Field effects explain the unintuitive potential response of electrochemical oxygen evolution in acid

Abstract

Electrochemical water oxidation (OER) is the most important electrode reaction in electrocatalysis, representing the default counter-reaction in the plethora of modern electroreductions. Given this prominent role in the electrochemistry-based green transition, improving its efficiency is of utmost importance. Here, identifying novel catalysts by means of computational screening necessitates clarity on the reaction mechanism as this is used to decide on appropriate activity descriptors. To date, however, the mechanism of OER, even on the most widely used catalyst in acid, IrO₂, is still debated, and the debate is fuelled by the consistent appearance of Tafel slopes indicative of a non-electrochemical rate-limiting step. Here, we employ density functional calculations and microkinetic modelling to analyse the mechanism of acidic OER on IrO₂(110), with an emphasis on the polarization of reaction intermediates. Introducing this degree of freedom shows that the electrostatic destabilization of surface-bound oxygen atoms with increasingly positive potentials increases the effective potential response of the reaction. Thus, a reaction mechanism through OOH*-formation could be confused with a non-electrochemical rate-limiting step. Furthermore, we highlight that a mechanism limited by the desorption of adsorbed O₂ is unlikely, as this step is facile at room temperature, but caution is needed in treating adsorbed O₂ in GGA-DFT. By incorporating these elements into our model, we simulate Tafel curves that reproduce the experimental potential response in both the low and high overpotential regions, pointing out that including surface dipole effects is essential for understanding and reproducing experiments.

---

Sustainability spotlight

The oxygen evolution reaction (OER) plays a critical role in the development of efficient and sustainable energy solutions, particularly in water splitting for hydrogen production. However, the dependence on trial-and-error experiments has made it difficult to find promising electrocatalysts. By applying DFT calculations and microkinetic modeling to OER, we can pinpoint key intermediates, rate-determining steps, and reaction pathways that are central to improving the catalyst performance. This approach can significantly minimize the discrepancy between theory and experiment, making it easier to identify promising materials and conditions that lead to higher efficiency and lower environmental impact. This aligns with the goals of the creation of energy-efficient technologies for renewable energy production where understanding of the OER mechanism offers a promising route for advancing sustainable energy technologies.

Introduction

The oxygen evolution reaction (OER) is crucial to achieve a fossil fuel-free economy.¹ When powered by renewable energy, OER supports the sustainable production of hydrogen, hydrocarbons, and other valuable chemicals. However, oxidizing potentials and the corrosive environment at the anode limit the efficiency of OER, making it a key area for improvement. Further, state of the art catalysts (IrO₂ and RuO₂) require significant overpotentials (∼300 mV) to function effectively, which adds to energy losses in nearly all electroreduction reactions of interest.¹ The overpotential and stability could be reduced slightly through modifications such as, varying catalyst supports² or introducing alternative metals into IrO₂/RuO₂.³ However, although representing the likely most applied half-reaction in electrocatalytic technology, designing better OER catalysts remains a challenge, even down to the level of knowing the relevant reaction steps, as the mechanism of e.g. acidic OER on its historically most used catalyst, IrO₂, is still under debate.

OER requires the transfer of four electrons across the electrode/electrolyte interface and the generation of four protons via the stepwise decomposition of water followed by the formation of an O–O chemical bond, as shown in Scheme 1. In the 1960s, Bockris et al. suggested 14 possible routes for OER on Pt, proposing primary water discharge as the rate-determining step.⁴ Conversely, on RuO₂(110), OER was suggested to occur via the Eley-Rideal (ER) mechanism, with the coupling of surface-bound oxygen with H₂O from the solution being reported as the rate-limiting step (RLS).⁵ In contrast, the Langmuir–Hinshelwood (LH) mechanism (such as by coupling two oxygen atoms on the surface) was deemed energetically less favoured and weakly influenced by the applied potential. Finally, a participation of lattice oxygen in the reaction could also be hypothesized (Mars–Van Krevelen mechanism). Kasian et al. and Scott et al. addressed this possibility by O-isotope labelling of the reacting water and the oxide catalyst, respectively. Both studies concluded that on rutile IrO₂, the vast majority of oxygen is formed out of interfacial water.^6,7 While lattice oxygen could be a minor contributor in RuO₂ and IrO₂, it can be important in other materials, such as perovskite (e.g. SrIrO₃,⁸ LaCoO₃,⁹) and Co-based catalysts (e.g. Co₃O₄).¹⁰

Scheme 1 Schematic illustration of the possible reaction mechanism for OER on IrO₂(110). The O₂ molecule is formed by O–O bond formation either by a Langmuir–Hinshelwood (LH) mechanism or Eley–Rideal (ER) mechanism via a coupled proton–electron transfer. Possible rate-limiting steps (RLS) are marked in blue and green colors.

Computational analysis of the thermodynamic landscape in OER reveals that the formation of OOH* is the most difficult step for many electrocatalysts including IrO₂,^11,12 and a further analysis by Dickens et al., including explicit calculations of potential-dependent activation energies confirmed that O–OH bond formation is most likely the RLS in all cases.¹³ However, the O–O coupling pathway via a LH mechanism, involving a chemical RLS between two oxygen atoms, was suggested in earlier studies due to OER's potential response above ∼1.5 V vs. RHE.^14–16 Additionally, S. Kwon et al. concluded that the OER mechanism and RLS depend on the facet and potential of IrO₂.¹⁷ They concluded that direct oxygen coupling is favourable on the (101)-facet of IrO₂, while the other facets follow a mechanism limited by the nucleophilic attack of water.

Recent theoretical analyses further suggested that, at high overpotentials on IrO₂, the final oxygen desorption step may become thermodynamically unfavourable.^18,19 As an alternative to direct O₂-desorption from the catalyst surface, recent findings by Binninger et al. suggested that OER on IrO₂ may follow the association of two O–O* species, especially at high overpotentials.²⁰ Exner further validated this result^21,22 concluding that the *OO–OO* recombination mechanism is crucial and should not be overlooked in future screening studies of OER.

All these deviating mechanistic interpretations need clarification to justify specific catalyst screening strategies. Turning to experiments, one of the strongest mechanistic tools in electrocatalysis for a distinction between the varying pathways is the interpretation of the potential needed to change the current by one order of magnitude, the so-called Tafel slope. From empirical models, such as Butler–Volmer theory in the absence of mass transport limitations,²³ the Tafel slope is a consequence of the transfer coefficient α following the relationship:

with referring to the change of current density j with applied potential U and k_B, T, and e representing the Boltzmann constant, temperature, and the charge per electron, respectively. Fig. 1 presents a collection of experimental data for OER on IrO_x-based catalysts in acid, including both films and nanoparticles (NPs).^24–31 Although few data span a broad potential window, for those cases, it is evident that OER exhibits two distinct Tafel slope regions. The potential at which this transition occurs defines the low and high-potential Tafel regions for the data below and above, respectively. The low-potential Tafel region slope is about 40 mV dec⁻¹, representing α ≈ 1.5. However, the more commonly investigated (and commercially more relevant) high-potential region exhibits Tafel slopes of 60–72 mV dec⁻¹ (α between 0.83 and 1) for films and around 50 mV dec⁻¹ for NPs (α ≈ 1.2). Previous theoretical studies successfully reproduced low-potential region behaviours and overestimated values for higher potential ones,¹³ indicating that there is still a gap in understanding mechanistic details and the origin of the Tafel slope values in the high-potential region.

Fig. 1 Experimental Tafel plots for OER on IrO_x-based catalysts in acidic conditions. Square and circle symbols represent films and nanoparticles (NPs), respectively.^24–31 Note that the reported current densities (j_total) vary in their normalization, making the direct comparison of j_total unjustified. This does not affect the highlighted Tafel slope values.

The interaction of intermediate species and transition states with the interfacial field during acidic OER might be the key to solving this conundrum as it adds a degree of freedom to the potential response of the thermodynamic landscape of the reaction. Its relevance is likely, as the intermediate steps involve highly electronegative oxygen species. Electron donation to them upon adsorption creates the formation of distinct surface dipoles, whose interaction with the interfacial field leads to significant electrostatic (de-)stabilization. Further, a variation of this interaction with altering applied potentials leads to contributions to Tafel slopes specific to the surface species and transition states determining the measured current.

The role of such electrostatic effects have recently been experimentally studied by Liang et al., highlighting the role of the interfacial water structure in acidic and alkaline electrolytes on the binding energetics of O* species.^31,32 Further, Kelly et al. showed that interfacial field interactions are responsible for selectivity changes within the ORR on noble metal based surfaces like Au(100), Au(111) and Pt(111).³³ Both findings emphasize the importance of accounting for interfacial effects on intermediates for mechanistic analyses, which are often overlooked in conventional models.

In this paper, we analyse the possibilities for the reaction mechanism from microkinetic considerations. We show that both the low and high-potential Tafel slopes can be explained by the OOH*-formation mechanism if the interaction of O* and OH* with the interfacial field are accounted for. Further, we will show that the combination of two oxygens from the surface is unlikely as it would lead to negligible current densities that would marginally benefit from an increase in overpotential, and that the desorption of O₂* is never rate-limiting but is poorly captured by DFT.

Results

In an atomistic picture, α results from the potential dependence of the effective activation free energy, ΔG_act,³⁴ which is the free energy cost to reach the RLS transition state starting from the catalysts resting state (RS), at constant pH, i.e.Here G^‡_RLS and G_RS denote the free energies of the RLS transition state and the RS with respect to a common reference state (e.g. the empty catalyst surface and gaseous molecular references). While the RLS is a well-known concept, the RS is often poorly defined. It represents the state that defines the predominant coverage on the surface under the reaction conditions, including empty catalytic sites.³⁵

The two derivatives in eqn (2) can formally be further simplified into

andwhere (N^‡_pe,i − N⁰_pe) is the number of produced proton–electron pairs under acidic and neutral conditions or the number of hydroxides consumed alongside producing electrons (in base) up to state i from a common reference state (e.g. empty surface and H₂O(l)). β_RLS further represents the symmetry factor of the RLS. As decisive characteristics, N_pe is generally limited to integer numbers, while β_RLS is fractional and often simplified to −0.5 (note our choice of sign for β_RLS to reflect the potential dependence of G^‡_RLS instead of that of the current).³⁶ Combining eqn (2)–(4) leads to the expression

α = N^‡_pe − N_pe,RS − β_RLS. (5)

Interpreting the Tafel slopes in the high overpotential region in Fig. 1 (60–72 mV dec⁻¹) might indicate an RLS whose rate was independent of potential, i.e. β_RLS ≈ 0, as it suggests that α is close to an integer value (cf. eqn (1)). Conversely, DFT-based studies suggest that sequential water dissociation is a more feasible pathway.¹³ Employing such an ER-based mechanism, where OOH* formation is the RLS, it is possible to reproduce the experimental Tafel slope (∼40 mV dec⁻¹) behaviour in the potential region below ∼1.5 V vs. RHE on rutile metal oxides such IrO₂, while a Tafel slope of about 120 mV dec⁻¹ is predicted in the higher potential region in disagreement with experiments. Thus, an interpretation based purely on eqn (5) would indicate that the mechanism changes from a proton-coupled electron transfer (PCET)-based RLS at low overpotential (β_RLS < 0), to a RLS defined by a potential-independent chemical step (β_RLS = 0).

The picture of expected Tafel slopes changes once the system is allowed to deviate from the idealized values. Two deviations can be envisioned; pinning the value of β_RLS to −0.5 for PCET steps or zero for formally non-electrochemical steps has no strong justification, where β_RLS can, in principle, adopt any value between the effective potential responses of the initial state and final state of the elementary steps.^37,38 Further, neglecting the contribution of the polarization of reaction intermediates, γ,³⁴ is a crude approximation. Here, the field response of the RS, γ_RS, is particularly important, as it will directly influence . While often negligible, particularly the binding of oxygen-containing adsorbates can exhibit a substantial inherent dipole, which changes α into:

α = N^‡_pe − N_pe,RS − β_RLS + γ_RS (6)

Note that, analogous to β_RLS, we chose the sign of γ_RS to be consistent with rather than α.

Fig. 2 shows the variations in the Tafel slope, resulting from variations in γ_RS and β_RLS. We highlight the combination of Tafel slopes for RS conditions of a monolayer of OH* (y-axis) and O* (x-axis) defining the RS of the catalyst. The two cases differ in N^‡_pe − N_pe,RS, being 1 and 0 for OH* and O* coverage, respectively. This difference results from the need of OH* to traverse an O*-intermediate to reach the RLS, while O* does not have an equilibrated elementary step preceding the RLS.

Fig. 2 Tafel slopes considering (a) the ER mechanism (O–OH formation) and (b) the LH mechanism (O–O coupling). Contours show the variation in the Tafel slope considering the potential response (γ) of OH* and O* for estimating low (y-axis) and high (x-axis) Tafel slopes, respectively. Experimentally observed Tafel slopes are marked with a dark green box.

Fig. 2a focuses on the mechanism involving O–OH* formation as the RLS. Here, β_RLS = −0.5 together with γ_RLS of both OH* and O* being zero (light turquoise line, γ_OH − γ_O = 0) results in the expected combination of 120 and 40 mV dec⁻¹ on the x and y-axes, respectively. While keeping β_RLS constant, increasing γ_OH and γ_O results in a reduction of their respective Tafel slopes, where e.g. β_RLS = −0.5, γ_O = 0.2 and γ_OH = 0.1 lead to Tafel slopes of 86 and 38 mV dec⁻¹.

The dependency of the Tafel slopes on γ_RS in the LH mechanism, shown in Fig. 2b, is even more prominent as its effect is doubled due to the participation of two O*-species in the RLS. Equally, N^‡_pe − N_pe,RS in this case takes the values of 2 and 0, for OH* and O* covered surfaces, respectively. Note that, in this mechanism, β_RLS → 0 is likely, making the potential response purely defined by γ_RS and leading to large Tafel slopes in the high overpotential region.

Overall, Fig. 2 shows that γ_RS is a central component of the measured potential response and leads to a large variety of possible Tafel slope combinations in OER, independent of the actual mechanism at play.

To estimate the magnitude of γ_RS, in Fig. 3 we show the DFT-predicted response of the differential formation free energy of the relevant intermediates of OER to an applied homogeneous electric field perpendicular to the electrode surface at a full background coverage of OH* (Fig. 3a) and O* (Fig. 3b) on the CUS sites of IrO₂(110) (see ESI Section 1† for Computational details). Analogous results for the field dependence of the change of surface phases by means of average formation free energies are shown in ESI Section 3,† with nearly identical values.

Fig. 3 Field response of the relevant intermediates in OER on IrO₂(110) under (a) OH* coverage and (b) O* coverage on Ir_CUS sites. (c) Table with fitted values for the change in surface dipole (Δμ,[eÅ]) and polarizability associated with a change in surface phase. Additionally, the net potential response for each adsorbate is indicated where Ũ = U_SHE − U_PZC.

We found that, in the vicinity of the potential of zero charge (PZC) of the electrode, O*, OH*, and O₂* are destabilized by negative field strengths, corresponding to more anodic conditions, while H₂O* and OOH* are stabilized. This varying behaviour results from the varying surface dipole changes upon adsorption, Δμ, and, thus, γ, as summarized in Fig. 3c. We provide the framework to define γ from the change in surface dipole Δμ and polarizability Δη in ESI Section 4.†

γ_O is generally enhanced relative to γ_OH, which can be attributed to its binding motif in a top site on the IrO₂(110) CUS, forming a distinct dipole perpendicular to the catalyst surface.³⁹ Conversely, OH* tends to form a hydrogen bond network with the hydrogen pointing parallel to the surface, reducing its overall dipole perpendicular to the surface.

We now show how γ, and particularly its relative differences influence phase stabilities. Fig. 4a shows the calculated Pourbaix diagrams for IrO₂(110) including interfacial field effects (see ESI Section 5† for calculation details). In agreement with previous results,³² we identified that IrO₂(110) is covered by OH* on the IrO₂(110) CUS when ramping up the potential to 1.52 V vs. RHE, where it transitions into a monolayer of O*. We also identified that the deprotonation of the bridge-O (O_b) is likely responsible for the capacitive peaks in cyclovoltammetry (CV) appearing at intermediate positive RHE potential, as reported in ref. 26 for single-crystal IrO₂(110). This phenomenon has also been documented in amorphous IrO_x and rutile IrO₂ in acid.^31,32

Fig. 4 Surface phase diagram for different coverage conditions on the pristine IrO₂(110) surface at the full coverage limit with field effects (a). Potential vs. RHE where full OH* coverage transitions to full O* coverage at different pH when no field effect is included (white circles), when a field effect is included (solid black circles) and from experimental data (black triangles)²⁶ (b). *Ir_CUS represents empty Ir_CUS sites and O_b an oxygen bridge.

The field response of the varying surface phases has a minor effect on the transition from OH*- to O*-covered IrO₂(110) CUS sites when compared to the case without the inclusion of the field effect shown in ESI Sections 6 & 7.† Conversely, OH* formation on IrO₂(110) CUS shifts by ∼−0.7 V. This behavior is a consequence of our choice of PZC in the field response model, which we chose based on the calculated value for the bare IrO₂ surface (see Fig. S2†). As the OH*- to O*-covered IrO₂(110) CUS-transition happens close to the PZC, the field is small and thus has little influence on it. We note that the PZC does influence the specific transition potential, but its change with potential, our central benchmark, is less affected.

Differences in γ of the two phases involved in the transition are expressed as pH-dependence on the RHE potential scale,³⁴ which allows us to directly benchmark our determined values against experimental observations. In Fig. 4b, we benchmarked the potential where the RS changes from a monolayer of OH* to a monolayer of O* on the CUS of IrO₂ against experimental validations from Kuo et al., who studied the transition between the two phases based on the appearance of oxidation/reduction waves in CVs.²⁶ The fingerprint CVs of IrO₂(110) were recorded in a wide pH range, exhibiting a non-Nernstian shift in the peak position of two phase transitions between 0.8 and 1.6 V vs. RHE. Based on Fig. 4a, we can attribute the two waves to the electrochemical desorption of H* from the O_b sites (0.87 V vs. RHE) and the transition from OH* to O* (1.52 V vs. RHE) on IrO₂(110) CUS. With increasing pH, the experimental peak positions shifted in the negative direction against the RHE potential scale, which allows us to directly probe the γ_O with respect to γ_OH. The experimental behaviour is in line with the results from our calculations including the calculated γ_i, with 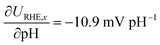. This proves the qualitative behavior that O* is destabilized by increasingly anodic potentials more than OH*, strongly indicating that γ_O may substantially influence on the Tafel slopes in the high overpotential region. Spin polarized results for the same are shown in Fig. S3.†

After having identified the relevant surface phases at reaction conditions and estimating γ_OH and γ_O, we now show how both these aspects influence experimental OER observations. For this, Fig. 5 shows the calculated free energy diagram at pH zero for all the intermediates involved in the (a) ER and (b) LH pathways. The effective changes of the free energy of each state with U at constant pH, , are explicitly given. For clarity, only the energetics on an O*-covered surface are shown, while corresponding energetics with a full OH* coverage as the RS are shown in Fig. S6,† and the qualitative picture is equal in both cases. The direct link to experimental observations is made in the corresponding lower panels (c and d) of Fig. 5 resulting from a microkinetic model (see section 8 in ESI† for more detail).

Fig. 5 Free energy diagrams and simulated current densities for OER including effects of the electric field on IrO₂(110). Panels (a) and (b) show free energy diagrams for the ER and LH mechanisms, respectively, under full O* coverage. The mean values of the effective changes of the free energy of each state with U at constant pH, , are noted for each step. Panels (c) and (d) show the simulated current density (j) at pH = 0 for the ER and the LH pathways, respectively. The solid lines represent the effective current taking into account the change in surface phase. Coverages obtained from the microkinetic model are shown in blue for OH (θ_OH) and O (θ_O). The obtained Tafel slopes for the pre-kink and post-kink regions are given in panels (c) and (d).

Starting from an empty IrO₂(110) CUS-site, the adsorption of water to form H₂O* does not involve a proton–electron pair (N_pe,*H2O = 0). However, H₂O* is considerably stabilized by increasing the potential, and when calculating γ_H2O at 1.23, 1.43, and 1.63 vs. RHE the average value is γ_H2O = −0.29, defining its whole potential response. Next, one proton–electron pair is produced for reaching OH* (N_pe,*OH = 1). Combined with γ_OH, the effective potential response of OH* formation resulted in −0.98 eV/V. Subsequently, to produce O*, two proton–electron pairs are created with respect to the empty site (N_pe,*O = 2). However, the considerable γ_O partially counters the purely Nernstian potential response leading to an effective 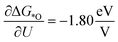. O* is followed by the RLS in both considered reaction mechanisms. For the ER mechanism shown in panel (a), we used the activation energy and β_O–OH = −0.58 as determined in our previous work.¹³ Here, Dickens et al. calculated the activation energy for the formation of OOH* on oxides and investigated its dependence on the applied potential (See ESI Section 8† for further details). as no extra proton or OH⁻ are involved for reaching the transition state under acidic conditions. After crossing the RLS barrier in the ER mechanism, OOH* is reached, which, in contrast to O* and OH*, is stabilized by an increase in the negative field (more positive potential), resulting in an enhanced potential response compared to the field free case (i.e. α_OOH* − α_O* = 1.71).

Finally, O₂* results from the deprotonation of OOH*, which exhibits a net potential response of −3.93 eV/V. Note that we did not use the bare DFT calculated formation free energy of O₂* in the free energy diagram in Fig. 5, as it is overstabilized by the applied GGA-DFT methodology. Instead, we used a value benchmarked by employing the Redhead analysis of experimental temperature-programmed profiles (TPD) of O₂ desorption from IrO₂(110).^40–42 We describe the process of determining the energy in more detail in ESI Section 9† and will discuss the need for this correction for a correct mechanistic analysis in the discussion of the microkinetic results below.

For the definition of α in the ER mechanism (α_ER), we can invoke eqn (6), hence simply calculating the potential response difference between the RLS transition state (−2.58 eV/V) and the RS, i.e. −0.98 eV/V and −1.80 eV/V at low and high overpotentials, respectively. Thus, the predicted α_ER values are 1.6 and 0.78. In the LH mechanism, shown in Fig. 5b, 2O* species act as the reactants of the RLS. Thus, the energy landscape is altered involving two adsorbates throughout up to the RLS. Analogously, the potential response of each step before the RLS is doubled as well. As the RLS represents a formally non-electrochemical step in this mechanism, the potential response between 2O* and O₂(g) only varies by 0.4 eV/V, purely defined by the quenching of γ_O upon desorption. Thus, α_LH calculated from Fig. 5b results in 2.04 and 0.4 for the low and high overpotential regions, respectively.

A comparison of the simulated polarization curves in Fig. 5c and d reveals that the ER mechanism aligns much more closely with experimental data both in terms of Tafel slopes and absolute current densities, which approach at 1 mA cm⁻² at ∼1.6 V. Conversely, the LH mechanism, exhibits negligible reaction rates throughout the potential range because of the huge thermodynamic barrier connected to the formation of O₂ from two O* species.

As expected, α_ER directly translates into the Tafel slope estimates of 37 mV dec⁻¹ and 77 mV dec⁻¹ for the low and high overpotential regions, respectively, under O* coverage (see Fig. 5c). Note that this result is only obtained when the O₂* to O₂(g) energy value is set to ∼0.31 eV, as fitted from the TPD analysis shown in Fig. S7,† as O–OH* formation remains the RLS within the simulated potential range. Specifically, including the field effect for O₂* shows that this species destabilizes at oxidative potentials, weakening its interaction with the surface compared with pure TPD-derived data, then when the potential increases, the O₂* to O₂(g) value is even smaller than 0.31 eV. However, this picture changes when using the desorption energy predicted by GGA-DFT (∼0.81 eV). As the activation energy for O–OH* formation is potential-dependent, it decreases as the potential increases. At a certain potential, it becomes smaller than the desorption energy of O₂*, as predicted by GGA-DFT, making the latter the apparent RLS. This shift alters the Tafel curve behaviour, resulting in a near complete loss of potential response, in strict disagreement with experiments.

In contrast to the ER reaction path, the simulated LH mechanism exhibited Tafel slopes of 29 and 150 mV dec⁻¹ (see Fig. 5d), which also disagrees with the measurements shown in Fig. 1. A degree of rate control analysis (cf. Fig. S8 & S9 in ESI†) for this mechanism shows that the chemical O–O coupling step and the energy of O₂* do not influence the overall rate of the reaction, as O₂(g) defines the highest barrier to the product starting from the RS.

Note that we have chosen constant values of C_H (i.e. 25 μF cm⁻²) and U_pzc (1.5 V vs. SHE) in our model. These choices directly affect the quantitative values of the Tafel slopes and the potentials of surface phase changes. Therefore, we also probed the sensitivity of simulated Tafel plots to variations of C_H (Fig. S10†) and U_pzc (Fig. S11 and S12†). The results show that the trends in Tafel slopes are mostly unaffected by the choice of parameters. That is, while the low overpotential region (*OH-covered surface) is virtually unaffected by the interfacial field, the high overpotential region (*O-covered surface) shows a substantial field response, leading to reduced Tafel slopes compared to the case without the field effects.

While in the present study, we focussed only on the most stable (110)-surface of IrO₂, we are confident that analogous characteristic field interactions are present on other facets. Further, the stronger binding of *O on less coordinated surface sites likely even reduces the probability of the LH mechanism. However, specific evaluations on other facets would be needed to confirm these hypotheses.

Overall, our analysis shows that while the proximity of experimental Tafel slopes to the characteristic value of 60 mV dec⁻¹ might make it tempting to assign a chemical RLS. This can be equally well explained by the combined potential response of the RLS and RS in a PCET-limited step, as is the case for the ER mechanism. Conversely, the LH mechanism would never have a value approaching 60 mV dec⁻¹, as it would formally (from purely Nernstian behaviour) only exhibit Tafel slopes of ∼30 mV dec⁻¹ or infinity. However, including γ_O leads to non-zero potential responses, which still deviate strongly from the experimentally observed values.

This a priori unintuitive Tafel behaviour likely extends beyond IrO₂(110), both in terms of alternative surface facets and other rutile oxides. To account for the behaviour, a further simplified model directly applicable in large scale screening studies can be applied: conventional DFT calculations for the relevant reaction intermediates directly provide μ from the ground state charge density (mostly given in the output of DFT codes) and the work function as an estimate for U_pzc. Utilizing them allows a first order estimate of relevant γ values without the need for field dependent (or even more sophisticated) calculations.

Conclusions

In this study, we used DFT calculations and microkinetic modelling to analyse the mechanism of acidic OER on IrO₂(110) including the polarization of reaction intermediates. We have shown that the ER type mechanism through a coupled proton–electron transfer RLS to form OOH* suggested by Dickens et al.¹³ does not contradict the experimentally measured Tafel slopes as long as the field response of reaction intermediates is considered. Further, our results suggest that the combination of two oxygen atoms from the surface via the LH mechanism is unlikely, as it would result in negligible current densities that would be marginally affected by the increase in overpotential. Additionally, by analysing experimental data of temperature-programmed desorption profiles, we emphasized that the desorption of O₂* is fast. Hence, it is unlikely to be a RLS. However, GGA-DFT poorly captures this, overestimating the O₂* adsorption energies.

Data availability

All the data for DFT calculated energies are summarized in the ESI.† Data such as inputs for the figures and the atomic structures will be made available at https://github.com/CatTheoryDTU/OER_mechanism_IrO2_acid upon acceptance of the article.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

AT and VKOR were funded from Villum Fonden V-Sustain I+II (grant no. 9455 + grant no. 54345) and GK received funding from the Novo Nordisk Foundation grant 0085735. We further acknowledge support from the Novo Nordisk Foundation Data Science Research Infrastructure 2022 grant: a high-performance computing infrastructure for data-driven research on sustainable energy materials, grant no. NNF22OC0078009.

References

1. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining Theory and Experiment in Electrocatalysis: Insights into Materials Design, Science, 2017, 355(6321), eaad4998,  DOI:10.1126/science.aad4998.
2. G. Li, H. Jia, H. Liu, X. Yang and M.-C. Lin, Nanostructured IrOx Supported on N-Doped TiO₂ as an Efficient Electrocatalyst towards Acidic Oxygen Evolution Reaction, RSC Adv., 2022, 12(45), 28929–28936,  10.1039/D2RA05374H.
3. H.-W. Lv, H.-B. Zhao, X.-Y. Peng, Z.-G. Ye, Q.-B. Huang, X.-T. Yuan, D.-S. Li and Z. Jin, Rhenium-Boosted Electrocatalytic Activity and Durability of Pyrolytic IrO2 for Acidic Oxygen Evolution, Rare Met., 2024, 43(12), 6758–6764,  DOI:10.1007/s12598-024-02830-6.
4. A. Damjanovic, A. Dey and J. O. Bockris, Kinetics of Oxygen Evolution and Dissolution on Platinum Electrodes, Electrochim. Acta, 1966, 11(7), 791–814,  DOI:10.1016/0013-4686(66)87056-1.
5. Y.-H. Fang and Z.-P. Liu, Mechanism and Tafel Lines of Electro-Oxidation of Water to Oxygen on RuO₂ (110), J. Am. Chem. Soc., 2010, 132(51), 18214–18222,  DOI:10.1021/ja1069272.
6. O. Kasian, S. Geiger, T. Li, J.-P. Grote, K. Schweinar, S. Zhang, C. Scheu, D. Raabe, S. Cherevko, B. Gault and K. J. J. Mayrhofer, Degradation of Iridium Oxides via Oxygen Evolution from the Lattice: Correlating Atomic Scale Structure with Reaction Mechanisms, Energy Environ. Sci., 2019, 12(12), 3548–3555,  10.1039/C9EE01872G.
7. S. B. Scott, J. E. Sørensen, R. R. Rao, C. Moon, J. Kibsgaard, Y. Shao-Horn and I. Chorkendorff, The Low Overpotential Regime of Acidic Water Oxidation Part II: Trends in Metal and Oxygen Stability Numbers, Energy Environ. Sci., 2022, 15(5), 1988–2001,  10.1039/D1EE03915F.
8. G. Wan, J. W. Freeland, J. Kloppenburg, G. Petretto, J. N. Nelson, D.-Y. Kuo, C.-J. Sun, J. Wen, J. T. Diulus, G. S. Herman, Y. Dong, R. Kou, J. Sun, S. Chen, K. M. Shen, D. G. Schlom, G.-M. Rignanese, G. Hautier, D. D. Fong, Z. Feng, H. Zhou and J. Suntivich, Amorphization Mechanism of SrIrO3 Electrocatalyst: How Oxygen Redox Initiates Ionic Diffusion and Structural Reorganization, Sci. Adv., 2021, 7(2), eabc7323,  DOI:10.1126/sciadv.abc7323.
9. Y. Lu, A. Ma, Y. Yu, R. Tan, C. Liu, P. Zhang, D. Liu and J. Gui, Engineering Oxygen Vacancies into LaCoO3 Perovskite for Efficient Electrocatalytic Oxygen Evolution, ACS Sustain. Chem. Eng., 2019, 7(3), 2906–2910,  DOI:10.1021/acssuschemeng.8b05717.
10. H. M. A. Amin, P. Königshoven, M. Hegemann and H. Baltruschat, Role of Lattice Oxygen in the Oxygen Evolution Reaction on Co3 O4 : Isotope Exchange Determined Using a Small-Volume Differential Electrochemical Mass Spectrometry Cell Design, Anal. Chem., 2019, 91(20), 12653–12660,  DOI:10.1021/acs.analchem.9b01749.
11. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, Electrolysis of Water on Oxide Surfaces, J. Electroanal. Chem., 2007, 607(1–2), 83–89,  DOI:10.1016/j.jelechem.2006.11.008.
12. J. Rossmeisl, A. Logadottir and J. K. Nørskov, Electrolysis of Water on (Oxidized) Metal Surfaces, Chem. Phys., 2005, 319(1–3), 178–184,  DOI:10.1016/j.chemphys.2005.05.038.
13. C. F. Dickens, C. Kirk and J. K. Nørskov, Insights into the Electrochemical Oxygen Evolution Reaction with Ab Initio Calculations and Microkinetic Modeling: Beyond the Limiting Potential Volcano, J. Phys. Chem. C, 2019, 123(31), 18960–18977,  DOI:10.1021/acs.jpcc.9b03830.
14. M. H. P. Santana, L. A. D. Faria and J. F. C. Boodts, Electrochemical Characterisation and Oxygen Evolution at a Heavily Boron Doped Diamond Electrode, Electrochim. Acta, 2005, 50(10), 2017–2027,  DOI:10.1016/j.electacta.2004.08.050.
15. M. H. P. Santana and L. A. De Faria, Oxygen and Chlorine Evolution on RuO₂+TiO₂+CeO₂+Nb₂O₅ Mixed Oxide Electrodes, Electrochim. Acta, 2006, 51(17), 3578–3585,  DOI:10.1016/j.electacta.2005.09.050.
16. J. Jirkovský, H. Hoffmannová, M. Klementová and P. Krtil, Particle Size Dependence of the Electrocatalytic Activity of Nanocrystalline RuO₂ Electrodes, J. Electrochem. Soc., 2006, 153(6), E111–E118.
17. S. Kwon, K. A. Stoerzinger, R. Rao, L. Qiao, W. A. Goddard and Y. Shao-Horn, Facet-Dependent Oxygen Evolution Reaction Activity of IrO2 from Quantum Mechanics and Experiments, J. Am. Chem. Soc., 2024, 146(17), 11719–11725,  DOI:10.1021/jacs.3c14271.
18. T. Binninger and M.-L. Doublet, The Ir–OOOO–Ir Transition State and the Mechanism of the Oxygen Evolution Reaction on IrO2 (110), Energy Environ. Sci., 2022, 15(6), 2519–2528,  10.1039/D2EE00158F.
19. K. S. Exner and H. Over, Beyond the Rate-Determining Step in the Oxygen Evolution Reaction over a Single-Crystalline IrO2 (110) Model Electrode: Kinetic Scaling Relations, ACS Catal., 2019, 9(8), 6755–6765,  DOI:10.1021/acscatal.9b01564.
20. T. Binninger, P. M. Kowalski and M. H. Eikerling, Oxygen Desorption–Critical Step for the Oxygen Evolution Reaction, Curr. Opin. Electrochem., 2023, 42, 101382,  DOI:10.1016/j.coelec.2023.101382.
21. K. S. Exner, Implications of the M-OO-OO-M Recombination Mechanism on Materials Screening and the Oxygen Evolution Reaction, JPhys Energy, 2023, 5(1), 014008,  DOI:10.1088/2515-7655/aca82a.
22. K. S. Exner, On the Mechanistic Complexity of Oxygen Evolution: Potential-Dependent Switching of the Mechanism at the Volcano Apex, Mater. Horiz., 2023, 10(6), 2086–2095,  10.1039/D3MH00047H.
23. O. Van Der Heijden, S. Park, R. E. Vos, J. J. J. Eggebeen and M. T. M. Koper, Tafel Slope Plot as a Tool to Analyze Electrocatalytic Reactions, ACS Energy Lett., 2024, 9(4), 1871–1879,  DOI:10.1021/acsenergylett.4c00266.
24. Y. Lee, J. Suntivich, K. J. May, E. E. Perry and Y. Shao-Horn, Synthesis and Activities of Rutile IrO2 and RuO2 Nanoparticles for Oxygen Evolution in Acid and Alkaline Solutions, J. Phys. Chem. Lett., 2012, 3(3), 399–404,  DOI:10.1021/jz2016507.
25. H.-S. Oh, H. N. Nong, T. Reier, A. Bergmann, M. Gliech, J. Ferreira De Araújo, E. Willinger, R. Schlögl, D. Teschner and P. Strasser, Electrochemical Catalyst–Support Effects and Their Stabilizing Role for IrOx Nanoparticle Catalysts during the Oxygen Evolution Reaction, J. Am. Chem. Soc., 2016, 138(38), 12552–12563,  DOI:10.1021/jacs.6b07199.
26. D.-Y. Kuo, J. K. Kawasaki, J. N. Nelson, J. Kloppenburg, G. Hautier, K. M. Shen, D. G. Schlom and J. Suntivich, Influence of Surface Adsorption on the Oxygen Evolution Reaction on IrO2 (110), J. Am. Chem. Soc., 2017, 139(9), 3473–3479,  DOI:10.1021/jacs.6b11932.
27. G. Li, S. Li, J. Ge, C. Liu and W. Xing, Discontinuously Covered IrO2 –RuO2 @Ru Electrocatalysts for the Oxygen Evolution Reaction: How High Activity and Long-Term Durability Can Be Simultaneously Realized in the Synergistic and Hybrid Nano-Structure, J. Mater. Chem. A, 2017, 5(33), 17221–17229,  10.1039/C7TA05126C.
28. D. Weber, L. M. Schoop, D. Wurmbrand, S. Laha, F. Podjaski, V. Duppel, K. Müller, U. Starke and B. V. Lotsch, IrOOH Nanosheets as Acid Stable Electrocatalysts for the Oxygen Evolution Reaction, J. Mater. Chem. A, 2018, 6(43), 21558–21566,  10.1039/C8TA07950A.
29. H. N. Nong, L. J. Falling, A. Bergmann, M. Klingenhof, H. P. Tran, C. Spöri, R. Mom, J. Timoshenko, G. Zichittella, A. Knop-Gericke, S. Piccinin, J. Pérez-Ramírez, B. R. Cuenya, R. Schlögl, P. Strasser, D. Teschner and T. E. Jones, Key Role of Chemistry versus Bias in Electrocatalytic Oxygen Evolution, Nature, 2020, 587(7834), 408–413,  DOI:10.1038/s41586-020-2908-2.
30. D. Choudhury, R. Das, R. Maurya, H. Kumawat and M. Neergat, Kinetics of the Oxygen Evolution Reaction (OER) on Amorphous and Crystalline Iridium Oxide Surfaces in Acidic Medium, Langmuir, 2023, 39(38), 13748–13757,  DOI:10.1021/acs.langmuir.3c02293.
31. C. Liang, Y. Katayama, Y. Tao, A. Morinaga, B. Moss, V. Celorrio, M. Ryan, I. E. L. Stephens, J. R. Durrant and R. R. Rao, Role of Electrolyte pH on Water Oxidation for Iridium Oxides, J. Am. Chem. Soc., 2024, 146(13), 8928–8938,  DOI:10.1021/jacs.3c12011.
32. C. Liang, R. R. Rao, K. L. Svane, J. H. L. Hadden, B. Moss, S. B. Scott, M. Sachs, J. Murawski, A. M. Frandsen, D. J. Riley, M. P. Ryan, J. Rossmeisl, J. R. Durrant and I. E. L. Stephens, Unravelling the Effects of Active Site Density and Energetics on the Water Oxidation Activity of Iridium Oxides, Nat. Catal., 2024, 7(7), 763–775,  DOI:10.1038/s41929-024-01168-7.
33. S. R. Kelly, C. Kirk, K. Chan and J. K. Nørskov, Electric Field Effects in Oxygen Reduction Kinetics: Rationalizing pH Dependence at the Pt(111), Au(111), and Au(100) Electrodes, J. Phys. Chem. C, 2020, 124(27), 14581–14591,  DOI:10.1021/acs.jpcc.0c02127.
34. G. Kastlunger, L. Wang, N. Govindarajan, H. H. Heenen, S. Ringe, T. Jaramillo, C. Hahn and K. Chan, Using pH Dependence to Understand Mechanisms in Electrochemical CO Reduction, ACS Catal., 2022, 12(8), 4344–4357,  DOI:10.1021/acscatal.1c05520.
35. C. T. Campbell and Z. Mao, Analysis and Prediction of Reaction Kinetics Using the Degree of Rate Control, J. Catal., 2021, 404, 647–660,  DOI:10.1016/j.jcat.2021.10.002.
36. J. O. Bockris and Z. Nagy, Symmetry Factor and Transfer Coefficient. A Source of Confusion in Electrode Kinetics, J. Chem. Educ., 1973, 50(12), 839,  DOI:10.1021/ed050p839.
37. R. Guidelli, R. G. Compton, J. M. Feliu, E. Gileadi, J. Lipkowski, W. Schmickler and S. Trasatti, Defining the Transfer Coefficient in Electrochemistry: An Assessment (IUPAC Technical Report), Pure Appl. Chem., 2014, 86(2), 245–258,  DOI:10.1515/pac-2014-5026.
38. A. M. Limaye, J. S. Zeng, A. P. Willard and K. Manthiram, Bayesian Data Analysis Reveals No Preference for Cardinal Tafel Slopes in CO2 Reduction Electrocatalysis, Nat. Commun., 2021, 12(1), 703,  DOI:10.1038/s41467-021-20924-y.
39. H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. T. K. K. Gunasooriya, C. S. Abraham, S. Vijay, J. M. Gregoire and J. K. Nørskov, Analysis of the Limitations in the Oxygen Reduction Activity of Transition Metal Oxide Surfaces, Nat. Catal., 2021, 4(6), 463–468,  DOI:10.1038/s41929-021-00618-w.
40. Y. D. Kim, A. P. Seitsonen, S. Wendt, J. Wang, C. Fan, K. Jacobi, H. Over and G. Ertl, Characterization of Various Oxygen Species on an Oxide Surface: RuO₂ (110), J. Phys. Chem. B, 2001, 105(18), 3752–3758,  DOI:10.1021/jp003213j.
41. V. K. Ocampo-Restrepo, S. Vijay, G. T. K. K. Gunasooriya and J. K. Nørskov, Characterization of Adsorption Sites on IrO2 via Temperature Programmed O2 Desorption Simulations, Phys. Chem. Chem. Phys., 2024, 26(24), 17396–17404,  10.1039/D4CP01213E.
42. P. A. Redhead, Thermal desorption of gases, Vacuum, 1962, 12(4), 203–211,  DOI:10.1016/0042-207X(62)90978-8.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5su00080g

‡ These authors contributed equally to this work.

---