DOI:
10.1039/D4YA00577E
(Paper)
Energy Adv., 2025, Advance Article
A machine learning approach for estimating supercapacitor performance of graphene oxide nano-ring based electrode materials†
Received
23rd October 2024
, Accepted 20th November 2024
First published on 5th December 2024
Abstract
This work utilizes a novel approach leveraging the machine learning (ML) technique to predict the electrochemical supercapacitor performance of graphene oxide nano-rings (GONs) as electrode nanomaterials. Initially, the experimental procedure was carried out to synthesize GO via a modified Hummers method, followed by GONs preparation using the water-in-oil (W/O) emulsion technique. High-resolution transmission electron microscopy (HRTEM) analysis reveals the formation of a typical two-dimensional GO nanosheet and multilayer-GO nano-rings. The X-ray diffraction (XRD), Raman spectroscopy, X-ray photoelectron spectroscopy (XPS), and Brunauer–Emmett–Teller (BET) analysis results show that the GONs possess similar structural and surface chemistry properties as of GO, with a slight reduction in oxygenous functionalities, enhancing the capacitive behaviours through facile electron migration at the electrode surface. The electrochemical assessment of GO and GONs samples indicates outstanding specific capacitances of 164 F g−1 and 294 F g−1 at 1 mV s−1, showcasing capacitive retention of up to 63% and 60% after 2500 cycles. In addition, four different machine learning models were tested to estimate the role of electrochemical parameters in determining the specific capacitance of GONs.
1. Introduction
Graphene and graphene-based derivatives, including graphene oxide (GO) and reduced graphene oxide (rGO), have been widely explored in nanoelectronics,1,2 catalysis,3–5 medical imaging,6,7 and energy storage/conversion devices.8–10 Unlike pristine black graphite, GO exhibits a partly brownish-yellow colour owing to the electronic conjugation loss caused by graphite oxidation.11 On the chemical oxidation of graphite, various functional groups like carboxyls, hydroxyls, and epoxy become attached to the basal plane of graphitic sheets,7,12,13 which makes GO a suitable candidate for GO nanosphere fabrication through various techniques like water/oil emulsion,11,14,15 template-assisted,16–18 pulsed laser ablation,7 hydrothermal,19 chemical vapour deposition20 and microwave-assisted methods.21 Due to its unique configuration of a few atomic layers of carbon, it exhibits hydrophilic oxygen functionalities on its hydrophobic graphitic structure, giving it an amphiphilic nature.11,15 This negatively charged oxygenous functionalities on the hydrophobic graphitic structure allow GO to develop a spherical shape by attaching to the surface of the positively charged template.14,22 A novel extrinsic GO morphology like a hollow/solid GO spherical morphology demonstrated improved electrochemical performance such as higher gravimetric/volumetric capacitance, higher aerial capacitance, and higher energy density attributed to the synergistic effect of GO morphology, and its chemical and structural properties.16,18,23 Supercapacitors (SCs) are becoming more prominent in various industries, including communications, aviation, and transportation, because of their high-power density and quick charge/discharge cycle.
Inevitably, the intrinsic 2D graphene materials exhibit an electrical double-layer capacitance (EDLC) of <200 F g−1; meanwhile, the novel extrinsic GO morphology-like nanosphere shows a higher value of EDLC under different electrolytes.16,24,25 Guo et al. first prepared the hollow GONs using the W/O emulsion technique and successfully demonstrated their application in lithium-ion batteries.11 A groundbreaking study was introduced by Lee et al.20 creating mesoporous graphene nanoballs (MGBs) for energy storage applications. The as-synthesized MGB displays a specific capacitance of 206 F g−1, highlighting the excellent performance of the MGB as an electrode material for SCs.20 In 2014, his group26 proposed the synthesis of high-performance 3D hollow porous graphene balls (HPGBs) from coal tar pitch.26 The KOH activation and nano-MGO template strategy enhance the HPGBs, achieving a high specific capacitance (321 F g−1 at 0.05 A g−1) and cyclic stability for over 1000 cycles.26 Yuan and colleagues explored the template-assisted synthesis of n-doped hierarchical porous carbon for an electrical double-layer capacitor with the highest specific capacitance of 363.7 F g−1 at 1 A g−1.27 Fan et al.16 proposed a template-assisted synthesis of n-doped GONs, which showed a specific capacitance of 381 F g−1 at a current density of 1 A g−1.16 The introduction of heteroatoms in the graphite structure is attributed to increased active sites, electrical conductivity, and specific surface area.16,18 The synergistic effect of heteroatoms in the graphitic basal plane and micro-spherical graphene structure improves the capacitance value of SCs.16,28,29 Yan and his group19 have shown that the graphene nanospheres can be tailored to possess a high gravimetric capacitance of 529 F g−1 at 1 A g−1, with a specific surface area of 2794 m2 g−1.19 Numerous studies prompted the utilization of spherical-shaped graphene nanostructures in SCs, which has shown significant potential over vertical graphene nanosheet as an electrode material, with notable properties such as high energy density and exceptional cyclic stability.19 These findings collectively reflect the significant role of the unique morphology of graphene such as nanosphere or nanorings in advancing performance of symmetrical SCs.
Apart from the experimental investigation of GO-based electrode nanomaterials for SCs, researchers have explored the machine learning (ML) approach that reduces the time-consuming process of manual selection and optimization of the experimental parameters for electrode fabrication.30–34 ML is expected to reduce the trial-and-error aspect of experiments and estimate the SCs performance of electrodes before the actual electrochemical investigation of nanomaterials.35 Several reports demonstrated an interdisciplinary approach, combining ML with material science in estimating the performance of energy systems, especially in SCs,30–34 batteries,36–39 and fuel cells.35,40–43 Researchers leverage ML to investigate how different carbon-related physiochemical parameters affect the EDLC and pseudocapacitance of carbon nanomaterials.44 Su et al.44 have taken into account the nitrogen and oxygen atomic percentage, cyclic potential window, specific surface area, pore size, pore volume, and the ratio of D-band to G-band Raman intensity as an input variable to determine the specific capacitance of carbon-based EDL SCs.44 The researchers observed that multilayer perceptron (MLP) or an artificial neural network (ANN) shows the best performance and identifies the relative contribution of the input variable to the capacitance.44 Zhu et al.45 examined the impact of these variables using the ANN method and compared it with different levels of crystallinity of carbon materials to predict the energy storage capabilities of GO samples.45
Meanwhile, Gheytanzadeh's group46 observed that the support vector machine (SVM) by Grey Wolf Optimization (SVM-GWO) algorithm for carbon-based nanomaterials outperforms the other ML model.46 With an R2 value of 0.92, the suggested SVM-GWO demonstrated greater accuracy than any of the other suggested ML models used in this context.46 In 2022, Mishra et al.34 used the physiochemical properties to determine the SCs performance of carbon-based electrode materials.34 An extreme gradient boost (XGBoost) model was found to co-relate the features with the capacitance of the carbon electrode. The specific surface area, nitrogen doping, and potential window are the most significant descriptors impacting the capacitance of carbon electrodes.34 Jha and group32 attempted the four different ML models, including decision tree (DT), linear regression (LR), SVM, and ANN, to analyze the charge/discharge cycle of lignin-based SCs. The ANN model shows superior performance, with the highest accuracy, applicability, and extreme robustness.32 Various researchers examined the SC performance of non-carbonaceous nanomaterials using the ML approach. Ghosh et al.31 estimated the performance of cerium oxynitride nanomaterials. The random forest (RF) and MLP predicted the possible capacitance of 214 F g−1 and capacity retention of about 90% over the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.31 The RF and principal component analysis (PCA) are essential as they produced the best accurate prediction, which was verified experimentally. In addition, researchers modeled the cyclic voltammetry of a fabricated nanostructured Ni(OH)2 electrode using ANN for SC application.33 The ANN model estimated the electrode performance, showing satisfactory agreement with experimental results with a minimum error of 0.14%.
000 cycles.31 The RF and principal component analysis (PCA) are essential as they produced the best accurate prediction, which was verified experimentally. In addition, researchers modeled the cyclic voltammetry of a fabricated nanostructured Ni(OH)2 electrode using ANN for SC application.33 The ANN model estimated the electrode performance, showing satisfactory agreement with experimental results with a minimum error of 0.14%.
Studies have shown that machine learning techniques, such as XGBoost, LR, DT, SVM, RF, and ANN or MLP, can precisely predict specific capacitance and electrode characteristics of carbon-based SCs. Additionally, the performance and accuracy of the ML model depend on doping of heteroatoms like nitrogen, oxygen, and sulfur on graphene. The physiochemical properties have been found to significantly enhance the pseudocapacitance and energy density of SCs. Thus the ML models that can effectively predict capacitance of electrode materials by using the physiochemical and electrochemical parameters as input and output variable. This research trend in SCs underscores the significance of graphene-based nanocomposites, and the proper utilization of the ML approach significantly reduces the optimization time and load of input/output parameters to access the performance of materials under specific conditions. In the previous reports, researchers pivotally explored the influence of physiochemical characteristics on the specific capacitance of carbon electrodes and estimated the relative contribution of physiochemical descriptors on SC performance. However, no reports explicitly considered new experimental data for testing the ML model appropriately. This work aims to study the fabricated metal-free GONs-based electrode materials for SC application. For comparison, the electrochemical performance of the as-prepared samples was categorically tested using four different ML models, including the ANN, RT, SVM, and LR. By employing advanced machine learning techniques, we aim to interpret the intricate roles of electrochemical features in the electrochemical performance of GONs concerning GO. This dual approach provides deeper insight into the electrochemical parameter's role in electrode performance and paves the way for optimizing SCs performance through targeted morphological modifications.
2. Materials and methods
This experiment used commercially available analytical grade chemicals without further treatment such as graphite powder (Asbury carbon, USA, particle size <20 μm), sodium nitrate NaNO3 (ACL Labscan, Thailand), potassium permanganate KMnO3 (Samchun, Korea, 99.3%), hydrogen peroxide H2O2 (QReC, Thailand, 35%), sulphuric acid H2SO4 (Samchun, Korea, 98.00 vol%) and olive oil (Sabroso, Thailand).
2.1. GO synthesis
A schematic representation of the synthesis of graphene oxide using a modified Hummers method is shown in Fig. 1, as reported in previous literature.47 In a 200 mL beaker with 150 mL of concentrated H2SO4, 5 g of graphite powder and 2.5 g of NaNO3 powder was combined. The mixture was stirred in an ice bath for an hour to keep the temperature below 5 °C. Potassium permanganate (15 g of KMnO4) was slowly added to the mixture and stirred continuously for 4 h until the solution turned green, indicating incomplete exfoliation. The solution was continuously stirred for 3 hours at 40 °C until it changed to dark grey. The thick mixture appears dark brown after being left overnight at room temperature for 10 h. The thick pastry mixture was diluted with 40 mL of DI water while constantly stirring at 40 °C for an hour, followed by stirring with 500 mL of DI water for two hours at 95 °C. After cooling the mixture to room temperature, a further 700 mL of DI water and 150 mL of a 15% hydrogen peroxide H2O2 solution are added until the GO slurry turns yellow. 120 mL of a 5% HCl solution is added to the GO slurry to eliminate excess salt. Ultimately, the pH of the colloidal suspension is raised to 6–7 by cleaning, rinsing, and centrifuging. The collected sample was filtered and dried at 75 °C for 36 hours to measure the yield of finished product, GO. The production yield of GO was around 3.75 g after washing and drying.
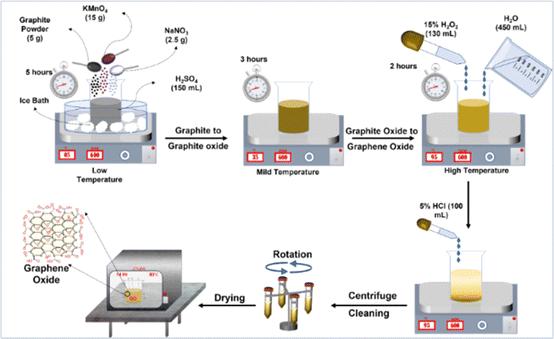 |
| | Fig. 1 Schematic diagram of GO synthesis using the modified Hummer's method. | |
2.2. GO nano-rings (GONs) synthesis
In this experimental procedure, approximately 0.5 g of graphene oxide (GO) powder was introduced into 250 ml of deionized (DI) water and stirred at 1000 rpm for nearly 30 minutes, forming a homogeneous GO solution. Subsequently, the stirred solution underwent ultrasonication for an additional 30 minutes, during which 5 ml of ammonia solution was added to adjust the pH to 11, ensuring the stability of the GO emulsion. Following this, approximately 25 ml of olive oil was incorporated into the GO suspension, and the resultant solution was stirred for 3.5 h at 1500 rpm. Over this duration, the solution viscosity exhibited a progressive increase. After the stirring period, the GO solution was allowed to stand overnight, facilitating the spontaneous separation of oil and water. The obtained GONs powder underwent thorough cleaning and rinsing before the annealing process. The GONs suspension was subsequently heated at 90 °C, and the resulting dried GONs powder underwent further investigation.
Researchers regarded that the water-in-oil (W/O) emulsion technique tuned the graphene oxide nanosheet into spherical graphene oxide.15 The partially reduced GO acted as a tailored surfactant in the W/O emulsion to prepare GONs.15 The synthesis of graphene oxide nano-rings (GONs) through the W/O emulsion method is elucidated with the aid of a schematic diagram in Fig. 2. The amphiphilic characteristics of graphene oxide (GO) endow it with a hydrophobic basal plane, while hydrophilic moieties, primarily comprising hydroxyl, carbonyl, and ether functional groups, envelop both the basal plane and the edges of the GO sheet.11,14 Notably, GO is a Pickering agent that effectively stabilizes W/O emulsions.48,49 The inherent flexibility of the GO sheet allows it to conformably stack around water droplets, eliminating the need for surfactants.48 Furthermore, the electrostatic interaction between graphene sheets facilitates the formation of a tightly knit graphene shell, contributing to the compact structure of the resulting nano-rings.
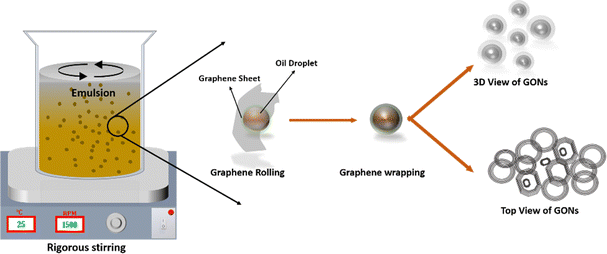 |
| | Fig. 2 Schematic representation of GON synthesis from W/O emulsion technique. | |
3. Characterizations
Morphological properties of the synthesized electrode materials were analyzed using a high-resolution transmission electron microscope (JEOL JEM-2100F, Japan). For HRTEM imaging, samples were characterized by depositing a few drops of the colloidal solution of the samples onto a carbon-coated copper wire grid and allowing it to dry at room temperature before analysis. The chemical compositions of the samples were examined using X-ray photoelectron spectroscopy (XPS) with an Al Kα X-ray source (1487 eV) on a ULVAC-PHI, Inc. instrument. The structural properties were studied using X-ray diffraction spectra (XRD, Rigaku, SmartLab 9 kW) and laser Raman spectroscopy (Renishaw microscope) using a 532 nm laser source wavelength. The presence of functional groups on the samples was characterized using the Fourier transform infrared (FTIR) spectrum using PerkinElmer 2 instrument, FTIR spectrometer, scanned between 4000 and 400 cm−1. Brunauer–Emmett–Teller (BET) analysis was performed using the Nova Touch LX2 model by Quantachrome Instruments, USA, to determine surface properties such as specific surface area and pore size. The Gaussian function was used for curve fitting and plotting Raman, XRD, and XPS after Shirley background subtraction using Origin 2019b software. Finally, the electrochemical experiments were conducted using a two-electrode configuration with an electrochemical workstation (CHI-760E, Instrument, USA).
3.1. Electrochemical analysis
The as-synthesized GO nanosheets and GONs were used as active materials to prepare the SCs electrode. Firstly, the GO or GONs were mixed with the carbon black and PVDF as a binder at a ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 with N-methyl-2-pyrrolidone as a solvent for paste formation, which was coated onto the nickel foam sheet with a covered area of 1 cm2. The electrode was dried at 70 °C for 12 h in the oven. The active materials mass loading on the Ni foam was about 3 mg cm−2. The device was assembled as a symmetric electrode for the SCs test in a 6 M KOH electrolyte solution. The specific capacitance (C) was calculated from CV and GCD curves using the following eqn (1) and (2), respectively,50
10 with N-methyl-2-pyrrolidone as a solvent for paste formation, which was coated onto the nickel foam sheet with a covered area of 1 cm2. The electrode was dried at 70 °C for 12 h in the oven. The active materials mass loading on the Ni foam was about 3 mg cm−2. The device was assembled as a symmetric electrode for the SCs test in a 6 M KOH electrolyte solution. The specific capacitance (C) was calculated from CV and GCD curves using the following eqn (1) and (2), respectively,50| | 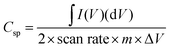 | (1) |
| | 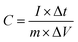 | (2) |
where I (A), m (g), ΔV (V), and Δt (s) represent the charge/discharge current, mass of active materials, voltage range, and discharging time of voltage, respectively. The following eqn (3) and (4) was used to determine the power (P, W kg−1) and energy density (E, W h kg−1) of the as-fabricated GO and GONs samples.| | 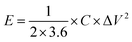 | (3) |
| | 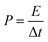 | (4) |
where the voltage, discharging time, and specific capacitance of the GO and GONs are represented by the variables Δt (s), ΔV (V), and C (F g−1). Cyclic voltammetry (CV) testing with different scan rates of 1 to 100 mV s−1 was used to electrochemically analyze the redox process occurs in the GO and GONs samples. While the charge/discharge studies was carried out at a current density of 1–6 A g−1 to estimate the capacitance and cyclic stability of the samples, respectively. Using the EIS analysis, the electron transport properties of GO and GONs were examined with an open circuit potential with an amplitude of 5 mV and a frequency range of 1 Hz–100 kHz.
4. Results and discussion
4.1. Morphological analysis
Fig. 3 presents the HRTEM images of as-synthesized GO and graphene oxide nano-rings (GONs) samples. A typical transparent sheet-like morphology was observed in GO, as shown in Fig. 3(a). The partially transparent GO nanosheet exhibits a lateral dimension of several hundred nanometers, confirming the fully exfoliated GO sheets. The apparent transparent sheet is attributed to the existence of oxygen-containing functional groups.11 The HRTEM image analysis of GONs reveals both solid and hollow multilayer onion-like structures with shapes lying in the range of regular polygonal structures like spherical, oblate, and ellipsoid, as highlighted in the yellow encircled regions in Fig. 3(b) and (c). It has also been observed that small sized GONs particles were encaged into bigger sized GONs, as displayed in Fig. 3(d). HRTEM images of GONs appear with a typical nano-rings-like morphology, as reported in previous papers.17,18,51 An observable 10–12 layers in the GONs sample indicate the successful formation of GONs by wrapping the GO nanosheet over the water droplet using the W/O emulsion technique. The inset image of Fig. 3(b) shows the statistical evaluation of various GONs nanoparticles. The GON sample shows a wide range of particle size distribution, varying from 10 to 40 nm with an average size of 21 nm.
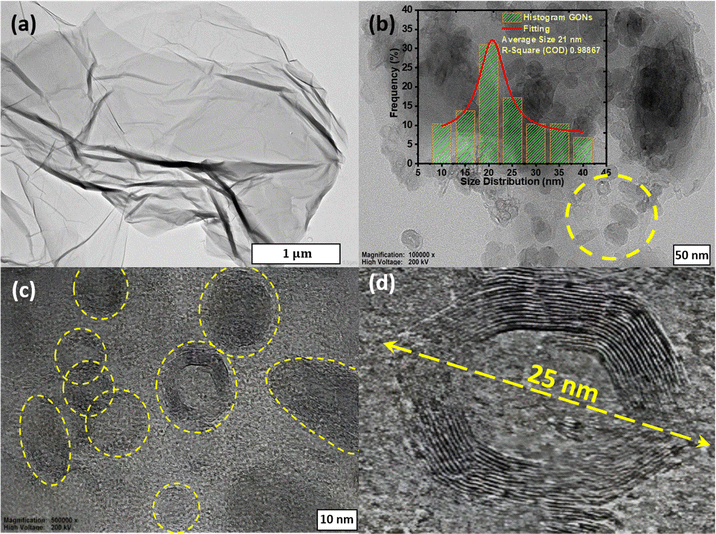 |
| | Fig. 3 HRTEM images of (a) GO, (b) GONs, (c) enlarged section of GONs, and (d) encaged GONs. | |
It is pertinent to note that the morphology of GO and GONs can play a crucial role in improving the electronic properties of electrode materials, as displayed in HRTEM images. The GO sheet typically shows the disordered structure with smaller sp2-domains interspersed with amorphous regions due to the oxygenous functional groups. Oxygenous functional groups primarily disrupt the π-conjugations, leading to lower conductivity, eventually affecting the charge-storage capacity and resulting in lower specific capacitance. In contrast, GONs display smaller nano-rings with an average diameter of around 21 nm with 10–12 layers of graphene sheets, exhibiting a more ordered structure than the GO, and providing more active sites for charge storage. The layered structure can facilitate a better electron transport pathway for higher conductivity and specific capacitance. The layered structure of GONs provides a more accessible path for ion diffusion, reducing the resistance and enhancing overall capacitance.
4.2. Structural analysis
The XRD pattern for graphite powder, GO, and GONs is presented in Fig. 4(a). The characteristic peak of graphite shows a strong peak at 2θ = 26.4° and minor peaks at 44.5 and 54.5° were observed specific to the (002), (101), and (004) planes, respectively. After the successful exfoliation of graphite, a broad and less intense diffraction peak appears at 2θ = 11.53°, which corresponds to the (001) diffraction peak of GO,11 indicating the c-axis spacing increases from ∼0.338 nm to ∼0.77 nm, confirming the GO formation.6 Furthermore, a weak peak was confirmed in GO and GONs with JCPDS Card No. 065-1528 at 2θ = 26.4° and 42.3°, corresponding to the (002) and (100) planes of a graphitic-type carbon structure.6 After the W/O emulsion process, it was found that the (001) diffraction peak of GO is slightly weakened and shifted to the higher diffraction angle from 2θ = 12.07°, as shown in Fig. 4(b), which is possibly due to the consumption of oxygenous moieties and bound moisture during the reaction with ammonia.11,52 Earlier, Guo et al.11 observed a similar diffraction peak at 2θ ≈ 12.7° for GO and GO nanospheres while producing a GO nanosphere from GO through emulsion.11 In the meantime, the (002) diffraction peak was partially restored in GONs, showing the recovery of the graphitic structure and the elimination of functional groups during the emulsion process, as per the previously reported results.11,12,15 In addition, to correctly assign the crystal structure of GONs, the XRD data of GONs have been compared with carbon nano-rings and graphite oxide (GrO). The typical XRD spectra of carbon nano-onions do not contain the peak at 2θ = 11°. Instead, they display a sharp peak at 2θ = 26.4° corresponding to the (002) of the graphitic carbon structure, which is widely reported in previous literature. The GrO displays a generally broad and less intense peak than GO due to the multiple layers of graphene oxide that are staked together, leading to a more disordered structure. In contrast, the synthesized GONs display a slightly less intense peak around 2θ = 12.07°, primarily arising due to partial recovery of the graphitic arrangement and removal of oxygenous moieties leading to more disorder in the structure from the emulsion and carbonization process of GONs.11
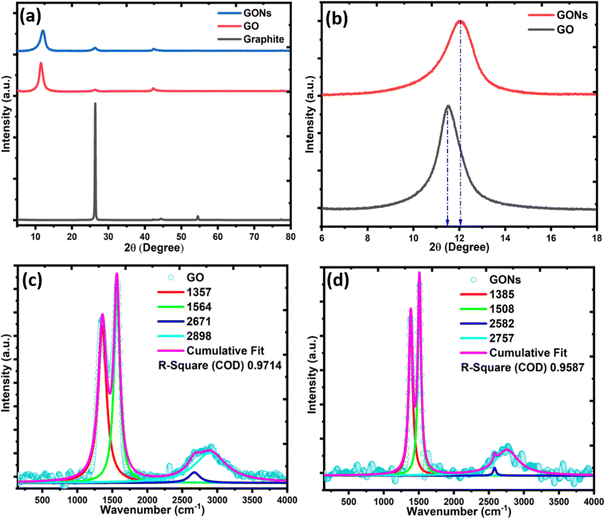 |
| | Fig. 4 (a) XRD spectra, (b) magnified view of the (001) peak, and (c)–(d) Raman spectra of GO and GONs. | |
Raman spectroscopy is a versatile technique for analyzing the structural and electronic properties of carbon-based nanomaterials.21,53,54 A summary of the fitting parameter of the laser Raman spectrum is presented in Table 1. Fig. 4(c) and (d) display the typical Raman spectrum of GO and GONs with three major bands between 150–4000 cm−1. The characteristics of D-band peaks at 1357–1385 cm−1 arise from the out-of-plane A1g breathing mode of sp2 carbon. This is usually ascribed to the disorders or defects in the graphitic carbon structure. The G-band at 1508–1564 cm−1 corresponds to the first-order in-plane stretching vibration (E2g phonon) of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond at the center of the Brillion zone of graphite. Lastly, a broad peak centered around 2600–2900 cm−1 is called the 2D and D + G-band, resulting from the breathing-like modes of the D-band of carbon rings triggered by the defects via the double resonance process.55 The relative intensity of the 2D band concerning the G-band provides information on the number of graphene layers in GO and GONs. An observable decrease in the I2D/IG ratio from 0.050 to 0.039 suggests that an increase in the number of layers of the graphene sheet in GONs compared to the GO. The intensity ratio of D-band to G-band (ID/IG) measures the size of sp3/sp2 domains, indicating the presence of defects.56 The ID/IG ratio remains the same, indicating that the GO structure remains intact after the emulsion process. However, the increased intensity of the D-band and G-bands in GONs compared to GO can be attributed to the formation of new graphitic or sp2 domains.21,55,57 The overtone of the D-band refers to the 2D-band in GONs, which appears at 2582 cm−1 and is blue-shifted by 89 cm−1 compared to the GO nanosheet. This difference is mainly due to the increased π–π staking in the GONs sample, as confirmed by the HRTEM images. In addition, a shift of the G-band to a lower frequency for GONs compared to GO can be attributed to various factors, such as the presence of functional groups or defects on the surface of GONs. Studies have shown that the reduction in the primary band edge of GO leads to a decrease in the bandgap. The alterations in the electronic properties of GONs due to oxidation levels contribute to the observed G-band shift to lower frequencies in GONs nanoparticles compared to pristine graphite and GO.58
C bond at the center of the Brillion zone of graphite. Lastly, a broad peak centered around 2600–2900 cm−1 is called the 2D and D + G-band, resulting from the breathing-like modes of the D-band of carbon rings triggered by the defects via the double resonance process.55 The relative intensity of the 2D band concerning the G-band provides information on the number of graphene layers in GO and GONs. An observable decrease in the I2D/IG ratio from 0.050 to 0.039 suggests that an increase in the number of layers of the graphene sheet in GONs compared to the GO. The intensity ratio of D-band to G-band (ID/IG) measures the size of sp3/sp2 domains, indicating the presence of defects.56 The ID/IG ratio remains the same, indicating that the GO structure remains intact after the emulsion process. However, the increased intensity of the D-band and G-bands in GONs compared to GO can be attributed to the formation of new graphitic or sp2 domains.21,55,57 The overtone of the D-band refers to the 2D-band in GONs, which appears at 2582 cm−1 and is blue-shifted by 89 cm−1 compared to the GO nanosheet. This difference is mainly due to the increased π–π staking in the GONs sample, as confirmed by the HRTEM images. In addition, a shift of the G-band to a lower frequency for GONs compared to GO can be attributed to various factors, such as the presence of functional groups or defects on the surface of GONs. Studies have shown that the reduction in the primary band edge of GO leads to a decrease in the bandgap. The alterations in the electronic properties of GONs due to oxidation levels contribute to the observed G-band shift to lower frequencies in GONs nanoparticles compared to pristine graphite and GO.58
Table 1 Gaussian fitting parameters of the Raman spectra of GO and GONs
| GO |
GONs |
| Band |
Center |
Height |
Ratio |
Band |
Center |
Height |
Ratio |
| D |
1357 |
133 |
I
D/IG = 0.82 |
D |
1385 |
229 |
I
D/IG = 0.81 |
| G |
1564 |
162 |
G |
1508 |
280 |
| |
| 2D |
2671 |
9 |
I
2D/IG = 0.05 |
2D |
2582 |
11 |
I
2D/IG = 0.039 |
| D + G |
2898 |
25 |
D + G |
2757 |
37 |
4.3. Surface chemistry analysis
Fig. 5(a) illustrates the FTIR spectra of GO and GONs displaying the characteristics of various functional groups on their surface. The intensive chemical oxidation and emulsion procedure results in sharp infrared absorption bands. These absorption bands are indicative of various functional groups. Specifically, bands indicating epoxy/carboxylic (C–O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) groups appear at 1049 and 1720 cm−1.57 In contrast, the hydroxyl groups characterized by C–OH were identified at around 1380 cm−1, respectively. The absorption band at 1616 cm−1 is associated with the carbon skeleton structure (C
O) groups appear at 1049 and 1720 cm−1.57 In contrast, the hydroxyl groups characterized by C–OH were identified at around 1380 cm−1, respectively. The absorption band at 1616 cm−1 is associated with the carbon skeleton structure (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), primarily regarded as graphitic carbon.12 The broad absorption band ranges from 2800–3800 cm−1, signifying the stretching vibration of hydroxyl functional groups.23,57 These functional groups are primarily covalently bonded to the carbon skeleton structure or interspersed within the graphene layers. This observation demonstrated the amphiphilic nature comparable to surfactants in water-in-oil (W/O) emulsion systems.11 The strategic inculcation of acidic/hydroxyl groups at the edge sites or basal plane graphene sheets significantly improves the dispersibility of GONs in the ammonia solution, which is an efficient dispersion agent.11
C), primarily regarded as graphitic carbon.12 The broad absorption band ranges from 2800–3800 cm−1, signifying the stretching vibration of hydroxyl functional groups.23,57 These functional groups are primarily covalently bonded to the carbon skeleton structure or interspersed within the graphene layers. This observation demonstrated the amphiphilic nature comparable to surfactants in water-in-oil (W/O) emulsion systems.11 The strategic inculcation of acidic/hydroxyl groups at the edge sites or basal plane graphene sheets significantly improves the dispersibility of GONs in the ammonia solution, which is an efficient dispersion agent.11
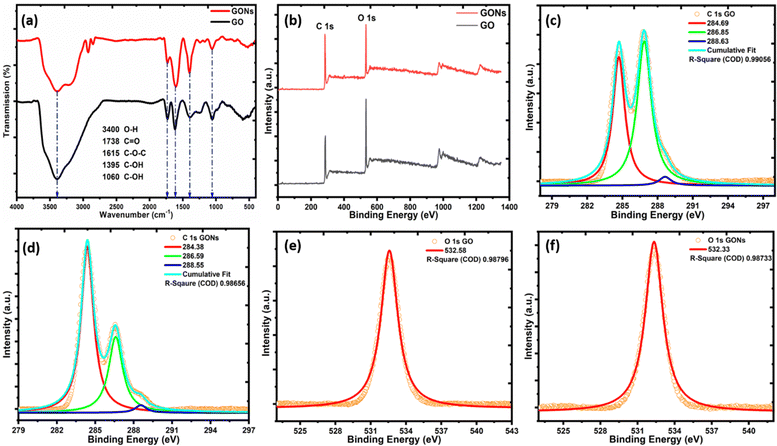 |
| | Fig. 5 (a) FTIR spectra, (b) XPS survey scan, (c)–(d) deconvolution of the C 1s peak, and (e)–(f) O 1s peak of GO and GONs. | |
XPS analysis is a versatile technique for evaluating the chemical and structural properties of materials. Fig. 5(b) depicts the XPS survey spectra of GO and GONs. The XPS survey scan reveals two major peaks at 284 and 532 eV, corresponding to single C 1s and O 1s peaks, respectively.6,59 Furthermore, the C 1s spectra were deconvoluted via Gaussian peak shape after exerting a Shirley background correction, as shown in Fig. 5(c) and (d). The C 1s peak for GO and GONs was observed at the same peak position at 284.6 ± 2 eV for C–C bonding of the carbon skeleton of the graphitic structure.11,21 In addition, peaks at ∼286.8 and ∼288.5 eV can be assigned to the C–OH/C–O–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species, respectively.57,60 The main peak at 286.8 eV is attributed to C–OH/C–O–C functional groups, consistent with the FTIR results. The epoxide group (C–O–C) in the structural model of graphene oxide has a binding energy comparable to that of C–OH.11 The presence of abundant C–O–C groups on the surface of the basal plane in contrast to the edges of the graphene sheet of GO and GONs is confirmed by a notable difference in the intensity of the C–O–C peak compared to C
O species, respectively.57,60 The main peak at 286.8 eV is attributed to C–OH/C–O–C functional groups, consistent with the FTIR results. The epoxide group (C–O–C) in the structural model of graphene oxide has a binding energy comparable to that of C–OH.11 The presence of abundant C–O–C groups on the surface of the basal plane in contrast to the edges of the graphene sheet of GO and GONs is confirmed by a notable difference in the intensity of the C–O–C peak compared to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. The reduction in the epoxide groups from the surface of the basal plane of GONs is shown by a notable decrease in the strength of the C–O–C peak.11,59
O. The reduction in the epoxide groups from the surface of the basal plane of GONs is shown by a notable decrease in the strength of the C–O–C peak.11,59
Meanwhile, Fig. 5(e) and (f) display the singlet O 1s peak in GO and GONs, which shared the same peak position centered around ∼532.3 ± 2 eV corresponding to similar oxygenous species (C–O–C/C–OH) even after the conversion of GO to GONs via a W/O emulsion process.11 The relative ratio of the atomic percentage of C and O in GO and GONs was found to be around 61.2% and 38.8%, and 75% and 25%, respectively. The relative oxygen content in GO and GONs further confirmed the formation of graphene oxide, not graphite oxide.
Table 2 presents the Gaussian fitting parameter of XPS spectra obtained after Shirley background correction. The relative intensity ratio of non-oxygenous carbon to oxygenous carbon (IC–C/IC–O) for GO and GONs was found to be around 0.73 and 1.80, confirming that fewer oxygenous species were present on the surface of GONs than in the GO sample.6 It is also evident that the atomic ratio (IC/IO) of GO and GONs increases from 1.13 to 1.25, revealing the increase in stacked layers, formation of newer graphitic domains, and the reduction of oxygen functional groups leading to decreased surface defects and improved electronic transport properties of the GON.21,55,57 Furthermore, the results of the XPS spectra for the GO and GONs samples are consistent with the FTIR and Raman spectra, revealing that the true nature of GO remains unaltered even after the rigorous W/O emulsion process for GONs formation.
Table 2 Gaussian fitting parameter for the XPS spectra of GO and GON samples
| Element |
Binding energy (eV) |
Intensity (a.u.) |
FWHM |
Species |
Atomic (%) |
Atomic ratio |
| GO |
| C |
284.69 |
4346 |
1.25 |
C–C |
61.2 |
I
C–C/IC–O = 0.73 |
| 286.85 |
5691 |
1.47 |
C–OH/C–O–C |
| 288.63 |
239 |
1.10 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
| O |
532.58 |
8982 |
2.05 |
C–O–C/C–OH |
38.8 |
I
C/IO = 1.13 |
| GONs |
| C |
284.38 |
6834 |
1.18 |
C–C |
75 |
I
C–C/IC–O = 1.80 |
| 286.59 |
3500 |
1.32 |
C–OH/C–O–C |
| 288.55 |
278 |
1.05 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
| O |
532.33 |
8483 |
1.71 |
C–O–C/C–OH |
25 |
I
C/IO = 1.25 |
4.4. Pore structure
The specific surface area (SSA) and pore structure of GO and GONs were evaluated by the N2 adsorption–desorption technique. Fig. 6(a) and (b) present the Brunauer–Emmett–Teller (BET) adsorption/desorption isotherms of GO and GONs, respectively. The insets of Fig. 6(a) and (b) show the pore-size distribution of GO and GONs, respectively. The isotherm shows a hysteresis loop in the 0.03–1.0 range of relative pressures (P/P0), indicating a type IV isotherm. In addition, the Barrett–Joyner–Halenda (BJH) approach is used to investigate the pore-size distribution. The measured specific surface areas were around 24 and 20 m2 g−1, and their average pore size were around 1.79 and 2.59 nm for the GO and GONs samples, respectively, indicating mesoporous nanomaterial formation. Herein, the GONs exhibit slightly lower SSA than GO nanosheets due to differences in shape, structure, and dimensions. Since the GONs were derived from the same GO, they have a more compact and circular morphology, which reduces the overall SSA available for N2 adsorption/desorption compared to the planar structure of GO. Researchers have observed that the planar and lateral size of GO plays a crucial role in determining its SSA.61 Additionally, the synthesis and size reduction methods used in producing GONs from GO can influence their final SSA, with smaller GO nanosheets often showing higher surface areas than larger GONs.62,63 Such differences in lateral dimensions, morphological and chemical changes in GONs can contribute to the slightly lower surface area than GO.
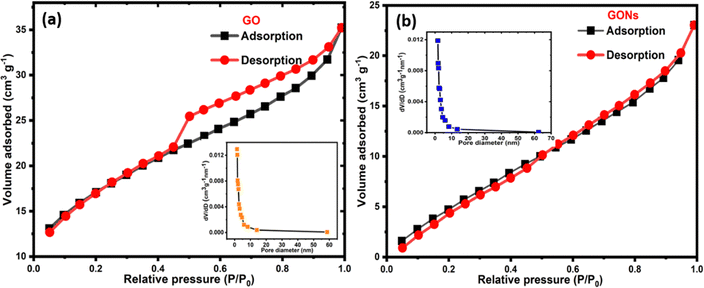 |
| | Fig. 6 BET isotherms of (a) GO and (b) GONs and the corresponding insets show pore-size distribution. | |
4.5. Electrochemical performance of GO and GONs
Various electrochemical studies have been carried out to assess the electrochemical SCs performance of GO and GONs comprehensively, as shown in Fig. 7(a)–(f). Fig. 7(a) and (d) display the CV results of GO and GONs at various scan rates from 1 mV s−1 to 100 mV s−1. GO and GONs samples possess ideal capacitive behaviour, indicated by the quasi-rectangular symmetric CV curves, corroborated by the nearly triangular-shaped GCD curves at various current densities.64–66Fig. 7(b) and (e) show the GCD curves of the GO and GONs samples at different current densities (1, 2, 3, 4, 5, and 6 A g−1) within a voltage range from −0.5 V to 0.5 V. The calculated specific capacitance values of GO and GONs from CV and GCD methods differ due to the nature of the measuring techniques, as presented in Fig. 7(c)–(f). However, both techniques are considered valid for the electrochemical performance testing of materials. In general, the specific capacitance measured at low scan rates (1 mV s−1 and 5 mV s−1) is more reliable, as these conditions allow sufficient time for ion diffusion and charge transfer, resulting in high capacitance. GCD measures the direct voltage response to a constant current, providing a direct charge storage ability in real devices, but it may underestimate pseudocapacitance. The maximum specific capacitance for GO and GONs measured from CV reaches 164 F g−1 and 294 F g−1 at 1 mV s−1. Although the capacitance value decreases from 164 F g−1 to 97 F g−1 for GO and from 294 to 68 F g−1 for GONs, as the scan rate increases from 1 mV s−1 to 100 mV s−1. The specific capacitance for GO and GONs decreases from 62 F g−1 to 45 F g−1 and 110 F g−1 to 51 F g−1 as the current density increases from 1 A g−1 to 6 A g−1, as shown in Fig. 7(f). It is interesting to note that the ratio of maximum capacitance (CCV/CGCD) observed for GO and GONs using CV and GCD are almost the same, 2.64 and 2.67, respectively. This indicates that the characteristic features of specific capacitance measured from CV and GCD remain the same under different measuring techniques. The CV test at a low scan rate reflects the combined effects of the electrical double layer and pseudocapacitance due to the electrolytic ions having sufficient time to diffuse into the graphene layers, leading to higher specific capacitance. However, a higher scan rate does not provide enough time for ions to diffuse, resulting in lower capacitance, as observed in Fig. 7(c). The absence of redox peaks in GO and GONs suggest excellent electrochemical stability to withstand numerous charge/discharge cycles.
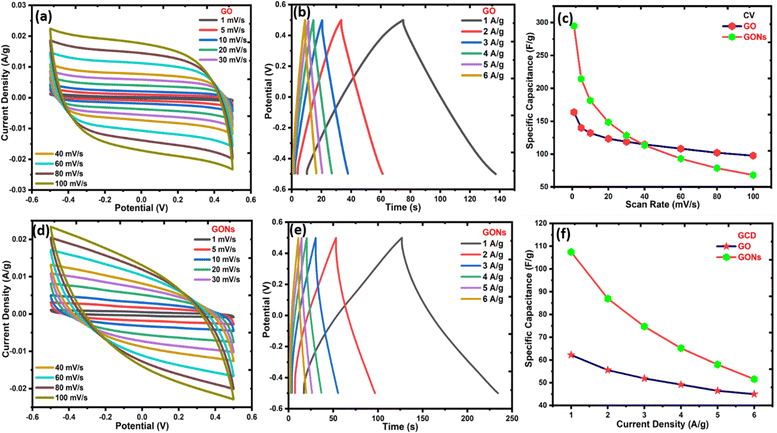 |
| | Fig. 7 Cyclic voltammogram, GCD curve, and specific capacitance vs. scan rate and current density for (a)–(c) GO and (d)–(f) GONs. | |
The cyclic stability of GO and GONs has been tested to unveil the potential of the as-prepared electrode materials for energy storage application. The capacitance retention capabilities of GO and GONs samples were around 63.5 and 60.8% after the 2500 cycles, as illustrated in Fig. 8(a) and (b). However, both samples show capacitance retention of around 60%, indicating reasonable electrochemical stability. The inset images in Fig. 8(a) and (b) present the charging/discharging curves for the last 20 cycles. The cyclic stability of GONs possesses superior performance among the previously reported metal-free graphene oxide nanospheres for SCs. Although retaining up to 60% of its capacity after 2500 cycles is not the highest result among the recent literature reports, as it still reflects a reasonable level of stability. Table 3 summarizes the previously reported results of metal-free GO nanostructures. Based on the previous literature, GONs show a reasonable increase in electrochemical capacitance but are not as competitive against advanced MXene and perovskite-based electrode materials for SCs.67–69 Previously, several researchers reported that increased cyclic stability comes at the expense of reduced specific capacitance. As a result, this work demonstrates that morphology-tailored GONs outperform most metal-free graphene and GO nanosheet electrode materials in terms of efficiency. Fig. 8(c) presents the Ragone plot of GO and GONs, wherein the maximum energy density was calculated to be 8.6 W h kg−1 and 14.9 W h kg−1 at 1 A g−1, respectively.
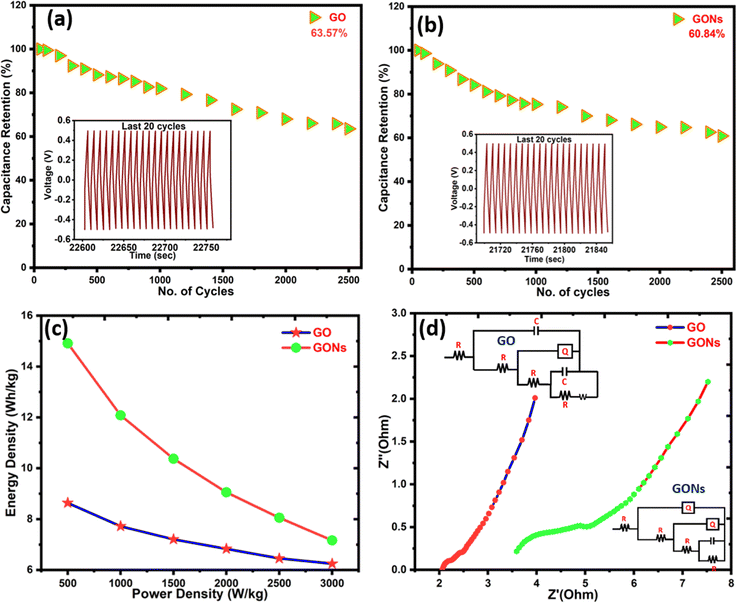 |
| | Fig. 8 (a) and (b) Cyclic stability after 2500 cycles; the inset image represents the last 20 cycles of the GCD curves, (c) Ragone plot of GO and GONs, and (d) impedance spectra of GO and GONs with Nyquist plot fit and the corresponding equivalent circuit diagrams. | |
Table 3 Supercapacitative performance of metal-free graphene oxide-based nanostructures
| S. No. |
Electrode |
Electrolyte |
Scan rate (mV s−1) or Curr. Den. (A g−1) |
Pot. Win. (V) |
Sp. Cap. (F g−1) |
Ret. (%) |
Cycles (numbers) |
Ref. |
| 1 |
S-PGHS-900 |
2 M KOH |
2.0 |
1.0 |
236 |
50.8 |
1000 |
18
|
| 2 |
HGSs |
6 M KOH |
0.2 |
0.8 |
207 |
86 |
1000 |
70
|
| 3 |
HGSs |
6 M KOH |
1.0 |
0.8 |
193 |
— |
— |
70
|
| 4 |
HMCNs |
1 M H2SO4 |
1.0 |
1.0 |
253 |
96 |
5000 |
71
|
| 5 |
N-HMCSs |
6 M KOH |
1.0 |
1.0 |
170 |
94 |
5000 |
72
|
| 6 |
PNHCS |
6 M KOH |
0.5 |
1.0 |
213 |
56 |
5000 |
73
|
| 7 |
Si-MCFs |
2 M KOH |
0.5 |
0.7 |
208 |
70 |
1000 |
74
|
| 8 |
N-HMCSs |
1 M H2SO4 |
1.0 |
0.8 |
240 |
97 |
5000 |
75
|
| 9 |
HCNSs |
6 M KOH |
0.2 |
1.0 |
225 |
71 |
3000 |
76
|
| 10 |
NGHS |
6 M KOH |
1.0 |
1.0 |
159 |
99 |
5000 |
77
|
| 11 |
MGB |
1 H2SO4 |
1.0 |
0.8 |
206 |
96 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
78
|
| 12 |
GMs |
3 KOH |
0.1 |
1.0 |
205 |
90 |
1200 |
24
|
| 13 |
rGONC |
6 KOH |
1.0 |
1.0 |
214 |
86 |
1000 |
79
|
| 14 |
hGO |
0.1 LiTFSI |
0.5 |
3.5 |
99 |
80 |
100 |
80
|
| 15 |
Ap-rGO |
6 KOH |
0.1 |
1.0 |
97 |
85 |
5000 |
81
|
| 16 |
Graphene |
0.5 Na2SO4 |
1.04 |
0.8 |
141 |
47 |
2000 |
82
|
| 17 |
GO
|
6 M KOH
|
1.0
|
1.0
|
164
|
63
|
2500
|
This work
|
| 18 |
GONs
|
6 M KOH
|
1.0
|
1.0
|
294
|
60
|
2500
|
This work
|
In addition, the Nyquist diagram and corresponding electrochemical circuit diagram of GO and GONs are shown in the inset image of Fig. 8(d). The Nyquist plot usually comprises a semicircle in a high-frequency region related to the charge transfer resistance (Rct) between electrode materials and electrolytes.67,83 The straight line in the low-frequency region represents Warburg impedance, which is related to the diffusion resistance of ions (Rs) in the electrolyte.84,85 The internal resistance Rs of the our electrode materials (the intercept of the curve from the horizontal axis) and the charge transfer impedance (Rct) values obtained through the diameter of the semicircular arc indicate that GONs have higher charge transfer resistance and exhibit excellent impedance characteristics, consistent with the reduced stability and higher specific capacitance than GO. Their internal resistance (Rs) of GO and GONs were obtained as 2.02 Ω and 3.59 Ω, and the charge transfer resistance (Rct) was 0.25 Ω and 0.85 Ω, respectively. Despite the GONs possessing a lower specific surface area and higher internal resistance than GO, their higher specific capacitance can be attributed to their unique ring-like morphology, which provides a more accessible active site for charge storage for ion transport, compensating for the specific surface area and internal resistance. These structural and morphological tailored electrochemical properties contribute to the higher specific capacitance in GONs over GO.
4.6. Capacitive and diffusive charge distribution
To further understand the charge storage mechanism behind the GONs, a semi-quantitative approach (Dunn's method) was carried out on the CV curve. A power law fitting approach was applied to the CV curves to determine which electrochemical process dominates in GO and GONs.86–88 The analysis focuses on the correlation between the logarithm of peak current (log(i)) and the logarithm of scanning rate (log(v)). The fitted power law is represented by the equation i = avb, where ‘i’ denotes peak current, ‘v’ indicates scanning rate, and ‘b’ is a dynamic variable. A ‘b’ value nearing 0.5 implies the prevalence of diffusion-driven behaviour, which means charge storage is limited by ion diffusion. A ‘b’ value near 1 signifies a capacitive storage mechanism, which means charge storage is surface-controlled and not limited by ion diffusion.86 The estimated ‘b’ values for GO and GONs are 0.5 and 0.6, indicating that diffusion-controlled battery type behaviour83,85 controls the electrode materials. The cathodic peaks of the GO electrodes have ‘b’ values closer to 0.5, indicating that the GO electrodes have pseudocapacitance-type behaviour rather than capacitive behaviour, as shown in Fig. 9(a)–(d).86 To intuitively estimate the proportion of capacitive-control and diffusion-control contributions in the GO and GONs, they were quantified by the power fitting formula. The capacitance at various scan rates can be further examined using eqn (5).87where k1v and k2v1/2 represent the contributions of current resulting from diffusion and capacitive mechanisms,87 respectively. The values of k1 and k2 were determined through a linear fit of the plot of 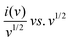 .
.
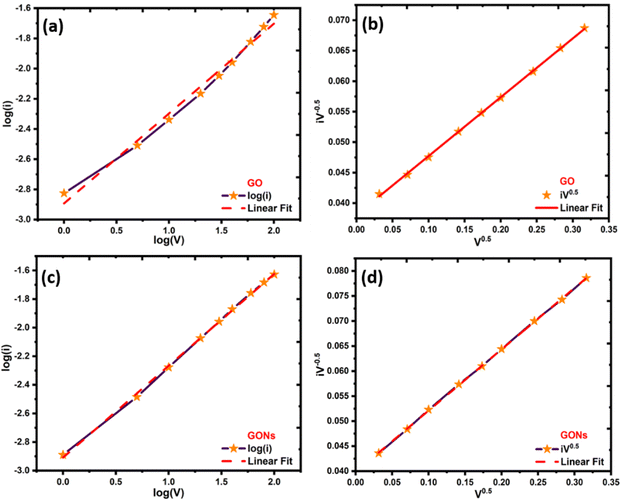 |
| | Fig. 9 Plot of log(i) vs. log(V) and log(i) vs. V0.5 for (a)–(b) GO and (c)–(d) GONs. | |
Fig. 10(a) and (c) display the diffusion-controlled and capacitive-controlled contribution at a scan rate of 100 mV s−1 for both electrode materials. In the CV graph, the blue region denotes the diffusive contribution, and the green shows capacitive contributions. These findings reveal that the diffusion contribution is predominant at lower scan rates, while at higher scan rates, the capacitive contribution becomes more significant.54 This observation suggests that electrolyte ions have adequate time for faradaic interactions with the electrode materials at lower scan rates, whereas at higher scan rates, ions do not have sufficient time to engage with the electrodes, resulting in non-faradaic charge storage.64Fig. 10(b) and (d) display the diffusive and capacitive contributions of GO and GONs expressed in the bar chart diagram at different scan rates. At a lower scan rate (1 mV s−1), the diffusive contribution was higher in the case of the GO electrode, with ∼7%, as evident from the ‘b’ value compared to GONs. As the scan rate increases for GONs, capacitive contribution grows from 3% (1 mV s−1) to 47% (100 mV s−1), indicating that the pseudocapacitive behaviour mainly dominates.
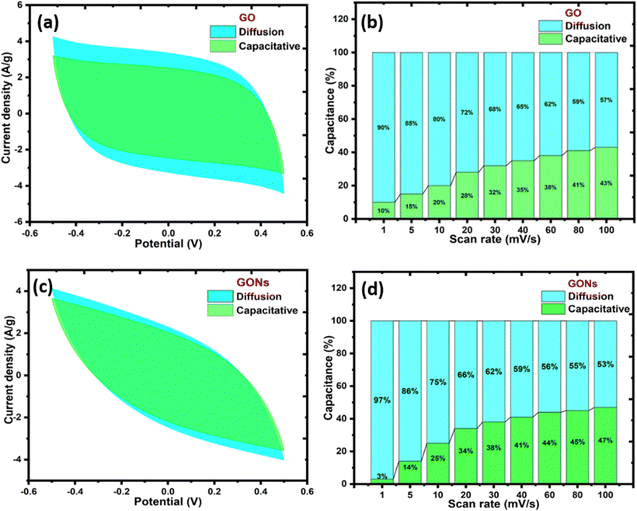 |
| | Fig. 10 (a) and (c) Percentage contribution separation of intercalation and capacitive current to the scan rates of GO and GONs, and (b) and (d) capacitive and diffusion contributions of the supercapacitor device at 100 mV s−1 of GO and GONs. | |
The success of a SCs is determined by its long-term cyclic stability, i.e., the ability to retain the charge storage after several thousand cycles of the charge–discharge process. The characteristic cyclic stability curve of GO and GONs shows a significant drop in capacitance to 63% and 60% after 2500 charge–discharge cycles. Li et al. suggested that stability degradation can be directly linked to the pseudocapacitance introduced by the excess surface oxygen-containing functional groups and the charge loss caused by the internal charge transfer resistance.23,89,90 However, unlike the electrical double layer, which arises due to the charge rearrangement, pseudocapacitance is related to the redox reaction caused by the surface functional group. At a constant scan rate of 100 mV s−1, a marginal increase in the capacitive behaviour from 43% for GO to 47% for GONs can be attributed to the rise in surface Faradaic redox reaction of oxygenous functional groups. The following surface redox reaction can be written as follows in eqn (6), (7) and (8).
| | ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C–OH ↔ C–O + H+ + e− C–OH ↔ C–O + H+ + e− | (6) |
| | | –COOH ↔ –COO + H+ + e− | (7) |
| | ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C–O + e− ↔ C–O + e− ↔ ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C–O− C–O− | (8) |
Additionally, reducing oxygen-containing functional groups during the synthesis of GONs leads to a smoother surface and reduced defect density, enhancing its charge storage ability.91 Furthermore, the structural and surface modifications in GONs contribute to their superior electrochemical performance over GO. Despite the GO possessing a higher specific surface area than GONs, leading to lower specific capacitance, it is influenced by various factors. GO materials exhibit better capacitance due to strong electrostatic interactions with species like K+ but suffers from inhibited ion mobility due to constriction of the interlayer spacing.92 Meanwhile, GONs with controlled assembly enable higher gravimetric capacitance than GO, making them suitable for energy storage applications.93
5. ML models selection
Fig. 11 presents the schematic diagram of ML operation for estimating the specific capacitance of the GONs sample. The dataset was manually prepared for ML model training by extracting electrochemical features information from 64 research articles on metal-free graphene oxide-based nanomaterials, as presented in Table S1 (ESI†). A limited number of input variables are chosen, such as electrolyte type, electrolyte concentration (M), current density (A g−1), and potential window (V) as predictors, while specific capacitance (F g−1) is the response variable to reduce the overfitting and complexity of ML models. In this work, four distinct ML models were used to predict the capacitance of GONs using MATLAB R2023b software. The selection of the best-fitted ML model is based on high prediction accuracy, such as root mean square error (RMSE), mean absolute error (MAE), coefficient of determination (R2), and coefficient of correlation (R) values.30,32,34 Herein, the supervised learning models like artificial neural network (ANN), regression tree (RT), support vector machine (SVM), and linear regression (LR) algorithm were used for predicting specific capacitance using electrochemical variables of GONs.
 |
| | Fig. 11 Schematic illustration of ML modeling of GONs for electrochemical SCs performance prediction. | |
5.1. ML performance metrics
The coefficient of correlation (R) measures the strength and direction of a linear relationship between two variables. The values of R ranges from +1 to −1, wherein +1 displays the perfect positive relationship, −1 represents the perfect negative relationship, and 0 means no relationship, as shown in eqn (9). Fig. S1 (ESI†) displays the actual and revised outlier capacitance of GO-based materials. The R-value is an important parameter to evaluate the linear regression model.| | 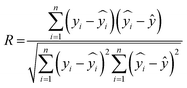 | (9) |
The R2 value defines the goodness of fitting of the regression model and varies between 0 and 1,32,34 as expressed in eqn (10)| | 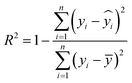 | (10) |
Here, yi is the predicted value, 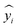 is the actual value, and ȳ is the mean of n actual values. A value equal to 1 represents the ideal fitted regression line, and a value equal to 0 shows that the regression model explains none of the data.
is the actual value, and ȳ is the mean of n actual values. A value equal to 1 represents the ideal fitted regression line, and a value equal to 0 shows that the regression model explains none of the data.
The root means square error (RMSE) measures the square root of variance of the residuals at each predicted value,32,34 which is expressed as in eqn (11)
| | 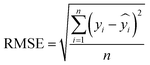 | (11) |
The mean absolute error (MAE) presents the average error magnitude between the actual and predicted values; compared to RMSE, this metric value varies linearly with increasing error, as described in
eqn (12)| | 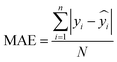 | (12) |
5.1.1. Artificial neural network (ANN).
ANN is a computational model mimicking human brain cells, the interconnecting cells known as neurons.42,94 The ANN model can easily recognize complex data and patterns. The optimized ANN model contains one input layer, one output layer, and three hidden layers. The input layer receives the input features or variables, typically electrolyte type, electrolyte concentration, current density, and potential window from the dataset, and it passes the data to the hidden layer without computation. In the next step, the hidden layer performs a complex activation function on each neuron layer that can be trained on the input data using techniques like backpropagation. The activation functions are sigmoid, tanh, and ReLU.32 The output layer finally computes the specific capacitance based on the learned model from the input features, thus completing the prediction process. Detailed information on the ANN model results is presented in the ESI.† The ANN model optimization process was completed after 30 objective evaluations, reaching the maximum allowed evaluations, as shown in Table S2 (ESI†). The best observed feasible point involved a neural network with a ReLU activation function, no standardization, a regularization parameter (Lambda) of 0.070108, and a three hidden layer size configuration with 3, 1, and 2 neurons in each hidden layer, respectively Fig. S2 (ESI†). Fig. S3 and S4 (ESI†) show the predicted capacitance over actual capacitance and an estimation of the electrochemical parameter's role.
5.1.2. Regression tree.
A regression tree is a powerful and interpretable ML method for predicting continuous outcomes based on multiple input variables. The regression tree algorithm iteratively splits the data into subsets based on the input variables, creating decision rules that predict the response variable. Each node in the tree represents a decision point, while the branches represent the possible outcomes, leading to leaf nodes that provide the final prediction values, as shown in Fig. 12. This hierarchical structure allows for easy interpretation of the relationships between the predictors and the response variable. Fig. 12 presents the regression tree analysis for predicting specific capacitance based on predictor variables: concentration, electrolyte, current density, and potential window. Each split represents a decision rule that leads to the final predicted value. This highlights the hierarchical structure and significance of each variable in the prediction process of the model. This regression tree diagram helps us to understand the contribution and interaction of different predictor variables in determining the specific capacitance of GONs. For instance, if the concentration is less than 0.2, the predicted capacitance is around 99.04 F g−1. The concentration is greater than or equal to 0.2, and the current density is less than 1.35; further conditions involving concentration and electrolyte determine the capacitance, ranging from 172.45 F g−1 to 212.33 F g−1. Higher current density ≥1.35 or specific ranges of the potential window led to different predicted capacitances. Each path through the tree represents a combination of these input variables, showing how they influence the specific capacitance. Table S3 (ESI†) presents the optimization process for the regression tree after 30 evaluations. The best observed feasible point had a minimum leaf size of 7, resulting in an objective function value of 8.3909, consistent with the estimated value of 8.391. This setting appeared optimal, as it was repeatedly selected as the best point during the process, as shown in Fig. S5 (ESI†). The runtime for these evaluations was efficiently low, demonstrating the robustness and reliability of using a minimum leaf size of 7 for the RT model. Fig. S6–S8 (ESI†) display RT model-based predicted capacitance over actual capacitance, visualization of the decision obtained from the regression tree, and estimation of the electrochemical parameters’ role, respectively.
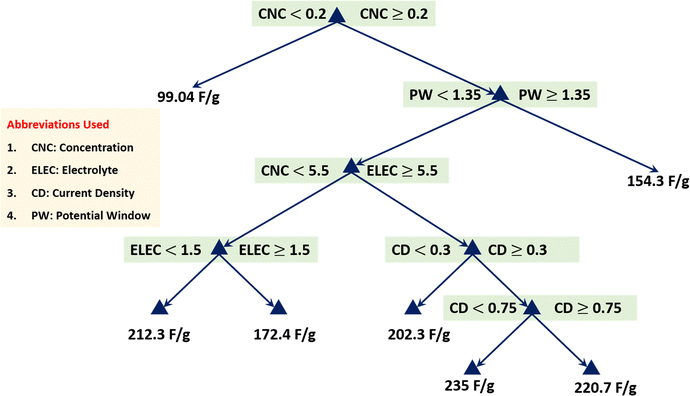 |
| | Fig. 12 Visualization of the decision obtained from the regression tree. | |
5.1.3. Support vector machine (SVM).
SVM is a machine learning approach widely applicable to solving classification and regression problems.37 It works by constructing hyperplanes around the training data into classes within a certain error threshold. SVM aims to find the optimal hyperplane in an N-dimensional space that maximizes the margin between the closest points of different classes.42 SVM uses mathematical functions called Kernels to transform an input space into a non-linear feature space, which can be linear, polynomial, sigmoid, Gaussian, or radial basis functions. The optimization problem in SVM involves the Gaussian Kernel function to maximize the margin and minimize the regression error, as shown in eqn (13).46 This study uses the Gaussian programming technique to find the optimal hyperplane. SVM has been applied to regression problems using structural risk minimization. Since SVM is less sensitive to minute changes, it is significantly more resilient than LR.| | | K(xj, xk) = exp(−‖xj − xk‖2) | (13) |
where xj, xk are arbitrary samples from the input space. To fit a hyperplane that minimizes the soft margin between the classes, training an SVM is equivalent to solving a Gaussian optimization problem. Fig. S9 and S10 (ESI†) display SVM model-based predicted capacitance over actual capacitance and estimation of the parameters’ role, respectively.
5.1.4. Linear regression (LR).
LR is a linear model constructing a relationship between dependent and independent variables.32,45 This study utilizes the LR model to determine the marginal effect of each variable, as shown in eqn (14).| | | y = I + β1x1 + β1x2 + ⋯ + βnxn | (14) |
Here, I is the intercept, βn is the coefficient, xn is the independent variable, and y is the predicted value. A linear model is efficient but suffers from a highly constrained nature. The basic elementary LR model considers the linear relationship between predictors and responses. In Table S2 (ESI†), the linear regression model suggests that the independent variables (x1, x2, x3, and x4) influence the dependent variable (y). The coefficient estimates for x1, x2, and x4 are statistically significant, with p-values below 0.05, indicating that these variables significantly impact y. In contrast, x3 is not statistically significant. The model explains 25% of the variance in y (R-squared = 0.25) (Fig. S11, ESI†). The overall model fit is statistically significant (p-value = 0.0017), but the relatively low adjusted R-squared (0.2) suggests other variables could influence the y or specific capacitance of GONs. The illustration of the LR model's fit and its predictor estimation are shown in Fig. S12 and S13 (ESI†), respectively.
The performance of different models (ANN, RT, SVM, and LR) has been compared using the regression plot, as shown in Fig. 13. The regression plot represents the predicted response vs. actual or true response, which helps in comparing the model by visualizing how close or far the predicted value is from the actual value.30 A cluster of points tightly close to a straight line passes diagonally, representing the better model performance for any given task. The scatter points around the diagonal line result in a large error between the predicted and actual values. The comparison of different ML models for predicting specific capacitance reveals distinct performances and strengths. The neural network (Fig. 13(a)) shows a fairly tight clustering of points around the diagonal, suggesting a strong prediction capability and effective learning of complex relationships. The regression tree (Fig. 13(b)) provides a somewhat less accurate fit, with more spread around the diagonal line, indicating it captures non-linear relationships but might struggle with more intricate patterns. The support vector machine (Fig. 13(c)) exhibits a more dispersed pattern, reflecting variability in prediction accuracy, which might be due to its sensitivity to the choice of kernel and hyperparameters. Lastly, the linear regression (Fig. 13(d)) shows a more widespread distribution of points, highlighting its limitations in capturing non-linear dependencies. This comparison underscores the importance of selecting the appropriate model based on the complexity and nature of the dataset, with neural networks typically excelling in capturing intricate patterns, while simpler models like LR might fall short.
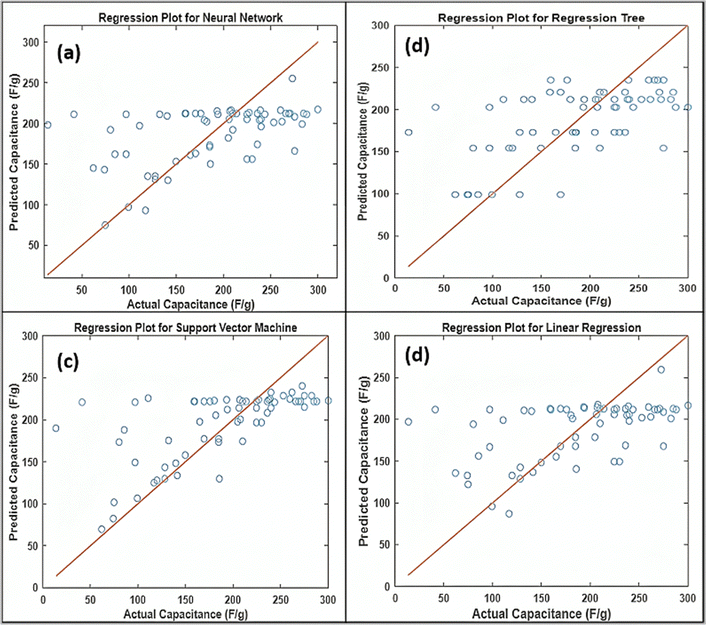 |
| | Fig. 13 Comparison of regression results of different ML models, (a) ANN, (b) RT, (c) SVM, and (d) LR. | |
Table 4 provides the ML model performance using RMSE, R2, R, MAE, and predicted capacitance. The predicted capacitance for GONs was determined using the current electrochemical parameters: a 6 M KOH electrolyte concentration, a current density of 1 A g−1, and a potential window of 1 V. The ANN model shows a solid performance with an RMSE of 59.02 and an R2 of 0.2602, demonstrating decent accuracy and predicting a capacitance of 212.4 F g−1. The regression tree (RT) fares slightly better with an RMSE of 55.98 and an R2 of 0.3364, predicting 220.7 F g−1, indicating it captures non-linear relationships effectively. The SVM model excels with the lowest RMSE of 52.71 and the highest R2 of 0.4100, making it the most accurate among the models, predicting 221.6 F g−1.
Table 4 Results summary of different ML models for GONs as supercapacitor electrode materials
| Model type |
RMSE |
R
2
|
R
|
MAE |
Predicted capacitance (F g−1) |
| ANN |
59.02 |
0.2602 |
0.5101 |
44.54 |
212.4 |
| RT |
55.98 |
0.3364 |
0.5785 |
13.87 |
220.7 |
| SVM |
52.71 |
0.4100 |
0.6501 |
37.16 |
221.6 |
| LR |
59.41 |
0.2504 |
0.5004 |
45.42 |
212.3 |
However, the LR model, with an RMSE of 59.41 and an R2 of 0.2504, shows limitations in capturing non-linear dependencies, predicting 212.3 F g−1. Table S4 (ESI†) shows the estimation of the coefficient from the LR model. This comparison highlights SVM's superior performance in accurately modeling data, while the ANN and RT models provide a reasonable balance between complexity and predictive power. LR lags in its ability to capture the intricacies of the dataset. Although the measured specific capacitance of GONs was around 110 F g−1, the ML models predicted a specific capacitance of around 220 F g−1. This significant discrepancy can be attributed to our model's selection of predictor variables. Due to their direct influence on electrochemical performance, we focused on electrolyte type, concentration, current density, and potential window. However, critical variables such as specific surface area, carbon content, pore size, and pore volume were excluded to simplify the model. The exclusion of this predictor variable has arisen due to limited research reports mentioning the values. The absence of these variables likely led to the machine learning overestimation. Incorporating additional variables into our model may help develop a more comprehensive and accurate predictive tool. This iterative process will enhance our understanding and predictive capability for electrode materials for SCs application, providing a more reliable approximation of specific capacitance based on a broader range of material properties. The current model prediction serves as an initial approximation, and we are committed to refining it for improved accuracy.
Fig. 14 presents an importance plot for understanding the influence of different predictor variables in ANN, RT, SVM, and LR. It helps us to identify the features contribution in model prediction, aiding in simplifying and interpreting ML models. By comparing the importance plot, the contribution of features decreases in the order of concentration, electrolytes, potential window, and current density. All the ML models indicated that electrolyte concentration significantly impacts the capacitive performance of the GONs compared to the other predictor variables. Incorporating other predictor variables, such as specific surface area, carbon content, pore size, and pore volume, may further improve the performance of ML models in estimating the specific capacitance.
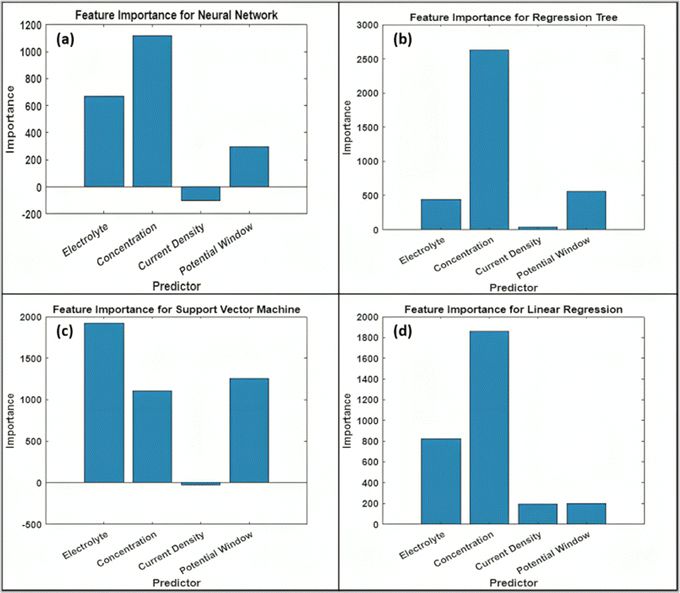 |
| | Fig. 14 Importance plot for predictor variables of (a) ANN, (b) RT, (c) SVM, and (d) LR. | |
6. Conclusion
In this work, we prepared GONs using the W/O emulsion technique from GO nanosheet as an initial precursor. HRTEM analysis reveals the spherical-shaped GO nanoparticles with an average particle size of around 21 nm. The GO and GONs samples display similar structural and surface characteristics, which confirms that the GONs preserve the GO structure even after the W/O emulsion process. The electrochemical studies show that GONs show significantly higher specific capacitance than GO, which is attributed to the surface Faradaic redox reaction by the oxygenous functional groups at the electrode surface. In addition, a data-driven ML approach has been used to analyze models to predict the performance of GONs as electrode materials for SCs. The prediction of a supercapacitor as a function of input variables: electrolyte type, concentration of electrolyte, current density, and potential window. The accuracy of ML models follows the ranking of SVM > RT > NN > LR based on the RMSE values of 52.71, 55.98, 59.02, and 59.41, respectively. Despite the deviation of predicted specific capacitance (∼220 F g−1) from actual capacitance (∼110 F g−1). The optimized ML models suggest that electrolyte concentration significantly contributes to determining the specific capacitance of GONs, followed by electrolyte type, potential window, and then finally current density. Thus, using ML has provided a deeper understanding of the underlying role of different electrochemical features interaction, paving the way for targeted material modifications to achieve superior energy storage capabilities.
Author contributions
G. K. Yogesh: conceptualization, methodology, investigation, formal analysis, writing – original draft, writing – review & editing. D. Nandi: conceptualization, methodology, investigation, formal analysis, writing – original draft, writing – review & editing. R. Yeetsorn: conceptualization, methodology, investigation, writing – original draft. C. Devi, R. P. Singh: investigation, formal analysis, writing – review & editing. A. Vasistha, M. Kumar: formal analysis. W. Wanchan: formal analysis. P. Koinkar, K. Yadav: conceptualization, methodology, writing – original draft, writing – review & editing.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†
Conflicts of interest
The authors declare that they have no known financial or interpersonal conflicts that would seem to impact the research presented in this study.
Acknowledgements
D. Nandi acknowledges support from the Horizon Europe Marie Skłodowska-Curie Action project MESTUM (No. 101108310).
References
-
T. Radsar, H. Khalesi and V. Ghods, Graphene properties and applications in nanoelectronic, Springer, US, 2021 DOI:10.1007/s11082-021-02839-6.
- V. S. Prudkovskiy, Y. Hu, K. Zhang, Y. Hu, P. Ji, G. Nunn, J. Zhao, C. Shi, A. Tejeda, D. Wander, A. De Cecco, C. B. Winkelmann, Y. Jiang, T. Zhao, K. Wakabayashi, Z. Jiang, L. Ma, C. Berger and W. A. de Heer, An epitaxial graphene platform for zero-energy edge state nanoelectronics, Nat. Commun., 2022, 13, 7814–7824, DOI:10.1038/s41467-022-34369-4.
- R. Yeetsorn, G. K. Yogesh, W. Wanchan, P. Koinkar and K. Yadav, Molybdenum-based Nanocatalysts for CO Oxidation Reactions in Direct Alcohol Fuel Cells: A Critical Review, ChemCatChem, 2023, 15, 1–23, DOI:10.1002/cctc.202301040.
- S. Nagappan, M. Duraivel, S. H. Han, M. Yusuf, M. Mahadadalkar, K. M. Park, A. Dhakshinamoorthy, K. Prabakar, S. Park, C. S. Ha, J. M. Lee and K. H. Park, Electrocatalytic Oxygen Reduction Reaction of Graphene Oxide and Metal-Free Graphene in an Alkaline Medium, Nanomaterials, 2023, 13, 1315–1334, DOI:10.3390/nano13081315.
- G. K. Yogesh, R. Yeetsorn, W. Wanchan, M. Fowler, K. Yadav and P. Koinkar, Molybdenum – Based Electrocatalysts for Direct Alcohol Fuel Cells: A Critical Review, J. Electrochem. Sci. Technol., 2024, 15, 67–95, DOI:10.33961/jecst.2023.00528.
- G. K. Yogesh, E. P. Shuaib, P. Roopmani, M. B. Gumpu, U. M. Krishnan and D. Sastikumar, Synthesis, characterization and bioimaging application of laser-ablated graphene-oxide nanoparticles (nGOs), Diamond Relat. Mater., 2020, 104, 107733–107746, DOI:10.1016/j.diamond.2020.107733.
- G. K. Yogesh, M. B. Gumpu, E. P. Shuaib and D. Sastikumar, Laser-induced transformation of graphene into graphene oxide nanospheres (GONs), Mater. Res. Bull., 2019, 115, 227–234, DOI:10.1016/j.materresbull.2019.03.030.
- G. K. Yogesh, S. Shukla, D. Sastikumar and P. Koinkar, Progress in pulsed laser ablation in liquid (PLAL) technique for the synthesis of carbon nanomaterials: a review, Appl. Phys. A: Mater. Sci. Process., 2021, 127, 810–850, DOI:10.1007/s00339-021-04951-6.
- A. G. Olabi, M. A. Abdelkareem, T. Wilberforce and E. T. Sayed, Application of graphene in energy storage device – A review, Renewable Sustainable Energy Rev., 2021, 135, 110026, DOI:10.1016/j.rser.2020.110026.
- L. Zhu, H. J. Peng, J. Liang, J. Q. Huang, C. M. Chen, X. Guo, W. Zhu, P. Li and Q. Zhang, Interconnected carbon nanotube/graphene nanosphere scaffolds as free-standing paper electrode for high-rate and ultra-stable lithium-sulfur batteries, Nano Energy, 2015, 11, 746–755, DOI:10.1016/j.nanoen.2014.11.062.
- P. Guo, H. Song and X. Chen, Hollow graphene oxide spheres self-assembled by W/O emulsion, J. Mater. Chem., 2010, 20, 4867–4874, 10.1039/b927302f.
- M. T. H. Aunkor, I. M. Mahbubul, R. Saidur and H. S. C. Metselaar, The green reduction of graphene oxide, RSC Adv., 2016, 6, 27807–27825, 10.1039/c6ra03189g.
- L. Shahhriary and A. A. Athawale, Graphene Oxide Synthesized by using Modified Hummers Approach, Int. J. Renew. Energy Environ. Eng., 2014, 02, 58–63, DOI:10.1016/j.aca.2014.02.025.
- A. W. Kuziel, K. Z. Milowska, P. L. Chau, S. Boncel, K. K. Koziol, N. Yahya and M. C. Payne, The True Amphipathic Nature of Graphene Flakes: A Versatile 2D Stabilizer, Adv. Mater., 2020, 32, 1–7, DOI:10.1002/adma.202000608.
- T. D. Gamot, A. R. Bhattacharyya, T. Sridhar, F. Beach, R. F. Tabor and M. Majumder, Synthesis and Stability of Water-in-Oil Emulsion Using Partially Reduced Graphene Oxide as a Tailored Surfactant, Langmuir, 2017, 33, 10311–10321, DOI:10.1021/acs.langmuir.7b02320.
- W. Fan, Y. Y. Xia, W. W. Tjiu, P. K. Pallathadka, C. He and T. Liu, Nitrogen-doped graphene hollow nanospheres as novel electrode materials for supercapacitor applications, J. Power Sources, 2013, 243, 973–981, DOI:10.1016/j.jpowsour.2013.05.184.
- B. G. Kim, D. H. Nam, S. M. Jeong, M. H. Lee, W. S. Seo and S. M. Choi, One-step growth of multilayer-graphene hollow nanospheres via the self-elimination of SiC nuclei templates, Sci. Rep., 2017, 7, 1–8, DOI:10.1038/s41598-017-13143-3.
- X. Chen, X. Xu, Z. Yang, Z. Liu, L. Zhang, X. Xu, Y. Chen and S. Huang, Sulfur-doped porous reduced graphene oxide hollow nanospheres framework as metal-free electrocatalysts for oxygen reduction reaction and supercapacitor electrode materials, Nanoscale, 2014, 6, 13740–13747, 10.1039/c0xx00000x.
- Z. Yan, Z. Gao, Z. Zhang, C. Dai, W. Wei and P. K. Shen, Graphene Nanosphere as Advanced Electrode Material to Promote High Performance Symmetrical Supercapacitor, Small, 2021, 17, 1–12, DOI:10.1002/smll.202007915.
- J. S. Lee, S. I. Kim, J. C. Yoon and J. H. Jang, Chemical vapor deposition of mesoporous graphene nanoballs for supercapacitor, ACS Nano, 2013, 7, 6047–6055, DOI:10.1021/nn401850z.
- J. Zheng, H. Liu, B. Wu, Y. Guo, T. Wu, G. Yu, Y. Liu and D. Zhu, Production of graphene nanospheres by annealing of graphene oxide in solution, Nano Res., 2011, 4, 705–711, DOI:10.1007/s12274-011-0126-9.
- A. S. Lemine, M. M. Zagho, T. M. Altahtamouni and N. Bensalah, Graphene a promising electrode material for supercapacitors—A review, Int. J. Energy Res., 2018, 42, 4284–4300, DOI:10.1002/er.4170.
- Z. Li, S. Gadipelli, Y. Yang and Z. Guo, Design of 3D Graphene-Oxide Spheres and Their Derived Hierarchical Porous Structures for High Performance Supercapacitors, Small, 2017, 13, 1702474–1702482, DOI:10.1002/smll.201702474.
- Y. Wang, Z. Shi, Y. Huang, Y. Ma, C. Wang, M. Chen and Y. Chen, Supercapacitor Devices Based on Graphene Materials, J. Phys. Chem. C, 2009, 113, 13103–13107 CrossRef CAS.
- Q. Ke and J. Wang, Graphene-based materials for supercapacitor electrodes – A review, J. Mater., 2016, 2, 37–54, DOI:10.1016/j.jmat.2016.01.001.
- X. He, H. Zhang, H. Zhang, X. Li, N. Xiao and J. Qiu, Direct synthesis of 3D hollow porous graphene balls from coal tar pitch for high performance supercapacitors, J. Mater. Chem. A, 2014, 2, 19633–19640, 10.1039/c4ta03323j.
- X. Yuan, L. Xu, J. Zhang, Y. Dai, J. Meng, X. Wang, C. Bu, C. Liu and H. Xie, Template Synthesis of Nitrogen Self-Doped Hierarchical Porous Carbon with Supermicropores and Mesopores for Electrical Double-Layer Capacitors, BioResources, 2023, 18, 87–99 CAS.
- M. Nazarian-Samani, H. K. Kim, S. H. Park, H. C. Youn, D. Mhamane, S. W. Lee, M. S. Kim, J. H. Jeong, S. Haghighat-Shishavan, K. C. Roh, S. F. Kashani-Bozorg and K. B. Kim, Three-dimensional graphene-based spheres and crumpled balls: Micro- and nano-structures, synthesis strategies, properties
and applications, RSC Adv., 2016, 6, 50941–50967, 10.1039/c6ra07485e.
- D. Arvind and G. Hegde, Activated carbon nanospheres derived from bio-waste materials for supercapacitor applications – a review, RSC Adv., 2015, 5, 88339–88352, 10.1039/c5ra19392c.
- V. Sawant, R. Deshmukh and C. Awati, Machine learning techniques for prediction of capacitance and remaining useful life of supercapacitors: A comprehensive review, J. Energy Chem., 2023, 77, 438–451, DOI:10.1016/j.jechem.2022.11.012.
- S. Ghosh, G. R. Rao and T. Thomas, Machine learning-based prediction of supercapacitor performance for a novel electrode material: Cerium oxynitride, Energy Storage Mater., 2021, 40, 426–438, DOI:10.1016/j.ensm.2021.05.024.
- S. Jha, S. Bandyopadhyay, S. Mehta, M. Yen, T. Chagouri, E. Palmer and H. Liang, Data-Driven Predictive Electrochemical Behavior of Lignin-Based Supercapacitors via Machine Learning, Energy Fuels, 2022, 36, 1052–1062, DOI:10.1021/acs.energyfuels.1c03270.
- P. E. Lokhande, Cyclic voltammetry behavior modeling of fabricated nanostructured Ni(OH)2 electrode using artificial neural network for supercapacitor application, J. Mech. Eng. Sci., 2020, 234, 2563, DOI:10.1177/0954406220907615.
- S. Mishra, R. Srivastava, A. Muhammad, A. Amit, E. Chiavazzo, M. Fasano and P. Asinari, The impact of physicochemical features of carbon electrodes on the capacitive performance of supercapacitors: a machine learning approach, Sci. Rep., 2023, 13, 1–16, DOI:10.1038/s41598-023-33524-1.
- T. Gao and W. Lu, Machine learning toward advanced energy storage devices and systems, iScience, 2021, 24, 101936, DOI:10.1016/j.isci.2020.101936.
- C. V. Prasshanth, A. K. Lakshminarayanan, B. Ramasubramanian and S. Ramakrishna, Progress of machine learning in materials design for Li-Ion battery, Next Mater., 2024, 2, 100145, DOI:10.1016/j.nxmate.2024.100145.
- M. Faraji Niri, K. Aslansefat, S. Haghi, M. Hashemian, R. Daub and J. Marco, A Review of the Applications of Explainable Machine Learning for Lithium–Ion Batteries: From Production to State and Performance Estimation, Energies, 2023, 16, 6360–6397, DOI:10.3390/en16176360.
- S. Müller, C. Sauter, R. Shunmugasundaram, N. Wenzler, V. De Andrade, F. De Carlo, E. Konukoglu and V. Wood, Deep learning-based segmentation of lithium-ion battery microstructures enhanced by artificially generated electrodes, Nat. Commun., 2021, 12, 1–12, DOI:10.1038/s41467-021-26480-9.
- G. Wang, T. Fearn, T. Wang and K. L. Choy, Machine-Learning Approach for Predicting the Discharging Capacities of Doped Lithium Nickel-Cobalt-Manganese Cathode Materials in Li-Ion Batteries, ACS Cent. Sci., 2021, 7, 1551–1560, DOI:10.1021/acscentsci.1c00611.
- K. Deng, Y. Liu, D. Hai, H. Peng, L. Löwenstein, S. Pischinger and K. Hameyer, Deep reinforcement learning based energy management strategy of fuel cell hybrid railway vehicles considering fuel cell aging, Energy Convers. Manage., 2022, 251, 115030–115041, DOI:10.1016/j.enconman.2021.115030.
- R. Ma, T. Yang, E. Breaz, Z. Li, P. Briois and F. Gao, Data-driven proton exchange membrane fuel cell degradation predication through deep learning method, Appl. Energy, 2018, 231, 102–115, DOI:10.1016/j.apenergy.2018.09.111.
- A. Legala, J. Zhao and X. Li, Machine learning modeling for proton exchange membrane fuel cell performance, Energy AI, 2022, 10, 100183, DOI:10.1016/j.egyai.2022.100183.
- H. Chen, W. Shan, H. Liao, Y. He, T. Zhang, P. Pei, C. Deng and J. Chen, Online voltage consistency prediction of proton exchange membrane fuel cells using a machine learning method, Int. J. Hydrogen Energy, 2021, 46, 34399–34412, DOI:10.1016/j.ijhydene.2021.08.003.
- H. Su, S. Lin, S. Deng, C. Lian, Y. Shang and H. Liu, Predicting the capacitance of carbon-based electric double layer capacitors by machine learning, Nanoscale Adv., 2019, 1, 2162–2166, 10.1039/c9na00105k.
-
S. Zhu, J. Li, L. Ma, C. He, E. Liu, F. He, C. Shi and N. Zhao, Machine Learning Enabled Capacitance Prediction for Carbon-Based Supercapacitors, ChemRxiv, 2018, preprint, 1–8 DOI:10.26434/chemrxiv.6222221.v2.
- M. Gheytanzadeh, A. Baghban, S. Habibzadeh, A. Mohaddespour and O. Abida, Insights into the estimation of capacitance for carbon-based supercapacitors, RSC Adv., 2021, 11, 5479–5486, 10.1039/d0ra09837j.
- R. Thangappan, M. Arivanandhan, S. Kalaiselvam, R. Jayavel and Y. Hayakawa, Molybdenum Oxide/Graphene Nanocomposite Electrodes with Enhanced Capacitive Performance for Supercapacitor Applications, J. Inorg. Organomet. Polym. Mater., 2018, 28, 50–62, DOI:10.1007/s10904-017-0699-1.
- P. Xie, X. Ge, B. Fang, Z. Li, Y. Liang and C. Yang, Pickering emulsion polymerization of graphene oxide-stabilized styrene, Colloid Polym. Sci., 2013, 291, 1631–1639, DOI:10.1007/s00396-013-2897-x.
- Y. He, F. Wu, X. Sun, R. Li, Y. Guo, C. Li, L. Zhang, F. Xing, W. Wang and J. Gao, Factors that affect pickering emulsions stabilized by graphene oxide, ACS Appl. Mater. Interfaces, 2013, 5, 4843–4855, DOI:10.1021/am400582n.
- D. Nandi, A. Jayakumar, S. Radoor, R. Srisuk and S. Siengchin, High-rate electrochemical performance and structure elucidation of hydrothermally synthesized nickel zincate nanorods, J. Solid State Electrochem., 2022, 27(1), 195–206, DOI:10.1007/S10008-022-05318-4.
- Q. Chen, C. Zhang, F. Xue, Y. Zhou, W. Li, Y. Wang, W. Tu, Z. Zou, X. Wang and M. Xiao, Enhanced hot-carrier luminescence in multilayer reduced graphene oxide nanospheres, Sci. Rep., 2013, 3, 2315–2321, DOI:10.1038/srep02315.
- D. Nandi, S. Radoor, A. Jayakumar, C. Devi and S. Siengchin, Hexagonal nanoplatelets of Ni–Mn oxide implanted reduced graphene oxide for high response in humidity sensing, Chem. Pap., 2024, 78, 3099–3110, DOI:10.1007/s11696-023-03296-z.
- C. Devi, J. Gellanki, H. Pettersson and S. Kumar, High sodium ionic conductivity in PEO/PVP solid polymer electrolytes with InAs nanowire fillers, Sci. Rep., 2021, 11, 1–8, DOI:10.1038/s41598-021-99663-5.
- R. P. Singh, P. S. Alegaonkar, C. Devi, G. K. Yogesh and K. Yadav, Selenium-enriched MoSe2 as an effective electrode material for supercapacitors and a photocatalyst for dye degradation, Mater. Today Commun., 2024, 40, 109671, DOI:10.1016/j.mtcomm.2024.109671.
- A. Ganguly, S. Sharma, P. Papakonstantinou and J. Hamilton, Probing the Thermal Deoxygenation of Graphene Oxide Using, J. Phys. Chem., 2011, 115, 17009–17019 CAS.
- V. Giegold, L. Lange, R. Ciesielski and A. Hartschuh, Non-linear Raman scattering intensities in graphene, Nanoscale, 2020, 12, 5612–5617, 10.1039/c9nr10654e.
- J. Shen, M. Shi, B. Yan, H. Ma, N. Li and M. Ye, One-pot hydrothermal synthesis of Ag-reduced graphene oxide composite with ionic liquid, J. Mater. Chem., 2011, 21, 7795–7801, 10.1039/c1jm10671f.
- I. Mushtaq, S. Naseem, W. Khan and S. Husain, Investigation of optical and electrical properties of graphene oxide/TiO2 nanocomposite, AIP Conf. Proc., 2020, 2265, 030167–0304670, DOI:10.1063/5.0016746.
- G. K. Yogesh, E. P. Shuaib, P. Roopmani, M. B. Gumpu, U. M. Krishnan and D. Sastikumar, Fluorescent carbon nanoparticles from laser-ablated Bougainvillea alba flower extract for bioimaging applications, Appl. Phys. A: Mater. Sci. Process., 2019, 125, 379–389, DOI:10.1007/s00339-019-2673-y.
- G. K. Yogesh, E. P. Shuaib, A. Kalai Priya, P. Rohini, S. V. Anandhan, U. M. Krishnan, V. Kalyanavalli, S. Shukla and D. Sastikumar, Synthesis of water-soluble fluorescent carbon nanoparticles (CNPs) from nanosecond pulsed laser ablation in ethanol, Opt. Laser Technol., 2021, 135, 106717–106726, DOI:10.1016/j.optlastec.2020.106717.
- M. Atawneh, S. Makharza, S. Zahran, K. Titi, F. Takrori and S. Hampel, The cross-talk between lateral sheet dimensions of pristine graphene oxide nanoparticles and Ni2+ adsorption, RSC Adv., 2021, 11, 11388–11397, 10.1039/d1ra00400j.
- H. Zhang, C. Peng, J. Yang, M. Lv, R. Liu, D. He, C. Fan and Q. Huang, Uniform ultrasmall graphene oxide nanosheets with low cytotoxicity and high cellular uptake, ACS Appl. Mater. Interfaces, 2013, 5, 1761–1767, DOI:10.1021/am303005j.
- F. Absalan, M. Seyed Sadjadi, N. Farhadyar and M. Hossaini Sadr, Synthesis and characterization of mesoporous HA/GO nanocomposite in the presence of chitosan as a potential candidate for drug delivery, Chem. Pap., 2021, 75, 4565–4578, DOI:10.1007/s11696-021-01686-9.
- Y. Gong, D. Li, Q. Fu and C. Pan, Influence of graphene microstructures on electrochemical performance for supercapacitors, Prog. Nat. Sci. Mater. Int., 2015, 25, 379–385, DOI:10.1016/j.pnsc.2015.10.004.
- C. Shen, Y. Xie, B. Zhu, M. Sanghadasa, Y. Tang and L. Lin, Wearable woven supercapacitor fabrics with high energy density and load-bearing capability, Sci. Rep., 2017, 7, 1–9, DOI:10.1038/s41598-017-14854-3.
- Z. Ren, J. Li, Y. Ren, S. Wang, Y. Qiu and J. Yu, Large-scale synthesis of hybrid metal oxides through metal redox mechanism for high-performance pseudocapacitors, Sci. Rep., 2016, 6, 1–10, DOI:10.1038/srep20021.
- X. Liang, Y. Chen, Z. Jiao, M. Demir, M. Du and J. Han, MXene-transition metal sulfide composite electrodes for supercapacitors: Synthesis and electrochemical characterization, J. Energy Storage, 2024, 88, 111634, DOI:10.1016/j.est.2024.111634.
- J. He, Y. Zhou, S. Wu, L. Jin, J. Cao, M. Demir and P. Ma, Cr-Substituted SrCoO3−δ Perovskite with Abundant Oxygen Vacancies for High-Energy and Durable Low-Temperature Antifreezing Flexible Supercapacitor, Inorg. Chem., 2024, 63, 13755–13765, DOI:10.1021/acs.inorgchem.4c02115.
- G. Liu, L. Liu, G. Li, S. Wu, J. He, Y. Zhou, M. Demir and P. Ma, Temperature-Dependent Electrochemical Performance of Ta-Substituted SrCoO3 Perovskite for Supercapacitors, Chem. – Eur. J., 2024, 30, 1–10, DOI:10.1002/chem.202303267.
- J. Cao, Y. Wang, P. Xiao, Y. Chen, Y. Zhou, J. H. Ouyang and D. Jia, Hollow graphene spheres self-assembled from graphene oxide sheets by a one-step hydrothermal process, Carbon, 2013, 56, 389–391, DOI:10.1016/j.carbon.2012.12.075.
- Y. Dai, H. Jiang, Y. Hu, Y. Fu and C. Li, Controlled synthesis of ultrathin hollow mesoporous carbon nanospheres for supercapacitor applications, Ind. Eng. Chem. Res., 2014, 53, 3125–3130, DOI:10.1021/ie403950t.
- A. Chen, Y. Wang, Y. Yu, H. Sun, Y. Li, K. Xia and S. Li, Nitrogen-doped hollow carbon spheres for supercapacitors, J. Alloys Compd., 2016, 688, 878–884, DOI:10.1016/j.jallcom.2016.07.163.
- J. Han, G. Xu, B. Ding, J. Pan, H. Dou and D. R. MacFarlane, Porous nitrogen-doped hollow carbon spheres derived from polyaniline for high performance supercapacitors, J. Mater. Chem. A, 2014, 2, 5352–5357, 10.1039/c3ta15271e.
- Q. Li, R. Jiang, Y. Dou, Z. Wu, T. Huang, D. Feng, J. Yang, A. Yu and D. Zhao, Synthesis of mesoporous carbon spheres with a hierarchical pore structure for the electrochemical double-layer capacitor, Carbon, 2011, 49, 1248–1257, DOI:10.1016/j.carbon.2010.11.043.
- C. Liu, J. Wang, J. Li, M. Zeng, R. Luo, J. Shen, X. Sun, W. Han and L. Wang, Synthesis of N-Doped Hollow-Structured Mesoporous Carbon Nanospheres for High-Performance Supercapacitors, ACS Appl. Mater. Interfaces, 2016, 8, 7194–7204, DOI:10.1021/acsami.6b02404.
- D. He, Y. Gao, Z. Wang, Y. Yao, L. Wu, J. Zhang, Z. H. Huang and M. X. Wang, One-step green fabrication of hierarchically porous hollow carbon nanospheres (HCNSs) from raw biomass: Formation mechanisms and supercapacitor applications, J. Colloid Interface Sci., 2021, 581, 238–250, DOI:10.1016/j.jcis.2020.07.118.
- K. Xia, G. Wang, H. Zhang, Y. Yu, L. Liu and A. Chen, Synthesis and characterization of nitrogen-doped graphene hollow spheres as electrode material for supercapacitors, J. Nanopart. Res., 2017, 19, 254–264, DOI:10.1007/s11051-017-3954-z.
- J. S. Lee, S. I. Kim, J. C. Yoon and J. H. Jang, Chemical vapor deposition of mesoporous graphene nanoballs for supercapacitor, ACS Nano, 2013, 7, 6047–6055, DOI:10.1021/nn401850z.
- Z. Shen, J. Du, Y. Mo and A. Chen, Nanocomposites of reduced graphene oxide modified with mesoporous carbon layers anchored by hollow carbon spheres for energy storage, Carbon, 2021, 173, 22–30, DOI:10.1016/j.carbon.2020.10.087.a.
- S. D. Perera, R. G. Mariano, N. Nijem, Y. Chabal, J. P. Ferraris and K. J. Balkus, Alkaline deoxygenated graphene oxide for supercapacitor applications: An effective green alternative for chemically reduced graphene, J. Power Sources, 2012, 215, 1–10, DOI:10.1016/j.jpowsour.2012.04.059.
- E. Y. L. Teo, H. N. Lim, R. Jose and K. F. Chong, Aminopyrene functionalized reduced graphene oxide as a supercapacitor electrode, RSC Adv., 2015, 5, 38111–38116, 10.1039/c5ra02578h.
- D. Yang and C. Bock, Laser reduced graphene for supercapacitor applications, J. Power Sources, 2017, 337, 73–81, DOI:10.1016/j.jpowsour.2016.10.108.
- D. Peyrow Hedayati, G. Singh, M. Kucher, T. D. Keene and R. Böhm, Physicochemical Modeling of Electrochemical Impedance in Solid-State Supercapacitors, Materials, 2023, 16, 1232–1252, DOI:10.3390/ma16031232.
- I. Shaheen, K. S. Ahmad, C. Zequine, R. K. Gupta, A. G. Thomas and M. A. Malik, Electrochemical energy storage by nanosized MoO3/PdO material: Investigation of its structural, optical and electrochemical properties for supercapacitor, J. Energy Storage, 2021, 36, 102447, DOI:10.1016/j.est.2021.102447.
- N. H. Basri, M. Deraman, M. Suleman, N. Syahirah and M. Nor, Energy and Power of Supercapacitor Using Carbon Electrode Deposited with Nanoparticles Nickel Oxide, Int. J. Electrochem. Sci., 2016, 11, 95–110 CrossRef CAS.
- J. Liu, J. Wang, C. Xu, H. Jiang, C. Li, L. Zhang, J. Lin and Z. X. Shen, Advanced Energy Storage Devices: Basic Principles, Analytical Methods, and Rational Materials Design, Adv. Sci., 2018, 5, 1700322–1700340, DOI:10.1002/advs.201700322.
- J. Lu, L. Pu, W. Wang and Y. Dai, Construction of hierarchical cobalt-molybdenum selenide hollow nanospheres architectures for high performance battery-supercapacitor hybrid devices, J. Colloid Interface Sci., 2020, 563, 435–446, DOI:10.1016/j.jcis.2019.12.101.
- D. M. K. Vijaya Sankara and R. Kalai Selvana, Electrochemical performances of CoFe2O4 nanoparticles and rGO based asymmetric supercapacitor, RSC Adv., 2015, 5, 99959–99967 RSC.
- S. Chen, J. Zhu, X. Wu, Q. Han and X. Wang, Graphene Oxide-MnO2 Nanocomposites for Supercapacitors, ACS Nano, 2010, 4, 2822–2830, DOI:10.1021/nn901311t.
- J. Zhao, Y. Jiang, H. Fan, M. Liu, O. Zhuo, X. Wang, Q. Wu, L. Yang, Y. Ma and Z. Hu, Porous 3D Few-Layer Graphene-like Carbon for Ultrahigh-Power Supercapacitors with Well-Defined Structure–Performance Relationship, Adv. Mater., 2017, 29, 1604569–1604575, DOI:10.1002/adma.201604569.
-
S. Rai, R. Bhujel and B. P. Swain, Electrochemical Analysis of Graphene Oxide and Reduced Graphene Oxide for Super Capacitor Applications, Proc. Int. Conf. 2018 IEEE Electron Device Kolkata Conf. EDKCON 2018, (2018), pp. 489–492 DOI:10.1109/EDKCON.2018.8770433.
- W. J. Paschoalino, N. A. Payne, T. M. Pessanha, S. M. Gateman, L. T. Kubota and J. Mauzeroll, Charge Storage in Graphene Oxide: Impact of the Cation on Ion Permeability and Interfacial Capacitance, Anal. Chem., 2020, 92, 10300–10307, DOI:10.1021/acs.analchem.0c00218.
- T. Islam, M. M. Hasan, S. Sarker and A. J. S. Ahammad, Intrinsic Properties of GO/RGO Bilayer Electrodes Dictate Their Inter-/Intralayer Intractability to Modulate Their Capacitance Performance, ACS Omega, 2023, 8, 14013–14024, DOI:10.1021/acsomega.3c00573.
- P. E. Lokhande and U. S. Chavan, Cyclic voltammetry behavior modeling of fabricated nanostructured Ni(OH)2 electrode using artificial neural network for supercapacitor application, Proc. Inst. Mech. Eng., Part C, 2020, 234, 2563–2568, DOI:10.1177/0954406220907615.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Debabrata
Nandi‡
a,
Debabrata
Nandi‡
 b,
Rungsima
Yeetsorn
c,
Waritnan
Wanchan
c,
Chandni
Devi
ad,
Ravi Pratap
Singh
b,
Rungsima
Yeetsorn
c,
Waritnan
Wanchan
c,
Chandni
Devi
ad,
Ravi Pratap
Singh
 e,
Aditya
Vasistha
a,
Mukesh
Kumar
a,
Pankaj
Koinkar
e,
Aditya
Vasistha
a,
Mukesh
Kumar
a,
Pankaj
Koinkar
 *f and
Kamlesh
Yadav
*f and
Kamlesh
Yadav
 *g
*g
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.31 The RF and principal component analysis (PCA) are essential as they produced the best accurate prediction, which was verified experimentally. In addition, researchers modeled the cyclic voltammetry of a fabricated nanostructured Ni(OH)2 electrode using ANN for SC application.33 The ANN model estimated the electrode performance, showing satisfactory agreement with experimental results with a minimum error of 0.14%.
000 cycles.31 The RF and principal component analysis (PCA) are essential as they produced the best accurate prediction, which was verified experimentally. In addition, researchers modeled the cyclic voltammetry of a fabricated nanostructured Ni(OH)2 electrode using ANN for SC application.33 The ANN model estimated the electrode performance, showing satisfactory agreement with experimental results with a minimum error of 0.14%.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 with N-methyl-2-pyrrolidone as a solvent for paste formation, which was coated onto the nickel foam sheet with a covered area of 1 cm2. The electrode was dried at 70 °C for 12 h in the oven. The active materials mass loading on the Ni foam was about 3 mg cm−2. The device was assembled as a symmetric electrode for the SCs test in a 6 M KOH electrolyte solution. The specific capacitance (C) was calculated from CV and GCD curves using the following eqn (1) and (2), respectively,50
10 with N-methyl-2-pyrrolidone as a solvent for paste formation, which was coated onto the nickel foam sheet with a covered area of 1 cm2. The electrode was dried at 70 °C for 12 h in the oven. The active materials mass loading on the Ni foam was about 3 mg cm−2. The device was assembled as a symmetric electrode for the SCs test in a 6 M KOH electrolyte solution. The specific capacitance (C) was calculated from CV and GCD curves using the following eqn (1) and (2), respectively,50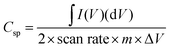
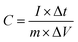
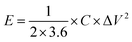
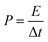

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond at the center of the Brillion zone of graphite. Lastly, a broad peak centered around 2600–2900 cm−1 is called the 2D and D + G-band, resulting from the breathing-like modes of the D-band of carbon rings triggered by the defects via the double resonance process.55 The relative intensity of the 2D band concerning the G-band provides information on the number of graphene layers in GO and GONs. An observable decrease in the I2D/IG ratio from 0.050 to 0.039 suggests that an increase in the number of layers of the graphene sheet in GONs compared to the GO. The intensity ratio of D-band to G-band (ID/IG) measures the size of sp3/sp2 domains, indicating the presence of defects.56 The ID/IG ratio remains the same, indicating that the GO structure remains intact after the emulsion process. However, the increased intensity of the D-band and G-bands in GONs compared to GO can be attributed to the formation of new graphitic or sp2 domains.21,55,57 The overtone of the D-band refers to the 2D-band in GONs, which appears at 2582 cm−1 and is blue-shifted by 89 cm−1 compared to the GO nanosheet. This difference is mainly due to the increased π–π staking in the GONs sample, as confirmed by the HRTEM images. In addition, a shift of the G-band to a lower frequency for GONs compared to GO can be attributed to various factors, such as the presence of functional groups or defects on the surface of GONs. Studies have shown that the reduction in the primary band edge of GO leads to a decrease in the bandgap. The alterations in the electronic properties of GONs due to oxidation levels contribute to the observed G-band shift to lower frequencies in GONs nanoparticles compared to pristine graphite and GO.58
C bond at the center of the Brillion zone of graphite. Lastly, a broad peak centered around 2600–2900 cm−1 is called the 2D and D + G-band, resulting from the breathing-like modes of the D-band of carbon rings triggered by the defects via the double resonance process.55 The relative intensity of the 2D band concerning the G-band provides information on the number of graphene layers in GO and GONs. An observable decrease in the I2D/IG ratio from 0.050 to 0.039 suggests that an increase in the number of layers of the graphene sheet in GONs compared to the GO. The intensity ratio of D-band to G-band (ID/IG) measures the size of sp3/sp2 domains, indicating the presence of defects.56 The ID/IG ratio remains the same, indicating that the GO structure remains intact after the emulsion process. However, the increased intensity of the D-band and G-bands in GONs compared to GO can be attributed to the formation of new graphitic or sp2 domains.21,55,57 The overtone of the D-band refers to the 2D-band in GONs, which appears at 2582 cm−1 and is blue-shifted by 89 cm−1 compared to the GO nanosheet. This difference is mainly due to the increased π–π staking in the GONs sample, as confirmed by the HRTEM images. In addition, a shift of the G-band to a lower frequency for GONs compared to GO can be attributed to various factors, such as the presence of functional groups or defects on the surface of GONs. Studies have shown that the reduction in the primary band edge of GO leads to a decrease in the bandgap. The alterations in the electronic properties of GONs due to oxidation levels contribute to the observed G-band shift to lower frequencies in GONs nanoparticles compared to pristine graphite and GO.58![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) groups appear at 1049 and 1720 cm−1.57 In contrast, the hydroxyl groups characterized by C–OH were identified at around 1380 cm−1, respectively. The absorption band at 1616 cm−1 is associated with the carbon skeleton structure (C
O) groups appear at 1049 and 1720 cm−1.57 In contrast, the hydroxyl groups characterized by C–OH were identified at around 1380 cm−1, respectively. The absorption band at 1616 cm−1 is associated with the carbon skeleton structure (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), primarily regarded as graphitic carbon.12 The broad absorption band ranges from 2800–3800 cm−1, signifying the stretching vibration of hydroxyl functional groups.23,57 These functional groups are primarily covalently bonded to the carbon skeleton structure or interspersed within the graphene layers. This observation demonstrated the amphiphilic nature comparable to surfactants in water-in-oil (W/O) emulsion systems.11 The strategic inculcation of acidic/hydroxyl groups at the edge sites or basal plane graphene sheets significantly improves the dispersibility of GONs in the ammonia solution, which is an efficient dispersion agent.11
C), primarily regarded as graphitic carbon.12 The broad absorption band ranges from 2800–3800 cm−1, signifying the stretching vibration of hydroxyl functional groups.23,57 These functional groups are primarily covalently bonded to the carbon skeleton structure or interspersed within the graphene layers. This observation demonstrated the amphiphilic nature comparable to surfactants in water-in-oil (W/O) emulsion systems.11 The strategic inculcation of acidic/hydroxyl groups at the edge sites or basal plane graphene sheets significantly improves the dispersibility of GONs in the ammonia solution, which is an efficient dispersion agent.11

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species, respectively.57,60 The main peak at 286.8 eV is attributed to C–OH/C–O–C functional groups, consistent with the FTIR results. The epoxide group (C–O–C) in the structural model of graphene oxide has a binding energy comparable to that of C–OH.11 The presence of abundant C–O–C groups on the surface of the basal plane in contrast to the edges of the graphene sheet of GO and GONs is confirmed by a notable difference in the intensity of the C–O–C peak compared to C
O species, respectively.57,60 The main peak at 286.8 eV is attributed to C–OH/C–O–C functional groups, consistent with the FTIR results. The epoxide group (C–O–C) in the structural model of graphene oxide has a binding energy comparable to that of C–OH.11 The presence of abundant C–O–C groups on the surface of the basal plane in contrast to the edges of the graphene sheet of GO and GONs is confirmed by a notable difference in the intensity of the C–O–C peak compared to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. The reduction in the epoxide groups from the surface of the basal plane of GONs is shown by a notable decrease in the strength of the C–O–C peak.11,59
O. The reduction in the epoxide groups from the surface of the basal plane of GONs is shown by a notable decrease in the strength of the C–O–C peak.11,59![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O
O

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000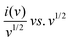 .
.
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C–OH ↔ C–O + H+ + e−
C–OH ↔ C–O + H+ + e−![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C–O + e− ↔
C–O + e− ↔ ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C–O−
C–O−
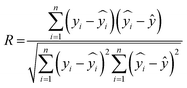
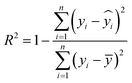
 is the actual value, and ȳ is the mean of n actual values. A value equal to 1 represents the ideal fitted regression line, and a value equal to 0 shows that the regression model explains none of the data.
is the actual value, and ȳ is the mean of n actual values. A value equal to 1 represents the ideal fitted regression line, and a value equal to 0 shows that the regression model explains none of the data.