A Raman spectroscopy algorithm based on convolutional neural networks and multilayer perceptrons: qualitative and quantitative analyses of chemical warfare agent simulants

Abstract

Rapid and reliable detection of chemical warfare agents (CWAs) is essential for military defense and counter-terrorism operations. Although Raman spectroscopy provides a non-destructive method for on-site detection, existing methods show difficulty in coping with complex spectral overlap and concentration changes when analyzing mixtures containing trace components and highly complex mixtures. Based on the idea of convolutional neural networks and multi-layer perceptrons, this study proposes a qualitative and quantitative analysis algorithm of Raman spectroscopy based on deep learning (RS-MLP). The reference feature library is built from pure substance spectral features, while multi-head attention adaptively captures mixture weights. The MLP-Mixer then performs hierarchical feature matching for qualitative identification and quantitative analysis. The recognition rate of spectral data for the four types of combinations used for validation reached 100%, with an average root mean square error (RMSE) of less than 0.473% for the concentration prediction of three components. Furthermore, the model exhibited robust performance even under conditions of highly overlapping spectra. At the same time, the interpretability of the model is also enhanced. The model has excellent accuracy and robustness in component identification and concentration identification in complex mixtures and provides a practical solution for rapid and non-contact detection of persistent chemicals in complex environments.

---

1 Introduction

Chemical warfare agents (CWAs) are a class of highly toxic chemicals that rapidly incapacitate or kill enemy personnel in a short period. In addition to being highly toxic and acting quickly, another important characteristic is their persistent effects, which are why they are often used in military conflicts and terrorist attacks.^1,2 Chemical warfare agent simulants are often used as substitutes in the detection technology research and equipment evaluation of CWAs due to their similar molecular structure to chemical warfare agents and their non-toxic or low-toxicity properties. For example, the simulant of the nerve agent sarin (GB) is dimethyl methylphosphonate (DMMP),^3,4 the simulant of VX (Viex) is triethyl phosphate (TEP),⁵ and the simulant of the erosive agent mustard gas (HD) is 2-chloroethyl ethyl sulfide (2-CEES).^6,7 Persistent chemical agents not only cause casualties but also result in long-term contamination of the ground, reducing military combat effectiveness and operational efficiency and hindering military operations.^8,9 Therefore, whether in response to chemical warfare or chemical terrorist attacks, it is urgent to develop rapid, non-contact, and accurate on-site detection methods for persistent chemical agents contaminated on the soil surface, which provides accurate and reliable information for command decision-making and minimizes casualties while reducing operational risks.^10–13

Raman spectroscopy is a spectroscopic technique that is used to analyze molecular structures by examining their rotational and vibrational modes through non-elastic energy exchange.^14,15 The technology is straightforward to operate, has high sensitivity, and does not require sample pretreatment or preparation of experimental reagents, meeting the urgent needs for chemical defense, counter-terrorism, and emergency monitoring tasks for sudden accidents.^16–18 As a non-destructive analytical technique, Raman spectroscopy can quickly characterize molecular structures and is widely used in chemical analysis, biological detection, and materials science.¹⁹ Although each substance displays unique Raman spectral features that theoretically allow the identification and quantification of components in mixtures, in practical applications, especially in the application of detecting substances at very low concentrations, the sensitivity of Raman spectroscopy is very poor and susceptible to interference by environmental factors. The complexity of the interactions and reactions of the substances in the mixtures will further complicate the identification of the Raman spectral features, such as complex spectral overlap, non-linear combination of pure substance spectra, and unavoidable noise interferences, making Raman spectroscopy a great challenge.²⁰

In the past, traditional chemometric methods, such as partial least squares regression (PLSR), partial least squares discriminant analysis (PLS-DA), and spectral peak matching algorithms, have typically been used to analyze Raman spectra of mixtures.^21,22 These methods usually require preprocessing steps, including denoising (such as SG smoothing or wavelet transform), baseline correction, and normalization, to mitigate the effects of instrument noise and environmental interference on the Raman spectra. After preprocessing, the Raman spectra are analyzed. When using the PLSR method, it first divides the spectral subintervals through slope comparison and then combines the LMF algorithm to extract peak parameters. PLSR then extracts the principal components (LVs) that maximize covariance, and cross-validation is used to determine the optimal number of components. Finally, an overdetermined equation is constructed using Beer's law, which allows for the qualitative identification of components in the mixture. This method demonstrates relatively high accuracy when applied to mixtures with fewer spectral peaks. However, as the number of spectral peaks and the diversity of components in the mixture increase, its effectiveness significantly diminishes.^23,24

The emergence of machine learning has brought revolutionary advancements to spectral analysis. Unlike traditional chemometric methods, machine learning can automatically extract complex features and handle nonlinear relationships, allowing for more accurate identification of spectral features and component information in complex mixtures, particularly in the classification and identification of chemical warfare agent simulants.^25,26 Chen et al.²⁷ used simulated spectra to tackle challenges like data scarcity and invisible spectral regions but did not validate their accuracy. Fan applied DeepCID,²⁸ leveraging convolutional neural networks (CNNs) for Raman spectroscopy component analysis, achieved over 95% accuracy under controlled conditions but struggled with complex spectra. Models like Long Short-Term Memory (LSTM),²⁹ K-Nearest Neighbors (KNNs),³⁰ Random Forests (RFs), and Backpropagation Artificial Neural Networks (BP-ANNs)³¹ have reduced training sample requirements and improved accuracy in complex mixtures, often exceeding 95% even across wide concentration ranges. Despite their strengths in component identification, these methods are constrained by limited interpretability and versatility. Their performance degrades markedly when dealing with unknown mixtures, with prediction errors rising by a factor of 3 to 4. Zhang et al.³² achieved a 4.1% improvement in recognition accuracy over CNNs by leveraging transfer learning for Raman spectroscopy. However, the limited interpretability of existing models continues to hinder their practical applications.

This paper presents an RS-MLP framework, a novel multilayer perceptron architecture for Raman spectral analysis. This manuscript selects chemical agent simulants as the object of study, aiming to achieve qualitative and quantitative analyses of chemical agent simulant mixtures, thus providing a methodological reserve for future real agent analysis. Currently, using simulated agents to conduct methodological research is a common practice in the international academic community.^33–36 Leveraging the principles of the MLP-Mixer architecture, this framework constructs a reference feature library from pure spectral fragments, combines attention mechanisms with hierarchical feature matching strategies, and performs dual-channel matching of convolution-extracted mixed spectral features against the reference library. Accurate analysis of mixtures is achieved through adaptive capture of spectral region contributions. RS-MLP ensures end-to-end interpretability via feature importance weighting and attention heatmaps, enabling traceable results. The model demonstrates exceptional performance in handling complex mixtures with high spectral overlap and significant concentration variations, particularly in the quantitative analysis of chemical agent simulant mixtures, achieving an extremely low concentration prediction error of only 0.473% RMSE. Furthermore, it maintains high accuracy even under extreme concentration ratios. Its stability and robustness are rigorously validated on low-concentration samples and independent datasets.

2 Method

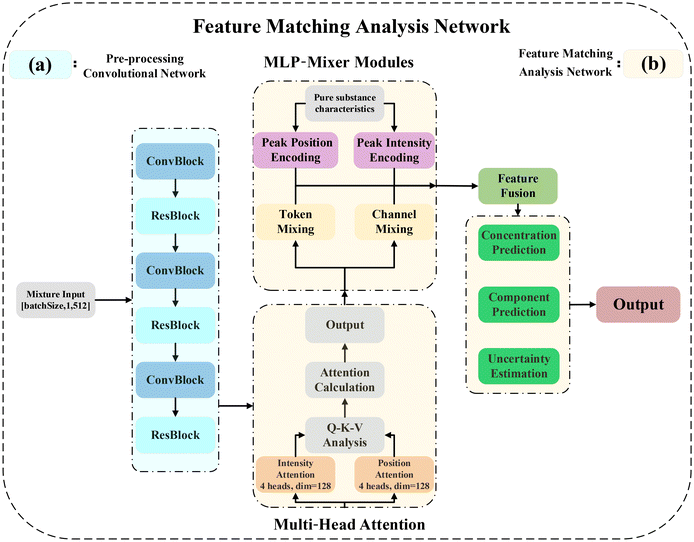
Herein, we elucidate a novel Raman spectral multi-layer perceptron (RS-MLP) framework for qualitative and quantitative analyses of chemical mixtures. As illustrated in Fig. 1, the RS-MLP framework encompasses three interconnected modules: pure substance feature extraction, data augmentation, and RS-MLP analytical networks.

Fig. 1 RS-MLP Analysis of the flowchart. Arrow 1 represents the construction of the reference feature library of the pure substance. Arrow 2 represents simulated data mixing and concentration gradient filling. After matching and analysis through the RS-MLP analytical network, the probabilities of the three pure substances are output as 0 or 1.

Initially, in the pure substance feature extraction module, the framework constructs a reference feature library by using convolution for feature extraction and labeling pure substance features. Specifically, eight key Raman peaks from the spectra of pure DIMP, DMMP, and TEP are labeled based on critical characteristics such as position, intensity, sharpness, width, and area. Next, the spectral features are reduced into 64 feature segments using convolution. These features collectively build the reference library, providing a foundation for subsequent spectral matching and integration.

Subsequently, we designed a simulation mixing algorithm to simulate linear and nonlinear mixing effects, concentration-dependent nonlinear responses, and pairwise spectral interactions. This algorithm was applied to the pure substance data to generate 45 binary and ternary mixtures with different concentration ratios. To address practical challenges like concentration gradients and extreme concentration scenarios, we used the Wasserstein Generative Adversarial Network with Gradient Penalty (WGAN-GP)^26,37 to perform concentration gradient filling for 45 mixtures with different concentration ratios.

In the RS-MLP analysis network, Raman spectral data from the mixtures, augmented with simulated mixing and GAN-based concentration gradient filling, are the input. The network first extracts features using a multi-scale dilated convolutional network with residual blocks. The multi-head attention mechanism then focuses on the key peak positions and intensities. These features are labeled using position and intensity encoders and matched to a reference feature library through the MLP-Mixer's token and channel feature mixing. The output is a 0–1 probability for each of the three components, where 0 indicates absence and 1 indicates the presence of a pure substance, enabling both qualitative and quantitative analyses.

2.1 Raman dataset and processing

In this experimental study, according to the requirements of the project on environmental risk assessment and mitigation of chemical warfare agents, we systematically collected the Raman spectral data for three chemical agent simulants in their pure states: DMMP, DIMP, and TEP, simulating real-world detection scenarios for agents such as GB and VX. Due to the partial similarity in their molecular structures, the Raman spectra of these simulants exhibit significant overlap and high resemblance (Fig. S1†). The minimal differences in the positions and intensities of their main peaks make distinguishing them accurately by visual inspection challenging. For each compound, 50 spectra were recorded under different laser power settings and integration times. The spectra for each pure substance under different conditions were then averaged. Based on the predefined concentration gradient table (Table 1), we used the averaged spectra of the pure substances, combined with a simulated spectral mixing algorithm and minimal Gaussian noise perturbation, to generate 21 binary mixtures and 24 ternary mixtures, each containing 50 spectra.

Table 1 The predefined concentration gradients for binary and ternary mixture simulations were categorized as follows: three categories—‘balanced’, ‘imbalanced’, and ‘trace’—were established, covering all cases from equal to extreme ratios

Mixture type	Category	Concentration combinations (%)	Total combinations
Binary	Balanced	75/25, 50/50, and 25/75	21
	Imbalanced	10/90 and 5/95
	Trace	1/99 and 0.5/99.5
Ternary	Regular	60/30/10, 60/10/30, 30/60/10, 30/10/60, 10/60/30, and 10/30/60	24
	Balanced	40/35/25, 40/25/35, 35/40/25, 35/25/40, 25/40/35, and 25/35/40
	Imbalanced	80/15/5, 80/5/15, 15/80/5, 15/5/80, 5/80/15, and 5/15/80
	Trace	90/9/1, 90/1/9, 9/90/1, 9/1/90, 1/90/9, and 1/9/90

---

The binary and ternary mixture concentration gradients were expanded to 200 samples per ratio using WGAN-GP. These samples were then merged with the original dataset for use in this study. The data were divided into training, validation, and test sets. The test set was uniformly sampled across the concentration gradient to ensure that each concentration was represented, with a sampling ratio of 1/5. The sampled data were used as the test set after sampling was complete, ensuring that it was completely independent and did not participate in the training or validation process. The remaining data were randomly sampled by the index, and the training and validation sets were divided in a ratio of 7 : 3.

The experimental measurements were carried out using a Beijing Zhuo Li Han Guang FE1064-Pro Handheld Raman spectrometer.

2.1.1 Data augmentation. In the context of chemical warfare or chemical terrorist attacks, it is unlikely that a single persistent chemical agent will be present on the contaminated surface. More often, multiple chemical agents coexist in the environment. Therefore, the qualitative and quantitative detection of chemical agent simulants in mixtures becomes crucial for practical applications. The inherent similarities between pure substances result in highly overlapping and broadened spectral bands in the mixed spectra (Fig. S2 and S3†), complicating both identification and quantitative analysis. Deep learning models, which require diverse datasets to avoid overfitting and improve generalization, are particularly challenged by the limited availability of Raman spectroscopy data due to constraints in sample availability and experimental conditions.³⁸ To overcome these challenges, the use of simulated data mixing techniques and appropriate mixing methods proves invaluable, as they significantly reduce both experimental costs and time. In this study, we simulated spectral mixtures using predefined concentration gradients (Table 1) to better represent real-world scenarios. We categorized the mixtures into three groups—‘balanced’, ‘imbalanced’, and ‘trace’—to simulate a broad spectrum of scenarios, from equal proportions to extreme ratios. This emphasizes the challenge of identifying components and predicting concentrations in such scenarios, highlighting the need for advanced analytical techniques. This approach enables a comprehensive evaluation of the model's predictive capabilities under boundary conditions and simulates real concentration scenarios of CWAs, ensuring reliable analysis in specialized cases.

For binary mixtures composed of DIMP, DMMP, and TEP, we defined seven concentration ratios, including extreme values as shown in Table 1, based on practical use scenarios. The specified concentration gradients were systematically combined to generate 21 unique binary mixtures. These mixtures were constructed as weighted linear combinations of the concentration ratios, while also accounting for nonlinear concentration effects. The binary mixing process is modeled as:

Binary_mix = ∑(C_i(1 − αC_i)S_i) (1)

where binary_mix represents the mixed spectrum, C_i represents the concentration ratio, S_i is the spectrum of the pure compound (i = 1 and 2), and α = 0.05 modulates the nonlinear response to maintain peak independence.

For the ternary mixture, we further improved the fidelity of the simulated spectrum by incorporating both linear and nonlinear mixing effects, as well as concentration-dependent nonlinear responses and pairwise spectral interactions. The ternary mixing process is represented as:

In this model, α = 0.05 regulates the concentration's nonlinear response, and β = 0.02 determines the strength of interactions between components. The term I(S_i,S_j) represents the spectral interaction between compounds i and j. M(S_i,S_j) serves as a masking function, confining interactions to regions where either compound exhibits significant spectral peaks, defined as greater than 10% of the maximum intensity. This formulation strikes a balance between preserving the integrity of individual spectral peaks and accounting for realistic minor interactions between components, enhancing both the model's physical relevance and predictive accuracy.

Subsequently, we verified the accuracy and authenticity of the simulated mixtures and examined whether the simulation method could effectively overcome the scarcity of Raman spectral experimental data and the challenges associated with data acquisition by accurately replicating the spectral data of chemical agent simulants. Binary mixtures were simulated as weighted linear combinations of pure component spectra based on concentration ratios, while ternary mixtures incorporated both linear and nonlinear mixing effects to emulate real spectral interactions. For validation, we selected a balanced binary mixture and an extreme ternary mixture, simulating the mixing of pure components according to specified ratios to verify against real mixed data. For the validation and comparison results between simulated and real mixtures, refer to Fig. S4.†

Finally, we designed 24 combinations of ternary mixtures with different concentrations, which were divided into four groups: conventional mixtures, mixtures with extreme components, mixtures with medium to trace components and mixtures with equilibrium components. Due to space limitations, the dataset is not presented here. For the complete visualization and data comparison of all binary and ternary simulated mixtures, please refer to Fig. S1–S3.†

2.1.2 Concentration gradient filling. Considering that the concentration ratio of the substances to be measured in practical applications differs to some extent from our predefined concentration ratio, we choose WGAN-GP to address the challenge of limited concentration combinations by filling the concentration gradient. As shown in Fig. 2, the network architecture consists of a generator and a discriminator, incorporating residual connections and self-attention mechanisms to ensure spectral fidelity.

Fig. 2 GAN network architecture diagram: (a) the network structure of the generator and (b) the network structure of the discriminator.

The generator architecture comprises three core components: an initial upsampling module that expands the input noise vector dimensions via transposed convolution; a feature refinement module with three residual blocks and a self-attention layer to capture complex spectral features and correlations; and a progressive upsampling path that enhances spectral resolution over five stages while preserving spectral characteristics. Residual connections and batch normalization in each stage ensure training stability and maintain spectral details, while a final smoothing layer ensures spectral continuity.

The discriminator is designed with a complementary architecture that progressively down-samples the input spectrum through four convolutional layers and one residual block to extract hierarchical features. Batch normalization ensures training stability, and activation functions enable the model to capture complex nonlinear relationships. A dropout layer is incorporated to prevent mode collapse in the GAN. To improve gradient flow and stabilize training, the Wasserstein distance with gradient penalty is employed as the primary loss function, which is formulated as:

where x̌ denotes the generated spectrum, x denotes the true spectrum, and x̂ denotes the interpolated sample. The gradient penalty coefficient λ is optimized to 10 according to experience. In the final layer, a sigmoid activation function generates probability scores, which are used to assess the authenticity of the spectrum. This setup ensures that the discriminator is effectively trained to distinguish between real and generated spectra while maintaining stable gradient flow throughout the network.

2.2 Qualitative and quantitative analysis networks

The network architecture used in this study is shown in Fig. 3. The network consists of a pre-processing convolutional network and a feature matching fusion network.

Fig. 3 Network architecture diagram. Block (a) represents the pre-processing convolutional network, where the mixture features are extracted in depth through the convolutional module with the residual module. Block (b) represents the feature matching analysis network, where the mixture features are mixed and matched with the encoded pure substances in an MLP-Mixer after attention through multiple heads, and finally the prediction of the mixture components and the concentration of each component is the output.

2.2.1 Pre-processing convolutional networks. Fig. 3(a) illustrates the detailed architecture of the pre-processing convolutional network. The network facilitates the hierarchical extraction of features using three cascaded convolutional-residual modules. Each stage integrates two complementary feature processing modules: ConvBlock for feature transformation and ResBlock for feature enhancement. The convolutional module employs dilated convolution with progressive channel expansion (32 → 64 → 128) and decreasing kernel sizes (7 → 5 → 3) to facilitate multi-scale extraction of features (Fig. S5†): larger kernels in early stages capture global spectral characteristics, while smaller kernels in later stages focus on localized peak features. The dilated convolution expands the receptive field without increasing parameters, effectively integrating spectral correlations over the global range.

Subsequently, ResBlock with pre-activation architecture is used to perform deep feature extraction (Fig. S6†). This architecture not only enables deeper feature propagation but also preserves original spectral information while allowing the network to learn complementary features for enhanced spectral data extraction. The feature extraction module employs stride-2 convolution operations to systematically downsample the 512-dimensional spectral vector to a 64-dimensional feature representation. Each feature corresponds to an 8.26 cm⁻¹ (512/64) spectral region.

The network maintains stable feature distributions across different scales through batch normalization in ConvBlock and layer normalization in ResBlock. ConvBlock combines dilated convolution and progressive channel expansion for multi-scale feature extraction, while ResBlock's pre-activation architecture ensures effective feature propagation and enhancement. The final output is a feature map of shape (128, 64), where each spectral segment is represented by a 128-dimensional feature vector.

In the subsequent feature matching and analysis network, the mixture features after convolutional feature extraction are processed by multi-head attention, and the two sets of multi-head attention focus on Raman shift and peak intensity features, respectively. Combined with pure substance feature encoding, a mixture of token and channel is used in the MLP, and the similarity between the mixture features and each pure substance is computed through the multi-head attention mechanism, so that the mixture can be analyzed qualitatively and quantitatively.

2.2.2 Feature matching analysis networks. The feature matching and fusion network aims to systematically analyze the contribution of spectral features to component recognition and quantification. Fig. 3(b) illustrates the detailed network architecture. The network takes a feature map of size (128, 64) as the input, where 128 represents the feature channel and 64 corresponds to the spectral segment extracted from the convolutional network.

In view of the fact that Raman spectroscopy contains two distinct types of basic information: determining the peak position of the molecular structure and the peak intensity representing the concentration of the component.³⁹ In order to efficiently capture spectral properties, the network uses two parallel multi-head attention modules, and the number of heads for each multi-head attention is set to 8, aiming to focus on the characteristics of position and intensity, respectively. In each attention header, the input features are projected into the query, key, and value spaces through linear transformations. The attention mechanism calculates the score according to the following formula:

where d_k is the dimension of each attention head. This mechanism enables the network to selectively focus on relevant spectral regions while suppressing noise, resulting in different representations of location and intensity. The output of all heads is connected and projected back to the original dimension to form a fine feature map customized for spectral features.

In order to further improve the accuracy of feature matching and enhance the ability of global correlation of tandem spectra, this study used a multi-layer perceptron (MLP-Mixer) module to align the extracted spectral features with the reference pure component features. The module encodes position and intensity information separately using two independent encoders for pure substances. The coding features are processed by a token-wise and channel-wise hybrid network. The token-wise network processes each spectral segment independently, combines the multi-head attention of the mixture with the position coding of the pure substance, and deeply captures the correlation features to achieve preliminary matching. The channel-wise network captures the correlation between different feature channels and enhances the ability of global feature matching and fusion. Both networks use residual connection and layer normalization (layer norm) to maintain a stable feature distribution. Using pure substance feature encoding, the MLP performs token and channel mixing. The multi-head attention mechanism then calculates the similarity between the mixture features and each pure substance, enabling both qualitative and quantitative analyses of the mixture.

The final prediction phase consists of a multi-task learning framework built with three fully connected networks, each targeting specific aspects of mixture analysis. The component prediction module uses a stepwise dimension reduction structure to transform high-dimensional spectral features into concentration predictions for the three substances, generating probability scores for each chemical component. The concentration prediction network employs a three-tier architecture to optimize feature transformation and ensure precise outputs. The first layer enriches the representation space while maintaining the original feature dimensions, followed by dimensional compression to retain critical information for concentration estimation. The final layer maps the refined features to predicted concentrations, ensuring that output values represent the effective proportions of the three components, constrained within the range of 0 to 1. The uncertainty quantification module shares features through dimensionality reduction and generates confidence scores (0–1) for each component, providing a quantitative measure of prediction reliability.

2.3 Loss calculation

The primary challenge in the qualitative and quantitative analyses of complex mixtures, particularly in Raman spectroscopy, lies in achieving high sensitivity for component identification, precise concentration prediction, and accurate detection of trace components.⁴⁰ To address these challenges, we frame the problem as multi-task learning, where the model simultaneously optimizes several objectives.

The model's output consists of the predicted concentration of each pure substance in the mixture, represented as probabilities ranging from 0% to 100%. To achieve robust performance across various mixture types, we designed a comprehensive loss function that integrates multiple components, each addressing a specific aspect of the problem. This loss function is constructed to optimize the model holistically, enabling it to perform well in both classification and concentration prediction tasks.

The primary component of the loss function is the mean squared error (MSE) loss, formulated as:

where y_i is the true concentration of the i-th component, and ŷ_i is the model's predicted concentration. MSE is employed due to its effectiveness in regression tasks, particularly for continuous-valued outputs such as concentration predictions. However, standard MSE loss tends to underrepresent low-abundance components, necessitating a dedicated mechanism for trace component enhancement.

To enhance the model's sensitivity to trace components, defined as those with concentrations below 15%, a dynamic weighting mechanism is introduced. This mechanism assigns higher loss contributions to low-concentration samples, ensuring that they are not overshadowed by dominant components. The dynamic weight is computed as:

where 1(·) is an indicator function that selects low-concentration samples, and ε is a small numerical constant to prevent division by zero. The weighted loss for trace components is then defined as:

It is ensured that trace components contribute proportionally more to the total loss function, improving model sensitivity to low-abundance species.

Beyond concentration prediction, uncertainty quantification plays a crucial role in ensuring the reliability of model outputs. To penalize predictions with high uncertainty, an uncertainty-weighted error loss is incorporated, given as follows:

L_uncertainty = E[|ŷ − y| × uncertainty] (8)

where the absolute prediction error is weighted by the associated uncertainty. This formulation ensures that uncertain predictions contribute more to the loss function, encouraging the model to reduce uncertainty while improving accuracy. Furthermore, to prevent excessive uncertainty values that could degrade model performance, an uncertainty regularization term is introduced:

R_uncertainty = 0.01 × E[uncertainty²] (9)

where the regularization coefficient (0.01) was empirically chosen to balance model stability and learning efficiency.

In addition to predicting concentration values, the model must correctly classify whether a component is present or absent in a given sample. To achieve this, binary cross-entropy (BCE) loss is employed for presence detection:

where y_i is a binary indicator (0 or 1) representing the presence of a component, with a detection threshold set at 0.001. This loss ensures that the model effectively distinguishes between the present and absent components while handling imbalanced dataset distributions.

The final total loss function integrates these components into a single objective:

L_total = L_conc. + 2 × L_{low\_conc.} + 0.1 × (L_uncert + R_uncert) + 0.1 × L_pres (11)

where weighting coefficients were empirically determined to prioritize accurate concentration prediction, enhance trace component detection, regulate uncertainty estimation, and ensure robust presence classification. The factor of 2.0 assigned to L_{low_conc.} reinforces the model's focus on trace components, while the 0.1 weighting of L_uncertainty and R_uncertainty ensures that uncertainty is accounted for without overwhelming the optimization process. Similarly, the 0.1 weighting assigned to L_pres ensures reliable component detection while maintaining a balance with other objectives. This loss function formulation enables the model to achieve optimal performance in complex mixture analysis by ensuring accurate concentration prediction, heightened sensitivity to trace components, robust uncertainty regulation, and reliable component detection, making it well-suited for real-world Raman spectral mixture analysis.

3 Results and discussion

In order to validate the analytical capability of the network and critically assess its generalisation ability, a strategy of uniformly extracted data was used to compose the test set. Specifically, the original dataset, sampled by uniform extraction according to the concentration gradient, was extracted for each concentration combination, and the data extracted in the ratio of 1/5 formed the test set. The test set is completely independent of the training and validation sets. The data after sampling the test set is divided into training and validation sets in the ratio of 7 : 3, which is done by random sampling according to the index.

3.1 Model validation

Considering that most data in this study were generated using a GAN network, we first evaluated its performance using multiple indicators, including the correlation coefficient to assess overall distribution similarity and mean square error (MSE) to identify deviations in local details. The evaluation of the GAN model demonstrated its exceptional learning capability, with correlation coefficients for binary and ternary mixtures reaching as high as 0.9997 (Fig. S6(a)†) and MSE values on the order of 10⁻⁵ (Fig. S6(b)†). The inverse relationship between MSE and the correlation coefficient (Fig. S6(c)†) further highlighted the robustness and accuracy of the GAN network across various complex systems. Additionally, the subsequent training process illustrated the stability of the GAN network, with progressive improvements observed at every stage of training (Fig. S8–S10†), confirming the effectiveness of the loss function. The comparison between generated and real data further validated the authenticity of the GAN-generated data (Fig. S9–S12†), where the minor intensity differences aligned with the intended purpose of filling concentration gradients. Fig. S12† shows a comparison of the effect of traditional data enhancement methods with WGAN-GP concentration gradient amplification.

To validate the model's performance, we uniformly sampled 20% of the binary and ternary mixtures at different concentration gradients, totaling 1800 test samples. These were excluded from the training and validation processes to rigorously assess the model's robustness and generalization.

The model is designed to identify components in the mixture and predict their concentrations with high accuracy. To evaluate this, we classify all mixtures in the test set based on their components. For binary mixtures, we used three component combinations: DMMP + DIMP, DMMP + TEP, and DIMP + TEP. Ternary mixtures, containing all three components, form a single combination. These mixtures were then categorized based on the components identified during the data processing phase.

The model's effectiveness is measured by its classification accuracy and concentration prediction. Fig. 4 illustrates the model's evaluation of classification and prediction accuracy. Fig. 4(a) shows that the model correctly identifies the component combinations, achieving 100% classification accuracy using multi-head attention mechanisms to focus on Raman shifts. The confusion matrix confirms the model's accurate classification, with no errors in categorizing the mixtures.

Fig. 4 Multi-dimensional evaluation of predictive and classification accuracy in the matching network. (a) Confusion matrix illustrating the classification accuracy for four mixture types. The model achieves 100% accuracy, with all spectra correctly classified into their respective categories. (b) Error metrics analyses (MAE, MSE, and RMSE) for DIMP, DMMP, and TEP, demonstrating excellent predictive accuracy and low error rates for all components. (c) Scatter plots of predicted versus true concentration values for DIMP, DMMP, and TEP, showcasing an almost perfect linear correlation (R² > 0.99) with a negligible bias, as indicated by the regression equations. Uncertainty across predictions is also visualized using a color gradient. (d) Comparison of true versus predicted concentration values for representative samples of DIMP, DMMP, and TEP, highlighting the strong agreement between predictions and actual measurements with minimal deviation.

The model's error metrics for concentration predictions, as illustrated in Fig. 4(b), highlight its predictive accuracy. The exceptionally low values of MAE, MSE, and RMSE across all components highlight the model's precision, with MAE values of 0.0035 for DIMP, 0.0032 for DMMP, and 0.0031 for TEP. Such robust performance demonstrates the model's ability to predict component concentrations with high accuracy and consistency across diverse mixture types. Building upon the accurate classification of component categories, the model further demonstrates its effectiveness in predicting individual component concentrations.

This strong classification accuracy provides a solid foundation for the concentration prediction of each component. Fig. 4(c) demonstrates that the predicted concentrations exhibit near-perfect linear correlations with the true values (R² > 0.99), with regression slopes approaching unity for DIMP (0.999), DMMP (0.998), and TEP (1). This result reflects the model's ability to match spectral features with those from the reference feature library, enabled by its attention-based architecture. Additionally, the incorporation of uncertainty quantification further enhances the model's interpretability, with the color gradient representation in Fig. 4(c) illustrating the model's confidence in its predictions.

To further validate the model's performance, a comparative analysis of 20 representative samples is presented in Fig. 4(d). This analysis underscores the model's accuracy and stability in handling both binary and ternary mixtures. The close agreement between the predicted values (orange) and true values (blue) confirms the efficacy of the hierarchical feature extraction and matching strategy. This success is closely tied to the interpretable architecture adopted in the study, which employs convolutional residual features to identify feature peak positions, followed by position-intensity matching via an attention mechanism. Such a structured approach ensures not only high predictive accuracy but also a deeper understanding of the underlying decision-making process, making the model highly applicable for analyzing complex mixtures in real-world scenarios. By monitoring the learning process, the decline in training and validation losses (Fig. S13(a)†) indicates that the model is used for effective learning. Although occasional fluctuations were observed in the validation loss, the small gap between training and validation losses suggests strong generalization capability and the absence of overfitting. The final model successfully achieved a balance between loss minimization and learning rate adjustment.

3.2 Model weight visualization

According to the MSE index, this study selected an optimal binary and ternary mixture to illustrate the reasoning process of the network. In the analysis of the matching network, given that the attention mechanism might face challenges in modeling complex scenarios, a dynamic weighting method was implemented to aggregate the attention weights across layers. Initially, the attention weights of each layer were normalized independently to retain their unique characteristics while restoring the attention regions as accurately as possible. This normalization ensures a clearer representation of the model's reasoning process.

Subsequently, attention from different layers, with dimensions of 256, 128, and 64, respectively, was combined and projected onto a unified attention layer for aggregation. To preserve the precision of the attention weight distribution in the first and second layers, point correspondence mapping was applied to align their attention to the spectral dimension, preventing the loss of fine positional information. Finally, a masking technique was employed to map the 512 data points from the first and second layers onto the attention weights of the third layer. This step accurately captures the true weight distribution of attention across spectral bands, which is crucial for final component discrimination and concentration prediction.

The attention weights at the corresponding positions across all three layers were then accumulated, and the total weights were renormalized to ensure consistency within a unified visual range. Finally, using linear interpolation, the 64 attention weight blocks were mapped to their corresponding spectral regions, providing detailed visualization of the weight distribution within the analysis matching network and enhancing the interpretability of the model. Here we show the visualization and analysis of binary and ternary mixtures to illustrate the inference process of the model.

To achieve spectral alignment and enhance the clarity of visualization, all spectra were aligned to the origin of the coordinate axis to ensure consistency. The inference process of the model is depicted in Fig. 5. Fig. 5(a) presents a heatmap of attention weight distribution over the mixture spectrum during the analysis. By visualizing the attention weights, the network's focus on mixture features during the matching analysis phase can be intuitively observed.

Fig. 5 (a) & (d) Showing the global attention weight distribution on the Raman spectra of ternary and binary mixtures, respectively. (b) & (e) Peak matching analysis showing the correspondence between the peaks of the mixture and the characteristic peaks of DIMP, DMMP and TEP. (c) & (f) Histogram showing the predicted concentration of each component in the mixture.

Although linear interpolation was applied to the aggregated attention weights, the mapping relationships remain neither entirely intuitive nor detailed due to changes in feature dimensions after convolution. Nevertheless, it is evident that the attention weights exhibit significant emphasis around Raman shifts of 0–100 cm⁻¹, 600–780 cm⁻¹, 1100–1220 cm⁻¹, and approximately 1450 cm⁻¹. These regions, highlighted in the figure, serve as the foundation for subsequent network matching analysis phases. Given the high similarity in the characteristic peaks of the three pure substances, Fig. 5(b) further illustrates the network's stepwise matching analysis process. The differently colored triangles in the figure represent distinct substances, and their marked positions within the mixture's Raman spectrum correspond to the results of attention mechanism matching with Raman shifts in the reference feature library. The heights of the dashed lines represent the network's comparison of peak intensities between the mixture's features and the reference feature library. These positions are crucial indicators for the network to determine the presence of specific substances in the mixture. The dashed line heights further reflect the network's analysis of mixture concentrations based on the peak intensities of pure substances and the attention weights. These two figures illustrate the inference process and working principles of the network: after assigning weights to regions with significant spectral peak variations in the mixture using a multi-head attention mechanism, the reference feature library is introduced. By independently encoding the Raman peak positions and intensities in the reference feature library, the network implements a dual-channel matching strategy between the attention weights of the mixture and the reference feature library. Positional correspondence determines the components of the mixture, while proportional correspondence in intensity reveals the concentration ratios of individual components. For example, in the peak matching analysis plot, at the highest peak corresponding to the Raman shift of 780 cm⁻¹, the network identifies the characteristic peaks of three substances, with significant differences in the dashed line heights for each substance. By normalizing the Raman characteristic peak intensities in the reference feature library to 100%, it is evident that the network derives the concentration ratios of each component by comparing the peak intensities with those in the reference feature library. The height proportions of the dashed lines can be visually correlated with the predicted component concentration distribution of the mixture in Fig. 5(c).

Fig. 5(d–f) shows the attentional weight distributions, the locations of the attentional distributions, and the concentration prediction histograms for the spectra of binary mixtures. Since the analysis of ternary mixtures has already been elaborated in detail previously, and the case of the spectra of binary mixtures is quite similar to that of ternary mixtures, the details of such analysis will not be repeated in this section.

The network employs a dual-channel matching strategy between the attention weights and the reference feature library to identify the components and concentration information of pure substances within the mixture, enabling interpretable analysis of the mixture. Although cumulative effects lead to a significant overall increase in attention weights, this does not impede the visualization of regions with high attention.

3.3 Model generalization validation and comparison

Since the construction of this model is done using both simulated data and GAN-generated data, in order to test the representation of the model in real mixtures, we select ten concentration gradients for each of the binary and ternary mixtures according to the concentration gradients in Table 1 above for the testing of real mixture data, and 10 Raman spectral data are collected for each concentration gradient, and the real mixture data measured above are treated as a test set to test the model trained with the simulated data to test the performance of the model and to verify the realism and feasibility of the simulated mixture. The validation results are shown in Fig. S14.† The results show the reliable performance of the model, but also reflect the shortcomings of the simulation hybrid algorithm.

To further validate the applicability of the RS-MLP algorithm and evaluate its generalization capability, we tested the model using a hazardous chemical dataset from Raman spectra and compared the results with those of CNNs,⁴¹ Residual Networks (ResNet),⁴² and Long Short-Term Memory (LSTM) + CNNs.⁴³ A self-constructed hazardous chemical dataset comprising 75 substances was used for evaluation, including 15 pure substances, 20 binary mixtures, 15 ternary mixtures, 15 quaternary mixtures, and 10 quinary mixtures, with 50 samples collected per category. The dataset and detailed validation information can be found in Fig. S15.†

Following the modeling procedures outlined earlier in this manuscript, we collected data and established models. To further validate the model's qualitative analysis capability for hazardous chemical mixtures in practical application scenarios, random baseline noise was introduced as an interference signal. The validation was divided into 75 categories based on different component combinations. For a clear and comparative evaluation of the model, these categories were grouped into five major classes. Multiple tests were conducted under identical experimental conditions, and the validation results are summarized in Table 2, where “F” denotes values below the threshold or recognition errors.

Table 2 Verification results and comparison table of hazardous chemical datasets

Concentration	Accuracy/R^2
	GAN & random baseline noise				No GAN & random baseline noise
	CNN	ResNet	LSTM + CNN	RS-MLP	CNN	ResNet	LSTM + CNN	RS-MLP
Pure	0.954	0.966	0.961	0.998/0.999	0.931	0.92	0.92	0.982/0.99
Binary	0.932	0.944	0.878	0.992/0.999	0.863	0.76	0.823	0.974/0.982
Ternary	0.898	0.91	0.866	0.99/0.999	0.799	0.76	0.75	0.963/0.969
Quaternary	0.729	0.833	0.752	0.984/0.99	0.5	F	0.72	0.952/0.96
Quinary	F	0.712	0.7	0.98/0.986	F	F	F	0.938/0.96

---

Table 2 highlights the significant advantage gained by incorporating GAN-generated data. For all mixture categories, the accuracy and R² values of the models improved substantially with the GAN compared to the baseline without the GAN. For example, in ternary and quinary mixtures, where spectral overlap and concentration gradients present considerable challenges, the inclusion of the GAN augmented the data diversity and mitigated overfitting, thereby enhancing the generalization capability. The RS-MLP model particularly benefited from this augmentation, reaching the highest accuracy and R² values across all mixture types, with values of 0.998/0.999 in pure substances and 0.98/0.986 in quinary mixtures.

The RS-MLP model consistently outperformed ResNet, LSTM + CNNs, and CNNs under identical experimental conditions, highlighting its superior capability for feature extraction and matching. This capability is crucial for handling complex chemical mixtures. In challenging scenarios, such as quinary mixtures, RS-MLP maintained high prediction accuracy, indicating its robustness and adaptability. By contrast, models like ResNet and LSTM + CNN faced challenges in capturing subtle spectral variations and conducting feature matching, resulting in lower accuracy and R² values, particularly in high-order mixtures.

RS-MLP excels at handling complex Raman spectra, particularly in mixtures with overlapping peaks, by combining multi-head attention with convolutional and residual blocks. The multi-head attention allows the model to focus on different parts of the spectrum simultaneously, while the residual blocks refine predictions by learning from errors. This structure enables RS-MLP to capture nonlinear interactions and efficiently extract both positional and intensity features, which are crucial for accurately identifying and quantifying components in mixtures.

Unlike traditional methods that extract all spectral features at once, potentially missing small but important variations, RS-MLP separates the positional and intensity information. By using a reference library of pure substance features and an MLP-based matching technique, it combines these two aspects, offering a more comprehensive and accurate representation of the spectral data.

In contrast, traditional models like CNNs, ResNet, and LSTM + CNNs struggle with nonlinear interactions, lack multi-scale feature matching, and do not account for the nuanced positional and intensity relationships in Raman spectra.⁴⁴ These limitations make them less effective for analyzing complex mixtures, where RS-MLP outperforms them by handling intricate spectral patterns and extracting crucial information more precisely.

In summary, the results demonstrate that integrating the GAN with RS-MLP significantly enhances the model's capability to perform precise qualitative and quantitative analyses of hazardous chemical mixtures, even under challenging conditions. Future work should focus on optimizing data augmentation strategies and further refining network architectures to improve model performance, especially in quinary mixtures where slight discrepancies remain. This would ensure greater accuracy and robustness in practical applications, such as real-time CWA detection and analysis.

4 Conclusion

In conclusion, we developed a novel deep learning network for the qualitative and quantitative analyses of Raman spectral mixtures. This network determines the components of mixtures and their concentrations by using the features of pure substances as references, enabling spectral matching and concentration prediction. The network demonstrated excellent performance in the qualitative and quantitative analyses of Raman spectral mixtures of chemical warfare agent simulants and exhibited remarkable results in independent validation using the laboratory hazardous chemicals database, highlighting its strong feature extraction and generalization capabilities. While obtaining real Raman spectra from chemical warfare agents on complex matrices remains a challenge due to data scarcity, we addressed this issue by generating high-quality simulated mixture spectra based on predefined concentration gradients to supplement real data. This approach effectively mitigates the lack of available data. By combining both real and simulated data in the training dataset, the proposed model has shown great potential for applications in military chemical defense, chemical warfare detection, environmental monitoring, and complex mixture analysis.

Author contributions

Jie Wu: methodology, code, formal analysis, and writing – original draft. Fei Li: formal analysis and writing – original draft. Jing-Wen Zhou: investigation. Hongmei Li: formal analysis. Zilong Wang: investigation. Xian-Ming Guo: formal analysis. Yue-Jiao Zhang: formal analysis. Lin Zhang: data curation, review manuscript, and formal analysis. Pei Liang: review manuscript and formal analysis. Shisheng Zheng: conceptualization, writing – review & editing, and formal analysis. Jian-Feng Li: conceptualization, resources, writing – review & editing, and funding acquisition.

Data availability

Data will be made available from the corresponding author upon reasonable request. The relevant source code and data of machine learning can be found at https://github.com/JasonBourneeee/RS-MLP.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This project was supported by the National Natural Science Foundation of China (grant no. 21876402)under the title Environmental Risk Assessment and Disposal of Chemical Weapons Abandoned by Japan in China.

References

1. M. Schwenk, Toxicol. Lett., 2018, 293, 253–263.
2. Z. Witkiewicz, S. Neffe, E. Sliwka and J. Quagliano, Crit. Rev. Anal. Chem., 2018, 45, 337–371.
3. P. G. Wilcox and J. A. Guicheteau, Proc. SPIE, 2018, 10629, 106290M,  DOI:10.1117/12.2303968.
4. J.-C. Wolf, M. Schaer, P. Siegenthaler and R. Zenobi, Anal. Chem., 2014, 87, 723–729.
5. S. K. Choi, Y. S. Jeong, Y. J. Koh, J. H. Lee and S. Kim, Bull. Korean Chem. Soc., 2019, 40, 483–484.
6. E. Budzyńska, M. Grabka, J. Kopyra, M. Maziejuk, Z. Safaei, B. Fliszkiewicz, M. Wiśnik and J. Puton, Talanta, 2018, 194, 259–265.
7. M. Liu, Z. Zeng and H. Fang, J. Chromatogr., A, 2005, 1076, 16–26.
8. H. John, F. Balszuweit, K. Kehe, F. Worek and H. Thiermann, in Handbook of Toxicology of Chemical Warfare Agents, ed. R. C. Gupta, Academic Press, San Diego, 2009, pp. 755–790.
9. H. Jung and H. W. Lee, J. Hazard. Mater., 2014, 273, 78–84.
10. C. E. Davidson, M. M. Dixon, B. R. Williams, G. K. Kilper, S. H. Lim, R. A. Martino, P. Rhodes, M. S. Hulet, R. W. Miles, A. C. Samuels, P. A. Emanuel and A. E. Miklos, ACS Sens., 2020, 5, 1102–1109.
11. S. Ha, M. Lee, H. O. Seo, S. G. Song, K.-s. Kim, C. H. Park, I. H. Kim, Y. D. Kim and C. Song, ACS Sens., 2017, 2, 1146–1151.
12. P. Jarosław and N. Jacek, Trends Anal. Chem., 2016, 85, 10–20.
13. M. S. J. Khan, Y.-W. Wang, M. O. Senge and Y. Peng, J. Hazard. Mater., 2017, 342, 10–19.
14. X.-M. Lin, Y.-L. Sun, Y.-X. Chen, S.-X. Li and J.-F. Li, eScience, 2024, 100352.
15. C. Yi, Z. Hulin and S. Mengtao, Chin. J. Light Scattering, 2023, 35, 189–205.
16. K. Y. Noonan, L. A. Tonge, O. S. Fenton, D. B. Damiano and K. A. Frederick, Appl. Spectrosc., 2009, 63, 742–747.
17. T. Kondo, R. Hashimoto, Y. Ohrui, R. Sekioka, T. Nogami, F. Muta and Y. Seto, Forensic Sci. Int., 2018, 291, 23–38.
18. G. Mogilevsky, L. Borland, M. Brickhouse and A. W. Fountain III, Int. J. Spectrosc., 2012, 808079.
19. Z. Jiaqian, W. Yukai, W. Hongqiu and G. Lin, Chin. J. Light Scattering, 2022, 34, 1.
20. W. Huang, J. Chen, H. Xiong, T. Tan, G. Wang, K. Liu, C. Chen and X. Gao, Talanta, 2025, 289, 127756.
21. P. Liu, J. Wang, Q. Li, J. Gao, X. Tan and X. Bian, Spectrochim. Acta, Part A, 2019, 206, 23–30.
22. X. Bian, D. Chen, W. Cai, E. Grant and X. Shao, Chin. J. Chem., 2011, 29, 2525–2532.
23. Q. Yang, L. Wu, C. Shi, X. Wu, X. Chen, W. Wu, H. Yang, Z. Wang, L. Zeng and Y. Peng, IEEE Access, 2021, 9, 140008–140021.
24. S. Wu, S.-X. Li, J. Qiu, H.-M. Zhao, Y.-W. Li, N.-X. Feng, B.-L. Liu, Q.-Y. Cai, L. Xiang, C.-H. Mo and Q. X. Li, Environ. Sci. Technol., 2024, 58, 15100–15110.
25. E. R. K. Neo, J. S. C. Low, V. Goodship and K. Debattista, Resour., Conserv. Recycl., 2023, 188, 106718.
26. R. Xu, J. Tang, C. Li, H. Wang, L. Li, Y. He, C. Tu and Z. Li, Meta-Radiology, 2024, 2, 100069.
27. T. Chen and S.-J. Baek, ACS Omega, 2023, 8, 37482–37489.
28. X. Fan, W. Ming, H. Zeng, Z. Zhang and H. Lu, Analyst, 2019, 144, 1789–1798.
29. K. Greff, R. K. Srivastava, J. Koutnik, B. R. Steunebrink and J. Schmidhuber, IEEE Trans. Neural Networks Learn. Syst., 2017, 28, 2222–2232.
30. L. Le, Y. Xie and V. V. Raghavan, Fundam. Inform., 2021, 182, 95–110.
31. H. Tian, L. Zhang, M. Li, Y. Wang, D. Sheng, J. Liu and C. Wang, Infrared Phys. Technol., 2019, 102, 103003.
32. R. Zhang, H. Xie, S. Cai, Y. Hu, G.-k. Liu, W. Hong and Z.-q. Tian, J. Raman Spectrosc., 2020, 51, 176–186.
33. X. Li, J. Dong, H. Liu, X. Sun, Y. Chi and C. Hu, J. Hazard. Mater., 2018, 344, 994–999.
34. Y. Liu, S.-Y. Moon, J. T. Hupp and O. K. Farha, ACS Nano, 2015, 9, 12358–12364.
35. M. P. Willis, M. J. Varady, T. P. Pearl, J. C. Fouse, P. C. Riley, B. A. Mantooth and T. A. Lalain, J. Hazard. Mater., 2013, 263, 479–485.
36. Q.-Y. Wang, Z.-B. Sun, M. Zhang, S.-N. Zhao, P. Luo, C.-H. Gong, W.-X. Liu and S.-Q. Zang, J. Am. Chem. Soc., 2022, 144, 21046–21055.
37. T. Feng, T. Hu, W. Liu and Y. Zhang, Int. J. Mol. Sci., 2023, 24, 17548.
38. M. Yu, L. Li, R. You, X. Ma, C. Zheng, L. Zhu and T. Zhang, Microchem. J., 2024, 199, 109990.
39. A. Guleng, H. Siqingaowa, B. Lin and H. Wuliji, Chin. J. Light Scattering, 2024, 36, 142–147.
40. P. L. De Reeder, Anal. Chim. Acta, 1953, 8, 6–15.
41. Y. Wan, Y. Jiang, W. Zheng, X. Li, Y. Sun, Z. Yang, C. Qi and X. Zhao, Spectrochim. Acta, Part A, 2025, 329, 125608.
42. Y. Xie, S. Yang, S. Zhou, J. Liu, S. Zhao, S. Jin, Q. Chen and P. Liang, J. Raman Spectrosc., 2023, 54, 191–200.
43. Y. Cai, G. Xu, D. Yang, H. Tian, F. Zhou and J. Guo, Anal. Chim. Acta, 2023, 1259, 341200.
44. M. Kazemzadeh, M. Martinez-Calderon, W. Xu, L. W. Chamley, C. L. Hisey and N. G. R. Broderick, Anal. Chem., 2022, 94, 12907–12918.

---

Footnotes

† Electronic supplementary information (ESI) available: Fig. S1–S14. See DOI: https://doi.org/10.1039/d5an00075k

‡ These authors contributed equally.

---