Describing dynamic electron correlation beyond a large active space†
Yinxuan
Song
a,
Yifan
Cheng
*b and
Haibo
Ma
 *c
*c
aSchool of Environmental Science and Engineering, Shandong University, 72 Binhai Road, Qingdao 266237, China
bSchool of Chemistry and Chemical Engineering, Nanjing University, Nanjing 210023, China. E-mail: yifan@smail.nju.edu.cn
cKey Laboratory for Colloid and Interface Chemistry, Ministry of Education, School of Chemistry and Chemical Engineering, Shandong University, 72 Binhai Road, Qingdao 266237, China. E-mail: haibo.ma@sdu.edu.cn
First published on 22nd May 2025
Abstract
The pursuit of quantitatively accurate electron correlation calculations for realistic large strongly correlated systems presents significant theoretical and computational challenges. These challenges stem primarily from two fundamental aspects: the inherent complexity of treating static correlations within extensive active spaces and the additional difficulty of incorporating dynamic correlation effects from the external space. In this comprehensive perspective, we systematically review and analyze state-of-the-art methodologies that address dynamic correlation beyond large active spaces, with particular emphasis on approaches that circumvent the computational burden associated with high-order reduced density matrices. Through careful classification, we have organized these advanced techniques into seven distinct categories. To illustrate the practical application and comparative performance of these newly developed methods, we present a detailed case study involving the calculation of potential energy curves for the neodymium oxide (NdO) molecule. It is our expectation that this work will not only provide valuable insights for future multi-reference calculations in large strongly correlated systems but also stimulate the development of innovative methodologies specifically tailored for handling extensive active spaces in multi-reference calculations.
1 Introduction
The electronic structure of atoms and molecules is determined by simultaneous pairwise interactions among electrons and nuclei. These quantum many-body interactions form the foundation of chemical behaviors and can be fully described by the solutions of the unrelativistic Schrödinger equation or relativistic Dirac equation. Due to the well-known “curse of dimensionality” difficulty for the quantum many-body systems, one usually has to resort to approximate rather than exact solutions to their respective equations. The Hartree–Fock (HF) mean field theory is the most straightforward and widely used approximate wave function theory (WFT) method. It simplifies the complex problem of many electrons into a single-electron problem, depicting the electron's interaction with its surrounding electrons as an interaction with an average field. However, to achieve higher accuracy, it is crucial to adequately describe how the movement of each electron is influenced by the movements of the other electrons. This corresponds to the “electron correlation” issue, which is often the largest error source in quantum chemistry calculations. It is usually considered that there are two sources of correlation beyond the mean field single-particle approximation (Hartree product): symmetry and Coulomb repulsion.1,2 The first source stems from the collective spin and permutation symmetry requirements, electrons’ Fermionic characteristics, and is consequently also termed as “Fermi correlation”. This can be effectively depicted by HF theory through the use of Slater determinants instead of simple Hartree products. Therefore, in modern day's quantum chemistry community, the term “electron correlation” is typically used to refer specifically to the second source of error, known as “Coulomb correlation”. The electron correlation energy is then usually defined as the difference between the exact full configuration interaction (FCI) energy of the molecular system and the HF energy, in a given basis set.The mean field approximation employed in the derivation of the HF theory assumes independent electron motion, neglecting instantaneous Coulomb repulsion with dynamic neighboring electrons. Therefore, HF systematically underestimates the average distances between electron pairs and thus overestimates the average electron repulsion energies, which can be observed in the calculated ground-state potential energy curves of H2 and N2 shown in Fig. 1. This effect is known as “dynamic correlation” because it is directly related to electron's instantaneous motion, and it can be efficiently described by single-reference (SR) electron correlation methods such as the coupled cluster (CC) approach or perturbation theory (PT) by considering determinant configurations (CFGs) with electrons excited from occupied HF orbitals to unoccupied (virtual) orbitals. The dynamic correlation is expected to decrease in the bond dissociated limit due to the suppressed likelihood of electron repulsion when the two neutral atoms are spatially well separated from each other. However, from Fig. 1, one can find that the correlation energy (energy difference between HF solution and the exact result at the given basis set) increases from 40 (470) mEh at the equilibrium structure to 168 (1065) mEh at the dissociated structure with an inter-atomic distance of 3 Å for H2 (N2). More interestingly, SR correlation methods shown in Fig. 1, including second-order Møller–Plesset perturbation (MP2) and coupled cluster singles and doubles (CCSD) augmented with perturbative triples correction [CCSD(T)], also cannot correctly describe the energy behaviors in the bond-dissociation regime. This phenomenon originates from another Coulomb correlation effect known as “non-dynamic correlation”, also termed “static correlation” or “strong correlation”, because it is not related to electron dynamics. This issue arises because the wave function in the HF model is represented by a single Slater determinant, which may not adequately represent the state of specific systems. In certain situations, such as bond stretching, an electronic state can only be accurately described by a linear combination of multiple near-degenerate Slater determinants due to the presence of near-degenerate frontier molecular orbitals (MOs) constituting a complete active space (CAS). Such static correlations are also often observed in various conjugated molecules and transition metal compounds that possess energetically near-degenerate π orbitals or d/f orbitals, and can be well described by multi-configurational (MC) quantum chemical methods, such as valence bond (VB) theory, complete active space configuration interaction (CASCI) or complete active space self-consistent field (CASSCF).
 | ||
| Fig. 1 Calculated ground-state potential energy curves of (a) H2 and (b) N2 dissociation with the cc-pVQZ basis set via ORCA 4.2.13 unless otherwise specified. The exact curves are calculated by FCI (H2) and density matrix renormalization group (DMRG)-FCI (N2, m = 1000, using Kylin4), respectively. The uncontracted MRCISD calculations are performed by BDF.5 | ||
Quantitatively accurate electron correlation calculations for realistic large strongly correlated systems are highly challenging, due to the difficulties of both treating static correlations in a large active space and incorporating further the dynamic correlation outside the large active space. The first difficulty is because the dimension of the Hilbert space scales exponentially with the number of the active orbitals. Nowadays, the largest exactly solved active space comprises 26 electrons and 23 orbitals, i.e. (26e, 23o), for C3H8/STO-3G with 1.31 trillion determinants, by virtue of utilizing high-performance distributed computations on supercomputers.6 In recent decades, advancements in selected configuration interaction (sCI),7–11 quantum Monte Carlo (QMC),12–14 and density matrix renormalization group (DMRG)15–19 and others20,21 have significantly enhanced the computational ability of accurately describing static correlations within very large active spaces, encompassing several tens or even over 100 active orbitals.4,9,22 These improvements stem from the screening of important configurations or the compression of information through iterative renormalization of truncated many-electron bases. However, to quantitatively comprehend the behaviors of strongly correlated molecular systems, it is imperative to account for both static and dynamic electron correlations. This requirement necessitates the combination of sCI, QMC or DMRG as a CASCI solver and traditional multi-reference (MR) methods, such as MR configuration interaction (MRCI), MR perturbation theory (MRPT), and MR coupled cluster (MRCC). The MR methods address both CFGs within the CAS and excited CFGs involving electron excitations from the CAS to virtual inactive orbitals. To circumvent the explicit handling of the vast number of excited configurations in MR computations, the fully internally contracted (FIC) approximation23–25 has been extensively utilized. Nevertheless, this introduces a new computational challenge due to the emergence of costly third-order and fourth-order reduced density matrices (3-RDM, 4-RDM) associated with the CAS. This limitation confines conventional MR calculations to the small CAS with less than 20 active orbitals, which is incompatible with the rapid progression of sCI, QMC and DMRG in managing the large CAS with up to 100 active orbitals. Although the straightforward implementation of MR methods, such as the MR Møller–Plesset method (MRMP),26 multi-configuration quasi-degenerate perturbation theory (MC-QDPT)27 and spin-adapted state-specific MRPT (SA-SSMRPT),28,29 without using FIC approximations can avoid the use of expensive high-order RDMs, their application to large systems is also computationally infeasible due to the combinatorial explosion of excited configurations. Consequently, a prominent trend in quantum chemistry for strongly correlated systems is to develop novel methodologies to capture dynamic correlations beyond large active spaces without using high-order RDMs.
This perspective focuses on new MR methods for a large CAS with more than 20 active orbitals and is organized as follows. Section 2 provides a brief introduction to the widely used contraction approximations in conventional MR quantum chemical methods and also discusses about their limitations in treating a large CAS. Then Sections 3–8 outline recent progresses for breaking through the bottlenecks of computing expensive high-order RDMs or including a huge number of reference CFGs to describe dynamic electron correlation beyond a large CAS. These developments include approximating high-order RDMs (Section 3), restricting the summation items (Section 4), using renormalized many-electron states instead of primitive CFGs (Section 5), using the effective Hamiltonian (Section 6), hybridization between MC-WFT and SR-WFT or density functional theory (Section 7) and using time-dependent formulation (Section 8). Then a numerical benchmark test for calculating the potential energy curve of the neodymium oxide (NdO) molecule by different methods is shown and discussed in Section 9. Finally, a brief summary and outlook is given in Section 10.
2 Contraction approximations in conventional MR quantum chemical methods
The exponentially increasing number of CAS configurations quickly leads to a bottleneck in MR calculations. Therefore, compressing the Hilbert space becomes essential for practical calculations. A commonly used technique in MR calculations is the contraction approximation, where certain configurations are grouped together in advance. The most basic contraction is the internally contracted (IC) approximation,23–25 in which configurations with the same excitation pattern are contracted. This means that the excitation operator acts on the contracted reference wavefunction rather than on individual configurations. The resulting excited electronic states are formed by applying the same creation and annihilation operators to different configurations within the reference space, and the contraction coefficients are determined by the corresponding configuration coefficients in the reference wavefunction. Since, in the original scheme, all configurations in the first order interaction space (FOIS),30 which can directly couple to the reference wave function via the Hamiltonian, are contracted, this approach is often referred to as the fully internally contracted (FIC) scheme.25 While the FIC approximation significantly reduces the size of the final matrix to be computed, the cost of computing matrix elements is relatively high. For instance, calculating matrix elements in the FIC scheme requires high-order RDMs, | (1) |
 is the electron integral, and
is the electron integral, and  is acquired as
is acquired as  . The spin-free excitation operator is given by:
. The spin-free excitation operator is given by:  with
with  . The highest order RDM involved is the 4-RDM
. The highest order RDM involved is the 4-RDM  , which comes from the single excitation space (semi-internally excited states):
, which comes from the single excitation space (semi-internally excited states): 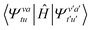 . To avoid the high computational cost brought by the highest-order RDM from the single excitation space, the “partially contracted” (PC) scheme was further proposed, including the Werner–Knowles (WK)31,32 and Celani–Werner (CW)33 schemes. In these schemes, the reference space and the single excitation space are no longer contracted, and the CFG basis vectors are fully utilized. This reduces the 4-RDM to a 3-RDM and minimizes the error introduced by the contraction approximation. However, at the same time, the variational space once again grows exponentially due to the increase in configuration basis vectors.
. To avoid the high computational cost brought by the highest-order RDM from the single excitation space, the “partially contracted” (PC) scheme was further proposed, including the Werner–Knowles (WK)31,32 and Celani–Werner (CW)33 schemes. In these schemes, the reference space and the single excitation space are no longer contracted, and the CFG basis vectors are fully utilized. This reduces the 4-RDM to a 3-RDM and minimizes the error introduced by the contraction approximation. However, at the same time, the variational space once again grows exponentially due to the increase in configuration basis vectors.
In addition to the FIC and PC internally contracted schemes, there is another scheme called strong contraction (SC),34,35 commonly used in the n-electron valence state perturbation theory (NEVPT) method. As its name suggests, in the SC approximation, the subspaces in the FIC method are further contracted using electron integrals. Internally contracted electronic states with the same excitation pattern in the active space are multiplied by integrals and summed to be further contracted, and accordingly there are no more active space indices in the final SC electronic states.
Another contraction approximation, in contrast to internal contraction, is the external contraction (EC)36 approximation. After determining the contraction coefficients through second-order perturbation, configurations in the FOIS with the same external space are contracted into a single electronic state. Therefore, the size of the external space does not affect the dimensionality of the variational space after EC contraction, making it particularly suitable for large basis set calculations. However, since its computational cost is directly related to the size of the reference space, the cost becomes prohibitive as the active space grows. It often needs to be combined with the idea of selected CI to handle large active space calculations.
3 Approximating high-order RDMs
The many-particle correlation information stored in an n-RDM can be partitioned into two parts, an irreducible part (the cumulant) describing genuine n-particle correlations and a reducible part describing remaining n-particle correlations as products of lower-rank cumulants.37,38 In typical situations, genuine many-particle correlations beyond a certain rank can be neglected, making it possible to approximate high-order RDMs using their cumulant expansion. Under such cumulant approximations, an n-RDM (n = 3, 4) is written using the anti-symmetrized products among the l-RDMs (l = 1, 2, …, n − 1) along with neglecting the n-rank cumulant. For example, 4-RDMs can be decomposed as:39 | (2) |
 refers to the fully-connected cumulant and is regarded as small in the cumulant approximation. The cumulant approximation has been extensively used in MR quantum chemistry. It has been adopted in strongly contracted (SC) second-order n-electron valence state perturbation (NEVPT2),40 FIC-MRCI,39,41 FIC-CAS second-order perturbation theory (FIC-CASPT2),42,43etc. While the cumulant approximation significantly reduces the computational costs, it may disrupt the variational nature of MRCI or introduce spurious intruder states into MRPT, due to the presence of nonphysical interactions within the Hamiltonian matrix.
refers to the fully-connected cumulant and is regarded as small in the cumulant approximation. The cumulant approximation has been extensively used in MR quantum chemistry. It has been adopted in strongly contracted (SC) second-order n-electron valence state perturbation (NEVPT2),40 FIC-MRCI,39,41 FIC-CAS second-order perturbation theory (FIC-CASPT2),42,43etc. While the cumulant approximation significantly reduces the computational costs, it may disrupt the variational nature of MRCI or introduce spurious intruder states into MRPT, due to the presence of nonphysical interactions within the Hamiltonian matrix.
It is worth noting that high-order RDMs can also be approximated using alternative techniques. For instance, one can use a simplified approximate reference wave function to evaluate RDMs with much reduced computational costs. On top of the DMRG reference wave function, Guo et al.44 estimated the 4-RDM with a lower bond dimension than that employed in the DMRG energy optimization. Similarly, in Roemelt et al.'s implementation of SC-NEVPT2 on top of the DMRG reference, both the perturber functions and the unperturbed Hamiltonian are projected onto a reduced Hilbert space.45 This space is defined by the renormalized states in the middle of the DMRG lattice, rather than the full variational matrix product state (MPS) space in usual DMRG calculations. High-order RDMs can also be efficiently computed using the resolution of identity (RI)46 approximation, which factorizes many-index matrices into a sum of products involving only fewer-index matrices.
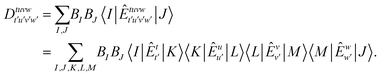 | (3) |
Here, the zeroth-order wave function is taken as  and the set of
and the set of  represents suitable many-particle state functions. By applying pre-screening (PS) and extended PS (EPS) approximations to the CASCI reference wave function, the number of state functions within the RI space can be significantly reduced.47 By factorizing the matrix elements of the Dyall Hamiltonian in a similar manner, the computational cost for all matrices involved in the FIC-NEVPT2 method can also be reduced to that of evaluating only 3-RDMs.48,49
represents suitable many-particle state functions. By applying pre-screening (PS) and extended PS (EPS) approximations to the CASCI reference wave function, the number of state functions within the RI space can be significantly reduced.47 By factorizing the matrix elements of the Dyall Hamiltonian in a similar manner, the computational cost for all matrices involved in the FIC-NEVPT2 method can also be reduced to that of evaluating only 3-RDMs.48,49
4 Restricting the summation items
Another way to characterize dynamic correlations beyond a large active space is to completely avoid the use of high-order RDMs. As discussed in Section 2, this necessitates the costly computation of Hamiltonian elements, owing to the immense number of summation terms over the vast array of excited CFGs. Instead of employing the extensive CASCI expansion (easily exceeding one billion terms) within a large CAS, a straightforward strategy to reduce the number of excited CFGs is to utilize the compact sCI wave function as the reference. This reference comprises only a limited number (usually less than one hundred thousand) of truncated, significant CFGs. Ma et al.50,51 have successfully implemented spin-adapted MRCI on top of the sCI reference in conjunction with EC approximation. This approach, termed as sCI-EC-MRCI, has been effectively utilized for active spaces encompassing over 40 active orbitals. The impact of overlooked reference CFGs can be further taken into account through a static-dynamic-static (SDS) framework proposed by Liu et al.52 This is achieved by introducing not just the primary space (P), which is composed of reference CFGs, and the external space (Q), comprised of excited CFGs, but also a secondary space (S) that consists of the remaining CFGs within the CAS.The concept of stochastic sampling can also be utilized to decrease the number of summation terms when evaluating matrix elements in MR approaches. Alavi et al.53 proposed a stochastic evaluation of MR linearized coupled cluster (LCC) theory. In this method, both the zeroth-order and first-order wave functions are sampled stochastically by the full configuration interaction quantum Monte Carlo (FCIQMC)12 method. Recently, Booth et al.54 further utilized FCIQMC to develop a stochastic FIC-NEVPT2 method. Sharma et al.55,56 also suggested stochastic versions for both SC-MRCI and SC-NEVPT2 by employing variational Monte Carlo (VMC) to directly sample contributions from CFGs in the FOIS. One benefit of these stochastic methods is their excellent parallel efficiency, which allows them to be easily implemented on large-scale parallel computers, as has been demonstrated in numerous QMC studies.
Another straightforward strategy for simplifying the complexity in MR calculations involves focusing solely on single excitations from the reference, while disregarding contributions from double and higher excitations. For example, in the adiabatic connection (AC) method introduced by Pernal et al.,57–61 the two-electron RDMs at the given coupling constant α (ranging between 0 and 1) are approximately expressed by one-electron reduced properties, namely, 1-RDM and one-electron transition RDM (1-TRDM) in a non-perturbative way, and the α-dependent 1-TRDMs are obtained by employing Rowe's equation of motion theory in the extended random phase approximation (ERPA),62 which requires knowledge of only the 1-RDM and 2-RDM at α = 0 (i.e., those RDMs derived from CASSCF). However, the excitation operator is constrained to only single excitations within the working ERPA framework. This approach is found to be able to efficiently capture the dynamic correlation beyond a large CAS, as it avoids the use of high-order RDMs. But it is also noticed to be less accurate than other MR methods for strongly correlated systems and excited states due to its neglect of doubly excited configurations.63
5. Using renormalized many-electron states instead of primitive CFGs
While utilizing a subset of important CFGs as a reference or employing stochastic sampling can markedly reduce the computational demands associated with summation operations during matrix element evaluations, the convergence patterns concerning the chosen/sampled primitive CFGs are system dependent. In the case of extremely highly correlated systems, a vast array of CFGs possess nearly identical and non-negligible weights, thereby rendering these techniques ineffective for achieving converged outcomes. Therefore, for such systems, the idea of DMRG could be followed, where renormalized many-electron states are utilized instead of CFG bases to represent the entire Hilbert space. This approach could significantly compress the Hilbert space while maintaining high accuracy.Since the computational cost of quantum chemistry (QC)-DMRG scales steeply (O(k4m2) + O(k3m3)) with system size (k, the number of active orbitals) and necessitates a substantial number (m ∼ 103–4) of truncated renormalized bases, also known as auxiliary bond dimensions, directly applying it to the entire MO space is often prohibitive. Since the MPS in the QC-DMRG is block-sparse when particle number symmetry is considered, and each block's indices are associated with well-defined quantum numbers, the required bond dimension could be reduced during the sweep process by discarding blocks with specific quantum numbers. For example, by virtue of restricting the particle numbers of the MPS within an external space to not exceed two, the configurations corresponding to processes involving more than double excitations could be discarded (similar to limiting excitation patterns in MR calculations), thus the bond dimension is reduced. This approach was first implemented in the MPS-PT method,64,65 where the second-order energy is obtained by variationally minimizing the Hylleraas functional in the space of MPS. Consequently, the first-order wavefunction can be optimized by a sweep algorithm, while overlaps and transition operator elements can be easily obtained through contractions between two MPSs with one MPO. This method theoretically recovers exact uncontracted MRPT energies in the limit of a reasonable MPS bond dimension and can be applied to various MRPT theories such as NEVPT2, retaining excitation degree-perturbation theory (REPT2),66,67 and linearized multireference coupled-cluster method (MRLCCM),68 with different choices of zeroth-order Hamiltonian.
However, even if the bond dimension is reduced, one still needs to construct the long-chain MPO in quantum chemistry and perform multiple sweeps over a long chain of MO sites. For systems with hundreds of external orbitals, the MPS-PT method remains very expensive. Therefore, Larsson and others proposed fusing the external space sites into large sites.69,70 These large sites directly represent all possible electron configurations in the external space, i.e., residues of configurations in the external space. By constructing operator matrices with these configuration residues as basis vectors in the external space, the long orbital chain of the external orbitals in the standard MPS-PT method is compressed into one large site. Thus, the final number of sites is only the number of active orbitals plus one or two (depending on whether core orbitals and external orbitals are further fused together), avoiding the extensive sweep process in the external space. In addition to the MPS-PT with big sites, the MPS-MRCI, also known as the DMRG-RAS method, with big sites has also been implemented.
Since many MPS blocks are discarded by restricting quantum numbers, the MPS-PT/MRCI methods achieve a significant speedup compared to the standard DMRG. However, due to the appearance of “long-range interactions” caused by forcibly mapping MOs onto a one-dimensional chain, the MPS-PT/MRCI methods over the entire orbital space still require a much larger bond dimension than that used in DMRG calculations within the active space. Therefore, Ma et al.71 proposed a spin-adapted MPS-MRCI method to reduce the large bond dimension in the non-spin-adapted version and ensure spin-adapted results. Building on this, they further proposed adopting a divide-and-conquer approach, optimizing and obtaining the renormalized many-electron states in the active space, called renormalized residues (RRs), separately and then connecting them with configuration residues in the external space to describe the entire space. Since the entanglement within the external space is weak, the external orbitals can be partitioned and treated as the buffer environment space for parts of the active space, obtaining renormalized residues for the active space portion by portion. The resulted RR-MRCI method has been proved that it can improve the computational efficiency of the MPS-MRCI method while keeping the error controlled within chemical accuracy.
Although the RRs account for the environment's effect, resulting in fewer RRs representing the Hilbert space than contracted residues for the same accuracy, this also means that the computational cost for a single RR is often higher than that for a contracted residue, as the calculation needs to include the environment's degrees of freedom. Therefore, as a balance, contracted residues can be used in the double excitation space, while RRs are used in the single excitation space. This avoids the 4-RDM problem caused by contracted residues in the single excitation space and the excessive renormalization cost due to too many environmental degrees of freedom in the double excitation space. As a result, methods that mix RRs and contracted residues in MPS-PT and MRCI have also been proposed.71,72
6 Using the effective Hamiltonian
Rather than assessing the dynamic correlation with the bare many-electron Hamiltonian Ĥ, an alternative approach is to employ effective Hamiltonian theories, which allows one to encapsulate a vast array of degrees of freedom into a small part of![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) that is decoupled from the rest of the world via similarity transformations
that is decoupled from the rest of the world via similarity transformations  . Therefore, the main focus in the effective Hamiltonian theories is on Ĥ and its transformed version
. Therefore, the main focus in the effective Hamiltonian theories is on Ĥ and its transformed version ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) and the wave function plays a much more minor role.
and the wave function plays a much more minor role.
CC theory can be viewed as an effective Hamiltonian theory when one reformulates the exponential term in the wave function ansatz into the form of the transformed Hamiltonian. For example, the unitary canonical transformation (CT) method, initially proposed by White,73 and later advanced by Yanai and Chan et al.,74–78 is an approximated internally contracted MR unitary CC (ic-MRUCC) theory. However, this framework further incorporates operator decomposition approximations to systematically eliminate all three-body and higher-order interactions within the Baker-Campbell–Hausdorff (BCH) expansion of the transformed Hamiltonian, thereby simplifying the computational complexity.
Also using a formalism similar to that of unitary CC theory, Li and Evangelista79,80 proposed a MR-driven similarity renormalization group (DSRG) approach, which writes the unitary operator  in terms of an exponential operator eÂ(s), where Â(s) is the s-dependent anti-Hermitian operator in terms of standard cluster operator
in terms of an exponential operator eÂ(s), where Â(s) is the s-dependent anti-Hermitian operator in terms of standard cluster operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (s) as Â(s) =
(s) as Â(s) = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (s) −
(s) − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) †(s). As s increases, the DSRG transformation gradually reduces the magnitude of the non-diagonal components of
†(s). As s increases, the DSRG transformation gradually reduces the magnitude of the non-diagonal components of ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) (s) to zero. For finite values of s, the DSRG Hamiltonian possesses a band-diagonal structure in the Fock space. Due to the simplicity of the transformed Hamiltonian
(s) to zero. For finite values of s, the DSRG Hamiltonian possesses a band-diagonal structure in the Fock space. Due to the simplicity of the transformed Hamiltonian ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) (s), the highest body rank of RDM cumulants appearing in the expressions of the second-order perturbative approximation of the MR-DSRG, denoted as DSRG-MRPT2, is only three, therefore the expensive terms involving 4-RDMs are avoided. Recently, Feldmann and Reiher81 further combined the MR-DSRG with the FIC-MRCC and demonstrated that the unitary flow equation approach can be adapted for non-unitary transformations, rationalizing the renormalization of FIC-MRCC amplitudes. Meanwhile, DSRG suffers from a notable drawback, i.e. its performance is dependent on the choice of the flow parameter s.
(s), the highest body rank of RDM cumulants appearing in the expressions of the second-order perturbative approximation of the MR-DSRG, denoted as DSRG-MRPT2, is only three, therefore the expensive terms involving 4-RDMs are avoided. Recently, Feldmann and Reiher81 further combined the MR-DSRG with the FIC-MRCC and demonstrated that the unitary flow equation approach can be adapted for non-unitary transformations, rationalizing the renormalization of FIC-MRCC amplitudes. Meanwhile, DSRG suffers from a notable drawback, i.e. its performance is dependent on the choice of the flow parameter s.
In addition, the transcorrelated Hamiltonian, a non-Hermitian effective Hamiltonian, typically used for accounting for the explicit electron correlation in the electronic Hamiltonian, has also been incorporated into FCIQMC and DMRG calculations.82–85 Transcorrelation86 is a technique in which a similarity transformation is applied to the many-electron Hamiltonian Ĥ in order to absorb an exponential Jastrow correlation factor ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) :
: ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = e−
= e−![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) Ĥe
Ĥe![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) . By virtue of using the transcorrelated Hamiltonian, part of the dynamic correlation induced by the electron–electron cusp can be efficiently dealt with, and accordingly much faster energy convergence with respect to the basis set size can be achieved. However, the other remaining dynamic correlations still have to be considered with other standard MR methods.
. By virtue of using the transcorrelated Hamiltonian, part of the dynamic correlation induced by the electron–electron cusp can be efficiently dealt with, and accordingly much faster energy convergence with respect to the basis set size can be achieved. However, the other remaining dynamic correlations still have to be considered with other standard MR methods.
7 Hybridization between MC-WFT and SR-WFT or density functional theory
A computationally cheap strategy to obtain dynamic correlations beyond large active spaces is to combine MC-WFT methods with SR-WFT ones or density functional theory (DFT), thereby exploiting the high efficiency in treating dynamic correlation by SR-WFT or DFT, while maintaining the success of describing static correlation by MC-WFT.One representative example along this direction is tailored CC (TCC),87–90 which employs the following split-amplitude wave function ansatz
 | (4) |
Here the cluster operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) comprises two parts: a CAS part (
comprises two parts: a CAS part (![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) CAS) and an external part (
CAS) and an external part (![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ext). Note that
ext). Note that  is a single determinant reference, so
is a single determinant reference, so ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) CAS and
CAS and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ext commute naturally. Therefore,
ext commute naturally. Therefore, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) CAS can be seen as the static correlation with respect to the HF single reference and its associated CC amplitudes can be acquired by a SCI, QMC or DMRG procedure and then kept frozen during the TCC calculation.91–97 As for the
CAS can be seen as the static correlation with respect to the HF single reference and its associated CC amplitudes can be acquired by a SCI, QMC or DMRG procedure and then kept frozen during the TCC calculation.91–97 As for the ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ext amplitudes, they are optimized by the following linked CC equation analogous to that in the standard SRCC method:
ext amplitudes, they are optimized by the following linked CC equation analogous to that in the standard SRCC method:
 | (5) |
 is the excited CFG that does not lie in the CAS.
is the excited CFG that does not lie in the CAS.
Different from TCC, the externally corrected CC (ecCC) method98–100 extracts static correlation from an approximate CASCI solver and then uses this wave function as an “external” source of high-order CC amplitudes. For instance, in ecCC singles and doubles (ecCCSD), the cluster operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is given by
is given by
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) = = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 + 1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 + 2 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ec3 + ec3 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ec4, ec4, | (6) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ec3 and
ec3 and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ec4 excite the HF single reference determinant into the space of triples and quadruples determinants extracted from the external source. The
ec4 excite the HF single reference determinant into the space of triples and quadruples determinants extracted from the external source. The ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 and
1 and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 amplitudes are obtained by solving the ecCCSD equation using fixed
2 amplitudes are obtained by solving the ecCCSD equation using fixed ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ec3 and
ec3 and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ec4.
ec4.
DFT is nowadays the most prevalent electronic structure method in quantum chemistry. This popularity stems from its optimal balance between computational accuracy and efficiency. However, challenges persist in addressing its delocalization error and static correlation error. The combination of MC-WFT and DFT presents ambiguity due to the difficulty in separating static and dynamic correlations strictly. A minor fraction of static correlation is inherently incorporated into DFT computations through empirical functional parameters. Consequently, without implementing appropriate treatments, this can result in the double-counting of correlation effects.
To address the issue of double-counting correlation effects, Savin and Flad101 introduced the MC range-separated short-range DFT (MC-srDFT) method. In this approach, the two-electron operator is bifurcated into long-range (lr) and short-range (sr) components. Consequently, the short-range segment of electron interaction is managed by DFT, while the long-range segment is allocated to MC-WFT. MC-srDFT necessitates the development of new short-range exchange–correlation functionals because the standard functionals, which were engineered to encapsulate the entire electron correlation, are ill-suited for this purpose. As a result, variants such as short-range local density approximation (srLDA), short-range generalized gradient approximation (srGGA), and meta-srGGA have been devised.
The symmetry dilemma, in addition to the double-counting error, represents one of the most significant theoretical challenges to the proper combination of MC-WFT and DFT. Conventional DFT models' treatment of open-shell systems hinges on the employment of unphysical ρα and ρβ densities, derived from unrestricted (i.e., spin-polarized) Slater determinants with incorrect spin symmetry. This is incompatible with the preserved spin symmetry in MC-WFT, whose eigenfunctions are Ŝ2 and Ŝz (where S represents the total electron spin). A potential solution to this symmetry dilemma is multi-configurational pair-density functional theory (MC-PDFT).102–108 In this framework, the functional is expressed in terms of the total density ρ along with the on-top two-particle pair density Π, rather than being a function of the spin-up and spin-down densities as in usual DFT. The on-top pair density is expressed in terms of the 2-RDM as
 | (7) |
8 Using time-dependent formulation
In MRPT, the initial zeroth-order wave function is not an eigenstate of a one-electron Hamiltonian but rather of an interacting Hamiltonian. This implies that functions of the zeroth-order Hamiltonian, such as the resolvent operator in PT, are not explicitly known in computational form. Nevertheless, executing time-evolution with this identical Hamiltonian is comparatively more manageable. Therefore, Sokolov and colleagues109,110 have proposed a time-dependent formulation of MRPT, which builds on the framework of time-dependent perturbation theory. This formulation has been applied to time-dependent NEVPT2, yielding the fully uncontracted NEVPT2 wave function and energy but with a lower computational scaling than the usual contracted variants, and also bypassing the construction of high-order RDMs. Nonetheless, the efficiency and accuracy of wave function compression during imaginary-time evolution warrant further investigation.9 Benchmarking over the NdO molecule
Rare-earth elements (REEs) are crucial components in numerous high-technology products, advanced materials, and computing devices. To evaluate the effectiveness of the aforementioned methodologies, we examine the potential energy curve for the ground state of the neodymium oxide (NdO) molecule employing multiple available MR approaches. Previously, this molecule was studied using several methods including single-reference CCSD(T) based on the complex-valued wave function111 and the second-order generalized Van Vleck perturbation theory (GVVPT2) method with an active space comprising 10 orbitals and 10 electrons.112 Although GVVPT2 provided a reasonable estimate for the equilibrium bond length (1.780 Å), the calculated harmonic frequency (891 cm−1) exhibited significant discrepancies from the experimental measurements. Consequently, in this study, we employ a larger active space to compute this molecule.We performed DMRG-SCF (m = 1000) calculations using the OpenMolcas software113 in combination with Block2114 to optimize the orbitals. Subsequently, we generated the FCIDUMP file of molecular orbital integrals using the DMRG-SCF natural orbitals (with external orbitals canonicalized), which were then read into the PySCF115 and Kylin4 software to compute additional results. The methods employed include DMRG-FIC-CASPT2 (OpenMolcas + Block2), DMRG-PDFT (OpenMolcas + QCMaquis116), DMRG-AC0 (PySCF + Block2), DMRG-uLDSRG(2) (Forte117 + Block2), DMRG-FIC-NEVPT2 (Block2), DMRG-SC-NEVPT2 (Block2), MPS-NEVPT2 (Block2), MPS-MRREPT2 (Block2), MPS-MRCI (Block2/Kylin), DMRG2sCI-EC-MRCI (Kylin), DMRG2sCI-ENPT2 (Kylin), and RR-UC-MRCI (Kylin). The molecular point group of NdO was set to C2v, and the “Linear” keyword was used during the DMRG-SCF calculations to account for its supersymmetry. The basis set used was ANO-RCC-VQZP, and second-order scalar relativistic corrections were included via the Douglas–Kroll–Hess (DKH) Hamiltonian.
We selected an active space of (18e, 20o) for NdO, encompassing the 5s, 5p, 5d, 4f, and 6s orbitals of Nd and the 2p orbital of O, with all occupied inactive orbitals frozen. The calculated electronic state was the ground state of NdO: 15Π. The results are presented in Fig. 2. Note that DMRG-PDFT does not approach the FCI limit within this basis set but rather aims to approach the basis set limit. Therefore, its results are not presented in the figure. The original data for these methods can be found in the ESI.† The equilibrium bond length and spectroscopic parameters of NdO were fitted using a sixth-order polynomial, with detailed values provided in Table 1.
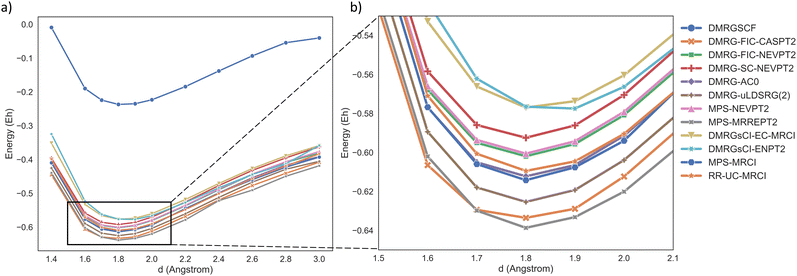 | ||
| Fig. 2 Potential energy curve of the ground state (15Π) of the NdO molecule. The energy values in the graph have been shifted by −9691 Hartree. | ||
| R e/angstrom | Error (%) | ω e/cm−1 | Error (%) | B e/cm−1 | Error (%) | Average errorh (%) | |
|---|---|---|---|---|---|---|---|
a DMRG-CASSCF (m = 500) followed by a DMRG-complete active space configuration interaction (DMRG-CASCI) (m = 1000) calculation using DMRG-CASSCF (m = 500) natural orbitals.
b The DMRG (m = 1000) wave function of CAS(20o, 18e) is used as the reference wave function.
c The maximum discarded weight is set to be 5 × 10−4, and as a result, the completeness of all calculations 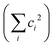 is over 0.989.
d The MPS with a large-site strategy is utilized, and the m used for the MPS-MR calculation is 5000.
e The parameter s in the DSRG is assigned a value of 0.5.
f The external space is evenly divided into 5 buffer spaces, and the total bond dimension is over 0.989.
d The MPS with a large-site strategy is utilized, and the m used for the MPS-MR calculation is 5000.
e The parameter s in the DSRG is assigned a value of 0.5.
f The external space is evenly divided into 5 buffer spaces, and the total bond dimension  is 5 × 2000.
g The GVVPT2 data were adopted from Sepehri's work,112 which involved the use of a smaller active space characterized by (10e, 10o).
h The average error is calculated by averaging the absolute values of the percentage errors in Re, ωe, and Be. is 5 × 2000.
g The GVVPT2 data were adopted from Sepehri's work,112 which involved the use of a smaller active space characterized by (10e, 10o).
h The average error is calculated by averaging the absolute values of the percentage errors in Re, ωe, and Be.
|
|||||||
| DMRG-SCFa | 1.827 | 2.07 | 778.2 | −6.24 | 0.351 | −3.04 | 3.78 |
| DMRG-PDFT (T:BLYP)b | 1.832 | 2.35 | 744.8 | −10.27 | 0.349 | −3.59 | 5.41 |
| DMRG-PDFT (FT:BLYP)b | 1.828 | 2.12 | 748.08 | −9.87 | 0.350 | −3.31 | 5.10 |
| DMRG2sCI-ENPT2ac | 1.845 | 3.07 | 763.5 | −8.01 | 0.344 | −4.97 | 5.35 |
| DMRG-PDFT (FT:revPBE)b | 1.808 | 1.01 | 764.96 | −7.84 | 0.358 | −1.10 | 3.32 |
| DMRG-PDFT (T:revPBE)b | 1.809 | 1.06 | 765.85 | −7.73 | 0.358 | −1.10 | 3.30 |
| DMRG2sCI-EC-MRCIac | 1.814 | 1.34 | 781.1 | −5.89 | 0.356 | −1.66 | 2.96 |
| DMRG-PDFT (T:PBE)b | 1.804 | 0.78 | 770.99 | −7.11 | 0.359 | −0.83 | 2.91 |
| DMRG-PDFT (FT:PBE)b | 1.802 | 0.67 | 772.24 | −6.96 | 0.360 | −0.55 | 2.73 |
| DMRG-PDFT (FT:OPBE)b | 1.762 | −1.56 | 809.47 | −2.47 | 0.377 | 4.14 | 2.72 |
| DMRG-PDFT (T:OPBE)b | 1.760 | −1.68 | 818.99 | −1.33 | 0.378 | 4.42 | 2.48 |
| DMRG-PDFT (FT:LSDA)b | 1.769 | −1.17 | 814.4 | −1.88 | 0.374 | 3.31 | 2.12 |
| DMRG-PDFT (T:LSDA)b | 1.773 | −0.95 | 808.6 | −2.58 | 0.372 | 2.76 | 2.10 |
| DMRG-FIC-NEVPT2b | 1.787 | −0.17 | 793.4 | −4.41 | 0.366 | 1.10 | 1.89 |
| MPS-MRREPT2d | 1.797 | 0.39 | 786.8 | −5.21 | 0.362 | 0.14 | 1.91 |
| DMRG-FIC-CASPT2b | 1.776 | −0.78 | 813.2 | −2.02 | 0.371 | 2.49 | 1.76 |
| DMRG-SC-NEVPT2b | 1.786 | −0.22 | 809.2 | −2.51 | 0.367 | 1.38 | 1.37 |
| MPS-NEVPT2d | 1.788 | −0.12 | 799.7 | −3.65 | 0.366 | 1.16 | 1.64 |
| DMRG-uLDSRG(2)e | 1.790 | −0.03 | 804.7 | −3.05 | 0.366 | 0.97 | 1.35 |
| RR-UC-MRCIf | 1.802 | 0.67 | 807.6 | −2.70 | 0.360 | −0.55 | 1.31 |
| MPS-MRCId | 1.789 | −0.06 | 833.6 | 0.43 | 0.366 | 1.10 | 0.86 |
| DMRG-AC0b | 1.792 | 0.11 | 820.8 | −1.11 | 0.365 | 0.83 | 0.68 |
| Ref (GVVPT2)g | 1.780 | −0.56 | 891.0 | 7.30 | 0.359 | −0.83 | 2.90 |
| Experiment118 | 1.79 | — | 830 | — | 0.362 | — | — |
The obtained results demonstrate that the DMRG-SCF method is capable of qualitatively describing the dissociation behavior of NdO with reasonable accuracy. However, it should be noted that a systematic energy shift is observed when compared to other MR calculations due to its neglect of dynamic correlation. Moreover, the error in the estimated harmonic frequency for the DMRG-SCF exceeds 5%, also highlighting the importance of dynamic correlation. All other MR methods that incorporate dynamic correlation beyond DMRG generally provide a close estimation of dynamic correlation energy, around 0.4 Hartree. For the equilibrium bond length, most MR methods yield excellent fitting results with relative errors less than 1%, except for the DMRG2sCI-EC-MRCI/ENPT2 methods. Regarding the harmonic frequency, most methods result in fitting errors larger than 2%, except for MPS-MRCI and DMRG-AC0, as well as DMRG-PDFT when using FT:LSDA or T:LSDA on-top pair density functionals. Notably, the performance of PDFT is clearly sensitive to the choice of functional. Overall, the DMRG-SC-NEVPT2, DMRG-uLDSRG(2), DMRG-AC0, MPS-MRCI, and RR-UC-MRCI approaches yield results that are close to the experimental values118 for this system. We hope that the insights from this calculation can serve as a reference for other chemical systems or as a benchmark for future novel MR methods.
10 Summary and outlook
The integration of innovative approaches for addressing dynamic electron correlation with advanced approximate FCI-solvers is increasingly being acknowledged as the standard methodology for handling strongly correlated chemical molecules and complexes. In this perspective, we reviewed the state-of-the-art approaches for treating dynamic correlation beyond large active spaces while avoiding the usage of expensive high-order RDMs and classified them into seven types. These works have demonstrated their ability to treat dynamic correlation, with varying levels of accuracy and efficiency resulting from their distinct theoretical frameworks. Recent numerical tests, exemplified by the NdO molecules’ potential energy curve, demonstrate that these methods can achieve promising accuracy in capturing both static and dynamic correlations.Despite the many impressive schemes that have been proposed and tested, their accessibility and ease of use remain major challenges. To this day, the most commonly used MR methods within the quantum chemistry community are still CASPT2 and NEVPT2. Aside from the good balance between accuracy and efficiency offered by these two methods, the fact that many novel methods have not been integrated into popular quantum chemistry programs is another reason for their limited adoption. Therefore, user-friendly implementations in commonly-used software packages remain a major task for this field. Additionally, the use of MR methods is always associated with the choice of active space.119,120 In some cases, the need for a large active space arises from the inability to select a suitable medium-sized active space or from changes in active space composition along reaction pathways or potential energy surfaces.121 Thus, the selection of active space is a significant challenge faced by all methods aiming to treat dynamic correlation. Finally, due to the high computational cost of these methods, progress related to calculations of excited states, molecular spectra, and non-Born–Oppenheimer effects remains limited. Therefore, combining these methods with techniques such as the resolution of identity, local correlation, explicit correlation, and high-performance computing is becoming increasingly important.
Author contributions
All authors contributed to data analysis and paper writing.Data availability
Data for this article, including the original NdO potential curve data and the files required for generating the FCIDUMP of DMRGSCF orbitals are available at https://github.com/zhaivanczha/PCCP_NdO_CAS20o18e.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the National Natural Science Foundation of China (22325302) is gratefully acknowledged. The authors thank Prof. Yang Guo, Dr Ke Liao, Dr Ning Zhang, Dr Huanchen Zhai and Dr Rulin Feng for their stimulating discussions. Special thanks are extended to Prof. Chenyang Li for supplying the DMRG-DSRG data.Notes and references
- E. Wigner and F. Seitz, Phys. Rev., 1934, 46, 509–524 CrossRef CAS.
- D. P. Tew, W. Klopper and T. Helgaker, J. Comput. Chem., 2007, 28, 1307–1320 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- Z. Xie, Y. Song, F. Peng, J. Li, Y. Cheng, L. Zhang, Y. Ma, Y. Tian, Z. Luo and H. Ma, J. Comput. Chem., 2023, 44, 1316–1328 CrossRef CAS.
- Y. Zhang, B. Suo, Z. Wang, N. Zhang, Z. Li, Y. Lei, W. Zou, J. Gao, D. Peng, Z. Pu, Y. Xiao, Q. Sun, F. Wang, Y. Ma, X. Wang, Y. Guo and W. Liu, J. Chem. Phys., 2020, 152, 064113 CrossRef.
- H. Gao, S. Imamura, A. Kasagi and E. Yoshida, J. Chem. Theory Comput., 2024, 20, 1185–1192 CrossRef CAS.
- J. B. Schriber and F. A. Evangelista, J. Chem. Phys., 2016, 144, 161106 CrossRef PubMed.
- A. A. Holmes, N. M. Tubman and C. J. Umrigar, J. Chem. Theory Comput., 2016, 12, 3674–3680 CrossRef CAS PubMed.
- N. M. Tubman, C. D. Freeman, D. S. Levine, D. Hait, M. Head-Gordon and K. B. Whaley, J. Chem. Theory Comput., 2020, 16, 2139–2159 CrossRef CAS PubMed.
- N. Zhang, W. Liu and M. R. Hoffmann, J. Chem. Theory Comput., 2021, 17, 949–964 CrossRef CAS.
- J. Li and J. Yang, J. Phys. Chem. Lett., 2022, 13, 10042–10047 CrossRef CAS.
- G. H. Booth, A. J. W. Thom and A. Alavi, J. Chem. Phys., 2009, 131, 054106 CrossRef.
- B. M. Austin, D. Y. Zubarev and W. A. J. Lester, Chem. Rev., 2012, 112, 263–288 CrossRef CAS.
- J. Hermann, Z. Schätzle and F. Noé, Nat. Chem., 2020, 12, 891–897 CrossRef CAS PubMed.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef.
- U. Schollwöck, Rev. Mod. Phys., 2005, 77, 259–315 CrossRef.
- G. K.-L. Chan and S. Sharma, Annu. Rev. Phys. Chem., 2011, 62, 465–481 CrossRef CAS PubMed.
- A. Baiardi and M. Reiher, J. Chem. Phys., 2020, 152, 040903 CrossRef CAS PubMed.
- H. Ma, U. Schollwöck and Z. Shuai, Density Matrix Renormalization Group (DMRG)-based Approaches in Computational Chemistry, Elsevier, 2022, pp. 91–147 Search PubMed.
- J. Greiner, I. Gianni, T. Nottoli, F. Lipparini, J. J. Eriksen and J. Gauss, J. Chem. Theory Comput., 2024, 20, 4663–4675 CrossRef CAS PubMed.
- X. Ren, J. Zou, H. Zhang, W. Li and S. Li, J. Phys. Chem. Lett., 2024, 15, 693–700 CrossRef CAS PubMed.
- H. Zhai and G. K.-L. Chan, J. Chem. Phys., 2021, 154, 224116 CrossRef CAS.
- W. Meyer, in Configuration Expansion by Means of Pseudonatural Orbitals, ed. H. F. Schaefer, Springer US, Boston, MA, 1977, pp. 413–446 Search PubMed.
- P. E. Siegbahn, Int. J. Quantum Chem., 1980, 18, 1229–1242 CrossRef CAS.
- H.-J. Werner and E.-A. Reinsch, J. Chem. Phys., 1982, 76, 3144–3156 CrossRef CAS.
- K. Hirao, Chem. Phys. Lett., 1992, 190, 374–380 CrossRef CAS.
- H. Nakano, J. Chem. Phys., 1993, 99, 7983–7992 CrossRef CAS.
- S. Mao, L. Cheng, W. Liu and D. Mukherjee, J. Chem. Phys., 2012, 136, 024105 CrossRef.
- S. Mao, L. Cheng, W. Liu and D. Mukherjee, J. Chem. Phys., 2012, 136, 024106 CrossRef.
- A. McLean and B. Liu, J. Chem. Phys., 1973, 58, 1066–1078 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- P. E. Siegbahn, Int. J. Quantum Chem., 1983, 23, 1869–1889 CrossRef CAS.
- C. Valdemoro, Phys. Rev. A:At., Mol., Opt. Phys., 1992, 45, 4462–4467 CrossRef PubMed.
- D. A. Mazziotti, Phys. Rev. A:At., Mol., Opt. Phys., 1998, 57, 4219–4234 CrossRef CAS.
- M. Saitow, Y. Kurashige and T. Yanai, J. Chem. Phys., 2013, 139, 044118 CrossRef.
- D. Zgid, D. Ghosh, E. Neuscamman and G. K.-L. Chan, J. Chem. Phys., 2009, 130, 194107 CrossRef.
- M. Saitow, Y. Kurashige and T. Yanai, J. Chem. Theory Comput., 2015, 11, 5120–5131 CrossRef CAS PubMed.
- Y. Kurashige, J. Chalupský, T. N. Lan and T. Yanai, J. Chem. Phys., 2014, 141, 174111 CrossRef PubMed.
- Q. M. Phung, S. Wouters and K. Pierloot, J. Chem. Theory Comput., 2016, 12, 4352–4361 CrossRef CAS PubMed.
- S. Guo, M. A. Watson, W. Hu, Q. Sun and G. K.-L. Chan, J. Chem. Theory Comput., 2016, 12, 1583–1591 CrossRef CAS PubMed.
- M. Roemelt, S. Guo and G. K.-L. Chan, J. Chem. Phys., 2016, 144, 204113 CrossRef PubMed.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- Y. Guo, K. Sivalingam and F. Neese, J. Chem. Phys., 2021, 154, 214111 CrossRef CAS PubMed.
- K. Chatterjee and A. Y. Sokolov, J. Chem. Theory Comput., 2020, 16, 6343–6357 CrossRef CAS PubMed.
- C. Kollmar, K. Sivalingam, Y. Guo and F. Neese, J. Chem. Phys., 2021, 155, 234104 CrossRef CAS.
- Z. Luo, Y. Ma, X. Wang and H. Ma, J. Chem. Theory Comput., 2018, 14, 4747–4755 CrossRef CAS PubMed.
- Y. Song, W. Huang, C. Liu, Y. Lei, B. Suo and H. Ma, J. Phys. Chem. A, 2024, 128, 958–971 CrossRef CAS PubMed.
- Y. Lei, W. Liu and M. R. Hoffmann, Mol. Phys., 2017, 115, 2696–2707 CrossRef CAS.
- G. Jeanmairet, S. Sharma and A. Alavi, J. Chem. Phys., 2017, 146, 044107 CrossRef PubMed.
- R. J. A. James, J. Halson and G. H. Booth, Mol. Phys., 2020, 118, e1802072 CrossRef.
- A. Mahajan, N. S. Blunt, I. Sabzevari and S. Sharma, J. Chem. Phys., 2019, 151, 211102 CrossRef PubMed.
- N. S. Blunt, A. Mahajan and S. Sharma, J. Chem. Phys., 2020, 153, 164120 CrossRef CAS PubMed.
- K. Pernal, Phys. Rev. Lett., 2018, 120, 013001 CrossRef CAS PubMed.
- E. Pastorczak and K. Pernal, J. Phys. Chem. Lett., 2018, 9, 5534–5538 CrossRef CAS PubMed.
- E. Maradzike, M. Hapka, K. Pernal and A. E. I. DePrince, J. Chem. Theory Comput., 2020, 16, 4351–4360 CrossRef CAS PubMed.
- P. Beran, M. Matoušek, M. Hapka, K. Pernal and L. Veis, J. Chem. Theory Comput., 2021, 17, 7575–7585 CrossRef CAS PubMed.
- D. Drwal, P. Beran, M. Hapka, M. Modrzejewski, A. Sokól, L. Veis and K. Pernal, J. Phys. Chem. Lett., 2022, 13, 4570–4578 CrossRef CAS PubMed.
- K. Chatterjee and K. Pernal, J. Chem. Phys., 2012, 137, 204109 CrossRef PubMed.
- Y. Guo and K. Pernal, Faraday Discuss., 2024, 254, 332–358 RSC.
- S. Sharma and G. K. Chan, J. Chem. Phys., 2014, 141, 111101 CrossRef PubMed.
- S. Sharma and A. Alavi, J. Chem. Phys., 2015, 143, 102815 CrossRef PubMed.
- R. F. Fink, Chem. Phys. Lett., 2006, 428, 461–466 CrossRef CAS.
- R. F. Fink, Chem. Phys., 2009, 356, 39–46 CrossRef CAS.
- W. D. Laidig and R. J. Bartlett, Chem. Phys. Lett., 1984, 104, 424–430 CrossRef CAS.
- H. R. Larsson, H. Zhai, K. Gunst and G. K.-L. Chan, J. Chem. Theory Comput., 2022, 18, 749–762 CrossRef CAS PubMed.
- G. Barcza, M. A. Werner, G. Zaránd, A. Pershin, Z. Benedek, O. Legeza and T. Szilvási, J. Phys. Chem. A, 2022, 126, 9709–9718 CrossRef CAS PubMed.
- Y. Cheng and H. Ma, J. Chem. Theory Comput., 2024, 20, 1988–2009 CrossRef PubMed.
- S. Sharma, G. Knizia, S. Guo and A. Alavi, J. Chem. Theory Comput., 2017, 13, 488–498 CrossRef CAS PubMed.
- S. R. White, J. Chem. Phys., 2002, 117, 7472–7482 CrossRef CAS.
- T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2006, 124, 194106 CrossRef PubMed.
- T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 104107 CrossRef PubMed.
- T. Y. Eric Neuscamman and G. K.-L. Chan, Int. Rev. Phys. Chem., 2010, 29, 231–271 Search PubMed.
- E. Neuscamman, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2010, 132, 024106 CrossRef PubMed.
- T. Yanai, Y. Kurashige, E. Neuscamman and G. K.-L. Chan, J. Chem. Phys., 2010, 132, 024105 CrossRef PubMed.
- C. Li and F. A. Evangelista, J. Chem. Theory Comput., 2015, 11, 2097–2108 CrossRef CAS PubMed.
- C. Li and F. A. Evangelista, Annu. Rev. Phys. Chem., 2019, 70, 245–273 CrossRef CAS PubMed.
- R. Feldmann and M. Reiher, J. Chem. Theory Comput., 2024, 7126–7143 CrossRef CAS PubMed.
- S. Sharma, T. Yanai, G. H. Booth, C. J. Umrigar and G. K.-L. Chan, J. Chem. Phys., 2014, 140, 104112 CrossRef PubMed.
- A. J. Cohen, H. Luo, K. Guther, W. Dobrautz, D. P. Tew and A. Alavi, J. Chem. Phys., 2019, 151, 061101 CrossRef.
- A. Baiardi, M. Lesiuk and M. Reiher, J. Chem. Theory Comput., 2022, 18, 4203–4217 CrossRef CAS PubMed.
- K. Liao, H. Zhai, E. M. C. Christlmaier, T. Schraivogel, P. L. Ríos, D. Kats and A. Alavi, J. Chem. Theory Comput., 2023, 19, 1734–1743 CrossRef CAS PubMed.
- S. F. Boys, N. C. Handy and J. W. Linnett, Proc. R. Soc. London, Ser. A, 1969, 310, 43–61 CAS.
- P. Piecuch, N. Oliphant and L. Adamowicz, J. Chem. Phys., 1993, 99, 1875–1900 CrossRef CAS.
- T. Kinoshita, O. Hino and R. J. Bartlett, J. Chem. Phys., 2005, 123, 074106 CrossRef PubMed.
- M. Mörchen, L. Freitag and M. Reiher, J. Chem. Phys., 2020, 153, 244113 CrossRef PubMed.
- K. Liao, L. Ding and C. Schilling, J. Phys. Chem. Lett., 2024, 15, 6782–6790 CrossRef CAS PubMed.
- L. Veis, A. Antalk, J. Brabec, F. Neese, O. Legeza and J. Pittner, J. Phys. Chem. Lett., 2016, 7, 4072–4078 CrossRef CAS PubMed.
- J. Lang, A. Antalk, L. Veis, J. Brandejs, J. Brabec, O. Legeza and J. Pittner, J. Chem. Theory Comput., 2020, 16, 3028–3040 CrossRef CAS PubMed.
- J. Brandejs, J. Višnák, L. Veis, M. Maté, Ö. Legeza and J. Pittner, J. Chem. Phys., 2020, 152, 174107 CrossRef CAS PubMed.
- E. Vitale, A. Alavi and D. Kats, J. Chem. Theory Comput., 2020, 16, 5621–5634 CrossRef CAS PubMed.
- E. Vitale, G. Li Manni, A. Alavi and D. Kats, J. Chem. Theory Comput., 2022, 18, 3427–3437 CrossRef CAS PubMed.
- A. Leszczyk, M. Máté, O. Legeza and K. Boguslawski, J. Chem. Theory Comput., 2022, 18, 96–117 CrossRef CAS PubMed.
- O. Demel, J. Brandejs, J. Lang, J. Brabec, L. Veis, Ö. Legeza and J. Pittner, J. Chem. Phys., 2023, 159, 224115 CrossRef CAS PubMed.
- J. Paldus, J. Math. Chem., 2017, 55, 477–502 CrossRef CAS.
- S. Lee, H. Zhai, S. Sharma, C. J. Umrigar and G. K.-L. Chan, J. Chem. Theory Comput., 2021, 17, 3414–3425 CrossRef CAS PubMed.
- I. Magoulas, K. Gururangan, P. Piecuch, J. E. Deustua and J. Shen, J. Chem. Theory Comput., 2021, 17, 4006–4027 CrossRef CAS PubMed.
- A. Savin and H.-J. Flad, Int. J. Quantum Chem., 1995, 56, 327–332 CrossRef CAS.
- G. Li Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2014, 10, 3669–3680 CrossRef CAS PubMed.
- L. Gagliardi, D. G. Truhlar, G. Li Manni, R. K. Carlson, C. E. Hoyer and J. L. Bao, Acc. Chem. Res., 2017, 50, 66–73 CrossRef CAS PubMed.
- M. Mostafanejad, M. D. Liebenthal and A. E. I. DePrince, J. Chem. Theory Comput., 2020, 16, 2274–2283 CrossRef CAS PubMed.
- R. Pandharkar, M. R. Hermes, D. G. Truhlar and L. Gagliardi, J. Phys. Chem. Lett., 2020, 11, 10158–10163 CrossRef CAS PubMed.
- R. Pandharkar, M. R. Hermes, C. J. Cramer, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2021, 17, 2843–2851 CrossRef CAS PubMed.
- P. Sharma, A. J. Jenkins, G. Scalmani, M. J. Frisch, D. G. Truhlar, L. Gagliardi and X. Li, J. Chem. Theory Comput., 2022, 18, 2947–2954 CrossRef CAS PubMed.
- R. Feng, I. Y. Zhang and X. Xu, Nat. Commun., 2025, 16, 235 CrossRef CAS PubMed.
- A. Y. Sokolov and G. K.-L. Chan, J. Chem. Phys., 2016, 144, 064102 CrossRef PubMed.
- A. Y. Sokolov, S. Guo, E. Ronca and G. K.-L. Chan, J. Chem. Phys., 2017, 146, 244102 CrossRef PubMed.
- M. C. Babin, M. DeWitt, J. A. DeVine, D. C. McDonald, S. G. Ard, N. S. Shuman, A. A. Viggiano, L. Cheng and D. M. Neumark, J. Chem. Phys., 2021, 155, 114305 CrossRef CAS PubMed.
- A. Sepehri, A. Azenkeng and M. R. Hoffmann, J. Phys. Chem. A, 2024, 128, 3137–3148 CrossRef CAS PubMed.
- G. Li Manni, I. Fdez Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao, S. Battaglia, L. Birnoschi, A. Blanco-González, S. I. Bokarev, R. Broer, R. Cacciari, P. B. Calio, R. K. Carlson, R. Carvalho Couto, L. Cerdán, L. F. Chibotaru, N. F. Chilton, J. R. Church, I. Conti, S. Coriani, J. Cuéllar-Zuquin, R. E. Daoud, N. Dattani, P. Decleva, C. de Graaf, M. G. Delcey, L. De Vico, W. Dobrautz, S. S. Dong, R. Feng, N. Ferré, M. Filatov Gulak, L. Gagliardi, M. Garavelli, L. González, Y. Guan, M. Guo, M. R. Hennefarth, M. R. Hermes, C. E. Hoyer, M. Huix-Rotllant, V. K. Jaiswal, A. Kaiser, D. S. Kaliakin, M. Khamesian, D. S. King, V. Kochetov, M. Krosnicki, A. A. Kumaar, E. D. Larsson, S. Lehtola, M.-B. Lepetit, H. Lischka, P. López Ros, M. Lundberg, D. Ma, S. Mai, P. Marquetand, I. C. D. Merritt, F. Montorsi, M. Mörchen, A. Nenov, V. H. A. Nguyen, Y. Nishimoto, M. S. Oakley, M. Olivucci, M. Oppel, D. Padula, R. Pandharkar, Q. M. Phung, F. Plasser, G. Raggi, E. Rebolini, M. Reiher, I. Rivalta, D. Roca-Sanjuán, T. Romig, A. A. Safari, A. Sánchez-Mansilla, A. M. Sand, I. Schapiro, T. R. Scott, J. Segarra-Mart, F. Segatta, D.-C. Sergentu, P. Sharma, R. Shepard, Y. Shu, J. K. Staab, T. P. Straatsma, L. K. Sørensen, B. N. C. Tenorio, D. G. Truhlar, L. Ungur, M. Vacher, V. Veryazov, T. A. Voß, O. Weser, D. Wu, X. Yang, D. Yarkony, C. Zhou, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2023, 19, 6933–6991 CrossRef CAS PubMed.
- H. Zhai, H. R. Larsson, S. Lee, Z.-H. Cui, T. Zhu, C. Sun, L. Peng, R. Peng, K. Liao, J. Tölle, J. Yang, S. Li and G. K.-L. Chan, J. Chem. Phys., 2023, 159, 234801 CrossRef CAS PubMed.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen and Z.-H. Cui, et al. , J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- K. Szenes, N. Glaser, M. Erakovic, V. Barandun, M. Mörchen, R. Feldmann, S. Battaglia, A. Baiardi and M. Reiher, arXiv, 2025, preprint, arXiv:2505.01405 Search PubMed.
- F. A. Evangelista, C. Li, P. Verma, K. P. Hannon, J. B. Schriber, T. Zhang, C. Cai, S. Wang, N. He and N. H. Stair, et al. , J. Chem. Phys., 2024, 161, 062502 CrossRef CAS PubMed.
- C. Linton, C. Effantin, P. Crozet, A. Ross, E. Shenyavskaya and J. dIncan, J. Mol. Spectrosc., 2004, 225, 132–144 CrossRef CAS.
- V. Veryazov, P. Å. Malmqvist and B. O. Roos, Int. J. Quantum Chem., 2011, 111, 3329–3338 CrossRef CAS.
- S. Keller, K. Boguslawski, T. Janowski, M. Reiher and P. Pulay, J. Chem. Phys., 2015, 142, 244104 CrossRef PubMed.
- A. Khedkar and M. Roemelt, Phys. Chem. Chem. Phys., 2021, 23, 17097–17112 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00998g |
| This journal is © the Owner Societies 2025 |
