Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Membrane potential fluctuations and water asymmetry on plasma cell and model lipid membranes: origins, implications and properties
Zhi Li†
,
Iwona Swiderska† ,
Lena Dalifoski,
Seonwoo Lee
,
Lena Dalifoski,
Seonwoo Lee ,
Nelson Alonso Correa-Rojas
,
Nelson Alonso Correa-Rojas ,
David Roesel,
Maksim Eremchev,
Mischa Flor
,
David Roesel,
Maksim Eremchev,
Mischa Flor ,
Orly B. Tarun,
Arianna Marchioro
,
Orly B. Tarun,
Arianna Marchioro and
Sylvie Roke
and
Sylvie Roke *
*
Laboratory for Fundamental BioPhotonics (LBP), Institute of Bioengineering (IBI), and Institute of Materials Science (IMX), School of Engineering (STI), and Lausanne Centre for Ultrafast Science (LACUS), École Polytechnique Fédérale de Lausanne (EPFL), CH-1015, Lausanne, Switzerland. E-mail: sylvie.roke@epfl.ch
First published on 31st January 2025
Abstract
Membrane potential fluctuations have previously been detected using second harmonic (SH) water imaging on neuronal cells and model lipid bilayer membranes. We report that such fluctuations are also visible when membrane potential-sensitive fluorophores are used as contrast agents, and fluctuations are imaged on both free-standing lipid membranes (FLMs) and on the plasma membranes of neuroblastoma cells. We show that upon K+ depolarization, non-uniform recovery responses occur across cells and within single cells. We discuss the origins and implications of such fluctuations, and investigate the molecular-level details of membrane potential distributions on FLMs and compare it to those on giant unilamellar vesicles (GUVs). SH water imaging shows that the hydrated part of lipid membranes is most likely composed of regions having a diffuse double layer, and other regions having an additional condensed double layer, with a high concentration of ions/ionic groups. In terms of transmembrane potential distributions, FLMs and GUVs show similar signatures, as expected from electrostatics. Comparing passive ion transport, FLMs and GUVs of identical composition behave differently, with GUVs being more permeable for proton transport (∼20×). This is likely caused by differences in the hydrophobic cores of the membranes, which create different energetic barriers for the proton transport.
1. Introduction
The inner and outer leaflets of cellular and organelle membranes are compositionally diverse, which is crucial for cell function. Leaflet composition is often non-random and occurs in eukaryotic membranes.1–4 Transmembrane asymmetry can be achieved actively and passively.5–7 Active pathways use regulating proteins and peptides to induce asymmetry, whereas passive pathways derive from a balance of intermolecular interactions.8 Interactions that are strong enough to impart asymmetry are, in decreasing order of strength,9 electrostatic, and hydrogen (H) bonding interactions, followed by dispersive and steric interactions. Although electrostatic and H-bonding interactions are the most relevant in terms of strength and responsible for stabilizing membranes in water, they are rarely studied in the context of membrane asymmetry.10–12 These interactions are the topic of this work.The part of lipid membranes that is immersed in water is the hydrated head group region. The charged head group moieties (e.g. R2PO4−, COO−, NH3+, and N(CH3)3+) as well as their counterions (e.g. Na+, K+, Cl−), and water and ionic species from the bulk aqueous phase, form the electric double layer (EDL, sketched in Fig. 1A).13,14 The EDL comprises a concentration gradient of co- and counterions, as well as oriented and interacting water molecules, and is part of every aqueous interface and membrane.15 In the vicinity of a charged interface, dipolar molecules and ions distribute in a manner that lowers the free energy. A balance between enthalpic and entropic driving forces creates a layer of charge separation, as sketched in Fig. 1A. According to the Gouy–Chapman (GC) theory or Gouy–Chapman–Stern (GCS) theory, this gradient can be either gradual, giving rise to a diffuse double layer (DDL), or composed of a condensed part (Stern layer) in combination with a diffuse part. The GC and GCS models comprise linearized solutions to the Poisson–Boltzmann equation, which describe the distribution of point charges in the vicinity of a homogeneously charged interface in contact with a mean-field dielectric medium. In the GCS model, the surface potential (Φ0) of a charged planar surface with surface charge density σ0 in contact with an aqueous solution having a symmetric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte with concentration c is given by:15
1 electrolyte with concentration c is given by:15
 | (1) |
 , εr, kBT, e, NA, are the Stern layer thickness, the permittivity of vacuum, the dielectric constant in the Stern layer, the dielectric constant of the bulk medium (water), the Boltzmann constant, the temperature, the elementary charge and Avogadro’s number, respectively.
, εr, kBT, e, NA, are the Stern layer thickness, the permittivity of vacuum, the dielectric constant in the Stern layer, the dielectric constant of the bulk medium (water), the Boltzmann constant, the temperature, the elementary charge and Avogadro’s number, respectively.
 | ||
| Fig. 1 Electric double layer, lipid hydration and SH imaging of hydration asymmetry. (A) Illustration of the molecular structure of the hydrated lipid headgroup region which forms an electric double layer in the aqueous phase. The electrostatic potential arising from the distribution of ions is modelled by the Gouy–Chapman–Stern model and a typical potential decay in the solution as a function of distance is depicted. (B) Energy level diagram of a non-resonant second harmonic process. (C) (i) Fully symmetric bilayer with symmetric hydration (no coherent SH emission), and three ways in which this symmetry can be broken (with coherent SH emission): (ii) on-average asymmetric lipid/protein distributions, (iii) specific ion binding or (iv) by spatiotemporal fluctuations. (D) SH imaging configuration for imaging free standing lipid membranes (FLMs) in aqueous solution.36,40–44 (E) SH imaging configuration for SH imaging GUVs45–47 and cells.48 | ||
Although other idealized models of this charge separation phenomena exist,16,17 many aspects remain unknown, such as when/how exactly a Stern layer is formed, how different ionic species influence this formation (known as specific ion effects), and what is the effect of interfacial heterogeneities. Historically, the understanding of the EDL on lipid membranes has been driven by theoretical/computational efforts,14,18 aided primarily by electrical recordings.17 This has led to the conceptual idea that electrostatic interfacial potentials are ‘fixed’ properties of membranes. This is perhaps best exemplified by the notion that every cell has a specific resting potential and that, upon (de)polarization, the whole cell changes its membrane potential.19 Recent imaging developments are beginning to alter this picture. It has become possible to image interfacial water on sub-second time scales. This is important, as water is generally the main compound in any biological system, and the obtained data provides quantified information about the electric double layer on the molecular level.20 The enabling imaging method is called high throughput non-resonant second harmonic (SH) imaging and is described in detail in ref. 20–22.
SH imaging was invented in the 1970s,23–25 and became an important tool for biomedical applications, whereby either non-centrosymmetric bulk structures were probed, see e.g. ref. 26–31, or interfaces, combined with the use of resonant dyes, see e.g. ref. 32–35. These strategies were necessary to obtain sufficient imaging contrast for the generally weak nonlinear optical process. Non-resonant SH generation, is a process in which two photons with frequency ω are converted into a photon with frequency 2ω via a series of non-resonant interactions (illustrated in Fig. 1B). Using an approach with a medium-repetition rate near-infrared femtosecond illumination with gated detection, it became possible to perform non-resonant wide-field SH imaging of interfacial water on sub-second time scales.20,36 SHG has a unique sensitivity to interfaces,37 by virtue of a spatial symmetry selection rule that applies to all even-order nonlinear optical techniques within the electric dipole approximation.37 Anisotropic molecular arrangements of non-isotropic molecules generate coherent SH photons, while isotropic arrangements do not. Therefore, coherent SH photons are uniquely generated in the phase matching direction from an interface if it is sandwiched between isotropic media. This offers a unique optical contrast mechanism for bilayer imaging. A fully symmetric bilayer (Fig. 1C(i)), with all components superimposable by reflection, generates no coherent SH photons.38 An asymmetric bilayer that lacks such a symmetry does generate coherent SH photons.36 The asymmetry can be static, by having 2 different leaflets with on-average asymmetric lipid/protein distributions (Fig. 1C(ii)), specific interactions in the EDL of one leaflet, e.g. with divalent ions or protons (Fig. 1C(iii)), or by spatio-temporal fluctuations (Fig. 1C(iv)). When a liquid interface is probed, coherent SH photons are emitted only from a 2–3 molecular diameter layer. It has been determined in ref. 20 that ∼60% of all SH photons emerge from a 0.6 nm-thick region at high ionic strength. Note that the probed region is located in the aqueous phase and that the lipids do not contribute to the SHG signal intensity, which will be further explained in Section 2.4. The thickness of this layer is determined by the optical geometry and the ionic strength of the solution, not by the nature of the substance in contact with water.39
High-throughput SH imaging has shed new light on the electrostatics/EDL properties of interfaces. SH imaging of a variety of surfaces has generated surface potential videos of glass–water,20 electrode–water,49,50 membrane and cellular interfaces.42,44,45,47,48,50 In terms of lipid membranes, SH imaging was applied to free-standing lipid membranes (FLMs)40,41,44 and giant unilamellar vesicles (GUVs),45,47 whose importance as a model membrane system is detailed in ref. 51 and 52. All interfaces displayed membrane potential fluctuations. The source of these fluctuations lies in the fact that interfacial surface chemistry is spatially varying and that transport of chemicals in the EDL is not a diffusion-limited motion but rather determined by jamming, field gradients and nanoscale fluctuations, which are also found in concentrated electrolyte solutions,47 as further explained below in Section 3.4. The spatiotemporal variation of the charged state of lipids and ions along lipid leaflets induces transient electrostatic fields that aid in the formation of transient nanopores46,47 and water wires/needles,40 which have both been predicted previously by simulations.40,47
Here, we report membrane potential fluctuations as seen by water molecules as well as the intensity variations of a potential-sensitive fluorophore on both model and plasma membranes of cells. We also show that upon K+ depolarization, non-uniform recovery responses occur across cells and within single cells. The origins and implications of such fluctuations are considered in detail, which warrant investigating the molecular level details of membrane potential distribution on FLMs and GUVs on the molecular level using water as a probe. The hydrated region of lipid membranes is composed of areas having a diffuse double layer, and other regions having an additional condensed double layer. The condensed regions have a high concentration of ionic groups. In terms of transmembrane potential distributions, FLMs and GUVs behave similarly, as expected from electrostatics. Comparing the passive ion transport properties, FLMs and GUVs of identical composition behave differently, with GUVs being much more permeable for ions, which is illustrated by examining proton transport. Protons transport on average ∼20× faster through GUV membranes than through FLMs having identical composition. This transport difference is likely caused by differences in the hydrophobic cores of the membranes.
2. Experimental section
2.1. Chemicals
1,2-Diphytanoyl-sn-glaycero-3-phosphocholine (DPhPC), 1,2-diphytanoyl-sn-glycero-3-phospho L-serine (DPhPS), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phospho-L-serine (DOPS), and 1,2-diphytanoyl-sn-glycero-3-phosphate were obtained in powder form (>99%, Avanti Polar Lipids, Alabama, USA). Hexadecane (C16H34, 99.8%, Sigma-Aldrich), hexane (C6H14, 99%, Sigma-Aldrich), chloroform (CHCl3, 99.8%, Merck), hydrogen peroxide (H2O2, 30–32%, Reactolab SA), sulfuric acid (H2SO4, 95–97%, ISO, Merck), hydrochloric acid (HCl, 36–38%, Sigma-Aldrich), potassium chloride (KCl, 99.999%, Aros), monosodium phosphate (NaH2PO4 ≥ 99.0%, Sigma-Aldrich), disodium phosphate (Na2HPO4 ≥ 99.0%, Sigma-Aldrich), N-(3-triethylammoniumpropyl)-4-(6-(4-(diethylamino)phenyl)hexatrienyl)pyridinium dibromide (FM4-64 dye (Sigma-Aldrich)), calcium chloride (CaCl2, 99.999%, Sigma-Aldrich), 4-(2-hydroxyethyl)piperazine-1-ethane-sulfonic acid (HEPES), poly-D-lysine (PDL), and agar ((C12H18O9)n, >99%, Sigma-Aldrich) were used as received. All aqueous solutions were made with 18.2 MΩ cm ultra-pure water (H2O, Milli-Q UF plus, Millipore, Inc.), and filtered with 0.1 μm Millex filters. For each experiment, the coverslips were taken fresh from the packaging and were pre-cleaned by soaking them thoroughly in piranha solution (a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of 30–32% H2O2
3 mixture of 30–32% H2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95–97% H2SO4) for 30 min after which they were thoroughly rinsed with ultrapure water. For FLM formation, 13 mM lipid in CHCl3 solutions were used, which is sufficient to make a well-packed lipid monolayer on an air/water interface. The pH was adjusted (Fig. 6) by micro-pipetting a 3 M HCl solution to the bottom compartment of the membrane.
95–97% H2SO4) for 30 min after which they were thoroughly rinsed with ultrapure water. For FLM formation, 13 mM lipid in CHCl3 solutions were used, which is sufficient to make a well-packed lipid monolayer on an air/water interface. The pH was adjusted (Fig. 6) by micro-pipetting a 3 M HCl solution to the bottom compartment of the membrane.
2.2. Sample preparation and characterization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 vol% mixture of n-hexane and n-hexadecane. The bilayer was created by apposition. Wide-field white light imaging, the electrical recording of resistance and SH imaging were performed after ∼15 min. Capacitance and resistance measurements were taken with a HEKA patch clamp amplifier. Only bilayers with specific capacitance, Cm > 0.7 μF cm−2 and specific resistance, Rm ∼ 108 Ω cm2 were used for SH imaging experiments.
0.5 vol% mixture of n-hexane and n-hexadecane. The bilayer was created by apposition. Wide-field white light imaging, the electrical recording of resistance and SH imaging were performed after ∼15 min. Capacitance and resistance measurements were taken with a HEKA patch clamp amplifier. Only bilayers with specific capacitance, Cm > 0.7 μF cm−2 and specific resistance, Rm ∼ 108 Ω cm2 were used for SH imaging experiments.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per cm2 per coverslip. Cultured neurons were maintained at 37 °C in a humidified atmosphere of 95% air/5% CO2 and were used for experiments after 17 days in vitro (Fig. 2D–G). Coverslips with plated cells were inserted in a 3 ml laminar flow (1 ml min−1) Quick Change Imaging Chamber from Warner Instruments (Series 40 RC-41LP). The extracellular solution contained 140 mM NaCl, 5 mM KCl, 3 mM CaCl2·2H2O, 2 mM MgCl2·6H2O, 5 mM glucose and 10 mM Hepes. During the depolarization experiments the solution was switched for 2 min to one that had 93 mM NaCl, 5 mM KCl. For more details, see ref. 48. Neuroblastoma cells were cultured in the same extracellular solution and imaged following the same protocol. For imaging applications that require glass-bottomed dishes, the dish was coated with poly-D-lysine (PDL) before use. Cells were seeded evenly in a 35 mm glass-bottomed well dish, while avoiding air bubbles at the bottom of the dish. The cells were imaged 48–72 hours after seeding. For resonant SHG imaging 10 μM FM4-64 was added to the extracellular solution. For K+ depolarization experiments, 50 mM aqueous KCl solution was added to the extracellular solution and flushed out after ∼1 min.
000 cells per cm2 per coverslip. Cultured neurons were maintained at 37 °C in a humidified atmosphere of 95% air/5% CO2 and were used for experiments after 17 days in vitro (Fig. 2D–G). Coverslips with plated cells were inserted in a 3 ml laminar flow (1 ml min−1) Quick Change Imaging Chamber from Warner Instruments (Series 40 RC-41LP). The extracellular solution contained 140 mM NaCl, 5 mM KCl, 3 mM CaCl2·2H2O, 2 mM MgCl2·6H2O, 5 mM glucose and 10 mM Hepes. During the depolarization experiments the solution was switched for 2 min to one that had 93 mM NaCl, 5 mM KCl. For more details, see ref. 48. Neuroblastoma cells were cultured in the same extracellular solution and imaged following the same protocol. For imaging applications that require glass-bottomed dishes, the dish was coated with poly-D-lysine (PDL) before use. Cells were seeded evenly in a 35 mm glass-bottomed well dish, while avoiding air bubbles at the bottom of the dish. The cells were imaged 48–72 hours after seeding. For resonant SHG imaging 10 μM FM4-64 was added to the extracellular solution. For K+ depolarization experiments, 50 mM aqueous KCl solution was added to the extracellular solution and flushed out after ∼1 min.
 | ||
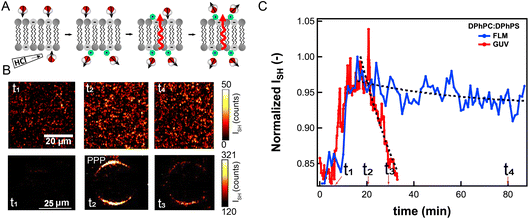
Fig. 2 Electrical recording and SH water imaging of FLMs and living mouse brain neurons. (A) SH intensity (ISH) and corresponding transmembrane potential difference (ΔΦ0) images (acquisition times 1 s) of a symmetric membrane composed of a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mol% (i) DPhPC 30 mol% (i) DPhPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPS and (ii) DOPC DPhPS and (ii) DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPS lipids. (B) Image averaged SH intensity (blue squares) as a function of external bias (U) for the membrane (i) in A and image-averaged trans-membrane potential ΔΦ0. The red curve is a parabolic fit according to eqn (4). (C) Capacitance as a function of applied bias U for a symmetric membrane. (D) Whole cell current patch clamp potential recording. The orange area represents the time lapse application of the K+ enriched solution and the arrow shows when the K+ solution reaches the neurons. (E and F) SH imaging of K+ depolarization: phase contrast image (E) of cortical neurons, 15 days in vitro. Three cell bodies are seen in the image. The black line indicates the area in which the membrane potential calculations were made. (F) Membrane potential map at a time point indicated by (x) in (G). The scale bar is 20 μm. (G) Spatially-averaged SH intensity changes (left axis) and extracted average membrane potential (right axis) as a function of time during two applications and recovery cycles of a 50 mM K+ enriched extracellular solution (orange areas). The data and analysis procedure of (D–G) are from ref. 48. DOPS lipids. (B) Image averaged SH intensity (blue squares) as a function of external bias (U) for the membrane (i) in A and image-averaged trans-membrane potential ΔΦ0. The red curve is a parabolic fit according to eqn (4). (C) Capacitance as a function of applied bias U for a symmetric membrane. (D) Whole cell current patch clamp potential recording. The orange area represents the time lapse application of the K+ enriched solution and the arrow shows when the K+ solution reaches the neurons. (E and F) SH imaging of K+ depolarization: phase contrast image (E) of cortical neurons, 15 days in vitro. Three cell bodies are seen in the image. The black line indicates the area in which the membrane potential calculations were made. (F) Membrane potential map at a time point indicated by (x) in (G). The scale bar is 20 μm. (G) Spatially-averaged SH intensity changes (left axis) and extracted average membrane potential (right axis) as a function of time during two applications and recovery cycles of a 50 mM K+ enriched extracellular solution (orange areas). The data and analysis procedure of (D–G) are from ref. 48. | ||
2.3. SH imaging
SH images were obtained with custom-built wide-field second harmonic microscopes that have been previously characterized in detail, see ref. 21 and 36 for details on the microscope used to image FLMs, and ref. 45 and 47 for the microscopes used to image GUVs and cells. Briefly, in both cases the fundamental (ω) beam consisted of a pulsed 190 fs, 200 kHz, 1030 nm light source that is polarization controlled. The coherent SH light (2ω) is emitted in the phase-matched direction, spectrally filtered, polarization controlled and imaged with an electronically amplified intensified gated CCD camera. White-light imaging was performed in parallel.2.4. Transmembrane potential obtained from non-resonant high throughput SH imaging
Wide-field high-throughput SH imaging increases the SH imaging throughput by a factor of >5000,20 compared to scanning confocal approaches that are typically applied to study resonant SHG.56 This approach allows for imaging interfacial water with ∼400 nm spatial resolution and sub-second acquisition times. Although the non-resonant interaction scheme (Fig. 1B) is not chemically selective, it is used to specifically detect the orientation distribution of interfacial water, and the recorded intensity is proportional to the square of the transmembrane potential difference , and the transmembrane potential difference in mV can be determined from each pixel.
, and the transmembrane potential difference in mV can be determined from each pixel.
In a non-resonant nonlinear optical interaction, the molecular response is independent of the molecular species, and the number of non-zero nonlinear optical parameters is small, with each of these being frequency independent.37 At most interfaces, water outnumbers every other molecule with typical ratios >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (typically ∼10–50 for lipids12,57), resulting in >102
1 (typically ∼10–50 for lipids12,57), resulting in >102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 SH intensity ratio in favor of water. This ability to SH image water has been demonstrated and exploited for solid–liquid, liquid–liquid, and cellular membrane interfaces.20,44,48 The surface potential information derives from the proportionality of the emitted SH field to the nonlinear optical polarization (P(NL)(2ω)). P(NL)(2ω) depends on the incoming electromagnetic fields (E1(ω), E2(ω)) from the light source having frequency ω, and EDC(z), the electrostatic field in the aqueous phase that emerges from the surface (Fig. 1A). This field relates to the electrostatic potential, since
1 SH intensity ratio in favor of water. This ability to SH image water has been demonstrated and exploited for solid–liquid, liquid–liquid, and cellular membrane interfaces.20,44,48 The surface potential information derives from the proportionality of the emitted SH field to the nonlinear optical polarization (P(NL)(2ω)). P(NL)(2ω) depends on the incoming electromagnetic fields (E1(ω), E2(ω)) from the light source having frequency ω, and EDC(z), the electrostatic field in the aqueous phase that emerges from the surface (Fig. 1A). This field relates to the electrostatic potential, since  , and the expression for P(NL)(2ω) becomes:39
, and the expression for P(NL)(2ω) becomes:39
 | (2) |
 are the second-order surface susceptibility and the third-order effective susceptibility, respectively. For non-resonant SH imaging of interfacial water, these tensors reduce to scalars (χs(2) and
are the second-order surface susceptibility and the third-order effective susceptibility, respectively. For non-resonant SH imaging of interfacial water, these tensors reduce to scalars (χs(2) and 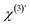 ).39,57 They report on the orientational distribution of interfacial water in the direction of the surface normal due to chemical interactions (χs(2)), and due to electrostatic field–driven interactions
).39,57 They report on the orientational distribution of interfacial water in the direction of the surface normal due to chemical interactions (χs(2)), and due to electrostatic field–driven interactions  , respectively. The intensity is related to the polarizability by: I(2ω) ∝ |P(NL)(2ω)|2. For a lipid membrane with two opposing leaflets (i = 1 or 2) and I(ω) = |E1(ω)|2 = |E2(ω)|2, the total emitted SH intensity I(2ω, x, y) originating from the spatial coordinates x, y is related to the membrane surface potential on the aqueous side of each leaflet (Φ0,i):36
, respectively. The intensity is related to the polarizability by: I(2ω) ∝ |P(NL)(2ω)|2. For a lipid membrane with two opposing leaflets (i = 1 or 2) and I(ω) = |E1(ω)|2 = |E2(ω)|2, the total emitted SH intensity I(2ω, x, y) originating from the spatial coordinates x, y is related to the membrane surface potential on the aqueous side of each leaflet (Φ0,i):36
 | (3) |
 (ref. 36 and 57)) and it does not change significantly upon the addition of ions. The SH intensity variations in the images are attributed to the transmembrane potential difference ΔΦ0(x, y) = Φ0,1(x, y) − Φ0,2(x, y). For a structurally symmetric bilayer, Eqn (3) becomes:
(ref. 36 and 57)) and it does not change significantly upon the addition of ions. The SH intensity variations in the images are attributed to the transmembrane potential difference ΔΦ0(x, y) = Φ0,1(x, y) − Φ0,2(x, y). For a structurally symmetric bilayer, Eqn (3) becomes:
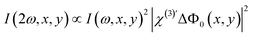 | (4) |
 . To obtain ΔΦ0(x, y) in voltage, the image-integrated SH intensity is recorded as a function of external electric bias across the membrane (U). Using this curve, the intensity is converted into a membrane potential difference in mV (see ref. 36 for details). An example of such a curve is shown in Fig. 2B. Because there is only one connecting parameter, which is the effective third-order susceptibility of water
. To obtain ΔΦ0(x, y) in voltage, the image-integrated SH intensity is recorded as a function of external electric bias across the membrane (U). Using this curve, the intensity is converted into a membrane potential difference in mV (see ref. 36 for details). An example of such a curve is shown in Fig. 2B. Because there is only one connecting parameter, which is the effective third-order susceptibility of water 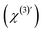 , eqn (4) is the same for all on-average symmetric lipid membranes, no matter the membrane composition or type of solutes at physiological concentration in the aqueous solution, as they do not contribute to
, eqn (4) is the same for all on-average symmetric lipid membranes, no matter the membrane composition or type of solutes at physiological concentration in the aqueous solution, as they do not contribute to  . For an asymmetric membrane, |χs,1(2) − χs,2(2)| can be determined with a parabolic fit to a plot of the image averaged intensity recorded as a function of external bias.36,40,42 With
. For an asymmetric membrane, |χs,1(2) − χs,2(2)| can be determined with a parabolic fit to a plot of the image averaged intensity recorded as a function of external bias.36,40,42 With  and |χs,1(2) − χs,2(2)| determined, the transmembrane potential ΔΦ0(x, y) of every pixel in a SH image can then be computed in mV using eqn (3) or (4). This procedure was previously tested in three ways: (1) by comparing the image averaged membrane potential difference to the one measured with capacitance minimization, a purely electrical recording.36 This gave identical values. (2) By determining membrane-averaged binding constants of divalent ions (Ca2+, Ba2+) that complex with certain lipids; the image-averaged values compared well to reported values in the literature.42 (3) By performing simulations.36 In addition, inverse experiments in which a know DC field is interacting with bulk water were used to relate field strength to SH intensity.20
and |χs,1(2) − χs,2(2)| determined, the transmembrane potential ΔΦ0(x, y) of every pixel in a SH image can then be computed in mV using eqn (3) or (4). This procedure was previously tested in three ways: (1) by comparing the image averaged membrane potential difference to the one measured with capacitance minimization, a purely electrical recording.36 This gave identical values. (2) By determining membrane-averaged binding constants of divalent ions (Ca2+, Ba2+) that complex with certain lipids; the image-averaged values compared well to reported values in the literature.42 (3) By performing simulations.36 In addition, inverse experiments in which a know DC field is interacting with bulk water were used to relate field strength to SH intensity.20
3. Results and discussion
3.1. Hydration/membrane potential asymmetry of model lipid and cellular membranes
We start by reviewing SH water imaging of model free-standing lipid membranes (FLMs), and then consider living mouse brain neurons. Fig. 2A–C shows several measurements of FLMs. Fig. 2A shows SH images of membranes having a symmetric composition, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mol% DPhPC
30 mol% DPhPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPS (i) and DOPC
DPhPS (i) and DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPS (ii), in contact with a pH 7.3, 50 mM KCl and 10 mM phosphate buffer solution, from a single frame with a 1 s acquisition time. The SH intensity is converted to membrane surface potential as described in Section 2.4. and published in ref. 36, 40–42. Fig. 2B shows image averaged SH intensity values (blue squares) plotted as a function of external bias (U) for membrane (i) in Fig. 2A. The computed image-averaged trans-membrane potential ΔΦ0 values are also plotted on the bottom axis, and they are the same as the external bias.36 The red curve is a parabolic fit to eqn (4). The symmetry of the membrane is experimentally confirmed by capacitance minimization measurements shown in Fig. 2C. The minimum of the capacitance for a symmetric membrane occurs when the applied external bias U = 0 mV. Transient membrane potential fluctuations are observed for both membrane compositions and reach absolute values of up to 350 mV. Such fluctuations agree with previous observations.36,40,42,43,46,47
DOPS (ii), in contact with a pH 7.3, 50 mM KCl and 10 mM phosphate buffer solution, from a single frame with a 1 s acquisition time. The SH intensity is converted to membrane surface potential as described in Section 2.4. and published in ref. 36, 40–42. Fig. 2B shows image averaged SH intensity values (blue squares) plotted as a function of external bias (U) for membrane (i) in Fig. 2A. The computed image-averaged trans-membrane potential ΔΦ0 values are also plotted on the bottom axis, and they are the same as the external bias.36 The red curve is a parabolic fit to eqn (4). The symmetry of the membrane is experimentally confirmed by capacitance minimization measurements shown in Fig. 2C. The minimum of the capacitance for a symmetric membrane occurs when the applied external bias U = 0 mV. Transient membrane potential fluctuations are observed for both membrane compositions and reach absolute values of up to 350 mV. Such fluctuations agree with previous observations.36,40,42,43,46,47
Fig. 2D shows an electrophysiological recording in whole-cell current clamp mode, of a mouse brain neuron, 17 days in vitro, that is being subjected to a temporary increase in extracellular concentration of K+ ions from 5 mM (normal concentration) to 50 mM (indicated by the shaded area). The membrane averaged potential of the neuron 〈ΔΦ0〉 (which corresponds to the difference in surface potentials of the two membrane leaflets) changes from −65 to −34 mV, in response, after which it recovers back to its original value. The electrophysiological recording suggests that the membrane potential of the neuron is constant over the whole cell membrane. The neurons in Fig. 2E are SH imaged with 300 ms acquisition time (Fig. 2F), and the interfacial water response around the neuron is extracted and processed into membrane potential changes (ΔΦ0). Fig. 2G shows the average membrane potential change over the entire image. This graph shows that the average SH response matches with the electrical recording in Fig. 2E, as it should. However, the spatiotemporal distribution of membrane potential values in the snapshot of Fig. 2F is not constant. This suggests that ion channels are opening and closing at different times, and with different efficiencies. It also implies that the charge distribution on the cell membrane is dynamically fluctuating. This data set was previously published in ref. 48.
Fig. 2 illustrates that both free-standing lipid membranes as well as the plasma membrane of neurons display drastic membrane potential fluctuations on sub-second time scales. These fluctuations have a spatial correlation of ∼1 μm, a temporal correlation <300 ms, and membrane potential fluctuations reaching values of several hundreds of millivolts.
Next, the following aspects are examined:
• Do fluorescence imaging methods also display membrane potential fluctuations?
• Do the distributions depend on the alkyl chains and ionic composition of the adjacent solution?
• Are they different for FLMs and GUVs?
• Is passive proton transport, a process that depends on membrane potential fluctuations, different across FLMs and GUVs?
3.2. Membrane potential fluctuations imaged using a voltage sensitive fluorophore
To investigate if membrane potential fluctuations are also seen when imaged by other means, we use a membrane potential sensitive fluorophore, FM4-64 (Fig. 3A),58 which resonantly enhances the SH intensity by a factor of ∼107 compared to water.45 FM4-64 is commonly used for neuro-imaging.59–63 The spectrum shown in Fig. 3A shows that the SH emission (515 nm) is spectrally sharp and isolated from the 2-photon fluorescence of the dye (550–750 nm). Fig. 3B shows SH images of an asymmetric FLM composed of DPhPA/DPhPC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 mol%) + 165 μM KCl on the top leaflet and DPhPC + 165 μM KCl on the bottom leaflet. Fig. 3B(i) was generated by SH imaging of membrane water (1 s snapshot), while Fig. 3B(ii) was SH imaged after 10 μM of FM4-64 in 165 μM KCl was added to the solution adjacent to the top leaflet. The square root of the SH intensity that is emitted by FM4-64 correlates linearly with an applied voltage bias35 and is therefore used as an indicator of the transmembrane potential. Fig. 3C shows a superimposed bright field and SH image of neuroblastoma cells stained with 10 μM FM4-64. Several ROIs are indicated for which intensity histograms are shown in Fig. 3D. It can be seen that the intensity and thus also the membrane potential varies drastically across the membrane surface. Repeating the same K+ depolarization experiment as in Fig. 2D–G, neuronal depolarization is SH imaged using FM4-64 in Fig. 3E, and analyzed in Fig. 3F. Different response curves are seen for different cells, and even different regions within the same cells. Interestingly, similar fluctuations in the intensity of FM4-64 have been observed previously with scanning confocal 2-photon imaging within the context of several neuroimaging studies60,64 by the Yuste lab, but were not published (Yuste, personal communication, 2022). Scanning confocal measurements, in contrast to wide-field imaging, record one pixel at a time, with some time, on the order of micro-milliseconds between different pixel recordings. In such a measurement scheme transient effects are not easily spotted. Thus, both the membrane potential fluctuations observed at FLMs and neuronal cell membranes are seen with two different optical methods, and agree with three different types of electric recordings (patch clamp, free space electrical recording and capacitance minimization). The presence of membrane potential fluctuations in different membrane systems, model membranes, and cell membranes of living neurons indicates that the membrane potential and thus also the electrostatic free energy (ΔG = eΔΦ0) is a dynamic feature of lipid membranes. Next, we consider the origin of these fluctuations in more detail, and then examine their dependence on several parameters such as clustering of ionic species and fluctuating gradient in concentration of ions in FLMs and GUVs.
7 mol%) + 165 μM KCl on the top leaflet and DPhPC + 165 μM KCl on the bottom leaflet. Fig. 3B(i) was generated by SH imaging of membrane water (1 s snapshot), while Fig. 3B(ii) was SH imaged after 10 μM of FM4-64 in 165 μM KCl was added to the solution adjacent to the top leaflet. The square root of the SH intensity that is emitted by FM4-64 correlates linearly with an applied voltage bias35 and is therefore used as an indicator of the transmembrane potential. Fig. 3C shows a superimposed bright field and SH image of neuroblastoma cells stained with 10 μM FM4-64. Several ROIs are indicated for which intensity histograms are shown in Fig. 3D. It can be seen that the intensity and thus also the membrane potential varies drastically across the membrane surface. Repeating the same K+ depolarization experiment as in Fig. 2D–G, neuronal depolarization is SH imaged using FM4-64 in Fig. 3E, and analyzed in Fig. 3F. Different response curves are seen for different cells, and even different regions within the same cells. Interestingly, similar fluctuations in the intensity of FM4-64 have been observed previously with scanning confocal 2-photon imaging within the context of several neuroimaging studies60,64 by the Yuste lab, but were not published (Yuste, personal communication, 2022). Scanning confocal measurements, in contrast to wide-field imaging, record one pixel at a time, with some time, on the order of micro-milliseconds between different pixel recordings. In such a measurement scheme transient effects are not easily spotted. Thus, both the membrane potential fluctuations observed at FLMs and neuronal cell membranes are seen with two different optical methods, and agree with three different types of electric recordings (patch clamp, free space electrical recording and capacitance minimization). The presence of membrane potential fluctuations in different membrane systems, model membranes, and cell membranes of living neurons indicates that the membrane potential and thus also the electrostatic free energy (ΔG = eΔΦ0) is a dynamic feature of lipid membranes. Next, we consider the origin of these fluctuations in more detail, and then examine their dependence on several parameters such as clustering of ionic species and fluctuating gradient in concentration of ions in FLMs and GUVs.
3.3. The origin and implications of membrane potential fluctuations
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 and, more recently, also molecular dynamics simulations68 show that at concentrations exceeding the Kirkwood limit, ions are partially and dynamically distributed in quasi-periodic lattices spaced by more dilute regions of ions.69 Segregation over longer length scales in ionic solutions has also been observed with dynamic light scattering, where domains on the length scale of 0.1–0.5 microns are observed.70 The autocorrelation function of scattered light decays on time scales ranging from 10 μs–0.1 s, depending on the type of salt and concentration used. This type of clustering behavior is a manifestation of the statistical distribution of matter.
67 and, more recently, also molecular dynamics simulations68 show that at concentrations exceeding the Kirkwood limit, ions are partially and dynamically distributed in quasi-periodic lattices spaced by more dilute regions of ions.69 Segregation over longer length scales in ionic solutions has also been observed with dynamic light scattering, where domains on the length scale of 0.1–0.5 microns are observed.70 The autocorrelation function of scattered light decays on time scales ranging from 10 μs–0.1 s, depending on the type of salt and concentration used. This type of clustering behavior is a manifestation of the statistical distribution of matter.Lipid membrane interfaces have hydrated headgroup regions that make up ∼40% of a bilayer thickness.12,71 Such regions can be considered as partially confined electrolyte solutions, that are open ended on the diffuse double layer side. Being a half-open highly concentrated electrolyte solution, such systems are likely displaying the same kind of behavior as observed in 3D concentrated ionic solutions. The relevant time scale for the observed transient membrane potential fluctuations thus falls in the same time scale as the one measured by DLS in concentrated salt solutions (10 μs–0.1 s). The clustering of ionic species and the dynamically fluctuating gradient in concentration leads to dynamic fluctuations in the distribution of ions, which manifests itself as membrane potential fluctuations.47 To get to the bottom of this process, more research is needed.
Another aspect that contributes to charge segregation is that the fluctuation-induced electrostatic fields create strain in the membrane. This strain arises from a surface pressure gradient across the membrane in combination with steric pressure along the membrane.42,72,73 Although the details have not been worked out completely, this interaction most likely leads to nano/micron scale curvature changes and charge segregation.42 The coupling between mechanical curvature changes and the electrostatic properties of the membrane in relation to its EDL structure is complex, and more research in this direction is needed as well.
Besides curvature fluctuations,42 another biophysical process that is strongly affected is passive ion transport.46,47,74–76 This is illustrated in Fig. 4. A transient electrostatic field drastically lowers the free energy to form a transient nanopore (Fig. 4A) for the transport of cations, or a transient water wire/needle (Fig. 4B) for the transport of protons.40,77,78 Water wire transport involves the transport of protons through water molecules that are connected by hydrogen bonds. The protons move across via the breaking and making of correlated hydrogen bonds along the water molecules whose connected hydrogen bond network forms the wire (the Grotthuss mechanism).79 This passive ion transport – either ions through nanopores or protons through water wires – depends on the magnitude of the transmembrane potential47 and on the hydrophobic barrier formed by the alkyl chains of the lipids and other molecules such as cholesterol.46 The electrostatic free energy, ΔG = eΔΦ0, contributes to the probability Ppore to form a transient pore via: Ppore ∼ e−ΔGpore/kBT ∼ 1/τ, where ΔGpore is the free energy of the pore relative to the unperturbed membrane, kB is the Boltzmann constant, T the temperature, and τ is the translocation time of ions.47 The transport of protons and divalent ions can be SH imaged. Ions that interact with the lipid headgroups on one leaflet, such as Ca2+, associate/bind with charged (e.g. PS or PA) head groups and neutralize charges on one leaflet. This severely distorts the water orientation on this leaflet. The opposing leaflet, which is uncoupled to the first, has not been neutralized, and its water orientation has not been changed. This difference in the orientational distribution of water creates a SH contrast, which can be imaged and converted into a membrane potential value. This mechanism is illustrated in Fig. 4C(i), and a SH image of a GUV composed of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole% mixture of DOPC
1 mole% mixture of DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPA immersed in an osmolarity-balanced solution with 5 mM CaCl2 added to the outside, is shown in the inset of Fig. 4D(i). When a transient nanopore is formed, ions transport though the membrane (Fig. 4C(ii)), which will restore the imbalance of Ca2+ ions that are complexed on both leaflets. The difference in the orientational distributions of water molecules on both leaflets becomes smaller (Fig. 4C(iii)), which decreases the SH intensity. This process continues until the distribution of divalent ions on both leaflets is equal. Fig. 4D shows the GUV averaged reduction in SH intensity, finally resulting in a non-existent SH contrast. Adding cholesterol to the membrane slows down the transport process.47 Branched lipids slow it down further, as can be seen in Fig. 4D, and no decrease in the SH intensity is seen on the time scale of the experiment (∼2–3 h).
DOPA immersed in an osmolarity-balanced solution with 5 mM CaCl2 added to the outside, is shown in the inset of Fig. 4D(i). When a transient nanopore is formed, ions transport though the membrane (Fig. 4C(ii)), which will restore the imbalance of Ca2+ ions that are complexed on both leaflets. The difference in the orientational distributions of water molecules on both leaflets becomes smaller (Fig. 4C(iii)), which decreases the SH intensity. This process continues until the distribution of divalent ions on both leaflets is equal. Fig. 4D shows the GUV averaged reduction in SH intensity, finally resulting in a non-existent SH contrast. Adding cholesterol to the membrane slows down the transport process.47 Branched lipids slow it down further, as can be seen in Fig. 4D, and no decrease in the SH intensity is seen on the time scale of the experiment (∼2–3 h).
 | ||
Fig. 4 Transient membrane potential fluctuations drive passive ion transport. (A) Molecular dynamics snapshot of a transient nanopore,47 (B) illustration of a water wire or needle that facilitates H+ transport, (C) illustration of the nanopore formation process proposed in ref. 47 and (D) single GUV averaged SH intensity over time (blue data points: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole% DOPC 1 mole% DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPA; orange data points: 1 DOPA; orange data points: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole% DPhPC 1 mole% DPhPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPA) after a 5 mM CaCl2 solution is added to the outer solution. The lines are exponential fits (dark blue). The SH images show two 1 s acquisitions taken of the GUV composed of unsaturated lipids at 2 min and 27 min after addition of CaCl2. DPhPA) after a 5 mM CaCl2 solution is added to the outer solution. The lines are exponential fits (dark blue). The SH images show two 1 s acquisitions taken of the GUV composed of unsaturated lipids at 2 min and 27 min after addition of CaCl2. | ||
Previously, symmetric and asymmetric FLMs of the following lipids were studied: DPhPC, DPhPA, DPhPS, DOPC, DOPA, DOPS, DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine), DPPS (1,2-dipalmitoyl-sn-glycero-3-phospho-L-serine), with ionic species Na+, K+, Mg2+, Ca2+, Ba2+, Cu2+, H+.40,41,46,47 While divalent cations change the membrane potential distribution of FLMs they do not lead to changes to the SHG intensity over time, which means they do not translocate through the membrane. Protons, however, do change the transmembrane potential distribution and also transfer through the FLM, albeit on a time scale of hours.40 GUVs with compositions DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PA interacting with Ca2+, Ba2+, Cu2+ ions have been investigated and simulated.46,47 Here, as shown in Fig. 4D, divalent cations can transfer through the membrane on timescales of minutes, depending on the composition of the membrane and the type of ion, and the magnitude of the transmembrane potential. For both FLMs and GUVS the magnitude of the transmembrane potential changes that are induced by the divalent cations is determined by the strength of the divalent ion–headgroup complex, and follows the order Cu2+ > Ca2+ > Mg2+ > Ba2+ and the density of the charged lipid headgroup. Membrane potential changes only occur when ions form complexes with the charged groups of the lipids, and this is higher for charged lipids that have smaller footprints. PA headgroups, with their small areas generate higher interfacial charge densities/transmembrane potential differences than PS headgroups. Adding monovalent K+ ions does not change the membrane potential distribution up to and above physiological concentrations.
PA interacting with Ca2+, Ba2+, Cu2+ ions have been investigated and simulated.46,47 Here, as shown in Fig. 4D, divalent cations can transfer through the membrane on timescales of minutes, depending on the composition of the membrane and the type of ion, and the magnitude of the transmembrane potential. For both FLMs and GUVS the magnitude of the transmembrane potential changes that are induced by the divalent cations is determined by the strength of the divalent ion–headgroup complex, and follows the order Cu2+ > Ca2+ > Mg2+ > Ba2+ and the density of the charged lipid headgroup. Membrane potential changes only occur when ions form complexes with the charged groups of the lipids, and this is higher for charged lipids that have smaller footprints. PA headgroups, with their small areas generate higher interfacial charge densities/transmembrane potential differences than PS headgroups. Adding monovalent K+ ions does not change the membrane potential distribution up to and above physiological concentrations.
Having considered the origin of the membrane potential fluctuations, and discussed the implications for passive ion transport, we next investigate membrane potential distributions on FLMs, whether these depend on the alkyl chain length and the adjacent solution (with or without buffer), and what we can learn from the measured distributions. We then make a comparison with GUVs, considering the amount of charged lipids in the membrane. Finally, we will compare passive proton transport across FLM and GUV membranes having identical composition, and explain the observed differences.
3.4. The structure of the hydrated interface in FLMs and GUVS
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mol% DOPC
30 mol% DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPS and DPhPC
DOPS and DPhPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPS lipid mixtures surrounded by an aqueous solution containing 50 mM KCl. The SH contrast was shown to arise from an asymmetric distribution of charges per leaflet, which modifies the measured water structure. This is asymmetry caused by spatio-temporal fluctuations (Fig. 1C(iv)). The intensity scale as well as the converted transmembrane potentials (ΔΦ0) were shown. Fig. 5A shows a histogram of the ΔΦ0 values obtained from an analysis of the domain intensity of the image stack from which the images of Fig. 2A are taken. Fig. 5A also shows histograms obtained for a symmetric FLM composed of a 70
DPhPS lipid mixtures surrounded by an aqueous solution containing 50 mM KCl. The SH contrast was shown to arise from an asymmetric distribution of charges per leaflet, which modifies the measured water structure. This is asymmetry caused by spatio-temporal fluctuations (Fig. 1C(iv)). The intensity scale as well as the converted transmembrane potentials (ΔΦ0) were shown. Fig. 5A shows a histogram of the ΔΦ0 values obtained from an analysis of the domain intensity of the image stack from which the images of Fig. 2A are taken. Fig. 5A also shows histograms obtained for a symmetric FLM composed of a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mol% DOPC
30 mol% DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPS lipid mixture, surrounded by an aqueous solution containing 50 mM KCl or 10 mM PBS buffer. The lines are fits to a Gaussian distribution. All three bilayer membranes have very similar transmembrane potential distributions with an average domain transmembrane potential of |ΔΦ0| ∼ 122 mV, and a maximum (transient) value of |ΔΦ0| ∼ 390 mV. This confirms the notion that the transmembrane potential distribution is a phenomenon that is independent of the alkyl chain structure and relatively insensitive to pH (which is 5.3 without buffer and 7.3 with buffer).
DOPS lipid mixture, surrounded by an aqueous solution containing 50 mM KCl or 10 mM PBS buffer. The lines are fits to a Gaussian distribution. All three bilayer membranes have very similar transmembrane potential distributions with an average domain transmembrane potential of |ΔΦ0| ∼ 122 mV, and a maximum (transient) value of |ΔΦ0| ∼ 390 mV. This confirms the notion that the transmembrane potential distribution is a phenomenon that is independent of the alkyl chain structure and relatively insensitive to pH (which is 5.3 without buffer and 7.3 with buffer).
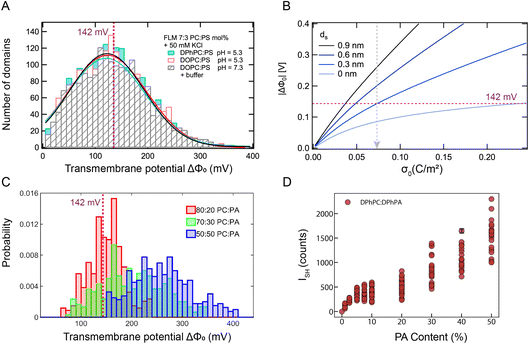 | ||
Fig. 5 Transmembrane potential distributions on FLMs and GUVs. FLMs: (A) transmembrane potential values per domain (〈ΔΦdomain〉, taken from 1 s SH images and averaged over 20 images) from 3 different symmetric FLMs composed of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mol% DPhPC 30 mol% DPhPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPS (turquoise), 70 DPhPS (turquoise), 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mol% DOPC 30 mol% DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPS (red/white) immersed in a pH 5.3, 50 mM KCl solution, and the same DOPC DOPS (red/white) immersed in a pH 5.3, 50 mM KCl solution, and the same DOPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOPS mixture but with 10 mM PBS buffer added to both sides (dashed grey). The lines are Gaussian fits to the data. (B) Computed curves (eqn (1)) of the surface potential difference (|ΔΦ0|) as a function of the surface charge density (σ0) plotted for different thicknesses of the Stern layer (ds). The x axis spans a neutral surface up to a fully ionized DPhPS layer. (C) Transmembrane potential values per 20 μm2 domains obtained for GUVs composed of DPhPC DOPS mixture but with 10 mM PBS buffer added to both sides (dashed grey). The lines are Gaussian fits to the data. (B) Computed curves (eqn (1)) of the surface potential difference (|ΔΦ0|) as a function of the surface charge density (σ0) plotted for different thicknesses of the Stern layer (ds). The x axis spans a neutral surface up to a fully ionized DPhPS layer. (C) Transmembrane potential values per 20 μm2 domains obtained for GUVs composed of DPhPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPA with 3 different mole% ratios of 1 DPhPA with 3 different mole% ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (blue), 7 1 (blue), 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (green), and 8 3 (green), and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (red). The solution inside the GUV contains 45 mM sucrose, and the solution outside the GUV contains 30 mM glucose and 5 mM CaCl2. (D) Bar graph showing how the distribution of average SH intensity per GUV changes for different GUVs prepared according to the same protocol. Each marker represents one GUV. Between 9 and 29 GUVs were imaged per lipid composition. 2 (red). The solution inside the GUV contains 45 mM sucrose, and the solution outside the GUV contains 30 mM glucose and 5 mM CaCl2. (D) Bar graph showing how the distribution of average SH intensity per GUV changes for different GUVs prepared according to the same protocol. Each marker represents one GUV. Between 9 and 29 GUVs were imaged per lipid composition. | ||
Next, we analyze the structural implications of the ΔΦ0 values using the GC and GCS models (eqn (1)). This determines the degree of ionization and whether there is a Stern layer present. In this analysis we assume that for a given domain, the charge is on one leaflet only. Fig. 5B shows the computed surface potential (ΔΦ0) vs. surface charge density (σ0) curves using the GC and GCS models in light and progressively darker blue curves, whereby the Stern layer is varied from 0 nm (absent, GC model) to one with a thickness of 0.3, 0.6, and 0.9 nm corresponding to a thickness of ∼1, ∼2 and ∼3 hydration layers, respectively (GCS model). The graph shows that, in absence of a condensed charge or Stern layer, the maximum membrane potential value that can be reached is 142 mV. The potential measured above this value, can only be generated when a Stern layer is present. Considering a hypothetical 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mol% PC
3 mol% PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PS lipid leaflet with a uniform surface charge density and 100% ionization, the surface charge density is σ0 = 0.0735 C m−2, which corresponds to an area of 212 Å2 per charge, indicated by the dashed grey arrow. Such a charge density leads to surface potentials of 85 mV, 142 mV, 199 mV and 259 mV for Stern layer thicknesses of 0, 0.3, 0.6 and 0.9 nm, respectively. A 100% PS membrane with 100% ionization, in which a PS headgroup has a cross-sectional area of ∼65 Å2 per charge (σ0 = 0.245 C m−2),10 can have a surface potential of 142 mV (ds = 0 nm, GC model), 338 mV (ds = 0.3 nm), 530 mV (ds = 0.6 nm), 730 mV (ds = 0.9 nm).
PS lipid leaflet with a uniform surface charge density and 100% ionization, the surface charge density is σ0 = 0.0735 C m−2, which corresponds to an area of 212 Å2 per charge, indicated by the dashed grey arrow. Such a charge density leads to surface potentials of 85 mV, 142 mV, 199 mV and 259 mV for Stern layer thicknesses of 0, 0.3, 0.6 and 0.9 nm, respectively. A 100% PS membrane with 100% ionization, in which a PS headgroup has a cross-sectional area of ∼65 Å2 per charge (σ0 = 0.245 C m−2),10 can have a surface potential of 142 mV (ds = 0 nm, GC model), 338 mV (ds = 0.3 nm), 530 mV (ds = 0.6 nm), 730 mV (ds = 0.9 nm).
Examining the measured domain values in Fig. 5A, ∼73% of the ΔΦ0 values are above 85 mV and ∼40% of the ΔΦ0 values are above 142 mV. This means that most of the charged domains will have charge condensation or Stern layers in them, as the measured potential exceeds the theoretical GC potential maximum. In addition, there needs to be a higher percentage of PS than present in the ‘average’ 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mole% structure. Also, for the highest potentials, >300 mV, which comprises ∼1.5% of the charged domains, the Stern layer is more than 1–2 hydration layers thick (>0.3 nm).
3 mole% structure. Also, for the highest potentials, >300 mV, which comprises ∼1.5% of the charged domains, the Stern layer is more than 1–2 hydration layers thick (>0.3 nm).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPA having 3 different mole ratios of 1
DPhPA having 3 different mole ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 7
1, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 8
3, and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Fig. 5D shows the GUV averaged intensity for different measurements on GUVs, in which between 9 and 29 GUVs were measured for each lipid composition indicated in the graph. In each case, the solution inside the GUV contains 45 mM sucrose, and the solution outside the GUV contains 30 mM glucose and 5 mM CaCl2. In these experiments, the SH contrast observed in the GUV images is enhanced by the complexation of Ca2+ ions with the phosphate headgroups of the outer leaflet. The asymmetry here is caused by specific divalent ion–head group interactions on top of spatio-temporal fluctuations (Fig. 1C(iii)). Note that adding additional ionic strength to the aqueous solution does not change the observations in any way. Also note that, in using branched lipids, divalent ion transport is halted.
2. Fig. 5D shows the GUV averaged intensity for different measurements on GUVs, in which between 9 and 29 GUVs were measured for each lipid composition indicated in the graph. In each case, the solution inside the GUV contains 45 mM sucrose, and the solution outside the GUV contains 30 mM glucose and 5 mM CaCl2. In these experiments, the SH contrast observed in the GUV images is enhanced by the complexation of Ca2+ ions with the phosphate headgroups of the outer leaflet. The asymmetry here is caused by specific divalent ion–head group interactions on top of spatio-temporal fluctuations (Fig. 1C(iii)). Note that adding additional ionic strength to the aqueous solution does not change the observations in any way. Also note that, in using branched lipids, divalent ion transport is halted.Increasing the amount of charged lipids increases the surface charge density, as well as the membrane potential, as expected (Fig. 5B). It is clear though that the spread per GUV (Fig. 5C) and between GUVs (Fig. 5D) is very large. The values for the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 PA
7 PA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC membrane, −117 < ΔΦ0 < −235 are consistent with those of the PC
PC membrane, −117 < ΔΦ0 < −235 are consistent with those of the PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PS FLM membranes in Fig. 5A. The graphs also show that as with the FLMs, the degree of ionization varies across the domains as does the presence of a Stern layer. The potential limit above which a condensed charged layer is formed is indicated by the dashed line.
PS FLM membranes in Fig. 5A. The graphs also show that as with the FLMs, the degree of ionization varies across the domains as does the presence of a Stern layer. The potential limit above which a condensed charged layer is formed is indicated by the dashed line.
Thus, for both FLMs and GUVs the hydrated lipid membrane is most likely composed of some regions having a diffuse double layer, and regions having an additional condensed double layer, with a high concentration of ionic groups, and this is the same whether the asymmetry is due to having different amounts of charged lipids, or asymmetry induced by specific ion interactions. In terms of transmembrane potential distribution FLMs and GUVs behave similarly. This is expected as the determining factor is the amount of charge and the structure of the electric double layer, which are properties of the aqueous phase in contact with the lipid membrane.17 As discussed in Section 3.3, transient transmembrane potentials of several 100 mVs are sufficient to induce passive ion transport, via transient nanopores (divalent cations) or transient water wires. The probability to create such nanopores or water nanowires/needles depends also on the nature of the hydrophobic core of the membrane. Divalent ion transport through GUVs is slowed down/halted when branched lipids are used or when cholesterol is added to the membrane,46 and has not been observed for FLMs. Proton transport does occur through FLMs, and is faster in a symmetric FLM having unsaturated alkyl chains than in a symmetric FLM made with branched lipids that have the same head group composition.40 Because of the difference between divalent ion transport through FLMs (not detected on the time scale of the measurement) and GUVs (depends on the strength of specific ion–head group interactions, and alkyl chain/membrane composition) is different, proton transport may be different through FLMs and GUVs as well. We investigate this next.
3.5. Passive proton translocation in FLMs vs. GUVs
To compare passive proton transport through FLMs and GUVs, we examine proton transport across both types of membranes using the same lipid membrane composition, and the same ionic strength. FLMs and GUVs were made having symmetric lipid membranes composed of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 mol% DPhPC
30 mol% DPhPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPS. Both leaflets are initially in contact with a 50 mM KCl solution having identical pH values for both leaflets (pH = 5.3/pH = 5.3). For the experiment on FLMs the pH of the bottom leaflet was changed by adding (HCl)aq to the solution, and for GUVs the pH was changed by changing the outer solution. In both cases the pH was brought down to 2.5.
DPhPS. Both leaflets are initially in contact with a 50 mM KCl solution having identical pH values for both leaflets (pH = 5.3/pH = 5.3). For the experiment on FLMs the pH of the bottom leaflet was changed by adding (HCl)aq to the solution, and for GUVs the pH was changed by changing the outer solution. In both cases the pH was brought down to 2.5.
After changing the pH of the solution in contact with one leaflet, the initially, on average, symmetric distribution of interfacial water is distorted by the interaction with (H+)aq, which changes the orientational distribution of water (Fig. 6A). Proton transport through the membrane diminishes the interfacial asymmetry, eventually resulting in symmetric interfacial orientational distributions of water. The SH contrast is very low before adding (H+)aq. It increases when protons reach the interface and then decays back to the initial value. The decay time is related to the proton translocation time across the membrane. Fig. 6B shows three SH images of an FLM (top row), and a GUV (bottom row) obtained before changing the pH (t1), and at times t2, t3, and t4 after changing the pH. Fig. 6C shows the image-averaged SH intensity over time after addition of (HCl)aq, for the GUV (red data), and an FLM (blue data). The times t1–t4 are indicated in the graph. Both bilayers display the above-described rise-and-fall behavior. The increase in intensity occurs on the same time scale, but the decrease is much faster for the GUV than for the FLM. Exponential fits provide average membrane translocation times (τ). The fitted decay time for DPhPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DPhPS GUVs is τGUV = 14 min, and for the FLM it is τFLM = 332 min. Note that the distributions in translocation time for each system is ∼50%, which is a manifestation of the spatial heterogeneity of the process. The value obtained for FLM is close to the value obtained previously for translocations of protons on membranes having the same composition but with the pH buffered to 7.3 and 4.1, respectively (442 min (ref. 40)).
DPhPS GUVs is τGUV = 14 min, and for the FLM it is τFLM = 332 min. Note that the distributions in translocation time for each system is ∼50%, which is a manifestation of the spatial heterogeneity of the process. The value obtained for FLM is close to the value obtained previously for translocations of protons on membranes having the same composition but with the pH buffered to 7.3 and 4.1, respectively (442 min (ref. 40)).
This experiment shows that the translocation of protons is much faster across GUV membranes compared to FLMs. Even though both membranes are composed of the same lipids, there is a difference of a factor of ∼20 in the translocation time. This difference is likely caused by the hydrophobic core being somewhat different, e.g. in thickness, for the FLM compared to the GUV. The FLMs in these experiments are produced using a tiny amount of hexadecane oil, which results in a sub-monolayer amount of oil that interdigitates with the membrane.44 This likely results in a larger hydrophobic barrier for passive proton transport, as it increases the energetic barrier for creating a water wire needle.
4. Conclusions
We investigated membrane potential fluctuations as seen by water as well as a potential sensitive fluorophore on FLMs, GUVs and living cells. We also showed that upon K+ depolarization, non-uniform recovery responses occur across cells and within single cells, which are detected both by SH water and SH fluorophore imaging. The origins and implications of such fluctuations are considered in detail, arising from molecular level processes in the EDL. Next, the molecular-level details of membrane potential distribution on FLMs and GUVs using water as a probe were considered. Hydrated lipid membranes are most likely heterogeneous in structure, and composed of regions having a diffuse double layer, and other regions having an additional condensed double layer. The condensed double layer/Stern regions have a high concentration of ionic groups. In terms of transmembrane potential distributions, FLMs and GUVs behave similarly, displaying the same magnitude and spread in fluctuations, as expected from electrostatics. However, comparing the passive ion transport properties, FLMs and GUVs of identical composition behave differently, with GUVs being much more permeable for proton transport (∼20×). This is likely caused by differences in the hydrophobic cores of the membranes.Data availability
The authors confirm that the raw data supporting the findings of this study are available from the corresponding author, upon reasonable request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Julia Jacobi Foundation, the European Union’s Horizon 2020 research and innovation program under Marie Skłodowska-Curie grant agreement 860592 (H2020-MSCA-ITN, PROTON), and the European Research Council grant agreement No. 951324 (H2020, R2-tension).References
- P. F. Devaux, Static and dynamic lipid asymmetry in cell membranes, Biochemistry, 1991, 30(5), 1163–1173 CrossRef CAS.
- J. H. Lorent, K. R. Levental, L. Ganesan, G. Rivera-Longsworth, E. Sezgin and M. Doktorova, et al., Plasma membranes are asymmetric in lipid unsaturation, packing and protein shape, Nat. Chem. Biol., 2020, 16(6), 644–652 CrossRef CAS PubMed.
- G. van Meer, D. R. Voelker and G. W. Feigenson, Membrane lipids: where they are and how they behave, Nat. Rev. Mol. Cell Biol., 2008, 9(2), 112–124 CrossRef CAS PubMed.
- Z. Wang, J. M. Jumper, S. Wang, K. F. Freed and T. R. Sosnick, A Membrane Burial Potential with H-Bonds and Applications to Curved Membranes and Fast Simulations, Biophys. J., 2018, 115(10), 1872–1884 CrossRef CAS PubMed.
- D. Marquardt, B. Geier and G. Pabst, Asymmetric Lipid Membranes: Towards More Realistic Model Systems, Membranes, 2015, 5(2), 180–196 CrossRef CAS.
- M. Markones, C. Drechsler, M. Kaiser, L. Kalie, H. Heerklotz and S. Fiedler, Engineering Asymmetric Lipid Vesicles: Accurate and Convenient Control of the Outer Leaflet Lipid Composition, Langmuir, 2018, 34(5), 1999–2005 CrossRef CAS PubMed.
- M. Doktorova, F. A. Heberle, B. Eicher, R. F. Standaert, J. Katsaras and E. London, et al., Preparation of asymmetric phospholipid vesicles for use as cell membrane models, Nat. Protoc., 2018, 13(9), 2086–2101 CrossRef CAS.
- G. van Meer and A. I. P. M. de Kroon, Lipid map of the mammalian cell, J. Cell Sci., 2011, 124(1), 5–8 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 2010, p. 706 Search PubMed.
- H. I. Petrache, S. Tristram-Nagle, K. Gawrisch, D. Harries, V. A. Parsegian and J. F. Nagle, Structure and Fluctuations of Charged Phosphatidylserine Bilayers in the Absence of Salt, Biophys. J., 2004, 86(3), 1574–1586 CrossRef CAS PubMed.
- E. A. Disalvo, F. Lairion, F. Martini, E. Tymczyszyn, M. Frías and H. Almaleck, et al., Structural and functional properties of hydration and confined water in membrane interfaces, Biochim. Biophys. Acta, Biomembr., 2008, 1778(12), 2655–2670 CrossRef CAS PubMed.
- E. A. Disalvo, Membrane Hydration: the Role of Water in the Structure and Function of Biological Membranes, Springer, 2015, p. 295 Search PubMed.
- S. Y. Bhide and M. L. Berkowitz, Structure and dynamics of water at the interface with phospholipid bilayers, J. Chem. Phys., 2005, 123(22), 224702 CrossRef PubMed.
- R. Vácha, M. L. Berkowitz and P. Jungwirth, Molecular Model of a Cell Plasma Membrane With an Asymmetric Multicomponent Composition: Water Permeation and Ion Effects, Biophys. J., 2009, 96(11), 4493–4501 CrossRef.
- R. J. Hunter, Foundations of Colloid Science, Oxford University Press, 2001, p. 824 Search PubMed.
- H. Ohshima, Electrical Phenomena at Interfaces and Biointerfaces: Fundamentals and Applications in Nano-, Bio-, and Environmental Sciences, John Wiley & Sons, 2012, p. 870 Search PubMed.
- S. McLaughlin, The Electrostatic Properties of Membranes, Annu. Rev. Biophys., 1989, 18, 113–136 CrossRef CAS.
- K. Bohinc, M. Špadina, J. Reščič, N. Shimokawa and S. Spada, Influence of Charge Lipid Head Group Structures on Electric Double Layer Properties, J. Chem. Theory Comput., 2022, 18(1), 448–460 CrossRef CAS PubMed.
- Neuroscience, ed. D. Purves, G. J Augustine, D. Fitzpatrick, L. C. Katz, A.-S. La Mantia, J. O. McNamara and S. Mark Williams, Sinauer Associates, Sunderland (MA), 2nd edn, 2001 Search PubMed.
- C. Macias-Romero, I. Nahalka, H. I. Okur and S. Roke, Optical imaging of surface chemistry and dynamics in confinement, Science, 2017, 357(6353), 784–788 Search PubMed.
- C. Macias-Romero, M. E. P. Didier, P. Jourdain, P. Marquet, P. Magistretti and O. B. Tarun, et al., High throughput second harmonic imaging for label-free biological applications, Opt. Express, 2014, 22(25), 31102–31112 CrossRef CAS.
- C. Macias-Romero, M. E. P. Didier, V. Zubkovs, L. Delannoy, F. Dutto and A. Radenovic, et al., Probing rotational and translational diffusion of nanodoublers in living cells on microsecond time scales, Nano Lett., 2014, 14(5), 2552–2557 CrossRef CAS PubMed.
- R. Hellwarth and P. Christensen, Nonlinear optical microscopic examination of structure in polycrystalline ZnSe, Opt. Commun., 1974, 12(3), 318–322 CrossRef CAS.
- C. Sheppard, J. Gannaway, R. Kompfner and D. Walsh, The scanning harmonic optical microscope, IEEE J. Quantum Electron., 1977, 13(9), 912 Search PubMed.
- B. R. Masters and P. So, Handbook of Biomedical Nonlinear Optical Microscopy, Oxford University Press, 2008, p. 895 Search PubMed.
- E. J. Gualtieri, F. Guo, D. J. Kissick, J. Jose, R. J. Kuhn and W. Jiang, et al., Detection of Membrane Protein Two-Dimensional Crystals in Living Cells, Biophys. J., 2011, 100(1), 207–214 CrossRef CAS.
- E. L. DeWalt, V. J. Begue, J. A. Ronau, S. Z. Sullivan, C. Das and G. J. Simpson, Polarization-resolved second-harmonic generation microscopy as a method to visualize protein-crystal domains, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2013, 69(1), 74–81 Search PubMed.
- P. J. Campagnola, A. C. Millard, M. Terasaki, P. E. Hoppe, C. J. Malone and W. A. Mohler, Three-dimensional high-resolution second-harmonic generation imaging of endogenous structural proteins in biological tissues, Biophys. J., 2002, 82(1), 493–508 Search PubMed.
- S. V. Plotnikov, A. C. Millard, P. J. Campagnola and W. A. Mohler, Characterization of the myosin-based source for second-harmonic generation from muscle sarcomeres, Biophys. J., 2006, 90(2), 693–703 Search PubMed.
- D. A. Dombeck, K. A. Kasischke, H. D. Vishwasrao, M. Ingelsson, B. T. Hyman and W. W. Webb, Uniform polarity microtubule assemblies imaged in native brain tissue by second-harmonic generation microscopy, Proc. Natl. Acad. Sci., 2003, 100(12), 7081–7086 CrossRef CAS.
- G. Latour, L. Kowalczuk, M. Savoldelli, J. L. Bourges, K. Plamann and F. Behar-Cohen, et al., Hyperglycemia-induced abnormalities in rat and human corneas: the potential of second harmonic generation microscopy, PLoS One, 2012, 7(11), e48388 Search PubMed.
- B. A. Nemet, V. Nikolenko and R. Yuste, Second harmonic imaging of membrane potential of neurons with retinal, J. Biomed. Opt., 2004, 9(5), 873 Search PubMed.
- M. A. Kriech and J. C. Conboy, Imaging Chirality with Surface Second Harmonic Generation Microscopy, J. Am. Chem. Soc., 2005, 127(9), 2834–2835 CrossRef CAS PubMed.
- K. L. Sly, T. T. Nguyen and J. C. Conboy, Lens-less surface second harmonic imaging, Opt. Express, 2012, 20(20), 21953–21967 CrossRef PubMed.
- M. Nuriya, S. Fukushima, A. Momotake, T. Shinotsuka, M. Yasui and T. Arai, Multimodal two-photon imaging using a second harmonic generation-specific dye, Nat. Commun., 2016, 7(1), 11557 CrossRef CAS PubMed.
- O. B. Tarun, C. Hannesschläger, P. Pohl and S. Roke, Label-free and charge-sensitive dynamic imaging of lipid membrane hydration on millisecond time scales, Proc. Natl. Acad. Sci, 2018, 115(16), 4081–4086 CrossRef CAS.
- R. W. Boyd, Nonlinear Optics, Academic Press, 2020, p. 636 Search PubMed.
- R. S. Ries, H. Choi, R. Blunck, F. Bezanilla and J. R. Heath, Black Lipid Membranes: Visualizing the Structure, Dynamics, and Substrate Dependence of Membranes, J. Phys. Chem. B, 2004, 108(41), 16040–16049 CrossRef CAS.
- G. Gonella, C. Lütgebaucks, A. G. F. De Beer and S. Roke, Second Harmonic and Sum-Frequency Generation from Aqueous Interfaces Is Modulated by Interference, J. Phys. Chem. C, 2016, 120(17), 9165–9173 CrossRef CAS.
- S. Lee, C. S. Poojari, A. Maznichenko, D. Roesel, I. Swiderska and P. Pohl, et al., Dynamic Second Harmonic Imaging of Proton Translocation Through Water Needles in Lipid Membranes, J. Am. Chem. Soc., 2024, 146(29), 19818–19827 CrossRef CAS.
- S. Lee, D. Roesel and S. Roke, Imaging Cu2+ binding to charged phospholipid membranes by high-throughput second harmonic wide-field microscopy, J. Chem. Phys., 2021, 155(18), 184704 CrossRef CAS.
- O. B. Tarun, H. I. Okur, P. Rangamani and S. Roke, Transient domains of ordered water induced by divalent ions lead to lipid membrane curvature fluctuations, Commun. Chem., 2020, 3(1), 1–8 Search PubMed.
- O. B. Tarun, M. Y. Eremchev, A. Radenovic and S. Roke, Spatiotemporal Imaging of Water in Operating Voltage-Gated Ion Channels Reveals the Slow Motion of Interfacial Ions, Nano Lett., 2019, 19(11), 7608–7613 Search PubMed.
- O. B. Tarun, M. Y. Eremchev and S. Roke, Interaction of Oil and Lipids in Freestanding Lipid Bilayer Membranes Studied with Label-Free High-Throughput Wide-Field Second-Harmonic Microscopy, Langmuir, 2018, 34(38), 11305–11310 Search PubMed.
- M. Eremchev, D. Roesel, P. M. Dansette, A. Michailovas and S. Roke, High throughput wide field second harmonic imaging of giant unilamellar vesicles, Biointerphases, 2023, 18(3), 031202 Search PubMed.
- M. Eremchev, D. Roesel, C. S. Poojari, A. Roux, J. S. Hub and S. Roke, Passive transport of Ca2+ ions through lipid bilayers imaged by widefield second harmonic microscopy, Biophys. J., 2023, 122(4), 624–631 CrossRef CAS.
- D. Roesel, M. Eremchev, C. S. Poojari, J. S. Hub and S. Roke, Ion-Induced Transient Potential Fluctuations Facilitate Pore Formation and Cation Transport through Lipid Membranes, J. Am. Chem. Soc., 2022, 144(51), 23352–23357 CrossRef CAS PubMed.
- M. E. P. Didier, O. B. Tarun, P. Jourdain, P. Magistretti and S. Roke, Membrane water for probing neuronal membrane potentials and ionic fluxes at the single cell level, Nat. Commun., 2018, 9(1), 5287 CrossRef CAS PubMed.
- I. Nahalka, G. Zwaschka, R. K. Campen, A. Marchioro and S. Roke, Mapping Electrochemical Heterogeneity at Gold Surfaces: A Second Harmonic Imaging Study, J. Phys. Chem. C, 2020, 124(37), 20021–20034 CrossRef CAS PubMed.
- H. I. Okur, O. B. Tarun and S. Roke, Chemistry of Lipid Membranes from Models to Living Systems: A Perspective of Hydration, Surface Potential, Curvature, Confinement and Heterogeneity, J. Am. Chem. Soc., 2019, 141(31), 12168–12181 CrossRef CAS PubMed.
- R. Dimova and C. Marques, The Giant Vesicle Book, CRC Press, 2019, p. 677 Search PubMed.
- R. Dimova, Giant Vesicles and Their Use in Assays for Assessing Membrane Phase State, Curvature, Mechanics, and Electrical Properties, Annu. Rev. Biophys., 2019, 48, 93–119 Search PubMed.
- M. Montal and P. Mueller, Formation of Bimolecular Membranes from Lipid Monolayers and a Study of Their Electrical Properties, Proc. Natl. Acad. Sci, 1972, 69(12), 3561–3566 CrossRef CAS PubMed.
- A. Horner, S. A. Akimov and P. Pohl, Long and Short Lipid Molecules Experience the Same Interleaflet Drag in Lipid Bilayers, Phys. Rev. Lett., 2013, 110(26), 268101 CrossRef PubMed.
- A. Weinberger, F. C. Tsai, G. H. Koenderink, T. F. Schmidt, R. Itri and W. Meier, et al., Gel-Assisted Formation of Giant Unilamellar Vesicles, Biophys. J., 2013, 105(1), 154–164 CrossRef CAS PubMed.
- D. A. Dombeck, M. Blanchard-Desce and W. W. Webb, Optical Recording of Action Potentials with Second-Harmonic Generation Microscopy, J. Neurosci., 2004, 24(4), 999–1003 CrossRef CAS PubMed.
- C. Lütgebaucks, G. Gonella and S. Roke, Optical label-free and model-free probe of the surface potential of nanoscale and microscopic objects in aqueous solution, Phys. Rev. B, 2016, 94(19), 195410 CrossRef.
- E. Reeve J, L. Anderson H and K. Clays, Dyes for biological second harmonic generation imaging, Phys. Chem. Chem. Phys., 2010, 12(41), 13484–13498 Search PubMed.
- D. A. Dombeck, L. Sacconi, M. Blanchard-Desce and W. W. Webb, Optical Recording of Fast Neuronal Membrane Potential Transients in Acute Mammalian Brain Slices by Second-Harmonic Generation Microscopy, J. Neurophysiol., 2005, 94(5), 3628–3636 CrossRef PubMed.
- M. Nuriya, J. Jiang, B. Nemet, K. B. Eisenthal and R. Yuste, Imaging membrane potential in dendritic spines, Proc. Natl. Acad. Sci., 2006, 103(3), 786–790 CrossRef CAS PubMed.
- M. Nuriya and M. Yasui, Membrane potential dynamics of axons in cultured hippocampal neurons probed by second-harmonic-generation imaging, J. Biomed. Opt., 2010, 15(2), 020503 Search PubMed.
- L. Sacconi, D. A. Dombeck and W. W. Webb, Overcoming photodamage in second-harmonic generation microscopy: Real-time optical recording of neuronal action potentials, Proc. Natl. Acad. Sci, 2006, 103(9), 3124–3129 Search PubMed.
- S. Rama, L. Vetrivel and A. Semyanov, Second-harmonic generation voltage imaging at subcellular resolution in rat hippocampal slices, J. Biophotonics, 2010, 3(12), 784–790 CrossRef PubMed.
- J. Jiang and R. Yuste, Second-Harmonic Generation Imaging of Membrane Potential with Photon Counting, Microsc. Microanal., 2008, 14(6), 526–531 Search PubMed.
- J. G. Kirkwood, Statistical Mechanics of Liquid Solutions, Chem. Rev., 1936, 19(3), 275–307 Search PubMed.
- J. E. Enderby, W. S. Howells and R. A. Howe, The structure of aqueous solutions, Chem. Phys. Lett., 1973, 21(1), 109–112 CrossRef CAS.
- J. A. Prins, X-ray diffraction in ionic solutions, Physica, 1934, 1(7), 1171–1173 Search PubMed.
- E. O. Fetisov, C. J. Mundy, G. K. Schenter, C. J. Benmore, J. L. Fulton and S. M. Kathmann, Nanometer-Scale Correlations in Aqueous Salt Solutions, J. Phys. Chem. Lett., 2020, 11(7), 2598–2604 Search PubMed.
- M. A. Marques, M. I. Cabaço, M. I. Marques, B. de and A. M. Gaspar, Intermediate-range order in aqueous solutions of salts constituted of divalent ions combined with monovalent counter-ions, J. Phys.: Condens. Matter, 2002, 14(32), 7427 CrossRef CAS.
- Y. Georgalis, A. M. Kierzek and W. Saenger, Cluster Formation in Aqueous Electrolyte Solutions Observed by Dynamic Light Scattering, J. Phys. Chem. B, 2000, 104(15), 3405–3406 CrossRef CAS.
- J. F. Nagle and S. Tristram-Nagle, Structure and Interactions of Lipid Bilayers: Role of Fluctuations, in Lipid Bilayers: Structure and Interactions, ed. J. Katsaras and T. Gutberlet, Springer, Berlin, Heidelberg, 2001, pp. 1–23, DOI:10.1007/978-3-662-04496-4_1.
- J. C. Stachowiak, F. M. Brodsky and E. A. Miller, A cost–benefit analysis of the physical mechanisms of membrane curvature, Nat. Cell Biol., 2013, 15(9), 1019–1027 Search PubMed.
- D. Marsh, Lateral Pressure Profile, Spontaneous Curvature Frustration, and the Incorporation and Conformation of Proteins in Membranes, Biophys. J., 2007, 93(11), 3884–3899 CrossRef CAS PubMed.
- M. Tarek, Membrane Electroporation: A Molecular Dynamics Simulation, Biophys. J., 2005, 88(6), 4045–4053 Search PubMed.
- E. Duboué-Dijon, P. E. Mason, H. E. Fischer and P. Jungwirth, Hydration and Ion Pairing in Aqueous Mg2+ and Zn2+ Solutions: Force-Field Description Aided by Neutron Scattering Experiments and Ab Initio Molecular Dynamics Simulations, J. Phys. Chem. B, 2018, 122(13), 3296–3306 CrossRef PubMed.
- M. Kohagen, P. E. Mason and P. Jungwirth, Accurate Description of Calcium Solvation in Concentrated Aqueous Solutions, J. Phys. Chem. B, 2014, 118(28), 7902–7909 CrossRef CAS PubMed.
- H. L. Tepper and G. A. Voth, Protons May Leak through Pure Lipid Bilayers via a Concerted Mechanism, Biophys. J., 2005, 88(5), 3095–3108 CrossRef CAS PubMed.
- S. J. Marrink, F. Jähnig and H. J. Berendsen, Proton transport across transient single-file water pores in a lipid membrane studied by molecular dynamics simulations, Biophys. J., 1996, 71(2), 632–647 Search PubMed.
- N. Agmon, H. J. Bakker, R. K. Campen, R. H. Henchman, P. Pohl and S. Roke, et al., Protons and Hydroxide Ions in Aqueous Systems, Chem. Rev., 2016, 116(13), 7642–7672 Search PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |