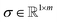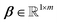Open Access Article
Open Access ArticleAutoSpect: an all-in-one software solution for automated processing of LA-ICP-TOF-MS datasets†
Andrew M. Crawford *abc,
David Z. Zee
*abc,
David Z. Zee abc,
Qiaoling Jin
abc,
Qiaoling Jin d,
Aaron Sue
d,
Aaron Sue abc,
Niharika Sinha
abc,
Niharika Sinha abc,
Soo Hyun Ahn
abc,
Soo Hyun Ahn ae,
Thomas V. O'Halloran
ae,
Thomas V. O'Halloran *abc and
Keith W. MacRenaris
*abc and
Keith W. MacRenaris *abc
*abc
aDepartment of Microbiology, Genetics, Immunology, Michigan State University, East Lansing, MI, USA. E-mail: macrenar@msu.edu; ohallor8@msu.edu; crawf472@msu.edu
bDepartment of Chemistry, Michigan State University, East Lansing, MI, USA
cElemental Health Institute, Michigan State University, East Lansing, MI, USA
dDepartment of Physics and Astronomy, Northwestern University, Evanston, IL, USA
eDepartment of Pathobiology and Diagnostics Investigation, Michigan State University, East Lansing, MI, USA
First published on 2nd July 2025
Abstract
LA-ICP-TOF-MS provides rapid, high resolution elemental analysis of biological and non-biological samples. However, accurate real-time data analysis frequently requires the user to account for several instrumental and experimental variables that can change during data acquisition. AutoSpect is a novel software tool designed to automate the processing and fitting of LA-ICP-TOF-MS data, addressing key challenges such as time-dependent spectral drift, instrument sensitivity drift, calibration inaccuracies, and peak deconvolution, enabling researchers to rapidly and accurately process complex datasets. The tool is optimized to be robustly applicable across scientific fields (e.g., geochemistry, biology, and materials science), providing a streamlined solution for end users seeking to maximize the potential of LA-ICP-TOF-MS for high-resolution elemental mapping and isotopic analysis.
1. Introduction
Time-of-flight mass spectrometry (TOF-MS) has fast become the technique of choice for analyzing fast transient signals following ionization via inductively coupled plasma (ICP) sources due to the dramatic improvement in high-speed detection electronics.1 This has been especially true for single particle (SP), single cell (SC), and laser ablation (LA) ICP-TOF-MS applications ranging from nanoparticle and microplastic characterization to elemental mapping in geological and biological samples.2–4 By combining high frequency LA with ICP-TOF-MS, rapid, high-resolution analyses at scales ranging from microns to millimeters are achievable. Additionally, with recent advancements in benchtop instrumentation, LA-ICP-TOF-MS is now capable of measuring all isotopes at frequencies from 10 Hz up to 1000 Hz helping to move elemental mapping into the realm of more routine, robust, quantitative analysis. These advancements are improving our fundamental understanding of how the distribution and concentration of elements play a role in dynamic processes; and, by combining elemental mapping with complementary imaging modalities such as matrix assisted laser desorption ionization TOF-MS, near infrared, Raman, histochemistry, immunofluorescence, and brightfield microscopy we can begin to unlock the complexity of a multitude of sample types.5–7The major advantage of ICP-TOF-MS is the ability to provide near simultaneous detection of all isotopes across the whole mass spectrum which makes it well-suited for the analysis of short transient events such as LA.8 However, using TOF-MS for detecting these short transient events generated from single pulse-resolved laser ablation presents challenges, including time-dependent spectral drift, instrument sensitivity drift, and the need for precise calibration and interference correction. Addressing these hurdles is crucial to ensuring accurate data interpretation, particularly for multi-element and isotopic analyses and quantitative elemental mapping. Although there are several software options for mass spectrometry image analysis9–11 there remain few commercially available spectral fitting tools for modern ICP-TOF-MS systems that handle spectral post-processing for ICP-TOF-MS datasets including LA.9 Each of these tools have independent advantages but sequential application can lead to bottlenecks and inefficiencies in ICP-TOF-MS workflow. Most software12–14 requires manual user input to identify optimal peaks for drift correction, mass axis calibration, and peak profile modeling, which can introduce subjectivity and user error. With larger specimens, a laser ablation imaging experiment can require several hours, exposing the spectra to greater possibility of drift due to external factors like temperature changes.15,16 While some commercially available software packages can accommodate peak drift up to a user-defined limit, the process is not automatic and can fail to accurately fit peaks that drift beyond that limit. Ideally, users would benefit from inspection of the accuracy of the drift correction process. Overcoming these challenges is particularly important when the goal is a quantitative comparison of dozens of analytes over a broad dynamic range in small regions of interest.
Herein, we describe the workflow of a new integrated and automated software solution called AutoSpect, that integrates multiple stages of data processing, beginning with raw data import, and proceeds through data sorting, peak identification, time dependent peak drift correction, mass-to-charge (m/z, or μ) calibration, peak profile creation, and spectral fitting to generate reliable outputs. Finally, we demonstrate AutoSpect use cases illustrating elemental map generation and data visualization as well as isotope accumulation.
2. AutoSpect workflow
AutoSpect software provides a user-friendly graphical interface for analysis of complex ICP-TOF-MS datasets. This is accomplished through an automated process composed of the following six steps (Fig. 1):(i) Processing and partitioning raw data: first, LA-ICP-TOF-MS data is imported in the raw hierarchical data format (HDF5), where each component is automatically defragmented to produce three distinct datasets (i.e. gas blanks, references, and samples). These three datasets are partitioned into hundreds of independently manageable data chunks with associated metadata (e.g., average integrated mass spectra, acquisition time, and m/z calibration coefficients).
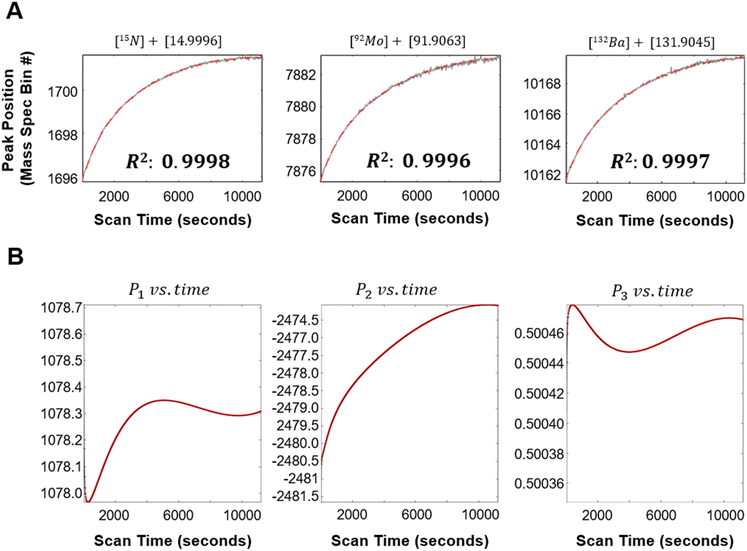
(ii) Measuring peak drift: following processing of raw data, peaks are identified in the integrated spectrum and then tracked across spectral partitions to extract centroid positions. The centroids are modeled as smooth functions of acquisition time and used to characterize drift.
(iii) Drift correction: using a reference set of centroids, partition-specific mass calibration parameters are optimized, modeled over time, and used to interpolate each partition onto the reference mass axis. Finally, a drift-corrected integrated spectrum is computed as a weighted average of the aligned partitions.
(iv) Mass-to-charge (m/z) calibration: the global mass calibration parameters are recalibrated using a refined set of well-isolated peaks with known mass-to-charge (m/z) values. Each is fitted with Gaussian and Lorentzian models to extract centroids and widths. A smooth polynomial model is used to identify and iteratively remove outliers, leaving a final set of peaks for recalibrating the global parameters. The parameters are then refined iteratively until convergence, and the updated calibration parameters are propagated to update drift correction results.
(v) Peak profiling: empirical peak profiles are generated based on isolated peaks that are automatically identified by AutoSpect. These profiles are used to create a look up table (LUT) of all possible peaks contained in the range of the spectra. This ensures accurate representation of spectral features corresponding to the main peak centers. AutoSpect then accounts for instrumental notching effects and models peak tailing.
(vi) Spectral fitting: the generated peak profiles are applied to fit spectra, resolving overlapping peaks and deconvoluting interferences. Linear optimization algorithms refine the fitting process, ensuring high precision in determining elemental and isotopic abundances. Fitted spectra are saved and a new HDF5 file is generated that can be used in a variety of downstream image processing programs such as iolite.17–19
3. Materials and methods for AutoSpect use cases
Datasets to test the key functionality of AutoSpect such as peak fitting and branching were obtained from fresh frozen murine kidney and epididymis as well as sea urchin egg samples. Mice organs were dissected from Balb/c and C57BL/6 mice and were embedded in optimal cutting temperature (OCT) media in a plastic mold and flash frozen using chilled isopentane over liquid nitrogen as described elsewhere.20 Briefly, samples were sectioned at 10 μm using a conventional cryostat (Leica Biosystems) onto SuperFrost charged slides (Thermofisher Scientific) and stored in −20 °C prior to ablation. Sea urchin eggs from Arbacia punctulata (Marine Biology Laboratory, Woods Hole, MA, USA) were isolated following standard procedures,21 deposited onto Kapton thin film (SPEX SamplePrep) and allowed to air dry at ambient temperature for 8 hours prior to ablation.Experimental setup begins with outlining the regions of interest on the sample (i.e. kidney, epididymis). Additionally, the instrument is set to measure at least 50 seconds of gas blanks throughout a scan for the collection of signals that can be used for background subtraction.
All samples were ablated using the Elemental Scientific Lasers BioImage 266 nm laser ablation system (Elemental Scientific Lasers, Bozeman, MT, USA) equipped with an ultra-fast low dispersion TwoVol3 ablation chamber and a dual concentration injector and connected to icpTOF S2 mass spectrometer (TOFWERK AG, Thune, Switzerland). Elemental content was initially analyzed in real time according to m/z ratio windowing. Tuning was performed using NIST SRM612 glass certified reference material (National Institute for Standards and Technology, Gaithersburg, MD, USA). Torch alignment, lens voltages, and nebulizer gas flow were optimized using 140Ce and 55Mn while maintaining low oxide formation based on the 232Th16O+/232Th+ ratio (<0.5). Murine samples were ablated in a raster pattern with a laser repetition rate of 100 Hz using a 10 μm circular spot with a 10 μm spacing and zero raster overlap. Sea urchin samples were ablated in a raster pattern with a laser repetition rate of 100 Hz, a 2 μm circular spot, 2 μm spacing, and zero raster overlap. Scanning data were recorded using TofPilot 1.3.4.0 (TOFWERK AG) and saved in the HDF5 format v1.8.20.22 Laser ablation images were visualized using Iolite.17–19
4. AutoSpect software
4.1 LA-ICP-TOF-MS
Laser ablation works by ablating material from the sample and introducing it to a plasma torch where the material is converted to positively charged ions. In TOF-MS, these ions are injected between a pair of extraction plates and accelerated toward a detector. For each extraction, the time of collision is recorded for each detection event, culminating in a spectrum of total detected collisions as a function of time. Current elemental mapping via LA groups each set of laser shots as a line scan, whereas a single image dataset is represented by as many line scans as there are rasters in the image. Thus, a single image can correspond to the aggregate of thousands of individual line scans each corresponding to hundreds to thousands of individual spectra representing ion extraction events. Furthermore, as an LA-ICP-TOF-MS instrument collects an image, it alternates between segmented scans of sample regions, reference standards, and gas blanks. This results in fragmented, discontinuous data spread across thousands of individual scans that cannot be immediately interpreted and require users to manually assign the identity of each individual line scan, or raster, which is time consuming. AutoSpect software preprocesses this LA-ICP-TOF-MS data in the raw hierarchical data format (HDF5), automatically defragmenting each component, and producing three distinct datasets. These three groups are then partitioned into hundreds of independently manageable data partitions with associated metadata (e.g., average integrated mass spectra, acquisition time, and m/z calibration coefficients, derived below).| KE = ½mv2 = qV | (1) |
 | (2) |
This yields a square-root dependence of t on m/z, consistent with the idealized flight model. However, to account for instrumental delays and nonlinearities in practical TOF-MS systems, this relationship is generalized as:
| t = P1(m/z)3P3 − P2 | (3) |
Since each ion undergoes the same accelerative force, the more massive an ion is the slower the acceleration it undergoes. This separates the ions in space based on their mass-to-charge ratio (m/z, or μ), such that the corresponding digital spectral time bin, bi, for a particular μi is given by eqn (4) and the corresponding μi for a given time bin, bi, is given by eqn (5).
| mz2bin(μi;P1, P2, P3), bi = P1 × (μi)P3 − P2 | (4) |
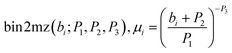 | (5) |
4.2 Partitioning and processing raw data
Laser ablation based elemental mapping is acquired using line scans. As such, a single image dataset is represented by as many line scans as there are rasters in the image. Thus, a single image corresponds to the aggregate of thousands of individual line scans. Furthermore, as an LA-ICP-TOF-MS instrument collects an image, it alternates between segmented scans of the sample, reference standards, and gas blanks. As the instrument alternates between segmented scans of the sample, reference standards, and gas blanks, the resulting spectra are fragmented and dispersed across numerous acquisitions. To facilitate structured data handling, spectra from all measurements—sample, gas blank, and references—are sorted accordingly and grouped into smaller partitions, each containing approximately 1600 spectra consisting of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616 spectral time points.
616 spectral time points.
For each partition, the average acquisition time and spectrum are computed and stored. The spectral data is structured into a partition matrix,  , where N represents the number of spectral bins, and Q denotes the number of partitions. Each column S(:,q) in the matrix corresponds to a partition containing the mean spectrum for that subset:
, where N represents the number of spectral bins, and Q denotes the number of partitions. Each column S(:,q) in the matrix corresponds to a partition containing the mean spectrum for that subset:
 | (6) |
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) n,q represents the average intensity at spectral bin n within partition q. The partition-wise averaged spectrum is then computed (eqn (S1)†). The columns of S are then sorted in ascending order of their mean acquisition times,
n,q represents the average intensity at spectral bin n within partition q. The partition-wise averaged spectrum is then computed (eqn (S1)†). The columns of S are then sorted in ascending order of their mean acquisition times,  , with the qth entry of t corresponding to the qth column of S. Lastly, the integrated spectrum,
, with the qth entry of t corresponding to the qth column of S. Lastly, the integrated spectrum, 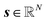 , is obtained by averaging over all individual raw pixel spectra.
, is obtained by averaging over all individual raw pixel spectra.
4.3 Peak identification, tracking peaks, and measuring peak drift
TOF instruments can be sensitive to fluctuations in physical parameters such as temperature.15,16 This can lead to time-dependent peak centroid drift of the ions of interest over the course of sample analysis. As such, the peak centroids' positions at the initiation of a scan may not reflect their corresponding positions throughout the scan. Therefore, this time-dependent peak drift must be accounted for before any processing/fitting of the resultant spectra to produce the most accurate isotope maps. The major drawback for peak fitting is the subjective nature of removing peaks prior to fitting and the time constraints of full spectrum peak fitting. AutoSpect solves these issues through development of an automated process to identify peaks and measure peak drift. , where each column, j, contains the raw intensity values
, where each column, j, contains the raw intensity values  such that
such that
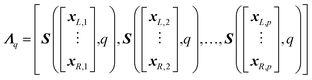 | (7) |
Here, each column in Λq represents the 19-bin peak region, centered at xj. Similarly, the corresponding bins for the intensity values of the peak regions in S(:,q) are extracted and assembled into a matrix 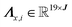 , such that
, such that
 | (8) |
Each peak region Λq(:,j) is first corrected by subtracting a linear baseline computed using a first-order polynomial fit. The baseline is subtracted from the raw peak region, yielding a corrected peak region. This baseline-corrected region is then fitted to a Lorentzian function. The optimal parameters are determined by minimizing the sum of squared residuals (see Section 3 in ESI†).
From each spectral partition, q, and peak region, j, the fitted centroid, x0, is stored to the q-th and j-th entry of matrix 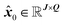 , where J is the number of peaks and Q is the number of spectral partitions (see Fig. 2A, gray lines).
, where J is the number of peaks and Q is the number of spectral partitions (see Fig. 2A, gray lines).
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) 0 is the array of fitted centroids from our Lorentzian modeling to the peaks across the spectral partitions, we seek to solve for
0 is the array of fitted centroids from our Lorentzian modeling to the peaks across the spectral partitions, we seek to solve for ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) f, the smooth temporal trend of the centroids across the partitions. To do this, each row of the peak centroid matrix,
f, the smooth temporal trend of the centroids across the partitions. To do this, each row of the peak centroid matrix, ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) 0, is independently fitted to a smooth function of the mean acquisition time, t, (Fig. 2A, red fitted line, eqn (S10)†). Using the R2 calculated from the fit to each row (peak centroid as a function of time), only the rows corresponding to the top 20 R2 values are retained and used in the following section to solve spectral drift as a function of acquisition time. This ensures that the most temporally coherent and well-modeled peaks are used for spectral drift correction.
0, is independently fitted to a smooth function of the mean acquisition time, t, (Fig. 2A, red fitted line, eqn (S10)†). Using the R2 calculated from the fit to each row (peak centroid as a function of time), only the rows corresponding to the top 20 R2 values are retained and used in the following section to solve spectral drift as a function of acquisition time. This ensures that the most temporally coherent and well-modeled peaks are used for spectral drift correction.4.4 Modeling peak drift and applying drift correction
 , each representing a vector of length Q corresponding to the spectral partition specific entries for P1, P2, and P3, respectively (eqn (S11)†).
, each representing a vector of length Q corresponding to the spectral partition specific entries for P1, P2, and P3, respectively (eqn (S11)†).AutoSpect solves for the coefficients ρ1, ρ2, and ρ3, by first assigning a basis set for comparison. This basis set provides a reference set of peak centroids for comparison with the time-dependent peak centroids derived above. This set of basis peaks is determined by assigning one of the partitions as a reference. To determine the reference partition, total peak region counts per spectral partition are computed and the partition with the fourth-highest total counts is chosen as the reference.
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) f, the peak centroids are converted from bin# to μ (eqn (5)) and become the basis set against which the rest will be compared.
f, the peak centroids are converted from bin# to μ (eqn (5)) and become the basis set against which the rest will be compared.
μref = bin2mz(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) f(:,j); P1, P2, P3) f(:,j); P1, P2, P3)
| (9) |
μq = bin2mz(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) f(:,q); ρ1q, ρ2q, ρ3q) f(:,q); ρ1q, ρ2q, ρ3q)
| (10) |
Using the theoretical centroids calculated above, ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) f, the partition specific calibration parameters (ρ1, ρ2, and ρ3) are solved by minimizing the residuals between expected/basis (μref, eqn (9)) and fitted (μq, eqn (10)) values.
f, the partition specific calibration parameters (ρ1, ρ2, and ρ3) are solved by minimizing the residuals between expected/basis (μref, eqn (9)) and fitted (μq, eqn (10)) values.
Following optimization of the ρ1, ρ2, and ρ3 calibration parameters, each parameter is fitted as a function of the mean acquisition time, t, using polynomial fitting, Gaussian Process Regression fitting, or a simple cubic spline interpolation. The resulting root-mean-squared-deviations from each approach for all three parameters are compared and the approach with the corresponding lowest value is used going forward (Fig. 2B).
Once the spectra of S are drift corrected, the integrated spectrum is recalculated (Fig. 3 bottom row, Fig. 6A and 8 bottom row) as the weighted mean of the drift corrected spectral partitions.
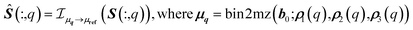 | (11) |
 is the interpolation operator, implemented using a piecewise cubic Hermite interpolation polynomial, that maps the spectrum from the local axis μq to the global reference axis μref, Ŝ(:,q) is the drift-corrected spectrum matrix for partition q.
is the interpolation operator, implemented using a piecewise cubic Hermite interpolation polynomial, that maps the spectrum from the local axis μq to the global reference axis μref, Ŝ(:,q) is the drift-corrected spectrum matrix for partition q.An overlay of the various spectral partitions following drift correction can be seen in Fig. 3A and B, which show drift correction of low, mid, and high range m/z regions. This can be seen by the top and middle rows. Where the top rows show noticeable peak drift in the centroid positions, the middle row shows that the drift corrected spectra are perfectly aligned.
The deblurring of spectra following drift correction can be seen in Fig. 3 (and later in the bottom row of Fig. 8) by looking at the bottom row of plots and comparing the original integrated spectrum with the integrated spectrum from drift correction. Although the peaks are narrower for all three regions, the impact, at least in this example, is most noticeable for m/z of 18, where it is easily seen that the peak is much more clearly defined.
4.5 Optimizing mass spectrum calibration
The global mass calibration parameters are recalibrated using a refined set of well-isolated peaks with known m/z values. Each is fitted with Gaussian and Lorentzian models to extract centroids and widths. A smooth polynomial model is used to identify and iteratively remove outliers, leaving a final set of peaks for recalibrating the global parameters. The parameters are then refined iteratively until convergence, and the updated calibration parameters are propagated to update drift correction results.This begins by using the preset integration windows for the 315 ions in the LUT available from TofWare. All peaks that have integration windows that do not overlap with any other window are considered isolated peak regions. For the icpTOF S2 instrument, of the 315 available peak regions in the LUT, 118 peaks are considered isolated. Then in a process similar to peak identification above (Section 4.3), each peak region of the drift corrected weighted integral spectrum, ŝ, is checked to verify two things.
(1) The highest point (peak) is contained in the window but not at the boundaries of the window.
(2) The spectral intensities are monotonically decreasing to the left and right (similar to eqn (S2) and (S3)†).
Next, the fitted centroid and width from the Gaussian fitting are used as initial values for fitting the same region to a Lorentzian function (eqn (S17), ESI†). From this, the centroids (xfitted) and peak widths (σfitted) are saved. To avoid spurious fits, the xfitted is verified to be contained within the windowed region. If it is not, then the peak region and its associated xfitted and σfitted are discarded. Using the R2 from the Lorentzian fitting, all fitted peak regions with R2 > 0.75 are carried forward. Using eqn (5), the xfitted is converted to μfitted. Then xfitted, μfitted, and σfitted are stored into column vectors for further refinement (eqn (S18), ESI†).
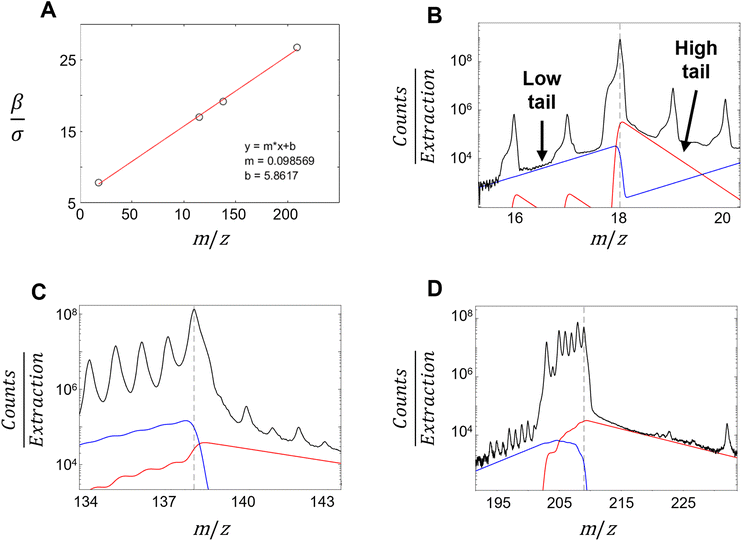
To model the expected smooth dependence of σfitted on the corresponding fitted centroid positions μfitted, a second-order polynomial model is constructed using non-negative least squares regression. In addition, the expected peak width for each centroid is then estimated using a fitted polynomial model, the most extreme outlier is then removed, and the polynomial fit is recomputed with the remaining peaks. This process is repeated until only 10 peaks remain (Fig. 4A and ESI Section 10†).
From these 10 peaks, the associated xfitted and μfitted are used to optimize the coefficients P1, P2, and P3. The optimization problem is solved using nonlinear least squares (eqn (S20), ESI†). The associated σexpected from the ten peaks are used to calculate the expected peak centroid width for all spectral bins for use in Sections 4.6 and 4.7.
4.6 Peak profile calculations
 | (12) |
Each transformed peak is then interpolated onto a fixed standard deviation grid, s ∈ [−20, 20], with k uniformly spaced points. The peak profiles corresponding to a centroid positioned anywhere on the mass-axis are interpolated across all detector bins using first-order polynomial regression at each s-coordinate, forming a continuous 2D surface of peak shape profiles. This creates the empirical LUT used below:
•  : empirical peak profile intensities in standard deviation space, with each column corresponding to the measured profile at each of the N integer value digital spectral bins.
: empirical peak profile intensities in standard deviation space, with each column corresponding to the measured profile at each of the N integer value digital spectral bins.
•  : empirical peak profile spectral bin indices in standard deviation space, with each column corresponding to the bin coordinate of the corresponding intensity value in LUTy.
: empirical peak profile spectral bin indices in standard deviation space, with each column corresponding to the bin coordinate of the corresponding intensity value in LUTy.
This LUT facilitates accurate, calibration-driven construction of empirical peak shapes during fitting.
 , for each of m peaks, the corresponding empirical peak shape is retrieved via interpolation from the precomputed LUTs. This process involves several variables, an interpolation operator, and a series of transformation steps (ESI Section 13†).
, for each of m peaks, the corresponding empirical peak shape is retrieved via interpolation from the precomputed LUTs. This process involves several variables, an interpolation operator, and a series of transformation steps (ESI Section 13†).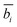 , using the calibration parameters using eqn (4) and global calibration coefficients (P1, P2, and P3). Since
, using the calibration parameters using eqn (4) and global calibration coefficients (P1, P2, and P3). Since ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) i will only extremely rarely be a whole integer (i.e., an exact match to a column of LUTx and LUTy), the two nearest corresponding integer bins are blended to generate the intermediate profile corresponding to
i will only extremely rarely be a whole integer (i.e., an exact match to a column of LUTx and LUTy), the two nearest corresponding integer bins are blended to generate the intermediate profile corresponding to ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) i. Then, using xi and yi, the peak shape yi, defined over non-integer spectral bin coordinates xi, in standard deviation space, is mapped onto the uniform detector bin grid via interpolation and then normalized to unit area. This yields
i. Then, using xi and yi, the peak shape yi, defined over non-integer spectral bin coordinates xi, in standard deviation space, is mapped onto the uniform detector bin grid via interpolation and then normalized to unit area. This yields  , the empirical core peak shapes for each centroid μ0,i.
, the empirical core peak shapes for each centroid μ0,i.| Region | Peaks | Tails | ||||||
|---|---|---|---|---|---|---|---|---|
| Intensity | Percentage of peak intensity | |||||||
| Isotope | Intensity | Fe | Cu | Zn | Fe | Cu | Zn | |
| 0 | 56Fe | 1526 | 0.2408 | — | — | 0.02% | — | — |
| 1 | 59Co | 2.526 | 0.0998 | — | — | 3.95% | — | — |
| 2 | 60Ni | 2.291 | 0.0725 | — | — | 3.16% | — | — |
| 3 | 61Ni | 0.1542 | 0.0520 | 0.0027 | — | 33.74% | 1.76% | — |
| 4 | 62Ni | 0.3078 | 0.0380 | 0.0092 | — | 12.33% | 2.99% | — |
| 5 | 69Ga | 0.2553 | 0.0039 | 0.0106 | 0.0283 | 1.52% | 4.15% | 11.08% |
| 6 | 71Ga | 0.1671 | 0.0020 | 0.0063 | 0.0175 | 1.22% | 3.76% | 10.45% |
Let:
The tails are defined as:
 | (13) |
Each tail matrix is normalized column-wise (eqn (S34), ESI†).
 contains the asymmetric, resolution-constrained, and normalized peak shapes for each spectral signal prior to application of instrumental notching and isotopic branching.
contains the asymmetric, resolution-constrained, and normalized peak shapes for each spectral signal prior to application of instrumental notching and isotopic branching.To correct for this effect, AutoSpect uses the stored notching parameters from the raw data file to automatically optimize and account for these changes. These values are used to compute a set of scaling factors, referred to as FLOAT, which are applied to the branching ratios of affected isotopes.
To model isotopic structure, each elemental peak in GT is condensed into one or more isotopic peaks using the notch-corrected branching ratio matrix ![[B with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0042_0303.gif) iso.
iso.
Let:
• 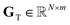 : asymmetric, tailed, normalized elemental peak profiles,
: asymmetric, tailed, normalized elemental peak profiles,
• 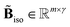 : corrected branching ratio matrix,
: corrected branching ratio matrix,
• 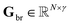 : final modeled isotope-resolved asymmetric, tailed peak profiles.
: final modeled isotope-resolved asymmetric, tailed peak profiles.
Then, the isotopic peak shapes are computed as:
Gbr = GT × ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) iso iso
| (14) |
Each column of ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) iso contains fractional contributions from isotopes of a given element. These are derived from known natural abundances and adjusted to account for notching. Each column is then normalized to unit area (eqn (S34), ESI†). This step allows each species to be represented by a single equation, incorporating all isotopes and correcting for instrument-induced artifacts. It improves both interpretability and robustness in spectral deconvolution, particularly for peaks that are partially resolved or overlapping (Fig. 6).
iso contains fractional contributions from isotopes of a given element. These are derived from known natural abundances and adjusted to account for notching. Each column is then normalized to unit area (eqn (S34), ESI†). This step allows each species to be represented by a single equation, incorporating all isotopes and correcting for instrument-induced artifacts. It improves both interpretability and robustness in spectral deconvolution, particularly for peaks that are partially resolved or overlapping (Fig. 6).
4.7 Spectral fitting and peak deconvolution
In the final steps of AutoSpect, using the drift calibration and the branched equations defined in the previous sections, the spectra for the samples, gas blanks, and reference standards are fitted to deconvolute peak overlap. Typically, with LA data, the individual pixel spectra are sparsely populated where most of the spectral bins contain zeros. This is especially the case with biological tissues. Because of this, interpolating the pixel spectra into a common grid for drift correction can result in significant errors. To avoid such potential errors, the composite model matrix Gbr is interpolated to the local drift-corrected mass axis for each partition. Then, prior to spectral fitting, background correction is applied using either measured gas blanks or an automated SNIP-based background estimation algorithm.26 Once the spectra are background corrected and the model matrix is aligned with the measured data, the corrected spectra are deconvolved using standard linear least squares:
Cq(:,k) = (![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) Tq Tq![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) q)−1 q)−1![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) Tq(Fq(:,k) − Bq(:,k)) Tq(Fq(:,k) − Bq(:,k))
| (15) |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) q) across all spectra in partition q. Since each column of
q) across all spectra in partition q. Since each column of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) q is normalized to unit area, the resulting coefficients in Cq represent the total extracted counts for each modeled peak component, and no additional normalization or post-processing is required (ESI Section 19†).
q is normalized to unit area, the resulting coefficients in Cq represent the total extracted counts for each modeled peak component, and no additional normalization or post-processing is required (ESI Section 19†).
Once fitted, AutoSpect copies the original data file and then updates fitted peak data. Since AutoSpect outputs the data in the native TofWerk format, the fitted data can be seamlessly incorporated to any of the existing data reduction pipelines currently in the field using the TofWerk hdf5 structure.
5. AutoSpect use case examples
5.1 Single cell and tissue section imaging
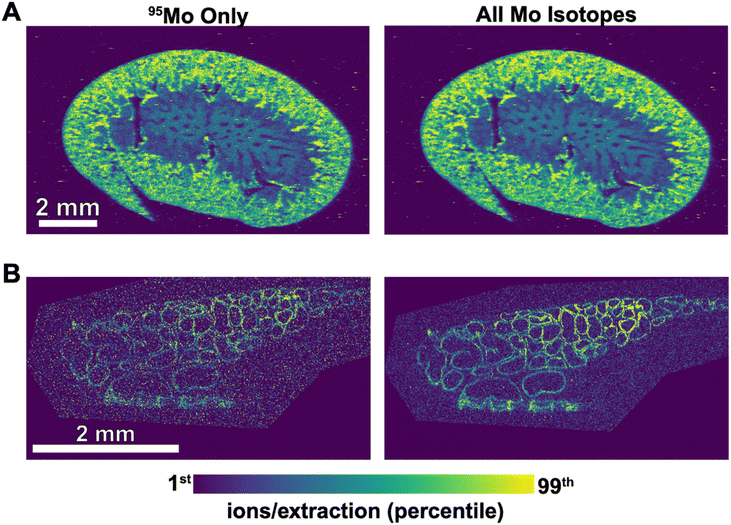
AutoSpect functionality was tested on freshly isolated sea urchin eggs from Arbacia punctulata, which have an average diameter of 70 μm. This dataset required ∼ around 4.5 hours per sample and exhibited noticeable signal drift resulting from observed peak position drift with potentially contributing factors from instrument drift, ablation drift and transport drift (Fig. 7). For 24Mg, 31P, and 66Zn, the peak drift was quantified as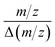 yielding values of 480, 344, and 507, respectively. This is on the order of 50% the instrument specified resolution. Additional datasets were collected from 10 μm thick sections of epididymis and kidney tissues, which respectively showed low and high localized abundance of molybdenum, an essential enzymatic cofactor.
yielding values of 480, 344, and 507, respectively. This is on the order of 50% the instrument specified resolution. Additional datasets were collected from 10 μm thick sections of epididymis and kidney tissues, which respectively showed low and high localized abundance of molybdenum, an essential enzymatic cofactor.
AutoSpect was compared to currently existing software for spectral analysis, Tofware, to benchmark performance. A laser ablation dataset of sea urchin eggs was analyzed using both Autospect and Tofware to compare their workflows, speed, and performance. This dataset was chosen due to its large file size, with 987 raster lines of 1305 spots, each 2 μm in size, giving a field of 2610 μm × 1974 μm, and a file size of 9.08 GB. The Tofware workflow totaled 53 min and 24 s, comprising peak shape optimization and peak fitting across 315 masses ranging from 6Li+ to 238U+ (see Table 2). The analogous peak fitting by Autospect was accomplished in 41 min 50 s. The Autospect workflow took 10 min 14 s to complete drift correction, and an additional 27 s to perform peak profiling, totaling 52 min 31 s for all operations. The resulting fitted laser ablation images and the original, uncorrected data are shown in Fig. 7. Notably, this dataset has fluctuating 24Mg+, 31P+, 66Zn+ signals arising from time dependent peak centroid drift. The decrease in 24Mg+ for Tofware is a result of the imperfect calibration of the mass axis. This can be seen in Fig. 8 with the spectral partitions projected onto the Tofware mass axis, where the peak centroid for 24Mg+ is shifted further out of focus to higher apparent m/z. For 66Zn+, Tofware improved the mass axis calibration for the latter ca. 70% of the image, improving the bottom of the map, but worsening the top. For 31P+, peak broadening in Tofware leads to an inability to separate the 31P+ intensity from that of an apparent unknown satellite gas peak. None of the pitfalls in Tofware are a reflection of the software, rather these reflect the need for a robust and automated mass axis drift correction. As can be seen, when mass axis drift correction is robustly performed, as in AutoSpect, it eliminates these fluctuations and gives a stable response over the course of the experiment.
| Data processing task | Time taken by AutoSpect (mm:ss) | Time taken by Tofware (mm:ss) |
|---|---|---|
| a Includes data loading and writing tasks.b Function not available. | ||
| Dataset 1: sea urchin eggs (experimental scan time = 4:37:15) | ||
| Peak fittinga | 41:50 | 53:24 |
| Drift correction | 10:14 | —b |
| Peak profiling | 00:27 | —b |
| Total | 52:31 | 53:24 |
| Dataset 2: tissue slide 2 (experimental scan time = 1:10:02) | ||
| Peak fittinga | 05:17 | 07:18 |
| Drift correction | 03:11 | —b |
| Peak profiling | 00:15 | —b |
| Total | 08:43 | 07:18 |
| Dataset 3: tissue slide 3 (experimental scan time = 1:10:04) | ||
| Peak fittinga | 06:09 | 09:12 |
| Drift correction | 03:25 | —b |
| Peak profiling | 00:22 | —b |
| Total | 09:56 | 09:12 |
| Dataset 4: tissue slide 5 (experimental scan time = 1:20:54) | ||
| Peak fittinga | 08:33 | 11:06 |
| Drift correction | 03:42 | —b |
| Peak profiling | 00:22 | —b |
| Total | 12:37 | 11:06 |
 | ||
| Fig. 8 Spectral analysis of peak fitting and drift correction by AutoSpect and Tofware. The average spectrum for each of the 806 spectral partitions determined in AutoSpect from the sea urchin eggs from Fig. 7 are shown for the three masses 24Mg+, 31P+, and 66Zn+. Row 1 shows the original spectra prior to any drift correction. Row 2 shows the scan partitions from AutoSpect projected onto the mass axis calibration from Tofware. Row 3 shows the spectra from the partitions after drift correction. Row 4 shows the average of the uncorrected spectra projected to the mass axis from AutoSpect (blue) and Tofware (black), along with the average spectrum from the drift corrected (red) spectra from AutoSpect, showing significant changes to the apparent peak position and peak morphology post AutoSpect drift correction. | ||
Another demonstration for AutoSpect involves showing the effectiveness of isotope ratio branching in revealing spatial localization of low isotopic abundance elements such as molybdenum in biological tissues (Fig. 9). Molybdenum acts as an essential metal cofactor to enzymes that participate in redox reactions due to its ability to shuttle between three oxidation states.27 Therefore, detection of molybdenum in biological samples most likely indicate the presence of these enzymes. While molybdenum was detectable using Iolite software, the isotope ratio branching capability of AutoSpect improved signal to noise, allowing for increased accurate assessment of localization within the sample.
6. Discussion
AutoSpect provides an approach that is useful at many levels to LA-ICP-TOF-MS analysis, addressing longstanding challenges in data processing. By automating drift correction and peak profile determination, profiling low and high peak tailing, and fitting spectra, it improves both accuracy and efficiency of analysis. AutoSpect's flexible design allows for adaptation to other fields requiring high-resolution elemental and isotope analyses. Future updates will incorporate additional functionality, such as advanced multiply charged species handling and enhanced matrix-matching algorithms.The approach employed in AutoSpect, and many of the underlying algorithms, were directly borrowed from or built upon ideas and algorithms developed for X-ray fluorescence microscopy (XFM).28–31 In particular, the implementation of branching ratios, introduction of the low and high m/z tailing, use of directly subtracting the gas blank, and the partitioning and chunking of spectra were adapted from the M-BLANK program used for fitting XFM spectra.
Recalibration of the mass axis: when identifying isolated peaks to calculate the smooth function of peak broadening as a function of m/z, the field largely supports the use of a first order polynomial. However, a second order polynomial was used rather than a first order (ESI Section 10†) as it was found that allowing for subtle curvature adhering to a square component yielded peaks that aligned with their tabulated m/z values across the dynamic range of individual atoms to a much better degree than a slope component alone (Fig. 4A).
Automatic generation of peak profiles: empirical peak profiles are generated based on isolated peaks that are automatically identified by the software and used to create a LUT of all possible peaks contained in the range of the spectra. This ensures accurate representation of spectral features corresponding to the main peak centers. AutoSpect then accounts for instrumental notching effects and models peak tailing. The incorporation of peak tailing and accounting for these tails is quantitatively important, especially concerning the high m/z tailing which persists for tens of m/z. This explains the difficulty of fitting an isotope neighboring another isotope with an intensity that is greater than 4 orders of magnitude larger.
Peak tailing: peak tailing is a new feature that has not been implemented into peak shape modeling of mass spectra. The functional forms have been adapted from XFM for modeling inefficient electron capture in energy-dispersive detectors. In XFM and related XRF systems, only a low-energy tail is observed, corresponding to post-detection charge dissipation—an effect analogous to the high m/z tail observed in TOF. In the context of TOF mass spectrometry, however, an additional low m/z tail emerges, requiring a new physical interpretation. Despite the differing origins, both tails are modeled using mirrored functional forms, and distinct interpretations are warranted for each side of the peak.
High m/z tailing is hypothesized to result from residual charge persisting on the detector, which dissipates over time, analogous to charge retention artifacts in energy dispersive X-ray detectors.23–25 This leads to a slowly decaying signal that extends tens of m/z units beyond the peak and must be modeled to avoid misattributing ion counts.
In contrast, the low m/z tail appears to reflect a phenomenon that precedes the actual arrival of the ion at the detector. While it may seem counterintuitive to detect a signal before the particle arrives, electrostatics provides a rationale. As a charged ion approaches the detector, its electric field induces a mirror charge within the conductive surface of the detector, an effect that can be understood using the method of image charges from electrostatics. This induced field, and the resulting current, could plausibly begin to rise before the ion physically reaches the detector. Notably, the slope of this low-m/z tail would depend on ion velocity: heavier ions (higher m/z) move more slowly, resulting in a more gradual leading slope. This matches observations from empirical fits, which show shallower low-side tailing for higher masses.
Thus, the peak tailing model captures both a post-arrival dissipation component (high m/z tail) and a pre-arrival induction component (low m/z tail). While both features are needed to accurately model the observed peaks asymmetry, and failure to account for them can significantly impact spectral deconvolution especially in dense or overlapping regions, the proposed explanation should be viewed as speculative at this time.
In TOF-MS it is difficult to reliably quantify a weaker peak that is positioned near a much more intense peak differing by four or more orders of magnitude in intensity. For example, if 55Mn is present at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 counts and 56Fe is only 10 counts, the 56Fe signal is traditionally considered unreliable due to interference from the more intense neighboring peak. Notably, such quantitation has never invoked tailing, as tails had not previously been modeled or recognized as a source of interference in TOF-MS. The identification and modeling of peak tails in AutoSpect represents a new advancement that helps explain and correct this increased noise in the weaker neighboring peak. With the inclusion of explicit tail modeling in AutoSpect, such weaker peaks can now be meaningfully quantified even in the presence of nearby intense signals, challenging this long-standing assumption and extending the quantifiable dynamic range of TOF-MS. This assumption likely stems from historical limitations in peak modeling that failed to incorporate tailing behavior. The inclusion of accurate tail models in AutoSpect directly challenges this assumption by enabling quantification even in cases of extreme dynamic range and overlap, thereby extending the practical limits of spectral resolution and trace detection.
000 counts and 56Fe is only 10 counts, the 56Fe signal is traditionally considered unreliable due to interference from the more intense neighboring peak. Notably, such quantitation has never invoked tailing, as tails had not previously been modeled or recognized as a source of interference in TOF-MS. The identification and modeling of peak tails in AutoSpect represents a new advancement that helps explain and correct this increased noise in the weaker neighboring peak. With the inclusion of explicit tail modeling in AutoSpect, such weaker peaks can now be meaningfully quantified even in the presence of nearby intense signals, challenging this long-standing assumption and extending the quantifiable dynamic range of TOF-MS. This assumption likely stems from historical limitations in peak modeling that failed to incorporate tailing behavior. The inclusion of accurate tail models in AutoSpect directly challenges this assumption by enabling quantification even in cases of extreme dynamic range and overlap, thereby extending the practical limits of spectral resolution and trace detection.
Building on this, we can examine how tail contributions manifest in real datasets. For example, the contribution from the peak tail for 56Fe is ca. 0.02% the amplitude of the main centroid contributing negligibly to the quantitative estimate of 56Fe. However, because LA exists across a dynamic range of 8 to 10 orders of magnitude, these tails can have significant non-negligible impacts on neighboring peaks near and far in unpredictable manners that are sample dependent. For example, comparing the amplitudes of the raw peak and tails present for 61Ni (region 3), 35.5% of the peak amplitude corresponds to the combined contributions from the Cu and Fe tails (Fig. 6). Similarly, 15.32% of the peak amplitude for 62Ni (region 4) corresponds to these two tails. For 69Ga (region 5) and 71Ga (region 6), 16.76% and 15.43% of the peak amplitudes correspond to the combined contributions of the Fe, Cu, and Zn tails. By comparison, the 3.95% and 3.16% contributions to 59Co (region 1) and 60Ni (region 2), are less significant.
Spectral fitting: AutoSpect applies background correction using either gas blanks or a SNIP-based algorithm, with the residual spectra fitted using the generated peak profiles to resolve overlapping peaks and deconvolute interferences. The fitted peak intensities are then saved in the native HDF5 format for compatibility with existing data pipelines allowing further analysis and reporting.
7. Conclusion
AutoSpect represents a significant advancement in the field of LA-ICP-TOF-MS, providing researchers with a robust, automated tool for spectral fitting and data reduction. Case use studies indicate that AutoSpec supports:(1) Enhanced spectral deconvolution, resolving interferences with high precision.
(2) Accurate drift corrections, ensuring consistent results across extended analytical sessions.
(3) Efficient handling of complex datasets, reducing analysis times significantly compared to manual methods.
By streamlining workflows and addressing critical analytical challenges, AutoSpect empowers users to fully leverage the capabilities of this powerful analytical technique, paving the way for new discoveries in fields from geology to biology, from medicine to material sciences.
Ethical statement
All animal procedures were conducted in compliance with National Institutes of Health's Guide for the Care and Use of Laboratory Animals32 and were approved by the Institutional Animal Care and Use Committee at Michigan State University (protocol approval number: 202200021). Mice were maintained on a 12 h light/dark cycle with chow and water available ad libitum.Data availability
Data and software are available upon request and can be found at https://qemap.ehi.msu.edu/resources.Author contributions
AMC conceived, designed, developed, wrote, and validated all software, including AutoSpect, InSpect, and affiliated subroutines, and performed testbed analyses with input from KWM, DZZ, and TVO. AMC also contributed to the interpretation of results and preparation of the methods description. AMC, DZZ, SHA, KWM, TVO wrote the manuscript. DZZ performed software comparisons, isolated samples, collected and analyzed results for the sea urchin data sets. Mouse kidneys were harvested by QJ. KWM, DZZ, SHA, NS, and AS sectioned murine tissues and collected data.Conflicts of interest
The authors have no conflicts to declare aside from the AutoSpec copyright which is held by AMC, KWM and TVO at Michigan State University.Acknowledgements
Metal analysis and quantitative elemental mapping was performed at the Michigan State University Quantitative Bio Element Analysis and Mapping (QBEAM) Center generously supported by the MSU Office for Research and Innovation, the National Institute of General Medical Sciences of the National Institutes of Health award for the resource entitled “Quantitative Elemental Mapping for the Life Sciences” (QE-Map, P41 GM135018) and by the Office of The Director, National Institutes of Health (S10OD026786). D. Z. Z. thanks the National Institute of General Medical Sciences of the National Institutes of Health for a Ruth L. Kirschstein NRSA postdoctoral fellowship (F32GM139401). SHA acknowledges support from National Institute of Child Health and Disease R01 HD100832 for supporting acquisition of mouse epididymal tissue, and TVO acknowledges R01 GM038784 for supporting sea urchin samples. The content of this publication is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors thank Dr Andy Drews for suggesting image charge induction as a possible mechanism for low m/z tailing in TOF-MS.References
- A. Gundlach-Graham, Chapter Three - Multiplexed and Multi-Metal Single-Particle Characterization with ICP-TOFMS, in Comprehensive Analytical Chemistry, ed. Milačič R., Ščančar J., Goenaga-Infante H. and Vidmar J., Elsevier, 2021, vol 93, pp. 69–101, DOI:10.1016/bs.coac.2021.01.008.
- B. Paul, K. Kysenius, J. B. Hilton, M. W. M. Jones, R. W. Hutchinson, D. D. Buchanan, C. Rosty, F. Fryer, A. I. Bush, J. M. Hergt, J. D. Woodhead, D. P. Bishop, P. A. Doble, M. M. Hill, P. J. Crouch and D. J. Hare, An Integrated Mass Spectrometry Imaging and Digital Pathology Workflow for Objective Detection of Colorectal Tumours by Unique Atomic Signatures, Chem. Sci., 2021, 12, 10321–10333, 10.1039/D1SC02237G.
- B. Paul, D. J. Hare, D. P. Bishop, C. Paton, V. T. Nguyen, N. Cole, M. M. Niedwiecki, E. Andreozzi, A. Vais, J. L. Billings, L. Bray, A. I. Bush, G. McColl, B. R. Roberts, P. A. Adlard, D. I. Finkelstein, J. Hellstrom, J. M. Hergt, J. D. Woodhead and P. A. Doble, Visualising Mouse Neuroanatomy and Function by Metal Distribution Using Laser Ablation-Inductively Coupled Plasma-Mass Spectrometry Imaging, Chem. Sci., 2015, 6, 5383–5393, 10.1039/c5sc02231b.
- C. Neff, P. Keresztes Schmidt, P. S. Garofalo, G. Schwarz and D. Günther, Capabilities of Automated LA-ICP-TOFMS Imaging of Geological Samples, J. Anal. At. Spectrom., 2020, 35, 2255–2266, 10.1039/D0JA00238K.
- D. Z. Zee, K. W. MacRenaris and T. V. O'Halloran, Quantitative imaging approaches to understanding biological processing of metal ions, Curr. Opin. Chem. Biol., 2022, 69, 102152, DOI:10.1016/j.cbpa.2022.102152.
- S. A. Iakab, P. Ràfols, X. Correig-Blanchar and M. García-Altares, Perspective on Multimodal Imaging Techniques Coupling Mass Spectrometry and Vibrational Spectroscopy: Picturing the Best of Both Worlds, Anal. Chem., 2021, 93, 6301–6310, DOI:10.1021/acs.analchem.0c04986.
- P. Niehaus, R. Gonzalez de Vega, M. T. Haindl, C. Birkl, M. Leoni, A. M. Birkl-Toeglhofer, J. Haybaeck, S. Ropele, M. Seeba, W. Goessler, U. Karst, C. Langkammer and D. Clases, Multimodal analytical tools for the molecular and elemental characterisation of lesions in brain tissue of multiple sclerosis patients, Talanta, 2024, 270, 125518, DOI:10.1016/j.talanta.2023.125518.
- L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, Characterization of a new ICP-TOFMS instrument with continuous and discrete introduction of solutions, J. Anal. At. Spectrom., 2017, 32, 548–561, 10.1039/C6JA00400H.
- R. Weiskirchen, S. Weiskirchen, P. Kim and R. Winkler, Software solutions for evaluation and visualization of laser ablation inductively coupled plasma mass spectrometry imaging (LA-ICP-MSI) data: a short overview, J. Cheminf., 2019, 11, 16, DOI:10.1186/s13321-019-0338-7.
- T. E. Lockwood, L. Schlatt and D. Clases, SPCal – an open source, easy-to-use processing platform for ICP-TOFMS-based single event data, J. Anal. At. Spectrom., 2025, 40, 130–136, 10.1039/D4JA00241E.
- H. B. Andrews, L. Hendriks, S. B. Irvine, D. R. Dunlap and B. T. Manard, TOFHunter—unlocking rapid untargeted screening of inductively coupled plasma–time-of-flight–mass spectrometry data, J. Anal. At. Spectrom., 2025, 40, 910–920, 10.1039/D4JA00331D.
- M. J. Cubison and J. L. Jimenez, Statistical precision of the intensities retrieved from constrained fitting of overlapping peaks in high-resolution mass spectra, Atmos. Meas. Tech., 2015, 8, 2333–2345, DOI:10.5194/amt-8-2333-2015.
- H. Stark, R. L. N. Yatavelli, S. L. Thompson, J. R. Kimmel, M. J. Cubison, P. S. Chhabra, M. R. Canagaratna, J. T. Jayne, D. R. Worsnop and J. L. Jimenez, Methods to extract molecular and bulk chemical information from series of complex mass spectra with limited mass resolution, Int. J. Mass Spectrom., 2015, 389, 26–38, DOI:10.1016/j.ijms.2015.08.011.
- H. Timonen, M. Cubison, M. Aurela, D. Brus, H. Lihavainen, R. Hillamo, M. Canagaratna, B. Nekat, R. Weller, D. Worsnop and S. Saarikoski, Applications and limitations of constrained high-resolution peak fitting on low resolving power mass spectra from the ToF-ACSM, Atmos. Meas. Tech., 2016, 9, 3263–3281, DOI:10.5194/amt-9-3263-2016.
- V. A. Petyuk, N. Jaitly, R. J. Moore, J. Ding, T. O. Metz, K. Tang, M. E. Monroe, A. V. Tolmachev, J. N. Adkins, M. E. Belov, A. R. Dabney, W.-J. Qian, D. G. Camp and R. D. Smith, Elimination of Systematic Mass Measurement Errors in Liquid Chromatography−Mass Spectrometry Based Proteomics Using Regression Models and a Priori Partial Knowledge of the Sample Content, Anal. Chem., 2008, 80, 693–706, DOI:10.1021/ac701863d.
- I. V. Chernushevich, A. V. Loboda and B. A. Thomson, An introduction to quadrupole–time-of-flight mass spectrometry, J. Mass Spectrom., 2001, 36, 849–865, DOI:10.1002/jms.207.
- C. Paton, J. Hellstrom, B. Paul, J. Woodhead and J. Hergt, Iolite: Freeware for the visualisation and processing of mass spectrometric data, J. Anal. At. Spectrom., 2011, 26, 2508–2518, 10.1039/C1JA10172B.
- B. Paul, C. Paton, A. Norris, J. Woodhead, J. Hellstrom, J. Hergt and A. Greig, CellSpace: A module for creating spatially registered laser ablation images within the Iolite freeware environment, J. Anal. At. Spectrom., 2012, 27, 700–706, 10.1039/C2JA10383D.
- B. Paul, J. Petrus, D. Savard, J. Woodhead, J. Hergt, A. Greig, C. Paton and P. Rayner, Time resolved trace element calibration strategies for LA-ICP-MS, J. Anal. At. Spectrom., 2023, 38, 1995–2006, 10.1039/D3JA00037K.
- S. H. Ahn, K. Halgren, G. Grzesiak, K. W. MacRenaris, A. Sue, H. Xie, E. Demireva, T. V. O'Halloran and M. G. Petroff, Autoimmune regulator deficiency causes sterile epididymitis and impacts male fertility through disruption of inorganic physiology, bioRxiv, 2025, preprint, 2025.2001.2011.632558, DOI:10.1101/2025.01.11.632558.
- V. D. Vacquier, Laboratory on sea urchin fertilization, Mol. Reprod. Dev., 2011, 78, 553–564, DOI:10.1002/mrd.21360.
- M. Folk, G. Heber, Q. Koziol, E. Pourmal and D. Robinson, An overview of the HDF5 technology suite and its applications, in Proceedings of the EDBT/ICDT 2011 Workshop on Array Databases, Association for Computing Machinery, Uppsala, Sweden, 2011, pp. 36–47 Search PubMed.
- B. Vekemans, K. Janssens, L. Vincze, F. Adams and P. Van Espen, Analysis of X-ray spectra by iterative least squares (AXIL): New developments, X-Ray Spectrom., 1994, 23, 278–285, DOI:10.1002/xrs.1300230609.
- J. L. Campbell and J. A. Maxwell, A cautionary note on the use of the Hypermet tailing function in X-ray spectrometry with Si(Li) detectors, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 129, 297–299, DOI:10.1016/S0168-583X(97)00229-2.
- J. L. Campbell, A. Perujo and B. M. Millman, Analytic description of Si(Li) spectral lineshapes due to monoenergetic photons, X-Ray Spectrom., 1987, 16, 195–201, DOI:10.1002/xrs.1300160503.
- C. G. Ryan, E. Clayton, W. L. Griffin, S. H. Sie and D. R. Cousens, SNIP, a statistics-sensitive background treatment for the quantitative analysis of PIXE spectra in geoscience applications, Nucl. Instrum. Methods Phys. Res., Sect. B, 1988, 34, 396–402, DOI:10.1016/0168-583X(88)90063-8.
- G. Schwarz, R. R. Mendel and M. W. Ribbe, Molybdenum cofactors, enzymes and pathways, Nature, 2009, 460, 839–847, DOI:10.1038/nature08302.
- A. M. Crawford, N. J. Sylvain, H. Hou, M. J. Hackett, M. J. Pushie, I. J. Pickering, G. N. George and M. E. Kelly, A comparison of parametric and integrative approaches for X-ray fluorescence analysis applied to a Stroke model, J. Synchrotron Radiat., 2018, 25, 1780–1789, DOI:10.1107/s1600577518010895.
- A. M. Crawford, A. Deb and J. E. Penner-Hahn, M-BLANK: a program for the fitting of X-ray fluorescence spectra, J. Synchrotron Radiat., 2019, 26, 497–503, DOI:10.1107/S1600577519000651.
- A. M. Crawford, B. Huntsman, M. Y. Weng, O. Ponomarenko, C. D. Kiani, S. J. George, G. N. George and I. J. Pickering, Abridged spectral matrix inversion: parametric fitting of X-ray fluorescence spectra following integrative data reduction, J. Synchrotron Radiat., 2021, 28, 1881–1890, DOI:10.1107/S1600577521008419.
- A. M. Crawford, X-Ray Fluorescence Data Analysis Using A Blank Correction Approach, in Advances in X-Ray Analysis (AXA), Lombard IL, United States; 2019, vol 63, pp. 180–193 Search PubMed.
- National Research Council (US) Committee for the Update of the Guide for Care and Use of Laboratory Animals, Guide for the Care and Use of Laboratory Animals: Eighth Edition, The National Academies Press, Washington DC, United States, 8th edn, 2011, DOI:10.17226/12910.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ja00145e |
| This journal is © The Royal Society of Chemistry 2025 |