State-of-the-art heterogeneous polymerization kinetic modelling processes and their applications

Abstract

Heterogeneous polymerization systems have been widely used in large-scale industrial production. Utilizing kinetic simulations to effectively reveal the underlying mechanisms of complex heterogeneous systems is invaluable for both product design and process optimization. The aim of this study is to comprehensively review the recent research progress on the development of heterogeneous polymerization kinetic modelling. We first provide an overview of the kinetic modelling processes of heterogeneous polymerization systems, focusing on mass transfer models, phase-state treatment approaches, and numerical methods. Further, to illustrate the importance of heterogeneous polymerization kinetic modelling, we give examples of its utilization in three research domains, including understanding the kinetics and transfer features, enabling the performance-oriented polymer structure design and precise synthesis, and guiding reactor design, optimization, and scale-up. Finally, the challenges and perspectives of heterogeneous polymerization kinetic modelling are discussed for future development.

---

1 Introduction

Many large-scale polymer production processes (e.g., polystyrene (PS), polyvinyl chloride, and polypropylene (PP)) are carried out in heterogeneous systems. Heterogeneous polymerization is a system in which two or more phases exist during the polymerization process.^1,2 Based on the presence of the phase state, heterogeneous polymerization can be classified into two categories. In the first category, the initial reaction environment would be composed of multiple phases, (e.g., suspension polymerization^3–6 and emulsion polymerization^7–12); in the second category, the reaction medium would be initially homogeneous but phase separation would occur as the polymerization proceeds (e.g., production of high impact polystyrene (HIPS),^13–16 interpenetrating polymer networks,¹⁷ and precipitation polymerization^18–20). Compared with homogeneous polymerization, heterogeneous polymerization has the following advantages: (i) effective release of heat to avoid thermal runaway^21,22 (except in some precipitation or bulk polymerization systems); (ii) effective control of product morphology, which is beneficial to the preparation of high molecular weight polymers,^23,24 (iii) easier separation of polymer products for aqueous-based heterogeneous systems, reducing the post-processing costs.

From the point of view of polymerization reaction engineering, the complexity of heterogeneous polymerization not only lies in the competing polymerization loci but also involves the mass transfer process, which can influence the concentrations of components in each phase and affect the structures and performances of the products. However, owing to the limitations of conventional characterization techniques, it is difficult to monitor the composition and distribution of each phase in real time. Moreover, the comprehensive characterization of the hierarchical structure of polymer products is challenging, especially for the topological structure. Since the successful development of the first electronic computer in 1946, the modelling of chemical processes has been rapidly developed, and the models and algorithms have been gradually adopted for kinetic studies. As supplementary tools for experimental research, modelling and simulation can be used to study the reaction and transfer features efficiently and safely, providing detailed information on the microstructure of the polymer chain. In addition, such modelling techniques can guide the optimization of process conditions, thereby shortening the product development cycles effectively and economically.^25,26 The development of efficient and accurate kinetic models combining the reactions and mass transfer is the key to promoting heterogeneous polymerization engineering.

In recent years, kinetic models of various heterogeneous polymerization systems have been developed. In this study, we systematically review advances in the development of kinetic models for heterogeneous polymerization, including mass transfer models, pseudo-homogeneous assumptions, and numerical solution methods. Then, we focus more on the applications of heterogeneous polymerization kinetic modelling in the understanding of kinetics and transfer characteristics, the development of performance-oriented polymer materials, and the guidance of design, optimization, and scale-up of heterogeneous reactors. This is complementary to the existing reviews on kinetic modelling.^22,27 Finally, we make an outlook on the development trend of heterogeneous polymerization kinetic modelling.

2 Advances in heterogeneous polymerization modelling

2.1 Mass transfer model of the heterogeneous polymerization system

In the heterogeneous polymerization system, the components transfer between phases due to the presence of a concentration gradient or chemical potential gradient, which affects the results of polymerization.^28,29 Since the interphase mass transfer of components and chemical reactions occur simultaneously and compete with each other, the adequate interphase mass transfer model is crucial to accurately predict the kinetics and transfer features of heterogeneous polymerization processes. In this section, we describe several universal mass transfer models, such as the equilibrium thermodynamic model, simple partition model (with the chemical potential gradient as the driving force), and the two-film theory (with the concentration gradient as the driving force). There are also a few mass transfer models applicable to specific heterogeneous systems, such as the radical entry and exit in emulsion polymerization, which are not described in detail in this review but are available in the literature.^30–32

2.1.1. Equilibrium thermodynamic model. The equilibrium thermodynamic model assumes that the system is in phase equilibrium throughout and that the chemical potentials of components are equal in each phase. According to the Flory–Huggins solution theory,³³ the Gibbs energy of a binary mixture can be expressed as:

ΔG_mix = RT(n₁ ln v₁ + n₂ ln v₂ + χn₁v₂) (1)

in which R is the gas constant, T is the temperature, n_i and v_i are the number of molecules and volume fraction of the component i, and χ is the Flory–Huggins interaction parameter.

The chemical potential of each component is the partial derivation of Gibbs energy with respect to the number of molecules at constant pressure and temperature:

Based on the equality of μ_i in the two phases, the distribution of components in each phase can be calculated. In studying the kinetics of HIPS, Luciani et al.³⁴ assumed that the system was always in thermodynamic equilibrium after phase separation. They applied the Flory–Huggins theory to estimate the partition of styrene (St) and initiators in the PS-rich phase and the rubber phase. Moreover, the Flory–Huggins theory was applied to predict the point of phase separation.^34,35 The equilibrium thermodynamic model is simple and easy to understand and apply, but the calculation is heavy. Moreover, χ is not always available, which often needs to be fitted to adequately reproduce experimental data on monomer partitioning. In a heterogeneous polymerization reaction process, if the mass transfer step becomes a control step, the model may not accurately describe the actual situation.

2.1.2. Simple partition model. The simple partition model is an extreme simplification of thermodynamic phase equilibrium, assuming that the concentration ratio of the reactant in the two phases always maintains a certain value. Luo's group³⁶ established a two-phase model of HIPS. It was assumed that after the phase separation, the mass transfer rates of the initiator and monomer molecules were much larger than the rate of polymerization in the phases; thus, the small molecules were evenly distributed between the two phases according to the partition coefficients and the partition coefficients could not be affected by the temperature, conversion, degree of grafting, etc. The results showed that the larger the St partition coefficient, the lower the conversion of the phase inversion. The simple partition model is very convenient but may neglect the changes during the polymerization process and ignore some details.

2.1.3. Two-film theory. The two-film theory uses the concentration gradient as the mass transfer driving force. It assumes that the components are uniformly distributed within the bulk of the phases and that there is a laminar boundary layer on both sides of the phase interface. These boundary layers contribute to the mass transfer resistance. Since there is no accumulation of components at the phase interface, the molar fluxes of component i transferring from phase II to phase I, from phase II to the phase interface, and from the phase interface to phase I are equal:

ṅ_i = β^II_i(c^II_i − c^II_i,s) = β^I_i(c^I_i − c^I_i,s) (3)

in which β^I_i and β^II_i are the mass transfer coefficients of component i through the boundary layers of phases I and II, respectively, c^I_i and c^II_i are the bulk concentrations of component i in phase I and phase II, respectively, and c^I_i,s and c^II_i,s are the concentrations of films in phases I and II, respectively. Since it is difficult to measure the concentration at the boundary layer, the components are assumed to be in thermodynamic equilibrium at the phase boundary:

c^I_i,s = K_ic^II_i,s (4)

in which K_i is the partition coefficient of component i. Thus, the molar flux of component i from phase II to phase I can be calculated:

Morbidelli's group^37,38 carried out experimental studies on the polymerization of vinylidene fluoride in supercritical carbon dioxide (scCO₂) and simulated this process with a detailed kinetic model. They used the two-film theory to describe the mass transfer of high molecular weight species and confirmed that the interphase mass transfer of radicals was the key reason for the bimodal molecular weight distribution (MWD) of the products. For the suspension polymerization of vinyl chloride, Wieme et al.³⁹ constructed a two-film model to quantify the liquid–liquid mass transfer of the migration of radicals and revealed the effects of radical transfer on the monomer conversion and total moments of the MWD. The two-film theory can also be used to simulate the release of medicines. Aguiar et al.⁴⁰ tested the controlled release of D-fructose in hydrogels of acrylic acid cross-linked with trimethylolpropane triacrylate using the experiment and mathematical model, and the resistance to mass transfer was taken into account in the form of a film model. The modelling results were in good agreement with the experiment data.

As listed above, it is necessary to select an appropriate mass transfer model based on the actual conditions. Both the equilibrium thermodynamic model and the simple partition model are used for situations where the equilibrium is reached quickly. But the former one requires the available χ. The two-film theory is mainly used when the resistance at the interface is very large and the mass transfer is the rate-determining step.

2.2 Pseudo-homogeneous assumption

For heterogeneous polymerization systems, sometimes for simplicity, researchers use the pseudo-homogeneous assumption to study the kinetics. For example, the HIPS system is homogeneous in the low conversion range, and the partition coefficients of the monomer and initiator between the phases are close to 1 even after phase separation. Therefore, several studies^{13,15,41–44} have used the pseudo-homogeneous model to predict important global variables (e.g., conversion of components and grafting efficiencies). Meira's group^13,15 experimentally and theoretically investigated the role of bifunctional initiators in the synthesis of HIPS, assuming homogeneous polymerization, and developed a mathematical model to predict the chemical composition distributions of free PS and grafted copolymer (GC), monomer conversion, St grafting efficiency, and free PS molecular weight. Subsequently, they simulated the polymerization process of HIPS using a heterogeneous model.⁴⁵ After the phase inversion, the PS produced by the residual St in the polybutadiene-rich (PB-rich) phase had lower molecular weights with respect to the PS in the PS-rich phase. Thus, in the late stage of polymerization, the dispersity of free PS of the heterogeneous model is larger than that of the pseudo-homogeneous model. Figueira et al.⁴⁶ compared the heterogeneous and pseudo-homogeneous modelling results for the main polymer properties, as illustrated in Fig. 1. The results of the two models were approximately the same at low conversion (less than 20%), not only the dispersity of free PS but also other properties (e.g., St conversion, dispersity of PB, dispersity of GC); at higher conversion, the pseudo-homogeneous model tended to underestimate the dispersity of free PS.

Fig. 1 Comparison of pseudo-homogeneous and heterogeneous model simulation results for the dispersity of free PS as a function of the conversion of St.⁴⁶ Reproduced with permission from ref. 46, Copyright 2024 Elsevier.

Overall, the pseudo-homogeneous model is simple. When the partition coefficients of substances are close to 1, the system seems to be pseudo-homogeneous, and a pseudo-homogeneous model can be used instead of a heterogeneous model to predict the kinetics at low conversion. For more complex systems or at higher conversion, especially those involving significant phase-to-phase differences, the pseudo-homogeneous model differs in the results of microstructure evolution compared with experimental data.

For example, Giudici's group⁴⁷ developed a pseudo-homogeneous model to simulate maleic anhydride (MAH)-grafted PP, ignoring the thermodynamic incompatibility of MAH with PP, and the results of the model were compared with the experimental data. Subsequently, they⁴⁸ developed two heterogeneous models for the first time to study this grafting polymerization with the consideration of the incomplete solubility of MAH. The heterogeneous model 2 considered mass transfer between the phases, while the heterogeneous model 1 ignored it. Both of the heterogeneous results had modest improvements in the trends of grafting degree and number average molecular weights compared with the pseudo-homogeneous one. Heterogeneous model 1 was in agreement with the experimental data at low initiator concentrations; while heterogeneous model 2 could better reflect the experimental trends of grafting degree and average molecular weight.

Interpenetrating polymer networks (IPNs) are specialized polymer blends consisting of two or more cross-linked polymers that are spatially interpenetrated but without chemical bonds.^49–51 Similarly, IPNs are homogeneous at the beginning of the reaction, then two components turn to thermodynamic incompatibility with the increase in the degree of polymerization. Luo's group^52,53 established a pseudo-homogeneous and a two-stage model, respectively, to investigate the kinetics and molecular structure of polyurethane/poly(methyl methacrylate) PU/PMMA IPN. Both models could adequately explain the interaction mechanism between the two networks, i.e., the formed PU network first restricted the mobilities of acrylic chains, thereby accelerating the formation of the PMMA network. For the network structures, due to the differences in the composition of the phases and the control of acrylic acid chains by diffusion limitation, the predicted cross-linking density of the PMMA network was higher in the two-stage model.

3 Numerical methods for homogeneous and heterogeneous polymerization kinetics

Numerical algorithms for polymerization kinetic models are the heart of the whole simulation. Polymerization kinetics are governed by partial or ordinary differential equations, which are difficult to solve analytically and need to be discretized numerically to provide approximate solutions. Generally, the polymerization kinetic numerical methods are divided into deterministic (e.g., method of moments (MoM), fixed pivot method, probability generation function method) and stochastic (e.g., kinetic Monte Carlo (kMC), random graph theory). Table 1 summarizes the heterogeneous polymerization systems and their kinetic models that have been widely studied in recent years. Here, we mainly introduce MoM and kMC.

Table 1 Summary of the kinetic models of heterogeneous polymerization systems

Reaction system	Numerical method	Phase-state treatment	Mass transfer model		Ref.
			Radical	Monomer
a The copolymerization of the gas monomers, ethylene and propylene, happens in the liquid phase, which includes n-hexane as the solvent. Then, this system is classified as solution polymerization.
Suspension polymerization	MoM	Heterogeneous	Two-film theory	Simple partition model	39
	MoM	Heterogeneous	—	Equilibrium thermodynamic model	54
Emulsion polymerization	MoM	Heterogeneous	Radical entry and exit	—	55
	kMC	Heterogeneous	Radical entry and exit	Simple partition model	56
	kMC	Heterogeneous	—	Simple partition model	57
HIPS	MoM	Pseudo-homogeneous	—	—	58, 59
	MoM	Heterogeneous	—	Simple partition model	36
	kMC	Pseudo-homogeneous	—	—	60, 61, 62
	kMC	Heterogeneous	—	Equilibrium thermodynamic model	46
IPN	kMC	Pseudo-homogeneous	—	—	52
	Fixed pivot	Pseudo-homogeneous	—	—	63
	kMC	Heterogeneous	Two-film theory	Two-film theory	53
Polymer grafting modification	MoM	Heterogeneous	—	Simple partition model	64
	kMC	Pseudo-homogeneous	—	—	65, 66
	kMC	Heterogeneous	Two-film theory	Two-film theory	67
Solution polymerization	MoM	Pseudo-homogeneous	—	—	68, 69
	MoM	Heterogeneous	—	Two-film theory	70
Melt copolycondensation	MoM	Heterogeneous	—	Two-film theory	71

---

3.1 Deterministic method: method of moments

The deterministic method considers chemical reactions to be continuous and deterministic, always yielding the same results without any variation when the same reaction conditions are used as input. It is usually derived from the mass balance equations of the reactants, e.g.:in which C_i (i = 1, …N) is the concentration of component i, the form of f_i is defined by the specific reaction mechanism, and k is the relevant kinetic parameter.

Considering all the possible chain lengths and other variates, the number of species N will be numerous. One has to solve ordinary differential equations on a large scale, which may give rise to numerical difficulties.^72,73 Due to the complex kinetic mechanism, the systems usually exhibit stiffness and complicate the solution procedure. Bamford and Tompa proposed the MoM and applied it for the first time to simulate the kinetic schemes of vinyl polymerization.^74,75 The n-th moments of living and dead chains are given by eqn (7) and (8), respectively:

in which [R] represents the concentration of living chains, [P] represents the concentration of dead chains, and r is the chain length. The method reduces a large number of mass balance differential equations to a smaller number of moment balance differential equations.

MoM has a low computational expense and is widely used to study the average properties of polymers.^76,77 Li et al.⁶⁴ developed a heterogeneous model using MoM for the study of grafting copolymerization of St and acrylonitrile in the presence of polypropylene glycol, which well-described the copolymer composition, molecular weight, dispersity, grafting efficiency, grafting ratio, and the conversions of monomer, polypropylene glycol, and macromer. Kiparissides⁵⁴ established a mathematical model with MoM in the study of suspension polymerization of polyvinyl chloride, describing the evolutions of polymerization rate, number average molecular weight, weight average molecular weight, and morphology. The predictions were in good agreement with the experimental results. López-Domínguez et al.⁷⁸ used MoM and the perturbed-chain statistical associating fluid theory equations of state to investigate the nitroxide-mediated polymerization of St in scCO₂ with benzoyl peroxide and 2,2,6,6-tetramethylpiperidin-1-yloxy as the initiator and control agent, respectively. The effects of pressure on monomer conversion and molecular weight were estimated.

To enable MoM to output distribution properties (e.g., chain length distribution (CLD), MWD), Wu et al.⁷⁹ proposed the distribution-numerical method-moment method (D-NF-MoM). The prediction framework of this method is shown in Fig. 2. Firstly, they used the multidimensional MoM that could realize the quick and efficient solution of the average properties.

Fig. 2 Prediction framework for distributed polymer properties in HIPS.

Then, they assumed the initial PB MWD obeying a Schulz–Zimm distribution and solved the moment equation of the GC species with different topologies by introducing some closure relations. Then, the distribution properties (e.g., MWD, chemical composition distribution of GC) could be reconstructed by appropriate prior distribution functions. Since each topology needs the corresponding moment equation, D-NF-MoM may lose simplicity and convenience, which are the advantages of MoM. The use of D-NF-MoM requires suitable closure relations, which may influence the accuracy and applicability of the model.

Although the D-NF-MoM is proposed to output distribution properties, prior distribution is needed. MoM still has the limitation in describing the full distribution.

3.2 Stochastic method: kinetic Monte Carlo

The stochastic approach considers each reaction event to be discrete and randomly executed. It is based on the chemical master equation (CME) to predict the temporal stochastic evolution of the reaction system:⁸⁰

X(t) ≡ (X₁(t), …, X_N(t)) (9)

X_i(t) is the number of component i at time t, X(t) is the state vector, P(x, t|x₀, t₀) is the probability of the initial state X(t₀) = x₀ changing to the state at t, X(t) = x, a_j(x) is the event probability of reaction j under the state X(t) = x, v_j is the variation of the system state caused by reaction j. Since CME is difficult to solve, Gillespie^80,81 proposed a Markov chain-based stochastic simulation algorithm named Monte Carlo (MC). MC can accurately generate time trajectories of molecular populations based on CME, and it is called kMC when used for reaction kinetic simulations.

The prediction accuracy of kMC depends on the sample size. The large sample size contributes to more accurate results, but it also increases the computational expense. Therefore, the first step of kMC is to carry out the volume independence analysis and choose the optimal volume to balance the simulation accuracy and operation cost. Since kMC can record the reaction history and track the detailed structures chain by chain, it can obtain the distribution properties of the polymers (e.g., CLD, MWD).²² Moreover, D'Hooge's group⁶⁰ introduced a coupled matrix-based concept to record the structural information of nonlinear polymers and copolymers (e.g., T-grafts, H-grafts, and the copolymer composition of each molecule), as shown in Fig. 3. Based on this matrix, it allowed one to reconstruct the complete molecular structure of the molecule. Then, the grafting degree distribution, copolymer sequence structure quality, and bivariate number St-Bd distribution of GCs can be gained by post-processing.

Fig. 3 Concept of coupled matrices to represent linear and branched/crosslinked multicomponent macrospecies illustrated for free radical-induced grafting of polybutadiene (PB) precursor chains with styrene (St).⁶⁰ Reproduced with permission from ref. 60, Copyright 2021, the Royal Society of Chemistry.

4 Applications of heterogeneous polymerization kinetic modelling

4.1 Understanding the kinetics and transfer features

With the progress of numerical algorithms and computational capacity, kinetic modelling allows for a deeper investigation of microscopic molecular behaviours (e.g., reaction path, intermolecular interaction), which are elusive to be captured experimentally.

As we all know, emulsion polymerization involves the mass transfer of various small molecules between the aqueous phase and the particle. Marien et al.⁸² used kMC to simulate miniemulsion free radical polymerization, acknowledging the difference in radical and monomer concentrations per particle. Through the simulation, they successively estimated the importance of the exit/entry of initiator radicals, monomeric radicals, macroradicals, monomers, and initiators, as illustrated in Fig. 4. The results unveiled that the temporal evolutions of the CLD and the particle size distribution are correlated and affected by the radical exit/entry and monomer mass transfer.

Fig. 4 Micro-scale reaction and meso-scale mass transfer events in a miniemulsion free radical polymerization.⁸² Reproduced with permission from ref. 82, Copyright 2019, the American Chemical Society.

In scCO₂ dispersion polymerization, radicals can be generated in dispersed particles and a continuous supercritical phase. When the rates of propagation and termination are slower than the rate of radical entry into the particles, most polymers are produced in dispersed particles; conversely, polymers can be generated in the continuous phase. The main reaction locus is still debated. Mueller et al.⁸³ developed two models and compared the results with experimental data in the case of supercritical dispersion polymerization of methyl methacrylate (MMA). The two limiting models are the radical separation model (RS), which assumed a much slower interphase mass transfer rate of radicals than the termination rate in the phase where the radicals had been initiated, and the radical partitioning model (RP), which assumed that the diffusion rate of radicals between the two phases was very fast and thus reached thermodynamic equilibrium. As a result, the molecular weight was largely underestimated by the RS model and reproduced well by the RP one. In the case of MMA polymerization, the shortest active chains (no longer than 10 units) remained and terminated in the continuous phase; hence, a slight shoulder at the low molecular weight could be observed experimentally. The RP model assumed the shortest active chains to move in the polymer particles and terminated with longer chain lengths, resulting in the disappearance of the slight shoulder. It seems that much attention should be paid to the mass transfer of radicals, including the reversible mass transfer of radicals with short chain lengths.

The kinetic model can be used to estimate the contributions of the side reaction events to the polymerization system. To provide a more realistic description of the heterogeneous reaction mechanism during the synthesis of waterborne polyurethane/acrylic adhesives, Leiza's group⁵⁶ developed a kinetic model with kMC for the miniemulsion polymerization of mixtures of isocyanate and acrylic monomers containing hydroxyl functional groups. The simultaneous polyaddition and free-radical polymerization were taken into account, as well as all reactions in the aqueous and polymer particles, and then the complex mechanism of the polyurethane/acrylic hybrids was explained in detail for the first time. The simulation results showed that once the water was neglected in the monomer droplet where the isocyanate groups existed, the consumption rate of isocyanate would deviate from the experimental data, reflecting the importance of the side reaction of isocyanate groups with water.

Zeinali et al.⁸⁴ combined a deterministic four-dimensional Smith–Ewart model with MoM to simulate nitroxide N-(2-methyl-2-propyl)-N-(1-diethylphosphono-2,2-dimethylpropyl)-N-oxyl mediated polymerization of n-butyl acrylate in a miniemulsion. Considering a more comprehensive reaction mechanism and interphase mass transfer, this more detailed modelling approach revealed seven distinct regimes as a function of average particle size. This model enhanced the knowledge of the radical dispersed phase polymerization kinetics. Zeinali et al.⁸⁵ utilized this model in a systematic investigation of comparing N-(2-methyl-2-propyl)-N-(1-diethylphosphono-2,2-dimethylpropyl)-N-oxyl and 2,2,6,6-tetramethylpiperidine-1-oxyl for the nitroxide-mediated polymerization of n-butyl acrylate in a miniemulsion. Their findings emphasized the importance of describing interphase mass transfer for accurate predictions.

Overall, the utilization of heterogeneous polymerization kinetic modelling helps to figure out microscopic molecular behaviours. However, a critical prerequisite is that the established heterogeneous kinetic model must be sufficiently accurate and reliable. This requires us to comprehensively consider all relevant kinetic reaction processes during model construction and to develop and select appropriate mass transfer models.

4.2 Modulation of the polymer structure and properties

The polymer structure determines its performance and application. Kinetic modelling can trace the evolution process of the structure and comprehensively analyse the influence of the reaction conditions on the structure, which in turn guide the performance-oriented polymer structure design and precise synthesis.

The monomer sequence has an essential impact on the physical properties of copolymers. Polymers with well-controlled sequences have broader potential applications. Based on the experimental results at different molar ratios of St and butyl acrylate, Jiang et al.⁵⁵ derived a reversible addition-fragmentation chain transfer miniemulsion copolymerization chain and sequence model. Then, this model was incorporated into a semi-batch model for designing and synthesizing polymers with different uniform number-average sequence lengths of St and butyl acrylate, as shown in Fig. 5. Subsequently, they developed a visualization technology with MC to present the evolution of the ternary sequence composition and copolymer sequence length distributions. The method they proposed can readily be adopted to produce the polymers with precisely designed copolymer sequence lengths and tailor-made material properties.

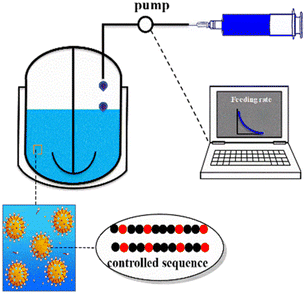Fig. 5 Schematic experimental setup for programmed semi-batch RAFT miniemulsion copolymerization.⁵⁵ Reproduced with permission from ref. 55. Copyright 2019, the American Chemical Society.

The branching density is an important parameter that significantly affects the physical and mechanical properties of branched polymers. For reversible addition-fragmentation chain transfer miniemulsion copolymerization of St and triethylene glycol dimethacrylate, Li et al.⁸⁶ established the corresponding kinetic model, then combined it with a semi-batch reactor model to study the control of branching density distribution. They optimized the monomer feeding strategy to successfully synthesize a series of hyperbranched PS with designed branching density distributions.

Structural parameters related to cross-linked polymers, such as cross-linking density and network uniformity, reflect the hardness, melting behaviours, and swelling capacity of the material. Hydrogels are three-dimensional networks formed via the cross-linking of hydrophilic polymers. Karageorgos et al.⁸⁷ developed a four-dimensional MC model to simulate the cross-linking reaction of a polymer–phenol conjugated system in the presence of horseradish peroxidase (HRP)/H₂O₂ and quantified the effects of the concentrations of HRP and H₂O₂ on the onset of gelation and viscoelastic hydrogel properties (e.g., storage modulus). The polymer-phenol conjugates (e.g., tyramine-modified hyaluronic acid, HA-Tyr) could form three-dimensional networks via a free-radical oxidation mechanism in the presence of HRP and H₂O₂. The cross-linking mechanism of the HA-Tyr polymer chains included the following elementary reactions: (i) activation of the HRP enzyme by hydrogen peroxide, (ii) generation of “live” polymer chains via the activation of phenol rings, (iii) enzyme deactivation by a combination of “live” polymer chains, (iv) termination by a combination of “live” polymer chains, and (v) internal cyclization reaction. The reaction (v) was considered to only occur in the gel phase.⁸⁸ The cyclization probability depended on the length and flexibility of the connecting path(s) and on the site's interdiffusion rate. In the solution phase, where the diffusion was fast, intermolecular reactions were more likely to happen compared with intramolecular ones. In the gel phase, where diffusion control became dominant, the unimolecular cyclization reactions occurred. The onset of gelation for HA-Tyr increased with HRP and accelerated with H₂O₂. The storage modulus equilibrium rose with HRP but peaked and then declined with H₂O₂ due to enzyme inactivation. The results were in good agreement with experimental data, and could be used to optimize the design of hydrogels with desirable viscoelastic and molecular properties for specific biomedical applications.

The functionality of traditional hydrogels is often too limited to address the needs of complex applications. The advancement of double-network (DN) hydrogels has broadened the scope of hydrogel applications. Liu et al.⁸⁹ conducted an in-depth study on the antifreeze property of polyvinyl alcohol (PVA)/poly(N-(2-hydroxyethyl)acrylamide) PHEAA DN hydrogels. They first developed a ‘random walk reactive polymerization’ kinetic model to construct the PVA/PHEAA DN hydrogels. Following molecular dynamics simulations, they studied the water structures, dynamics, and interactions confined in the DN hydrogels at different water contents and temperatures to reveal the antifreeze mechanism at atomic levels. With the same water content, the number of hydrogen bonds between the polymer networks decreased as the temperature decreased, implying that the polymer networks provided more binding sites for water molecules at lower temperatures. At the same temperature, the packing density of the polymer chains was higher at a lower water content, which was more effective for attracting and trapping the surrounding water molecules. The simulation results indicate that the combination of polymerization kinetics and molecular dynamics enables precise design materials at the molecular scale or even smaller scale.

These examples demonstrate the importance of heterogeneous polymerization kinetic modelling in regulating polymer structures and properties. However, challenges still remain. The current structure–property relationships are overly simplified (typically assuming a one-to-one correspondence between the key structures and properties). In reality, polymer properties emerge from the complex interplay of multi-structural factors. There is a need to develop more comprehensive structure–property relationships and optimize specific properties through the coordinated adjustment of multiple structural parameters based on kinetic models.

4.3 Guidelines for reactor design, optimization, and scale-up

In the field of polymerization reaction engineering, suitable reactor geometry is important but challenging for the preparation of high-performance polymeric materials. Building upon cold model studies, the reactor is further optimized, combining polymerization kinetics to provide a scientific basis for the efficient and safe operation of polymerization reactions.

Luo's group^90–92 established the polymerization kinetic model with MoM and adopted the key parameter transfer technique to combine the computational fluid dynamics (CFD) model with the polymerization kinetic model. For the suspension polymerization system, the CFD single-phase flow model was extended to a multi-phase model, and the particle population balance model was used to describe the droplet size distribution, then a multiscale model was proposed as shown in Fig. 6. The presence of baffles offered a shearing force and promoted the breakage of droplets. The MWD was mainly determined by the size of the droplet, and the droplets of small diameter were conducive for obtaining a narrower MWD.⁹³ The breakage and coalescence rates depended on the flow fields. The smaller off-bottom clearance of an impeller was inconducive to the mixing of the fluid, and thus the coalescence rate was far from well-distributed. With the increase in the off-bottom clearance, the distribution of the coalescence rate became more uniform in both the lower and upper zones of the reactor due to the improved recirculation rate. This multi-scale model is useful for the reactor design and process optimization in suspension polymerization.

Fig. 6 Solution procedure for a multiscale model.⁹¹ Reproduced with permission from ref. 91. Copyright 2017, the American Chemical Society.

For a stationary continuous stirred tank reactor for MMA suspension polymerization, Lee's group⁹⁴ combined MoM with the multi-scale CFD model based on multi-phase particle-in-cell combined with the population balance equation to investigate the effect of different paddle inclination angles (30°, 45°, 60°) on mixing, particle size, particle flow pattern, and polymer properties. In the reactor, the injected particles were the monomer MMA and initiator benzoyl peroxide. The density of MMA was lower than that of water; thus, the particles first accumulated at the top of the reactor. Then, with the movement of the paddles, the solvent drove the particles from the top to the bottom of the reactor with good mixing. A lower inclination angle induced the particles to be transported downward, which improved the mixing efficiency. A higher inclination angle enlarged and strengthened the area and rate of turbulent dissipation in the reactor, and the particle fragmentation rate could be higher. When the inclination angle was 45°, the particle flow could mix well. Larger paddles could also result in smaller particles, but they would deteriorate the mixing effect. The simulation results provide guidance for paddle design in the continuous stirred tank reactor applied to liquid–solid heterogeneous polymerization reactions.

Microreactors have outstanding features in mixing efficiency, mass transfer, heat transfer, and precise control of process parameters, making them advantageous over conventional reactors for highly exothermic reactions (e.g., polymerization). The microreactor is a promising platform for the continuous synthesis of polymer lattices when combined with emulsion polymerization. Qiu et al.⁵⁷ carried out differential microemulsion polymerization in a liquid–liquid slug-flow microreactor to achieve the rapid and stable preparation of PMMA nanoparticles. The increase in the flow ratio of the aqueous phase to the organic phase and the reduction in the size of the capillary microreactor could both intensify the interphase mass transfer. As the mass transfer coefficients increased, the polymerization rate increased, the degree of polymerization and diameter of polymer particles rose rapidly and then dropped to a fixed level, and the dispersity dropped, indicating the significance of efficient mass transfer in controlling the MWD.

Xu et al.⁷⁰ combined the Euler–Euler two-fluid model, copolymerization kinetics, and copolymer microstructural distribution model for the ethylene-propylene gas–liquid heterogeneous copolymerization process in a bubble column reactor. They applied this comprehensive CFD model to analyse the hydrodynamic properties, interface mass transfer, and the influence of different operating conditions on the molecular weight (distribution) and copolymer component (distribution). At the beginning of the polymerization, due to the gas–liquid mass transfer, the gas monomers were not saturated in the solvent. Then, the ratio of the two monomer concentrations fluctuated, leading to the nonuniformity of the copolymer component. When the gas was rapidly and continuously fed, the monomers saturated quickly in the liquid phase, and the copolymer composition remained unchanged during the process. The copolymer composition could be fixed at different values by controlling the molar ratio of the two monomers and the feeding rate. The comprehensive images showed that the MWD and copolymer component distribution were wider at the bottom of the reactor due to the inefficient mixing at the inlet and narrower at the outlet because of the developed flow and polymerization. As such, the model is of guiding significance to improving the polymer products and process control in industrial ethylene-propylene reactors.

In terms of scale-up, Pan et al.⁹⁵ incorporated a comprehensive polymerization kinetic model into the CFD model to describe the polymer properties in the gas–liquid–solid three-phase polyethylene fluidized bed reactor. Furthermore, the impact of scale-up was studied by modelling three different reactor sizes, and the conditions were set according to the simplified Glicksman scaling law.⁹⁶ Due to the scale-up effect, the differences in flow hydrodynamics at the macroscale level would affect the particle mixing, mass transfer and heat transfer among the phases, which in turn influenced the differences in microscale structures. The simulation results for polymerization rates indicated that the simplified Glicksman scaling law performed poorly. Thus, more combined models need to be developed to evaluate various scaling laws for scaling up multi-phase reactors in the near future.

The above cases demonstrate the great potential of combining heterogeneous polymerization kinetic modelling with CFD models in guiding the reactor design, optimization, and scale-up. Future research should focus on the acceleration of multi-scale model computations, mixing enhancement methods in heterogeneous systems, and establishing scaling laws for heterogeneous systems.

5 Outlook

In this review, the kinetic modelling processes of various heterogeneous polymerization systems have been comprehensively and thoughtfully reviewed, highlighting the mass transfer models, phase state assumptions, numerical methods, and applications of heterogeneous polymerization kinetic modelling. Considerable investigations have confirmed the importance of kinetic simulations in revealing the heterogeneous system complexity and interplay between the reaction and mass transfer. The effects of reaction conditions on the chain microstructure obtained based on kinetic modelling can guide performance-oriented polymer structure design and precise synthesis. Besides, the integration of kinetic modelling with CFD has enabled the development of non-ideal reaction models, which facilitate reactor optimization and support the industrial scale-up for polymer production.

Although significant progress has been made in modelling heterogeneous polymerization, several key areas require further attention in future research. (i) Development of more advanced characterization techniques to monitor the mass transfer behaviour in heterogeneous polymerization systems. This could help better understand the mass transfer features and the interactions between the reactions and mass transfer and further develop more accurate and reliable mass transfer models to provide theoretical guidance for process optimization and process scale-up. (ii) Accurately characterize the quantitative relationship between the polymer structure and properties. The existing quantitative structure–property relationships are either too simplistic in their structural hierarchy (e.g., focusing solely on the molecular weight of the polymer) or restricted to considering only one or two properties. Methods such as density functional theory, molecular dynamics simulation, etc., can be combined to comprehensively construct the structure–property relationships and realize the rational design of polymer structure. (iii) Integrating kinetic modelling with machine learning to develop an intelligent manufacturing technology is a promising direction.⁹⁷ Data-driven is the new paradigm of scientific research. Since a large amount of data has been generated in kinetic simulations, the machine learning toolbox can effectively and intelligently process massive datasets for the accelerated production of well-defined functional and high-value-added polymers.

Data availability

No primary research results, software or code have been included, and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 22408224) and the Postdoctoral Fellowship Program of CPSF (No. GZB20240433).

References

1. J. Ma, J. Li, B. Yang, S. Liu, B. P. Jiang, S. Ji and X. C. Shen, Polymers, 2022, 14, 3269.
2. Y. Kohno, T. Makino and M. Kanakubo, React. Chem. Eng., 2019, 4, 627–633.
3. J. P. Han, Y. N. Yang, Q. Niu, Z. H. Luo and Y. N. Zhou, Chem. Eng. Sci., 2023, 275, 118753.
4. S. You, X. Wei, R. Liu, C. Zhao, M. Zhao, Q. Shi, G. Gong and Y. Wu, Polymer, 2022, 256, 125183.
5. I. A. A. Gritskova, N. I. I. Prokopov, A. A. A. Ezhova, A. E. E. Chalykh, S. A. A. Gusev, S. M. M. Levachev, V. P. P. Zubov, V. I. I. Gomzyak, I. V. V. Skopintsev, A. N. N. Stuzhuk, I. D. D. Kovtun, A. M. M. Shulgin, D. S. S. Ivashkevich, G. A. A. Romanenko, V. G. G. Lakhtin and S. N. N. Chvalun, Polymers, 2023, 15, 2464.
6. J. Cao, L. Zhang, X. Jiang, C. Tian, X. Zhao, Q. Ke, X. Pan, Z. Cheng and X. Zhu, Macromol. Rapid Commun., 2013, 34, 1747–1754.
7. P. Lopez-Dominguez, E. Saldivar-Guerra, M. E. Trevino and I. Zapata-Gonzalez, Polymers, 2023, 15, 38006191.
8. G. K. K. Clothier, T. R. Guimaraes, L. T. Strover, P. B. Zetterlund and G. Moad, ACS Macro Lett., 2023, 12, 331–337.
9. A. Jimenez-Victoria, R. D. Peralta-Rodriguez, E. Saldivar-Guerra, G. Y. Cortez-Mazatan, L. A. A. Soriano-Melgar and C. Guerrero-Sanchez, Polymers, 2022, 14, 3475.
10. K. Yan and Y. Luo, React. Chem. Eng., 2017, 2, 159–167.
11. M. Khan, T. R. Guimaraes, D. Zhou, G. Moad, S. Perrier and P. B. Zetterlund, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 1938–1946.
12. Z. Li, W. Chen, Z. Zhang, L. Zhang, Z. Cheng and X. Zhu, Polym. Chem., 2015, 6, 1937–1943.
13. D. A. Estenoz, G. R. Meira, N. Gomez and H. M. Oliva, AIChE J., 1998, 44, 427–441.
14. G. R. Meira, C. V. Luciani and D. A. Estenoz, Macromol. React. Eng., 2007, 1, 25–39.
15. D. A. Estenoz, G. P. Leal, Y. R. Lopez, H. M. Oliva and G. R. Meira, J. Appl. Polym. Sci., 1996, 62, 917–939.
16. J. M. Maffi and D. A. Estenoz, Chem. Eng. Sci., 2022, 247, 117027.
17. E. Hasa, J. P. Scholte, J. L. P. Jessop, J. W. Stansbury and C. A. Guymon, Macromolecules, 2019, 52, 2975–2986.
18. T. Lü and G. R. Shan, AIChE J., 2011, 57, 2493–2504.
19. T. Lü and G. R. Shan, J. Appl. Polym. Sci., 2009, 112, 2859–2867.
20. P. López-Domínguez, J. E. Rivera-Peláez, G. Jaramillo-Soto, J. F. Barragán-Aroche and E. Vivaldo-Lima, React. Chem. Eng., 2020, 5, 547–560.
21. D. N. Lin, L. Zhang and J. B. Tan, Acta Polym. Sin., 2023, 54, 761–777.
22. E. Saldívar-Guerra, Curr. Opin. Chem. Eng., 2024, 44, 101026.
23. R. A. Olson, M. E. Lott, J. B. Garrison, C. L. G. Davidson, L. Trachsel, D. I. Pedro, W. G. Sawyer and B. S. Sumerlin, Macromolecules, 2022, 55, 8451–8460.
24. Y. Kohno and T. Makino, React. Chem. Eng., 2021, 6, 2014–2017.
25. D. Constales, G. S. Yablonsky, D. R. D'hooge, J. W. Thybaut and G. B. Marin, Advanced data analysis and modelling in chemical engineering, Elsevier, 2017.
26. B. M. Guy, S. Y. Gregory and C. Denis, Kinetics of chemical reactions: decoding complexity, John Wiley & Sons, 2018.
27. D. R. D'Hooge, P. H. M. Van Steenberge, M. F. Reyniers and G. B. Marin, Prog. Polym. Sci., 2016, 58, 59–89.
28. F. J. Schork, Biomacromolecules, 2024, 25, 3249–3260.
29. E. K. Gelinski, N. Sheibat-Othman and T. F. L. McKenna, Can. J. Chem. Eng., 2024, 102, 532–547.
30. J. Herrera-Ordonez, Adv. Colloid Interface Sci., 2023, 320, 103005.
31. J. M. Asua, Macromolecules, 2003, 36, 6245–6251.
32. N. Sheibat-Othman, H. M. Vale, J. M. Pohn and T. F. L. McKenna, Macromol. React. Eng., 2017, 11, 1600059.
33. P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, New York, 1953.
34. C. V. Luciani, D. A. Estenoz, G. R. Meira, N. L. Garcia and H. M. Oliva, Macromol. Theory Simul., 2007, 16, 703–710.
35. H. Jeong, J. Gu, P. Mwasame, K. Patankar, D. Yu and C. E. Sing, Soft Matter, 2024, 20, 681–692.
36. C. X. Zhu, J. Jin, Y. Y. Wu, F. L. Figueira, M. Edeleva, P. H. M. Van Steenberge, D. R. D'Hooge, Y. N. Zhou and Z. H. Luo, AIChE J., 2023, 70, e18297.
37. P. A. Mueller, G. Storti, M. Morbidelli, M. Apostolo and R. Martin, Macromolecules, 2005, 38, 7150–7163.
38. P. A. Mueller, G. Storti, M. Morbidelli, I. Costa, A. Galia, O. Scialdone and G. Filardo, Macromolecules, 2006, 39, 6483–6488.
39. J. Wieme, D. R. D'Hooge, M. F. Reyniers and G. B. Marin, Macromol. React. Eng., 2009, 3, 16–35.
40. L. G. Aguiar, D. C. Iwakura, A. T. S. Semeano, R. W. C. Li, E. F. Souza, J. Gruber and R. Giudici, Can. J. Chem. Eng., 2018, 96, 1221–1227.
41. D. A. Estenoz, I. M. González, H. M. Oliva and G. R. Meira, J. Appl. Polym. Sci., 1999, 74, 1950–1961.
42. D. A. Estenoz and G. R. Meira, J. Appl. Polym. Sci., 1993, 50, 1081–1098.
43. M. Fischer and G. P. Hellmann, Macromolecules, 1996, 29, 2498–2509.
44. C. V. Luciani, D. A. Estenoz, G. R. Meira and H. M. Oliva, Ind. Eng. Chem. Res., 2005, 44, 8354–8367.
45. N. Casis, D. Estenoz, L. Gugliotta, H. Oliva and G. Meira, J. Appl. Polym. Sci., 2006, 99, 3023–3039.
46. F. L. Figueira, P. Reyes, M. Edeleva, Y. W. Marien, Y. Y. Wu, Y. N. Zhou, Z. H. Luo, P. H. M. Van Steenberge and D. R. D'Hooge, Chem. Eng. J., 2024, 481, 148349.
47. R. Giudici, Macromol. Symp., 2007, 259, 354–364.
48. L. G. Aguiar, P. A. Pessoa-Filho and R. Giudici, Macromol. Theory Simul., 2011, 20, 837–849.
49. E. S. Dragan, Chem. Eng. J., 2014, 243, 572–590.
50. D. Sophiea, D. Klempner, V. Sendijarevic, B. Suthar and K. C. Frisch, in Interpenetrating Polymer Networks, ed. D. Klempner, L. H. Sperling and L. A. Utracki, 1994, ch. 2, vol. 239, pp. 39–75.
51. I. Calvez, C. R. Szczepanski and V. Landry, Macromolecules, 2022, 55, 3129–3139.
52. J. Jin, Y. N. Zhou and Z. H. Luo, AIChE J., 2022, 68, e17838.
53. J. Jin, Y. N. Zhou and Z. H. Luo, AIChE J., 2023, 69, e18041.
54. C. Kiparissides, in Polymer Reaction Engineering of Dispersed Systems, ed. W. Pauer, Springer Cham, 2018, vol. 280, pp. 121–193.
55. J. Jiang, W. J. Wang, B. G. Li and S. P. Zhu, Ind. Eng. Chem. Res., 2019, 58, 18997–19008.
56. S. Hamzehlou, N. Ballard, P. Carretero, M. Paulis, J. M. Asua, Y. Reyes and J. R. Leiza, Polymer, 2014, 55, 4801–4811.
57. M. Qiu, Y. H. Wang, M. J. Shang and Y. H. Su, Chem. Eng. J., 2023, 475, 146363.
58. C. X. Zhu, Y. Y. Wu, F. L. Figueira, P. H. M. Van Steenberge, D. R. D'Hooge, Y. N. Zhou and Z. H. Luo, Chem. Eng. J., 2022, 444, 136595.
59. Y. Y. Wu, F. L. Figueira, P. H. M. Van Steenberge, D. R. D'Hooge, Y. N. Zhou and Z. H. Luo, Chem. Eng. J., 2021, 425, 130463.
60. F. L. Figueira, Y. Y. Wu, Y. N. Zhou, Z. H. Luo, P. H. M. Van Steenberge and D. R. D'Hooge, React. Chem. Eng., 2021, 6, 640–661.
61. J. C. Hernandez-Ortiz, P. H. M. Van Steenberge, M.-F. Reyniers, G. B. Marin, D. R. D'Hooge, J. N. E. Duchateau, K. Remerie, C. Toloza, A. L. Vaz, F. Schreurs and D. R. D'Hooge, AIChE J., 2017, 63, 4944–4961.
62. J. C. Hernandez-Ortiz, P. H. M. Van Steenberge, J. N. E. Duchateau, C. Toloza, F. Schreurs, M.-F. Reyniers, G. B. Marin and D. R. D'Hooge, Macromol. Theory Simul., 2018, 27, 1800036.
63. W. J. Lin, L. T. Biegler and A. M. Jacobson, Macromol. Theory Simul., 2011, 20, 146–165.
64. L. Li, L. B. Wu, Z. Y. Bu, C. Gong, B. G. Li and K. D. Hungenberg, Macromol. React. Eng., 2012, 6, 365–383.
65. Y. T. Zhu, L. J. An and W. Jiang, Macromolecules, 2003, 36, 3714–3720.
66. T. R. Pietrafesa, A. Brandolin, C. Sarmoria and M. Asteasuain, Macromol. Theory Simul., 2023, 32, 2300018.
67. J. C. Hernandez-Ortiz, P. H. M. Van Steenberge, J. N. E. Duchateau, C. Toloza, F. Schreurs, M. F. Reyniers, G. B. Marin and D. R. D'Hooge, Chem. Eng. J., 2019, 377, 119980.
68. C. Z. Xu, J. J. Wang, X. P. Gu and L. F. Feng, Chem. Eng. Res. Des., 2017, 125, 46–56.
69. C. Z. Xu, J. J. Wang, X. P. Gu and L. F. Feng, Chem. Eng. Commun., 2018, 205, 857–870.
70. C. Z. Xu, J. J. Wang, X. P. Gu and L. F. Feng, AIChE J., 2019, 65, e16632.
71. Y. M. Zhang, Y. L. Xing, J. Jiang, L. Zhao and Z. H. Xi, Huagong Xuebao, 2022, 73, 4722–4733.
72. Y. N. Zhou and Z. H. Luo, Macromol. React. Eng., 2016, 10, 516–534.
73. E. Mastan and S. Zhu, Eur. Polym. J., 2015, 68, 139–160.
74. C. H. Bamford and H. Tompa, J. Polym. Sci., 1953, 10, 345–350.
75. C. H. Bamford and H. Tompa, Trans. Faraday Soc., 1954, 50, 1097–1115.
76. E. Mastan, X. Li and S. Zhu, Prog. Polym. Sci., 2015, 45, 71–101.
77. I. Zapata-González and E. Saldívar-Guerra, Can. J. Chem. Eng., 2023, 101, 5324–5356.
78. P. López-Domínguez, M. Rios-Lopez, J. Eduardo Rivera-Pelaez, J. Fernando Barragan-Aroche and E. Vivaldo-Lima, Can. J. Chem. Eng., 2023, 101, 5179–5188.
79. Y. Y. Wu, F. L. Figueira, M. Edeleva, P. H. M. Van Steenberge, D. R. D'Hooge, Y. N. Zhou and Z. H. Luo, AIChE J., 2022, 68, e17559.
80. D. T. Gillespie, Annu. Rev. Phys. Chem., 2007, 58, 35–55.
81. D. T. Gillespie, J. Phys. Chem., 1977, 81, 2340–2361.
82. Y. W. Marien, P. H. M. Van Steenberge, D. R. D'Hooge and G. B. Marin, Macromolecules, 2019, 52, 1408–1423.
83. P. A. Mueller, G. Storti and M. Morbidelli, Chem. Eng. Sci., 2005, 60, 377–397.
84. E. Zeinali, Y. W. Marien, S. R. George, M. F. Cunningham, D. R. D'Hooge and P. H. M. Van Steenberge, Chem. Eng. J., 2023, 470, 144162.
85. E. Zeinali, Y. W. Marien, M. Edeleva, S. R. George, M. F. Cunningham, D. R. D'Hooge and P. H. M. Van Steenberge, React. Chem. Eng., 2024, 9, 1334–1353.
86. X. H. Li, W. J. Wang, B. G. Li and S. P. Zhu, Macromol. React. Eng., 2015, 9, 90–99.
87. F. F. Karageorgos and C. Kiparissides, Int. J. Mol. Sci., 2021, 22, 7317.
88. D. L. Kurdikar, J. Somvarsky, K. Dusek and N. A. Peppas, Macromolecules, 1995, 28, 5910–5920.
89. Y. Liu, D. Zhang, Y. Tang, X. Gong and J. Zheng, npj Comput. Mater., 2023, 9, 209.
90. L. Xie, Q. Liu and Z. H. Luo, Chem. Eng. Res. Des., 2018, 130, 1–17.
91. L. Xie and Z. H. Luo, Ind. Eng. Chem. Res., 2017, 56, 4690–4702.
92. L. Xie, L. T. Zhu, Z. H. Luo and C. W. Jiang, Macromol. React. Eng., 2017, 11, 1600022.
93. Z. D. Liu, Y. C. Lu, B. D. Yang and G. S. Luo, Ind. Eng. Chem. Res., 2011, 50, 11853–11862.
94. S. H. Kim, J. H. Lee and R. D. Braatz, Comput. Chem. Eng., 2021, 152, 107391.
95. H. Pan, Y. X. Liu and Z. H. Luo, Asia-Pac. J. Chem. Eng., 2019, 14, e2265.
96. L. R. Glicksman, M. Hyre and K. Woloshun, Powder Technol., 1993, 77, 177–199.
97. B. G. Li, Y. W. Luo and P. W. Liu, Huagong Jinzhan, 2023, 42, 3905–3909.

---