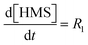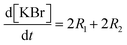DOI:
10.1039/D5RE00082C
(Paper)
React. Chem. Eng., 2025, Advance Article
Reaction kinetics for the synthesis of an anti-cancer drug (adavosertib) precursor†
Received
18th February 2025
, Accepted 14th April 2025
First published on 15th April 2025
Abstract
The development of kinetic models which can accurately describe drug synthesis reactions is an important part of process design in the pharmaceutical industry. Correctly identifying these models can be difficult, since the reaction pathways used to manufacture new pharmaceutical compounds are often extremely complex. Consequently, many kinetic modelling and parameter estimation tools have been developed in recent years to allow drug manufacturers to test and compare a variety of reaction models before selecting the one which provides the best predictions. The present paper employs a multistart parameter estimation code (in MATLAB®) to parameterise a range of kinetic models describing the synthesis of a key intermediate required for the production of a new anti-cancer drug, Adavosertib (AZD1775). Furthermore, the Akaike and Bayesian Information Criteria are used to rank these models based upon their complexity and fidelity to reflect real-world experimentation.
1. Introduction
Since 2005, public spending on anti-cancer drugs has steadily increased across Europe (Fig. 1a) and the United States; leading to a total global spending of 150 billion USD in 2020.1,2 Whilst some of this spending can be attributed to rising incidence rates of various cancer types around the world2–6 (with 18.1 million new cases and 10 million deaths reported in 2020 alone7), it is clear that rising drug prices have contributed to this landscape (Fig. 1b). Consequently, pharmaceutical companies must find a way to reduce the price of their medications if treatments are to be affordable in the future.1,2
 |
| | Fig. 1 Anti-cancer spending in Europe, 2005–2018 (data: ref. 2 and 3). (a) Anti-cancer drug expenditure; (b) drug cost fraction. | |
To accomplish this goal, drug manufacturers must first find a way to intensify their manufacturing processes. Moreover, they must do so whilst minimising experimentation so as to not simply inflate costs elsewhere in their pipeline. Therefore, many authors8–16 propose that fit-for-purpose process models should be developed, to accurately describe the different unit different operations involved in pharmaceutical processes. Once these models are correctly parameterised, they can provide an efficient way to visualise and optimise processes. This has already been demonstrated by Jolliffe et al.,15 Diab et al.,8 and Cuthbertson et al.17 for ibuprofen, diphenhydramine and amoxicillin, respectively.
Numerous studies have been published in recent years on the importance of developing and parameterising kinetic models for chemical synthesis11,18–36 and crystallisation processes;37,38 with the former receiving particular attention (Table 1). For example, Schenk et al.39 demonstrated how parameter estimation tools can be used to compare different kinetic models available to describe drug synthesis processes, using the production of an asymmetrical urea compound required to manufacture various active pharmaceutical ingredients (APIs) as a case study. Earlier, Grom et al.22 had shown that computational modelling techniques can be used to study the reaction mechanisms underpinning Lorcaserin synthesis (a complicated reaction network, consisting of 27 reaction steps and 15 chemical species), leading to the robust development of a temperature-dependent kinetic model with 29 parameters. Published studies have been conducted to show how kinetic modelling can be used to comparatively assess the benefits of batch vs. continuous manufacturing processes.12,40 The paper of Kraus et al.41 considered the eco-friendly production of carbamazepine from urea and iminostilbene. Because of these efforts, various established software packages are now available to conduct this type of studies, and they are summarised in Table 2.
Table 1 Summary of published reaction modelling and kinetic parameter estimation studies conducted for different APIs and drug precursors
| API/precursor |
Condition treated |
Study outcomes |
Software |
Ref. |
| Carbamazepine |
Epilepsy |
Kinetic model & Arrhenius rate law |
MATLAB® |
41 |
| Unspecified |
Unspecified |
Kinetic model & isothermal rate constants |
KIPET |
39 |
| Lorcaserin |
Obesity |
Kinetic model & Arrhenius rate law |
— |
22 |
| Lomustine |
Brain tumours, Hodgkin's lymphoma |
Kinetic models, isothermal rate constants |
MATLAB® |
18 |
| Osimertinib intermediate |
Non-small cell lung cancer |
Kinetic model & Arrhenius rate law |
Dynochem® |
19 |
| Carfilozomib intermediate |
Myeloma |
Kinetic model & Arrhenius rate law |
Dynochem® |
20 |
| Merestinib intermediate |
Biliary tract & non-small cell lung cancer |
Kinetic model & isothermal rate constants |
— |
21 |
| Paracetamol |
Moderate pain, fevers |
Kinetic model & isothermal rate constants |
MATLAB® |
23 |
| Metoprolol |
High blood pressure |
Kinetic model & isothermal rate constants |
MATLAB® |
23 |
| Unspecified |
Unspecified |
Kinetic model & isothermal rate constants |
KIPET |
24 |
| Ibuprofen |
Moderate pain, fevers, inflammation |
Kinetic model & isothermal rate constants |
MATLAB® |
25 |
| Diphenhydramine |
Hay fever, common cold, short-term insomnia |
Kinetic model & isothermal rate constants |
MATLAB® |
8 |
| Nevirapine |
HIV |
Arrhenius rate law |
MATLAB® |
11 |
| Aziridines (building block) |
Cancer therapies (mitomycin, azinomycin) |
Arrhenius rate law |
gPROMS® |
26 |
| Pyrroles (building block) |
Cancer therapies (sunitinib), pain relief (ketorolac), heart disease (atorvastatin) |
Kinetic models & Arrhenius rate law |
COMSOL Multiphysics® |
27 |
| Abemaciclib |
Advanced/metastatic breast cancers |
Arrhenius rate law |
Dynochem® |
28 |
| Thiazolidine intermediate |
Diabetes |
Kinetic model & Arrhenius rate law |
— |
29 |
| Glitazone intermediate |
Diabetes |
Kinetic model & Arrhenius rate law |
— |
30 |
| Tryptophol |
Insomnia |
Kinetic model & Arrhenius rate law |
COMSOL Multiphysics® |
31 |
| Dolutegravir intermediate |
HIV |
Kinetic model & Arrhenius rate law |
COMSOL Multiphysics® |
32 |
Table 2 Software packages for kinetic parameter estimation (CT = concentration-time data; AT = absorbance-time data; V = various data types)
| |
Software elements |
Required packages |
Input data |
Open source |
| Dynochem42 |
• ODE solvers (e.g., Rosenbrock) |
• Dynochem® |
V |
 |
| • Local-optimisation algorithms (e.g., Levenberg–Marquardt) and search tools (e.g., multiple start-point) |
| MATLAB43 |
• ODE solvers (e.g., Rosenbrock, Runge–Kutta, variable step variable order solvers) |
• MATLAB® |
V |
 |
| • Global optimisation toolbox |
| • Various optimisation algorithms (e.g., Levenberg–Marquardt, trust-region-reflective, simulated annealing, Nelder–Mead, genetic algorithm, particle swarm, surrogate polynomial optimisation, pattern search) and search tools (e.g., multiple start-point) |
| gPROMS44,45 |
• ODE solvers (e.g., DAEBDF, or DASOLV variable step variable order backward differentiation formulae, SRADAU variable step Runge–Kutta) |
• gPROMS® Process or Formulated Products |
V |
 |
| • Local-optimisation algorithms (e.g., maximum likelihood) and search tools (e.g., multiple start-point) |
| SciPy46 |
• ODE solvers (e.g., Runge–Kutta, variable step variable order solvers) |
• Python |
V |
 |
| • SciPy |
| • NumPy |
| • Local-optimisation algorithms (e.g., Nelder–Mead, trust region reflective, Newton-CG, sequential least squares programming) |
| KIPET24,47,48 |
• ODE solvers (e.g., orthogonal collocation on finite elements) |
• Python |
CT AT |
 |
| • Pyomo |
| • Local-optimisation algorithms (e.g., maximum likelihood) and search tools (e.g., multiple start-point) |
| • SciPy |
| • NumPy |
| • KIPET |
| GEKKO49 |
• ODE solvers (e.g., orthogonal collocation on finite elements) |
• Python |
V |
 |
| • GEKKO |
| • Local optimisation algorithms and Hyperopt search tools (e.g., grid search, random search, tree-structured parzen estimator, adaptive tree-structured parzen estimator) |
• NumPy |
| GDOC33,35,36,50 |
• ODE solvers (e.g., CVODES) |
• Fortran, C, or C++ |
CT |
 |
| • Local-optimisation algorithms (e.g., sequential quadratic programming via NPSOL, etc.) and search tools (e.g., branch and bound algorithm coupled with convex relaxation considerations) |
| • NPSOL |
| • Any ANSI compliant Fortran, C, or C++ compiler |
| COMSOL51,52 |
• ODE solvers and optimisation modules (e.g., optimisation module, LiveLink™ for MATLAB) |
• COMSOL Multiphysics® |
V |
 |
| • Local-optimisation algorithms (e.g., Levenberg–Marquardt, bound optimisation BY quadratic approximation) |
Several studies have also been conducted to show how computational modelling can simplify conceptualising and ranking the kinetic models developed for these reactions.53 Tsu et al.54 recently used integer linear programming (ILP) to identify stoichiometric coefficients for synthetic chemical reactions, whilst August et al.55 used it to identify promising chemical reaction networks for biological systems. Meanwhile, Taylor et al.23,56 and Willis et al.57 have shown that Mixed Integer Linear Programming (MILP) can be used to automatically generate and test different rate laws and reaction networks for systems where the reagents, products and intermediates are already known. Ultimately, the grand vision is allowing all feasible unimolecular and bimolecular reactions between different chemical species to be determined automatically,53,54,57 before leveraging metrics such as the Akaike23,56,58 and Bayesian information criterions59 to identify models which have the simplest structure, yet can accurately predict experimental observations.23,60
A promising cancer therapy which can particularly benefit from accelerated process R&D is Adavosertib (AZD1775) – an experimental oral medication which may inhibit tyrosine kinase WEE1 activity during cell signalling, growth and division61 – since it has shown clinical efficacy as a monotherapy against a range of cancers. Most notably, it is potent against non-small cell lung cancer (NSCLC) and pancreatic cancers,62 which together account for over 50% of all cancer-related deaths in Europe today.4 This compound has also shown promise as a combinatorial therapy when treating NSCLC, ovarian cancer and leukemia using Sotorasib,63 chemotherapy62 and Cytarabine64 as partner therapies.
Considering this, in the present paper we propose a range of kinetic models which can be used to describe the synthesis of an important precursor required for adavosertib production: AZD1775 hydroxymethylsulfanyl (HMS). Neither a reaction mechanism nor any kinetic model have ever been previously proposed for the synthesis of this compound, but understanding its synthesis and production is critical for the cost-effective manufacture of Adavosertib. To conduct this kinetic study, we have used an original parameter estimation code written in MATLAB® to parameterise 64 candidate kinetic models, before ranking them based on their complexity and fidelity to reflect lab-scale experimentation. Remarkably, each of the models hereby postulated and considered have been developed by invoking knowledge of similar chemical reactions.
2. Experimental
The experimental data required for kinetic modelling is obtained once AZD1775 HMS is synthesised from a feedstock of pyrimidine (Pyr) and bromopyridine (PyBr) in the presence of potassium acetate (KOAc), using copper(I) iodide (Cu(I)I) and racemic ± trans-N,N′-dimethylcyclohexane-1,2-diamine (CyDMEDA) acting as a catalyst and ligand, respectively (Fig. 2).
 |
| | Fig. 2 The overall reaction scheme for AZD1775 hydroxymethylsulfanyl (HMS) batch synthesis. | |
The chemical synthesis protocol involves first weighing appropriate amounts of solids (i.e. Pyr, PyBr, KOAc, Cu(I)I and CyDMEDA) into vials, before purging them with nitrogen, and adding the reaction solvent (degassed MeCN) to these reagents under inert conditions only. Consequently, an Amigo Chem® workstation (Fig. 3) has been used to carry out the synthesis reaction, over a range of reaction temperatures (338.15, 348.15, and 355.15 K) and initial reagent concentrations (cf. ESI,† Table S1). High Performance Liquid Chromatography (HPLC) has been used to determine the concentration-time profile of each reagent during these reactions (hereafter, referred to as experiments a–n), measuring the concentration of species Pyr, PyBr, PyI and HMS over the course of the reaction. For the final experimental run (experiment ‘n’), Pyr concentration was not recorded.
 |
| | Fig. 3 Schematic representation of a magnetically stirred Amigo Chem® batch reactor used for AZD1775 HMS synthesis. | |
Key properties of these compounds are provided in Table 3.
Table 3 Properties of compounds used in AZD1775 HMS synthesis
| Species |
Role |
#CAS |
Chemical formula |
M [g mol−1] |
Tbp [K] |
Tmp [K] |
| Ref. 65. Ref. 66. |
| Pyr |
Reagent |
955368-90-8 |
C9H10N4OS |
222.27 |
671.05a |
— |
| PyBr·HBr |
Reagent |
— |
C8H11Br2NO |
296.99 |
— |
— |
| PyBr |
Reagent |
638218-78-7 |
C8H10BrNO |
216.08 |
546.35a |
339.36a |
| HBr |
Reagent |
10035-10-6 |
HBr |
80.91 |
206.15b |
186.15b |
| KOAc |
Reagent |
127-08-2 |
C2H3KO2 |
98.14 |
— |
565.15b |
| PyI |
Intermediate |
— |
C8H10INO |
263.08 |
— |
— |
| KBr |
By-product |
7758-02-3 |
KBr |
119.00 |
1708.15b |
1003.15b |
| HOAc |
By-product |
64-19-7 |
C2H4O2 |
60.05 |
391.15b |
289.85b |
| HMS |
Product |
955369-56-9 |
C17H19N5O2S |
357.43 |
838.75a |
— |
| Cu(I)I |
Catalyst |
7681-65-4 |
CuI |
190.45 |
1563.15a |
878.15a |
| CyDMEDA |
Ligand |
67579-81-1 |
C8H18N2 |
142.25 |
459.95a |
283.38a |
| MeCN |
Solvent |
75-05-8 |
C2H3N |
41.05 |
354.82b |
228.15b |
3. Reaction mechanism & kinetic model development
To develop a reaction mechanism which can accurately describe AZD1775 HMS synthesis, inspiration has been taken from a similar reaction already studied by Strieter et al.67 (specifically, the copper-catalysed N-arylation of amides), since HMS synthesis occurs via Ullmann-type coupling.68,69 Herein, we have adapted the reaction mechanism presented by these authors to allow the consideration of several characteristics unique to HMS synthesis. These include:
1. The production of an aryl iodide compound (PyI), due to the presence of a side reaction involving PyBr (Fig. 4).
2. The production of acetic acid (HOAc), which can hinder the progress of the reaction (Fig. 4).
3. The presence of potassium acetate (KOAc), which may influence reaction rates (Fig. 4).
 |
| | Fig. 4 Proposed reaction mechanism for AZD1775 HMS synthesis: UICi denotes unidentified compounds due to inhibitory HOAc action. | |
Using this approach, we have defined three fundamental regimes under which different kinetic models can be developed to describe HMS synthesis (Fig. 4). These are:
• Case 1: AZD1775 HMS synthesis disregarding PyI production.
• Case 2: AZD1775 HMS synthesis considering irreversible PyI production.
• Case 3: AZD1775 HMS synthesis considering reversible PyI production.
Each of these cases can be described using systems of differential algebraic equations (DAEs), as shown in Table 4, where R1 and R2 denote HMS synthesis from PyBr and PyI, respectively, whilst R3 and R4 denote the production and reversible consumption of PyI, respectively (Fig. 4). To summarise their differences, we note that in Case 1 the production of PyI from PyBr is completely ignored, allowing us to treat PyBr and PyI as a single pseudo-aryl halide (PyHal). Conversely, in cases 2 and 3, we explicitly consider rate laws for PyI production via irreversible (Case 2) and reversible (Case 3) halide substitution reactions. Thereby, we allow for PyBr and PyI to both react with Pyr independently in order to produce HMS.
Table 4 System of DAEs corresponding to each case developed
Within each case different rate laws describe:
1. The mechanism by which HMS synthesis occurs (from PyBr, PyI or the pseudo-aryl halide PyHal).
2. The influence of HOAc on reaction rate.
3. The impact of KOAc concentration on reaction rate.
4. PyI production.
Consequently, candidate rate laws for each of these aspects have been covered in section 3.1 for each case.
3.1. Candidate rate laws for cases 1–3
Full kinetic models developed for each case have been provided in the ESI† (Case 1: Table S2, Case 2: Table S3, and Case 3: Table S4). The individual rate laws used in each of these kinetic models are discussed in the following sections.
3.1.1. AZD1775 HMS synthesis disregarding PyI production (Case 1). The production of HMS occurs via Ullmann-type coupling as per the study of Strieter et al.67 Thus, assuming PyBr and PyI can be treated as a single compound (PyHal), HMS synthesis may be described using the rate law presented in eqn (1) and (2).| | |
R1 = k1[LCuPyr][PyHal]
| (1) |
| |
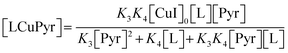 | (2) |
Moreover, we postulate that potassium acetate (KOAc) may impact reaction rate. Thus, an alternative rate law for HMS synthesis is defined, to account for this possibility, as shown in eqn (3).| | |
R1 = k1[LCuPyr][PyHal](Ksp[KOAc])α where: α ∈ [0, 1]
| (3) |
HMS may also be produced via a two-step Ullmann-type coupling reaction (Fig. 5). Hence, it is also possible that the reaction proceeds with 2nd order dependence on the ligated Pyrimidine compound (LCuPyr);68,69 leading to the development of a second candidate rate law, as shown in eqn (4).| | |
R1 = k1[LCuPyr]2[PyHal](Ksp[KOAc])α where: α ∈ [0, 1]
| (4) |
Beyond these considerations, it is also important to consider the possibility that acetic acid (HOAc) impacts the rate of reaction. Hence, reversible processes are defined, which temporarily take reactants off-cycle from the main reaction to model this effect (eqn (5) and (6)).| |
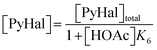 | (5) |
| |
 | (6) |
The nature of the compounds produced by these side processes (eqn (5) and (6)) is unknown. Thus, we have simply represented them as UIC1 and UIC3 in this study (Fig. 4).
 |
| | Fig. 5 Ullmann-type coupling68,69 hypothesis for AZD1775 HMS formation. | |
Considering each of these options, it is clear that either eqn (3) or (4) can be used to describe HMS synthesis, by setting α to 0 or 1. Moreover, eqn (5) and (6) can be used to augment eqn (3) and (4) to account for the effects of HOAc. Consequently, a total of 16 kinetic models can be built for Case 1 – full details of which can be found in the ESI† (Table S2). These models are named 1–16.
3.1.1.1. Calculating ligand concentration. To calculate the free ligand concentration required for each model, according to eqn (2), we define its concentration in terms of observable species only. To do this, we note that the concentration of the catalyst and free-ligand may be defined in terms of the Cu-bound and ligated species as per eqn (7) and (8): when combined and rearranged, these yield eqn (9).| | |
[L]total = [L] + [LCu]+ + [LCuPyr]
| (7) |
| | |
[CuI]total = [CuI]0 = [LCu]+ + [LCuPyr] + [CuPyr2]−
| (8) |
| | |
[L] = [L]total − [CuI]0 + [CuPyr2]−
| (9) |
Accordingly, we use Fig. 4 to define eqn (10), before combining it with eqn (2) and (9) to produce eqn (11) (after extensive algebraic rearrangement).| |
 | (10) |
Eqn (11) is a simple quadratic equation, solvable at each timestep for the reaction.| | |
(K3K4[Pyr] + K4)[L]2 + (K3[Pyr]2 + K3K4[CuI]0[Pyr] + K4[CuI]0 − K4[L]total − K3K4[Pyr][L]total)[L] − K3[Pyr]2[L]total = 0
| (11) |
3.1.2. AZD1775 HMS synthesis considering irreversible PyI production (Case 2). For Case 2, HMS synthesis is modelled assuming Ullmann-type coupling, just as in Case 1. Herein, however, we also consider PyI formation, assuming that it is produced irreversibly from PyBr. Consequently, HMS production for Case 2 is defined using eqn (12) and (13) to describe HMS synthesis from PyBr (eqn (12): one-step coupling, eqn (13): two-step coupling), whilst eqn (14) and (15) are used to describe its production from PyI (eqn (14): one-step coupling, eqn (15): two-step coupling).| | |
R1 = k1[LCuPyr][PyBr](Ksp[KOAc])α where: α ∈ [0, 1]
| (12) |
| | |
R1 = k1[LCuPyr]2[PyBr](Ksp[KOAc])α where: α ∈ [0, 1]
| (13) |
| | |
R2 = k2[LCuPyr][PyI](Ksp[KOAc])α where: α ∈ [0, 1]
| (14) |
| | |
R2 = k2[LCuPyr]2[PyI](Ksp[KOAc])α where: α ∈ [0, 1]
| (15) |
Following these definitions, expressions (as per eqn (5) and (6) of Case 1) are defined to describe the inhibitory effect of HOAc on PyBr, PyI and Pyr independently (eqn (16)–(18)).| |
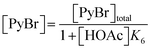 | (16) |
| |
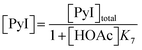 | (17) |
| |
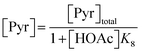 | (18) |
A variety of rate laws are tested for the production of PyI from PyBr, all of which are reminiscent of those in other areas of chemistry where halogenic substitution takes place.70–79 For example, it is noted that some studies71–73 have found that halogenic substitution reactions involving pyridines follow second-order rate laws (which are first-order in both the substrate and solvent). Moreover, a recent study by Kundu et al.74 explored reaction mechanisms underpinning ligand-assisted substitutions involving pyridines and their derivatives, concluding that they proceed via third-order reactions (first-order in catalyst and second-order in aryl halide substrate).74 Other authors70,71 have suggested that such reactions proceed with rate laws of non-integer order (i.e., between 1 and 2). Consequently, two variable-order rate laws are hereby tested to allow each of these possibilities to be examined simultaneously, limiting the reaction order with respect to PyBr to between 1 and 2 (eqn (19) and (20)). This is a critical problem simplification, removing the need to explicitly quantify acetonitrile and copper(I) iodide concentrations, whilst defining β as an extra kinetic parameter to be estimated.| |
 | (19) |
| | |
R3 = k5[CuI]0[PyBr]β
| (20) |
This approach results in a total of 32 models for Case 2 (named models 17–48), with details in the ESI† (Table S3).
3.1.3. AZD1775 HMS synthesis considering reversible PyI production (Case 3). For Case 3, we retain eqn (2) from Case 1 and eqn (12)–(18) from Case 2 to describe the production of HMS from PyBr and PyI. However, we replace our treatment of PyI to consider its reversible production from PyBr. Specifically, this is postulated to occur via a reversible copper-catalysed Finkelstein reaction (eqn (21) and (22)).75–79| | |
R3 = k5[CuI]0[PyBr][I−] where: [I−] ≈ [I−]0 + [CuI]0 − [PyI]
| (21) |
This leads to the development of 16 kinetic models for Case 3, resulting in a total of 64 models across all three cases. Consequently, the kinetic models arising from Case 3 are named models 49–64. A full description of each model developed as part of Case 3 can be found in the ESI† (Table S4).
3.2. Kinetic rate law temperature dependence
To capture the temperature dependence of each reaction step, Arrhenius and van't Hoff relationships are embedded within each of the kinetic models proposed (eqn (23)–(25)).| |
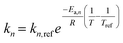 | (23) |
| |
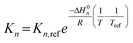 | (24) |
| |
 | (25) |
The temperature dependence of the solubility of KOAc within HOAc80 has also been estimated using the van't Hoff equation (eqn (26) and (27))81 (Fig. 6).| |
 | (27) |
 |
| | Fig. 6 Temperature-dependent KOAc solubility in HOAc (data: ref. 80). | |
4. Parameter estimation & model discrimination
Parameter estimation and model discrimination methods are hereby used in tandem to identify the highest-fidelity kinetic model for HMS synthesis from the 64 models developed in section 3. Consequently, the computational procedure is summarised in Fig. 7, and sections 4.1 and 4.2 are provided below to offer detailed explanations of each of the blocks in the software architecture illustrated in this diagram.
 |
| | Fig. 7 The computational procedure for kinetic parameter estimation and reaction model discrimination, implemented in MATLAB®. | |
Each case (and model) has been studied independently using multistart nonlinear programming (NLP). Hence, parameter estimation efforts are conducted for each model individually, and model discrimination methods are subsequently employed to analyse the results from each of these studies.
4.1. Kinetic parameter estimation methodology
The parameter estimation problem is formulated as a multistart constrained optimisation problem for each model, using the objective function and constraints of eqn (28)–(30).| |
 | (29) |
| |
 | (30) |
Using this approach, parameter estimations are initialised from 1000 different start-points for each model, using 1000 different random guess-vectors containing different parameter values within the specified bounds (Table 5). To avoid divergence, parameter estimations resulting in non-numeric, infinite or imaginary objective function values must be rejected, forcing the optimisation algorithm to modify the search vector space.
Table 5 Parameter bounds
| |
kn,ref [various] |
Kn,ref [various] |
Ea,n [kJ mol−1] |
ΔH0n [kJ mol−1] |
ΔH0d [kJ mol−1] |
ΔS0d [kJ mol−1 K−1] |
β [—] |
| Lower bound (θlb) |
10−10 |
0.01 |
1 |
−1000 |
10.702 |
0.0184 |
1 |
| Upper bound (θub) |
6 × 1011 |
100 |
150 |
1000 |
12.365 |
0.0230 |
2 |
A detailed discussion of the code structure is provided in section 4.1.1 below. The kinetic parameters and reaction orders required by each model are estimated using an in-house parameter estimation code written in MATLAB® (Fig. 7), employing its fminsearch command (which implements the Nelder–Mead algorithm) at the centre of a while loop, so as to iteratively minimise the sum of weighted least squares (eqn (30)) for each model: this occurs by setting weights (Wi) to the reciprocal of the square uncertainties of experimental measurements, whilst also placing user-specified bounds on each of the parameters to be estimated (Table 5).
To enable this approach, it has been stipulated that kinetic rate constants within the kinetic models tested can take values between 0–6 × 1011, since liquid-phase bimolecular reactions do not exceed rates of 6 × 1011 M−1 min−1.82–86 Likewise, it has been specified that activation energies (Ea,n) take values between 1–150 kJ mol−1, to align with data from classical organic synthesis reactions.87 Moreover, it has been acknowledged that standard reaction enthalpies (ΔH0n) for organic reactions are within ±1000 kJ mol−1, whilst their equilibrium constants (Kn) have values of 0.01–100, whenever equilibrium concentrations are measurable.88 Reaction orders, β, must be bounded between 1 and 2 (for the reasons discussed in section 3), and KOAc dissolution properties (ΔH0d and ΔS0d) are set within limits equal to their 95% confidence intervals (as per Fig. 6).
Given the range of each of these bounds, the search space for each problem is reduced by natural logarithm transforms of parameters kref,n, Ea,n and Kref, as per recent studies.89,90 This approach is not possible for ΔH0n parameters, as it would result in imaginary solutions with no physical meaning (it is also not required for β parameters due to range brevity).
4.1.1. Code structure. Parameter estimation has been carried out for each kinetic model independently (i.e., models 1–64) using original MATLAB® code based on the next concepts:1) Local optimisation: MATLAB®'s fminsearch command (implementing the Nelder–Mead algorithm) is used to minimise the objective function of each model (eqn (28)–(30)) by varying the value of their model parameters (θ) within their specified bounds. Moreover, it continues to do so until one of the following criteria is met:
a) The minimum step size (10−6) has been violated, and the objective function cannot be improved upon by more than 10−6.
b) The maximum number of iterations or objective function evaluations is exceeded (MATLAB default settings used).
Once one of these criteria is met, fminsearch releases any parameter estimates held (θcurrent). The algorithm then checks whether one of the following criteria has also been satisfied:
c) The kinetic parameters have not changed compared to the values last supplied to the optimiser.
d) The user-specified maximum allowable time for estimations (48 h) has been exceeded.
If one of (c) or (d) has been satisfied, then the current parameter estimates (θcurrent) are saved against their associated start-point identification number (Ns) for later analysis. However, if neither of these criteria have been achieved, then the output parameter estimates (θcurrent) are provided to fminsearch again, as a new initial guess. This serves to enhance convergence by repeating step 1 until (a)–(b), plus one of (c) or (d), are satisfied (Fig. 7).
2) Multistart problem initialisation: to improve estimations, step 1 is repeated using 1000 different initial guesses (θguess) before selecting the set of parameters which yield the lowest objective function value. Following this, the 95% confidence intervals are calculated for the selected parameter set, and parameters which give unacceptably high confidence intervals (i.e., greater than 15%23,24,48,56) should be fixed39,91 (Fig. 7).
The parameter estimation code used can be run in series or parallel – depending on the computing facilities available. Running parameter estimations in parallel (splitting jobs across multiple CPU/GPU cores) will invariably provide faster results, as computational cost scales linearly with the number of starting points used.
4.2. Model discrimination
Following parameter estimation, the Akaike Information criterion (AICc) is used to rank each model based on its: (i) simplicity, and (ii) fidelity vs. experimental observations23,56 (eqn (31)). Consequently, models with lower AICc values are favoured, since this indicates accurate reproduction of experimental findings whilst avoiding the use of unnecessary terms, thus preventing overfitting and unjustifiable over-parameterisation.23| |
 | (31) |
Relative Akaike likelihood metrics (eqn (32) and (33)) are simultaneously used to determine the probability that the model with the lowest AICc for a given case is indeed better than all other model candidates available for the same case. Evidence ratios (eqn (34)) and normalized probabilities (eqn (35)) are also calculated for each model, to assess the likelihood that the selected model is better than the next-best model (i.e. the probability that model i is more suitable compared to model j).58,60,92,93| |
 | (32) |
| | |
Δ(AICc)i = (AICc)i − (AICc)min
| (33) |
| |
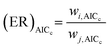 | (34) |
| |
 | (35) |
The Bayesian Information Criterion (BIC) is also estimated for each model via eqn (36) to corroborate this analysis, by calculating normalised probabilities as done for AICc. Hence, lower BIC values represent more promising models (higher fidelity), with BIC penalising model complexity more harshly than AICc.59| |
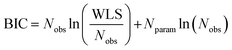 | (36) |
5. Results & discussion
Three distinct cases are considered for kinetic models describing HMS synthesis:
• Case 1: AZD1775 HMS synthesis disregarding PyI production.
• Case 2: AZD1775 HMS synthesis considering irreversible PyI production.
• Case 3: AZD1775 HMS synthesis considering reversible PyI production.
Consequently, Fig. 8 provides an overview of AICc and BIC values for every single model, ranking all 64 models hereby considered within these three cases.
 |
| | Fig. 8 AICc and BIC values for: (a) Case 1 (no PyI production); (b) Case 2 (irreversible PyI production); and (c) Case 3 (reversible PyI production). | |
Models 14, 42 and 62 are determined to be the most promising ones from Cases 1, 2 and 3, respectively. The normalised AICc and BIC probabilities both sit at 1.0 for each of these models when compared with the next-best model from their respective cases. Moreover, we observe that among models considering PyI production (Cases 2 and 3), model 62 outperformed model 42 by a significant margin, as it exhibited WLS, AICc and BIC values 50.10, 16.03 and 14.66% lower than the latter, respectively. Hence, model 42 is rejected, rendering model 62 as the most reliable vs. all other models describing PyI production.
The reaction profiles predicted by models 14 and 62 are compared with experimental data in Fig. 9 and 10, respectively; final kinetic parameters for both these models are provided in Table 6. Both models 14 and 62 provide looser fits for experiment “l” than for the rest of the experiments, most likely due to undercalculation of HMS concentrations for this experiment only (possibly caused by non-uniform mixing), since less HMS was produced than Pyr consumed in this experiment (no other species were observed during HPLC measurements for this experiment). The use of Weighted Least Squares (WLS) regression during our original analysis is able to successfully mitigate the effects of this suspected effect, especially since similar percentage uncertainties are computed for each experimental data point measured – leading to larger absolute experimental uncertainties for species with higher concentrations (e.g. HMS in experiment “l”).
 |
| | Fig. 9 Kinetic model predictions vs. experimental data (model 14). | |
 |
| | Fig. 10 Kinetic model predictions vs. experimental data (model 62). | |
Table 6 Kinetic parameters (estimated and fixed) for models 14 and 62
| |
Model 14 |
Model 62 |
| k1,ref [M−2 min−1] |
131.339 (± 1.140%) |
852.151 (± 2.164%) |
| k2,ref [M−2 min−1] |
— |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 273.399 (fixed) 273.399 (fixed) |
| k5,ref [M−2 min−1] |
— |
1.482 (± 0.014%) |
| K3,ref [M] |
99.993 (± 0.011%) |
8.004 (± 0.086%) |
| K4,ref [—] |
0.166 (± 0.148%) |
0.052 (± 0.063%) |
| K5,ref [M−1] |
— |
9.284 (fixed) |
| K6,ref [M] |
4.112 (± 10.168%) |
0.549 (± 2.408%) |
| K7,ref [M] |
— |
6.977 (fixed) |
| K8,ref [M] |
8.057 (± 6.120%) |
2.296 (± 5.839%) |
| Ea,1 [kJ mol−1] |
146.134 (± 7.539%) |
31.272 (± 9.268%) |
| Ea,2 [kJ mol−1] |
— |
1.045 (fixed) |
| Ea,5 [kJ mol−1] |
— |
60.497 (± 3.047%) |
| ΔH03 [kJ mol−1] |
200.464 (± 1.030%) |
−309.601 (± 1.146%) |
| ΔH04 [kJ mol−1] |
0.825 (± 1.045%) |
9.908 (± 2.465%) |
| ΔH05 [kJ mol−1] |
— |
253.532 (fixed) |
| ΔH06 [kJ mol−1] |
404.302 (± 6.580%) |
−515.590 (± 3.211%) |
| ΔH07 [kJ mol−1] |
— |
−584.127 (± 10.448%) |
| ΔH08 [kJ mol−1] |
102.235 (fixed) |
−217.411 (± 8.344%) |
From these findings, we observe that both highest-fidelity models share all their main pathway features, with the sole exception of PyI production treatment (cf. model structures in Tables S2 and S4 within the ESI†). Thus, we conclude that each of the aspects accounted for by these models plays a key role in the AZD1775 HMS synthesis mechanism. For example, since the production of HMS from aryl halides and Pyr is second-order in LCuPyr concentration for both models, it is likely that a two-step Ullmann coupling (Fig. 5) occurs instead of a single-step mechanism. Conversely, the characteristics ignored by these models (e.g. KOAc concentration dependence) are unlikely to have any significant effect on the HMS synthesis reaction.
Furthermore, we can also conclude that PyI is most likely produced via a copper-catalysed Finkelstein reaction, since the kinetic models employing this assumption (those in Case 3) often outperform their equivalent counterparts (those in Case 2). However, further experimentation focused on analysing the production of PyI is required to fully confirm this hypothesis. Similarly, because both highest-fidelity models consider inhibitory effects brought about by the presence of HOAc, acetic acid may indeed inhibit the action of Pyr, PyBr and PyI. The exact mechanism by which this inhibition may occur remains unclear (as per section 3, Fig. 4), however. Consequently, future studies should establish the true mechanism by which this HOAc inhibition occurs – a possible explanation is that the presence of HOAc creates a buffer system impacting the deprotonation of pyrimidine, thus slowing down the oxidative addition of aryl halides (Fig. 5).
6. Conclusions
The present paper performs an original parameter estimation and extensive model discrimination to arrive at a novel reaction mechanism (Fig. 4) which successfully captures all known key features of AZD1775 HMS synthesis, with three broad kinetic model classes (Cases 1–3) and 64 individual models developed, tested and comparatively evaluated for the first time. Specifically, the model collection comprises those addressing HMS synthesis by disregarding PyI production entirely (Case 1: models 1–16), as well as those which considered irreversible (Case 2: models 17–48) and reversible (Case 3: models 49–64) PyI production. Thus, a total of 64 candidate kinetic models have been proposed, parameterised and evaluated to describe the copper-catalysed and ligand-assisted HMS synthesis. Candidates 14 and 62 have the highest model fidelity, demonstrating the most promising results by a significant margin and exhibiting the lowest objective function values and the most favourable Akaike and Bayesian (AICc and BIC) metrics following their successful parameterisation. Consequently the authors propose that manufacturing facilities and research groups should use model 14 to model HMS synthesis if PyI production can be ignored (as this model has a far simpler structure and a concise parameter set), but employ model 62 if PyI production is to be considered for explicit quantification.
The original parameter estimation and model development and discrimination method and code proposed herein does not guarantee uniqueness. Consequently, alternative models may yield comparable results to those achieved here, but they also be far more complex than those presented. Accordingly, future studies should focus on using the kinetic models presented here for the first time, to identify optimal reaction conditions for HMS synthesis, by manipulating process variables such as temperature, reaction time and initial reagent concentrations to maximise product yield whilst minimising side product generation. Furthermore, future parameter estimation studies can incorporate parameter identifiability and estimability analyses94,95 in the respective workflows. Bootstrapping methods can also be incorporated into future workflows, especially for codes which may study similarly many kinetic model scenarios under limited experimental data availability.
Nomenclature & acronyms
Latin letters
| Cexpti,j | Experimental concentration of species i at datapoint j [M] |
| Cmodeli,j | Modelled concentration of species i at datapoint j [M] |
| Ea,n | Activation energy associated with forward reaction n [kJ mol−1] |
| f(θ) | Temperature dependent fitting objective function [—] |
| ΔH0d | Standard enthalpy of dissolution for KOAc in HOAc [kJ mol−1] |
| ΔH0n | Standard reaction enthalpy with reaction n [kJ mol−1] |
| [i] | Molar concentration of component i [M] |
| [i]0 | Initial molar concentration of component i [M] |
| kn | Kinetic rate constant associated with forward reaction n [various] |
| kn,ref | Pre-exponential reference constant for forward reaction n [various] |
| k−n | Kinetic rate constant associated with reverse reaction n [various] |
| Kn | Equilibrium rate constant associated with reaction n [various] |
| Ksp | Solubility product [M2] |
| M | Molecular weight [g mol−1] |
| Ndata | Number of experimental data points [—] |
| Nmdl | Number of models tested [—] |
| Nobs | Number of experimental observations (i.e., time-points) [—] |
| Nparam | Number of parameters [—] |
| Ns | Number of start-points [—] |
| Nspecies | Number of species [—] |
| R | Universal gas constant [J mol−1 K−1] |
| Rj | Reaction rate j [mol L−1 min−1] |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) | Real numbers [—] |
| ΔS0d | Standard entropy of dissolution for KOAc in HOAc [kJ mol−1 K−1] |
| t | Reaction time [min] |
| T | Reaction temperature [K] |
| Tbp | Boiling point temperature [K] |
| Tmp | Melting point temperature [K] |
| Tref | Reference temperature [K] |
| wi,AICc | Normalised relative Akaike likelihoods [—] |
| Wi | Objective function weight associated with measurement i [M−2] |
| xKOAc | Solubility of KOAc in HOAc at a given temperature [mol mol−1] |
Greek letters
| α | Binary decision variable [—] |
| β | Unknown rate order [—] |
| θ | Parameter vector [various] |
| θcurrent | Parameter vector outputted at interim points during estimations [various] |
| θguess | Initial parameter vector guess for a given start-point [various] |
| θlb | Parameter vector lower bounds [various] |
| θub | Parameter vector upper bounds [various] |
Acronyms
| AICc | Corrected Akaike's information criterion [—] |
| (AICc)i | Corrected Akaike information criterion of model i [—] |
| (AICc)min | Minimum corrected Akaike information criterion obtained [—] |
| Δ(AICc)i | Corrected Akaike differences of model i [—] |
| BIC | Bayesian information criterion [—] |
| (ER)AICc | Corrected Akaike evidence ratios [—] |
| (NP)AICc | Corrected Akaike normalized probabilities [—] |
| WLS | Weighted least squares [—] |
Data availability
A legal confidentiality agreement (2020) is in effect and has been signed between the University of Edinburgh and AstraZeneca plc, governing the publication of results (under the auspices of the Engineering & Phys. Sciences Research Council, EPSRC). Tabulated, literature reference and digitised reaction (concentration) data are all provided and suffice for the reproduction of all Figs./results presented in the article. Specific requests for original (raw) experimental data and/or the software (MATLAB®) code by Mr M. Blair can be considered in writing, to ensure the above is not violated.
Conflicts of interest
The authors report no conflict of interest whatsoever.
Acknowledgements
This study has employed computational resources provided by the University of Edinburgh's Compute and Data Facility (ECDF) (https://www.ecdf.ed.ac.uk/). M. Blair acknowledges the financial support provided by the Engineering and Physical Sciences Research Council (EPSRC) and AstraZeneca UK via an Industrial CASE (iCASE) PhD Fellowship. Prof. D. I. Gerogiorgis also acknowledges financial support from UKRI/EPSRC (RAPID: ReAl-time Process Modeling and Diagnostics: Powering Digital Factories, EP/V028618/1) as well as a recent Royal Society Short Industrial Fellowship (2020-22), and an ongoing Royal Society International Exchanges Programme grant (IES\R2\232014, 2023-25). All authors acknowledge the critical leadership and support of Dr. Martin Jones, Principal Scientist (Process Design, AstraZeneca U.K.), for the inception and critical support of this research project.
References
- V. Prasad, K. De Jesus and S. Mailankody, The high price of anticancer drugs: origins, implications, barriers, solutions, Nat. Rev. Clin. Oncol., 2017, 14(6), 381 CrossRef PubMed.
- B. Jönsson, T. Hofmarcher, P. Lindgren and N. Wilking, The cost and burden of cancer in the European Union 1995–2014, Eur. J. Cancer, 2016, 66, 162 CrossRef PubMed.
- T. Hofmarcher, P. Lindgren, N. Wilking and B. Jönsson, The cost of cancer in Europe 2018, Eur. J. Cancer, 2020, 129, 41 CrossRef PubMed.
- T. Dyba, G. Randi and F. Bray, et al., The European cancer burden in 2020: Incidence and mortality estimates for 40 countries and 25 major cancers, Eur. J. Cancer, 2021, 157, 308 CrossRef PubMed.
- Cancer Research UK, Cancer Statistics for the UK, [cited 2023 23rd March]; Available from: https://www.cancerresearchuk.org/health-professional/cancer-statistics-for-the-uk.
- R. L. Siegel, K. D. Miller, H. E. Fuchs and A. Jemal, Cancer Statistics, 2021, Ca-Cancer J. Clin., 2021, 71(1), 7 CrossRef PubMed.
- Cancer Research UK, Worlwide cancer statistics, [cited 2023 25th May]; Available from: https://www.cancerresearchuk.org/health-professional/cancer-statistics/worldwide-cancer#heading-Zero.
- S. Diab and D. I. Gerogiorgis, Process Modeling, Simulation, and Technoeconomic Evaluation of Separation Solvents for the Continuous Pharmaceutical Manufacturing (CPM) of Diphenhydramine, Org. Process Res. Dev., 2017, 21(7), 924 CrossRef CAS.
- S. Diab and D. I. Gerogiorgis, Process modelling, simulation and technoeconomic evaluation of crystallisation antisolvents for the continuous pharmaceutical manufacturing of rufinamide, Comput. Chem. Eng., 2018, 111, 102 CrossRef CAS.
- S. Diab and D. I. Gerogiorgis, Process modelling, simulation and technoeconomic optimisation for continuous pharmaceutical manufacturing of (S)-warfarin, in Computer Aided Chemical Engineering, ed. A. Friedl, et al., Elsevier, 2018, p. 1643 Search PubMed.
- S. Diab, D. T. McQuade, B. F. Gupton and D. I. Gerogiorgis, Process Design and Optimization for the Continuous Manufacturing of Nevirapine, an Active Pharmaceutical Ingredient for HIV Treatment, Org. Process Res. Dev., 2019, 23(3), 320 CrossRef CAS.
- S. Diab, N. Mytis, A. G. Boudouvis and D. I. Gerogiorgis, Process modelling, design and technoeconomic Liquid–Liquid Extraction (LLE) optimisation for comparative evaluation of batch vs. continuous pharmaceutical manufacturing of atropine, Comput. Chem. Eng., 2019, 124, 28 CrossRef CAS.
- O. L. Watson, S. Jonuzaj and J. McGinty, et al., Computer Aided Design of Solvent Blends for Hybrid Cooling and Antisolvent Crystallization of Active Pharmaceutical Ingredients, Org. Process Res. Dev., 2021, 25(5), 1123 CrossRef CAS PubMed.
- H. G. Jolliffe and D. I. Gerogiorgis, Plantwide design and economic evaluation of two Continuous Pharmaceutical Manufacturing (CPM) cases: Ibuprofen and artemisinin, Comput. Chem. Eng., 2016, 91, 269 CrossRef CAS.
- H. G. Jolliffe and D. I. Gerogiorgis, Technoeconomic Optimization of a Conceptual Flowsheet for Continuous Separation of an Analgaesic Active Pharmaceutical Ingredient (API), Ind. Eng. Chem. Res., 2017, 56(15), 4357 CrossRef CAS.
- M. A. McDonald, G. D. Marshall and A. S. Bommarius, et al., Crystallization Kinetics of Cephalexin Monohydrate in the Presence of Cephalexin Precursors, Cryst. Growth Des., 2019, 19(9), 5065 CrossRef CAS.
- A. B. Cuthbertson, A. D. Rodman, S. Diab and D. I. Gerogiorgis, Dynamic Modelling and Optimisation of the Batch Enzymatic Synthesis of Amoxicillin, Processes, 2019, 7(6), 318 CrossRef CAS.
- S. Diab, M. Raiyat and D. I. Gerogiorgis, Flow synthesis kinetics for lomustine, an anti-cancer active pharmaceutical ingredient, React. Chem. Eng., 2021, 6(10), 1819 RSC.
- C. A. Hone, A. Boyd and A. O'Kearney-McMullan, et al., Definitive screening designs for multistep kinetic models in flow, React. Chem. Eng., 2019, 4(9), 1565 RSC.
- E. Içten, A. J. Maloney and M. G. Beaver, et al., A Virtual Plant for Integrated Continuous Manufacturing of a Carfilzomib Drug Substance Intermediate, Part 1: CDI-Promoted Amide Bond Formation, Org. Process Res. Dev., 2020, 24(10), 1861 CrossRef.
- K. P. Cole, B. M. Campbell and M. B. Forst, et al., An Automated Intermittent Flow Approach to Continuous Suzuki Coupling, Org. Process Res. Dev., 2016, 20(4), 820 CrossRef CAS.
- M. Grom, G. Stavber, P. Drnovšek and B. Likozar, Modelling chemical kinetics of a complex reaction network of active pharmaceutical ingredient (API) synthesis with process optimization for benzazepine heterocyclic compound, Chem. Eng. J., 2016, 283, 703 CrossRef CAS.
- C. J. Taylor, M. Booth and J. A. Manson, et al., Rapid, automated determination of reaction models and kinetic parameters, Chem. Eng. J., 2021, 413, 127017 CrossRef CAS.
- C. Schenk, M. Short and J. S. Rodriguez, et al., Introducing KIPET: A novel open-source software package for kinetic parameter estimation from experimental datasets including spectra, Comput. Chem. Eng., 2020, 134, 106716 CrossRef CAS.
- H. G. Jolliffe and D. I. Gerogiorgis, Process modelling and simulation for continuous pharmaceutical manufacturing of ibuprofen, Chem. Eng. Res. Des., 2015, 97, 175 CrossRef CAS.
- A. Echtermeyer, Y. Amar, J. Zakrzewski and A. Lapkin, Self-optimisation and model-based design of experiments for developing a C–H activation flow process, Beilstein J. Org. Chem., 2017, 13, 150 CrossRef CAS PubMed.
- K. C. Aroh and K. F. Jensen, Efficient kinetic experiments in continuous flow microreactors, React. Chem. Eng., 2018, 3(1), 94 RSC.
- M. O. Frederick, M. A. Pietz and D. P. Kjell, et al., Development of a Leuckart–Wallach Reaction in Flow for the Synthesis of Abemaciclib, Org. Process Res. Dev., 2017, 21(9), 1447 CrossRef CAS.
- R. R. de Oliveira Silva, P. V. Cuesta Calvo and M. Fernandes da Silva, et al., Flow Synthesis of a Thiazolidine Drug Intermediate in Capillary Microreactors, Chem. Eng. Technol., 2019, 42(2), 465 CrossRef.
- D. D. S. Pinheiro, R. R. D. O. Silva and P. V. C. Calvo, et al., Microreactor Technology as a Tool for the Synthesis of a Glitazone Drug Intermediate, Chem. Eng. Technol., 2018, 41(9), 1800 CrossRef CAS.
- Y. R. Dubhashe, V. M. Sawant and V. G. Gaikar, Process Intensification of Continuous Flow Synthesis of Tryptophol, Ind. Eng. Chem. Res., 2018, 57(8), 2787 CrossRef CAS.
- C. T. Armstrong, C. Q. Pritchard and D. W. Cook, et al., Continuous flow synthesis of a pharmaceutical intermediate: a computational fluid dynamics approach, React. Chem. Eng., 2019, 4(3), 634 RSC.
- A. B. Singer, Global Dynamic Optimization, PhD Thesis, Department of Chemical Engineering, Massachusetts Institute of Technology (MIT), Cambridge, MA, USA, 2004 Search PubMed.
- A. B. Singer and P. I. Barton, Global solution of optimization problems with parameter-embedded linear dynamic systems, J. Optim. Theory Appl., 2004, 121(3), 613 CrossRef.
- A. B. Singer and P. I. Barton, Global Optimization with Nonlinear Ordinary Differential Equations, J. Glob. Optim., 2006, 34(2), 159 CrossRef.
- A. B. Singer, J. W. Taylor, P. I. Barton and W. H. Green, Global Dynamic Optimization for Parameter Estimation in Chemical Kinetics, J. Phys. Chem., 2006, 110, 971 CrossRef CAS PubMed.
- M. Trampuž, D. Teslić and B. Likozar, Crystallization of fesoterodine fumarate active pharmaceutical ingredient: Modelling of thermodynamic equilibrium, nucleation, growth, agglomeration and dissolution kinetics and temperature cycling, Chem. Eng. Sci., 2019, 201, 97 CrossRef.
- A. Pohar and B. Likozar, Dissolution, Nucleation, Crystal Growth, Crystal Aggregation, and Particle Breakage of Amlodipine Salts: Modeling Crystallization Kinetics and Thermodynamic Equilibrium, Scale-up, and Optimization, Ind. Eng. Chem. Res., 2014, 53(26), 10762 CrossRef CAS.
- C. Schenk, L. T. Biegler, L. Han and J. Mustakis, Kinetic Parameter Estimation from Spectroscopic Data for a Multi-Stage Solid–Liquid Pharmaceutical Process, Org. Process Res. Dev., 2021, 25(3), 373 CrossRef CAS.
- Q. Su, Z. K. Nagy and C. D. Rielly, Pharmaceutical crystallisation processes from batch to continuous operation using MSMPR stages: Modelling, design, and control, Chem. Eng. Process.: Process Intesif., 2015, 89, 41 CrossRef CAS.
- H. F. Kraus, D. Acevedo and W. Wu, et al., Kinetic modelling of
an environmentally friendly carbamazepine synthesis via urea and iminostilbene in batch and continuous processes, React. Chem. Eng., 2023, 8(2), 402 RSC.
- Scale-up Systems Ltd., Dynochem, Scale-up Systems Ltd. Search PubMed.
- The MathWorks Inc., MATLAB, MathWorks Search PubMed.
- Process Systems Enterprise, gPROMS Process, PSE Search PubMed.
- Process Systems Enterprise, gPROMS Formulated Products, PSE Search PubMed.
- P. Virtanen, R. Gommers and T. E. Oliphant, et al., SciPy 1.0: fundamental algorithms for scientific computing in Python, Nat. Methods, 2020, 17(3), 261 CrossRef CAS PubMed.
- M. Short, L. T. Biegler, S. García-Muñoz and W. Chen, Estimating variances and kinetic parameters from spectra across multiple datasets using KIPET, Chemom. Intell. Lab. Syst., 2020, 203, 104012 CrossRef CAS.
- M. Short, C. Schenk and D. Thierry, et al., KIPET – An Open-Source Kinetic Parameter Estimation Toolkit, Comput.-Aided Chem. Eng., 2019, 47, 299 Search PubMed.
- L. D. R. Beal, D. Hill, R. A. Martin and J. D. Hedengren, GEKKO Optimization Suite, Processes, 2018, 6(8), 106 CrossRef.
- A. B. Singer and P. I. Barton, Bounding the Solutions of Parameter Dependent Nonlinear Ordinary Differential Equations, SIAM J. Sci. Comput., 2006, 27(6), 2167 CrossRef.
- COMSOL, COMSOL Multiphysics, COMSOL Search PubMed.
- COMSOL, Chemical Reaction Engineering Module, COMSOL Search PubMed.
- S. C. Burnham, D. P. Searson, M. J. Willis and A. R. Wright, Inference of chemical reaction networks, Chem. Eng. Sci., 2008, 63(4), 862 CrossRef CAS.
- J. Tsu, V. H. G. Díaz and M. J. Willis, Computational approaches to kinetic model selection, Comput. Chem. Eng., 2019, 121, 618 CrossRef CAS.
- E. August and A. Papachristodoulou, Efficient, sparse biological network determination, BMC Syst. Biol., 2009, 3(25), 1752 Search PubMed.
- C. J. Taylor, H. Seki and F. M. Dannheim, et al., An automated computational approach to kinetic model discrimination and parameter estimation, React. Chem. Eng., 2021, 6(8), 1404 RSC.
- M. J. Willis and M. V. Stosch, Inference of chemical reaction networks using mixed integer linear programming, Comput. Chem. Eng., 2016, 90, 31 CrossRef CAS.
- H. Akaike, A new look at the statistical model identification, IEEE Trans. Autom. Control, 1974, 19(6), 716 CrossRef.
- N. N. Narisetty, Chapter 4 - Bayesian model selection for high-dimensional data, in Handbook of Statistics, ed. A. S. R. Srinivasa Rao and C. R. Rao, Elsevier, 2020, p. 207 Search PubMed.
- K. P. Burnham, Model selection and multimodel inference: a practical information-theoretic approach, ed. D. R. Anderson and K. P. Burnham, Springer, New York, 2nd edn, 2002 Search PubMed.
- N. Takebe, A. R. Naqash and G. O'Sullivan Coyne, et al., Safety, Antitumor Activity, and Biomarker Analysis in a Phase I Trial of the Once-daily Wee1 Inhibitor Adavosertib (AZD1775) in Patients with Advanced Solid Tumors, Clin. Cancer Res., 2021, 27(14), 3834 CrossRef CAS PubMed.
- A. A. Mortlock, D. M. Wilson and J. G. Kettle, et al., 5.02 - Selective Kinase Inhibitors in Cancer, in Comprehensive Medicinal Chemistry III, 2017, p. 39 Search PubMed.
- G. Yamamoto, K. Tanaka and R. Kamata, et al., WEE1 confers resistance to KRASG12C inhibitors in non-small cell lung cancer, Cancer Lett., 2025, 611, 217414 CrossRef CAS PubMed.
- G. O. Rodríguez-Vázquez, A. O. Diaz-Quiñones and N. Chorna, et al., Synergistic interactions of cytarabine-adavosertib in leukemic cell lines proliferation and metabolomic endpoints, Biomed. Pharmacother., 2023, 166, 115352 CrossRef PubMed.
- Royal Society of Chemistry, ChemSpider, 2023, [cited 2023 10/03/2023]; Available from: https://www.chemspider.com/ Search PubMed.
- S. Kim, J. Chen and T. Cheng, et al., PubChem 2023 update, Nucleic Acids Res., 2023, 51(D1), D1373 CrossRef PubMed.
- E. R. Strieter, B. Bhayana and S. L. Buchwald, Mechanistic Studies on the Copper-Catalyzed N-Arylation of Amides, J. Am. Chem. Soc., 2009, 131(1), 78 CrossRef CAS PubMed.
- X. Ribas and I. Güell, Cu(I)/Cu(III) catalytic cycle involved in Ullmann-type cross-coupling reactions, Pure Appl. Chem., 2014, 86(3), 345 CAS.
- C. Sambiagio, S. P. Marsden, A. J. Blacker and P. C. McGowan, Copper catalysed Ullmann type chemistry: from mechanistic aspects to modern development, Chem. Soc. Rev., 2014, 43(10), 3525 RSC.
- J. F. Bunnett, Mechanism and reactivity in aromatic nucleophilic substitution reactions, Q. Rev., Chem. Soc., 1958, 12(1), 1 RSC.
- A. J. Kirby and A. G. Varvoglis, The reactivity of phosphate esters: reactions of monoesters with nucleophiles. Nucleophilicity independent of basicity in a bimolecular substitution reaction, J. Chem. Soc. B, 1968, 135 RSC.
- T. Cohen and I. Cristea, Kinetics and mechanism of the copper(I)-induced homogeneous Ullmann coupling of o-bromonitrobenzene, J. Am. Chem. Soc., 1976, 98(3), 748 CrossRef CAS.
- H. K. Oh, M. H. Ku, H. W. Lee and I. Lee, Nucleophilic Substitution Reactions of Aryl Dithioacetates with Pyridines in Acetonitrile, J. Org. Chem., 2002, 67(11), 3874 CrossRef CAS PubMed.
- A. Kundu, M. Inoue and H. Nagae, et al., Direct ortho-C–H Aminoalkylation of 2-Substituted Pyridine Derivatives Catalyzed by Yttrium Complexes with N,N′-Diarylethylenediamido Ligands, J. Am. Chem. Soc., 2018, 140(23), 7332 CrossRef CAS PubMed.
- G. Evano, A. Nitelet, P. Thilmany and D. F. Dewez, Metal-Mediated Halogen Exchange in Aryl and Vinyl Halides: A Review, Front. Chem., 2018, 6, 114 CrossRef PubMed.
- X. Jin and R. P. Davies, Copper-catalysed aromatic-Finkelstein reactions with amine-based ligand systems, Catal. Sci. Technol., 2017, 7(10), 2110 RSC.
- A. Klapars and S. L. Buchwald, Copper-Catalyzed Halogen Exchange in Aryl Halides: An Aromatic Finkelstein Reaction, J. Am. Chem. Soc., 2002, 124(50), 14844 CrossRef CAS PubMed.
- R. D. Pace and Y. Regmi, The Finkelstein Reaction: Quantitative Reaction Kinetics of an SN2 Reaction Using Nonaqueous Conductivity, J. Chem. Educ., 2006, 83(9), 1344 CrossRef CAS.
- D. S. Surry and S. L. Buchwald, Diamine ligands in copper-catalyzed reactions, Chem. Sci., 2010, 1(1), 13 RSC.
- DECHEMA, DETHERM, [accessed 05/10/2022]; Available from: https://detherm.cds.dechema.de/ Search PubMed.
- M. Tao, Z. Wang and J. Gong, et al., Determination of the Solubility, Dissolution Enthalpy, and Entropy of Pioglitazone Hydrochloride (Form II) in Different Pure Solvents, Ind. Eng. Chem. Res., 2013, 52(8), 3036 CrossRef CAS.
- J. Keizer, Diffusion effects on rapid bimolecular chemical reactions, Chem. Rev., 1987, 87(1), 167 CrossRef CAS.
- A. I. Awaji, B. Köksoy and M. Durmuş, et al., Novel Hexadeca-Substituted Metal Free and Zinc(II) Phthalocyanines; Design, Synthesis and Photophysicochemical Properties, Molecules, 2019, 24(1), 77 CrossRef PubMed.
- G. B. Dutt and N. Periasamy, Electron-transfer distance in intermolecular diffusion-limited reactions, J. Chem. Soc., Faraday Trans., 1991, 87(24), 3815 RSC.
- T. R. Waite, General Theory of Bimolecular Reaction Rates in Solids and Liquids, J. Chem. Phys., 1958, 28(1), 103 CrossRef CAS.
- F. C. Collins and G. E. Kimball, Diffusion-controlled reaction rates, J. Colloid Sci., 1949, 4(4), 425 CrossRef CAS.
- R. R. Shaydullin, A. S. Galushko and V. V. Ilyushenkova, et al., Are activation barriers of 50–70 kcal mol−1 accessible for transformations in organic synthesis in solution?, Chem. Sci., 2025, 16(12), 5289 RSC.
- R. J. Ouellette and J. D. Rawn, 3 - Introduction to Organic Reaction Mechanisms, in Organic Chemistry, ed. R. J. Ouellette and J. D. Rawn, Academic Press, 2018, 2nd edn, p. 51 Search PubMed.
- D. M. Espie, The use of nonlinear parameter estimation for dynamic chemical reactor modelling, University of London, 1987 Search PubMed.
- D. J. Pritchard and D. W. Bacon, Statistical assessment of chemical kinetic models, Chem. Eng. Sci., 1975, 30(5), 567 CrossRef CAS.
- K. A. P. McLean and K. B. McAuley, Mathematical modelling of chemical processes—obtaining the best model predictions and parameter estimates using identifiability and estimability procedures, Can. J. Chem. Eng., 2012, 90(2), 351 CrossRef CAS.
- H. T. Banks and M. L. Joyner, AIC under the framework of least squares estimation, Appl. Math. Lett., 2017, 74, 33 CrossRef.
- P. Kletting and G. Glatting, Model selection for time-activity curves: The corrected Akaike information criterion and the F-test, Z. Med. Phys., 2009, 19(3), 200 CrossRef PubMed.
- A. D. Rodman and D. I. Gerogiorgis, Parameter estimation and sensitivity analysis for dynamic modelling and simulation of beer fermentation, Comput. Chem. Eng., 2020, 136, 106665 CrossRef CAS.
- D. W. Pilarski and D. I. Gerogiorgis, Systematic Parameter Estimation And Dynamic Simulation of Cold Contact Fermentation for Alcohol-Free Beer Production, Processes, 2022, 10(11), 2400 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Mazaher M. Chalchooghib,
Robert J. Cox
a,
Mazaher M. Chalchooghib,
Robert J. Cox b and
Dimitrios I. Gerogiorgis
b and
Dimitrios I. Gerogiorgis *a
*a











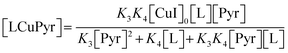
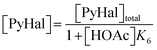



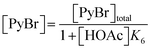
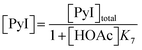
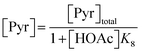

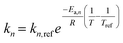
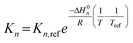








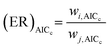

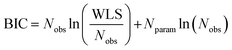

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 273.399 (fixed)
273.399 (fixed)![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif)