Evidence of ferrimagnetism in Fe₃GaTe₂ via neutron diffraction studies

Abstract

The van der Waals material Fe₃GaTe₂ is known to exhibit long-range ferromagnetism above room temperature, making it highly attractive for potential two-dimensional spintronic applications. Using a combination of single crystal X-ray diffraction, powder X-ray diffraction, and neutron diffraction, we report that Fe₃GaTe₂ is best described as a self-intercalated ferrimagnet with interstitial iron sites that stabilize its long-range magnetic order at high temperatures. We find the amount of interstitial sites to vary between 7% and 11%, and its total moment to be approximately 1.6(6)μ_B at 1.5 K by neutron diffraction analysis; the other two iron sites have total moments of 0.7(2)μ_B and 1.65(6)μ_B at base temperature. Group theory analysis reveals that only one magnetic space group is consistent as the maximal isomorphic subgroup of the parent paramagnetic group P6₃/mmc. The resulting magnetic space group of P6₃/mm′c′ leads to a collinear antiferromagnetic arrangement of the interstitial iron sites with respect to those in the telluride layers and with the iron moments all out of plane. Through DFT studies based on the experimental crystal structure, we find that the ferrimagnetic state is favorable over that of the ferromagnetic state by 66 meV. The calculated band structures for the ferromagnetic and ferrimagnetic models show that a significant re-distribution of the electronic density of states occurs near the Fermi level due to the presence of the antiferromagnetically coupled interstitial iron.

---

Introduction

Two-dimensional (2D) or van der Waals (vdW) materials hold great promise for advancing technologies and also uncovering new physical phenomena. However, many common vdW materials are not intrinsically magnetic, so the search for magnetic vdW systems remains of great interest, especially for integration into applications such as spintronics.¹ An interesting challenge is in stabilizing long-range 2D ferromagnetism in vdW layers at room temperature or above. The Mermin–Wagner theorem places hard constraints on 2D magnetism since it rigorously demonstrates that an isotropic Heisenberg system cannot host any long-range magnetic order in one or two dimensions.² To circumvent the Mermin–Wagner limit, researchers have designed magnetic vdW materials by introducing magnetocrystalline anisotropy.^3,4 Another potential way is through the intercalation of magnetic atoms into vdW materials. Here we examine the case of self-intercalation of the vdW material Fe₃GaTe₂ (Fig. 1) and elucidate the role of iron atoms located in the vdW gap in modulating the magnetic structure.

Fig. 1 The structural model of Fe₃GaTe₂ and powder diffraction data with X-rays. The three representations of the crystal show the iron in 3 different coordination geometries: Fe1, Fe2, and Fe3. Both Fe1 and Fe3 are not fully occupied, and Fe3 is considered interstitial. Rietveld refinement of the structure fitted to powder XRD using Cu Kα radiation (λ₁ = 1.540562 Å/λ₂ = 1.544398 Å).

The search for magnetic vdW materials that exhibit high Curie temperatures T_C is largely driven by their potential utilization in device applications. Several interesting candidates include CrGeTe₃³ and Fe₃GeTe₂.^5,6 The T_C in CrGeTe₃ was found to be 67 K, while the large magnetocrystalline anisotropy in Fe₃GeTe₂ raised T_C to anywhere from 140 K to 234 K, depending on its iron stoichiometry.⁷ However, Fe₃GaTe₂ was found to exhibit an even higher T_C compared to its Ge-based analogue with a reported transition temperature between 340 K and 380 K.^8–12 Therefore, Fe₃GaTe₂ stands as a viable candidate to translate the fundamental science of magnetic vdW materials into real applications. For example, Fe₃GaTe₂ has been found to display magnetoresistance^13–15 and facile magnetic switching.^16,17 Furthermore, its vdW nature has made it easy to integrate into heterostructured architectures that can support magnetic tunnel junctions^18–24 and spin valves.^23,25 Finally, Fe₃GaTe₂ has also been reported to exhibit Néel-type skyrmions above room temperature.^26–31

Despite the growing number of studies on thin flakes or exfoliated layers of Fe₃GaTe₂, little attention has been paid to elucidating the crystal and magnetic structures of its bulk crystals. Recently, single crystal X-ray diffraction (XRD) studies were reported,^27,28 yet many crystallographic details remain unclear. Neutron diffraction studies are also conspicuously missing; this important technique not only discerns the crystal structure but also provides detailed insights into the microscopic magnetic order in a material. Neutron diffraction is a powerful tool for distinguishing whether Fe₃GaTe₂ is a simple ferromagnet or a more complex ferrimagnet while also providing the total magnetic moment size per iron site (Table 1).

Table 1 Selected parameters from single crystal X-ray diffraction of Fe₃GaTe₂

Empirical formula	Fe2.97(2)Ga0.93(1)Te2
Space group	P63/mmc
a (Å)	4.0724(3)
c (Å)	16.0928(15)
Crystal system	Hexagonal
Volume (Å^3)	231.13(4)
Calc. density (g cm^−3)	6.981
Radiation	MoKα (λ = 0.71073 Å)
Reflections collected	2096
Independent reflections	162
F(000)	420.0
R1	0.0319
wR2	0.0694
Goodness of fit	1.2
Temperature (K)	250

---

Results and discussion

Structure and composition from X-ray diffraction studies

Nearly isostructural to Fe₃GeTe₂,⁷ the title compound comprises 5-atom thick layers arranged in a hexagonal lattice. Fig. 1 shows the coordination of the two major iron sites: Fe1 and Fe2. The middle layer consists of a hexagonal lattice with Fe1 coordinated in a trigonal bipyramidal fashion to the Ga and Te atoms. This Fe1 layer is, in turn, enveloped by another layer consisting of the Fe2 site. Unlike Fe1, Fe2 is in an octahedral coordination to the Ga and Te atoms.

Notably, Fe₃GaTe₂ departs from its Ge counterpart with the addition of a third Fe site that is located in the vdW gap directly above the Fe2 site by about 2.78 Å (Fig. 1). On average, Fe3 is octahedrally coordinated to the Te anions and is located at the 2a Wyckoff position with a partial occupancy of about 7%. Additionally, the 2d Wyckoff site for Fe1 is slightly vacant by about 10%, which suggests that some of the iron in the Fe1 site migrates to the Fe3 site during crystal growth. Given these vacancies, the final composition is substoichiometric at Fe_2.97(2)Ga_0.93(1)Te₂. Structural parameters such as occupancies and fractional coordinates can be found in Table S2 (ESI†) and the crystallographic information files.

The iron stoichiometry in Fe₃GaTe₂ was also observed by Li et al.,²⁸ where they noted that both the Fe1 and Fe2 sites can be slightly vacant, Fe1 being the preferred site of vacancy formation. They also observed that if less iron metal is used during the self-flux growth, the crystal symmetry shifts to trigonal P3m1, with a sample composition of Fe_2.83GaTe₂. Interestingly, this non-centrosymmetric and polar space group could be the basis of non-collinear antiferromagnetic order that leads to Néel-type skyrmion lattices in Fe₃GaTe₂. In fact, Li et al.²⁸ and Saha et al.²⁷ argue that the space group is P3m1 based on the observation of certain (hhl) reflections for l = 2n + 1, which should be systematically absent in the space group P6₃/mmc. We did not observe those reflections in our single crystal XRD measurements within the resolution and detection of our single crystal diffractometer (Table S6, ESI†). Thus, we conclude that, in our single crystal sample, the interstitial iron is disordered in the vdW gap to retain the centrosymmetric space group although we cannot discard that locally some inversion-symmetry breaking may occur on account of short-range iron ordering.

Neutron diffraction and magnetic structure

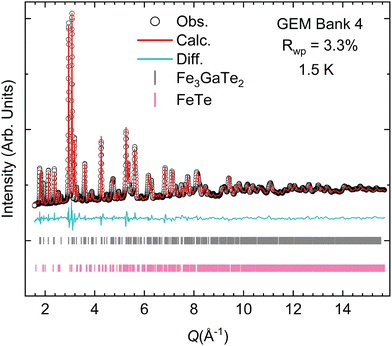
Neutron powder diffraction (NPD) data were collected at the GEM beamline of the ISIS user facility (Rutherford Appleton Laboratory, UK)³² at temperatures varying from 1.5 K to 473 K. The GEM instrument is a time-of-flight neutron diffractometer and provides six sets of detector banks covering a wide range in Q-space, allowing us to further substantiate the evidence of interstitial iron occupancy through Rietveld analysis (Fig. 2). Utilizing all the data banks (Fig. S2–S9, ESI†) during our structural refinements, we find a higher occupancy of the interstitial Fe3 site at nearly 10.5(1)% and a lower occupancy of Fe1 at 87.5(1)%. Clearly, these two sites are correlated. With increasing Fe3, a decrease in Fe1 is observed. Our Rietveld refinement with the NPD data collected at 348 K suggests that the intensities of the (10l) reflections for l = 0, 1, 2, 3, 4 are primarily responsible for determining the occupancy of the interstitial site. Indeed, fixing the occupancy of Fe3 to zero resulted in the model substantially under-fitting the intensity of the abovementioned reflections.

Fig. 2 Neutron powder diffraction (NPD) pattern of Fe₃GaTe₂ at 1.5 K. The Rietveld refinement was performed using the structural model obtained from X-ray diffraction studies, and the magnetic space group was used to fit the magnetic intensity of the low-Q reflections. The NPD was collected at the GEM beamline, which is a time-of-flight diffractometer. The impurity phase was found to be Fe_1+xTe, which was nearly 10 wt%.

We also noted in our refinement analysis that there is a measurable amount of microstrain in our crystal structure solution. This observation indicates that there is some non-uniform distribution of d-spacing, which is not anisotropic but isotropic. Potential sources of this strain could be the partial occupancy of the Fe3 site in the interstitial position. Considering the variation in the occupancy of the Fe3 site in the structural models derived from single-crystal XRD and neutron diffraction results, it is plausible that different Fe occupancies could affect the van der Waals layer distance, which could affect the d-spacing between the nuclear reflections. An interesting comparison would be to compare the microstrain with the sister compound Fe₃GeTe₂.

After obtaining an accurate structural model with the high-temperature NPD patterns, we focused on finding new intensities due to long-range magnetic order in the low-temperature NPD patterns. We interpret the divergence in the magnetic susceptibility as the ferromagnetic transition in our powder sample. Taking the first derivative of the magnetic susceptibility data reveals T_C near 334 K (Fig. S11, ESI†). Powder magnetization data imply a potential T_C between 340 K and 360 K (Fig. S10–S12, ESI†). Therefore, we were able to obtain the structure in both paramagnetic and ferromagnetic states. Comparison of the 348 K and 1.5 K NPD data (Fig. 2 and Fig. S5, ESI†) reveals that no new magnetic peaks were observed. Instead, we observed an increase in the intensity of certain reflections as a function of temperature. The lack of new magnetic reflections means that the magnetic propagation vector is q = (0,0,0), i.e., the chemical and magnetic unit cells are coincident. Furthermore, a q = 0 vector is also consistent with a ferromagnetic order, already suggested by previous magnetic susceptibility and magnetization studies.^9,12,33–36 The impurity phase Fe_1+xTe is itself an antiferromagnet, but it was found in such a low amount that its weak magnetic reflections did not interfere with our fits to the NPD patterns. Incidentally, the long-range ordering temperature in Fe_1+xTe varies from 55 K to 75 K and the nature of the order (collinear vs. non-collinear) depends on the amount of interstitial iron, x, present in that telluride.^37–40

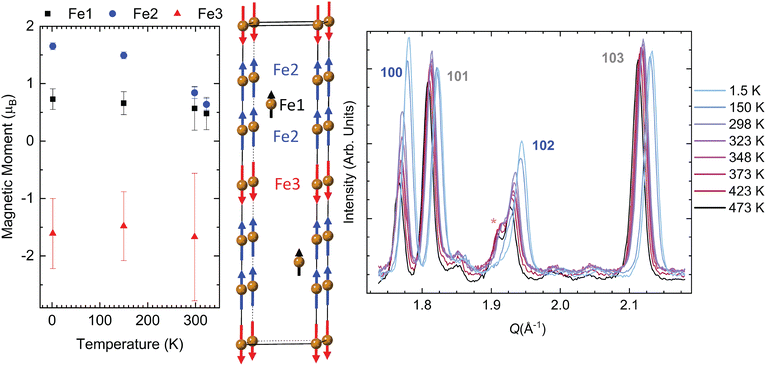
Our Rietveld refinement with the NPD data at 1.5 K demonstrates that the magnetism in Fe₃GaTe₂ is best modeled as a ferrimagnet instead of a ferromagnet. Once the interstitial iron, Fe3, site is included in the structure, then one of the magnetic space groups results in an antiferromagnetic arrangement. Briefly, when one includes the parent paramagnetic space group as P6₃/mmc with a q = 0 propagation vector, then the maximal subgroups include 8 magnetic space groups. When one includes the Wyckoff sites of the 2 magnetically active iron sites, Fe1 and Fe2, then the result narrows down to two possible groups. Finally, if one includes the Wyckoff position of the interstitial iron, Fe3, as being magnetically active, then the solution reduces to only one maximal subgroup of the paramagnetic group P6₃/mmc.

The magnetic space group P6₃/mm′c′ (no. 194.270 in the BNS setting and no. 194.8.1501 in the OG setting) allowed for a stable fit that converged when the moments of Fe1 and Fe2 are parallel to the c-axis, which is the ferromagnetic model assumed in most of the published literature. This structure is also the proposed magnetic space group of the Ge-analogue.⁷ However, this magnetic space group results in Fe3 being antiparallel to both Fe1 and Fe2. Fig. 3 illustrates this ferrimagnetic arrangement. The key reflections for evaluating the effects of long-range magnetic order are the (100) and (102) reflections; these exhibit the greatest rise in intensity below 348 K.

Fig. 3 The proposed magnetic order in Fe₃GaTe₂ from neutron diffraction analysis. (left) Evolution of the total magnetic moment size for all three iron sites, including the interstitial iron Fe3. The magnetic structure resulting from the space group P6₃/mm′c′ showing how Fe3 is anti-aligned within the vdW gaps. (right) Select Q-range of the temperature-dependent NPD data set (GEM Bank 4, ISIS) showing the key reflections that have the largest magnetic contribution. The asterisk marks the impurity Fe_1xTe.

Fig. 3 also displays these magnetic reflections along with other nuclear reflections (101) and (103). As one can see, the intensities vary little for nuclear reflections, with only a slight shift in intensity due to 1.5 K and 150 K measurements occurring in a different sample environment at the GEM instrument (note that there is slightly less background at low temperatures as well due to this change in the sample environment). From the Q-axis, we see that the nuclear reflection generally shifts to a higher Q value as the temperature decreases. This change indicates that the lattice parameters are contracting as a function of temperature, and the large shift in the reflections is due to large changes in lattice parameters below 300 K. Detailed plots on the relationship between the lattice parameters and temperature can be found in Fig. S10 (ESI†).

The (110) reflection also exhibits an increase in intensity at lower temperatures, and this can be seen in comparison to the neighboring reflection (106), whose intensity does not change appreciably with temperature. Interestingly, eliminating the magnetic moments on the Fe3 sites results in a poorer fit since it causes a decrease in intensity for the (102) reflection and an overfit of the (100) reflection. Forcing Fe3 to be ferromagnetic by discarding symmetry constraints placed by P6₃/mm′c′ does not result in an optimal intensity for the (102) or (100) reflection. In short, not only does the interstitial iron lead to real differences in the nuclear peak intensities, but its magnetic moment also contributes to the key reflections that have significant magnetic structure factors in the NPD patterns.

Table 2 lists the values of the total magnetic moment for each Fe site at 1.5 K. The evolution of the moment size for the temperatures of 1.5 K, 150 K, 298 K, and 323 K is consistent with a larger moment at base temperature (Table S7, ESI†). The weighted residual from the Rietveld refinement is also listed in Table S7 (ESI†) to show that more reliable parameters are derived from the low-temperature measurements. The higher residual for 298 K and 323 K likely arises from the furnace sample environment utilized in that temperature range, leading to poorer diffraction statistics. All the moments obtained from NPD exhibit a clear downward trend with the increase of temperature (Fig. 3), except for Fe3 at 323 K, for which the moment suddenly increases to almost 3μ_B. However, this value has a high uncertainty of ±1.4μ_B. In general, the larger error bars for the Fe3 moment likely stem from the low occupancy of this interstitial site. If we compare our base temperature NPD results with those of Fe₃GeTe₂, the moments are lower in Fe₃GaTe₂. However, they are more similar to the Ge-analogue with low iron content.⁷

Table 2 Comparison of the moment size for different magnetic orders from DFT calculations and neutron diffraction results. The models include ferromagnetic (FM) Fe₃GeTe₂ (FGT), ferromagnetic Fe₃GaTe₂ (FGaT) with only 2 sites and ferrimagnetic (FiM) with the interstitial site added (3-site). The experimental values from neutron diffraction are included for comparison

Material	FGT	FGaT	FGaT	FGaT
Model	DFT	2-sites (DFT)	3-sites (DFT)	(Exp.)
Magnetic state	FM	FM	FiM	FiM
Magnetic moment (μB)
−Fe1 (Avg.)	1.54	1.54	1.68	0.73 (18)
−Fe2 (Avg.)	2.39	2.35	2.32	1.65 (6)
−Fe3 (Avg.)	—	—	−2.82	−1.6 (6)
Total magnetization (μB per cell)	12.53	12.11	11.18	—
Absolute magnetization (μB per cell)	14.10	13.99	14.30	—

---

We now compare our results from NPD with those of magnetization studies with respect to the total magnetic moment size per iron atom. Our M vs. H isotherms shown in Fig. S13 (ESI†) were measured from room temperature up to 380 K. Although it is difficult to obtain a saturation magnetization due to the powder-like nature of our sample, we estimate a moment size of 0.61μ_B from the 300 K isotherm. This value compares well with that from our NPD analysis, which was found to be 0.8(1)μ_B at 300 K. The moment sizes for the rest of the NPD temperature scans can be found in Table S7 (ESI†). We compare our base temperature NPD analysis (1.5 K) results with the values reported in the literature. The work by Zhang et al.³³ investigated Fe₃GaTe₂ single crystals, and the most useful value for our purposes is the out-of-plane saturation moment. If we consider the total magnetic moment for Fe2 from the NPD data, which represents the majority of the active magnetic atoms, the value at 1.5 K is close to 1.65(6)μ_B per Fe. This value agrees remarkably well with the saturation magnetic moment of 1.68μ_B per Fe observed by Zhang et al. Therefore, our NPD results should be useful for future magnetization studies of Fe₃GaTe₂, given their agreement with our work and past studies.

First-principles calculations and model comparison

To gain further insights on the role of the third Fe site on the magnetic properties, we performed first-principles calculations using density functional theory (DFT). Based on experimental crystallographic data, Fe1 and Fe2 spins are co-aligned, while Fe3, located at the interstitial position, has an inverted spin. To simulate this, we used DFT to investigate two different magnetic configurations: the ferromagnetic (FM) state, where all Fe spins are aligned, and the ferrimagnetic (FiM) state based on the experimental data. The results in Table 2 show that the FiM state is more favorable than the FM state, with a total energy that is 66 meV lower than that of the FM state, validating the experimental data obtained from neutron diffraction. Fe2 exhibits a larger average magnetic moment than Fe1 in all three modeled structures, which also matches the experimental results. In interstitial Fe₃GaTe₂, the interstitial atom Fe3 has a larger absolute average magnetic moment than Fe1, which aligns with the trends observed in experimental data.

While DFT may overestimate the magnetic moment of Fe atoms due to over-localization of the Fe 3d electrons, it can accurately capture trends in magnetic moment changes and directions. DFT methods provide the ground-state magnetic moments of Fe atoms based on an idealized structural configuration in vacuum at 0 K. Discrepancies in the magnetic moment between DFT and experimental neutron diffraction results can arise from temperature effects under experimental conditions and localized defects, as well as from the choice of DFT functionals. While the DFT-idealized moments are below the spin-only theoretical maximum for high-spin Fe (4.9μ_B for Fe²⁺ and 4.9μ_B for Fe³⁺), the observed site-dependent variation is consistent with the intermetallic nature of the compounds, and it reflects the influence of the local electronic structure rather than a well-defined formal oxidation state.

Based on the comparison of the projected density of states (PDOS) in Fig. 4, the primary difference is observed in the behavior of the Fe3 3d orbitals (dark blue curve in Fig. 4b). In the case of Fe3, these 3d orbitals appear at higher energies compared to their counterparts in Fe1 and Fe2. Once the interstitial sites are introduced, the Fe3 site interacts with the Te 5p orbitals from adjacent layers, which significantly alters the electronic structure. This interaction results in the formation of both new bonding states (near the Fermi level) and anti-bonding states (above the Fermi level). Consequently, the 3d orbitals of Fe3 experience both broadening and a shift in their energy levels when compared to Fe1 and Fe2. The higher absolute magnetic moment of Fe3 is likely due to its distinct coordination environment. Specifically, the hybridization between Fe3 3d orbitals and the relatively weak-field Te 5p orbitals in the interstitial position fosters a high-spin configuration. This increased spin state contributes to a larger magnetic moment for Fe3, distinguishing it from Fe1 and Fe2, where the spin state is more constrained by their respective coordination environment (Fig. 1). Thus, the differences in magnetic moments between Fe sites are not solely due to magnetic ordering but also reflect variations in 3d orbital energy, hybridization, and local electron density-features strongly tied to the distinct coordination of each site.

Fig. 4 The band structure and projected density of states (a) of ideal Fe₃GaTe₂ (FGaT) and (b) Fe₃GaTe₂ (FGaT) with 12.5% interstitial iron occupancy. The orange dashed line on the left-hand side of each plot represents the Fermi level at 0 eV.

Conclusions

We have performed X-ray and neutron diffraction studies on Fe₃GaTe₂ and propose that the existence of an interstitial Fe site within the van der Waals gap turns this compound into a ferrimagnet with a T_C between 323 K and 348 K. The NPD diffraction patterns of Fe₃GaTe₂ coupled with the symmetry constraints of the magnetic space group P6₃/mmc lead to only certain reflections such as the (102) to be properly fit with an oppositely aligned magnetic moment for the interstitial Fe sites. DFT calculations are in agreement with the experimental results and further reveal that mixing between the Fe3 3d-orbitals and Te 5p-orbitals gives rise to a high-spin state for the interstitial iron site. Since the amount of interstitial iron seems to be correlated to the occupation of the Fe1 site, then it is likely that the greater self-intercalation of Fe₃GaTe₂ over its Ge-analogue also causes the stabilization of its ferrimagnetic order at higher temperatures. These insights from neutron diffraction and DFT studies could be the basis of manipulating the composition of Fe₃GaTe₂ to enhance some of its properties including its transition temperature and its magnetic symmetry within the context of spintronic applications.

Experimental

Single crystals of Fe₃GaTe₂ were grown by the flux method. Fe (Alfa Aesar, 99.5%), Ga (Thermo Fisher, 99.99%), and Te (Sigma-Aldrich, 99.8%) were mixed in a 1 : 1 : 2 ratio in a glove box and placed in a quartz ampoule. The ampoule was heated to 1000 °C over 3 hours. Afterwards, it was dwelled at 1000 °C for 24 hours. Next, the sample was quenched to 880 °C within 1 hour, followed by slow cooling to 780 °C at a rate of 1 °C h⁻¹. Then, the sample was quenched to room temperature. A large molten, metallic rock-like substance was extracted from the ampoule. This metallic rock was observed to be magnetic under ambient conditions, which is an indication that FGaT has grown within the rock sample. However, it was mixed with the rest of the flux, which mostly comprised Ga₂Te₃. To isolate Fe₃GaTe₂ from the self-flux rock, a razor blade was carefully applied to scrape some flakes on the more metallic flat surfaces on the rock. These flakes were collected and used for SCXRD.

Powder Fe₃GaTe₂ was synthesized as follows: GaTe was synthesized in an ampoule prepared in an Ar-filled glovebox at 900 °C for 3 days. The ampoule contained one part Ga (Thermo Fisher, 99.99%) and one part Te (Sigma-Aldrich, 99.8%) with the addition of an additional 0.1–0.3% Ga to ensure the production of GaTe instead of Ga₂Te₃ based on the binary phase diagram. Afterwards, inside an Ar filled glovebox, one part of GaTe, one part Te (Sigma-Aldrich, 99.8%) and three parts of Fe (Alfa Aesar, 99.5%) were mixed using a mortar and pestle and placed in an ampoule. The reaction mixture was heated to 700 °C within 1–2 hours and held at that temperature for 6 days. The ampoule was then allowed to naturally cool in the furnace before extraction.

Single crystal XRD results revealed that the best fit consists of a structure with the centrosymmetric space group P6₃/mmc (no. 194). However, our best model includes three Fe sites instead of just two. The third site, which we label Fe3 throughout this manuscript, arises from the interstitial amounts of iron present in the vdW gaps (Fig. 1 and Fig. S1, ESI†). Second, the chemical composition is slightly substoichiometric at Fe_2.97(2)Ga_0.93(1)Te₂ (Tables S1–S6, ESI†). Our single crystal model was then successfully used to fit the powder X-ray and neutron diffraction patterns via the Rietveld method (Fig. 1). The structural models found through both measurements were highly consistent; the powder XRD revealed, however, that the common impurity in the samples was tetragonal Fe_1+xTe, which was typically around 7 wt% for the polycrystalline sample. More detailed information regarding the Rietveld refinement procedure can be found in the ESI.†

First-principles calculations were performed using the open-source software package QUANTUM ESPRESSO,⁴¹ based on periodic plane-wave density functional theory (DFT).^42,43 The Perdew–Burke–Ernzerhof (PBE)⁴⁴ generalized gradient approximation (GGA) was adopted, along with the van der Waals (vdW) interaction correction in Grimme's DFT-D2 method⁴⁵ (with the global scaling factor S₆ = 0.5) for all calculations. GBRV⁴⁶ ultrasoft pseudopotentials were used to describe all atoms, with a plane-wave basis cutoff of 40 Ry for the primitive bulk structures. Lattice optimization calculations were performed using a 6 × 6 × 6 Monkhorst–Pack k-point grid.¹⁴ All self-consistent calculations were carried out with a convergence criterion of 1 × 10⁻⁷ eV and a force tolerance of 1–5 meV per Å per atom. The optimized lattices were then used for band structure and projected density of states (PDOS) calculations, employing a 10 × 10 × 10 Monkhorst–Pack k-point grid.⁴⁷

Author contributions

ML and EER conceived and planned the research presented in this publication. ML and AJ prepared the polycrystalline and single crystals. PY and JWB performed the first-principles calculations. PYZ solved the single crystal structure from X-ray diffraction. IdS performed the neutron scattering measurements. ZW and SR performed the magnetic susceptibility and magnetization studies.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for Fe₃GaTe₂ have been deposited at the Cambridge Structural Database under 2440606. Crystallographic information files are available for download. Neutron diffraction data from GEM (ISIS, UK) are available at https://doi.org/10.5286/ISIS.E/ISIS.E.RB2410408.

Acknowledgements

The authors wish to acknowledge the support from DTRA through grant number HDTRA12410015. All calculations were performed using the UMBC High Performance Computing Facility (HPCF), supported by the National Science Foundation through the MRI grants CNS-0821258, CNS-1228778, and OAC-1726023 and the SCREMS grant DMS-0821311. This work was supported in part by the X-ray Crystallographic Center at The University of Maryland. Experiments at the ISIS Neutron and Muon Source were supported through beamtime allocation RB2410408 from the Science and Technology Facilities Council.

References

1. M. Mi, H. Xiao, L. Yu, Y. Zhang, Y. Wang, Q. Cao and Y. Wang, Mater. Today Nano, 2023, 24, 100408.
2. N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133.
3. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269.
4. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273.
5. H. Deiseroth, K. Aleksandrov, C. Reiner, L. Kienle and R. K. Kremer, Eur. J. Inorg. Chem., 2006, 1561–1567.
6. V. Y. Verchenko, A. A. Tsirlin, A. V. Sobolev, I. A. Presniakov and A. V. Shevelkov, Inorg. Chem., 2015, 54, 8598–8607.
7. A. F. May, S. Calder, C. Cantoni, H. Cao and M. A. McGuire, Phys. Rev. B, 2016, 93, 014411.
8. M. Yang, Q. Li, R. V. Chopdekar, C. Stan, S. Cabrini, J. W. Choi, S. Wang, T. Wang, N. Gao, A. Scholl, N. Tamura, C. Hwang, F. Wang, Z. Qiu, M. Yang, Q. Li, S. Wang, T. Wang, N. Gao, F. Wang, Z. Qiu, R. V. Chopdekar, C. Stan, S. Cabrini, A. Scholl, N. Tamura, J. W. Choi and C. Hwang, Adv. Quantum Technol., 2020, 3, 2000017.
9. H. Algaidi, C. Zhang, Y. Ma, C. Liu, A. Chen, D. Zheng and X. Zhang, APL Mater., 2024, 12, 11124.
10. A. M. Ruiz, D. L. Esteras, D. López-Alcalá and J. J. Baldoví, Nano Lett., 2024, 24(26), 7886–7894.
11. M. Wang, B. Lei, K. Zhu, Y. Deng, M. Tian, Z. Xiang, T. Wu and X. Chen, npj 2D Mater. Appl., 2024, 8, 1–7.
12. G. Zhang, J. Yu, H. Wu, L. Yang, W. Jin, W. Zhang and H. Chang, Appl. Phys. Lett., 2023, 123, 101901.
13. G. Hu, H. Guo, S. Lv, L. Li, Y. Wang, Y. Han, L. Pan, Y. Xie, W. Yu, K. Zhu, Q. Qi, G. Xian, S. Zhu, J. Shi, L. Bao, X. Lin, W. Zhou, H. Yang and H. Jun Gao, Adv. Mater., 2024, 36, 2403154.
14. Y. Deng, M. Wang, Z. Xiang, K. Zhu, T. Hu, L. Lu, Y. Wang, Y. Ma, B. Lei and X. Chen, Nano Lett., 2024, 24, 9302–9310.
15. Z. C. Pan, D. Li, X. G. Ye, Z. Chen, Z. H. Chen, A. Q. Wang, M. Tian, G. Yao, K. Liu and Z. M. Liao, Sci. Bull., 2023, 68, 2743–2749.
16. S. Yan, S. Tian, Y. Fu, F. Meng, Z. Li, H. Lei, S. Wang and X. Zhang, Small, 2024, 20, 2311430.
17. S. N. Kajale, T. Nguyen, C. A. Chao, D. C. Bono, A. Boonkird, M. Li and D. Sarkar, Nat. Commun., 2024, 15, 1–8.
18. W. Jin, X. Li, G. Zhang, H. Wu, X. Wen, L. Yang, J. Yu, B. Xiao, F. Guo, W. Zhang, J. Zhang, H. Chang, W. Jin, G. Zhang, H. Wu, X. Wen, L. Yang, J. Yu, B. Xiao, W. Zhang, H. Chang, X. Li, J. Zhang and F. Guo, Adv. Funct. Mater., 2024, 34, 2402091.
19. H. Pan, A. K. Singh, C. Zhang, X. Hu, J. Shi, L. An, N. Wang, R. Duan, Z. Liu, S. S. Parkin, P. Deb and W. Gao, InfoMat, 2024, 6, e12504.
20. L. Zhang, M. He, X. Wang, H. Zhang, K. Han, Y. Liu, L. Zhang, Y. Cheng, J. Pan, Z. Qu and Z. Wang, J. Phys. D: Appl. Phys., 2025, 58, 105005.
21. H. Wu, L. Yang, G. Zhang, W. Jin, B. Xiao, J. Yu, A. Annas, W. Zhang, K. Wang and H. Chang, Small Methods, 2025, 2401117.
22. Y. Zhang, X. Li, J. Sheng, S. Yu, J. Zhang and Y. Su, Appl. Phys. Lett., 2023, 123, 192402.
23. W. Jin, G. Zhang, H. Wu, L. Yang, W. Zhang and H. Chang, ACS Appl. Mater. Interfaces, 2023, 15, 36519–36526.
24. W. Zhu, S. Xie, H. Lin, G. Zhang, H. Wu, T. Hu, Z. Wang, X. Zhang, J. Xu, Y. Wang, Y. Zheng, F. Yan, J. Zhang, L. Zhao, A. Patané, J. Zhang, H. Chang and K. Wang, Chin. Phys. Lett., 2022, 39, 128501.
25. H. Yin, P. Zhang, W. Jin, B. Di, H. Wu, G. Zhang, W. Zhang and H. Chang, CrystEngComm, 2023, 25, 1339–1346.
26. C. Liu, S. Zhang, H. Hao, H. Algaidi, Y. Ma and X. X. Zhang, Adv. Mater., 2024, 36, 2311022.
27. R. Saha, H. L. Meyerheim, B. Göbel, I. Mertig and S. S. P. Parkin, npj Spintronics, 2024, 2, 1–7.
28. Z. Li, H. Zhang, G. Li, J. Guo, Q. Wang, Y. Deng, Y. Hu, X. Hu, C. Liu, M. Qin, X. Shen, R. Yu, X. Gao, Z. Liao, J. Liu, Z. Hou, Y. Zhu and X. Fu, Nat. Commun., 2024, 15, 1–11.
29. S. Mi, J. Guo, G. Hu, G. Wang, S. Li, Z. Gong, S. Jin, R. Xu, F. Pang, W. Ji, W. Yu, X. Wang, X. Wang, H. Yang and Z. Cheng, Nano Lett., 2024, 24, 13094–13102.
30. H. Shi, J. Zhang, Y. Xi, H. Li, J. Chen, I. Ahmed, Z. Ma, N. Cheng, X. Zhou, H. Jin, X. Zhou, J. Liu, Y. Sun, J. Wang, J. Li, T. Yu, W. Hao, S. Zhang and Y. Du, Nano Lett., 2024, 22, 39.
31. J. Ryu, S. N. Kajale and D. Sarkar, MRS Commun., 2024, 14, 1113–1126.
32. A. C. Hannon, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 551, 88–107.
33. G. Zhang, F. Guo, H. Wu, X. Wen, L. Yang, W. Jin, W. Zhang and H. Chang, Nat. Commun., 2022, 13, 1–8.
34. J. E. Lee, S. Yan, S. Oh, J. Hwang, J. D. Denlinger, C. Hwang, H. Lei, S. K. Mo, S. Y. Park and H. Ryu, Nano Lett., 2023, 23, 11526–11532.
35. H.-B. Ahn, H. Lim, J. Song, J. Lee, S.-Y. Park, M. Joe, C.-J. Kang, K.-W. Kim, T.-E. Park, T. Park and C. Lee, Nanoscale, 2024, 16, 20252–20259.
36. J. Lee, J. Yun, Y. Lee, B. T. Kang, J. S. Kim, N. Haberkorn and J. Kim, J. Appl. Phys., 2024, 136, 123905.
37. E. E. Rodriguez, C. Stock, P. Y. Hsieh, N. P. Butch, J. Paglione and M. A. Green, Chem. Sci., 2011, 2, 1782–1787.
38. E. E. Rodriguez, C. Stock, P. Zajdel, K. L. Krycka, C. F. Majkrzak, P. Zavalij and M. A. Green, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 064403.
39. E. E. Rodriguez, D. A. Sokolov, C. Stock, M. A. Green, O. Sobolev, J. A. Rodriguez-Rivera, H. Cao and A. Daoud-Aladine, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 165110.
40. C. Stock, E. E. Rodriguez, M. A. Green, P. Zavalij and J. A. Rodriguez-Rivera, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045124.
41. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. D. Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
42. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
43. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
45. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
46. K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452.
47. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2440606. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5tc01719j

---