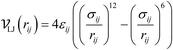Computational investigation of the impact of metal–organic framework topology on hydrogen storage capacity

Abstract

Metal–organic frameworks (MOFs) are promising, tunable materials for hydrogen storage. For application under cryogenic operating conditions, past work has run into a ceiling on performance due to a trade-off in the volumetric deliverable capacity (VDC) versus the gravimetric deliverable capacity (GDC). In this study, we computationally constructed and screened 105 230 MOF structures based on 529 nets to explore the effect of underlying topology on the hydrogen storage performance of the resulting materials. A machine learning model was developed based on simulated hydrogen uptake to facilitate screening of the entire dataset, and it successfully identified the top 10% of materials with a root-mean-square error of approximately 1 g L⁻¹ as validated by subsequent grand canonical Monte Carlo simulations. We identified a promising structure based on the tsx topology that exhibits both VDC and GDC higher than the current benchmark material, MOF-5. Our data-driven analysis indicates that nets with higher net density yield MOFs with enhanced volumetric and gravimetric surface areas, thereby improving maximum VDC while shifting the capacity trade-off toward higher GDC.

---

Design, System, Application

Hydrogen is projected to play an important role in decarbonization efforts, but storing hydrogen is challenging due to its low volumetric density. In recent years, molecular simulation has played an important role in screening nanoporous metal–organic frameworks (MOFs) for hydrogen storage, and simulations have helped uncover how the storage performance depends on material “textural” properties such as the surface area, pore size, and void fraction. MOFs can be tailored by the selection of their constituent metal nodes and organic linkers, which control the textural properties and surface chemistry but also the topology or net of the framework. In this work, we investigated the effect of MOF topology on cryogenic hydrogen storage by creating 105 230 MOF structures based on 529 nets on the computer and modeling their hydrogen uptake and release. We identified topological descriptors that correlate with high hydrogen capacities and showed that nets with higher interconnectivity lead to some of the best performing MOFs with enhanced volumetric and gravimetric surface areas at the optimal pore volume. The findings provide new directions for topology-based MOF design for storage of hydrogen and other gases.

1. Introduction

As efforts towards decarbonization and a more sustainable energy economy accelerate, hydrogen has emerged as a pivotal energy carrier, boasting the highest energy density per unit mass among all fuels and water vapor as its only combustion product. However, its extremely low volumetric density poses a significant challenge in developing efficient, reliable, and cost-effective hydrogen storage technologies. Existing hydrogen storage methods struggle to simultaneously meet safety, durability, and capacity requirements.¹

Sorption-based storage, particularly using metal–organic frameworks (MOFs),^2,3 is an attractive option that enables storage under milder conditions (i.e., lower pressure) compared to compressed gas tanks, which allows the use of a less expensive type I metal tank.⁴ The development of new adsorbent materials for hydrogen storage is a key component of the comprehensive strategy of the U.S. Department of Energy's (DOE) Energy Efficiency and Renewable Energy (EERE) office.⁵ MOFs have demonstrated promising results for hydrogen storage under both ambient temperature and cryogenic conditions.^2,6–8 Under the operating conditions set by EERE for cryogenic hydrogen storage (filling at 77 K/100 bar and discharge at 160 K/5 bar), MOF-5 (ref. 9) exhibits the highest volumetric deliverable capacity at 51.9 g L⁻¹ to date and a gravimetric deliverable capacity of 7.8 wt%.¹⁰ To achieve the system-level goal of 50 g L⁻¹ deliverable capacity, further material-level enhancements are necessary to compensate for losses in packing and to accommodate other system components. However, it has proven challenging to make further improvements in volumetric deliverable capacity (VDC) as demonstrated by previous computational studies.^10–12 Ahmed and Siegel recently screened nearly a million MOFs¹³ computationally and identified 95 materials (∼0.01% of the MOFs screened) with VDC surpassing that of MOF-5. One of the better-performing MOFs is a MOF-5 variant where the linker is functionalized with fluorine, resulting in an approximately 5% enhancement over MOF-5. Previous screening studies have provided guidelines on optimal textural properties,^4,11,12 such as pore volume and surface area, which provide indirect design parameters in the search for better performing MOFs.

MOFs can be designed by judiciously selecting organic building blocks (linkers) and metal clusters based on a targeted underlying periodic net (a crystal net),^14,15 also referred to as the topology of the MOF.¹⁶ While recent studies have focused on several design pathways such as isoreticular expansion¹⁷ and metal substitution, the role of topology has been underexplored.^18,19 Computational screening studies^20–26 have generally focused on a handful of topologies and did not emphasize the effect of topology. Thus, its relationship to the textural properties as well as gas storage performance remains unclear. Colón and coworkers showed that the relationship between volumetric and gravimetric capacity varies among different topologies considered in the ToBaCCo MOF database.²⁷ Their ToBaCCo database considers 41 different edge-transitive nets. Edge-transitive nets, under the Principle of Minimal Transitivity,^15,28 are considered as the “default” nets and regarded as the most easily targetable subset of topologies, although there are exceptions. There are a number of non-edge-transitive nets that serve as reliable, non-default topology platforms for isoreticular expansion and MOF synthesis,^28–30 with the qom net (MOF-177 family)^31–33 being the most studied example without considering supermolecular building blocks.

Following previous studies,^27,34,35 we reasoned that a deeper understanding of the effect of topologies on the textural properties and gas adsorption would aid in the design of MOFs with improved hydrogen storage performance and in addressing the observed tradeoff to date between volumetric and gravimetric capacity.³⁶ Currently, there are over 3000 3-periodic crystal nets in the Reticular Chemistry Structure Resource (RCSR) database,³⁷ but there are a very limited number of edge-transitive nets given a particular set of common MOF building blocks.²⁹ For example, there is only one type of edge-transitive net when combining a square node and a hexagonal node, the 4,6-c she net. To include a reasonable number of nets, we extend our investigation beyond the edge-transitive nets and focus on non-derived nets (basic nets)²⁸ that are geometrically compatible with common organic nodes and metal clusters,²⁷ by including nets where all edges connect the same kind of vertices. This approach allows us to consider slightly over 500 nets from the RCSR database,³⁷ resulting in 105 230 predicted MOF structures.

To elucidate the relationship between topology and H₂ storage capacity, we predict the hydrogen capacity landscape of all 105 230 MOFs as outlined in Fig. 1b. To reduce computational cost, we develop a machine learning model to predict the deliverable capacity, achieving state-of-the-art accuracy with a root mean square error of 1.2 g L⁻¹. The machine learning model reliably identifies the top performing candidates as validated by subsequent grand canonical Monte Carlo (GCMC) simulations. Furthermore, we study one of the top structures in detail, which exhibits higher simulated volumetric (+1.5%) and gravimetric capacities (+47%) compared to MOF-5.

Fig. 1 Workflow of the study: (a) dataset construction, (b) hydrogen capacity prediction leveraging ML techniques based on energy grid descriptors and validation of model performance of the top performing candidates, (c) data analysis probing into the effect of underlying topology on structural properties and gas adsorption performance. Dashed lines suggest relationships that are understudied.

With this large dataset, we analyze the relationship between the underlying topology and the volumetric deliverable capacity, using multivariate analysis, dimensionality reduction, and data visualization (Fig. 1c). The connectivity and coordination of crystal nets are described by a set of numerical features, such as the coordination number of vertices, net density, td10, and genus.³⁷ We examine whether the current topological descriptors are sufficient for correlating with the gas adsorption performance of the resulting materials. Finally, we also identify promising topology platforms that have been less studied in the MOF literature and discuss the mathematical nature of these nets.

2. Methodology

Building block selection and construction

We considered a total of 14 organic node building blocks, 12 metal cluster building blocks, and 61 edge building blocks as the building block pool in this study. Details are provided in ESI† section 1 including a list of the building blocks and their abbreviated names (e.g. mc9 for metal cluster #9). We included the most common linker fragments from the CoRE MOF 2019 database³⁸ by decomposing the structures with the MOFid algorithm.³⁹ For metal cluster building blocks, we used the building blocks from the ToBaCCo database,²⁷ with an additional beryllium metal cluster based on Be-MOF-5 that has been reported experimentally.⁴⁰ Note that due to the toxicity of beryllium,⁴¹ we excluded the Be-MOFs from the top candidate pool, but they were considered in all other data analysis.

To construct the organic node and edge building blocks, an in-house code “linkergen” was used, which uses Open Babel⁴² to convert the SMILES⁴³ string into a 3d structure in a format readable by the ToBaCCo algorithm.³⁴ Specifically we used the unique SMILES^44,45 to handle isomerism. After creating the building blocks, manual checks and edits were performed to ensure that the geometry and chiral configuration correctly matched the chemical diagrams.

Generation of the topology files

Topologies and their corresponding information were taken from the RCSR database as of February 2020 (ref. 37) in Systre⁴⁶ input data (.cgd) format. Only 3-periodic nets¹⁴ were considered.

Selection of topologies

The edges and vertices of a periodic net are distinguished by their symmetry,^47,48 and nets with only one kind of edge are referred as edge-transitive nets. Here, we consider the equivalence of edges based on the connection of the same pair of vertices and coin the concept of “chemical” kind of edge in contrast to the usual symmetry equivalence for the net inclusion. Only nets with one or two kinds of vertex can meet this criterion. Among 2697 nets available in the RCSR database as of February 2020, a total of 474 single-vertex nets and 60 multi-vertex nets are compatible with the building block pool. However, after structural checks, relaxation with a classical force field, and cleaning, we noticed that the assembled structures from 9 single-vertex nets all had structural issues such as having unexpected number of assigned bonds, and they were discarded, resulting in only 469 of 474 single-vertex nets being included in the final dataset, which is available on the Zenodo repository.⁴⁹ We also note that there are no MOFs based on the metal cluster mc9 (10-c Zr node) and mc11 (24-c supermolecular building block from 12 Cu₂-paddlewheels); this is due to a limitation of the bonding algorithm used.

Structural assembly

We used a slightly modified version of the ToBaCCo 3.0 algorithm³⁴ based on its January 2020 version. During the assembly, no structures were generated for the 10-c Zr node (mc9) and a 24-c Cu-based supermolecular building block (mc11) included in the building block pool. For the 10-c Zr node, the algorithm encountered a runtime error related to edge placement when assembling structures based on compatible nets such as bct. For the 24-c node, the algorithm could not find the correct orientation for the metal node due to the high coordination. As discussed in prior works,^25,27 a key step in structural assembly is to identify the orientation of the metal node by aligning the vectors from its connection points (carbon atoms) to the centroid of the connection points with the vectors formed by the topological vertex-edge connections.

Structural optimization

We optimized all structures by geometric relaxation using LAMMPS⁵⁰ with the classical UFF4MOF⁵¹ force field as described by Anderson and coworkers³⁴ with slight modification of the optimization algorithm. Specifically, we used conjugated gradient (CG) as the minimizer throughout the minimization instead of using both the CG and FIRE algorithms.⁵² We started overall relaxation by relaxing only the atom positions, followed by a series of cycles, each consisting of two minimizations: first, relaxation of atomic positions and all cell parameters with a maximal fractional volume change of 0.001 per iteration (v_max = 0.001), then, a minimization of only atom positions in the fixed cell. We considered the system to be converged when the relative energy difference between these two steps was within 10⁻⁶. For each minimization process (referred to as a “minimizer” in LAMMPS⁵³), both the energy tolerance and force tolerance were 10⁻⁶, in relative unit for energy and (kcal mol⁻¹)/angstrom for force, and the maximum iteration was set to 1 000 000. We removed the structures that contained overlapping atoms after the geometry optimization and prepared a total of 105 230 optimized structures for the dataset, with 105 206 structures available with calculated textural properties.

For benchmark and validation purposes, we optimized a few selected top candidate structures using two different methods: extended tight-binding (xTB)⁵⁴ and density functional theory (DFT). The geometric optimization with the xTB methods (GFN1-xTB⁵⁴ followed by GFN2-xTB⁵⁵) was carried out using the DFTB+ software⁵⁶ with the rational function based optimizer and a convergence threshold of 10⁻⁴ hartree per bohr maximum absolute gradient in one geometry step. Density functional theory (DFT) calculations were performed using the Vienna Ab Initio Simulation Package (VASP) (version: 5.4.4)⁵⁷ with spin-polarization considered. The initial spin states for all atoms were determined by the program's default settings, which assign an initial magnetic moment of 1.0 for each atom. The projector augmented wave (PAW) pseudopotentials⁵⁸ and Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional⁵⁹ were employed (version: 5.4, files dated: H: “15Jun2001”, C: “08Apr2002”, O: “08Apr2002”, Cu: “05Jan2001”, Cr: “06Sep2000”). A plane-wave energy cutoff of 500 eV was used, and convergence criteria for force and energy were set to 0.01 eV Å⁻¹ and 10⁻⁵ eV, respectively. A gamma-centered k-point grid was applied for Brillouin zone sampling, ensuring that the product of the cell parameter and the number of k-points along each axis was approximately 30 Å. van der Waals interactions were accounted for with the DFT-D3(BJ) method.^60,61 Structural optimizations (all the cell parameters and the atom positions) were performed using the conjugate gradient algorithm.⁶²

Molecular simulation

We modeled the energy interactions in the same manner as described by Liu et al.³⁶ in the Monte Carlo simulations and the energy grid calculations, both of which were conducted using the RASPA2 code.⁶³ Specifically, the nonbonded interaction energies were modeled using a Lennard-Jones (LJ) potential with Feynman–Hibbs effective potential which accounts for quantum diffraction effects^64–66 plus a Coulomb potential.


We used the Universal Force Field⁶⁷ for the LJ parameters for framework atoms, and no partial charges were assigned to the framework atoms. Previous works^36,68 have showed that for cryogenic H₂ adsorption the host–guest electrostatic interactions contribute minimally under the conditions considered.^36,69 We used the Darkrim–Levesque model^70,71 for H₂ molecules, which is a three-site model with a LJ site on the center of mass and charges of +0.468 on the H nuclei and −0.936 on the center of mass. Lennard-Jones interactions were truncated at a cutoff distance of 12.8 Å without tail corrections, and all LJ cross terms were calculated by Lorentz–Berthelot mixing rules. The Feynman-Hibbs correction was calculated following the work of Johnson et al.⁷²

We conducted grand canonical Monte Carlo (GCMC) simulations to predict hydrogen uptake under two operating conditions: 77 K/100 bar (filling state) and 160 K/5 bar (discharge state). MOF framework atoms were assumed fixed at their crystallographic coordinates throughout the simulations. We used 2500 initialization cycles and 2500 production cycles which were shown to be sufficient for convergence in prior work.¹¹ In every cycle, max(20,N) Monte Carlo moves were executed, where N is the number of molecules in the system at the start of the cycle. The Monte Carlo moves were randomly selected from five categories with equal probability: translation, rotation, insertion, deletion and reinsertion at a new position.

Energy grid, energy histogram calculation and machine learning parameter tuning

We trained LASSO and random forest models to predict hydrogen deliverable capacity. We used energy histograms as features, proposed by Bucior et al.,⁶⁸ which are histograms of the energy felt by a probe species at grid points of a 3d unit cell. These “energy grids” are calculated based on nonbonded interactions with a H₂ probe. Hyperparameters related to the energy histogram features, namely, the bin width and range, were tuned using the LASSO model as used by Bucior and coauthors. Based on Table S5,† increasing the bin range from −10 kJ mol⁻¹ to −12 kJ mol⁻¹ reduced the model accuracy, whereas refining the bin width increased the model accuracy. Therefore, we used a bin range of −10 to 0 kJ mol⁻¹ with a bin width of 0.5 kJ mol⁻¹ (right closed intervals), coupled with one bin for the grid points with positive energy and one bin for the grid points with energy below −10 kJ mol⁻¹, which led to a total of 22 bins. The data preprocessing and hyperparameter tuning for the LASSO and random forest models were performed using the ‘caret’ and ‘randomforest’ package in R. For the random forest model, the default number of trees (500) was used. The number of variables at each node (‘mtry’) was tuned as a hyperparameter using cross validation, which gives the optimal mtry value of 12. The model performance results are shown in Table S8.†

Textural property calculation

The textural properties of all MOFs were calculated with Zeo++.⁷³ We used the UFF force field for interatomic potential parameters. To measure pore accessibility, we used a spherical N₂ model with radius of 1.86 Å as the probe.⁷⁴ In prior work, it was shown that the equilibrium distance should be used to estimate the surface area.⁷⁵ Therefore, we used the repulsive wall distance (σ) for measuring pore diameters and pore volume and the equilibrium distance (2^1/6σ) for measuring the surface area. Example scripts for textural property calculation can be found on the Zenodo repository.⁴⁹

3. Results

3.1. Generation and overview of the dataset

Using the method described above, we created a dataset of 105 230 MOF structures, named “NU-topoMOF-2025”. Fig. 2 provides a comprehensive overview of the structural diversity within the dataset. Due to the bonding algorithm and subsequent cleanup, the dataset contains MOFs resulting from 469 of the 474 selected single-vertex nets, equivalent to having ditopic linkers, and all 60 of the 60 selected multi-vertex nets, equivalent to having multitopic linkers. We note that there are roughly an equal number of MOFs from single-vertex nets (ditopic linkers) and from multi-vertex nets (multitopic linkers). These MOFs span a wide range of topological diversity, measured by td10,³⁷ from 188 (very low topological neighbor counts) up to 6747 (very high topological neighbor counts). A more detailed discussion on td10 is provided in the ESI† section 3.

Fig. 2 Overview of the 105 206 MOFs. Top six panels: histograms of topologies and building blocks in the dataset. The metal node and organic node histograms are shown based on the node IDs (Tables S1 and S2†). Bottom six panels: textural property histograms of the dataset: the distribution of unit cell volume, largest cavity diameter (LCD), pore limiting diameter (PLD), pore volume (nonporous MOFs excluded for log scale plotting), volumetric surface area (VSA) and gravimetric surface area (GSA).

The 60 chosen edge building blocks have lengths from 0 to over 12 Å. The unit cell volume of the MOFs follows a log-normal distribution, with the largest MOF, f5_anaf_21, having unit cell lengths over 200 Å (Fig. 3), being more than 10 000 times larger than the smallest MOF. The tremendous size of some of the MOFs is another reason to use a machine learning model over molecular simulation to predict gas adsorption. On the other hand, the dataset also contains 229 nonporous structures and hundreds of structures with low surface areas (below 200 m² g⁻¹), and the pore volume ranged from 0 cm³ g⁻¹ to over 100 cm³ g⁻¹. This gives us a wide range of structural property space to determine the structure–property relationships.

Fig. 3 The crystal structure of MOF f5_anaf_21: (a) parallel view, (b) perspective view, (c) perspective view of the ana-f net. Its unit cell volume of 9 141 330 ų renders it extremely costly for GCMC simulations.

3.2. H₂ storage performance based on machine learning predictions

Our random forest (RF) model was trained on deliverable capacity using a subset of 16 953 MOFs from the dataset where hydrogen capacity was simulated using GCMC. We reserved 20% as the test data with data stratification based on deciles of VDC (Fig. 4a). Since RF is an ensemble learning method,⁷⁶ the learning performance can be evaluated with an out-of-bag (OOB) estimate, where predictions are made using only the trees that did not see the specific data point, as illustrated in Fig. 4b. Our learning curve (Fig. 4c) suggests that the RF model performance converges with around 8000 training samples, based on the testing set and OOB results. Our final model reaches an excellent accuracy, with R² of 0.97 and a root mean square error (RMSE) of 1.2 g L⁻¹ on the testing set (Fig. 4d and S5†). The model reaches state-of-the-art accuracy in H₂ capacity predictions under cryogenic conditions.^{13,68,77–79}

Fig. 4 Machine learning performance with random forest (RF) model. (a) Data preprocessing details. The subset is split 80/20 for training and testing (hold out) with stratification based on simulated VDC, and subsequently the validation set was created for five-fold cross-validation of the RF model. (b) Illustration of the prediction of RF model training as an average of all decision tree results. As training involves bootstrap sampling, the model creates out-of-bag estimates using trees that do not see the specific training samples. (c) Learning curve with RMSE plotted as a function of training set size. Blue: testing set; orange: OOB estimate; red: training set. (d) Parity plot for testing set samples with ML predicted capacity plotted against GCMC simulated capacity. Color shows the counts of MOFs.

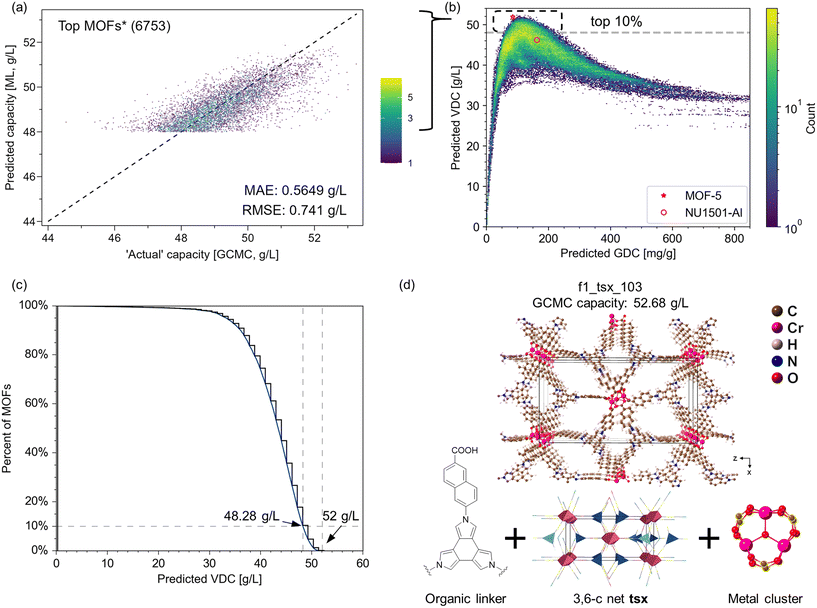
We further tested the ML model on the top 10% of candidates in terms of VDC by performing GCMC simulations. Fig. 5a presents the model performance based on 6753 MOFs predicted by the model to have a VDC above 48 g L⁻¹, where the model achieves an RMSE of less than 1 g L⁻¹. These MOFs are not seen by the model during the training process. Thus, the model can not only distinguish high-performing from low-performing MOFs, but it can also provide accurate estimates of the deliverable capacity even for the top materials. Fig. 5b shows the overall landscape of the dataset, where the well-known trade-off between volumetric and gravimetric deliverable capacities can be recognized. While 10% of MOFs have predicted VDC greater than 48.28 g L⁻¹, the number of structures falls off very quickly beyond (Fig. 5c). This is consistent with Siegel's work that MOFs with VDC greater than 51.9 g L⁻¹ under this condition are very difficult to find.^10,13

Fig. 5 Top performing MOF structures based on ML predictions. (a) Parity plot of hydrogen deliverable capacity for 6753 selected MOFs from the top 10%. (b) Overall deliverable capacity landscape of 105 230 MOFs from ML. The top 10% MOFs have deliverable capacity >48.28 g L⁻¹, shown as the dashed line. The experimental capacities for MOF-5 and NU-1501-Al are plotted with a red star and a red circle, respectively. (c) Cumulative distribution showing the percentage of MOFs with predicted VDC greater than specific value. (d) One of the selected top performing candidates, f1_tsx_103, after DFT optimization.

The experimentally measured capacity of MOF-5 (red star in Fig. 5b) remains among the highest in the predicted landscape. Based on our GCMC simulation results, we identified 73 MOFs with a simulated VDC > 52 g L⁻¹, which means that less than 0.1% of the structures are predicted to have a VDC that exceeds MOF-5's performance (51.9 g L⁻¹). On the other hand, NU-1501-Al, known for its good balance between volumetric and gravimetric deliverable capacities,⁸⁰ falls within a densely populated region on the plot, indicated by the brightness of the area, suggesting that there is still room for enhancement to reach the Pareto front.

We further examined the 73 structures with VDC > 52 g L⁻¹. These MOFs come from 10 topologies (Table S10†) including underlying nets reported in existing MOFs, those identified in natural minerals, and purely theoretical nets. We validated a few selected structures by relaxing them with periodic DFT. For example, f1_tsx_103 has an energetically stable structure that showed minimal structural changes from the classically optimized structure upon DFT optimization. The DFT-optimized structure maintained a high simulated VDC of 52.68 g L⁻¹. The composition of f1_tsx_103 is interesting: the net tsx has been observed in experimental MOFs as a polymorph net,^81,82 and the Cr metal cluster is also known. The organic linker has a twisted geometry that is helpful in targeting non-default topologies.³⁰ However, the synthesis of tsx-MOFs based on this cluster has not be reported. We also note that Zn₄O-based tsx MOFs are predicted to have capacity up to 51.8 g L⁻¹, which is on par with the experimental VDC of MOF-5.¹⁰

As shown in Fig. S23,† the ranges of the textural properties of the top 10% MOFs are in good agreement with previous studies of top performing materials for hydrogen storage.^4,11,83 For example, the pore volume of the top structures is between 1.0–2.0 cm³ g⁻¹, the VSA is between 1500–2500 m² cm⁻³ and centered around 2000 m² cm⁻³, and the GSA is between 4000–5000 m² g⁻¹.

Compared to the distribution of the overall dataset (Fig. 2), we notice an increased relative frequency of MOFs with metal node mc4, the octahedral Zn₄O cluster, as in MOF-5 (Fig. S23†). In contrast, there is a decreased relative frequency of MOFs with metal node mc6, the octahedral Zr₆O₄(OH)₄ cluster. We also see twice as many MOFs with multi-topic linkers (multi-vertex nets) as those with ditopic linkers (single-vertex nets), which highlights the advantage of having organic nodes for attaining ideal porosity and surface areas. These observations will be further discussed below based on the differences in their compatible nets.

3.3. Impact of topology on porosity and predicted capacities

One of our primary goals was to understand how the hydrogen capacity and porosity of MOFs correlate with the underlying topology. In Fig. 6, MOFs are grouped by their underlying nets as vertical lines, indicating the range, interquartile range, median, and mean for various properties, analogous to a boxplot. We discovered that different nets exhibit different average and median VDC values (Fig. 6a). While many of the nets have an upper range above 48 g L⁻¹, we identified only 10 nets that resulted in MOFs with simulated VDC above 52 g L⁻¹ (Table S10†), and 4 of them come from synthesized MOFs.

Fig. 6 Distribution of properties of MOFs grouped by underlying topologies, (a) volumetric deliverable capacity (VDC), (b) pore volume (PV), (c) gravimetric surface area (GSA), (d) volumetric surface area (VSA). The x axis is the rank based on the mean VDC of each MOF topology. Zero denotes the topology with the highest mean VDC, and higher rank means lower mean VDC. The grey line represents the range of the property of interest, dark blue represents the intermediate (25/75) quartile range (IQR), light blue denotes the median, and yellow denotes the mean value of the respective property. (e) Two nets with high net density, whose resulting MOFs can attain high VDC: ssc and ilc. (f) Two nets with low net density, whose resulting MOFs are extremely vacant and can attain high GDC as a result.

We observed interesting clustering patterns in the low average VDC region in Fig. 6a. Specifically, nets with low average VDC form two distinct clusters with different structural properties. The first cluster (outlined by the black rectangle in Fig. 6a) consists of nets that show lower upper VDC and a narrower spread in VDC. They also possess very high pore volumes (PV) (Fig. 6b) and exhibit highly similar distributions in gravimetric surface area (GSA) (Fig. 6c). These nets result in MOFs with high void space and will be denoted as the “vacant topologies” in this work (Fig. 6f). Further analysis in section 3.4 shows that a topological descriptor, net density, best captures the trend. The net density is defined as ρ = N/V where N is the number of circles or spheres with non-overlapping unit diameter in a volume V.⁸⁴

The second cluster (outlined by the green dashed rectangles in Fig. 6) consists of nets with low average VDC but which achieve a very high upper VDC. These “crowded” nets (Fig. 6e) result in nonporous MOFs when assembled with short edge building blocks but can reach optimal porosity and high surface area when assembled with longer edge building blocks. They have lower PV (Fig. 6b) and lower GSA (Fig. 6c), compared to the vacant topologies. Notably, the ssc net resulted in a hypothetical MOF with the highest VDC in the dataset.

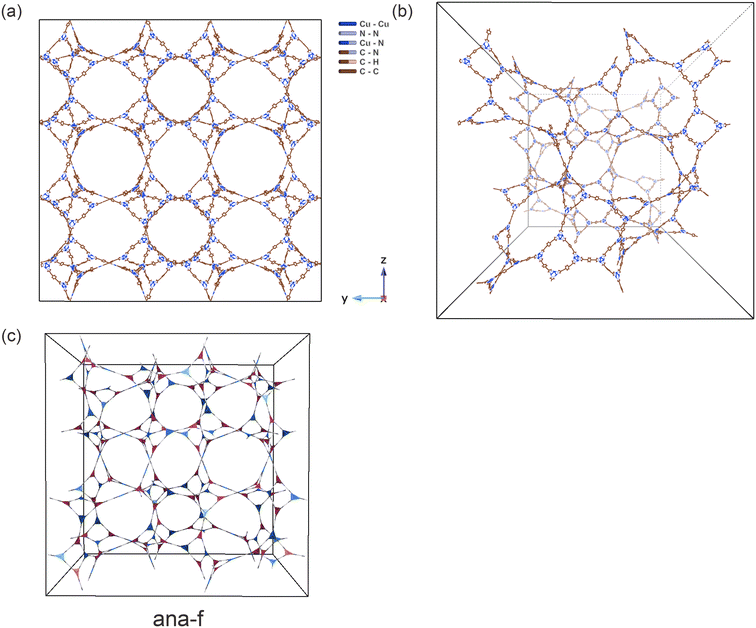
These observations suggest that some nets share similar features and lead to MOFs occupying a similar structural property space regarding porosity and surface areas. As examples, we show two vacant hypothetical MOFs and their underlying nets: srs-a and ana-f in Fig. 7. These two MOFs (Table S9†) feature very high gravimetric deliverable capacities (1017 mg g⁻¹ and 1018 mg g⁻¹). It may be possible to describe this similarity by appropriate topological descriptors. We also note that Fig. 6d shows that VSA is capped around 3000 m² cm⁻³ for the MOFs studied. There is also an interesting pattern in the PV-LCD and PV-PLD scatter plots, which indicates there are topological differences in how pore volume increases as the pore diameters increase (Fig. S24†).

Fig. 7 Example structures with “vacant” topologies, (a) srs-a and (b) dia-f. The corresponding MOF structures (c) and (d) reach 1017 mg g⁻¹ and 1018 mg g⁻¹ gravimetric deliverable capacity, respectively.

3.4. Correlation between the net density and porosity

We conducted dimensionality reduction with the Uniform Manifold Approximation and Projection (UMAP)⁸⁵ algorithm to explore whether the numerical topological features, such as coordination number of vertices, net density, and td10 (Table S14†), could effectively distinguish nets or resulting MOFs for interesting patterns. We first aggregated the MOFs into groups based on their net and computed various statistical measures for textural properties and storage performance, such as mean, upper and lower VSA and VDC, for each net. The UMAP analysis on the aggregated data (Fig. S17 and S18†) showed that merely using the topological descriptors, these net data points can be separated into clusters with distinguishable patterns of gas adsorption performance. On the other hand, if the analysis is performed on the individual MOF data points, we see many clusters of nets corresponding to groups of single-vertex nets and multi-vertex nets. More discussion can be found in ESI† section 10.

Based on these findings, we performed Spearman correlation analysis (Fig. 8) to investigate the relationship between the aggregate structural properties for the 529 nets. The correlation coefficients suggest that net density and td10 are positively correlated with the highest VDC of the nets (i.e. higher net density leads to higher upper VDC) and negatively correlated with the lowest VDC of the nets, which is due to the creation of nonporous MOFs. These correlations can be seen in Fig. S26 and S27.†

Fig. 8 Heatmap of Spearman correlation coefficients between aggregate structural and performance properties and topological descriptors. The aggregated property variables include predicted VDC, VSA, and PV. Each cell represents the correlation coefficient between a pair of variables, with color intensity indicating the strength and direction of the correlation. Color gradients are specified in the accompanying legend. Associated p-values are listed in Table S16.†

The correlation between net density and VDC is further illustrated in Fig. 9. MOFs with nets of different net densities exhibit different performance trade-offs in the bivariate plots of the VDC versus GDC (Fig. 9a) and VSA versus GSA (Fig. 9b). Comparing Fig. 9a and b, we see that there are qualitative similarities between the VDC/GDC tradeoff and the VSA/GSA tradeoff. We observe that the volcano pattern's peak location shifts to the upper right as net density increases, with the exception of MOFs with net density over 3, whose volcano peak (the trade-off) is unclear based on the data. The optimal pore volume that maximizes surface area also increases (Fig. S32†). Our findings suggest that denser nets lead to MOFs with higher GSA and GDC at the peak point, with less compromise on volumetric performance compared to nets with lower net density, provided that the pore volume attains its optimal value for that specific net (larger for denser nets).

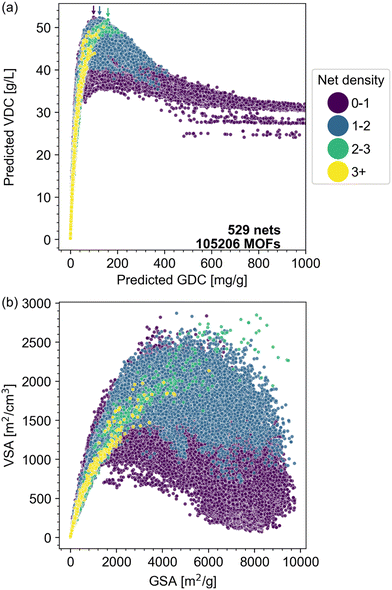Fig. 9 Analysis of MOF data points colored by net density. (a) Scatter plot comparing predicted VDC versus predicted GDC, color-coded into four subgroups by net density: purple (0–1), blue (1–2), green (2–3), and yellow (>3). The peak performance of each subgroup is indicated with a color-matched arrow except for yellow (>3). (b) Scatter plot comparing VSA versus GSA, with the same color scheme. Higher density MOFs are plotted on the top. Fig. S28–S31† show the data points of subgroups separately.

Our observation that net density influences both surface area and deliverable capacity is based on the entire dataset. The topology inherently limits the organic nodes and metal clusters that can be employed, which serve as confounding variables due to their impact on both the structural and the chemical properties of the resulting structures. To further elucidate the effects of net density on structural properties and deliverable capacities, we analyzed the patterns within subgroups defined by having the same net coordination (Fig. S43–S58†), metal clusters (Fig. S59–S68†), or organic nodes (Fig. S69–S82†) to control for variance attributable to these factors. We observe that in general, the correlation between higher net density and higher VSA and GSA, and subsequently higher deliverable capacities, still holds in different subgroups of MOFs. Not surprisingly, the choice of metal clusters has a clear impact on the structural space (Fig. S33†), as lighter metals can lead to higher gravimetric properties like GSA independent of the topology choices. This is also seen in Fig. 10. The metal clusters considered herein include trimetallic metal clusters (mc12 – beryllium, mc4 – zinc, mc5 – chromium) and a hexanuclear zirconium cluster (mc6). The MOFs show different GSA following the trend of metal mass as well as the cluster size – the Be-based mc12 is lightest, followed by Cr-based mc5 and Zn-based mc4. The size of mc6 is larger than the trimetallic nodes and also results in a reduction in the VSA. Its molar mass of 1193 g mol⁻¹ is twice of that of the trimetallic Zn node (560 g mol⁻¹) and around three times of that of the trimetallic Be node (350 g mol⁻¹).

Fig. 10 Surface areas of the MOFs with 6-c nets, colored by net density. The dashed contour lines encompass approximately 97% of the data for MOFs with their respective metal clusters (Table S2†): dark blue: mc12, purple: mc4, red: mc5, orange: mc6. Marginal plots on the upper and right borders show density curves for the MOF subgroups defined by the metal clusters.

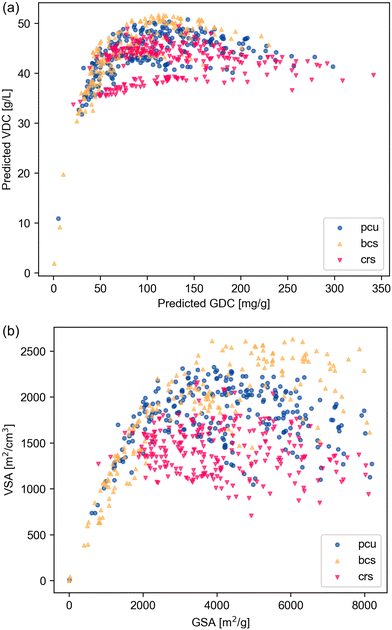
Nets with the same coordination figures (the vertex coordination and geometry) can form polymorphs from the same building blocks.^29,30 To explore whether net density can serve as a criterion for selecting better topologies, we investigated MOFs based on the pcu net and its polymorph nets, bcs and crs.²⁹ The net density of pcu is 1; the bcs net has a net density of 1.23, and the crs has a net density of 0.707. Fig. 11 shows that bcs-MOFs exhibit higher surface areas and higher deliverable capacities, in both volumetric and gravimetric units, compared to pcu-MOFs and crs-MOFs. The bcs net ranks among the top 10 nets we identified and results in 3 MOFs in the dataset with simulated VDC above 52 g L⁻¹.

Fig. 11 Analysis of MOFs with pcu net and its polymorph nets, bcs and crs. Scatter plots displaying (a) predicted VDC against predicted GDC and (b) VSA against GSA. Data points are represented with blue circles for pcu-MOFs, orange upward triangles for bcs-MOFs (with higher net density than pcu), and red downward triangles for crs-MOFs (with lower net density than pcu).

4. Discussion

The ultimate goal set by the U.S. DOE for on-board hydrogen storage is to achieve 50 g L⁻¹ system level deliverable capacity for light-duty vehicles.⁸⁶ Our results suggest that it will be difficult to raise the material performance much beyond the current benchmark of 51.9 g L⁻¹ (on a material basis) under the currently suggested cryogenic operating conditions. The current adsorbent-based H₂ storage tank designs consist of the vessel, insulation, safety components and balance of plant in addition to the adsorbent.⁸⁷ These components occupy 30–40% of the total system volume, and the full-system volumetric capacity has been estimated to be approximately 60% of that of the material system.⁸⁷ Therefore, it is unlikely that a MOF-based material can meet the ultimate VDC goals for on-board, light-duty vehicle applications given the current tank design requirements and operating conditions. It is, however, possible to identify more materials with high volumetric and gravimetric storage performance concurrently. Our results exemplify two pathways: 1) using lighter and smaller metal clusters, 2) constructing MOFs from denser net platforms, where the MOFs with optimal VDC possess higher pore volume and higher GDC compared to those with the less dense nets. The strategy of targeting topologies with higher net density is not exclusive to hydrogen storage, as the resulting MOFs are shown to have simultaneously enhanced VSA and GSA, which should benefit other gas storage applications where physisorption is prominent.

Mathematical studies on the packing of spheres go back several centuries⁸⁴ and provide a foundation for understanding the packing observed in more complex crystal structures. The underlying representation of most crystal structures, the periodic 3d graphs, were examined in early work by Wells⁸⁸ and O'Keeffe and Hyde⁸⁹ and set the stage for further research on the topological representation of crystal structures aimed at understanding the mathematical structure and identifying reliable descriptors for the underlying periodic graphs.^14,48,90 For example, td10 and net density both describe the interconnectivity between vertices in the net, but there are nuances (see ESI† sections 3 and 4 for detailed discussions).

Slack analyzed the relation between packing density (described by the occupied fractional volume, ϕ) and the coordination number η of sphere packing in three dimensions and of circle packing in two dimensions.⁹¹ He compiled a non-exhaustive list of the densest and least-dense 3D sphere-packing nets per η. Slack highlighted that the most-dense limit of ϕ depends on the definition of the next-nearest-neighbor distance, D₁, which serves as a constraint for the construction of the densest nets. The densest nets discussed therein were constructed by stacking the densest 2D nets in the way that maximizes the coordination between the vertical layers. There are two implications: first, non-sphere-packing nets can reach a higher net density because the next-nearest neighbors do not have to be a certain distance away and can be connected to the center vertex. While fcu is the densest sphere-packing net with a coordination of 12 and a net density of 1.414, ild, as a non-sphere-packing 12-c net (Fig. S36†), attains a higher net density of 1.556, with also a higher td10. The vertex of ild net (Fig. S37†) is connected to neighbors in two different distances as shown in Fig. S36.†

While much of the focus in MOF synthesis has been on edge-transitive nets,^29,90 our results suggest that non-sphere-packing nets should be given additional consideration. Metal clusters may not always be symmetrically coordinated,³⁰ which may result in forms of connectivity deviating from the sphere-packing prerequisites outlined by Slack.⁹¹ For instance, in the literature, ild-MOFs have been synthesized with dodecanuclear Zn(II) carboxylate wheels.⁹² The 6-c hxg net (Fig. S41†) displays a net density of 1.414, higher than the densest sphere-packing net of this coordination (pcu, Fig. S39†). Using the MOFid³⁹ algorithm, we identified a MOF⁹³ in the CoRE MOF database³⁸ featuring an hxg topology when the Ag(I) dimers are considered as metal clusters. Furthermore, both bcs and crs are non-sphere-packing nets (Fig. S42†) and have been discussed in reticular MOF design due to their edge-transitive nature.²⁹ The vertex of the bcs net is an octahedron compressed to trigonal antiprism shape, which can also be viewed as a regular hexahedron (cube) with two missing connections (Fig. S42b†), and a bcs-MOF was reported with the Zn₄O metal cluster (mc4).⁹⁴ These examples underscore that non-sphere-packing nets with high net density may be targetable by reticular synthesis. In the nets discussed, hxg, bcs, and crs are edge-transitive, whereas ild, qom,³³ and tsx⁸¹ are non-edge-transitive.

5. Conclusions

In this work, we developed a dataset of over 100 000 predicted MOF structures based on more than 500 3-periodic nets. In addition, we created a machine learning model that accurately predicts H₂ deliverable capacity with an RMSE of around 1 g L⁻¹ compared to Monte Carlo simulations and used it to screen for the top-performing structures. We identified a new MOF structure with both higher volumetric and gravimetric deliverable capacities compared to MOF-5, which is the current benchmark material. We also analyzed the large dataset to shed light on how topology impacts the structural properties and H₂ adsorption performance. We identified two key descriptors, net density and td10, which correlate with the peak performance in the trade-off between volumetric and gravimetric deliverable capacities (VDC vs. GDC) as well as the related trade-off between volumetric and gravimetric surface areas (VSA vs. GSA). By analyzing over 100 000 MOFs with various underlying nets, coordination of vertices, and edge lengths, we found that nets with high net density lead to MOFs with tighter spatial packing. When combined with short edge lengths, these nets result in MOFs with small pores unsuitable for gas storage. However, by increasing the edge length and reaching optimal pore volume, MOFs based on the nets with higher net density can attain higher surface areas and achieve higher maximal deliverable capacities. This finding suggests a possible mechanism to break the current ceiling for volumetric deliverable capacity seen in the current literature and to improve the balanced performance between volumetric and gravimetric deliverable capacities. By integrating concepts from mathematics and materials science, we provide new perspectives on the design of MOFs with optimal gas storage capabilities.

Data availability

Detailed information on dataset generation, results of ML model training, discussions on topological densities, supplementary data analysis, details on validation of models and case studies on MOFs (pdf). This material is available free of charge via the Internet at https://doi.org/10.1039/d5me00078e. Additional data for this article, including the structure files of the hypothetical structures and building blocks, molecular simulation input and force field parameters, the dataset with structural composition, textural properties, GCMC results, and additional data analysis figures are available on the Zenodo repository⁴⁹ at the following DOI: https://doi.org/10.5281/zenodo.14997970.

Author contributions

K. L.: conceptualization, methodology, validation, data curation, formal analysis, visualization, writing – original draft. H. C., T. I., A. S. R., X. W.: data curation. O. K. F.: supervision, funding acquisition. R. Q. S.: conceptualization, supervision, funding acquisition. All authors contributed to manuscript editing and review and have given approval to the final version of the manuscript.

Conflicts of interest

O. K. F. and R. Q. S. have a financial interest in NuMat Technologies, a startup company that is seeking to commercialize MOFs.

Acknowledgements

K. L. thanks Dr. Olaf Delgado-Friedrichs for sharing data of the RCSR database and valuable discussions. In addition, K. L. extends gratitude to Dr. Zhijie Chen for valuable insights on derived nets, to Dr. David C Palmer for inspiring guidance on crystal visualization, and to Yin Wang for valuable inputs on graphic design. K. L. acknowledges the use of CrystalMaker, ToposPro, and VESTA software for crystal and topology visualization. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 using NERSC award BES-ERCAP0032203. This research was also supported through the computational resources and staff contributions provided for the Quest high performance computing facility at Northwestern University which is jointly supported by the Office of the Provost, the Office for Research, and Northwestern University Information Technology. The authors gratefully acknowledge the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (DE-EE0008816) for funding the early part of this work and the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences (DE-SC0023454) for funding the latter part of this work. O. K. F. acknowledges support from the Catalyst Design for Decarbonization Center, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences (award number DE-SC0023383). H. C. acknowledges Southern Methodist University for start-up funds.

References

1. U.S. Department of Energy, U.S. National Clean Hydrogen Strategy and Roadmap, 2023, https://www.hydrogen.energy.gov/library/roadmaps-vision/clean-hydrogen-strategy-roadmap (accessed 2024-10-24).
2. Z. Chen, K. O. Kirlikovali, K. B. Idrees, M. C. Wasson and O. K. Farha, Porous Materials for Hydrogen Storage, Chem, 2022, 8(3), 693–716,  DOI:10.1016/j.chempr.2022.01.012.
3. M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Hydrogen Storage in Metal–Organic Frameworks, Chem. Rev., 2012, 112(2), 782–835,  DOI:10.1021/cr200274s.
4. M. D. Allendorf, Z. Hulvey, T. Gennett, A. Ahmed, T. Autrey, J. Camp, E. Seon Cho, H. Furukawa, M. Haranczyk, M. Head-Gordon, S. Jeong, A. Karkamkar, D.-J. Liu, J. R. Long, K. R. Meihaus, I. H. Nayyar, R. Nazarov, D. J. Siegel, V. Stavila, J. J. Urban, S. P. Veccham and B. C. Wood, An Assessment of Strategies for the Development of Solid-State Adsorbents for Vehicular Hydrogen Storage, Energy Environ. Sci., 2018, 11(10), 2784–2812,  10.1039/C8EE01085D.
5. Hydrogen and Fuel Cell Technologies Office, Hydrogen and Fuel Cell Technologies Office Multi-Year Program Plan, https://www.energy.gov/sites/default/files/2024-05/hfto-mypp-2024.pdf (accessed 2024-10-24).
6. D. P. Broom, C. J. Webb, K. E. Hurst, P. A. Parilla, T. Gennett, C. M. Brown, R. Zacharia, E. Tylianakis, E. Klontzas, G. E. Froudakis, Th. A. Steriotis, P. N. Trikalitis, D. L. Anton, B. Hardy, D. Tamburello, C. Corgnale, B. A. Van Hassel, D. Cossement, R. Chahine and M. Hirscher, Outlook and Challenges for Hydrogen Storage in Nanoporous Materials, Appl. Phys. A: Mater. Sci. Process., 2016, 122(3), 151,  DOI:10.1007/s00339-016-9651-4.
7. L. Zhang, M. D. Allendorf, R. Balderas-Xicohténcatl, D. P. Broom, G. S. Fanourgakis, G. E. Froudakis, T. Gennett, K. E. Hurst, S. Ling, C. Milanese, P. A. Parilla, D. Pontiroli, M. Riccò, S. Shulda, V. Stavila, T. A. Steriotis, C. J. Webb, M. Witman and M. Hirscher, Fundamentals of Hydrogen Storage in Nanoporous Materials, Prog. Energy, 2022, 4(4), 042013,  DOI:10.1088/2516-1083/ac8d44.
8. D. Sengupta, P. Melix, S. Bose, J. Duncan, X. Wang, M. R. Mian, K. O. Kirlikovali, F. Joodaki, T. Islamoglu, T. Yildirim, R. Q. Snurr and O. K. Farha, Air-Stable Cu(I) Metal–Organic Framework for Hydrogen Storage, J. Am. Chem. Soc., 2023, 145(37), 20492–20502,  DOI:10.1021/jacs.3c06393.
9. N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keeffe and O. M. Yaghi, Hydrogen Storage in Microporous Metal-Organic Frameworks, Science, 2003, 300(5622), 1127–1129,  DOI:10.1126/science.1083440.
10. A. Ahmed, S. Seth, J. Purewal, A. G. Wong-Foy, M. Veenstra, A. J. Matzger and D. J. Siegel, Exceptional Hydrogen Storage Achieved by Screening Nearly Half a Million Metal-Organic Frameworks, Nat. Commun., 2019, 10(1), 1568,  DOI:10.1038/s41467-019-09365-w.
11. N. S. Bobbitt, J. Chen and R. Q. Snurr, High-Throughput Screening of Metal–Organic Frameworks for Hydrogen Storage at Cryogenic Temperature, J. Phys. Chem. C, 2016, 120(48), 27328–27341,  DOI:10.1021/acs.jpcc.6b08729.
12. A. W. Thornton, C. M. Simon, J. Kim, O. Kwon, K. S. Deeg, K. Konstas, S. J. Pas, M. R. Hill, D. A. Winkler, M. Haranczyk and B. Smit, Materials Genome in Action: Identifying the Performance Limits of Physical Hydrogen Storage, Chem. Mater., 2017, 29(7), 2844–2854,  DOI:10.1021/acs.chemmater.6b04933.
13. A. Ahmed and D. J. Siegel, Predicting Hydrogen Storage in MOFs via Machine Learning, Patterns, 2021, 2(7), 100291,  DOI:10.1016/j.patter.2021.100291.
14. O. Delgado-Friedrichs and M. O'Keeffe, Crystal Nets as Graphs: Terminology and Definitions, J. Solid State Chem., 2005, 178(8), 2480–2485,  DOI:10.1016/j.jssc.2005.06.011.
15. Y. Liu and M. O'Keeffe, Regular Figures, Minimal Transitivity, and Reticular Chemistry, Isr. J. Chem., 2018, 58(9–10), 962–970,  DOI:10.1002/ijch.201800060.
16. Z. Chen, H. Jiang, M. O'Keeffe and M. Eddaoudi, Minimal Edge-Transitive Nets for the Design and Construction of Metal–Organic Frameworks, Faraday Discuss., 2017, 201, 127–143,  10.1039/C7FD00119C.
17. O. M. Yaghi, M. J. Kalmutzki and C. S. Diercks, Introduction to Reticular Chemistry: Metal-Organic Frameworks and Covalent Organic Frameworks, John Wiley & Sons, 2019.
18. Z. Chen, H. Jiang, M. Li, M. O'Keeffe and M. Eddaoudi, Reticular Chemistry 3.2: Typical Minimal Edge-Transitive Derived and Related Nets for the Design and Synthesis of Metal–Organic Frameworks, Chem. Rev., 2020, 120(16), 8039–8065,  DOI:10.1021/acs.chemrev.9b00648.
19. H. Jiang, S. Benzaria, N. Alsadun, J. Jia, J. Czaban-Jóźwiak, V. Guillerm, A. Shkurenko, Z. Thiam, M. Bonneau, V. K. Maka, Z. Chen, Z. O. Ameur, M. O'Keeffe and M. Eddaoudi, Merged-Nets Enumeration for the Systematic Design of Multicomponent Reticular Structures, Science, 2024, 386(6722), 659–666,  DOI:10.1126/science.ads7866.
20. C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Large-Scale Screening of Hypothetical Metal–Organic Frameworks, Nat. Chem., 2012, 4(2), 83–89,  DOI:10.1038/nchem.1192.
21. Y. Bao, R. L. Martin, M. Haranczyk and M. W. Deem, In Silico Prediction of MOFs with High Deliverable Capacity or Internal Surface Area, Phys. Chem. Chem. Phys., 2015, 17(18), 11962–11973,  10.1039/C5CP00002E.
22. Y. Lan, T. Yan, M. Tong and C. Zhong, Large-Scale Computational Assembly of Ionic Liquid/MOF Composites: Synergistic Effect in the Wire-Tube Conformation for Efficient CO ₂ /CH ₄ Separation, J. Mater. Chem. A, 2019, 7(20), 12556–12564,  10.1039/C9TA01752F.
23. P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. M. Moosavi, M. M. Maroto-Valer, J. A. Reimer, J. A. R. Navarro, T. K. Woo, S. Garcia, K. C. Stylianou and B. Smit, Data-Driven Design of Metal–Organic Frameworks for Wet Flue Gas CO2 Capture, Nature, 2019, 576(7786), 253–256,  DOI:10.1038/s41586-019-1798-7.
24. S. Majumdar, S. M. Moosavi, K. M. Jablonka, D. Ongari and B. Smit, Diversifying Databases of Metal Organic Frameworks for High-Throughput Computational Screening, ACS Appl. Mater. Interfaces, 2021, 13(51), 61004–61014,  DOI:10.1021/acsami.1c16220.
25. S. Lee, B. Kim, H. Cho, H. Lee, S. Y. Lee, E. S. Cho and J. Kim, Computational Screening of Trillions of Metal–Organic Frameworks for High-Performance Methane Storage, ACS Appl. Mater. Interfaces, 2021, 13(20), 23647–23654,  DOI:10.1021/acsami.1c02471.
26. A. Nandy, S. Yue, C. Oh, C. Duan, G. G. Terrones, Y. G. Chung and H. J. Kulik, A Database of Ultrastable MOFs Reassembled from Stable Fragments with Machine Learning Models, Matter, 2023, 6(5), 1585–1603,  DOI:10.1016/j.matt.2023.03.009.
27. Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Topologically Guided, Automated Construction of Metal–Organic Frameworks and Their Evaluation for Energy-Related Applications, Cryst. Growth Des., 2017, 17(11), 5801–5810,  DOI:10.1021/acs.cgd.7b00848.
28. M. Li, D. Li, M. O'Keeffe and O. M. Yaghi, Topological Analysis of Metal–Organic Frameworks with Polytopic Linkers and/or Multiple Building Units and the Minimal Transitivity Principle, Chem. Rev., 2014, 114(2), 1343–1370,  DOI:10.1021/cr400392k.
29. H. Jiang, D. Alezi and M. Eddaoudi, A Reticular Chemistry Guide for the Design of Periodic Solids, Nat. Rev. Mater., 2021, 6(6), 466–487,  DOI:10.1038/s41578-021-00287-y.
30. V. Guillerm and D. Maspoch, Geometry Mismatch and Reticular Chemistry: Strategies To Assemble Metal–Organic Frameworks with Non-Default Topologies, J. Am. Chem. Soc., 2019, 141(42), 16517–16538,  DOI:10.1021/jacs.9b08754.
31. H. K. Chae, D. Y. Siberio-Pérez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, A Route to High Surface Area, Porosity and Inclusion of Large Molecules in Crystals, Nature, 2004, 427(6974), 523–527,  DOI:10.1038/nature02311.
32. Y.-B. Zhang, H. Furukawa, N. Ko, W. Nie, H. J. Park, S. Okajima, K. E. Cordova, H. Deng, J. Kim and O. M. Yaghi, Introduction of Functionality, Selection of Topology, and Enhancement of Gas Adsorption in Multivariate Metal–Organic Framework-177, J. Am. Chem. Soc., 2015, 137(7), 2641–2650,  DOI:10.1021/ja512311a.
33. H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Ultrahigh Porosity in Metal-Organic Frameworks, Science, 2010, 329(5990), 424–428,  DOI:10.1126/science.1192160.
34. R. Anderson and D. A. Gómez-Gualdrón, Increasing Topological Diversity during Computational “Synthesis” of Porous Crystals: How and Why, CrystEngComm, 2019, 21(10), 1653–1665,  10.1039/C8CE01637B.
35. H. Chen and R. Q. Snurr, Computational Screening of Metal-Catecholate-Functionalized Metal–Organic Frameworks for Room-Temperature Hydrogen Storage, J. Phys. Chem. C, 2021, 125(39), 21701–21708,  DOI:10.1021/acs.jpcc.1c06549.
36. K. Liu, Z. Chen, T. Islamoglu, S.-J. Lee, H. Chen, T. Yildirim, O. K. Farha and R. Q. Snurr, Exploring the Chemical Space of Metal–Organic Frameworks with rht Topology for High Capacity Hydrogen Storage, J. Phys. Chem. C, 2024, 128(18), 7435–7446,  DOI:10.1021/acs.jpcc.4c00638.
37. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, The Reticular Chemistry Structure Resource (RCSR) Database of, and Symbols for, Crystal Nets, Acc. Chem. Res., 2008, 41(12), 1782–1789,  DOI:10.1021/ar800124u.
38. Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019, J. Chem. Eng. Data, 2019, 64(12), 5985–5998,  DOI:10.1021/acs.jced.9b00835.
39. B. J. Bucior, A. S. Rosen, M. Haranczyk, Z. Yao, M. E. Ziebel, O. K. Farha, J. T. Hupp, J. I. Siepmann, A. Aspuru-Guzik and R. Q. Snurr, Identification Schemes for Metal–Organic Frameworks To Enable Rapid Search and Cheminformatics Analysis, Cryst. Growth Des., 2019, 19(11), 6682–6697,  DOI:10.1021/acs.cgd.9b01050.
40. W. W. Porter, A. Wong-Foy, A. Dailly and A. J. Matzger, Beryllium Benzene Dicarboxylate: The First Beryllium Microporous Coordination Polymer, J. Mater. Chem., 2009, 19(36), 6489–6491,  10.1039/B912092K.
41. S. L. Griffin and N. R. Champness, A Periodic Table of Metal-Organic Frameworks, Coord. Chem. Rev., 2020, 414, 213295,  DOI:10.1016/j.ccr.2020.213295.
42. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, Open Babel: An Open Chemical Toolbox, J. Cheminf., 2011, 3(1), 33,  DOI:10.1186/1758-2946-3-33.
43. D. Weininger, SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules, J. Chem. Inf. Comput. Sci., 1988, 28(1), 31–36,  DOI:10.1021/ci00057a005.
44. Online SMILES Translator, https://cactus.nci.nih.gov/translate/trans_info.html#unique (accessed 2024-10-09).
45. Daylight Theory: SMILES, Daylight Chemical Information Systems Inc., https://www.daylight.com/dayhtml/doc/theory/theory.smiles.html (accessed 2024-11-26).
46. Github - odf/gavrog, Java code for programs Systre and 3dt, https://github.com/odf/gavrog.
47. O. Delgado-Friedrichs, M. D. Foster, M. O'Keeffe, D. M. Proserpio, M. M. J. Treacy and O. M. Yaghi, What Do We Know about Three-Periodic Nets?, J. Solid State Chem., 2005, 178(8), 2533–2554,  DOI:10.1016/j.jssc.2005.06.037.
48. J.-G. Eon, Euclidian Embeddings of Periodic Nets: Definition of a Topologically Induced Complete Set of Geometric Descriptors for Crystal Structures, Acta Crystallogr., Sect. A: Found. Crystallogr., 2011, 67(1), 68–86,  DOI:10.1107/S0108767310042832.
49. K. Liu, H. Chen, T. Islamoglu, A. S. Rosen, X. Wang, O. K. Farha and R. Q. Snurr, Supplementary Data for “Computational Investigation of the Impact of Metal-Organic Framework Topology on Hydrogen Storage Capacity”,  DOI:10.5281/zenodo.14997970.
50. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In 'T Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales, Comput. Phys. Commun., 2022, 271, 108171,  DOI:10.1016/j.cpc.2021.108171.
51. D. E. Coupry, M. A. Addicoat and T. Heine, Extension of the Universal Force Field for Metal–Organic Frameworks, J. Chem. Theory Comput., 2016, 12(10), 5215–5225,  DOI:10.1021/acs.jctc.6b00664.
52. E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Structural relaxation made simple, Phys. Rev. Lett., 2006, 97, 170201.
53. minimize command — LAMMPS documentation, https://docs.lammps.org/minimize.html.
54. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended Tight-binding Quantum Chemistry Methods, WIREs Comput. Mol. Sci., 2021, 11(2), e1493,  DOI:10.1002/wcms.1493.
55. C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671,  DOI:10.1021/acs.jctc.8b01176.
56. B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. Van Der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-z. Yu and T. Frauenheim, DFTB+, a Software Package for Efficient Approximate Density Functional Theory Based Atomistic Simulations, J. Chem. Phys., 2020, 152(12), 124101,  DOI:10.1063/1.5143190.
57. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
58. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979,  DOI:10.1103/PhysRevB.50.17953.
59. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
60. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
61. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465,  DOI:10.1002/jcc.21759.
62. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes: The Art of Scientific Computing, Cambridge University Press, Cambridge, 3rd edn, 2007.
63. D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, RASPA: Molecular Simulation Software for Adsorption and Diffusion in Flexible Nanoporous Materials, Mol. Simul., 2016, 42(2), 81–101,  DOI:10.1080/08927022.2015.1010082.
64. H. Tanaka, H. Kanoh, M. Yudasaka, S. Iijima and K. Kaneko, Quantum Effects on Hydrogen Isotope Adsorption on Single-Wall Carbon Nanohorns, J. Am. Chem. Soc., 2005, 127(20), 7511–7516,  DOI:10.1021/ja0502573.
65. L. M. Sesé, Study of the Feynman-Hibbs Effective Potential against the Path-Integral Formalism for Monte Carlo Simulations of Quantum Many-Body Lennard-Jones Systems, Mol. Phys., 1994, 81(6), 1297–1312,  DOI:10.1080/00268979400100891.
66. Q. Wang, J. K. Johnson and J. Q. Broughton, Path Integral Grand Canonical Monte Carlo, J. Chem. Phys., 1997, 107(13), 5108–5117,  DOI:10.1063/1.474874.
67. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations, J. Am. Chem. Soc., 1992, 114(25), 10024–10035,  DOI:10.1021/ja00051a040.
68. B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Energy-Based Descriptors to Rapidly Predict Hydrogen Storage in Metal–Organic Frameworks, Mol. Syst. Des. Eng., 2019, 4(1), 162–174,  10.1039/C8ME00050F.
69. G. Garberoglio, A. I. Skoulidas and J. K. Johnson, Adsorption of Gases in Metal Organic Materials: Comparison of Simulations and Experiments, J. Phys. Chem. B, 2005, 109(27), 13094–13103,  DOI:10.1021/jp050948l.
70. F. Darkrim and D. Levesque, Monte Carlo Simulations of Hydrogen Adsorption in Single-Walled Carbon Nanotubes, J. Chem. Phys., 1998, 109(12), 4981–4984,  DOI:10.1063/1.477109.
71. R. B. Getman, Y.-S. Bae, C. E. Wilmer and R. Q. Snurr, Review and Analysis of Molecular Simulations of Methane, Hydrogen, and Acetylene Storage in Metal–Organic Frameworks, Chem. Rev., 2012, 112(2), 703–723,  DOI:10.1021/cr200217c.
72. J. Liu, J. T. Culp, S. Natesakhawat, B. C. Bockrath, B. Zande, S. G. Sankar, G. Garberoglio and J. K. Johnson, Experimental and Theoretical Studies of Gas Adsorption in Cu3(BTC)2: An Effective Activation Procedure, J. Phys. Chem. C, 2007, 111(26), 9305–9313,  DOI:10.1021/jp071449i.
73. T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Algorithms and Tools for High-Throughput Geometry-Based Analysis of Crystalline Porous Materials, Microporous Mesoporous Mater., 2012, 149(1), 134–141,  DOI:10.1016/j.micromeso.2011.08.020.
74. D. Ongari, P. G. Boyd, S. Barthel, M. Witman, M. Haranczyk and B. Smit, Accurate Characterization of the Pore Volume in Microporous Crystalline Materials, Langmuir, 2017, 33(51), 14529–14538,  DOI:10.1021/acs.langmuir.7b01682.
75. Y.-S. Bae, A. O. Yazaydin and R. Q. Snurr, Evaluation of the BET Method for Determining Surface Areas of MOFs and Zeolites That Contain Ultra-Micropores, Langmuir, 2010, 26(8), 5475–5483,  DOI:10.1021/la100449z.
76. L. Breiman, Random Forests, Mach. Learn., 2001, 45(1), 5–32,  DOI:10.1023/A:1010933404324.
77. G. Anderson, B. Schweitzer, R. Anderson and D. A. Gómez-Gualdrón, Attainable Volumetric Targets for Adsorption-Based Hydrogen Storage in Porous Crystals: Molecular Simulation and Machine Learning, J. Phys. Chem. C, 2019, 123(1), 120–130,  DOI:10.1021/acs.jpcc.8b09420.
78. G. S. Fanourgakis, K. Gkagkas, E. Tylianakis and G. Froudakis, A Generic Machine Learning Algorithm for the Prediction of Gas Adsorption in Nanoporous Materials, J. Phys. Chem. C, 2020, 124(13), 7117–7126,  DOI:10.1021/acs.jpcc.9b10766.
79. A. I. Osman, W. Abd-Elaziem, M. Nasr, M. Farghali, A. K. Rashwan, A. Hamada, Y. M. Wang, M. A. Darwish, T. A. Sebaey, A. Khatab and A. H. Elsheikh, Enhanced Hydrogen Storage Efficiency with Sorbents and Machine Learning: A Review, Environ. Chem. Lett., 2024, 22(4), 1703–1740,  DOI:10.1007/s10311-024-01741-3.
80. Z. Chen, P. Li, R. Anderson, X. Wang, X. Zhang, L. Robison, L. R. Redfern, S. Moribe, T. Islamoglu, D. A. Gómez-Gualdrón, T. Yildirim, J. F. Stoddart and O. K. Farha, Balancing Volumetric and Gravimetric Uptake in Highly Porous Materials for Clean Energy, Science, 2020, 368(6488), 297–303,  DOI:10.1126/science.aaz8881.
81. S. R. Caskey, A. G. Wong-Foy and A. J. Matzger, Phase Selection and Discovery among Five Assembly Modes in a Coordination Polymerization, Inorg. Chem., 2008, 47(17), 7751–7756,  DOI:10.1021/ic800777r.
82. K. Kim and J. Kim, Development of a Transferable Force Field between Metal–Organic Framework and Its Polymorph, ACS Omega, 2023, 8(46), 44328–44337,  DOI:10.1021/acsomega.3c06937.
83. D. A. Gómez-Gualdrón, T. C. Wang, P. García-Holley, R. M. Sawelewa, E. Argueta, R. Q. Snurr, J. T. Hupp, T. Yildirim and O. K. Farha, Understanding Volumetric and Gravimetric Hydrogen Adsorption Trade-off in Metal–Organic Frameworks, ACS Appl. Mater. Interfaces, 2017, 9(39), 33419–33428,  DOI:10.1021/acsami.7b01190.
84. M. O'Keeffe, Some Properties of Three-Periodic Sphere Packings, in Science of Crystal Structures: Highlights in Crystallography, ed. I. Hargittai and B. Hargittai, Springer International Publishing, Cham, 2015, pp. 155–163,  DOI:10.1007/978-3-319-19827-9_17.
85. L. McInnes, J. Healy and J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, arXiv, 2018, preprint,  DOI:10.48550/ARXIV.1802.03426.
86. Hydrogen Storage Tech Team, U.S. DRIVE. Hydrogen Storage Tech Team Roadmap, 2017, https://www.energy.gov/eere/vehicles/articles/us-drive-hydrogen-storage-technical-team-roadmap (accessed 2025-03-10).
87. C. Grady, S. McWhorter, M. Sulic, S. J. Sprik, M. J. Thornton, K. P. Brooks and D. A. Tamburello, Design Tool for Estimating Adsorbent Hydrogen Storage System Characteristics for Light-Duty Fuel Cell Vehicles, Int. J. Hydrogen Energy, 2022, 47(69), 29847–29857,  DOI:10.1016/j.ijhydene.2022.06.281.
88. A. F. Wells, Three Dimensional Nets and Polyhedra, John Wiley and Sons, New York, 1977.
89. M. O'Keeffe and B. G. Hyde, Plane Nets in Crystal Chemistry, Philos. Trans. R. Soc., A, 1980, 295(1417), 553–618,  DOI:10.1098/rsta.1980.0150.
90. V. A. Blatov and D. M. Proserpio, Periodic-Graph Approaches in Crystal Structure Prediction, in Modern Methods of Crystal Structure Prediction, ed. A. R. Oganov, Wiley, 2010, pp. 1–28,  DOI:10.1002/9783527632831.ch1.
91. G. Slack, The Most-Dense and Least-Dense Packings of Circles and Spheres, Z. Kristallogr., 1983, 165, 1.
92. A. A. Lysova, D. G. Samsonenko, P. V. Dorovatovskii, V. A. Lazarenko, V. N. Khrustalev, K. A. Kovalenko, D. N. Dybtsev and V. P. Fedin, Tuning the Molecular and Cationic Affinity in a Series of Multifunctional Metal–Organic Frameworks Based on Dodecanuclear Zn(II) Carboxylate Wheels, J. Am. Chem. Soc., 2019, 141(43), 17260–17269,  DOI:10.1021/jacs.9b08322.
93. L.-L. Han, Y.-X. Wang, Z.-M. Guo, C. Yin, T.-P. Hu, X.-P. Wang and D. Sun, Synthesis, Crystal Structure, Thermal Stability, and Photoluminescence of a 3-D Silver(I) Network with Twofold Interpenetrated Dia-f Topology, J. Coord. Chem., 2015, 68(10), 1754–1764,  DOI:10.1080/00958972.2015.1028380.
94. S. Ma, X.-S. Wang, C. D. Collier, E. S. Manis and H.-C. Zhou, Ultramicroporous Metal−Organic Framework Based on 9,10-Anthracenedicarboxylate for Selective Gas Adsorption, Inorg. Chem., 2007, 46(21), 8499–8501,  DOI:10.1021/ic701507r.

---

Footnotes

† Electronic supplementary information (ESI) available: Detailed information on dataset generation, results of ML model training, discussions on topological densities, supplementary data analysis, details on validation of models and case studies on MOFs (pdf). See DOI: https://doi.org/10.1039/d5me00078e

‡ Present address: UL Research Institutes, Materials Discovery Research Institute, 8045 Lamon Avenue, Skokie, Illinois 60077, USA.

§ Present address: Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA.

---