In situ TEM and synchrotron SAXS/WAXS study on the impact of different iron salts on iron-catalysed graphitization of cellulose

Abstract

Carbon materials are essential for emerging energy applications and there is a pressing need to be able to produce carbons with controlled properties from sustainable precursors. Iron-catalysed graphitization of biomass is an attractive approach, where simple iron salts are used to convert organic matter to graphitic carbons at relatively low temperature. The choice of iron salt can have a significant impact on the chemical and structural properties of carbons derived from biomass. In this paper, we report a detailed mechanistic investigation of iron catalysed graphitization of cellulose by Fe(NO₃)₃ and FeCl₃. In situ small and wide angle X-ray scattering and electron microscopy show that the evolution of catalyst particles from the two salts follows very different pathways. Remarkably, graphitization by FeCl₃ is an order of magnitude faster than by Fe(NO₃)₃.

---

Introduction

Graphitic carbon is an essential component of existing and emerging energy applications.¹ Limitations on natural graphite supply and process sustainability have meant that graphite is listed as a critical material by many governments.^2,3 As an alternative, graphite can be manufactured from petroleum products⁴ or biomass⁵ such as cellulosic materials. However, production of synthetic graphite requires very high temperatures (>2500 °C), making it a very energy intensive process. In addition, while biomass is renewable and abundant, its sources are non-graphitizable by traditional methods. A potential solution is catalytic graphitization, where catalysts from abundant elements such as iron are used to convert amorphous carbon to graphitic carbon at relatively low temperatures (∼800 °C).^6,7 The process of iron-catalysed graphitization of biomass is very simple and involves mixing biomass with soluble iron salts then pyrolyzing in an inert atmosphere. The biomass decomposes to amorphous carbon and the iron salts decompose to form iron nanoparticles dispersed throughout the carbon. On further heating, the iron nanoparticles move through the amorphous carbon matrix (Fig. 1a) to produce graphitic carbon nanostructures (Fig. 1b) via a dissolution–precipitation mechanism.⁸

Fig. 1 (a) Schematic showing proposed mechanism of iron-catalysed graphitization and (b) scanning electron microscope image of graphitic nanotubes produced by iron-catalysed graphitization of softwood (image reproduced with permission from ref. 13).

Previous studies have shown that the type of biomass can have a dramatic effect on the structure and properties of carbons produced by iron-catalysed graphitization. For example, the branched gel network of starch produces amorphous carbon that is resistant to graphitization even in the presence of catalysts.⁹ This makes it easier to control the degree of graphitization and, in turn, the porosity. The choice of iron catalyst can also have a significant effect on the mechanism of catalytic graphitization and thus on the microstructure of the resulting carbons.^10,11 For example, our previous work showed that cellulose pyrolyzed with Fe(NO₃)₃ produces a mesoporous graphitic carbon whereas cellulose pyrolyzed with FeCl₃ generates a carbon with a much wider range of pore sizes.¹² This is believed to be partially due to the different iron salts driving different decomposition mechanisms in the cellulose. In addition, cellulose treated with FeCl₃ produced very large intermediate iron oxide particles whereas no crystalline iron oxide intermediates were observed in the cellulose-Fe(NO₃)₃ system. Our in situ transmission electron microscopy of the cellulose-Fe(NO₃)₃ system showed that the graphitization catalyst moves in a liquid-like way through the amorphous carbon.⁸ However, no such experiments have been conducted with cellulose-FeCl₃. Therefore, the role of the large iron oxide crystallites in producing the active catalyst and multimodal porosity is unknown. Furthermore, since all the experiments with cellulose-FeCl₃ have been ex situ it is not known whether the large iron oxide crystallites actually play a role in the mechanism or whether they only form on quenching.

Cellulose is the most abundant biopolymer on Earth and comprises many different types of renewable biomass. If cellulosic biomass is to become a viable precursor for synthetic graphite, it is therefore essential that we understand how different graphitization catalysts influence the properties of carbons produced from cellulose. In this paper, we use in situ synchrotron small and wide angle X-ray scattering (SAXS and WAXS) and in situ transmission electron microscopy (TEM) to compare the graphitization mechanism of microcrystalline cellulose pyrolyzed with Fe(NO₃)₃ and FeCl₃. These techniques enable us to determine the evolution and progression of crystalline phases and also the distribution of particle sizes at different stages of the graphitization process. This offers unprecedented insight into the mechanism of iron-catalysed graphitization of cellulose.

Results and discussion

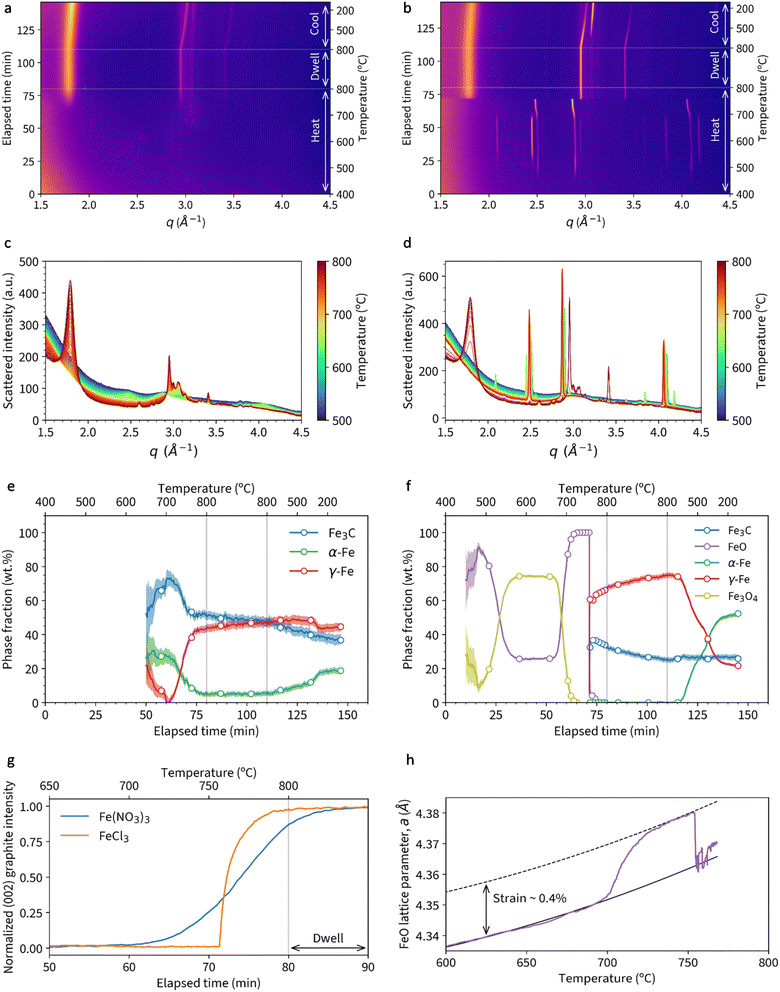
Fig. 2a shows a heatmap of in situ WAXS data for a sample of microcrystalline cellulose treated with Fe(NO₃)₃ and heated to 800 °C under nitrogen, followed by a 30 minute dwell and then cooling to 100 °C. The bright orange/pink bands represent crystalline phases and, as expected based on previous studies, there is little evidence of crystalline content below 700 °C.¹² Between 700 °C and 800 °C, a broad band emerges at q ≈ 1.8 Å⁻¹, corresponding to the 002 peak for graphitic carbon. Alongside this, peaks in the q = 2.5–3.5 Å⁻¹ region indicate the formation of crystalline iron phases. In contrast, a heatmap for a sample of microcrystalline cellulose with FeCl₃ (Fig. 2b) displays well-defined orange bands from ∼500 °C. There is a peak shift to lower q at ∼60 minutes (700 °C) followed by a sudden transition to a different crystalline phase. At the same point, there is a sudden appearance of a strong graphitic carbon band. In both heatmaps, there is very little change during the dwell stage of the experiment. During the cooling stage of the experiment, the shift in peak positions from ∼110 minutes represents crystalline contraction and there also appears to be a phase transformation.

The change in crystalline phase composition can be more readily seen in plots of the Bragg peaks (Fig. 2c and d). Around 600 °C in the cellulose-Fe(NO₃)₃ system, the system is largely amorphous, with peaks for iron-containing crystalline phases only appearing above 700 °C. In contrast, the cellulose-FeCl₃ system undergoes a large number of phase transformations. The gradual emergence of the graphite peak in the cellulose-Fe(NO₃)₃ system also contrasts very clearly with the very fast growth of the same peak in the cellulose-FeCl₃ system. A plot of normalised graphite peak intensity against time and temperature (Fig. 2e) shows this even more strikingly, with the maximum rate of peak growth nearly an order of magnitude higher for the cellulose-FeCl₃ system. It should be noted that the data shown here for the cellulose-FeCl₃ system is for a sample repeated at a higher scan rate to confirm the rapid phase changes and provide more data points during the transition. The data for the original sample, run at the same scan rate as the cellulose-Fe(NO₃)₃ system, can be seen in (Fig. S1†).

Fig. 2 Heatmaps of WAXS data for samples of (a) cellulose + Fe(NO₃)₃ and (b) cellulose + FeCl₃ heated to 800 °C under nitrogen. Also diffraction data for (c) cellulose + Fe(NO₃)₃ and (d) cellulose + FeCl₃ with an additional panel showing the temperature for each pattern during heating to 800 °C. Phase fractions extracted from Rietveld refinement of data for (e) cellulose + Fe(NO₃)₃ and (f) cellulose + FeCl₃. A plot of (g) normalised graphite (002) peak intensity vs. time and temperature. (h) Plot showing expansion of FeO lattice parameter a with increasing temperature.

Rietveld refinement of the diffraction data was used to extract phase fractions of the iron-containing crystalline phases throughout the experiments. In the cellulose-Fe(NO₃)₃ system (Fig. 2f), the peaks above q = 2.5 Å⁻¹ correspond to a mixture of Fe₃C, α-Fe and γ-Fe. The decrease in α-Fe and concurrent increase in γ-Fe corresponds to the expected transition in the iron–carbon phase diagram.¹⁴ The increase of the γ-Fe phase fraction occurs alongside the emergence of the graphite phase (from 60 minutes), suggesting that γ-Fe may be an active catalyst for graphitization. During the same time frame, there is a decrease in Fe₃C fraction, which may indicate a second or alternative route of graphitic carbon formation via Fe₃C decomposition. Both catalysts have been identified during chemical vapour deposition (CVD) synthesis of carbon nanotubes, with the conclusion in that paper that two routes of graphitization occur simultaneously.¹⁵ There is very little change during the dwell stage of the experiment, other than a slight decrease in Fe₃C and increase in γ-Fe fraction. This could correspond to decomposition of the Fe₃C to graphitic carbon. However, the bulk of graphitization occurs before the dwell phase of the experiment. On cooling, a small fraction of the γ-Fe transforms to the lower temperature α-Fe, but surprisingly a large amount remains trapped as γ-Fe. Trapping of γ-Fe has been demonstrated during chemical vapour deposition synthesis of carbon nanotubes due to stabilization by carbon in the interstitial sites.¹⁶

A plot of phase fractions for the cellulose-FeCl₃ system (Fig. 2g) shows the presence of various iron oxide phases during the heating stage. Interestingly, FeO (wüstite, more accurately written as Fe_1−xO, where 0.04 < x < 0.1) is the first iron oxide phase to emerge, followed by Fe₃O₄. Rather than some of the FeO transforming to Fe₃O₄ (unlikely in the reducing conditions) we believe that the two phases form via different mechanisms. The sample preparation involves combining cellulose powder with aqueous FeCl₃. FeCl₃ hydrolyses on contact with water and, as a result, there will be some iron(oxyhydr)oxide species present alongside the FeCl₃.¹⁷ These iron (oxyhydr)oxide species decompose to FeO. Separately, we suggest that the FeCl₃ undergoes halide vapour hydrolysis,¹⁸ where volatile iron chloride reacts with water vapour released from decomposing cellulose to produce crystalline magnetite.¹⁹ The magnetite then undergoes carbothermal reduction to form additional FeO. At ∼700 °C, there is a shift in the FeO peaks to a smaller q value, indicating a lattice expansion. The trend in lattice parameter a is shown in Fig. 2h and could indicate strain in the lattice in the initial stages of carbothermal reduction. At 755 °C, the FeO quickly transforms to a mixture of γ-Fe and Fe₃C. This occurs at the same time as the rapid emergence of the peak for graphitic carbon. The presence of both phases again makes it impossible to identify a single graphitization catalyst, suggesting that both may be active. During the dwell stage, there is a similar decrease in Fe₃C content and concurrent increase in γ-Fe, suggesting gradual decomposition of the Fe₃C to graphitic carbon. On cooling, a significant fraction of the γ-Fe transforms to the lower temperature α-Fe phase. A final point to note is that energy dispersive X-ray analysis (ex situ) of a sample heated to 800 °C under N₂ in a furnace showed no evidence of chlorine (Fig. S2†), supporting the theory that all the FeCl₃ is converted into iron oxide.

Further insight into the different mechanisms operating in the Fe(NO₃)₃ and FeCl₃ systems comes from in situ transmission electron microscopy (TEM) footage. We have previously reported that catalyst particles in the cellulose-Fe(NO₃)₃ system move in a liquid-like manner during the graphitization step.⁸ Before this point, the catalyst particles emerge from material that appears amorphous, consistent with the in situ WAXS data. In the cellulose-FeCl₃ system, large particles can be observed in snapshots (Fig. 3a) of in situ TEM data (Video S1†) even below 400 °C. As the system is heated, the large particles can be seen to vaporise (Video S2†), consistent with the halide vapour hydrolysis mechanism proposed above. The disappearance of the large particles occurs alongside the appearance of smaller particles, presumed to be caused by deposition of iron oxide.²⁰ During continued heating from 500 °C to 600 °C, the particles grow (Fig. 3b) and then start to move in a similar erratic manner to those observed in the cellulose-Fe(NO₃)₃ system (Fig. 3c and Video S3†). The particles move through the even-textured amorphous carbon of the decomposed cellulose, leaving a trail of graphitic carbon nanotubes (Fig. 4 and Video S4†), again as observed in the cellulose-Fe(NO₃)₃ system. Remarkably, however, the particles from the cellulose-FeCl₃ system move a lot faster than those in the cellulose-Fe(NO₃)₃ system (Video S5,† data for cellulose-Fe(NO₃)₃ reproduced with permission from ref. 8). For example, the fastest particle observed is highlighted in Fig. 3c and has an estimated speed of 300 nm s⁻¹, which is an order of magnitude faster than even the fastest particles observed in the cellulose-Fe(NO₃)₃ system. Other particles did not move quite as quickly (Fig. S3 and S4†) but were still considerably faster than the average speed of particles in the cellulose-Fe(NO₃)₃ system. This is surprising but is consistent with the in situ WAXS data above, which shows the rate of graphitization to be considerably faster for the FeCl₃-cellulose system. It should be noted that the temperature of graphitization in the TEM experiments is lower than recorded in the in situ WAXS experiment. This could be due to electron beam heating, but this is unlikely as it would also have affected the cellulose-Fe(NO₃)₃ sample. Given that the cellulose-FeCl₃ decomposition mechanism is believed to involve a vapour-phase step, it is more likely that the vacuum conditions of the TEM accelerated the progress of the pyrolysis or changed the catalyst formation mechanism. In situ SAXS/WAXS experiments at 700 °C show that graphitization is possible at lower temperatures (Fig. S5†). However, TEM experiments under atmospheric pressure or vacuum phase synchrotron experiments would be necessary to verify the exact reason for variation in this system.

Fig. 3 Snapshots from in situ TEM videos showing heating of a cellulose + FeCl₃ sample (a) up to 500 °C (scale bar = 50 nm), (b) from 500 °C to 600 °C (scale bar = 100 nm) and (c) held at 600 °C (scale bar = 100 nm). Circles show the positions of a single particle as it moves.

Fig. 4 Snapshots from TEM video showing a region of the cellulose-FeCl₃ sample during the graphitization step, showing (a) amorphous carbon with some Fe nanoparticles and (b) a trail of graphitic carbon nanotubes left by a moving catalyst particle. Scale bar = 20 nm.

In situ small angle X-ray scattering (SAXS) offers further insight into the different graphitization mechanisms. Fig. 5a shows the SAXS data for the microcrystalline cellulose-Fe(NO₃)₃ system during heating from 400 °C to 800 °C at 25 °C intervals. During the early stages of heating (400–700 °C), there is a gradual increase in scattering intensity in the q range 0.2–1.2 nm⁻¹, indicating an increase in scattering features around 5–30 nm in size. Above 700 °C, the data shows an increase in scattering intensity at lower q, indicating the formation of larger scattering features. Selected scans were fitted and analysed using McSAS, a Monte Carlo method for extracting form-free size distributions, for q range 0.027 ≤ q (nm⁻¹) ≥ 2.88 (data with fit lines in Fig. S6†).²¹ The histograms support observations from the raw data and correlate with WAXS and TEM data. At 700 °C, the sample consists of only very small scattering features (Fig. 5b), presumably the emerging nuclei of Fe₃C and Fe nanoparticles. The distribution moves to larger scattering features at 750 °C (Fig. 5c) and 800 °C (Fig. 5d) as the catalyst particles grow. It should be noted that the graphitic nanotubes created by the catalyst particles will also contribute to scattering due to the presence of a carbon–air interface within the pore of each nanotube. The scattering length density contrast for the iron–carbon interface is roughly twice that of the carbon–air interface. This corresponds to ∼4× difference in scattering intensity. However, as there is a high proportion of pores compared to iron particles in the sample, the contribution in the SAXS pattern from the pores is likely to be significant. To gain more insight into the evolution of different features, normalised scattering intensity was plotted alongside graphite (002) peak intensity for two different q values. The graph for q = 0.439 nm⁻¹ (corresponding to scattering features ∼7 nm in radius) shows both scattering intensity and graphite peak evolution track each other exactly (Fig. 5e). In contrast, the scattering intensity at q = 0.133 nm⁻¹ (corresponding to scattering features ∼23 nm in radius) increases in advance of the graphite peak evolution (Fig. 5f). The graphitic nanotubes formed in these systems are multi-walled, meaning that the internal pore will be smaller than the catalyst nanoparticle. Therefore, the features ∼23 nm in radius are likely to be the catalyst particles and the smaller scattering features are likely to be the graphitic nanotubes. This data therefore shows convincing evidence of the emergence of catalyst particles followed by the growth of graphitic nanostructures, with both contributing to the broad distribution of sizes of scattering features. The SAXS pattern did not change during the dwell and cooling phase of the experiment (Fig. S7†).

Fig. 5 (a) SAXS data for the heating range 400–800 °C and corresponding particle size histograms for data scans at (b) 700 °C, (c) 750 °C and (d) 800 °C for cellulose-Fe(NO₃)₃. Normalised graphite (002) peak intensity alongside scattering intensity at (e) q = 0.439 nm⁻¹ and (f) q = 0.133 nm⁻¹.

For the microcrystalline cellulose-FeCl₃ system, the SAXS data is very different (Fig. 6a), with no significant change in the scattering profile until 750 °C, when there is a very sudden increase in scattering intensity. This corresponds to the fast graphitization step observed in the WAXS data. Selected scans were fitted and analysed using McSAS, a Monte Carlo method for extracting form-free size distributions, for q range 0.027 ≤ q (nm⁻¹) ≥ 2.88 (data with fit lines in Fig. S8†).²¹ The particle size histogram extracted from the SAXS data at 750 °C (Fig. 6b) shows particles in the size range 10–100 nm (radius). The shape of the data suggests that there may also be a distribution of particles above 100 nm in radius. This is consistent with the wide range of particle sizes observed in both in situ and ex situ TEM experiments.¹² At 760 °C (Fig. 6c), the approximate temperature for onset of graphitization, the histogram shows the presence of features below 10 nm in radius, consistent with the observation of Fe/Fe₃C particles less than 10 nm in radius by in situ TEM (Fig. 3c and 4b). A simple calculation shows that a FeO particle of radius 50 nm would contract to a Fe particle with a radius of ∼40 nm. Therefore, the distribution of scattering features <10 nm cannot be due to particle contraction during carbothermal reduction. Another possibility is that the FeO–Fe transition could involve splitting of the particles into fragments. Crack formation and propagation is a well-known phenomenon on a bulk scale in the carbothermal reduction of iron ore.²² This occurs due to volume/density changes and gas evolution. Therefore, particle splitting during carbothermal reduction is a plausible explanation for the observed change in scattering intensity. Once graphitization is complete, at 770 °C (Fig. 6d), the most significant contribution in the histogram is from features below 10 nm in radius. As above, this is likely to be due to a combination of catalyst nanoparticles and pores. This is corroborated by TEM footage, which shows that the catalyst particles do not grow significantly in size during graphitization. As above, more insight can be gained by comparing normalised scattering intensity at certain q values to graphite (002) peak intensity. For q = 0.439 nm⁻¹ (corresponding to scattering features ∼7 nm in radius), the normalised scattering and graphite peak intensities track each other closely (Fig. 6e). However, the data for q = 0.133 nm⁻¹ (corresponding to scattering features ∼23 nm in radius) shows firstly a gradual increase in scattering intensity up to 70 minutes (Fig. 6f). We know there is a population of FeO that comes from iron hydroxide (from hydrolysis of FeCl₃ in sample preparation) and the growth and sintering of these particles could cause this small intensity increase. The most dramatic observation is that the fast increase in scattering intensity occurs more quickly than the corresponding evolution of the graphite peak. As with the cellulose-Fe(NO₃)₃ system, this indicates that the catalyst particles are larger than the internal pores of the multiwalled graphitic nanotubes they produce. The catalyst particles also form first, with a time lag during which the graphitic nanotubes are produced. As with the cellulose-Fe(NO₃)₃ system, the SAXS patterns for cellulose-FeCl₃ do not change significantly during the dwell and cooling phase of the experiment (Fig. S9†).

Fig. 6 (a) SAXS data for the heating range 400–800 °C and corresponding particle size histograms for data at (b) 750 °C, (c) 760 °C and (d) 770 °C for cellulose-FeCl₃. Normalised graphite (002) peak intensity alongside scattering intensity at (e) q = 0.439 nm⁻¹ and (f) q = 0.133 nm⁻¹.

The data above enable us to propose a mechanism for the very different graphitization behaviour of catalyst particles formed from Fe(NO₃)₃ and FeCl₃. The first point is the very sudden onset of graphitization for the cellulose-FeCl₃ system compared to the gradual increase in graphitic content in the cellulose-Fe(NO₃)₃ system. Pyrolysis of cellulose with Fe(NO₃)₃ results in the formation of a largely amorphous mixture of carbon with iron presumably present as very small amorphous iron oxide clusters or dispersed throughout the carbon (Fig. 7a). Carbothermal reduction at ∼700 °C is followed by gradual growth of the Fe/Fe₃C crystals and then the onset of graphitization. These data point to the need for catalyst particles to reach a critical size before graphitization can commence. An interesting exercise we can do at this point is estimate the minimum carbon concentration required for precipitation of single-atom thick graphene sheets around catalyst particles of different diameters. Because of surface/volume ratio effects, the concentration of carbon needed to form a graphene ‘cap’ or layer around an iron catalyst particle rises steeply with decreasing catalyst diameter (Fig. 8). The model is extremely simple, but it clearly shows that catalyst particles would have to achieve a minimum diameter before graphitization can occur, given that the solubility of carbon in γ-Fe at the 723 °C eutectic is only 0.8%. In contrast, pyrolysis of cellulose with FeCl₃ results in the formation of large iron oxide crystallites (Fig. 7b). These appear to break apart during carbothermal reduction, followed by a very sudden onset of graphitization. If breaking up of the large oxide particles results in a lot of γ-Fe particles above the minimum size for graphitization, this could explain the very fast onset of graphitization.

Fig. 7 Schematic showing the two proposed mechanisms of graphitization catalyst formation from cellulose with (a) Fe(NO₃)₃ and (b) FeCl₃.

Fig. 8 Estimation of carbon concentration required to cover a catalyst sphere with a single-atom thick layer of graphene.

The very fast rate of catalyst movement in the cellulose-FeCl₃ is harder to rationalize. We concluded in our previous study of the cellulose-Fe(NO₃)₃ system that the process of graphitization occurs via dissolution of carbon atoms at the front face of the Fe catalyst particle, diffusion of carbon atoms through the solid γ-Fe particle and precipitation of graphitic carbon structures at the rear face of the catalyst. Movement of the catalyst occurs through self-diffusion of iron atoms away from the site of precipitation. The speed of catalyst movement in the cellulose-Fe(NO₃)₃ system was consistent with diffusion constants listed in the literature. If catalyst movement is considerably faster in the cellulose-FeCl₃ system, then there are several possible considerations. Firstly, it is possible that different diffusion mechanisms operate in the two systems (i.e. bulk diffusion of Fe in the Fe(NO₃)₃ system and surface diffusion in the FeCl₃ system). Surface diffusion is a lot faster than bulk diffusion but given the two systems have very similar crystalline compositions during graphitization, it seems unlikely that diffusion mechanisms would be significantly different. Another possibility is that the catalyst particles in the cellulose-FeCl₃ system are liquid, compared to the solid catalyst particles in the cellulose-Fe(NO₃)₃ system. Again, this seems unlikely. The iron–carbon phase diagram and molecular dynamics simulations both provide strong evidence that Fe and Fe₃C cannot be liquid under the conditions of these experiments.⁸ Another possibility is the properties of the amorphous carbon. We know that the Lewis acidic nature of FeCl₃ changes the decomposition pathway of cellulose.¹² We also know that changes in the molecular structure and composition of biochar can lead to different rates of graphitization, e.g. with high-nitrogen biochar undergoing very slow graphitization.²³ The different decomposition pathway for cellulose with FeCl₃ could result in an amorphous carbon with a different structure, which may be more soluble, accelerating graphitization.

A final possibility is that the primary graphitization catalyst is different between the two systems. Fig. 9 is a schematic of the different crystalline phases (from Rietveld refinements in Fig. 2). The solid black vertical line in each panel marks the onset of graphitization and it can be clearly seen that graphitization in the cellulose-Fe(NO₃)₃ system begins when Fe₃C is the dominant crystalline iron phase, with some α-Fe also present. As graphitization progresses (and the temperature increases), the α-Fe converts to γ-Fe. In contrast, the sudden onset of graphitization in the cellulose-FeCl₃ is concurrent with the carbothermal reduction of FeO to γ-Fe, with Fe₃C as a significant secondary phase. Both Fe₃C and γ-Fe are known to act as catalysts for graphitization but the diffusion coefficients of carbon in Fe₃C (D ≈ 10⁻¹¹ cm² s⁻¹)²⁴ and in γ-Fe (D ≈ 10⁻⁸ cm² s⁻¹)²⁵ at 725 °C indicate that carbon moves much faster in γ-Fe. Given that γ-Fe is the dominant crystalline iron phase at the onset of graphitization in the cellulose-FeCl₃ system, it is reasonable to presume that this is the dominant catalyst. The much larger carbon diffusion rate in γ-Fe would be consistent with the much faster catalyst particle speed. In contrast, Fe₃C is the dominant phase in the cellulose-Fe(NO₃)₃ system. Given the much smaller C diffusion coefficient for Fe₃C, it is reasonable that catalysis will be much slower in this system. Additionally, it has been shown that carbon diffusion in supersaturated γ-Fe is much slower.^26,27 It is possible that the sudden formation of γ-Fe in the cellulose-FeCl₃ system results in a lower concentration of carbon compared to the slow evolution of γ-Fe in the cellulose-Fe(NO₃)₃ system. Based on this, it is reasonable that γ-Fe-catalysed graphitization would be faster in the cellulose-FeCl₃ system, even though γ-Fe is present in both systems.

Fig. 9 Schematic of the evolution of iron phases and graphitic carbon during pyrolysis of microcrystalline cellulose with (a) Fe(NO₃)₃ and (b) FeCl₃ from 700 °C.

Conclusion

The in situ data in this paper show that the choice of iron salt can have a big impact on the graphitization pathway in catalytic graphitization of cellulose. This is due to the decomposition of the salt, the impact of the salt on cellulose decomposition and the influence of the changed decomposition pathways on particle size of solid-state catalyst precursors. Cellulose-Fe(NO₃)₃ decomposes to very small iron–oxygen clusters which are carbothermally reduced to small Fe₃C catalyst particles. This results in a gradual onset of graphitization. In contrast, the larger iron oxide particles formed during pyrolysis of cellulose-FeCl₃ undergo sudden carbothermal reduction to γ-Fe and Fe₃C, alongside strain-induced shattering of the particles. The onset of graphitization is equally sudden. This data indicates that there is a critical size required for the onset of graphitization to occur. In situ TEM and SAXS/WAXS data show that graphitization is considerably faster in the cellulose-FeCl₃ system and we ascribe that to γ-Fe being a much faster catalyst, consistent with reported diffusion coefficients. Given that cellulose is the most abundant component of biomass, this understanding of cellulose graphitization mechanisms is essential for moving towards carbon materials with controlled structure and properties.

Experimental

Preparation of iron-doped cellulose

For cellulose samples, 0.68 mmol of iron salt (Fe(NO₃)₃·9H₂O or FeCl₃·6H₂O) was dissolved in 10 mL of water and added to 5 g of microcrystalline cellulose. The mixtures were manually stirred until all the solution was absorbed. Samples were then dried in a 70 °C oven overnight. The samples were then preheated for experiments by heating in an alumina crucible in a tube furnace and heated to 400 °C at a rate of 5 °C per minute under the flow of nitrogen and held for 1 hour. This is to remove water and avoid expansion in the capillary during the SAXS/WAXS experiment.

In situ synchrotron small and wide angle X-ray scattering measurements

In situ SAXS/WAXS experiments were performed at Diamond Light Source using the I22 beamline. Pre-heated samples were placed in a quartz capillary (1 mm OD) and packed at either end with quartz wool to prevent movement during the experiment. Samples were heated at 20 °C per minute to 400 °C and held for 5 minutes to equilibrate before beginning the experiment. It should be noted that although every effort was made to ensure consistency between experiments, it was difficult to ensure that the capillary was the exact same distance from the hot air blower in every experiment. Therefore there may be some error in the temperatures stated. The capillary was heated using a hot air blower. Measurements were performed using a 14 keV beam (wavelength = 0.8856 Å), a sample to detector distance of 2.730 m, and a beam size of 200 μm × 180 μm. The scattered X-rays were detected using a Pilatus P3-2M unit from Dectris, which has a pixel size of 172 μm × 172 μm. A schematic of the set-up of the experiment is shown in Fig. S10,† alongside details of the refinement method.

TEM measurements

Approx. 50 mg of amorphous carbon (prepared from FeCl₃-doped cellulose at 400 °C) was dispersed in 1 mL of ethanol by sonication for 10 minutes. One drop of the dispersion was pipetted on to a Protochips Thermal E-chip (E-FHDC). In situ TEM footage was collected on a JEOL JEM-ARM200F equipped with a Schottky field emission gun. The sample was heated at 1 °C per second up to 500 °C. Samples were then heated at 0.5 °C per second up to 600 °C and held for approx. 10 minutes inside the microscope.

Estimation of critical catalyst diameter

For catalyst spheres of diameter 1–50 nm, the surface area and volume were calculated and the mass of iron calculated using an austenite density of 7.65 g cm⁻³ (800 °C).²⁸ The areal density of a single graphene sheet can be calculated as 7.6 × 10⁻⁴ g m⁻² and from this, we can estimate the mass of carbon required to form a single-atom thick graphene layer around a catalyst sphere. From this, we can calculate the mass% of carbon required if all the carbon was to precipitate from a catalyst sphere to form a single-atom thick graphene layer.

Data availability

All the data for this project can be found at the following https://doi.org/10.25500/edata.bham.00001281.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Leverhulme Trust (RPG-2020-076) for funding and Diamond Light Source for synchrotron beamtime access.

References

1. Y. Liu, H. Shi and Z. S. Wu, Energy Environ. Sci., 2023, 16, 4834–4871.
2. European Commission, Critical Raw Materials Factsheets (2020), 2020.
3. BEIS, Resilience for the Future: the United Kingdom's Critical Minerals Strategy, 2022.
4. J. L. Rowlandson, K. J. Edler, M. Tian and V. P. Ting, ACS Sustainable Chem. Eng., 2020, 8, 2186–2195.
5. Z. Shi, S. Wang, Y. Jin, L. Zhao, S. Chen, H. Yang, Y. Cui, R. Svanberg, C. Tang, J. Jiang, W. Yang, P. G. Jönsson and T. Han, SusMat, 2023, 3, 402–415.
6. M. Mennani, A. Ait Benhamou, A. A. Mekkaoui, F. El Bachraoui, M. El Achaby, A. Moubarik and Z. Kassab, J. Mater. Chem. A, 2024, 12, 6797–6825.
7. R. D. Hunter, J. Ramírez-Rico and Z. Schnepp, J. Mater. Chem. A, 2022, 10, 4489–4516.
8. R. D. Hunter, M. Takeguchi, A. Hashimoto, K. M. Ridings, S. C. Hendy, D. Zakharov, N. Warnken, J. Isaacs, S. Fernandez-Muñoz, J. Ramirez-Rico and Z. Schnepp, Adv. Mater., 2024, 36, 2404170.
9. R. D. Hunter, J. L. Rowlandson, G. J. Smales, B. R. Pauw, V. P. Ting, A. Kulak and Z. Schnepp, Mater. Adv., 2020, 1, 3281–3291.
10. J. Hoekstra, A. M. Beale, F. Soulimani, M. Versluijs-Helder, J. W. Geus and L. W. Jenneskens, J. Phys. Chem. C, 2015, 119, 10653–10661.
11. J. Hoekstra, A. M. Beale, F. Soulimani, M. Versluijs-Helder, D. Van De Kleut, J. M. Koelewijn, J. W. Geus and L. W. Jenneskens, Carbon, 2016, 107, 248–260.
12. E. C. Hayward, G. J. Smales, B. R. Pauw, M. Takeguchi, A. Kulak, R. D. Hunter and Z. Schnepp, RSC Sustainability, 2024, 3490–3499.
13. E. Thompson, A. E. Danks, L. Bourgeois and Z. Schnepp, Green Chem., 2015, 17, 551–556.
14. J. Chipman, Metall. Trans., 1972, 3, 55–64.
15. C. T. Wirth, B. C. Bayer, A. D. Gamalski, S. Esconjauregui, R. S. Weatherup, C. Ducati, C. Baehtz, J. Robertson and S. Hofmann, Chem. Mater., 2012, 24, 4633–4640.
16. B. Alemán, R. Ranchal, V. Reguero, B. Mas and J. J. Vilatela, J. Mater. Chem. C, 2017, 5, 5544–5550.
17. C. M. Flynn, Chem. Rev., 1984, 84, 31–41.
18. L. B. Robinson, W. B. White and R. Roy, J. Mater. Sci., 1966, 1, 336–345.
19. S. Soares, G. Camino and S. Levchik, Polym. Degrad. Stab., 1995, 49, 275–283.
20. A. A. Battiston, J. H. Bitter, F. M. F. De Groot, A. R. Overweg, O. Stephan, J. A. Van Bokhoven, P. J. Kooyman, C. Van Der Spek, G. Vankó and D. C. Koningsberger, J. Catal., 2003, 213, 251–271.
21. I. Bressler, B. R. Pauw and A. F. Thünemann, J. Appl. Crystallogr., 2015, 48, 962–969.
22. J. E. Ogbezode, O. O. Ajide, O. Ofi and O. O. Oluwole, J. Alloys Metall. Syst., 2024, 6, 100071.
23. R. D. Hunter, E. C. Hayward, G. J. Smales, A. Kulak, S. G. De and Z. Schnepp, Mater. Adv., 2023, 4, 2070–2077.
24. A. Schneider and G. Inden, Calphad, 2007, 31, 141–147.
25. T. A. Timmerscheidt, J. Von Appen and R. Dronskowski, Comput. Mater. Sci., 2014, 91, 235–239.
26. C. T. Wirth, B. C. Bayer, A. D. Gamalski, S. Esconjauregui, R. S. Weatherup, C. Ducati, C. Baehtz, J. Robertson and S. Hofmann, Chem. Mater., 2012, 24, 4633–4640.
27. J. Cermak and L. Kral, J. Alloys Compd., 2014, 586, 129–135.
28. M. Lyassami, D. Shahriari, E. Ben Fredj, J.-B. Morin and M. Jahazi, J. Manuf. Mater. Process., 2018, 2(2), 34.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta03584h

---