Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The interplay of composition and mechanics in the thermodynamics of asymmetric ternary lipid membranes
Malavika Varma and
Markus Deserno
and
Markus Deserno *
*
Department of Physics, Carnegie Mellon University, Pittsburgh, PA 15213, USA
First published on 14th January 2025
Abstract
Eukaryotic lipid membranes are both compositionally complex and strongly asymmetric. Preferential lipid interactions enable coexistence between two fluid phases and an associated critical point, while bilayer asymmetry leads to leaflet-specific values for many observables—most saliently composition, but also a difference in leaflet tensions, for which we introduced the term “differential stress.” Lipid mixing thermodynamics has been extensively studied, notably in idealized ternary model systems, and interest in asymmetry has grown significantly in the past decade, but their interplay remains poorly understood. Here we propose a conceptual framework for the thermodynamics of asymmetric ternary lipid membranes. Cholesterol emerges as an essential actor playing two different roles: first, it controls lipid mixing; second, it couples the compositional phase points of the two leaflets by achieving chemical equilibrium between them. Since differential stress can squeeze cholesterol from one leaflet into the other, this couples mechanical properties such as lateral stresses and curvature torques directly to mixing thermodynamics. Using coarse-grained simulations, we explore implications for leaflet coexistence, mechanical stability of giant vesicles, and differential stress driven phase segregation in a single leaflet. We hope this framework enables a fresh look at some persistent puzzles in this field, most notably the elusive nature of lipid rafts.
1 Introduction
Our overarching goal in this contribution is to develop a theoretical framework, largely based on thermodynamics, within which we can describe lipid membranes that are both compositionally complex and asymmetric. The scope for the composition degree of freedom will remain ostensibly modest: we do not aim to grapple with the enormous richness of biological lipid mixtures, and we will eschew proteins entirely. Instead, we will restrict our study to the widely studied case of ternary systems comprising a saturated lipid species, an unsaturated one, and cholesterol. These are the simplest known lipid mixtures that capture a phenomenon widely believed to be of physiological significance: the possibility of coexistence between two fluid phases exhibiting different degrees of order. Considering bilayer asymmetry we will go beyond the usual discussion of leaflet-specific lipidomes and emphasize the importance of other thermodynamic variables that can differ between the two sides of the membrane, with an emphasis on stresses and torques.This introduction serves to very briefly set the stage for these two main players—reminding our readers of a few key facts of complex biomembranes, and how these tend to be captured in simplified model systems.
1.1 Compositional complexity in nature
Biomembranes feature an astoundingly diverse lipidome:1,2 thousands of chemically distinct lipids are synthesized in the endoplasmic reticulum (ER) of a typical eukaryotic cell, whose individual membrane organelles are kept at unique compositions while still hosting hundreds of individual species.3 This complexity is challenging to even categorize,4 but it is anything but random, even though its purpose is not well understood.Since chemically distinct lipids interact differently with one another, we should expect that they do not mix ideally. If the interactions are sufficiently dissimilar, phase separation might occur. The by far most extensively studied instances of this possibility are “lipid rafts”,5–9 whose 2006 consensus definition describes them as “small (10–200 nm), heterogeneous, highly dynamic, sterol- and sphingolipid-enriched domains that compartmentalize cellular processes.”10 While having many putative effects on a wide spectrum of biomembrane functions, their precise nature (and even existence) has been famously controversial.11,12 All the same, decades of data on highly non-ideal mixing need to be explained. Recent reviews13,14 suggest that rafts will remain protagonists in this story, even though almost surely as more subtle actors than originally envisioned.
Of course, in addition to lipids, biomembranes also contain a host of peripheral or integral membrane proteins, which add further complexity, but for the sake of the present discussion we will summarily ignore them. This smacks of impermissible simplification, so let us offer a few thoughts to ease the discomfort:
(1) We will subsequently also ignore more than 99% of all lipid species, aiming for a model system that captures some emergent phase behavior, not an intricate lipidomic fingerprint.
(2) If the lipid matrix becomes laterally inhomogeneous, this will subsequently affect the proteins, but in a first step we can imagine them simply adjusting their distribution in response to the spatially nontrivial lipid background.
(3) In a second step, uneven protein partitioning between different lipid phases will in turn change the properties of these phases, further tweaking the distribution of lipids.
We can think of points 2 and 3 as the beginnings of an iterative process that adjusts the lipids, then the proteins, then again the lipids, then again the proteins—and so on. Mathematically, this constitutes a perturbation expansion in some lipid–protein coupling parameter. We will proceed on the hope that its first terms capture the main physics reasonably well. This is rigorously true if that coupling parameter is (in some sense) small—but, of course, this almost surely depends on the situation, and so we have to remain vigilant.
1.2 Ternary model systems
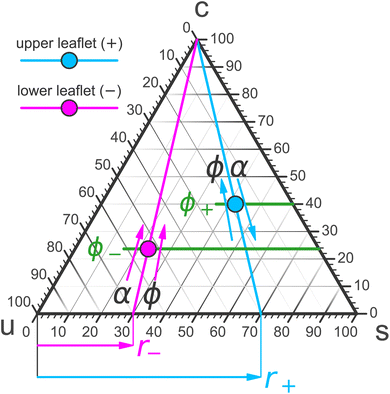
Mixed membranes comprising hundreds of distinct lipid species cannot be studied with any expectation of experimental reproducibility and precise theoretical understanding. Model systems are clearly needed, but from the outset it is not obvious how far we may simplify. Remarkably, more than two decades of research strongly suggest that ternary systems consisting of a saturated lipid species, an unsaturated species, and cholesterol capture many of the key physical properties at the heart of biomembrane phase behavior.15–31 Specifically, these systems exhibit the phenomenon of liquid–liquid phase separation, which offers tantalizing connections to raft-like domains. A particularly intriguing aspect is that the liquid–liquid coexistence region terminates in a critical point,32–38 which has also been observed in cellular membranes (including its Ising-like critical exponents!).39 This underscores the presence of universality—which often justifies the use of even highly simplified models.The constraint that the three mole fractions {ϕu, ϕs, ϕc} must sum to 100% reduces the independent degrees of freedom from 3 to 2. An elegant way to turn this into a “plotting strategy” is to exploit Viviani's theorem: the sum of the shortest distances from any interior point of an equilateral triangle to its sides is constant and equal to the triangle's height. As a corollary, the three symmetric lines radiating out from this point parallel to the triangle's sides can be used to set up coordinates which add up to a fixed number, conveniently chosen as 100%. This is illustrated in Fig. 1 using the point ϕu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕs
ϕs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕc = 20
ϕc = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30. We can hence represent ternary mixtures as follows: pure components correspond to the corners of the triangle, binary mixtures live on the sides connecting the respective two pure corners, and ternary mixtures are located anywhere in the interior of the triangle.
30. We can hence represent ternary mixtures as follows: pure components correspond to the corners of the triangle, binary mixtures live on the sides connecting the respective two pure corners, and ternary mixtures are located anywhere in the interior of the triangle.
Adding cholesterol (i.e., “moving up”), opens a second 2-phase region near the saturated corner (tie-lines are shown in green) with a cholesterol-poor gel-phase coexisting with a more cholesterol-rich so-called “liquid ordered” (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o) fluid phase. Both 2-phase regions border at a 3-phase triangle, on whose third side a third 2-phase region is attached. Unlike the other two, it does not extend to its nearest triangle side (namely, uc), since at the chosen temperature cholesterol and the unsaturated species mix well (except that cholesterol precipitates at sufficiently high concentration—see below). Instead, the two phases coexisting across this region—the
o) fluid phase. Both 2-phase regions border at a 3-phase triangle, on whose third side a third 2-phase region is attached. Unlike the other two, it does not extend to its nearest triangle side (namely, uc), since at the chosen temperature cholesterol and the unsaturated species mix well (except that cholesterol precipitates at sufficiently high concentration—see below). Instead, the two phases coexisting across this region—the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o phase and its “partner”, a less ordered (since more unsaturated) “liquid disordered” (
o phase and its “partner”, a less ordered (since more unsaturated) “liquid disordered” (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d) phase, become more similar and merge at a critical point. “Beyond” this point there is no meaningful distinction between a fluid ordered or disordered phase, any more than a meaningful distinction between liquid water and steam can be made past water's critical point—both merely being fluid phases of the same symmetry.
d) phase, become more similar and merge at a critical point. “Beyond” this point there is no meaningful distinction between a fluid ordered or disordered phase, any more than a meaningful distinction between liquid water and steam can be made past water's critical point—both merely being fluid phases of the same symmetry.
The solubility limit of cholesterol in PC-phospholipids is typically around 66%,40 above which it precipitates from the bilayer into crystals of cholesterol monohydrate. Once this happens, a point in the Gibbs phase triangle no longer reflects the membrane composition, but the resulting states still feature a stable membrane. In fact, they are experimentally very useful, because they anchor cholesterol's chemical potential to that of its monohydrate, permitting quantitative calibration between different membrane systems.41
If the temperature is such that even the saturated lipid is in a fluid phase, then the two gel-fluid coexistence regions vanish from the phase diagram, and with it also the 3-phase triangle. They are effectively “pushed down” to the us-binary line and all that survives is the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o/
o/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d coexistence. This may look like a very different phase diagram, but recall that gel phases are rarely physiologically relevant. What matters is the fluid–fluid coexistence region and its critical point, which remains intact, not gel-phase physics created by the pure-s-corner. We will subsequently discuss simpler “gel-free” versions of the ternary phase diagram and argue that for the purpose of understanding physiologically interesting ternary lipid mixtures these will suffice.
d coexistence. This may look like a very different phase diagram, but recall that gel phases are rarely physiologically relevant. What matters is the fluid–fluid coexistence region and its critical point, which remains intact, not gel-phase physics created by the pure-s-corner. We will subsequently discuss simpler “gel-free” versions of the ternary phase diagram and argue that for the purpose of understanding physiologically interesting ternary lipid mixtures these will suffice.
1.3 Membrane asymmetry
Lipid membrane asymmetry is not a recent addition to a biomembrane's complexity list. It was discovered at the very dawn of modern biomembrane science: Mark Bretscher's seminal paper42 on the subject appeared just 12 days after Singer and Nicholson published their “Fluid Mosaic Model.”43 The following year, Verkleij et al. proposed the first rough leaflet distribution in a human red blood cell,44 followed by similar results from other authors for platelets,45 the plasma membrane of nucleated cells,46–48 and some membrane organelles.49 Recent work by Lorent et al.50 confirmed these early findings and added highly fine-grained detail. Moreover, their bioinformatics analysis of transmembrane proteins anchored by a single-pass α-helix (in particular, that anchor's surface area imbalance) strongly suggests that plasma membrane asymmetry is evolutionarily conserved across all eukarya.It is worth highlighting that leaflet-specific lipidomes can exist only because spontaneous transitions of phospholipids between leaflets (“flip-flop” events) happen so slowly—between hours and days51—that active but slow cellular transmembrane sorting mechanisms can successfully counter the decay into a fully scrambled state. An important exception is cholesterol, whose flip-flop time is believed to be somewhere in the sub-microsecond to millisecond range.51–54 Hence, its concentration is thermodynamically equilibrated between leaflets on most experimentally and biophysically relevant timescales.
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o/
o/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d-like critical fluctuations in biomembranes were first observed in GPMVs.39
d-like critical fluctuations in biomembranes were first observed in GPMVs.39However, such bio-derived systems as exemplars for asymmetry have a number of drawbacks. The most obvious one is that they are very complicated: they consist of far more than just a few types of lipids, besides also containing many proteins.58–60 This not only makes it difficult to know (let alone control) their composition; if the goal is to specifically probe asymmetry, their substantial complexity adds numerous confounding factors. Furthermore, it appears that whatever asymmetric composition the plasma membrane has, GPMVs have lost at least some of it (they appear to be at least partially scrambled).60,61
Luckily, this situation has changed dramatically over the past decade: by now more than 70 protocols for synthesizing asymmetric bilayers have been published, which Krompers and Heerklotz have recently reviewed, classified into four major categories, and analyzed in terms of advantages and drawbacks.62 We believe that the availability of such clean model systems is a key driver of asymmetry's renaissance. And yet, the community has only just begun to explore the exciting opportunities this affords. This includes many now feasible research questions that are waiting to be realized, likely offering consequential insights into the biological situation.
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) .
.Differential stress is the difference between the two individual mechanical leaflet tensions,
| ΔΣ = Σ+ − Σ−, | (1) |
Bilayer torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is the thermodynamic observable conjugate to a membrane's extrinsic curvature J, i.e., the (generalized) force that drives bending,
is the thermodynamic observable conjugate to a membrane's extrinsic curvature J, i.e., the (generalized) force that drives bending,
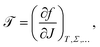 | (2) |
Differential stress can be rephrased as the existence of a preferred bilayer curvature J0,s at which this stress vanishes, because at fixed lipid content bending changes the leaflet reference areas measured some distance z0 away from the bilayer midsurface, to lowest order linear in the curvature. (The relevant reference surface at this distance z0 is the so-called “neutral surface,” at which bending and stretching energies decouple.) This implies that we should be able to write63
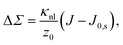 | (3) |
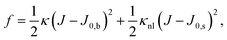 | (4) |
 | (5a) |
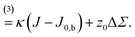 | (5b) |
Fig. 2 illustrates the sign conventions for these two terms.
Demanding that a flat membrane is torque free (i.e., it will voluntarily stay flat) yields
 | (6) |
Using common values on the right hand side (such as κ ≃ 30kBT, J0,b ≃ few ×10−2 mN m−1, and z0 ≃ 1 nm) shows that we should expect ΔΣ to be on the order of a few mN m−1, which is between one and two orders of magnitude larger than typical cellular membrane tensions.68
2 Towards ternary asymmetric phase diagrams
Whatever the precise physics of asymmetric ternary lipid mixtures will be, it is clear that these systems have more degrees of freedom than their symmetric counterparts—most obviously since we now have to deal with two nontrivial leaflet compositions. This means that we will not merely be asking how the phases in a diagram such as the one in Fig. 1 might change. The more profound question is: what type of phase diagrams should we be drawing in the first place? What are good thermodynamic variables to put on the axes of what kind of plot? How many degrees of freedom do we have, and what are they?2.1 Effective binary modeling
So far experiments offer little guidance, since leaflet-resolved phase diagrams are practically nonexistent. The first (and so far only) measurement of a leaflet-resolved binary phase diagram (a mixture of two phospholipids, DOPC and DPPC) was only published in 2023.69 While experimentally challenging, it is conceptually straightforward: the mole-fraction on each side is a single number, which yields a straightforward two-dimensional diagram for which theoretical predictions exist.70–72 Ternary lipid systems have also been studied theoretically, but the cholesterol component has been treated implicitly, essentially by considering a single order parameter that distinguishes![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o from
o from ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d (rendering the problem effectively that of a binary mixture), to which a rapidly flip-flopping cholesterol component is locked.70–75 At any rate, differential stress or considerations regarding torque have not been part of any analysis.
d (rendering the problem effectively that of a binary mixture), to which a rapidly flip-flopping cholesterol component is locked.70–75 At any rate, differential stress or considerations regarding torque have not been part of any analysis.
2.2 Counting degrees of freedom
 | (7) |
First the removal. Since cholesterol rapidly flip-flops between the leaflets, we need to satisfy the condition of equal chemical potential,
| μ+chol = μ−chol. | (8) |
This constraint reduces the number of degrees of freedom from 4 to 3. The cholesterol fractions ϕ+ and ϕ− in the two leaflets cannot be set to whatever values we desire; instead, we can only decide on the total mole fraction ϕ of cholesterol, defined via
 | (9) |
Now the addition. Compositional ternary diagrams such as the one in Fig. 1 only record mole fractions; they know nothing about the absolute number of lipids on the two different sides. It proves useful to include this missing thermodynamic information not via the individual lipid numbers N± but in terms of total lipid content, N+ + N−, and number difference, N+ − N−. The former captures potentially interesting physics pertaining to system size (which we will sidestep in this paper), while the latter homes in more directly on asymmetry. Considering that cholesterol rapidly flip-flops, it is more convenient to specify the abundance asymmetry via the phospholipid contingent, which does not change under cholesterol redistribution; let us hence define the phospholipid abundance asymmetry
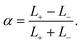 | (10) |
In the absence of cholesterol, changing the abundance by Δα changes the differential stress by ΔΔΣ = −KAΔα (assuming area additivity, since abundance then couples directly to area difference, the observable conjugate to differential stress). Shifting α by just a few percentage points would then change differential stress by several mN m−1, rendering α a fairly “stiff” degree of freedom.
We will see that once cholesterol is present, its ability to offset a phospholipid imbalance by redistributing into the less crowded leaflet permits much larger changes of α without incurring huge differential stress. Of note, recent experiments have claimed that the cytosolic leaflet of the human red blood cell contains about twice as many phospholipids as the exoplasmic one (i.e., α ∼ −33%),76 in line with the raw data of no less than five previous studies (see Table S1 in that reference). Such an enormous abundance asymmetry would profoundly affect cholesterol distribution and leaflet-specific phase behavior, both fields rife with their own controversial claims. We expect that further work dedicated to this complex interplay has the potential to resolve numerous contentious issues. Our goal here is to develop a theoretical framework that accounts for phospholipid abundance asymmetry, however large it may prove to be, such that its thermodynamic implications can be quantitatively examined.
Small changes in ϕ and α trigger small changes in the ϕ±, which are presumably linear. This shows that
 | (11) |
 | (12) |
To be clear: we are not guaranteed that we can always make every conceivable pair {ϕ+, ϕ−} coexist, since this local argument does not clarify global reach. Besides the fact that cholesterol does not dissolve in a membrane beyond ∼66%,40,41 permissible Δϕ and especially Δα will have feasibility limits of their own. Additionally, edge cases are likely problematic. For instance, it will be impossible to make a nonzero ϕ+ coexist with a vanishing ϕ−, because mixing entropy terms of the form ϕ log ϕ will create an infinite driving force at ϕ → 0 that cannot be balanced by any finite enthalpic terms.
To summarize the present discussion: we have argued that the thermodynamic phase space of our system is four-dimensional—already disregarding “obvious” variables such as the total number of lipids N = N+ + N− (i.e., the system size) and the temperature T, both of which we imagine fixed once and for all. Possible independent degrees of freedom are {r+, r−, ϕ+, ϕ−} or alternatively {r+, r−, ϕ, α}. The former can be easily visualized as two points in a ternary phase diagram, and realizing them requires a judicious choice of ϕ and α. The latter may be more easily tunable experimentally and yield leaflet-specific cholesterol fractions ϕ+ and ϕ− that arise after flip-flop assisted chemical potential equilibration.
2.3 Some important new linear response functions
The matrix elements in eqn (11) describe the local linear relation for how {ϕ+, ϕ−} vary with {ϕ, α}. In other words, they quantify the linear response of the leaflet cholesterol fractions to the external control parameters of cholesterol content and phospholipid abundance.More generally, we can define susceptibilities that measure the response to changes in external control variables—as is routinely done in thermodynamics. For now, let us focus on responses to changing {ϕ, α}, which are most closely related to the question of asymmetry and ternary mixtures, even though we could also include {r+, r−} into the mix.
The observables whose perturbation we will discuss in a bit more detail here are differential stress ΔΣ and bilayer torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , so let us define their α-related susceptibilities
, so let us define their α-related susceptibilities
 | (13a) |
 | (13b) |
 | (13c) |
 | (13d) |
These would almost surely benefit from easier notations (at least this one is informative), as well as some intuitive names, since cumbersome attempts like “iso-compositional differential stressability” for χΔΣα|ϕ are not likely to catch on. Nevertheless, as linear response functions they satisfy the joint differential relation
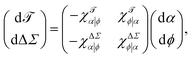 | (14) |
 | (15) |
While it might be difficult to determine these susceptibilities quantitatively in experiment, they will all have a noticeable impact on the response of vesicles, especially micron-scale giant unilamellar vesicles (GUVs), to the respective changes (see Section 3 below). At the very least, their signs would be straightforward to observe, and possibly even whether the response is “strong” or “mild”. Of course, in simulations they are very accessible, and we will discuss some examples below.
Let us elaborate on the sign. We expect the susceptibilities with respect to changes in α to have a definite sign, because α itself has a definite sign baked into it. Recall that increasing α means that we will increase the phospholipid content in leaf+ relative to leaf−. This will put leaf+ under compression and leaf− under tension. Since stress is the negative of pressure, this change will make the derivative ∂ΔΣ/∂α negative, and for that reason we propose the extra minus sign in the definition of χΔΣα|ϕ, which would then render it positive. A similar argument explains the extra minus sign in the definition of χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ: pushing more phospholipids into leaf+ gives rise to a torque that would drive “down-bending” (i.e., leaf+ will bulge “out”), and from eqn (5b) or (6) it is clear that this corresponds to a negative torque, which the extra minus sign then turns into a positive susceptibility.
α|ϕ: pushing more phospholipids into leaf+ gives rise to a torque that would drive “down-bending” (i.e., leaf+ will bulge “out”), and from eqn (5b) or (6) it is clear that this corresponds to a negative torque, which the extra minus sign then turns into a positive susceptibility.
The situation is slightly more subtle, though, because in the presence of cholesterol the membrane can relax the differential stress induced by a change in α by cholesterol relocation from the compressed to the tense leaflets. The same holds for the torque: its change, too, will be curtailed by cholesterol flip-flop. Unless this cholesterol relocation triggers a compositional instability (which might happen if we push one side into a phase coexistence region), we would expect it to reduce the changes in ΔΣ or ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (compared to the cholesterol-free case), but not to actually flip the sign. This is not a rigorous argument, though.
(compared to the cholesterol-free case), but not to actually flip the sign. This is not a rigorous argument, though.
Importantly, the response functions with respect to cholesterol, χΔΣϕ|α and χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α, behave very differently. If we increase ϕ, this neither means that cholesterol will increase in a specific leaflet, nor does it distribute in equal amounts between the two leaflets (even though it will distribute such that μchol+ = μchol− remains true). Consider the following illustrative scenarios:
ϕ|α, behave very differently. If we increase ϕ, this neither means that cholesterol will increase in a specific leaflet, nor does it distribute in equal amounts between the two leaflets (even though it will distribute such that μchol+ = μchol− remains true). Consider the following illustrative scenarios:
(1) A cholesterol-free compositionally symmetric membrane is under some lipid abundance asymmetry α > 0. If we add cholesterol, the chemical partitioning forces are equal, but the differential stress ΔΣ due to α will guide cholesterol preferentially into the leaflet whose tension is larger, thus reducing the magnitude of ΔΣ. This will render χΔΣϕ|α negative if the differential stress is positive and positive if the differential stress is negative.
(2) A compositionally asymmetric membrane is under vanishing differential stress. If we add cholesterol, there is no driving force coming from the stress, but the compositional difference will now bias cholesterol—away from the phase that already contains a higher mole fraction of cholesterol but also towards the side into which cholesterol partitions better (say, the more saturated one). The resulting change in differential stress—and hence the sign of χΔΣϕ|α—can be either positive or negative, depending on how these drivers pan out.
We have previously observed both of these cases in simpler binary systems.77 Notice that the undetermined sign of χΔΣϕ|α, rather than being annoying, means that the mere direction of an effect will be informative about some conceivably difficult to ascertain membrane observables—such as, is there a cholesterol imbalance between the leaflets, or is there pre-existing differential stress. Experiments that change ϕ might thus be very informative.
We expect the situation for χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α to be similar: the sign is not pre-determined and instead depends on the specifics of the underlying situation. It is unfortunately more difficult to make analogous arguments, because the response of cholesterol's inter-leaflet distribution to changes in torque are more subtle. The differential stress contribution to the torque,
ϕ|α to be similar: the sign is not pre-determined and instead depends on the specifics of the underlying situation. It is unfortunately more difficult to make analogous arguments, because the response of cholesterol's inter-leaflet distribution to changes in torque are more subtle. The differential stress contribution to the torque, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) Σ = z0ΔΣ is of course the same, but the part of the torque due to lipid shape,
Σ = z0ΔΣ is of course the same, but the part of the torque due to lipid shape, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) J = −κJ0,b, requires an answer to the question how J0,b changes with cholesterol concentration—a famously tricky problem that might not be simply captured by a linear combination of some “bare” intrinsic lipid curvatures.78–80 It seems to us that a workable rule of thumb is that at sufficiently large cholesterol content, any further increase will tend to reduce the magnitude of torque. One way of seeing this is that in the “theorist's limit” of ϕ → 1 we reach a perfectly symmetric membrane, which hence has zero torque (and also zero differential stress). The “ultimate” direction into which
J = −κJ0,b, requires an answer to the question how J0,b changes with cholesterol concentration—a famously tricky problem that might not be simply captured by a linear combination of some “bare” intrinsic lipid curvatures.78–80 It seems to us that a workable rule of thumb is that at sufficiently large cholesterol content, any further increase will tend to reduce the magnitude of torque. One way of seeing this is that in the “theorist's limit” of ϕ → 1 we reach a perfectly symmetric membrane, which hence has zero torque (and also zero differential stress). The “ultimate” direction into which ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) must change as ϕ increases is hence clear, even though at intermediate concentrations additional drivers may well complicate matters. (Of course, the same argument can be made for the differential stress.)
must change as ϕ increases is hence clear, even though at intermediate concentrations additional drivers may well complicate matters. (Of course, the same argument can be made for the differential stress.)
2.4 Zero torque foliations
After identifying a set of variables that specify the thermodynamic state, all other observables will be functions of those. For instance, if we initially pick two desired leaflet compositions {r−, ϕ−} and {r+, ϕ+}, then the {ϕ, α} values needed to realize them are functions of those. Likewise, observables such as differential stress, ΔΣ, or bilayer torque,![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , are now set, and neither of them is generally zero. For the differential stress that is intuitively easy to see: two arbitrarily chosen leaflet compositions generally do not coexist in their cholesterol content across the leaflets. To prevent a net flux from one leaflet to the other, we need to set up a stress difference that opposes such a translocation.
, are now set, and neither of them is generally zero. For the differential stress that is intuitively easy to see: two arbitrarily chosen leaflet compositions generally do not coexist in their cholesterol content across the leaflets. To prevent a net flux from one leaflet to the other, we need to set up a stress difference that opposes such a translocation.
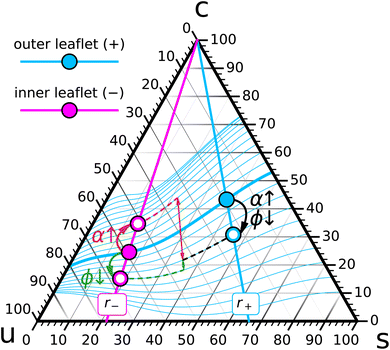
Let us follow this idea a bit further. Pick a composition {r−, ϕ−} for leaf− (the magenta point in Fig. 4) and try to arrange for chemical coexistence with compositions in leaf+ that have a fixed saturation ratio r+ but different values of ϕ+ (points on the bold cyan r+ line in Fig. 4). Each such point will require some specific {ϕ, α} combination, and once we have found it, it will result in a bilayer with some differential stress, and some torque, whose value depends on ϕ+:
| ΔΣ(ϕ+) = ΔΣ(ϕ+|r−, ϕ−, r+), | (16a) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ+) = (ϕ+) = ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ+|r−, ϕ−, r+). (ϕ+|r−, ϕ−, r+).
| (16b) |
Consider for instance the torque: the function ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ+) varies with ϕ+ in some conceivably complicated and yet-to-be-determined way, and for some value of ϕ+ it might vanish (the cyan point on the bold cyan r+ line in Fig. 4). At this special point the two ternary compositions in the two leaflets do not just chemically coexist; they coexist at zero torque, which constitutes an additional mechanical condition. Constraint counting of this type does not answer the question how many solutions
(ϕ+) varies with ϕ+ in some conceivably complicated and yet-to-be-determined way, and for some value of ϕ+ it might vanish (the cyan point on the bold cyan r+ line in Fig. 4). At this special point the two ternary compositions in the two leaflets do not just chemically coexist; they coexist at zero torque, which constitutes an additional mechanical condition. Constraint counting of this type does not answer the question how many solutions ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ+) = 0 has. However, in light of the underlying physical situation we expect this equation to identify a small number of points along the r+ curve, likely just a single one, that coexist with the composition {r−, ϕ−} at vanishing bilayer torque.
(ϕ+) = 0 has. However, in light of the underlying physical situation we expect this equation to identify a small number of points along the r+ curve, likely just a single one, that coexist with the composition {r−, ϕ−} at vanishing bilayer torque.
Let us now also vary the r+ line, and for each one find the special zero-torque-point(s) on it (a few are illustrated as smaller cyan points in Fig. 4). Their collection forms a one-dimensional curve in the ternary phase diagram, namely, the locus of all leaflet compositions in leaf+ that can coexist at vanishing torque with the given point {r−, ϕ−} in leaf−. This curve has to pass through the {r−, ϕ−} point, because this gives rise to a symmetric bilayer, and we know that such a system would also have zero torque.
Finally, we can construct such zero-torque-curves for any cholesterol fraction ϕ− on the r− line. This yields a foliation of the ternary phase diagram into zero torque coexistence curves: a specified composition {r−, ϕ−} in leaf− can in principle coexist with any composition {r+, ϕ+} in leaf+ (a set of dimension two), but only a one-dimensional subset ϕ+(r+|r−, ϕ−) coexists at zero torque.
We hasten to clarify that the zero-torque-curves we constructed depend on the points {r−, ϕ−} in leaf− to which we pinned them. We are not claiming that any two points selected on a given curve will coexist with one another at zero torque—this is a stronger condition that does not follow from the simple counting argument we have presented.
3 Zero torque states and their perturbations
We concluded the previous section by specifically discussing a coexistence between the two leaflets that ensures a vanishing torque. Why is this interesting?3.1 Stability of giant unilamellar vesicles
There is no reason why compositionally asymmetric membranes should be flat: we have broken the reflection symmetry of a membrane (with respect to its midplane) in terms of chemical identity, so we should expect that membrane shape itself also fails to obey that symmetry: it will generally be curved—meaning, it will be driven into a curved state by a nonzero torque![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) . Let us estimate how much curvature we should expect. If the membrane is free of any additional stresses (especially differential stress) then its spontaneous bilayer curvature should be the difference of the individual spontaneous leaflet curvatures J0,m±, weighted by their respective monolayer bending rigidities κm±:
. Let us estimate how much curvature we should expect. If the membrane is free of any additional stresses (especially differential stress) then its spontaneous bilayer curvature should be the difference of the individual spontaneous leaflet curvatures J0,m±, weighted by their respective monolayer bending rigidities κm±:
 | (17) |
Considering the J0,m values of typical lipids,81 equilibrium radii R0,b = 2/J0,b of asymmetric vesicles are usually on the order of a few tens of nanometers (the size of small unilamellar vesicles, SUVs), unless we pick two lipid species that just happen to have very similar spontaneous curvatures. However, many techniques have been developed to create asymmetric giant unilamellar vesicles (GUVs),62 whose curvature radii are easily two orders of magnitude larger than those of SUVs. Why are they stable against submicroscopic tubulation?
A possible answer is that despite the large spontaneous bilayer curvature J0,b originating from the lipid shape asymmetry, the net torque is actually very small, because a counter-torque arising from differential stress cancels the spontaneous curvature torque.63,64,66,67 As we argued following eqn (6), this would mean that an asymmetric flat membrane—and hence, essentially any asymmetric GUV—has to experience a differential stress of a few mN m−1.
Conversely, that asymmetric GUVs should have ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ≃ 0 implies that the zero torque foliations discussed in Section 2.4 become constraints on the compositions that may coexist across a GUV's leaflet: once the composition on one side is fixed, the composition on the other is limited to a one-dimensional slice through the ternary phase diagram.
≃ 0 implies that the zero torque foliations discussed in Section 2.4 become constraints on the compositions that may coexist across a GUV's leaflet: once the composition on one side is fixed, the composition on the other is limited to a one-dimensional slice through the ternary phase diagram.
As an example: we propose that the ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0 constraint will fix the abundance asymmetry of GUVs during their creation. The precise mechanism is likely complicated and will depend on the protocol for making asymmetric GUVs in the first place, but our stability argument sidesteps such details and simply notes the following: if the saturation ratios {r+, r−} are set, then all that needs to be determined are the {ϕ+, ϕ−} values, via suitable choices of {ϕ, α}. However, the condition
= 0 constraint will fix the abundance asymmetry of GUVs during their creation. The precise mechanism is likely complicated and will depend on the protocol for making asymmetric GUVs in the first place, but our stability argument sidesteps such details and simply notes the following: if the saturation ratios {r+, r−} are set, then all that needs to be determined are the {ϕ+, ϕ−} values, via suitable choices of {ϕ, α}. However, the condition ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0 selects a one-dimensional subset from those. For instance, if the asymmetric creation protocol somehow fixes ϕ, then the condition
= 0 selects a one-dimensional subset from those. For instance, if the asymmetric creation protocol somehow fixes ϕ, then the condition ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0 sets α, because any other choice of α would not produce a GUV that is mechanically stable against tubulation. Almost the same argument holds if the creation process instead fixes ϕ−. The very existence of a stable asymmetric GUV means that we must have achieved torque balance, and whatever compositional arrangements materialized, there is only one corresponding α that will do so.
= 0 sets α, because any other choice of α would not produce a GUV that is mechanically stable against tubulation. Almost the same argument holds if the creation process instead fixes ϕ−. The very existence of a stable asymmetric GUV means that we must have achieved torque balance, and whatever compositional arrangements materialized, there is only one corresponding α that will do so.
3.2 Perturbing cholesterol content and abundance
Since perturbations of a vesicle's thermodynamic state need not keep the two leaflet compositions on the same zero-torque-foliation, we expect that they trigger shape deformations—anywhere from mild ones such as sphere → prolate → oblate → stomatocyte,82,83 up to the formation of membrane tubules.84–87 Let us discuss two specific examples, related to changes of ϕ and α.Lowering ϕ will reduce the cholesterol leaflet concentrations ϕ±, even though not necessarily by the same amount. More importantly, we generally have no guarantee that the two new points will still share a zero-torque foliation curve. Stated in terms of the response functions defined in Section 2.3, there is no reason to believe the susceptibility χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α vanishes (we will see it might, but only for very special conditions). As a consequence, we expect that the GUV would want to deform—if it can. Deflated GUVs should therefore have a tendency to assume new shapes, and since the shape diagrams for deflated vesicles are well understood,82,83 the nature of these deformations will alert us at the very least to the sign of χ
ϕ|α vanishes (we will see it might, but only for very special conditions). As a consequence, we expect that the GUV would want to deform—if it can. Deflated GUVs should therefore have a tendency to assume new shapes, and since the shape diagrams for deflated vesicles are well understood,82,83 the nature of these deformations will alert us at the very least to the sign of χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α under the present conditions.
ϕ|α under the present conditions.
To simplify the discussion, we will assume that the saturation ratio r+ on the outer leaflet of the GUV remains fixed during the lipid addition process. This can be done by loading the cyclodextrins with a ratio of u- and s-lipids that reflects r+ (possibly adjusted to account for different complexation strengths). Alternatively, we could appeal to the fact that percent-level changes in α require percent-level changes in L+ (in fact, ΔL+/L = Δα/(1 − α)), but these do generally not change the saturation ratio r+ significantly, unless it is close to 0.
As Fig. 5 indicates, the change in abundance α has opposite effects on the leaflets. Adding phospholipids to the outer leaflet will put it under compression and hence squeeze cholesterol into the inner leaflet, which had been put under tension due to the change of α. Unlike in the cholesterol depletion scenario from Section 3.2.1, where the compositions moved into the same directions and so could potentially remain quite close to ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0, this is not an option when we tune α: ϕ+ moves down while ϕ− moves up, and so the membrane will definitely develop a net torque. While it is difficult to directly compare the magnitudes of effects driven by ϕ and α, since these two variables (albeit dimensionless) measure different things, we could compare the change in
= 0, this is not an option when we tune α: ϕ+ moves down while ϕ− moves up, and so the membrane will definitely develop a net torque. While it is difficult to directly compare the magnitudes of effects driven by ϕ and α, since these two variables (albeit dimensionless) measure different things, we could compare the change in ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) under conditions that give rise to the same change in ϕ+, as is illustrated in Fig. 5. It appears evident that such a change in abundance would perturb the torque balance more strongly. Rather loosely speaking, this might translate to the statement that ternary GUVs are easier to mechanically perturb with phospholipids than with cholesterol.
under conditions that give rise to the same change in ϕ+, as is illustrated in Fig. 5. It appears evident that such a change in abundance would perturb the torque balance more strongly. Rather loosely speaking, this might translate to the statement that ternary GUVs are easier to mechanically perturb with phospholipids than with cholesterol.
4 Computational illustrations
Many of the connections we have described so far cannot (yet) be checked experimentally, but we are convinced that the rapidly growing sophistication of experimental techniques will change this in the near future. Until then, it will be useful to employ computational techniques to not just check the theoretical picture but also identify unexpected phenomena that warrant further study.4.1 Coarse-graining as the arena for modeling
The reality of finitely available computing time puts limits on how big a system we can simulate, and for how long. Coarse-grained (CG) simulations are a popular way to overcome this constraint: develop a force field at a lower level of resolution that strives to capture physics at longer time scales and larger length scales by summarily encoding finer-scale physics in effective interactions between CG degrees of freedom. While pragmatically expedient, we would like to add that this is also good physics: a universally intriguing property of nature is that large-scale physics almost always depends on only a small number of effective parameters, with much of the intricate finer-scale detail having been rendered irrelevant. If so, it behooves us to leave such irrelevant detail out of our models, too. Notice that if we happen to ignore too much and our model no longer works, we thereby learn a deep lesson about what constitutes relevant physics.Recall, though, that (i) in particle-based simulations we are (for better or worse) not interested in the long scales but the short ones and (ii) we will also need to sample compositional fluctuations, which relax on the diffusive scale rD = Dq2, with D being the lipid diffusion constant. Comparing q3 vs. q2 shows that diffusive modes will actually relax even slower than curvature modes at sufficiently small scales. Where is the cross-over? From κq×3/4η = Dq×2 we get λ× = 2π/q× = πκ/2Dη, and using typical values κ ≃ 30kBT, D ≃ 5 μm2 s−1 and η = 10−3 Pa s yields λ× ≃ 40 μm. Hence, at any computational scale that bothers to actually represent lipids, we are deeply in the regime where compositional relaxation is the bottleneck.
Since the largest wavelength at which we need to sample in a simulation is the box length L, the characteristic relaxation time is rD−1 = L2/4π2D. Taking L ≃50 nm (chosen to host raft-like heterogeneities at the few tens of nanometer scale), we find rD−1 ≃ 13 μs. While doable at the atomistic level with modern high performance computing, this remains a serious challenge and is not a feasible means to scan parameter space.
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o/
o/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d phase coexistence in ternary mixtures, as illustrated in Fig. 6.
d phase coexistence in ternary mixtures, as illustrated in Fig. 6.
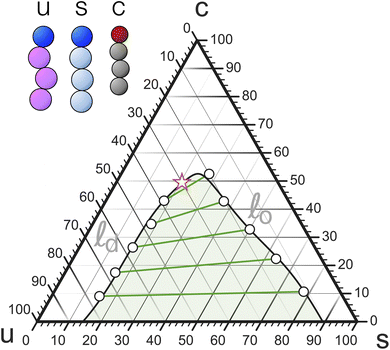 | ||
Fig. 6 Phase diagram of a ternary mixture in the Cooke lipid model of a lipid mixture, showing ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o/ o/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d coexistence and (the approximate location of) its critical point (adapted from ref. 98). d coexistence and (the approximate location of) its critical point (adapted from ref. 98). | ||
The time scale is more subtle. In principle, CG degrees of freedom also have a mass m, and this defines a time scale  , but this scale only matters for the calculation of instantaneous dynamical quantities, such as the kinetic energy. Longer time scale dynamics—diffusion, bending mode or chain relaxations, lipid flip-flop, etc.—is not well described by τbare, because CG models are virtually always tuned to reproduce thermodynamic equilibrium properties, not to also rescue the dynamics. In fact, the strongly sped-up dynamics resulting from a much smoother free energy landscape is a major redeeming quality of coarse-graining.
, but this scale only matters for the calculation of instantaneous dynamical quantities, such as the kinetic energy. Longer time scale dynamics—diffusion, bending mode or chain relaxations, lipid flip-flop, etc.—is not well described by τbare, because CG models are virtually always tuned to reproduce thermodynamic equilibrium properties, not to also rescue the dynamics. In fact, the strongly sped-up dynamics resulting from a much smoother free energy landscape is a major redeeming quality of coarse-graining.
The way to translate CG dynamics into real world units is then to agree on a specific dynamical process—say, diffusion—and interpret the CG unit τ such that CG simulations of that process quantitatively map to those in the real world. For example, when a CG lipid diffusion constant is D = 0.01σ2/τ (as measured for the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d phase in our model98) and D = 5 μm2 s−1 in the lab,103 setting those equal (and recalling σ = 0.75 nm) defines τ ≈ 1 ns. This for instance shows that diffusive relaxation over a 50 nm = 67σ scale happens over the time scale 11
d phase in our model98) and D = 5 μm2 s−1 in the lab,103 setting those equal (and recalling σ = 0.75 nm) defines τ ≈ 1 ns. This for instance shows that diffusive relaxation over a 50 nm = 67σ scale happens over the time scale 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ, which in our case takes about 20 h on a 32 core node.
000τ, which in our case takes about 20 h on a 32 core node.
We ran our simulations using the ESPResSo package,104 using an integration time step δt = 0.005τ. We reach the canonical ensemble via a standard Langevin thermostat,105 with a friction constant γ = 1m/τ. To realize membranes under zero lateral tension we employed semi-anisotropic boundary conditions using a barostat of Kolb/Dünweg106 type with a box mass Q = 0.01m/σ4 and a friction constant γQ = 2 × 10−4m/σ4. Our simulations typically contained 2048 lipids and ran between 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ and 100
000τ and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ, with the first 20
000τ, with the first 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ being used for thermalization.
000τ being used for thermalization.
4.2 Coexisting leaflets at very different saturation ratios
We will start by exploring coexisting leaflets that differ markedly in their saturation ratio, which creates sizable driving forces for cholesterol from one into the other. Specifically, we picked| r− = 1/8 = 0.125, | (18a) |
| r+ = 5/6 ≈ 0.833. | (18b) |
The low-saturation r− line in leaf− bypasses the coexistence region, while the more ordered high-saturation r+ line in leaf+ stays outside it for ϕ ≳ 20%. Given how far the coexistence region reaches on the s-side for low cholesterol content, it is difficult to entirely avoid it, unless we move very close to the triangle's sc-side, which might bring us uncomfortably close to some not fully resolved gel complications98 in the s-corner of the diagram. Observe that with this choice, cholesterol chemically prefers to partition into leaf+.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ, and sampled for typically another 80
000τ, and sampled for typically another 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ during which we measured a variety of observables, in particular the cholesterol distribution and asymmetry, differential stress, and torque. We found that within this domain the torque
000τ during which we measured a variety of observables, in particular the cholesterol distribution and asymmetry, differential stress, and torque. We found that within this domain the torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ,α) can be represented remarkably well by a quadratic (reduced χ2 = 0.11), so we empirically fit it to
(ϕ,α) can be represented remarkably well by a quadratic (reduced χ2 = 0.11), so we empirically fit it to
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ,α) = c0 + c1,ϕϕ + c1,αα + c2,ϕϕϕ2 + c2,ααα2 + c2,ϕαϕα. (ϕ,α) = c0 + c1,ϕϕ + c1,αα + c2,ϕϕϕ2 + c2,ααα2 + c2,ϕαϕα.
| (19) |
We will refer to this as the “torque surface”.
Fig. 7 shows a contour plot of that surface. For sufficiently negative values of the abundance α, i.e. when leaf+ becomes increasingly depleted of phospholipids, the torque is positive (i.e., the membrane would want to “curl up” if not prevented by the periodic boundary conditions; see Fig. 2 for a clarification of the torque's sign). Conversely, if leaf+ is sufficiently overcrowded, the torque becomes negative. In between the torque crosses zero at a location dependent on the overall cholesterol content ϕ. This zero-torque-curve describes the possible states of mechanically stable GUVs, which due to their essential flatness cannot harbor any significant torque before deforming or even tubulating.
 | ||
Fig. 7 Contour plot of the (empirically fitted) torque surface ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ,α) for the saturation ratios r− = 0.125 and r+ = 0.833. The bold solid curve is the location where the torque vanishes and hence GUVs would be mechanically stable, the thin teal dashed curve is the nullcline at which ∂ (ϕ,α) for the saturation ratios r− = 0.125 and r+ = 0.833. The bold solid curve is the location where the torque vanishes and hence GUVs would be mechanically stable, the thin teal dashed curve is the nullcline at which ∂![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) /∂ϕ = χ /∂ϕ = χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α = 0, i.e., where the torque does not change upon small variations of overall cholesterol content. The bold white dashed curve is the locus of states for which ΔΣ = 0 (see also Fig. 10). ϕ|α = 0, i.e., where the torque does not change upon small variations of overall cholesterol content. The bold white dashed curve is the locus of states for which ΔΣ = 0 (see also Fig. 10). | ||
In the absence of cholesterol, ϕ = 0, when the abundance asymmetry vanishes as well, α = 0, but the torque is nevertheless not zero but slightly positive. This happens because the system is still not symmetric; most notably, leaf+ contains an approximately six times larger fraction of saturated lipids, which have (at least in pure phases) an approximately 25% smaller area per lipid.98 Since for α = 0 the number of phospholipids is the same in both leaflets, the relaxed leaflet area in leaf+ is smaller than in leaf−, giving rise to a positive differential stress, whose torque contribution ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) Σ = z0ΔΣ wants to bend the bilayer up (see Fig. 2b).
Σ = z0ΔΣ wants to bend the bilayer up (see Fig. 2b).
Adding cholesterol to this state will preferentially recruit it into leaf+ to release the area strain, an effect that will become even stronger when we lower α. Independent of these mechanical considerations, the higher saturation ratio r+ in leaf+ will also favor the partitioning of cholesterol into it. Hence, there are two reasons that favor ϕ+ growing faster than ϕ−, and as a consequence, the torque decreases. Notice, though, that as we increase the abundance asymmetry α, the stress-derived torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) Σ weakens and at some point reverses, as leaf− becomes depleted. Where will the cholesterol go, now that the two drivers compete? As the contour lines in Fig. 7 show, the trend is indeed non-monotonic: initially,
Σ weakens and at some point reverses, as leaf− becomes depleted. Where will the cholesterol go, now that the two drivers compete? As the contour lines in Fig. 7 show, the trend is indeed non-monotonic: initially, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) still decreases, since chemical partitioning bias still drives more cholesterol into leaf+. But at some point it reverses, as the increasing ϕ+ value weakens further recruitment of even more cholesterol and entropy favors a more even distribution, which together ends up reducing the magnitude of the torque. The teal dashed line in Fig. 7 marks the location of that reversal: at it, the contour lines are horizontal and χ
still decreases, since chemical partitioning bias still drives more cholesterol into leaf+. But at some point it reverses, as the increasing ϕ+ value weakens further recruitment of even more cholesterol and entropy favors a more even distribution, which together ends up reducing the magnitude of the torque. The teal dashed line in Fig. 7 marks the location of that reversal: at it, the contour lines are horizontal and χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α = 0 (which is exactly the nullcline of ∇
ϕ|α = 0 (which is exactly the nullcline of ∇![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) for the variable α).
for the variable α).
![[scr T, script letter T]](https://www.rsc.org/images/entities/b_char_e533.gif) ϕ|α. If we cut the torque surface at some fixed value of α, we can single out the dependence of torque on ϕ:
ϕ|α. If we cut the torque surface at some fixed value of α, we can single out the dependence of torque on ϕ: ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ|α). The derivative of this function with respect to ϕ is exactly the susceptibility χ
(ϕ|α). The derivative of this function with respect to ϕ is exactly the susceptibility χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α defined in eqn (13d), which measures how the torque changes with cholesterol content at a fixed value of α. This response function is shown in Fig. 8—itself as a function of ϕ and parametrized for a set of α-values. Due to our simple quadratic representation (19) of
ϕ|α defined in eqn (13d), which measures how the torque changes with cholesterol content at a fixed value of α. This response function is shown in Fig. 8—itself as a function of ϕ and parametrized for a set of α-values. Due to our simple quadratic representation (19) of ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (ϕ,α), we find simple lines. For most of the values the response function is negative, showing that addition of cholesterol tends to reduce the torque. However, this reduction weakens as cholesterol increases, and the χ
(ϕ,α), we find simple lines. For most of the values the response function is negative, showing that addition of cholesterol tends to reduce the torque. However, this reduction weakens as cholesterol increases, and the χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α(ϕ) lines cross zero and become positive. This happens earlier when the abundance asymmetry is already larger. These zero crossings reflect the “trend reversal” we discussed in the previous section, i.e., the nullcline included in Fig. 7.
ϕ|α(ϕ) lines cross zero and become positive. This happens earlier when the abundance asymmetry is already larger. These zero crossings reflect the “trend reversal” we discussed in the previous section, i.e., the nullcline included in Fig. 7.
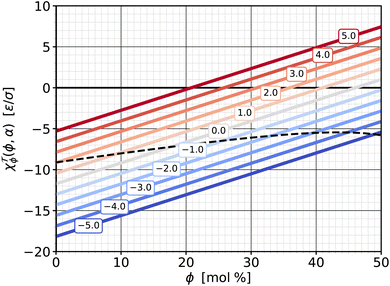 | ||
Fig. 8 Susceptibility χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α from eqn (13d) as a function of cholesterol content ϕ, parametrized by different values of phospholipid abundance α, as indicated in the boxed labels, and the saturation ratios from eqn (18). The dashed line shows the susceptibility for the special ϕ-dependent α values at which ϕ|α from eqn (13d) as a function of cholesterol content ϕ, parametrized by different values of phospholipid abundance α, as indicated in the boxed labels, and the saturation ratios from eqn (18). The dashed line shows the susceptibility for the special ϕ-dependent α values at which ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0 (i.e., on the zero-torque contour in Fig. 7). = 0 (i.e., on the zero-torque contour in Fig. 7). | ||
![[scr T, script letter T]](https://www.rsc.org/images/entities/b_char_e533.gif) α|ϕ. We can also cut the torque surface along constant-ϕ-slices, which gives us the complementary function
α|ϕ. We can also cut the torque surface along constant-ϕ-slices, which gives us the complementary function ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (α|ϕ), whose derivative with respect to α leads to the other torque-related response function, χ
(α|ϕ), whose derivative with respect to α leads to the other torque-related response function, χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ from eqn (13b). This susceptibility—again as a function of ϕ and for a set of different α is shown in Fig. 9.
α|ϕ from eqn (13b). This susceptibility—again as a function of ϕ and for a set of different α is shown in Fig. 9.
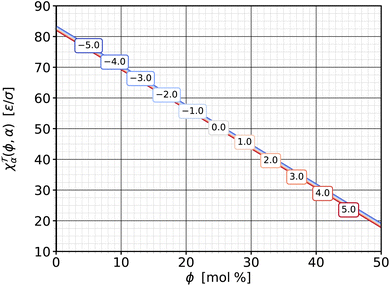 | ||
Fig. 9 Susceptibility χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ from eqn (13b) as a function of cholesterol content ϕ, parametrized by different values of phospholipid abundance α, as indicated in the boxed labels. The lines almost coincide, with smaller α values having ever so slightly larger susceptibilities. α|ϕ from eqn (13b) as a function of cholesterol content ϕ, parametrized by different values of phospholipid abundance α, as indicated in the boxed labels. The lines almost coincide, with smaller α values having ever so slightly larger susceptibilities. | ||
Several observations are notable here. First, the susceptibilities hardly depend on α. This means that ∂χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ/∂α = −∂2
α|ϕ/∂α = −∂2![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) /∂α2 ≈ 0: the cuts of the torque surface along constant ϕ are essentially straight lines. In Fig. 7 this can be recognized by the fact that the contour curves intersect any line with a fixed ϕ value at very evenly spaced points. These lie closer together for smaller ϕ, leading to larger slopes and higher χ
/∂α2 ≈ 0: the cuts of the torque surface along constant ϕ are essentially straight lines. In Fig. 7 this can be recognized by the fact that the contour curves intersect any line with a fixed ϕ value at very evenly spaced points. These lie closer together for smaller ϕ, leading to larger slopes and higher χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ values. Physically this means that a change Δ
α|ϕ values. Physically this means that a change Δ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) in membrane torque due to a change Δα in phospholipid abundance does not depend on the pre-existing abundance α. A change ΔΔA of the area excess ΔA between the two leaflets always changes the curvature in the same way—and the parallel surface theorem107,108 agrees: ΔΔA = 2Az0ΔJ, provided that adding or removing phospholipids always adds or removes the same area.
in membrane torque due to a change Δα in phospholipid abundance does not depend on the pre-existing abundance α. A change ΔΔA of the area excess ΔA between the two leaflets always changes the curvature in the same way—and the parallel surface theorem107,108 agrees: ΔΔA = 2Az0ΔJ, provided that adding or removing phospholipids always adds or removes the same area.
Second, the susceptibility χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ is positive. The definite sign (unlike what we have seen for the complementary partner χ
α|ϕ is positive. The definite sign (unlike what we have seen for the complementary partner χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α) derives from the expectation that adding phospholipids on one side invariably bends the membrane away from that side. Since adding lipids to leaf+ increases α, but a downward bending counts as a negative torque (cf. again Fig. 2), we have added an additional minus sign to the definition (13b) of χ
ϕ|α) derives from the expectation that adding phospholipids on one side invariably bends the membrane away from that side. Since adding lipids to leaf+ increases α, but a downward bending counts as a negative torque (cf. again Fig. 2), we have added an additional minus sign to the definition (13b) of χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ to arrange for a convenient positive sign. This mimics definitions such as κT = −(∂V/∂P)T/V for the isothermal compressibility (whose sign is fixed by a rigorous thermodynamic argument, though, not merely a strong expectation).
α|ϕ to arrange for a convenient positive sign. This mimics definitions such as κT = −(∂V/∂P)T/V for the isothermal compressibility (whose sign is fixed by a rigorous thermodynamic argument, though, not merely a strong expectation).
Third, the magnitude of χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ is noticeably larger than that of χ
α|ϕ is noticeably larger than that of χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ϕ|α. Small changes of the phospholipid abundance α change the torque more strongly than comparably small changes of the cholesterol content ϕ. As mentioned above, the reason is that changes in α have a sign built into it: all phospholipids are added or removed from the same leaflet, while cholesterol addition or removal is shared between the two leaflets (besides the fact that cholesterol molecules are also smaller).
ϕ|α. Small changes of the phospholipid abundance α change the torque more strongly than comparably small changes of the cholesterol content ϕ. As mentioned above, the reason is that changes in α have a sign built into it: all phospholipids are added or removed from the same leaflet, while cholesterol addition or removal is shared between the two leaflets (besides the fact that cholesterol molecules are also smaller).
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) as a function of the two thermodynamic variables ϕ and α, we can do the same with the differential stress ΔΣ. The procedure mirrors the one for the torque surface from Section 4.2.1; in particular, we again find that a quadratic fit captures the simulated data very well. Fig. 10 shows the result via a contour plot, amended again by the nullcline at which ∂ΔΣ/∂ϕ = χΔΣϕ|α = 0, a bold contour curve to highlight the place where the differential stress vanishes, and for comparison also the location of the curve where the torque vanishes. Let us summarize several notable points:
as a function of the two thermodynamic variables ϕ and α, we can do the same with the differential stress ΔΣ. The procedure mirrors the one for the torque surface from Section 4.2.1; in particular, we again find that a quadratic fit captures the simulated data very well. Fig. 10 shows the result via a contour plot, amended again by the nullcline at which ∂ΔΣ/∂ϕ = χΔΣϕ|α = 0, a bold contour curve to highlight the place where the differential stress vanishes, and for comparison also the location of the curve where the torque vanishes. Let us summarize several notable points:
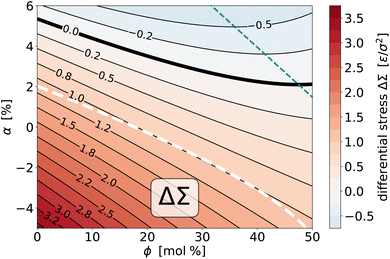 | ||
Fig. 10 Contour plot of the (empirically fitted) differential stress surface ΔΣ(ϕ, α) for the saturation ratios r− = 0.125 and r+ = 0.833. The bold solid curve is the location where the differential stress vanishes, the thin teal dashed curve is the nullcline at which ∂ΔΣ/∂ϕ = χΔΣϕ|α = 0, i.e., where the differential stress does not change upon small variations of overall cholesterol content. The bold white dashed curve is the locus of states for which ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0 (see also Fig. 7). = 0 (see also Fig. 7). | ||
(1) As we deplete phospholipids from leaf+ (i.e., reduce α), the differential stress increases.
(2) The variation with ϕ is again a bit more subtle, since for sufficiently large α an initial reduction in ΔΣ, driven by preferential partitioning, can reverse direction for sufficiently large ϕ, when stress and entropy take over.
(3) Torque and differential stress never vanish at the same time: zero torque states have a positive differential stress, while zero differential stress states have a negative torque.
(4) The ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0 curve lies very close to the ΔΣ = 1.0ε/σ2 contour line, which shows that all possible zero torque states have (within about ±7%) the same differential stress.
= 0 curve lies very close to the ΔΣ = 1.0ε/σ2 contour line, which shows that all possible zero torque states have (within about ±7%) the same differential stress.
(5) Just as for the torque, we could also plot the two susceptibilities χΔΣϕ|α and χΔΣα|ϕ, but they behave qualitatively very similarly to their torque counterparts. Briefly, the χΔΣϕ|α are lines with positive slope that at the nullcline transition from negative to positive values, and this happens earlier for larger α. The χΔΣα|ϕ are positive, generally larger in magnitude, decreasing with ϕ, and again hardly dependent on α.
κJ0,b = z0ΔΣ − ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (flat membrane). (flat membrane).
| (20) |
Since we now have both the torque and the differential stress surface available, we can obtain the lipid-shape affiliated spontaneous bilayer curvature torque κJ0,b for a wide range of conditions, assuming we know z0. Taking z0 ≃ 2σ for our model, we find that κJ0,b varies fairly little over the explored parameter range (mostly between 1.5ε/σ and 2.5ε/σ). This is surprising, since we would expect that changing cholesterol content or compressing/stretching a leaflet affects the conformational ensemble of lipids, and hence their preferred curvature. Clearly, the extent to which this happens will also depend on details of the lipid model, and this question should be revisited with different models, especially those at a more refined resolution.
Let us map this finding to realistic units: recalling that σ ≈ 0.75 nm and kBT = 1.4ε, we find z0 ≈ 1.5 nm and κJ0,b ≈ 2ε/σ ≈ 1.9kBT/nm. If we recall that the bending rigidity of our CG membranes is around κ ≈ 30kBT,99 which is similar to real lipid membranes, the lipid torque translates to a spontaneous bilayer curvature of J0,b ≈ 0.063 nm−1. This corresponds to an equilibrium vesicle radius R0 = 2/J0,b ≈ 32 nm, in line with the typical expectations we have outlined in Section 3.1. This reiterates that unless differential stress cancels the torque associated with lipid shape, these systems cannot exist as stable GUVs. But it also shows that our fairly simple CG model reproduces the orders of magnitude of some of these effects quite well.
From Fig. 7 we see that the zero-torque contour intersects ϕ = 40% at a phospholipid abundance of α ≈ −3.1%. Explicit simulations at this state point confirm that the torque vanishes within error (![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0.12(12)ε/σ) but the differential stress does not: ΔΣ = 1.01(06)ε/σ2, in agreement with Fig. 10. The cytosolic leaflet hence contains more phospholipids than the exoplasmic one, an abundance asymmetry partially balanced by cholesterol: we find ϕ+ = 45% and ϕ− = 34%, showing that about 57% of all cholesterol is in leaf+.
= 0.12(12)ε/σ) but the differential stress does not: ΔΣ = 1.01(06)ε/σ2, in agreement with Fig. 10. The cytosolic leaflet hence contains more phospholipids than the exoplasmic one, an abundance asymmetry partially balanced by cholesterol: we find ϕ+ = 45% and ϕ− = 34%, showing that about 57% of all cholesterol is in leaf+.
That the exoplasmic leaflet contains fewer phospholipids is a subtle balance between several competing factors: at first one might think that a leaflet richer in more saturated lipids, which have a smaller specific area, should contain more of those lipids. This is indeed true when we remove all cholesterol: as we have seen, the zero-torque contour intersects ϕ = 0% at α ≃ 2%, i.e., at a slightly positive phospholipid abundance. But we have two competing effects: first, the excess of saturated lipids in the outer leaflet renders J0,b slightly positive. This creates a negative bilayer torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) κ which we must “undo” by a positive differential stress to stay at
κ which we must “undo” by a positive differential stress to stay at ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0 (see eqn (5b)); this favors reducing the phospholipid contingent in leaf+ even in the absence of cholesterol. And second, the saturated lipids in the outer leaflet recruit cholesterol more avidly. As we increase ϕ, the cholesterol mole fraction ϕ+ will hence grow more strongly than ϕ−.
= 0 (see eqn (5b)); this favors reducing the phospholipid contingent in leaf+ even in the absence of cholesterol. And second, the saturated lipids in the outer leaflet recruit cholesterol more avidly. As we increase ϕ, the cholesterol mole fraction ϕ+ will hence grow more strongly than ϕ−.
Taking everything together, the initial exoplasmic abundance “flips” beyond ϕ ≈ 18%: torque-free membranes now have more phospholipids in their cytosolic leaflet. This is qualitatively in line with experimental observations, but the quantitative comparison is far off: in our case, at 40% cholesterol the cytosolic leaflet contains about 6% more phospholipids than the exoplasmic one, while recent experiments argue that the excess can be 100% or even more—a factor of 2.76 Of course, we must be careful with predictions based on coarse-grained models as simplified as ours: while we have tried to capture many important characteristics of this system when we developed our force-field (such as lipid area, cholesterol partitioning, and the overall phase behavior),98 more subtle phenomena (e.g., how does lipid spontaneous curvature depend on saturation and cholesterol content) need to be further examined. That being said, this large discrepancy serves to remind us how extraordinary the experimental claims are, and how difficult it would be to achieve a torque balanced state with an acceptable differential stress at a much larger abundance asymmetry (assuming, of course, that torque balance is relevant to begin with).
4.3 Demixing driven by differential stress
As a final illustration we show how a system of fixed overall lipid content can be driven to phase segregate in one leaflet by depleting its cholesterol content via a suitably induced differential stress.![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o domains in an
o domains in an ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d background, and so we will pick the
d background, and so we will pick the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d-leaflet (which for consistency we make leaf−) to be the one to phase separate. Specifically, let us pick a saturation ratio r− = 0.2, which results in a line that intersects the
d-leaflet (which for consistency we make leaf−) to be the one to phase separate. Specifically, let us pick a saturation ratio r− = 0.2, which results in a line that intersects the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o/
o/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d coexistence region in the vicinity of ϕ− = 20% (see Fig. 11). To keep matters simple, we will choose the composition in leaf+ to be as far away from coexistence as possible, namely, on the binary sc-side of the triangle (i.e., at r+ = 1).
d coexistence region in the vicinity of ϕ− = 20% (see Fig. 11). To keep matters simple, we will choose the composition in leaf+ to be as far away from coexistence as possible, namely, on the binary sc-side of the triangle (i.e., at r+ = 1).
 | ||
Fig. 11 The set of saturation ratios r+ = 1 for leaf+ (cyan line) and r− = 0.2 for leaf− (magenta line), combined with an overall cholesterol content ϕ = 30%, yields a pair of coexisting points (solid cyan and magenta symbols) of which the leaf− composition resides very close to the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d-side of the binodal. Increasing the abundance asymmetry α → +10% squeezes cholesterol from leaf+ to leaf− and pushes the latter further away from the two phase region. Reducing α → −10% instead removes cholesterol from leaf− and plunges it into d-side of the binodal. Increasing the abundance asymmetry α → +10% squeezes cholesterol from leaf+ to leaf− and pushes the latter further away from the two phase region. Reducing α → −10% instead removes cholesterol from leaf− and plunges it into ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o/ o/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d coexistence (see Fig. 12 for illustrations). The compositions in leaf+ pivot oppositely but always stay in a homogeneous d coexistence (see Fig. 12 for illustrations). The compositions in leaf+ pivot oppositely but always stay in a homogeneous ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o phase. o phase. | ||
With this choice of r±, we ran a set of simulations at α = 0 over a range of overall cholesterol concentrations ϕ ∈ {10%, 15%, 20%, …, 50%} and let these relax until both sides found their equilibrium cholesterol content ϕ±. The purpose is to find the ϕ-value that lets ϕ− sit as close as possible to the binodal of the coexistence region, so that subsequent changes in differential stress, which raise or lower ϕ−, will move leaf− further away or more deeply into the coexistence region.
Since the specific area of s-lipids is about 25% smaller than that of u-lipids, we expect a system with the same number of phospholipids on both sides (i.e., α = 0) to be under negative differential stress (i.e., leaf+ is under tension while leaf− is compressed). The presumably cleanest way to run the simulations is to compensate for this and increase the abundance until ΔΣ = 0. This is technically challenging, though, since the necessary increase is itself ϕ-dependent (recall the nontrivial ϕ–α relation on the ΔΣ = 0 contour of the differential stress surface shown in Fig. 10). To avoid an extra round of iterations, we decided to forgo this ambition and instead select an overall cholesterol content ϕ that results in a ϕ− slightly above the coexistence region, as we expect the slight net compression in leaf− to assist the formation of ordered domains. With this in mind, we selected ϕ = 30%, which resulted in ϕ− ≈ 24.5%, about 5 percentage points above the local cholesterol content of the binodal. Fortuitously, the resulting system has an almost vanishing torque, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = −0.33(17)ε/σ ≃ −1.3(7) pN, meaning, it would be voluntarily (close to) flat.
= −0.33(17)ε/σ ≃ −1.3(7) pN, meaning, it would be voluntarily (close to) flat.
Observe that the r− line and the binodal intersect at a relatively small angle, such that small movements of the binodal to the left or right would shift the intersection by a fairly large amount. The binodal is indeed not known very precisely, as its location is not merely dependent on sampling (slow) statistical fluctuations in the compositions of coexisting ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o/
o/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d phases (see ref. 98 for details) but also on difficult to quantify systematic errors inherent in the Hidden Markov Model's phase identification.98,109 With these complications in mind, we chose to not over-engineer the precise location of ϕ−.
d phases (see ref. 98 for details) but also on difficult to quantify systematic errors inherent in the Hidden Markov Model's phase identification.98,109 With these complications in mind, we chose to not over-engineer the precise location of ϕ−.
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d-side of the binodal, leaf+ is far from coexistence and manifestly in a homogeneous
d-side of the binodal, leaf+ is far from coexistence and manifestly in a homogeneous ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o phase at r+ = 1 and ϕ+ = 34.8%, see again the phase diagram in Fig. 11. We now create two new systems in which we change the abundance asymmetry to α = +10% and α = −10%. The former increases the number of phospholipids in leaf+ relative to leaf− and hence expels some of the cholesterol into leaf−, where its concentration increases to about ϕ− = 32.5%, moving it further away from the binodal. In the other case we instead deplete leaf+ relative to leaf− and thus draw additional cholesterol from leaf−, where its concentration hence drops even more, to about ϕ− = 16.7%, thereby plunging this leaflet into the coexistence region.
o phase at r+ = 1 and ϕ+ = 34.8%, see again the phase diagram in Fig. 11. We now create two new systems in which we change the abundance asymmetry to α = +10% and α = −10%. The former increases the number of phospholipids in leaf+ relative to leaf− and hence expels some of the cholesterol into leaf−, where its concentration increases to about ϕ− = 32.5%, moving it further away from the binodal. In the other case we instead deplete leaf+ relative to leaf− and thus draw additional cholesterol from leaf−, where its concentration hence drops even more, to about ϕ− = 16.7%, thereby plunging this leaflet into the coexistence region.Fig. 12 shows stylized snapshots of the leaf− lipid configuration for the three systems with α ∈ {−10%, 0%, + 10%}. As the abundance changes from negative to positive, and as a consequence the leaflet's cholesterol content from a small to a larger value, we observe that very distinct stable ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o domains visible at α = −10% melt away, with merely some remnant transient non-ideally mixed “flakes” remaining, which dynamically fluctuate in and out of existence.
o domains visible at α = −10% melt away, with merely some remnant transient non-ideally mixed “flakes” remaining, which dynamically fluctuate in and out of existence.
 | ||
Fig. 12 Stylized representative lipid configurations in leaf− of the three systems discussed in Section 4.3 and represented in the phase diagram of Fig. 11. Colors indicate lipid type—red: unsaturated, blue: saturated, black: cholesterol—while style indicates the phase state—open circles: ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d, filled circles: d, filled circles: ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o—as identified by a Hidden Markov Model analysis.98,109 At zero abundance, the phase state in leaf− is very close to the o—as identified by a Hidden Markov Model analysis.98,109 At zero abundance, the phase state in leaf− is very close to the ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) d-side of the coexistence binodal and we see only fleeting occurrences of small transient d-side of the coexistence binodal and we see only fleeting occurrences of small transient ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o regions. At α = −10% cholesterol is drawn out of leaf− which pushes the phase state into the coexistence region and we get a small but persistent o regions. At α = −10% cholesterol is drawn out of leaf− which pushes the phase state into the coexistence region and we get a small but persistent ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o domain. Conversely, at α = +10% cholesterol is pushed from leaf+ into leaf−, increasing the state's distance from the coexistence region and further melting any remaining ordered domains. All systems contain 2048 lipids, and the box length is approximately L ≈ 32σ ≈ 24 nm. o domain. Conversely, at α = +10% cholesterol is pushed from leaf+ into leaf−, increasing the state's distance from the coexistence region and further melting any remaining ordered domains. All systems contain 2048 lipids, and the box length is approximately L ≈ 32σ ≈ 24 nm. | ||
 | (21a) |
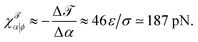 | (21b) |
Interestingly, the value for χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ is essentially the same we found in Section 4.2.3 (see Fig. 9 at ϕ = 30%), even though the r± values were different. This suggests that the response to a change in lipid abundance is dominated by mechanics. We already saw that χ
α|ϕ is essentially the same we found in Section 4.2.3 (see Fig. 9 at ϕ = 30%), even though the r± values were different. This suggests that the response to a change in lipid abundance is dominated by mechanics. We already saw that χ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) α|ϕ itself hardly depends on α; here we get additional support from the fact that the change in torque is almost exclusively driven by the change in differential stress.
α|ϕ itself hardly depends on α; here we get additional support from the fact that the change in torque is almost exclusively driven by the change in differential stress.
Using eqn (20) to calculate the intrinsic torque κJ0,b, and taking again z0 = 2σ ≃1.5 nm, we find that κJ0,b ≃10 pN within error for all three systems. The value itself is quite reasonable (using again κ ≈ 30kBT we get J0,b ≃0.08 nm−1), but its ϕ-independence appears surprising, given that the α = +10% system has about twice as much cholesterol in leaf− as the α = −10% system, with a slightly smaller but opposite effect in leaf+, and so we would expect some effect at the spontaneous curvature level. Of course, the precise answer depends on exactly what value we use for z0, and that value itself can change as leaflets become more or less ordered and hence lipids stretch or shrink. Furthermore, the mechanism by which cholesterol affects intrinsic lipid curvature is notoriously subtle,78,80 and we should not expect this to be fully captured by a coarse-grained model as simple as ours.
The magnitude of these stresses and torques raises concerns about whether under experimental conditions these systems would remain stable. Unbalanced torques of order 18 pN may be associated with characteristic curvature radii R ∼ 2κ/![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ∼ 14 nm. Our box length L ≈ 24 nm is not much larger than this, and so curvature deformations such as tubulation are not an option, but they would be for macroscopic systems at the micron scale. To still observe a single leaflet phase transition we have to relocate enough cholesterol with less stress. We suspect the experimental situation is easier, though, as we will not need to change a leaflet's cholesterol content by as much as 15% to affect a very noticeable difference in its phase state. Macroscopic systems respond much more sharply when crossing first order phase boundaries. However, considering that transitions from nanoscopic domains to macroscopic phase separation appear to be another characteristic of these systems,110–112 we must be careful not to over-interpret findings obtained from small simulations.
∼ 14 nm. Our box length L ≈ 24 nm is not much larger than this, and so curvature deformations such as tubulation are not an option, but they would be for macroscopic systems at the micron scale. To still observe a single leaflet phase transition we have to relocate enough cholesterol with less stress. We suspect the experimental situation is easier, though, as we will not need to change a leaflet's cholesterol content by as much as 15% to affect a very noticeable difference in its phase state. Macroscopic systems respond much more sharply when crossing first order phase boundaries. However, considering that transitions from nanoscopic domains to macroscopic phase separation appear to be another characteristic of these systems,110–112 we must be careful not to over-interpret findings obtained from small simulations.
Conclusions
We have proposed a thermodynamic framework that describes the conditions for coexistence between the two leaflets of an asymmetric ternary lipid membrane comprising a saturated lipid, an unsaturated lipid, and cholesterol. Our goal was not to make specific predictions—the discussion remains fully agnostic about the detailed form of the system's free energy. Instead, we clarified the dimensionality of the underlying thermodynamic state space, arguing that even though cholesterol will transition between leaflets to equilibrate its chemical potential, two essentially arbitrary ternary compositions can still coexist. However, doing so will generally require a nonzero differential stress ΔΣ that creates a mechanical counter-pressure to act against a generally non-zero chemical driving force. This implies that ΔΣ is an essential thermodynamic variable that must be part of any description of the asymmetric ternary system, for otherwise not the entire available state space is also accessible.Differential stress not only helps achieve a certain desired cholesterol imbalance; since individual leaflet tensions act some distances ±z0 displaced from the membrane midplane, ΔΣ creates a torque. This torque, in turn, will combine with the generally nonzero intrinsic torque due to lipid compositional asymmetry into an overall torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) that will try to bend the membrane. We argue that large membranes such as GUVs are therefore only stable against small-scale tubulation if the overall torque indeed vanishes.
that will try to bend the membrane. We argue that large membranes such as GUVs are therefore only stable against small-scale tubulation if the overall torque indeed vanishes.
Keeping track of the accessible degrees of freedom is hence rather subtle: two two-dimensional composition spaces (i.e., two Gibbs triangles per leaflet) combine to 4 degrees of freedom, but the equilibrium condition μchol+ = μchol− removes one, leaving only 3. However, differential stress can help balance cholesterol, so including it we bounce back to 4. Except, if the resulting torque is not also close to zero, the membrane is unstable against tubulation, so we again drop down to 3.
All these complications can be traced back to cholesterol, a remarkable actor that plays two entirely different roles here: on the one hand it co-determines the phase behavior as one of the compositional axes in the Gibbs triangles. On the other hand it can transition between leaflets and hence change the inter-leaflet stresses. Recall now that cholesterol also affects the intrinsic curvature of mixtures, usually not additively, and that its effect on leaflet area is not just non-additive but maybe also non-positive (because under certain conditions adding cholesterol will condense the membrane). This shows that writing down an actual free energy, or equations of state, for these coexisting asymmetric ternary systems is going to be a significant challenge, which we probably have to approach by adding complications one step at a time. This was not the goal of this paper, but we hope that the conceptual framework we have provided here will make it easier to progress on this difficult journey.
Data availability
The code used to set up the simulations, along with various data analysis scripts used in this article, are available on GitHub: https://github.com/m-varma-phys/asymmetric_ternary_mixtures.Author contributions
Malavika Varma: conceptualization (supporting); formal analysis (lead); investigation (equal); methodology (lead); software (lead); visualization (supporting); writing—review & editing (equal). Markus Deserno: conceptualization (lead); investigation (equal); funding acquisition (lead); visualization (lead); project administration (lead); supervision (lead); writing—original draft (lead); writing—review & editing (equal).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for many stimulating discussions on the subject with Ilya Levental, Kandice Levental, Sarah Veatch, Milka Doktorova, Fred Heberle, Thais Enoki, Alex Sodt, Gerald Feigenson, Samuel Foley, Seamus Gallagher, and Tyler Reagle. This material is based upon work supported by the National Science Foundation under Award No. NSF/CHE 2102316.Notes and references
- G. van Meer, EMBO J., 2005, 24, 3159–3165 CrossRef CAS PubMed.
- M. R. Wenk, Nat. Rev. Drug Discovery, 2005, 4, 594–610 CrossRef CAS PubMed.
- G. van Meer, Annu. Rev. Cell Biol., 1989, 5, 247–275 CrossRef CAS PubMed.
- J. E. Kyle, L. Aimo, A. J. Bridge, G. Clair, M. Fedorova, J. B. Helms, M. R. Molenaar, Z. Ni, M. Orešič, D. Slenter, E. Willighagen and B.-J. M. Webb-Robertson, Metabolomics, 2021, 17, 55 CrossRef CAS PubMed.
- K. Simons and E. Ikonen, Nature, 1997, 387, 569–572 CrossRef CAS PubMed.
- D. A. Brown and E. London, Annu. Rev. Cell Dev. Biol., 1998, 14, 111–136 CrossRef CAS PubMed.
- D. A. Brown and E. London, J. Biol. Chem., 2000, 275, 17221–17224 CrossRef CAS PubMed.
- K. Simons and D. Toomre, Nat. Rev. Mol. Cell Biol., 2000, 1, 31–39 CrossRef CAS PubMed.
- K. Simons and M. J. Gerl, Nat. Rev. Mol. Cell Biol., 2010, 11, 688 CrossRef CAS PubMed.
- L. J. Pike, J. Lipid Res., 2006, 47, 1597–1598 CrossRef CAS PubMed.
- S. Munro, Cell, 2003, 115, 377–388 CrossRef CAS PubMed.
- I. Levental and S. L. Veatch, J. Mol. Biol., 2016, 428, 4749–4764 CrossRef CAS PubMed.
- F. M. Goñi, Chem. Phys. Lipids, 2019, 218, 34–39 CrossRef PubMed.
- I. Levental, K. R. Levental and F. A. Heberle, Trends Cell Biol., 2020, 30, 341–353 CrossRef CAS PubMed.
- G. W. Feigenson and J. T. Buboltz, Biophys. J., 2001, 80, 2775–2788 CrossRef CAS PubMed.
- S. L. Veatch and S. L. Keller, Phys. Rev. Lett., 2002, 89, 268101 CrossRef PubMed.
- S. L. Veatch and S. L. Keller, Biophys. J., 2003, 85, 3074–3083 CrossRef CAS PubMed.
- D. Scherfeld, N. Kahya and P. Schwille, Biophys. J., 2003, 85, 3758–3768 CrossRef CAS PubMed.
- S. L. Veatch, I. V. Polozov, K. Gawrisch and S. L. Keller, Biophys. J., 2004, 86, 2910–2922 CrossRef CAS PubMed.
- S. L. Veatch and S. L. Keller, Biochim. Biophys. Acta, Biomembr., 2005, 1746, 172–185 CrossRef CAS PubMed.
- S. L. Veatch and S. L. Keller, Phys. Rev. Lett., 2005, 94, 148101 CrossRef PubMed.
- H. McConnell, Biophys. J., 2005, 88, L23–L25 CrossRef CAS PubMed.
- S. L. Veatch, K. Gawrisch and S. L. Keller, Biophys. J., 2006, 90, 4428–4436 CrossRef CAS PubMed.
- G. W. Feigenson, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 63–77 CrossRef CAS PubMed.
- T. Baumgart, G. Hunt, E. R. Farkas, W. W. Webb and G. W. Feigenson, Biochim. Biophys. Acta, Biomembr., 2007, 1768, 2182–2194 CrossRef CAS PubMed.
- A. Bunge, P. Müller, M. Stöckl, A. Herrmann and D. Huster, Biophys. J., 2008, 94, 2680–2690 CrossRef CAS PubMed.
- D. Marsh, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2114–2123 CrossRef CAS PubMed.
- Y. Z. Yoon, J. P. Hale, P. G. Petrov and P. Cicuta, J. Phys.: Condens. Matter, 2010, 22, 062101 CrossRef PubMed.
- F. A. Heberle, J. Wu, S. L. Goh, R. S. Petruzielo and G. W. Feigenson, Biophys. J., 2010, 99, 3309–3318 CrossRef CAS PubMed.
- F. A. Heberle and G. W. Feigenson, Cold Spring Harbor Perspect. Biol., 2011, 3, a004630 Search PubMed.
- M. C. Blosser, J. B. Starr, C. W. Turtle, J. Ashcraft and S. L. Keller, Biophys. J., 2013, 104, 2629–2638 CrossRef CAS PubMed.
- S. L. Veatch, O. Soubias, S. L. Keller and K. Gawrisch, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17650–17655 CrossRef CAS PubMed.
- A. R. Honerkamp-Smith, P. Cicuta, M. D. Collins, S. L. Veatch, M. Den Nijs, M. Schick and S. L. Keller, Biophys. J., 2008, 95, 236–246 CrossRef CAS PubMed.
- A. R. Honerkamp-Smith, S. L. Veatch and S. L. Keller, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 53–63 CrossRef CAS PubMed.
- L. S. Hirst, P. Uppamoochikkal and C. Lor, Liq. Cryst., 2011, 38, 1735–1747 CrossRef CAS.
- S. L. Veatch and P. Cicuta, Physics of Biological Membranes, Springer, 2018, pp. 141–168 Search PubMed.
- E. Cammarota, C. Soriani, R. Taub, F. Morgan, J. Sakai, S. L. Veatch, C. E. Bryant and P. Cicuta, J. R. Soc. Interface, 2020, 17, 20190803 CrossRef CAS PubMed.
- T. R. Shaw, S. Ghosh and S. L. Veatch, Annu. Rev. Phys. Chem., 2021, 72, 51–72 CrossRef CAS PubMed.
- S. L. Veatch, P. Cicuta, P. Sengupta, A. Honerkamp-Smith, D. Holowka and B. Baird, ACS Chem. Biol., 2008, 3, 287–293 CrossRef CAS PubMed.
- J. Huang, J. T. Buboltz and G. W. Feigenson, Biochim. Biophys. Acta, Biomembr., 1999, 1417, 89–100 CrossRef CAS PubMed.
- J. Huang and G. W. Feigenson, Biophys. J., 1999, 76, 2142–2157 CrossRef CAS PubMed.
- M. S. Bretscher, Nature (London), New Biol., 1972, 236, 11 CrossRef CAS PubMed.
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CrossRef CAS PubMed.
- A. J. Verkleij, R. F. A. Zwaal, B. Roelofsen, P. Comfurius, D. Kastelijn and L. L. M. Van Deenen, Biochim. Biophys. Acta, Biomembr., 1973, 323, 178–193 CrossRef CAS PubMed.
- P. K. Schick, K. B. Kurica and G. K. Chacko, J. Clin. Invest., 1976, 57, 1221–1226 CrossRef CAS PubMed.
- A. Sandra and R. E. Pagano, Biochemistry, 1978, 17, 332–338 CrossRef CAS PubMed.
- J. A. F. Op den Kamp, Annu. Rev. Biochem., 1979, 48, 47–71 CrossRef CAS PubMed.
- P. F. Devaux, Biochemistry, 1991, 30, 1163–1173 CrossRef CAS PubMed.
- M. G. P. Vale, Biochim. Biophys. Acta, Biomembr., 1977, 471, 39–48 CrossRef CAS PubMed.
- J. H. Lorent, K. R. Levental, L. Ganesan, G. Rivera-Longsworth, E. Sezgin, M. Doktorova, E. Lyman and I. Levental, Nat. Chem. Biol., 2020, 16, 644–652 CrossRef CAS PubMed.
- M. M. Sperotto and A. Ferrarini, The Biophysics of Cell Membranes: Biological Consequences, Springer Singapore, Singapore, 2017, pp. 29–60 Search PubMed.
- W. F. D. Bennett, J. L. MacCallum, M. J. Hinner, S. J. Marrink and D. P. Tieleman, J. Am. Chem. Soc., 2009, 131, 12714–12720 CrossRef CAS PubMed.
- S. Jo, H. Rui, J. B. Lim, J. B. Klauda and W. Im, J. Phys. Chem. B, 2010, 114, 13342–13348 CrossRef CAS PubMed.
- R.-X. Gu, S. Baoukina and D. P. Tieleman, J. Chem. Theory Comput., 2019, 15, 2064–2070 CrossRef CAS PubMed.
- R. E. Scott, Science, 1976, 194, 743–745 CrossRef CAS PubMed.
- R. E. Scott and P. B. Maercklein, J. Cell Sci., 1979, 35, 245–252 CrossRef CAS PubMed.
- D. Holowka and B. Baird, Biochemistry, 1983, 22, 3466–3474 CrossRef CAS PubMed.
- E. Sezgin, H.-J. Kaiser, T. Baumgart, P. Schwille, K. Simons and I. Levental, Nat. Protoc., 2012, 7, 1042–1051 CrossRef CAS PubMed.
- D. M. Engelman, Nature, 2005, 438, 578–580 CrossRef CAS PubMed.
- T. Baumgart, A. T. Hammond, P. Sengupta, S. T. Hess, D. A. Holowka, B. A. Baird and W. W. Webb, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3165–3170 CrossRef CAS PubMed.
- H. Keller, M. Lorizate and P. Schwille, ChemPhysChem, 2009, 10, 2805–2812 CrossRef CAS PubMed.
- M. Krompers and H. Heerklotz, Membranes, 2023, 13, 267 CrossRef CAS PubMed.
- A. Hossein and M. Deserno, Biophys. J., 2020, 118, 624–642 CrossRef CAS PubMed.
- A. Hossein and M. Deserno, J. Chem. Phys., 2021, 154, 014704 CrossRef CAS PubMed.
- S. L. Foley, A. Hossein and M. Deserno, Biophys. J., 2022, 121, 2997–3009 CrossRef CAS PubMed.
- S. L. Foley, M. Varma, A. Hossein and M. Deserno, Emerging Top. Life Sci., 2023, 7, 95–110 CrossRef CAS PubMed.
- M. Deserno, Curr. Opin. Struct. Biol., 2024, 87, 102832 CrossRef CAS PubMed.
- C. E. Morris and U. Homann, J. Membr. Biol., 2001, 179, 79–102 CrossRef CAS PubMed.
- T. A. Enoki and F. A. Heberle, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2308723120 CrossRef CAS PubMed.
- A. J. Wagner, S. Loew and S. May, Biophys. J., 2007, 93, 4268–4277 CrossRef CAS PubMed.
- G. G. Putzel and M. Schick, Biophys. J., 2008, 94, 869–877 CrossRef CAS PubMed.
- S. May, Soft Matter, 2009, 5, 3148–3156 RSC.
- J. J. Williamson and P. D. Olmsted, Biophys. J., 2015, 108, 1963–1976 CrossRef CAS PubMed.
- J. J. Williamson and P. D. Olmsted, Soft Matter, 2015, 11, 8948–8959 RSC.
- J. J. Williamson and P. D. Olmsted, Biophys. J., 2018, 115, 1956–1965 CrossRef CAS PubMed.
- M. Doktorova, J. L. Symons, X. Zhang, H.-Y. Wang, J. Schlegel, J. H. Lorent, F. A. Heberle, E. Sezgin, E. Lyman, K. R. Levental and I. Levental, Cell, 2025, 188, 1–17 CrossRef PubMed.
- M. Varma and M. Deserno, Biophys. J., 2022, 121, 4001–4018 CrossRef CAS PubMed.
- A. J. Sodt, R. M. Venable, E. Lyman and R. W. Pastor, Phys. Rev. Lett., 2016, 117, 138104 CrossRef CAS PubMed.
- D. W. Allender, A. J. Sodt and M. Schick, Biophys. J., 2019, 116, 2356–2366 CrossRef CAS PubMed.
- A. H. Beaven, K. Sapp and A. J. Sodt, Biophys. J., 2023, 122, 2162–2175 CrossRef CAS PubMed.
- R. M. Venable, F. L. Brown and R. W. Pastor, Chem. Phys. Lipids, 2015, 192, 60–74 CrossRef CAS PubMed.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- R. Lipowsky, Faraday Discuss., 2013, 161, 305–331 RSC.
- Y. Liu, J. Agudo-Canalejo, A. Grafmüller, R. Dimova and R. Lipowsky, ACS Nano, 2016, 10, 463–474 CrossRef CAS PubMed.
- R. Lipowsky, Adv. Biol., 2022, 6, 2101020 CrossRef PubMed.
- T. Reagle, Y. Xie, Z. Li, W. Carnero and T. Baumgart, Soft Matter, 2024, 20, 4291–4307 RSC.
- R. Zidovetzki and I. Levitan, Biochim. Biophys. Acta, Biomembr., 2007, 1768, 1311–1324 CrossRef CAS PubMed.
- S. Mahammad and I. Parmryd, Methods in membrane lipids, 2015, pp. 91–102 Search PubMed.
- L. Szente and É. Fenyvesi, Struct. Chem., 2017, 28, 479–492 CrossRef CAS.
- M. Rahimi, D. Regan, M. Arroyo, A. B. Subramaniam, H. A. Stone and M. Staykova, Biophys. J., 2016, 111, 2651–2657 CrossRef CAS PubMed.
- E. London, Acc. Chem. Res., 2019, 52, 2382–2391 CrossRef CAS PubMed.
- Z. Huang and E. London, Langmuir, 2013, 29, 14631–14638 CrossRef CAS PubMed.
- Q. Lin and E. London, PLoS One, 2014, 9, e87903 CrossRef PubMed.
- G. Li, J. Kim, Z. Huang, J. R. St. Clair, D. A. Brown and E. London, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14025–14030 CrossRef CAS PubMed.
- G. Li, S. Kakuda, P. Suresh, D. Canals, S. Salamone and E. London, PLoS One, 2019, 14, e0223572 CrossRef CAS PubMed.
- P. Suresh and E. London, Biochim. Biophys. Acta, Biomembr., 2022, 1864, 183774 CrossRef CAS PubMed.
- M. Varma, F. Khuri-Makdisi and M. Deserno, J. Chem. Phys., 2024, 161, 114103 CrossRef CAS PubMed.
- S. Foley and M. Deserno, J. Chem. Theory Comput., 2020, 16, 7195–7206 CrossRef CAS PubMed.
- I. R. Cooke, K. Kremer and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011506 CrossRef PubMed.
- I. R. Cooke and M. Deserno, J. Chem. Phys., 2005, 123, 224710 CrossRef PubMed.
- M. Deserno, Macromol. Rapid Commun., 2009, 30, 752–771 CrossRef CAS PubMed.
- G. Orädd, P. W. Westerman and G. Lindblom, Biophys. J., 2005, 89, 315–320 CrossRef PubMed.
- F. Weik, R. Weeber, K. Szuttor, K. Breitsprecher, J. de Graaf, M. Kuron, J. Landsgesell, H. Menke, D. Sean and C. Holm, Eur. Phys. J.: Spec. Top., 2019, 227, 1789–1816 Search PubMed.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628 CrossRef CAS PubMed.
- A. Kolb and B. Dünweg, J. Chem. Phys., 1999, 111, 4453–4459 CrossRef CAS.
- M. Deserno, Chem. Phys. Lipids, 2015, 185, 11–45 CrossRef CAS PubMed.
- M. P. Do Carmo, Differential geometry of curves and surfaces: revised and updated, Courier Dover Publications, 2nd edn, 2016 Search PubMed.
- A. J. Sodt, M. L. Sandar, K. Gawrisch, R. W. Pastor and E. Lyman, J. Am. Chem. Soc., 2014, 136, 725–732 CrossRef CAS PubMed.
- T. M. Konyakhina, S. L. Goh, J. Amazon, F. A. Heberle, J. Wu and G. W. Feigenson, Biophys. J., 2011, 101, L8–L10 CrossRef CAS PubMed.
- F. A. Heberle, R. S. Petruzielo, J. Pan, P. Drazba, N. Kucerka, R. F. Standaert, G. W. Feigenson and J. Katsaras, J. Am. Chem. Soc., 2013, 135, 6853–6859 CrossRef CAS PubMed.
- R. D. Usery, T. A. Enoki, S. P. Wickramasinghe, M. D. Weiner, W.-C. Tsai, M. B. Kim, S. Wang, T. L. Torng, D. G. Ackerman and F. A. Heberle, et al., Biophys. J., 2017, 112, 1431–1443 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |