Open Access Article
Open Access ArticlePhosphatidylserine affinity for and flip-flop dependence on Ca2+ and Mg2+ ions
Preston P. Hymas and
John C. Conboy *
*
Department of Chemistry, University of Utah, 315 S. 1400 E. RM 2020, Salt Lake City, UT 84112, USA. E-mail: John.Conboy@utah.edu
First published on 18th February 2025
Abstract
Ca2+ ions are believed to play a crucial role in regulating lipid membrane asymmetry by modulating the activity of flippases, floppases, and scramblases. Dysregulation of Ca2+ homeostasis, and subsequent loss of phosphatidylserine (PS) lipid asymmetry, is associated with physiological conditions such as blood clotting, neurodegeneration, and apoptosis. Yet, despite the prominence of Ca2+ with regards to PS flip-flop, the specific actions of Ca2+ are not fully understood and detailed mechanisms remain elusive. Much focus has been placed on enzymatic interactions, while the endogenous interactions of Ca2+ ions with PS and the direct role Ca2+ ions play on maintaining PS asymmetry have not been characterized in detail, a potentially crucial gap in understanding. In the current study the binding affinities of Ca2+ ions to planar supported lipid membranes containing PS were measured via sum-frequency vibrational spectroscopy (SFVS). Evaluation of binding affinity obtained from SFVS peak area analysis yielded an affinity of 1.3 × 105 M−1. The rate of PS flip-flop was also measured in the presence and absence of Ca2+ via SFVS, with a nearly five-fold decrease in the rate of translocation when Ca2+ ions are present. Controls which tested Mg2+ with PS or phosphatidylcholine (PC) with Ca2+ did not show similar slowing effects, highlighting the specificity of the PS–Ca2+ interaction. For the binary lipid mixture tested, the disparity in the PS flip-flop rate would be sufficient to produce an 82% PS asymmetry if Ca2+ ions are localized to one side of the membrane. These studies have important implications for the non-enzymatic role Ca2+ ions may play in the maintenance of PS asymmetry.
Introduction
Lipid asymmetry in living cells has long been recognized,1–5 though the details of how phospholipid asymmetry is established, maintained, and destroyed is the subject of continued debate. What is known is that lipids are asymmetrically distributed between the cytosolic and extracellular leaflets of the plasma membrane based on both headgroup structure and alkyl chain saturation.6,7 Lipids facing the extracellular environment are predominantly phosphatidylcholine (PC) and sphingomyelin (SM) lipids; conversely, the aminophospholipids phosphatidyl-ethanolamine (PE) and phosphatidylserine (PS) are found enriched on the cytoplasmic leaflet. Of these lipid species, PC, SM, and PE are net neutral zwitterions, while PS headgroups are net negative. Notably, while detectable levels of externalized PE are known to be present, PS sequestration to the inner leaflet is essentially absolute. An outer neutral leaflet with an underlying negative inner leaflet contributes to a physiologically vital membrane potential.8 The charge differential maintained by this arrangement has been shown to be important to intracellular fusion, budding, and ion diffusion processes which help maintain internal homeostasis.4,9–15 Meanwhile, loss of asymmetry and the subsequent externalization of PS is essential to blood coagulation and the inability to express PS is a key characteristic of the clotting disorder Scott's syndrome.9,12,15–18 Externalization of PS to the extracellular leaflet also serves as a signal for phagocytes to engulf and clear apoptotic cells.19The origin of the asymmetric lipid distribution found in cells has been ascribed to the action of ATP-dependent enzymes known as flippases and floppases that flip or flop lipids inward or outward, respectively.2,4,12,20–24 Several PS-active flippases have been identified, such as ATP11A, ATP11C, and aminophospholipid translocase (APLT).22,24–28 The ability of these enzymes to deliver PS lipids to the inner leaflet has been established through various means, including monitoring the uptake of fluorescent PS lipid analogues such as 7-nitro-2-1,3-benzoxadiazol-4-yl–PS (NBD–PS) with or without active flippases or floppases present.26–30 Yet, while deactivation of these enzymes will slow the uptake and transfer of newly delivered PS, loss of flippase activity does not itself lead to loss of existing PS asymmetry. PS externalization in dead or dying cells has therefore been attributed to a third class of proteins, scramblases, which are believed to actively destroy PS asymmetry as part of apoptosis.2,9,12,24,27,30–37
Activation of the scrambling process is routinely linked to Ca2+ ions. Elevation of cytosolic Ca2+ through either the incorporation of ionophores such as A23187, which increases inward flux, or deactivation of Ca-ATPase via agonists like thapsigargan, which decreases outward flux, reliably result in PS externalization.1,16,33,35,38–41 Williamson et al. have, through a series of papers involving PS staining with FTIC-labeled Annexin V, quenching of NBD- or doxylpentanoyl-labeled lipids, and examination of phospholipase degradation products, established scrambling activity to affect a wide variety of lipid species.4,28,31,35,36,42–44 Williamson's group has found that not only will elevated cytosolic Ca2+ lead to mixing of the native PC, SM, PE, and PS lipids, but also NBD or doxylpentanoyl-labeled variants. Further, Ca-induced mixing of even non-natural lipid analogues such as fatty-acid carnitine esters and trimethylammonium–diphenylhexatriene has also been shown.29,40 These data establish the scrambling process to be quite indiscriminate toward lipid structure, yet the mechanism for how exactly Ca2+ enhanced scramblases lead to lipid translocation is not well understood.
Despite the demonstration of Ca-induced lipid mixing over a wide range of cell strains and lipid types, the identities of the specific enzymes responsible are currently unclear. Several potential scramblases have been identified, such as phospholipid scramblase (PLSCR) and ABCA1, yet studies on their activity are decidedly mixed. PLSCR−/− knockout in mice platelets did not inhibit PS exposure.45 In addition, studies on lymphocytes, macrophages, and fibroblasts of Tangier disease patients who do not express ABCA1 found Ca-induced scrambling of PS to remain active.46,47
The lack of a defined, well-established mechanism for how Ca2+ may lead to externalized PS is notable, a deficiency compounded by the fact that the direct effect Ca2+ ions have on the rates of protein-free PS flip-flop are unknown. There is a wide body of literature, beyond the discussion of scramblase activation, which suggests that PS–Ca pairing is quite important. When observing mixed monolayers and bilayers of PS and PC in the presence of Ca2+ ions, phase segregation of PS and PC was observed.48–50 Janshoff et al. found the process can be reversed via removal of the Ca2+ with ethylene glycol tetraacetic acid (EGTA), a chelating agent with a strong affinity for Ca2+. Similar results were found by Papahadjopoulos, who noted both Ca2+ and Mg2+ ions affect PS-containing membranes.49,51,52 Interestingly, although PS was responsive to both ions, only Ca2+ leads to phase segregation, and while Mg2+ elevated the lipid melting point, Ca2+ completely abolished the transition within the tested temperature range. The ability for Ca2+ to induce membrane disruptions over Mg2+ has also been observed in lipid vesicles. PS-containing vesicles have enhanced fusion and aggregation in the presence of Ca2+, behaviors which were either absent or reduced in the presence of Mg2+.10,14,50–53
The divergence in Ca2+ and Mg2+ behavior toward PS is notable considering that, like PS, the concentrations of these species differ drastically over the cell membrane boundary. In the extracellular media, Ca2+ is in the range of 1–2 mM, yet exists in the 100–200 nM range within the cytoplasm.54,55 Conversely, Mg2+ ions within the cytoplasm are in the range of 0.6–1 mM.54 While Ca2+ influx is commonly stated as the cause of scramblase activation, there is data to suggest the existing concentration gradient of Ca2+ is an equally important factor. Hampton et al. found complexation of internal Ca2+ using the chelating agent 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid tetrakis(acetoxymethyl ester) (BAPTA-AM) did not inhibit PS exposure, whereas chelation of external Ca2+ with EGTA lead to a reduction of exposed PS by 50% to 65%.56 Further, Bratton et al. found PS expression could be achieved via UV irradiation of human leukaemia (HL-60) cells, but that the degree of expression was directly related to the external concentration of Ca2+.25 To test if irradiation had caused the cells to become more permeable to Ca2+ resulting in Ca2+ influx, the authors used fluorescence from fura-2-acetoxymethylester-loaded cells and found intracellular Ca2+ had only risen by 100 nM in an external media containing 1 mM Ca. Their results indicate the presence of Ca2+ was required for externalization even though Ca2+ flux was minimal.
The results of Hampton and Bratton, combined with the previously detailed evidence of strong a Ca–PS interaction, suggest the presence of Ca2+ may directly influence the rate of PS flip-flop and, by extension, the maintenance of PS lipid asymmetry in cellular membranes irrespective of postulated scramblase activity. The interaction of solvated ions and membrane lipids have previously been shown to have a pronounced effect on rates of translocation. Cheng and Conboy found that exposure to Yb3+ ions slowed 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) flip-flop by an order of magnitude, demonstrating the potency of ion–lipid interactions to modulate lipid flip-flop dynamics.57 It is hypothesized here that PS externalization may, at least in part, be attributed to an equilibration of PS toward the Ca2+ exposed leaflet of the bilayer by way of unequal rates of native, nonenzymatic flip and flop. Such a hypothesis does not preclude enzymatic activity, but rather aims to assist in the interpretation of enzymatic data by clarifying what behaviors can be explained through direct Ca–PS and Mg–PS competitive effects in the extracellular and intercellular environments, respectively.
The importance of the nonenzymatic flip-flop of PS is less characterized than the enzymatic behaviors, as lipid mixing dynamics are often approached with the starting assumption that the non-enzymatic or “native” lipid flip-flop is too slow to be relevant. Leaflet mixing is therefore viewed largely through the lens of active transport, hence an overall focus on scramblase-driven PS movement. While there are several studies which find native flip-flop to be quite slow, the literature contains a wide variance in the reported rates of translocation. Methods such as electron paramagnetic resonance (EPR),3 nuclear magnetic resonance (H1 NMR),58 small angle neutron scattering (SANS),59–61 fluorescence,27,44 and sum-frequency vibrational spectroscopy (SFVS)62–67 have been applied to the problem, yet there is little consensus on specific rates.
Divergent results are generally ascribed to two experimental factors. Firstly, determined rates of flip-flop can be highly dependent on the presence of chemical labels like the 2,2,6,6-tetramethylpiperidine 1-oxyl (TEMPO) label used by Kornberg and McConnell's EPR study.3,64 Analyzing the influence of the TEMPO label employed in Kornberg and McConnell's original work, Liu and Conboy showed that native DPPC lipids flip-flopped nearly 50-fold faster than the TEMPO-DPPC analogue. Liu and Conboy's study was performed using SFVS of planar supported lipid bilayers (PSLBs), a methodology advantaged by being capable of measuring the flip-flop rates of unlabelled lipids. The PSLBs methodology is, however, counter to Kornberg and McConnell who had utilized vesicle membranes. The membrane model, planar or vesicle, is another factor which can influence flip-flop measurements.
An example of a label-free method which has been employed for vesicle models is 1HNMR analysis of asymmetric large unilamellar vesicles (aLUVs).58,68–72 aLUV analysis provides DPPC flip-flop rates several orders of magnitude slower than those measured in PSLBs, hypothesized by Marquardt et al. to be due to defect-enhanced translocation in PSLBs near sub-micron holes in surface coverage.69 The effect of surface defects can be minimized through the incorporation of a highly hydrated polymer cushion between the bilayer and surface support, but cannot be removed entirely.73–77 The influence of surface defects on PSLB flip-flop kinetics may not, therefore, be entirely discounted. However, inconsistencies in reported flip-flop rates are not entirely explainable purely by planar versus vesicle membrane dynamics. The TEMPO-PC flip-flop observed by Kornberg and McConnell in DPPC is several orders of magnitude faster than DPPC flip-flop rates observed in aLUVs,3,69 despite the presence of the bulky TEMPO label. As both studies utilized vesicle models, the discrepancy would not be explainable by surface coverage defects.
While it is clear that methodological differences can influence the flip-flop rates obtained, the study herein is interested primarily in relative kinetic shifts which may affect the equilibrium of PS expression. In order to validate the Ca-modulated PS flip-flop hypothesis, the present study used SFVS of PS-containing PSLBs in the presence of physiologic 1 mM concentrations of Ca2+ or Mg2+ ions to compare their effects on PS flip-flop dynamics. Solutions were ionic strength matched and use a baseline comparison to 100 mM KCl to mimic the cytosolic environment where K+ ions predominate.78 As the utilized methodology was consistent among all samples examined, the Ca2+ or Mg2+ induced changes in lipid flip-flop kinetics are used to make inferences on in vivo PS lipid behaviour. Gel phase mixtures of DPPC and 1,2-dipalmitoyl-sn-glycero-3-phosphoserine (DPPS) were utilized due to the inability to measure the rapid flip-flop mixing of liquid crystalline (LC) phase lipids by SFVS using PSLB model membranes. While binary mixtures of DPPC and DPPS are not physiologic, the simplified mixture allowed the variable of PS-selective Ca2+ or Mg2+ interactions to be isolated. Aside from headgroup identity these two lipids are structurally identical. Thus, any divergence in response to Ca2+ or Mg2+ exposure is attributed to differences in the binding of these two ions to PC and PS headgroups. Additionally, compression isotherms of lipid monolayers on subphases with or without Ca2+ and Mg2+ were used to probe the effects these ions have on the packing and compressibility of DPPS and DPPC lipids. Finally, SFVS of hybrid bilayers, composed of lipid monolayers deposited to a methylated silica surface, was utilized to determine the affinity of DPPS for Ca2+ and Mg2+ and characterize structural changes occurring within the headgroups, water solvation layer, and lipid alkyl chains.
Sum-frequency vibrational spectroscopy
Sum-frequency vibrational spectroscopy is a coherent nonlinear optical method which involves simultaneous infrared (IR) excitation and anti-stokes Raman scattering to generate an outgoing photon at the sum of the two input energies.79 In the present case, the system employed uses a tunable IR (ωIR) and a fixed 532 nm visible (ω532) laser to generate the sum-frequency beam (ωS.F.):| ωS.F. = ω532 + ωIR | (1) |
Generation of the sum-frequency is dependent on the second order nonlinear susceptibility of the material (χ(2)) and scaled by the linear transmission Fresnel coefficients of the IR (fIR) and 532 nm (f532) beams, as well as the nonlinear Fresnel coefficient of the outgoing sum-frequency (![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) S.F.):
S.F.):
IS.F. = |![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) S.F.f532fIRχ(2)|2 S.F.f532fIRχ(2)|2
| (2) |
The second order susceptibility is a third order, 27 element tensor which describes the coupling of the three electric field vectors (IR, visible, and sum-frequency) in three-dimensional space (x, y, and z). χ(2) contains both resonant (χR(2)) and non-resonant (χN.R.(2)) contributions, however the non-resonant component is small compared to the resonant component when dealing with dielectric materials and may usually be ignored:
| χ(2) = χR(2) + χN.R.(2) ≈ χR(2) | (3) |
The resonant component (χR(2)) is proportional to the number of molecules (N) at the interface, scaled by the IR (Ai) and Raman (Mjk) transition probabilities (eqn (4)). Resonance will reach a maximum when the tunable IR (ωIR) is matched to a vibrational mode (ωv), though will be limited by the linewidth of the transition (Γv). Expressed as a sum over all possible vibrational modes, the sum-frequency dependence on the total resonant contribution can be expressed as follows:
 | (4) |
The orientation of the molecules is implicit via the bra (〈) and ket (〉) operators, which denote an average of all molecular orientations. In isotropic media where the orientational averaging results in no net directionality, the expected sum-frequency is zero. Only in anisotropic media, or at an interface, should sum-frequency be observed.80 Due to the symmetry dependence of the sum-frequency, SFVS can be utilized to great advantage when observing interleaflet mixing. Bilayer systems contain a natural plane of inversion between the leaflets, and thus any sum-frequency generated is proportional to the number difference of species in the proximal (Nproximal) and distal (Ndistal) leaflets:63,81
| ISF ∝ (Nproximal − Ndistal)2 | (5) |
One technique to achieve lipid leaflet asymmetry is through the use of PSLBs prepared via the Langmuir–Blodgett/Langmuir–Schaffer (LB/LS) transfer methods. Selective deuteration of the lipid tails in one leaflet shifts the resonances out of the C–H region into the C–D region, removing any interference of sum-frequency from the antiparallel orientation of the tails. This bilayer asymmetry allows the alkyl chain C–H vibrations to become sum-frequency active. Fig. 1A illustrates this principal for the C–H vibrational region recorded for an asymmetric DPPC/DPPCd62 bilayer and a symmetric DPPC/DPPC bilayer. Five key vibrational modes are observed: the CH2 symmetric stretch at 2850 cm−1, CH3 symmetric stretch at 2875 cm−1, CH2 Fermi resonance at 2905 cm−1, CH3 Fermi resonance at 2935 cm−1, and CH3 asymmetric stretch at 2960 cm−1.64,65 The spectra in Fig. 1 were collected with s-polarized sum-frequency, s-polarized 532 nm and p-polarized IR. This optical configuration probes the component of the vibrational transitions parallel to the surface normal. For this reason, the terminal CH3 stretch appears most prominently in ssp spectra.
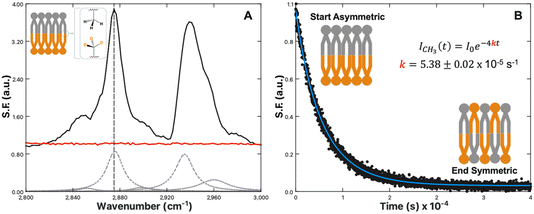 | ||
| Fig. 1 (A) SFVS spectrum scan of an asymmetric DPPC/DPPC-d62 bilayer (black) and symmetric DPPC/DPPC bilayer (red). Inset image shows an illustration of an isotopically asymmetric lipid bilayer highlighting the terminal CH3 symmetric stretch. The CH3 symmetric stretch is located at 2875 cm−1, denoted with a vertical grey dashed line. The grey dashed curves are the fits to the various C–H resonances obtained by fitting the SFVS spectrum to eqn (4), with the data offset for clarity. (B) SFVS intensity decay of the CH3 symmetric stretch at 2875 cm−1 for an asymmetric DPPC/DPPCd62 bilayer recorded at 28 °C. The solid blue line is the fit of the decay data using eqn (7). | ||
As the sum-frequency is proportional to the lipid number difference between the leaflets, changes in the sum-frequency (SF) intensity can therefore be attributed directly to mixing between the two leaflets:
 | (6) |
| ICH3,t = I0e−4kt | (7) |
Experimental
Materials
All materials were used as received without further purification. 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-dipalmitoyl-d62-sn-glycero-3-phosphocholine (DPPC-d62), 1,2-dipalmitoyl-sn-glycero-3-phosphoserine (DPPS), and 1,2-dipalmitoyl-d62-sn-glycero-3-phosphoserine (DPPS-d62) (Fig. 2) were purchased from Avanti Polar Lipids (Alabaster, AL). 99.995% pure KCl (metals basis), ultra dry, 99.9% pure MgCl2 (metals basis), Tris Base, HPLC-grade chloroform, and deuterium oxide were purchased from Thermo Fisher Scientific (Waltham, MA). Nanopure, 18.2 MΩ cm water from a Barnstead Thermolyne (Dubuque, IA) system was used for all aqueous solutions.Lipid stock solutions of DPPC, DPPC-d62, DPPS, and DPPS-d62 were made at 1 mg mL−1 in HPLC-grade chloroform. Mixtures of various PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PC mol fractions were made using these parent solutions.
PC mol fractions were made using these parent solutions.
Compression isotherms
Pressure–area isotherms were collected on a Langmuir trough (KSV, Helsinki, Finland). Prior to lipid additions, each subphase was checked for surface contaminants with a barrier sweep over the surface, with barrier compressions resulting in less than a 0.2 mN m−1 lateral surface pressure increase considered sufficient for lipid deposition. Lipid solutions in chloroform were deposited dropwise at the air–water interface and allowed to evaporate for 10 min. All monolayers were compressed at a rate of 4 mm min−1 at room temperature (21 °C).Silica supports
Custom IR-grade fused silica prisms were purchased from Almaz Optics (Marlton, NJ). Before each use, prisms were cleaned for at least 10 min under ozone (Jetlight Co., Irvine, CA), followed by submersion in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of concentrated sulfuric acid and 30% H2O2 for at least one hour. CAUTION: Piranha solutions contain strong oxidants which react violently, potentially explosively, with organics. Submerged prisms should be absolutely free of any residual organic solvents, and extreme care with proper personal protective equipment should be used when handling these corrosive mixtures. Finally, each prism was rinsed with 18.2 MΩ cm water, dried under N2, and treated with argon plasma (Harrick Scientific, Ithaca, NY) for at least 10 min.
1 mixture of concentrated sulfuric acid and 30% H2O2 for at least one hour. CAUTION: Piranha solutions contain strong oxidants which react violently, potentially explosively, with organics. Submerged prisms should be absolutely free of any residual organic solvents, and extreme care with proper personal protective equipment should be used when handling these corrosive mixtures. Finally, each prism was rinsed with 18.2 MΩ cm water, dried under N2, and treated with argon plasma (Harrick Scientific, Ithaca, NY) for at least 10 min.
Planar supported lipid bilayers
PSLBs were deposited to silica prisms at a surface pressure of 30 mN m−1 to mimic physiological conditions.82 Compressions were performed following the same procedure listed in the ‘Compression isotherms’ section. To prevent interactions between the lipid headgroups and the silica surface, particularly salt bridging with PS, a 3% C16-PEG(5000)PE lipid fraction was incorporated for LB depositions (proximal leaflet). The highly water-soluble PEG groups attached to the lipid heads form a PEG polymer cushion to act as a spacer between the support and lipids.74–76,83 For LB depositions the prism was pulled up through the interface at a rate of 4 mm min−1. For the LS deposition the prism was rotated 90° and aligned to be as perfectly level with the trough as possible. The trough was reset with a fresh subphase, new lipids of the desired composition, and compressed to 30 mN m−1 as previously. The prism was then brought back through the interface to deposit the distal leaflet.Hybrid bilayers
Silica prisms were surface modified by submersion in a solution of 2% trimethoxymethylsilane in dry toluene (v/v) with an incubation time of at least one hour. Incubation should be performed in a covered container to prevent evaporation of the toluene. Following incubation, the surface was rinsed with methanol and placed into an oven at >80 °C for at least one hour. Finally, a lipid monolayer was deposited via a single LS transfer at 30 mN m−1 on the methylated surface to create a hybrid bilayer.Results and discussion
Compression isotherms
The effect of Ca2+ and Mg2+ ions on lipid packing and compression were examined by way of pressure–area isotherms for three lipid systems: control monolayers of 100% DPPC (Fig. 3A), monolayers of 10% DPPS in DPPC as a physiologically appropriate PS fraction (Fig. 3B), and monolayers of 100% DPPS (Fig. 3C). The subphases for all experiments were ionic strength matched, with a base solution of 100 mM KCl and 50 mM Tris buffer for a total ionic strength of 133.4 mM at pH 7.4. The amount of KCl present was reduced to 97 mM to compensate for the addition of 1 mM CaCl2 or MgCl2 when those species were present. Each experiment was performed at least three times and averaged. | ||
| Fig. 3 Pressure–area isotherms of (A) DPPC, (B) 10% DPPS in DPPC, and (C) DPPS obtained with a subphases of 100 mM KCl (black), 97 mM KCl + 1 mM CaCl2 (blue) or 1 mM MgCl2 (green). Each line represents the average of at least three replicate measurements. All subphases are buffered with 50 mM Tris at pH 7.4. (D) Compression moduli of DPPS as a function of surface pressure, calculated from the isotherms displayed in (C) using eqn (7) for 100 mM KCl (black), 97 mM KCl + 1 mM CaCl2 (blue) or 1 mM MgCl2 (green). Compression moduli were obtained by employing a 50-point rolling average on the corresponding π–A isotherm. | ||
In the absence of either Ca2+ or Mg2+, the mean molecular areas (MMAs) at a physiological surface pressure of 30 mN m−1 were determined to be 49.3 ± 0.5, 45.9 ± 0.7, and 46.7 ± 0.7 Å2 per molecule for the 100% PS, 100% PC, and 10% PS systems, respectively. The values determined for pure PC and PS agree favorably with those reported elsewhere.84,85 Upon the addition of 1 mM Ca2+ or Mg2+, no net change in the MMA of DPPC was observed. A previous report from Adams et al. found DPPC monolayers expand in the presence of Ca2+;86 however, those studies were carried out at much higher concentrations of Ca2+, starting at 300 mM CaCl2 compared to 1 mM here. Additionally, their baseline of comparison was a pure water subphase rather than ionic strength matched buffer. The divergent results can therefore likely be attributed to experimental differences between their study and the results found here.
More notable results are found in the DPPS mixtures where, when in the presence of Ca2+, but not Mg2+, there is a reduction in the MMA of −0.2 ± 0.7 and −2.4 ± 0.6 Å2 per molecule for 10% and 100% DPPS, respectively, at 30 mN m−1 surface pressure. In the case of the 10% DPPS system the differential is within the margin of error; however, the differential for the 100% DPPS system is significant and suggests a net condensation of the DPPS monolayer in the presence of Ca2+ ions. Given the low mol fraction in the 10% mixture, one might expect only one-tenth the response of that in the neat DPPS monolayer, corresponding to a shift of around −0.2 Å2 per molecule, which is within the standard deviation of the experiment. The 10% DPPS data therefore agrees within error. The condensing behavior observed for Ca2+ with pure PS monolayers is additionally consistent with behavior observed by Narayanan who found a contraction of 1,2-dilauroyl-sn-glycero-3-phospho-L-serine (DLPS) in the presence of 10 mM Ca2+.87 Narayanan observed Mg2+ to have a weaker condensing effect than Ca2+, with the condensation disappearing at higher surface pressures. A similar trend was observed here, with the Mg2+-induced condensation effect disappearing above 20 mN m−1.
There is additionally a shift in the compression moduli of the DPPS monolayer in the presence of both the Ca2+ and Mg2+. The compression modulus was computed from the first derivative of the isotherm in Fig. 3C, using the following expression:88
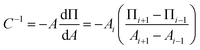 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ion
2 ion![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lipid ratio, the binding modality was found to be quite different. The most stable conformation of Ca–PS complexation is a motif of four oxygens per Ca2+ ion, with each lipid coordinating one phosphate oxygen and one carboxylate oxygen to form a cage around the central ion (Fig. 4). Conversely, the two most stable forms of the Mg–PS complex were found to involve only two total oxygens, with Mg2+ bridging either the lipid phosphate or carboxylate regions, but not both simultaneously as calculated for Ca2+. These conformations represented the most likely states, though Martin-Molina observed other binding modes at lower probabilities. The average of all possible states found Mg2+ to bind 2.7 oxygens, while Ca2+ bound 4.2. Overall, Mg2+ was found to occupy more superficial positions than Ca2+, which penetrated more deeply into the membrane and led to a loss of more associated waters.
lipid ratio, the binding modality was found to be quite different. The most stable conformation of Ca–PS complexation is a motif of four oxygens per Ca2+ ion, with each lipid coordinating one phosphate oxygen and one carboxylate oxygen to form a cage around the central ion (Fig. 4). Conversely, the two most stable forms of the Mg–PS complex were found to involve only two total oxygens, with Mg2+ bridging either the lipid phosphate or carboxylate regions, but not both simultaneously as calculated for Ca2+. These conformations represented the most likely states, though Martin-Molina observed other binding modes at lower probabilities. The average of all possible states found Mg2+ to bind 2.7 oxygens, while Ca2+ bound 4.2. Overall, Mg2+ was found to occupy more superficial positions than Ca2+, which penetrated more deeply into the membrane and led to a loss of more associated waters.
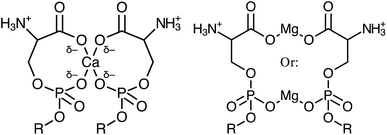 | ||
| Fig. 4 Schematic diagrams comparing the simultaneous bridging of carboxylate and phosphate oxygens by Ca2+ (left) versus Mg2+ bridged carboxylate or phosphate regions (right). These represent the most favourable configurations determined by MD simulations by Martin-Molina et al.89 | ||
The MD simulations by Martin-Molina are consistent with X-ray diffraction studies by Papahadjopoulos which support the conclusions of a larger dehydration effect of Ca2+ ions on PS.51 Tighter bridging of the headgroups by Ca2+ would additionally explain the Ca-induced abolishment of the PS lipid phase transition and enhanced fusogenic activity also observed by Papahadjopoulos.10,52 These data make clear that while both ions impact the behavior of PS, an overall stronger binding interaction exists between PS and Ca2+ than with Mg2+. SFVS was used to determine whether the binding of either species results in changes within the C–H stretch or H-bonding regions, which can elucidate how differences in binding modality influence the lipid monolayer structure, both in terms of tail packing and headgroup solvation.
Sum-frequency analysis
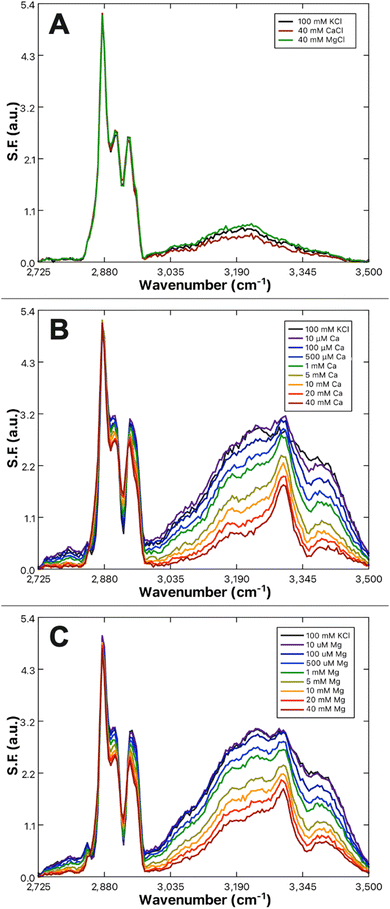
The vibrational spectra of DPPS and DPPC hybrid bilayers were examined to determine whether significant changes to the alkyl chain or hydrogen bonding structure were occurring as a result of Ca2+ and Mg2+ binding the DPPS headgroups. The use of hybrid bilayers (lipid monolayers) rather than lipid bilayers is important, as equivalent hydration environments across the bilayer interface would result in interference of sum-frequency generation between the two leaflets. The use of hybrid bilayers removes the antiposed hydration layer associated with headgroups on the opposite leaflet of a symmetric bilayer. Fig. 5A–C illustrate how the SFVS spectra of DPPC and DPPS hybrid bilayers change as a function of Ca2+ or Mg2+ concentration. The sum-frequency spectra of these hybrid bilayers can be broken into three general regions of interest: the C–H region from 2800 to 3000 cm−1, the water region from 3000 to 3500 cm−1, and an amine peak centered at 3300 cm−1 originating from the hydrogen bonded –NH3 group of the PS headgroup. Each of these vibrational features will be analyzed in turn to determine how the structure of the headgroups, associated water layer, and lipid tails respond to bound Ca2+ and Mg2+.Amine peak analysis
The resonance observed at ∼3300 cm−1 is attributed to the symmetric stretch of the primary amine moiety present on the serine headgroup. The resonance observed here is similar to the sum-frequency spectra obtained from mixtures of ammonia and water, where a 3300 cm−1 band appears due to the ordering of ammonia near the air/water interface.90 A very prominent 3300 cm−1 also appears within the sum-frequency spectra of fibrinogen-coated surfaces as reported by both the Chen and Cremer groups.91,92 Chen and Cremer both attributed the peak to N–H stretches, though disagreed on whether the peak indicated an ordering of the backbone amides (R–NH2–R) or side-chain amines (R–NH3). Further analysis by Weidner and Castner using a lysine-containing protein analogue LKα14 supports the hypothesis of the peak being related to the amine groups, as replacement of the lysine nitrogens with 15N resulted in a shift of the peak.93 The amine peak, for the purposes of this study, was considered a reporter of the reordering of serine headgroup amines resulting from Ca2+ or Mg2+ complexation, in line with the lipid complexing behavior predicted by Martin-Molina et al.89 as well as phospholipid reorientations observed by Seelig et al.94The amine peak, present only in the PS system, gains in prominence as the bulk Ca2+ (Fig. 5B) or Mg2+ (Fig. 5C) content is increased. The prominence of the amine peak reports directly on structural changes resulting from Ca2+ or Mg2+ complexation. Therefore, correlation of the net area change in the amine peak to the concentration of bulk Ca2+ or Mg2+ present was used to derive the binding affinity of Ca2+ and Mg2+ to PS by way of a fit to a Frumkin model binding isotherm, eqn (9):95,96
 | (9) |
Here it was found that while both Ca2+ and Mg2+ bind to the PS monolayer, Ca2+ will do so with both a higher affinity and a greater impact on the headgroup structure. Fig. 6 shows the amine peak area as a function of Ca2+ and Mg2+ concentration, with the lines representing the best Frumkin model fit of each dataset to eqn (9). The increase in amine peak area for Ca2+ is roughly double that of Mg2+. A more pronounced ordering of the amines in the case of Ca2+ is consistent with both the tighter caging of the ion as predicted in Martin-Molina's MD simulations as well as the condensation effect of Ca2+ on DPPS observed in compression isotherms. The Ka values of 1.3 ± 0.3 × 105 and 7.3 ± 2.5 × 103 M−1 for Ca–PS and Mg–PS, respectively, additionally indicate Ca2+ ions have around a 20-fold higher affinity toward PS. Newton and Papahadjopoulos reported a 10-fold difference between Ca2+ and Mg2+, roughly matching the order of magnitude relation found here, though their Ka values of 0.35 and 0.04 M−1 are much smaller.51 These values were based on dialysis equilibrium experiments and assumptions were made regarding the permeability and “probable amount of lipid exposed to the bulk solution”. It is possible there was less exposure of the lipids to the Ca2+ and Mg2+ solutions than anticipated, which could explain the variance.
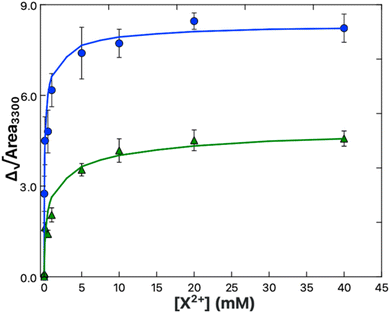 | ||
| Fig. 6 Binding isotherm data for Ca2+ (blue) and Mg2+ (green) obtained from the areas of the 3300 cm−1 amine peak in the spectra shown in Fig. 5B and C respectively. The solid lines are the fits to the data using a Frumkin model (eqn (9)). | ||
An alternate comparison with the results of Hauser et al., who examined Ca–PS affinity via measurement of the surface-enhanced radioactivity of solutions containing 45Ca in the presence and absence of PS monolayers was also made.97 Based on increases in surface radioactivity in the presence of PS, representing surface enrichment of 45Ca2+ relative to the bulk, Hauser determined the Ca–PS affinity to be anywhere from 104 to 106 M−1. Hauser could not go above 1 mM Ca2+ due to the cost and health concerns related to the use of radioactive isotopes. Ka values were therefore reported as single point measurements not fit to an isotherm model, however the results of Hauser are in relative agreement with the SFVS results. Mg2+ was not tested by Hauser, so a comparison of relative Mg2+/Ca2+ affinities cannot be made.
Finally, Sinn et al. characterized the binding affinity of PS and Ca2+ by way of ion selective electrode (ISE) measurements.98 Known amounts of Ca2+ were used to titrate a solution containing vesicles composed of 20% DOPS in 80% DOPC. The free concentration of Ca2+ measured by the probe was compared to the injected amount of Ca2+ to deduce the amount of Ca2+ ions bound to the vesicle membranes. Results indicated a binding constant of 650 M−1, roughly 200-fold lower than that determined by SFVS. The authors do note however that repeat calibrations of the ISE probe showed drift indicative of lipids depositing to the hydrophobic surfaces of the probe and that the presence of charged lipid on the probe surface could shift the measured Ca2+ concentration. Sinn et al. hypothesized the lipid coating could either decrease the measured [Ca2+] via reduced ion transport across the electrode membrane or increase the measured [Ca2+] through electrostatic enrichment in the local Ca2+ concentration due to the presence of negatively charged PS lipids. The former would increase the determined Ka by reporting an overly large differential in the injected and detected amounts of bulk Ca2+ whereas the latter would lead to a reduction in the measured Ka. Given Hauser's finding of a great local enrichment of Ca2+ ions in the presence of PS lipids, it is possible the deviation in results between ISE and SFVS are due to the second scenario put forward by Sinn.
Water peak analysis
The water region from 3000 to 3500 cm−1 reports on the hydrogen bonding structure within the membrane associated water layer and contains two characteristic water peaks centered at 3200 cm−1 and 3400 cm−1, representing the ice-like O–H symmetric and liquid-like O–H symmetric stretches.80,99–101 While both result from the symmetric O–H stretch of water, the ice-like resonance is indicative of a strong, tetrahedral H-bonding structure like that seen in ice. Conversely, the liquid-like peak results from a weaker H-bonding structure, namely bifurcated H-bonding whereby hydrogens are shared unevenly between neighboring oxygens. It can be seen that the intensity of the water sum-frequency is far higher with DPPS (Fig. 5B and C) as compared to DPPC (Fig. 5A), results which are in line with previous observations by Chen et al.102 Chen attributed sum-frequency enhancement in the presence of negatively charged lipids to the ordering of water at the lipid interface, with waters orienting their hydrogens toward the charged lipid headgroups. The observed reduction in water sum-frequency for a DPPS monolayer exposed to either Ca2+ or Mg2+ is therefore hypothesized to result from neutralization of the membrane surface charge and relaxation of the electrostatically imposed ordering of water. Conversely, the lack of an increase in sum-frequency from the water region of the DPPC hybrid bilayer when exposed to Ca2+ or Mg2+ ions implies the neutral DPPC lipids have not increased in charge. It is therefore hypothesized that either no binding of Ca2+ or Mg2+ has occurred, or that any bound Ca2+ and Mg2+ simply displace previously bound Na+ ions in a surface charge conserving manner. Both the hypothesized rationales for the DPPS and DPPC sum-frequency water band responses to Ca2+ or Mg2+ rely upon the interpretation that sum-frequency in the water region is sensitive to the charge state of the lipids.The influence of interfacial charge on the observed sum-frequency intensity has been previously considered by others as a third order, χ(3) effect.103–110 Just as the χ(2) tensor describes a material's response to the coupling of two incident electric fields, the χ(3) tensor describes a material's response to three incident fields. In the present case, two are the E532 and EIR from the incoming 532 nm and IR beams and the third is a static field, EDC, which is produced by the charged DPPS/water interface. The total sum-frequency generated is expressed as a summation of the respective second and third order contributions:105–108,110–113
| ISF ∝ |(χ(2) + χ(3)EDC)EIRE532|2 | (10) |
Depending on the material properties, EDC may influence χ(3) in various ways. As noted by Allen, Eisenthal, Levine and others, dipolar molecules, like water, will realign within a static electric field.100,102,105–107,110,114 As χ(2) depends on the molecular axis being probed, realignment of interfacial molecules can yield changes in sum-frequency generation without necessarily resulting directly from third-order coupling. Therefore, the static field (EDC) contributions can be expressed as a summation of two components, one dependent on third-order molecular hyperpolarizability (γ) and the other dependent on molecular rearrangement of the second-order molecular hyperpolarizability (β). χ(3) can then be expressed as:105–107
 | (11) |
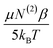 term.107,110 Substitution of eqn (11) into eqn (10) yields the relationship between the generated sum-frequency and EDC field strength:
term.107,110 Substitution of eqn (11) into eqn (10) yields the relationship between the generated sum-frequency and EDC field strength:
 | (12) |
The magnitude of the static EDC field is itself ultimately determined by the surface charge density and the ionic strength of the solution. The surface charge will generate a surface potential in accordance with eqn (13):8,13,115–117
 | (13) |
| ϕx = ϕ0e−κx | (14) |
 | (15) |
The charge density of the DPPS membrane was computed using the MMA of the DPPS monolayer obtained from the pressure–area isotherms. Given a mean molecular area of 49.3 ± 0.5 Å2 for DPPS at a deposition pressure of 30 mN m−1, the theoretical maximum charge density for a pure DPPS monolayer is −0.33 C m−2. Conversely, at a saturating concentration of Ca2+, one would expect the PS lipids to have a charge state of zero, assuming a binding ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PS
1 PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca. Using these surface charge limits and the isotherm data in Fig. 6, Table 1 lists the surface saturation, charge density (σ), surface potential (ϕ0), and electric field strength one Debye length away from the surface (Eκ−1) for each bulk concentration of Ca2+. The Debye length for all calculations was taken to be 0.828 nm as the ionic strength was held constant at 133.4 mM.
Ca. Using these surface charge limits and the isotherm data in Fig. 6, Table 1 lists the surface saturation, charge density (σ), surface potential (ϕ0), and electric field strength one Debye length away from the surface (Eκ−1) for each bulk concentration of Ca2+. The Debye length for all calculations was taken to be 0.828 nm as the ionic strength was held constant at 133.4 mM.
| [Ca] (mM) | ΓCa2+ | σi (C m−2) | ϕ0 (V) | EDC (V m−1) × 10−7 | |
|---|---|---|---|---|---|
| 0 | 0 | 100% | −0.33 | −0.142 | 6.30 |
| 0.01 | 27% | 73% | −0.25 | −0.126 | 5.59 |
| 0.1 | 54% | 46% | −0.16 | −0.103 | 4.57 |
| 0.5 | 72% | 28% | −0.094 | −0.078 | 3.48 |
| 1 | 79% | 21% | −0.070 | −0.065 | 2.89 |
| 5 | 92% | 8% | −0.028 | −0.031 | 1.40 |
| 10 | 95% | 5% | −0.017 | −0.020 | 8.67 |
| 20 | 97% | 3% | −0.009 | −0.010 | 4.95 |
| 40 | 100% | 0% | 0 | 0 | 0 |
The validity of the calculated surface saturation and surface charge density values were evaluated as follows. The spectra of Fig. 5B were fit using eqn (4) to obtain the transition probability amplitudes [PA = (NAiMjk)] for the ice-like 3200 cm−1 and water-like 3400 cm−1 resonances. Equating eqn (4) and (12) at a specific resonance yields:
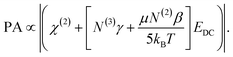 | (16) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PS
1 PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca complexation. Under such a motif, the EDC should be reduced due to charge neutralization of PS upon binding Ca2+. A linear drop in the ice- and water-like transition probabilities with respect to EDC supports these previous assumptions. There does, however, seem to be a deviation from linearity beyond an EDC of 5.59 × 107 V m−1. The 10 μM Ca2+ and zero Ca2+ data have roughly equal water intensity despite the binding isotherm predicting around 27% neutralization of the surface charge should have occurred. The deviation from linearity seen in Fig. 7 is explained by considering the two types of contributions to χ(3) detailed in eqn (11). As observed by both Richmond and Kielich, EDC scaling reaches a saturation point beyond which there is no further change in intensity.99,110 Saturation occurs in instances where χ(3) has significant contributions from molecular reorientations,
Ca complexation. Under such a motif, the EDC should be reduced due to charge neutralization of PS upon binding Ca2+. A linear drop in the ice- and water-like transition probabilities with respect to EDC supports these previous assumptions. There does, however, seem to be a deviation from linearity beyond an EDC of 5.59 × 107 V m−1. The 10 μM Ca2+ and zero Ca2+ data have roughly equal water intensity despite the binding isotherm predicting around 27% neutralization of the surface charge should have occurred. The deviation from linearity seen in Fig. 7 is explained by considering the two types of contributions to χ(3) detailed in eqn (11). As observed by both Richmond and Kielich, EDC scaling reaches a saturation point beyond which there is no further change in intensity.99,110 Saturation occurs in instances where χ(3) has significant contributions from molecular reorientations,  , as opposed to being purely third-order coupling, (N(3)γ). Both Richmond and Kielich attributed saturation to a limit on the alignment of the interfacial water within the EDC field.99,110 Once the EDC strength is sufficient to orient the water dipoles along the EDC field vector, further increases in field strength will not yield further alignment. The realignment term,
, as opposed to being purely third-order coupling, (N(3)γ). Both Richmond and Kielich attributed saturation to a limit on the alignment of the interfacial water within the EDC field.99,110 Once the EDC strength is sufficient to orient the water dipoles along the EDC field vector, further increases in field strength will not yield further alignment. The realignment term, 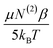 , is thus maximized and higher EDC fields further magnify only the N(3)γ component of χ(3). The deviation seen here is therefore ascribed to maximal water alignment beyond EDC = 5.59 × 107 V m−1. Accordingly, the line fits of Fig. 7 were limited to the linear region.
, is thus maximized and higher EDC fields further magnify only the N(3)γ component of χ(3). The deviation seen here is therefore ascribed to maximal water alignment beyond EDC = 5.59 × 107 V m−1. Accordingly, the line fits of Fig. 7 were limited to the linear region.
 | ||
| Fig. 7 3200 cm−1 (black) and 3400 cm−1 (blue) peak transition probabilities from spectral fits of Ca-exposed DPPS (Fig. 5B) plotted as a function of the electric field strength one Debye length away from the lipid surface (Table 1). The determined slopes, representing the relative χ(3), are 3.4 ± 0.1 × 106 m V−1 for the ice-like 3200 cm−1 and 1.6 ± 0.1 × 106 for the water-like 3400 cm−1. | ||
The ice-like peak results from tightly ordered water structures, whereas the water-like peak results from more transient and disordered H-bonding. As previously detailed by Gragson and Richmond, application of an electric field will lead to sequential conversion of disordered bulk water to the semi-ordered population resonant at 3400 cm−1 and from the semi-ordered population to the tetrahedrally ordered population resonant at 3200 cm−1.99 Gragson and Richmond altered the EDC field strength through modulation of either the density of charged sodium dodecyl sulfate (SDS) molecules at the air/water interface or the bulk ionic strength. In both cases it was found the 3200 cm−1 peak responded more strongly to the electric field due to population migration of water molecules toward the more ordered state.
The rate of change of the ice-like and water-like amplitudes |NAiMjk|, with respect to EDC were used to examine the relative χ(3) of each peak. In Fig. 7, the χ(3) for the ice-like and water-like peaks is represented by the slope of each line (eqn (10)). The data yield χ(3) values of 3.4 ± 0.1 × 106 m V−1 for the ice-like 3200 cm−1 and 1.6 ± 0.1 × 106 m V−1 for the water-like 3400 cm−1. The relative ice-like to water-like χ(3) ratio is thus found to be 2.1 ± 0.1. A larger χ(3) for the 3200 cm−1 peak is in agreement with Gragson and Richmond's findings of net population conversion of water molecules toward the more ordered ice-like state at higher EDC. As the water population conversion requires reordering of the water molecules, it is concluded EDC dependent molecular rearrangements are occurring within the solvation layer. These data are limited, however, in that while the presence of molecular rearrangement is suggested, the magnitude of 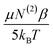 relative to the static component, N(3)γ, of χ(3) remains unclear.
relative to the static component, N(3)γ, of χ(3) remains unclear.
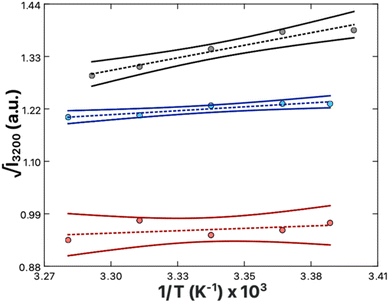
The relative magnitude of the molecular rearrangement and third-order contributions was assessed as follows. From eqn (12), only the molecular rearrangement term,  , of χ(3) has a 1/T dependence. Determination of the relative contributions of the dynamic and static components of χ(3),
, of χ(3) has a 1/T dependence. Determination of the relative contributions of the dynamic and static components of χ(3),  and N(3)γ, respectively, was therefore performed by measurement of the sum-frequency intensity as a function of 1/T for the 3200 cm−1 ice-like peak, Fig. 8.105,106 The ice-like resonance was chosen due to its larger χ(3), as found in Fig. 7. A linear relationship between the square root of the sum-frequency intensity and 1/T should be observed if EDC induced reorganization of water is occurring,105 with the slope and intercept terms equal to:
and N(3)γ, respectively, was therefore performed by measurement of the sum-frequency intensity as a function of 1/T for the 3200 cm−1 ice-like peak, Fig. 8.105,106 The ice-like resonance was chosen due to its larger χ(3), as found in Fig. 7. A linear relationship between the square root of the sum-frequency intensity and 1/T should be observed if EDC induced reorganization of water is occurring,105 with the slope and intercept terms equal to:
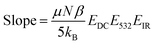 | (17) |
| Intercept = (χ(2) + N(3)γEDC)E532EIR | (18) |
The relative influences of the dynamic realignment,  , and static third-order, N(3)γ, contributions to χ(3) were calculated as follows. Intensity data was collected in the absence of Ca2+, as well as in the presence of 1 mM Ca2+ or 40 mM Ca2+. These data contain three important trends. Firstly, a linear trend is observed in the zero and 1 mM Ca2+ systems. As the realignment contribution,
, and static third-order, N(3)γ, contributions to χ(3) were calculated as follows. Intensity data was collected in the absence of Ca2+, as well as in the presence of 1 mM Ca2+ or 40 mM Ca2+. These data contain three important trends. Firstly, a linear trend is observed in the zero and 1 mM Ca2+ systems. As the realignment contribution, 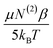 , is the only temperature dependent term in eqn (12), the results validate the hypothesis of electrostatically induced water reorganization. Secondly, it is shown the 1/T dependence decreases as the concentration of Ca2+ increases. As per eqn (17), the slope, representing the dynamic term
, is the only temperature dependent term in eqn (12), the results validate the hypothesis of electrostatically induced water reorganization. Secondly, it is shown the 1/T dependence decreases as the concentration of Ca2+ increases. As per eqn (17), the slope, representing the dynamic term 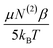 , is scaled by EDC. The observation of reduced EDC as Ca2+ content is increased is further evidence of charge neutralization of PS lipids as Ca2+ binds. Lastly, at 40 mM Ca2+ the slope of the line becomes indistinct from zero (180 ± 200). The conclusion is that complete neutralization of PS headgroup charges has occurred resulting in EDC = 0. Complete neutralization supports the previous assumption of a 2
, is scaled by EDC. The observation of reduced EDC as Ca2+ content is increased is further evidence of charge neutralization of PS lipids as Ca2+ binds. Lastly, at 40 mM Ca2+ the slope of the line becomes indistinct from zero (180 ± 200). The conclusion is that complete neutralization of PS headgroup charges has occurred resulting in EDC = 0. Complete neutralization supports the previous assumption of a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PS
1 PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca2+ binding ratio. Further, the neutralization point agrees with the amine peak-derived binding isotherm (Fig. 6), which indicates surface saturation at 40 mM Ca2+.
Ca2+ binding ratio. Further, the neutralization point agrees with the amine peak-derived binding isotherm (Fig. 6), which indicates surface saturation at 40 mM Ca2+.
From the previous analysis, it becomes possible to determine the relative contributions (eqn (12)) to χ(3). The contribution from molecular rearrangements,  , at any temperature T is simply the product of the measured slope and 1/T (eqn (17)). As all sum-frequency spectra shown in Fig. 5A–C were collected at 21 °C, T = 294.15 K is used here. The determined slopes of 960 ± 130 K and 300 ± 60 K yield
, at any temperature T is simply the product of the measured slope and 1/T (eqn (17)). As all sum-frequency spectra shown in Fig. 5A–C were collected at 21 °C, T = 294.15 K is used here. The determined slopes of 960 ± 130 K and 300 ± 60 K yield 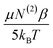 values of 3.26 ± 0.44 and 1.02 ± 0.35 for the zero Ca2+ and 1 mM Ca2+ data, respectively. The static third-order contributions, N(3)γ, can be determined from rearrangement of eqn (18). To accomplish this, however, the value of χ(2) must be known. χ(2) is obtained from the 40 mM Ca2+ data set, as complete neutralization of surface charge results in an EDC of zero. The average of all the measured 3200 cm−1 sum-frequency intensities at 40 mM Ca2+ yields a relative χ(2) of 0.958 ± 0.008. Using this χ(2) value, the static third-order contributions, N(3)γ, were calculated for the zero Ca2+ and 1 mM Ca2+ systems. From the determined intercepts of −1.85 ± 0.42 and 0.21 ± 0.21, N(3)γ values of −2.81 ± 0.43 and −0.75 ± 0.22 are obtained for the zero Ca2+ and 1 mM Ca2+ data, respectively. The relative contribution of dynamic realignment
values of 3.26 ± 0.44 and 1.02 ± 0.35 for the zero Ca2+ and 1 mM Ca2+ data, respectively. The static third-order contributions, N(3)γ, can be determined from rearrangement of eqn (18). To accomplish this, however, the value of χ(2) must be known. χ(2) is obtained from the 40 mM Ca2+ data set, as complete neutralization of surface charge results in an EDC of zero. The average of all the measured 3200 cm−1 sum-frequency intensities at 40 mM Ca2+ yields a relative χ(2) of 0.958 ± 0.008. Using this χ(2) value, the static third-order contributions, N(3)γ, were calculated for the zero Ca2+ and 1 mM Ca2+ systems. From the determined intercepts of −1.85 ± 0.42 and 0.21 ± 0.21, N(3)γ values of −2.81 ± 0.43 and −0.75 ± 0.22 are obtained for the zero Ca2+ and 1 mM Ca2+ data, respectively. The relative contribution of dynamic realignment  to χ(3) is therefore 54 ± 9% and 57 ± 8% for the zero Ca2+ and 1 mM Ca2+ data, respectively. The results suggest an equal contribution of the dynamic and static components to χ(3), within error. At saturation, where maximum dipole alignment and maximum
to χ(3) is therefore 54 ± 9% and 57 ± 8% for the zero Ca2+ and 1 mM Ca2+ data, respectively. The results suggest an equal contribution of the dynamic and static components to χ(3), within error. At saturation, where maximum dipole alignment and maximum  is reached, further increases in EDC are predicted to increase the contribution from the negative N(3)γ term while contributions from
is reached, further increases in EDC are predicted to increase the contribution from the negative N(3)γ term while contributions from  would remain constant. Increases in EDC beyond saturation are therefore expected to reduce the total χ(3) and result in a drop in generated sum-frequency. From Fig. 7 it can be seen that maximum 3200 cm−1 amplitude is reached at 5.59 × 107 V m−1, which then decreases at 6.30 × 107 V m−1. These data are consistent with maximal water alignment at 5.59 × 107 V m−1.
would remain constant. Increases in EDC beyond saturation are therefore expected to reduce the total χ(3) and result in a drop in generated sum-frequency. From Fig. 7 it can be seen that maximum 3200 cm−1 amplitude is reached at 5.59 × 107 V m−1, which then decreases at 6.30 × 107 V m−1. These data are consistent with maximal water alignment at 5.59 × 107 V m−1.
Alkyl chain analysis
The alkyl chain C–H stretches, found between 2800 and 3000 cm−1, were characterized to determine whether the lipid tails undergo any structural changes as PS binds Ca2+ or Mg2+. All five peaks previously detailed for the bilayer system of Fig. 1 are present, with an additional peak at 2920 cm−1 due to the CH3 symmetric stretch of the methylated surface. The C–H region of the DPPC system in Fig. 5A displays no change when comparing the 100 mM KCl, 40 mM CaCl2, and 40 mM MgCl2 solutions. Conversely, changes are quite apparent within the C–H bands of DPPS as Ca2+ (Fig. 5B) or Mg2+ (Fig. 5C) content is increased. At first glance this may imply an alteration in the packing structure of the lipid tails; however, the C–H region of the DPPS sits atop the trailing edge of the water stretches, the magnitudes of which are highly influenced by both Ca2+ and Mg2+ association due to charge screening.The direct effect of Ca2+ ions on DPPS tail structure was determined by isolation of the C–H region from the water region. SFVS spectra were recorded in buffered D2O to remove the water features from the spectra. Fig. 9 illustrates the influence Ca2+ has on the C–H region, absent any O–H bands. Comparing the 100 mM KCl (zero Ca2+) and 40 mM Ca2+ solutions, it is clear the changes observed in Fig. 5B are not due to changes in the C–H bands intensities, but rather result from Ca2+ induced disruption of the underlying water resonance.
 | ||
| Fig. 9 SFVS spectra of DPPS in D2O with 100 mM KCl (black) or 40 mM CaCl2 (red). The offset curves (dashed lines) are the spectral fits of the CH2 vs and CH3 vs peaks at 2850 cm−1 and 2875 cm−1 respectively, obtained using eqn (4). All solutions were buffered with Tris at pH = 7.4 with a total ionic strength of 133.4 mM. Spectra were recorded at 21 °C. | ||
The ratio of the CH2 symmetric stretch (vs) at 2850 cm−1 and the CH3 vs at 2875 cm−1 has previously been used to evaluate net changes in gauche content within the chain structure.81,119–122 Increased ordering of the alkyl chains is expected to result in reduced gauche content, which is observed in sum-frequency spectra as a reduced CH2 vs character relative to the CH3 vs due to cancellation of sum-frequency within the locally symmetric trans configuration.79,119,120 Ordering of the alkyl chains from Ca2+ induced condensation of DPPS would be expected to result in a decrease in the CH2 vs to CH3 vs peak ratio. The sum-frequency spectra of Fig. 9 were fit using eqn (4) to calculate the CH2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH3 ratio for the 100 mM KCl and 40 mM CaCl2 data, which remains unchanged within error at 0.20 ± 0.05 and 0.17 ± 0.06, respectively. The observed invariance of the CH2
CH3 ratio for the 100 mM KCl and 40 mM CaCl2 data, which remains unchanged within error at 0.20 ± 0.05 and 0.17 ± 0.06, respectively. The observed invariance of the CH2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH3 ratio with respect to Ca2+ induced condensation of DPPS is taken to simply be a result of minimal initial gauche content within the alkyl chains. The membranes under measurement here were deposited at 30 mN m−1, within the gel phase where gauche content of saturated lipids is expected to be minimal, for example H1NMR and FT-IR analysis place the gauche vs. trans conformation of DPPC at less than 3%.123,124 Given DPPS has the same 16-carbon alkyl chain lengths as DPPC, a similarly low gauche content would be expected.
CH3 ratio with respect to Ca2+ induced condensation of DPPS is taken to simply be a result of minimal initial gauche content within the alkyl chains. The membranes under measurement here were deposited at 30 mN m−1, within the gel phase where gauche content of saturated lipids is expected to be minimal, for example H1NMR and FT-IR analysis place the gauche vs. trans conformation of DPPC at less than 3%.123,124 Given DPPS has the same 16-carbon alkyl chain lengths as DPPC, a similarly low gauche content would be expected.
Flip-flop kinetics
The central hypothesis of the current work is that PS expression can be influenced by Ca2+. At equilibrium, a net population difference in the number density of PS lipids is possible if the rate constants for PS flip and flop are not equal:
 | (19) |
To achieve this, Ca2+ ions need to alter the flip-flop mixing behavior of PS lipids such that PS lipids will flip and flop at different rates in the presence and absence of Ca2+. To test the hypothesis, DPPS flip-flop kinetics of asymmetric PSLBs containing physiologic levels of 10% PS were performed to determine if the binding interactions observed between PS and Ca2+ or Mg2+ affect the rate of DPPS flip-flop. The concentration of Ca2+ and Mg2+ were 1 mM to mimic the physiologic concentrations of the extracellular fluid and cytosol, respectively.54,55 KCl controls without Ca2+ or Mg2+ were also collected as a baseline for comparison. Fig. 10A–C show representative DPPS flip-flop decays for both DPPC and DPPS with Ca2+ or Mg2+, while Fig. 10D and E show linearized Eyring plots of all determined flip-flop rates.
 | ||
| Fig. 10 Representative SFVS intensity decays of the CH3 symmetric stretch at 2875 cm−1 for (A) DPPC/DPPCd62 bilayers in the presence of 100 mM KCl (black) and 97 mM KCl + 1 mM CaCl2 (blue) recorded at 26.9 and 26.6 °C, respectively; (B) 10% DPPS in DPPCd62 bilayers in the presence of 100 mM KCl (black) and 97 mM KCl + 1 mM CaCl2 (blue) recorded at 24.7 and 24.5 °C, respectively; (C) 10% DPPS in DPPCd62 bilayers in the presence of 100 mM KCl (black) and 97 mM KCl + 1 mM MgCl2 (green) recorded at 24.7 and 24.5 °C, respectively. The solid lines in (A–C) are the fits to the data using eqn (7). (D and E) show the linearized Eyring plots of the measured flip-flop rates for DPPC and 10% DPPS in DPPCd62, respectively obtained in 100 mM KCl (gray circles), 97 mM KCl + 1 mM CaCl2 (blue triangles) and 97 mM KCl + 1 mM MgCl2 (green squares). The dashed lines are the fits to the data using eqn (21) with the corresponding confidence intervals (solid lines). (D) also contains measured flip-flop rates for DPPC in the presence of 10% DPPSd62 (red diamonds) with 97 mM KCl + 1 mM CaCl2. | ||
Eyring plots were generated from the Eyring equation, which relates the rate of flip-flop, k, to the transition state free energy, ΔG‡:63,66,125
 | (20) |
 | (21) |
Considering the DPPC controls first, no effect of Mg2+ or Ca2+ on the rate of DPPC flip-flop was observed. A representative comparison of DPPC flip-flop behavior is shown in Fig. 10A, where the rate of DPPC flip-flop is found to be 3.35 ± 0.03 × 10−5 s−1 at 26.9 °C or 3.45 ± 0.04 × 10−5 s−1 at 26.6 °C in the presence and absence of 1 mM Ca2+, respectively. The slight deviation in rate is considered to be within the experimental variance as, from Fig. 10D, the 95% confidence intervals of the DPPC flip-flop rates in the presence and absence of 1 mM Ca2+ overlap. Likewise, measured flip-flop rates for DPPC in the presence of 1 mM Mg2+ fall within the 95% confidence intervals for DPPC flip-flop rates both in the presence and absence of 1 mM Ca2+. The lack of any influence of Ca2+ or Mg2+ on DPPC flip-flop rates is in agreement with the compression isotherms which found no change in the MMA in the presence of Ca2+ or Mg2, results which indicate neither ion had bound DPPC. Likewise, bound Ca2+ or Mg2+ would be expected to increase the surface charge density of the neutral DPPC lipids and, through χ(3) (eqn (13)), scale the sum-frequency generated by the 3200 cm−1 and 3400 cm−1 water peaks. No such effect was observed in sum-frequency scans of DPPC hybrid bilayers in the presence and absence of Ca2+ or Mg2+ (Fig. 5A). The sum-frequency spectra, compression isotherms, and flip-flop data are all consistent with no observable binding interaction between the PC headgroup and either Ca2+ or Mg2+.
Determination of the flip-flop kinetics for 10% DPPS + 90% DPPC membranes was performed with respect to both the DPPS and DPPC fractions. The effect of 10% DPPS on the parent DPPC matrix was examined by measurement of the flip-flop rate of 90% DPPC in the presence of 10% DPPS with 1 mM Ca2+ (87.3% DPPC + 9.7% DPPSd62 + 3% PEG5000-PE/90% DPPCd62 + 10% DPPSd62, proximal/distal). The flip-flop rates fall within the 95% confidence intervals of the flip-flop rates obtained for a pure DPPC membrane shown in Fig. 10D. This result indicates that the presence of 10 mol% DPPS has no influence on DPPC flip-flop. The flip-flop behavior of the PS fraction, however, yields more interesting results. The rate of DPPS flip-flop in DPPC (87.3% DPPCd62 + 9.7% DPPS + 3% PEG5000-PE/90% DPPCd62 + 10% DPPSd62, proximal/distal) show a pronounced effect of Ca2+ on the rate of DPPS flip-flop. The rate of DPPS flip-flop decreased from 7.11 ± 0.08 × 10−5 s−1 (24.7 °C) in the absence of Ca2+ to 1.46 ± 0.07 × 10−5 s−1 (24.5 °C) when in the presence of 1 mM Ca2+, roughly a 5-fold decrease. Alternatively, Fig. 10C shows a comparison of DPPS flip-flop measured in the presence of 1 mM Mg2+ at 24.5 °C compared to DPPS flip-flop in the absence of Ca2+ or Mg2+ at 24.7 °C (same as Fig. 10B). The measured flip-flop rate of 6.8 ± 0.1 × 10−5 s−1 for the 1 mM Mg2+ exposed DPPS is essentially identical to the 7.11 ± 0.08 × 10−5 s−1 flip-flop rate measured in the absence of Mg2+. All flip-flop rates measured for DPPS in the presence of 1 mM Mg2+ fall within the 95% confidence intervals of DPPS flip-flop in the absence of Ca2+ or Mg2+, whereas all flip-flop rates measured for DPPS in the presence of 1 mM Ca2+ fall outside (Fig. 10E). Ca2+ exposure has a pronounced and specific slowing effect on DPPS translocation. From eqn (19), the slowed flip-flop kinetics of DPPS in the presence of Ca2+ (Fig. 10B) results from an increase in ΔG‡ from 96.6 ± 0.1 kJ mol−1 in the absence of Ca2+ to 100.5 ± 0.2 kJ mol−1 in the presence of 1 mM Ca2+, an increase of 3.9 ± 0.2 kJ mol−1. In the presence of 1 mM Mg2+, the ΔG‡ of 96.7 ± 0.2 kJ mol−1 remains within error of the ΔG‡ in the absence of Ca2+ or Mg2+.
The divergence in DPPS response to the presence of Ca2+ and Mg2+ can be attributed to two important factors. Firstly, Mg2+ was found to have a PS binding affinity roughly 20-fold lower than Ca2+. Yet further, the binding data from Fig. 6 shows bound Mg2+ does not produce as great of an impact on the ordering of the serine headgroup amines. A 1 mM concentration of Mg2+ resulted in an amine peak area increase roughly equivalent to just 10 μM Ca2+. These results track well with Papahadjopoulos, who observed a 10-fold differential in Ca2+ and Mg2+ binding affinity, and noted only Ca2+ lead to fusion of PS-containing vesicles or phase segregation of PS.10,50–53 Mg2+ ions have lower PS affinity, more muted impact on headgroup structure, and lower denticity binding to the membrane as predicted by MD simulations,89 and it is therefore not surprising to find that Mg's binding modality is simply too weak to influence translocation.
Ca2+ has a unique ability to slow the rate of DPPS translocation relative to Mg2+, which has no measurable effect. The finding has potentially important implications for PS expression in vivo. The extracellular concentration of Ca2+ is far higher than within the cytosol, at 1 mM and 100 nM, respectively.55 Some degree of Ca2+ induced PS externalization could therefore be explained in terms of the difference in the rate of PS flip and flop (eqn (19)).63,65,126 In the case where kflip = kflop, one would expect the system to mix to homogeneity, where Nproximal = Ndistal. Such is observed in the flip-flop measurements in Fig. 10A–C, where sum-frequency signal trends toward zero due to the increasing symmetry of the system (eqn (5)). However, in the case of unequal rates of kflip and kflop, the equilibrium expression (eqn (19)) dictates accumulation toward the side of lower k, as the rate of inward movement is greater than the rate of outward transfer. Using the flip-flop rates determined in Fig. 10C as an example, a Ca2+ concentration differential whereby the distal leaflet is exposed to 1 mM Ca2+ while the proximal leaflet is unexposed to Ca2+ would result in a DPPS kflip of 1.46 ± 0.07 × 10−5 s−1 and kflop of 7.11 ± 0.08 × 10−5 s−1 at 24.5 °C. Applied to eqn (19), DPPS would be expected to enrich in the Ca2+ exposed leaflet by a factor of 4.87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, or approximately 80% of the total DPPS population (Fig. 11). Ongoing research aims to further validate the Ca-induced PS expression model by way of SFVS of surface-tethered vesicles where the concentration of Ca2+ of the external and internally encapsulated solution can be independently controlled. From the data shown here, an initially symmetric PS population should produce asymmetric vesicles upon exposure to a calcium concentration gradient and thus yield an increase in sum frequency. Such experiments would additionally allow a comparison of lipid flip-flop rates determined from PSLB and vesicle systems and aid in the examination of inconsistencies between methods.
1, or approximately 80% of the total DPPS population (Fig. 11). Ongoing research aims to further validate the Ca-induced PS expression model by way of SFVS of surface-tethered vesicles where the concentration of Ca2+ of the external and internally encapsulated solution can be independently controlled. From the data shown here, an initially symmetric PS population should produce asymmetric vesicles upon exposure to a calcium concentration gradient and thus yield an increase in sum frequency. Such experiments would additionally allow a comparison of lipid flip-flop rates determined from PSLB and vesicle systems and aid in the examination of inconsistencies between methods.
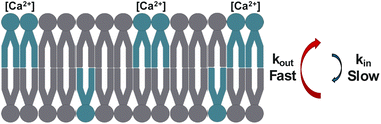 | ||
| Fig. 11 Illustration of the enrichment of PS lipids (blue) on the Ca2+-exposed distal leaflet, driven by unequal rates of slow inward flip (kin) and fast outward flop (kout). | ||
While the flip-flop rates used in the prior calculation are particular to the non-physiologic binary mixture tested, Ca–PS interactions in vivo can reasonably be inferred to slow PS lipid flip-flop in an analogous fashion. The extent of the effect is very likely to depend on the membrane matrix and experimental parameters, which precludes any universal statement on how the effect may manifest. However, the theorized enrichment of PS toward the Ca-exposed leaflet is in agreement with the observations of both the Hampton and Bratton groups where the degree of PS expression was dependent on a Ca2+ concentration differential over the bilayer as opposed to Ca2+ influx.25,56
On the surface, migration of PS lipids toward Ca2+ would seem incompatible with the usual observations of internally held PS, where Ca2+ content is minimal.55 However, PS externalization is normally induced in vivo by some intentional perturbation of the cells. For example, common methods of achieving PS externalization include UV irradiation, incorporation of membrane-permeating ionophores, ATP-depletion, deoxygenation, and other treatments which may destabilize cell functioning in some unforeseen ways.16,29,33,35,36,39,40,43,47,127 As the mechanisms by which PS asymmetry is maintained in healthy cells are not fully understood, the effects of such treatment on the cell's ability to maintain PS asymmetry is not fully detailed. Destabilized cell functionality may simply lead to PS lipids becoming free to equilibrate across the membrane boundary. Many studies on PS externalization utilize high concentrations of external Ca2+ to mimic physiologic conditions, make use of Ca-dependent Annexin V staining, or test the dependence of scramblases2,4,11,17,19,24,25,28,31–36 on Ca2+ content.39,43,44,47,127–138 Due to PS experiencing differing flip and flop rates, some amount of PS expression may simply be attributed to the high external concentrations of Ca2+.
The hypothesized effect of Ca-induced PS enrichment does not preclude the effects of scramblases or signalling processes which may also serve to externalize PS. Multiple pathways of externalization may coexist. The potential presence of a direct PS–Ca2+ mechanism of externalization does however suggest that determinations of cooperative actions between Ca2+ and scramblases may first require disentanglement from effects driven purely by PS–Ca2+ interactions. The data reported here demonstrates the importance of considering the influence of Ca2+ concentration differentials when interpreting PS expression data.
Conclusions
Compression isotherms of DPPC and DPPS monolayers in the presence and absence of 1 mM Ca2+ or 1 mM Mg2+ revealed a specific interaction between DPPS and Ca2+ ions. When in the presence of Ca2+, but not Mg2+, a −2.4 ± 0.6 Å2 per molecule reduction in the MMA of DPPS was observed at 30 mN m−1. No change in MMA was observed for DPPC. A net condensation of the DPPS monolayer in the presence of Ca2+ is consistent with a headgroup-bridging binding interaction whereby neighboring headgroups are brought into closer contact. A 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PS
1 PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca2+ binding ratio was hypothesized.
Ca2+ binding ratio was hypothesized.
SFVS spectra of DPPS and DPPC hybrid bilayers were examined at concentrations between 0 and 40 mM Ca2+ or Mg2+ to determine whether the binding of either Ca2+ or Mg2+ to PS or PC headgroups impacted the membrane structure. No effect on DPPC was observed for either Ca2+ or Mg2+, whereas DPPS responded to both Ca2+ and Mg2+. As the concentration of Ca2+ or Mg2+ was increased, DPPS hybrid bilayers showed an increase in the amine peak sum-frequency at 3300 cm−1, as well as decreases in sum-frequency of the ice- and water-like O–H peaks at 3200 cm−1 and 3400 cm−1, respectively. The growth in the amine peak is attributed to complexation of the PS headgroup and ordering of the amine moiety. Ca2+ ions were shown to have a more pronounced influence on ordering of the amine groups, resulting in double the 3300 cm−1 peak area at saturation when compared to Mg2+. Frumkin model binding isotherms were calculated through relation of the change in amine peak area with the bulk concentration of either Ca2+ or Mg2+ present. The binding isotherms showed both Ca2+ and Mg2+ demonstrate binding behaviors toward PS lipids, with affinity values of 1.3 ± 0.3 × 105 M−1 and 7.3 ± 2.5 × 103 M−1, respectively.
The amine peak binding isotherm for Ca2+ was used in conjunction with the assumed 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PS
1 PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca2+ binding ratio to calculate the membrane charge state and EDC field strength. The peak amplitudes of both the ice- and water-like O–H peaks of the DPPS associated water layer were found to track linearly with EDC values projected from the Ca–PS binding isotherm. These results are in line with EDC scaling of χ(3) and the reorientation of water within the surface charge dependent EDC field. At saturating concentrations of Ca2+, loss of temperature dependence of sum-frequency at the 3200 cm−1 ice-like water resonance was observed. These data indicate an EDC of zero and complete charge neutralization at Ca2+ saturation, consistent with the assumed 2
Ca2+ binding ratio to calculate the membrane charge state and EDC field strength. The peak amplitudes of both the ice- and water-like O–H peaks of the DPPS associated water layer were found to track linearly with EDC values projected from the Ca–PS binding isotherm. These results are in line with EDC scaling of χ(3) and the reorientation of water within the surface charge dependent EDC field. At saturating concentrations of Ca2+, loss of temperature dependence of sum-frequency at the 3200 cm−1 ice-like water resonance was observed. These data indicate an EDC of zero and complete charge neutralization at Ca2+ saturation, consistent with the assumed 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PS : Ca2+ binding ratio.
1 PS : Ca2+ binding ratio.
SFVS measurements of DPPS and DPPC flip-flop rates in the presence and absence of physiologic 1 mM Ca2+ and 1 mM Mg2+ were utilized to determine the impact of bound Ca2+ or Mg2+ on DPPS and DPPC lipid translocation. The measured rate of translocation of 10% DPPS in DPPC decreased from 7.11 ± 0.08 × 10−5 s−1 (24.7 °C) in the absence of Ca2+ to 1.46 ± 0.07 × 10−5 s−1 (24.5 °C) when in the presence of 1 mM Ca2+, roughly a 5-fold decrease. No effect of Mg2+ on DPPS flip-flop rate or Ca2+ or Mg2+ on DPPC flip-flop rate was observed. From these data it is inferred that a Ca2+ concentration differential over the bilayer would produce differing rates of PS lipid flip and flop between the leaflets. For the tested binary mixture of 10% DPPS in DPPC, the differential in the zero Ca2+ and 1 mM Ca2+ flip-flop rates at ∼24.6 °C would be expected to result in an approximate 80% sequestration of DPPS toward the Ca2+-exposed leaflet. Given the large differential in Ca2+ concentration over the cell membrane in vivo, the endogenous effects of Ca2+ on PS lipids may influence PS lipid externalization even absent enzymatic action. These results illustrate the importance of considering direct Ca–PS interactions when interpreting PS locality and expression.
Data availability
The data that supports these findings are available from the corresponding author upon reasonable request.Author contributions
J. C. C and P. P. H designed the research. P. P. H. performed the research. P. P. H. and J. C. C. analysed the data and wrote the article. P. P. H. and J. C. C. edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The following work was supported by the National Science Foundation (NSF) (No. 2304682).Notes and references
- R. Chandra, P. C. Joshi, V. K. Bajpai and C. M. Gupta, Biochim. Biophys. Acta, 1987, 902, 253–262 CrossRef CAS PubMed.
- D. L. Daleke, Curr. Opin. Hematol., 2008, 15, 191–195 CrossRef CAS PubMed.
- R. D. Kornberg and H. M. Mcconnell, Biochemistry, 1971, 10, 1111–1120 CrossRef CAS PubMed.
- G. Lenoir, P. Williamson and J. C. Holthuis, Curr. Opin. Chem. Biol., 2007, 11, 654–661 CrossRef CAS PubMed.
- J. A. Op den Kamp, Annu. Rev. Biochem., 1979, 48, 47–71 Search PubMed.
- A. J. Verkleij, R. F. Zwaal, B. Roelofsen, P. Comfurius, D. Kastelijn and L. L. van Deenen, Biochim. Biophys. Acta, 1973, 323, 178–193 CrossRef CAS PubMed.
- J. H. Lorent, K. R. Levental, L. Ganesan, G. Rivera-Longsworth, E. Sezgin, M. Doktorova, E. Lyman and I. Levental, Nat. Chem. Biol., 2020, 16, 644–652 CrossRef CAS PubMed.
- G. Cevc, Biochim. Biophys. Acta, 1990, 1031, 311–382 CrossRef CAS PubMed.
- B. Fadeel and D. Xue, Crit. Rev. Biochem. Mol. Biol., 2009, 44, 264–277 Search PubMed.
- N. Duzgunes, J. Wilschut, R. Fraley and D. Papahadjopoulos, Biochim. Biophys. Acta, 1981, 642, 182–195 CrossRef CAS PubMed.
- J. W. Gauer, K. J. Knutson, S. R. Jaworski, A. M. Rice, A. M. Rannikko, B. R. Lentz and A. Hinderliter, Biophys. J., 2013, 104, 2437–2447 CrossRef CAS PubMed.
- J. G. Kay and G. D. Fairn, Cell Commun. Signal., 2019, 17, 1–8 CrossRef CAS PubMed.
- S. Ohki and R. Sauve, Biochim. Biophys. Acta, 1978, 511, 377–387 CrossRef CAS PubMed.
- A. Portis, C. Newton, W. Pangborn and D. Papahadjopoulos, Biochemistry, 1979, 18, 780–790 CrossRef CAS PubMed.
- J. Wang, C. Yu, J. Zhuang, W. Qi, J. Jiang, X. Liu, W. Zhao, Y. Cao, H. Wu, J. Qi and R. C. Zhao, Biomark. Res., 2022, 10, 4 CrossRef PubMed.
- E. M. Bevers, P. Comfurius and R. F. Zwaal, Biochim. Biophys. Acta, 1983, 736, 57–66 CrossRef CAS PubMed.
- A. D. Ide, E. M. Wight and C. K. Damer, PLoS One, 2021, 16, e0250710 CrossRef CAS PubMed.
- A. K. Kimura and T. Kimura, FASEB J., 2021, 35, e21177 CrossRef CAS PubMed.
- I. Vermes, C. Haanen, H. Steffens-Nakken and C. Reutelingsperger, J. Immunol. Methods, 1995, 184, 39–51 CrossRef CAS PubMed.
- P. F. Devaux, A. Herrmann, N. Ohlwein and M. M. Kozlov, Biochim. Biophys. Acta, Biomembr., 2008, 1778, 1591–1600 CrossRef CAS PubMed.
- A. Papadopulos, S. Vehring, I. López-Montero, L. Kutschenko, M. Stöckl, P. F. Devaux, M. Kozlov, T. Pomorski and A. Herrmann, J. Biol. Chem., 2007, 282, 15559–15568 CrossRef CAS PubMed.
- K. Segawa, S. Kurata and S. Nagata, J. Biol. Chem., 2016, 291, 762–772 CrossRef CAS PubMed.
- K. Segawa, S. Kurata, Y. Yanagihashi, T. R. Brummelkamp, F. Matsuda and S. Nagata, Science, 2014, 344, 1164–1168 CrossRef CAS PubMed.
- H. Takatsu, M. Takayama, T. Naito, N. Takada, K. Tsumagari, Y. Ishihama, K. Nakayama and H. W. Shin, Nat. Commun., 2017, 8, 1423 CrossRef PubMed.
- D. L. Bratton, V. A. Fadok, D. A. Richter, J. M. Kailey, L. A. Guthrie and P. M. Henson, J. Biol. Chem., 1997, 272, 26159–26165 CrossRef CAS PubMed.
- T. Pomorski, A. Herrmann, P. Müller, G. Van Meer and K. Burger, Biochemistry, 1999, 38, 142–150 CrossRef CAS PubMed.
- T. Pomorski, P. Müller, B. Zimmermann, K. Burger, P. F. Devaux and A. Herrmann, J. Cell Sci., 1996, 109, 687–698 Search PubMed.
- X. Tang, M. S. Halleck, R. A. Schlegel and P. Williamson, Science, 1996, 272, 1495–1497 CrossRef CAS PubMed.
- E. M. Bevers, P. F. Verhallen, A. J. Visser, P. Comfurius and R. F. Zwaal, Biochemistry, 1990, 29, 5132–5137 CrossRef CAS PubMed.
- E. F. Smeets, P. Comfurius, E. M. Bevers and R. F. Zwaal, Biochim. Biophys. Acta, 1994, 1195, 281–286 Search PubMed.
- E. M. Bevers and P. L. Williamson, FEBS Lett., 2010, 584, 2724–2730 Search PubMed.
- M. Ikeda, A. Kihara and Y. Igarashi, Biol. Pharm. Bull., 2006, 29, 1542–1546 Search PubMed.
- A. Momchilova, L. Ivanova, T. Markovska and R. Pankov, Arch. Biochem. Biophys., 2000, 381, 295–301 CrossRef CAS PubMed.
- J. Suzuki, M. Umeda, P. J. Sims and S. Nagata, Nature, 2010, 468, 834–838 CrossRef CAS PubMed.
- P. Williamson, E. M. Bevers, E. F. Smeets, P. Comfurius, R. A. Schlegel and R. F. Zwaal, Biochemistry, 1995, 34, 10448–10455 CrossRef CAS PubMed.
- P. Williamson, A. Christie, T. Kohlin, R. A. Schlegel, P. Comfurius, M. Harmsma, R. F. Zwaal and E. M. Bevers, Biochemistry, 2001, 40, 8065–8072 CrossRef CAS PubMed.
- M. Seigneuret and P. F. Devaux, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 3751–3755 Search PubMed.
- B. J. Abbott, D. S. Fukuda, D. E. Dorman, J. L. Occolowitz, M. Debono and L. Farhner, Antimicrob. Agents Chemother., 1979, 16, 808–812 CrossRef CAS PubMed.
- J. Dachary-Prigent, J. M. Pasquet, J. M. Freyssinet and A. T. Nurden, Biochemistry, 1995, 34, 11625–11634 CrossRef CAS PubMed.
- U. Henseleit, G. Plasa and C. Haest, Biochim. Biophys. Acta, 1990, 1029, 127–135 CrossRef CAS PubMed.
- A. Jaskulska, A. E. Janecka and K. Gach-Janczak, Int. J. Mol. Sci., 2020, 19, 131–135 Search PubMed.
- J. K. Paterson, K. Renkema, L. Burden, M. S. Halleck, R. A. Schlegel, P. Williamson and D. L. Daleke, Biochemistry, 2006, 45, 5367–5376 CrossRef CAS PubMed.
- P. Williamson, A. Kulick, A. Zachowski, R. A. Schlegel and P. F. Devaux, Biochemistry, 1992, 31, 6355–6360 CrossRef CAS PubMed.
- D. W. Dekkers, P. Comfurius, E. M. Bevers and R. F. Zwaal, Biochem. J., 2002, 362, 741–747 CrossRef CAS PubMed.
- Q. Zhou, J. Zhao, T. Wiedmer and P. J. Sims, Blood, 2002, 99, 4030–4038 CrossRef CAS PubMed.
- J. R. Nofer, G. Herminghaus, M. Brodde, E. Morgenstern, S. Rust, T. Engel, U. Seedorf, G. Assmann, H. Bluethmann and B. E. Kehrel, J. Biol. Chem., 2004, 279, 34032–34037 CrossRef CAS PubMed.
- P. Williamson, M. S. Halleck, J. Malowitz, S. Ng, X. Fan, S. Krahling, A. T. Remaley and R. A. Schlegel, PLoS One, 2007, 2, e729 CrossRef PubMed.
- M. Ross, C. Steinem, H.-J. Galla and A. Janshoff, Langmuir, 2001, 17, 2437–2445 Search PubMed.
- K. Jacobson and D. Papahadjopoulos, Biochemistry, 1975, 14, 152–161 Search PubMed.
- D. Papahadjopoulos, G. Poste, B. E. Schaeffer and W. J. Vail, Biochim. Biophys. Acta, 1974, 352, 10–28 CrossRef CAS PubMed.
- C. Newton, W. Pangborn, S. Nir and D. Papahadjopoulos, Biochim. Biophys. Acta, 1978, 506, 281–287 CrossRef CAS PubMed.
- D. Papahadjopoulos and A. Portis, Ann. N. Y. Acad. Sci., 1978, 05467, 50–66 CrossRef PubMed.
- D. Papahadjopoulos, W. J. Vail, C. Newton, S. Nir, K. Jacobson, G. Poste and R. Lazo, Biochim. Biophys. Acta, 1977, 465, 579–598 CrossRef CAS PubMed.
- R. Vink and M. Nechifor, Magnesium in the Central Nervous System, University of Adelaide Press, South Australia, 2011 Search PubMed.
- D. K. Atchison and W. H. Beierwaltes, Pfluegers Arch., 2013, 465, 59–69 CrossRef CAS PubMed.
- M. B. Hampton, D. M. Vanags, M. I. Porn-Ares and S. Orrenius, FEBS Lett., 1996, 399, 277–282 CrossRef CAS PubMed.
- V. Cheng and J. C. Conboy, J. Phys. Chem. B, 2022, 126, 7651–7663 CrossRef CAS PubMed.
- F. A. Heberle, D. Marquardt, M. Doktorova, B. Geier, R. F. Standaert, P. Heftberger, B. Kollmitzer, J. D. Nickels, R. A. Dick, G. W. Feigenson, J. Katsaras, E. London and G. Pabst, Langmuir, 2016, 32, 5195–5200 CrossRef CAS PubMed.
- M. Nakano, M. Fukuda, T. Kudo, H. Endo and T. Handa, Phys. Rev. Lett., 2007, 98, 238101–238104 CrossRef PubMed.
- M. Nakano, M. Fukuda, T. Kudo, N. Matsuzaki, T. Azuma, K. Sekine, H. Endo and T. Handa, J. Phys. Chem. B, 2009, 113, 6745–6748 CrossRef CAS PubMed.
- B. Wah, J. M. Breidigan, J. Adams, P. Horbal, S. Garg, L. Porcar and U. Perez-Salas, Langmuir, 2017, 33, 3384–3394 CrossRef CAS PubMed.
- J. S. Allhusen and J. C. Conboy, Acc. Chem. Res., 2017, 50, 58–65 CrossRef CAS PubMed.
- T. C. Anglin and J. C. Conboy, Biochemistry, 2009, 48, 10220–10234 CrossRef CAS PubMed.
- J. Liu and J. C. Conboy, Biophys. J., 2005, 89, 2522–2532 CrossRef CAS PubMed.
- J. Liu and J. C. Conboy, J. Am. Chem. Soc., 2004, 126, 8376–8377 CrossRef CAS PubMed.
- A. Timothy, C. Michael, L. Hao, C. Katherine and C. John, J. Phys. Chem. B, 2010, 114, 1903–1914 CrossRef PubMed.
- K. L. Brown and J. C. Conboy, J. Phys. Chem. B, 2013, 117, 15041–15050 CrossRef CAS PubMed.
- D. Marquardt, B. Geier and G. Pabst, Membranes, 2015, 5, 180–196 CrossRef CAS PubMed.
- D. Marquardt, F. A. Heberle, T. Miti, B. Eicher, E. London, J. Katsaras and G. Pabst, Langmuir, 2017, 33, 3731–3741 CrossRef CAS PubMed.
- M. Doktorova, F. A. Heberle, B. Eicher, R. F. Standaert, J. Katsaras, E. London, G. Pabst and D. Marquardt, Nat. Protoc., 2018, 13, 2086–2101 CrossRef CAS PubMed.
- L. Marx, M. P. K. Frewein, E. F. Semeraro, G. N. Rechberger, K. Lohner, L. Porcar and G. Pabst, Faraday Discuss., 2021, 232, 435–447 RSC.
- M. P. K. Frewein, P. Piller, E. F. Semeraro, K. C. Batchu, F. A. Heberle, H. L. Scott, Y. Gerelli, L. Porcar and G. Pabst, J. Membr. Biol., 2022, 255, 407–421 CrossRef CAS PubMed.
- H. M. McConnell, L. K. Tamm and R. M. Weis, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 3249–3253 CrossRef CAS PubMed.
- M. L. Wagner and L. K. Tamm, Biophys. J., 2000, 79, 1400–1414 CrossRef CAS PubMed.
- V. Kiessling and L. K. Tamm, Biophys. J., 2003, 84, 408–418 CrossRef CAS PubMed.
- V. Kiessling, C. Wan and L. K. Tamm, Biochim. Biophys. Acta, 2009, 1788, 64–71 CrossRef CAS PubMed.
- V. Kiessling, J. M. Crane and L. K. Tamm, Biophys. J., 2006, 91, 3313–3326 CrossRef CAS PubMed.
- M. Zacchia, M. L. Abategiovanni, S. Stratigis and G. Capasso, Kidney Dis., 2016, 2, 72–79 CrossRef PubMed.
- P. Guyot-Sionnest, J. H. Hunt and Y. R. Shen, Phys. Rev. Lett., 1987, 59, 1597–1600 CrossRef CAS PubMed.
- V. Ostroverkhov, G. A. Waychunas and Y. R. Shen, Chem. Phys. Lett., 2004, 386, 144–148 CrossRef CAS.
- J. Liu and J. C. Conboy, Langmuir, 2005, 21, 9091–9097 CrossRef CAS PubMed.
- D. Marsh, Biochim. Biophys. Acta, 1996, 1286, 183–223 CrossRef CAS PubMed.
- A. J. Diaz, F. Albertorio, S. Daniel and P. S. Cremer, Langmuir, 2008, 24, 6820–6826 CrossRef CAS PubMed.
- O. Bouffioux, A. Berquand, M. Eeman, M. Paquot, Y. F. Dufrene, R. Brasseur and M. Deleu, Biochim. Biophys. Acta, 2007, 1768, 1758–1768 CrossRef CAS PubMed.
- J. Miñones, J. M. Rodríguez Patino, O. Conde, C. Carrera and R. Seoane, Colloids Surf., A, 2002, 203, 273–286 CrossRef.
- E. M. Adams, C. B. Casper and H. C. Allen, J. Colloid Interface Sci., 2016, 478, 353–364 CrossRef CAS PubMed.
- S. Narayanan, PhD thesis, The Pennsylvania State University, 2019.
- J. T. Davies and E. K. Rideal, Interfacial Phenomena, Academic Press, New York, 2nd edn, 1963 Search PubMed.
- A. Martin-Molina, C. Rodriguez-Beas and J. Faraudo, Biophys. J., 2012, 102, 2095–2103 CrossRef CAS PubMed.
- D. Simonelli, S. Baldelli and M. J. Shultz, Chem. Phys. Lett., 1998, 298, 400–404 CrossRef CAS.
- M. L. Clarke, J. Wang and Z. Chen, J. Phys. Chem. B, 2005, 109, 22027–22035 CrossRef CAS PubMed.
- S. Y. Jung, S. M. Lim, F. Albertorio, G. Kim, M. C. Gurau, R. D. Yang, M. A. Holden and P. S. Cremer, J. Am. Chem. Soc., 2003, 125, 12782–12786 CrossRef CAS PubMed.
- T. Weidner, N. F. Breen, G. P. Drobny and D. G. Castner, J. Phys. Chem. B, 2009, 113, 15423–15426 CrossRef CAS PubMed.
- J. Seelig, P. M. Macdonald and P. G. Scherer, Biochemistry, 1987, 26, 7535–7541 CrossRef CAS PubMed.
- T. T. Nguyen and J. C. Conboy, Anal. Chem., 2011, 83, 5979–5988 CrossRef CAS PubMed.
- T. T. Nguyen, K. Rembert and J. C. Conboy, J. Am. Chem. Soc., 2009, 131, 1401–1403 CrossRef CAS PubMed.
- H. Hauser, A. Darke and M. C. Phillips, Eur. J. Biochem., 1976, 62, 335–344 CrossRef CAS PubMed.
- C. G. Sinn, M. Antonietti and R. Dimova, Colloids Surf., A, 2006, 282–283, 410–419 CrossRef.
- D. E. Gragson and G. L. Richmond, J. Am. Chem. Soc., 1998, 120, 366–375 CrossRef CAS.
- G. L. Richmond, Chem. Rev., 2002, 102, 2693–2724 CrossRef CAS PubMed.
- A. G. de Beer and S. Roke, J. Chem. Phys., 2016, 145, 044705 CrossRef PubMed.
- X. Chen, W. Hua, Z. Huang and H. C. Allen, J. Am. Chem. Soc., 2010, 132, 11336–11342 CrossRef CAS PubMed.
- P. E. Ohno, H. F. Wang and F. M. Geiger, Nat. Commun., 2017, 8, 1032 CrossRef PubMed.
- P. E. Ohno, H. F. Wang, F. Paesani, J. L. Skinner and F. M. Geiger, J. Phys. Chem. A, 2018, 122, 4457–4464 CrossRef CAS PubMed.
- S. Ong, X. Zhao and K. B. Eisenthal, Chem. Phys. Lett., 1992, 191, 327–335 CrossRef CAS.
- X. Zhao, S. Ong and K. B. Eisenthal, Chem. Phys. Lett., 1993, 202, 513–520 CrossRef CAS.
- B. F. Levine and C. G. Bethea, J. Chem. Phys., 1976, 65, 2429–2438 CrossRef CAS.
- P. D. Maker and R. W. Terhune, Phys. Rev., 1965, 137, A801–A818 CrossRef.
- R. W. Terhune, P. D. Maker and C. M. Savage, Phys. Rev. Lett., 1962, 8, 404–406 CrossRef CAS.
- S. Kielich, IEEE J. Quantum Electron., 1969, 5, 562–568 CrossRef CAS.
- G. Gonella, C. Lütgebaucks, A. G. F. de Beer and S. Roke, J. Phys. Chem. C, 2016, 120, 9165–9173 CrossRef CAS.
- J. A. Armstrong, N. Bloembergen, J. Ducuing and P. S. Pershan, Phys. Rev., 1962, 127, 1918–1939 CrossRef CAS.
- P. A. Franken and J. F. Ward, Rev. Mod. Phys., 1963, 35, 23–39 CrossRef CAS.
- M. A. Habib and J. O. Bockris, Langmuir, 2002, 2, 388–392 CrossRef.
- A. Chachaj-Brekiesz, J. Kobierski, A. Wnetrzak and P. Dynarowicz-Latka, Membranes, 2021, 11, 53 CrossRef CAS PubMed.
- M. Eisenberg, T. Gresalfi, T. Riccio and S. McLaughlin, Biochemistry, 1979, 18, 5213–5223 CrossRef CAS PubMed.
- Y. A. Ermakov, Membranes, 2023, 13, 883–905 CrossRef CAS PubMed.
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 185–206 CAS.
- J. C. Conboy, M. C. Messmer and G. L. Richmond, Langmuir, 1998, 14, 6722–6727 CrossRef CAS.
- J. C. Conboy, M. C. Messmer and G. L. Richmond, J. Phys. Chem., 1996, 100, 7617–7622 CrossRef CAS.
- R. N. Ward, D. C. Duffy, P. B. Davies and C. D. Bain, J. Phys. Chem., 2002, 98, 8536–8542 Search PubMed.
- X. Zhuang, P. B. Miranda, D. Kim and Y. R. Shen, Phys. Rev. B, 1999, 59, 12632–12640 CrossRef CAS.
- R. Mendelsohn, M. A. Davies, J. W. Brauner, H. F. Schuster and R. A. Dluhy, Biochemistry, 1989, 28, 8934–8939 CrossRef CAS PubMed.
- J. r. Tuchtenhagen, W. Ziegler and A. Blume, Eur. Biophys. J., 1994, 23, 323–335 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- C. M. Guldberg and P. Waage, Forh. Vidensk.–Selsk., 1864, 35–45 Search PubMed.
- E. Weiss, D. C. Rees and J. S. Gibson, Anemia, 2011, 2011, 379894 CrossRef PubMed.
- P. Meers, D. Daleke, K. Hong and D. Papahadjopoulos, Biochemistry, 1991, 30, 2903–2908 CrossRef CAS PubMed.
- P. Raynal and H. B. Pollard, Biochim. Biophys. Acta, 1994, 1197, 63–93 CrossRef CAS PubMed.
- M. A. Swairjo, N. O. Concha, M. A. Kaetzel, J. R. Dedman and B. A. Seaton, Nat. Struct. Biol., 1995, 2, 968–974 CrossRef CAS PubMed.
- G. Kohler, U. Hering, O. Zschornig and K. Arnold, Biochemistry, 1997, 36, 8189–8194 CrossRef CAS PubMed.
- K. Balasubramanian, E. M. Bevers, G. M. Willems and A. J. Schroit, Biochemistry, 2001, 40, 8672–8676 CrossRef CAS PubMed.
- K. G. Maffey, L. B. Keil and V. A. DeBari, Ann. Clin. Lab. Sci., 2001, 31, 85–90 CAS.
- J. F. Tait, D. F. Gibson and C. Smith, Anal. Biochem., 2004, 329, 112–119 CrossRef CAS PubMed.
- M. A. Lizarbe, J. I. Barrasa, N. Olmo, F. Gavilanes and J. Turnay, Int. J. Mol. Sci., 2013, 14, 2652–2683 CrossRef CAS PubMed.
- H. Yang, A. Kim, T. David, D. Palmer, T. Jin, J. Tien, F. Huang, T. Cheng, S. R. Coughlin, Y. N. Jan and L. Y. Jan, Cell, 2012, 151, 111–122 CrossRef CAS PubMed.
- Y. Furuta, O. Pena-Ramos, Z. Li, L. Chiao and Z. Zhou, PLoS Genet., 2021, 17, e1009066 CrossRef CAS PubMed.
- T. Sakuragi and S. Nagata, Nat. Rev. Mol. Cell Biol., 2023, 24, 576–596 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |