In situ synchrotron X-ray diffraction with laser-heated diamond anvil cells study of Pt up to 95 GPa and 3150 K†
Xiaoli Huang,
Fangfei Li,
Qiang Zhou,
Gang Wu,
Yanping Huang,
Lu Wang,
Bingbing Liu and
Tian Cui*
State Key Laboratory of Superhard Materials, College of Physics, Jilin University, Changchun 130012, People's Republic of China. E-mail: cuitian@jlu.edu.cn
First published on 12th January 2015
Abstract
Platinum (Pt) has been widely studied for pressure calibration in high pressure–temperature ranges. We have for the first time performed in situ synchrotron X-ray diffraction (XRD) with laser-heated diamond anvil cells to study the P–V–T equation of state (EOS) for Pt up to 95 GPa and 3150 K. MgO was used for pressure calibration. A detailed analysis of the room-temperature compression curve was fitted with the third-order Birch–Murnaghan (BM) EOS, which yields ambient volume V0 = 60.3 Å3, isothermal bulk modulus K0 = 308 GPa, and its pressure derivative K′0 = 4.1. A least-squares fit of the P–V–T data to a high-temperature (BM) EOS yielded K′0 = 5.5 ± 2, K0 = 274 ± 36 GPa, αKT(V0, T) = 0.003 ± 0.0003 GPa K−1 and (∂KT/∂T)V = 0.03 ± 0.01 GPa K−1 with V0 = 60.3 Å3. Within a reasonable range, it is found that the EOS of this study is consistent with the known EOS of Pt. The present technique and results cover the P–T range between the resistive heating and the shock compression experimental data in the literature.
Introduction
The P–V–T equation of state (EOS) is fundamental and crucial in physics as it contains plentiful information to describe a particular system.1,2 Accurate determination of the high-temperature EOS is extremely important for condensed matter physics and experimental geophysics in terms of the development of consistent high-pressure scales.3–5 The EOS of some elemental metals has been used as an internal pressure gauge in high-pressure X-ray diffraction (XRD) studies using diamond anvil cell (DAC) or multi-anvil press experiments.6,7 However, there has been much debate on the proposed pressure scales. So the EOS of most metals needs to be further refined with new data under simultaneous static high pressure and temperature conditions.Platinum (Pt) has been the subject of extensive theoretical and experimental investigations, because Pt is used not only as a high pressure scale in XRD measurements but also a laser absorber for laser-heating experiments, but it is not totally stable when with some elements such as hydrogen.8 The available EOS data of Pt include static compression experiments, shock compression experiments and theoretical calculations. The earliest EOS of Pt to 660 GPa by Holmes et al.9 has been used for the pressure estimation, which based on experimental data from a two stage light gas gun combined with the first-principles theoretical simulation. However, the P–V–T EOS of Pt by Holmes et al.9 was derived from shock compression data, and the static compressed volume data at 300 K or higher temperature is absent. As for the static compression with DACs, Dewaele et al.10 measured the volume compression data of Pt at 300 K from synchrotron XRD with helium served as pressure medium and a newly developed ruby luminescent pressure calibration. After that, Zha et al.11 derived the P–V data of Pt at 300 K with the MgO scale from Speziale et al.12 Compared with the 300 K EOS by Dewaele et al.,10 the EOS given by Holmes et al.9 increasingly overestimates pressure with increasing pressure. Recently, there are three main developed high P–T EOS of Pt reported by Fei et al., Zha et al. and Matsui et al., respectively. Fei et al.13 have measured the P–V–T up to 28 GPa and 1873 K, and derived the EOS of Pt based on the revised ruby scale using the 300 K volume data by Dewaele et al.10 Zha et al.11 have designed and modified the internal resistive heating technique in DAC and obtained XRD data of Pt up to 80 GPa and 1900 K. Lately, the P–V–T data of Pt up to 42 GPa and 1600 K was reported by Matsui et al.14 Obviously, there is a temperature gap between the resistive heating and shock wave compression measurements, reliable P–V–T data in this temperature range is urgently needed for completing data and cross-checking the reported results.
To obtain the precise P–V–T EOS by combining static compression and XRD methods, pressure measurement and its relationship with volume and temperature is the most challenging issue. In situ laser-heated DAC is a unique static technique for reaching ultrahigh P–T conditions (P > 100 GPa, T > 1500 K) and has been widely used. Numerous important discoveries and novel phenomena have been reported based on this technique.15–17 The major technical progress has been made in the areas of heating capability and stability, as well as temperature control and measurement.18,19 The issue of an axial temperature gradient in the sample layer has been resolved by introducing the double-sided laser heating technique.20 Therefore, laser-heated DAC has been becoming an increasingly powerful tool for P–V–T EOS research. In this work, we have firstly performed in situ synchrotron XRD with double-sided laser-heated DACs to study the P–V–T EOS of Pt up to 95 GPa and 3150 K.
Experimental details and methods
Both Pt and MgO powder with purity 99.9% were purchased from Alfa Aesar Company. The original sample consists of fine ground and well mixed Pt and MgO powder, and its XRD pattern at ambient conditions was measured confirming no impurity phase, as shown in Fig. S1.† Then the mixed sample was compressed to a flake with thickness of ∼10 μm, and one small piece of that is loaded into the sample hole of the DAC with a preindented and drilled rhenium gasket. Neon (Ne) was loaded into the sample chamber using COMPRES/GSECARS gas-loading equipment,21 which served as a thermal insulator and pressure transmitting medium. Under this condition, the sample flake was suspended in the Ne surroundings to guarantee good hydrostatic condition and thermal insulation.The high pressure and high temperature XRD experiments using the laser-heated DAC were performed at the 16ID-B beamline at the APS facility in Argonne National Laboratory. We have conducted five static compression experiments in this work. During each compression run, the sample was compressed with certain pressure point and then was heated with Nd:YLF laser (Photonics GS40, wavelength λ = 1053 nm) to high temperature for several minutes. The heating laser beam, which is a combination of the two YLF:Nd lasers, is split into two beams that pass through the opposing diamond anvils to heat the high-pressure sample simultaneously from both sides. Temperatures are measured separately from both sides with an imaging spectrograph and equalized by adjusting the power ratio of beam splitting. Temperatures are determined by fitting the visible portion of the black-body radiation (600–800 nm) from the heating spot to the Planck radiation function. The setup and methods are described elsewhere.17,20 In this work, the temperatures reported for each diffraction pattern are from the peak intensities at the center of the hotspot and the measured temperature for both sides is used with the average temperature. And the temperature was determined with an average uncertainty of ∼100 K. The detailed experimental conditions for all the compression runs are also listed in Table SI.†
The synchrotron angle-dispersive XRD patterns of the sample were collected with imaging plate and exposure time of 1 min for each point under P–T conditions. The monochromatic incident X-ray beam with a wavelength of 0.4066 Å was collimated to 6 × 7 μm2, while the laser heating spot during experiments was about 48 μm in diameter, which ensures that the collected diffraction pattern and measured temperature are consistent. Two-dimensional XRD images were integrated as a function of 2θ angle in order to give a conventional one-dimensional diffraction pattern using the Fit2D program.22
As indicated by Fei et al.,13 the MgO pressure scale is most useful in practice, because its EOS has been most extensively studied and is the least controversial one. The experimental results, which obtained based on the thermal EOS of MgO, is generally consistent with that determined by the theoretical molecular dynamics simulations.12,23 Additionally, the previous experiments using the MgO scale have shown that the pressures of post-spinel and post-perovskite phase transitions match the observed depths of seismic discontinuities at 660 and 2600 km, respectively.13,24 Here, for all of the compression runs, MgO scale proposed by Speziale et al.12 was used as the internal standards under P–T conditions. Table 1 listed the detailed data for all the compression runs.
| T (K) | MgO | Pt | |||
|---|---|---|---|---|---|
| a (Å) | V (Å3) | P (GPa) | a (Å) | V (Å3) | |
| Pt + MgO + Ne_1 | |||||
| 1476 (31) | 4.0769 | 67.76 | 26.2 | 3.8512 | 57.12 |
| 1529 (6) | 4.0779 | 67.81 | 26.3 | 3.8541 | 57.25 |
| 1718 (17) | 4.0825 | 68.04 | 26.8 | 3.8568 | 57.37 |
| 1786 (17) | 4.0847 | 68.15 | 26.9 | 3.8584 | 57.44 |
| 1947 (15) | 4.0861 | 68.22 | 27.7 | 3.8641 | 57.69 |
| Pt + MgO + Ne_2 | |||||
| 1416 | 3.9338 | 60.87 | 56.5 | 3.7636 | 53.31 |
| 1559 (17) | 3.9379 | 61.07 | 56.4 | 3.7640 | 53.33 |
| 1751 (15) | 3.9429 | 61.30 | 56.4 | 3.7673 | 53.47 |
| 2034 (82) | 3.9448 | 61.39 | 58.0 | 3.7746 | 53.78 |
| 2209 (114) | 3.9522 | 61.73 | 57.4 | 3.7834 | 54.16 |
| 2298 (80) | 3.9533 | 61.78 | 57.7 | 3.7852 | 54.23 |
| 2474 (72) | 3.9582 | 62.01 | 57.8 | 3.7924 | 54.54 |
| 2537 (129) | 3.9599 | 62.09 | 57.8 | 3.7939 | 54.61 |
| 2580 (145) | 3.9616 | 62.17 | 57.7 | 3.7963 | 54.71 |
| Pt + MgO + Ne_3 | |||||
| 1810 (53) | 3.8971 | 59.19 | 69.4 | 3.7608 | 53.19 |
| 2188 (39) | 3.9033 | 59.47 | 70.4 | 3.7732 | 53.72 |
| 2275 (77) | 3.9043 | 59.52 | 70.7 | 3.7805 | 54.03 |
| 2660 (78) | 3.9115 | 59.84 | 71.6 | 3.7818 | 54.09 |
| 3002 (55) | 3.9144 | 59.98 | 73.2 | 3.7849 | 54.22 |
| Pt + MgO + Ne_4 | |||||
| 1357 (7) | 3.8727 | 58.08 | 73.5 | 3.7525 | 52.84 |
| 1406 (5) | 3.8744 | 58.16 | 73.3 | 3.7488 | 52.68 |
| 1543 (27) | 3.8762 | 58.24 | 73.8 | 3.7518 | 52.81 |
| 1663 (38) | 3.8775 | 58.30 | 74.2 | 3.7559 | 52.98 |
| 1828 (39) | 3.8799 | 58.41 | 74.7 | 3.7663 | 53.42 |
| 2012 (54) | 3.8812 | 58.47 | 75.7 | 3.7855 | 54.24 |
| 2205 (67) | 3.8836 | 58.58 | 76.4 | 3.7873 | 54.32 |
| 2383 (18) | 3.8841 | 58.60 | 77.6 | 3.7910 | 54.48 |
| 2465 (70) | 3.8850 | 58.64 | 77.9 | 3.7928 | 54.56 |
| 2588 (42) | 3.8873 | 58.74 | 78.1 | 3.7973 | 54.75 |
| Pt + MgO + Ne_5 | |||||
| 1570 (11) | 3.8428 | 56.74 | 84.8 | 3.7497 | 52.72 |
| 1801 (37) | 3.8468 | 56.92 | 85.2 | 3.7555 | 52.97 |
| 1956 (20) | 3.8492 | 57.03 | 85.6 | 3.7604 | 53.18 |
| 2149 (27) | 3.8504 | 57.08 | 86.7 | 3.7653 | 53.38 |
| 2322 (10) | 3.8512 | 57.12 | 87.7 | 3.7657 | 53.40 |
| 2464 (27) | 3.8529 | 57.20 | 88.2 | 3.7709 | 53.62 |
| 2633 (3) | 3.8519 | 57.15 | 89.8 | 3.7728 | 53.70 |
| 2886 (32) | 3.8502 | 57.08 | 92.3 | 3.7646 | 53.35 |
| 3152 (58) | 3.8523 | 57.17 | 93.7 | 3.7708 | 53.61 |
Results and discussion
Representative XRD patterns under different pressure and temperature are shown in Fig. 1. As is shown in Fig. 1a, the typical XRD patterns before and after heating are listed for comparison. For both Pt and MgO, there are at least five peaks for each phase to calculate the lattice constants and volume. In Fig. 1b, one typical XRD pattern collected under 89.8 GPa and 2633 K is presented. The diffraction peaks of Pt and MgO are identified and indicated, and the other peaks are either from the Re gasket or crystallized pressure medium.A. Cold compression curve
At ambient conditions, the Rietveld refinement results of the XRD pattern (Fig. S1†) determine the lattice constants and unit cell volume with a = 3.9116 (9) Å, V = 59.9 Å3 for Pt and a = 4.2100 (2) Å, V = 74.6 Å3 for MgO, respectively. We have measured volume of Pt in Ne pressure medium up to 78 GPa at room temperature. And the crystal structure of Pt remained in fcc phase with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m up to the highest pressure. The ambient temperature EOS data are presented in Fig. 2. The choice of the EOS at 300 K is critical for determining the model parameters of the thermal EOS from the measured thermal pressure. Therefore, to provide useful physical parameters (namely, volume V0, bulk modulus K0, and its pressure derivative K′0 under ambient conditions), the P–V data points have been fitted by two EOS functional forms at 300 K. Firstly, the data were fitted by the third-order Birch–Murnaghan (BM) EOS25 as follow:
m up to the highest pressure. The ambient temperature EOS data are presented in Fig. 2. The choice of the EOS at 300 K is critical for determining the model parameters of the thermal EOS from the measured thermal pressure. Therefore, to provide useful physical parameters (namely, volume V0, bulk modulus K0, and its pressure derivative K′0 under ambient conditions), the P–V data points have been fitted by two EOS functional forms at 300 K. Firstly, the data were fitted by the third-order Birch–Murnaghan (BM) EOS25 as follow:
 | (1) |
 | (2) |
 | ||
| Fig. 2 Summary of 300 K isotherm P–V measured in this study, compared with previous experimental results. The solid blue curve represents the BM EOS fit to the experimental data of this study. | ||
From the fitted parameters by the two EOS forms, it is found that the bulk modulus and its pressure derivative in the BM EOS are interchangeable with those in the RV EOS used more commonly in the high pressure physics community. Fig. 2 has also shown the recent compression experimental results for comparison with our experimental results. The data collected by Holmes et al.9 were obtained from shock compression, and it is clearly seen that the Holmes Pt scale is deviated from other experimental results especially above 70 GPa. The results obtained from this study are close to Fei et al.'s scale13 under lower pressure and are nearly close with Dewaele et al.'s scale.10 Besides, the data of Zha et al.11 are a little stiffer than other studies.
B. Thermal equation of state
If the electron thermal contribution was included, the thermal EOS of a solid normally has the following form as:| P(V, T) = P0(V, T0) + Pth latt(V, T) + Pth elec(V, T) | (3) |
| P(V, T) = P0(V, T0) + Pth(V, T) | (4) |
In the thermodynamic approach, the Pth(V, T) beyond the 300 K isothermal is conveniently evaluated by integration at constant volume presented as:28
 | (5) |
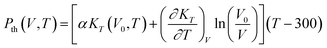 | (6) |
Therefore, in the thermodynamic approach, the pressure determined in the eqn (3) shown as follows:
 | (7) |
In the thermodynamic approach, the linear temperature dependence of thermal pressure at constant volume is assumed. The total data points at high temperature and high pressure with different volumes (Table 1) is fitted using eqn (7). The fitting yields K′0 = 5.5 ± 2, K0 = 274 ± 36 GPa, αKT(V0, T) = 0.003 ± 0.0003 GPa K−1 and (∂KT/∂T)V = 0.03 ± 0.01 GPa K−1 with V0 = 60.3 Å3 for all the measured data of Pt in Table 1). Zha et al.11 have reported the thermo-elastic parameters of Pt scale, so we have compared the thermo-elastic parameters with those of Zha et al. and the consistency between previous work and this study is good. The isothermal P–V data at any desired temperature can be calculated from eqn (7) with the parameters obtained above.
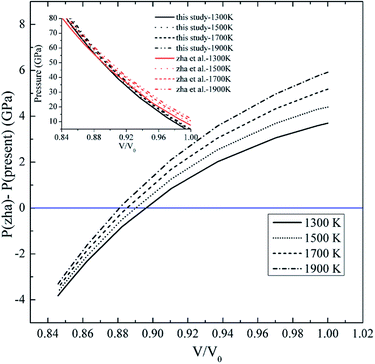
Recently, Pt has been widely studied for pressure calibration in high pressure–temperature ranges. Recently, Zha et al.11 has extended the P–V–T EOS up to 80 GPa and 1900 K from the internal resistive heating DAC and XRD measurements. It is noted that they used the MgO scale of the Speziale et al.12 as the pressure calibration for their P–V–T EOS of Pt, which is the same pressure calibration used in our present EOS calculation. Fig. 3 compares the present EOS with the EOS by Zha et al. at temperatures of 1300 K, 1500 K, 1700 K, 1900 K and pressures up to 80 GPa. It is seen that all the four isotherms from the two results cross at intermediate pressure point in inset of Fig. 3. The present study gives a lower pressure at first, and the EOS by Zha et al. increasingly underestimates pressure in comparison to our EOS at high pressure (Fig. 3). Among the four isotherms, the 1900 K isotherm has the largest pressure difference with ∼6 GPa at low pressure. The difference is reasonable based on two possibilities. Firstly, although we have used the same MgO pressure scale proposed by Speziale et al., the pressure is directly determined by the lattice constants or volume of MgO, so the volume of MgO needs to be accurate. For the study by Zha et al., they sometimes have used only one peak for the calculation volume of MgO, which also influences the pressure value. Secondly, for the EOS of Zha et al., the high temperature is obtained from the internal resistive heating while the laser-heating is used for the present study. The internal resistive heating by Zha et al. is with ∼20 K temperature uncertainty, while the temperature uncertainty from the present study is with ∼100 K temperature. The larger temperature uncertainty from the present study may contribute to the pressure differences, which determines the accuracy of the EOS.
Besides Zha Pt scale, Fei et al.13 have measured the P–V–T data for Pt at pressures up to 28 GPa and temperatures up to 1873 K. They performed multi-anvil experiments at simultaneous high pressures and temperatures using multiple internal pressure standards. The pressure for Pt EOS is calculated from the Au scale obtained from their measurement. They have derived the isotherms (1473, 1673, and 1873 K) of Pt (Fig. 4). Comparing with our calculated isotherms, it is found that the pressure determined from Fei et al. is larger than our results below 30 GPa. The pressure differences grow larger with the increasing temperature, and the maximum pressure difference among all the isotherms is with ∼5 GPa. It is known that a different pressure scale is able to generate large uncertainty in calculating the thermal pressure, and in some cases, the calculated pressures based on different standards could differ as much as 4 GPa.13 So the small pressure differences ∼5 GPa between the Fei et al. and this study are reasonable.
 | ||
| Fig. 4 Solid curves represent calculated isotherms for Pt at 1473, 1673, and 1873 K from this study, and the solid squares, solid circles and solid triangles represent experimental data collected from Fei et al.13 | ||
Fig. 5 compares the present EOS of Pt and the EOS by Matsui et al.,14 by Dorogokupets et al.,32 by Sun et al.33 and Holmes et al.9 at selected temperature of (a) 1000 K, and (b) 2000 K and pressures up to 200 GPa. The EOS of Pt by Sun et al. is calculated by using density-functional theory. The other reported EOS of Pt in Fig. 5 is obtained from the shock compression experiment. It is observed that the EOS in Fig. 5 has a small difference with our EOS. The EOS by Matsui et al. gives lower pressure than others with increasing pressure, as shown in Fig. 5, which has been developed without any pressure scale. The EOS of Pt by Dorogokupets et al. underestimates pressure with the present study from 80 GPa to 200 GPa. Dorogokupets et al. have recommended a new ruby pressure scale and used it as the pressure scale for the EOS of Pt. As pointed out by Fei et al., different pressure scale is able to generate large uncertainty in calculating the thermal pressure, and in some cases, the calculated pressures based on different standards could differ. So the small pressure differences among Matsui et al., Dorogokupets et al. and this study are reasonable. When compared with this study, the EOS by Holmes et al.9 firstly overestimates pressure and then underestimates pressure with increasing pressure. But the pressure differences between this study and Holmes et al.9 are less than 10 GPa up to 2000 K and 200 GPa. The difference may be attributed to the temperature accuracy derived from different temperature generation methods. Sun et al. have used density-functional theory to calculate the thermal EOS of Pt up to 550 GPa and 5000 K. The real cause of the discrepancy between experimental and theoretical studies might be a combination of several factors.
 | ||
| Fig. 5 Pressure differences between the present EOS of Pt and the EOS by Matsui et al.,14 by Dorogokupets et al.,32 by Sun et al.33 and Holmes et al.9 at selected temperature of (a) 1000 K, and (b) 2000 K. | ||
Conclusion
In summary, we have obtained the P–V–T dataset for Pt up to 95 GPa and 3150 K using in situ synchrotron XRD with laser-heated diamond anvil cells. The thermal EOS of MgO by Speziale et al. is used as the pressure calibration. A detailed analysis of room-temperature compression curve fitted with the third-order BM EOS, which yields ambient volume V0 = 60.3 Å3, isothermal bulk modulus K0 = 308 GPa, and its pressure derivative K′0 = 4.1. The ambient P–V results obtained from this study are close to Fei et al.'s scale under lower pressure and are nearly close with Dewaele et al.'s scale. A least-squares fit of the P–V–T data to a high-temperature BM EOS yields K′0 = 5.5 ± 2, K0 = 274 ± 36 GPa, αKT(V0, T) = 0.003 ± 0.0003 GPa K−1 and (∂KT/∂T)V = 0.03 ± 0.01 GPa K−1 with V0 = 60.3 Å3 for all the P–V–T data measured of Pt. Within the reasonable range, it is found that the EOS of this study is consistent with the known EOS of Pt. This study is the first in situ laser-heated DAC experiment for the P–V–T EOS of Pt. The present technique and results cover the P–T range between the resistive heating and the shock compression experimental data in the literature.Acknowledgements
The authors are grateful to Yue Meng and Jesse Smith for their technical support during the experiment. This work was performed at HPCAT (Sector 16), Advanced Photon Source (APS), Argonne National Laboratory. HPCAT operations are supported by DOE-NNSA under Award no. DE-NA0001974 and DOE-BES under Award no. DE-FG02-99ER45775, with partial instrumentation funding by NSF. The Advanced Photon Source is a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract no. DE-AC02-06CH11357. This work was also supported by the National Basic Research Program of China (no. 2011CB808200), Program for Changjiang Scholars and Innovative Research Team in University (no. IRT1132), National Natural Science Foundation of China (no. 51032001, 11074090, 10979001, 51025206, 11274137, 11004074, 11204100), and National Found for Fostering Talents of basic Science (no. J1103202).Notes and references
- High Pressure Phenomena, ed. R. J. Hemley, G. L. Chiarotti, M. Bernasconi, and L. Ulivi, IOS, Amsterdam, 2002 Search PubMed.
- C.-S. Zha, H.-K. Mao and R. J. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 13494–13499 CrossRef CAS PubMed.
- Y. Fei, A. Ricolleau, M. Franck, K. Mibe, G. Shen and V. Prapapenka, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9182–9186 CrossRef CAS PubMed.
- Y. Al-Khatatbeh, K. K. M. Lee and B. Kiefer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 144106 CrossRef.
- R. A. Fischer, A. J. Campbell, G. A. Shofner, O. T. Lord, P. Dera and V. B. Prakapenka, Earth Planet. Sci. Lett., 2011, 304, 496–502 CrossRef CAS PubMed.
- M. Matsui and N. Shima, J. Appl. Phys., 2003, 93, 9679–9682 CrossRef CAS PubMed.
- Y. Ueda, M. Matsui, A. Yokoyama, Y. Tange and K. Funakoshi, J. Appl. Phys., 2008, 103, 113513 CrossRef PubMed.
- T. Scheler, O. Degtyareva, M. Marqués, C. L. Guillaume, J. E. Proctor, S. Evans and E. Gregoryanz, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 214106 CrossRef.
- N. C. Holmes, J. A. Moriarty, G. R. Gathers and W. J. Nellis, J. Appl. Phys., 1989, 66, 2962–2967 CrossRef CAS PubMed.
- A. Dewaele, P. Loubeyre and M. Mezouar, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094112 CrossRef.
- C.-S. Zha, K. Mibe, W. A. Bassett, O. Tschauner, H.-K. Mao and R. J. Hemley, J. Appl. Phys., 2008, 103, 054908 CrossRef PubMed.
- S. Speziale, C.-S. Zha, T. S. Duffy, R. J. Hemley and H.-K. Mao, J. Geophys. Res., 2001, 106, 515–528 CrossRef CAS.
- Y. Fei, J. Li, K. Hirose, W. Minarik, J. V. Orman, C. Sanloup, W. van Westrenen, T. Komabayashi and K. Funakoshi, Phys. Earth Planet. Inter., 2004, 143, 515–526 CrossRef PubMed.
- M. Matsui, E. Ito, T. Katsura, D. Yamazaki, T. Yoshino, A. Yokoyama and K. Funakoshi, J. Appl. Phys., 2009, 105, 013505 CrossRef PubMed.
- R. Boehler, Nature, 1993, 363, 534–536 CrossRef CAS.
- M. Murakami, K. Hirose, K. Kawamura, N. Sata and Y. Ohishi, Science, 2004, 304, 855–858 CrossRef CAS PubMed.
- G. Shen, V. B. Prakapenka, M. L. Rivers and S. R. Sutton, Phys. Rev. Lett., 2004, 92, 185701 CrossRef.
- R. Boehler, N. V. Bargen and A. Chopelas, J. Geophys. Res., 1990, 95, 21731–21736 CrossRef.
- G. Shen, M. L. Rivers, Y. Wang and S. R. Sutton, Rev. Sci. Instrum., 2001, 72, 1273–1282 CrossRef CAS PubMed.
- Y. Meng, G. Shen and H. K. Mao, J. Phys.: Condens. Matter, 2006, 18, S1097–S1103 CrossRef CAS PubMed.
- M. Rivers, V. B. Prakapenka, A. Kubo, C. Pullins, C. M. Holl and S. D. Jacobsen, High Pressure Res., 2008, 28, 273–292 CrossRef CAS.
- A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235–248 CrossRef.
- M. Matsui, S. C. Parker and M. Leslie, Am. Mineral., 2000, 85, 312–316 CAS.
- K. Hirose, R. Sinmyo, N. Sata and Y. Ohishi, Geophys. Res. Lett., 2006, 33, L01310 CrossRef.
- F. Birch, J. Appl. Phys., 1938, 9, 279–288 CrossRef PubMed.
- P. Vinet, J. R. Smith, J. Ferrante and J. H. Rose, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 1945 CrossRef CAS.
- T. Tsuchiya and K. Kawamura, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 094115 CrossRef.
- I. Jackson and S. M. Rigden, Phys. Earth Planet. Inter., 1996, 96, 85–112 CrossRef CAS.
- O. L. Anderson, Crit. Rev. Anal. Chem., 1984, 1, 185 Search PubMed.
- O. L. Anderson, Phys. Earth Planet. Inter., 1999, 112, 267–283 CrossRef CAS.
- O. L. Anderson, D. G. Isaak and S. Yamamoto, J. Appl. Phys., 1989, 65, 1534–1543 CrossRef CAS PubMed.
- P. I. Dorogokupets and A. R. Oganov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 024115 CrossRef.
- T. Sun, K. Umemoto, Z. Wu, J.-C. Zheng and R. M. Wentzcovitch, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 024304 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra12769b |
| This journal is © The Royal Society of Chemistry 2015 |