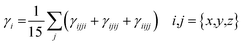Open Access Article
Open Access ArticleExploring key electronic and non-linear optical amplitute with bilateral intramolecular charge transfer into thieno[3,2-b]thiophene-based compounds: a DFT approach†
Muhammad Khalid *ab,
Memoona Arshadab,
Muhammad Haroonc,
Ataualpa Albert Carmo Braga
*ab,
Memoona Arshadab,
Muhammad Haroonc,
Ataualpa Albert Carmo Braga d and
Norah Alhokbanye
d and
Norah Alhokbanye
aInstitute of Chemistry, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan. E-mail: muhammad.khalid@kfueit.edu.pk; khalid@iq.usp.br
bCentre for Theoretical and Computational Research, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
cDepartment of Chemistry and Biochemistry, Miami University, Oxford, OH, USA
dDepartamento de Química Fundamental, Instituto de Química, Universidade de São Paulo, Av. Prof. Lineu Prestes, 748, São Paulo, 05508-000, Brazil
eDepartment of Chemistry, College of Science, King Saud University, P. O. Box 2455, Riyadh 11451, Saudi Arabia
First published on 25th February 2025
Abstract
Organic molecules are considered important NLO materials in the modern age because of their potential optoelectronic features. Therefore, a series of organic molecules (DBTD1–DBTD7) with a D–π–A architecture was designed from the reference compound (DBTR) by structurally tailoring it with effective donors and making significant modifications to the π-spacers. All derivatives and references were initially optimized at the M06 functional with a 6-311G(d,p) basis set. Furthermore, the optimized structures (DBTR and DBTD1–DBTD7) were used to determine the density of states (DOS), frontier molecular orbitals (FMOs), natural bond orbital (NBO), UV-Visible, transition density matrix (TDM) analyses, and the most significant NLO properties. Among the compounds, DBTD4 had the smallest band gap (2.882 eV) which was further supported by DOS analysis. The global reactivity parameters were also related to the HOMO–LUMO band gap, where the compound with the lowest band gap showed a lower hardness value and higher softness value. NBO analysis was used to explain the molecular stability and hyperconjugation. DBTD4 and DBTD5 demonstrated comparable low bandgaps with the highest comparable NLO parameter values. However, we also observed efficient NLO characteristics for DBTD6 and DBTD7. The highest μtot value is observed in DBTD6 as 10.362 D, whereas the highest αtot (1.48 × 10−22 and 1.47 × 10−22 esu) is observed in DBTD6 and DBTD7. Further, βtot (6.68 × 10−28 and 6.23 × 10−28 esu) in DBTD4 and DBTD5 and γtot (6.20 × 10−33 and 6.59 × 10−33 esu) values are observed in DBTD5 and DBTD6. To acquire favorable NLO responses in molecules, structural modelling utilizing efficient donor units played significant role. Thus, current research insights encourage researches to develop efficient NLO materials for optoelectronic applications.
Introduction
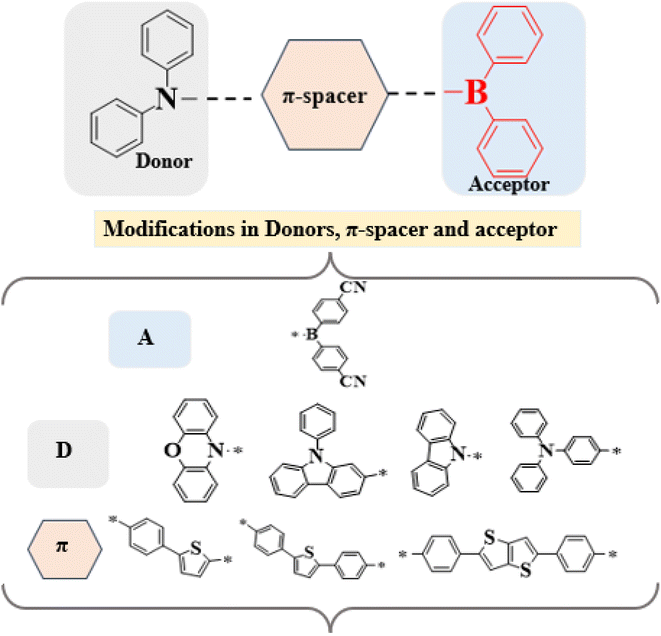
Nonlinear optics is an emerging topic in physical sciences that explores the interaction of intense light with materials. It has significant scientific and technological implications.1,2 NLO materials and their application in photometric materials have been important in the past several decades.3 Non-linear optic studies first, second, and third-order characteristics such as photorefractive, optoelectronic, and frequency doubling. The development of NLO substances is an area of experimental and theoretical investigations.4Among these, understanding and finding new and better NLO materials to fulfil the needs of advanced technologies is the most important research field. Some years ago, several manufactured polymers, coloured compounds, and inorganic or organic diodes were semi-conductors.5 Although each kind of NLO material has its merits and demerits. Currently, organic based non-linear optical materials are more popular in the field of NLO research due to high non-linear optical parameters and the versatility of structures.6,7 Recent findings show that organic chemicals are valued for their excellent non-linear optical characteristics, attributed to their application in contemporary technologies, and can be synthesized cost-effectively.8 Therefore, currently much experimental and theoretical attention has been paid to π-conjugated molecular systems, based on donor moiety (D) linked through a π-bridge to an acceptor moiety (A) due to their exceptional NLO response.9,10 The design strategy of NLO in the D–π–A arrangement is characterized as a push–pull mechanism, which further enhances the internal charge transfer. Theoretical and experimental investigations confirm that careful selection of the π-spacer, donor, and acceptor units plays a crucial role in tuning NLO efficiency.11 The literature reports indicate that π-conjugated moieties provide an efficient charge transfer pathway under an electric field.12,13
Moreover, it is observed that incorporating π-conjugated linkers of an appropriate length enhances the NLO characteristics.7,14 By enhancing charge transfer between donor and acceptor units, non-centrosymmetric π-linker derivatives exhibiting first, second and third-order nonlinear polarizabilities can be achieved.15,16 To design the push–pull mechanism various schemes, for example, donor–acceptor, donor–π–acceptor, acceptor–π–donor–π–acceptor, and donor–donor–π–acceptor, are reported.17 Among them D–π–A framework, which facilitates photoinduced charge transfer, has been extensively explored in the design of high-performance NLO materials. At higher wavelengths, the push–pull mechanism can increase the asymmetric electronic distribution, improve the NLO response, lower the HOMO/LUMO band gap, and increase the light penetration range.18,19 The diphenylborane moiety enhances electron affinity and charge transfer process through its vacant p-orbital, lowering the LUMO level and boosting NLO and optoelectronic performance.20 The thiophene-based π-spacers enhance charge transport due to their high conjugation efficiency and rigidity, which aid in stabilizing the charge-separated states.21 Similarly, phenoxazine, triphenylamine, and carbazole units, with their strong electron-donating capabilities, enhance charge asymmetry and boost hyperpolarizability.22
Given these advantages, we designed a series of D–π–A derivatives, DBTD1–DBTD7, from a synthesized compound 4-(5-(diphenylboraneyl)thiophen-2-yl)-N,N-diphenylaniline23 utilized as reference compound for current study. This reference compound consists of a diphenylborane acceptor and a diphenylaniline donor, bridged by phenylthiophene π-spacers to promote efficient charge transfer. To further enhance intramolecular charge transfer (ICT), and electronic properties, the phenylthiophene unit in DBTR was replaced with tolyl thiophene and diphenyl thieno thiophene rings. Additionally, strategic donor modifications and central core adjustments were introduced to optimize π-conjugation and improve NLO efficiency.
This study explores the structure–property relationship of entitled compounds with distinct π-spacers and donor groups. A literature review revealed that their NLO properties remain unexplored. Our structural modifications significantly enhance the NLO response, making these compounds promising candidates for optoelectronic applications such as electro-optic switching, second-harmonic generation, and photonic devices. Furthermore, these findings provide valuable insights into the rational design of next-generation NLO materials, contributing to the development of more efficient and high-performance optoelectronic devices. The chemical structures and schematic representation of the reference and investigated compounds are presented in Fig. 1 and 2.
Computational procedure
New thieno[3,2-b]thiophene-based compounds were designed with different structural modifications via various donor moieties with the configuration of the D–π–A framework. All the quantum calculations were performed using the Gaussian 16 program.24 The designed and reference compounds were optimized using the M06 functional25 with the 6-311G(d,p) basis set.26 Various electronic and optical properties were investigated using the same DFT functional and basis set. These include the density of states (DOS), frontier molecular orbital (FMO), transition density matrix (TDM), natural population (NPA), UV-Visible, natural bond orbital analyses (NBO), global reactivity parameter (GRPs), and the most important non-linear optical studies. DOS was performed using pyMolyze software27 utilizing Gaussian log files, to investigate the electronic density relating to the FMO results. A natural bond orbital analysis was carried out to estimate the stabilization energy of the designed compound. UV-Visible absorption spectra in tetrahydrofuran solvent and gas were obtained to analyse the optical properties using Origin 8.0,28 and GaussSum29 software from Gaussian outputs. The solvent effect was investigated using the conductor-like polarizable continuum model (CPCM).30 Using Multiwfn 3.7,31 we constructed a transition density matrix to investigate the electronic transitions. Chemcraft,32 Avogadro,33 and Gaussview34 were used for various type of data interpretation from Gaussian outputs. The convergence graphs of reference and designed compounds are shown in Fig. S6.†Dipole moment35 was calculated by using following eqn (1)
| μ = (μx2 + μy2 + μz2)½ | (1) |
Average polarizability (α)36 was examined using the eqn (2)
| (α) = 1/3(axx + ayy + azz) | (2) |
The magnitude of βtot37 is defined in eqn (3).
| βtot = (βx2 + βy2 + βz2)½ | (3) |
Eqn (4) was utilized to get the second hyperpolarizability (γtot)38
 | (4) |
Koopman's theorem39 was used to calculate global reactivity descriptors using the following eqn (5)–(9):
 | (5) |
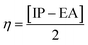 | (6) |
 | (7) |
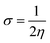 | (8) |
 | (9) |
Results and discussions
The designed compounds comprised an acceptor, π-conjugated linkers, and a donor. The compound characteristics were modified by structural modifications, including adding donors and π-conjugated linkers. Generally, theoretical and experimental studies indicate that unifying strong donor and acceptor groups at the periphery of an adequately conjugated system may result in a significant NLO response.40 The present study uses DBTR with IUPAC name, 4-(5-(diphenylboraneyl)thiophen-2-yl)-N,N-diphenylaniline as reference compound with D–π–A configuration. DBTR underwent modification to design different derivatives. Literature shows that cyano moieties are widely used in FREAs due to their strong electron-withdrawing ability, which lowers FMOs energy levels and enhances charge transfer.41 Therefore, to improve the acceptor character of the molecule, DBTD1 was designed, in which electrons with drawing cyano units were added to the terminal acceptors. To, further enhance the resonance, a benzene ring was integrated between the terminal acceptor and thiophene spacer in DBTD2. Additionally, conjugation was improved by substituting a single thiophene ring with fused double thiophene ring, leading to the design of DBTD3. Building on this structure, various donors were introduced at the left terminal of DBTD3, resulting in additional derivatives (DBTD4–DBTD7) with 4,4′-((4-(5(4(9-H-carbazol-9-yl)phenyl)thieno[3,2-b]thiophenyl)phenyl)boranediyl)dibenzonitrile as the central core. A double thiophene ring was incorporated as a π-spacer to further enhance the NLO characteristics of these derivatives. The following parameters for entitled compounds were calculated (i) linear polarizability, (ii) first hyperpolarizability, (iii) second hyperpolarizability, (iv) optical properties, and (v) NBO transitions and HOMO–LUMO energies through DFT/TD-DFT approaches. The optimized structures obtained via DFT analysis is shown in Fig. 3, respectively. Their Cartesian coordinates are presented in Tables S1–S8.† Moreover, the IUPAC names of examined compounds are given in Table S59.† Nevertheless, the current research provides theoretical insights into the design of efficient NLO materials, but their practical applicability requires further experimental synthesis and characterization.Frontier molecular orbitals (FMOs)
Frontier molecular orbitals (FMOs) analysis is a significant method for studying electronic transitions, molecular reactivities, chemical stability, and optical characteristics in organic systems.42 This parameter is crucial for determining the transfer of charge probability among compounds.43 In a conjugated framework, the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) determine the different interactions and reactions between molecules.44,45 According to band theory, valence and conduction bands are another way to describe the HOMO and LUMO of compounds.46,47 HOMOs demonstrate the electron-donating capacity of nucleophiles, whereas LUMOs indicate the electron-accepting ability of electrophiles from nucleophiles.48 Molecules with higher energy gap (ΔE) values are difficult because they resist changes in electronic configuration, resulting in low reactivity and high kinetic stability.49 On the other hand, substances with low band gaps are thought of as soft molecular structures that are unstable and likely to give a reaction.50 These substances exhibit efficient nonlinear optical properties and have high polarizability.51 Transferring electrons from HOMO to LUMO is crucial to comprehend a molecule's electronic properties and optical behavior.52The visual depiction of entitled chromophores depicts electronic distribution patterns in HOMO/LUMO during intramolecular charge transfer using red and blue areas in Fig. S1.† In the same way, the pictographs of charge transferred in other orbitals (HOMO−1/LUMO+1 and HOMO−2/LUMO+2) are represented in Table S10 and Fig. S1.†
The energy findings of FMOs as illustrated in Table S9† represented that EHOMO of reference compound and designed derivatives are calculated as −5.631, −5.711, −5.576, −5.662, −5.553, −5.583, −5.786 and −5.915 eV while ELUMO values are found as −2.106, −2.613, −2.663, −2.667, −2.671, −2.690, −2.688 and −2.706 eV. We calculated the band gaps of the studied compounds using the HOMO–LUMO energies. The band gaps of DBTR–DBTD7 are computed as follows: 3.525, 3.098, 2.913, 2.995, 2.882, 2.893, 3.098 and 3.209 eV. Here, we observed that all the designed compounds showed smaller band gaps than the reference compound. The insertion of cyano units in derivatives, replacement of thiophene with thieno[3,2-b]thiophene, and enhanced resonance effect cause this reduction and enhance charge transfer. DBTD4 has the smallest band gap because of the introduction of a donor (N-methyl-N-phenylaniline) with the highest electron-donating effect. The data of FMOs along with molecular orbital energies also tells us about internal charge transfer between orbitals.53 The compound DBTD4 with lowest band gap has efficient charge transfer from donor to acceptor through π-bridge. The decreasing trend of band gaps for tailored compounds and reference are as follows: DBTR (3.525) > DBTD7 (3.209) > DBTD6 > DBTD1 (3.098) > DBTD3 (2.995) > DBTD2 (2.913) > DBTD5 (2.893) > DBTD4 (2.882) in eV. DBTD6, DBTD1, and DBTD7 had the largest band gaps among all the derivatives. This might be due to a varied chemical framework and various associated donors with a lower electron-donating impact and hence does not cause effective charge transfer.
The pictograms of FMO indicate the contribution of charge density. In DBTR, the electronic clouds related to the HOMO are mainly present on the donor and π-spacer. In contrast, the acceptor primarily contributes to the LUMO and a minor contribution from the π-spacer. However, a diverse charge density distribution was observed for the tailored compounds (DBTD1–DBTD7). The HOMOs of all the developed compounds demonstrated that their electronic clouds were primarily centred on the donor portion, with a modest contribution to the π-spacer.
On the other hand, the LUMO has focused electron clouds toward the acceptor part while leaving a tiny area on the π-spacer portion. This suggests that π-spacers facilitate the charge transfer between the donor and acceptor units. All investigated compounds may be considered significant NLO components owing to this charge flow. The pictorial representation of band gaps is presented in Fig. 4.
Density of states (DOS)
To support the FMOs data and explore the electron delocalization seen in the HOMOs and LUMOs of the compounds, a density of states (DOS) analysis was carried out.45,54 By measuring the density of states per unit of energy and volume, we can determine the number of electrons occupying a particular energy level. The energy distribution of electron scattering and the general distribution of energy levels concerning energy are disclosed through DOS calculations.55 The π-conjugated bridge, which functions as a facilitator between electron-donating and electron-accepting moieties, is essential for improving the electron transfer processes within the molecule.56 One important component of the band structure is the band gap, which significantly affects the optical and electrical properties of the compounds.57 Left side peaks values in the graphical representation of DOS denote the HOMOs connected to the valence band. In contrast, right side values along the x-axis reflect the LUMOs connected to the conduction band.58 The Fermi level, also referred to as the difference between the lowest and highest occupied single-electronic states, is the area with zero intensity between the HOMOs and LUMOs peaks. The Fermi level in n-type semiconductors is located near the conduction band (HOMO), but in p-type semiconductors, it is more likely to be located near the valence band.59To investigate the DOS, we further divided the reference compound and its derivatives into three segments: donor, π-spacer, and acceptor parts, represented by red, green, and blue lines, respectively. The density of states (DOS) examination at the M06 functional was conducted using the 6-311G(d,p) basis set to elucidate the findings of DBTR and DBTD1–DBTD7. The alteration of donors and π-spacers resulted in a change in the electronic distribution pattern. This transition can be explained very well by studying the percentages of moieties in HOMOs and LUMOs.60 Regarding DBTR, the findings indicated that the donor moiety showed contributions of 57.4% towards HOMO and 2.4% towards LUMO. Similarly, the acceptor moiety displayed substantial contributions of 53.8% towards the LUMO and 2.3% towards the HOMO. The π-spacer contributed to the LUMO by 43.7% and 40.3% towards the HOMO, respectively. In same way, in the case of DBTD1–DBTD7, the notable electronic charge distributions for the LUMO were 71.0, 74.1, 73.6, 73.4, 72.4, 72.8, 72.9% for the acceptor moiety. The electron density in the HOMO is distributed over the acceptor is noted as 2.5, 0.8, 1.1, 0.7, 0.3, 1.0, and 1.2%. Similarly, the charge contributions on the donors for the LUMO are as follows: 1.4, 0.3, 0.1, 0.2, 0.1, 0.0, 0.1%, and 27.7, 25.5, 26.3, 26.4, 27.6, 27.1, and 27.0% on π-spacer, respectively. Whereas in HOMO, the charge contributions on donor are 58.1, 49.5, 25.2, 42.9, 50.1, 17.8, 35.4% and 39.4, 18.7, 73.7, 56.4, 49.5, 81.2, 63.5% on π-spacer, accordingly. The acceptor significantly contributes to the LUMO. In the HOMO, all compounds displayed a significant contribution towards the donor, except for DBTD3, DBTD4, DBTD6, and DBTD7. However, these compounds have a major contribution to the π-spacers. The recorded images for studied compounds are presented in Fig. 5, and their percentages are presented in Table S11.†
Global reactivity parameters (GRPs)
The global reactivity parameters are calculated using the HOMO and LUMO energies, such as the ionization potential (IP),61 chemical potential (μ),62 electron affinity (EA),63 electronegativity (X),64 global electrophilicity index (ω),51 global hardness (η),65 global softness (σ)66 and charge transfer index (ΔNmax).67 The chemical hardness [η = −(ELUMO − EHOMO)/2] of a compound determines its activity and stability. It measures the resistance to changes in electron density or charge.65 Similarly, the ability of an atom in a species to attract electrons to itself is known as electronegativity [X = −(EHOMO + ELUMO)/2].64 The values of GRPs are depicted in Table 1.| Compounds | IP | EA | X | η | μ | ω | σ | ΔNmax |
|---|---|---|---|---|---|---|---|---|
| a Ionization potential (I), electron affinity (A), electronegativity (X), global hardness (η), chemical potential (μ), global electrophilicity (ω), global softness (σ), and maximum charge transfer index (ΔNmax). | ||||||||
| DBTR | 5.631 | 2.106 | 3.868 | 1.762 | −3.868 | 4.246 | 0.284 | 2.195 |
| DBTD1 | 5.711 | 2.613 | 4.162 | 1.549 | −4.162 | 5.592 | 0.323 | 2.687 |
| DBTD2 | 5.576 | 2.663 | 4.119 | 1.456 | −4.119 | 5.826 | 0.343 | 2.828 |
| DBTD3 | 5.662 | 2.667 | 4.164 | 1.497 | −4.164 | 5.791 | 0.334 | 2.781 |
| DBTD4 | 5.553 | 2.671 | 4.112 | 1.441 | −4.112 | 5.867 | 0.347 | 2.854 |
| DBTD5 | 5.583 | 2.690 | 4.136 | 1.446 | −4.136 | 5.915 | 0.346 | 2.859 |
| DBTD6 | 5.786 | 2.688 | 4.237 | 1.549 | −4.237 | 5.795 | 0.323 | 2.736 |
| DBTD7 | 5.915 | 2.706 | 4.310 | 1.604 | −4.310 | 5.790 | 0.312 | 2.686 |
The association between the hardness (η), energy gaps, stability of a molecule, and chemical potential (μ) is direct. However, the relationship between reactivity and softness is inverse.45
Based on the GRPs, we observed that the electron affinity values were higher in derivatives than the reference chromophore. The hardness values of DBTR–DBTD7 are 1.762, 1.549, 1.456, 1.497, 1.441, 1.446, 1.549, and 1.604 eV. The softness values of the tailored compounds were greater than those of the reference compound: 0.284, 0.323, 0.343, 0.334, 0.347, 0.346, 0.323, and 0.312 eV−1. Another parameter used to examine the stability and reactivity of the substances under study is the chemical potential (μ). It varies directly with stability and inversely with the compound reactivity. A D–π–A system is predicted to be more reactive and less stable because its μ values are more negative.68 The chemical potential values are presented in Table 2. Moreover, the decreasing trend in hardness was DBTR > DBTD7 > DBTD6 = DBTD1 > DBTD3 > DBTD2 > DBTD5 > DBTD4. The order of increasing softness was DBTR < DBTD7 < DBTD6 = DBTD1< DBTD3 < DBTD2 < DBTD5 < DBTD4. The values of the global electrophilicity index of DBTR–DBTD7 were 4.246, 5.592, 5.826, 5.791, 5.867, 5.915, 5.795, and 5.790 eV, respectively. Since the compound (DBTD4) has the lowest hardness (1.441 eV) and the highest softness (0.347 eV−1), which matches its lower energy band gap (2.882 eV), it is expected to be the most advantageous designed compound with good NLO properties.
| Comp. | DFT λ (nm) | E (eV) | fos | MO contributions |
|---|---|---|---|---|
| a MO = molecular orbital, H = HOMO, L = LUMO, fos = oscillator strength, DFT = density functional theory. | ||||
| DBTR | 430.097 | 2.883 | 0.921 | H → L (95%) H−1 → L (2%) H → L+1 (2%) |
| DBTD1 | 485.242 | 2.555 | 0.758 | H → L (96%) |
| DBTD2 | 502.265 | 2.469 | 0.741 | H → L (93%) H−1 → L (3%) H → L+1 (3%) |
| DBTD3 | 490.657 | 2.527 | 0.984 | H → L (93%) H−1 → L (3%) H → L+1 (3%) |
| DBTD4 | 502.591 | 2.467 | 0.885 | H → L (92%) H−1 → L (4%) H → L+1 (3%) |
| DBTD5 | 488.088 | 2.540 | 1.024 | H−1 → L (14%) H → L (81%), H → L+1 (3%) |
| DBTD6 | 473.276 | 2.620 | 1.248 | H → L (87%) H−1 → L (8%) H → L+1 (3%) |
| DBTD7 | 459.116 | 2.701 | 1.163 | H → L (86%) H−1 → L (9%) H → L+1 (3%) |
UV-Visible analysis
The nature of a molecular transition and its charge-transfer properties are understood by UV-Vis investigation.69 A conductor-like polarizable continuum model70 is used to compute absorption bands to comprehend the system's optical characteristics in tetrahydrofuran solvent through DFT. This model considers the polarity of the solvent and its capacity to stabilize the n → π* and π → π* transition states at suitable energy levels, which generally advances our knowledge of optimal behavior.71 The λmax value indicates the amount of photon energy required to excite an electron from the HOMO to the LUMO. The fos reflects the potential of transition, and the E represents the energy required for a transition.72 Broader absorption at greater λmax, high fos, and low excitation energy are expected to result in efficient intramolecular charge transfer (ICT).73 UV-Visible analysis of the modified compounds was performed at the M06/6-311G(d,p) level in gaseous and tetrahydrofuran, to investigate their absorption shifts. The separate and combined absorption spectra in tetrahydrofuran solvent and gaseous phase are shown in Fig. S2–S4.†The values of λmax, along with the associated aspects, such as transition energy, oscillation strength, and molecular contributions in the solvent and gaseous phases, are presented in Tables 2 and 3. In contrast, Tables S12–S27† indicate the lowest six transitions. The data show that all of the compounds under investigation have absorption levels in the visible region of the electromagnetic spectrum, except DBTD2, DBTD3, and DBTD4 in tetrahydrofuran solvent. They displayed low absorption values in the ultraviolet region, which might be due to the presence of double thiophene, which can lead to increased steric hindrance, conjugational distortion, and complex geometry alterations. When the oscillation strength was preferred over the wavelength, the absorption maxima (λmax) in THF solvent were as follows: DBTD5 (488.088) > DBTD1 (485.242) > DBTD6 (473.276) > DBTD7 (459.116) > DBTR (430.097) > DBTD4 (394.013) > DBTD2 (387.693), and DBTD3 (377.333) (Tables S12–S19†). Here, DBTD5 has the highest wavelength, which might be due to the presence of auxochrome, leading to a redshift with lowest excitation energy of 2.540 eV.
| Comp. | DFT λ (nm) | E (eV) | fos | MO contributions |
|---|---|---|---|---|
| a MO = molecular orbital, H = HOMO, L = LUMO, fos = oscillator strength, DFT = density functional theory. | ||||
| DBTR | 413.391 | 2.999 | 0.836 | H → L (95%) |
| DBTD1 | 472.555 | 2.624 | 0.667 | H → L (97%) |
| DBTD2 | 506.203 | 2.449 | 0.600 | H → L (96%) |
| DBTD3 | 496.056 | 2.499 | 0.810 | H → L (96%) H−1 → L (2%) |
| DBTD4 | 509.468 | 2.434 | 0.710 | H → L (95%) H−1 → L (3%) |
| DBTD5 | 502.754 | 2.466 | 0.667 | H → L (90%) H−1 → L (7%) |
| DBTD6 | 481.380 | 2.576 | 0.988 | H → L (90%) H−1 → L (6%) |
| DBTD7 | 463.579 | 2.675 | 0.867 | H−1 → L (10%) H → L (86%) H → L+1 (2%) |
However, there are variations in the wavelength values if we favor wavelength over oscillation strength in the THF solvent. In this case, the absorption maxima in THF decreased in the following order in nm: DBTD4 (502.591) > DBTD2 (502.265) > DBTD3 (490.657) > DBTD5 (488.088) > DBTD1 (485.242) > DBTD6 (473.276) > DBTD7 (473.276), and DBTR (459.116).
At the lowest excitation energy of 2.467 eV, the maximum absorption value was recorded for DBTD4 at 502.591 nm. Because of its narrowest band gap, it can take less energy to transition, and more electrons might move into excited states, accounting for its highest wavelength.
All derivatives exhibited higher absorption values in the gaseous phase than the reference compound. The compounds exhibited absorption values in the range from 413.391 nm to 509.468 nm. The DBTD4 had the highest wavelength with an excitation energy of 2.434 eV in the gas phase. This might be due to the development of a more efficient push–pull mechanism. These findings were obtained when we prioritized wavelengths above oscillation strength. The gaseous phase exhibited a declining trend in λmax values measured in nm, as follows: DBTD4 (509.468) > DBTD2 (506.203) > DBTD5 (502.754) > DBTD3 (496.056) > DBTD6 (481.380) > DBTD1 (472.555) > DBTD7 (463.579), and DBTR (413.391). When we prefer oscillation frequency to wavelength, the proposed compounds exhibit absorption values ranging from 370 to 496 nm regarding oscillation strength preference. All the substances exhibited UV absorption values except for DBTD3, DBTD7,DBTD1, and DBTR. (Tables S20–S36†).
In summary, DBTD4 had the strongest affinity for decreasing the transition energy, the smallest energy difference, and exhibited a bathochromic shift. These features make it a desirable optically active material for nonlinear optics applications.
Light-harvesting efficiency (LHE) is a crucial factor that determines the optical performance of the designed compounds. It can be evaluated using the oscillator strength (fos) obtained from TD-DFT calculations. A higher LHE value indicates an improved photocurrent response of the compound. The LHE for the designed chromophores was calculated using eqn (10) (ref. 74) and the results are presented in Table S36.†
| LHE = 1 − 10−f | (10) |
Oudar and Chemla introduced a two-state model35 that has been widely used in the literature to analyze the NLO response, incorporating the key contributions of the ground and excited states in a sum-over-states approach. This model establishes a relationship between charge transfer transitions and second-order polarizability, which serves as the foundation for the push–pull architecture in designing high-performance NLO compounds.
| βCT = (Δμgm × fgm)/Egm3 | (11) |
Eqn (11) represents the two-state model for calculating first hyperpolarizability (βCT). In this model, βCT depends on three key factors: the dipole moment difference between the ground and excited states (Δμgm), the oscillator strength of the transition (fgm), and the cube of the transition energy (Egm3). According to this model, βCT is directly proportional to Δμgm and fgm, meaning that a larger dipole moment difference and higher oscillator strength enhance the NLO response. Conversely, βCT is inversely proportional to Egm3, indicating that a lower transition energy leads to better NLO performance. Therefore, molecules with strong NLO properties should have a significant dipole moment difference, strong oscillator strength, and lower transition energy. In this study, these parameters for entitled compounds were determined and are presented in Table S36.†
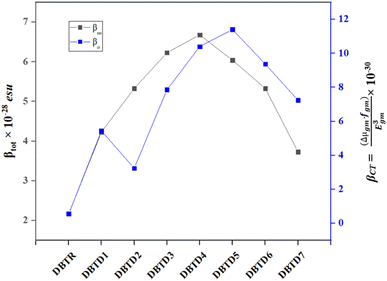
The results indicate that among the studied compounds, reference compound exhibits the highest Egm3 value at 3.862 eV, while the lowest value is observed for DBTD4 at 2.435 eV. This suggests that DBTD4 compound might exhibit a stronger NLO response due to its lower transition energy. Additionally, to further analyze the NLO properties, the relationship between the two-state model (βCT) and the total hyperpolarizability (βtot) for all compounds (DBTR, DBTD1–DBTD7) is illustrated in Fig. 6. The variations in the graph reflect the influence of different π-spacers and terminal acceptor units on βtot, which align with the trends predicted by the two-state model (βCT), supporting their potential as efficient NLO materials.
Transition density matrix (TDM)
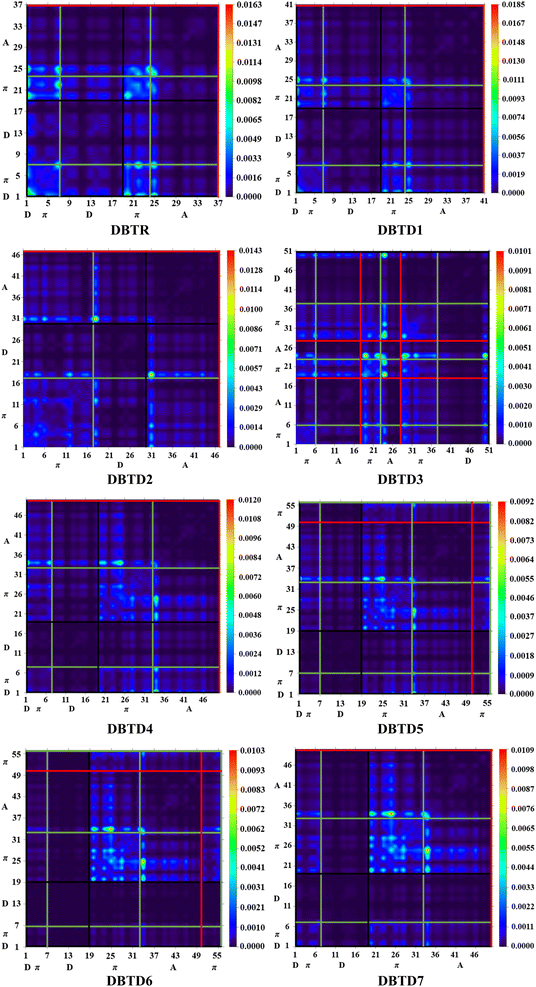
One widely used method for estimating electronic transitions in organic compounds is TDM analysis.75,76 In the excited state, TDM assists in determining the (a) donor–acceptor moiety interface, (b) electronic charge promotions, and (c) vitality of charge separation or charge compensation whereby electron–hole pairs are localized or delocalized.58 It is possible to visually depict the distribution of charges using an electrostatic potential map.56 Owing to minimal contribution in transition of hydrogen atoms their impact is neglected in these TDM maps. The M06/6-311G(d,p) functional was used for TDM analysis of the studied compounds. The investigated compounds were divided into the following parts: donor, π-spacer, and acceptor. The TDM heat maps are shown in Fig. 7, where the colored dots represent the electron flow pattern. Here, the vertical and horizontal lines define the electron coherence regions. The donor is represented by a black line, whereas the π-spacer and acceptor are represented by green and red lines, respectively. The electron densities in the reference compound (DBTR) and derivatives (DBTD1–DBTD3) were present along the diagonal and off-diagonal portions. For further derivatives (DBTD4–DBTD7), electron densities are present along the diagonal section. We observed that charge was transferred from the donor to the acceptor through the π-bridge. The radiant portions in the TDM pictographs show that the electron density was concentrated at that spot. In the studied compounds, bright portions were mainly present on the acceptor and π-spacer and showed minor contribution towards the donor. This outcome is important for the development of NLO materials. This TDM analysis also supports the FMO and DOS investigations.Natural bond orbital (NBO) analysis
NBO analysis examines the electron-transfer pathway, bonding characteristics, bond-to-bond interactions, charge distribution, and hyper-conjugative association relationships.77 Moreover, the intramolecular delocalization is precisely shown by NBO analysis.78 To explain the uniform depiction of the donor–π–acceptor framework and the charge density shift from fully bound to half-filled non-bonded orbitals, the NBO analysis is useful.79 Delocalization reactions are calculated using a second-order perturbation technique.80 The following eqn (12) is used to determine the stabilizing energy E(2) that aids in delocalization i → j, transition donor (i), and acceptor (j).81
 | (12) |
Different transitions are observed in the natural bond orbital analysis, such as π → π*, σ → σ*, LP → π*, and LP → σ*. The π–π * transition is the most significant of all the transitions. Charge transfer in the π → π* transition is more dominant than that in σ → σ*. The stabilization energy is the most important parameter to consider in NBO analysis. Table 4 illustrates the selected NBO values, whereas the other values are presented in Tables S37–S44.†
| Compounds | Donor(i) | Type | Acceptor(j) | Type | E(2) [kcal mol−1] | E(j) − E(i) [a.u] | F(i,j) [a.u] |
|---|---|---|---|---|---|---|---|
| DBTR | C2–C4 | π | C7–C9 | π* | 24.54 | 0.3 | 0.077 |
| C35–C37 | π | C32–C33 | π* | 15.88 | 0.3 | 0.064 | |
| C37–B39 | σ | C35–C37 | σ* | 7.21 | 1.17 | 0.082 | |
| S34–C37 | σ | C33–C35 | σ* | 0.52 | 1.22 | 0.023 | |
| S34 | LP (2) | C32–C33 | π* | 27.12 | 0.27 | 0.078 | |
| N1 | LP (1) | C22–C23 | σ* | 3.55 | 0.85 | 0.052 | |
| DBTD1 | C50–C52 | π | C55–C57 | π* | 26.37 | 0.28 | 0.077 |
| C32–C33 | π | C32–C33 | π* | 0.55 | 0.3 | 0.012 | |
| C57–C64 | σ | C64–N65 | σ* | 8.85 | 1.61 | 0.107 | |
| C37–B39 | σ | S34–C37 | σ* | 0.52 | 0.8 | 0.018 | |
| S34 | LP (2) | C32–C33 | π* | 27.7 | 0.27 | 0.079 | |
| N63 | LP (1) | C47–C62 | σ* | 11.87 | 1.06 | 0.1 | |
| DBTD2 | C18–C20 | π | C23–C25 | π* | 26.26 | 0.3 | 0.079 |
| C23–C25 | π | C23–C25 | π* | 0.64 | 0.29 | 0.012 | |
| C66–C72 | σ | C72–N73 | σ* | 8.86 | 1.61 | 0.107 | |
| B49–C50 | σ | C25–B49 | σ* | 0.57 | 1.08 | 0.022 | |
| N28 | LP (1) | C13–C15 | π* | 25.54 | 0.29 | 0.08 | |
| N73 | LP (1) | C66–C72 | σ* | 11.87 | 1.06 | 0.1 | |
| DBTD3 | C11–C12 | π | C14–C17 | π* | 26.02 | 0.28 | 0.076 |
| C1–C3 | π | C1–C3 | π* | 0.64 | 0.29 | 0.012 | |
| C40–N41 | σ | C26–C40 | σ* | 8.2 | 1.58 | 0.102 | |
| C42–S44 | σ | C42–C43 | σ* | 0.52 | 1.25 | 0.023 | |
| N74 | LP (1) | C50–C52 | π* | 32.39 | 0.32 | 0.094 | |
| N39 | LP (1) | C17–C38 | σ* | 11.87 | 1.06 | 0.1 | |
| DBTD4 | C43–C45 | π | C48–C50 | π* | 26.1 | 0.3 | 0.079 |
| C48–C50 | π | C48–C50 | π* | 0.64 | 0.29 | 0.012 | |
| C71–C76 | σ | C76–N77 | σ* | 8.86 | 1.61 | 0.107 | |
| C32–S34 | σ | C32–C33 | σ* | 0.52 | 1.25 | 0.023 | |
| N1 | LP (1) | C2–C4 | π* | 28.23 | 0.29 | 0.084 | |
| N75 | LP (1) | C61–C74 | σ* | 11.87 | 1.06 | 0.1 | |
| DBTD5 | C43–C45 | π | C48–C50 | π* | 25.9 | 0.3 | 0.079 |
| C35–C37 | π | C40–C41 | π* | 17.08 | 0.32 | 0.067 | |
| C61–C74 | σ | C74–N75 | σ* | 8.86 | 1.61 | 0.107 | |
| C81–H86 | σ | C81–C82 | σ* | 0.96 | 1.12 | 0.029 | |
| S42 | LP (2) | C35–C37 | π* | 25.38 | 0.26 | 0.075 | |
| N75 | LP (1) | C61–C74 | σ* | 11.87 | 1.06 | 0.1 | |
| DBTD6 | C41–C43 | π | C46–C48 | π* | 25.88 | 0.3 | 0.079 |
| C21–C22 | π | C21–C22 | π* | 0.69 | 0.29 | 0.013 | |
| C74–N75 | σ | C69–C74 | σ* | 8.21 | 1.58 | 0.102 | |
| C30–S32 | σ | C30–C31 | σ* | 0.54 | 1.25 | 0.023 | |
| N1 | LP (1) | C2–C3 | π* | 36.4 | 0.31 | 0.097 | |
| N73 | LP (1) | C59–C72 | σ* | 11.87 | 1.06 | 0.1 | |
| DBTD7 | C39–C41 | π | C44–C46 | π* | 25.71 | 0.3 | 0.079 |
| C44–C46 | π | C44–C46 | π* | 0.57 | 0.29 | 0.011 | |
| C72–N73 | σ | C67–C72 | σ* | 8.21 | 1.58 | 0.102 | |
| C2–C4 | σ | N1–C10 | σ* | 0.5 | 1.16 | 0.022 | |
| N1 | LP (1) | C19–C20 | π* | 40.32 | 0.31 | 0.101 | |
| N71 | LP (1) | C57–C70 | σ* | 11.87 | 1.06 | 0.1 |
In the case of reference compound (DBTR), the value of the highest stabilization energy for π (C2–C4) → π* (C2–C4) transition is 24.4 kcal mol−1 while the lowest energy for π (C35–C37) → π* (C32–C33) is about 15.88 kcal mol−1. The weak transitions σ → σ* show greatest and lowest stabilization energy as 7.21 and 0.52 for σ (C37–B39) → σ* (S35–C37) and σ (S34–C37) → σ* (C33–C35). The lone pair transitions show values as 27.12 and 3.55 kcal mol−1 for LP (S34) → π* (C32–C33) and LP (N1) → σ* (C22–B23).
The stabilization energy values for DBTD1 are 26.37, 0.55, 8.85, 0.52, 27.7, and 11.87 kcal mol−1 with corresponding transition as π (C50–C52) → π* (C55–C57), π (C32–C33) → π*(C32–C33), σ (C57–C64) → σ* (C64–N65), σ (C37–B39) → σ* (S34–C37), LP (S34) → π* (C32–C33), LP (N63) → σ*(C47–C62). We observed that DBTD1 had a higher stabilization energy than the reference compound.
The designed compound (DBTD2) has a maximum stabilization energy of 26.26 kcal mol−1 for the π (C18–C20) → π* (C23–C25) transition and a minimum of 0.64 kcal mol−1 for the π (C23–C25) → π* (C23–C25) transition. The weak σ → σ* transitions exhibit the highest and lowest stabilization energies of 8.86 and 0.57, respectively, for σ (C66–C72) → σ* (C72–N73) and σ (B49–C50) → σ* (C25–B49). The lone pair transitions for LP (N28) → π* (C13–C15) and LP(N73) → σ* (C66–C72) gave values of 25.54 and 11.87, respectively.
For the π (C11–C12) → π* (C14–C17) transition, the proposed compound (DBTD3) had a maximum stabilization energy of 26.02 kcal mol−1, whereas for the π (C1–C3) → π* (C1–C3) transition, it had a minimum stabilization energy of 0.64 kcal mol−1. The stabilization energies of the weak transitions σ → σ* are the lowest at 0.52 and the highest at 8.2 for σ (C42–S44) → σ* (C42–C43) and σ (C40–N41) → σ* (C26–C40). For LP (N74) → π* (C50–C52) and LP(N39) → σ* (C17–C38), the lone pair transitions provided values of 32.39 and 2.34, respectively.
Regarding DBTD4, there is a minimum stabilization energy of 0.64 kcal mol−1 for the π (C48–C50) → π* (C48–C50) transition and a maximum stabilization energy of 26.1 kcal mol−1 for the π (C43–C45) → π* (C48–C50) transition. When discussing weak transitions σ (C71–C76) → σ* (C76–N77) and σ (C32–S34) → σ* (C32–C33), the highest and lowest stabilization energies of the transitions σ → σ* are 8.86 and 0.52 kcal mol−1. Analysing further transitions for LP (N1) → π* (C2–C4) and LP (S42) → σ* (C33–C35), the values are 28.23 and 11.87 kcal mol−1.
With respect to DBTD5, the π (C35–C37) → π* (C40–C41) transition had a minimum stabilization energy of 17.08 kcal mol−1, whereas the π (C43–C45) → π* (C48–C50) transition had a maximum stabilization energy of 25.9 kcal mol−1. The weak transitions σ (C61–C74) → σ* (C74–N75) and σ (C81–H86) →σ* (C81–C82) have the greatest and lowest stabilization energy, respectively, at 8.86 and 0.96 kcal mol−1. The results of the analysis of lone pair transitions for LP (S42) → π* (C35–C37) and LP (N75) → σ* (C61–C74) are 25.38 and 11.87 kcal mol−1, respectively.
A comparison of the stabilization energies for all the electronic transitions occurring in the DBTD6 molecule shows that the energy transition π (C41–C43) →π* (C46–C48) has the maximum energy stabilized at 25.88 kcal mol−1. The transition π (C21–C22) →π* (C21–C22) requires a small energy of only 0.69 kcal mol−1. Quantitatively, we found that the maximum energy of σ → σ * transition is 8.21 kcal mol−1 for (C74–N75) and (C69–C74). Conversely, the minimum energy in the case of σ (C30–S32) → σ* (C30–C31) was 0.54 kcal mol−1. It was noted that LP → π* held the maximum value of 36.4 kcal mol−1 in LP (N1) and (C2–C3) transition, while a minimum value of 11.87 kcal mol−1 was found in LP (N73) → σ * (C59–C72) transition.
Analysis of the DBTD7 molecule showed that the π (C39–C41) → π* (C44–C46) transitions have the largest stabilization energy of 25.71 kcal mol−1, while the π (C44–C46) → π* (C44–C46) transitions have the lowest value, 0.57 kcal mol−1. The weak interaction transitions σ (C72–N73) →σ* (C67–C72) and σ (C2–C4) → σ*(N1–C10) have the highest and lowest stabilization energies of 8.21 and 0.5 kcal mol−1, respectively. Furthermore, the LP (N71) → σ* (C57–C70) and LP (N1) → π* (C19–C20) transitions, which have stabilization energies of 11.87 and 40.32 kcal mol−1, respectively, are caused by resonance effects in the molecule. For DBTD7, many other transitions are shown in Table S37.†
The above discussion indicates that the NBO findings of all the chemicals examined are interrelated. However, it should be noted that, unlike other designed compounds, DBTD1 gave the highest stabilization energies. This could be due to the presence of cyano groups, as they often enhance electron delocalization, leading to molecular stability. The stability of the compound is also evidenced by the charges of the NBOs. We can observe that ICT and hyperconjugation play a vital role in developing materials with strong NLO characteristics.
Natural population analysis (NPA)
The distribution of charges on an atom significantly influences numerous characteristics of the chemical system, including dipole moment, chemical reactivity, and electrostatic interactions between atoms and compounds. A more accurate interpretation of the conjugated system depends on calculating the atomic charges of the selected compounds.83,84 Fig. S5† shows the charges of DBTR and DBTD1–DBTD7 calculated using the M06/6-311G(d,p) functional. To gain a better understanding of their molecular structures, it is important to calculate the atomic charge of the reference DBTR and the developed compounds (DBTD1–DBTD7), as boron, sulfur, and hydrogen atoms have a net positive charge in NBO analysis. However, because of steric effects, carbon primarily carries negative charges, while it may also carry positive charges because of its accepting and donating properties. In comparison to all other atoms in all the molecules under investigation (DBTR–DBTD7), nitrogen has the highest electronegativity. Thus, it exhibited the strongest intensity peak in the negative direction. There is an unequal distribution of charges when strongly electronegative elements are present.85 NPA analysis is a useful method to gain information about reactivity since all of the derivatives have effective charge transfer mechanisms and are useful NLO materials. The graphs of the NPA investigation are depicted in Fig. S5.†Non-linear optical (NLO) properties
The development of NLO research has increased following the emergence of lasers. It is considered the most promising technology for the advancement of biomedicine, photonics, and optoelectronics.86,87 The electrical characteristics of a compound, such as its polarizability (linear response) and hyperpolarizability (non-linear response), dictate its nonlinear features. Therefore, the linear and NLO potentials of materials are estimated by evaluating both polarizability and hyper-polarizability. In most cases, obtaining significant hyperpolarizability requires linear polarizability.88 By altering the compound's non-centrosymmetric characteristics, the NLO qualities are improved.89 A push–pull architecture that relies on the donor and acceptor, connected by a π-spacer, has been designed to establish the NLO response.90 The NLO qualities are ascertained by quantum chemical approaches employing metrics such as the first hyper-polarizability (βtot),37 second hyper-polarizability (γtot), linear polarizability (α),36 and dipole moment (μtot),35 using eqn (1)–(4) mentioned earlier. To check the solvent effect on polarizability of investigated compounds the NLO analysis was performed in both the gas and solvent phase. The total values of the computed NLO parameters in tetrahydrofuran solvent and are presented in Tables S45 and S51,† respectively. However, in gaseous phase gas phase these values are presented in Tables S52–58,† respectively.An essential component for determining the polarizability of organic compounds is the dipole moment (μ).91 For entitled molecules, their μ values are calculated in Debye (D), in solvent and gas phase shown in Tables S45 and S52,† respectively. As observed here, all developed compounds exhibited higher values than the reference compound. The highest μtot was found in DBTD6 and DBTD3 (10.362 and 10.223D, respectively) in solvent phase because of the strong donor moieties, which may be due to their non-centrosymmetric structure. Urea was used as a reference compound for comparison analysis in NLO studies, according to the literature data its dipole moment is 1.3732D.16 The μtot in Debye for all other compounds and references in tetrahydrofuran are as the following: DBTD1 (9.920D), DBTD4 (9.610), DBTD2 (9.090), DBTD5 (8.828), DBTD7 (5.402), DBTR (2.328). All the designed derivatives had higher values than urea. Higher values of μtot indicate high polarizability. For all the studied compounds, larger polarizability values were analyzed along the x-axis (DBTD1 = −9.573, DBTD2 = 8.874, DBTD3 = 10.167, DBTD4 = 9.610, DBTD5 = −8.827, DBTD6 = −10.258, and DBTD7 = −5.401 in D).
For DBTR and DBTD1–DBTD7, Table S46† displays the 〈α〉 values in solvent phase. It also reveals crucial 3-D tensors for polarizability. The linear polarizability value of DBTR was the lowest, and all other designed compounds had the highest values. Along the z-axis all compounds showed major contributing tensor in the (αtot) value compared with the x- and y-axes with comparable values. The 〈α〉 values for entitled molecules in declining order are represented as follows in solvent phase: DBTD5 (1.48 × 10−22) > DBTD6 (1.47 × 10−22) > DBTD4 (1.31 × 10−22) > DBTD7 (1.29 × 10−22) = DBTD3 (1.29 × 10−22) > DBTD2 (1.19 × 10−22) > DBTD1 (1.02 × 10−22) and DBTR (0.916 × 10−22) in esu. The computed linear polarizability in gas phase is presented in Table S53.†
According to the literature, the FMO bandgap has a distinct impact on the polarizability of compounds; that is, the narrower the bandgap, the higher the polarizability values, and vice versa.50 The compounds to be studied in our case have a similar pattern: DBTD4 has the highest βtot value (6.68 × 10−28 esu) with the smallest band gap of 2.882 eV due to the extended conjugated system and strong push–pull framework. A decreasing trend in all entitled compounds in solvent phase is as follows: DBTD4 (6.68 × 10−28) > DBTD3 (6.23 × 10−28) > DBTD5 (6.04 × 10−28) > DBTD2 (5.33 × 10−28) = DBTD6 (5.33 × 10−28) > DBTD1 (4.23 × 10−28) > DBTD7 (3.73 × 10−28) and DBTR (2.17 × 10−28) Table S47.† The calculated βtot in gas phase of all examined compounds is presented in Table S55.†
In the second hyper-polarizability, the values of γtot are the highest for the DBTD5 and DBTD4 compounds for solvent phase, which have the lowest band gaps. All values of γtot were comparable to each other and greater than that of the reference compound (Table S48†). The order of declining trend of γtot in solvent medium in esu is following: DBTD5 (6.59 × 10−33) > DBTD4 (6.20 × 10−33) > DBTD6 (5.32 × 10−33) > DBTD3 (5.07 × 10−33) > DBTD7 (3.54 × 10−33) > DBTD2 (4.42 × 10−33) > DBTD1 (2.75 × 10−33) and DBTR (1.43 × 10−33). The second hyper-polarizability of examined compounds in gas phase is presented in Table S56.†
We computed frequency-dependent first hyperpolarizability coefficients for electro-optic Pockel's effect (EOPE) with β(ω;ω,0) and second-harmonic generation of first hyperpolarizability (SHG) with β(−2ω;ω,ω) at commonly used laser wavelengths of 532 nm and 1064 nm to give insights for experimental studies. At 532 nm, the EOPE values fall between 2.84 × 10−28 to 10.1 × 10−28, whereas at 1064 nm, the response is in the range of 20.5 × 10−28 to 773 × 10−28 in solvent phase. We found significant EOPE values at 1064 nm, which might be attributed to an enhancement of resonance. Similarly, the SHG values are high for all derivatives except DBTD5 and DBTD6 at both 532 and 1064 as shown in the Table S49.† Therefore, it can be concluded that increased wavelength produces significant SHG responses.
At 532 nm and 1064 nm, third order nonlinear optical response coefficients, such as the electric field induced second harmonic generation (ESHG) γ(−2ω;ω,ω,0) and the dc-Kerr effect γ(−ω;ω,0,0) were also calculated. Higher dc-Kerr effect and ESHG values are mostly seen at 1064 nm, showing that the entitled compounds can significantly improve their performance at higher wavelengths as depicted in Table S50† might be due to increased polarizability.
Overall, it has been noted that all derivatives have polarizable characteristics and a smaller band gap than DBTR. Among all derivatives, DBTD4, DBTD5, and DBTD6 had the highest NLO values. Furthermore, these compounds have low hardness and high softness values, indicating that these are more polarizable. Therefore, the entitled compounds are considered as good NLO materials for optoelectronic devices. The frequency dependent second order and third order optical response in gas phase is illustrated in Tables S56–S57.†
Conclusion
A quantum chemical study was performed on the designed molecules (DBTD1–DBTD7) to clarify the relationship among the donor, π-spacer, and acceptor; all the designed compounds showed a notable reduction in the band gaps compared to the reference compound. The smallest band gap is obtained for DBTD4, which has the highest softness value, as illustrated in GRPs among all compounds (DBTD1–DBTD7). Similarly, their UV-Visible spectra were obtained in the range of bathochromic shifts with the lowest transition energies. Additionally, NBO investigations revealed the stabilization energies of the compounds. According to the TDM heat maps, the charge is transported from the donor to the acceptor via the π-spacer along the diagonal and off-diagonal portions. Moreover, it observed that the efficient NLO response is shown not only by DBTD4 but also by DBTD5 and DBTD6. The highest μtot value was observed for DBTD6 at 10.362 D, whereas the highest values of αtot, βtot, and γtot were observed for DBTD4 and DBTD5. Consequently, these compounds exhibited better NLO performance. Therefore, the above mentioned significant findings suggest that these compounds may be used in different application of photonic fields.Data availability
All data generated or analyzed during this study are included in this published article and its ESI Files.†Conflicts of interest
There is no conflict of interest.Acknowledgements
Dr Muhammad Khalid gratefully acknowledges the financial support from HEC Pakistan (Project No. 20-14703/NRPU/R&D/HEC/2021). The authors are thankful for the cooperation and collaboration of A. A. C. B. from IQ-USP, Brazil, especially for his continuous support and for providing computational lab facilities. A. A. C. B. (grant 2015/01491-3) is highly grateful to Fundação de Amparo á Pesquisa do Estado de São Paulo for their cooperation and financial assistance. The authors extend their sincere appreciation to Researchers Supporting Project number (RSP2025R253), King Saud University, Riyadh, Saudi Arabia.References
- R. W. Boyd, J. Opt. Soc. Am. B, 2011, 28, A38–A44 CrossRef CAS.
- J. Zyss, Molecular Nonlinear Optics: Materials, Physics, and Devices, Academic press, 2013 Search PubMed.
- A. Karakaş, A. Elmali, H. Ünver and I. Svoboda, Spectrochim. Acta, Part A, 2005, 61, 2979–2987 CrossRef PubMed.
- M. Akram, M. Adeel, M. Khalid, M. N. Tahir, M. U. Khan, M. A. Asghar, M. A. Ullah and M. Iqbal, J. Mol. Struct., 2018, 1160, 129–141 CrossRef.
- A. Datta, J. Phys. Chem. C, 2009, 113, 3339–3344 CrossRef CAS.
- S. Basu, Ind. Eng. Chem. Prod. Res. Dev., 1984, 23, 183–186 Search PubMed.
- S. Muhammad, J. Mol. Graphics Modell., 2015, 59, 14–20 CrossRef CAS PubMed.
- S. Muhammad, H. Xu, Z. Su, K. Fukuda, R. Kishi, Y. Shigeta and M. Nakano, Dalton Trans., 2013, 42, 15053–15062 Search PubMed.
- M. Panneerselvam, A. Kathiravan, R. V. Solomon and M. Jaccob, Phys. Chem. Chem. Phys., 2017, 19, 6153–6163 Search PubMed.
- A. Shanthi, C. Krishnan and P. Selvarajan, J. Cryst. Growth, 2014, 393, 7–12 Search PubMed.
- R. Canton-Vitoria, Y. Sayed-Ahmad-Baraza, M. Pelaez-Fernandez, R. Arenal, C. Bittencourt, C. P. Ewels and N. Tagmatarchis, npj 2D Mater. Appl., 2017, 1, 13 CrossRef.
- N. S. Abdel-Kader, S. A. Abdel-Latif, A. L. El-Ansary and A. G. Sayed, J. Mol. Struct., 2021, 1223, 129203 CrossRef CAS.
- M. R. S. A. Janjua, J. Iran. Chem. Soc., 2017, 14, 2041–2054 Search PubMed.
- M. R. S. A. Janjua, M. U. Khan, B. Bashir, M. A. Iqbal, Y. Song, S. A. R. Naqvi and Z. A. Khan, Comput. Theor. Chem., 2012, 994, 34–40 CrossRef CAS.
- M. Khalid, M. U. Khan, I. Shafiq, R. Hussain, K. Mahmood, A. Hussain, R. Jawaria, A. Hussain, M. Imran and M. A. Assiri, Arabian J. Chem., 2021, 14, 103295 CrossRef CAS.
- P. N. Prasad and D. J. Williams, Introduction to Nonlinear Optical Effects in Molecules and Polymers, Wiley, New York, 1991 Search PubMed.
- C. Yao, Y. Yang, L. Li, M. Bo, J. Zhang, C. Peng, Z. Huang and J. Wang, J. Phys. Chem. C, 2020, 124, 23059–23068 Search PubMed.
- M. Haroon, R. Mahmood and M. R. S. A. Janjua, J. Cluster Sci., 2017, 28, 2693–2708 Search PubMed.
- M. R. S. A. Janjua, C.-G. Liu, W. Guan, J. Zhuang, S. Muhammad, L.-K. Yan and Z.-M. Su, J. Phys. Chem. A, 2009, 113, 3576–3587 CrossRef CAS PubMed.
- S. Muhammad, M. R. S. A. Janjua and Z. Su, J. Phys. Chem. C, 2009, 113, 12551–12557 Search PubMed.
- A. Ammasi and X.-H. Ju, J. Phys. Chem. Solids, 2024, 193, 112155 CrossRef CAS.
- F. Liu, Y. Yang, H. Wang, J. Liu, C. Hu, F. Huo, S. Bo, Z. Zhen, X. Liu and L. Qiu, Dyes Pigm., 2015, 120, 347–356 CrossRef CAS.
- L. Wan, Z. Cheng, F. Liu and P. Lu, Mater. Chem. Front., 2023, 7, 4420–4444 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. P. Andersson and P. Uvdal, J. Phys. Chem. A, 2005, 109, 2937–2941 CrossRef CAS PubMed.
- M. Khalid, I. Shafiq, S. C. Ojha, A. A. Braga, T. Ahamad and M. Arshad, J. Photochem. Photobiol., A, 2023, 445, 115091 CrossRef CAS.
- K. J. Stevenson, J. Am. Chem. Soc., 2011, 133, 5621 CrossRef CAS.
- N. M. O'boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 Search PubMed.
- G. A. Zhurko and D. A. Zhurko, ChemCraft, version 1.6, 2009, https://www.chemcraftprog.com. Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- R. Dennington, T. A. Keith, and J. M. Millam, GaussView, Version 6, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- J.-L. Oudar and D. S. Chemla, J. Chem. Phys., 1977, 66, 2664–2668 Search PubMed.
- A. Alparone, Chem. Phys., 2013, 410, 90–98 CrossRef CAS.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J.-L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 Search PubMed.
- F. Ullah, K. Ayub and T. Mahmood, New J. Chem., 2020, 44, 9822–9829 Search PubMed.
- T. Koopmans, Physica, 1934, 1, 104–113 Search PubMed.
- M. G. Papadopoulos, A. J. Sadlej and J. Leszczynski, Non-linear Optical Properties of Matter, Springer, 2006 Search PubMed.
- H. Wang, C. Zhao, Z. Burešová, F. Bureš and J. Liu, J. Mater. Chem. A, 2023, 11, 3753–3770 RSC.
- S. Uzun, Z. Esen, E. Koç, N. C. Usta and M. Ceylan, J. Mol. Struct., 2019, 1178, 450–457 Search PubMed.
- I. Shafiq, M. Khalid, M. Muneer, M. A. Asghar, R. Baby, S. Ahmed, T. Ahamad, S. F. de Alcântara Morais and A. A. Braga, Mater. Chem. Phys., 2023, 308, 128154 Search PubMed.
- M. N. Arshad, A.-A. M. Al-Dies, A. M. Asiri, M. Khalid, A. S. Birinji, K. A. Al-Amry and A. A. Braga, J. Mol. Struct., 2017, 1141, 142–156 CrossRef CAS.
- M. N. Tahir, M. Khalid, A. Islam, S. M. A. Mashhadi and A. A. Braga, J. Mol. Struct., 2017, 1127, 766–776 CrossRef CAS.
- M. Srnec and E. I. Solomon, J. Am. Chem. Soc., 2017, 139, 2396–2407 CrossRef CAS PubMed.
- M. U. Khan, M. Ibrahim, M. Khalid, A. A. C. Braga, S. Ahmed and A. Sultan, J. Cluster Sci., 2019, 30, 415–430 Search PubMed.
- M. Khalid, M. Ali, M. Aslam, S. H. Sumrra, M. U. Khan, N. Raza, N. Kumar and M. Imran, Int. J. Pharm. Sci. Res., 2017, 8, 457–469 CAS.
- A. J. Garza, O. I. Osman, N. A. Wazzan, S. B. Khan, A. M. Asiri and G. E. Scuseria, Theor. Chem. Acc., 2014, 133, 1–8 Search PubMed.
- M. Khalid, H. M. Lodhi, M. U. Khan and M. Imran, RSC Adv., 2021, 11, 14237–14250 RSC.
- P. K. Chattaraj and D. R. Roy, Chem. Rev., 2007, 107, PR46–PR74 CrossRef CAS.
- M. Khalid, I. Shafiq, K. Mahmood, R. Hussain, M. F. Ur Rehman, M. A. Assiri, M. Imran and M. S. Akram, Sci. Rep., 2023, 13, 1395 Search PubMed.
- A. Mahmood, M. I. Abdullah and M. F. Nazar, Bull. Korean Chem. Soc., 2014, 35, 1391–1396 Search PubMed.
- T. Hassan, R. Hussain, M. U. Khan, U. Habiba, Z. Irshad, M. Adnan and J. Lim, Mater. Sci. Semicond. Process., 2022, 151, 107010 Search PubMed.
- P. Goszczycki, K. Stadnicka, M. Z. Brela, J. Grolik and K. Ostrowska, J. Mol. Struct., 2017, 1146, 337–346 Search PubMed.
- A. Mahmood, A. Irfan, F. Ahmad and M. R. S. A. Janjua, Comput. Theor. Chem., 2021, 1204, 113387 Search PubMed.
- A. Mahmood, M. I. Abdullah and S. U.-D. Khan, Spectrochim. Acta, Part A, 2015, 139, 425–430 Search PubMed.
- M. Khalid, I. Shafiq, M. Zhu, M. U. Khan, Z. Shafiq, J. Iqbal, M. M. Alam, A. A. C. Braga and M. Imran, J. Saudi Chem. Soc., 2021, 25, 101305 Search PubMed.
- C. Zhao, C. G. Tang, Z.-L. Seah, Q.-M. Koh, L.-L. Chua, R.-Q. Png and P. K. Ho, Nat. Commun., 2021, 12, 2250 CrossRef CAS PubMed.
- M. N. Arshad, I. Shafiq, M. Khalid, M. Asad, A. M. Asiri, M. M. Alotaibi, A. A. Braga, A. Khan and K. A. Alamry, Polymers, 2023, 15, 1508 CrossRef CAS PubMed.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- P. Politzer, in Chemical Applications of Atomic and Molecular Electrostatic Potentials: Reactivity, Structure, Scattering, and Energetics of Organic, Inorganic, and Biological Systems, Springer, 1981, pp. 7–28 Search PubMed.
- K. Fukui, Science, 1982, 218, 747–754 CrossRef CAS PubMed.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. Parthasarathi, J. Padmanabhan, M. Elango, V. Subramanian and P. Chattaraj, Chem. Phys. Lett., 2004, 394, 225–230 CrossRef CAS.
- J. Padmanabhan, Z. Arif, P. Singh and R. Parthasarathi, ACS Omega, 2021, 6, 21514–21524 Search PubMed.
- R. G. Pearson, J. Mol. Struct.: THEOCHEM, 1992, 255, 261–270 Search PubMed.
- Z. Zhao, C. Xu, Y. Ma, K. Yang, M. Liu, X. Zhu, Z. Zhou, L. Shen, G. Yuan and F. Zhang, Adv. Funct. Mater., 2022, 32, 2203606 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- W. Rahmalia, J.-F. Fabre, T. Usman and Z. Mouloungui, Spectrochim. Acta, Part A, 2014, 131, 455–460 CrossRef CAS PubMed.
- D. Liu, B. Kan, X. Ke, N. Zheng, Z. Xie, D. Lu and Y. Liu, Adv. Energy Mater., 2018, 8, 1801618 CrossRef.
- R. Saleem, A. Farhat, R. A. Khera, P. Langer and J. Iqbal, Comput. Theor. Chem., 2021, 1197, 113154 CrossRef CAS.
- R. H. Xie, in Handbook of Advanced Electronic and Photonic Materials and Devices, Elsevier, 2001, pp. 267–307 Search PubMed.
- M. Chahkandi and H. A. R. Aliabad, Chem. Phys., 2019, 525, 110418 CrossRef CAS.
- M. Chahkandi, A. Keivanloo Shahrestanaki, M. Mirzaei, M. Nawaz Tahir and J. T. Mague, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 591–603 CrossRef CAS PubMed.
- N. Sadlej-Sosnowska, J. Org. Chem., 2001, 66, 8737–8743 CrossRef CAS PubMed.
- R. T. Ulahannan, C. Y. Panicker, H. T. Varghese, R. Musiol, J. Jampilek, C. Van Alsenoy, J. A. War and S. Srivastava, Spectrochim. Acta, Part A, 2015, 151, 184–197 CrossRef CAS PubMed.
- M. Szafran, A. Komasa and E. Bartoszak-Adamska, J. Mol. Struct., 2007, 827, 101–107 CrossRef CAS.
- M. Khalid, M. U. Khan, E.-T. Razia, Z. Shafiq, M. M. Alam, M. Imran and M. S. Akram, Sci. Rep., 2021, 11, 19931 CrossRef CAS PubMed.
- F. Weinhold and C. R. Landis, Valency and Bonding: a Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, 2005 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- Z. Demircioğlu, Ç. A. Kaştaş and O. Büyükgüngör, Mol. Cryst. Liq. Cryst., 2017, 656, 169–184 CrossRef.
- Z. Demircioğlu, G. Kaştaş, Ç. A. Kaştaş and R. Frank, J. Mol. Struct., 2019, 1191, 129–137 CrossRef.
- L. Li, C. Wu, Z. Wang, L. Zhao, Z. Li, C. Sun and T. Sun, Spectrochim. Acta, Part A, 2015, 136, 338–346 CrossRef CAS PubMed.
- N. Z. Hakim, B. E. Saleh and M. C. Teich, J. Lightwave Technol., 1991, 9, 318–320 CrossRef.
- D. F. Eaton, Science, 1991, 253, 281–287 CrossRef CAS PubMed.
- C. Qin and A. E. Clark, Chem. Phys. Lett., 2007, 438, 26–30 CrossRef CAS.
- A. Mahmood, J. Cluster Sci., 2019, 30, 1123–1130 CrossRef CAS.
- M. Khalid, M. U. Khan, I. Shafiq, R. Hussain, A. Ali, M. Imran, A. A. Braga, M. Fayyaz ur Rehman and M. S. Akram, R. Soc. Open Sci., 2021, 8, 210570 CrossRef CAS PubMed.
- L. Kara Zaitri and S. M. Mekelleche, Mol. Phys., 2020, 118, 1618508 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra08662g |
| This journal is © The Royal Society of Chemistry 2025 |