Revealing thermophysical and mechanical responses of graphene-reinforced polyvinyl alcohol nanocomposites using molecular dynamics simulations†
Pabitra Narayan
Samanta
 ,
Devashis
Majumdar
and
Jerzy
Leszczynski
,
Devashis
Majumdar
and
Jerzy
Leszczynski
 *
*
Center for Computational Chemistry, Department of Chemistry, Physics and Atmospheric Sciences, Jackson State University, Jackson, MS 39217, USA. E-mail: jerzy@icnanotox.org
First published on 9th April 2025
Abstract
The effects of graphene (G) nanofiller content on enhancing the mechanical and thermal resistance of the polyvinyl alcohol (PVA) matrix are disentangled by performing all-atom classical molecular dynamics (MD) simulations. The crux of the computational work is to assess several key performance-limiting factors of the functional hybrid material, including the strain rate, temperature, and the size and distribution of the graphene nanofiller. Adding graphene nanofiller to the polymer results in more compact polymer chains, with the most significant impact observed in the 2% graphene composite. Uniaxial compression MD simulations revealed that the yield strength of the material is impacted by the proportion of nanofiller present. Specifically, the calculated stress–strain responses at a strain rate of 1.5 × 108 s−1 show that incorporating 2% graphene nanofiller remarkably enhances the yield strength. Conversely, increasing the graphene content to 5–10% led to a reduction in yield stress, which is primarily attributed to the disruption of hydrogen bond networks and destabilization of non-covalent interactions. Further analysis shows that increasing the strain rate led to higher yield stress in the G-PVA composite, while elevated temperatures caused its yield stress to decrease. Additionally, the glass transition temperature of the PVA composite rises with the graphene content and strongly correlates with the polymer chain mobility. The proposed theoretical approach may serve as a quantitative framework for elucidating the crucial role of interfacial interaction between polymers and nanomaterials in modulating the conformational, thermodynamic, and macroscopic properties of the hybrid materials.
1. Introduction
Due to the unique properties of graphene nanostructures including high electrical conductivity, mechanical robustness, and large surface area, there is a strong zeal to employ them in the diverse fields of materials science and engineering.1–8 Graphene is a two-dimensional carbon structure with a hexagonal atomic arrangement that offers a promising approach for creating multifunctional hybrid materials with polymer materials.9–14 To modulate the electrical conductivity, thermal conductivity, gas barrier properties, and mechanical resistance of graphene-reinforced polymer composites, there has been a plethora of research work focused on examining the critical factors influencing the functionality of the nanocomposites including the compatibility between polymers and graphene-like materials, the nature of interaction between the nanomaterial and polymer, the functionalization of graphene surface and cross-linking, the distribution of the nanofiller, the mobility of polymer chains, and the effectiveness of stress transfer between the nanofiller and the polymer matrix.15–19To produce a graphene–polymer-based functional material with excellent strength and toughness, polyvinyl alcohol (PVA), which is a synthetic vinyl polymer, has emerged as a promising polymeric material due to its exceptional film-forming, emulsifying, and adhesive properties.20 When graphene nanofiller is added to the PVA matrix, the resulting nanocomposite shows enhanced gas barrier performance, superior mechanical strength, and improved thermal stability.10,11,16,21–23 In addition to this, the charge transport properties of the PVA matrix are significantly enhanced by the addition of graphene nanofiller, which in turn extends its potential use in electronic and electrochemical applications.24–28 Moreover, the unique morphology and interfacial interactions between the PVA polymer and graphene filler can be tailored using feasible experimental techniques which expands the utility of the composite material for diverse applications ranging from water resistance to drug delivery.29–32
To date, numerous theoretical and experimental investigations have been carried out to assess the compatibility between the PVA and graphene-based materials including graphene oxide (GO) to yield high-performance graphene–polymer composite materials.11,16,33–39 The presence of oxygen-containing functional groups on GO produces strong hydrogen bonding and molecular interactions with the thermosetting polymers. By performing molecular dynamics (MD) simulations, Ding et al.40 demonstrated that the interaction between the GO nanosheets and the PVA matrix increases with an increase in the extent of GO oxidation, leading to the enhancement of the mechanical strength and glass transition temperature of the PVA/GO composite. In another study, Wang et al.41 employed MD simulation-based techniques to explore the impact of diverse functional groups including carboxyl (–COOH), carboxamide (–CONH2), ether (–O–), and hydroxyl (–OH) on the mechanical properties of a PVA matrix reinforced by functional graphene nanofiber (FGF). The study revealed that the elastic modulus, tensile strength, and stretchability of the PVA/FGF composite could be competently improved by introducing edge functionalization with hydroxyl and carboxyl groups. Later, the researchers demonstrated that the PVA composite coated with GO nanofibers (GO–C-PVA) is one of the more promising materials for enhancing both the mechanical strength and glass transition temperature, compared to pristine PVA and PVA integrated with randomly dispersed GO.42 Moreover, the mechanical properties and glass transition temperature of the GO–C-PVA composite material could be improved by increasing the aspect ratio and concentration of GO nanofibers. In another work, Wang and co-workers43 explored the impact of diverse graphene oxide nanofiber (GOF) structures on the mechanical and thermal properties of PVA/GOF composites by employing classical MD simulation-based methods. The study revealed that the columnar arrangement of GOF around the PVA matrix significantly increased the tensile strength and glass transition temperature of the composite material, compared to the random dispersion or 3D core–shell structures of the GOF.
An extensive comparative experimental study44 revealed that graphene (G) is more effective than GO toward the enhancement of the properties of the PVA matrix including mechanical strength, thermal strength, and electrical conductivity. Moreover, the interfacial binding strength and dispersion effect were identified to be the critical factors for yielding graphene–polymer nanocomposites with distinct features. In a prior study, Zhao et al.45 proposed a simple method to create a highly exfoliated G-PVA nanocomposite with excellent nanofiller dispersion. The resultant G-PVA nanocomposite was demonstrated to possess remarkable mechanical properties, including a 150% increase in tensile strength and a nearly 10-fold rise in Young's modulus, due to the incorporation of 1.8 vol% G-nanosheets. Furthermore, a comparative experimental and theoretical study on the Young's modulus of the G-PVA nanocomposite suggested that the graphene nanosheets are randomly dispersed throughout the polymer matrix in the nanocomposite films. In another study,46 a solution blending method was used to produce the G-PVA composite with a homogeneous dispersion of the nanosheets, where water was used as the processing solvent and the partially reduced GO was used as the nanofiller. Due to the enhanced interfacial interaction between the nanofiller and the polymer matrix, the G-PVA nanocomposites were shown to exhibit significant improvement in their mechanical and thermal properties with just 0.8 wt% graphene loadings. Notably, the tensile strength was increased by 116%, and there was a 19 °C enhancement in the inception of thermal degradation. A prior theoretical study47 used MD simulations to explore the effects of G and GO nanofillers on the structural and dynamic properties of two different polymer systems comprising an apolar polymer (poly(propylene)) and a polar polymer (poly(vinyl alcohol)). MD pullout simulations were utilized to estimate the interaction energies between the polymers and nanofillers. The obtained results showed that polymer chains near the G and GO nanofillers exhibit greater orientation and slower dynamics compared to the bulk polymer. The orientation of the polymer chains at the interface was impacted by the nanofiller type. The polymer chains were demonstrated to be more oriented with the G-based nanofiller. However, the increased roughness and heterogeneous shape of the GO nanofiller, caused by the presence of oxygen-containing functional groups, were mainly responsible for the lower amount of polymer orientation in the GO-based nanocomposite.
Despite such advances, optimization of the chemical composition and the binding strength between the G nanofiller and the PVA matrix is required for designing multifunctional materials with the desired thermomechanical and transport properties. Although the inclusion of graphene nanofiller in the polymer matrix has been demonstrated to improve the thermal resistance and tensile strength of the material, the mitigation of graphene agglomeration during the fabrication of graphene–polymer nanocomposites is a dauting task. The performance of such nanocomposites relies heavily on the distribution of graphene nanofiller as well as the amount of graphene loading. For instance, high graphene loading is indispensable to enhance the electrical conductivity of the polymer composites, while lower graphene loading is desirable for augmenting the mechanical strength. In addition to the distribution state of the graphene filler, the nature of the interfacial interactions between the polymer matrix and the nanofiller plays a significant role in modulating the properties of the graphene-reinforced polymer composites. A stronger interfacial interaction enables effective load transfer, which in turn improves the tensile strength and toughness of the composite. On the other hand, the estimation of structural, mechanical, and thermophysical properties such as density, Young's modulus, and glass transition temperature necessitates the access to long polymer chains for eliminating the discrepancies between the computed data and the experimental results that stem from the finite size effects. Previous studies40,42,43,47 have primarily focused on model systems with short PVA chains (10–20 monomer units). However, the typical degree of PVA polymerization ranges from 200–3000, which demands probing into the effects of the longer PVA chains on the properties of graphene-modified composites. Furthermore, despite the abundance of MD simulation studies on the mechanical properties of graphene–PVA composites, a detailed theoretical investigation on predicting the structure–property relationship with the alteration of performance limiting factors such as temperature, stress rate, chain length, and filler loading, remains an area of interest. This article provides atomic-scale insights into the interfacial binding strength, in particular to elucidate the nature of noncovalent interactions between the longer PVA chains and the graphene nanofiller that control the conformational, thermal, mechanical, and surface properties of the nanocomposites. In the present computational study, several key factors that influence the performance characteristics of the G-PVA nanocomposite, including the strain rate, temperature, and graphene content, are also critically assessed. The structural aspects of polymer chain dynamics induced by graphene nanofiller incorporation are captured through analyses of density profiles, radii of gyration, and mean squared displacements. In addition to the conformational analysis, the impact of graphene nanofiller on the mechanical and thermophysical properties of the PVA nanocomposite is probed by performing uniaxial deformation simulations and simulated annealing-based molecular dynamics simulations.
2. Computational details
To investigate the impact of graphene nanofillers on the mechanical and glass transition properties of the PVA composite, all-atom classical MD simulations were performed for the pristine PVA matrix and the G-PVA nanocomposites using the GROMACS code (GPU version 2023).48–54 The model system of the G-PVA nanocomposite was created by combining long PVA polymer chains, each containing 300 monomers, with a small number of single-layer graphene nanosheets comprising hydrogen-terminated dangling bonds. An earlier benchmark study demonstrated that the glass transition temperature of diverse polymer systems, comprising 6 chains with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms and more than 300 monomers, remains unaltered due to the enhancement of system size consisting of 16
000 atoms and more than 300 monomers, remains unaltered due to the enhancement of system size consisting of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–20
000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms.55 The lateral dimensions and number of graphene nanosheets were varied to unveil the influence of graphene content on the mechanical response of the G-PVA nanocomposite. Detailed structural information for the G-PVA nanocomposite model systems is provided in Table 1.
000 atoms.55 The lateral dimensions and number of graphene nanosheets were varied to unveil the influence of graphene content on the mechanical response of the G-PVA nanocomposite. Detailed structural information for the G-PVA nanocomposite model systems is provided in Table 1.
| Model systems | Component | Chemical formula | No. of components | Total no. of atoms | Total mass (amu) | Nanofiller proportion (%) |
|---|---|---|---|---|---|---|
| PVA matrix | PVA chain (300 monomers) | C600H1202O300 | 10 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
132173.76 | |
| G-PVA composite | G nanosheet | C30H14 | 3 | 132 | 1123.23 | 0.84 |
| PVA chain | C600H1202O300 | 10 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
132173.76 | ||
| (Model 1) |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 152 152
|
133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 296.99 296.99
|
||||
| G-PVA composite | G nanosheet | C198H38 | 1 | 236 | 2416.28 | 1.80 |
| PVA chain | C600H1202O300 | 10 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 173.76 173.76 |
||
| (Model 2) |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 256 256
|
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 590.04 590.04
|
||||
| G-PVA composite | G nanosheet | C198H38 | 3 | 708 | 7248.83 | 5.20 |
| PVA chain | C600H1202O300 | 10 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 173.76 173.76 |
||
| (Model 3) |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 728 728
|
139![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 422.59 422.59
|
||||
| G-PVA composite | G nanosheet | C198H38 | 6 | 1416 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 497.66 497.66 |
9.88 |
| PVA chain | C600H1202O300 | 10 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 173.76 173.76 |
||
| (Model 4) |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 436 436
|
146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 671.42 671.42
|
The inaccessibility of experimental morphology imposes constraints on modeling the polymer–nanomaterial composites. Theoretically, searching for the lowest-energy structures of such nanocomposites on the potential energy surface is a dauting task as it requires large-scale MD simulation as well as the critical assessment of statistical averages of polymer chain configurations. To obtain a reliable starting conformation of the pristine PVA composite, the model system of the amorphous polymer matrix was generated by using a coarse-grained (CG) model as implemented in the CHARMM-GUI polymer builder.56 The parameterization of the CG model of the polymer builder was formulated by incorporating solubility parameters and machine learning methods, which were extensively validated against diverse experimental data and all-atom MD simulations. The steps used to generate polymer systems could be summarized as follows – first, the PVA polymer chains are built using the monomer units. Each of these polymer structures is then fragmented into coarse-grained (CG) beads based on an estimated bead size tied to the monomer units i.e., Kuhn length. To fit the all-atom Kuhn fragment structure to a corresponding CG bead, spherical and positional restraints are applied. The polymer builder tool can be used to examine the chemical composition, bead diameter, and interaction strength between CG beads. The estimation of interaction parameters relies on the Flory–Huggins χ parameter derived from the solubility parameters. In the next step, to examine the spatial correlation in the bead-spring model, a 20 nanosecond (ns) CG simulation of the PVA polymers was conducted using the OpenMM software.57 Finally, the equilibrated CG beads from the previous step were replaced by the all-atom segments to obtain the all-atom model system of the PVA composite. For constructing the G-PVA nanocomposites, the CHARMM generalized force field (CGenFF) parameters58 were employed to estimate the molecular mechanics (MM) energies of the PVA polymer chains, while the interface force field (IFF) parameters59 were used to model the graphene surface, as implemented in the polymer builder and nanomaterial modeler of the CHARMM-GUI.56,60
The model systems of pristine PVA and G-PVA nanocomposites were fully relaxed by performing energy minimization using the steepest descent algorithm to eliminate any steric clashes. Next, four independent molecular dynamics (MD) simulations were executed for each system to commensurate the simulation box size and achieve the desired system density. The initial MD run was conducted for 10 ns under NVT dynamics at 500 K, followed by a 50 ns relaxation period using NPT dynamics at 500 K. Subsequently, a temperature annealing process was performed under the NPT ensemble for 100 ns, gradually cooling the system down to room temperature (300 K), since the tensile measurements are commonly performed at room temperature.34 The target temperature was further varied to explore the thermomechanical properties of the G-PVA composite beyond the glass transition temperature of the PVA especially in the region of rubbery state. Before the production stage, each graphene–polymer nanocomposite system and the pristine PVA composite were further equilibrated by running 200 ns of MD simulations under the NPT ensemble. Finally, production runs of 200 ns were executed using the NPT dynamics at the target temperature. Furthermore, to minimize the underlying uncertainty in the computed properties, the equilibrium structures were verified by repeating the simulated annealing, NPT equilibration and production MD runs with varying the annealing reference temperature (e.g., 800 K → 300 K, 600 K → 300 K and 500 K → 300 K) as well as the rates of heating and cooling. All MD simulations were performed using periodic boundary conditions in all three directions to mitigate edge effects. The leapfrog algorithm was applied to integrate Newton's equations of motion, with a time step of 2 femtosecond (fs). Long-range electrostatic interactions were computed using the particle mesh Ewald (PME) method, and Lennard-Jones (LJ) and Coulomb interactions were truncated at 1.2 nanometer (nm). Bonds involving hydrogen atoms were restrained using the LINCS algorithm,61 with an expansion order of four and a single iteration to correct for rotational lengthening. Temperature was maintained at a constant value using a velocity-rescaling thermostat with a coupling constant of τT = 1.0 picosecond (ps). The pressure was controlled at 1 bar using a C-rescale barostat, with a coupling constant of τp = 4.0 ps and a compressibility of β = 4.5 × 10−5 bar−1. The isotropic pressure coupling was applied for the MD simulations of PVA and G-PVA nanocomposites under the NPT ensemble.
3. Results and discussion
The structural and thermodynamic properties of the simulated systems are consecutively analyzed to assess the reliability of the force field parameters, the simulation workflow, and the model structure of the PVA composite. The adequacy of the equilibration strategy adopted for obtaining the thermally equilibrated structure of the pristine PVA and graphene-modified PVA composites is probed by analyzing the temporal changes in the volume and density of the composites as well as the end-to-end distance and radii of gyration of the polymer chains. Fig. S1–S5 (ESI†) illustrate the relative changes of the calculated volume (V), density (ρ), end-to-end distance (Ree) and radii of gyration (Rg) of the simulated systems of PVA matrix and the 10% graphene-incorporated PVA composite as a function of total simulation time, as derived from the 200 ns NPT equilibration and production MD trajectories at different temperatures. The relative changes together with the estimated error for the ensemble-average of the simulation box dimension before and after the equilibration and production MD simulations are also provided in Table S1 (ESI†). The thermodynamic stability of the equilibrated structures of the pristine polymer and the G-PVA composite at a given temperature is evidenced by the uniform changes of the measured observables over the period of MD simulations. The comparison of ensemble-averaged quantities extracted from NPT equilibration and production MD runs (Fig. S1–S5, ESI†) shows that the structural parameters remain almost unaltered, suggesting substantial convergence of the MD trajectories. To reveal the convergence of energetics of the pristine PVA and the graphene-reinforced PVA composites, the temporal changes of dispersion energy (Edisp), potential energy (Epot), kinetic energy (Ekin), total energy (Etot), and enthalpy (H) of the PVA and G-PVA composites derived from the 200 ns production MD trajectory are compared in Fig. S6–S13 (ESI†), due to the alteration of temperature and the proportion of graphene nanofiller. The steady fluctuations with reference to the ensemble-averages of the measured quantities vindicate the viability of further analysis of equilibrium properties of the simulated systems. To ascertain the simulation quality and the extent of uncertainty in predicting the equilibrium properties of the composites, we performed statistical error analysis of a few observables over multiple block lengths. The error estimation was executed over 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 points, accumulated from the 200 ns NPT production MD trajectory at different temperatures. Tables S2–S6 (ESI†) illustrate the estimated error for the volume, density, pressure, temperature, and total energy of the simulated systems of PVA and 10% graphene-filled PVA composites. The viability of simulated systems is reflected by the legitimate error bar produced by alteration of block averaging size.
001 points, accumulated from the 200 ns NPT production MD trajectory at different temperatures. Tables S2–S6 (ESI†) illustrate the estimated error for the volume, density, pressure, temperature, and total energy of the simulated systems of PVA and 10% graphene-filled PVA composites. The viability of simulated systems is reflected by the legitimate error bar produced by alteration of block averaging size.
Next, we place emphasis on the analysis of density profiles of the pristine polymer material and the graphene-modified PVA composites. Fig. 1(a) displays the thermally equilibrated structure of the PVA composite along with the temporal evolution of the polymer matrix density, as obtained from the 200 ns production MD trajectory. The calculated ensemble-averaged density at 300 K is 1254.29 kg m−3 (1.25 g cm−3), which is in accordance with the previous simulated density of PVA at 300 K.39 The ensemble-averaged density of the PVA at 400 K is predicted to be 1218.4 kg m−3 (1.22 g cm−3) (Fig. S2, ESI†). The obtained results also correlate well with the experimental data which showed that the average density of the PVA could be achieved as 1.19 g cm−3 and 1.31 g cm−3, respectively, for the amorphous and crystalline sample.62,63 After that, the density of the graphene-reinforced polymer nanocomposites was estimated from the 200 ns MD trajectory. Fig. 1(b) shows the equilibrium structure of the 10% graphene-filled PVA nanocomposite, along with the computed density values at 300 K across different graphene nanofiller loadings. The obtained results clearly show that the ensemble-averaged density of the G-PVA nanocomposite is enhanced by the addition of graphene nanofiller, thereby indicating the augmented compactness of the PVA polymer chains. The impact of temperature on the density of the graphene-reinforced PVA composite is also investigated. Fig. S3–S5 (ESI†) compare the temporal changes of the simulated density at 200 K, 300 K, and 400 K for the 10% graphene-filled PVA composite. As revealed by the calculated ensemble-averaged density values at different temperatures, the density value reduces from 1302.0 kg m−3 at 200 K to 1286.28 kg m−3 at 300 K and 1251.0 kg m−3 at 400 K.
To obtain a more intuitive understanding of the polymer conformation, the radii of gyration (Rg) of PVA chains were estimated for each composite. Fig. 2(a) demonstrates the relative changes of the calculated Rg of the simulated systems of the PVA matrix and the graphene-incorporated PVA composites as a function of total simulation time, as derived from the 200 ns production MD trajectories at 300 K. The influence of graphene nanofiller on the probability distribution of the Rg values of PVA chains is represented in Fig. 2(b)–(f). As shown in Fig. 2, the calculated Rg of the polymer chains decreases significantly after the addition of graphene nanofiller. The reduction of Rg is more significant for the G-PVA composite containing 2% graphene nanofiller. This indicates that the inclusion of graphene nanofiller produces stronger intermolecular interactions between the PVA chains, leading to a more compact conformation of the polymer chains. However, the addition of 5–10% graphene nanofiller raises the Rg value. This is probably due to the disruption of the folding of the PVA chains caused by the addition of excessive graphene nanofiller to the PVA matrix. The calculated Rg for the pristine PVA material is 2.49 nm, which agrees well with the previously reported value of 2.2–2.5 nm.64 The attenuation of Rg for the 2% graphene-filled composite may contribute to the enhanced mechanical strength of the material. Furthermore, the increased compactness of the PVA chains in the 2% graphene-filled nanocomposite could enhance the glass transition temperature of the polymer. The influence of temperature on the structural ordering of polymer chains is also examined. Fig. S1 and S2 (ESI†) compare the time dynamics of calculated end-to-end distances and radii of gyration of the PVA matrix extracted from 200 ns MD simulations under NPT ensemble at 300 K and 400 K, respectively. As evidenced by the ensemble-averages of the Ree and Rg, the enhancement of temperature perturbs the structural ordering of PVA chains. The values of Ree and Rg augments from 4.86 nm and 2.49 nm, respectively, at 300 K to 4.94 nm and 2.54 nm, respectively, at 400 K. Furthermore, increasing the temperature beyond the glass transition temperature of PVA yields fluctuation over the 200 ns MD trajectory, however, the deviation of Ree and Rg values with respect to the ensemble-average is within 0.1 nm. Fig. S3–S5 (ESI†) illustrate the impact of temperature on the Ree and Rg values of the PVA chains after the incorporation of graphene filler. The calculated Ree and Rg values anticipate that the compactness of PVA chains is curtailed by rising temperature. However, the enhanced structural ordering of PVA chains in the presence of graphene nanofiller remains unchanged beyond the room temperature (>300 K). The calculated ensemble-averaged Ree and Rg at 400 K for the 10% graphene-filled PVA composite are 4.33 nm and 2.11 nm, respectively. Thus, the estimated values of Ree and Rg at 400 K are found to be lowered by 0.61 nm and 0.43 nm, respectively, due to the introduction of 10% graphene filler within the PVA matrix. Next, we explored the impact of graphene nanofiller distribution on the mechanical and thermophysical characteristics of the PVA composites.
3.1. Mechanical properties
Uniaxial compression simulations were conducted on the fully equilibrated G-PVA nanocomposite structures to analyze their stress–strain profiles. To achieve uniaxial deformation, the deformation velocities were applied in the X-direction to the box elements, and a semi-isotropic pressure coupling was used. In the stress response calculations, we used a compressibility of β = 4.5 × 10−7 bar−1 for the transverse direction but set the compressibility to zero along the direction of deformation. To control the semi-isotropic pressure coupling, the reference pressure was set to 1 bar, and a coupling constant of τp = 4.0 ps was applied. This allowed the simulation box to elongate in the deformation direction while compressing in the perpendicular directions. The relative strain (ε) and stress responses (σ) were calculated as follows.| σ = −Pi |
| ε = (Li − L0i)/L0i |
The pressure tensor component Pi in the direction of deformation is calculated using the simulation box size Li, which changes due to the uniaxial deformation. The original simulation cell size before deformation is denoted as L0i. The pressure tensor is derived from the kinetic energy tensor Ek and the virial tensor Ξ, using the formula P = 2(Ek − Ξ)/V, where V is the volume of the simulation cell. The kinetic energy tensor Ek is calculated as  , and the virial tensor Ξ is
, and the virial tensor Ξ is  , where Fij are the pairwise-additive forces between particles i and j. Notably, the adequacy of uniaxial deformation simulation executed by GROMACS code has been previously assessed in estimating the influence of cooling rate, deformation rate, temperature and pressure on the mechanical properties of the thermoplastic polyimides.65 Furthermore, the atomic-scale MD simulations are also indicated to be advantageous for exploring the mechanical properties of such thermoplastic polymers reinforced by carbon nanofiller with distinct shape and size.
, where Fij are the pairwise-additive forces between particles i and j. Notably, the adequacy of uniaxial deformation simulation executed by GROMACS code has been previously assessed in estimating the influence of cooling rate, deformation rate, temperature and pressure on the mechanical properties of the thermoplastic polyimides.65 Furthermore, the atomic-scale MD simulations are also indicated to be advantageous for exploring the mechanical properties of such thermoplastic polymers reinforced by carbon nanofiller with distinct shape and size.
To demonstrate the impact of graphene nanofiller on the mechanical properties of the PVA composites, the stress–strain responses were derived from the uniaxial deformation of the simulation cell at a strain rate of 1.5 × 108 s−1 along the principal X-axis. The calculated stress–strain curves for the pristine PVA and graphene-reinforced nanocomposites, as acquired from the uniaxial deformation MD simulations at 300 K, are compared in Fig. 3(a). The pristine PVA matrix has an ultimate tensile strength of about 611 MPa, as estimated from the maxima in the stress–strain curve. The addition of about 0.8% and 2% graphene nanofiller to the PVA matrix increases the tensile strength to 626 MPa and 636 MPa, respectively. The findings are in accordance with the previous studies which demonstrated that incorporating 1.8 volume percent graphene into PVA composite substantially enhanced their tensile strength.45 In another study, it was demonstrated that the tensile strength only slightly changes from 69 MPa to 71 MPa when graphene loading is increased from 0.8 to 1.0 wt%.46 On the other hand, as shown in Fig. 3(a), the tensile strength reduces to around 579 MPa and 572 MPa, respectively, due to the incorporation of 5% and 10% graphene nanofiller to the PVA matrix. The calculated stress–strain plots thus suggest that there is an optimum amount of graphene addition to the PVA matrix for controlling the mechanical properties of the G-PVA nanocomposite. This observation accords with previous experimental findings that the tensile strength of GO/PVA films decreases significantly when the GO loading exceeds 20 wt%.66 The PVA chains may produce a crystalline structure during solidification at room temperature from the melt yielded at higher temperature. A higher degree of crystallinity is typically responsible for enhancing the mechanical strength and stiffness of the polymer as well as reducing the flexibility and impact resistance. Notably, a previous experimental study demonstrated that the crystallite size of PVA increases due to the addition of 2% GO compared to the pristine PVA.67 However, the crystallite size of GO-modified PVA successively decreases with the increase of GO nanofiller loading from 2% to 3% and 20%. On the other hand, the incorporation of higher amounts of graphene nanofiller may develop the formation of nanoaggregates instead of being evenly distributed in the PVA matrix, which in turn restrains the interfacial interaction between the graphene surface and the polymer chains. This weak interaction may reduce the overall mechanical strength at higher graphene nanofiller concentrations.
Next, we place emphasis on the estimation of non-bonded energy to explore the key role of noncovalent interactions controlling the stress–strain behavior of the graphene-reinforced PVA composites. The non-bonded interactions are estimated from the Lennard-Jones/6-12 interaction (LJ) and Coulombic (Coul) energy terms, where Enon-bonded = E(LJ) + E(Coul). The E(LJ) term is computed from the sum of the energy contributions corresponding to the 1–4 pair interactions (ELJ-14), short-range interactions (ELJ-SR), and long-range dispersion corrections (EDisp-corr). The E(Coul) term is calculated from the energy contributions related to 1-4 pair Coulombic interactions (ECoul-14), short-range Coulombic interactions (ECoul-SR), and long-range reciprocal space Coulombic interactions (ECoul-recip). Fig. 3(b) illustrates the change in calculated non-bonded energy (Enon-bonded) as a function of applied strain, for both the pristine polymer material and polymer composites containing 2% to 10% graphene nanofiller. In the pristine PVA matrix, the contribution of non-bonded energy to the potential energy is comparatively higher in the absence of any strain. This is because the hydrogen bond network established by vinylic –OH groups is stronger in the pristine material, whereas these interactions are disrupted by the addition of graphene nanofiller. The disruption is more pronounced at higher graphene loadings, leading to weaker non-bonded energy. When the applied strain exceeds 30%, the non-bonded energy reaches a plateau and contributes more favorably to the potential energy in the case of the 2% graphene-modified composite. This indicates that the lower amount of graphene loading resulted in more compact PVA polymer chains, thereby minimizing the non-bonded interaction energy. Fig. 4(a) shows the variation of hydrogen-bond interactions with the percentage of graphene nanofiller, as extracted as an ensemble-average from the production MD simulation trajectory. Fig. 4(b)–(f) demonstrate the impact of graphene nanofiller on the probability distribution of hydrogen-bond interactions, and the values are normalized by accounting contributions from monomers of each PVA chain in the G-PVA nanocomposites. The obtained results corroborate well with the predicted trends in the yield strength of the graphene-reinforced nanocomposites.
To explore the impact of strain rate on the mechanical responses of the G-PVA nanocomposites, the uniaxial deformation simulation was further conducted at different strain rates. Fig. 5(a) compares the calculated stress–strain curves of a G-PVA composite with 10% graphene nanofiller obtained from deformation MD simulations conducted at 300 K using three different strain rates: 1.5 × 109 s−1, 1.5 × 108 s−1, and 1.5 × 107 s−1. As manifested by the calculated stress–stress responses, the yield strength of the G-PVA nanocomposite increases with higher strain rates. At a high strain rate of 1.5 × 109 s−1, the G-PVA nanocomposite exhibited a yield strength of 677 MPa. This is significantly higher than the predicted yield strengths of 572 MPa and 402 MPa, respectively, as derived from the uniaxial tension of the simulation cell with lower strain rates of 1.5 × 108 s−1 and 1.5 × 107 s−1.
Next, we emphasize evaluating the impact of temperature on the mechanical properties of the G-PVA composite. To perform the uniaxial compression simulations, the model system of the G-PVA composite consisting of 10% graphene nanofiller was appropriately equilibrated at a given temperature. As mentioned above in the computational details section, the G-PVA composite was subjected to four independent MD simulations: (a) a 10 ns MD simulation under NVT ensemble at 500 K, (b) a temperature annealing process under the NPT ensemble for 100 ns, gradually cooling the system to the target temperatures of 200 K, 300 K, and 400 K, (c) 200 ns of MD simulations under the NPT ensemble, and (d) 200 ns production runs using NPT dynamics at the target temperatures. The stress–strain responses were then extracted from the uniaxial deformation of the simulation cell at a strain rate of 1.5 × 108 s−1 along the principal X-axis. Fig. 5(b) delineates the temperature dependence of the stress–strain curves of the 10% graphene-modified PVA composite. The yield stress reaches approximately 723 MPa when the temperature decreases to 200 K, which is higher than the estimated yield stresses of 572 MPa and 262 MPa at 300 K and 400 K, respectively. As the temperature increases, the yield stress of the G-PVA composite decreases. This is because the higher temperature allows the polymer chains to move more freely, allowing them to more easily accommodate the strain during deformation, which in turn produces a lower yield stress. Fig. 6 illustrates the temperature dependence of the mean square displacement (MSD) curves for the 10% graphene-filled PVA composite. We calculated the MSD over the 200 ns of the production MD trajectories to demonstrate the influence of temperature on the mobility of the polymer chains in the G-reinforced PVA composites. The values of MSD are calculated as:
| MSD(t) = 〈|ri(t) − ri(0)|2〉 |
 | ||
| Fig. 6 Demonstration of temperature dependence of the calculated mean square displacement (MSD) curves for the PVA chains in the graphene–PVA composites comprising 10% graphene nanofiller. | ||
3.2. Thermophysical properties
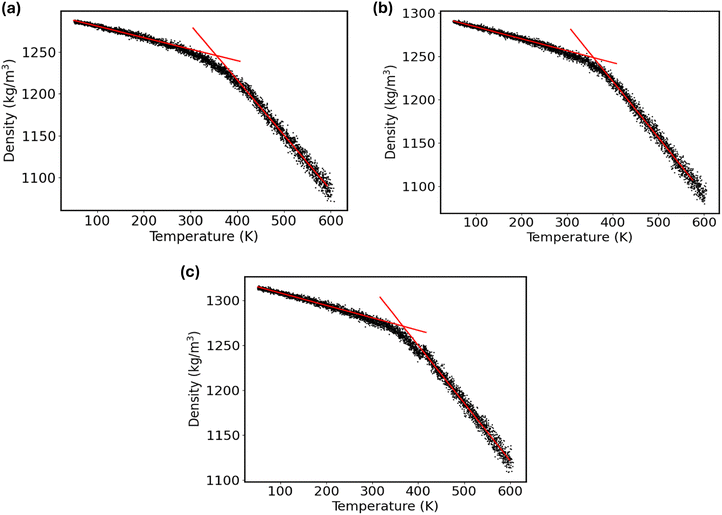
To investigate the impact of graphene nanofiller on the glass transition temperature (Tg) of the PVA composite, the simulated annealing-based NPT MD simulations were performed. This allows one to capture how the density of the graphene–polymer nanocomposite changes with temperature. To accomplish the measurement of Tg, first, each nanocomposite system was heated from 300 K to 600 K at a rate of 0.3 K ps−1. Then, the system was equilibrated for 10 ns using NPT dynamics at 600 K to ensure the density distribution had stabilized. Next, to collect the density–temperature data, the system was progressively cooled from 600 K to 50 K at a rate of 12 K ns−1, dynamically reducing the reference temperature in the thermostat algorithm. It is noteworthy to mention that the glass transition temperature may vary with the quenching rate applied for the simulated annealing MD simulations. For instance, an earlier MD simulation study68 revealed that the Tg for the poly(4-hydroxybutyrate) with 100 monomers reduces from 270.64 K to 242.91 K due to the lowering of quenching rate from 100 K ns−1 to 10 K ns−1. This indicates that higher cooling rates yield higher estimates of Tg. Conversely, another study69 demonstrated that the Tg of polyethylene film confined between graphene surfaces is not significantly impacted by the cooling rate. On the other hand, the MD simulation with an extremely slow cooling rate or experimental timescale (e.g., 1 K s−1) demands immense computational resources. Thus, the impact of further reducing the cooling rate below 12 K ns−1 on the glass transition temperature of the PVA composite was not investigated. Furthermore, extracting the macroscopic property from the atomistic simulation strongly relies on the initial configuration of the system. Consequently, there is inherent uncertainty in estimating Tg from MD simulations. In previous studies, a range of independent MD simulations were carried out to obtain a statistically meaningful average value of Tg, including single, three, four, five, six, and ten simulations of the same system.70 Therefore, to obtain better statistics, we considered three independent thermally equilibrated starting configurations for each system to estimate the Tg values from the density–temperature data.The calculated density–temperature curves for the pristine PVA composite and the G-PVA composites with 2% and 10% graphene nanofiller are compared in Fig. 7. Using a bilinear fit with an R2 value of at least 0.99, the glass transition temperature was estimated from the low-temperature (glassy) and high-temperature (rubbery) regions of the curves. The value of Tg was then determined as the intersection point of these two fitted lines. The fitting protocol basically seeks to minimize the following objective function:71
Fig. S14–S16 (ESI†) illustrate the effect of the fitting ranges on Tg values as acquired from the bilinear fit of the glassy and rubbery states on the density vs. temperature curve for three independent thermally equilibrated starting configurations of the pristine PVA, 2% graphene-filled PVA composite, and 10% graphene-filled PVA composite, respectively. Noticeably, the calculated Tg values due to the alteration of fitting ranges of 150–250 K are not deviated much. Since the maximum R2 value is less than 0.9 especially for the rubbery states on the density vs. temperature curve, the fitting range of 300 K is excluded in obtaining the statistical average of Tg. On the other hand, the Tg estimated with the fitting ranges of 150 K and 200 K show better agreement with the experimental value for the pristine PVA material. Thus, the fitting ranges of 150 K and 200 K are selected to estimate the statistics of Tg from three independent MD simulations for each system. Fig. 7 illustrates the predicted Tg for the pristine PVA and graphene-modified PVA nanocomposites, as estimated from the bilinear fit of the glassy and rubbery states on the density vs. temperature curves using the 200 K fitting range. The 95% confidence interval for the calculated Tg values of the pristine PVA composite from the three initial configurations is 84.7 ± 3.6 °C. The predicted Tg value aligns with the typical literature range of 75–85 °C (348–358 K) for PVA.73 To demonstrate the influence of graphene reinforcement on the glass transition temperature of the PVA composite, the Tg values are further estimated for the inclusion of 2% and 10% graphene filler into the PVA matrix. The estimated Tg of the 2% graphene-filled PVA composite, across the three initial configurations, falls within a 95% confidence interval of 86.7 ± 4.5 °C. The calculated Tg of the 10% graphene-filled PVA composite, derived from three initial configurations, exhibits a 95% confidence interval of 91.5 ± 1.2 °C. This shift toward higher temperatures indicates that adding graphene fillers to the PVA polymer matrix enhanced the thermal stability of the composite systems.
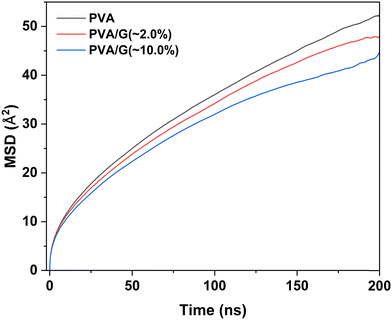
The higher glass transition temperature of nanocomposites of polymeric systems is commonly associated with reduced chain mobility and intermolecular interactions. To examine the influence of graphene nanofiller on the PVA chain mobility, we estimated the MSD of PVA chains across 200 ns of the production MD trajectories accumulated from the NPT dynamics of the pristine PVA matrix and G-PVA nanocomposites at 400 K. As revealed by the calculated MSD curves shown in Fig. 8, the polymer chain mobility consecutively decreases with the addition of graphene nanofiller to the PVA matrix. The analyses of hydrogen-bond interactions and MSD data, as shown in Fig. 4 and 8, indicate that the reduced chain mobility effects outweigh the hydrogen-bond reduction effect when higher amounts of graphene nanofillers are incorporated into the PVA matrix. The overall effect is an increase in the Tg of the 10% graphene-filled PVA composite compared to the 2% graphene-filled PVA composite.
4. Conclusions
The influence of graphene nanofiller on the structural, mechanical, and thermophysical properties of PVA composites is explored within the framework of classical MD simulations. The calculated ensemble-average density of the PVA matrix, obtained from a 200 ns NPT dynamics trajectory, is approximately 1.25 g cm−3. Increasing the graphene nanofiller proportion from 0.8% to 10% enhances the density of the G-PVA nanocomposite by around 2.6%. Analysis of the computed average radii of gyration for the PVA chains reveals that the incorporation of graphene filler causes the polymer chains to become more folded. This compactness is most pronounced in the composite with 2% graphene. Uniaxial deformation MD simulations were used to derive the mechanical properties of graphene-reinforced PVA composites. The results show that the mechanical strength of the G-PVA composites is highly dependent on the weight percentage of the graphene nanofiller added to the PVA matrix. Specifically, the calculated stress–strain responses from the uniaxial deformation of the simulation cell at a strain rate of 1.5 × 108 s−1 reveal that the yield strength of the G-PVA composite is maximized when the graphene loading is just 2%. The predicted trends in the yield strength of the pristine PVA matrix and the graphene-modified PVA nanocomposites align with the calculated non-bonded energy derived from the energy components of the Lennard-Jones and Coulombic interactions. The analysis of hydrogen-bond interactions anticipates that the reduction of the yield stress of the G-PVA composite at a higher percentage of graphene nanofiller addition (5–10%) is correlated with the disruption of hydrogen bond networks established between polymer segments. The stress responses of the G-PVA polymer are consistent with the mobility of its polymer chains, as demonstrated by the analysis of mean-squared displacement (MSD) curves. The impact of strain rate on the mechanical properties of the G-PVA nanocomposite is studied by calculating stress–strain responses at different strain rates: 1.5 × 109 s−1, 1.5 × 108 s−1, and 1.5 × 107 s−1. As the strain rate increases, the PVA oligomers and graphene nanostructures in the composite material are unable to adequately relax and accommodate the strain during deformation. Consequently, the composite exhibits a higher yield stress compared to when the strain rate is lower. The effect of temperature on the mechanical responses of the polymer and graphene–polymer composites is also investigated. As evidenced by the calculated stress–strain curves at different temperatures, elevated temperatures cause the yield stress of the G-PVA composite to decrease. This occurs because the increased molecular motion at higher temperatures enables the PVA chains to more readily rearrange and conform to strain during deformation, thereby lowering the yield stress. Finally, computational analysis of the glass transition temperatures confirms the enhanced thermal stability of the graphene-reinforced polymer nanocomposites. The enhancement of glass transition temperature is strongly correlated with the suppression of polymer chain mobility. The atomistic MD simulations of graphene–polymer nanocomposites thus provide the detailed structural basis for enhancing the mechanical and thermal resistance of the G-PVA nanocomposites. The acquired information could guide the development of functional hybrid materials of polymers and nanomaterials with superior mechanical properties. The simulation strategy laid out in this study could be expanded to analyze the thermomechanical behavior of other polymer–nanofiller composite systems. Furthermore, the development of a more generalized MD simulation approach along with transferable force fields becomes a subject of concern in the ongoing research studies to predict the thermal conductivity and dielectric properties of such nanocomposites.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This research was funded by the Department of Defense (DoD) (Award No. W911NF-21-S-0011) and the CA BO340 497014 Project “Graphene Applications for Military Engineering,” under Contract W912HZ-21C0040, managed by the US Army Engineer Research and Development Center. The work described in this document was conducted in the Center for Computational Chemistry at Jackson State University. The authors would like to acknowledge the support provided by the US Army Engineer Research and Development Center (ERDC) and the Military Engineering Research and Development Area under contract W912HZ-21C0040. Permission to publish was granted by the ERDC Geotechnical and Structures Laboratory. The research described and the resulting data presented herein were funded under CA BO340 497014 Project, “Graphene Applications for Military Engineering,” under Contract W912HZ-21C0040, managed by the US Army Engineer Research and Development Center.References
- M. J. Allen, V. C. Tung and R. B. Kaner, Honeycomb Carbon: A Review of Graphene, Chem. Rev., 2010, 110, 132–145 CrossRef CAS PubMed.
- F. Farjadian, S. Abbaspour, M. A. A. Sadatlu, S. Mirkiani, A. Ghasemi, M. Hoseini-Ghahfarokhi, N. Mozaffari, M. Karimi and M. R. Hamblin, Recent Developments in Graphene and Graphene Oxide: Properties, Synthesis, and Modifications: A Review, ChemistrySelect, 2020, 5, 10200–10219 CrossRef CAS.
- G. Zhao, X. Li, M. Huang, Z. Zhen, Y. Zhong, Q. Chen, X. Zhao, Y. He, R. Hu, T. Yang, R. Zhang, C. Li, J. Kong, J.-B. Xu, R. S. Ruoff and H. Zhu, The physics and chemistry of graphene-on-surfaces, Chem. Soc. Rev., 2017, 46, 4417–4449 RSC.
- L. Rodríguez-Pérez, M. Á. Herranz and N. Martín, The chemistry of pristine graphene, Chem. Commun., 2013, 49, 3721 RSC.
- A. Kaplan, Z. Yuan, J. D. Benck, A. G. Rajan, X. S. Chu, Q. H. Wang and M. S. Strano, Current and future directions in electron transfer chemistry of graphene, Chem. Soc. Rev., 2017, 46, 4530–4571 RSC.
- H. Huang, H. Shi, P. Das, J. Qin, Y. Li, X. Wang, F. Su, P. Wen, S. Li, P. Lu, F. Liu, Y. Li, Y. Zhang, Y. Wang, Z. Wu and H. Cheng, The Chemistry and Promising Applications of Graphene and Porous Graphene Materials, Adv. Funct. Mater., 2020, 30, 1909035 CrossRef CAS.
- A. Razaq, F. Bibi, X. Zheng, R. Papadakis, S. H. M. Jafri and H. Li, Review on Graphene-, Graphene Oxide-, Reduced Graphene Oxide-Based Flexible Composites: From Fabrication to Applications, Materials, 2022, 15, 1012 CrossRef CAS PubMed.
- H. Faye, T. M. Subrahmanya, O. Setiawan, J. Widakdo, Y.-H. Chiao, W.-S. Hung, C.-F. Wang, C.-C. Hu, K.-R. Lee and J.-Y. Lai, A review on the recent advancements in graphene-based membranes and their applications as stimuli-responsive separation materials, J. Mater. Chem. A, 2021, 9, 21510–21531 RSC.
- K. Hu, D. D. Kulkarni, I. Choi and V. V. Tsukruk, Graphene-polymer nanocomposites for structural and functional applications, Prog. Polym. Sci., 2014, 39, 1934–1972 CrossRef CAS.
- H. Kim, A. A. Abdala and C. W. Macosko, Graphene/Polymer Nanocomposites, Macromolecules, 2010, 43, 6515–6530 CrossRef CAS.
- P. Govindaraj, B. Fox, P. Aitchison and N. Hameed, A Review on Graphene Polymer Nanocomposites in Harsh Operating Conditions, Ind. Eng. Chem. Res., 2019, 58, 17106–17129 CrossRef CAS.
- M. Silva, N. M. Alves and M. C. Paiva, Graphene-polymer nanocomposites for biomedical applications, Polym. Adv. Technol., 2017, 29, 687–700 CrossRef.
- A. Díez-Pascual, J. L. Sánchez, R. P. Capilla and P. G. Díaz, Recent Developments in Graphene/Polymer Nanocomposites for Application in Polymer Solar Cells, Polymers, 2018, 10, 217 CrossRef PubMed.
- S. J. Lee, S. J. Yoon and I.-Y. Jeon, Graphene/Polymer Nanocomposites: Preparation, Mechanical Properties, and Application, Polymers, 2022, 14, 4733 CrossRef CAS PubMed.
- M. Zhang, Y. Li, Z. Su and G. Wei, Recent advances in the synthesis and applications of graphene–polymer nanocomposites, Polym. Chem., 2015, 6, 6107–6124 RSC.
- W. K. Chee, H. N. Lim, N. M. Huang and I. Harrison, Nanocomposites of graphene/polymers: a review, RSC Adv., 2015, 5, 68014–68051 RSC.
- X. Sun, C. Huang, L. Wang, L. Liang, Y. Cheng, W. Fei and Y. Li, Recent Progress in Graphene/Polymer Nanocomposites, Adv. Mater., 2020, 33, 2001105 CrossRef PubMed.
- D. G. Papageorgiou, Z. Li, M. Liu, I. A. Kinloch and R. J. Young, Mechanisms of mechanical reinforcement by graphene and carbon nanotubes in polymer nanocomposites, Nanoscale, 2020, 12, 2228–2267 RSC.
- P. Govindaraj, A. Sokolova, N. Salim, S. Juodkazis, F. K. Fuss, B. Fox and N. Hameed, Distribution states of graphene in polymer nanocomposites: A review, Composites, Part B, 2021, 226, 109353 CrossRef CAS.
- S. Lee, J.-Y. Hong and J. Jang, The effect of graphene nanofiller on the crystallization behavior and mechanical properties of poly(vinyl alcohol), Polym. Int., 2013, 62, 901–908 CrossRef CAS.
- J. Ashfaq, I. A. Channa, A. G. Memon, I. A. Chandio, A. D. Chandio, M. A. Shar, M. S. Alsalhi and S. Devanesan, Enhancement of Thermal and Gas Barrier Properties of Graphene-Based Nanocomposite Films, ACS Omega, 2023, 8, 41054–41063 CrossRef CAS PubMed.
- B. Van der Schueren, H. El Marouazi, A. Mohanty, P. Lévêque, C. Sutter, T. Romero and I. Janowska, Polyvinyl Alcohol-Few Layer Graphene Composite Films Prepared from Aqueous Colloids. Investigations of Mechanical, Conductive and Gas Barrier Properties, Nanomaterials, 2020, 10, 858 CrossRef CAS PubMed.
- C.-H. Tsou, L. Zhao, C. Gao, H. Duan, X. Lin, Y. Wen, J. Du, S.-M. Lin, M.-C. Suen, Y. Yu, X. Liu and M. Reyes, Characterization of network bonding created by intercalated functionalized graphene and polyvinyl alcohol in nanocomposite films for reinforced mechanical properties and barrier performance, Nanotechnology, 2020, 31, 385703 CrossRef CAS PubMed.
- L. Yang, W. Weng, X. Fei, L. Pan, X. Li, W. Xu, Z. Hu and M. Zhu, Revealing the interrelation between hydrogen bonds and interfaces in graphene/PVA composites towards highly electrical conductivity, Chem. Eng. J., 2020, 383, 123126 CrossRef CAS.
- L. Mahmoud, Y. Abdul Samad, M. Alhawari, B. Mohammad, K. Liao and M. Ismail, Combination of PVA with Graphene to Improve the Seebeck Coefficient for Thermoelectric Generator Applications, J. Electron. Mater., 2014, 44, 420–424 CrossRef.
- S. Karadaş, S. A. Yerişkin, M. Balbaşı and Y. Azizian-Kalandaragh, Complex dielectric, complex electric modulus, and electrical conductivity in Al/(Graphene-PVA)/p-Si (metal-polymer-semiconductor) structures, J. Phys. Chem. Solids, 2021, 148, 109740 CrossRef.
- D. Chen, X. Wang, T. Liu, X. Wang and J. Li, Electrically Conductive Poly(vinyl alcohol) Hybrid Films Containing Graphene and Layered Double Hydroxide Fabricated via Layer-by-Layer Self-Assembly, ACS Appl. Mater. Interfaces, 2010, 2, 2005–2011 CrossRef CAS.
- S. Lim, B. Kang, D. Kwak, W. H. Lee, J. A. Lim and K. Cho, Inkjet-Printed Reduced Graphene Oxide/Poly(Vinyl Alcohol) Composite Electrodes for Flexible Transparent Organic Field-Effect Transistors, J. Phys. Chem. C, 2012, 116, 7520–7525 CrossRef CAS.
- J. Wang, X. Wang, C. Xu, M. Zhang and X. Shang, Preparation of graphene/poly(vinyl alcohol) nanocomposites with enhanced mechanical properties and water resistance, Polym. Int., 2011, 60, 816–822 CrossRef CAS.
- H. Liu, S.-H. Hu, Y. Chen and S.-Y. Chen, Characterization and drug release behavior of highly responsive chip-like electrically modulated reduced graphene oxide–poly(vinyl alcohol) membranes, J. Mater. Chem., 2012, 22, 17311 RSC.
- R. Surudžić, A. Janković, M. Mitrić, I. Matić, Z. D. Juranić, L. Živković, V. Mišković-Stanković, K. Y. Rhee, S. J. Park and D. Hui, The effect of graphene loading on mechanical, thermal and biological properties of poly(vinyl alcohol)/graphene nanocomposites, J. Ind. Eng. Chem., 2016, 34, 250–257 CrossRef.
- E. F. Gulino, M. C. Citarrella, A. Maio and R. Scaffaro, An innovative route to prepare in situ graded crosslinked PVA graphene electrospun mats for drug release, Composites, Part A, 2022, 155, 106827 CrossRef CAS.
- N. Zhao, M. Yang, Q. Zhao, W. Gao, T. Xie and H. Bai, Superstretchable Nacre-Mimetic Graphene/Poly(vinyl alcohol) Composite Film Based on Interfacial Architectural Engineering, ACS Nano, 2017, 11, 4777–4784 CrossRef CAS PubMed.
- J. Ma, Y. Li, X. Yin, Y. Xu, J. Yue, J. Bao and T. Zhou, Poly(vinyl alcohol)/graphene oxide nanocomposites prepared by in situ polymerization with enhanced mechanical properties and water vapor barrier properties, RSC Adv., 2016, 6, 49448–49458 RSC.
- G. T. Park and J.-H. Chang, Comparison of Properties of PVA Nanocomposites Containing Reduced Graphene Oxide and Functionalized Graphene, Polymers, 2019, 11, 450 CrossRef PubMed.
- J.-H. Chang, Comparative Analysis of Properties of PVA Composites with Various Nanofillers: Pristine Clay, Organoclay, and Functionalized Graphene, Nanomaterials, 2019, 9, 323 CrossRef CAS PubMed.
- X. Wang, X. Liu, H. Yuan, H. Liu, C. Liu, T. Li, C. Yan, X. Yan, C. Shen and Z. Guo, Non-covalently functionalized graphene strengthened poly(vinyl alcohol), Mater. Des., 2018, 139, 372–379 CrossRef CAS.
- M. Y. Zhou, J. Liu and L. Q. Zhang, Structure and properties of polymer/two-dimensional nanomaterials studied via molecular dynamics simulation: a review, Mol. Syst. Des. Eng., 2023, 8, 11–31 RSC.
- S. Yang, W. Zhang, R. Ma, H. Li, Y. Lu, X. Zhao, L. Zhang and Y. Gao, Manipulating the Thermal Conductivity of the Graphene/Poly(vinyl alcohol) Composite via Surface Functionalization: A Multiscale Simulation, Langmuir, 2023, 39, 9703–9714 CrossRef CAS PubMed.
- N. Ding, X. Chen, C.-M. L. Wu and X. Lu, Computational Investigation on the Effect of Graphene Oxide Sheets as Nanofillers in Poly(vinyl alcohol)/Graphene Oxide Composites, J. Phys. Chem. C, 2012, 116, 22532–22538 CrossRef CAS.
- Y. Wang, G. Yang, W. Wang, S. Zhu, L. Guo, Z. Zhang and P. Li, Effects of different functional groups in graphene nanofiber on the mechanical property of polyvinyl alcohol composites by the molecular dynamic simulations, J. Mol. Liq., 2019, 277, 261–268 CrossRef CAS.
- Y. Wang, W. Wang, S. Zhu, G. Yang, Z. Zhang and P. Li, The evolution of the thermodynamic property of graphene oxide nanofiber coated poly(vinyl alcohol) resin surface by the molecular dynamic simulations, J. Mol. Liq., 2020, 316, 113723 CrossRef CAS.
- Y. Wang, W. Wang, G. Yang, Z. Zhang and P. Li, The theoretical study of mechanical property and thermostability analysis of poly(vinyl alcohol)/graphene oxide nanofiber composites with different architecture: Molecular dynamics simulation, Polym. Compos., 2021, 42, 6478–6487 CrossRef CAS.
- C. Bao, Y. Guo, L. Song and Y. Hu, Poly(vinyl alcohol) nanocomposites based on graphene and graphite oxide: a comparative investigation of property and mechanism, J. Mater. Chem., 2011, 21, 13942 RSC.
- X. Zhao, Q. Zhang, D. Chen and P. Lu, Enhanced Mechanical Properties of Graphene-Based Poly(vinyl alcohol) Composites, Macromolecules, 2010, 43, 2357–2363 CrossRef CAS.
- X. Yuan, Enhanced interfacial interaction for effective reinforcement of poly(vinyl alcohol) nanocomposites at low loading of graphene, Polym. Bull., 2011, 67, 1785–1797 CrossRef CAS.
- M. Azimi, S. S. Mirjavadi, A. M. S. Hamouda and H. Makki, Heterogeneities in Polymer Structural and Dynamic Properties in Graphene and Graphene Oxide Nanocomposites: Molecular Dynamics Simulations, Macromol. Theory Simul., 2017, 26, 1600086 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: Fast, flexible, and free, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- E. Lindahl, B. Hess and D. van der Spoel, GROMACS 3.0: a package for molecular simulation and trajectory analysis, J. Mol. Model., 2001, 7, 306–317 CrossRef CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: A message-passing parallel molecular dynamics implementation, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- M. Abraham, A. Alekseenko, C. Bergh, C. Blau, E. Briand, M. Doijade, S. Fleischmann, V. Gapsys, G. Garg, S. Gorelov, G. Gouaillardet, A. Gray, M. Eric Irrgang, F. Jalalypour, J. Jordan, C. Junghans, P. Kanduri, S. Keller, C. Kutzner, J. A. Lemkul, M. Lundborg, P. Merz, V. Miletić, D. Morozov, S. Páll, R. Schulz, M. Shirts, A. Shvetsov, B. Soproni, D. V. D. Spoel, P. Turner, C. Uphoff, A. Villa, S. Wingbermühle, A. Zhmurov, P. Bauer, B. Hess and E. Lindahl, GROMACS 2023 Source code (Version 2023), Zenodo, 2023. DOI:10.5281/zenodo.7588619.
- M. A. F. Afzal, A. R. Browning, A. Goldberg, M. D. Halls, J. L. Gavartin, T. Morisato, T. F. Hughes, D. J. Giesen and J. E. Goose, High-Throughput Molecular Dynamics Simulations and Validation of Thermophysical Properties of Polymers for Various Applications, ACS Appl. Polym. Mater., 2021, 3, 620–630 CrossRef CAS.
- Y. Choi, S. M. Park, S. Park, S. H. Kim, N. R. Kern, J. Lee and W. Im, CHARMM-GUI Polymer Builder for Modeling and Simulation of Synthetic Polymers, J. Chem. Theory Comput., 2021, 17, 2431–2443 CrossRef CAS PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, OpenMM 7: Rapid development of high performance algorithms for molecular dynamics, PLoS Comput. Biol., 2017, 13, e1005659 CrossRef PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields, J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS PubMed.
- H. Heinz, T.-J. Lin, R. K. Mishra and F. S. Emami, Thermodynamically Consistent Force Fields for the Assembly of Inorganic, Organic, and Biological Nanostructures: The INTERFACE Force Field, Langmuir, 2013, 29, 1754–1765 CrossRef CAS PubMed.
- Y. K. Choi, N. R. Kern, S. Kim, K. Kanhaiya, Y. Afshar, S. H. Jeon, S. Jo, B. R. Brooks, J. Lee, E. B. Tadmor, H. Heinz and W. Im, CHARMM-GUI Nanomaterial Modeler for Modeling and Simulation of Nanomaterial Systems, J. Chem. Theory Comput., 2022, 18, 479–493 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: A linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- F. L. Marten, Vinyl Alcohol Polymers, Encycl. Polym. Sci. Technol., 2002, 8, 399–437 Search PubMed.
- R. L. Miller, Crystallographic Data and Melting Points for Various Polymers, in The Wiley Database of Polymer Properties, ed. J. Brandrup, E. H. Immergut and E. A. Grulke, Wiley, 2003 DOI:10.1002/0471532053.bra038.
- R. Nagarkar and J. Patel, Polyvinyl Alcohol: A Comprehensive Study, Acta Sci. Pharm. Sci., 2019, 3(4), 34–44 Search PubMed.
- V. M. Nazarychev, A. V. Lyulin, S. V. Larin, A. A. Gurtovenko, J. M. Kenny and S. V. Lyulin, Molecular dynamics simulations of uniaxial deformation of thermoplastic polyimides, Soft Matter, 2016, 12, 3972–3981 RSC.
- C. Tao, H. Zhang, F. Wang, H. Zhu, X. Zou and J. Wang, Mechanical Properties of Graphene Oxide/Polyvinyl Alcohol Composite Film, Polym. Polym. Compos., 2017, 25, 11–16 CAS.
- L. Gahramanli, M. Muradov, G. Eyvazova, M. B. Baghirov, S. Mammadyarova, G. Aliyeva, E. Hajiyev, F. Mammadov and S. Bellucci, Investigating the Effect of Thermal Annealing and Changing the Concentration of GO in GO/PVA Nanocomposites on Their Structural, Electrical, and Optical Properties, ChemEngineering, 2023, 7, 92 CrossRef CAS.
- K. K. Bejagam, C. N. Iverson, B. L. Marrone and G. Pilania, Molecular dynamics simulations for glass transition temperature predictions of polyhydroxyalkanoate biopolymers, Phys. Chem. Chem. Phys., 2020, 22, 17880–17889 RSC.
- D. McKechnie, J. Cree, D. Wadkin-Snaith and K. Johnston, Glass transition temperature of a polymer thin film: Statistical and fitting uncertainties, Polymer, 2020, 195, 122433 CrossRef CAS.
- J. L. Suter, W. A. Müller, M. Vassaux, A. Anastasiou, M. Simmons, D. Tilbrook and P. V. Coveney, Rapid, Accurate and Reproducible Prediction of the Glass Transition Temperature Using Ensemble-Based Molecular Dynamics Simulation, J. Chem. Theory Comput., 2025, 21, 1405–1421 CrossRef CAS PubMed.
- F. J. Carmona, Y. Zhang, Y. J. Colón and E. J. Maginn, Molecular Dynamics Simulation of the Influence of External Electric Fields on the Glass Transition Temperature of the Ionic Liquid 1-Ethyl-3-methylimidazolium Bis(trifluoromethylsulfonyl)imide, J. Phys. Chem. B, 2023, 127, 4623–4632 CrossRef PubMed.
- K.-H. Lin, L. Paterson, F. May and D. Andrienko, Glass transition temperature prediction of disordered molecular solids, npj Comput. Mater., 2021, 7, 179 CrossRef CAS.
- C. Tsioptsias, D. Fardis, X. Ntampou, I. Tsivintzelis and C. Panayiotou, Thermal Behavior of Poly(vinyl alcohol) in the Form of Physically Crosslinked Film, Polymers, 2023, 15, 1843 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04706k |
| This journal is © the Owner Societies 2025 |