Open Access Article
Open Access ArticleOuter-sphere effects on ligand-field excited-state dynamics: solvent dependence of high-spin to low-spin conversion in [Fe(bpy)3]2+†
Jennifer N.
Miller
and
James K.
McCusker
 *
*
Department of Chemistry, Michigan State University, 578 South Shaw Lane, East Lansing, Michigan 48824, USA. E-mail: jkm@chemistry.msu.edu
First published on 12th May 2020
Abstract
In condensed phase chemistry, the solvent can have a significant impact on everything from yield to product distribution to mechanism. With regard to photo-induced processes, solvent effects have been well-documented for charge-transfer states wherein the redistribution of charge subsequent to light absorption couples intramolecular dynamics to the local environment of the chromophore. Ligand-field excited states are expected to be largely insensitive to such perturbations given that their electronic rearrangements are localized on the metal center and are therefore insulated from so-called outer-sphere effects by the ligands themselves. In contrast to this expectation, we document herein a nearly two-fold variation in the time constant associated with the 5T2 → 1A1 high-spin to low-spin relaxation process of tris(2,2′-bipyridine)iron(II) ([Fe(bpy)3]2+) across a range of different solvents. Likely origins for this solvent dependence, including relevant solvent properties, ion pairing, and changes in solvation energy, were considered and assessed by studying [Fe(bpy)3]2+ and related derivatives via ultrafast time-resolved absorption spectroscopy and computational analyses. It was concluded that the effect is most likely associated with the volume change of the chromophore arising from the interconfigurational nature of the 5T2 → 1A1 relaxation process, resulting in changes to the solvent–solvent and/or solvent–solute interactions of the primary solvation shell sufficient to alter the overall reorganization energy of the system and influencing the kinetics of ground-state recovery.
Introduction
When running a reaction in solution – be it thermal or photochemical – one must consider how the solvent itself may influence the chemistry of the system. Even under static or steady-state conditions, the solvent medium can impact a molecule's physical properties.1 For example, interactions between the solute and the solvent can shift the potential energy surfaces of reactants and products relative to the gas phase, the effects of which can be seen in changes to absorption and fluorescence spectra.2 Similarly, the position, shape, and intensity of absorption features can vary across solvents due to solvatochromism,3 effects that can be particularly pronounced for transitions associated with a rearrangement of charge. Additional intermolecular effects of solvation can manifest through structural modifications,4 electrostatic interactions,5 polarization effects,6 or even aggregation of the solute molecules.7 The dipole moment of a molecule can also change,8 an indication that the solvent environment can modify intramolecular charge distribution.Despite the wealth of knowledge available on the impact of solvation, there is still much to be learned when it comes to understanding the effect of solvent under non-equilibrium conditions. For example, the microscopic details by which solvent responses couple to and/or influence reactions is an area of continued interest both experimentally and theoretically,9,10 particularly in the case of charge-transfer events where the process in question involves a significant spatial redistribution of charge. If, for example, the solute molecule is promoted to a metal-to-ligand charge transfer (MLCT) state following irradiation, an electron will be shifted from an orbital localized primarily on the metal center to a new location within the solute molecule (in this case, the ligand). Since this charge transfer is instantaneous relative to any solvent response, the solvent molecules will still be oriented as they were prior to the excitation of the chromophore. The solvent environment must then reorganize in response to photoexcitation of the solute in order to stabilize the new charge distribution. Previous work from our group demonstrated how ultrafast solvent dynamics – particularly those associated with inertial solvent response11 – can modulate the nature of the excited state to the extent of driving charge localization within the chromophore.12 Solvent dynamics (or a lack thereof) can also have a significant impact on the thermodynamics of photoinduced electron transfer as evidenced by the shift in free energy that occurs upon decreasing the temperature of a charge transfer system below the freezing point of the solution.10 These are just a few of many examples in which solvation dynamics can influence the photophysics and photochemistry of chemical systems.
While charge-transfer excited states are known to be particularly responsive to solvent properties, ligand-field excited states, which correspond to electronic structure rearrangements that are largely localized on the metal center, are generally viewed as being insensitive to these perturbations. For example, the 2E → 4A2 ground-state recovery dynamics of Cr(acac)3 (where acac = acetylacetonate) that follows 4A2 → 4T2 ligand-field excitation are similar (though not identical) in both acetonitrile and dichloromethane, two solvents that differ substantially in their dipole moments, longitudinal relaxation times, and viscosities.13 Although examples certainly exist of ways in which ligand-field state dynamics can be modulated as a result of solvent–solute interactions – the lifetime of the 2E excited state of Cr(III)-amine complexes can be significantly altered upon deuteration of the amine ligands due to changes in non-radiative coupling to the solvent, for example14 – the relative insensitivity of ligand field-state dynamics to changes in the solvent can be attributed to the fact that metal-centered excited states are largely shielded from the solvent by the ligands. The primary driver of dynamics associated with this class of excited states is therefore usually inner-sphere in nature, with the solvent having little influence on a compound's photophysics. It is for this reason that, upon changing the solvent from water to acetonitrile, the observation of a ∼50% increase in the lifetime of the 5T2 ligand-field excited state of [Fe(bpy)3]2+ (where bpy = 2,2′-bipyridine) was surprising. Given the recent attention that has been paid to the photophysics of this and related compounds,15–17 the fact that little information is available as to the possible origin of this effect compelled us to take a closer look at the solvent dependence of the photophysics of this class of prototypical Fe(II) chromophores (Chart 1). By examining a range of solvents with varying physical properties – and after accounting for factors including ion pairing, and the accessibility of the metal center by the solvent – we demonstrate that variations in the lowest-energy excited-state lifetime are most likely linked to outer-sphere reorganization energy effects in which the solvent is responding to metal-localized intramolecular dynamics to an extent sufficient for it to manifest in the time-dependent photophysics of the chromophore.
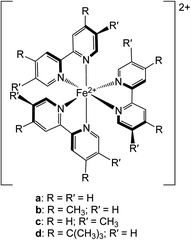 | ||
| Chart 1 Molecular structures of the chromophores examined in this study: (a) [Fe(bpy)3]2+, (b) [Fe(dmb)3]2+, (c) [Fe(5,5′-dmb)3]2+ and (d) [Fe(dtbbpy)3]2+. See text for further details. | ||
Experimental details
Materials
Reagents were all commercially available and purchased from Alfa Aesar, Jade Scientific, Oakwood Chemical, Sigma-Aldrich, Spectrum Chemical, and Strem Chemicals. Solvents for spectroscopic measurements were used as received: 1-butanol (Jade Scientific, JS-B6000), 1,3-propanediol (Alfa Aesar, A10829), 1,4-butanediol (Sigma-Aldrich, 493732), 1,5-pentanediol (Fluka Analytical, 76892), 2-propanol (Sigma-Aldrich, 278475), acetonitrile (Sigma-Aldrich, 34851), butyronitrile (Alfa Aesar, L02999), dichloromethane (Jade Scientific, JS-D2735), diethyl ether (Sigma-Aldrich, 673811), dimethyl sulfoxide (EMD, MX1458-3), ethanol (KOPTEC, V1016), ethylene glycol (CCI, 2165CM), hexanenitrile (Aldrich, 166650), methanol (Jade Scientific, JS-M3650), propionitrile (Alfa Aesar, A13203), propylene carbonate (Sigma-Aldrich, 310328), tetrahydrofuran (Fisher Chemical, T427), and water (Sigma-Aldrich, 270733).Syntheses and characterization
[Fe(bpy)3]2+, tris-(4,4′-dimethyl-2,2′-bipyridine)iron(II) ([Fe(dmb)3]2+), tris-(5,5′-dimethyl-2,2′-bipyridine)iron(II) ([Fe(5,5′-dmb)3]2+), and tris-(4,4′-di-tert-butyl-2,2′-bipyridine)-iron(II) ([Fe(dtbbpy)3]2+) were prepared based on routes reported in the literature.18,19 All of the compounds were isolated as the bromide (Br−) salt, with the exception of [Fe(bpy)3]2+, which was also isolated with chloride (Cl−), iodide (I−), hexafluorophosphate (PF6−), tetraphenylborate (BPh4−), and tetrakis(3,5-bis(trifluoromethyl)phenyl)borate (BArF4−) as counterions. Reactions were performed under an inert atmosphere with deoxygenated solvents either in a nitrogen-filled glovebox or by standard Schlenk techniques. The composition and purity of all molecules were assessed by mass spectrometry, nuclear magnetic resonance (NMR) spectroscopy, and elemental analysis. 1H NMR spectroscopic data were collected with Agilent DD2 500 MHz NMR spectrometers at the MSU Max T. Rogers NMR facility. Mass spectra were acquired at the MSU Mass Spectrometry and Metabolomics Core facility with a Waters Xevo G2-XS QTof instrument. Elemental analyses were run by facilities in the MSU chemistry department with a PerkinElmer 2400 Series II CHNS/O Elemental Analyzer. Additional details can be found in the ESI.†Electronic absorption spectra
Ground state electronic absorption spectra of samples for time-resolved absorption measurements were measured on a Varian Cary 50 UV-visible spectrophotometer. Molar absorptivities were determined in matched 1 cm path length quartz cells on a PerkinElmer Lambda 1050 spectrophotometer from serial dilutions of the original solution (see Fig. S1–S9 in the ESI†).Time-resolved spectroscopic measurements
Femtosecond pump-probe measurements were collected on a laser system with approximately 130 fs resolution that has been described previously,13 modified with a 1035 mm stage (Aerotech, LMAC Series linear motor actuator with a Soloist CP controller) using a double-pass configuration on the pump beam line (Fig. S10†), that allows for data collection with delays of up to ∼13 ns.20 Samples were excited on the low energy shoulder of the MLCT band, corresponding to 530 nm for [Fe(5,5′-dmb)3]Br2 and 550 nm for [Fe(bpy)3]2+, [Fe(dmb)3]Br2, and [Fe(dtbbpy)3]Br2. A white light continuum was generated by focusing 805 nm light into a calcium fluoride window, which was continuously translated transverse to the direction of the laser beam. Probe wavelengths were selected from the white light continuum with 10 nm bandpass filters positioned after the sampling a spectral window 20–40 nm bluer than the pump wavelength in order to minimize pump scatter at the Si photodiode. Polarizations for the pump and probe beams were set at magic angle (54.7°) relative to one another. A neutral density (ND) filter slide was used to give pump energies of 5 μJ at the sample position, and all sample signals were checked to verify a linear response with respect to the pump power.Samples were prepared in air in a series of solvents at concentrations which yielded ground state absorbances in the range of 0.4–0.5 at the excitation wavelength in a 1 mm path length cell (with the exception of the concentration-dependent studies, where samples having absorbances of 0.1, 0.7, and 1.0 were also employed). All measurements were carried out at room temperature (ca. 20 °C). Time constants reported herein are the average of at least four data sets, where each of these data sets represents a signal average of at least sixteen scans. Each 16-scan signal-averaged data set was fit to a single exponential kinetic model using Igor Pro software (Version 6.37) with weighting to incorporate the standard deviation associated with each data point. The error associated with each reported lifetime was derived from propagating the error associated with the exponential fits from each of the complete data sets. Igor Pro software was also used to analyze the relationship between selected solvent properties and excited state lifetimes with linear regression, where the strength of the correlation is reflected by the coefficient of determination (R2).
Computational methods
Calculations were carried out using the Gaussian 09 software package21 on servers available through the High Performance Computing Center (HPCC) of the Institute for Cyber-Enabled Research (ICER) at Michigan State University. The singlet and quintet state geometries of each Fe(II) complex were optimized with UFF atomic radii under tight convergence criteria and an ultrafine integration grid at the spin-unrestricted B3LYP22–24 level, using the SDD effective core potential and associated basis set25 for the Fe atom, the 6-31G(d) basis set26,27 for C and N atoms, and the 6-31G(d,p) basis set26,27 for H atoms. No symmetry restrictions were imposed. The initial geometries of the molecules came from their crystal structures, downloaded from the Cambridge Structural Database28 under the refcodes: ADEJOK ([Fe(dtbbpy)3]2+), ECAKUP ([Fe(5,5′-dmb)3]2+), MEMSON ([Fe(dmb)3]2+), and NUZKOI ([Fe(bpy)3]2+). Optimized structures were assessed by vibrational frequency analysis, the results of which were ultimately used to determine Gibbs free energies for all compounds at 293.15 K and standard pressure under vacuum and in solution.The purpose of these calculations is to estimate how the gas-to-solution phase Gibbs free energy of solvation (ΔGsolv) changes between the quintet and singlet states. The conductor-like polarizable continuum model (CPCM)29,30 was used to compute solvation energy, with all solvents applied under the generic setting and distinguished by the following input parameters (DFT keywords): stoichiometry, static dielectric constant (eps), optical dielectric constant (epsinf), solvent radius (rsolv), molar volume (molarvolume), and temperature (TAbs). All CPCM calculations also included the keywords cav, dis, and rep (for cavitation, dispersion, and repulsion, respectively) to incorporate non-electrostatic contributions. To compute the ΔGsolv of an electronic state in a particular solvent, the difference was taken between the thermally-corrected Gibbs free energy in solvent versus under vacuum.31 From there, the differential solvation energy, or ΔΔGsolv, was calculated as the difference between the ΔGsolv values for the singlet and quintet states.
Results and discussion
Effect of solvent on the excited-state dynamics of [Fe(bpy)3]2+: empirical observations
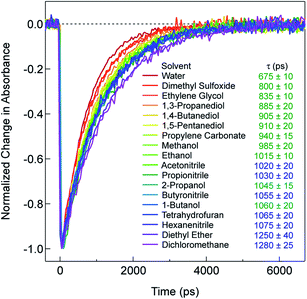
Recent research on the photophysics of Fe(II) polypyridyl complexes has focused primarily on the ultrafast relaxation dynamics that take place immediately following excitation from the 1A1 ground state to the 1MLCT state, with an eye toward their use in photovoltaic applications,32–35 molecular electronics,36 or as a platform for addressing fundamental questions about the photophysics of transition metal-based chromophores.37–42 In the case of [Fe(bpy)3]2+, a variety of experimental and theoretical studies carried out by a number of research groups around the world have succeeded in painting a reasonably detailed picture of the evolution of the electronic and geometric structure of this compound subsequent to charge transfer excitation. These studies have established that, after the initial formation of the 1MLCT Franck–Condon state, the molecule undergoes intersystem crossing (ISC) to populate the 3MLCT state in <50 fs, whereby it transiently samples the S = 1 ligand field manifold (specifically, the 3T1 and/or 3T2 states) as it relaxes to the 5T2 state.40,42 The net ΔS = 2 conversion just described is complete in <200 fs, a fact that underscores the remarkably fast rate at which transition metal complexes can undergo formally spin-forbidden processes within their non-thermalized excited state manifolds. Following vibrational cooling in the 5T2 state (∼5–10 ps) – which corresponds to the lowest energy excited state of [Fe(bpy)3]2+ – the compound undergoes non-radiative decay back to the ground state on a ∼1 ns timescale.As stated in the Introduction, while it is not uncommon for the solvent to influence the dynamics of charge transfer states, ligand field states tend to be regarded as relatively insulated from outer-sphere effects. However, the data presented in Fig. 1, which plots the kinetics for the 5T2 → 1A1 ground state recovery process in [Fe(bpy)3]2+ following 1A1 → 1MLCT excitation, clearly challenges this paradigm. The time constant for ground state recovery varies by nearly a factor of two across solvents that were selected to span a wide range of physical properties such as dielectric constant, viscosity, size, and dipole moment (Table S1†). It should be noted that this phenomenon does not appear to be restricted to [Fe(bpy)3]2+: work from our lab20,43 and others44 reveals variations in the time constant for the 5T2 → 1A1 conversion in [Fe(terpy)2]2+ (where terpy = 2,2':6′,2′′-terpyridine), ranging from ∼3 ns in water to ∼5 ns in both acetonitrile and dichloromethane. An effect was also noted by Tribollet et al.,45 where a ground state recovery time of 1.1 ± 0.1 ns for [Fe(phen)3]2+ (where phen = 1,10-phenanthroline) in acetonitrile solution differs from that published previously in aqueous solution (685 ± 30 ps).38,46 Most recently, X-ray transient absorption (TA) spectroscopy was used to study the photophysics of [Fe(dmb)3]2+ in water and acetonitrile. The data revealed not only a difference in the lifetime of the 5T2 state (830 ± 10 ps versus 1240 ± 12 ps in water and acetonitrile, respectively), but surprisingly also indicated a significant inner-sphere effect in the form of a difference in the magnitude of structural distortion along the Fe–N coordinate (ΔRHS–LS = 0.181 ± 0.003 Å in water as compared to 0.199 ± 0.003 Å in acetonitrile).47 This finding will be discussed in greater detail in the last section of the paper.
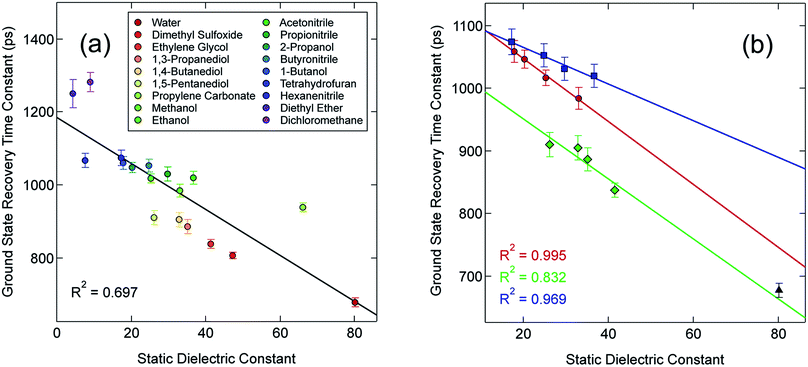
In an effort to identify possible trends linked to this solvent dependence, the observed ground state recovery lifetime was plotted against various macroscopic properties of the solvents (Fig. S11†). The strongest correlation across all of the solvent properties was found to exist between the measured time constant for the 5T2 → 1A1 relaxation process and the static dielectric constant (Fig. 2a). This correlation becomes more striking when one further subdivides the data according to solvent type, e.g., alcohols, nitriles, diols, etc. (Fig. 2b). Similar, though not as strong degrees of correlation become apparent with other solvent properties once the data are grouped in an analogous manner (Fig. S12†), suggesting that the correlation is not necessarily linked specifically to the static dielectric constant but rather to properties of the solvent that manifest themselves in certain of their macroscopic properties. It should be stressed that we are not ascribing a particular physical significance to the linear nature of the correlation, but it seems clear that the trends in ground state recovery dynamics are being influenced not just by the solvent, but by the nature of the solvent (Fig. S13†). The issue now is in identifying the underlying physical origin of this effect and what that tells us about the interplay between the intramolecular nature of the ligand field-state relaxation dynamics in this system and its surrounding environment.
Factors influencing 5T2 → 1A1 relaxation dynamics
Without a clear indication of what drives the observed solvent dependence of ground state recovery dynamics from solvent properties alone, it is important to understand the factors which contribute to the ground state recovery dynamics of these sorts of systems in general. For a six-coordinate, d6 metal complex, the 1A1 and 5T2 states are the lowest-energy term states arising from the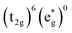 and
and 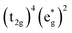 configurations, i.e., the low-spin (LS) and high-spin (HS) states, respectively; for compounds like [Fe(bpy)3]2+, the 1A1 state corresponds to the ground state. It is well-established that the HS-to-LS conversion in this class of compounds can be modeled using non-radiative decay theory.48,49 In the semi-classical limit (i.e., treating the electronic coupling quantum mechanically, but the nuclear term classically), we can employ a Marcus-type expression (eqn (1)),
configurations, i.e., the low-spin (LS) and high-spin (HS) states, respectively; for compounds like [Fe(bpy)3]2+, the 1A1 state corresponds to the ground state. It is well-established that the HS-to-LS conversion in this class of compounds can be modeled using non-radiative decay theory.48,49 In the semi-classical limit (i.e., treating the electronic coupling quantum mechanically, but the nuclear term classically), we can employ a Marcus-type expression (eqn (1)),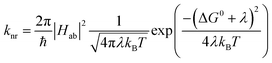 | (1) |
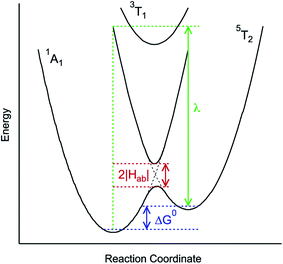 | ||
| Fig. 3 Generalized potential energy surface diagram for a low-spin d6 complex of O symmetry whose kinetics can be described by eqn (1). Electronic coupling between the S = 0 and S = 2 states is facilitated via mixing with a (thermally inaccessible) excited S = 1 state, resulting in an avoided crossing on the lower potential surface. The reorganization energy indicated corresponds to that associated with the 5T2 → 1A1 conversion. | ||
As can be seen from eqn (1), these three variables – Hab, ΔG0, and λ – are the primary factors that define the rate constant for ground state recovery. Since [Fe(bpy)3]2+ is not emissive nor does it represent a true spin-crossover complex where changes in temperature or pressure can modulate the equilibrium between the LS and HS states, we are left with three unknowns that present challenges in terms of experimentally determining their values. Our group recently published a report20 which described results from variable-temperature time-resolved ultrafast measurements on a series of Fe(II) polypyridyl complexes that indicated a value for Hab on the order of 4.5 ± 0.5 cm−1. Assuming that the second-order electronic coupling between the 1A1 and 5T2 states is not significantly influenced by the solvent environment, we can posit that the origin of the solvent-dependent kinetics observed for ground state recovery in [Fe(bpy)3]2+ is most likely associated with modulations of ΔG0 and/or λ as a result of changes in the nature of the solvent.
The electrostatic force of attraction between two charged ions, whose strength is dependent on the charge and size of the ions as well as the surrounding solvent, can be described by Coulomb's law according to eqn (2),52
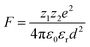 | (2) |
The ground state recovery kinetics of [Fe(bpy)3]Br2 were investigated at multiple concentrations in multiple solvents, with the expectation that any change in response to concentration in a given solvent would be suggestive of an ion pairing influence on ΔG0 and/or λ. One would also expect that, based on eqn (2), the influence and liklihood of ion pairing should increase both as the concentration of [Fe(bpy)3]2+ increases and as the static dielectric constant of the solvent decreases. For this study, the concentration of [Fe(bpy)3]Br2 was varied by an order of magnitude, from ca. 2.5 × 10−4 to 2.5 × 10−3 M, in solvents ranging in static dielectric constant from 80.1 (water) to 17.84 (1-butanol); across this range of dielectric constants, the force of attraction for ion pairing should vary by a factor of approximately 4.5. The results shown in Table 1 (and Fig. S14†) reveal that the excited state lifetimes for [Fe(bpy)3]Br2 are within error of one another for each concentration in all of the solvents tested, in stark contrast to the aforementioned observations of Hendrickson and co-workers, where a dependence of ground-state recovery on solute concentration was clearly observed.
| Ground state recovery (ps) | ||||
|---|---|---|---|---|
| Abs = 0.1 | Abs = 0.4 | Abs = 0.7 | Abs = 1.0 | |
| Water | 690 ± 10 | 675 ± 10 | 680 ± 25 | 690 ± 50 |
| Dimethyl sulfoxide | 805 ± 30 | 800 ± 10 | 790 ± 10 | 800 ± 30 |
| Methanol | 995 ± 20 | 985 ± 20 | 980 ± 25 | 975 ± 115 |
| Acetonitrile | 1020 ± 30 | 1015 ± 15 | 1015 ± 25 | 970 ± 90 |
| 1-Butanol | 1055 ± 25 | 1060 ± 20 | 1075 ± 20 | 1075 ± 60 |
The nature of the counterion – specifically its charge density – should also have an impact on the strength of any ion pairs formed in solution. Therefore, a series of salts were prepared, comprising a mixture of halides and polyatomic anions that spanned in size from chloride to the BArF4− ion (Fig. 4). Time-resolved spectroscopic measurements were carried out in acetonitrile, since it corresponded to the solvent having the lowest dielectric constant in which all of the [Fe(bpy)3]2+ salts were soluble across the same solute concentration range as described in the previous paragraph. The halide ions should be most susceptible to ion pairing, especially at higher solute concentrations, whereas the larger BArF4− ion should represent the opposite extreme due to its (relatively) low negative charge density and polarizability. As can be seen in Table 2 (and Fig. S15†), however, exchanging the counterions does not have any measurable influence on the ground state recovery lifetime.
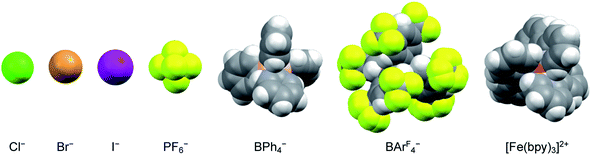 | ||
| Fig. 4 Size comparison of the various anions used as counterions for [Fe(bpy)3]2+ to yield the data listed in Table 2. The iron complex depicted here corresponds to the size of the low-spin form of the compound. | ||
| Ground state recovery (ps) | ||||
|---|---|---|---|---|
| Abs = 0.1 | Abs = 0.4 | Abs = 0.7 | Abs = 1.0 | |
| [Fe(bpy)3]Cl2 | 1015 ± 40 | 1020 ± 15 | 1005 ± 45 | 1010 ± 115 |
| [Fe(bpy)3]Br2 | 1020 ± 30 | 1015 ± 15 | 1015 ± 25 | 970 ± 90 |
| [Fe(bpy)3]I2 | 1040 ± 30 | 1015 ± 15 | 1010 ± 30 | 1045 ± 110 |
| [Fe(bpy)3](PF6)2 | 1025 ± 25 | 1020 ± 20 | 1005 ± 40 | 1020 ± 105 |
| [Fe(bpy)3](BPh4)2 | 1030 ± 40 | 1025 ± 15 | 1005 ± 30 | 1025 ± 110 |
| [Fe(bpy)3](BArF4)2 | 1045 ± 45 | 1020 ± 20 | 1030 ± 30 | 1035 ± 120 |
The insensitivity of the 5T2 → 1A1 conversion to changes in either solute concentration or the nature of the counterion does not provide definitive evidence as to the presence or absence of ion pairing in these solutions. Indeed, we consider it likely that some degree of ion pairing does exist (particularly in solvents with lower static dielectric constants), in part based on the conductivity data presented by Hendrickson and co-workers.51 What can be inferred, however, is that differences in the extent of ion pairing cannot be the underlying reason behind the solvent-dependent changes in the ground state recovery lifetime of [Fe(bpy)3]2+ illustrated in Fig. 1. In other words, if ion pairing is modulating the zero-point energy difference between the 5T2 and 1A1 states of [Fe(bpy)3]2+ under these various conditions, that modulation is too small to measurably impact the kinetics. We suspect that the effect was detected in the case of the [Fe(tren(py)3)]2+ system studied by Conti et al. because the zero-point energy difference in that system is substantially smaller than the estimated value of ΔG0 for [Fe(bpy)3]2+ (e.g., a 100 cm−1 perturbation to a 500 cm−1 zero-point energy difference will be far more impactful than that same perturbation imposed on a 5000 cm−1 energy gap).
It has already been mentioned that the conversion from a HS state to a LS state of an Fe(II) complex is accompanied by large geometric changes in the complex itself as a result of depopulating antibonding orbitals in the HS state; reductions in the metal–ligand bond length on the order of 0.2 Å55–58 and an overall volume contraction (ΔV) of 20–25 cm3 mol−1 are not uncommon.59–63 The energetics associated with these sorts of changes comprise the inner-sphere contributions to λtot. Typically, the outer-sphere effects are expected to be decoupled from the inner-sphere changes in the sense that, while the surrounding environment will respond to changes occurring as a result of the reaction in question, the specific structural changes that define λin are independent of this response.64
A relatively rare exception to this paradigm is actually associated with the Fe(II)-tris-polypyridyl platform we are considering herein. A study by Liu et al. detailing time-resolved X-ray spectroscopic measurements on [Fe(dmb)3]2+ in acetonitrile and water was previously mentioned.47 The application of high-resolution time-resolved X-ray spectroscopy allowed for an examination of the evolution of the spin, electronic, and nuclear degrees of freedom of this complex subsequent to photoexcitation, making it possible to detect structural changes within the iron complex due to solvent–solute interactions. The data revealed a difference in the structural change associated with the primary coordination sphere of the Fe(II) center upon conversion from the HS state to the LS state between the two solvents that was outside of experimental error. Specifically, the change in the Fe–N bond length, ΔRHS–LS, was 0.018 Å smaller in water as compared to acetonitrile. Since the Fe–N bond lengths for the compound in the two solvents were experimentally indistinguishable from one another in the ground state, this means that the Fe–N bond for the HS form was longer in the acetonitrile solution than that measured in water. Considering how this goes against conventional thinking regarding the influence of solvent on inner-sphere effects, we will need to revisit this topic later in the discussion.
This specific example notwithstanding, as a first approximation, we can still view the solvent response as passive with respect to the inner-sphere changes accompanying the 5T2 → 1A1 conversion. Solvation, which encompasses interactions between the solute and solvent that stabilize the solvated species, is largely electrostatic in nature and can include interactions such as hydrogen bonding, van der Waals forces, etc. The Gibbs free energy of solvation (ΔGsolv) can be estimated with the Born equation (eqn (3)),65
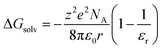 | (3) |
| ΔΔGsolv = ΔGproductsolv − ΔGreactantsolv | (4) |
Although the solvation model based on density (SMD)66,67 represents a generally accepted option for computing solvation energy, no correlation between the ground state recovery lifetime and ΔΔGsolv was observed (Fig. S17†). As a second option, we employed the conductor-like polarizable continuum model (CPCM)29,30 with solvent properties (from Table S1†) added to the input file for each solvent individually. As predicted by eqn (3), the estimated solvation energies are indeed more negative for the LS state than the HS state (Table S4†); no significant correlation with ΔΔGsolv is immediately obvious between the estimated differential solvation energy and the time constant for ground state recovery, that is, until the data are again separated into solvent families in a manner suggested by Fig. 2b (see Fig. S19b†). The similarity is especially striking in Fig. 5, where the calculated values for ΔΔGsolv are plotted with respect to the static dielectric constant of the solvent (Fig. 5a) and the experimentally measured time constants for 5T2 → 1A1 conversion (Fig. 5b). The data clearly reveal a correlation between ΔΔGsolv and the kinetics of ground state recovery (Fig. 5b): as ΔΔGsolv becomes more negative, the rate constant for the 5T2 → 1A1 relaxation process (i.e., τobs−1) increases.
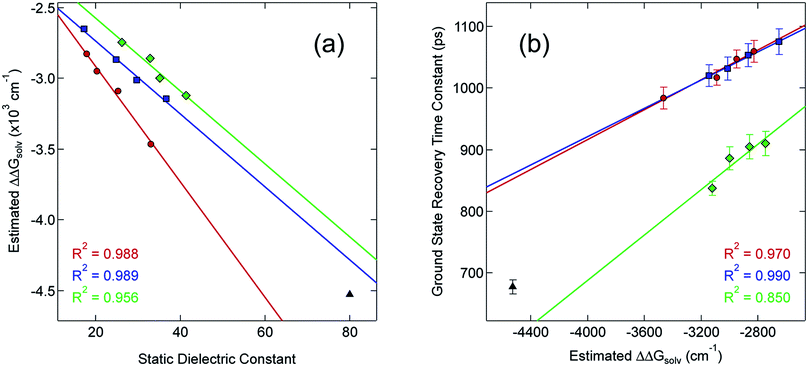 | ||
| Fig. 5 Correlating the estimated change in ΔGsolv (ΔΔGsolv, eqn (4)) between the HS and LS states of [Fe(bpy)3]2+ with (a) the static dielectric constant and (b) the time constants for ground state recovery in alcohol-based (red circles), nitrile-based (blue squares), and diol-based (green diamonds) solutions. The result for water (black triangle) is listed in both, but is not included in any of the linear fits. | ||
Given the correlations highlighted in Fig. 5, we posited that the change in molecular volume concomitant with the HS-to-LS conversion (ΔV) could be manifesting as an outer-sphere contribution to the overall reorganization energy due to changes in the energetics of solvent–solute and/or solvent–solvent interactions as the system relaxes back to the ground state. One way to probe this would be to examine the dynamics of ground state recovery across a homologous series of compounds in which this volume change is varied. If the observations we have documented originate from a given solvent's response to ΔV between the HS and LS states, then studying Fe(II) complexes with differing molecular volume changes should result in different slopes for ΔΔGsolv when compared to static dielectric constant. Therefore, we prepared three additional complexes to test this hypothesis: [Fe(dmb)3]Br2, [Fe(5,5′-dmb)3]Br2, and [Fe(dtbbpy)3]Br2 (Chart 1). The molecular volumes of the ground states of these complexes (as calculated68 from their crystal structures28) rank as follows: [Fe(bpy)3]2+ (404.90 Å3) < [Fe(5,5′-dmb)3]2+ (489.54 Å3) ∼ [Fe(dmb)3]2+ (489.61 Å3) < [Fe(dtbbpy)3]2+ (748.06 Å3). The change in the Fe–N bond length between the HS and LS states is expected to be roughly the same for all four of these complexes, so an increase in the molecular volume of the ground state will translate into a larger value for ΔV associated with ground state recovery.
Time-resolved absorption data for ground state recovery were acquired for all four of these compounds; given that the data presented in Fig. 2 clearly show strong correlations within particular families of solvents, for this study we chose to focus on the alcohol series based on the larger number of solvents available and the (relatively) broad range in static dielectric constants that can be accessed. The measured time constants are listed in Table 3. Upon inspection, we note that there is a significant difference in the lifetime of the 5T2 state for [Fe(dmb)3]2+ relative to [Fe(bpy)3]2+ in all of the solvents studied. The difference is more or less uniform across the solvent series, suggesting that this is an intrinsic feature of the compound rather than a solvent effect. Previous work from our group has shown that there is, in fact, a small shift in the zero-point energy difference between the LS and HS states upon the introduction of methyl groups at the para positions of the pyridyl rings.20 Specifically, those variable-temperature time-resolved absorption studies revealed that the dmb ligand presents a slightly smaller ligand field to Fe(II) than bpy, leading to a reduction in the 5T2/1A1 energy gap and a longer excited state lifetime, in accordance with the model depicted in Fig. 3. The weaker ligand field is due to increased π donation from the more electron-rich dmb ligand, an effect that is largely absent for [Fe(5,5′-dmb)3]2+ due to the nodes in the π system of bipyridine at the meta positions of the rings (hence, the similarity in lifetimes between [Fe(bpy)3]2+ and [Fe(5,5′-dmb)3]2+).69 Spectroscopic studies of Co(III) analogs of these compounds have since confirmed these conclusions,70 again reinforcing the notion that these small effects are ligand field in nature as opposed to solvent-driven.
| Ground state recovery (ps) | ||||
|---|---|---|---|---|
| [Fe(bpy)3]Br2 | [Fe(dmb)3]Br2 | [Fe(5,5′-dmb)3]Br2 | [Fe(dtbbpy)3]Br2 | |
| a [Fe(dtbbpy)3]Br2 is soluble, but not stable in water. | ||||
| Water | 675 ± 10 | 860 ± 10 | 635 ± 10 | N/Aa |
| Methanol | 985 ± 20 | 1210 ± 10 | 1010 ± 10 | 1035 ± 10 |
| Acetonitrile | 1015 ± 15 | 1285 ± 10 | 1040 ± 10 | 1055 ± 10 |
| Ethanol | 1015 ± 10 | 1210 ± 10 | 1045 ± 10 | 1125 ± 10 |
| 2-Propanol | 1045 ± 15 | 1225 ± 10 | 1065 ± 10 | 1235 ± 10 |
| 1-Butanol | 1060 ± 20 | 1285 ± 10 | 1130 ± 10 | 1300 ± 10 |
Given this small electronic perturbation, the effect of solvent on the ground state recovery dynamics of this system can be more clearly illustrated by normalizing the time constants for all of the Fe(II) compounds to a single value in one of the solvents, thereby allowing trends arising from changes in the solvent to become more evident: this is depicted in Fig. 6 (with the original data from Table 3 provided in the inset). While small differences in the effective slope can be seen across [Fe(bpy)3]2+ and the methylated analogs, a much more dramatic effect is visible for [Fe(dtbbpy)3]2+, which is, of course, the compound possessing a discontinuously larger change in molecular volume relative to the other three compounds in the series.
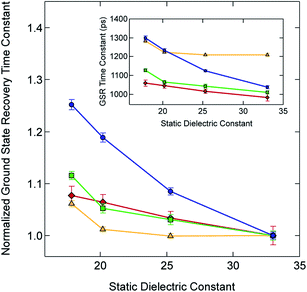 | ||
| Fig. 6 Time constants for ground state recovery (i.e., 5T2 → 1A1 conversion) for [Fe(bpy)3]Br2 (red diamonds), [Fe(dmb)3]Br2 (yellow triangles), [Fe(5,5′-dmb)3]Br2 (green squares) and [Fe(dtbbpy)3]Br2 (blue circles) in alcohol-based solutions, normalized to each complex's ground state recovery lifetime in methanol. The solid line between each data point is not a fit but is merely present to guide the eye. The inset shows the raw data listed in Table 3. See text for further details. | ||
While the data plotted in Fig. 6 are wholly consistent with our hypothesis linking changes in molecular volume to outer-sphere contributions of the reorganization energy, there exists the possibility that the difference in the change in molecular volume may alter the extent of solvent access to the primary coordination sphere. If this were indeed the case, then the solvent effect would be more properly considered to contribute to inner-sphere as opposed to being purely outer-sphere in nature. Although we have not acquired time-resolved X-ray data on these complexes (which would allow us to probe this question in a manner similar to Liu et al. for solutions of [Fe(bpy)3]2+),47 we can use a computational approach to gain a better sense of the degree to which exposure of the Fe(II) metal center changes between the HS and LS forms of these compounds. This should allow us to assess whether differences in direct access to the metal by the solvent may be influencing our observations.
Fig. 7 presents a visualization of the volume occupied by the coordinated bipyridine ligands for the DFT-optimized structures of [Fe(bpy)3]2+ in its LS and HS forms using the Solid-G approach described by Guzei and Wendt.71 This method essentially allows one to assess the degree of total coverage imposed by the ligands, which, in turn, gives an indication of the extent of metal-ion accessibility. It can be seen by inspection of Fig. 7 that there is indeed a difference in this accessibility between the LS and HS forms of [Fe(bpy)3]2+. If we look at the actual magnitude of the so-called “G” value – which is a more quantitative measure of the shielding of the metal center provided by the ligands – in methanol, for example, there is a decrease from ∼96% in the 1A1 state to ∼85% in the 5T2 state (Table 4). In other words, there is an 11% difference in the degree of exposed metal between the two spin states.
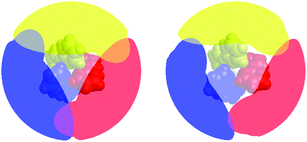 | ||
| Fig. 7 Visualization of the extent of ligand coverage of the coordination sphere of [Fe(bpy)3]2+ in its low-spin (left) and high-spin (right) configurations. | ||
| Fe–N (Å) | N–Fe–N (°) | G value (%) | |
|---|---|---|---|
| a Using optimized structures from DFT calculations with CPCM to represent the solvent. | |||
| LS state in methanol | 2.00 | 144.33 | 96.16 |
| HS state in methanol | 2.20 | 130.43 | 85.34 |
| LS state in ethanol | 2.00 | 144.10 | 95.95 |
| HS state in ethanol | 2.20 | 130.29 | 85.29 |
| LS state in 2-propanol | 2.01 | 143.92 | 95.96 |
| HS state in 2-propanol | 2.20 | 130.11 | 85.17 |
| LS state in 1-butanol | 2.01 | 143.83 | 95.91 |
| HS state in 1-butanol | 2.21 | 130.02 | 85.14 |
What is more striking – and more relevant to the present discussion – is the fact that this change in metal accessibility is essentially invariant not only for [Fe(bpy)3]2+ across the range of solvents we examined (Table 4), but also for all of the molecules examined in this study (Table 5). This appears to be due in large part to the fact that the substituents merely extend the ligand structure outward rather than blocking cavities that could provide direct access to the metal center (hence the similarity in G values in all the alkyl-substituted complexes as compared to [Fe(bpy)3]2+). Since there is no significant change in the percentage of the metal center left unshielded across these complexes, any direct interactions between solvent molecules and the metal center, if they exist, are unlikely to be the origin of the trends illustrated in Fig. 6.
| Fe–N (Å) | N–Fe–N (°) | G value (%) | |
|---|---|---|---|
| a Using optimized structures from DFT calculations in vacuum, i.e., no solvent continuum applied. | |||
| [Fe(bpy)3]2+ (LS) | 2.03 | 142.29 | 95.01 |
| [Fe(bpy)3]2+ (HS) | 2.23 | 128.57 | 84.16 |
| [Fe(dmb)3]2+ (LS) | 2.02 | 142.25 | 95.09 |
| [Fe(dmb)3]2+ (HS) | 2.23 | 128.56 | 84.16 |
| [Fe(5,5′-dmb)3]2+ (LS) | 2.03 | 142.39 | 94.98 |
| [Fe(5,5′-dmb)3]2+ (HS) | 2.23 | 128.61 | 84.20 |
| [Fe(dtbbpy)3]2+ (LS) | 2.02 | 142.41 | 95.20 |
| [Fe(dtbbpy)3]2+ (HS) | 2.23 | 128.55 | 84.16 |
Based on all of the results we have presented, we believe that the most likely origin of the solvent effect reflected in the data shown in Fig. 1 is an outer-sphere contribution to the reorganization energy associated with the 5T2 → 1A1 conversion. Specifically, we suggest that the large change in molecular volume that accompanies ground-state recovery in this class of chromophores is forcing a change in the energetics of solvent-solvent and/or solvent-solute interactions sufficient to modulate the kinetics associated with this (largely intramolecular) process.
Revisiting the dynamics of [Fe(bpy)3]2+ in aqueous solution
As a final point, we return briefly to a discussion of the ground state recovery dynamics of [Fe(bpy)3]2+ in water. The results we have described paint a consistent picture wherein changes in outer-sphere reorganization energy contributions from the solvent can explain the variation in the time constant for ground state recovery in [Fe(bpy)3]2+ depicted in Fig. 1 with one glaring exception: water. We are not the first to identify that water appears to interact with and/or influence the dynamics of this system in a manner distinct from all other solvents. In 2010, Lawson Daku and Hauser published an ab initio molecular dynamics study of [Fe(bpy)3]2+ in aqueous solution with the goal of exploring the influence of solvent on its excited state dynamics.72 An analysis of the radial distribution functions (g(r)) associated with the oxygen and hydrogen atoms of water in relation to their distance from the metal center suggested that water molecules intercalate between the bpy ligands. The depiction of the HS state in Fig. 7 clearly shows that, although the metal center is significantly shielded from its environment by the bipyridyl ligands, one can easily imagine a small molecule such as water wedging itself into and/or out of the compound's primary coordination sphere via the small channels evident in this representation.The calculations of Lawson Daku and Hauser actually suggest that water molecules are expelled upon conversion from the LS state to the HS state, a somewhat counterintuitive result given the increased metal accessibility evident in the right panel of Fig. 7. Computational work by Das et al. came to the same conclusion as Lawson Daku and Hauser, although they suggest that the effect is electronic in origin as opposed to structural.73 The time-resolved X-ray absorption, emission, and diffuse scattering studies previously alluded to have since supported the idea of water molecules being expelled, as data could only be fit when incorporating an increase in the solvent density of the bulk solvent.74–76 A more recent study by Lawson Daku with improved resolution now suggests that more solvent molecules can be found in the HS state than the LS state,77 which would be qualitatively more consistent with chemical intuition based on inspection of Fig. 7. While the details surrounding this issue still appear to be a somewhat open question, there is a broad consensus that there are specific solvent–solute interactions between water and [Fe(bpy)3]2+ that are perturbing the primary coordination sphere of the complex, which, in turn, would be expected to influence the excited state dynamics of the compound in a manner quite distinct from that of other solvent systems.
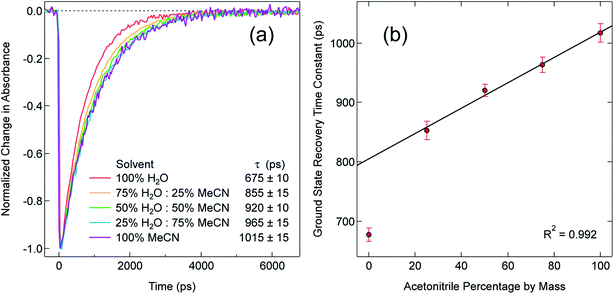
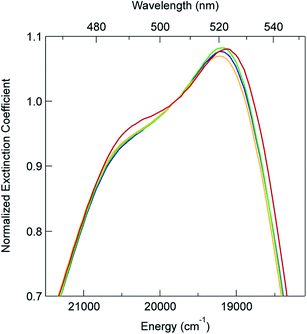
In order to explore this notion of water as something of an outlier in the context of our study, we carried out a series of dilution studies involving mixtures of water and acetonitrile to see what effect various (relative) concentrations of water would have on the ground state recovery dynamics of [Fe(bpy)3]2+. The results of this study are shown in Fig. 8. Starting with pure acetonitrile, successive addition of water to the solvent mixture results in a monotonic decrease in the ground state recovery lifetime i.e., an increase in the rate constant for 5T2 → 1A1 conversion. These additions of water systematically increase the overall static dielectric constant of the solvent (Table S6†),78 so this correlation is wholly consistent with the data and analyses that we have presented herein. An obvious discontinuity in this behavior occurs when we move to a purely aqueous environment, a strong indication that water has a unique effect on the photophysics of this system. This notion is further supported when one examines the ground state absorption spectrum of [Fe(bpy)3]2+ across the alcohol solvent series (Fig. 9). There are small variations in the band position and band shape of the 1A1 → 1MLCT absorption envelope for these solvents, which is to be expected given that charge transfer features are well-known to be sensitive to changes in the static dielectric constant of the solvent. What is striking, however, is the difference in the absorption profiles between the aqueous solution and the other solvents represented in Fig. 9. Specifically, the spectrum of [Fe(bpy)3]2+ in aqueous solution is characterized by a pronounced enhancement of what was a mild shoulder at 490 nm in the alcohol-based solutions, while at the same time exhibiting a somewhat larger shift of the main absorption feature to lower energy. We suggest that this change in the vibronic structure is an indication of a solvent-specific interaction between water and [Fe(bpy)3]2+, wherein the water molecules are interacting directly with the metal center and/or primary ligand environment of the complex in a manner wholly distinct from other solvents. In this regard, we believe that the influence of water on the excited state dynamics of [Fe(bpy)3]2+ is correspondingly unique, manifesting itself in both inner- and outer-sphere contributions to the system as opposed to the purely outer-sphere effects that we believe give rise to the effects we have documented herein for other solvent systems.
Concluding comments
Generally speaking, the dynamics of interconversion among ligand field excited states are expected to be largely insensitive to changes in the solvent environment due to the fact that, for a coordinatively saturated metal complex, the ligands largely insulate the metal ion from the surrounding environment. It was for this reason that the observation of a nearly 2-fold change in the dynamics for ground state recovery in [Fe(bpy)3]2+, while modest in an absolute sense, was nevertheless unexpected. An empirical correlation was found between the measured time constant for 5T2 → 1A1 relaxation and the static dielectric constant, a correlation that became significantly more pronounced once the solvents were grouped according to their type, e.g., alcohols versus diols versus nitriles, etc. Various origins for this observation were examined, including ion pairing perturbations to the zero-point energy difference between the two electronic states as well as direct solvent interaction with the metal center. Ultimately, it was concluded that the rate for this process was likely being influenced by changes to outer-sphere contributions from the solvent to the overall reorganization energy of the relaxation process in response to the large geometric change that characterizes the transition from a HS Fe(II) compound to its LS form. In effect, the perturbations in these interactions induced by the intramolecular dynamics of the chromophore were sufficient to manifest as a change in the kinetics of ground state recovery.Although our data and analysis yield a self-consistent picture, the conclusions we have presented are necessarily qualitative in nature owing to the fact that we have represented the solvent throughout as a dielectric continuum. We believe that the correlation between excited state dynamics and solvent dielectric constant that has been documented is simply reflecting much more complex changes associated with the solvent concomitant with the intramolecular dynamics of the chromophore. A proper assessment of these changes – which would provide tremendous insight into the details of how solvent couples to this sort of process – would require a molecular-level description of the solvent interacting with these complexes. Such an analysis is beyond the scope of the present study. That said, we believe that the driver for these outer-sphere effects is the interconfigurational nature of the HS-to-LS conversion. Although the structural changes that define a HS-to-LS transition in an octahedral d6 complex are among the largest one will come across in the transition block, the effect should still be manifest in a fairly wide range of chemical systems for which excited state processes involve a redistribution of electrons among σ- and π-based bonding/antibonding orbitals. The potential generality of this phenomenon suggests that a more detailed examination of these processes is certainly worth pursuing.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Dr Allison M. Brown for initial work on this project, Dr Amanda L. Smeigh for the preparation of the [Fe(bpy)3]Cl2 sample used in this study, and Sara L. Adelman and Jonathon T. Yarranton for mass spectral analyses. Geometry optimizations were completed after receiving valuable input from Dr Daniel Ashley and Professor Elena Jakubikova of North Carolina State University. The authors would also like to thank Professor Mark Maroncelli of The Pennsylvania State University for fruitful discussions. This research was supported by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Science, Office of Science, U.S. Department of Energy under Grant No. DE-FG02-01ER15282. J. N. M. was also funded by the U.S. Department of Education Graduate Assistance in Areas of National Need fellowship program at Michigan State University (grant no. P200A140215).Notes and references
- Solvents and solvent effects in organic chemistry, ed. C. Reichardt and T. Welton, Wiley-VCH, Weinheim, 4th edn, 2011 Search PubMed.
- M. F. Nicol, Appl. Spectrosc. Rev., 1974, 8, 183–227 CrossRef CAS.
- C. Reichardt, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS.
- J. Emsley and N. J. Freeman, J. Mol. Struct., 1987, 161, 193–204 CrossRef CAS.
- A. Balasubramanian and C. N. R. Rao, Spectrochim. Acta, 1962, 18, 1337–1352 Search PubMed.
- Y. Chen and B. A. Wallace, Biophys. Chem., 1997, 65, 65–74 CrossRef CAS PubMed.
- S. Nath, H. Pal and A. V. Sapre, Chem. Phys. Lett., 2002, 360, 422–428 CrossRef CAS.
- J. R. Mannekutla, B. G. Mulimani and S. R. Inamdar, Spectrochim. Acta, Part A, 2008, 69, 419–426 CrossRef CAS PubMed.
- R. M. Stratt and M. Maroncelli, J. Phys. Chem., 1996, 100, 12981–12996 CrossRef CAS.
- P. Chen and T. J. Meyer, Chem. Rev., 1998, 98, 1439–1478 CrossRef CAS PubMed.
- S. A. Passino, Y. Nagasawa and G. R. Fleming, J. Chem. Phys., 1997, 107, 6094–6108 CrossRef CAS.
- A. T. Yeh, C. V. Shank and J. K. McCusker, Science, 2000, 289, 935–938 CrossRef CAS PubMed.
- E. A. Juban and J. K. McCusker, J. Am. Chem. Soc., 2005, 127, 6857–6865 CrossRef CAS PubMed.
- J. F. Endicott, R. Tamilarasan and R. B. Lessard, Chem. Phys. Lett., 1984, 112, 381–386 CrossRef CAS.
- J. K. McCusker, Science, 2019, 363, 484–488 CrossRef CAS PubMed.
- O. S. Wenger, Chem.–Eur. J., 2019, 25, 6043–6052 CrossRef CAS PubMed.
- C. Förster and K. Heinze, Chem. Soc. Rev., 2020, 49, 1057–1070 RSC.
- J. K. McCusker, A. L. Rheingold and D. N. Hendrickson, Inorg. Chem., 1996, 35, 2100–2112 CrossRef CAS.
- Y. Yamamoto, E. Sumimura, K. Miyoshi and T. Tominaga, Anal. Chim. Acta, 1973, 64, 225–233 CrossRef CAS.
- M. C. Carey, S. L. Adelman and J. K. McCusker, Chem. Sci., 2019, 10, 134–144 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingfort CT, 2013 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- J. Ho and M. Z. Ertem, J. Phys. Chem. B, 2016, 120, 1319–1329 CrossRef CAS PubMed.
- S. Ferrere and B. A. Gregg, J. Am. Chem. Soc., 1998, 120, 843–844 CrossRef CAS.
- S. Ferrere, Inorg. Chim. Acta, 2002, 329, 79–92 CrossRef CAS.
- C. R. Tichnell, J. N. Miller, C. Liu, S. Mukherjee, E. Jakubikova and J. K. McCusker, J. Phys. Chem. C, 2020, 124, 1794–1811 CrossRef CAS.
- For a general resource on a range of related topics, see: Molecular Devices for Solar Energy Conversion and Storage, ed. H. Tian, G. Boschloo, and A. Hagfeldt, Springer Nature, Singapore, 2018 Search PubMed.
- A. Hauser, Top. Curr. Chem., 2004, 234, 155–198 CrossRef CAS.
- C. Creutz, M. Chou, T. L. Netzel, M. Okumura and N. Sutin, J. Am. Chem. Soc., 1980, 102, 1309–1319 CrossRef CAS.
- J. K. McCusker, K. N. Walda, R. C. Dunn, J. D. Simon, D. Magde and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 298–307 CrossRef CAS.
- J. E. Monat and J. K. McCusker, J. Am. Chem. Soc., 2000, 122, 4092–4097 CrossRef CAS.
- W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartstock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. N. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. Gaffney, Nature, 2014, 509, 345–348 CrossRef CAS PubMed.
- C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Chem.–Eur. J., 2013, 19, 17541–17551 CrossRef CAS PubMed.
- G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633 CrossRef PubMed.
- A. M. Brown, PhD dissertation, Michigan State University, 2011.
- S. E. Canton, X. Zhang, L. M. Lawson Daku, A. L. Smeigh, J. Zhang, Y. Liu, C.-J. Wallentin, K. Attenkofer, G. Jennings, C. A. Kurtz, D. Gosztola, K. Wärnmark, A. Hauser and V. Sundström, J. Phys. Chem. C, 2014, 118, 4536–4545 CrossRef CAS.
- J. Tribollet, G. Galle, G. Jonusauskas, D. Deldicque, M. Tondusson, J. F. Letard and E. Freysz, Chem. Phys. Lett., 2011, 513, 42–47 CrossRef CAS.
- It should be noted that, although the data presented in ref. 38 resulted from excitation at shorter wavelengths than those used in the present study, ground-state recovery kinetics in this class of chromophores have been found to be independent of excitation wavelength.
- C. Liu, J. Zhang, L. M. Lawson Daku, D. Gosztola, S. E. Canton and X. Zhang, J. Am. Chem. Soc., 2017, 139, 17518–17524 CrossRef CAS PubMed.
- E. Buhks, G. Navon, M. Bixon and J. Jortner, J. Am. Chem. Soc., 1980, 102, 2918–2923 CrossRef CAS.
- N. Sutin, Acc. Chem. Res., 1982, 15, 275–282 CrossRef CAS.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168 CrossRef CAS.
- A. J. Conti, C.-L. Xie and D. N. Hendrickson, J. Am. Chem. Soc., 1989, 111, 1171–1180 CrossRef CAS.
- M. R. Wright, in An Introduction to Aqueous Electrolyte Solutions, John Wiley & Sons Ltd, West Sussex, 2007, pp. 349–420 Search PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- M. Khalil, M. A. Marcus, A. L. Smeigh, J. K. McCusker, H. H. W. Chong and R. W. Schoenlein, J. Phys. Chem. A, 2006, 110, 38–44 CrossRef CAS PubMed.
- W. Gawelda, V.-T. Pham, M. Benfatto, Y. Zaushitsyn, M. Kaiser, D. Grolimund, S. L. Johnson, R. Abela, A. Hauser, C. Bressler and M. Chergui, Phys. Rev. Lett., 2007, 98, 057401 CrossRef PubMed.
- C. Bressler, C. Milne, V.-T. Pham, A. ElNahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492 CrossRef CAS PubMed.
- A. Britz, W. Gawelda, T. A. Assefa, L. L. Jamula, J. T. Yarranton, A. Galler, D. Khakhulin, M. Diez, M. Harder, G. Doumy, A. M. March, É. Bajnóczi, Z. Németh, M. Pápai, E. Rozsályi, D. S. Szemes, H. Cho, S. Mukherjee, C. Liu, T. K. Kim, R. W. Schoenlein, S. H. Southworth, L. Young, E. Jakubikova, N. Huse, G. Vankó, C. Bressler and J. K. McCusker, Inorg. Chem., 2019, 58, 9341–9350 CrossRef CAS PubMed.
- J. J. McGarvey, I. Lawthers, K. Heremans and H. Toftlund, J. Chem. Soc., Chem. Commun., 1984, 1575–1576 RSC.
- E. König, Struct. Bonding, 1991, 76, 51–152 CrossRef.
- P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427 RSC.
- A. Hauser, C. Enachescu, M. Lawson Daku, A. Vargas and N. Amstutz, Coord. Chem. Rev., 2006, 250, 1642–1652 CrossRef CAS.
- For a good general reference, see: P. Gütlich and H. Goodwin, Spin Crossover in Transition Metal Compounds I, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, vol. 233 Search PubMed.
- Cases where separation of inner- and outer-sphere contributions cannot be cleanly separated do occur in certain systems, e.g., reactions involving solvolysis.
- M. Born, Zeitschrift für Phys., 1920, 1, 45–48 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- The SMD model was applied under default conditions, without manually entering any solvent parameters, and only solvents already incorporated in Gaussian 09 were tested.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science, Sausalito, 2006 Search PubMed.
- Co(III) analogs were studied as isoelectronic surrogates for Fe(II) complexes, where the blue-shift of the CT absorptions leave the LF transitions relatively unobscured (J. Y. Yarranton and J. K. McCusker, manuscript in preparation).
- I. A. Guzei and M. Wendt, Dalton Trans., 2006, 3991–3999 RSC.
- L. M. Lawson Daku and A. Hauser, J. Phys. Chem. Lett., 2010, 1, 1830–1835 CrossRef CAS.
- A. K. Das, R. V. Solomon, F. Hofmann and M. Meuwly, J. Phys. Chem. B, 2016, 120, 206–216 CrossRef CAS PubMed.
- K. Haldrup, G. Vankó, W. Gawelda, A. Galler, G. Doumy, A. M. March, E. P. Kanter, A. Bordage, A. Dohn, T. B. van Driel, K. S. Kjær, H. T. Lemke, S. E. Canton, J. Uhlig, V. Sundström, L. Young, S. H. Southworth, M. M. Nielsen and C. Bressler, J. Phys. Chem. A, 2012, 116, 9878–9887 CrossRef CAS PubMed.
- C. Bressler, W. Gawelda, A. Galler, M. M. Nielsen, V. Sundström, G. Doumy, A. M. March, S. H. Southworth, L. Young and G. Vankó, Faraday Discuss., 2014, 171, 169–178 RSC.
- K. Haldrup, W. Gawelda, R. Abela, R. Alonso-Mori, U. Bergmann, A. Bordage, M. Cammarata, S. E. Canton, A. O. Dohn, T. B. van Driel, D. M. Fritz, A. Galler, P. Glatzel, T. Harlang, K. S. Kjær, H. T. Lemke, K. B. Møller, Z. Németh, M. Pápai, N. Sas, J. Uhlig, D. Zhu, G. Vankó, V. Sundström, M. M. Nielsen and C. Bressler, J. Phys. Chem. B, 2016, 120, 1158–1168 CrossRef CAS PubMed.
- L. M. Lawson Daku, Phys. Chem. Chem. Phys., 2018, 20, 6236–6253 RSC.
- L. G. Gagliardi, C. B. Castells, C. Ràfols, M. Rosés and E. Bosch, J. Chem. Eng. Data, 2007, 52, 1103–1107 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01506g |
| This journal is © The Royal Society of Chemistry 2020 |