A chemical map of NaSICON electrode materials for sodium-ion batteries†
Baltej
Singh‡
a,
Ziliang
Wang‡
a,
Sunkyu
Park
bcd,
Gopalakrishnan Sai
Gautam
 e,
Jean-Noël
Chotard
bdg,
Laurence
Croguennec
e,
Jean-Noël
Chotard
bdg,
Laurence
Croguennec
 cdf,
Dany
Carlier
cdf,
Anthony K.
Cheetham
cdf,
Dany
Carlier
cdf,
Anthony K.
Cheetham
 ag,
Christian
Masquelier
ag,
Christian
Masquelier
 bdf and
Pieremanuele
Canepa
bdf and
Pieremanuele
Canepa
 *ah
*ah
aDepartment of Materials Science and Engineering, National University of Singapore, Singapore 117575, Singapore. E-mail: pcanepa@nus.edu.sg
bLaboratoire de Réactivité et de Chimie des Solides (LRCS), CNRS UMR 7314, Université de Picardie Jules Verne, 80039 Amiens Cedex, France. E-mail: christian.masquelier@u-picardie.fr
cCNRS, Univ. Bordeaux, Bordeaux INP, ICMCB, UMR CNRS 5026, F-33600, Pessac, France
dRS2E, Réseau Français sur le Stockage Electrochimique de l'Energie, FR CNRS 3459, F-80039 Amiens Cedex 1, France
eDepartment of Materials Engineering, Indian Institute of Science, Bengaluru, 560012, Karnataka, India
fALISTORE-ERI European Research Institute, FR CNRS 3104, Amiens, F-80039 Cedex 1, France
gMaterials Department and Materials Research Laboratory, University of California, Santa Barbara, California 93106, USA
hChemical and Biomolecular Engineering, National University of Singapore, 4 Engineering Drive 4, Singapore 117585
First published on 23rd November 2020
Abstract
Na-ion batteries are promising devices for smart grids and electric vehicles due to the cost effectiveness arising from the overall abundance of sodium (Na) and its even geographical distribution. Among other factors, the energy density of Na-ion batteries is limited by the cathode electrode chemistry. NaSICON-based electrode materials are known for their wide range of electrochemical potentials, high ionic conductivity, and most importantly their structural and thermal stabilities. Using first-principles calculations, we chart the chemical space of 3d transition metal-based NaSICON phosphates with the formula NaxMM′(PO4)3 (with M and M′ = Ti, V, Cr, Mn, Fe, Co and Ni) to analyze their thermodynamic stabilities and the intercalation voltages for Na+ ions. Specifically, we compute the Na insertion voltages and related properties of 28 distinct NaSICON compositions. We investigate the thermodynamic stability of Na-intercalation in previously unreported NaxMn2(PO4)3 and NaxVCo(PO4)3. The calculated quaternary phase diagrams of the Na–P–O–Co and Na–P–O–Ni chemical systems explain the origin of the suspected instability of Ni and Co-based NaSICON compositions. From our analysis, we are also able to rationalize anomalies in previously reported experimental data in this diverse and important chemical space.
1. Introduction
Developing new battery systems capable of storing increasing quantities of energy poses extraordinary scientific and economic challenges. Lithium (Li)-ion batteries power the world's portable devices, such as mobile phones, cameras, laptops, etc., but the supply chains of Li and the required transition metals may soon be at risk due to geopolitical considerations.1,2 Sodium (Na) appears to be a viable alternative to Li for battery applications due to its earth abundance, as well as the possibility of harvesting it directly from sea water. With Na being ∼50 times more affordable compared to Li, Na-ion batteries (NIBs) are being explored by researchers worldwide, including a number of commercialization attempts.3–8 In addition, inexpensive stainless-steel current collectors are typically used in NIBs instead of the expensive copper ones found in Li-ion cells.Cathode materials factor prominently in the overall energy density stored by NIBs, and the optimization of electrode chemistries to provide high intercalation voltages and gravimetric/volumetric capacities remains a crucial aspect in the design of competitive NIBs. In theory, transition metal layered oxide-based cathode materials for NIBs would offer the largest theoretical energy densities.5–7,9,10 However, the dominant two dimensional character of their structures strongly affects the longevity of the cathode material, with the electrochemical cell exhibiting a shorter-than-desired cycle life.6,7,10–15 Promising alternatives to layered oxides are polyanion-based cathode materials.16 Polyanion electrode materials leverage a combination of multivalent cations (e.g., P5+, Si4+ and S6+) and anions (mostly O2−) arranging into phosphate, silicate and sulfate (PO43−, SiO44− and SO42−), which are thermodynamically stable by virtue of the strong binding energy of their polyanionic covalent bonds.17–19
An important class of phosphate electrodes discovered by Hong and Goodenough is the Natrium Super Ionic CONductors (NaSICONs),20,21 with the formula NaxMM′(XO4)3, where M and M′ are metals and X = Si, P and/or S. NaSICON electrode materials and electrolytes typically display significant Na+-mobility.22 The NaSICON framework is important for the development of new NIB materials,17,22–29 since its structural tunability enables the exploration of a vast chemical space, which greatly diversifies the potential, electrochemical properties and related structural features. In theory, a charged MM′(PO4)3 NaSICON framework with redox-active transition metals M and M′ would allow the intercalation of up to 4 Na+ ions,9 which make these materials promising in terms of energy density.30 Notwithstanding the challenges of working with carbon-based anodes in NIBs,9,31–33 one could benefit from the presence of 4 Na+ ions in NaSICONs, e.g., Na4MnIIVIII(PO4)3.34,35 However, the reversible extraction/intercalation of 4 Na+ ions is yet to be reported in NaSICON frameworks.
As an example of a NaSICON cathode electrode, Na3VIIIVIII(PO4)3 (NVP) can reversibly exchange two electrons (via the activation of the VIV/VIII redox couple) delivering Na1VIVVIV(PO4)3 at an average voltage of ∼3.4 V vs. Na/Na+ with a capacity of ∼110 mA h g−1 and an energy density of ∼370 W h kg−1.27,36,37 One additional Na+ can be inserted (electro)chemically into NVP to achieve Na4VIIVIII(PO4)3 with a voltage of ∼1.63 V vs. Na/Na+. The reversible extraction of 3 Na+ ions (i.e., starting from Na4VIIVIII(PO4)3 as the pristine material to Na1VIVVIV(PO4)3 is possible but not practical due to the 1.8 V difference between the two processes (VIV/VIII and VIII/VII) and the difficult synthesis of Na4V2(PO4)3. Uebou et al.38 demonstrated the extraction of ∼2.5 Na+ ions with partial reversibility.
Symmetric Na electrochemical cells entirely made of NaSICON frameworks adopt NVP as both the electrodes;39 in the charged state of the battery the anode is Na4VIIIVII(PO4)3 and the cathode is Na1VIVVIV(PO4)3 with Na3Zr2Si2PO12 as the electrolyte. This could deliver an average voltage of ∼1.8 V.39–41 NVP suffers from poor intrinsic electronic conductivity due to the isolated VO6 octahedra, which are never face-, edge- or corner-sharing with each other,25,42 in contrast to their arrangement in layered-oxide cathodes where edge-sharing exists between MO6 moieties.6,9
The Ti analogue of NVP is the TiIV-containing NaTiIVTiIV(PO4)3 composition, which is stable in air and can reversibly exchange two electrons by benefitting from the TiIV/TiIII redox couple, but at a lower voltage of ∼2.1 V vs. Na/Na+ compared to that of ∼3.4 V for VIV/VIII redox in NVP.25,26 NaTiIVTiIV(PO4)3 is also commonly used as a negative electrode material.28 The NaSICON Na3FeIIIFeIII(PO4)3 exhibits a voltage–composition plateau at ∼2.5 V vs. Na/Na+ with a discharge capacity of ∼61 mA h g−1 and is associated with the redox couple FeIII/FeII.43 The FeIV/FeIII redox couple was claimed to be observed in Na3FeIIIFeIII(PO4)3 at ∼3.4 V vs. Na/Na+, with a limited specific discharge capacity of ∼22 mA h g−1.44 Nevertheless, the formation of tetravalent iron ions has not yet been reproduced.
Yamada et al.45 reported a voltage of ∼4.5 V vs. Na/Na+ (enabled by the reversible CrIV/CrIII redox couple) when Na+ is extracted from Na3CrIIICrIII(PO4)3, which corresponds to the highest voltage ever reported among NaSICON materials with a single TM species. Importantly, the Mn, Co and Ni, NaxM2(PO4)3 NaSICON analogues have not yet been reported.
The high voltage delivered by the CrIV/CrIII redox couple offers scope for exploring new high-voltage/capacity materials using more than one TM, e.g., Na4CrIIIMnII(PO4)3.30,46 Other NaSICON materials, such as Na3VIIICrIII(PO4)3,47 Na2TiIVVIII(PO4)3,48,49 Na3TiIVMnII(PO4)3,50,51 Na2TiIVFeIII(PO4)3,52 Na4VIIIMnII(PO4)3,34,35,53–56 Na3VIIIFeIII(PO4)3 (ref. 29 and 35) and Na4VIIINiII(PO4)3,35 have also been studied to enable high reversible capacity and longevity as anode and cathode electrodes.
In general, to access three electrons (i.e., 3 Na+ ions per 2 TMs per formula unit) in any mixed TM NaSICON, two criteria must be met: (i) the TM must be in the +2 and +3 oxidation states in the fully discharged state (i.e., 4 Na+ ions) and (ii) at least one of the TMs must accommodate multiple redox active oxidation states. Compounds that meet these criteria are mainly either Mn or V-based NaSICONs, e.g., Na2TiIVVIII(PO4)3, Na3TiIVMnII(PO4)3, Na4MnIIVIII(PO4)3, and Na4CrIIIMnII(PO4)3, which undergo reversible electrochemical reactions up to three electrons with average voltages of ∼2.4, ∼3.2, ∼3.4, and ∼4.1 V vs. Na/Na+. While Na4CrIIIMnII(PO4)3 exhibits a high theoretical energy density (566 W h kg−1) for a gravimetric capacity of 160 mA h g−1,30 only ∼40 mA h g−1 was reported at voltages below 1.6 V vs. Na/Na+.
However, there remains a wide chemical space yet to be explored, which could yield new combinations of TMs enabling improved NaSICON electrode materials. A systematic study, either experimental or theoretical, of trends in voltages and the phase behavior of possible transition-metal combinations within NaSICON electrode materials has not yet been reported.
We present a first-principles study that charts the chemical space of 28 different NaxMM′(PO4)3-electrode chemistries, where M and M′ can be any of the 3d TM, Ti, V, Cr, Mn, Fe, Co and Ni, with the Na content varying in the range of 1 ≤ x ≤ 4. We derive the intercalation voltages for all the 28 NaxMM′(PO4)3 systems, validate our predictions with available experimental data, and identify promising NaSICON compositions to be targeted experimentally. We find new promising or not fully explored NaxMM′(PO4)3 compositions, e.g., NaxMn2(PO4)3 (1 ≤ x ≤ 4), NaxCo2(PO4)3 (3 ≤ x ≤ 4), NaxTiCo(PO4)3 (2 ≤ x ≤ 4), NaxVCo(PO4)3 (1 ≤ x ≤ 4), NaxCrCo(PO4)3 (2 ≤ x ≤ 4), NaxCoMn(PO4)3 (2 ≤ x ≤ 4) and NaxCrFe(PO4)3 (2 ≤ x ≤ 4). We analyze the possible origins of the difficulties in synthesizing specific NaSICON chemistries.
2. Results
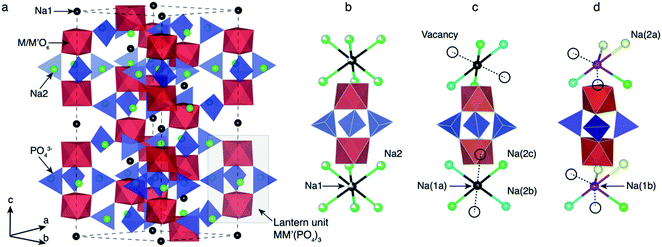
2.1 Structural features of NaxMM′(PO4)3 electrodes
Depending on the TM species, temperature and/or Na content (x) per formula unit (f.u.) NaSICON materials typically adopt a rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c),45,57 an ordered monoclinic (C2/c or Cc),20,21,47 or, in the specific case of α-Na3TiIIITiIII(PO4)3, a triclinic structure (P1).58 For example, Na4VIIVIII(PO4)3 and Na4FeIIFeIII(PO4)3 (ref. 59) are rhombohedral, while Na3VIIIVIII(PO4)3,57 Na3FeIIIFeIII(PO4)3,43 Na3TiIIITiIII(PO4)3 and Na3CrIIICrIII(PO4)3 tend to form monoclinic58 structures at room temperature due to Na/vacancy orderings. Fig. 1 shows the archetypal structure of the rhombohedral NaxMM′(PO4)3.
c),45,57 an ordered monoclinic (C2/c or Cc),20,21,47 or, in the specific case of α-Na3TiIIITiIII(PO4)3, a triclinic structure (P1).58 For example, Na4VIIVIII(PO4)3 and Na4FeIIFeIII(PO4)3 (ref. 59) are rhombohedral, while Na3VIIIVIII(PO4)3,57 Na3FeIIIFeIII(PO4)3,43 Na3TiIIITiIII(PO4)3 and Na3CrIIICrIII(PO4)3 tend to form monoclinic58 structures at room temperature due to Na/vacancy orderings. Fig. 1 shows the archetypal structure of the rhombohedral NaxMM′(PO4)3.
NaxMM′(PO4)3 materials consist of (M, M′)O6 octahedral and PO4 tetrahedral units. As shown in Fig. 1, three PO4 tetrahedra share all their corners with two (M,M′)O6 octahedra forming the “lantern units”—a recurrent motif of NaSICON structures. The lantern units assemble into a 3-D MM′(PO4)3 framework producing two types of available sites for Na in the rhombohedral phase (Fig. 1b): Na1 (one per f.u.) and Na2 (three per f.u.). The six-coordinated Na1 sites are located between two (M,M′)O6 octahedra, while the Na2 sites remain eight-coordinated with the O atoms of the PO4 tetrahedra. At x = 4 in NaxMM′(PO4)3, all the Na positions (i.e., 1 × Na1 and 3 × Na2 per f.u.) are fully occupied and the structure is ordered and rhombohedral. In several NaSICONs, the Na+ ions are fully ordered at x = 3 and the structure adopts monoclinic (C2/c) symmetry (Fig. 1c), where the Na1 site splits into two distinct sites (i.e., fully occupied Na1a and Na1b). The Na2 site splits into five sites (3 fully occupied, Na2a, Na2b and Na2c, and 2 vacancies).
2.2 Na intercalation in NaxM2(PO4)3 NaSICONs
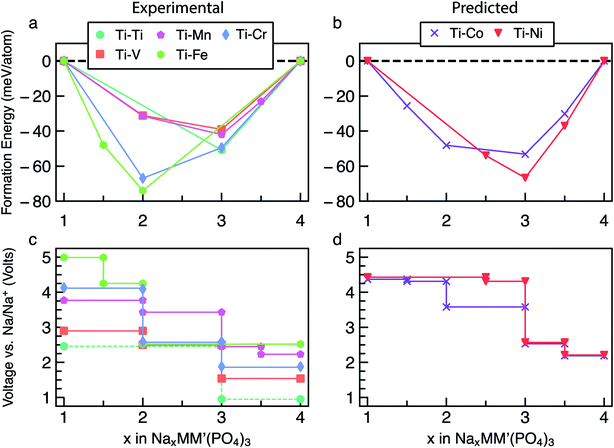
The energetics of Na intercalation and the corresponding average voltages (see Methodology in Section 5) for single TM (M = M′) NaSICON electrodes are shown in panels (a) and (b) of Fig. 2. The computed formation energies for the most stable orderings in NaxM2(PO4)3 are displayed in Fig. 2a as a function of Na concentration, where the lower energy envelopes form the so-called convex hull (solid lines) for a given NaxM2(PO4)3 system. The convex hull highlights the thermodynamic phase behavior at 0 K of Na (de)intercalation from/into the NaxM2(PO4)3 frameworks. Since the convex hull at 0 K does not include any entropic and pV effects, it informs on the propensity of Na to bond with the M2(PO4)3 frameworks. Among the M = Ti, V, Cr, Mn, Fe, Co and Ni compounds, NaSICONs based on Ti, V, Cr and Fe have been reported experimentally.28,36,43–45 From previous experimental work, the redox activities of Ti and V provide accessible Na concentrations ranging in 1 ≤ x ≤ 4, while NaxCr2(PO4)3 spans a narrower range of Na concentration (1 ≤ x ≤ 3), being limited by the CrIV/CrIII redox couple. Notably, the CrIII/CrII redox couple has not been cycled reversibly in NaSICON frameworks so far.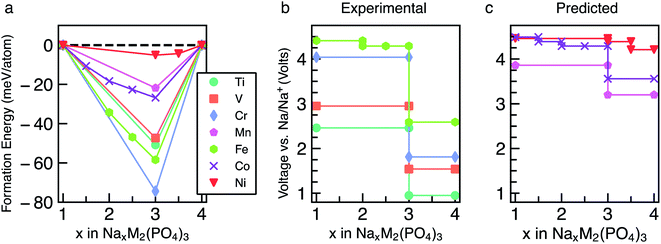 | ||
| Fig. 2 Panel (a) shows the computed formation energies and respective convex hulls for Na vacancy orderings as a function of Na concentration (x) in NaxM2(PO4)3 where M = Ti, V, Cr, Mn, Fe, Co and Ni. Panels (b) and (c) show the intercalation voltages vs. Na/Na+ for the experimentally known (M = Ti, V, Cr and Fe) and predicted (M = Mn, Co and Ni) NaxM2(PO4)3 compounds, respectively. Only the stable orderings forming the convex hull are displayed in panel (a). The energies of unstable configurations for each convex hull are shown in Fig. S1–S7 of the ESI.† | ||
The structures represented by specific Na/vacancy orderings falling above the convex hull are thermodynamically unstable/metastable and are shown in Fig. S1–S7 of the ESI.† Note that the unstable Na/vacancy orderings should decompose to the closest ground state(s) identified by the convex hulls in Fig. 2a. For example, in Fig. S2,† Na2V2(PO4)3 (C2) is found to be slightly metastable (∼1.8 meV per atom above the stability line) and will phase separate into Na1VIVVIV(PO4)3 and Na3VIIIVIII(PO4)3. Given the small metastability of Na2V2(PO4)3, we expect this compound to be stabilized by entropic effects. Consequently, the stable structures lying on the convex hull (e.g., Na3VIIIVIII(PO4)3) give rise to a “step” in the calculated Na voltage curve (see Fig. S2†). The convexity, that is the depth of the convex hull, is an indication of the thermodynamic stabilities of the specific Na/vacancy configurations. The calculated ground states on the convex hull do not necessarily correspond to topotactic structures since we allow changes to the symmetry (e.g., rhombohedral → monoclinic) of the host during deintercalation of Na from Na4MM′(PO4)3 in our calculations.
Analyzing Fig. 2a and b, the following general trends can be deduced:
(i) The end member compositions in NaxM2(PO4)3, i.e., x = 1 and 4, typically adopt the rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c or R
c or R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) space group. Exceptions to this trend are Na4CrIICrIII(PO4)3 and Na4MnIIMnIII(PO4)3, which are predicted to have triclinic (P
) space group. Exceptions to this trend are Na4CrIICrIII(PO4)3 and Na4MnIIMnIII(PO4)3, which are predicted to have triclinic (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) symmetry probably due to Jahn–Teller distortions of high-spin Cr2+ and Mn3+ d4 ions. These have not yet been observed experimentally.
) symmetry probably due to Jahn–Teller distortions of high-spin Cr2+ and Mn3+ d4 ions. These have not yet been observed experimentally.
(ii) A global minimum in the formation energy curves is present across all transition-metal NaxM2(PO4)3 systems at x = 3 (Fig. 2a).41
(iii) Among all the Na3MIIIMIII(PO4)3 compounds investigated, Na3CrIIICrIII(PO4)3 displays the deepest or lowest (i.e., most favorable) formation energy, followed by Na3FeIIIFeIII(PO4)3 > Na3TiIIITiIII(PO4)3 ≈ Na3VIIIVIII(PO4)3, respectively, which reflects the stability of the M3+ oxidation states of these TMs. The stability of Na3CrIIICrIII(PO4)3 is enhanced by the large ligand field stabilization energy of the Cr3+ (3d3) cation. The other compounds, Na3CoIIICoIII(PO4)3, Na3MnIIIMnIII(PO4)3 and Na3NiIIINiIII(PO4)3, display shallower (i.e., less favorable) formation energies (<25 meV per atom, Fig. 2a). The shallow convex hulls for NaXMn2(PO4)3 and NaxNi2(PO4)3 are caused by the Mn3+ and Ni3+ ions which are both Jahn–Teller active. The magnetic moment of Co3+ Na3CoIIICoIII(PO4)3 is ∼3.0 μB, indicating an intermediate spin state and possible Jahn–Teller activity.
(iv) Unsurprisingly, the deep minima in the convex hull plot of Fig. 2a lead to a large voltage step as shown in Fig. 2b and d, following the sequence Cr > Fe > Ti > V > Co > Mn > Ni.
(v) The M(III/II) redox couples that correspond to Na contents from x = 3 to x = 4, follow the voltage trend Ni > Co > Mn > Fe > Cr > V > Ti, while the M(IV/iII) couples (x = 1 to x = 3) follow the sequence Ni > Co > Fe > Cr > Mn > V > Ti. Thus, Ni and Co (V and Ti) display the highest (lowest) average voltages for both M redox couples.
To validate our methodology, we have benchmarked our results against experimental observations in NaxV2(PO4)3, which has been extensively studied.57,60 Experimentally, Na3VIIIVIII(PO4)3 adopts monoclinic symmetry (C2/c) at room temperature, which is in qualitative agreement with our DFT calculations identifying the monoclinic ordering (Cc) as the stable structure at x = 3. From Fig. 2a, Na3VIIIVIII(PO4)3 is on the convex hull with Na1VIVVIV(PO4) and Na4VIIVIII(PO4)3, which adopt the rhombohedral space groups R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c and R
c and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , respectively; this is consistent with X-ray diffraction experiments.36,57,61 In Fig. 2b, the extraction of 2 Na atoms from Na3VIIIVIII(PO4)3 gives rise to an average voltage of ∼2.96 V vs. Na/Na+ and corresponds to the VIV/VIII redox couple, while the insertion of Na into Na3VIIIVIII(PO4)3 results in a voltage of 1.54 V (associated with the VIII/VII redox couple). Experimentally, both the V redox couples (VIV/VIII and VIII/VII) are involved in two-phase reaction mechanisms, yielding average voltages of ∼3.40 V and ∼1.63 V vs. Na/Na+, respectively,60 which are in reasonable agreement with our computed values. Notably, both GGA+U and hybrid functionals underestimate the computed voltages of NaxV2(PO4)3 (see Section S2 in the ESI†). Another important assessment to verify the validity of our simulations is ensuring that changes in oxidation states of the TMs upon Na extraction/insertion are captured. We verify that the correct redox processes do occur in our calculations by tracking the on-site magnetic moments on the TM atoms (Table S1†), as well as the transition metal coordination environments (Table S2†), which are discussed in Section S3 of the ESI.†
, respectively; this is consistent with X-ray diffraction experiments.36,57,61 In Fig. 2b, the extraction of 2 Na atoms from Na3VIIIVIII(PO4)3 gives rise to an average voltage of ∼2.96 V vs. Na/Na+ and corresponds to the VIV/VIII redox couple, while the insertion of Na into Na3VIIIVIII(PO4)3 results in a voltage of 1.54 V (associated with the VIII/VII redox couple). Experimentally, both the V redox couples (VIV/VIII and VIII/VII) are involved in two-phase reaction mechanisms, yielding average voltages of ∼3.40 V and ∼1.63 V vs. Na/Na+, respectively,60 which are in reasonable agreement with our computed values. Notably, both GGA+U and hybrid functionals underestimate the computed voltages of NaxV2(PO4)3 (see Section S2 in the ESI†). Another important assessment to verify the validity of our simulations is ensuring that changes in oxidation states of the TMs upon Na extraction/insertion are captured. We verify that the correct redox processes do occur in our calculations by tracking the on-site magnetic moments on the TM atoms (Table S1†), as well as the transition metal coordination environments (Table S2†), which are discussed in Section S3 of the ESI.†
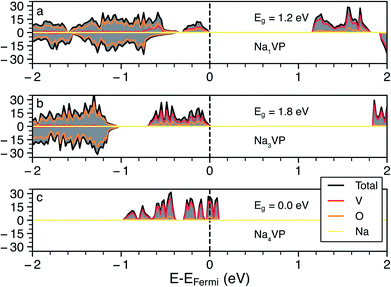
Whenever we could not assign the expected oxidation state of the TMs directly from the computed magnetic moments (e.g., in the cases of Fe, Co and Ni based NaSICONs), we inspected the density of states (DOS). Additional DOSs is are reported in Section S4 of the ESI (Fig. S9–S12).† As an example, we show in Fig. 3 the total and atom-projected DOS in NaxV2(PO4)3, for x = 1, 3 and 4, which are the ground states identified in Fig. 2. The DOS is displayed for spin up and spin down states in the range of interest (−2.5 to 2 eV) around the Fermi energy. Unless a given structure is metallic, the top of the Fermi energy is arbitrarily set to the top of the valence band.
Panels (a) and (b) in Fig. 3 show the results for Na1VIVVIV(PO4)3 and Na3VIIIVIII(PO4)3, respectively. From the projected DOS, the valence bands near the Fermi energy are occupied by 3d electrons of vanadium (red line), while the 2p O states (orange line) lie at lower energies. In general, the vanadium 3d states tend to dominate the valence band and shift at higher energies as more Na is inserted, closing the band gap (>1 eV for both compounds). The monoclinic distortion of Na3VIIIVIII(PO4)3 is responsible for an increase in the band gap (∼1.8 eV) contrary to the Na = 1 and Na = 4 trends. As expected, the intercalation of more Na+ ions as in Na4VIIIVII(PO4)3 (Fig. 3c) further increases (destabilizes) the valence band, with this composition becoming gapless and showing a Fermi energy dominated by V(3d) states when GGA+U is used. For the Na4VIIIVII(PO4)3, the band gap opens to ∼0.3 eV when the more accurate HSE06 hybrid functional is used at the relaxed HSE06 structure. Very recent hybrid functional simulations on NaxTi2(PO4)3 have verified these orders of magnitude, with Na4TiIIITiII(PO4)3 showing a small band gap of ∼0.59 eV.62
In the case of NaxNi2(PO4)3 the projected DOS of Fig. S12† suggests metallic behavior at all the Na concentrations explored (i.e., x = 1, 3 and 4). NaxMn2(PO4)3 and NaxCo2(PO4)3 show band gaps > 1.0 eV at x = 3 and 4, but become metallic at x = 1, as shown in Fig. S9 and S11.† Na1FeIVFeIV(PO4)3 also appears, surprisingly, metallic (Fig. S10†), which introduces difficulties in localizing the FeIII/FeIV redox couple. Therefore, due to the apparent metallic behavior of some of these systems (Fe, Co and Ni-based NaSICONs), we were unable to assign unique oxidation states to their TMs. Notably, DFT is a ground state theory and not adequate in the prediction of accurate band gaps.63
2.3 Na+ ion intercalation in NaxMM′(PO4)3 NaSICON structures
We extend our analysis to the reversible extraction of Na from mixed Na4MM′(PO4)3 compounds where, for the sake of simplicity, the ratio M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M′ is fixed as 1
M′ is fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. While all the M
1. While all the M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M′ combinations have been considered, to simplify our discussion we concentrate on the cases where M = Ti, while M′ = Ti, V, Cr, Mn, Fe, Co and Ni. Other mixed Na4MM′(PO4)3 are reported in Section S5 of the ESI (Fig. S13–S33).† The main reason behind choosing Ti-based mixed TM NaSICONs is their maximum experimental electrochemical data availability as compared to other combinations. Fig. 4a and b show the calculated convex hulls for experimentally reported and theoretical NaxTiM′(PO) compounds, with Na contents in the range 1 ≤ x ≤ 4. Fig. 4c displays the corresponding voltages. NaxTi2(PO4)3 is also reported in Fig. 4a and c as a reference.
M′ combinations have been considered, to simplify our discussion we concentrate on the cases where M = Ti, while M′ = Ti, V, Cr, Mn, Fe, Co and Ni. Other mixed Na4MM′(PO4)3 are reported in Section S5 of the ESI (Fig. S13–S33).† The main reason behind choosing Ti-based mixed TM NaSICONs is their maximum experimental electrochemical data availability as compared to other combinations. Fig. 4a and b show the calculated convex hulls for experimentally reported and theoretical NaxTiM′(PO) compounds, with Na contents in the range 1 ≤ x ≤ 4. Fig. 4c displays the corresponding voltages. NaxTi2(PO4)3 is also reported in Fig. 4a and c as a reference.
Among the NaxTiM′(PO4)3 systems, only NaxTi2(PO4)3, NaxTiV(PO4)3 and NaxTiMn(PO4)3 have been experimentally investigated over the entire Na composition range (1 ≤ x ≤ 4),28,48–51 while NaxTiCr(PO4)3 (ref. 52 and 64) and NaxTiFe(PO4)3 (ref. 52) have been studied in limited ranges of 1 ≤ x ≤ 3 and 2 ≤ x ≤ 4, respectively. NaxTiCo(PO4)3 and NaxTiNi(PO4)3 are theoretical compounds and have not yet been reported experimentally.
In general, the end member compositions at x = 1 and 4 (Fig. 4a and b) of the Ti–M′ NaSICON electrodes adopt rhombohedral symmetry (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c or R
c or R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , or R32) except for Na4TiIIICrII(PO4)3 (P
, or R32) except for Na4TiIIICrII(PO4)3 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and Na1TiIVFeIV(PO4)3 (P1), which are theoretically derived. This could be due to Jahn–Teller effects caused by the high-spin d4 electronic configurations of Cr2+ and Fe4+, respectively, as well as the low stability of Fe4+. For NaxTiM′(PO4)3 with M′ = V, Mn, Co and Ni, a global minimum in the convex hull is located at x = 3, and the magnitudes of the formation energy follow the trend Ni > Co > Mn > V. On the other hand, the global minima for the M′ = Ti, Cr and Fe NaSICONs are located at x = 2 (Fig. 4a), which is driven by the high stability of their stable oxidation states Ti4+, Cr3+ and Fe3+, respectively. Overall, the depth of the convex hulls (i.e., maximum magnitude of formation energies) for mixed TM NaSICONs follows the trend Fe > Cr ∼ Ni > Co > Ti > Mn ∼ V.
) and Na1TiIVFeIV(PO4)3 (P1), which are theoretically derived. This could be due to Jahn–Teller effects caused by the high-spin d4 electronic configurations of Cr2+ and Fe4+, respectively, as well as the low stability of Fe4+. For NaxTiM′(PO4)3 with M′ = V, Mn, Co and Ni, a global minimum in the convex hull is located at x = 3, and the magnitudes of the formation energy follow the trend Ni > Co > Mn > V. On the other hand, the global minima for the M′ = Ti, Cr and Fe NaSICONs are located at x = 2 (Fig. 4a), which is driven by the high stability of their stable oxidation states Ti4+, Cr3+ and Fe3+, respectively. Overall, the depth of the convex hulls (i.e., maximum magnitude of formation energies) for mixed TM NaSICONs follows the trend Fe > Cr ∼ Ni > Co > Ti > Mn ∼ V.
Fig. 4c and d present the computed voltages for Na extraction from NaxTiM′(PO4)3 in the composition range 1 ≤ x ≤ 4. Expectedly, the compound exhibiting the lowest intercalation voltage (∼0.96 V) is NaxTi2(PO4)3 for 3 ≤ x ≤ 4, which overestimates the experimental voltage (∼0.4 V) reported by Senguttuvan et al.28 The DFT data of Fig. 4a suggest that an unreported stable phase appears at Na1.5TiFe(PO4)3, but with an oxidation state for Fe of 3.5 (FeIV + FeIII). Although the highest Na intercalation voltage (∼4.99 V) is computed for NaxTiFe(PO4)3 between x = 1.5 and x = 1, the oxidation state of Fe would have to be +4, which may not be experimentally accessible in a reversible manner. We find that Na1FeIVFeIV(PO4)3, where iron is expected to be Fe4+ appears metallic from the DOS in Fig. S10.†
To assess the quality of our computed data, we analyzed in detail the experimentally reported data for NaxTiV(PO4)3. At x = 1, 2 and 4, NaxTiV(PO4)3 has rhombohedral symmetry (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c), while the structure of Na3TiV(PO4)3 is monoclinic (C2/c).48,49 Our calculations reproduce the rhombohedral symmetry (R
c), while the structure of Na3TiV(PO4)3 is monoclinic (C2/c).48,49 Our calculations reproduce the rhombohedral symmetry (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) at x = 1 and 4 and the monoclinic symmetry (Cc) at x = 3, whereas we find a triclinic structure (P
c) at x = 1 and 4 and the monoclinic symmetry (Cc) at x = 3, whereas we find a triclinic structure (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) for Na2TiV(PO4)3.48 The NaxTiV(PO4)3 convex hull (Fig. 4a) displays a minimum at x = 3, analogous to the observed minima in the NaxM2(PO4)3 systems (Fig. 2a); this also provides the largest step in the corresponding voltage profile of Fig. 4c. In particular, the Na extraction from Na4TiIIIVII(PO4)3 takes place through the redox couples VIII/VII 1.54 V (experimentally ∼1.6 V
) for Na2TiV(PO4)3.48 The NaxTiV(PO4)3 convex hull (Fig. 4a) displays a minimum at x = 3, analogous to the observed minima in the NaxM2(PO4)3 systems (Fig. 2a); this also provides the largest step in the corresponding voltage profile of Fig. 4c. In particular, the Na extraction from Na4TiIIIVII(PO4)3 takes place through the redox couples VIII/VII 1.54 V (experimentally ∼1.6 V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48,49), TiIV/TiIII 2.50 V (∼2.1 V), and VIV/VIII 2.90 V (∼3.4 V) vs. Na/Na+, respectively. The mechanism of Na extraction from Na4TiIIIVII(PO4)3 has been shown to occur via a solid-solution mechanism for the VIII/VII redox couple, followed by a two-phase reaction for both the TiIV/TiIII and VIV/VIII redox couples.48
48,49), TiIV/TiIII 2.50 V (∼2.1 V), and VIV/VIII 2.90 V (∼3.4 V) vs. Na/Na+, respectively. The mechanism of Na extraction from Na4TiIIIVII(PO4)3 has been shown to occur via a solid-solution mechanism for the VIII/VII redox couple, followed by a two-phase reaction for both the TiIV/TiIII and VIV/VIII redox couples.48
Due to the existence of multiple voltage steps in NaxMM′(PO4)3 (where M′ = Ti, V, Cr, Mn, Fe, Co and Ni and M = Ti), we directly compare the computed average voltage per Na+ exchanged over the entire composition range (i.e., 1 ≤ x ≤ 4), as shown in Fig. 5. Importantly, the overall average voltage monotonically increases from Ti to Ni in cases where M = M′ and M = Ti, which is consistent with trends in standard reduction potentials of the transition metals. We note that the M4+ ions, in particular, become more oxidizing as one crosses the transition series from Ti to Ni, with the lack of voltage increase from Mn to Fe reflecting the stability of their 3d5 configurations. Specifically, the calculated voltages increase from ∼1.96 V (for Ti) to ∼4.40 V vs. Na/Na+ (for Ni) in NaxM2(PO4)3 (green line in Fig. 5), while the maximum voltage is ∼3.73 V for Ti–Ni in the case of NaxMM′(PO4)3 (M = Ti) systems (orange line). Notably, the voltage values for NaxTiM′(PO4)3 are consistently lower than those for the corresponding NaxM′2(PO4)3, indicating that replacing Ti with another 3d metal will always lead to an increased average voltage in both M = M′ and Ti–M′ systems.
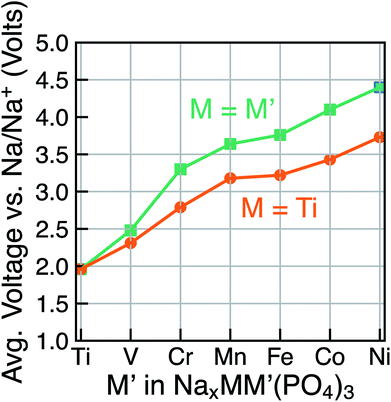 | ||
| Fig. 5 The calculated average voltage per extracted Na+ ion vs. Na/Na+ over the x range1–4 in NaxMM′(PO4)3 compounds, where M = M′ (green) or M = Ti (orange) and M′ = V, Cr, Mn, Fe, Co and Ni. | ||
2.4 Intercalation voltages of NaxMM′(PO4)3
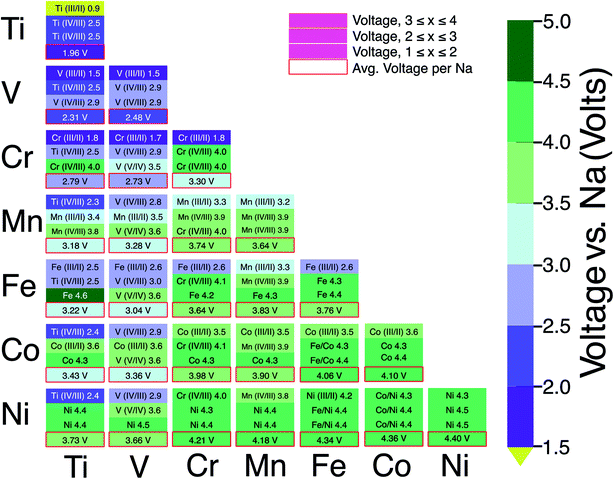
Fig. 6 consolidates the computed voltages of 28 plausible combinations of 3d TMs in NaxMM′(PO4)3 with M and M′ in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. In Fig. 6, the boxes outlined in red represent the average voltage per extracted Na in the entire 1 ≤ x ≤ 4 concentration range for each combination of TM. The NaSICON systems investigated cover a range of average voltages from ∼1.96 to ∼4.4 V vs. Na/Na+. Redox couples are indicated in each box whenever we could identify the appropriate oxidation states as described in Section 2.2. The diagonal of Fig. 6 displays the single-TM NaSICONs (M = M′), whose average voltages map directly to Fig. 5. Notably, the highest average voltages of ∼4.3 to 4.4 V are attained by the theoretical NaxNi2(PO4)3, NaxCoNi(PO4)3 and NaxFeNi(PO4)3 compounds. In general, voltages in NaSICONs are set by the redox couples MIII/MII and MIV/MIII but notable exceptions to this trend are for V and Nb-based NaSICONs, which can also operate on the VV/VIV couple (see the mixed NaxVM′(PO4)3 systems in Fig. 6) and the NbV/NbIV couple in NaxNbTi(PO4)3 not discussed here.65
1 ratio. In Fig. 6, the boxes outlined in red represent the average voltage per extracted Na in the entire 1 ≤ x ≤ 4 concentration range for each combination of TM. The NaSICON systems investigated cover a range of average voltages from ∼1.96 to ∼4.4 V vs. Na/Na+. Redox couples are indicated in each box whenever we could identify the appropriate oxidation states as described in Section 2.2. The diagonal of Fig. 6 displays the single-TM NaSICONs (M = M′), whose average voltages map directly to Fig. 5. Notably, the highest average voltages of ∼4.3 to 4.4 V are attained by the theoretical NaxNi2(PO4)3, NaxCoNi(PO4)3 and NaxFeNi(PO4)3 compounds. In general, voltages in NaSICONs are set by the redox couples MIII/MII and MIV/MIII but notable exceptions to this trend are for V and Nb-based NaSICONs, which can also operate on the VV/VIV couple (see the mixed NaxVM′(PO4)3 systems in Fig. 6) and the NbV/NbIV couple in NaxNbTi(PO4)3 not discussed here.65
2.5 Thermodynamic stabilities of selected NaxM2(PO4)3 compounds
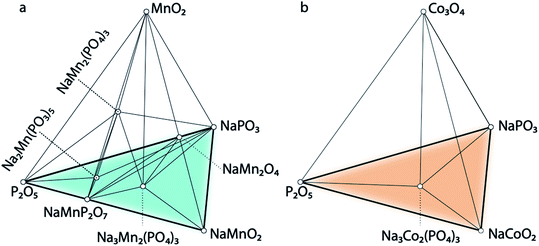
The calculated quaternary phase diagrams for the systems Na–P–O–Mn, Na–P–O–Co, and Na–P–O–Ni (Fig. 7 and S34 in the ESI†) reflect the stabilities of the unreported NaSICONs with these transition metals compared with the stable elemental, binary, ternary and quaternary phases. While it remains extremely challenging to characterize quaternary (and beyond) phase diagrams solely based on sparse experimental data, theory provides a viable alternative for investigating such complex systems. We calculated all the binary/ternary/quaternary compounds available in the inorganic crystal structure database (ICSD)66 within the Na–P–O–Mn, –Co and –Ni quaternary systems.
Fig. 7a shows the computed phase diagram of the Na–P–O–Mn system, where open circles correspond to stable phases in the global phase diagrams and the black lines show the equilibria among various compounds. The computed phase diagram of Na–Mn–P–O shows that Na3MnIIIMnIII(PO4)3 and Na1MnIVMnIV(PO4)3 are stable compounds. Na3MnIIIMnIII(PO4)3 has the structure of the monoclinic (Cc) polymorph, whereas Na1MnIVMnIV(PO4)3 has a rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) structure. From our computations, we observed a Jahn–Teller distortion driven by the Mn3+ 3d4 ions and highlighted by four longer equatorial bonds of ∼2.10 Å and two shorter axial bonds of ∼1.96 Å. No Ni-containing NaSICON phases appear stable in the Na–Ni–P–O system (Fig. S34†). In the Na–Co–P–O phase diagram (Fig. 7b), only Na3CoIIICoIII(PO4)3 appears stable and exhibits rhombohedral symmetry (R
) structure. From our computations, we observed a Jahn–Teller distortion driven by the Mn3+ 3d4 ions and highlighted by four longer equatorial bonds of ∼2.10 Å and two shorter axial bonds of ∼1.96 Å. No Ni-containing NaSICON phases appear stable in the Na–Ni–P–O system (Fig. S34†). In the Na–Co–P–O phase diagram (Fig. 7b), only Na3CoIIICoIII(PO4)3 appears stable and exhibits rhombohedral symmetry (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ). From this analysis, it is predicted that Na3MnIIIMnIII(PO4)3, Na1MnIVMnIV(PO4)3, and Na3CoIIICoIII(PO4)3 have the potential for successful experimental synthesis, given their thermodynamic stabilities.
). From this analysis, it is predicted that Na3MnIIIMnIII(PO4)3, Na1MnIVMnIV(PO4)3, and Na3CoIIICoIII(PO4)3 have the potential for successful experimental synthesis, given their thermodynamic stabilities.
3. Discussion
Using first-principles calculations, we investigated the electrochemical properties of 28 transition-metal-based NaSICONs as cathode materials for NIBs. To guide our discussion, we summarize the reported experimental voltages and the experimental gravimetric and the theoretical gravimetric capacities of some NaxMM′(PO4)3 systems in Table 1. For a transparent and fair comparison between the theoretical and experimentally reported capacities in Table 1, the reported capacities are renormalized from the reported composition (pristine) to the molecular weight of the Na4MM′(PO3)4. The theoretical capacities are also computed with respect to the Na4MM′(PO3)4 compounds.| M = M′ | x = 1 | 2 | 3 | 4 | Reported capacity | Theo. capacity |
|---|---|---|---|---|---|---|
| Ti–Ti28 | ? |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
142.7 | 170.1 | |
| 2.1 V, TiIV/TIIII, Rev. | 0.4 V, TiIII/TIII, Irrev. | |||||
| V–V37,39 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
C2/c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
156.7 | 167.9 | |
| 3.4 V, VV/VIII, Rev. | 1.6 V, VIII/VII, Irrev. | |||||
| Cr–Cr45 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
93.3 | 111.5 | ||
| 4.5 V, CrIV/CrIII, Rev. | ||||||
| Fe–Fe43,44 | ? | C2/c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
85.8 | 164.6 | |
| 3.4 V, FeIV/FeIII, Rev. | 2.5 V, FeIII/FeII, Rev. | |||||
| M–M′ | x = 1 | 2 | 3 | 4 | Reported capacity | Theo. capacity |
|---|---|---|---|---|---|---|
| Ti–V48,49 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
C2/c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
132.8 | 169.0 |
| 3.4 V, VIV/VIII, Rev. | 2.1 V, TiIV/TIIII, Rev. | 1.6 V, VIII/VII, Rev. | ||||
| Ti–Cr52 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
— | 112.4 | |
| 4.5 V, CrIV/CrIII, Rev. | 2.1 V, TiIV/TIIII, Rev. | |||||
| Ti–Mn50,51 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
? | 152.3 | 167.6 |
| 4. V, MnIV/MnIII, Rev. | 3.5 V, MnIII/MnII, Rev. | 2.1 V, TiIV/TIIII, Rev. | ||||
| Ti–Fe52 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
— | 111.5 | |
| 2.4 V, FeIII/FeII, Rev. | 2.1 V, TiIV/TIIII, Rev. | |||||
| V–Cr47 | ? | ? |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
85.7 | 111.7 | |
| 4.1 V, VV/VIV, Rev. | 3.4 V, VIV/VIII, Rev. | |||||
| V–Mn34,54,56 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
156.0 | 166.6 |
| 3.9 V, VV/VIV, Irrev. | 3.6 V, MnIII/MnII, Rev. | 3.4 V, VIV/VIII, Rev. | ||||
| V–Fe29,35 | ? | C2/c | ? | 98.1 | 110.8 | |
| 3.3 V, VIV/VIII, Rev. | 2.5 V, FeIII/FeII, Rev. | |||||
| V–Ni35 | ? | ? |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
80.0 | 110.2 | |
3.9 V,VV/VIV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NiIII/NiII, Rev. NiIII/NiII, Rev. |
3.5 V, VIV/VIII, Rev. | |||||
| Cr–Mn30,46 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
160.5 | 166.2 |
| 4.4 V, CrIV/CrIII, Rev. | 4.2 V, MnIV/MnIII, Rev. | 3.6 V, MnIII/MnII, Rev. | ||||
Among the NaxM2(PO4)3 compounds, NaxCr2(PO4)3 delivers the highest measured voltage of ∼4.5 V (∼4 V calculated theoretically) vs. Na/Na+,45 albeit with a limited capacity of just ∼98 mA h g−1 and corresponding to the extraction of 2 Na from Na3CrIIICrIII(PO4)3 to form Na1CrIVCrIII(PO4)3. Na4Cr2(PO4)3 has not yet been obtained by either a chemical or an electrochemical process. Na4CrIIICrII(PO4)3 would require Cr to exist in a mixed, CrIII/CrII oxidation state, with Cr2+ (high-spin d4) typically being an unstable oxidation state for Cr and easily prone to Jahn–Teller distortions in octahedral environments, e.g., NaSICON.67
NaxV2(PO4)3 exhibits the 2nd highest measured voltage of the single TM NaSICONs, with a computed average voltage of ∼2.48 V vs. Na/Na+ (Fig. 5). With the same number of maximum electrons exchanged in NaxM2(PO4)3 (where M = Ti or V), and Ti being lighter than V, NaxTi2(PO4)3 is expected to show the largest gravimetric capacity. NaxTi2(PO4)3 and NVP provide the largest reported theoretical gravimetric capacities (∼170.1 mA h g−1 and ∼167.9 mA h g−1 for Na4M2(PO4)3) in single TM NaSICONs. In theory, additional capacity and an increased voltage could be achieved by exploiting the VV/VIV redox couple in the reaction Na1VIVVIV(PO4)3 → Na+ + 1e− VVVIV(PO4)3. While the seminal report by Gopalakrishnan et al. suggested the possibility of chemically extracting the last Na+ ion to form VVVIV(PO4)3,68 subsequent attempts to do so have proven unsuccessful. Note that VVVIV(PO4)3 is not a thermodynamically stable compound69 and is predicted to decompose into VPO5 + VP2O7.
We assessed the existence of uncharted single-TM NaSICONs, which are Ni, Co and Mn. Except for Na1MnIVMnIV(PO4)3, Na3MnIIIMnIII(PO4)3 and Na3CoIIICoIII(PO4)3 that appear stable according to our convex hulls but have not been reported experimentally, our analysis of the phase diagrams indicates that Ni- and Co-NaSICONs are generally unstable. However, Mn has been mixed effectively with Ti, V and Cr, while Ni–V mixed NaSICONs have also been made (Table 1).34 In particular, Zhou et al.35 and later Chen and collaborators34 synthesized MnII-containing Na4MnIIVIII(PO4)3, which upon Na extraction exploits the MnIII/MnII redox couple and Mn3+ 3d4 is Jahn–Teller active.
In the case of mixed Na4MM′(PO4)3 NaSICONs, we kept the M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M′ ratio to 1
M′ ratio to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. From an extensive assessment of polyanion electrodes, Masquelier and Croguennec17 observed that the redox potentials of specific TMs remain nearly independent70 of those of other TMs that may be present. This general rule is also well supported by the simulations that are summarized in Fig. 6. Based on this general principle, one can envision selected combinations of TMs delivering reversible high voltages vs. Na/Na+. For example, the TiIV/TiIII redox couple showed a similar voltage17 (∼2.1 V vs. Na/Na+) in three related NaSICON systems: NaxTi2(PO4)3, NaxTiNb(PO4)3 and NaxTiFe(PO4)3. Notably, in experiments, there is a consistent shift of ∼0.3 V between the voltages measured vs. Na/Na+ compared to those measured vs. Li/Li+.
1. From an extensive assessment of polyanion electrodes, Masquelier and Croguennec17 observed that the redox potentials of specific TMs remain nearly independent70 of those of other TMs that may be present. This general rule is also well supported by the simulations that are summarized in Fig. 6. Based on this general principle, one can envision selected combinations of TMs delivering reversible high voltages vs. Na/Na+. For example, the TiIV/TiIII redox couple showed a similar voltage17 (∼2.1 V vs. Na/Na+) in three related NaSICON systems: NaxTi2(PO4)3, NaxTiNb(PO4)3 and NaxTiFe(PO4)3. Notably, in experiments, there is a consistent shift of ∼0.3 V between the voltages measured vs. Na/Na+ compared to those measured vs. Li/Li+.
The NaxTiV(PO4)3 system has been shown to provide the largest gravimetric capacity (∼187.1 mA h g−1, Table 1) among NaSICONs as a result of the accessibility of several VIV/VIII/VII and TiIV/TiIII redox couples. Nevertheless, the computed average voltage (∼2.3 V, Fig. 6) of NaxTiV(PO4)3 highlights the low energy density of the system.48,49 More promising in terms of overall capacities and voltages, and thus energy density, are NaxTiCr(PO4)3,52,64 NaxTiMn(PO4)3,50,51 NaxCrMn(PO4)3,30,46 NaxVCr(PO4)3,47 and NaxVMn(PO4)3,34,54 but the reversible extraction/insertion of Na from some of these systems remains to be verified. Excluding some specific exceptions, especially Fe, Co and Ni based NaSICONs since they appear metallic, our simulations are also able to capture the mechanism of Na intercalation in mixed NaSICON electrodes. For example, Na3VFe(PO4)3 has been reported to reversibly insert Na with the activation of the FeIII/FeII and VIII/VII redox couples (see Table 1),35 and this behavior is reproduced by our calculations (Fig. 6 and S21 of the ESI†). Similar conclusions can be advanced for mixed TiV, TiCr, VCr and CrMn NaSICON materials.
From our analysis (Fig. 6), specific unexplored combinations of TMs appear to be worthy of future study. Our calculations suggest promising NaSICON compositions in terms of average voltages, such as TiCo, VCo, CrFe and CrCo NaSICONs as reported in Fig. 5 and Table 1. Both CrFe and CrCo NaSICONs are predicted to exploit the high voltage CrIV/CrIII redox couple, which has been proven effective in other mixed NaSICONs, e.g., TiCr, VCr and MnCr.47,64 Although the addition of Co into Ti, V and Cr appears interesting, our analysis of the NaxCo2(PO4)3 system suggests that only Na3CoIIICoIII(PO4)3 with Co3+ 3d6 (low spin) is thermodynamically stable, but this compound has not yet been synthesized. While one would target compounds with Co2+ to ensure high voltages, it appears possible to introduce Co in smaller proportions71 than a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, but more experimental and theoretical work is required.
1 ratio, but more experimental and theoretical work is required.
We do not anticipate Ni to be of importance in mixed NaSICON systems due to the high instability of quaternary NaxNi2(PO4)3. Manoun et al.72 briefly reported the synthesis of Na4CrIIINiII(PO4)3. A recent report by Zhou et al.35 claimed the extraction of Na from NaxVNi(PO4)3 (Table 1) involving the redox couples VIV/VIII, VV/VIV, and NiIII/NiII. Nevertheless, we speculate that the Ni content of the materials is not in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio but appears to be significantly lower. Furthermore, the highest voltage accessed (<4.3 V vs. Na/Na+) during the electrochemical cycling is lower than that of the expected Ni redox couple. While our DFT calculations seem to verify the activity of the VIV/VIII and VV/VIV redox couples in NaxVNi(PO4)3 (Fig. 6), we are unable to verify the oxidation states involved in the NiIII/NiII reaction from the computed magnetic moments as the material becomes metallic in our simulations (Fig. S12†). Our findings also cast doubt on the activity of Ni in this compound as reflected by the limited gravimetric capacity reported experimentally (∼80 mA h g−1).35
1 ratio but appears to be significantly lower. Furthermore, the highest voltage accessed (<4.3 V vs. Na/Na+) during the electrochemical cycling is lower than that of the expected Ni redox couple. While our DFT calculations seem to verify the activity of the VIV/VIII and VV/VIV redox couples in NaxVNi(PO4)3 (Fig. 6), we are unable to verify the oxidation states involved in the NiIII/NiII reaction from the computed magnetic moments as the material becomes metallic in our simulations (Fig. S12†). Our findings also cast doubt on the activity of Ni in this compound as reflected by the limited gravimetric capacity reported experimentally (∼80 mA h g−1).35
4. Conclusions
Using ab initio density functional theory and thermodynamics, we explored the full chemical map of 3d TM-based NaSICON phosphate NaxMM′(PO4)3 (M, M′ = Ti, V, Cr, Mn, Fe, Co and Ni) cathode materials for high-energy density and safe sodium-ion batteries. We identified the ground state structures at various Na contents as well as the corresponding Na-intercalation voltages and redox processes for 28 distinct NaSICON compositions of which only 13 have been reported experimentally.Further, we investigated the Na-intercalation properties of previously unreported NaxMn2(PO4)3 and NaxVCo(PO4)3 (1 ≤ x ≤ 4), among others. The calculated quaternary phase diagrams of the Na–P–O–M (M = Mn, Co and Ni) chemical systems indicate the instability of Ni and most Co-based NaSICONs, though the Na1MnIVMnIV(PO4)3, Na3MnIIIMnIII(PO4)3 and Na3CoIIICoIII(PO4)3 compounds are identified as stable compositions. We performed a complete analysis of the wide-ranging chemical space of NaSICON phosphate cathode materials for Na-ion batteries, and our work can be used to guide further experimental synthesis of the new and promising compositions identified here. We plan to synthesize the promising electrode compositions identified in this work.
5. Methodology
We used the Vienna ab initio simulation package (VASP)73,74 for ab initio density functional theory (DFT) total energy calculations. The projector augmented wave (PAW) potentials were used for the core wave-functions. The Perdew–Burke–Ernzerhof (PBE) parameterized spin-polarized generalized gradient approximation (GGA) was used for the exchange and correlation energy.75 The strong on-site coulomb correlation of 3d electrons of the TM (Ti, V, Cr, Mn, Fe, Co and Ni) is addressed with Hubbard's U correction76 according to the Dudarev method.77 The effective U parameters used were 4.0 eV for Ti,28 3.1 for V, 3.5 for Cr, 3.9 for Mn, 4.0 for Fe, 3.4 for Co, and 6.0 for Ni,78 and they were fitted to match the experimental formation energies of binary oxides. We also introduced an empirical correction of 1.36 eV per O2 (ref. 79) to remedy the spurious error originating from the well-known over-binding of O while using GGA.The periodic wave functions were expanded in terms of plane waves up to a kinetic energy cut-off of 520 eV. The PAW potentials used to describe the core electrons of the following atomic species were: Na 08Apr2002 3s1, P 17Jan2003 2s23p3, O 08Apr2002 2s22p4, Ti 08Apr2002 3d34s1, V_pv 07Sep2000 3p63d44s1, Cr 06Sep2000 3d54s1, Mn 06Sep2000 3d64s1, Fe 06Sep2000 3d74s1, Co 06Sep2000 3d84s1, and Ni 06Sep2000 3d94s1. Additionally, a Γ-centered Monkhorst–Pack80k-point mesh with 25 subdivisions along each reciprocal lattice vector was applied to all structures. Using these settings, the total energy of each structure was converged to within 10−5 eV per cell, atomic forces within 10−2 eV per Å and the stress within 0.29 GPa.
An intercalation battery based on the NaSICON cathode electrodes implies the reversible insertion/extraction of Na+-ions into/from the NayMM′(PO4)3 framework according to the redox reaction of eqn (1).
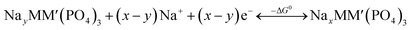 | (1) |
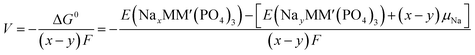 | (2) |
To establish the general phase behavior of Na (de)intercalation into the NayMM′(PO4)3 structure, we monitored, using eqn (3), the formation energies (Ef(x)) of various Na/vacancy orderings at different Na concentrations, x (1 ≤ x ≤ 4), with respect to the DFT energies of the fully discharged (i.e., E[Na4MM′(PO4)3]) and fully charged (E[NaMM′(PO4)3]) configurations.
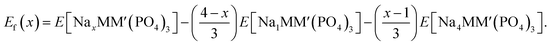 | (3) |
Different NaSICON structures were studied according to specific Na concentrations in NaxMM′(PO4)3 with M and M′ = Ti, V, Cr, Mn, Fe, Co, and Ni. In choosing the amount of mixing of TM in these NaSICON structures, we have considered only two distinct situations: (i) M = M′, which leads to NaxM2(PO4)3, and (ii) M and M′ in the ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
When fully sodiated, the fully ordered rhombohedral symmetry (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) of the high temperature NaSICON structure is typically observed (e.g., Na4FeIIIFeII(PO4)3 (ref. 59)) and is therefore our starting model to study Na removal and TM mixing. Na vacancies are created in the fully sodiated structure Na4MM′(PO4)3, resulting in NaxMM′(PO4)3, where the Na content varies in the range of 1 ≤ x ≤ 4 in steps of Δx = 0.5. The possible configurations originating from the various orderings of Na and vacancies (Va) in the NaSICON are obtained using the pymatgen library.81 A ranking according to the classical Ewald energy82 based on integer charges (i.e., Na = +1, P = +5, O = −2) and the variable charge on the TM (+2, +3 and +4) is applied to limit the number of possible structures to a computationally tractable level. For mixed TM NaSICONs, the ordering of M and M′ is simultaneously performed with that of Na and Va. DFT calculations are performed on the primitive cell and supercells (2 × 1 × 1) of these orderings. A formula unit of the fully discharged NaSICON (Na4MM′(PO4)3) contains 21 atoms.
c) of the high temperature NaSICON structure is typically observed (e.g., Na4FeIIIFeII(PO4)3 (ref. 59)) and is therefore our starting model to study Na removal and TM mixing. Na vacancies are created in the fully sodiated structure Na4MM′(PO4)3, resulting in NaxMM′(PO4)3, where the Na content varies in the range of 1 ≤ x ≤ 4 in steps of Δx = 0.5. The possible configurations originating from the various orderings of Na and vacancies (Va) in the NaSICON are obtained using the pymatgen library.81 A ranking according to the classical Ewald energy82 based on integer charges (i.e., Na = +1, P = +5, O = −2) and the variable charge on the TM (+2, +3 and +4) is applied to limit the number of possible structures to a computationally tractable level. For mixed TM NaSICONs, the ordering of M and M′ is simultaneously performed with that of Na and Va. DFT calculations are performed on the primitive cell and supercells (2 × 1 × 1) of these orderings. A formula unit of the fully discharged NaSICON (Na4MM′(PO4)3) contains 21 atoms.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. C., C. M., A. K. C., and J.-N. C. are grateful to the ANR-NRF NRF2019-NRF-ANR073 Na-MASTER. P. C. and B. S. acknowledge funding from the National Research Foundation under the NRF Fellowship NRFF12-2020-0012. L. C., D. C. and C. M. acknowledge the ANRT and TIAMAT for the funding of S. P.'s PhD thesis as well as the financial support from the Région Nouvelle Aquitaine and from the French National Research Agency (STORE-EX Labex Project ANR-10-LABX-76-01). The computational work was performed using resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg).References
- E. A. Olivetti, G. Ceder, G. G. Gaustad and X. Fu, Joule, 2017, 1, 229 CrossRef.
- J. M. Tarascon, Nat. Chem., 2010, 2, 510 CrossRef CAS PubMed.
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19 CrossRef CAS PubMed.
- S. W. Kim, D. H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2012, 2, 710 CrossRef CAS.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Energy Environ. Sci., 2012, 5, 5884 RSC.
- J. L. Kaufman, J. Vinckevičiūtė, S. K. Kolli, J. G. Goiri and A. Van Der Ven, Philos. Trans. R. Soc., A, 2019, 377, 20190020 CrossRef CAS PubMed.
- Q. Bai, L. Yang, H. Chen and Y. Mo, Adv. Energy Mater., 2018, 8, 1 Search PubMed.
- A. Mukherjee, T. Sharabani, R. Sharma, S. Okashy and M. Noked, Batteries Supercaps, 2020, 3, 510 CrossRef CAS.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636 CrossRef CAS PubMed.
- I. Hasa, S. Mariyappan, D. Saurel, P. Adelhelm, A. Y. Koposov, C. Masquelier, L. Croguennec and M. Casas-Cabanas, J. Power Sources, 2021, 482, 228872 CrossRef CAS.
- S. H. Bo, X. Li, A. J. Toumar and G. Ceder, Chem. Mater., 2016, 28, 1419 CrossRef CAS.
- J.-M. Tarascon, Joule, 2020, 4, 1613–1620 CrossRef.
- K. Kubota, T. Asari, H. Yoshida, N. Yaabuuchi, H. Shiiba, M. Nakayama and S. Komaba, Adv. Funct. Mater., 2016, 26, 6047 CrossRef CAS.
- P. F. Wang, Y. You, Y. X. Yin and Y. G. Guo, Adv. Energy Mater., 2018, 8, 1701912 CrossRef.
- J. L. Kaufman and A. Van der Ven, Phys. Rev. Mater., 2019, 3, 015402 CrossRef CAS.
- T. Jin, H. Li, K. Zhu, P. F. Wang, P. Liu and L. Jiao, Chem. Soc. Rev., 2020, 49, 2342 RSC.
- C. Masquelier and L. Croguennec, Chem. Rev., 2013, 113, 6552 CrossRef CAS PubMed.
- S. C. Chung, J. Ming, L. Lander, J. Lu and A. Yamada, J. Mater. Chem. A, 2018, 6, 3919 RSC.
- P. Barpanda, G. Oyama, S. Nishimura, S.-C. Chung and A. Yamada, Nat. Commun., 2014, 5, 4358 CrossRef CAS PubMed.
- H. Y. P. Hong, Mater. Res. Bull., 1976, 11, 173 CrossRef CAS.
- J. B. Goodenough, H. Y. P. Hong and J. A. Kafalas, Mater. Res. Bull., 1976, 11, 203 CrossRef CAS.
- Q. Ma, C. L. Tsai, X. K. Wei, M. Heggen, F. Tietz and J. T. S. Irvine, J. Mater. Chem. A, 2019, 7, 7766 RSC.
- Z. Jian, Y. S. Hu, X. Ji and W. Chen, Adv. Mater., 2017, 29 DOI:10.1002/adma.201601925.
- R. V. Panin, O. A. Drozhzhin, S. S. Fedotov, N. R. Khasanova and E. V. Antipov, Electrochim. Acta, 2018, 289, 168 CrossRef CAS.
- C. Delmas, F. Cherkaoui, A. Nadiri and P. Hagenmuller, Mater. Res. Bull., 1987, 22, 631 CrossRef CAS.
- C. Delmas, A. Nadiri and J. L. Soubeyroux, Solid State Ionics, 1988, 28–30, 419 CrossRef.
- X. Zhang, X. Rui, D. Chen, H. Tan, D. Yang, S. Huang and Y. Yu, Nanoscale, 2019, 11, 2556 RSC.
- P. Senguttuvan, G. Rousse, M. E. Arroyo y de Dompablo, H. Vezin, J.-M. Tarascon and M. R. Palacín, J. Am. Chem. Soc., 2013, 135, 3897 CrossRef CAS PubMed.
- B. M. de Boisse, J. Ming, S. Nishimura and A. Yamada, J. Electrochem. Soc., 2016, 163, A1469 CrossRef.
- J. Wang, Y. Wang, D. Seo, T. Shi, S. Chen, Y. Tian, H. Kim and G. Ceder, Adv. Energy Mater., 2020, 10, 1903968 CrossRef CAS.
- D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 1271 CrossRef CAS.
- M. Dahbi, M. Kiso, K. Kubota, T. Horiba, T. Chafik, K. Hida, T. Matsuyama and S. Komaba, J. Mater. Chem. A, 2017, 5, 9917 RSC.
- H. Kim, J. Hong, G. Yoon, H. Kim, K.-Y. Park, M.-S. Park, W.-S. Yoon and K. Kang, Energy Environ. Sci., 2015, 8, 2963 RSC.
- F. Chen, V. M. Kovrugin, R. David, O. Mentré, F. Fauth, J. Chotard and C. Masquelier, Small Methods, 2019, 3, 1800218 CrossRef CAS.
- W. Zhou, L. Xue, X. Lü, H. Gao, Y. Li, S. Xin, G. Fu, Z. Cui, Y. Zhu and J. B. Goodenough, Nano Lett., 2016, 16, 7836 CrossRef CAS PubMed.
- X. Yao, Z. Zhu, Q. Li, X. Wang, X. Xu, J. Meng, W. Ren, X. Zhang, Y. Huang and L. Mai, ACS Appl. Mater. Interfaces, 2018, 10, 10022 CrossRef CAS PubMed.
- K. Saravanan, C. W. Mason, A. Rudola, K. H. Wong and P. Balaya, Adv. Energy Mater., 2013, 3, 444 CrossRef CAS.
- Y. Uebou, T. KiyabuI, S. Okada and J. Yamaki, Rep. Inst. Adv. Mater. Study, Kyushu Univ., 2002, 16, 1 CAS.
- F. Lalère, J. B. Leriche, M. Courty, S. Boulineau, V. Viallet, C. Masquelier and V. Seznec, J. Power Sources, 2014, 247, 975 CrossRef.
- Y. Noguchi, E. Kobayashi, L. S. Plashnitsa, S. Okada and J. I. Yamaki, Electrochim. Acta, 2013, 101, 59 CrossRef CAS.
- Z. Deng, G. Sai Gautam, S. K. Kolli, J.-N. Chotard, A. K. Cheetham, C. Masquelier and P. Canepa, Chem. Mater., 2020, 32, 7908 CrossRef CAS.
- J. Kang, S. Baek, V. Mathew, J. Gim, J. Song, H. Park, E. Chae, A. K. Rai and J. Kim, J. Mater. Chem., 2012, 22, 20857 RSC.
- Y. Liu, Y. Zhou, J. Zhang, Y. Xia, T. Chen and S. Zhang, ACS Sustainable Chem. Eng., 2017, 5, 1306 CrossRef CAS.
- R. Rajagopalan, B. Chen, Z. Zhang, X.-L. Wu, Y. Du, Y. Huang, B. Li, Y. Zong, J. Wang, G.-H. Nam, M. Sindoro, S. X. Dou, H. K. Liu and H. Zhang, Adv. Mater., 2017, 29, 1605694 CrossRef PubMed.
- K. Kawai, W. Zhao, S. Nishimura and A. Yamada, ACS Appl. Energy Mater., 2018, 1, 928 CrossRef CAS.
- W. Zhang, H. Li, Z. Zhang, M. Xu, Y. Lai and S. L. Chou, Small, 2020, 16, 2001524 CrossRef CAS PubMed.
- R. Liu, G. Xu, Q. Li, S. Zheng, G. Zheng, Z. Gong, Y. Li, E. Kruskop, R. Fu, Z. Chen, K. Amine and Y. Yang, ACS Appl. Mater. Interfaces, 2017, 9, 43632 CrossRef CAS PubMed.
- F. Lalère, V. Seznec, M. Courty, J. N. Chotard and C. Masquelier, J. Mater. Chem. A, 2018, 6, 6654 RSC.
- D. Wang, X. Bie, Q. Fu, D. Dixon, N. Bramnik, Y. S. Hu, F. Fauth, Y. Wei, H. Ehrenberg, G. Chen and F. Du, Nat. Commun., 2017, 8, 1 CrossRef PubMed.
- T. Zhu, P. Hu, X. Wang, Z. Liu, W. Luo, K. A. Owusu, W. Cao, C. Shi, J. Li, L. Zhou and L. Mai, Adv. Energy Mater., 2019, 9, 2 Search PubMed.
- H. Gao, Y. Li, K. Park and J. B. Goodenough, Chem. Mater., 2016, 28, 6553 CrossRef CAS.
- S. Patoux, G. Rousse, J. B. Leriche and C. Masquelier, Chem. Mater., 2003, 15, 2084 CrossRef CAS.
- H. Li, T. Jin, X. Chen, Y. Lai, Z. Zhang, W. Bao and L. Jiao, Adv. Energy Mater., 2018, 8, 1801418 CrossRef.
- S. Ghosh, N. Barman, M. Mazumder, S. K. Pati, G. Rousse and P. Senguttuvan, Adv. Energy Mater., 2020, 10, 1902918 CrossRef CAS.
- M. V. Zakharkin, O. A. Drozhzhin, I. V. Tereshchenko, D. Chernyshov, A. M. Abakumov, E. V. Antipov and K. J. Stevenson, ACS Appl. Energy Mater., 2018, 1, 5842 CrossRef.
- M. V. Zakharkin, O. A. Drozhzhin, S. V. Ryazantsev, D. Chernyshov, M. A. Kirsanova, I. V. Mikheev, E. M. Pazhetnov, E. V. Antipov and K. J. Stevenson, J. Power Sources, 2020, 470, 228231 CrossRef CAS.
- J. N. Chotard, G. Rousse, R. David, O. Mentré, M. Courty and C. Masquelier, Chem. Mater., 2015, 27, 5982 CrossRef CAS.
- H. Kabbour, D. Coillot, M. Colmont, C. Masquelier and O. Mentré, J. Am. Chem. Soc., 2011, 133, 11900 CrossRef CAS PubMed.
- F. Hatert, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, i30 CrossRef CAS PubMed.
- F. Lalère, V. Seznec, M. Courty, R. David, J. N. Chotard and C. Masquelier, J. Mater. Chem. A, 2015, 3, 16198 RSC.
- Z. Jian, C. Yuan, W. Han, X. Lu, L. Gu, X. Xi, Y. S. Hu, H. Li, W. Chen, D. Chen, Y. Ikuhara and L. Chen, Adv. Funct. Mater., 2014, 24, 4265 CrossRef CAS.
- D. Gryaznov, S. K. Stauffer, E. A. Kotomin and L. Vilčiauskas, Phys. Chem. Chem. Phys., 2020, 22, 11861 RSC.
- M. K. Y. Chan and G. Ceder, Phys. Rev. Lett., 2010, 105, 196403 CrossRef CAS PubMed.
- J. Zhang, G. Liang, C. Wang, C. Lin, J. Chen, Z. Zhang and X. S. Zhao, ACS Appl. Mater. Interfaces, 2020, 12(25), 28313–28319 CrossRef CAS PubMed.
- O. Tillement, J. C. Couturier, J. Angenault and M. Quarton, Solid State Ionics, 1991, 48, 249 CrossRef CAS.
- G. Bergerhoff, R. Hundt, R. Sievers and I. D. Brown, J. Chem. Inf. Comput. Sci., 1983, 23, 66 CrossRef CAS.
- P. A. Cox, Transition Metal Oxides: An Introduction to Their Electronic Structure and Properties, Oxford Univeristy Press, Oxford, UK, 2010 Search PubMed.
- J. Gopalakrishnan and K. K. Rangan, Chem. Mater., 1992, 4, 745 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- A. K. Padhi, K. S. Nanjundaswamy, C. Masquelier and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 2581 CrossRef CAS.
- H. Wang, C. Chen, C. Qian, C. Liang and Z. Lin, RSC Adv., 2017, 7, 33273 RSC.
- B. Manoun, A. El Jazouli, S. Krimi and A. Lachgar, Powder Diffr., 2004, 19, 162 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- S. Dudarev and G. Botton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- A. Jain, G. Hautier, C. J. Moore, S. Ping Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50, 2295 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta10688g |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |