Refined molecular microstructure and optimized carrier management of multicomponent organic photovoltaics toward 19.3% certified efficiency†
Shuixing
Li‡
a,
Chengliang
He‡
a,
Tianyi
Chen‡
a,
Jiale
Zheng‡
b,
Rui
Sun
 c,
Jin
Fang
d,
Yiyao
Chen
e,
Youwen
Pan
a,
Kangrong
Yan
a,
Chang-Zhi
Li
c,
Jin
Fang
d,
Yiyao
Chen
e,
Youwen
Pan
a,
Kangrong
Yan
a,
Chang-Zhi
Li
 a,
Minmin
Shi
a,
Minmin
Shi
 a,
Lijian
Zuo
a,
Lijian
Zuo
 a,
Chang-Qi
Ma
a,
Chang-Qi
Ma
 d,
Jie
Min
d,
Jie
Min
 c,
Yujing
Liu
c,
Yujing
Liu
 *b and
Hongzheng
Chen
*b and
Hongzheng
Chen
 *a
*a
aState Key Laboratory of Silicon Materials, International Research Center for X Polymers, Department of Polymer Science and Engineering, Zhejiang University, Hangzhou 310027, P. R. China. E-mail: hzchen@zju.edu.cn
bCollege of Materials Science and Engineering, Zhejiang University of Technology, Hangzhou 310014, P. R. China. E-mail: yujingliu@zjut.edu.cn
cThe Institute for Advanced Studies, Wuhan University, Wuhan 430072, P. R. China
di-Lab & Printable Electronics Research Centre, Suzhou Institute of Nano-tech and Nano-bionics, Chinese Academy of Sciences, Suzhou 215123, P. R. China
eVacuum Interconnected Nanotech Workstation (Nano-X), Suzhou Institute of Nano-Tech and Nano-Bionics, Chinese Academy of Sciences, Suzhou 215123, P. R. China
First published on 4th April 2023
Abstract
Intuitive nanoscale visualization of sensitive donor–acceptor (D–A) heterojunction interfaces is still a huge challenge in organic photovoltaics (OPVs) but plays a critical role in carrier management. Herein, nanoscale visualization of the interfaces of newly developed asymmetric non-fullerene acceptors (NFAs) with an ideal absorption edge is realized and some interesting molecular microstructural features, including the alloy-like symbiosis of two NFAs in one domain and curved-crystal behavior in the D:A blend, are uncovered and further correlated with the charge transport and non-radiative loss properties in binary and ternary systems. It is also unveiled that for wide bandgap donor and narrow bandgap acceptor systems, the interfacial bending energy obtained on the ionization potential side is negatively correlated with non-radiative loss in small driving force systems, another factor in manipulating energy loss. Finally, double-channel recombination suppression leads to a record efficiency of 19.3% (certified: 19.3%) for asymmetric acceptor-based quaternary OPVs. This work brings interface research into a new era that enables the discovery of intrinsic interfacial features at under sub-nanometer resolution, thus facilitating intrinsic correlations between molecular microstructure and carrier management.
Broader contextDespite the rapid rise in power conversion efficiency (PCE) for organic photovoltaics (OPVs), there is still the main challenge of large non-radiative recombination loss, which hinders the performance of approaching the Shockley–Queisser (SQ) limit. The opportunity to mitigate non-radiative loss may lie in the heterojunction interfaces, a clear picture of which is waiting to be unveiled via nanoscale research. Herein, we developed various asymmetric acceptors and performed nanoscale studies on their interfaces, thus uncovering hidden molecular microstructural features, which are further correlated with charge transport and non-radiative loss, and disclosing the critical role of interfacial bending energy in energy loss. With optimized carrier management, a record certified efficiency of 19.3% was achieved for asymmetric acceptor-based OPVs. This work sheds light on solving the energy loss issue and leading OPV research into the nanoscale level. |
Introduction
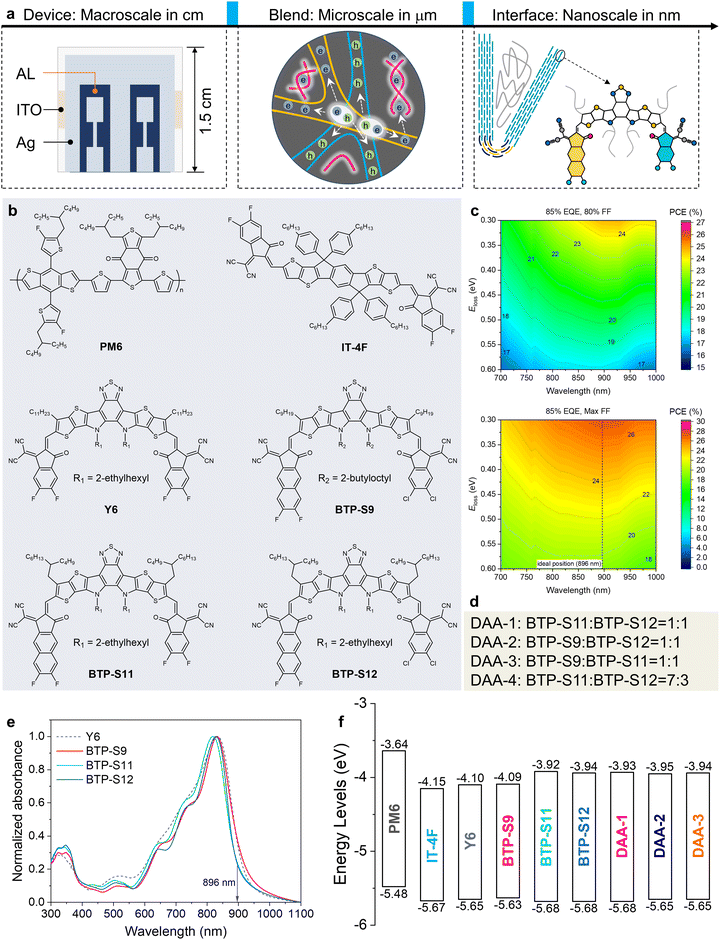
Single-junction organic photovoltaics (OPVs) based on non-fullerene acceptors (NFAs) have achieved an efficiency of over 19% recently, thanks to the emergence of Y-series molecules with high luminescence and multiple charge transport channels.1–13 The continuous increase of efficiency is closely related to the careful management of carrier dynamics, including the processes of charge separation, recombination, transport, and collection.14 Hence, research at different scales has been performed to disclose and optimize carrier behaviours (Fig. 1(a)). At the macroscopic level, designing suitable buffer layers between the active layer (AL) and electrode and constructing an island-like electrode have been found effective to improve the charge collection for a higher short-circuit current density (Jsc).15–18 At the microscopic level, forming a double-fibril network morphology is a feasible way to achieve both efficient charge separation and transport for a better fill factor (FF).8,19 As a result, both the Jsc and FF have progressed significantly toward their Shockley–Queisser (SQ) limits, while open-circuit voltage (Voc) still lags.20 The large Voc loss is mainly caused by the existence of disadvantageous non-radiative recombination loss.21–23One established rule is the approximately linear relationship between non-radiative recombination loss and the energetic offset (ΔELE–CT), which is the energetic difference between the local exciton (LE) state and the charge transfer (CT) state, but this no longer holds true if the energetic offset is less than 0.1 eV.24 It is thus desirable to explore the rules for mitigating non-radiative recombination loss in small driving force systems (ΔELE–CT < 0.1 eV).25–28
In OPVs, the donor–acceptor (D–A) heterojunction interfaces are the main locations for the carrier dynamics of charge transfer, separation and recombination and are also where the CT state occurs.29 As non-radiative recombination loss mainly occurs in the CT state, the D–A heterojunction interfaces play a crucial role in affecting non-radiative recombination loss.30 Despite their importance, the D–A heterojunction interfaces remain a mystery, as unveiling the detailed packing behaviors at nanoscale is quite challenging. In previous research, interface studies were mostly performed in indirect ways or at limited resolutions and are thus unable to reveal intrinsic interfacial features, like structural ordering and defects, under sub-nanometer resolution.31–33 In addition, a multicomponent strategy introducing extra donor or acceptor components to binary systems is commonly used to improve the carrier dynamics and device parameters, especially in pursuing a higher Voc.34–41 However, how the extra component combines with the host materials at the nanoscale level is not yet well understood, building barriers to acquiring design rules for successful multicomponent blends.42 In summary, the field of nanoscale study on interfaces is still blank but is critical to the exploration of successful multicomponent systems with comprehensive carrier management, particularly with non-radiative recombination loss mitigation.
In this work, based on a series of asymmetric Y-series NFAs (Fig. 1(b)), besides a traditional macroscale study on the device and a microscale study on the blend, we performed nanoscale visualization on the interfaces of the binary and multicomponent systems, uncovering some interesting molecular microstructural features, including the alloy-like symbiosis of two NFAs in one domain and curved-crystal behavior in the D:A blend, which are further correlated with carrier management, including non-radiative recombination loss and charge transport. Finally, double channel recombination suppression (DCRS) via a triple asymmetric acceptor (TAA) strategy enables a highest power conversion efficiency (PCE) of 19.3% (certified 19.3%) with an improved Voc of 0.89 V and an enhanced FF of 80%. This work achieves a visualization study on D/A interfaces under sub-nanometer resolution, thus bringing interface research into a new era.
Results and discussion
Material systems design
According to the SQ limits, there exists an ideal bandgap where the highest potential efficiency can be reached. Designing NFAs with an absorption edge close to the ideal bandgap is beneficial for solving the trade-off between photovoltage and photocurrent, thus maximizing the efficiency more easily. For example, by utilizing the quinoid resonance effect, Y6 shows an absorption edge (∼930 nm) closer to the ideal bandgap relative to IT-4F and is thus a current state-of-the-art NFA. For an accurate value of the ideal bandgap, theoretical efficiency calculations were performed, as illustrated in Fig. S1 and Note S1 (ESI†) and depicted in Fig. 1(c). It was found that the ideal absorption wavelength edge is around 896 nm, corresponding to a bandgap of 1.384 eV, which means further modifications should still be performed on Y6 to get a NFA with the ideal bandgap. This also indicated that, under the reasonable set of 85% external quantum efficiency (EQE) and 80% FF, an Eloss of 0.506 eV will be required for 20% efficiency based on photovoltaic materials with the ideal bandgap.Based on the skeleton of Y6, the molecular design strategies of asymmetric terminals, branched alkyl side chains and halogen atom tuning were used, yielding the NFAs BTP-S9, BTP-S11 and BTP-S12 (Fig. 1(b)), among which BTP-S11 and BTP-S12 possess an absorption edge of ∼896 nm. The synthetic details of the asymmetric acceptors can be found in ESI† (Fig. S2–S7). Based on the above three asymmetric NFAs, a dual asymmetric acceptor (DAA) strategy is proposed for multicomponent study (Fig. 1(d)). The basic absorption and energy level properties of the various NFAs are displayed in Fig. 1(e)–(f) and Fig. S8, S9 (ESI†).
Device performance study
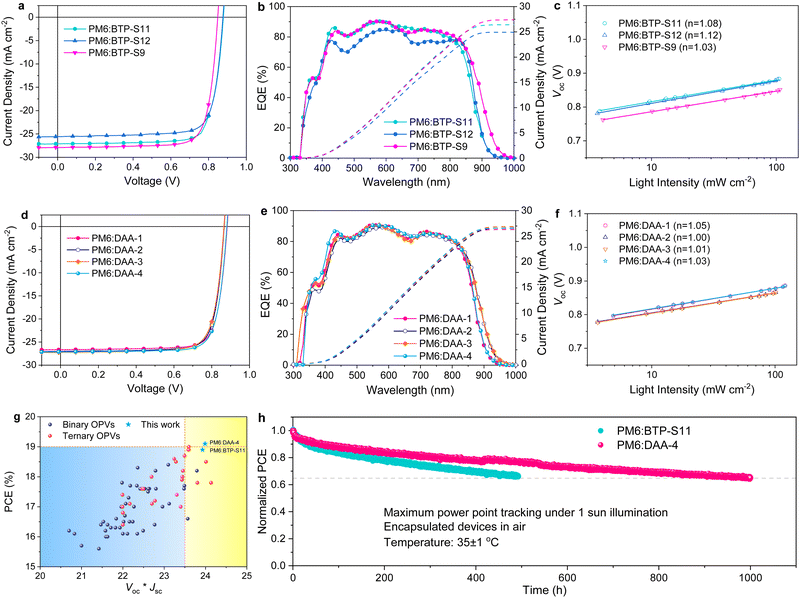
Binary and ternary OPVs were fabricated with the conventional device structure of indium tin oxide (ITO)/poly(3,4-ethylenedioxythiophene) polystyrene sulfonate (PEDOT:PSS)/active layer/bisfulleropyrrolidinium tris(methoxyethoxy) phenyl iodide (Bis-FIMG)/Ag to check the photovoltaic performance (Fig. S10, ESI†). The fabrication details can be found in ESI.† As shown in Fig. 2 and Table 1, binary OPVs based on a PM6:BTP-S11 blend delivered a maximum PCE of 18.9% with a high Voc of 0.878 V, large Jsc of 27.1 mA cm−2 and outstanding FF of 79.3%, better than the binary OPVs based on PM6:BTP-S12 (PCE of 17.7%) or PM6:BTP-S9 (PCE of 18.8%). The above three binary systems show similar FFs of ∼79%, comparing favourably with FF variations in ternary systems. The efficiency variations among these three binary systems originate from the change of voltage and photocurrent. The variation trend of voltage conforms to the relationship presented in the lowest unoccupied molecular (LUMO) levels of the relevant NFAs (Fig. 1(f)). The significantly lower photocurrent (25.6 mA cm−2) for PM6:BTP-S12-based OPVs is partly limited by the formation of large domains caused by the strong aggregation of BTP-S12, as discussed below.| Device type | Active layera | V oc (V) | J sc (mA cm−2) | FF (%) | PCE (%) |
|---|---|---|---|---|---|
a The total D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A weight ratio is fixed as 1 A weight ratio is fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2.
b TAA-1 is BTP-S11 1.2.
b TAA-1 is BTP-S11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BTP-S12 BTP-S12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BTP-S2 = 0.7 BTP-S2 = 0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2.
c Certified result by National Photovoltaic Industry Metrology and Testing Center, China. 0.2.
c Certified result by National Photovoltaic Industry Metrology and Testing Center, China.
|
|||||
| Binary | PM6:BTP-S11 | 0.878 (0.881 ± 0.002) | 27.1 (26.8 ± 0.2) | 79.3 (79.0 ± 0.4) | 18.9 (18.7 ± 0.1) |
| PM6:BTP-S12 | 0.876 (0.877 ± 0.002) | 25.6 (25.2 ± 0.3) | 78.8 (78.6 ± 0.5) | 17.7 (17.3 ± 0.2) | |
| PM6:BTP-S9 | 0.849 (0.850 ± 0.001) | 27.9 (27.7 ± 0.1) | 79.2 (78.7 ± 0.3) | 18.8 (18.5 ± 0.1) | |
| Ternary | PM6:DAA-1 | 0.881 (0.881 ± 0.001) | 26.7 (26.6 ± 0.1) | 80.0 (79.8 ± 0.2) | 18.8 (18.7 ± 0.1) |
| PM6:DAA-2 | 0.866 (0.866 ± 0.001) | 27.0 (26.9 ± 0.1) | 79.8 (79.8 ± 0.1) | 18.7 (18.6 ± 0.1) | |
| PM6:DAA-3 | 0.865 (0.866 ± 0.001) | 27.3 (27.0 ± 0.1) | 78.5 (78.4 ± 0.3) | 18.5 (18.3 ± 0.1) | |
| PM6:DAA-4 | 0.880 (0.882 ± 0.001) | 27.1 (27.0 ± 0.1) | 79.9 (79.6 ± 0.2) | 19.1 (18.9 ± 0.1) | |
| Quaternary | PM6:TAA-1b | 0.890 (0.891 ± 0.002) | 27.2 (27.1 ± 0.1) | 80.0 (79.6 ± 0.3) | 19.3 (19.1 ± 0.1) |
| PM6:TAA-1c | 0.885 | 27.5 | 79.3 | 19.3 | |
For ternary OPVs, a common rule is that compositional dependent voltage variation normally shows a linear relationship,40 as seen in the PM6:DAA-3 system (Fig. S11, ESI†). However, neither the PM6:DAA-1 nor the PM6:DAA-2 system follow a linear relationship and some even show higher voltages than the linear values. Correspondingly, an increase in FF is observed in both the PM6:DAA-1 and PM6:DAA-2 systems, but not in the PM6:DAA-3 system (Fig. S12, ESI†), indicating that PM6:DAA-1 and PM6:DAA-2 are ternary systems behaving differently from that of PM6:DAA-3.
Subsequently, we optimized the weight ratio of BTP-S11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BTP-S12 composite to 7
BTP-S12 composite to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, termed DAA-4, and achieved an optimized PCE of 19.1% with a Voc of 0.880 V, Jsc of 27.1 mA cm−2 and FF of 79.9%. A full copy of the certification report from the National Photovoltaic Industry Measurement and Testing Center (NPVIM) of China for PM6:DAA-4-based OPVs is provided as Fig. S13 (ESI†). Notably, the (Voc × Jsc) values are positively correlated with the PCE values (Fig. 2(g) and Table S1, ESI†), as designing photovoltaic materials with an absorption edge close to the ideal bandgap is beneficial for maximizing the (Voc × Jsc) values.
3, termed DAA-4, and achieved an optimized PCE of 19.1% with a Voc of 0.880 V, Jsc of 27.1 mA cm−2 and FF of 79.9%. A full copy of the certification report from the National Photovoltaic Industry Measurement and Testing Center (NPVIM) of China for PM6:DAA-4-based OPVs is provided as Fig. S13 (ESI†). Notably, the (Voc × Jsc) values are positively correlated with the PCE values (Fig. 2(g) and Table S1, ESI†), as designing photovoltaic materials with an absorption edge close to the ideal bandgap is beneficial for maximizing the (Voc × Jsc) values.
EQE tests were synchronously performed to cross-check the photocurrent generation, as shown in Fig. 2(b) and (e). High and broad photoresponses are observed for PM6:BTP-S11 and PM6:BTP-S9-based binary OPVs with the highest EQE values exceeding 90%, with a lower response for the PM6:BTP-S12-based one, which conforms to the Jsc values presented in the J–V curves (Fig. 2(a)). The integrated current densities from the EQE curves are found to be 26.39 mA cm−2, 24.93 mA cm−2 and 27.40 mA cm−2 for the PM6:BTP-S11-based, PM6:BTP-S12-based and PM6:BTP-S9-based OPVs, respectively, with errors of less than 3% of the Jsc values (Fig. 2(b)). For the ternary OPVs, the photoresponse intensities are similar and the differences mainly lie in the absorption ranges. The PM6:DAA-4-based OPVs show slightly higher EQE values in the 350–450 nm range than the PM6:DAA-1-based OPVs, enabling the higher current density detected in the J–V curves (Fig. 2(d)). The integrated current densities are calculated to be 26.30 mA cm−2, 26.59 mA cm−2, 26.87 mA cm−2 and 26.56 mA cm−2 for the PM6:DAA-1-based, PM6:DAA-2-based, PM6:DAA-3-based and PM6:DAA-4-based OPVs with errors within 2% of the Jsc values (Fig. 2(e)).
Light intensity variation measurements were conducted to examine the charge recombination situations. The relationship between Jsc and light intensity (Plight) can be expressed as Jsc ∝ Pαlight. For both the binary and ternary OPVs, the α values all approach 1, indicating similar situations in bimolecular recombination (Fig. S14, ESI†). The relationship between Voc and Plight can be expressed as Voc ∝ nkT/qln(Plight). Similarly, only minor differences are presented among the ideal factor values of n, which are all close to 1 (Fig. 2(c) and (f)).
Long-term light stability with maximum power point (MPP) tracking under 1 sun illumination was tested for the best binary OPV PM6:BTP-S11 and the best ternary OPV PM6:DAA-4. As shown in Fig. 2(h), the ternary OPV shows a shorter burn-in region and a better long-term linear decay region than the binary OPV, with 65% initial efficiency maintained after 1000 h illumination at MPP condition, implying that the ternary blend effectively improves the device stability.
The charge transport property was examined by the space-charge limited current (SCLC) method. The results are plotted in Fig. S15 (ESI†) and summarized in Table S2 (ESI†). Among the three binary systems, both the PM6:BTP-S11-based and PM6:BTP-S9-based devices show higher hole (μh) and electron (μe) mobilities and also more balanced μh/μe ratios than the PM6:BTP-S12-based one. Among the four ternary systems, the PM6:DAA-1-based device retains a high μh comparable to that of the PM6:BTP-S11-based one and acquires a higher μe than the binary systems of PM6:BTP-S11 and PM6:BTP-S12. However, both μh and μe are negatively affected in the PM6:DAA-2-based and PM6:DAA-3-based devices compared with their relevant binary ones. The benefits in mobility for the PM6:DAA-1-based OPV might contribute to the achievement of a higher FF relative to the PM6:DAA-2- and PM6:DAA-3-based OPVs. For the PM6:DAA-4-based device, both μh and μe are simultaneously enhanced, thus endowing a higher PCE relative to that of the PM6:DAA-1-based one.
Blend property study
To identify the blend properties, we performed multiple characterizations from the aspects of miscibility, aggregation, thermal property, and crystallinity. For miscibility, through contact angle experiments (Fig. S16 and Table S3, ESI†), a higher Flory–Huggins interaction parameter (χ) was found between PM6 and BTP-S9 relative to BTP-S11 and BTP-S12, indicating that alkyl side-chain induced molecular packing evolution is effective for miscibility tuning.4 Furthermore, a reduced miscibility was also presented between PM6 and DAA-1 relative to BTP-S11 and BTP-S12, which differs from DAA-2 or DAA-3, implying a ternary blend as another feasible way for miscibility tuning.43 For aggregation, through atomic force microscopy (AFM) images (Fig. S17 and S18, ESI†), except for BTP-S12 which shows a strong aggregation tendency, all the other films possess relatively smooth surfaces with a small roughness of 0.5–0.7 nm. For the thermal property, differential scanning calorimetry (DSC) measurements were conducted (Fig. S19, ESI†). BTP-S9, BTP-S11 and BTP-S12 have three different melting points (307.1 °C for BTP-S9, 315.1 °C for BTP-S11 and 329.1 °C for BTP-S12). For DAA-2 and DAA-3, two melting points appear and move to a lower temperature range relative to the relevant single acceptors. For DAA-1, only one melting point (312.8 °C), which differs from those of BTP-S11 and BTP-S12, was observed. The above thermal property variations imply that DAA-1 possibly works as an alloy-like model more than DAA-2 and DAA-3. For crystallinity, grazing-incidence wide-angle X-ray scattering (GIWAXS) measurements were performed and the results are displayed in Fig. S20–S24 (ESI†). Both BTP-S11 and BTP-S12 show a π–π stacking peak at q = 1.75 Å−1 (d = 3.59 Å) in the out-of-plane direction and a lamellar peak at q = 0.43 Å−1 (d = 14.60 Å) in the in-plane direction; for BTP-S9, the π–π stacking peak in the out-of-plane direction moves to q = 1.76 Å−1 (d = 3.57 Å) and the lamellar peak in the in-plane direction moves to q = 0.40 Å−1 (d = 15.70 Å). All the NFAs adopt a face-on orientation and possess good crystallinity. For the binary blends, high crystallinity is retained in the PM6:BTP-S9 and PM6:BTP-S11 systems, but not in PM6:BTP-S12, which explains why the PM6:BTP-S12 system shows lower mobilities and worse performance, as shown above. For the ternary blends, PM6:DAA-1 shows higher crystallinity than the PM6:DAA-2 and PM6:DAA-3 systems. In addition, the π–π stacking peak of PM6:DAA-1 film is located at q = 1.74 Å−1 (d = 3.61 Å), a bit tighter than those of the PM6:DAA-2 and PM6:DAA-3 films (q = 1.73 Å−1, d = 3.63 Å). The PM6:DAA-4 system is similar to the PM6:DAA-1 system.Molecular microstructure visualization
To directly observe the molecular interfaces with angstrom-level resolution, high resolution transmission electron microscopy (HR-TEM) technology was applied. As shown in Fig. 3, BTP-S11 shows an interplanar crystal spacing ranging from 0.20 to 0.25 nm, smaller than that of BTP-S12 (0.26–0.29 nm), a typical feature to distinguish between these two NFAs’ crystalline regions. In the DAA-1 film, BTP-S11 and BTP-S12 coexist in one domain of ∼50 nm instead of forming individual crystalline domains. This phenomenon, where two NFAs co-crystallize edge-to-edge to form one homogenous domain, is termed alloy-like symbiosis. It was also found that such alloy-like symbiosis renders the formation of sphero-crystals with exceptionally high crystallinity. As shown in Fig. S25 (ESI†), BTP-S9 possesses a larger interplanar crystal spacing of ∼0.35 nm. When BTP-S9 and BTP-S12 are mixed to form DAA-2, the alloy-like symbiosis phenomenon can still be observed but is not as distinct as in DAA-1. When BTP-S9 and BTP-S11 are mixed to form DAA-3, the alloy-like symbiosis phenomenon disappears, probably due to the large discrepancy (>0.1 nm) in the interplanar crystal spacings of the two molecules. This alloy-like symbiosis may explain why the PM6:DAA-1 and PM6:DAA-2 systems acquire an enhancement in FF, but the PM6:DAA-3 system does not. It seems that lattice matching is one of the prerequisites for forming alloy-like symbiosis and an interplanar crystal spacing difference of no more than 0.1 nm between the two NFAs is preferred. To further confirm our supposition, another asymmetric NFA BTP-15 with four chlorine atoms was synthesized for study (Fig. S26, ESI†), as it has a significantly large interplanar crystal spacing of ∼0.45 nm (Fig. S27, ESI†). When BTP-S9 and BTP-S15 are blended to form DAA-5 (BTP-S9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BTP-S15 = 1
BTP-S15 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), no alloy-like symbiosis domains are identified, while an individual large domain is formed for BTP-S9/BTP-S15 itself, certifying the importance of lattice matching in the formation of alloy-like symbiosis. As a result, reduced Jsc and FF values were observed in the PM6:DAA-5-based ternary device relative to those of the PM6:BTP-S9-based binary device, similar to that observed in the PM6:DAA-3 system (Fig. S28, ESI†).
1), no alloy-like symbiosis domains are identified, while an individual large domain is formed for BTP-S9/BTP-S15 itself, certifying the importance of lattice matching in the formation of alloy-like symbiosis. As a result, reduced Jsc and FF values were observed in the PM6:DAA-5-based ternary device relative to those of the PM6:BTP-S9-based binary device, similar to that observed in the PM6:DAA-3 system (Fig. S28, ESI†).
Then, we studied the molecular microstructure in D:A blends, as shown in Fig. 3 and Fig. S29 (ESI†). Relatively, the NFAs show a higher crystallinity than PM6 and their features can thus be observed in the D:A blends more easily. Surprisingly, a new curved-crystal phenomenon from the NFAs was observed, connecting with the straight crystal in a uniform interplanar crystal spacing, especially in the PM6:BTP-S9 and PM6:BTP-S11 systems. Such a curved crystal only appears in the D:A blends and cannot be found in the neat donor or acceptor films, implying its formation may be related to the molecular interaction between D and A. Curved crystal is beneficial for creating sufficient D/A interfaces for charge separation, but also risks forming more CT states, thus providing more opportunities for the formation of non-geminate triplet CT states that normally recombine in a non-radiative way.44,45 In the PM6:DAA-1 system, the curved-crystal behavior is relieved to some extent, which further affects the non-radiative recombination loss mitigation, as revealed below. Further, the relief of curved-crystal behavior in the PM6:DAA-1 blend might be from the reduced miscibility and formed sphero-crystals demonstrated above.
Energy loss analysis
To explain the different voltage variation trends in the ternary OPVs, we performed detailed energy loss analyses for the binary and ternary OPVs studied in this work. The relevant results are displayed in Fig. 4 and the detailed parameters are summarized in Table 2. We determined the bandgaps via the integral method of EQE curves (Fig. S30, ESI†), which considers effects from both the absorption of active layer materials and the whole device, by applying eqn (1)46 | (1) |
ΔE3 = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(EQEEL) ln(EQEEL) | (2) |
| Active layer | E g (eV) | V SQoc (V) | V radoc (V) | ΔE1 (eV) | ΔE2 (eV) | ΔE3 (eV) | E loss (eV) | EQEEL (%) |
|---|---|---|---|---|---|---|---|---|
| PM6:BTP-S11 | 1.425 | 1.168 | 1.075 | 0.257 | 0.093 | 0.194 | 0.544 | 4.12 × 10−2 |
| PM6:BTP-S12 | 1.409 | 1.155 | 1.086 | 0.254 | 0.069 | 0.210 | 0.533 | 3.12 × 10−2 |
| PM6:BTP-S9 | 1.379 | 1.128 | 1.050 | 0.251 | 0.078 | 0.201 | 0.530 | 3.17 × 10−2 |
| PM6:DAA-1 | 1.425 | 1.171 | 1.060 | 0.254 | 0.111 | 0.179 | 0.544 | 8.67 × 10−2 |
| PM6:DAA-2 | 1.393 | 1.142 | 1.056 | 0.251 | 0.086 | 0.190 | 0.527 | 6.38 × 10−2 |
| PM6:DAA-3 | 1.378 | 1.122 | 1.064 | 0.256 | 0.058 | 0.199 | 0.513 | 3.62 × 10−2 |
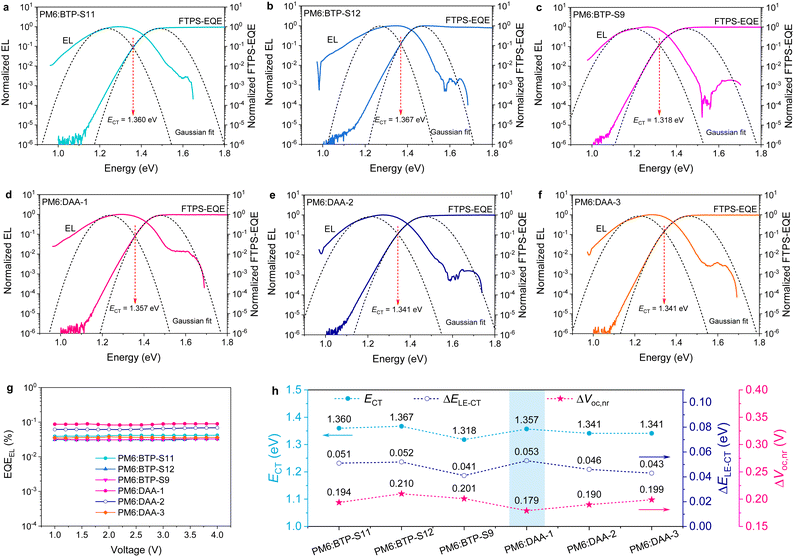
The three binary OPVs exhibit various EQEEL values of 3–4 × 10−2%, giving ΔE3 values of 0.194 eV for the PM6:BTP-S11 device, 0.210 eV for the PM6:BTP-S12 device and 0.201 eV for the PM6:BTP-S9 device (Table 2). However, we observe two different phenomena in the luminescence properties of the three ternary OPVs. For the PM6:DAA-3-based device, the EQEEL value (3.62 × 10−2%) lies between those of the PM6:BTP-S11-based and PM6:BTP-S9-based ones, which is a normal result. But, exceptional (over two times) enhancements in EQEEL values are found for the PM6:DAA-1-based (8.67 × 10−2%) and PM6:DAA-2-based (6.38 × 10−2%) devices relative to the relevant binary ones, thus enabling specifically low ΔE3 values of 0.179 eV for the PM6:DAA-1-based device and 0.190 eV for the PM6:DAA-2-based device. Such obvious luminescence enhancement in the PM6:DAA-1-based and PM6:DAA-2-based ternary OPVs is likely partly responsible for the non-linear voltage variation (Fig. S11, ESI†).
To explain the variations in ΔE2, we compare the energetic disorders in these binary and ternary systems by extracting the Urbach energy (EU) through exponential fitting of the Fourier transform photocurrent spectroscopy (FTPS)–EQE curves. The results can be found in Fig. S31 and S32 (ESI†). Among the three binary systems, the PM6:BTP-S12-based device possesses the lowest EU of 21.67 meV and also the lowest ΔE2 of 0.069 eV, implying that the relationship between EU and ΔE2 is positively related. Similarly, the PM6:DAA-3-based device has the lowest EU of 21.84 meV and also the lowest ΔE2 of 0.058 meV. In addition, the PM6:DAA-1-based device presents a reduced EU of 22.48 meV relative to the PM6:BTP-S11-based one (EU = 23.06 meV).
The CT state plays an important role during the working of OPVs, affecting charge recombination and charge separation.30 We determine the CT states for these binary and ternary OPVs by performing Gaussian fits to the FTPS–EQE and EL curves via the Marcus Equations,48
 | (3) |
 | (4) |
Interfacial bending energy
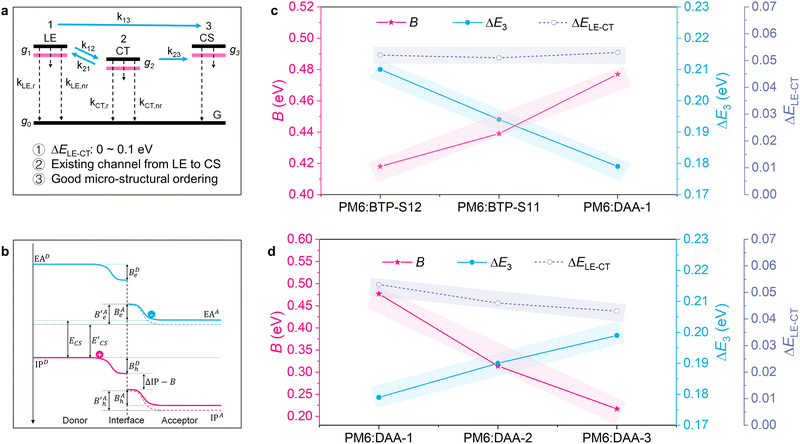
As shown in Fig. 5(a), for large driving force systems (ΔELE–CT > 0.1 eV), the large-enough energetic offset drives the Boltzmann equilibrium between the LE and CT states as the dominant way to determine the CT state ratio. Under this precondition, when the stationary state of the reaction between the LE and CT states is reached, the equilibrium constant K can be obtained as follows.28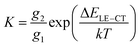 | (5) |
Thus, narrowing ΔELE–CT reduces the K value, giving a lower CT state ratio and lower ΔE3. However, for small driving force systems (ΔELE–CT < 0.1 eV), the above results show that ΔE3 is not simply decided by the lone factor of ΔELE–CT. A possible approach for resolving this puzzle is to take an extra process, from the LE state to a charge separation (CS) state, into consideration in the Boltzmann equilibrium (Fig. 5(a)). Such a process directly from the LE to CS states for Y-series NFAs has been confirmed in previous research.49–51 If we consider both processes of LE–CT and LE–CS in the Boltzmann equilibrium, when the stationary state of the reaction is reached, the modified equilibrium constant K′ will be obtained by
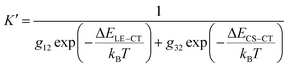 | (6) |
Next, we explore the factors existing at the D/A interfaces that affect ΔECS–CT. As shown in Fig. 5(b), an energy level bending phenomenon exists at the D/A interfaces, caused by the electrostatic interaction of charges with the quadrupole moments of surrounding molecules.52 The energy level bending phenomenon results in an important parameter named interfacial bending energy (B), through which we can identify the following relationship between ΔECS–CT and B.
| ΔECS–CT = ECS − ECT = ECTCoulomb − B | (7) |
Through the above equation, we learn that ΔECS–CT and B are negatively related, i.e., enlarging the value of B reduces ΔECS–CT (see analysis in Note S3, ESI†). The parameter B could be the factor that is responsible for the non-radiative loss mitigation in small driving force systems.
To calculate the value of B, we measured the ionization potential (IP) levels for all donors and acceptors (Fig. S33 and S34, ESI†) with which the value of B can be obtained through the following equation.
| B = ΔIP − ΔELE–CT | (8) |
The relevant results are analyzed in Note S4 (ESI†) and summarized in Table S4 (ESI†). We plotted the relationships among ΔE3, ΔELE–CT and B, shown in Fig. 5(c) and (d), for various systems. As shown in Fig. 5(c), the PM6:BTP-S12, PM6:BTP-S11 and PM6:DAA-1 systems possess nearly the same ΔELE–CT values and, with an increase in B, ΔE3 is gradually reduced. As displayed in Fig. 5(d), for the three ternary systems, a gradually reduced ΔELE–CT value does not result in the reduction of ΔE3; correspondingly, a gradually increased B value will lead to a reduced ΔE3. The above results uncover the correlation that the interfacial bending energy of B is negatively correlated with the non-radiative recombination loss of ΔE3 for small driving force systems. Thus, besides reducing energetic offset, enlarging the interfacial bending energy is another feasible approach for mitigating non-radiative recombination loss in small driving force systems.
Correlation analysis
During the process of exciton changing to free charge, one possible channel is LE–CT–CS, in which non-radiative recombination loss can be mitigated via tuning the CT state for a reduced ΔELE–CT. For classification, this recombination suppression is named “channel I recombination suppression” here. Another possible channel is LE–CS, in which non-radiative recombination loss can be mitigated via tuning the interfacial bending energy for a reduced ΔECS–CT, as revealed in this work. This recombination suppression is named “channel II recombination suppression” here. To check whether double-channel recombination suppression (DCRS) is possible, another asymmetric NFA of BTP-S2 (Fig. S35, ESI†), which allows a higher CT state energy (ECT = 1.444 eV) and a narrower energetic offset (ΔELE–CT = 0.039 eV) in the PM6:BTP-S2-based device (Fig. S36, ESI†), was introduced to DAA-4, yielding TAA-1 (BTP-S11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BTP-S12
BTP-S12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BTP-S2 = 0.7
BTP-S2 = 0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3
0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2).3Fig. 6(a) shows the J–V curves of the three types of OPVs (binary, ternary and quaternary) and Fig. 6(b) compares the photovoltaic parameters among the three types of OPVs. The photovoltaic parameters of quaternary OPVs are also summarized in Table 1.
0.2).3Fig. 6(a) shows the J–V curves of the three types of OPVs (binary, ternary and quaternary) and Fig. 6(b) compares the photovoltaic parameters among the three types of OPVs. The photovoltaic parameters of quaternary OPVs are also summarized in Table 1.
It was found that Voc further increased to 0.89 V in the quaternary OPVs while Jsc and FF were maintained as high as those of the PM6:DAA-4-based ternary OPVs, leading to an improved PCE of 19.3%, which is the highest efficiency reported to date for asymmetric acceptor-based OPVs. The PM6:TAA-1-based device was sent to NPVIM for certification and a certified PCE of 19.3% was obtained (Fig. S37, ESI†). The EQE spectrum of the relevant quaternary device is provided as Fig. S38 (ESI†). The above result proves DCRS is feasible for improved device performance. As to the photovoltaic parameter variation, although channel I and channel II affect both Voc and FF, “channel I recombination suppression” benefits the Voc more, while “channel II recombination suppression” benefits the FF more (Fig. 6(b)).
Finally, we perform correlation analysis between the molecular microstructure and carrier management. As shown in Fig. 6(c), in multicomponent systems, when two NFAs are blended together, if they have unmatched lattices (average interplanar crystal spacing difference >0.1 nm, as measured with HR-TEM), it will be difficult for the two different types of NFA crystals to integrate into the same domain during the course of crystallization; thus, the formation of multiple phases will be preferred. If they have matched lattice spacings (average interplanar crystal spacing difference <0.05 nm), two different NFAs will first crystallize individually to form small-sized crystals (∼10 nm), then fuse edge-to-edge when these two types of small-sized crystals meet to form a homogeneous large domain, thus forming alloy-like symbiosis. Alloy-like symbiosis is beneficial for the formation of sphero-crystals which help reduce the miscibility with the donor (Fig. S16, ESI†) and enhance crystallinity (Fig. S20–S24, ESI†). As a result, the charge transport property is promoted, leading to an improved FF.
When a polymer donor is blended with the NFAs, curved-crystal behavior from the NFAs appears at the D:A heterojunction interfaces, which act as bridges for constructing a fibril network. The existence of curved-crystal behavior creates more interfaces for charge separation, but also risks forming more CT states. Alloy-like symbiosis reduces the curved-crystal behavior to some extent, leads to enhanced crystallinity, and promotes intermolecular interaction and better mesoscale structural ordering, thus positively affecting the electrostatic interaction of charges with the enhanced quadrupole moment (Fig. S39, ESI†) and thereby enlarging the interfacial bending energy. An enlarged interfacial bending energy reduces ΔECS–CT, resulting in non-radiative loss mitigation. The above analysis reveals how molecular microstructural features, like alloy-like symbiosis and curved-crystal behavior, correlate with carrier management, including charge transport property and non-radiative loss mitigation. Furthermore, when the triple asymmetric acceptor strategy is applied, DCRS is achieved, leading to enhancements in both Voc and FF for a higher PCE. In the future, relative to FF, more efforts should be devoted to reducing non-radiative loss and DCRS could be a feasible approach (Fig. S40, ESI†).
Conclusions
In this work, we first performed theoretical efficiency calculations and developed asymmetric NFAs with an ideal absorption edge of ∼896 nm. Then, based on various asymmetric NFAs, besides a traditional macroscale study on the device and a microscale study on the blend, we initiated nanoscale study of the interfaces for binary and multicomponent OPV systems, through which some interesting molecular microstructural features were uncovered, including the alloy-like symbiosis of two NFAs in one domain and curved-crystal behavior in the D:A blend. Next, carrier management, including non-radiative loss and charge transport, was well studied, through which double-channel recombination suppression and the critical role of the interfacial bending energy on non-radiative loss mitigation were unveiled. Finally, the correlation between molecular microstructure and carrier management was made and a record certified efficiency of 19.3% was achieved in asymmetric acceptor-based OPVs with a high Voc of 0.89 V and a high FF of 80%. This work brings interface studies into a new era that opens the door for unveiling intrinsic interfacial features at the sub-nanometer resolution and provides a new strategy of DCRS for carrier management.Author contributions
S. L. and H. C. conceived the idea and designed the experiments. S. L. synthesized the asymmetric acceptors and performed the theoretical efficiency calculation. C. H. fabricated the binary and ternary devices and performed the related measurements. T. C. fabricated the quaternary devices and performed AFM measurement. J. Z. and Y. L. did the HR-TEM measurement. R. S. and J. M. carried out the energy loss test. J. F., Y. C. and C.-Q. M. did the GIWAXS measurement. C. H., T. C. and Y. P. conducted device fabrication for efficiency certification. K. Y. and C.-Z. L. provided Bis-FIMG. M. S. and L. Z. commented on this work. H. C. supervised the project. The manuscript was mainly written by S. L. and H. C., and all authors commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (no. 52127806, 21734008, 52273199, 61721005, 52173185, 52171225, 52102314), National Key Research and Development Program of China (no. 2019YFA0705902), the China Postdoctoral Science Foundation funded project (no. 2022M712737), the Fundamental Research Funds for the Central Universities (no. 226-2022-00133), and Shanxi-Zheda Institute of Advanced Materials and Chemical Engineering (2021SZ-FR001).Notes and references
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H.-L. Yip, T.-K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Joule, 2019, 3, 1140–1151 CrossRef CAS.
- Y. Cui, H. Yao, J. Zhang, K. Xian, T. Zhang, L. Hong, Y. Wang, Y. Xu, K. Ma, C. An, C. He, Z. Wei, F. Gao and J. Hou, Adv. Mater., 2020, 32, 1908205 CrossRef CAS PubMed.
- S. Li, L. Zhan, Y. Jin, G. Zhou, T.-K. Lau, R. Qin, M. Shi, C.-Z. Li, H. Zhu, X. Lu, F. Zhang and H. Chen, Adv. Mater., 2020, 32, 2001160 CrossRef CAS PubMed.
- C. Li, J. Zhou, J. Song, J. Xu, H. Zhang, X. Zhang, J. Guo, L. Zhu, D. Wei, G. Han, J. Min, Y. Zhang, Z. Xie, Y. Yi, H. Yan, F. Gao, F. Liu and Y. Sun, Nat. Energy, 2021, 6, 605–613 CrossRef CAS.
- Y. Cui, Y. Xu, H. Yao, P. Bi, L. Hong, J. Zhang, Y. Zu, T. Zhang, J. Qin, J. Ren, Z. Chen, C. He, X. Hao, Z. Wei and J. Hou, Adv. Mater., 2021, 33, 2102420 CrossRef CAS PubMed.
- S. Li, L. Zhan, N. Yao, X. Xia, Z. Chen, W. Yang, C. He, L. Zuo, M. Shi, H. Zhu, X. Lu, F. Zhang and H. Chen, Nat. Commun., 2021, 12, 4627 CrossRef CAS PubMed.
- L. Zhan, S. Li, Y. Li, R. Sun, J. Min, Z. Bi, W. Ma, Z. Chen, G. Zhou, H. Zhu, M. Shi, L. Zuo and H. Chen, Joule, 2022, 6, 662–675 CrossRef CAS.
- L. Zhu, M. Zhang, J. Xu, C. Li, J. Yan, G. Zhou, W. Zhong, T. Hao, J. Song, X. Xue, Z. Zhou, R. Zeng, H. Zhu, C.-C. Chen, R. C. I. MacKenzie, Y. Zou, J. Nelson, Y. Zhang, Y. Sun and F. Liu, Nat. Mater., 2022, 21, 656–663 CrossRef CAS PubMed.
- C. He, Y. Pan, Y. Ouyang, Q. Shen, Y. Gao, K. Yan, J. Fang, Y. Chen, C.-Q. Ma, J. Min, C. Zhang, L. Zuo and H. Chen, Energy Environ. Sci., 2022, 15, 2537–2544 RSC.
- K. Chong, X. Xu, H. Meng, J. Xue, L. Yu, W. Ma and Q. Peng, Adv. Mater., 2022, 34, 2109516 CrossRef CAS PubMed.
- C. He, Z. Chen, T. Wang, Z. Shen, Y. Li, J. Zhou, J. Yu, H. Fang, Y. Li, S. Li, X. Lu, W. Ma, F. Gao, Z. Xie, V. Coropceanu, H. Zhu, J.-L. Bredas, L. Zuo and H. Chen, Nat. Commun., 2022, 13, 2598 CrossRef CAS PubMed.
- J. Wang, P. Xue, Y. Jiang, Y. Huo and X. Zhan, Nat. Rev. Chem., 2022, 6, 614–634 CrossRef.
- G. Zhang, F. R. Lin, F. Qi, T. Heumüller, A. Distler, H.-J. Egelhaaf, N. Li, P. C. Y. Chow, C. J. Brabec, A. K. Y. Jen and H.-L. Yip, Chem. Rev., 2022, 122, 14180–14274 CrossRef CAS PubMed.
- M. Zhang, L. Zhu, G. Zhou, T. Hao, C. Qiu, Z. Zhao, Q. Hu, B. W. Larson, H. Zhu, Z. Ma, Z. Tang, W. Feng, Y. Zhang, T. P. Russell and F. Liu, Nat. Commun., 2021, 12, 309 CrossRef CAS PubMed.
- Y. Lin, B. Adilbekova, Y. Firdaus, E. Yengel, H. Faber, M. Sajjad, X. Zheng, E. Yarali, A. Seitkhan, O. M. Bakr, A. El-Labban, U. Schwingenschlögl, V. Tung, I. McCulloch, F. Laquai and T. D. Anthopoulos, Adv. Mater., 2019, 31, 1902965 CrossRef CAS PubMed.
- J. Yao, B. Qiu, Z.-G. Zhang, L. Xue, R. Wang, C. Zhang, S. Chen, Q. Zhou, C. Sun, C. Yang, M. Xiao, L. Meng and Y. Li, Nat. Commun., 2020, 11, 2726 CrossRef CAS PubMed.
- C. Cai, J. Yao, L. Chen, Z. Yuan, Z.-G. Zhang, Y. Hu, X. Zhao, Y. Zhang, Y. Chen and Y. Li, Angew. Chem., Int. Ed., 2021, 60, 19053–19057 CrossRef CAS PubMed.
- Y. Lin, Y. Firdaus, F. H. Isikgor, M. I. Nugraha, E. Yengel, G. T. Harrison, R. Hallani, A. El-Labban, H. Faber, C. Ma, X. Zheng, A. Subbiah, C. T. Howells, O. M. Bakr, I. McCulloch, S. D. Wolf, L. Tsetseris and T. D. Anthopoulos, ACS Energy Lett., 2020, 5, 2935–2944 CrossRef CAS.
- M. Zhang, L. Zhu, T. Hao, G. Zhou, C. Qiu, Z. Zhao, N. Hartmann, B. Xiao, Y. Zou, W. Feng, H. Zhu, M. Zhang, Y. Zhang, Y. Li, T. P. Russell and F. Liu, Adv. Mater., 2021, 33, 2007177 CrossRef CAS PubMed.
- P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Nat. Rev. Mater., 2019, 4, 269–285 CrossRef CAS.
- S. Liu, J. Yuan, W. Deng, M. Luo, Y. Xie, Q. Liang, Y. Zou, Z. He, H. Wu and Y. Cao, Nat. Photonics, 2020, 14, 300–305 CrossRef CAS.
- J. Yuan, H. Zhang, R. Zhang, Y. Wang, J. Hou, M. Leclerc, X. Zhan, F. Huang, F. Gao, Y. Zou and Y. Li, Chem, 2020, 6, 2147–2161 CAS.
- S. Li, C.-Z. Li, M. Shi and H. Chen, ACS Energy Lett., 2020, 5, 1554–1567 CrossRef CAS.
- X.-K. Chen, D. Qian, Y. Wang, T. Kirchartz, W. Tress, H. Yao, J. Yuan, M. Hülsbeck, M. Zhang, Y. Zou, Y. Sun, Y. Li, J. Hou, O. Inganäs, V. Coropceanu, J.-L. Bredas and F. Gao, Nat. Energy, 2021, 6, 799–806 CrossRef CAS.
- J. Liu, S. Chen, D. Qian, B. Gautam, G. Yang, J. Zhao, J. Bergqvist, F. Zhang, W. Ma, H. Ade, O. Inganäs, K. Gundogdu, F. Gao and H. Yan, Nat. Energy, 2016, 1, 16089 CrossRef CAS.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X.-K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- S. Li, L. Zhan, C. Sun, H. Zhu, G. Zhou, W. Yang, M. Shi, C.-Z. Li, J. Hou, Y. Li and H. Chen, J. Am. Chem. Soc., 2019, 141, 3073–3082 CrossRef CAS PubMed.
- A. Classen, C. L. Chochos, L. Lüer, V. G. Gregoriou, J. Wortmann, A. Osvet, K. Forberich, I. McCulloch, T. Heumüller and C. J. Brabec, Nat. Energy, 2020, 5, 711–719 CrossRef CAS.
- L. Zhan, S. Li, Y. Li, R. Sun, J. Min, Y. Chen, J. Fang, C.-Q. Ma, G. Zhou, H. Zhu, L. Zuo, H. Qiu, S. Yin and H. Chen, Adv. Energy Mater., 2022, 12, 2201076 CrossRef CAS.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Nat. Rev. Mater., 2019, 4, 689–707 CrossRef.
- C. He, Y. Pan, G. Lu, B. Wu, X. Xia, C.-Q. Ma, Z. Chen, H. Zhu, X. Lu, W. Ma, L. Zuo and H. Chen, Adv. Mater., 2022, 34, 2203379 CrossRef CAS PubMed.
- Y. Cai, Q. Li, G. Lu, H. S. Ryu, Y. Li, H. Jin, Z. Chen, Z. Tang, G. Lu, X. Hao, H. Y. Woo, C. Zhang and Y. Sun, Nat. Commun., 2022, 13, 2369 CrossRef CAS PubMed.
- Z. Zhou, S. Xu, J. Song, Y. Jin, Q. Yue, Y. Qian, F. Liu, F. Zhang and X. Zhu, Nat. Energy, 2018, 3, 952–959 CrossRef CAS.
- S. Li, L. Zhan, Y. Li, C. He, L. Zuo, M. Shi and H. Chen, Small Methods, 2022, 6, 2200828 CrossRef CAS PubMed.
- L. Zhan, S. Li, T.-K. Lau, Y. Cui, X. Lu, M. Shi, C.-Z. Li, H. Li, J. Hou and H. Chen, Energy Environ. Sci., 2020, 13, 635–645 RSC.
- L. Zhan, S. Li, X. Xia, Y. Li, X. Lu, L. Zuo, M. Shi and H. Chen, Adv. Mater., 2021, 33, 2007231 CrossRef CAS PubMed.
- Y. Cai, Y. Li, R. Wang, H. Wu, Z. Chen, J. Zhang, Z. Ma, X. Hao, Y. Zhao, C. Zhang, F. Huang and Y. Sun, Adv. Mater., 2021, 33, 2101733 CrossRef CAS PubMed.
- Y. Pan, X. Zheng, J. Guo, Z. Chen, S. Li, C. He, S. Ye, X. Xia, S. Wang, X. Lu, H. Zhu, J. Min, L. Zuo, M. Shi and H. Chen, Adv. Funct. Mater., 2022, 32, 2108614 CrossRef CAS.
- P. Bi, S. Zhang, Z. Chen, Y. Xu, Y. Cui, T. Zhang, J. Ren, J. Qin, L. Hong, X. Hao and J. Hou, Joule, 2021, 5, 2408–2419 CrossRef CAS.
- L. Zuo, S. B. Jo, Y. Li, Y. Meng, R. J. Stoddard, Y. Liu, F. Lin, X. Shi, F. Liu, H. W. Hillhouse, D. S. Ginger, H. Chen and A. K. Y. Jen, Nat. Nanotechnol., 2022, 17, 53–60 CrossRef CAS PubMed.
- Y. Li, Y. Guo, Z. Chen, L. Zhan, C. He, Z. Bi, N. Yao, S. Li, G. Zhou, Y. Yi, Y. Yang, H. Zhu, W. Ma, F. Gao, F. Zhang, L. Zuo and H. Chen, Energy Environ. Sci., 2022, 15, 855–865 RSC.
- N. Gasparini, A. Salleo, I. McCulloch and D. Baran, Nat. Rev. Mater., 2019, 4, 229–242 CrossRef.
- L. Ye, H. Hu, M. Ghasemi, T. Wang, B. A. Collins, J.-H. Kim, K. Jiang, J. H. Carpenter, H. Li, Z. Li, T. McAfee, J. Zhao, X. Chen, J. L. Y. Lai, T. Ma, J.-L. Bredas, H. Yan and H. Ade, Nat. Mater., 2018, 17, 253–260 CrossRef CAS PubMed.
- A. J. Gillett, A. Privitera, R. Dilmurat, A. Karki, D. Qian, A. Pershin, G. Londi, W. K. Myers, J. Lee, J. Yuan, S.-J. Ko, M. K. Riede, F. Gao, G. C. Bazan, A. Rao, T.-Q. Nguyen, D. Beljonne and R. H. Friend, Nature, 2021, 597, 666–671 CrossRef CAS PubMed.
- Z. Chen, X. Chen, Z. Jia, G. Zhou, J. Xu, Y. Wu, X. Xia, X. Li, X. Zhang, C. Deng, Y. Zhang, X. Lu, W. Liu, C. Zhang, Y. Yang and H. Zhu, Joule, 2021, 5, 1832–1844 CrossRef CAS.
- Y. Wang, D. Qian, Y. Cui, H. Zhang, J. Hou, K. Vandewal, T. Kirchartz and F. Gao, Adv. Energy Mater., 2018, 8, 1801352 CrossRef.
- J. Yao, T. Kirchartz, M. S. Vezie, M. A. Faist, W. Gong, Z. He, H. Wu, J. Troughton, T. Watson, D. Bryant and J. Nelson, Phys. Rev. Appl., 2015, 4, 014020 CrossRef.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125204 CrossRef.
- L. Zhu, J. Zhang, Y. Guo, C. Yang, Y. Yi and Z. Wei, Angew. Chem., Int. Ed., 2021, 60, 15348–15353 CrossRef CAS PubMed.
- X. Zhu, G. Zhang, J. Zhang, H.-L. Yip and B. Hu, Joule, 2020, 4, 2443–2457 CrossRef CAS.
- J. Xu, S. B. Jo, X. Chen, G. Zhou, M. Zhang, X. Shi, F. Lin, L. Zhu, T. Hao, K. Gao, Y. Zou, X. Su, W. Feng, A. K.-Y. Jen, Y. Zhang and F. Liu, Adv. Mater., 2022, 34, 2108317 CrossRef CAS PubMed.
- S. Karuthedath, J. Gorenflot, Y. Firdaus, N. Chaturvedi, C. S. P. De Castro, G. T. Harrison, J. I. Khan, A. Markina, A. H. Balawi, T. A. D. Peña, W. Liu, R.-Z. Liang, A. Sharma, S. H. K. Paleti, W. Zhang, Y. Lin, E. Alarousu, D. H. Anjum, P. M. Beaujuge, S. De Wolf, I. McCulloch, T. D. Anthopoulos, D. Baran, D. Andrienko and F. Laquai, Nat. Mater., 2021, 20, 378–384 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental procedures, NMR spectra, UV-vis, CV, certificate report, mobility, SCLC, contact angle, AFM, DSC, GIWAXS, HR-TEM, FTPS–EQE, UPS, EQE, etc. See DOI: https://doi.org/10.1039/d3ee00630a |
| ‡ S. Li, C. He, T. Chen and J. Zheng contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |