Planar pentacoordinate s-block metals

Abstract

The presence of a delocalized π-bond is often considered an essential criterion for achieving planar hypercoordination. Herein, we show that σ-delocalization could be sufficient to make the planar configuration the most stable isomer in a series of planar pentacoordinate s-block metals. High-level ab initio computations reveal that the global minimum of a series of interalkali and interalkali-alkaline earth clusters (LiNa₅, Li₅Mg⁺, Na₅Mg⁺, K₅Ca⁺, CaRb₅⁺, Rb₅Sr⁺, and SrCs₅⁺) adopts a singlet D_5h structure with a planar pentacoordinate lithium or alkaline earth metal (AE = Mg, Ca, Sr). These clusters are unusual combinations to stabilize a planar pentacoordinate atom, as all their constituents are electropositive. Despite the absence of π-electrons, Hückel's rule is fulfilled by the six σ-electrons. Furthermore, the systems exhibit a diatropic ring current in response to an external magnetic field and a strong magnetic shielding, so they might be classified as σ-aromatic. Therefore, multicenter σ-bonds and the resulting σ-delocalization stabilize these clusters, even though they lack π-aromaticity.

---

Introduction

Planar tetracoordinate carbons (ptCs) defy the standard paradigm of organic chemistry, yet they have been theoretically predicted, and experimentally isolated and characterized.^1,2 The story of these exotic molecules began with the report of a ptC transition state for methane in the stereomutation process of a tetrahedral carbon by Monkhorst.³ Subsequently, in a seminal paper, Hoffmann and co-workers analyzed bonding in planar methane and concluded that multicenter bond formation and lone pair delocalization on the central carbon atom are the key factors for the stability of ptC.⁴ Collins et al. followed these ideas to predict some ptC systems that are energetically more stable than their tetrahedral counterpart.⁵ This field has developed over time and now includes compounds containing planar tetra-, penta-, and even hexacoordinate carbon atoms.^6–23 In fact, planar hypercoordination is not restricted to carbon only,^24–38 other p-block elements have the ability to form these peculiar structures. However, as the electronegativity increases, stabilization of a planar hypercoordinate atom becomes more difficult since π-electrons would not be effectively delocalized. Although their number is relatively low, some planar hypercoordinate nitrogen and oxygen systems have been reported.^39–43 Merino and co-workers have recently designed one of the challenging systems, (quasi) planar tetracoordinate fluorine (ptF) in FIn₄⁺, FTl₄⁺, FGaIn₃⁺, FIn₂Tl₂⁺, FIn₃Tl⁺, and FInTl₃⁺.⁴⁴ Being the most electronegative element, the interactions of fluorine with the peripheral atoms are electrostatic in nature, affecting electron delocalization. So, the fluorine in these odd structures does not act as a σ-acceptor, restraining any back-donation.

So, a common feature of all these systems is that the hypercoordinate center is a p-block element. What about the s-block elements? Recently, some of us reported an intriguing set of systems with a planar pentacoordinate beryllium (ppBe) atom, BeM₅⁺ (M = Cu, Ag, Au), where three delocalized σ-orbitals support the bonding between Be and M₅ unit.⁴⁵ Beryllium is unique among the s-block elements because of its relatively large electronegativity and small radius. It has the highest capability to form covalent bonds between elements of the same block. Therefore, the σ-bonds in these ppBe clusters seem strong enough to prevent isomerization into a non-planar form. Is it plausible to obtain candidates having a planar pentacoordinate alkali metal or an alkaline earth metal?

Herein, we attempt to extend the list of compounds with planar pentacoordinate alkali (ppA) and alkaline-earth (ppAE) metals. LiNa₅ has a planar pentacoordinate lithium (ppLi) atom as the most stable isomer. Although this structure has previously been detected in the gas phase, its unusual form and way of stabilization were ignored. Gratifyingly, we found new planar pentacoordinate magnesium (Li₅Mg⁺ and Na₅Mg⁺), calcium (K₅Ca⁺ and CaRb₅⁺), and strontium (Rb₅Sr⁺ and SrCs₅⁺) atoms. To understand their stability, we have analyzed the nature of bonding and possible electron delocalization.

Computational details

The potential energy surfaces were systematically explored using the CALYPSO (Crystal structure Analysis by Particle Swarm Optimization) code.⁴⁶ Initial screening of both singlet and triplet configurations was performed at the PBE0-D3/def2-SVP level.⁴⁷ The resulting structures were re-minimized and characterized at the PBE0-D3/def2-QZVPP level. The final energies were refined at the CCSD(T)⁴⁸/def2-QZVPP level of theory. Therefore, the further discussion is based on the CCSD(T)/def2-QZVPP//PBE0-D3/def2-QZVPP results.

The multireference complete-active space self-consistent field (CASSCF)⁴⁹ computations were performed using MOLPRO.⁵⁰ The single-point computations of CASSCF and its second-order multireference perturbation theory (CASPT2)⁵¹ were conducted using the def2-QZVPP basis set on the PBE0-D3/def2-QZVPP geometries. For the active space, six orbitals (three occupied and three unoccupied) and six electrons were considered. Additionally, the geometries of the first three low-lying isomers were optimized using the CASPT2/def2-TZVPP level.

Electron delocalization was analyzed by computing the magnetic response to a unit external magnetic field (1.0 T). The magnetically induced current density⁵² (J^ind) and the induced magnetic field^53–55 (B^ind) were calculated using the GIMIC⁵² and Aromagnetic⁵⁶ programs, respectively. The external magnetic field was oriented parallel to the z-axis, perpendicular to the molecular plane. Under these conditions, the z-component of B^ind (B^ind_z) is equivalent to the NICS_zz index. Since the BHandHLYP functional⁵⁷ best matches the magnetic properties calculated at the CCSD(T) level, the magnetic response calculations were carried out using that functional together with the all-electron TZP-DKH⁵⁸ basis set, which includes scalar relativistic corrections. To quantify the degree of delocalization in the seven clusters, the ring current strengths (I^ind) were computed. These values are derived by integrating J^ind along a plane that begins at the center of the molecule, intersects a bond, and ends where J^ind vanishes. The contributions of the core electrons to the magnetic response were calculated using the RVE method, i.e., for highly charged molecules whose valence electrons have been removed but without relaxing the molecular structure. Therefore, the magnetic response of a system without its valence electrons is equivalent to the magnetic response of the core electrons.⁵⁹

Chemical bonding analyses were performed using the natural bonding orbitals (NBO) program.⁶⁰ To investigate the multicenter bonding feature, adaptive natural density partitioning (AdNDP)⁶¹ analysis was performed using the Multiwfn program code.⁶² The nature of the chemical bonding is further analyzed with interactive quantum atom analysis (IQA).^63–65 IQA was performed at the PBE-D3/TZ2P level using the ADF 2020 package.^66,67 All other calculations were performed with the Gaussian 16 package.⁶⁸

Planar pentacoordinate alkali metals

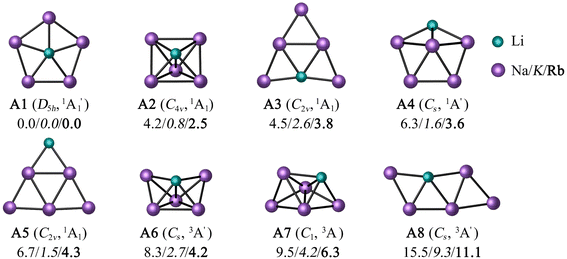
To minimize the computational cost, only the potential energy surfaces (PESs) of those combinations satisfying two conditions were explored: the first condition is that a perfect pentagon with a planar pentacoordinate alkali (ppA) at the center is a minimum. The second is that the ppA isomer is energetically more stable than the corresponding planar tetracoordinate alkali metal (ptA) form. Only three (LiNa₅, LiK₅, and LiRb₅) of the 25 possibilities satisfy both criteria at the CCSD(T)/def2-QZVPP//PBE0-D3/def2-QZVPP level (see Table S1 and Fig. S1†).

For these three combinations, the eight low-lying energy isomers are depicted in Fig. 1. According to global minimization, the most energetically stable configuration is a ppLi (A1). A C_4v square pyramid (A2) is the closest form in energy (4.2, 0.8, and 2.5 kcal mol⁻¹ for M = Na, K, and Rb, respectively), followed by a ptLi isomer (A3). Systems A4 and A5 contain a tricoordinate and dicoordinate A atom, respectively. Note that while the previous five isomers are in a singlet electronic state, the next three are triplets.

Fig. 1 PBE0-D3/def2-QZVPP geometries of the low-lying energy isomers of LiM₅ (M = Na/K/Rb). Relative energies in kcal mol⁻¹ were computed at the CCSD(T)/def2-QZVPP//PBE0-D3/def2-QZVPP level, including the zero-point energy computed at the DFT level. Point groups and spectroscopic states are given in parentheses.

The T₁-diagnostic was done to check the reliability of mono-determinantal methodologies in these systems. It is apparent from Table S2† that the LiK₅ clusters have somewhat higher T₁ values than LiNa₅ analogues. Particularly, the triplet states have very high T₁ values (0.08–0.15), which motivated us to perform CASPT2(6,6)/def2-QZVPP//PBE0-D3/def2-QZVPP computations. At the CASPT2 level, the ppLi isomer for LiNa₅ remains the lowest energy structure, unequivocally confirming its genuine candidacy in the flat world (see Fig. S2†). In contrast, the square pyramid becomes the lowest energy structure for LiK₅ and LiRb₅, 2.8 and 2.1 kcal mol⁻¹ more stable than the ppLi isomer, respectively (Fig. S2†). In fact, ptLi is 1.3 kcal mol⁻¹ more stable for the latter system than ppLi at the CASPT2 level. The first three low-lying isomers were optimized at the CASPT2/def2-TZVPP level to confirm if the energy trend of the isomers matches the results of the CASPT2//PBE0-D3 level. As shown in Table S3,† the difference in relative energies between these two levels ranged from 0.2 to 2.5 kcal mol⁻¹. However, the global minimum isomer remained the same in both cases. These findings suggest that the ppLi form is preferred for LiNa₅ due to both electronic and geometric factors, but for its heavier analogues, the larger ring size weakens the interaction between Li and peripheral atoms, resulting in others less symmetric structures being more stable than ppLi isomer.

In previous studies, pure and inter-alkali metal clusters with different combinations and sizes, including LiM₅, were detected in the gas phase by mass spectroscopy.^69a LiNa₅ has been identified experimentally and even Silva et al.^69b found that the ppLi arrangement is the most stable at the MP2 level. So, strictly speaking, we only confirm what has already been reported up to this point using multireference level.

Planar pentacoordinate alkali-earth metals

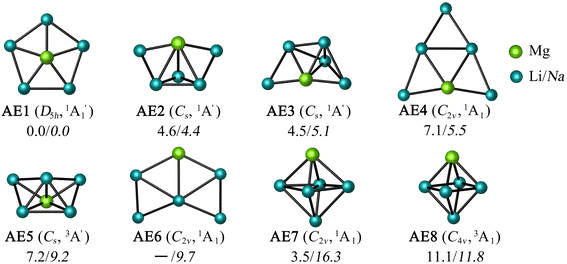
Let us expand this search to systems that contain a ppAE metal. Only six combinations (Li₅Mg⁺, Na₅Mg⁺, K₅Ca⁺, CaRb₅⁺, Rb₅Sr⁺, and SrCs₅⁺) satisfy both constraints following the same protocol established in the previous section (see Table S4†). Gratifyingly, the D_5h ppMg form, with an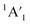 electronic state, is the most stable isomer for both Li₅Mg⁺ and Na₅Mg⁺ (AE1, see Fig. 2). The nearest energy isomer has a C_s three-dimensional configuration (AE2), being 4.6 (Li) and 4.4 (Na) kcal mol⁻¹ higher in energy than the global minimum. The ptMg isomer (AE4) lies 7.1 (Li) and 5.5 (Na) kcal mol⁻¹ above the ppMg. The closest triplet has a three-dimensional structure with a relative energy of 7.2 (Li) and 9.2 (Na) kcal mol⁻¹ with respect to the ppMg cluster. There is no significant difference in relative energy between CCSD(T) and CASPT2 levels (see Table S5 for T₁-diagnostics, and Table S3 and Fig. S3† for relative energies). The trend is same for CaM₅⁺ (M = K, Rb) and SrM₅⁺ (M = Rb, Cs) clusters (see Fig. S4–S7†). The ppAE form (AE = Ca, Sr) in all four cases is the most stable isomer at the CCSD(T) and CASPT2 levels. The relative energies with the closest three-dimensional isomer and the ptAE isomer are gradually reduced from Mg to Sr.

Fig. 2 PBE0-D3/def2-QZVPP geometries of the low-lying energy isomers of M₅Mg⁺ (M = Li/Na). Relative energies in kcal mol⁻¹ were computed at the CCSD(T)/def2-QZVPP//PBE0-D3/def2-QZVPP level, including the zero-point energy calculated at the DFT level. Point groups and spectroscopic states are given in parentheses. For Li₅Mg⁺, AE6 converges to AE2.

Structure and bonding

One of the most evident geometrical features is that the Li–M and AE–M bond lengths in LiM₅ (M = Na, K) and AEM₅⁺ are significantly longer (between 0.17 and 0.59 Å, see Table 1) than the typical covalent bond lengths proposed by Pyykkö and Atsumi,⁷⁰ which is typical for atoms bonded through multicenter bonds. The WBI values for Li–M and AE–M bonds range from 0.26 (Li–K) to 0.33 (Li–Mg), while they are smaller for M–M bonds (0.10–0.21). Since Na and K are more electropositive than Li, Li gets a negative CM5 charge of −0.18e in LiNa₅ and −0.17e in LiK₅. For the same reason, the natural charge on AE in the cationic clusters is also slightly negative (ranging between −0.13e and −0.18e).

Table 1 CM₅ charge (q) in |e|, bond lengths r in Å, and Wiberg bond indices (WBI) for the planar pentacoordinate s-block metal atoms

	q A/AE	q M	r A/AE–M	r M–M	WBIA/AE–M	WBIM–M
LiNa5	−0.18	+0.04	3.111	3.657	0.28	0.21
LiK5	−0.17	+0.03	3.797	4.464	0.26	0.19
Li5Mg^+	−0.13	+0.23	2.888	3.395	0.33	0.12
Na5Mg^+	−0.17	+0.23	3.234	3.802	0.31	0.10
K5Ca^+	−0.16	+0.23	4.123	4.847	0.32	0.11
CaRb5^+	−0.15	+0.23	4.337	5.098	0.31	0.10
Rb5Sr^+	−0.13	+0.22	4.490	5.278	0.28	0.11
SrCs5^+	−0.17	+0.23	4.764	5.600	0.29	0.10

---

To understand a little more about how atoms are bonded in these clusters, we performed an interacting quantum atom (IQA) analysis. Table 2 summarizes the values of the interatomic interaction energy (V_total) and their electrostatic (V_ionic) and exchange (V_coval) components. For Li/AE–M contacts, both ionic and covalent contributions are attractive, with the former being more dominant than the latter. Now, if we compare the values for ppLi with the corresponding ones in ppAE, both ionic and covalent interactions are improved in the latter cases. Note that the ionic attraction of AE–M bonds gradually decreases from Mg to Sr. On the other hand, for ppLi, there is a tiny electrostatic repulsion between the M–M bonds, which is compensated by the attractive covalent interaction. But for ppAE cases, a combination of enhanced ionic repulsion and weak covalent attraction makes the M–M contacts repulsive in nature.

Table 2 The results of IQA analysis of LiM₅ (M = Na, K) and AEM₅⁺ computed at the PBE-D3/QZ4P level, where inter-atomic interaction energy (V_total) and its electrostatic (ionic, V_ionic) and exchange (covalent, V_coval) contributions are provided in kcal mol⁻¹

	LiNa5	LiK5	Li5Mg^+	Na5Mg^+	K5Ca^+	CaRb5^+	Rb5Sr^+	SrCs5^+
V total (Li/AE–M)	−30.0	−35.9	−268.1	−116.1	−77.9	−65.9	−57.2	−58.6
V ionic (Li/AE–M)	−22.7	−10.6	−241.0	−80.7	−47.4	−37.1	−28.7	−31.9
V coval (Li/AE–M)	−7.3	−25.3	−27.1	−35.3	−30.6	−28.8	−28.5	−26.8
V total (M–M)	−23.7	−8.8	58.1	20.3	10.9	7.9	5.6	6.4
V ionic (M–M)	4.2	2.2	58.9	23.6	14.5	11.8	9.8	10.3
V coval (M–M)	−27.8	−11.0	−0.8	−3.4	−3.6	−4.0	−4.2	−3.9

---

Aromaticity

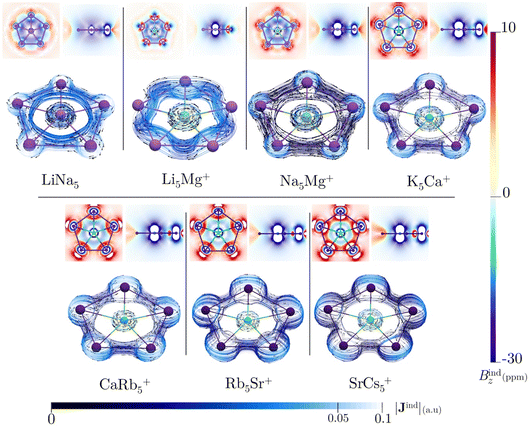
All of the ppA systems in this study have six valence electrons distributed in multicenter σ-orbitals, which include a degenerate HOMO and HOMO-1, as shown in Fig. S8† and AdNDP orbitals in Fig. S9†. Therefore, Hückel's rule is fulfilled by these σ-electrons. In previous studies, σ-aromaticity has been recognized as a crucial factor in stabilizing planar hypercoordination.^44,45,71 However, this phenomenon is usually accompanied by the delocalization of p orbitals or the presence of d orbitals in the ligands. In the present cases, the clusters only possess weak s-bonding, particularly for LiNa₅. This raises an intriguing question: can the limited σ-delocalization in these systems induce a diatropic ring current and a shielding cone when an external magnetic field is applied?

All these systems exhibit a diamagnetic magnetic response (negative B^ind_z values) and the formation of a shielding cone below and above the ring (Fig. 3), which is characteristic of an aromatic system. But, the B^ind_z values are strongly affected by the core electron magnetic response, mainly because heavy nuclei produce strong local shielding cones. So, to quantify the degree of delocalization in the seven clusters, the ring current strengths (I^ind) were computed. Since the integration domain covers the local atomic current of the central atom, the I^ind values for the seven planar pentacoordinate s-block metals systems (ranging from 17.94 to 88.04 nA T⁻¹) are relatively high compared to the benzene value of 12 nA T⁻¹, particularly for those with heavier elements (see Table 3). It is well-known that the effect of the core electron on ring-current strengths in organic molecules is typically negligible⁵⁹ but may be relevant for our molecules with heavy atoms,^72–74 even more so if the integration plane crosses a nucleus. This is also evident in the J^ind plots (Fig. 3), where the current–density pathways are distorted near the nuclei due to local atomic currents in the heaviest clusters. We also estimated the core-electron contribution of I^ind using the removing valence electrons (RVE) approach⁷⁵ to separate the influence of the core and valence electrons on these strengths. Consequently, the I^ind values derived exclusively from the σ-electrons range between 8.53 and 21.34 nA T⁻¹. So, we may claim that MgLi₅⁺ is the least aromatic while SrCs₅⁺ sustains the strongest ring current. These values are higher than those determined for benzene (a π-delocalized system) but lower than those obtained for Al₄²⁻ or CAl₄²⁻ (both (σ + π)-delocalized clusters).^76,77 So, these results emphasize the significance of σ-aromaticity in determining the stability and preferred geometry of the cluster.^78,79

Fig. 3 In the top panel: the B^ind_z isolines plotted in the molecular plane (left) and a transversal slide (right). In the bottom panel: J^ind maps plotted near the molecular plane. The arrows indicate the direction of the current density. The |J^ind| scale is in atomic units (1 au = 100.63 nA T⁻¹ Å⁻²). The external magnetic field is oriented parallel to the z-axis, perpendicular to the molecular plane.

Table 3 The ring-current strengths (I^ind) in nA T⁻¹ obtained from the integration of total (all-electron) J^ind and its core-electron (RVE) contribution for the ppLi and ppAE clusters computed at the BHandHLYP/TZP-DKH level. The valence (σ-electron) contribution is obtained by subtracting the core electron strength from the total

I ^ind	LiNa5	Li5Mg^+	Na5Mg^+	K5Ca^+	CaRb5^+	Rb5Sr^+	SrCs5^+
Total	17.94	27.79	33.22	50.50	50.59	81.95	88.04
Core	4.18	19.26	19.26	34.26	34.23	66.70	66.70
Valence (σ)	13.76	8.53	13.96	16.24	16.36	15.25	21.34

---

Conclusions

Is it plausible to obtain candidates with a planar pentacoordinate metal of the s-block? Yes, it is feasible. We have identified seven clusters with a planar pentacoordinate s-block metal as their global minimum by systematically exploring the potential energy surfaces of various combinations. Despite the electropositive nature of all their components, these clusters sustain a strong diatropic ring current and significant shielding, supporting their fully σ-delocalized character. So, multicentric σ-bonds and the resulting σ-delocalization stabilize these clusters, even in the absence of π-orbitals. These clusters push the covalent bonding tendency of alkali and alkaline earth metals to the limit and provide a basis for the design of rule-breaking planar hypercoordinate structures.

Data availability

Computational details, extra data, and the Cartesian coordinates for all compounds are provided in the ESI† accompanying this paper.

Author contributions

WT, AKG, SP, GM, and ZC designed the works and concepts, analyzed the data, wrote the draft, and finalized it. MW, AJK and MO-I performed the global minima search and aromaticity analysis. GY, CC and GC-T performed NBO and IQA. YB and MW performed CASPT2 calculations. All authors took part in the discussions and approved the final version. GM and SP wrote the final version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the National Natural Science Foundation of China (Grant no. 11922405, 11874178, 91961204) and was supported by the Fundamental Research Funds for the Central Universities. This work was funded in Mexico by Conacyt (Proyecto FORDECYT-PRONACES/1561802/2020). The partial calculations in this work are supported by the High Performance Computing Center of Jilin University, China. AKG acknowledges the financial support received from DST-SERB, INDIA (ECR/2016/001466). GCT thanks Conacyt for her PhD fellowship. M. O.-I. acknowledges the financial support from the Magnus Ehrnrooth Foundation. WT acknowledges the financial support of the National Agency for Research and Development (ANID) through FONDECYT projects 1211128.

References

1. V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 0114.
2. L. M. Yang, E. Ganz, Z. F. Chen, Z. X. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed. Engl., 2015, 54, 9468–9501.
3. H. J. Monkhorst, Chem. Commun., 1968, 1111–1112.
4. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4492–4493.
5. J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427.
6. G. Merino, M. A. Mendez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372.
7. R. Keese, Chem. Rev., 2006, 106, 4787–4808.
8. W. Siebert and A. Gunale, Chem. Soc. Rev., 1999, 28, 367–371.
9. D. R. Rasmussen and L. Radom, Angew. Chem., Int. Ed. Engl., 1999, 38, 2876–2878.
10. Z. X. Wang and P. v. R. Schleyer, Science, 2001, 292, 2465–2469.
11. Y. Pei, W. An, K. Ito, P. V. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394–10400.
12. O. Yanez, R. Baez-Grez, J. Garza, S. Pan, J. Barroso, A. Vasquez-Espinal, G. Merino and W. Tiznado, Chemphyschem, 2020, 21, 145–148.
13. M. H. Wang, X. Dong, Y. H. Ding and Z. H. Cui, Chem. Commun., 2020, 56, 7285–7288.
14. J. C. Guo, L. Y. Feng, J. Barroso, G. Merino and H. J. Zhai, Chem. Commun., 2020, 56, 8305–8308.
15. S. Pan, J. L. Cabellos, M. Orozco-Ic, P. K. Chattaraj, L. L. Zhao and G. Merino, Phys. Chem. Chem. Phys., 2018, 20, 12350–12355.
16. Z. H. Cui, V. Vassilev-Galindo, J. L. Cabellos, E. Osorio, M. Orozco, S. Pan, Y. H. Ding and G. Merino, Chem. Commun., 2017, 53, 138–141.
17. J. C. Guo, W. J. Tian, Y. J. Wang, X. F. Zhao, Y. B. Wu, H. J. Zhai and S. D. Li, J. Chem. Phys., 2016, 144, 244303.
18. Y. B. Wu, Y. Duan, H. G. Lu and S. D. Li, J. Phys. Chem. A, 2012, 116, 3290–3294.
19. J. O. C. Jimenez-Halla, Y. B. Wu, Z. X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776–8778.
20. R. Sun, B. Jin, B. Huo, C. X. Yuan, H. J. Zhai and Y. B. Wu, Chem. Commun., 2022, 58, 2552–2555.
21. K. Exner and P. v. R. Schleyer, Science, 2000, 290, 1937–1940.
22. Y. B. Wu, Y. Duan, G. Lu, H. G. Lu, P. Yang, P. V. Schleyer, G. Merino, R. Islas and Z. X. Wang, Phys. Chem. Chem. Phys., 2012, 14, 14760–14763.
23. L. Leyva-Parra, L. Diego, O. Yañez, D. Inostroza, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Angew. Chem., Int. Ed., 2020, 133, 8782–8786.
24. E.-U. Würthwein and P. V. R. Schleyer, Angew. Chem., Int. Ed. Engl., 1979, 18, 553–554.
25. F. L. Gu, X. M. Yang, A. C. Tang, H. J. Jiao and P. v. R. Schleyer, J. Comput. Chem., 1998, 19, 203–214.
26. H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827–833.
27. H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed. Engl., 2003, 42, 6004–6008.
28. S.-D. Li, G.-M. Ren, C.-Q. Miao and H.-J. Zhai, Angew. Chem., Int. Ed. Engl., 2004, 43, 1371–1373.
29. A. I. Boldyrev, X. Li and L. S. Wang, Angew. Chem., Int. Ed. Engl., 2000, 39, 3307–3310.
30. M.-h. Wang, X. Dong, Z.-h. Cui, M. a. Orozco-Ic, Y.-h. Ding, J. Barroso and G. Merino, Chem. Commun., 2020, 56, 13772–13775.
31. M. Garcon, C. Bakewell, G. A. Sackman, A. J. P. White, R. I. Cooper, A. J. Edwards and M. R. Crimmin, Nature, 2019, 574, 390–393.
32. W. L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 165–168.
33. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed. Engl., 2012, 51, 2101–2105.
34. F. Ebner and L. Greb, J. Am. Chem. Soc., 2018, 140, 17409–17412.
35. F. Ebner and L. Greb, Chem, 2021, 7, 2151–2159.
36. P. Ghana, J. Rump, G. Schnakenburg, M. I. Arz and A. C. Filippou, J. Am. Chem. Soc., 2021, 143, 420–432.
37. F. Ebner, H. Wadepohl and L. Greb, J. Am. Chem. Soc., 2019, 141, 18009–18012.
38. M. H. Wang, C. Chen, S. Pan and Z. H. Cui, Chem. Sci., 2021, 12, 15067–15076.
39. C. B. Shao and Y. H. Ding, Phys. Chem. Chem. Phys., 2010, 12, 13153–13157.
40. Z. H. Cui and Y. H. Ding, Phys. Chem. Chem. Phys., 2011, 13, 5960–5966.
41. X. M. Zhang, J. Lv, F. Ji, H. S. Wu, H. J. Jiao and P. V. R. Schleyer, J. Am. Chem. Soc., 2011, 133, 4788–4790.
42. Z. C. Liu, J. Y. Lei, M. Frasconi, X. H. Li, D. Cao, Z. X. Zhu, S. T. Schneebeli, G. C. Schatz and J. F. Stoddart, Angew. Chem., Int. Ed. Engl., 2014, 53, 9193–9197.
43. A. J. Kalita, S. S. Rohman, C. Kashyap, S. S. Ullah, I. Baruah and A. K. Guha, Inorg. Chem., 2020, 59, 17880–17883.
44. G. Castillo-Toraya, M. Orozco-Ic, E. Dzib, X. Zarate, F. Ortiz-Chi, Z. H. Cui, J. Barroso and G. Merino, Chem. Sci., 2021, 12, 6699–6704.
45. C. Chen, Y. Q. Liu and Z. H. Cui, Inorg. Chem., 2021, 60, 16053–16058.
46. J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, J. Chem. Phys., 2012, 137, 084104.
47. (a) M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305; (c) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
48. (a) G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918; (b) R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352.
49. K. Andersson, P.-Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinsk, J. Phys. Chem., 1990, 94, 5483–5488.
50. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
51. F. James, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306.
52. (a) J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963; (b) H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518; (c) D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev., 2016, 6, 639–678.
53. G. Merino, T. Heine and G. Seifert, Chem.–Eur. J., 2004, 10, 4367–4371.
54. T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309.
55. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
56. M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, Cinvestav- Mérida, México, 2016.
57. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
58. F. E. Jorge, A. C. Neto, G. G. Camiletti and S. F. Machado, J. Chem. Phys., 2009, 130, 064108.
59. M. Orozco-Ic, N. D. Charistos, A. Munoz-Castro, R. Islas, D. Sundholm and G. Merino, Phys. Chem. Chem. Phys., 2022, 24, 12158–12166.
60. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241.
61. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
62. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
63. A. M. Pendas, M. A. Blanco and E. Francisco, J. Chem. Phys., 2004, 120, 4581–4592.
64. A. M. Pendas, E. Francisco and M. A. Blanco, J. Comput. Chem., 2005, 26, 344–351.
65. M. A. Blanco, A. M. Pendas and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109.
66. ADF2020, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com/.
67. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
68. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
69. (a) M. M. Kappes, Chem. Rev., 1988, 88, 369–389; (b) F. T. Silva, A. Rocha-Santos, C. L. Firme, L. A. De Souza, I. C. Anjos and J. C. Belchior, J. Mol. Model., 2020, 26, 317–326.
70. P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197.
71. (a) H. Tanaka, S. Neukermans, E. Janssens, R. E. Silverans and P. Lievens, J. Am. Chem. Soc., 2003, 125, 2862–2863; (b) M. Kulichenko, W.-J. Chen, Y.-Y. Zhang, C.-Q. Xu, J. Li and L.-S. Wang, J. Phys. Chem. A, 2021, 125, 4606–4613; (c) A. J. Kalita, I. Baruah, K. Sarmah, R. R. Borah, F. Yashmin and A. K. Guha, Inorg. Chem., 2022, 61, 1259–1263; (d) A. J. Kalita, K. Sarmah, F. Yashmin, R. R. Borah, I. Baruah, R. P. Deka and A. K. Guha, Sci. Rep., 2022, 12, 10041; (e) E. Ravell, S. Jalife, J. Barroso, M. Orozco-Ic, G. Hernández-Juárez, F. Ortiz-Chi, S. Pan, J. L. Cabellos and G. Merino, Chem. – Asian J., 2018, 13, 1467–1473; (f) H. T. Pham, L. Q. Ngo, M. P. Pham-Ho and M. T. Nguyen, J. Phys. Chem. A, 2016, 120, 7964–7972.
72. C. Foroutan-Nejad, J. Vicha and A. Ghosh, Phys. Chem. Chem. Phys., 2020, 22, 10863–10869.
73. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789–4796.
74. G. Periyasamy, N. A. Burton, I. H. Hillier and J. M. H. Thomas, J. Phys. Chem. A, 2008, 112, 5960–5972.
75. M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Munoz-Castro and G. Merino, Chem.–Eur. J., 2020, 26, 326–330.
76. C.-G. Zhan, F. Zheng and D. A. Dixon, J. Am. Chem. Soc., 2002, 124, 14795–14803.
77. X. Li, H. F. Zhang, L. S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed. Engl., 2000, 39, 3630–3633.
78. S. E. Lewis, Chem. Soc. Rev., 2015, 44, 2221–2304.
79. (a) L.-M. Yang, V. Bačić, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, J. Am. Chem. Soc., 2015, 137, 2757–2762; (b) L.-M. Yang, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 17545–17551; (c) I. A. Popov, F.-X. Pan, X.-R. You, L.-J. Li, E. Matito, C. Liu, H.-J. Zhai, Z.-M. Sun and A. I. Boldyrev, Angew. Chem., Int. Ed., 2016, 55, 15344–15346; (d) I. A. Popov, A. A. Starikova, D. V. Steglenko and A. I. Boldyrev, Chem. –Eur. J., 2018, 24, 292–305; (e) H.-L. Xu, I. Popov, N. Tkachenko, Z.-C. Wang, A. Munoz-Castro, A. I. Boldyrev and Z.-M. Sun, Angew. Chem., Int. Ed., 2020, 59, 17286–17290.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc05939h

‡ Equal contribution.

---