Open Access Article
Open Access ArticleFirst principles modeling of composites involving TiO2 clusters supported on M2C MXenes†
Masoomeh
Keyhanian‡
 a,
Néstor
García-Romeral‡
a,
Néstor
García-Romeral‡
 b,
Ángel
Morales-García
b,
Ángel
Morales-García
 *b,
Francesc
Viñes
*b,
Francesc
Viñes
 b and
Francesc
Illas
b and
Francesc
Illas
 b
b
aDepartment of Physical Chemistry, Faculty of Chemistry, University of Mazandaran, Babolsar 47416-95447, Iran
bDepartament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, c/Martí i Franquès 1-11, 08028 Barcelona, Spain. E-mail: angel.morales@ub.edu
First published on 22nd July 2024
Abstract
First-principles calculations based on density functional theory are performed to investigate the formation of titania/MXene composites taking (TiO2)5/M2C (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) as cases of study. The present systematic analysis confirms a favorable, high exothermic interaction, which promotes important structural reconstructions of the (TiO2)5 cluster along with charge transfer from the MXene to titania. MXenes composed of d3 transition metals promote the strongest interaction, deformation energy, and charge transfer, followed by d4 and d5 M2C MXenes. We provide evidence that the formation of these (TiO2)5/M2C composites is governed by charge transfer, leading to scaling relationships. By using the electronegativity of the metal composing MXene and the MXene d-band center, we also establish linear correlations that can be used to predict the interaction strength of (TiO2)5/M2C composites just from the knowledge of the MXene composition. It is likely that the present trends hold for other TiO2/MXene composites.
1. Introduction
During recent decades, the relationship between semiconducting transition metal oxides (TMOs) and photocatalysis has been a topic of high interest in the scientific community, especially since the seminal paper published by Fujishima and Honda in 1972.1 Shortly, a photon of appropriate energy, ideally from sunlight, can be used to activate a catalyst generating electron–hole pairs to drive redox reactions.2,3 This solar-to-chemical energy transformation induced by semiconducting materials forms the basis of the so-called heterogeneous photocatalysis which plays an important role in a broad range of applications including microorganism inactivation, degradation of pollutants, water splitting, or CO2 photoreduction among others.4–7 Different semiconducting materials such as WO3, ZnO and TiO2 have been investigated as suitable photocatalysts, with the latter being the most broadly studied candidate.8–11 However, the full potential of this technology is still limited because of the too wide band gap of these materials—3.0 to 3.2 eV in the case of TiO2—and fast electron–hole recombination. These drawbacks seriously limit the activation of the semiconductor under sunlight and promote low photoactivity.12–14One proven strategy to enhance the photoactivity of a semiconductor is to integrate a new component. This is expected to facilitate charge carriers’ separation by forming an interface with the semiconducting photocatalyst. Also, the new component can participate as an active site for the surface reaction. Experimental and computational studies have proposed both metals (Pt, Pd, Ru, Ag, and Au)15–19 and nonmetals (C and N)19–22 as new constituents to anchor over or dope nanostructured TiO2 materials. The resulting systems show relative photocatalytic activity improvement due to the longer charge carrier lifetimes. In this quest for robust photocatalysts with superior charge carrier separation, low dimensional carbides and/or nitrides (called MXenes)23 appear as suitable candidates to generate hybrid catalysts together with TMOs to overcome the aforementioned limitations.24
MXenes exhibit a Mn+1XnTx general chemical formula where M stands for early transition metals, X corresponds to carbon and/or nitrogen elements, and Tx represents the terminal groups of MXene (i.e., OH, H, O, or F) derived from the top-down synthesis taking MAX phases as a precursor. Finally, n denotes the thickness of the MXene in terms of atomic layers and runs from 1 to 3. MXenes have shown to be versatile materials in a broad landscape of applications, including catalysis.25–30 In the realm of photocatalysis, a series of photoactive MXene-based compounds have been proposed as promising photocatalysts for efficient CO2 reduction, and H2 generation through water splitting.24,31–33
Concerning TiO2/MXene composites, several experimental studies have been reported.34–38 These studies show that the use of MXenes as co-catalysts could improve the photocatalytic activity compared to the use of isolated semiconductors as titania. One important aspect of such improvement resides in the interface contact type between both cocatalysts. A Schottky barrier formed at the interface prevents the back diffusion of the electrons, thus, preventing charge recombination of photogenerated electrons.
Instead of these reports, the interfacial structure and electronic properties of these composites remain largely unknown. Thus, theoretical analyses are necessary to identify and rationalize the structural and electronic aspects that could contribute to the enhancement of catalytic performance,39 and prior further theoretical studies regarding their reactivity in heterogeneous or photocatalytic reactions on these systems can be undertaken. Using extended periodic models, Xu and coauthors investigated the interfacial properties of Tin+1CnTx/TiO2 (n = 1, 2) heterostructures including O, OH, and F as Tx termination, and selected the (101) surface to represent the slab model of anatase TiO2.40 This study revealed the strong dependence of the interfacial interaction and properties of the TiO2/MXene heterostructures on the surface composition of the MXene. One step further was recently carried out by us investigating the TiO2/MXene composites but considering nanostructured TiO2 systems, (TiO2)5 and (TiO2)10 clusters, supported on a bare Ti2C surface.41 A remarkable exothermic interaction was reported, accompanied by significant deformation of the adsorbed titania clusters and substantial charge transfer from the MXene towards the TiO2 clusters. Nevertheless, all the heterostructures described so far, both theoretically and experimentally, involved only Ti-based MXenes as the substrate and a comprehensive study comparing the effect of other transition metals composing MXenes on the supported TiO2 cluster is missing. Thus, we focus here on a systematic computational analysis to gain further knowledge of the effects of MXene composition on the structural and electronic properties of TiO2/MXene composites. To this end, we select bare M2C (0001) MXenes (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) as substrates to support a (TiO2)5 cluster.
2. Computational details
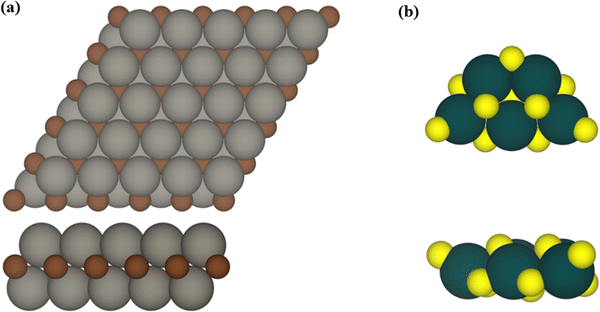
The influence of MXene composition when forming TiO2/MXene composites was investigated by considering extended M2C (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) MXene slabs exposing the (0001) surface with ABC stacking as depicted in Fig. 1. From a synthetic point of view, MXenes are generated using a top-down procedure using MAX phases as precursors. This involves chemical etching of the A-element in the MAX phase and further sonication to separate the generated MXenes exposing the basal (0001) surface. The (TiO2)5 titania cluster was selected as a representative example to study the interaction with the different MXene surfaces. The (TiO2)5 cluster was chosen as it provides a good representative model for experimental composites and a suitable theoretical case to study the chemical bonding in these systems. This selection was based on previous work on the (TiO2)5/Ti2C composite41 which constitutes an appropriate guide to compare both studies. The atomic structure of the gas phase (TiO2)5 cluster used as a reference was obtained using global optimization methods and exhibits the lowest energy in the potential energy surface (PES), see Fig. 1.42,43 An efficient analysis of the interacting landscape was carried out by generating different conformations by rotating the (TiO2)5 nanocluster over the M2C (0001) MXene surfaces. This screening procedure where a rotational angle α covers a 140° range with a step of 10° and guarantees a thorough assessment of PES attending to the inherent hexagonal symmetry exposed by the MXene slab models. Further details are described in ref. 41.The structural, electronic, and bonding properties of the (TiO2)5/M2C composites were investigated using periodic density functional theory (DFT) based calculations as implemented in the Vienna Ab Initio simulation package (VASP).44,45 Here, the Kohn–Sham equations are numerically solved using a plane wave basis set to expand the valence electron density with a kinetic energy cut-off of 415 eV. To account for the interaction between the core and valence electron density, the projector augmented wave (PAW) method was used.46 The generalized gradient approximation (GGA) Perdew–Burke–Ernzerhof (PBE) exchange correlation density functional was selected to pursue the geometry optimizations.47 PBE stands out as a widely recognized and broadly used DFT functional in computational materials science for its ability to accurately depict metallic systems, so it effectively characterizes the structural parameters of MXenes. To properly study the (TiO2)5/M2C composites, a p(5×5) M2C MXene supercell was selected as it is sufficiently large to minimize the lateral interactions between the periodically repeated titania clusters. A vacuum space of 18 Å along the direction normal to the MXene (0001) surface was included to prevent artificial electrostatic interactions between interleaved composite replicas. Given the rather large size of this supercell, calculations were carried out at the Γ k-point only.48 The convergence threshold for the electronic self-consistent field (SCF) calculations was established at 10−5 eV, and the structural optimization was reached when atomic forces were below 10−2 eV Å−1.
First, we analyzed the thermodynamic stability of the (TiO2)5/M2C (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W) composites based on the adsorption energy, Eads. This provides a measure of the exothermicity arising from supporting the (TiO2)5 cluster over the MXene (0001) surface, and is defined as:
| Eads = E(TiO2)5/M2C − EM2C − E(TiO2)5, | (1) |
The composite formation induces a deformation of its (0001) M2C MXene and (TiO2)5 cluster components relative to their isolated configurations, and this energy cost is compensated by the interaction strength, leading to the adsorption process. Therefore, one can define the deformation energy, Edef, of either M2C or (TiO2)5, and adhesion energy, Eadh, all defined as;
| Edef(X) = EspX − EX, | (2) |
| Eadh = Eads − Edef(TiO2) − Edef(Ti2C), | (3) |
Furthermore, a topological analysis of the electron density was carried out based on the quantum theory of atoms-in-molecules proposed by Bader,49 using the VASP-linked code developed by Henkelman et al.50 The charge transfer analysis was carried out by quantifying the total number of electrons in each structure in its gas phase and composite conformations. Furthermore, the charge density difference (CDD), and its plane-averaged (PA-CDD) counterpart along the normal direction were also computed as:
| Δρ = ρ(TiO2)5/M2C − ρM2C − ρ(TiO2)5, | (4) |
3. Results and discussion
We start this section by discussing in detail the trends of energetic features, i.e., adsorption, adhesion, and deformation energies. Next, we continue with the rationalization of these properties based on the chemical bonding analysis as the charge transfer, the CCD and PA-CDD. Finally, we will propose useful scaling relationships allowing one to establish the structural and bonding properties that govern the formation of titania/MXene composites.3.1. Energetic stability of (TiO2)5/M2C composites
Exploration of the potential energy surface (PES) of (TiO2)5/M2C systems is carried out by computing the interaction energy, this is, the Eads, between the (TiO2)5 nanocluster over the p(5×5) M2C (M = Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, and W) MXene supercell (cf.Fig. 1). This interacting process is systematically simulated by rotating the (TiO2)5 nanocluster over each M2C (0001) surface by varying the rotational angle as mentioned above, following a previous scheme recently used in the analysis of (TiO2)n/Ti2C (n = 5 and 10) and titania/titania interfaces.41,52 Due to the hexagonal symmetry of the MXene, analogous interacting conformations are expected to be found by shifting the titania cluster in the xy plane. See the ESI† for further details.Table 1 compiles the computed energy values defined by eqn (1)–(3) for the most stable configuration of each (TiO2)5/M2C composite. To avoid misunderstanding, we focus initially on the most stable configurations taking the most exothermic cases (i.e., largest Eads) for each composite (cf.Table 1). The complete analysis for all plausible conformations in each MXene surface is listed in Tables S1–S9 of the ESI.† First, Eads indicates an exothermic interaction ranging from −10.12 to −16.99 eV. The composition of the MXene surface promotes different adsorption energies. Indeed, the formation of (TiO2)5/M2C composites is the most exothermic over an MXene surface involving d3 transition metals (M = Ti, Zr, and Hf) with Eads values of −16.76, −16.78, and −16.99 eV, respectively. On the other hand, we find MXene surfaces composed of d5 transition metals (M = Cr, Mo, and W) expose the lowest, yet quite large, exothermicity with Eads values of −12.59, −10.12, and −10.37 eV, respectively. Finally, the MXenes composed of d4 transition metals (M = V, Nb, and Ta) present Eads values with energies between both extremes with values of −13.47, −13.08, and −14.11 eV, respectively. Attending to the location of the transition metal in the periodic table, one can capture some trends in Eads. In turn, the adsorption energy becomes less favorable when moving through the period. This indicates that the MXene surface reduces its reactivity with the titania cluster as the number of d electrons increases. This is consistent with the trends reported when M2C MXenes are used as template generating single-atom catalysts (SACs).53
| M2C | E ads | E adh | E def M2C | E def (TiO2)5 | ΔQ | Φ |
|---|---|---|---|---|---|---|
| Ti2C | −16.76 | −36.95 | 2.21 | 17.98 | −6.02 | 4.34 |
| Zr2C | −16.78 | −36.03 | 1.06 | 18.19 | −6.08 | 4.09 |
| Hf2C | −16.99 | −37.06 | 0.89 | 19.18 | −6.62 | 4.29 |
| V2C | −13.47 | −27.89 | 0.71 | 13.71 | −4.15 | 4.40 |
| Nb2C | −13.08 | −23.48 | 0.91 | 9.49 | −3.53 | 4.26 |
| Ta2C | −14.11 | −25.40 | 1.09 | 10.19 | −3.66 | 4.59 |
| Cr2C | −12.59 | −24.95 | 1.57 | 10.79 | −3.48 | 4.71 |
| Mo2C | −10.12 | −18.52 | 1.03 | 7.37 | −2.34 | 4.99 |
| W2C | −10.37 | −17.62 | 1.76 | 5.49 | −2.04 | 4.93 |
The Eadh follows a similar trend as Eads, see Table 1, running from −17.62 to −37.06 eV. Again, the most reactive MXenes are those involving d3 metals with the largest Eadh followed by d4 and d5 metal ones. In turn, this adhesion energy is directly related to the deformation energy (Edef) of the (TiO2)5 cluster and the M2C (0001) surface that takes place during the formation of titania/MXene composites as listed in Table 1. Here, one can readily see that the formation of (TiO2)5/M2C composites affects in a different way to the structural framework of each constituent. Starting with the M2C (0001) MXene surface, its Edef is relatively low and ranges in value between 2.21 and 0.71 eV only. On the other hand, one can see that this Edef is significantly larger for the (TiO2)5 nanocluster with values encompassing values between 5.49 and 19.18 eV. Clearly, the (TiO2)5 cluster always shows the largest deformation when a composite system is formed. Indeed, a quite linear trend emerges (R = 0.78) when plotting Eadsversus Edef (TiO2)5 as depicted in Fig. 2. Here, three different regions are delimited: (i) high Edef and Eads; (ii) intermediate Edef and Eads; and (iii) low Edef and Eads, corresponding to titania/MXene composites where the MXene (0001) surface is composed of d3, d4, and d5 transition metal. In short, the formation of titania/MXene composites induces a large reconstruction of the titania cluster.
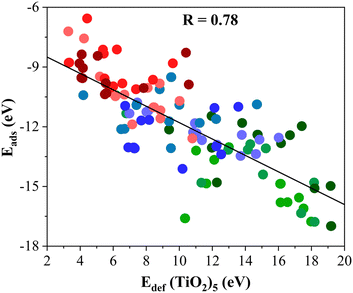 | ||
| Fig. 2 Linear trend between the Eads of (TiO2)5/M2C composites and Edef (TiO2)5. The solid black line is the linear correlation between both quantities where R stands for the regression coefficient between them. The spheres colors are consistent with the colored spheres of the metal atom in the MXene surface, depicted in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.† | ||
From a structural point of view, the fully relaxed geometries of the most exothermic configurations of each composite before and after adsorption are presented in Fig. 1 and 3, respectively. Fig. 3 clearly and consistently shows a deformation of titania clusters upon adsorption over M2C (0001) surfaces, in agreement with the above analyzed deformation energies. In fact, titania clusters are adsorbed in equivalent positions over M2C composed of d3 and d4 metals according to the inherent hexagonal symmetry of M2C (0001) surfaces and seem to follow the ABC MXene stacking. Despite titania clusters being adsorbed in different positions over M2C involving d5 metals, all titania clusters, regardless of the M2C metal composition, present O atoms in contact with the M2C surfaces occupying the high-symmetry adsorption sites (mainly hollow ones) upon adsorption. Indeed, some O atoms change plane in the cluster to maximize the number of contacts between the cluster and the surfaces and occupy the mentioned sites. Further structural analysis concerning atomic distances and angles are reported in Fig. S1 of the ESI.† The initial geometry found in the gas phase configuration of the (TiO2)5 cluster is lost when it is anchored on the MXene support.
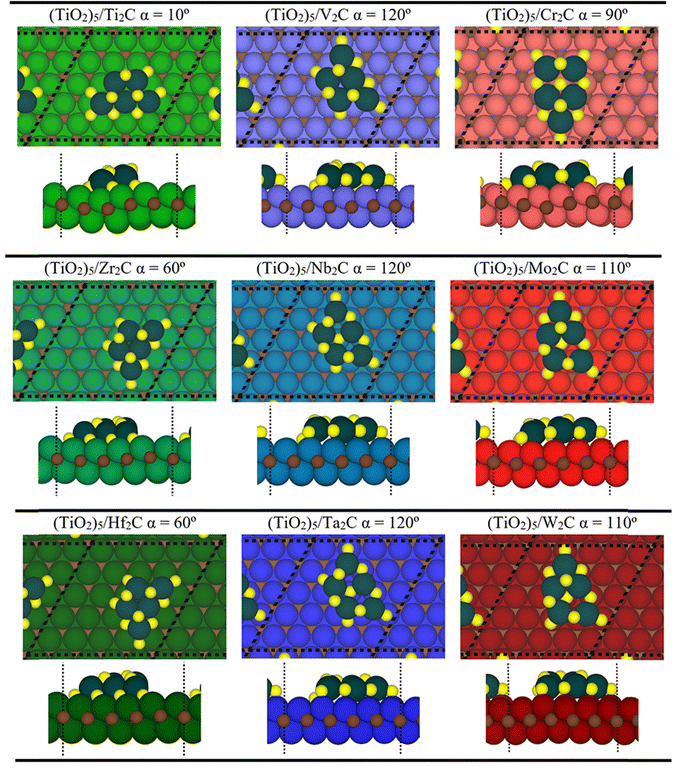 | ||
| Fig. 3 Top (top) and side (bottom) views of the optimized geometries of p(5×5) (dashed black line) (TiO2)5/M2C composite structures. Note that these structures correspond to the most stable configuration for each (TiO2)5/M2C. The color scheme of the C atom and (TiO2)5 cluster is the same as in Fig. 1. The green, blue, and red colors denote M atoms of groups IV, V, and VI, respectively, where light, solid, and darker shades imply 3d, 4d, or 5d series, respectively. | ||
3.2. Chemical bonding analysis of (TiO2)5/M2C composites
To gain further insight into the formation of titania/MXene composites depicted in Fig. 3, we conduct a topological analysis of the electron density to obtain Bader charges, and analyze CDD and PA-CDD plots, to investigate electron transfer between the components. Table 1 compiles ΔQ of the supported (TiO2)5 cluster resulting from Bader analysis. These data correspond to the most stable configuration for each MXene, while data for other configurations are reported in the ESI.† The ΔQ values in Table 1 represent the difference between the net charge on the titania nanocluster before and after adsorption. Since the isolated titania cluster is neutral, a negative ΔQ means the electron accumulation on the supported titania nanocluster. Thus, ΔQ < 0 implies an electron density excess on the supported cluster resulting from electron transfer from the M2C (0001) MXene surface towards the (TiO2)5 cluster. This electron excess is likely to promote the activation of the supported particle although further work involving study of the reactivity of the supported cluster is required to confirm this hypothesis. The electron density flow towards the titania cluster is systematically observed in all possible configurations regardless of the MXene composition, see Tables S1–S9 in the ESI.† ΔQ runs between −2.04 and −6.62 e and follows a similar trend as observed in Eads, confirming that a large adsorption energy is coupled with a large charge transfer, as shown in Fig. 4. The electron density accumulation at or near the (TiO2)5 cluster is accompanied by electron density depletion at the MXene surface. Usually, the excess electron density of an adsorbate results in structural changes. The case of the CO2 molecule interacting with MXenes is a clear example as the electron transfer towards CO2 promotes a considerable bending of the adsorbed molecule.54,55 To explore this effect in more detail, Fig. 5 plots Edef (TiO2)5vs. ΔQ of the supported titania cluster. This plot exhibits a quite clear linear trend (R = 0.91) that the charge transfer is the driving force that promotes the titania cluster deformation.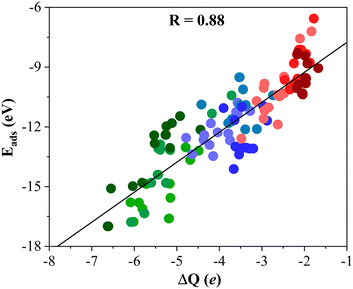 | ||
| Fig. 4 Linear trend between Eads and ΔQ of the titania cluster. The solid black line is the linear correlation between both quantities, and R stands for the regression coefficient. Color-coding as in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.† | ||
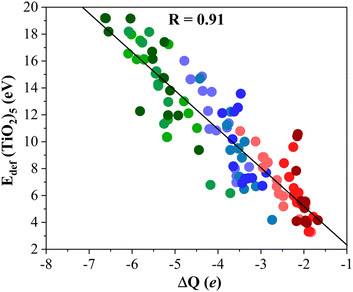 | ||
| Fig. 5 Linear correlation between Edef (TiO2)5 and ΔQ. Solid black line is the linear correlation between both quantities, while R stands for the linear correlation regression coefficient. Color coding as in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.† | ||
In addition, the CDD and the PA-CDD plots along the surface normal direction are presented in Fig. 6 for the most favorable composites (see Table 1 and Fig. 3). These plots complement the Bader analysis as they provide a visualization of the charge rearrangement induced by the formation of the composites. In all cases, a depletion of charge density is observed at the MXene M atoms and accumulation, at the Ti atoms from the (TiO2)5 cluster, consistent with previous work.41 The inset CDD plots in Fig. 6 show a clear redistribution of the electron density in the interface region. Altogether, both plots demonstrate that the electron density is mainly depleted in the MXene while it mainly accumulates in the (TiO2)5 cluster, in agreement with Bader charges. The strong charge transfer from MXene towards the (TiO2)5 cluster implies a high contribution of ionic bonding, however, the DOS projected per atomic orbital from Fig. S2 in the ESI† also shows a large mixing of orbitals, in this case, typical of a covalent bond. These two facts allow us to conclude that the chemical bond can be described as a mixture of covalent and ionic bonding. Furthermore, this electron transfer from the M2C MXene to (TiO2)5 clusters could generate a build-in electric field near the interface that can be beneficial in photocatalytic applications acting as a separator of charge carriers.56
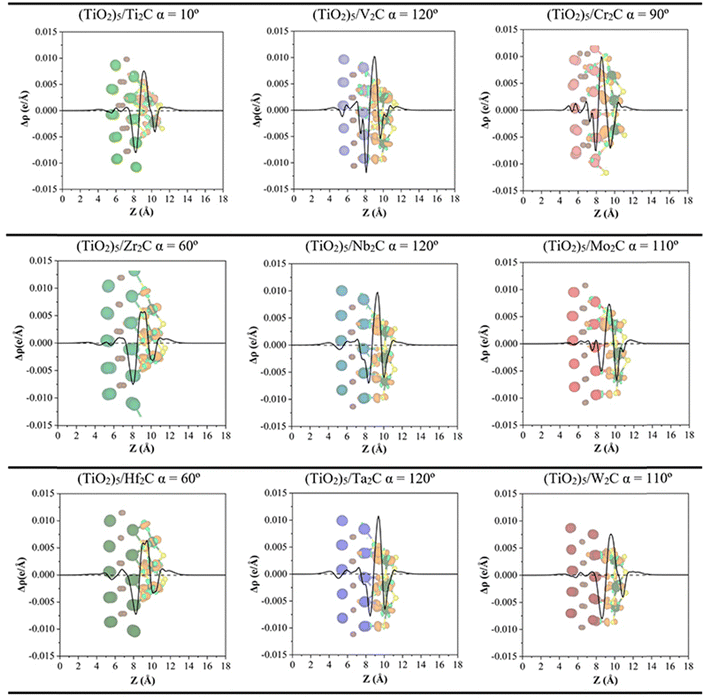 | ||
| Fig. 6 Plane-averaged charge density difference (PA-CDD) Δρ along the direction normal to the MXene surface, Z, for the most stable configurations of M2C/(TiO2)5 as listed in Table 1. Charge density differences, CDD, with an isosurface value of 0.015 e Å−3, are depicted inset where pale green and orange isosurfaces correspond to accumulation and depletion charges, respectively. Color coding as in Fig. 3. | ||
Further analysis is performed through the investigation of the work function, Φ, of each M2C MXene. One would, in general, expect that the lower the Φ, the easier the electron donation to the adsorbed titania cluster. Looking at the results reported in Table 1, the MXenes with the lowest Φ correspond to those composed of d3 transition metals followed by d4 and d5 ones. Indeed, the emerging trends when plotting Eads or Edef (TiO2)5versus Φ (cf.Fig. 7a and b) are analogous to those in Fig. 4 and 5. This is also consistent with the plot of Φ versus ΔQ in Fig. 7c indicating that, as expected, the electron transfer increased when Φ decreased, indeed with a relatively high regression coefficient, R, of 0.83.
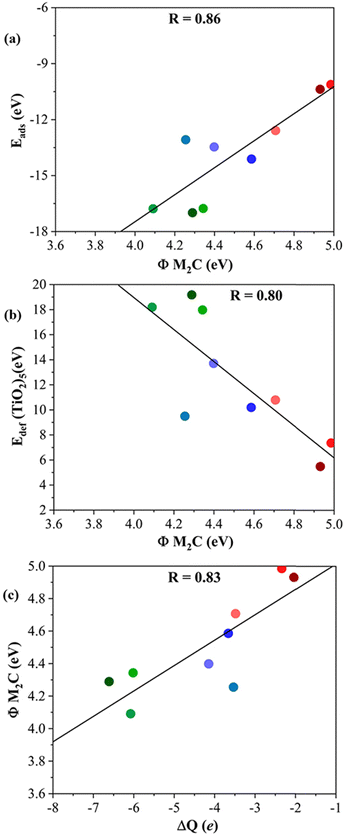 | ||
| Fig. 7 (a) Eadsvs. the work function, Φ, of bare (0001) MXene surfaces; (b) Edef (TiO2)5vs. Φ M2C; and (c) Φ M2C vs. ΔQ of (TiO2)5. The solid black lines correspond to the linear fitting associated with the regression coefficient, R. Color coding as in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.† | ||
3.3. Generalized trends of (TiO2)5/M2C composites
The main structural differences of these composites reside in the metal of the MXene. Hence, it is logical to investigate descriptors characteristic of transition metals such as the metal atom electronegativity, χM and the d-band center, εd, of the metal in the MXene structure.57 In particular, we focus on whether these descriptors would help tentatively predict the Eads and the Edef (TiO2)5 of a given M2C MXene. Fig. 8 shows clear linear correlations associated with the most favorable (TiO2)5/M2C composites listed in Table 1. Starting with the χM descriptor (cf.Fig. 8a and b), the adsorption energy increases as χM decreases. Thus, MXenes involving a d3 transition metal interact more strongly with the (TiO2)5 cluster than those MXene composed of d4 or d5 metal. This is consistent with the large Edef (TiO2)5 observed in MXene composed of d3 metals. In summary, we can conclude that (TiO2)5/M2C composites involving transition metals with a relatively low χM will exhibit a large exothermic interaction between the two constituents and a large structural modification on the (TiO2)5 nanoclusters.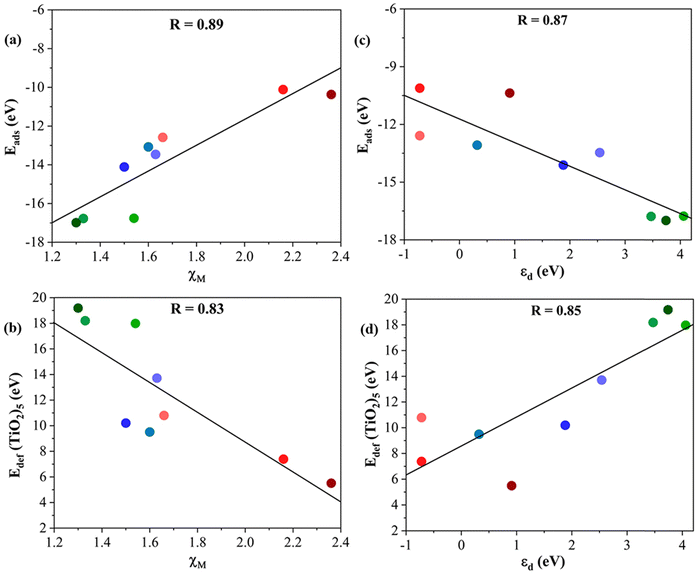 | ||
| Fig. 8 Tentative linear correlations of (a) Eadsvs. χM, (b) Edef (TiO2)5vs. χM, (c) Eadsvs. εd, and (d) Edef (TiO2)5vs. εd. The linear regression coefficient, R, is given in the inset in each panel. Color coding as in Fig. 3. Linear fitting analysis is reported in Table S12 of the ESI.† | ||
The trends corresponding to the second analyzed descriptor, εd, are depicted in Fig. 8c and d which also exhibit a reasonable linear trend. In general, MXenes involving a transition metal with a high εd lead to large exothermic adsorption energy and large deformation energy on (TiO2)5 nanoclusters. Based on the aforementioned analysis, χM and εd can be considered feasible descriptors to predict the formation of titania/MXene composites based on the MXene composition.
4. Conclusions
The formation of titania/MXene composites obtained by supporting a (TiO2)5 cluster on the basal surface of M2C MXenes with M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W has been investigated by means of periodic DFT based calculation on appropriate supercells. The present results systematically show a highly exothermic adsorption energy. The MXenes involving d3 metals (Ti, Zr, and Hf) have the largest interaction followed by d4 (V, Nb, Ta) and d5 (Cr, Mo, and W) metals. The composite formation involved an important change in the atomic structure of the supported (TiO2)5 cluster, relative to the most stable gas phase conformation in such a way that the largest adsorption promotes the largest deformation. The analysis of Bader charge and CDD plots shows a clear electron transfer from the MXene towards the (TiO2)5 cluster. The accumulation of electron density in the supported (TiO2)5 cluster is at the origin of its deformation.These systematic trends are rationalized using the MXene work function, the electronegativity of the metal atom, and the d-band center of the metal in the MXene. MXenes with a low work function are those that show high adsorption energy with a concomitant high deformation energy of the (TiO2)5 cluster and a large electron transfer. MXenes composed of metals with low electronegativity show high adsorption energies including the high deformation energy of the (TiO2)5 nanocluster and high electron transfer. Finally, the higher the d-band center of the metal in the MXene, the higher the adsorption and deformation energies and also the electron transfer. Finally, it has been shown that features of the metal element in the MXene can be used to predict trends in the interaction and in the extent of electron transfer when forming titania/MXene composites, valuable information for experimentalists interested in the synthesis, properties, and possible applications of these composites.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study has been supported by the Spanish Ministerio de Ciencia e Innovación and Agencia Estatal de Investigación (AEI) MCIN/AEI/10.13039/501100011033 through projects PID2020-115293RJ-I00, PID2021-126076NB-I00, TED2021-129506B-C22, la Unidad de Excelencia María de Maeztu CEX2021-001202-M granted to the IQTCUB and, in part, from COST Action CA18234, and Generalitat de Catalunya 2021SGR00079. N. G.-R. thanks the Generalitat de Catalunya for a predoctoral contract 2022 FISDU 00106. F. V. is thankful for the ICREA Academia Award 2023 Ref. Ac2216561.References
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- N. Serpone and A. V. Emeline, J. Phys. Chem. Lett., 2012, 3, 673–677 CrossRef CAS PubMed.
- B. Samanta, Á. Morales-García, F. Illas, N. Goga, J. A. Anta, S. Calero, A. Bieberle-Hütter, F. Libisch, A. B. Muñoz-García, M. Pavone and M. C. Toroker, Chem. Soc. Rev., 2022, 51, 3794–3818 RSC.
- P. K. J. Robertson, J. M. C. Robertson and D. W. Bahnemann, J. Hazard. Mater., 2012, 211–212, 161–171 CrossRef CAS PubMed.
- D. Zhu and Q. Zhou, Environ, Nanotechnol. Monit., 2019, 12, 100255 CrossRef.
- T. Hisatomi and K. Domen, Nat. Catal., 2019, 2, 387–399 CrossRef CAS.
- X. Jiao, K. Zheng, L. Liang, X. Li, Y. Sun and Y. Xie, Chem. Soc. Rev., 2020, 49, 6592–6604 RSC.
- E. Kozlova, A. Safatov, S. Kiselev, V. Y. Marchenko, A. Sergeev, M. Skarnovich, E. Emelyanova, M. Smetannikova, G. Buryak and A. Vorontsov, Environ. Sci. Technol., 2010, 44, 5121–5126 CrossRef CAS PubMed.
- Y. Li, Y.-K. Peng, L. Hu, J. Zheng, D. Prabhakaran, S. Wu, T. J. Puchtler, M. Li, K.-Y. Wong and R. A. Taylor, Nat. Commun., 2019, 10, 4421 CrossRef PubMed.
- A. Shahzad, K. Rasool, M. Nawaz, W. Miran, J. Jang, M. Moztahida, K. A. Mahmoud and D. S. Lee, Chem. Eng. J., 2018, 349, 748–755 CrossRef CAS.
- Y. Zhao, N. Liu, S. Zhou and J. Zhao, J. Mater. Chem. A, 2019, 7, 16294–16303 RSC.
- D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave and I. P. Parkin, Nat. Mater., 2013, 12, 798–801 CrossRef CAS PubMed.
- M. A. Henderson, Surf. Sci. Rep., 2011, 66, 185–297 CrossRef CAS.
- Y. Yamada and Y. Kanemitsu, Appl. Phys. Lett., 2012, 101, 133907 CrossRef.
- R. Reichert, Z. Jusys and R. J. Behm, J. Phys. Chem. C, 2015, 119, 24750–24759 CrossRef CAS.
- X. Wang, Y. Ruan, S. Feng, S. Chen and K. Su, ACS Sustainable Chem. Eng., 2018, 6, 11424–11432 CrossRef CAS.
- Y. Chen, Ll Soler, C. Cazorla, J. Oliveras, N. G. Bastús, V. F. Puntes and J. Llorca, Nat. Commun., 2023, 14, 6165 CrossRef CAS PubMed.
- M. Allès, E. R. Remesal, F. Illas and Á. Morales-García, Adv. Theory Simul., 2023, 10, 2200670 CrossRef.
- C. Di Valentin, E. Finazzi, G. Pacchioni, A. Selloni, S. Livraghi, M. C. Paganini and E. Giamello, Chem. Phys., 2007, 339, 44–56 CrossRef CAS.
- E. R. Remesal and Á. Morales-García, Phys. Chem. Chem. Phys., 2022, 24, 21381–21387 RSC.
- E. R. Remesal, Á. Morales-García and F. Illas, J. Phys. Chem. C, 2023, 127, 20128–20136 CrossRef PubMed.
- C. Di Valentin, G. Pacchioni, A. Selloni, S. Livraghi and E. Giamello, J. Phys. Chem. B, 2005, 109, 11414–11419 CrossRef CAS PubMed.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- J. Low, L. Zhang, T. Tong, B. Shen and J. Yu, J. Catal., 2018, 361, 255–266 CrossRef CAS.
- Á. Morales-García, F. Calle-Vallejo and F. Illas, ACS Catal., 2020, 10, 13487–13503 CrossRef.
- D. Dolz, R. De Armas, P. Lozano-Reis, Á. Morales-García, R. Sayós and F. Illas, ChemCatChem, 2024 DOI:10.1002/cctc.202400122.
- H. Zhou, Z. Chen, E. Kountoupi, A. Tsoukalou, P. M. Abdala, P. Florian, A. Fedorov and C. R. Müller, Nat. Commun., 2021, 12, 5510 CrossRef CAS PubMed.
- A. Jurado, Á. Morales-García, F. Viñes and F. Illas, ACS Catal., 2022, 12, 15658–15667 CrossRef CAS.
- S. Kazim, C. Huang, N. H. Hemasiri, A. Kulkarni, S. Mathur and S. Ahmad, Adv. Funct. Mater., 2024, 2315694, DOI:10.1002/adfm.202315694.
- A. Dey, S. Varagnolo, N. P. Power, N. Vangapally, Y. Elias, L. Damptey, B. N. Jaato, S. Gopalan, Z. Golrokhi, P. Sonar, V. Selvaraj, D. Aurbach and S. Krishnamurthy, Prog. Mater. Sci., 2023, 139, 101166 CrossRef CAS.
- G. Gao, A. P. O’Mullane and A. Du, ACS Catal., 2017, 7, 494–500 CrossRef CAS.
- Z. Guo, J. Zhou, L. Zhu and Z. Sun, J. Mater. Chem. A, 2016, 4, 11446–11452 RSC.
- D. Ontiveros, F. Viñes and C. Sousa, J. Mater. Chem. A, 2023, 11, 13754–13764 RSC.
- J. Chen, H. Zheng, Y. Zhao, M. Que, W. Wang and X. Lei, Ceram. Int., 2020, 46, 20088–20096 CrossRef CAS.
- S. Debow, T. Zhang, X. Liu, F. Song, Y. Qian, J. Han, K. Maleski, Z. B. Zander, W. R. Creasy and D. L. Kuhn, J. Phys. Chem. C, 2021, 125, 10473–10482 CrossRef CAS.
- L. Jiao, C. Zhang, C. Geng, S. Wu, H. Li, W. Lv, Y. Tao, Z. Chen, G. Zhou and J. Li, Adv. Energy Mater., 2019, 9, 1900219 CrossRef.
- R. Li, X. Ma, J. Li, J. Cao, H. Gao, T. Li, X. Zhang, L. Wang, Q. Zhang and G. Wang, Nat. Commun., 2021, 12, 1587 CrossRef CAS PubMed.
- M. M. Nair, A. C. Iacoban, F. Neatu, M. Florea and S. Neatu, J. Mater. Chem. A, 2023, 11, 12559–12592 RSC.
- S. A. Khan, B. Amin, L.-Y. Gan and I. Ahmad, Phys. Chem. Chem. Phys., 2017, 19, 14738–14744 RSC.
- L. Xu, T. Wu, P. R. Kent and D.-E. Jiang, Phys. Rev. Mater., 2021, 5, 054007 CrossRef CAS.
- N. García-Romeral, M. Keyhanian, Á. Morales-García, F. Viñes and F. Illas, Chem. Eur. J., 2024, 30, e202400255 CrossRef PubMed.
- O. Lamiel-García, A. Cuko, M. Calatayud, F. Illas and S. T. Bromley, Nanoscale, 2017, 9, 1049–1058 RSC.
- Á. Morales-García, R. Valero and F. Illas, J. Chem. Theory Comput., 2017, 13, 3746–3753 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1994 Search PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- G. Di Liberto, Á. Morales-García and S. T. Bromley, Nat. Commun., 2022, 13, 6236 CrossRef CAS PubMed.
- H. Oschinski, Á. Morales-García and F. Illas, J. Phys. Chem. C, 2021, 125, 2477–2484 CrossRef CAS.
- Á. Morales-García, A. Fernández-Fernández, F. Viñes and F. Illas, J. Mater. Chem. A, 2018, 6, 3381–3385 RSC.
- R. Morales-Salvador, Á. Morales-García, F. Viñes and F. Illas, Phys. Chem. Chem. Phys., 2018, 20, 17117–17124 RSC.
- M.-L. Tsai, S.-H. Su, J.-K. Chang, D.-S. Tsai, C.-H. Chen, C.-I. Wu, L.-J. Li, L.-J. Chen and J.-H. He, ACS Nano, 2014, 8, 8317–8322 CrossRef CAS PubMed.
- B. M. Abraham, O. Piqué, M. A. Khan, F. Viñes, F. Illas and J. K. Singh, ACS Appl. Mater. Interfaces, 2023, 15, 30117–30126 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Tables S1–S12 and Fig. S1 and S2. See DOI: https://doi.org/10.1039/d4cp01757a |
| ‡ Equally contributed. |
| This journal is © the Owner Societies 2024 |