Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sorption of metal ions onto PET-derived microplastic fibres†
H.
Frost
ab,
T.
Bond
 cd,
T.
Sizmur
cd,
T.
Sizmur
 e and
M.
Felipe-Sotelo
e and
M.
Felipe-Sotelo
 *a
*a
aSchool of Chemistry and Chemical Engineering, University of Surrey, Guildford, Surrey GU2 7XH, UK. E-mail: m.felipe-sotelo@surrey.ac.uk
bSchool of Civil Engineering and Surveying, University of Portsmouth, Portland Building, Portland Street, Portsmouth PO1 3AH, UK
cSchool of Sustainability, Civil and Environmental Engineering, University of Surrey, Guildford, GU2 7XH, UK
dWater Research Centre, Frankland Rd, Swindon SN5 8YF, UK
eDepartment of Geography and Environmental Science, University of Reading, Reading, RG6 6DW, UK
First published on 18th November 2024
Abstract
This study investigated microplastic polyester fibres representative of those shed during laundering as sorbents for metal ions. During sewage distribution and treatment, microplastics are exposed to elevated concentrations of metal ions, typically for several days. Cryogenic milling was used to generate polyethylene terephthalate (PET) fibres. Characterisation using optical microscopy and Raman spectroscopy revealed that milling did not cause significant chemical alteration to the fibres. Milled fibres were subsequently assessed in screening tests for their capacity to retain 12 metal ions—Sb(III), As(III), Cd(II), Cr(VI), Cu(II), Co(II), Pb(II), Hg(II), Mo(VI), Ni(II), V(V) and Zn(II)—at pH 8. All metal ions were sorbed onto PET fibres. The highest distribution coefficient (Kd) was observed for Pb2+ (939 mL g−1), followed by Cd2+ (898 mL g−1), Cu2+ (507 mL g−1), Hg2+ (403 mL g−1), and Zn2+ (235 mL g−1). The extent of sorption is largely explicable by electrostatic interactions between the PET surface (1.95 point of zero net charge) and the predicted metal ion species. The sorption behaviour of Cd2+ and Hg2+ was examined in more detail since both showed high sorption capacity and are highly toxic. Kinetic experiments revealed that the sorption of both elements was relatively fast, with a steady state reached within six hours. Experimental data from isotherm tests fitted well to the Langmuir sorption model and demonstrated that PET fibres had a much greater sorption capacity for Hg2+ (17.3–23.1 μg g−1) than for Cd2+ (4.3–5.3 μg g−1). Overall, the results indicate that retention of metal ions onto PET fibres originating from laundry is expected during full-scale sewage treatment, which facilitates the subsequent transfer of metals into the terrestrial environment, given that sewage sludge is commonly applied to agricultural land.
Environmental significanceDuring sewage treatment, microplastics are exposed to metal ions. Around 80% of microplastics are retained in sewage sludge, which is commonly applied to agricultural land. Polyethylene terephthalate (PET) microfibres derived from laundering synthetic clothes are an important fraction of microplastics entering the environment. After application to soils, metal ions are potentially accumulated by terrestrial organisms. This study aimed to determine whether microplastic fibres generated during laundering act as vectors for metals. Twelve metal ions were used for screening tests, all of which sorbed onto PET fibres. Maximum levels of adsorption for cadmium and mercury were reached within six hours. Overall, this study indicates that accumulation of metal ions on microplastic fibres is expected during sewage treatment. |
1. Introduction
Microplastics are a type of environmental contaminant that encompass a range of sizes (1–5 mm in diameter), shapes, and chemical compositions.1,2 Their small size, large surface area-to-volume ratio, wide environmental distribution, and general resistance to degradation have raised concerns because of their potential to sorb and transport co-pollutants in the environment, particularly through the food chain.3–6 Polyethylene terephthalate (PET), alternatively known as polyester, is the most widely produced synthetic fibre, representing 54% of the total global fibre production in 2021,7 and is the most commonly used fibre in the manufacturing of clothing.8 The laundering of textiles can release up to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fibres per kg of fabric into domestic wastewater systems.9
000 fibres per kg of fabric into domestic wastewater systems.9
During sewage treatment, ∼80% of microplastics are typically removed from the liquid fraction of sewage and retained in the solid fraction, known as sewage sludge, which accumulates during treatment. Sewage sludge can therefore contain large amounts of microplastics, over 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 microplastics per kg.10,11 The coexistence of microplastics, particularly PET, and metal ions in wastewater has raised concerns owing to the potential for metal ion sorption onto PET surfaces, which, in turn, enter the terrestrial environment when sewage sludge is added to agricultural land as a soil enhancer.5,12,13 It is relevant to note here that across Europe and North America, around 50% of sewage sludge is processed for agricultural use.14 PET microplastic fibres are among the most common microplastics reported in wastewater and sewage sludge, representing up to 90% of all microplastics.11,15 Corradini et al.16 found that the mass of microplastics in agricultural soils increased with successive biosolid application, from 1.37 to 4.38 mg kg−1 in soils that had received 1 and 5 biosolid applications, respectively. PET fibres are therefore thought to represent a large and important fraction of microplastics that enter agricultural soils through sewage sludge application.
000 microplastics per kg.10,11 The coexistence of microplastics, particularly PET, and metal ions in wastewater has raised concerns owing to the potential for metal ion sorption onto PET surfaces, which, in turn, enter the terrestrial environment when sewage sludge is added to agricultural land as a soil enhancer.5,12,13 It is relevant to note here that across Europe and North America, around 50% of sewage sludge is processed for agricultural use.14 PET microplastic fibres are among the most common microplastics reported in wastewater and sewage sludge, representing up to 90% of all microplastics.11,15 Corradini et al.16 found that the mass of microplastics in agricultural soils increased with successive biosolid application, from 1.37 to 4.38 mg kg−1 in soils that had received 1 and 5 biosolid applications, respectively. PET fibres are therefore thought to represent a large and important fraction of microplastics that enter agricultural soils through sewage sludge application.
Much attention has been paid to the sorption of organic contaminants, such as phthalates, polycyclic aromatic hydrocarbons (PAHs) and antibiotics, to microplastics.3,17,18 Interest in the capacity of microplastics to sorb inorganic pollutants such as metal ions has also grown considerably in recent years.2,6,19–22 Microplastics have been described as having an unexpectedly high affinity for heavy metals.23 For example, pristine polystyrene microplastics have been reported to sorb up to 655, and 1348 μg g−1 of cadmium (Cd2+), and lead (Pb2+), respectively.24 The sorption of metal ions onto microplastic surfaces is strongly influenced by the chemical properties of the metal ions and the physicochemical properties of the microplastic in question.2,25–29
Relatively few studies have quantified the sorption of metal ions onto polyethylene terephthalate (PET) microplastics.12,30,31 The sorption of some metal ions such as Cd2+, Pb2+, and Cr3+/CrO42− onto PET is reported in the literature (note that the oxidation state of Cr is not always indicated),12,30–33 with maximum sorption capacities ranging from 0.385 μg g−1 for Cr3+,21 to 4930 μg g−1 for Pb2+.12 Limited studies have compared the relative sorption of different metal ions onto PET microplastics however,30 and sorption data for key pollutants such as arsenic, cadmium, and mercury are either absent or extremely scarce. These represent important knowledge gaps because, upon application to soils, metal ions may potentially desorb and be accumulated by terrestrial organisms such as earthworms.34
Due to the limited information about the sorption of metal ions onto PET, this study aimed to fill key knowledge gaps surrounding this topic. Its overall aim was to determine whether microplastic fibres generated during laundering can act as vectors for metal ions into the terrestrial environment through sorption.5 Specific objectives were to (i) generate a reproducible source of PET fibres representative of those shed from fabrics during laundering, (ii) characterise their physicochemical properties, (iii) undertake screening tests to quantify sorption of 12 metal ions onto PET fibres and (iv) investigate the sorption behaviour of selected metal ions in more detail through kinetic and equilibrium tests. Combined, this information will allow an assessment of whether metal ion sorption onto PET fibres during sewage treatment facilitates their subsequent transfer into the terrestrial environment.
2. Materials and methods
2.1 Generation of PET fibres
For the experiment, 100% polyethylene terephthalate (PET) fabric (Mariella – microfibre nature-ecru) was supplied by Active Fabrics (Quakenbrück, Germany). Laundering was initially considered for generating PET fibres. However, conventional and accelerated laundering methods only produced 7–1507 mg fibres per kg of fabric35,36 and, therefore, can release large quantities of fibres into domestic wastewater, but this approach was deemed impractical for providing sufficient PET fibres for sorption experiments. Fibres were instead produced by grinding PET fabric in a cryogenic mill (6875 Freezer/Mill High Capacity Cryogenic Chamber, SPEX SamplePrep). Fabric (3.5 ± 0.1 g) was rinsed in water (solid-to-liquid ratio: 1/100) on an orbital shaker for 24 hours at 150 rpm, dried at room temperature and then cut into approximately 2 × 2 cm squares using scissors. The milling cycle lasted 45 minutes in total, consisting of 20 minutes pre-cooling, followed by three grinding cycles of seven minutes at 10 cps, with a cooling time of 2 minutes between each. Milled fibres were stored in a clean polypropylene container.2.2 Characterisation of PET microfibres
The surface morphology, chemical functionality, dimensions, and zeta potential of the microplastic fibres were characterised by SEM imaging (Apreo SEM, ThermoFisher Scientific), Raman spectroscopy (DXR3 Raman microscope, ThermoScientific; U-TV0.5XC-3 microscope, Olympus), optical microscopy (Olympus DSX500 microscope), and electrophoretic methods (Zetamaster, Malvern Instruments, UK) respectively. Specific surface area was estimated from the fibre length and width data. Full details of the material characterisation methods are provided in the paper's ESI.†2.3 Sorption screening tests
All sorption experiments were carried out at 20 (±1) °C, in 60 mL polytetrafluoroethylene (PTFE) screw-cap containers (Fisher Scientific UK). Prior to use, containers were soaked in 5% v/v HNO3 (PrimarPlus – Trace Analysis Grade Nitric Acid, >68%; Fisher Scientific) for 6 hours and then deionised water (18 mΩ cm−1) for 24 hours, before drying at room temperature in a fume hood. PET fibres (0.2 ± 0.005 g) were suspended in 40 mL of solution containing 200 μg L−1 of one of the following 12 metal ions: antimony (SbIIIO2−), arsenic (AsIIIO33−), cadmium (Cd2+), chromium (CrVIO42−), copper (Cu2+), cobalt (Co2+), lead (Pb2+), mercury (Hg2+), molybdenum (MoVIO42−), nickel (Ni2+), vanadium (VVO43−) or zinc (Zn2+), which were prepared from commercial stock solutions (1000 μg mL−1, PlasmaCAL). The final solid-to-liquid ratio was 1/200, with the initial pH adjusted to 8 ± 0.1, using 0.01 M NaOH or 0.01 M HCl solutions.Suspensions were placed on an orbital shaker at 200 rpm for 24 hours. Subsequently, 5 mL of each sample was filtered through a 0.45 μm filter (Millex 33 mm diameter mixed cellulose ester sterile membrane filter; Merck Millipore, Ireland). Sample filtrates were acidified to a final w/w concentration of 1% using HNO3, and refrigerated prior to analysis by inductively coupled plasma-mass spectrometry (ICP-MS) (Agilent 7800 ICP-MS). All sorption experiments were repeated 5 times.
The sorption of each metal ion to the PET fibres was calculated using eqn (1), where Cs is the concentration of the analyte adsorbed to the solid (μg g−1), [Ci] is the initial analyte concentration in the solution (μg L−1), [Caq] is the equilibrium analyte concentration in the solution (μg L−1), V is the solution volume (L), and Sm is the mass of the PET fibres (adsorbent) (g). Control experiments, which contained no fibres, were prepared for each metal ion. These were used to calculate the distribution factor Dd,w as in eqn (2), where [Ctot,C] is the total metal concentration added, and [Caq,C] is the final concentration in the controls, as determined by ICP-MS. This distribution factor Dd,w was used to correct [Caq] in eqn (1), to account for any losses of the metal ions in the solution due to retention onto the walls of the containers. Distribution coefficients (Kd) (mL g−1), quantifying the partitioning behaviour of metal ions between sorbed and aqueous phases, were calculated as a ratio of the sorbed metal ion concentration ({Cs}) to the aqueous phase metal ion concentration ([Caq]) (eqn (3)).2,25,37
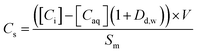 | (1) |
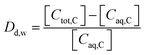 | (2) |
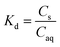 | (3) |
2.4 Sorption kinetics for Cd2+ and Hg2+
Materials are given in detail in 2.3, with the exception that the experiments were undertaken in 0.1 mol L−1 phosphate buffer at pH 7 (Table SI-3†), containing 200 μg L−1 of either Cd2+ or Hg2+. Experiments were conducted in triplicate, and controls, which contained metals but no fibres, were completed in duplicate to determine available metal concentrations, as discussed in section 2.3. Suspensions were placed on an orbital shaker at 200 rpm for time intervals of 5, 10, 20, 30, 60, 180, and 360 minutes. Subsequently, 5 mL of each sample were filtered (section 2.3) and the Cd2+ filtrates were then acidified using 2% v/v HNO3 prior to ICP-MS analysis. Meanwhile, Hg2+ filtrates were acidified using 1% v/v HCl (Trace Analysis Grade Hydrochloric Acid, 1 M; Fisher Scientific UK) and spiked with gold (Au) to a final concentration of 200 μg L−1. HCl and Au inhibit the reduction of Hg2+ into Hg0, the presence of which can lead to substantial carryover.38 All filtrates were refrigerated prior to analysis. The sorption of Cd2+ and Hg2+ to the PET fibres was evaluated using eqn (1)–(3).2.5 Sorption equilibrium isotherms for Cd2+ and Hg2+
For the isotherm experiments, 0.2 ± 0.003 g of fibres were suspended in 40 mL of solution containing either Hg2+ or Cd2+. For Hg2+, initial concentrations were 5, 25, 50, 100, 200, 300 and 500 μg L−1, and for Cd2+, initial concentrations were 5, 25, 50, 75, 100, 150 and 200 μg L−1. Experiments were conducted in triplicate and controls, which contained metals but no fibres, were completed in duplicate. Experiments were performed at pH 6, 7, and 8, using 0.1 mol L−1 phosphate buffers (Table SI-3†). These pH conditions have been selected in order to mimic typical operational ranges of wastewater treatment plants.39–41 Suspensions were placed on an orbital shaker at 200 rpm for 6 hours. Subsequently, samples were filtered and acidified as described above. Residual suspensions were also filtered using filter paper (Whatman no. 1), to obtain fibres for characterisation by Raman spectroscopy. The sorption of each metal ion onto the PET fibres (Cs) was calculated using eqn (1).2.6 Quantification of metal ions using ICP-MS
The signals of the isotopes 51V, 52Cr, 59Co, 60Ni, 63Cu, 66Zn, 75As, 95Mo, 111Cd, 121Sb, 201Hg, and 208Pb, were measured for the determination of each respective element, by inductively coupled plasma mass spectrometry (ICP-MS). Further details of the methodology used, including the instrumental limit of detection (LOD) and limit of quantification (LOQ), are given in the ESI.†2.7 Kinetics and isotherm modelling
From the kinetics data, the rate of sorption and equilibrium sorption capacity of the PET fibres for Cd2+ and Hg2+ were calculated using the pseudo-first-order (eqn (4)) and pseudo-second-order (eqn (5)) kinetic models, where qt is the sorption capacity at any given time (μg g−1), qe is the equilibrium sorption capacity (μg g−1), t is the time (min), k1 is the pseudo-first-order rate constant (min−1), and k2 is the pseudo-second-order rate constant (g μg−1 min).| qt = qe(1 − ek1t) | (4) |
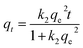 | (5) |
Equilibrium isotherm data were described using the Langmuir (eqn (6)) and Freundlich (eqn (7)) equations. The Langmuir model assumes that only monolayer sorption will occur and that there are no interactions between sorbate particles.42,43 The Freundlich model assumes that multi-layer sorption occurs, sorption sites have unequal affinities for the sorbent, and sites with the highest sorbent affinities are occupied first.42,43
In eqn (6) and (7), Cs is the sorption of each metal at equilibrium (μg g−1), CSM is the maximum monolayer sorption capacity of the sorbent (μg g−1), b is the binding constant (L μg−1), [Caq] is the aqueous concentration of metal at equilibrium (μg L−1), Kf is the Freundlich coefficient (μg1−n Ln g−1), and n is the Freundlich exponent.
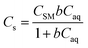 | (6) |
| Cs = KfCaq1/n | (7) |
Origin 2020 Academic (OriginLab Corporation; Massachusetts, USA) was used to model the experimental data, as shown in Table SI-4.† For the isotherm models, confidence bands were fitted showing the 95% confidence intervals.
2.8 Theoretical speciation modelling
The HYDRA (Hidra-Hydrochemical Database) and MEDUSA (Make Equilibrium Diagrams Using Sophisticated Algorithms) programmes44 were used to construct Pourbaix (pH vs. ESHE) diagrams and speciation graphs for cadmium and mercury. For each metal, the phosphate (PO43−) concentration was set to 0.1 M, the temperature was set to 20 °C, and the ionic strength was fixed at 0.1 M. The concentrations for cadmium and mercury were set to 1.78 μM (200 μg L−1) and 2.49 μM (500 μg L−1), respectively, to match experimental conditions.3. Results and discussion
3.1 Characterisation of PET microfibres
Fibres were imaged to visually assess the effect of cryo-milling on their surface topography (Fig. 1). A single fibre with an approximate length of 225 μm is shown in Fig. 1a. At higher magnifications, fibre surfaces appeared to be far more irregular than those imaged before cryo-milling (Fig. 1b and c). Cryo-milled fibre surfaces were rougher, more undulating, and often cracked, indicating physical damage caused by the milling procedure. Laundering experiments conducted by Pušić et al.45 reported similar but more limited damage, indicative of abrasion, after 25 washing cycles, with some indentations and cracks appearing. The fibres produced in our experiment probably experienced higher magnitude compressive and abrasive forces during cryo-milling than those exerted during home laundering. Fibre ends were typically irregular, with cracks and folds, suggesting that breakage was caused by fatigue failure, an important mechanism of fibre breakage during home laundering.46 Preliminary work verified that the 24 hours rinsing procedure was effective for removing residual particulates from the fabric surfaces (Fig. SI-1†). Before milling, PET fibres were uniform in width and shape, although their surface topography appeared to be rough and dimpled at higher magnifications (Fig. SI-2†).Normalised Raman spectra for the PET fabric and fibres show minimal fluorescence and noise, and well-resolved peaks (Fig. SI-3 and SI-4†). The fabric material was verified as PET, with a >94% match to known laboratory and environmental PET samples from a database search (see ESI† for details). Although SEM imaging indicated minor topographical differences between the PET fabric and cryo-milled fibres (Fig. 1, SI-1 and SI-2†), their Raman spectra were very similar (Fig. SI-3 and SI-4†), indicating that no significant chemical changes occurred as a result of cryo-milling.47
The average cryo-milled fibre length, estimated using optical microscopy, was 174 ± 132 μm (Table 1). Approximately 30% of fibres were 120–180 μm in length, with ∼90% of fibres below 300 μm in length (Fig. SI-5†). Conventional laundering experiments by Hernandez et al. (2017),48 using two kinds of polyester fabrics, revealed that the majority of shed fibres were 100 to 800 μm in length. Vassilenko and co-workers49 conducted conventional laundering experiments using 37 different fabrics (mainly polyester) and found that the most frequent size range of shed fibres was 163–283 μm in length, which is in good agreement with the results obtained here. Accelerated laundering experiments have also generated shed fibres of a similar size. Palacios-Marín et al.50 laundered various polyester, cotton, and polycotton blend fabrics using an accelerated laundering laboratory apparatus (Gyrowash), and found that 91% of shed fibres were less than 1000 μm in length, with most being 200–400 μm. Therefore, the length of cryo-milled fibres was broadly similar to the lengths of fibres shed during laundering.
The width of the cryo-milled fibres was highly uniform, with a small standard deviation (±2.4 μm). Approximately 75% of fibres had a width of 16–22 μm (Fig. SI-5†). This is typical of synthetic fibres such as polyester/PET, with fibre widths outside this range likely due to the compression of the fibres during cryo-milling.47
The average length and width data were collected using fibres from three separate milling cycles, and the means were compared with a one-way ANOVA. The mean fibre length and width were not significantly different (α = 0.5) between different milling cycles, showing that cryo-milling has good repeatability, yielding a consistent size distribution among milled fibres. Overall, length and width distributions of cryo-milled fibres are representative of those shed during both conventional and accelerated laundering experiments.
The specific surface area (SSA) of the fibres was calculated from the average length and width data, and the average density of PET (1.365 g cm3)51 was 0.156 ± 0.007 m2 g−1. It is important to note that this value is probably an underestimate because the method of calculation assumed that fibres are perfectly cylindrical, fibre ends are circular, and fibre surfaces are smooth. SSA calculations also did not account for porosity, although PET microplastics have been reported to have a lower total pore volume than other microplastics.12 Nonetheless, the calculated SSA of 0.156 m2 g−1 in this study is comparable with measured SSA values of PET microplastics published previously. Guo and Wang32 performed sorption experiments with irregular PET fragments that were smaller than those of this study (100–150 μm diameter), and reported an SSA of 0.162 m2 g−1. The SSA of virgin and aged PET fibres, approximately 2000–3000 μm in length, were reported to be 0.194 and 0.306 m2 g−1 respectively.33
Zeta potential experiments revealed that the PET fibres had a negative zeta potential over a pH range of 3–11 (Fig. SI-6†). The zeta potential remained constant as the pH decreased from 11 to 7, after which it steadily became less negative. An approximate point of zero charge (pHPZC) of 1.95 was derived from the intersection point on the pH axis when the zeta potential of the fibres in suspension was 0 mV. Below this pH, the zeta potential became positive. Using the pH drift method, the approximate pHPZC was determined to be 3.7 (Fig. SI-6†). Both pHPZC measurements are much lower than the typical pH of freshwater (6.5–7.1), seawater (7.5–8.4), and sewage sludge (5.0–8.0).25,52,53 The PET fibre surfaces are therefore expected to be negatively charged under the pH conditions of all sorption tests (pH 6–8), and therefore, under typical pH conditions of environmental water and sludge samples.39–41
The pHPZC value of microplastics depends on their surface chemistry and are generally reported to be between 2 and 5.43,54 A pHPZC value of 1.95 for the PET fibres obtained from the zeta potential experiment (Table 1) is in good agreement with that of Grancaric and co-workers,54 who estimated the pHPZC value of PET textiles fibres to be <2.5. The zeta potential steadily became less negative, as the pH decreased below approximately pH 6,54 again in good agreement with the data shown in Fig. SI-6.† The pHPZC value of 3.7, obtained from the pH drift experiment (Fig. SI-6†), matching with the results of Shih et al.,55 who reported a pHPZC value of 4.03 for virgin PET microplastics.
3.2 Sorption screening tests for twelve metal ions
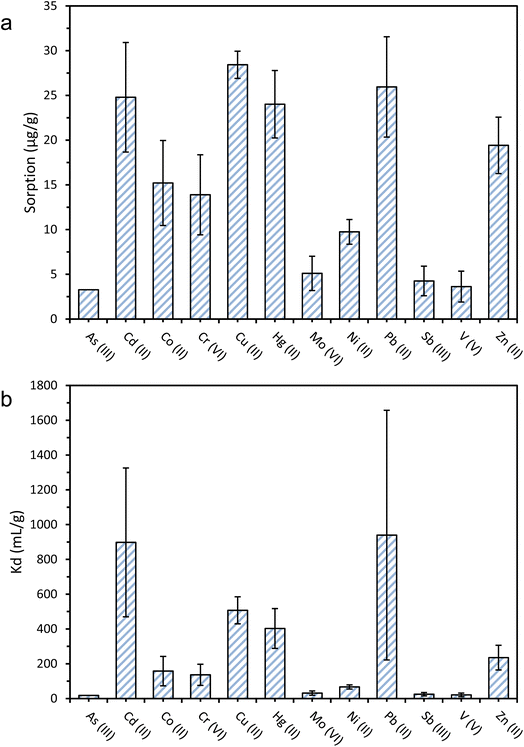
The sorption of 12 metal ions onto PET microfibres at pH 8 and an initial concentration of 200 μg L−1 ranged from 3.3 to 28.4 μg g−1 (Fig. 2). Cu2+ sorption was highest (28.4 ± 1.5 μg g−1), followed by Pb2+ (26.0 ± 5.6 μg g−1), Cd2+ (24.8 ± 6.1 μg g−1), Hg2+ (24.0 ± 3.8 μg g−1), and Zn2+ (19.4 ± 3.2 μg g−1). The net surface charge is likely to have influenced the relative sorption affinities of the metal ions investigated. Thus, the lowest sorption was observed for As(III) (3.2 μg g−1), V(V) (3.6 μg g−1), and Sb(III) (4.3 μg g−1). The low sorption of As(III) may be explained by electrostatic repulsion between the hydrogen arsenate (HAsO42−) oxyanion that predominates at pH 8, and the negatively charged surfaces of the PET fibres. The oxyanionic speciation of Sb(III) (SbO2−) and V(V) (VO43−) at an experimental pH of 8 may also explain their low sorption of 4.3 and 3.6 μg g−1, respectively.When comparing these results with previous reports of sorption of metal ions onto microplastics, Turner and Holmes2 found the sorption of a range of metal ions including Cd2+, Cu2+, Co2+ and Pb2+ onto virgin polyethylene (PE) microplastics to be two to three orders of magnitude lower than those reported here, ranging from 0.01 μg g−1 for Cd2+, to 0.19 μg g−1 for Pb2+. The differences observed between different plastic polymers (PE vs. PET) can be partially attributed to the presence of electronegative, oxygen-containing functional groups on the PET, which presents two ester groups in each monomer, and the subsequent increase in the relative strength of sorbent-sorbate electrostatic interactions.33,37,56 Other experimental factors that may also contribute to the differences observed with the work by Turner and Holmes2 could be their lower initial concentrations (2–20 μg L−1), compared with 200 μg L−1 in this work, since this would have subsequently resulted in a lower concentration gradient between the aqueous and sorbed phases. Furthermore, the microplastics used by Turner and Holmes2 were much larger (∼4 mm diameter) than the PET fibres used in this study (174 ± 132 μm length), implying that the surface area would likely have been much lower.2,37
The higher sorption observed in PET compared with other plastics agrees with the observations of Han et al.,30 who investigated the sorption of Cu2+, Pb2+, and Cr3+ onto polypropylene (PP), PE and PET microplastics and observed consistently higher sorption for PET. The sorption of Cu2+ onto PP and PET was 0.278 and 0.488 μg g−1, respectively, and the sorption of Pb2+ onto PP and PET was 0.370 and 1.04 μg g−1, respectively.30 It must be noted that in their study, Han and co-workers30 used an initial concentration of Cu2+ and Pb2+ of 5000 μg L−1, much higher than that in the present study (200 μg L−1) and used ground plastic pellets of bigger size (<0.9 mm to 5 mm), which would partially justify their lower sorption.
The sorption capacities reported by Ungureanu et al.57 and Ciobanu et al.58 for PET fibres and flakes are two to three orders of magnitude higher than any of the values found in the present study or previous reports by Han and co-workers.30 Ciobanu et al.58 reported that the sorption for Pb2+ onto PET fibres and flakes was 8.64 and 4.38 mg g−1 respectively, while Ungureano et al.57 observed a sorption of 2.48 mg g−1 for Cu2+ onto unmodified PET flakes. Those studies were completed at lower pH values (pK = 6.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 and pH = 2–6
57 and pH = 2–6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58) and at higher concentrations of metal ions (177.90 mg L−1
58) and at higher concentrations of metal ions (177.90 mg L−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 and 40–500 mg L−1
57 and 40–500 mg L−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58), but most importantly neither of the two studies reported the completion of any control experiment in order to estimate the losses of metal ions by retention onto containers, which may have resulted in the overestimation of the sorption to PET.
58), but most importantly neither of the two studies reported the completion of any control experiment in order to estimate the losses of metal ions by retention onto containers, which may have resulted in the overestimation of the sorption to PET.
Alongside absolute sorption (Cs), the distribution coefficient, Kd, values are useful in comparing sorption between metal ions, as they quantify the sorbed-aqueous phase partitioning behaviour. A higher Kd value indicates a higher propensity of the metal ions to sorb onto the PET fibre surface, as opposed to remaining in the aqueous phase. The highest Kd values were recorded for Pb2+ (939.4 mL g−1), followed by Cd2+ (898 mL g−1), Cu2+ (507 mL g−1), Hg2+ (403 mL g−1), and Zn2+ (235 mL g−1). These Kd values are generally in good agreement with the literature values for other microplastics.2,25,27,37 On the basis of the results of the sorption screening tests, Cd2+ and Hg2+ were selected to have their sorption kinetic and equilibrium behaviour studied in more detail. Both elements showed high sorption capacities and distribution coefficients, have very high toxicity compared to other metals, and there is a lack of data for their sorption onto PET microplastics. A similar argument could be made for including Pb2+, but Pourbaix speciation modelling predicted that insoluble lead phosphate species would predominate under selected experimental conditions (i.e., in the presence of phosphate buffer used during kinetic and equilibrium tests), so it was uncertain what proportion of Pb removal would be due to sorption to microplastics, and what proportion would be due to co-precipitation with phosphate.
3.3 Sorption kinetics for Cd2+ and Hg2+
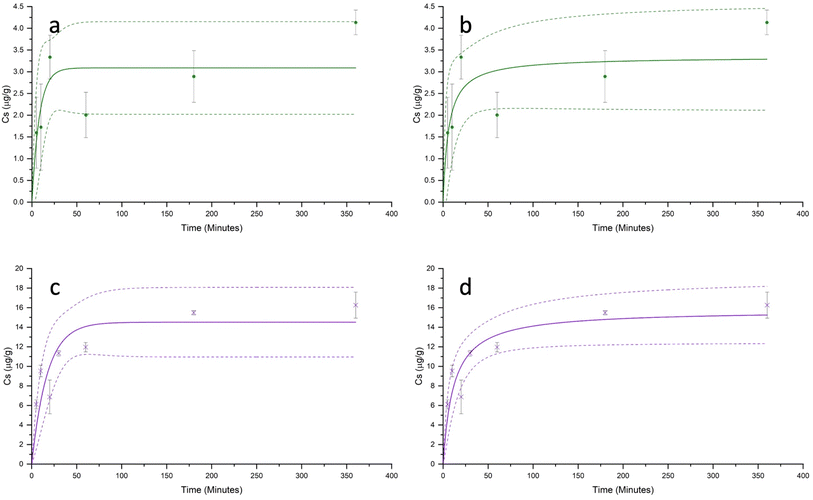
Both Cd2+ and Hg2+ sorption kinetics were characterised by a rapid initial period of sorption, which occurred within the first approximately 60 minutes of contact, followed by a much slower increase in sorption, reaching a plateau between 180 and 360 minutes (Fig. 3). For both metals, under all pH conditions, the sorption equilibrium was reached within 6 hours. The maximum experimental sorption capacities (Cs) of the PET fibres for Cd2+ and Hg2+ (after 6 hours) were 4.13 ± 0.28 μg g−1, and 16.26 ± 1.33 μg g−1 respectively.Table 2 summarises the adjusted parameters for the pseudo-first-order and pseudo-second-order kinetic models, constructed for Cd2+ and Hg2+. For both metal ions, the sorption kinetics data were better described by the pseudo-second-order model than the pseudo-first-order model. The pseudo-second-order model gave a higher coefficient of determination (r2), and modelled equilibrium sorption capacities (qe). This finding is consistent with most studies reported in the literature investigating the kinetics of metal sorption onto microplastics.26,28,30,31,33,43,56 While some researchers have concluded that the higher r2 value from the pseudo-second-order model suggests that the rate-limiting step is chemisorption, rather than physisorption,21,31,59 it is important to note that these kinetics models are empirical, and conclusions on the type of sorption mechanism should not be drawn purely from the goodness of model fit.60 The applicability of the pseudo-first-order and pseudo-second-order models is dependent not only on the sorption mechanism, but also on the relative initial sorbate concentration, the distribution and availability of active sites, and the stage of sorption, all of which have been shown to influence the r2 value.61,62
| Kinetic model | Parameter | Cd2+ | Hg2+ |
|---|---|---|---|
| Pseudo-first order | q e,exp (μg g−1) | 4.13 ± 0.28 | 16.26 ± 1.33 |
| q e,calc (μg g−1) | 3.09 ± 0.41 | 14.51 ± 1.45 | |
| k 1 (min−1) | 0.122 ± 0.066 | 0.58 ± 0.020 | |
| r 2 | 0.7441 | 0.8281 | |
| Pseudo-second order | q e,calc (μg g−1) | 3.34 ± 0.49 | 15.75 ± 1.35 |
| K 2 (g μg−1 min) | 0.049 ± 0.041 | 0.006 ± 0.002 | |
| r 2 | 0.7607 | 0.9025 |
3.4 Sorption equilibrium isotherms for Cd2+ and Hg2+
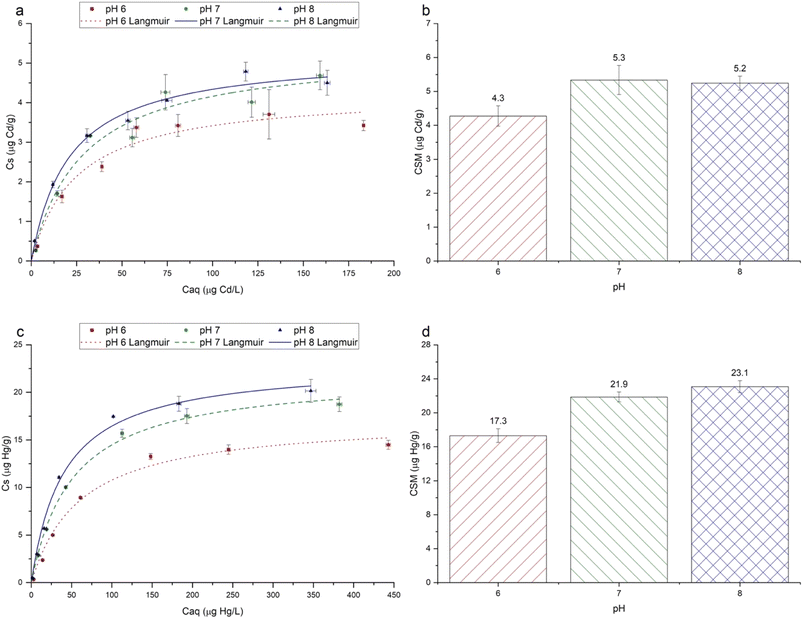
For both Cd2+ and Hg2+, under all pH conditions, sorption isotherms were characterised by greater sorption as [Caq] increased, followed by proportionally less sorption at higher [Caq] concentrations (Fig. 4). Langmuir and Freundlich models were fitted to the experimental data, with the Langmuir model consistently having a higher coefficient of determination (r2) for all metals under all pH conditions, hence only Langmuir models are shown in Fig. 4.The maximum Langmuir sorption capacities (CSM) for Cd2+ and Hg2+ ranged from 4.3 to 5.3 μg g−1, and from 17.3 to 23.1 μg g−1, respectively (Fig. 4). These values lie within the range reported in the available literature,2,63,64 although it should be noted that previous data are from studies that used a wide range of microplastics types and sizes, and experimental conditions. The sorption capacities of Cd2+ and Hg2+ (Fig. 4) were approximately 1–5 orders of magnitude higher than that reported by Holmes et al.,25 and Turner and Holmes.2 This may be partly explained by the much lower initial concentration gradient of 0–20 μg L−1 used in these studies, than ours (0–200 μg L−1 for Cd2+ and 0–500 μg L−1 for Hg2+), leading to a shallower concentration gradient between the aqueous phase and sorbed phase metals, and the larger size of the microplastics used in earlier work.2,25
Although data on the sorption of metal ions onto PET microplastics are scarce, our results are comparable with those reported in the available literature. Qiu and co-workers63 investigated the sorption of Hg2+ onto PET microplastics at pH 6.8 in the range from 1 to 50 μg L−1 Hg2+, reporting Langmuir CSM values of 6.6 and 35 μg g−1 for virgin and aged PET, respectively. Although size and surface area details were not presented by Qiu et al.,63 these values are in close agreement with our Hg2+ sorption data (17.3–23.1 μg g−1; Fig. 4). Data on the sorption of Cd2+ to PET microplastics are very scarce. However, the values reported in the literature for other microplastic types range greatly from 0.0004 μg g−1 for polyethylene in filtered seawater25 to 7485 μg g−1 for chlorinated polyethylene (CPE) in the pH range between 3 and 6.37
The experimental pH had a significant effect on the sorption of each metal ion (Fig. 4). For Hg2+, sorption followed the order pH 8 > pH 7 > pH 6, whereas for Cd2+, sorption followed the order pH 7 > pH 8 > pH 6. For Hg2+, sorption at pH 8 and 7 was significantly higher than that at pH 6 (p ≤ 0.05). For Cd2+, sorption at pH 7 was significantly higher than at pH 6, but sorption at pH 8 was not significantly different (p ≤ 0.05). For all metal ions, the order of the Langmuir CSM values (Fig. 4) matched the order of the experimental maximum Cs values (Fig. 4). Data are generally consistent with those reported in the literature in showing that the sorption of cationic metals onto microplastics increases as the experimental pH increases.30,31,37 This relationship can be attributed to several pH-dependent phenomena. First, as the solution pH increases, the concentration of hydronium ions (H3O+) decreases, leading to less competition between H3O+ and metal ions for sorption sites.28
Second, above the pHPZC value of approximately 1.95, the zeta potential of the PET microplastics became increasingly negative as the pH increased (Fig. SI-6†). The zeta potential of the PET microplastics decreased from approximately −55 mV at pH 6 to −60 mV at pH 7, and −65 mV at pH 8 (Fig. SI-6†). For Hg2+, the sorption capacity increased as the zeta potential decreased, suggesting the potential involvement of physisorption in the sorption mechanism.65 Tang et al.22 found that the sorption capacity of polyamide microplastics for Pb2+ increased as the pH increased (pH range 2.5–6). This was ascribed, in part, to the PA surface becoming more negative as the pH increased and the subsequent increase in the relative strength of the electrostatic interactions between the PA and the Pb2+.22 In the same study, the lowest sorption capacity was observed at the lowest pH of 2.5, which was close to the measured pHPZC value of 2.42. At this pH, it was suggested that the circumneutral net charge of the PA microplastic surfaces resulted in weaker electrostatic interactions with the Pb2+ ions in solution, and therefore, less sorption.22
Third, the aqueous metal speciation is influenced by solution pH (Fig. SI-7†), which may determine the type and relative strength of sorbent–sorbate interaction.21,65 Cd(II) sorption was not influenced by pH in the same way as Hg(II), which may be partly explained by its speciation in the phosphate buffer (Fig. SI-7†). The maximum Cs values at pH 7 (4.7 ± 0.6 μg g−1) and 8 (4.5 ± 0.5 μg g−1) were similar, but both higher than that at pH 6 (3.4 ± 0.2 μg g−1). According to the speciation modelling, at pH 6, the neutral CdHPO4 species predominates, yet as the pH increases from 6 to 8, the anionic Cd(HPO4)22− species becomes increasingly predominant (Fig. SI-7†). Wang and co-workers31 investigated the sorption of Cd(II) onto pristine polystyrene microplastics, over a pH range of 2–8, finding the highest sorption at pH 6. In that study, where no phosphate buffer was used, Cd2+ was expected to dominate at pH ≤ 6. As the pH increased further from pH 6 to 8, sorption decreased slightly but not significantly. This was attributed to the less electrostatically favourable interactions between the microplastic surfaces and Cd(II), as Cd(OH)+ predominates above pH 6.31 In our study, the optimum pH for sorption was 7, however, indicating that speciation is not the only factor influencing sorption. While the exact mechanism is unclear, as the pH increases from 6 to 8, there may be two antagonistic effects occurring simultaneously: (a) the increasing predominance of the anionic Cd(HPO4)22− species making electrostatic interactions weaker,21,31 and (b) the decrease in H3O+ ions, reducing competition for sorption.28
The sorption of Hg2+ onto the PET microplastics was approximately four times higher than that of Cd2+ (Fig. 4). Data on the sorption of Hg2+ onto microplastics are scarce in the literature,2,63 though our results are consistent with previous work that found a higher sorption affinity for Hg2+ than for Cd2+.66,67 One explanation for the relatively high sorption of Hg2+ is based on the classification of the metal ions according to the concept of hard and soft Lewis acids and bases. According to this criterion, Hg2+ would behave as a soft acid and would present a higher affinity for soft base groups in the PET structure, such as the aromatic rings.
3.5 Environmental relevance
Mercury and cadmium are both present in wastewater from various sources, including textile dyes.36 Our data indicate that sorption equilibrium occurs rapidly (within 6 hours) for both metals, under all pH conditions. The environmental significance of this finding is that microplastics, especially PET fibres, and metal ions such as Cd2+ and Hg2+ coexist in wastewater distribution networks, during wastewater treatment, and subsequent sludge treatment, typically for several days.68 It is therefore intuitive to conclude that the accumulation of metal ions by microplastic fibres is kinetically favourable and expected during full-scale sewage treatment.4. Conclusions
This study investigated the sorption of 12 metal ions onto PET microplastic fibres. Fibres were generated using cryogenic milling; characterisation confirmed that their dimensions and chemical functionality were representative of those generated during home laundering. The sorption distribution coefficients (Kd) for 12 metal ions at pH 8 showed that the highest levels of sorption were for Pb2+ (939 mL g−1), followed by Cd2+ (898 mL g−1), Cu2+ (507 mL g−1), Hg2+ (403 mL g−1), and Zn2+ (235 mL g−1). These data are largely explained by differences in their chemical speciation and charge at the experimental pH. Kinetic studies undertaken for Hg2+ and Cd2+ at pH 7 demonstrated that sorption was rapid, with the equilibration reached within 6 hours. Equilibrium isotherm data for Hg2+ and Cd2+ fitted well to the Langmuir model. The sorption of Hg2+ was approximately four times higher than that for Cd2+, which can be explained by the soft Lewis acid behaviour of Hg2+. Overall, this study indicates that the saturation of microplastic fibres by metals is expected during full-scale sewage treatment. In turn, this represents an important route for their transfer, as part of sewage sludge, into agricultural soils.Data availability
Data supporting this article, including SEM images, normalised Raman spectrum, fibre length and width distributions as well as zeta potential and pH drift data, have been included as part of the ESI.†Author contributions
H. Frost: conceptualisation, investigation, writing – original draft, writing – review & editing, visualisation; T. Bond: conceptualisation, writing – review & editing, supervision, funding acquisition; T. Sizmur: conceptualisation, writing – review & editing, supervision, funding acquisition; M. Felipe-Sotelo: conceptualisation, writing – review & editing, supervision, funding acquisition.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support from the NERC SCENARIO Doctoral Training Partnership for Harry Frost's PhD project (PhD studentship NE/S007261/1) is gratefully acknowledged.References
- M. A. Browne, P. Crump, S. J. Niven, E. Teuten, A. Tonkin, T. Galloway and R. Thompson, Environ. Sci. Technol., 2011, 45, 9175–9179 CrossRef CAS.
- A. Turner and L. A. Holmes, Environ. Chem., 2015, 12, 600–610 CrossRef CAS.
- L. Fu, J. Li, G. Wang, Y. Luan and W. Dai, Ecotoxicol. Environ. Saf., 2021, 217, 112207 CrossRef CAS PubMed.
- S. Liu, J. H. Huang, W. Zhang, L. X. Shi, K. X. Yi, H. B. Yu, C. Y. Zhang, S. Z. Li and J. N. Li, J. Environ. Manage., 2022, 302, 113995 CrossRef CAS PubMed.
- H. Frost, T. Bond, T. Sizmur and M. Felipe-Sotelo, Environ. Sci.: Processes Impacts, 2022, 24, 504–524 RSC.
- L. Zhou, T. Masset and F. Breider, Environ. Sci.: Processes Impacts, 2024, 26, 411–420 RSC.
- Textile Exchange, Preferred Fiber and Materials Market Report, 2022, https://textileexchange.org/knowledge-center/reports/materials-market-report-2022/accessed 21 October 2024 Search PubMed.
- A. Engelhardt, The Fibre Year 2008/09: A World Survey on Textile and Nonwovens Industry, Pfäffikon, Switzerland, 2009 Search PubMed.
- M. Sillanpää and P. Sainio, Environ. Sci. Pollut. Res., 2017, 24, 19313–19321 CrossRef.
- S. A. Carr, J. Liu and A. G. Tesoro, Water Res., 2016, 91, 174–182 CrossRef CAS PubMed.
- A. M. Mahon, B. O'Connell, M. G. Healy, I. O'Connor, R. Officer, R. Nash and L. Morrison, Environ. Sci. Technol., 2017, 51, 810–818 CrossRef CAS PubMed.
- V. Godoy, G. Blázquez, M. Calero, L. Quesada and M. A. Martín-Lara, Environ. Pollut., 2019, 255, 113363 CrossRef CAS PubMed.
- J. Sun, X. Dai, Q. Wang, M. C. M. van Loosdrecht and B. J. Ni, Water Res., 2019, 152, 21–37 CrossRef CAS PubMed.
- L. Nizzetto, M. Futter and S. Langaas, Environ. Sci. Technol., 2016, 50, 10777–10779 CrossRef CAS.
- P. U. Iyare, S. K. Ouki and T. Bond, Environ. Sci., 2020, 6, 2664–2675 CAS.
- F. Corradini, P. Meza, R. Eguiluz, F. Casado, E. Huerta-Lwanga and V. Geissen, Sci. Total Environ., 2019, 671, 411–420 CrossRef CAS.
- F. Fei Liu, G. Zhou Liu, Z. Lin Zhu, S. Chun Wang and F. Fei Zhao, Chemosphere, 2019, 214, 688–694 CrossRef PubMed.
- L. Zhang and Y. Tao, Environ. Sci.: Processes Impacts, 2022, 24, 2100–2107 RSC.
- L. A. Holmes, A. Turner and R. C. Thompson, Mar. Chem., 2014, 167, 25–32, DOI:10.1016/j.marchem.2014.06.001.
- W. Qiongjie, Z. Yong, Z. Yangyang, L. Zhouqi, W. Jinxiaoxue and C. Huijuan, J. Hazard. Mater., 2022, 424, 127340 CrossRef PubMed.
- Y. Dong, M. Gao, W. Qiu and Z. Song, Environ. Sci.: Processes Impacts, 2020, 22, 2388–2397 RSC.
- S. Tang, L. Lin, X. Wang, A. Feng and A. Yu, J. Hazard. Mater., 2020, 386, 121960 CrossRef CAS PubMed.
- W. K. Ho, J. C. F. Law, J. C. W. Lo, I. K. X. Chng, C. H. H. Hor and K. S. Y. Leung, Environ. Sci. Technol. Lett., 2023, 10, 27–32 CrossRef CAS.
- W. Yuan, Y. Zhou, Y. Chen, X. Liu and J. Wang, Sci. Total Environ., 2020, 746, 141254 CrossRef CAS PubMed.
- L. A. Holmes, A. Turner and R. C. Thompson, Environ. Pollut., 2012, 160, 42–48, DOI:10.1016/j.envpol.2011.08.052.
- D. Brennecke, B. Duarte, F. Paiva, I. Caçador and J. Canning-Clode, Estuar. Coast Shelf Sci., 2016, 178, 189–195 CrossRef CAS.
- S. Tang, L. Lin, X. Wang, A. Yu and X. Sun, J. Hazard. Mater., 2021, 403, 123548 CrossRef CAS.
- C. C. Chen, X. Zhu, H. Xu, F. Chen, J. Ma and K. Pan, Environ. Sci. Technol., 2021, 55, 13923–13931 CrossRef CAS PubMed.
- F. Yu, Q. Qin, X. Zhang and J. Ma, Environ. Sci.: Processes Impacts, 2024, 26, 882–890 RSC.
- X. Han, S. Wang, X. Yu, R. D. Vogt, J. Feng, L. Zhai, W. Ma, L. Zhu and X. Lu, Front. Mar. Sci., 2021, 8, 785146 CrossRef.
- H. Wang, C. Qiu, Y. Song, S. Bian, Q. Wang, Y. Chen and C. Fang, Sci. Total Environ., 2022, 845, 157109 CrossRef CAS PubMed.
- X. Guo and J. Wang, Environ. Pollut., 2019, 250, 737–745 CrossRef CAS PubMed.
- G. Bhagwat, T. K. A. Tran, D. Lamb, K. Senathirajah, I. Grainge, W. O'Connor, A. Juhasz and T. Palanisami, Environ. Sci. Technol., 2021, 55, 8877–8887 CrossRef CAS PubMed.
- M. C. Rillig, L. Ziersch and S. Hempel, Sci. Rep., 2017, 7, 1–6 CrossRef CAS PubMed.
- G. Dalla Fontana, R. Mossotti and A. Montarsolo, Environ. Pollut., 2020, 264, 113960 CrossRef CAS PubMed.
- S. Raja Balasaraswathi and R. Rathinamoorthy, J. Text. Inst., 2022, 113, 789–809 CrossRef CAS.
- J. Zou, X. Liu, D. Zhang and X. Yuan, Chemosphere, 2020, 248, 126064 CrossRef CAS.
- Y. Parikh, H. Lang, S. Mahmoud and J. Lallo, Spectrosc. Suppl., 2015, 30, 8–17 Search PubMed.
- J. Wang, C. P. Huang and H. E. Allen, Water Res., 2006, 40, 1333–1340, DOI:10.1016/j.watres.2005.12.044.
- M. F. Colmenarejo, A. Rubio, E. Sánchez, J. Vicente, M. G. García and R. Borja, J. Environ. Manage., 2006, 81, 399–404, DOI:10.1016/j.jenvman.2005.11.007.
- A. Taboada-Santos, E. Rivadulla, L. Paredes, M. Carballa, J. Romalde and J. M. Lema, Water Res., 2020, 169, 115258, DOI:10.1016/j.watres.2019.115258.
- R. Saadi, Z. Saadi, R. Fazaeli and N. E. Fard, Korean J. Chem. Eng., 2015, 32, 787–799 CrossRef CAS.
- Z. Lin, Y. Hu, Y. Yuan, B. Hu and B. Wang, Ecotoxicol. Environ. Saf., 2021, 208, 111451 CrossRef CAS.
- I. Puigdomènech, Program MEDUSA (Make Equilibrium Diagrams Using Sophisticated Algorithms), Department of Inorganic. Chemistry, The Royal Institute of Technology: Stockholm, Sweden, 2009 Search PubMed.
- T. Pušić, I. Soljačić and T. Dekanić, Household Pers. Care Today, 2014, 9, 26–32 Search PubMed.
- Y. Cai, T. Yang, D. M. Mitrano, M. Heuberger, R. Hufenus and B. Nowack, Environ. Sci. Technol., 2020, 54, 4847–4855 CrossRef CAS.
- A. Tamargo, N. Molinero, J. J. Reinosa, V. Alcolea-Rodriguez, R. Portela, M. A. Bañares, J. F. Fernández and M. V. Moreno-Arribas, Sci. Rep., 2022, 12, 1–15 CrossRef.
- E. Hernandez, B. Nowack and D. M. Mitrano, Environ. Sci. Technol., 2017, 51, 7036–7046 CrossRef CAS.
- E. Vassilenko, M. Watkins, S. Chastain, J. Mertens, A. M. Posacka, S. Patankar and P. S. Ross, PLoS One, 2021, 16, e0250346 CrossRef CAS.
- A. V. Palacios-Marín, A. Jabbar and M. Tausif, Text. Res. J., 2022, 92, 2265–2275 CrossRef.
- T. Bond, V. Ferrándiz-Mas, M. Felipe-Sotelo and E. van Sebille, Crit. Rev. Environ. Sci. Technol., 2018, 48, 685–722, DOI:10.1080/10643389.2018.1483155.
- A. Bakir, S. J. Rowland and R. C. Thompson, Environ. Pollut., 2014, 185, 16–23 CrossRef CAS.
- A. Pathak, M. G. Dastidar and T. R. Sreekrishnan, J. Environ. Manage., 2009, 90, 2343–2353 CrossRef CAS PubMed.
- A. M. Grancaric, A. Tarbuk and T. Pusic, Color. Technol., 2005, 121, 221–227 CAS.
- C. Y. Shih, Y. H. Wang, Y. J. Chen, H. A. Chen and A. Y. C. Lin, RSC Adv., 2021, 11, 32494–32504 RSC.
- M. Lang, X. Yu, J. Liu, T. Xia, T. Wang, H. Jia and X. Guo, Sci. Total Environ., 2020, 722, 137762 CrossRef CAS.
- O. I. Ungureanu, D. Bulgariu, A. Mi. Mocanu and L. Bulgariu, Water, 2020, 12, 2624, DOI:10.3390/w12092624.
- C.-Ş. Ciobanu, R. Copae, D. Bulgariu and L. Bulgariu, Desalination Water Treat., 2021, 222, 375–385, DOI:10.5004/dwt.2021.27075.
- X. Zong, J. Zhang, J. Zhu, L. Zhang, L. Jiang, Y. Yin and H. Guo, Ecotoxicol. Environ. Saf., 2021, 217, 112217 CrossRef CAS.
- J. Bujdák, Appl. Clay Sci., 2020, 191, 105630 CrossRef.
- Y. S. Ho and G. McKay, Water Res., 1999, 33, 578–584 CrossRef CAS.
- C. Sabarinathan, P. Karuppasamy, C. T. Vijayakumar and T. Arumuganathan, Microchem. J., 2019, 146, 315–326 CrossRef CAS.
- Y. Qiu, Z. Zhang, T. Zhang and P. Zhang, Sci. Total Environ., 2022, 848, 157802 CrossRef CAS PubMed.
- J. J. Guo, X. P. Huang, L. Xiang, Y. Z. Wang, Y. W. Li, H. Li, Q. Y. Cai, C. H. Mo and M. H. Wong, Environ. Int., 2020, 137, 105263 CrossRef CAS PubMed.
- O. D. Agboola and N. U. Benson, Front. Environ. Sci., 2021, 9, 678574 CrossRef.
- A. A. Atia, A. M. Donia and A. M. Yousif, React. Funct. Polym., 2003, 56, 75–82 CrossRef CAS.
- C. Xiong, Q. Jia, X. Chen, G. Wang and C. Yao, Ind. Eng. Chem. Res., 2013, 52, 4978–4986 CrossRef CAS.
- M. L. Sikosana, K. Sikhwivhilu, R. Moutloali and D. M. Madyira, Procedia Manuf., 2019, 35, 1018–1024 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4em00373j |
| This journal is © The Royal Society of Chemistry 2024 |