Open Access Article
Open Access ArticlePerylene-derivative singlet exciton fission in water solution†
Chloe
Magne
 a,
Simona
Streckaite
a,
Simona
Streckaite
 b,
Roberto A.
Boto
b,
Roberto A.
Boto
 c,
Eduardo
Domínguez-Ojeda
c,
Eduardo
Domínguez-Ojeda
 d,
Marina
Gromova
e,
Andrea
Echeverri
f,
Flavio Siro
Brigiano
f,
Minh-Huong
Ha-Thi
d,
Marina
Gromova
e,
Andrea
Echeverri
f,
Flavio Siro
Brigiano
f,
Minh-Huong
Ha-Thi
 g,
Marius
Fanckevičius
g,
Marius
Fanckevičius
 b,
Vidmantas
Jašinskas
b,
Vidmantas
Jašinskas
 b,
Annamaria
Quaranta
b,
Annamaria
Quaranta
 a,
Andrew A.
Pascal
a,
Andrew A.
Pascal
 a,
Matthieu
Koepf
a,
Matthieu
Koepf
 h,
David
Casanova
h,
David
Casanova
 ci,
Thomas
Pino
g,
Bruno
Robert
ci,
Thomas
Pino
g,
Bruno
Robert
 a,
Julia
Contreras-García
f,
Daniel
Finkelstein-Shapiro
a,
Julia
Contreras-García
f,
Daniel
Finkelstein-Shapiro
 d,
Vidmantas
Gulbinas
d,
Vidmantas
Gulbinas
 b and
Manuel J.
Llansola-Portoles
b and
Manuel J.
Llansola-Portoles
 *a
*a
aUniversité Paris-Saclay, CEA, CNRS, Institute for Integrative Biology of the Cell (I2BC), Gif-sur-Yvette, 91190, France. E-mail: manuel.llansola@i2bc.paris-saclay.fr
bDepartment of Molecular Compound Physics, Center for Physical Sciences and Technology, Saulėtekio Avenue 3, Vilnius, LT-10257, Lithuania
cDonostia International Physics Center (DIPC), Donostia, 20018, Euskadi, Spain
dInsituto de Química, Universidad Nacional Autónoma de México, Mexico City, 04510, Mexico
eUniversité Grenoble Alpes, CNRS, CEA, IRIG, MEM, Grenoble, F-38054, France
fSorbonne Université, CNRS, Laboratoire de Chimie Théorique, LCT, Paris, F. 75005, France
gUniversité Paris-Saclay, CNRS, Institut des Sciences Moléculaires d'Orsay, Orsay, 91405, France
hUniversité Grenoble Alpes, CNRS, CEA, IRIG, Laboratoire de Chimie et Biologie des Métaux, Grenoble, F-38054, France
iIKERBASQUE, Basque Foundation for Science, Bilbao, 48009, Euskadi, Spain
First published on 4th October 2024
Abstract
We provide direct evidence of singlet fission occurring with water-soluble compounds. We show that perylene-3,4,9,10-tetracarboxylate forms dynamic dimers in aqueous solution, with lifetimes long enough to allow intermolecular processes such as singlet fission. As these are transient dimers rather than stable aggregates, they retain a significant degree of disorder. We performed a comprehensive analysis of such dynamic assemblies using time-resolved absorption and fluorescence spectroscopy, nuclear magnetic resonance spectroscopy, and theoretical modelling, allowing us to observe the characteristic signatures of singlet fission and develop a model to characterize the different species observed. Our findings reveal that structure fluctuations within perylene-3,4,9,10-tetracarboxylate associations are key in favoring either singlet fission or charge separation. The efficiency of triplet formation is higher than 100%, and the disordered system leads to triplets living in the nanosecond time range.
Introduction
Singlet fission (SF) is a spin-allowed mechanism by which a photo-excited singlet state splits into two distinct spin-triplet excited states.1 SF was initially described in the 1960s for crystalline anthracene2 and tetracene,3–5 and it has experienced a surge of interest due to its potential to reach power conversion efficiencies up to 45%.6 Experimental studies have demonstrated that singlet fission processes can produce photon-to-charge conversion efficiencies exceeding 100% in electrodes.7,8 However, a variety of radiative and non-radiative alternative deactivation channels involving ultrafast electronic and vibrational dynamics may compete with SF, limiting these high efficiencies.9–11 A thorough description of SF mechanisms and the intermediate species involved can be found in several excellent reviews.12–15Currently, it is well accepted that the conversion from a singlet exciton (S1) to independent triplets involves the formation of a correlated triplet-pair state 1(TT), either directly from S1 or through the mediation of charge transfer (CT) states. Eventually, the system might evolve to form two independent triplets by the loss of electronic, 1(TT) → 1(T⋯T), and spin, 1(T⋯T) → T1 + T1, coherences.14 However, it is not trivial to determine this apparently simple sequence or even disentangle the role of parallel reactions. This is the case of singlet excimer (1Ex) formation, which has been suggested to act as a promoter for the population of 1(TT), but also as an inhibitor of SF.11–13,16–19 Moreover, the spectral signatures of several intermediates are unclear, since transient absorption spectroscopy can produce similar signatures for 1(TT), 1(T⋯T), and (T1 + T1). Even the employment of photon emission to assign 1(TT), trap states, or 1Ex is not unequivocal.11,18,20–23 The identification of the intermediate species becomes especially daunting when the molecular compounds are in solution, that is, with a large degree of configurational freedom, forming weak excitonic couplings, leading to small fluctuations of the electronic levels,17,24 and consequently of the spectral signatures. Finally, sensitization of triplets is the straightforward method to determine the spectroscopic signature of disentangled triplets and may assist to identify intermediate species.23,25 Whereas there have been many efforts to unravel the details of SF evolution in the solid state or even in non-aqueous solvents,11–13,16–19 there have been no major advances demonstrating SF in water. Indeed, the current scarcity of studies for SF in aqueous solution is remarkable, with only a few reports involving aqueous suspensions of diketopyrrolopyrrole nanoparticles,26 TIPS-pentacene nanoparticles,27–29 or carotenoid aggregates.30–32 Moreover, none of these involves molecular systems in solution, to create photocatalysts and open new research avenues. In this work, we explore the photophysics of a water-soluble organic system, characterizing the interaction(s) between molecules, the role of disorder, and unequivocally identifying intermediate species. Moreover, we present quantum chemistry simulations to show that the dynamic conformation controls the ability of the system to follow an SF process or charge separation.
Experimental
Preparation of rylene solutions
Perylene-3,4,9,10-tetracarboxylic dianhydride (PTCDA), and potassium hydroxide (KOH), were purchased from Sigma-Aldrich and used as received, with a purity of 97 and 90%, respectively. To prepare perylene-3,4,9,10-tetracarboxylate solutions, PTCDA was added to 0.5 M KOH in water at room temperature under continuous stirring. This results in hydrolysis of the terminal rings, yielding perylene-3,4,9,10-tetracarboxylic acid (PTC).UV-vis absorption spectra were measured on a Varian Cary E5 double-beam scanning spectrophotometer (Agilent). Hellma quartz cuvettes of varying pathlengths (10, 4, 2, 1, 0.1, and 0.01 mm) were used to accommodate the large range of PTC concentrations (over 5 orders of magnitude).
1H-NMR
Stock solutions of PTC (90 mM) were prepared in 0.5 M KOH in D2O (Sigma-Aldrich) just before use. The mixture was sonicated at room temperature for 45 min. All the NMR samples were prepared by diluting the corresponding volume of PTC stock solution with 0.1 M KOH, to obtain the following final concentrations: 1, 5, 10, 25, 40, 45, 50, 60, 70, 75, 80, 85 and 90 mM PTC. All samples were sonicated for 15 min just before taking the NMR spectra. 1H-NMR experiments were acquired at 400 MHz with 32 scans at 25 °C, in a JEOL JNM-ECZ400S spectrometer equipped with a 5 mm probe. The spectra were referenced to the solvent peak at 4.81 ppm, and the pure chemical shifts were reported along with the J coupling splitting. The fits are performed using the most-downfield-shifted resonance.DOSY experiments
The samples were prepared in deuterated water (D2O, 99.96%-d, Eurisotop) containing 100 μM sodium 3-(trimethylsilyl)propionate (d4-TMSP) as an internal reference. 54 mM, 39 mM, 31 mM, 22.3 mM, 18 mM, 13.3 mM, 9 mM and 4.6 mM solutions of PTC were obtained by dilution of a freshly prepared stock solution of PTC (80 mM, in 0.5 M KOH) in 0.1 M KOH. The accurate concentration of each sample was determined by quantitative 1H NMR measurements using sucrose solutions of known concentrations in deuterated water, as standards, and the ERETIC2 module to analyse the data. For the measurements, 600 μL of each solution was used. NMR spectra were recorded on a Bruker Avance spectrometer operating at 500.18 MHz for 1H, equipped with a 5 mm z-gradient BBI probe. All measurements were performed at 298 K. Chemical shifts were reported to the residual HDO signal fixed at 4.81 ppm. In pulsed field gradient 1H NMR mode, the diffusion-filtered spectra were recorded with the standard stimulated echo bipolar pulse gradient sequence (stebpgp1s). The amplitude of the trapezoidal gradient pulses (g) varied from 0.02 to 0.43 T m−1. The diffusion coefficients were determined according to the Stejskal–Tanner equation: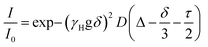 | (1) |
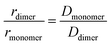 | (2) |
Nano-to-millisecond transient absorption was performed on an Edinburgh Instruments LP920 Flash Photolysis Spectrometer system, incorporating a Continuum Surelite OPO. The OPO was pumped by a Q-switched Nd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) YAG laser operating at 355 nm, having a pulse duration of 5 ns. The LP920 system is equipped with a 450 W pulsed Xenon arc lamp as the probe for the transient absorption measurements. Detection in the LP920 system is performed either via a Czerny–Turner blazed 500 nm monochromator (bandwidth 1–5 nm) coupled with a Hamamatsu R928 photomultiplier tube (kinetics mode), or via a 500 nm-blazed spectrograph (bandwidth 5 nm) coupled with a water-cooled ICCD nanosecond Andor DH720 camera (spectral mode). The samples had an absorbance of ∼0.8 at the excitation wavelength and the energy of the laser pulse was ∼10 mJ (∼15 mJ cm−2).
YAG laser operating at 355 nm, having a pulse duration of 5 ns. The LP920 system is equipped with a 450 W pulsed Xenon arc lamp as the probe for the transient absorption measurements. Detection in the LP920 system is performed either via a Czerny–Turner blazed 500 nm monochromator (bandwidth 1–5 nm) coupled with a Hamamatsu R928 photomultiplier tube (kinetics mode), or via a 500 nm-blazed spectrograph (bandwidth 5 nm) coupled with a water-cooled ICCD nanosecond Andor DH720 camera (spectral mode). The samples had an absorbance of ∼0.8 at the excitation wavelength and the energy of the laser pulse was ∼10 mJ (∼15 mJ cm−2).
Femto-to-nanosecond time-resolved transient absorption
The ultrafast transient absorption (TA) setup was based on an amplified femtosecond laser Pharos 10-600 PP (Light Conversion Ltd., Lithuania), operating at a fundamental wavelength of 1030 nm, with a repetition rate of 50 kHz and a pulse width of ∼230 fs. A collinear optical parametric amplifier Orpheus PO15F2L (Light Conversion Ltd., Lithuania) was used to obtain 415 nm wavelength pulses for sample excitation. The measurements were performed at a repetition rate of 4.554 kHz frequency, achieved by using the pulse picker. Excitation was modulated by a mechanical chopper synchronized to the output of the pulse picker. As a probe, we used laser pulses, spectrally broadened by means of continuum generation in a sapphire crystal. The time delay between the pump and probe pulses was varied by an optical delay line based on retroreflector optics mounted on an Aerotech PRO165LM electromechanical translation stage (Aerotech Ltd., UK). The detection equipment consisted of an Andor-Shamrock SR-500i-B1-R spectrometer (Andor Technology, UK) with 150 lines per mm diffraction grating equipped with Andor-Newton DU970 CCD camera (1600 × 200 pixels; Andor Technology Ltd., UK). The reading of the camera was synchronized with the chopper. The data was recorded and processed using home-written software in the LabView programming environment. The changes in absorption (ΔA) were measured as a function of both the wavelength and time delay between pump and probe pulses.Picosecond time-resolved fluorescence was performed with a streak camera system (Hamamatsu C5680) with synchroscan (M5675) unit coupled to a spectrometer. A femtosecond Yb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KGW oscillator (Light Conversion Ltd., Lithuania) generating 80 fs duration pulses at 1030 nm, which were frequency-tripled to 343 nm (HIRO harmonics generator, Light Conversion Ltd.) at a repetition rate of 76 MHz, was used for the sample excitation. Excitation energy density was attenuated using neutral density filters to about 15 nJ cm−2. The time resolution of the system was ∼8 ps. Signal acquisition time was 1–3 h for each measurement.
KGW oscillator (Light Conversion Ltd., Lithuania) generating 80 fs duration pulses at 1030 nm, which were frequency-tripled to 343 nm (HIRO harmonics generator, Light Conversion Ltd.) at a repetition rate of 76 MHz, was used for the sample excitation. Excitation energy density was attenuated using neutral density filters to about 15 nJ cm−2. The time resolution of the system was ∼8 ps. Signal acquisition time was 1–3 h for each measurement.
Pico-to-nanosecond time-resolved fluorescence was performed with an Edinburgh F920 spectrometer (Edinburgh Instruments, UK). Fluorescence decay kinetics were obtained using time-correlated single photon counting (TCSPC). The excitation source was a picosecond-pulsed diode laser EPL-375 (Edinburgh Instruments, UK) emitting ∼60 ps pulses (5 MHz repetition rate). The temporal resolution of this system was circa 200 ps.
Experimental time-resolved data treatment
Global analysis (sequential, parallel, and target) of time-resolved spectra was performed using commercial CarpetView data analysis software (Light Conversion) with reconvolution with the laser prompt.Simulations
Optimized molecular structures, vibrational frequencies, and excited states were calculated using Gaussian 16 software.34 These calculations have been performed with an implicit solvent model (PCM),35 where a dielectric constant of 78.35 was used to simulate the aqueous solvent. The configurational search for dimers was performed by placing the monomers in the center of cubes of various sizes and allowing them to evolve under annealing conditions, as implemented in the ASCEC program.36,37 Following the generation of candidate structures to be minima on the potential energy surface, these structures were subsequently optimised and classified as true minima by evaluation of the eigenvalues of the Hessian matrix at the DFT level of theory, using the M06 functional38 and the 3-21G basis set.39The dynamics of the most stable dimer structure were then simulated by ab initio molecular dynamics (AIMD) in the presence of bulk water at 300 K. The liquid phase was modelled with 432 water molecules in a cubic box with an edge length of 24.312 Å (ρ(H2O) ≈ 1.0 g cm3), generated by PACKMOL software.40,41 The final model was generated by adding to the simulation box the PTC dimer structure previously optimized by quantum static calculations in the presence of a few explicit molecules and in PCM. The neutrality of the box was ensured by adding four K+ ions into the simulation boxes, in positions close to the perylene carboxylate groups. We adopted Born–Oppenheimer molecular dynamics (BOMD), the PBE41 approximation of density functional theory in the spin-restricted Kohn–Sham scheme together with Grimme's D3(BJ) correction for the description of dispersion interactions,42,43 GTH pseudopotentials,44,45 combined plane-wave (600 Ry cut-off) and 909![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 879 DZVP-MOLOPT-SR basis sets. Before running the molecular dynamics simulations, the positions of all atoms in the simulation boxes were optimized. The dynamics were run with CP2K/Quickstep code46 for 30 ps adopting the Nosé–Hoover thermostat47,48 to control the average temperature at 300 K in the NVT ensemble. The length of the Nosé–Hoover chain was equal to 3, whereas the time constant of the thermostat was set to 100 fs, with the third-order Yoshida integrator and multiple time step set to 2. Trajectories of 1 ps, with a time step of 0.5 fs, were found to be sufficiently long to reach the target temperature. Only the last 17 ps were considered for analysis. It should be noted that the dimensions of the box lead to a minimal distance between replicas of 12.5 Å along the dynamics and that throughout the entire simulation, the K+ ions remained situated within the first solvation shell of the perylenes. VMD49 software was used to visualize the MD trajectories and the analysis of the dimer twist angle fluctuations was performed with the Travis package.50,51
879 DZVP-MOLOPT-SR basis sets. Before running the molecular dynamics simulations, the positions of all atoms in the simulation boxes were optimized. The dynamics were run with CP2K/Quickstep code46 for 30 ps adopting the Nosé–Hoover thermostat47,48 to control the average temperature at 300 K in the NVT ensemble. The length of the Nosé–Hoover chain was equal to 3, whereas the time constant of the thermostat was set to 100 fs, with the third-order Yoshida integrator and multiple time step set to 2. Trajectories of 1 ps, with a time step of 0.5 fs, were found to be sufficiently long to reach the target temperature. Only the last 17 ps were considered for analysis. It should be noted that the dimensions of the box lead to a minimal distance between replicas of 12.5 Å along the dynamics and that throughout the entire simulation, the K+ ions remained situated within the first solvation shell of the perylenes. VMD49 software was used to visualize the MD trajectories and the analysis of the dimer twist angle fluctuations was performed with the Travis package.50,51
Electronic couplings have been evaluated using a five-state excitonic model: two low-lying local excited states (LE), which are localized on the monomers, two low-lying CT states, and the 1(TT) state that determines the SF process. To compute electronic couplings, we follow a two-step procedure using the Q-Chem program:52,53 we first carry out restricted active space configuration interaction (RASCI)54,55 calculations to obtain the low-energy adiabatic states; we then obtain the diabatic state energies and couplings through a diabatization scheme. RASCI calculations have been performed using the Hartree-Fock singlet as the reference configurations, with four electrons and four orbitals in the RAS2 space, including hole and particle excitations, and with the 6-311G(d,p) basis set.56 Diabatization was performed following the boys localization scheme57 for the lowest nineteen excited singlet states.
Results
Steady-state absorption and fluorescence
Perylene-3,4,9,10-tetracarboxylic acid (PTC) is water soluble up to 100 mM. The absorption spectra in the range 0.01–90 mM (Fig. 1a, full lines) are devoid of scattering, indicating the absence of large-scale aggregation, and no absorption shifts are observed (which would be indicative of medium/strong excitonic interactions24,58,59). The vibronic peaks (414, 438, and 466 nm) display a strong concentration dependence in terms of the ratio of intensities between the first and second vibronic bands (Rabs = IA1/IA2), and the specific molar absorptivity (ε) (Fig. 1b). The decrease in Rabs is indicative of H-aggregation, whereas the lack of a blue shift, and the widening of the bands calculated as the difference of FWHM (ΔFWHM = 250 ± 50 cm−1 ≪ ωvib = 1400 cm−1), support the weak nature of the excitonic couplings involved.24,58,59 The hypochromism exhibited by H-aggregates has been associated with the formation of π–π-stacked species,58–60 and rationalized as the distortion, by the electronic excitation of one molecule, of the electronic states of neighboring chromophores.61 The fluorescence spectra (Fig. 1a, dashed lines), with vibronic peaks at 481, 509, and 550 nm, exhibit strong fluorescence quenching at higher concentrations along with an increase in the ratio of the vibronic emission bands (Rfluorescence = IF1/IF2), both of which are also consistent with the formation of H-aggregates.24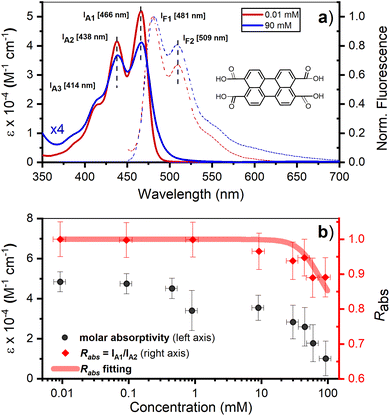 | ||
| Fig. 1 (a) Room temperature absorption (solid lines), represented as molar absorption coefficient (ε), and normalized fluorescence (dashed lines) of PTC at 0.01 and 90 mM. The maxima of the vibronic peaks for absorption and fluorescence are marked by vertical black dashed lines and the exact value is described on the side by IA1, IA2, IF1, IF2. Inset: chemical structure of PTC. (b) Concentration variation of ε at 466 nm (black circles – left y-axis) and Rabs (red diamonds – right y-axis). The red line is the fitting of Rabs using eqn (5) (vide infra). | ||
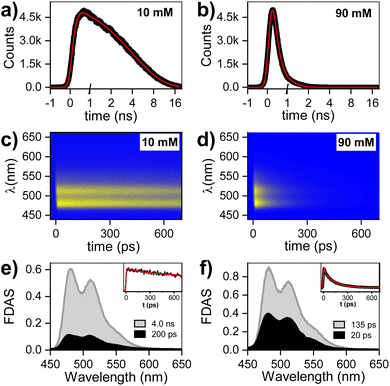
Time resolved fluorescence
The fluorescence decay for two PTC concentrations (10 and 90 mM) has been evaluated by single photon counting (SPC) with ca. 200 ps resolution, giving the following decay times: 10 mM (<200 ps and 4.0 ns), 90 mM (<200 ps). The fluorescence at higher temporal resolution was measured by streak camera, and fitted by fixing the long components obtained by SPC (see ESI† for 45 mM). The fluorescence decay associated species (FDAS) is obtained by multi-exponential parallel fitting and yields the following components for each of the samples: 10 mM (200 ps and 4.0 ns), and 90 mM (20 and 135 ps). This suggests the presence of π–π-stacked species even at low concentrations, which is consistent with the observations by steady state absorption and 1H-NMR, and probably results from hydrophobic interactions of the PTC core. The absence of any shift in the maxima is consistent with the presence of at least two weak H-aggregated species. It is reasonable to assume that the species decaying in 4.0 ns is monomeric PTC, while the species with shorter lifetimes correspond to the singlet-excited state of dimers/oligomers with different association geometries. We tentatively designate these entities as excimer states (1Ex), distinguishing them from the monomeric S1 state (Fig. 2).Transient absorption spectroscopy in the fs-to-ns window
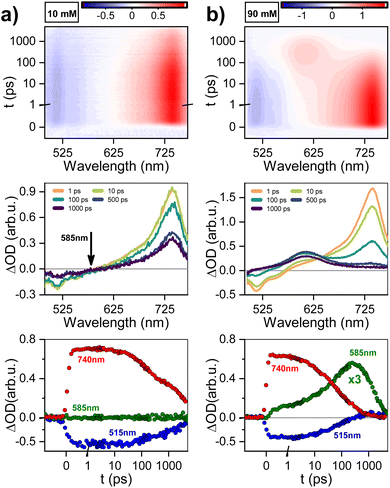
The evolution of excited states after photoexcitation at 415 nm in Fig. 3 shows: dataset, gated spectra, and selected kinetics for 10 and 90 mM PTC solutions. The 10 mM sample exhibits a distinct peak at 740 nm, which can be attributed to excited-state absorption (ESA) resulting from the S1–Sn transition. Additionally, a negative feature at 515 nm is observed, indicating stimulated emission (SE). From 1 to 10 ps, there is negligible change in the spectral features. Subsequently, both the positive and negative features maintain their shape and gradually diminish in intensity at 100 and 1000 ps. This dataset can be fitted to an exponential sequential model with 3 components, attributed to vibrationally-hot monomer/excimer ([hot-S1/1Ex]; 1 ps), singlet excimer (1Ex; 200 ps), and singlet monomer (S1; 4.0 ns) (see ESI†). It must be noted that for weak excitonic interactions, as in the present case, it has been reported that the S1–Sn and 1Ex1–1Exn transitions produce indistinguishable electronic signatures.16,62,63 This effect is particularly evident in the work of Marguilles et al.63 where the absorption spectrum of the weakly-interacting dyad shows minimal changes compared to the monomer, whereas strongly-interacting dyads exhibit distorted absorption profiles and a distinctive 1Ex1–1Exn transition. The spectral signatures of the S1–Sn and 1Ex1–1Exn transitions create an isosbestic point at 585 nm (ΔOD = 0). The 90 mM sample at time zero exhibits the 740 nm ESA attributed to S1–Sn and/or 1Ex1–1Exn transitions, which has a lifetime shorter than 500 ps. Associated to the S1–Sn and/or 1Ex1–1Exn decay, there is formation of a new species with ESA at 580–610 nm, which was not observed for 10 mM PTC. At the isosbestic point (585 nm), there is a first formation associated to short times (<100 ps), and a second ESA increase at longer times (100–500 ps). The sequential or parallel model fitting for 90 mM can give an approximation to the overall evolution of the system, but it is not able to produce an accurate physical description (see ESI†).To produce a sound model, it is necessary to first identify the unknown species with ESA at 580–610 nm, which unfortunately is subject to controversy. For highly-coupled perylene dimers, an ESA in the 614–625 nm region has been assigned to singlet excimers.64,65 However, it is unlikely in our weakly-coupled system, since we have already identified unambiguously the presence of weakly-coupled PTC in our dilute solutions associated to the 740 nm ESA, and we do not observe any associated fluorescence. Papadopoulos et al. attributed this feature to an entangled triplet 1(TT),25 but the detection of this feature in the nanosecond range rules out the presence of coherent species. A 580–610 nm ESA could be due to perylene cations,25,66 but it should have the paired anion signature circa 700–750 nm.25 The lack of any ESA for long-living species at 740 nm rules out CT in the ns time. However, polar solvents have been reported to favor CT,63 and the perylene anion signature could be obscured due to the overlap with the 740 nm 1Ex-ESA. A priori, the triplet species of PDI derivative dimers,25,67 and crystals68 are reported to appear in the 600 nm region, making them promising candidates for a preliminary tentative assignment.
Transient absorption spectroscopy in the ns-to-μs window
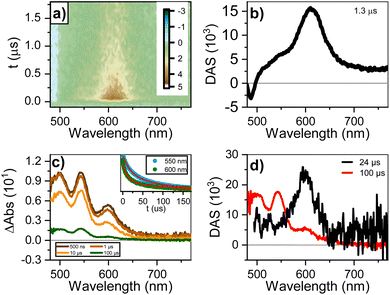
Fig. 4a and b shows the dataset and decay-associated spectra for ns-to-μs TA for the 90 mM sample. The dataset is fitted to a mono-exponential decay model, obtaining a component (1.3 μs) with GSB < 500 nm and ESA circa 610 nm. The lack of an ESA peak around 700–750 nm rules out the presence of perylene anions25 and reinforces the assignment to a triplet state. We designed a sensitization measurement using 1H-phenalen-1-one as sensitizer,69 which has ultrafast inter-system crossing (QYISC ∼ 100%), to make an unequivocal assignment. The sensitization of diluted (0.1 mM) PTC in water yields a transient signature similar to the monomeric triplet reported for perylenes,25 with the main absorption circa 550 nm and a small shoulder circa 600 nm (see ESI†). The most concentrated solution (90 mM) was not used since the addition of 1H-phenalen-1-one surpasses the solubility limit, causing precipitation (see ESI†). We therefore performed the sensitization at 45 mM, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio sensitizer/PTC, and in 70/30 (v/v) water/ethanol to maintain solubility. Fig. 4c and d shows the gated spectra and decay-associated spectra (DAS), yielding two components (24 and 100 μs). The 100 μs DAS is coincident with the monomeric triplet observed for the dilute solution, whereas the 24 μs DAS is similar to the feature observed in the ultra-fast measurements. Hence, the most plausible assignment for this species is the triplet state of perylene aggregates, which we henceforth denote as triplet excimers (3Ex). These triplets are exclusively generated at high concentrations and with remarkable speed, hinting at SF as their underlying formation mechanism.
1 ratio sensitizer/PTC, and in 70/30 (v/v) water/ethanol to maintain solubility. Fig. 4c and d shows the gated spectra and decay-associated spectra (DAS), yielding two components (24 and 100 μs). The 100 μs DAS is coincident with the monomeric triplet observed for the dilute solution, whereas the 24 μs DAS is similar to the feature observed in the ultra-fast measurements. Hence, the most plausible assignment for this species is the triplet state of perylene aggregates, which we henceforth denote as triplet excimers (3Ex). These triplets are exclusively generated at high concentrations and with remarkable speed, hinting at SF as their underlying formation mechanism.
Nuclear magnetic resonance
1H-NMR was used to characterize the interaction between PTC molecules and their resulting structure. We observe two distinct resonances (δ1, δ2) corresponding to dissimilar protons, with a coupling constant of J = 7.9 Hz. Increasing the concentration of PTC causes an upfield shift of both resonances, starting after 10 mM (Fig. 5a and b). The observation of a unique chemical shift for each distinct proton suggests a fast exchange between two or more chemical environments, and not the presence of two or more static species which would appear as two or more chemical shifts per distinct proton, reflecting the different static environments.70 Perylene dyes have been shown to form indefinite self-assemblies, where oligomers of different lengths coexist in dynamic equilibrium.71,72 We fit the data with three different association models (see ESI† for details of the three models):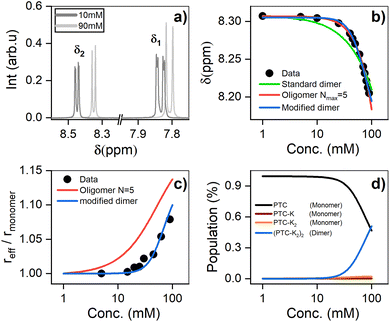 | ||
| Fig. 5 (a) 1H NMR chemical shifts showing two distinct environments for the protons (δ1 and δ2) (see ESI†). (b) 1H NMR chemical shift of PTC as a function of concentration, along with the fit to dimers and oligomers with a maximum cutoff of N = 5. (c) Effective radius (reff) extracted from DOSY measurements fit with the same models. (d) Species populations for the modified dimer model. | ||
Model 1: the formation of dimers from PTC monomers.
| PTC + PTC ↔ (PTC)2 |
Model 2: the formation of indefinite oligomers.
| (PTC + PTC ↔ (PTC)2 + PTC ↔ (PTC)3 ↔ …) |
Model 3: a modified dimer model where dimer formation is preceded by complexation with K+ ions as intermediate steps.
| PTC + K ↔ PTC-K + K ↔ PTC-K2 + PTC-K2 ↔ (PTC-K2)2 |
In all three cases, in the fast exchange limit, we can fit the observed chemical shift as a weighted average of the equilibrium fraction species i:
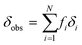 | (3) |
The simple (standard) dimer model does not reproduce the chemical shifts correctly – the onset of the chemical variation occurs from the lowest concentrations – and the values of the fit do not converge. In particular, the value of the chemical shift for the dimers tends to zero which is unphysical. Both the modified dimer and the oligomer model can explain the observed chemical shift trend; in particular, they both reproduce the onset of the chemical shift variation above 10 mM (Fig. 5b). This suggests either that higher size aggregates exist, or that the potassium ions play a role in aggregate formation. The oligomer model however also fails to account for 100% of the species: it requires a maximum cut-off size (Nmax) of the oligomers, and we find that for cut-off sizes of 5, 10, 15, and 20 there is a significant residual fractional population of 0.075, 0.048, 0.051 and 0.076, respectively. It indicates that the model might not be entirely appropriate for PTC as adding more oligomers does not make the model converge. To unambiguously discriminate between the oligomers and the modified dimer model, we carry out diffusion ordered spectroscopy (DOSY) at several concentrations. Since the system is in the fast exchange regime with respect to the chemical shift differences, we know that the exchange rate has to be much faster than 40 ms (taken as the inverse of the chemical shift difference between monomer and dimer). In this case, the DOSY experiment is also in the fast exchange regime with respect to the diffusion time (100 ms). We then expect to measure an average diffusion coefficient which is equal to the residence-time-weighted average of the diffusion coefficients for monomers and dimers, or oligomers of different sizes.
To minimize systematic errors, we measure the increase in the hydrodynamic radius of the aggregates as:
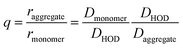 | (4) |
We reference the diffusion coefficients for PTC to that of HOD in the sample to remove the effect of varying viscosity (see ESI†) and assume that the diffusion coefficient of the PTC molecules at a concentration of 5 mM corresponds to that of the monomer. We estimate the ratio of radii of the monomer and dimer using structures optimized with DFT calculations and HYDROPRO, finding rdimer/rmonomer = 1.16. We assume that the oligomers grow proportionally larger by the same amount with each new molecule in the chain, which is a lower limit to its actual size. This estimate along with the calculated population fractions from the chemical shift fit provide a prediction free of fitting parameters for the effective radius in each model (Fig. 5c). We can see that the modified dimer explains the data while the oligomer overestimates the size of the aggregates – so it is reasonable to assume that we have a system of dynamic dimers. We can then use the modified dimer model to fit the vibrational progression observed in the absorption (Rabs) with the model in eqn (5):24
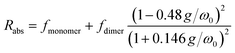 | (5) |
Modelling molecular aggregation
The 1H-NMR measurements cannot provide detailed information on the molecular organization, namely: distance, tilt, and twist angle between two molecules. We have run ab initio simulations to determine plausible structures to describe the behaviour observed. Given the solubility of PTC in water, the first tests were devoted to analyzing the charge upon solution. We carried out a M06/6-31g simulation with water as implicit solvent and checked the agreement of the experimental and simulated absorption spectra, obtaining a charge of (−2) on opposite sides of the molecule to present the best agreement with experimental absorption (see ESI†). We scanned all potential geometries and found one main dimer conformation with an intramolecular hydrogen bond. Explicit water molecules had to be added due to the carboxylates to obtain representative results (see ESI†). The most stable structure was re-optimized and simulated in water with AIMD, in order to determine the variability in the twist and tilt angles (Fig. 6). It resulted in a system exhibiting large conformational variation, with an average value of 37 ± 10° for the twist angle, a range between 0° and 15° for the tilt angle, and an average distance of 4.5 ± 0.2 Å (Fig. 6c and d).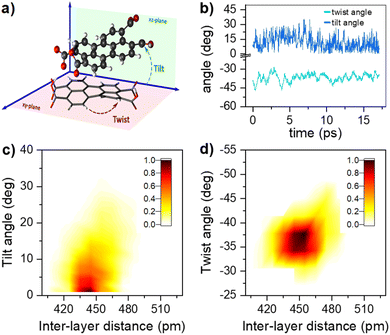 | ||
| Fig. 6 (a) Schematic representation of the dimer twist and tilt angles considered (see ESI† for the formal definition). (b) Temporal evolution of the twist and tilt angles (light and dark blue, respectively) along the AIMD trajectory at 300 K. Combined angular/radial probability of (c) the twist angle and (d) the tilt angle with respect to the distance between the two monomers computed from the 300 K AIMD trajectory. | ||
Modelling photophysical properties
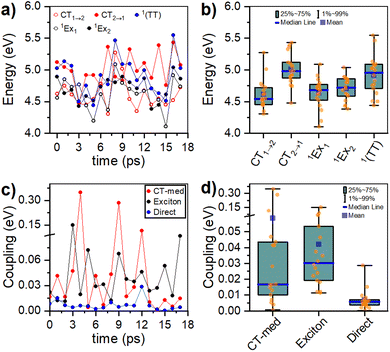
Computed singlet and triplet transition energies for the PTC molecular dianion predict the feasibility of SF, as E(S1) ≥ 2E(T1) (see ESI†). In addition to the right energetics, SF requires the interaction between S1 and the 1(TT) state.15 Interstate couplings evaluated for several conformations along the AIMD simulations for the lowest-energy dimer identify the viability of the formation of the triplet-pair state either by the direct S1 → 1(TT) transition or through the mediation of CT states (Fig. 7c). The conformational flexibility produces a wide spread of couplings that are statistically summarized in Fig. 7d (see ESI†). Moreover, the structural flexibility of the PTC dimer, as described in the previous section, allows the system to easily explore a considerable section of the conformational space. These structural changes induce important fluctuations in state energies and interstate couplings. Although the accuracy of the performed RASCI calculations is limited, preventing us from predicting the exact state energies at each conformation unequivocally, it is worth noting that the energy fluctuations are large enough to induce changes in the energy ordering of the states, selectively promoting the stabilization of either S1 or 1(TT), or even inducing charge-separated configurations (CT states). In essence, the system's flexibility enables the exploration of a range of structures that may favor either of the deactivation pathways, namely SF or CT formation. Interestingly, excitonic couplings between the two local S1 states in the dimer, although not directly involved in the SF process, are below 40 meV (322 cm−1), in very good agreement with the broadening of absorption bands and the analysis of the vibrational progression.Discussion
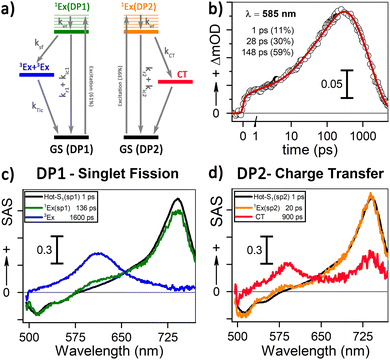
Our 1H-NMR data are consistent with the formation of dimers mediated by the coordination of PTC with K+ ions to form PTC-K2. Theoretical modelling confirms the conformational flexibility, with a distribution of distances and twist and tilt angles. The excitation energy evolution of this disordered system can be reasonably well described by a target model, featuring the parallel evolution of only two deactivation pathways (DP1 and DP2 in Fig. 8a). The deactivation rates of the singlets for each conformation are obtained from the streak camera (135 ± 5 ps and 20 ± 5 ps). To determine the formation rates of the new excited states for each deactivation pathway, we take advantage of the isosbestic point at 585 nm where only the new species absorb. Fig. 8b shows the kinetic trace at 585 nm, which can be fitted with three formation components (1, 28 and 148 ps). The 1 ps component suggests that a small proportion of the 600 nm ESA feature is formed from hot-S1. The target model was fitted globally, giving 39% of deactivation path 1 (DP1) and 61% of deactivation path 2 (DP2). For clarity, the species associated spectra (SAS) are shown separately for each decay channel (Fig. 8c and c, respectively). After photoexcitation, a hot-S1 is formed to evolve in 1 ps into 1Ex(DP1) and 1Ex(DP2). Surprisingly, the target analysis reveals notable differences between the two decay channels, not observable by sequential or parallel models. For DP1, 1Ex(DP1) (green traces) generates a triplet state (blue traces, ESA ca. 605 nm) via singlet fission (ksf = (148 ps)−1), which was already identified as a triplet excimer by sensitization measurements. The 1Ex(DP1) SAS overlaps the hot-S1(DP1) SAS, apart from a small ESA in the 605 nm region. This would suggest that some of the triplet excimer is already formed from the hot-S1(DP1). For DP2, we observe remarkable differences for the 2nd and 3rd SAS (orange, red traces, respectively) as compared to DP1. The 1Ex(DP2) SAS (orange traces) generates an excited state living 900 ps with no SE at 515 nm, and two ESA features at ca. 590 and 736 nm. The lack of fluorescence feature at 515 nm, and the long-living lifetime where no signal of fluorescence was recorded, suggest that the 736 nm ESA is not due to the 1Ex1–1Exn transition. These spectral features would be consistent with the formation of perylene cations and anions, i.e., a CT state.25,63 It is worth noting that 1Ex(DP2) SAS shows a weak ESA at 590 nm, which might be related to the CT state formation from hot-S1(DP2).From our computational analysis, the two possible decay channels of the photoexcited system, i.e., generation of two triplet excitons via SF (DP1) and formation of a CT state (DP2) can be rationalized by: (i) singlet-triplet energies adequate for SF, (ii) non-zero SF couplings, (iii) low energy CT states due to small intermolecular distances and strong polar medium, and (iv) dynamic fluctuations of state energies allowing for the simultaneous availability of DP1 and DP2. The presence of different geometries leading to two different processes (CT and SF) has been described for dimers of perylene73 and PDI74 in organic solvents. In molecular aggregates, overlapping wavefunctions on neighbouring molecules can lead to an additional CT-mediated exciton coupling with a vastly different spatial dependence and twist angle between two unslipped molecules. It has been shown that smaller changes in distance and twist and tilt angles than those modelled here can lead to a switch between CT and SF.63,73 However, further studies are necessary to assign each process to predominant conformations.
To calculate the efficiency of the processes (triplet and CT quantum yields; ΦT, ΦCT) in each conformation, we cannot rely on the change in ground state bleaching due to the overlap with the excimer triplet ESA. The most reliable method to calculate the yields of triplets and charge separation is by using the formation rates described in eqn (6)–(8):
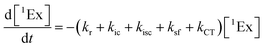 | (6) |
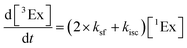 | (7) |
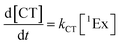 | (8) |
The rate constants are denoted as follows: radiative deactivation (kr), internal conversion (kic), inter-system crossing (kisc), singlet fission (ksf), and charge separation (kCT). The triplet and charge separation quantum yield are given by eqn (9) and (10). We consider that κisc can be approximated to zero, since no triplet formation is detected in dilute solutions. The overall singlet deactivation process is described by the singlet decay rate, measured by fluorescence and called effective singlet decay (keff) (Table 1).
 | (9) |
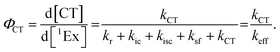 | (10) |
| % | k CT (ps−1) | k sf (ps−1) | k eff (ps−1) | QY triplet (%) | QY CT (%) | |
|---|---|---|---|---|---|---|
| DP1 | 61 | N/A | (148 ± 10)−1 | (135 ± 5)−1 | 182 ± 25 | N/A |
| DP2 | 39 | (28 ± 5)−1 | N/A | (20 ± 5)−1 | N/A | 71 ± 15 |
Conclusions
Our research has provided pioneering evidence of singlet fission in aqueous solutions of perylene-3,4,9,10-tetracarboxylate, and yields new insights into the photophysical properties of the system. Our results show that small changes in the molecular association modes can lead to different photophysical processes after photoexcitation such as singlet fission or charge transfer. We calculate that the efficiency of singlet fission/charge separation in aqueous perylene dimers depends strongly on their dynamic conformation, producing for DP1 an SF quantum efficiency close to 91% (triplet formation 182%), and for DP2 a charge separation efficiency of 70%. Overall, our study represents a major advance in the field of singlet fission and opens up exciting new directions for the development of water-compatible systems.Abbreviation
| PTCDA | Perylene-3,4,9,10-tetracarboxylic dianhydride |
| PTC | Perylene-3,4,9,10-tetracarboxylic acid |
| SF | Singlet-fission |
| LE | Local excited state |
| CT | Charge-transfer state |
Data availability
The data supporting this article have been included as part of the ESI.† The data analysis software is described in the materials and methods section and ESI.†Author contributions
The synthesis, FTIR, and steady state absorption and fluorescence was performed by Chloe Magne. Time resolved experiments were performed by Chloe Magne, Simona Streckaite, Marius Fanckevičius, Vidmantas Jašinskas, Annamaria Quaranta and Minh-Huong Ha-Thi. NMR measurements were performed by Chloe Magne, Marina Gromova, Matthieu Koepf, Eduardo Domínguez-Ojeda, and Daniel Finkelstein-Shapiro. Modelling and DFT calculations were performed by Roberto A. Boto, Andrea Echeverri, Flavio Siro Brigiano, David Casanova, Julia Contreras-García. The design of the experiments was done by Andrew A. Pascal, Vidmantas Gulbinas, Thomas Pino, Bruno Robert, Julia Contreras-García, David Casanova, Daniel Finkelstein-Shapiro, and Manuel J. Llansola-Portoles. All authors contributed to data analysis, interpreted the data, and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the French Infrastructure for Integrated Structural Biology (FRISBI) ANR-10-INBS-05, the French National Research Agency (SINGLETFISSION grant No: ANR-23-CE29-0007 and FISCIENCY grant No: ANR-23-CE50-009), the CNRS 80PRIME interdisciplinary program, and ECOS-Nord program (action #M21P02). DFS acknowledges funding from PAPIIT IA202821. We acknowledge Elisabet Huerta for technical assistance. The authors thank the Grand Equipement National de Calcul Intensif (GENCI) French National Supercomputing Facility for computer time (project Grant A0140814154). R. A. B and D. C. acknowledge the Spanish Government MICINN (project PID2022-136231NB-I00), the Gipuzkoa Provincial Council (project QUAN-000021-01), the European Union (project NextGenerationEU/PRTR-C17.I1), as well as by the IKUR Strategy under the collaboration agreement between Ikerbasque Foundation and DIPC on behalf of the Department of Education of the Basque Government. D.C. is thankful for financial support from IKERBASQUE (Basque Foundation for Science). The authors are thankful for the technical and human support provided by the Donostia International Physics Center (DIPC) Computer Center.References
- M. B. Smith and J. Michl, Singlet fission, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- S. Singh, W. J. Jones, W. Siebrand, B. P. Stoicheff and W. G. Schneider, Laser generation of excitons and fluorescence in anthracene crystals, J. Chem. Phys., 1965, 42, 330–342 CrossRef CAS.
- C. E. Swenberg and W. T. Stacy, Bimolecular radiationless transitions in crystalline tetracene, Chem. Phys. Lett., 1968, 2, 327–328 CrossRef CAS.
- N. Geacintov, M. Pope and F. Vogel, Effect of magnetic field on the fluorescence of tetracene crystals: exciton fission, Phys. Rev. Lett., 1969, 22, 593–596 CrossRef CAS.
- R. E. Merrifield, P. Avakian and R. P. Groff, Fission of singlet excitons into pairs of triplet excitons in tetracene crystals, Chem. Phys. Lett., 1969, 3, 155–157 CrossRef CAS.
- M. C. Hanna and A. J. Nozik, Solar conversion efficiency of photovoltaic and photoelectrolysis cells with carrier multiplication absorbers, J. Appl. Phys., 2006, 100, 074510–074518 CrossRef.
- L. Ye, Y. Zhao, R. Xu, S. Li, C. Zhang, H. Li and H. Zhu, Above 100% efficiency photocharge generation in monolayer semiconductors by singlet fission sensitization, J. Am. Chem. Soc., 2023, 145, 26257–26265 CrossRef CAS PubMed.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, External quantum efficiency above 100% in a singlet-exciton-fission-based organic photovoltaic cell, Science, 2013, 340, 334–337 CrossRef CAS PubMed.
- A. J. Musser, M. Liebel, C. Schnedermann, T. Wende, T. B. Kehoe, A. Rao and P. Kukura, Evidence for conical intersection dynamics mediating ultrafast singlet exciton fission, Nat. Phys., 2015, 11, 352–357 Search PubMed.
- H. L. Stern, A. Cheminal, S. R. Yost, K. Broch, S. L. Bayliss, K. Chen, M. Tabachnyk, K. Thorley, N. Greenham and J. M. Hodgkiss, et al. , Vibronically coherent ultrafast triplet-pair formation and subsequent thermally activated dissociation control efficient endothermic singlet fission, Nat. Chem., 2017, 9, 1205–1212 CrossRef CAS PubMed.
- C. B. Dover, J. K. Gallaher, L. Frazer, P. C. Tapping, A. J. Petty, M. J. Crossley, J. E. Anthony, T. W. Kee and T. W. Schmidt, Endothermic singlet fission is hindered by excimer formation, Nat. Chem., 2018, 10, 305–310 CrossRef CAS PubMed.
- R. Pandya, Q. Gu, A. Cheminal, R. Y. S. Chen, E. P. Booker, R. Soucek, M. Schott, L. Legrand, F. Mathevet and N. C. Greenham, et al. , Optical projection and spatial separation of spin-entangled triplet pairs from the S1(21 Ag−) state of pi-conjugated systems, Chem, 2020, 6, 2826–2851 CAS.
- A. J. Musser and J. Clark, Triplet-pair states in organic semiconductors, Annu. Rev. Phys. Chem., 2019, 70, 323–351 CrossRef CAS PubMed.
- R. Casillas, I. Papadopoulos, T. Ullrich, D. Thiel, A. Kunzmann and D. M. Guldi, Molecular insights and concepts to engineer singlet fission energy conversion devices, Energy Environ. Sci., 2020, 13, 2741–2804 RSC.
- D. Casanova, Theoretical modeling of singlet fission, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed.
- B. J. Walker, A. J. Musser, D. Beljonne and R. H. Friend, Singlet exciton fission in solution, Nat. Chem., 2013, 5, 1019–1024 CrossRef CAS PubMed.
- H. L. Stern, A. J. Musser, S. Gelinas, P. Parkinson, L. M. Herz, M. J. Bruzek, J. Anthony, R. H. Friend and B. J. Walker, Identification of a triplet pair intermediate in singlet exciton fission in solution, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7656–7661 CrossRef CAS PubMed.
- D. G. Bossanyi, M. Matthiesen, S. Wang, J. A. Smith, R. C. Kilbride, J. D. Shipp, D. Chekulaev, E. Holland, J. E. Anthony and J. Zaumseil, et al. , Emissive spin-0 triplet-pairs are a direct product of triplet–triplet annihilation in pentacene single crystals and anthradithiophene films, Nat. Chem., 2021, 13, 163–171 CrossRef CAS PubMed.
- M. J. Y. Tayebjee, S. N. Sanders, E. Kumarasamy, L. M. Campos, M. Y. Sfeir and D. R. McCamey, Quintet multiexciton dynamics in singlet fission, Nat. Phys., 2017, 13, 182–188 Search PubMed.
- M. Dvořák, S. K. K. Prasad, C. B. Dover, C. R. Forest, A. Kaleem, R. W. MacQueen, A. J. Petty, R. Forecast, J. E. Beves and J. E. Anthony, et al. , Singlet fission in concentrated TIPS-pentacene solutions: the role of excimers and aggregates, J. Am. Chem. Soc., 2021, 143, 13749–13758 CrossRef PubMed.
- E. A. Margulies, J. L. Logsdon, C. E. Miller, L. Ma, E. Simonoff, R. M. Young, G. C. Schatz and M. R. Wasielewski, Direct observation of a charge-transfer state preceding high-yield singlet fission in terrylenediimide thin films, J. Am. Chem. Soc., 2017, 139, 663–671 CrossRef CAS PubMed.
- N. V. Korovina, S. Das, Z. Nett, X. Feng, J. Joy, R. Haiges, A. I. Krylov, S. E. Bradforth and M. E. Thompson, Singlet fission in a covalently linked cofacial alkynyltetracene dimer, J. Am. Chem. Soc., 2016, 138, 617–627 CrossRef CAS PubMed.
- A. M. Alvertis, S. Lukman, T. J. H. Hele, E. G. Fuemmeler, J. Feng, J. Wu, N. C. Greenham, A. W. Chin and A. J. Musser, Switching between coherent and incoherent singlet fission via solvent-induced symmetry breaking, J. Am. Chem. Soc., 2019, 141, 17558–17570 CrossRef CAS PubMed.
- N. J. Hestand and F. C. Spano, Expanded theory of H- and J-molecular aggregates: the effects of vibronic coupling and intermolecular charge transfer, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- I. Papadopoulos, D. Gutiérrez-Moreno, Y. Bo, R. Casillas, P. M. Greißel, T. Clark, F. Fernández-Lázaro and D. M. Guldi, Altering singlet fission pathways in perylene-dimers; perylene-diimide versus perylene-monoimide, Nanoscale, 2022, 14, 5194–5203 RSC.
- M. Grzybowski and D. T. Gryko, Diketopyrrolopyrroles: synthesis, reactivity, and optical properties, Adv. Opt. Mater., 2015, 3, 280–320 CrossRef CAS.
- M. J. Y. Tayebjee, K. N. Schwarz, R. W. MacQueen, M. Dvořák, A. W. C. Lam, K. P. Ghiggino, D. R. McCamey, T. W. Schmidt and G. J. Conibeer, Morphological evolution and singlet fission in aqueous suspensions of TIPS-pentacene nanoparticles, J. Phys. Chem. C, 2016, 120, 157–165 CrossRef CAS.
- R. J. Hudson, J. M. de la Perrelle, R. D. Pensack, B. Kudisch, G. D. Scholes, D. M. Huang and T. W. Kee, Organizing crystalline functionalized pentacene using periodicity of poly(vinyl alcohol), J. Phys. Chem. Lett., 2020, 11, 516–523 CrossRef CAS PubMed.
- R. J. Hudson, A. N. Stuart, J. M. de la Perrelle, D. M. Huang and T. W. Kee, Nanoparticle size-dependent singlet fission and exciton dynamics in amorphous TIPS-pentacene, J. Phys. Chem. C, 2021, 125, 21559–21570 CrossRef CAS.
- A. J. Musser, M. Maiuri, D. Brida, G. Cerullo, R. H. Friend and J. Clark, The nature of singlet exciton fission in carotenoid aggregates, J. Am. Chem. Soc., 2015, 137, 5130–5139 CrossRef CAS PubMed.
- A. Quaranta, A. Krieger-Liszkay, A. A. Pascal, F. Perreau, B. Robert, M. Vengris and M. J. Llansola-Portoles, Singlet fission in naturally-organized carotenoid molecules, Phys. Chem. Chem. Phys., 2021, 23, 4768–4776 RSC.
- M. J. Llansola-Portoles, K. Redeckas, S. Streckaite, C. Ilioaia, A. A. Pascal, A. Telfer, M. Vengris, L. Valkunas and B. Robert, Lycopene crystalloids exhibit singlet exciton fission in tomatoes, Phys. Chem. Chem. Phys., 2018, 20, 8640–8646 RSC.
- A. Ortega, D. Amorós and J. García de la Torre, Prediction of hydrodynamic and other solution properties of rigid proteins from atomic- and residue-level models, Biophys. J., 2011, 101, 892–898 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16 Rev. C.01, 2019 Search PubMed.
- J. Tomasi and M. Persico, Molecular interactions in solution: an overview of methods based on continuous distributions of the solvent, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS.
- J. F. Pérez, C. Z. Hadad and A. Restrepo, Structural studies of the water tetramer, Int. J. Quant. Chem., 2008, 108, 1653–1659 CrossRef.
- J. Pérez and A. Restrepo, ASCEC V–02: Annealing Simulado con Energía Cuántica, in Property, development and implementation: Grupo de Química–Física Teórica, Instituto de Química, Universidad de Antioquia, Medellín, Colombia, 2008 Search PubMed.
- Y. Zhao and D. G. Truhlar, A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- J. S. Binkley, J. A. Pople and W. J. Hehre, Self-consistent molecular orbital methods. 21. Small split-valence basis sets for first-row elements, J. Am. Chem. Soc., 1980, 102, 939–947 CrossRef CAS.
- J. M. Martínez and L. Martínez, Packing optimization for automated generation of complex system's initial configurations for molecular dynamics and docking, J. Comput. Chem., 2003, 24, 819–825 CrossRef PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from H to Rn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- S. Nosé, A molecular dynamics method for simulations in the canonical ensemble, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, TRAVIS—A free analyzer for trajectories from molecular simulation, J. Chem. Phys., 2020, 152, 164105 CrossRef CAS PubMed.
- M. Brehm and B. Kirchner, TRAVIS – a free analyzer and visualizer for monte carlo and molecular dynamics trajectories, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al. , Software for the frontiers of quantum chemistry: an overview of developments in the Q-Chem 5 package, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- A. Carreras, O. Uranga-Barandiaran, F. Castet and D. Casanova, Photophysics of molecular aggregates from excited state diabatization, J. Chem. Theory Comput., 2019, 15, 2320–2330 CrossRef CAS PubMed.
- D. Casanova and M. Head-Gordon, Restricted active space spin-flip configuration interaction approach: theory, implementation and examples, Phys. Chem. Chem. Phys., 2009, 11, 9779–9790 RSC.
- D. Casanova, Restricted active space configuration interaction methods for strong correlation: recent developments, WIREs Computat. Mol. Sci., 2022, 12, e1561 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- S. F. Boys, Construction of some molecular orbitals to be approximately invariant for changes from one molecule to another, Rev. Mod. Phys., 1960, 32, 296–299 CrossRef CAS.
- V. Dehm, Z. Chen, U. Baumeister, P. Prins, L. D. A. Siebbeles and F. Würthner, Helical growth of semiconducting columnar dye assemblies based on chiral perylene bisimides, Org. Lett., 2007, 9, 1085–1088 CrossRef CAS PubMed.
- P. P. N. Syamala, B. Soberats, D. Görl, S. Gekle and F. Würthner, Thermodynamic insights into the entropically driven self-assembly of amphiphilic dyes in water, Chem. Sci., 2019, 10, 9358–9366 RSC.
- F. C. Spano, The spectral signatures of frenkel polarons in H- and J-aggregates, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS PubMed.
- C. R. Cantor and P. Schimmel, in Biophysical Chemistry: Part II: Techniques for the Study of Biological Structure and Function, 1980 Search PubMed.
- N. V. Korovina, C. H. Chang and J. C. Johnson, Spatial separation of triplet excitons drives endothermic singlet fission, Nat. Chem., 2020, 12, 391–398 CrossRef CAS PubMed.
- E. A. Margulies, C. E. Miller, Y. Wu, L. Ma, G. C. Schatz, R. M. Young and M. R. Wasielewski, Enabling singlet fission by controlling intramolecular charge transfer in π-stacked covalent terrylenediimide dimers, Nat. Chem., 2016, 8, 1120–1125 CrossRef CAS PubMed.
- R. E. Cook, B. T. Phelan, R. J. Kamire, M. B. Majewski, R. M. Young and M. R. Wasielewski, Excimer formation and symmetry-breaking charge transfer in cofacial perylene dimers, J. Phys. Chem. A, 2017, 121, 1607–1615 CrossRef CAS PubMed.
- W. Ni, G. G. Gurzadyan, J. Zhao, Y. Che, X. Li and L. Sun, Singlet fission from upper excited electronic states of cofacial perylene dimer, J. Phys. Chem. Lett., 2019, 10, 2428–2433 CrossRef CAS PubMed.
- A. Aster, G. Licari, F. Zinna, E. Brun, T. Kumpulainen, E. Tajkhorshid, J. Lacour and E. Vauthey, Tuning symmetry breaking charge separation in perylene bichromophores by conformational control, Chem. Sci., 2019, 10, 10629–10639 RSC.
- Z. Yu, Y. Wu, Q. Peng, C. Sun, J. Chen, J. Yao and H. Fu, Accessing the triplet state in heavy-atom-free perylene diimides, Chem.–Eur. J., 2016, 22, 4717–4722 CrossRef CAS PubMed.
- K. Nagarajan, A. R. Mallia, V. S. Reddy and M. Hariharan, Access to triplet excited state in core-twisted perylenediimide, J. Phys. Chem. C, 2016, 120, 8443–8450 CrossRef CAS.
- C. Flors and S. Nonell, On the phosphorescence of 1H-phenalen-1-one, Helv. Chim. Acta, 2001, 84, 2533–2539 CrossRef CAS.
- A. D. Bain, Chemical exchange in NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2003, 43, 63–103 CrossRef CAS.
- A. D. Shaller, W. Wang, H. Gan and A. D. Q. Li, Tunable molecular assembly codes direct reaction pathways, Angew. Chem., Int. Ed., 2008, 47, 7705–7709 CrossRef CAS PubMed.
- W. Wang, J. J. Han, L.-Q. Wang, L.-S. Li, W. J. Shaw and A. D. Q. Li, Dynamic π–π stacked molecular assemblies emit from green to red colors, Nano Lett., 2003, 3, 455–458 CrossRef CAS.
- N. J. Hestand and F. C. Spano, Interference between coulombic and CT-mediated couplings in molecular aggregates: H- to J-aggregate transformation in perylene-based π-stacks, J. Chem. Phys., 2015, 143, 244707 CrossRef PubMed.
- J. Idé, R. Méreau, L. Ducasse, F. Castet, Y. Olivier, N. Martinelli, J. Cornil and D. Beljonne, Supramolecular organization and charge transport properties of self-assembled π–π stacks of perylene diimide dyes, J. Phys. Chem. B, 2011, 115, 5593–5603 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc04732j |
| This journal is © The Royal Society of Chemistry 2024 |