Open Access Article
Open Access ArticleHigh-throughput screening of high-activity oxygen carriers for chemical looping argon purification via a machine learning – density functional theory method†
Shenglong
Teng‡
a,
Yiwen
Song
a,
Yu
Qiu
a,
Xinyu
Li
a,
Yixia
Hong
a,
Jian
Zuo
a,
Dewang
Zeng
 *a and
Kai
Xu
*b
*a and
Kai
Xu
*b
aKey Laboratory of Energy Thermal Conversion and Control of Ministry of Education, School of Energy and Environment, Southeast University, Nanjing 210096, PR China. E-mail: dwzeng@seu.edu.cn
bSuzhou Branch of Xi'an Thermal Power Research Institute Co., Ltd, Suzhou 215153, China
First published on 18th February 2025
Abstract
Argon, a protective gas, is susceptible to contamination by impurity gases in the production of monocrystalline silicon for solar cells. Chemical looping combustion (CLC) technology offers a solution for argon recycling by leveraging the cyclic conversion of oxygen carriers. However, the desorption of low-concentration impurity gases requires high-activity oxygen carriers, and current screening methods primarily rely on experimental trial and error, which is time-consuming and labor-intensive. Herein, we propose machine learning-assisted Density Functional Theory (DFT) for high-throughput screening of oxygen carriers. Quaternary iron-based spinel oxygen carriers A1xA21−xByFe2−y were used as the object of study. DFT calculations were conducted on 756 oxygen carriers, while the remaining 3619 were predicted through machine learning, achieving a prediction accuracy R2 of 0.87. Based on these predictions and a three-step screening criterion of synthesizability, thermodynamic stability, and reactivity, Cu0.875Ni0.125Al0.5Fe1.5O4 exhibited the highest reactivity and its desorption of impurity gases is 6 times higher than that of fresh Fe2O3. In the stability test, Cu0.875Ni0.125Al0.5Fe1.5O4 maintained 96% CO removal efficiency after 10 cycles, facilitating the cyclic purification of crude argon. This study provides new guidance for the design and discovery of high-activity materials through high-throughput screening.
1. Introduction
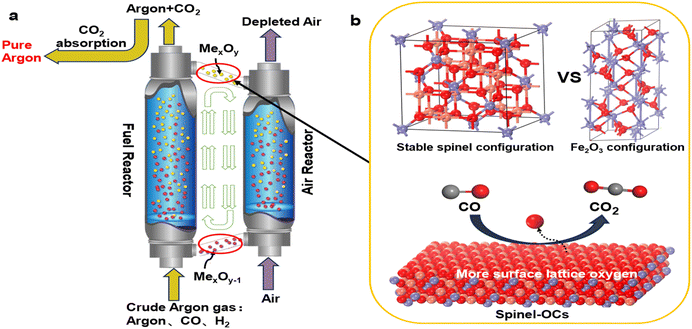
Argon is an inert gas commonly used as a shielding gas in various industrial applications, such as in the production of monocrystalline silicon, a primary component of solar cells,1–5 in protecting rotating nanostructures made of bent carbon nanotubes,6–8 and in steelmaking.9,10 However, during the production process, argon is prone to contamination by impurity gases (e.g.,CO and H2),11 thereby losing its protective function. To recycle the crude argon streams, techniques such as alloy adsorption12 and catalytic oxidation13,14 are employed. Alloy adsorption can achieve high purity but struggles to form irreversible chemical bonds at high temperatures, making it impractical for industrial recovery. Catalytic oxidation is a low-temperature process but requires the addition of extra oxygen, making it difficult to precisely control the oxygen demand.15 Therefore, there is an urgent need for an efficient and stable argon recycling technique.CLC technology provides a favorable pathway to cycle off impurity gases in a clean and efficient manner.16–18 As shown in Fig. 1(a), the primary principle of chemical looping argon purification is illustrated. This system mainly consists of a fuel reactor and an air reactor. In the fuel reactor, argon containing low-concentration impurity gases enter and are oxidized by metal oxygen carriers (OCs) to produce CO2 and H2O. The reduced OCs then enter the air reactor, where they regain lattice oxygen and continue back to the fuel reactor, thereby achieving cyclic purification of argon. Compared to traditional argon purification processes, chemical looping argon purification has the following advantages: (i) it uses lattice oxygen instead of gaseous oxygen to remove impurity gases, eliminating the need for oxygen regulation; (ii) the cyclic process can operate continuously when the two reactors are independently optimized; (iii) the cyclic process can operate at lower temperatures when using high-performance OCs, thus reducing process costs.
The argon purification process operates at low temperature and low impurity gas concentrations, placing higher demands on the activity and stability of the OCs. The oxygen carrier, a core component of the chemical looping process, is responsible for transporting lattice oxygen and heat. Common OCs include Fe2O3,19,20 CuO,21,22 and NiO.23,24 However, these oxygen carriers (OCs) fail to meet the high activity standards required. Spinel-type OCs, with their stable face-centered cubic structure, can accommodate more oxygen vacancies within the unit cell, thereby enhancing the oxygen transport rate (Fig. 1(b)). Extensive experimental studies have demonstrated that spinel-structured OCs exhibit superior reactivity and stability. Zhao et al.25 found that Ni–Fe spinel showed better reactivity and stability than fresh Fe2O3 OCs during chemical looping reactions, maintaining its cubic structure even after multiple cycles. Spinel structures possess numerous active sites and are easily doped. Zeng et al.26 investigated the performance of ternary mixed spinel OCs Cu–Co–Fe–O in chemical looping hydrogen production (CLHP) experiments, finding that these OCs exhibited strong reducibility and maintained high hydrogen production rates even at low temperatures. Similarly, Cui et al.27 studied the reaction performance of Zn–Fe–Al–O OCs in chemical looping processes, showing that this mixed oxygen carrier achieved twice the hydrogen production performance of fresh Fe2O3 and 100% fuel conversion. The above findings highlight the advantages of spinel OCs in terms of reactivity. However, current doping and selection of active elements for spinel OCs are primarily based on experimental trial and error, and a systematic method for screening OCs has yet to be developed.
The combination of machine learning (ML) and density functional theory (DFT) has become a new paradigm in the design of high-performance materials.28–31 DFT can provide the physicochemical properties of materials (such as conductivity, stability, and reactivity), thereby avoiding repetitive experimental synthesis and testing. The selection of DFT energy descriptors that accurately describe the properties of OCs is crucial for high-throughput screening. Singstock et al.32 chose the Gibbs reaction energy of OCs at different temperatures as descriptors, ultimately identifying 12 high-quality candidate OCs. Brorsson et al.33 proposed using oxygen chemical potential as the energy descriptor for the oxygen transfer capacity of reaction carriers, identifying Cu, Mn, and Fe as the most promising among 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials. Although these energy descriptors provide some reference value, none have demonstrated a clear correlation between the descriptors and oxygen carrier properties through calculations or experiments. The stringent conditions of chemical looping processes place high demands on oxygen carriers (OCs), necessitating a comprehensive consideration of stability, thermal resistance, and reactivity.21,34–36 Relying solely on DFT calculations is a significantly burdensome task. ML accelerates the high-throughput screening process by learning the mapping relationship between material structural features and energy properties. Wang et al.37 used ML to assist DFT calculations, predicting the properties of an additional 227
000 materials. Although these energy descriptors provide some reference value, none have demonstrated a clear correlation between the descriptors and oxygen carrier properties through calculations or experiments. The stringent conditions of chemical looping processes place high demands on oxygen carriers (OCs), necessitating a comprehensive consideration of stability, thermal resistance, and reactivity.21,34–36 Relying solely on DFT calculations is a significantly burdensome task. ML accelerates the high-throughput screening process by learning the mapping relationship between material structural features and energy properties. Wang et al.37 used ML to assist DFT calculations, predicting the properties of an additional 227![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 223 OCs based on the 2401 perovskite OCs obtained from DFT. Wen et al.38 employed a tree model to predict the performance of various deoxidizers, demonstrating high predictive accuracy. However, current research rarely addresses how to use computational language to describe the features of input oxygen carriers, which to some extent affects the generalization capability of the models. In summary, the appropriate selection of DFT energy descriptors and ML input features is critical to ensuring the accuracy and reliability of the DFT-ML method.
223 OCs based on the 2401 perovskite OCs obtained from DFT. Wen et al.38 employed a tree model to predict the performance of various deoxidizers, demonstrating high predictive accuracy. However, current research rarely addresses how to use computational language to describe the features of input oxygen carriers, which to some extent affects the generalization capability of the models. In summary, the appropriate selection of DFT energy descriptors and ML input features is critical to ensuring the accuracy and reliability of the DFT-ML method.
In this study, we propose a three-step high-throughput screening framework, utilizing synthesizability, high-temperature stability, and reactivity to identify target OCs. Focusing on A1xA21−xByFe2−y OCs, elements were doped at the A1, A2, and B sites. DFT calculations were performed to obtain the formation energy (Ef), Gibbs free energy (ΔG), and oxygen vacancy formation energy (Evac) for 756 groups of OCs, verifying the positive correlation between oxygen vacancy formation energy and reactivity. Based on the DFT results, we established a database of oxygen carrier characteristics and energy descriptors. Descriptors such as atomic number, ionization energy, and chemical potential of elements were selected to distinguish between different OCs. Four typical ML models were then employed to train and predict the performance of the remaining 3619 OCs. Finally, the four OCs with the best overall performance were selected, and reactivity and cycling stability tests for argon purification were conducted.
2. Methods
2.1 Calculation methods
DFT based first-principles calculations were performed using the Vienna ab initio Simulation Package (VASP). The gradient generalization for the approximation of an electron and plane wave basis set were used for the calculations. To represent the exchange–correlation energy, the projector augmented wave (PAW) potentials and Perdew–Burke–Ernzerhof (PBE) were used. Throughout the current studies, a fixed cutoff energy of 500 eV and energy convergence of 1.0 × 10−5 eV per atom were chosen. The magnetic moments were not taken into account for their small influence in the systematic energy trends. The addition of a model Hubbard-U term to the DFT energy functional was set for a correct qualitative description of the electronic structure of ceria surfaces. After being checked by spanning the values of U from 0–5 eV or the parameter results, the U-values for different transition state metal elements are shown in Table S1.† DFT+U calculations can improve the accuracy of conventional DFT calculations and provide valuable information on the structure of the active sites and the energy of adsorbed species interacting with the surfaces. Furthermore, detailed reaction pathways can be derived and characterized by the energy profile of the constituent elementary steps. At the same time, relying only on DFT calculations for high-throughput screening incurs significant computational costs. To alleviate this problem, an ML-assisted DFT screening approach is also introduced. The approach entails the execution of DFT computations on a subset of OCs, yielding energy descriptors. These descriptors then serve as the training data for an ML model. The efficacy of this method is evidenced by its ability to predict the attributes of the remaining OCs, thereby facilitating effective screening.All the studied systems were 2 × 2 × 2 cubic supercells, the surface slabs were made of 2 × 2 × 2 supercells with 15 Å of vacuum along the surface direction in order to indicate the aperiodic structure of surface atoms. Surface (100) was chosen for the calculation. The values of 4 × 4 × 4 k-point meshes employed in the calculations were generated according to the Monkhorst–Pack scheme. Dipole correction was considered for the slab calculations. The crystal structure of A1xA21−xB1yFe2−yO4 OCs is shown in Fig. S1.†
Overall, the chemical cycle for argon purification is similar to that for combustion, with the primary difference lying in the reaction pathways. In chemical cycle combustion, a large amount of energy is released through the reaction between fuel and metal oxides, whereas in chemical cycle argon purification, the focus is on separating metal oxides from impurities in the argon gas and driving the reduction process. In terms of energy distribution, the energy released during the chemical cycle combustion process is primarily used to generate electricity or heat, making it highly efficient in terms of energy utilization. In contrast, the chemical cycle for argon purification consumes less energy, which is mainly used to drive the reduction reaction, with some adjustments made to the model parameters. Four ML models are built autonomously using the python language, and the specific code can be found at https://github.com/ywsong1/Machine-learning-code-from-DFT-ML-for-high-throughput-screening-of-OCs. In order to refine the generalization ability of the models, we used grid partitioning to find the best hyperparameters for several models based on the accuracy of the prediction set. In evaluating the performance of different machine learning models, we chose the coefficient of determination (R2), the minimum absolute error (MAE), and the Pearson correlation index (Pearson) as the units of evaluation.
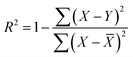 | (1) |
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) denotes the mean of all DFT calculations.
denotes the mean of all DFT calculations. | (2) |
 | (3) |
The Pearson correlation coefficient measures the linear correlation between two variables, ranging from −1 to 1. Here, Ȳ represents the mean of the predicted values for all samples.
2.2 Characterization of OCs
The crystalline phase composition of the OCs was analyzed using a Japanese D/max 2500VL/PC X-ray diffractometer (XRD). The measurement conditions were as follows: Cu Kα radiation source, graphite monochromator filter, tube voltage of 40 kV, tube current of 100 mA, scanning range from 2θ = 5° to 85°, step size of 0.02°, and X-ray wavelength λ = 1.5406 Å. H2-TPR characterization of the OCs was conducted using a Finesorb-3010 temperature-programmed reduction chemisorption analyzer. The experimental procedure was as follows: 200 mg of the oxygen carrier sample was weighed and pretreated at 400 °C for 1 hour with an Ar flow of 30 ml min−1. The sample was then cooled to 100 °C, followed by the introduction of 10 mol% H2 with a flow rate of 30 ml min−1. The temperature was linearly increased from 100 °C to 900 °C at a rate of 10 °C min−1, and the TCD signal was recorded simultaneously.2.3 Experimental tests
Spinel samples with the form of A1xA21−xB1yFe2−yO4 were synthesized by the sol–gel method. Metal nitrates were completely dissolved in a citric acid and polyethylene glycol solution by stirring for 12 h at 90 °C. Then the solution was dried at 105 °C. The dried gel was then calcined at 700 °C for 2 h, and then pulverized to powder.A batch of ∼0.5 g OCs were exposed to reducing gas (CO, 50 ml s−1, STP), inert gas (N2, 50 ml s−1, STP) and oxidizing gas (air, 50 ml s−1, STP) in the laboratory-scale fluidized bed. The temperature was set at 500 °C. Between the reduction and re-oxidation reactions, an insert period (1 l min−1 of N2) of about 1 min was inserted to prevent mixing between carbon monoxide and gas-phase oxygen. The performance of oxygen storage materials was estimated by the remaining reducing gas over multiple redox cycles.
3. Results and discussion
3.1 DFT high-throughput screening of oxygen carrier stability and activity
This study focuses on Fe-based spinel OCs A1xA21−xB1yFe2−yO4, systematically investigating the performance of various spinel OCs by doping divalent and trivalent metal elements at the A and B sites, respectively. Table 1 lists the selected metal elements for the A and B sites along with their corresponding doping ratios. Due to constraints in the crystal structure's lattice sites, the doping ratios for both A and B sites were limited to a range between 0 and 0.5. By combining these elements, a total of 4375 potential oxygen carriers (OCs) were generated. However, traditional experimental screening methods are inefficient for handling such a large number of combinations, making the screening of 4375 OCs a significant challenge. To address this, we employed a high-throughput screening method combining DFT with ML to accelerate the identification of target OCs. Fig. 2(a) illustrates the three-step process of this high-throughput screening. First, crystal structure stability is a crucial criterion for assessing the synthesizability of materials, with Ef serving as the key indicator of structural stability.39–41 When Ef < 0, the crystal structure is considered potentially synthesizable. However, due to the experimental reaction temperature being around 600 °C, composite OCs are prone to phase separation and microstructural changes at high temperatures, leading to performance degradation. Therefore, we used ΔG to evaluate the high-temperature stability of the materials.32,37,42,43 Based on this criterion, materials with a certain level of thermal stability were selected from the remaining candidate OCs. Next, to further identify OCs with excellent lattice oxygen transfer capabilities, we selected surface Evac as an energy descriptor. A lower Evac indicates less resistance to lattice oxygen transfer during the reaction, thus enhancing the reaction activity.44,45 Using these criteria, we ultimately selected four OCs with synthesizability, high-temperature stability, and superior reactivity.| A1, A2 | Cu, Mg, Zn, Ca, Ni, Co, Cd |
| B1 | Co, Ti, Al, Cr, Mn, In, V |
| x | 0, 0.125, 0.25, 0.375, 0.5 |
| y | 0, 0.25, 0.375, 0.5 |
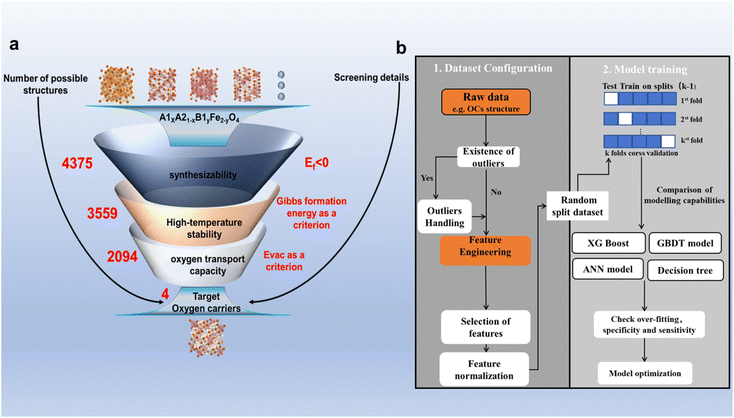 | ||
| Fig. 2 ML-assisted high-throughput screening flowchart. (a) DFT high-throughput screening process. (b) ML prediction flowchart. | ||
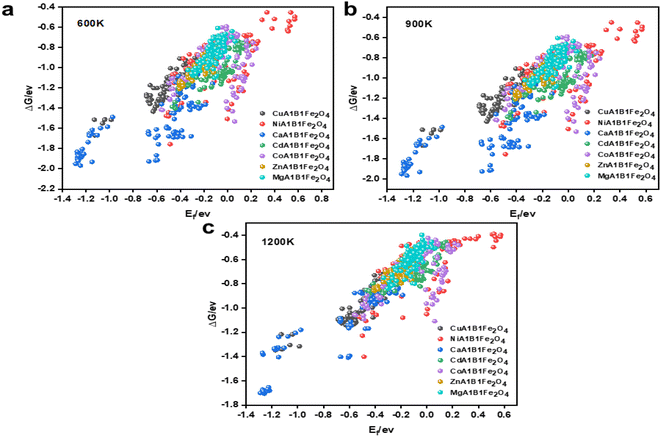
To ensure the ML models possess good generalization capability, the DFT calculation data must be as comprehensive and diverse as possible. Based on this, while fixing the A1 site element, we ensured that all possible elements were evenly distributed at the A2 and B1 sites, enabling the model to learn the interactions between different coordination elements during training. As a result, we obtained 756 spinel-type OCs with various elemental compositions through DFT calculations. The structural and thermal stability of OCs is crucial for maintaining activity under multi-cycle conditions. Fig. 3 shows the stability results of the 756 OCs calculated using DFT. A smaller Ef indicates higher structural stability of the OCs. When Ef < 0, the oxygen carrier is considered structurally stable. It is evident that Ca–Fe OCs exhibit better structural stability, while some Ni–Fe and Co–Fe OCs show poorer stability. The superior structural stability of Ca–Fe spinels is mainly attributed to the larger ionic radius of Ca2+, its good lattice matching, and the uniform distribution of its electronic structure.46,47 In contrast, Ni–Fe spinels exhibit reduced stability due to the smaller ionic radius of Ni2+ and the strong crystal field effect, which increase lattice stress and lead to coordination deformation. Co–Fe spinels, with Co2+ having an ionic radius between that of Ca2+ and Ni2+, show slightly better stability than Ni–Fe spinels, though still insufficient for optimal lattice matching. Furthermore, the complex electronic structure and spin states of Co2+ further diminish the symmetry and stability of the crystal, resulting in lower stability for Co–Fe spinels. Through the calculations, we found that 157 out of the 756 OCs had Ef > 0, indicating that these oxygen carriers were not suitable for further analysis.
To evaluate the stability of OCs under high-temperature conditions, we calculated the ΔG of these materials at 600 K, 900 K, and 1200 K. Encouragingly, all the OCs exhibited ΔG values greater than 0 eV at these temperatures, indicating a certain level of thermal resistance. As shown in Fig. 3(a)–(c), the ΔG values gradually increased with rising temperature, demonstrating a decline in stability under high-temperature conditions, which aligns with thermodynamic principles. The distribution of different OCs reveals that Ca–Fe OCs exhibit the best high-temperature stability, while Ni–Fe OCs perform the worst among the 756 materials. The superior thermal stability of Ca–Fe OCs is primarily attributed to the higher bond energy of Ca–O bonds, the resistance of the crystal structure to phase transitions at elevated temperatures, and a lower thermal expansion coefficient, which allows the structure to maintain integrity and stability under high-temperature conditions. In contrast, Ni–Fe OCs exhibit weaker Ni–O bond strength, making them more susceptible to phase transitions at high temperatures. Their higher thermal expansion coefficient also leads to greater lattice deformation and structural degradation, resulting in poorer thermal stability. Additionally, the thermal stability of OCs is closely linked to the ionic radius and crystal field effects. A larger ionic radius and moderate crystal field effects promote better lattice matching and structural integrity at high temperatures, reducing lattice stress and defects. This explains the similar trends observed in the structural and thermal stability of some OCs.
After analyzing the formation energy and Gibbs free energy of the OCs, we confirmed that the screened OCs possess sufficient stability. To further investigate the reaction kinetics of OCs in the CO removal process, we applied transition state theory (TST) to calculate the energy changes for seven groups of spinel OCs (Cu/Co/Ni/Ca/Cd/Mg/Zn–Fe) during their reactions with CO (Fig. 4). The results indicate that CO initially interacts with the surface of the OCs, forming a stable surface adsorption state. As the reaction proceeds, CO molecules react with the active lattice oxygen on the surface, causing lattice oxygen to shift and forming an intermediate COO*. During this process, COO* is further activated and gradually detaches from the surface, eventually transforming into a free CO2 molecule that is released into the gas phase. Meanwhile, the consumption of lattice oxygen creates oxygen vacancies on the surface of the oxygen carrier. This reaction mechanism highlights the critical role of lattice oxygen activation in controlling the reaction rate. In DFT calculations, the Evac reflects the ease of activating lattice oxygen; a lower Evac value indicates that lattice oxygen is more easily activated, thereby enhancing surface reaction rates. To verify the accuracy of Evac as a descriptor for oxygen carrier activity, we calculated the Evac values for seven groups of OCs. Fig. 5(a) shows the correlation between Evac and the activation energy of the reaction for these seven iron-based OCs. The results reveal a high degree of correlation between Evac and activation energy, with an R2 value of 0.92. This further confirms that Evac can effectively serve as an energy descriptor for describing the reaction activity of OCs. Using this descriptor, we calculated the Evac values for 756 OCs. The heatmaps in Fig. 5(b)–(h) illustrate the reaction activity of these OCs, showing that among the seven groups of OCs with fixed A1 sites, the Cu–Fe OCs exhibit the highest reaction activity, consistent with the activation energy calculation (Fig. 5(a)). Through high-throughput DFT calculations, we established a database of 756 OCs, encompassing synthesizability, high-temperature stability, and reaction activity (Table S2†).
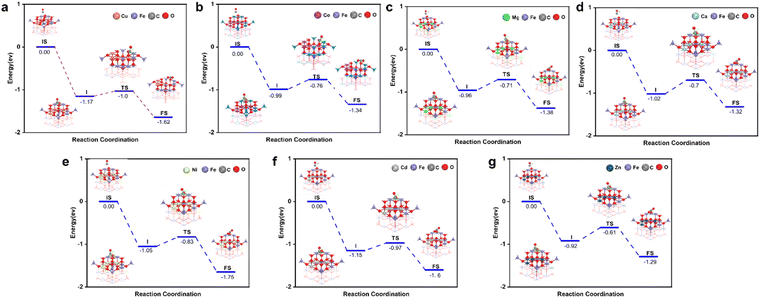 | ||
| Fig. 4 The reaction process of AFe2O4 spinel with CO. (a) A = Cu. (b) A = Co. (c) A = Mg. (d) A = Ca. (e) A = Ni. (f) A = Cd. (g) A = Zn. | ||
3.2 ML models' interpretability analysis
Based on the DFT-calculated database, this study trained ML models to efficiently predict the properties of the remaining OCs. Fig. 2(b) illustrates the ML workflow used in this research, which mainly consists of two core parts: database construction and model training. The database was generated from the DFT calculation results of a subset of OCs. The sample size of the database has a crucial impact on the model's performance. To explore the effect of sample size on model accuracy, we selected 150 to 750 samples from the database for analysis. The results demonstrate that when the sample size reached 600, the model's performance stabilized, suggesting that our database contains adequate data to meet the requirements for model training (Fig. S2(a)†). During the construction of the database, outlier analysis is a critical step, as addressing outliers can significantly enhance the quality of the dataset. Since ML models cannot directly interpret the chemical properties of OCs, we performed feature engineering to convert the structural information of the OCs into numerical matrices. A common issue in feature engineering is using only element symbols and proportions as feature descriptors (Fig. 6(a)), which can make it difficult for the model to capture complex relationships and may lead to overfitting. In this study, we transformed different chemical elements into unique physical and chemical properties, such as atomic number, electronegativity, atomic radius, electron affinity, and chemical potential, with the element proportions serving as weighted values for these properties. This process generated a unique feature matrix for each oxygen carrier (Fig. 6(b)). After completing the feature engineering, we analyzed the impact of different numbers of features on the model's prediction accuracy (Fig. S2(b)†). The results indicate that when the number of features increased from 1 to 4, model accuracy improved significantly. However, when the number of features increased to 5, the accuracy improvement leveled off. This suggests that as the number of features increases further, overfitting may occur, which not only increases computational complexity but also has the potential to reduce the model's accuracy. Considering both prediction accuracy and computational efficiency, setting the number of features to 5 was determined to be the optimal choice. Once feature engineering was completed, the database was randomly divided, with 75% of the data used for model training and 25% for validating the model's prediction accuracy on new-input data. The model's generalization ability was further validated using the k-fold cross-validation method. Finally, we employed four commonly used regression ML models for performance prediction, as these models have been proven to exhibit high accuracy in predicting material properties. Based on the predictive performance of each model, we selected the optimal model for subsequent applications. | ||
| Fig. 6 Descriptor representation of oxygen carrier information. (a) Widely used but erroneous descriptor representations. (b) Descriptors used in this paper that can be recognized by ML languages. | ||
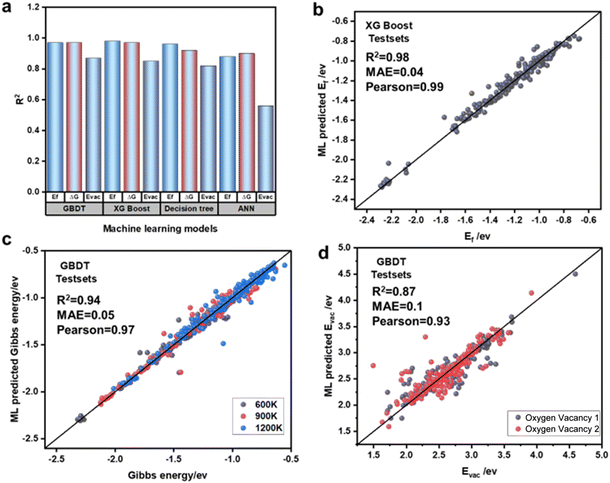
The ML models demonstrated significant differences in predicting various energy features. To address this, we used four models to predict Ef, ΔG and Evac, and selected the most suitable models for each case. Fig. 7(a) summarizes the R2 performance of each model in predicting these three energy features. For Ef prediction, the XGBoost model performed the best on the test set, achieving an R2 of 0.98, a MAE of 0.04, and a Pearson correlation coefficient of 0.99. The other three models also showed good performance in predicting Ef (Fig. S3†). For ΔG prediction, we modeled energy at 600 K, 900 K, and 1200 K, and found that both GBDT and XGBoost exhibited identical prediction accuracy, with R2 values of 0.97. The predicted values were highly consistent with the DFT-calculated values, making these models the top performers among the four (Fig. S4†). In predicting Evac, due to the presence of two distinct oxygen active sites on the surface of the OCs, we conducted separate predictions for these two sites. The results showed that the GBDT model had the highest prediction accuracy for Evac, with an R2 of 0.87, an MAE of 0.1, and a Pearson correlation coefficient of 0.93. In contrast, other models, especially the artificial neural network (ANN), exhibited larger discrepancies, with the ANN model achieving a lower R2 of only 0.58 (Fig. S5†). These differences can be attributed to the complexity of the physical and chemical properties of different materials, particularly in terms of crystal structure and electron distribution. The complex nonlinear relationships between energy features and material properties make certain energy features more sensitive to specific atomic interactions or local electronic states, resulting in variations in their ability to capture these features. After training and evaluating the four models, we confirmed that they demonstrated sufficient accuracy in predicting new data, making them suitable for oxygen carrier screening. Ultimately, the XGBoost model was selected for predicting the formation energy of oxygen carriers, while the GBDT model was chosen for predicting the Gibbs free energy and oxygen vacancy formation energy.
3.3 Application of ML models to screen OCs
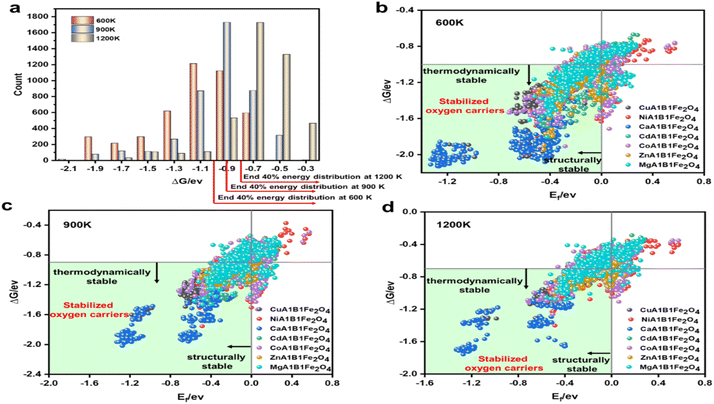
After ensuring that the selected models possessed sufficient generalization ability, we used the XGBoost and GBDT models to predict the properties of the remaining 3619 OCs. Combining these predictions with previous calculation results, we conducted high-throughput screening of all candidate OCs. The first screening criterion focused on structural stability. Fig. 8(b)–(d) show the distribution of structural stability for these OCs, with Ef values greater than 0 indicating structural instability. The results revealed that Co–Fe, Ni–Fe, and Mg–Fe spinel OCs had poorer structural stability, while Ca–Fe OCs exhibited the best structural stability, consistent with the DFT results. After this screening, 816 OCs were excluded due to insufficient structural stability. The thermal stability of the oxygen carriers was characterized by ΔG. Based on DFT calculations and ML model predictions, all candidate OCs showed ΔG values less than 0 eV, indicating that they possess theoretical high-temperature resistance. This can be attributed to the stable AB2O4 structure of Fe-based spinel oxides and the strong metal–oxygen bonds, which provide excellent thermal stability at high temperatures. Additionally, the half-filled 3d orbital electronic structure of Fe3+ and its favorable redox properties further enhance thermal stability.48,49Fig. 8(a) shows the ΔG distribution of 4375 OCs, which follows a normal distribution. Although the overall thermal stability was satisfactory, significant variations were observed among the OCs. To select those with superior thermal stability, we chose the top 60% in terms of stability at 600 K, 900 K, and 1200 K. The shaded regions represent OCs with good thermal stability (Fig. 8(b)–(d)). The results indicated that Ca–Fe and Cu–Fe spinel OCs exhibited excellent thermal stability, whereas a significant portion of Mg/Co/Ni–Fe OCs had ΔG values in the bottom 40%. Through high-throughput screening for structural and thermal stability, we excluded 2281 OCs that did not meet the required criteria. It is important to note that the exclusion of these OCs does not necessarily imply instability, but rather that they do not meet the specific application criteria we targeted.Finally, we screened out the four OCs with the highest reaction activity from the remaining 2094 candidates. Through DFT calculations, we validated the strong correlation between Evac and the CO desorption activation energy of the OCs. Fig. 9 presents the heatmap of −Evac values for all OCs, with the white regions representing those excluded during screening. It is evident that Cu–Fe OCs exhibit smaller Evac values compared to other compositions, indicating higher reaction activity. The high reactivity of Cu–Fe OCs is mainly attributed to the excellent catalytic properties of Cu, which effectively lowers the reaction activation energy.50 Moreover, strong electron transfer and interaction between Cu and Fe further enhance the active sites, accelerating the reaction process, which is consistent with experimental results.51–53 In addition to Cu–Fe, Ni–Fe and certain Ca–Fe OCs also exhibited high reaction activity, making them common materials in chemical looping reactions. By ranking these OCs based on their Evac values, we identified the four most reactive OCs: Cu0.875Ni0.125–Al0.5Fe1.5O4 (Evac = 1.25 eV), Cu0.625Mg0.375Al0.25Fe1.75O4 (Evac = 1.35 eV), Cu0.625Co0.375Al0.25–Fe1.75O4 (Evac = 1.39 eV), and Cu0.875Ca0.125Mn0.375Fe1.625O4 (Evac = 1.41 eV). Additionally, several other OCs, not previously reported in the literature, also demonstrated good reactivity. However, in this study, we focused on these four spinel OCs with the highest reaction activity and further explored their application potential.
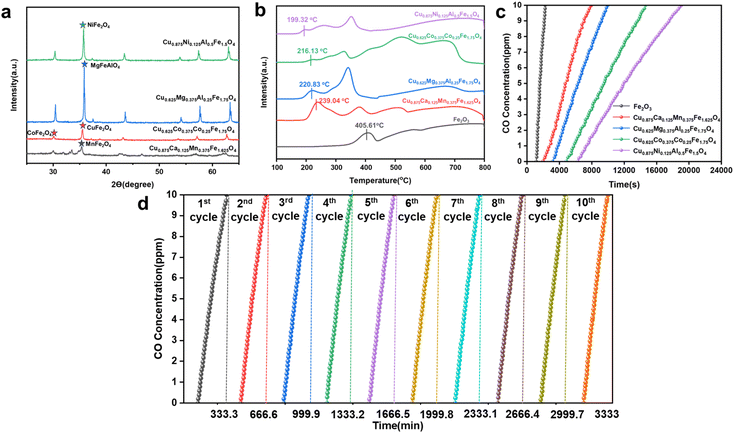
Chemical looping argon purification is a typical chemical reaction process that relies on highly active oxygen carriers to remove low concentrations of impurity gases. Using a high throughput screening method combining machine learning and DFT, we identified four theoretically high-activity OCs. Further experimental testing is required to verify their performance in low-concentration CO removal and their cycling stability. Fig. 10(a) shows the XRD characterization results for the four OCs, with diffraction peaks indicating that they all exhibit the characteristic spinel structure. Fig. 10(b) presents the H2-TPR (temperature-programmed reduction) test results for the four high-activity OCs and pure Fe2O3. All OCs exhibited two or more reduction peaks, corresponding to two reduction steps: the reduction of Fe2O3 and the reduction of the doped elements from higher to lower oxidation states. In the initial stage of the reduction reaction, the low-temperature reduction peak corresponds to the consumption of surface-active oxygen, and the reduction temperature is closely related to the activity of surface oxygen atoms, which is reflected in the Evac values obtained from DFT-calculations. A lower Evac value indicates higher surface oxygen activity, resulting in better low-temperature reaction activity and a lower initial reduction temperature. As shown in the figure, the low-temperature reduction peak temperatures for Cu0.875Ni0.125Al0.5Fe1.5O4, Cu0.625–Mg0.37–5Al0.25Fe1.75O4, Cu0.625Co0.375Al0.25Fe1.75O4, and Cu0.875Ca0.125Mn0.375Fe1.625O4 are 199.3–2 °C, 216.13 °C, 220.83 °C, and 230.94 °C, respectively. Among them, Cu0.875Ni0.125Al0.5Fe1.5O4 has the lowest initial reduction temperature, 206.29 °C lower than that of fresh Fe2O3,indicating its excellent low-temperature activity.
The concentration of impurity gases and the reaction temperature in the argon purification process significantly impact the system's reactivity and economic efficiency. Lower reaction temperatures can effectively reduce energy consumption, so we selected a temperature range of 350–650 °C to investigate the CO desorption characteristics of the oxygen carriers. Fig. S6† shows the CO removal performance of the OCs at different temperatures. The results indicate that, during the initial phase of the reaction, the OCs achieve complete CO removal, demonstrating high reactivity. Additionally, the reaction temperature has a significant effect on CO removal performance. As the temperature increases, the performance of the OCs improves, and the duration of complete CO removal extends. At 500 °C, after 6276 seconds (approximately 105 minutes) of reaction, no CO was detected in the outlet gas; when the temperature was raised to 650 °C, the complete CO removal time increased to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 seconds (217 minutes). Moreover, as the temperature rises, the rate of CO concentration increase slows down, further indicating that the reactivity of the OCs increases with rising temperature (Fig. S6(a)†). By analyzing the CO removal performance curves of other OCs, it can be observed that before 500 °C, the CO concentration increases rapidly, indicating that at lower temperatures, the surface-active oxygen content of the oxygen carriers is insufficient to sustain long-term reactions. After 500 °C, the activity of the OCs improves significantly. Therefore, 500 °C is considered the optimal balance point between system efficiency and reactivity. Fig. S7† shows the desorption performance of the OCs at different impurity gas concentrations. As the CO concentration increases, the reaction rate between the OCs and CO accelerates, and the consumption of active oxygen speeds up, shortening the time required for complete CO removal. When the gas concentration increased to 2000 ppm, the composite oxygen carrier Cu0.875Ni0.125Al0.5Fe1.5O4 was still able to achieve complete CO removal within approximately 500 seconds, further confirming its higher reactivity and oxygen release capacity. Fig. 10(c) illustrates the desorption performance of the four OCs and fresh Fe2O3 at 500 °C with a CO concentration of 100 ppm. The results show that Cu0.875Ni0.125Al0.5Fe1.5O4 outperforms fresh Fe2O3, achieving complete CO removal within 6500 seconds. This experimental result further validates the effectiveness of the OCs obtained through high-throughput screening in practical applications.
000 seconds (217 minutes). Moreover, as the temperature rises, the rate of CO concentration increase slows down, further indicating that the reactivity of the OCs increases with rising temperature (Fig. S6(a)†). By analyzing the CO removal performance curves of other OCs, it can be observed that before 500 °C, the CO concentration increases rapidly, indicating that at lower temperatures, the surface-active oxygen content of the oxygen carriers is insufficient to sustain long-term reactions. After 500 °C, the activity of the OCs improves significantly. Therefore, 500 °C is considered the optimal balance point between system efficiency and reactivity. Fig. S7† shows the desorption performance of the OCs at different impurity gas concentrations. As the CO concentration increases, the reaction rate between the OCs and CO accelerates, and the consumption of active oxygen speeds up, shortening the time required for complete CO removal. When the gas concentration increased to 2000 ppm, the composite oxygen carrier Cu0.875Ni0.125Al0.5Fe1.5O4 was still able to achieve complete CO removal within approximately 500 seconds, further confirming its higher reactivity and oxygen release capacity. Fig. 10(c) illustrates the desorption performance of the four OCs and fresh Fe2O3 at 500 °C with a CO concentration of 100 ppm. The results show that Cu0.875Ni0.125Al0.5Fe1.5O4 outperforms fresh Fe2O3, achieving complete CO removal within 6500 seconds. This experimental result further validates the effectiveness of the OCs obtained through high-throughput screening in practical applications.
In the chemical looping argon purification system, the cycling stability of OCs is critical—the better the stability, the higher the efficiency of impurity gas removal from crude argon. In this study, the oxygen carrier with the highest reactivity, Cu0.875Ni0.125Al0.5Fe1.5O4, was selected for cycling stability testing. The experimental conditions were set at 500 °C with a CO concentration of 100 ppm, and the number of cycles was set to 10, with each cycle lasting 333.3 minutes. The cycling stability of the oxygen carrier was analyzed by measuring the time it took for the CO concentration in the outlet gas to reach 10 ppm. When the CO concentration at the outlet reaches 10 ppm, it indicates that the reactivity of the oxygen carrier is no longer sufficient to maintain argon purification, at which point oxidation regeneration of the oxygen carrier is required. Fig. 10(d) shows the desorption performance of Cu0.875Ni0.125Al0.5Fe1.5O4 after 10 cycles. The results indicate that as the number of cycles increased, the CO removal capacity of the oxygen carrier experienced only a slight decrease. After a total reaction time of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 seconds and 10 cycles, the CO removal efficiency of the oxygen carrier remained at 96% of the initial cycle efficiency, demonstrating excellent cycling stability.
000 seconds and 10 cycles, the CO removal efficiency of the oxygen carrier remained at 96% of the initial cycle efficiency, demonstrating excellent cycling stability.
4. Conclusion
This study presents a high-throughput screening method combining DFT and machine learning for identifying high-activity oxygen carriers to remove low concentrations of CO. Through DFT calculations, we developed a screening framework for the synthesizability, high-temperature stability, and reactivity of OCs, and validated the correlation between their properties and energy characteristics. After analyzing data from 756 OCs, we evaluated the generalization performance of four different machine learning models. The results showed that the XGBoost and GBDT models achieved the best prediction accuracy for oxygen carrier properties, with R2 values of 0.98 and 0.87, respectively. Using the trained models, we predicted and screened the remaining 3619 OCs, ultimately identifying four previously unreported high-activity OCs: Cu0.875Ni0.125Al0.5Fe1.5O4, Cu0.625Mg0.375Al0.25Fe1.75O4, Cu0.625Co0.375Al0.25Fe1.75O4, and Cu0.875Ca0.125Mn0.375Fe1.625O4. Further experimental tests on these four OCs confirmed their CO removal performance. Cu0.875Ni0.125Al0.5Fe1.5O4 demonstrated effective CO removal for over 6500 seconds at a CO concentration of 100 ppm, and after 10 cycles, it maintained 96% of its CO removal efficiency. The other three high-activity oxygen carriers also exhibited excellent reactivity. This study demonstrates that the high-throughput screening method combining DFT and machine learning can efficiently and rapidly identify target materials, accelerating the development of related processes.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author information
All the authors contributed to the preparation of the final manuscript.Conflicts of interest
No potential conflict of interest was reported by the authors.Acknowledgements
The work was supported by the National Key R&D Program of China (Grant No. 2024YFB4106000), National Natural Science Foundation of China (Grant No. 52276105, 52336007) and the Fundamental Research Funds for the Central Universities (Grant No. 2242023k30026).References
- X. Qi, Y. Xue, W. Su, W. Ma and L. Liu, Crystals, 2021, 11, 421 CrossRef CAS
.
- A. Parashar, S. Kumar, J. Gope, C. Rauthan, P. Dixit and S. Hashmi, Sol. Energy Mater. Sol. Cells, 2010, 94, 892–899 CrossRef CAS
.
- M. Hou, C. Benazeth, P. Hecquet and N. Benazeth, Nucl. Instrum. Methods Phys. Res., Sect. B, 1990, 48, 625–629 CrossRef
.
- S. Sugunraj, G. Aravindan, M. Srinivasan and P. Ramasamy, Silicon, 2023, 15, 1701–1724 CAS
.
- H. J. Jeon, H. Park, G. Koyyada, S. Alhammadi and J. H. Jung, Processes, 2020, 8, 1077 CrossRef CAS
.
- J. Shi, Y. Li, A. Wang and K. Cai, Comput. Mater. Sci., 2018, 154, 132–137 CrossRef CAS
.
- M. Assali, M. P. Leal, I. Fernández and N. Khiar, J. Nanotechnol., 2013, 24, 085604 CrossRef PubMed
.
- C. Xu and K. L. Choy, Chem. Vap. Deposition, 2019, 153, 153–243 Search PubMed
.
- S. Lu, H. Fujii, H. Sugiyama, M. Tanaka and K. Nogi, ISIJ Int., 2003, 43, 1590–1595 CrossRef CAS
.
- J. Elmer, J. Vaja, R. Pong, T. Gooch and H. Barth, Weld. J., 2015, 2015, 313S–325S Search PubMed
.
- A. Streb and M. Mazzotti, Ind. Eng. Chem. Res., 2020, 59, 10093–10109 CrossRef CAS
.
- M. Wang, A. Lawal, P. Stephenson, J. Sidders and C. Ramshaw, Chem. Eng. Res. Des., 2011, 89, 1609–1624 CrossRef CAS
.
- H. I. Abdel-Shafy and M. S. Mansour, Egypt. J. Pet., 2018, 27, 1275–1290 CrossRef
.
- J. Hua, X. Cao, Y. Yi and J. Lin, J. Sound Vib., 2020, 464, 114985 CrossRef
.
- M. Maeda, Y. Muraki, Y. Anno, A. Sawa, Y. Kusama, M. Ishikane, N. Ohmagari and H. Ohge, J. Infect. Chemother., 2020, 26, 633–635 CrossRef PubMed
.
- J. Mao, Y. Wei, Z. Li, J. Chen, Z. Gu, H. Li, L. Huang, J. Yuan, D. Li and K. Li, Energy, 2024, 133148 CrossRef CAS
.
- X. Lin, X. Meng, H. Song and Y. Liu, Energy, 2024, 131945 CrossRef CAS
.
- Y. Lin, H. Wang, S. Fang, Z. Huang, G. Wei, Y. Zhang, H. Xia, Z. Zhao and H. Huang, Energy, 2022, 256, 124602 CrossRef CAS
.
- Y. Kang, Y. Han, M. Tian, C. Huang, C. Wang, J. Lin, B. Hou, Y. Su, L. Li and J. Wang, Appl. Catal., B, 2020, 278, 119305 CrossRef CAS
.
- Z. Ma, G. Liu, Y. Lu, J. Wang and H. Zhang, Fuel Process. Technol., 2021, 224, 107030 CrossRef CAS
.
- G. Liu and G. Lisak, Fuel, 2023, 342, 127828 CrossRef CAS
.
- A. Cabello, A. Abad, T. Mendiara, M. Izquierdo and L. de Diego, Chem. Eng. J., 2023, 455, 140484 CrossRef CAS
.
- Q. Zhang, B. Jiang, L. Li, K. Liu, N. He, J. Ma, X. Zhang and D. Tang, Fuel Process. Technol., 2021, 221, 106953 CrossRef CAS
.
- Y. Feng, X. Cai, X. Guo and C. Zheng, Chem. Eng. J., 2016, 295, 461–467 CrossRef CAS
.
- Y. Zhao, B. Jin, L. Zhang, W. Ji and Z. Liang, Chem. Eng. J., 2023, 454, 140226 CrossRef CAS
.
- D. Zeng, Y. Qiu, M. Li, D. Cui, L. Ma, Y. Lv, S. Zhang and R. Xiao, ACS Appl. Mater. Interfaces, 2019, 11, 44223–44232 CrossRef CAS PubMed
.
- D. Cui, M. Li, Y. Qiu, L. Ma, D. Zeng and R. Xiao, Chem. Eng. J., 2020, 400, 125769 CrossRef CAS
.
- Z. Ye, J. Li, W. Wang, F. Qin, K. Li, H. Tan and C. Zhang, J. Cleaner Prod., 2024, 449, 141410 CrossRef
.
- X. Zhu, M. Khosravi, B. Vaferi, M. N. Amar, M. A. Ghriga and A. H. Mohammed, J. Cleaner Prod., 2022, 363, 132465 CrossRef CAS
.
- H. Tiryaki, A. Yusuf and S. Ballikaya, Energy, 2024, 292, 130597 CrossRef CAS
.
- Y. Zhou, S. Zheng and G. Zhang, Energy, 2020, 192, 116608 CrossRef
.
- N. R. Singstock, C. J. Bartel, A. M. Holder and C. B. Musgrave, Adv. Energy Mater., 2020, 10, 2000685 CrossRef CAS
.
- J. Brorsson, V. Rehnberg, A. A. Arvidsson, H. Leion, T. Mattisson and A. Hellman, J. Phys. Chem. C, 2023, 127, 9437–9451 CrossRef CAS
.
- Y. De Vos, M. Jacobs, P. Van Der Voort, I. Van Driessche, F. Snijkers and A. Verberckmoes, Catalysts, 2020, 10, 926 CrossRef CAS
.
- Z. Cheng, L. Qin, J. A. Fan and L.-S. Fan, Engineering, 2018, 4, 343–351 CrossRef CAS
.
- L. Zeng, Z. Cheng, J. A. Fan, L.-S. Fan and J. Gong, Nat. Rev. Chem, 2018, 2, 349–364 CrossRef CAS
.
- X. Wang, Y. Gao, E. Krzystowczyk, S. Iftikhar, J. Dou, R. Cai, H. Wang, C. Ruan, S. Ye and F. Li, Energy Environ. Sci., 2022, 15, 1512–1528 RSC
.
- Z. Wen, N. Duan, R. Zhang, H. Li, Y. Wu, Z. Sun and Z. Sun, J. Cleaner Prod., 2024, 449, 141779 CrossRef CAS
.
- G. Hautier, S. P. Ong, A. Jain, C. J. Moore and G. Ceder, Phys. Rev. B, 2012, 85, 155208 CrossRef
.
- H. K. Singh, Z. Zhang, I. Opahle, D. Ohmer, Y. Yao and H. Zhang, Chem. Mater., 2018, 30, 6983–6991 CrossRef CAS
.
- Y. Mao, H. Yang, Y. Sheng, J. Wang, R. Ouyang, C. Ye, J. Yang and W. Zhang, ACS Omega, 2021, 6, 14533–14541 CrossRef CAS PubMed
.
- C. J. Bartel, S. L. Millican, A. M. Deml, J. R. Rumptz, W. Tumas, A. W. Weimer, S. Lany, V. Stevanović, C. B. Musgrave and A. M. Holder, Nat. Commun., 2018, 9, 4168 CrossRef PubMed
.
- J. Fan, W. Li, S. Li and J. Yang, Adv. Sci., 2022, 9, 2202811 CrossRef CAS PubMed
.
- Y. Feng, N. Wang, X. Guo and S. Zhang, Fuel, 2020, 276, 117942 CrossRef CAS
.
- F. Liu, J. Liu, Y. Li, R. Fang and Y. Yang, Energy, 2022, 239, 122100 CrossRef CAS
.
- A. V. Iskrina, A. V. Bobrov, A. V. Spivak, A. V. Kuzmin, S. Chariton, T. Fedotenko and L. S. Dubrovinsky, J. Phys. Chem. Solids, 2022, 171, 111031 CrossRef CAS
.
- T. Hidayat, D. Shishin, S. A. Decterov and E. Jak, Metall. Mater. Trans. B, 2016, 47, 256–281 CrossRef CAS
.
- V. Šepelák, L. Wilde, U. Steinike and K. Becker, Mater. Sci. Eng. A, 2004, 375, 865–868 CrossRef
.
- A. V. Kovalevsky, E. N. Naumovich, A. A. Yaremchenko, J. R. Frade and J. Eur, Ceram, 2012, 32, 3255–3263 CAS
.
- P. Hirunsit and K. Faungnawakij, J. Phys. Chem. C, 2013, 117, 23757–23765 CrossRef CAS
.
- Y. Li, L. Wang, D. Chen, J. Liu, W. Fan and J. Sun, Chem. Eng. J., 2024, 495, 153591 CrossRef CAS
.
- Y. Li, J. Liu, F. Liu and Y. Yang, J. Energy Inst., 2022, 105, 25–32 CrossRef CAS
.
- D. Cui, Y. Qiu, M. Li, L. Ma, S. Zhang, D. Zeng and R. Xiao, Int. J. Hydrogen Energy, 2020, 45, 11908–11915 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4se01575d |
| ‡ First author. |
| This journal is © The Royal Society of Chemistry 2025 |