The resolution of the weak-exchange limit made rigorous, simple and general in binuclear complexes†
Abstract
The correct interpretation of magnetic properties in the weak-exchange regime has remained a challenging task for several decades. In this regime, the effective exchange interaction between local spins is quite weak, of the same order of magnitude or smaller than the various anisotropic terms, which generates a complex set of levels characterized by spin mixing. Although the model multispin Hamiltonian in the absence of local orbital momentum, 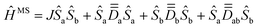 , is considered good enough to map the experimental energies at zero field and in the strong-exchange limit, theoretical works pointed out limitations of this simple model. This work revives the use of ĤMS from a new theoretical perspective, detailing point-by-point a strategy to correctly map the computational energies and wave functions onto ĤMS, thus validating it regardless of the exchange limit. We will distinguish two cases, based on experimentally characterized dicobalt(II) complexes from the literature. If centrosymmetry imposes alignment of the various rank-2 tensors constitutive of ĤMS in the first case, the absence of any symmetry element prevents such alignment in the second case. In such a context, the strategy provided herein becomes a powerful tool to rationalize the experimental magnetic data, since it is capable of fully and rigorously extracting the multispin model without any assumption on the orientation of its constitutive tensors. Furthermore, the strategy allows to question the use of the spin Hamiltonian approach by explicitly controlling the projection norms on the model space, which is showcased in the second complex where local orbital momentum could have occurred (distorted octahedra). Finally, previous theoretical data related to a known dinickel(II) complex is reinterpreted, clarifying initial wanderings regarding the weak exchange limit.
, is considered good enough to map the experimental energies at zero field and in the strong-exchange limit, theoretical works pointed out limitations of this simple model. This work revives the use of ĤMS from a new theoretical perspective, detailing point-by-point a strategy to correctly map the computational energies and wave functions onto ĤMS, thus validating it regardless of the exchange limit. We will distinguish two cases, based on experimentally characterized dicobalt(II) complexes from the literature. If centrosymmetry imposes alignment of the various rank-2 tensors constitutive of ĤMS in the first case, the absence of any symmetry element prevents such alignment in the second case. In such a context, the strategy provided herein becomes a powerful tool to rationalize the experimental magnetic data, since it is capable of fully and rigorously extracting the multispin model without any assumption on the orientation of its constitutive tensors. Furthermore, the strategy allows to question the use of the spin Hamiltonian approach by explicitly controlling the projection norms on the model space, which is showcased in the second complex where local orbital momentum could have occurred (distorted octahedra). Finally, previous theoretical data related to a known dinickel(II) complex is reinterpreted, clarifying initial wanderings regarding the weak exchange limit.



 Please wait while we load your content...
Please wait while we load your content...