Defects in the new oxide-fluoride Ba2PdO2F2: the search for fluoride needles in an oxide haystack
Tom
Baikie
a,
M. Saiful
Islam
*b and
M. Grazia
Francesconi
a
aDepartment of Chemistry, The University of Hull, Cottingham Rd, Hull, UK, HU6 7RX
bMaterials Chemistry Group, Chemistry Division, SBMS, University of Surrey, Guildford, UK, GU2 7XH. E-mail: M.Islam@surrey.ac.uk
First published on 29th November 2004
Abstract
The defect chemistry and fluorine insertion properties of the new Ba2−xSrxPdO2F2 system have been investigated using atomistic simulation techniques. The interatomic potential model produces good agreement between simulated and observed structures for the “parent” oxides Ba2PdO3 and Sr2PdO3, and the oxide-fluorides Ba2PdO2F2 and BaSrPdO2F2. The perfect lattice simulations confirm the most favourable structure type is the T′ (Nd2CuO4) structure for the oxide-fluoride phases comprised of square planar Pd, which accords with recent EXAFS studies. The fluorination reaction in the precursor oxide Ba2PdO3, involving substitution of two fluorine ions for one oxygen ion, is highly favourable. The formation of fluorine interstitials and holes in Ba2PdO2F2 is an unfavourable process in accord with the observed resistance to excess fluorine, and in contrast to the related cuprate superconductor Sr2CuO2F2+δ.
1. Introduction
Fluorination reactions at low temperature have become useful chemical routes in the search for novel materials with interesting properties. The first palladium oxide-fluorides have recently been synthesised by low temperature fluorination of the alkaline-earth palladates, Ba2−xSrxPdO3.1 Powder X-ray diffraction, EXAFS and magnetic measurements suggest that the fluorinated materials have the general formula Ba2−xSrxPdO2F2 (0 ≤ x ≤ 1.5) and that they adopt the T′-type (Nd2CuO4) structure shown in Fig. 1; in the T′ structure, palladium occupies a perovskite-like layer and is coordinated by four oxygens in a square-planar fashion.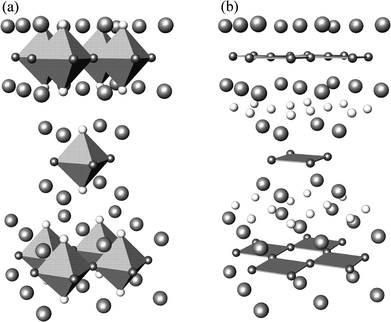 | ||
| Fig. 1 Crystal structure types of Ba2PdO2F2: (a) T-type, (b) T′-type. The polyhedra indicate the octahedral and square planar coordination of Pd in T and T′ respectively; small grey spheres (O); white spheres (F); large grey spheres (Ba). | ||
This work follows the important discovery of high temperature superconductivity in the copper oxide-fluoride Sr2CuO2F2+δ,2 which has stimulated considerable interest in the materials chemistry of ternary oxide-fluorides.3,4 The Sr2CuO2F2+δ phase displays the related T-type structure (La2CuO4) in which the Cu is octahedrally coordinated by four oxygen ions and two fluoride ions at equatorial and apical sites respectively (Fig. 1). Low temperature fluorination is thought to induce an interesting structural rearrangement in the “precursor” oxide Sr2CuO3, where one oxygen ion is substituted by two fluoride ions.2 The parent Pd-based oxides A2PdO3 (A = Ba, Sr) are isostructural with the cuprates A2CuO3 (A = Ca, Sr).
It is now well established that defect-related and fluorine insertion processes play a crucial role in determining the properties of these compounds. A key difference between palladium and copper oxide-fluorides is believed to be related to the fluoride stoichiometry in which Sr2CuO2F2+δ contains excess fluorine (δ) at interstitial defect sites, whereas Ba2PdO2F2 does not show such behaviour. However, it is acknowledged that it can be difficult to determine the precise F− positions in these structures since neither X-ray nor neutron diffraction techniques reliably distinguish between fluoride and oxide ions, thus motivating the title of this paper.
Atomic-scale studies in this area are amenable to advanced simulation techniques, which have been used in the present study to investigate the structural, defect and fluorine insertion properties of the precursor oxides and the novel fluorinated products, focusing on Ba2PdO3 and Ba2PdO2F2. The computational techniques are now well-tested methods for exploring solid-state properties at the microscopic level, and have been successfully applied to a range of inorganic materials5–8 including cuprate and oxyhalide superconductors.5,6 To the best of our knowledge, these are the first atomistic simulations of ternary palladium oxides and oxide-fluorides.
2. Simulation methods
Only a brief account of these widely used techniques (embodied within the GULP code9) will be described, as comprehensive reviews are given elsewhere.10 The basis of the lattice simulations is the specification of a potential model, which describes the potential energy of a system as a function of atomic coordinates and allows the modelling of perfect and defective lattices. The Born model representation is commonly used for polar solids, with the energy partitioned into long-range Coulombic and short-range pair potentials. An analytical function of the Buckingham form is used to describe the effective interatomic potentials: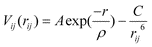 | (1) |
As charged defects will polarise other ions in the lattice, polarisability of the ions must be incorporated into the potential model. The “shell model” describes such effects by treating each ion in terms of a core (representing the nucleus and core electrons) connected via a harmonic spring to a shell (representing the valence electrons). Despite the simple mechanical representation of the ionic dipole, the shell model has been shown to effectively simulate both the dielectric and elastic properties of solid materials, by including the coupling between the short-range repulsive forces and ionic polarisation. It should be stressed, as argued previously,10 that employing such a potential model does not necessarily mean that the electron distribution corresponds to a fully ionic system, and that the general validity of the model is assessed primarily by its ability to reproduce observed crystal properties. In practice, it is found that potential models based on formal charges work well even for some semi-covalent compounds such as silicates and zeolites.10
An important feature of these calculations is the treatment of the extensive lattice relaxation about a point defect (e.g. vacancy or interstitial fluoride ion). The Mott–Littleton approach9,10 is to partition the crystal lattice into two spherical regions. Ions in the central inner region surrounding the defect (typically containing more than 300 ions) are relaxed explicitly. In contrast, the remainder of the crystal, where the defect forces are relatively weak, is treated by more approximate quasi-continuum methods.
It is recognised that there are limitations to such lattice simulation methods where the use of explicit electronic structure techniques may be more appropriate. However, such a large number of ions are not readily treated by quantum mechanical techniques, whereas previous studies on oxide and oxyhalide superconductors5,6 demonstrate the value (and versatility) of simulation methods in probing the nature of defect-related processes in complex materials.
3. Results and discussion
3.1 Crystal structures
The short-range potential parameters were transferred from previous work on cuprate oxide-fluoride superconductors,6 and fluorohalide luminescence compounds,8 and then adjusted slightly by simultaneous refinement to the complex crystal structures1,11 of four different phases Ba2PdO2F2, BaSrPdO2F2, Ba2PdO3 and Sr2PdO3. This provides considerable data within their structures and results in a common set of potentials across the composition range (listed in Table 1). We stress that reproduction of all four observed structures simultaneously is not a trivial exercise. This approach enables some information concerning the curvature of the energy surface to be included, and has the added advantage of improved transferability of the potential parameters. Additional experimental dielectric and elastic data are currently unavailable (in common with most novel ceramics), which would be useful for further validation or refinement of the potential models.| (a) Short range | |||
|---|---|---|---|
| Interaction | A/eV | ρ/Å | C/eV Å6 |
| Ba2+⋯O2− | 2096.8 | 0.3522 | 8.0 |
| Ba2+⋯F− | 4588.5 | 0.2725 | 0.0 |
| Pd2+⋯F− | 838.4 | 0.4600 | 0.0 |
| Pd2+⋯O2− | 1158.0 | 0.2927 | 0.1 |
| O2−⋯O2− | 22764.7 | 0.1490 | 43.0 |
| O2−⋯F− | 198.3 | 0.1110 | 73.8 |
| F−⋯F− | 507.5 | 0.4035 | 0.0 |
| Sr2+⋯O2− | 4630.4 | 0.2967 | 0.0 |
| Sr2+⋯F− | 757.2 | 0.2887 | 0.0 |
Energy minimisation of the perfect lattices was first performed to generate the equilibrium structures with the calculated and experimental lattice parameters (a, b, c), and selected bond lengths listed in Table 2. Examination of the data shows good agreement between simulated and observed structures; all the bond lengths are reproduced to within 0.06 Å for all four complex materials Ba2PdO2F2, BaSrPdO2F2, Ba2PdO3 and Sr2PdO3, providing additional support for the validity of our potential model.
| a) Unit cell parameters | |||
|---|---|---|---|
| Phase | Lattice parameter | Experimental/Å | Calculated/Å |
| Ba2PdO3 | a | 4.080 | 4.062 |
| b | 3.836 | 3.847 | |
| c | 13.335 | 13.311 | |
| Sr2PdO3 | a | 3.977 | 3.840 |
| b | 3.530 | 3.528 | |
| c | 12.820 | 12.871 | |
| Ba2PdO2F2 | a | 4.140 | 4.167 |
| c | 14.046 | 14.039 | |
| BaSrPdO2F2 | a | 4.091 | 4.074 |
| c | 13.409 | 13.413 | |
| b) Bond lengths | |||
|---|---|---|---|
| Phase | Bond | Experimental/Å | Calculated/Å |
| Ba2PdO3 | Ba–O | 2.708 | 2.769 |
| 2.802 | 2.799 | ||
| 2.724 | 2.779 | ||
| Pd–O | 2.025 | 1.995 | |
| 2.040 | 2.031 | ||
| Sr2PdO3 | Sr–O | 2.565 | 2.597 |
| 2.591 | 2.608 | ||
| 2.660 | 2.626 | ||
| Pd–O | 1.947 | 1.894 | |
| 1.989 | 1.920 | ||
| Ba2PdO2F2 | Ba–O | 2.806 | 2.836 |
| Ba–F | 2.627 | 2.618 | |
| Pd–O | 2.070 | 2.083 | |
| Pd–F | 4.076 | 4.082 | |
| BaSrPdO2F2 | (Ba,Sr)–O | 2.743 | 2.741 |
| (Ba,Sr)–F | 2.551 | 2.541 | |
| Pd–O | 2.046 | 2.039 | |
| Pd–F | 3.927 | 3.923 | |
XRD studies show that the Ba2PdO2F2 system adopts the T′-type (Nd2CuO4) structure in which Pd is coordinated by four oxygens in a square planar fashion, while Ba occupies a fluorite-like layer and coordinated by four oxygens and four fluorines in a distorted cubic arrangement (Fig. 1). The related T-type (La2CuO4) structure contains octahedral Cu with four oxygens and two fluorines at equatorial and apical sites respectively.
As noted, there are difficulties in determining the precise O2− and F− lattice positions using purely diffraction techniques based on their scattering power. In this context, our lattice simulation methods can be useful in comparing the energetics of different oxyfluoride structure types of the same stoichiometry. The calculated lattice energies for the specified T (La2CuO4) and T′ (Nd2CuO4) structure types of both Ba2PdO2F2 and BaSrPdO2F2 have been calculated and are listed in Table 3.
The comparison of the calculated lattice energies for the two alternative structures confirms that the T′structure is the most energetically favourable structure type for both Ba2PdO2F2 and BaSrPdO2F2. The expected fluorine positions are therefore confirmed by the modelling results, in which the substituting fluorines do not occupy an apical site of a Pd–O polyhedron but are located in the Ba fluorite-like layers, leaving Pd in a square planar coordination. This result is consistent with the structure type proposed from XRD and Pd K-edge EXAFS measurements.1 Further work on these materials will encompass studies on possible O/F (dis)ordering effects.
3.2 Intrinsic atomic defects
The basic defect properties of these new palladium-based compounds are not clearly characterised at the atomic level. Calculations were first performed on the energies of isolated point defects (vacancies and interstitials) focusing on the Ba2PdO3 and Ba2PdO2F2 (T′) materials. The isolated defect energies were then combined to give the energies of formation of Frenkel and Schottky type defects (Table 4) based on the following equations for Ba2PdO2F2, as an example. Kroger–Vink notation is used where, for instance, VO˙˙ is an oxygen vacancy and Fi′ is an interstitial fluoride ion.| Defect type | Ba2PdO3/eV defect−1 | Ba2PdO2F2/eV defect−1 |
|---|---|---|
| Full Schottky | 10.85 | 6.99 |
| BaO partial Schottky | 3.59 | 4.90 |
| PdO partial Schottky | 6.00 | 2.30 |
| BaF2 partial Schottky | — | 1.47 |
| F Frenkel | — | 2.10 |
Full Schottky:
| 2BaBax + PdPdx + 2OOx + 2FFx = 2VBa″ + VPd″ + 2VO˙˙ + 2VF˙ + Ba2PdO2F2 (surf) | (2) |
BaO partial Schottky-type:
| BaBax + OOx = VBa″ + VO˙˙ + BaO (surf) | (3) |
BaF2 partial Schottky-type:
| BaBax + 2FFx = VBa″ + 2VF˙ + BaF2 (surf) | (4) |
PdO partial Schottky-type:
| PdPdx + OOx = VPd″ + VO˙˙ + PdO (surf) | (5) |
Fluorine Frenkel:
| FFx = VF˙ + Fi′ | (6) |
Examination of Table 4 reveals that the calculated energies for the full Schottky, the BaO and PdO partial Schottky and the F Frenkel, suggest that intrinsic atomic defects of these reaction types are not expected at high levels within the oxide-fluoride. However, the relatively low energy for the BaF2 partial Schottky disorder suggests that non-stoichiometry related to BaF2 loss may be possible for the Ba2PdO2F2 system. It is interesting to note that recent experimental evidence indicates that the oxide-fluoride is metastable, decomposing slowly in air, with the increased formation of BaF2 over time.1 In addition, it is noted that BaF2 is often formed during the synthesis of Ba2PdO2F2, sometimes in an amorphous form, which is not detected satisfactorily using X-ray powder diffraction. This topic warrants further experimental investigation.
3.3 Fluorine incorporation
For the Sr2CuO2F2+δ superconductor, the substitution of two fluorine ions for one oxygen ion is believed to be the primary mechanism in the low temperature fluorination of the precursor oxide, Sr2CuO3.2 However, there is limited atomic-scale information on this process in the Pd-based system. We have therefore considered the energetics of the following fluorination reaction in Ba2PdO3 involving the incorporation of two fluoride ions for each oxygen ion lost:| F2 + OOx = VO˙˙ + 2Fi′ + ½ O2 | (7) |
To investigate the preferred fluorine site in Ba2PdO3, defect calculations were performed on the isolated fluorine interstitial. Following an extensive search of the potential energy surface, the lowest-energy interstitial position is found at the (¼ ¼ ¼) position in the orthorhombic structure (s.g. Immm). This is in good agreement with the fluorine site postulated by experimental structural studies.1
It is now well established that the crucial “hole-doping” mechanism for high Tc superconductivity in Sr2CuO2F2+δ is via excess fluorine (δ) accommodated at interstitial sites.2,6 It is not clear, however, whether this process occurs in the Pd-based material. We have therefore also considered the energetics for fluorine insertion (as interstitial defects) in Ba2PdO2F2 involving the creation of oxygen or palladium holes (h˙) as localised species represented by the following reaction:
| ½ F2 = Fi′ + h˙ | (8) |
The calculated energies for reactions 7 and 8 are listed in Table 5 and were derived using energies for relevant defect (hole) and intra-atomic terms (for O2− to ½ O2, and for ½ F2 to F−). Our approach to these reactions follows that first used for transition metal oxides and subsequently the cuprate superconductors.5,6 There may be uncertainties in the free-ion terms, but our main concern here is to probe the relative energetics of these processes; for this task our simulation procedures have proved to be reliable. The merit of our defect modelling approach is that it includes detailed estimates of lattice polarization and Coulomb energies, which are difficult to make from other sources.
| Compound/Process | E/eV per Fi′a |
|---|---|
| a Atomic energy terms in eV: Pd hole (4.15); O2− → ½ O2 (−9.86); ½ F2 → F− (−2.58). b From D'Arco and Islam.6 | |
| Ba2PdO3/Reaction (7) | −0.46 |
| Ba2PdO2F2/Reaction (8) | 3.33 |
| Sr2CuO2F2/Reaction (8)b | −0.36 |
Two main points emerge from the results presented in Table 5. First, the exothermic value for the fluorination of Ba2PdO3viareaction (7) indicates that the predicted mechanism is a highly favourable process. Our results therefore provide support that this reaction, involving substitution of one oxygen by two fluorine atoms, is the primary mechanism in the low temperature fluorination of the precursor oxide. Studies have already found that the synthesis of ternary oxide-fluorides is difficult by conventional solid-state reactions at high temperature, and that “soft-chemistry” pathways are required.2,3 Indeed, low temperature fluorination reactions have generally become useful chemical routes to novel materials, and are comparable with the more commonly used method of cation doping.
Second, the higher positive energy for reaction (8) in Ba2PdO2F2 suggests that excess fluorine to form Pd3+ holes is relatively unfavourable in this system. Indeed, recent XANES and EXAFS spectroscopy studies indicate that there is no change in local coordination or oxidation state (to Pd3+ or Pd4+) upon fluorination.1 For direct comparison, it is worth noting that our previous calculated value for the same reaction (8) in Sr2CuO2F2 is highly favourable (−0.36 eV),6 and found to be consistent with the available measured oxidation enthalpies of other cuprate materials. This result for the cuprate also agrees with observation as it is known that this reaction is responsible for the hole-doping in Sr2CuO2F2 necessary for superconductivity.2 Moreover, these results also assist in rationalising the observed difference between palladium and copper oxide-fluorides in that the fluoride stoichiometry of Sr2CuO2F2+δ has been reported to contain excess fluorine,2 whereas Ba2PdO2F2 does not show such behaviour.
4. Conclusion
Our simulation study has allowed us to gain significant insight as to the defect and fluorine insertion properties of the new Ba2PdO2F2 oxide-fluoride system on the atomic scale. The significance of the present study is that it provides some rationalisation, based upon quantitative simulations rather than qualitative proposals, as to the properties of the palladium oxide-fluoride, which show interesting comparisons with the analogous cuprate superconductor.Our discussion has highlighted three key points. First, the lattice simulations confirm that the most favourable structure type is the T′ (Nd2CuO4) structure for both Ba2PdO2F2 and BaSrPdO2F2, comprised of square planar Pd2+ and fluoride ions in the Ba(Sr) fluorite-like layer. This accords with recent studies using X-ray absorption (EXAFS) techniques. The lowest defect energy in Ba2PdO2F2 is calculated for the Ba/F vacancy disorder, which suggests possible non-stoichiometry related to BaF2 loss. Second, our calculated exothermic energy for the reaction involving the incorporation of two fluoride ions for each oxygen ion lost in the precursor oxide Ba2PdO3 provides support that this is the primary mechanism in the fluorination process. Finally, the formation of fluorine interstitials and holes in Ba2PdO2F2 is an energetically unfavourable process in accord with the observed resistance to excess fluorine, and in contrast to the related cuprate superconductor Sr2CuO2F2+δ.
Acknowledgements
We are grateful to the EPSRC and the Daresbury CCP5 group for financial support, to Dr J. Tolchard, Dr R. A. Davies and Dr P. R. Slater for helpful discussions, and to the Computational Chemistry Working Party for RAL computing facilities.References
- T. Baikie, E. L. Dixon, J. F. Rooms, N. A. Young and M. G. Francesconi, Chem. Commun., 2003, 1580 RSC.
- M. Al-Mamouri, P. P. Edwards, C. Greaves and M. Slaski, Nature, 1994, 369, 382 CrossRef CAS; M. G. Francesconi, P. R. Slater, J. P. Hodges, C. Greaves, P. P. Edwards, M. Al-Mamouri and M. Slaski, J. Solid State Chem., 1998, 135, 17 CrossRef CAS.
- R. L. Needs, M. T. Weller, U. Scheler and R. K. Harris, J. Mater. Chem., 1996, 6, 1219 RSC; P. R. Slater and R. K. B. Gover, J. Mater. Chem., 2002, 12, 291 RSC; L. D. Aikens, L. J. Gillie, R. K. Li and C. Greaves, J. Mater. Chem., 2002, 12, 264 RSC.
- A. K. Prodjosantoso, B. J. Kennedy, T. Vogt and P. M. Woodward, J. Solid State Chem., 2003, 172, 89 CrossRef CAS; H. Oesterreicher, Solid State Commun., 2003, 127, 563 CrossRef CAS; F. J. Brink, L. Noren and R. L. Withers, J. Solid State Chem., 2004, 177, 2177 CrossRef CAS; T. Hanaguri, C. Lupien, Y. Kohsaka, D. H. Lee, M. Azuma, M. Tanako, H. Takagi and J. C. Davis, Nature, 2004, 430, 1001 CrossRef CAS.
- M. S. Islam, M. S. D. Read and S. D'Arco, Faraday Discuss., 1997, 106, 367 RSC; N. L. Allan, P. S. Baram, A. Gormezano and W. C. Mackrodt, J. Mater. Chem., 1994, 4, 817 RSC; J. P. Hill, N. L. Allan and W. C. Mackrodt, Chem. Commun., 1996, 2703 RSC.
- S. D'Arco and M. S. Islam, Phys. Rev. B, 1997, 55, 3141 CrossRef CAS; M. S. Islam and S. D'Arco, Chem. Commun., 1996, 2291 RSC.
- M. S. D. Read, M. S. Islam, G. W. Watson and F. E. Hancock, J. Mater. Chem., 2001, 11, 2597 RSC; M. S. Islam, J. R. Tolchard and P. R. Slater, Chem. Commun., 2003, 1486 RSC; M. S. Islam and R. A. Davies, J. Mater. Chem., 2004, 14, 86 RSC.
- M. S. Islam and R. C. Baetzold, J. Phys. Chem. Solids, 1992, 53(8), 1105 CrossRef CAS.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629 RSC.
- Computer Modelling in Inorganic Crystallography, ed. C. R. A. Catlow, Academic Press, San Diego, 1997 Search PubMed.
- Y. Laligant, A. LeBail, G. Ferey, M. Hervieu, B. Raveau, A. Wilkinson and A. K. Cheetham, Eur. J. Solid State Inorg. Chem., 1998, 25, 237; H. D. Von Wasel-Nielsen and R. Hoppe, Z. Anorg. Allg. Chem., 1970, 375, 209 CrossRef.
| This journal is © The Royal Society of Chemistry 2005 |
