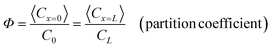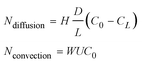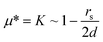Molecular sieving using nanofilters: Past, present and future

Abstract

Filtration of molecules by nanometer-sized structures is ubiquitous in our everyday life, but our understanding of such molecular filtration processes is far less than desired. Until recently, one of the main reasons was the lack of experimental methods that can help provide detailed, microscopic pictures of molecule–nanostructure interactions. Several innovations in experimental methods, such as nuclear track-etched membranes developed in the 70s, and more recent development of nanofluidic molecular filters, played pivotal roles in advancing our understanding. With the ability to make truly molecular-scale filters and pores with well-defined sizes, shapes, and surface properties, now we are well positioned to engineer better functionality in molecular sieving, separation and other membrane applications. Reviewing past theoretical developments (often scattered across different fields) and connecting them to the most recent advances in the field would be essential to get a full, unified view on this important engineering question.

---

Jongyoon Han

Jongyoon Han is currently an associate professor in the Department of Electrical Engineering and Computer Science and the Department of Biological Engineering, MIT. He received his BSc (1992) and MSc (1994) in physics from the Seoul National University, Seoul, Korea, and his PhD in applied physics from Cornell University in 2001. He was a research scientist in Sandia National Laboratories (Livermore, CA, Biosystems Research Department), until he joined the MIT faculty in 2002. He was awarded the NSF CAREER award (2003) and the Van Tassel Career Development Professorship (2004). His research is mainly focused on applying micro/nanofabrication techniques to biological problems, more specifically proteomic sample preparation. Jianping Fu is currently a postdoctoral fellow in the Research Laboratory of Electronics at the MIT. He received his BSc in mechanical engineering from the University of Science and Technology of China in 2000, and his PhD in mechanical engineering from MIT in 2007. Dr Fu’s doctoral thesis centered on developing various nanofluidic devices for rapid separation of physiologically-relevant macromolecules such as DNA and proteins. For his doctoral research, Dr Fu was awarded both the Halen Carr Peake Research Prize for Bioengineering Research of Extraordinary Quality and the Senturia Prize for Best Thesis in MEMS/NEMS. Reto B. Schoch obtained his degree in mechanical engineering from ETH Zurich, Switzerland, in 2003, majoring in micro- and nanotechnology and biomedical technology. In 2006 he received his PhD from EPF Lausanne, Switzerland, for his work on transport in nanofluidic channels. He worked as a Postdoctoral Associate at MIT until 2007, and is now a Senior Postdoctoral Associate at ETH Zurich. His current research interests are micro- and nanofluidics for systems nanobiology and biomedical applications on a chip.

---

1. Introduction: Molecular filtration

Molecular filtration and sieving is an important engineering problem, with very diverse applications ranging from chemical processing to bio-analytic separation, and to industrial desalination/water purification. However, our scientific understanding of molecular filtration processes is not as complete as the ubiquity of the phenomena seems to suggest. The simple, intuitive concept about filtration is well known to and understood by most people: When the pore is larger than the particles (molecules) to be filtered, there will be no filtration and all the particles will go through without retention. When the pore is smaller than the molecules, none of the molecules will pass. However, the detailed physical phenomena that happen at the filter–molecule interface are much more complicated, and therefore demand careful scientific study. To put it bluntly, the common notion of mechanical filtration is partially correct at best in most molecular filtration processes that involve small (bio-)molecules and particles at the nanometer size scale.

The chemical engineering community had pioneered the study of physical filtration back to the early 1900s, leading to the rather complete establishment of the hindered transport theory in the 1970s.¹ The key to such development was an innovative experimental technique, nuclear track-etched membranes, which allowed, for the first time, a well-controlled experiment to study the filtration phenomena. This was a significant development in terms of the science of molecular filtration (or, broadly defined, the problem of molecule–nanostructure interaction), and the theory of hindered transport of molecules in nanopores has been rather fully developed. Many aspects of the nanopore–molecule interaction, including hydrodynamic interaction, size-dependent partitioning, and even electrostatic partitioning due to the Debye-layer on the wall (and the net charges of molecules), have been well-characterized both theoretically and experimentally.

These old theories and experiments were revisited and rediscovered, when a new, innovative line of research emerged. Beginning in the early 1990s, the idea of using microfabricated regular structures for separating and sieving biomolecules came about.² Because molecules are usually considered small, and microfabricated structures are usually considered large, connecting the two (seemingly distant) dots was certainly an innovation. With the advances in nanofabrication, one can now build numerous kinds of artificial molecular filters, with characteristic dimensions comparable to biomolecules. In addition, these micro/nanofabricated molecular filters can be engineered and optimized, with the precision and flexibility that are not possible with polymer-based random nanoporous materials such as gels, or even track-etched nanopore membranes. The big question was: Would these highly engineered, regular molecular filter systems be any better than conventional gels and polymer-based membranes? (After all, conventional gels and membranes are inexpensive, provide ultra small, truly nanometer-scale pores with relatively high throughput.) In the following 15 years since the publication of the seminal paper by Volkmuth and Austin,² many regular, artificial molecular sieves and filters have been fabricated and tested for various applications, confirming that better controlling of the geometry of the sieves and filters by the micro/nanofabrication techniques can provide superior functionality and performance, if and only if the right application and right design principles have been chosen.

The new scientific and engineering fronts opened up by artificial molecular filters can be summarized as the following. First, the advances of fabrication techniques, including both conventional MEMS and other non-conventional techniques, allow one to have better control over nanopore system geometry and further to arrange numerous nanopores and nanofilters in an optimized manner to gain unique functionalities. Second, MEMS fabrication allows seamless integration of molecular sieving systems with other microfluidic channels, which is non-trivial for conventional, sheet-style gels and membranes. This will be important for future lab-on-a-chip applications. Lastly, these advances in nanoscale molecular sieving systems (integrated and implemented in a microfluidics format) will allow more detailed scientific study of membrane phenomena, and will enhance our understanding of nanoscale molecular sieving, sometimes beyond the hindered transport theory. Especially, recent theoretical and experimental studies have suggested that the phenomena at the bulk–membrane (or microchannel–nanochannel) interfaces,^3,4 as well as non-equilibrium filtration phenomena,^5,6 are important in determining the overall membrane performance, which have never been properly studied or characterized previously. Microfluidic channels that contain micro–nano junctions will allow direct access to the molecular transport phenomena in situ, as well as a good dimensional and convection control to simplify the problem for a detailed scientific study.

This review is our attempt to collect the relevant literature and work (both past and present) and arrange them in such a way that researchers can quickly identify the context of all the recent and future progress in the area of molecular sieving. As a result, this review is not fully exhaustive. We will begin by reviewing relevant theoretical developments in the hindered transport theory. Then, we will proceed to summarize the more recent (1990 and after) developments of artificial molecular sieving systems, both from a scientific and engineering point of view.

2. Molecular filtration using nanopore membranes

The theoretical study of molecular selectivity in nanopores or other porous systems dates back to the early 1900s. Ferry (1936)⁷ derived the hindrance factor (partition coefficient Φ) at the nanopore entrance, and Pappenheimer et al. (1951)⁸ and Renkin (1954)⁹ derived the other factor representing hydrodynamic hindrance. A must-read on the hindered transport process is Deen's 1987 review paper,¹ which listed all the relevant experimental and theoretical references in the field up to that time. Also, Deen's article discussed the effects of several interesting aspects such as osmosis and conformational dynamics of flexible polymers on the hindered transport. We believe this excellent review paper will still provide insights in further developing artificial sieving systems.

Hindered transport theory

The physical phenomena we are concerned about here are depicted in Fig. 1. Molecular sieving by filters (either artificial or natural, regular or random) can be abstracted by the interaction between molecules and a pore (or pores), while the molecules are driven into the pores. The molecules of interest could be larger than the size of the pores, which means the molecules have to change their shape or conformation to enter the pore. However, most often, molecules to be filtered are actually smaller than the pore dimensions. Even in such cases, the molecular motion can be significantly affected (or hindered) by the existence of the pore.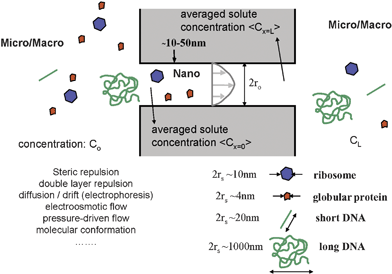

Fig. 1 Molecule–nanofilter interaction at the micro(macro)–nano–micro junction. Various factors are in play to affect the transport of biomolecules (with various shapes and sizes) through a nanopore or a nanofluidic filter. A solution for steady-state transport of this system was largely established in the hindered transport theory developed around 1970s.

There are two main reasons (which may be somewhat counterintuitive) for these sieving phenomena. First, the probability of the molecules finding the pore from the bulk solution would be affected by the sizes of both the molecule and the pore. This is due to the ‘steric hindrance’ (the larger the particle, the harder it is for the particle to fit in the porestatistically), or due to some additional long-range interactions such as electrostatic repulsions between the charged molecule and charged wall (Debye layer repulsion) when both the pore wall and the molecule are charged. One can describe this phenomenon by molecular partitioning between the micro (bulk) phase and nanopore phase, defining the partition coefficient Φ.

In the purely steric case, smaller molecules are more likely to find themselves in the pore compared with larger molecules, and their partition coefficients (between the bulk phase and the pore) would be size-dependent. The basic source of this partitioning is, essentially, the fast Brownian motion of the molecules, which is the dominant transport mechanism at small (nano) length scales. Therefore, when the size of the particle increases, this filtration mechanism would be modified because one enters a regime where random Brownian motion is becoming a less significant factor.

The second sieving effect in the nanopore is the hydrodynamic hindrance, which occurs within the nanopore, especially when molecules are transported either by pressure-driven flow or diffusion. In short, the motion of a particle within the pore is slowed down, because there are close-by static walls, generating drag forces on the particle. As a result, any particle motion within a nanopore (even Brownian motion) will be slowed down. Again, this effect will primarily be a function of both the particle and pore sizes. However, this picture should be modified significantly when one considers the molecular transport by electroosmotic flow, when the surface fluid layer on the nanopore wall is mobilized.

In the hindered transport theory, these two effects are quantified by the following two hindrance factors, as defined below. When a steady state is reached along a nanochannel or nanopore between the two reservoirs (with solute concentration of C₀ and C_L, respectively), effective solute fluxes caused by both diffusion and convection will be affected by these hindrance effects, which are quantified as the following,

where U is the average flow velocity within the pore, and L is the pore length. Two dimensionless factors (H and W) are used to describe the effective solute flux in this system, and represent the hindrance effects caused by both entrance partitioning and hydrodynamic hindrance. More specifically, H and W are represented by the function of the two factors (Φ and λ). Here Φ is the partition coefficient as defined above (at equilibrium) and λ is the ratio between the pore and solute dimension (λ = r_s/r₀).

Deen's review paper¹ summarized the derivation of these factors for both cylindrical and slit-like pores, which are also relevant to nanofluidic sieving systems. Cases involving electrostatic repulsion caused by the Debye layer were also studied by Malone and Anderson,¹⁰ and by Smith and Deen,¹¹ where both electrostatic repulsion (between the particle and the wall) and van der Waals forces were included in the calculation. These calculations were confirmed by the experiments done in track-etched nanopore membranes.

Track etched nanopores

In the early 1970s, nuclear track-etch processes,^12–14 which enabled fabrication of nanopore membranes that are straight and uniform in size, were introduced and had a significant impact on development of the hindered transport theory. The availability of such a well-controlled experimental system allowed researchers, for the first time, to verify the earlier theoretical models with a well-controlled experiment. The Renkin equation for steady state hindered diffusion of proteins through the nanopore with 10–100 nm pore diameters was directly tested by Beck and Schultz,^15,16 as early as in 1970 (Fig. 2). This seminal work should be regarded as the first controlled experiment on the molecular sieving and hindered transport, and has been the firm scientific basis for the full development of hindered transport and other nanoscale transport theory.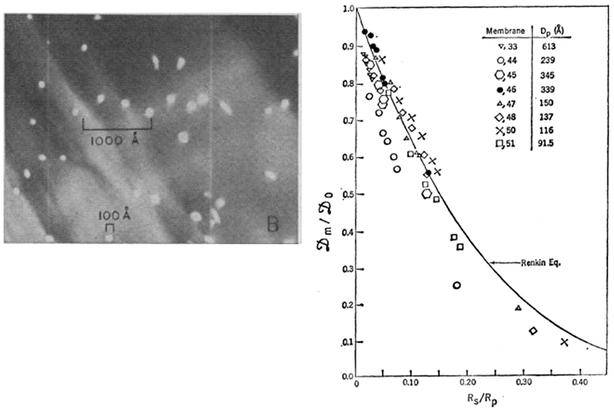

Fig. 2 Experiment by Beck and Schultz, from ref. 15, reprinted with permission from AAAS. Left: SEM of ∼12 nm pores. Right: Effective diffusivity across the nanopore membrane compared with the Renkin equation, from ref. 9.

These track-etched membranes are typically made in a polycarbonate membrane or other plastic membranes. Plastic membranes are exposed to a high-energy heavy ion beam, then followed by a wet etching process that will create (approximately) cylindrical pores along the tracks of nuclear ions through the membrane, the size of which can be controlled by the etching time and other conditions. The overall number density of the pores per unit area will be controlled by the dose of exposure. However, excessively high exposure doses will result in interconnected (overlapped) pores, compromising the pore regularity.

In a way, these track-etched nanopore systems provide (almost) the same capability as artificial nanofluidic channels/nanopores. Fluid in such systems is confined within a regular pore with known size and shape. Therefore, these systems provide valuable experimental tools to test some of the fundamental assumptions of the hindered transport theory. For example, the issue of whether the fluid properties in nanometer length scales would still follow the (macroscopic) Navier–Stokes equation can be tested in this system, using the track-etched nanopore systems. Transport experiments using track-etched nanopore systems could be fitted well to the transport model based on the standard Navier–Stokes equation, which provided an experimental evidence that the fluid behaviour can still be described by the continuum equations down to sub ∼10 nm length scale,^17–19 with nearly the same viscosity value as the bulk solution.

The first nanopore sieving studies by Beck and Schultz in 1970, which have been the basis of all theoretical developments that followed, did not get as much attention as they should have. Most polymer-based gels and other membranes, which were and still are used for filtration and other sieving applications primarily, have rather widely distributed pore sizes, which cannot be easily measured and controlled (due to their small sizes). Still, those polymer-based membranes are useful due to relatively low cost manufacturability. As long as most membrane pore sizes are widely distributed and not well-known, the utility of the ab initio molecular transport theory (with the pore size being the key parameter) might be quite limited, and optimization of filtration systems could only be done with phenomenological models.

Recent nanopore/nanofilter membranes

Nuclear track-etched membrane systems also provide inexpensive and ideal membranes, and researchers have found their use for various applications. Charles Martin's group pioneered the nanopore templating method starting from the early 1990s.^20,21 Using either a track-etched polycarbonate membrane or alumina nanopores as a template, they were able to build membranes with a good size control and known surface chemistry (metallic or polymeric) by depositing various materials directly on the pore wall. This method would enable one to decrease the pore size further, to a few nanometers. Since then, his group has been publishing several seminal papers using the technique, for size/charge selective separations, biosensing, and other applications.^22–25

One of the drawbacks of these film type nanopore membranes is the difficulty to integrate the filters with other (fluidic) systems. Shannon and coworkers recently developed a systematic approach to assemble and integrate track-etched nanopore membranes in a microfluidic format.^26,27

Another way to seamlessly integrate nanopores with microfluidic and other systems is to build the nanopores monolithically, by microfabrication techniques. Kittilsland et al.²⁸ demonstrated ∼50 nm pore systems using standard fabrication techniques. Chu and coworkers^29,30 demonstrated the fabrication of ∼15 nm pore systems using standard microfabrications, and used them for controlled drug delivery and immunoisolation.³¹ More recently, ultra-thin silicon-based nanopre membranes were demonstrated^32,33 (Fig. 3). One unique feature of this silicon-based membrane is the mechanical strength, even though the thickness of the membrane is only ∼10 nm.³³ Such an ultra-thin membrane, which has not been realized previously, could provide very high sample throughput for various applications.

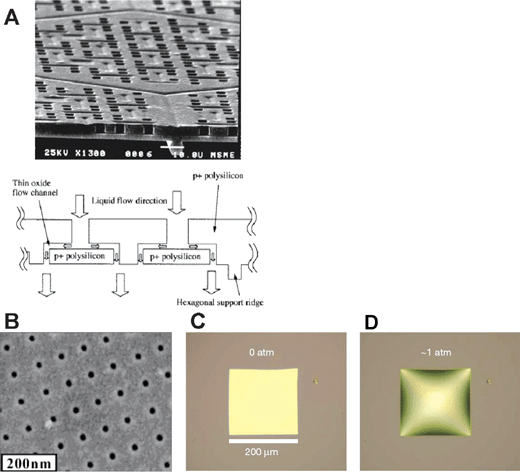Fig. 3 Various Si-nanopore membranes. A: Nanofilter membranes by Chu et al. (Ref. 30, copyright 1999, IEEE.) B: 10–25 nm diameter nanopore membranes (∼10 nm thickness) by Tong et al. (Reprinted with permission from ref. 32. Copyright (2004) American Chemical Society.) This membrane was made by FIB nanomachining technique. C: Nanopore membrane by Striemer et al. (Ref. 33, reprinted by permission from Macmillan Publishers Ltd: Nature, copyright (2007).) This membrane is only ∼10 nm thin (200 µm wide), but can withstand a pressure up to ∼1 atm pressure across the membrane (D).

3. Molecular separation in micro/nanofluidic systems: Theoretical and experimental developments

While various types of molecular filtration and sieving membranes have been developed and tested for different applications (as summarized in the previous section), the efficiency and accuracy of the molecular separation and fractionation (fundamentally an advanced dialysis system) is limited if there is only one sieving filter/step. Practically, high-resolution separations demand the integration of many (∼1000 or much more) such filtration/sieving steps into a system, and therefore when the analytes go through multiple sieving/filtration steps, they can separate from each other with high resolution.

The interaction between the molecules and the nanostructures (acting as “molecular sieves”) is much more complicated than our simple, macroscopic notion of the hard-filtration model might suggest. Such interactions can be affected by many different factors (other than the relative pore/molecule size), such as diffusion, electric and other driving forces for molecules, internal conformation of the molecules, and the surface conditions of both molecules and nanostructure surface. The hindered transport theory can indeed describe these various factors, as summarized in Deen's review. However, the hindered transport theory is limited in the sense that it only deals with steady-state situations. The partition coefficient (Φ) is essentially an equilibrium property, and the hindrance factors (H and W) were also calculated for the steady state transport through the nanopores between the two reservoir compartments. However, molecular sieving and filtering in most separation systems are essentially non-equilibrium, non-steady-state processes. Then, how can one relate a fundamentally non-equilibrium process (separation) with an equilibrium properties (hindered transport and partitioning)? While the traditional gel separation was operated under a moderate driving electric field, where the equilibrium partitioning model (Ogston model) works rather well, the importance of understanding non-equilibrium sieving process has increased as the new nanofilter-based separation systems are operated at high electric field conditions. These theoretical and experimental studies will deepen our understanding on molecular filtration and sieving, beyond the near-equilibrium theories.

At the same time, significant efforts have been directed toward developing better biomolecular separation systems (especially spurred by the interests in genomics and proteomics) during the last decade. Recently, various patterned regular micro/nanofluidic sieving structures have been developed to achieve more efficient biomolecule separation than gels and polymeric membranes in terms of separation speed and resolution. In addition to the application of biomolecule separation, these artificial sieving structures have proven ideal for the theoretical study of molecular dynamics and stochastic motion in confining spaces because of their precisely characterized structures.

Ogston sieving

The standard model for interpreting mobility µ in the Ogston sieving regime is the so-called extended Ogston model or Ogston–Morris–Rodbard–Chrambach model (OMRC model),^34–36 which is essentially a quasi-equilibrium model. In this model, it is argued that the field-driven sieving phenomena (gel electrophoresis, for example) can be described as a (equilibrium-like) partitioning process (between the gel pore and the open space). More specifically, the electrophoretic mobility of a molecule through porous gel systems was argued to be equal to the partition coefficient (Φ). In gel electrophoresis, sieving would occur mainly by the steric repulsion, and therefore the partition coefficient would be simply represented by the volume fraction (f) of the gel that is available to the molecule (free volume). If the molecule is larger, then the gel pore volume that is accessible to the molecule would be smaller, therefore leading to a lower electrophoretic mobility in the gel.

According to this model, the electrophoretic mobility of molecules in a nanopore system can be determined by simply calculating the fractional free volume available to the molecule. Ogston³⁴ theoretically estimated the average fractional free volume of a gel composed of randomly distributed matrix of fibers, which is;

µ* = K ∼ exp[–πl′(r + r_s)²C]

where l′ is the gel fiber length per unit volume, r is the gel fiber radius, and C is the total gel concentration. Here, the exponential factor came from the fact that the pore size is not constant but randomly distributed around an average pore size. This equation has been the basis of the OMRC model and the Fergusson method of sizing particles using gel electrophoresis.³⁷ For regular-shaped pores such as nanofluidic channels, Giddings et al.³⁸ calculated the partition coefficient for various regular and random nanopores, and for molecules with non-spherical, asymmetrical shapes. For a slit-like pore (with the depth d) and a spherical solute with the radius r_s, for example, the partition factor (and electrophoretic mobility) was calculated as:

The key assumption of the OMRC model (µ* = K) has never been rigorously tested or proven. Still, the OMRC model has been successful in predicting gel electrophoresis results, but mainly for low electric field experiments. In fact, the OMRC model should be viewed as a low-field approximation, since field-dependent deviations from the OMRC model had been observed in gel electrophoresis at relatively high fields (20–200 V cm^–1).^39,40

Recently, Fu et al. developed a nanofluidic filter (nanofilter) array system that extended the separation regime of regular sieving structures to physiologically-relevant macromolecules such as short DNA molecules and proteins.⁴¹ The design of the nanofilter array device is similar to the entropic trap array devised by Han et al.,⁴² but the device separates biomolecules based on the separation mechanism of Ogston sieving. The speed and resolution reported by Fuet al. was comparable to current state of the art systems (i.e., capillary gel electrophoresis). In a follow-up theoretical study by the same group,⁵ nanofilter array separation systems were used as a tool to test the assumption of the OMRC model (µ* = K). Using Kramer's rate theory, the same authors presented a theoretical model for the field-dependent electrophoretic mobility for the Ogston sieving in the system. This is the first detailed theoretical assessment of this ‘anomalous’ field-dependent mobility in Ogston sieving. More recently, Zeng and Harrison⁴³ used self-assembled silica bead arrays confined in microfluidic channels as three-dimensional nanofluidic sieves. By using colloidal arrays of different-sized particles, the sieve pore sizes have been tailored to separate biomolecules covering different size ranges. They have successfully demonstrated size-based separation of both DNA (0.05–50 kbp) and proteins (20–200 kDa) within a few minutes, both based on the Ogston sieving mechanism.

Entropic trapping

Whenever a flexible biopolymer (such as long DNA) enters a pore that is smaller than its radius of gyration (R_g), there is an (entropic) energy barrier for the molecule to overcome, which is the energy cost to be paid to stretch the polymer molecule. Therefore, flexible molecules can be trapped at the interface of nanopores, even when the pore size is much larger than its polymer backbone radius. Originally the concept of entropic trapping was introduced to understand the motion of diffusing long DNA polymers in porous environments such as gels.^44–46 Smisek and Hoagland,⁴⁷ based on the agarose gel electrophoresis experiments, further recognized the “entropic-barrier mediated transport” as an intermediate regime between the Ogston sieving regime and the reptation regime. It was experimentally demonstrated by Rousseau et al.⁴⁸ that there exists an entropic trapping transport regime in the polyacrylamide gel electrophoresis. DNA gel electrophoresis mobility in the entropic trapping regime had been reported to scale as µ ∼ 1/N^ν, with the exponent ν being 1.5–2.5 depending on the DNA size range. However, these studies in gels suffer from ambiguity of gel pore size, which is the critical parameter in entropic trapping. Direct experimental observations of entropic trapping have been recently achieved in artificial molecular sieving systems with precisely controlled geometries. A recent paper by Nykypanchuk and Hoagland⁴⁹ reported an approach to template a two-dimensional (2D) regular pore system with close-packed spherical beads, and direct observation of entropic trapping jump dynamics of long DNA between the cavities was achieved with fluorescence microscopy.

Han and Craighead designed an entropy-based nanofluidic separation system, where nanofluidic filters⁵⁰ were defined with a sequence of deep and shallow channels as an entropic trapping system for long DNA molecules. Han et al. had applied this entropy trap array device to observe the in situ jump dynamics of long DNA across the nanofilter constriction with fluorescence microscopy.⁴² Interestingly, longer DNA molecules were found to advance faster than shorter DNA molecules in their system. The reason for the seemingly counter-intuitive result is because the entropy involved in this process is the conformational entropy, and only a small portion of DNA molecules needs to be unravelled in order to initiate the escape of the entire DNA molecule. In other words, DNA molecules overcome the entropic energy barrier by unravelling themselves piece by piece, instead of fitting the entire molecule into the nanofilter simultaneously. This result demonstrates the complexity of molecular sieving and filtration and the importance of recognizing the biomolecule conformation dynamics involved in molecular sieving process.

Another example of entropy-based separation systems was demonstrated more recently based on the concept of entropic recoil.⁵¹ Long DNA molecules were driven into the densely pillared area by applied electric field. When the field was switched off, any DNA molecules resting entirely within the pillared area remained there, whereas those that had any region outside the pillared area relaxed back into the bulk liquid to maximize their conformational entropy. Since shorter DNA molecules have a greater probability to be driven entirely into the pillared area, they would not relax back and their effective mobility in the device would be greater.

Reptation and other conformation manipulation techniques

As the length of DNA molecule increases, its radius of gyration (R_g) becomes much larger than the average pore size of the gel. In such cases, DNA polyelectrolytes interact in a unique manner called reptation. The reptation model initially relied on DeGennes' theory of the motion of polymeric molecules in the presence of fixed obstacles.⁵² Under an electric field, DNA would slide between gel polymers along its own contour line, in a similar manner as snakes in bushes (where the name ‘reptation’ came from). However, as the length of DNA molecules increases (up to ∼50 kbp), DNA tends to line up in the direction of the field, which would make size-based separation very difficult. Robert Austin's group set out to solve this problem by microfabricating ‘artificial gel’, which was an array of microfabricated pillars.² Their initial attempt to separate long DNA in a microfabricated pillar array was not successful,⁵³ due to the same reason why agarose gel DNA electrophoresis fails for long DNA separation: DNA molecules in the pillar array always get stretched almost completely along the direction of the field. However, it was quickly discovered by the same group, that one can utilize this unavoidable stretching of DNA in the pillar array, by implementing an ingenious pulsed field operation (Fig. 4).^54,55 Here, DNA molecules will be completely stretched and driven into two different directions by switching the direction of the electric field. Depending on the (extended) DNA contour length and the switching frequency of the field, different sized DNA molecules can be quickly separated, and the fully stretched conformation of DNA in the pillar array is now helping to achieve better separation resolution.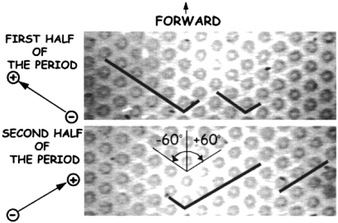

Fig. 4 Pillar array for long DNA separation. (Reprinted with permission from ref. 54. Copyright (2001) American Chemical Society.) This device is made of an array of circular pillars, where DNA molecules get hooked. Long and short DNA molecules (designated with black lines) are completely stretched in the direction of the field in this device. To separate, DNA molecules are driven (by an electric field) in one direction for the first half of the period, and then in another direction for the second half of the period. This will make shorter DNA proceed forward, but longer DNA will remain hooked and never move forward. Repetition of this process will separate DNA molecules based on their length.

Several other separation systems for long DNA molecules have been demonstrated, using different fabrication techniques and nanopore size ranges. Sano et al. recently reported a size-exclusion chromatography device that used an anodic porous alumina as the separation matrix.⁵⁶ The porous alumina membrane traps smaller biomolecules more frequently, therefore they elute slower than the larger biomolecules in the channel. Tabuchi et al. reported a technology using core–shell type nanospheres and nanoparticle medium in conjunction with a pressurization technique to carry out separation of a wide range of DNA fragments (100 bp to 20 kbp) with high speed and high resolution on a microchip format.⁵⁷ Fast long DNA separation was demonstrated using microfabricated submicron-size pillar arrays,⁵⁸ as well as self-assembled magnetic bead pillars.⁵⁹ While detailed sieving mechanisms in these regular sieving systems are not yet fully characterized, it is likely that a combination of several effects, including DNA hooking–unhooking on the pillars and/or Ogston-like sieving, are in play for separation.

Electrostatic sieving

Previously described separation and sieving processes are based on steric interactions of macromolecules with the sieving structure, and those experiments are typically done at relatively high ionic strengths, where the thickness of the electrical double layer (EDL) on the charged nanopore wall is small compared to the nanopore/nanofilter opening. However, if the Debye length gets comparable to the size of the pore (at lower ionic strengths), electrostatic interactions of the analyte with the EDL become prominent and start to dictate the molecular transport behaviour, resulting in charge-selective nanopores (see Fig. 5).^60,61 Co-ions (with the same polarity as the surface charges) will be more restricted from entering the nanochannels/nanopores than the counterions (with the opposite polarity as the surface charges). Such permselectivity can be an essential function for desalination and fuel cells. Nafion^®, for example, is a widely used permselective membrane in fuel cells, with estimated pore size of ∼5 nm.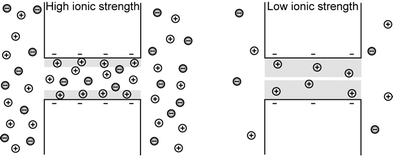

Fig. 5 Charge-selectivity is achieved by decreasing the ionic strength of the electrolyte such that the electrical double layer (EDL, shaded in grey) becomes comparable to the size of the opening. Enrichment of counterions and exclusion of co-ions at low ionic strength is schematically shown. (Adapted from ref. 104.)

Nanopore transport studies coupled with electrostatic interactions have been characterized theoretically as early as in the 1980s.^1,62 Such synthetic and permselective nanochannels have been used for a quantitative study of the exclusion of co-ions and the enrichment of counterions from the opening under passive diffusive transport.⁶³

The exclusion–enrichment coefficient increases exponentially with the net charge of the molecule, therefore, this presents a well-suited mechanism for the separation of biomolecules based on their charge density (or pI values). Depending on the pI value of the protein and the pH condition, partitioning across the perm-selective nanofilter would be charge-dependent.⁶⁴ This has been recently demonstrated⁶⁵ in the anisotropic nanofilter array (ANA) system (to be discussed later). When the ionic strength of the buffer was high, two similarly sized (but with different pI values) proteins followed along the same path without separation. However, at lower ionic strength conditions, two similar-sized proteins with different pI values (therefore different charge densities) were separated due to their different electrostatic interactions with the charged nanofilter wall. The electrostatic sieving mechanism will be useful in sorting complex protein mixtures based on pI values, without the need of pH-gradient generation by carrier ampholytes.

Brownian ratchets (rectified Brownian motion)

Diffusion (or Brownian motion) is usually the enemy for separation processes. However, diffusion can also be utilized for efficient separation if one can add asymmetry to the process: In other words, if diffusion (or random Brownian motion) in one direction is somehow made to be different from the diffusion in the other direction, then overall diffusive transport can be used to move things around or even be utilized for molecular separation. The idea of Brownian ratchet dates back to von Smoluchowski,⁶⁶ and has interested many researchers both in theoretical^67,68 and experimental research,⁶⁹ mainly due to its relevance in motor proteins and the protein translocation process through membranes. The actual implementation of Brownian ratchet-based molecular manipulation requires one to create an asymmetric energy field for molecules/particles to diffuse, which can be realized by dielectrophoresis,⁶⁹optical trapping,⁷⁰ and microfluidic sieving structures.^71–74

The challenge of the prior Brownian ratchet-based device was that the ratchet-based transport is rather slow. The application of Brownian ratchets to molecular separation using obstacle structure was theoretically suggested^71,72 and was later realized.^73,74 The key to this development was the realization that one can gain significantly, in terms of separation resolution and efficiency, simply by isolating the direction of separation (diffusion in this case) from the direction of migration (parallel separation). This allows one to utilize rectified Brownian motion in one dimension for separation, while streaming biomolecules and particles in the other dimension. So far, the Brownian ratchet systems have been demonstrated for a continuous-flow separation of long DNA^74,75 and phospholipids.⁷³ Since the diffusion constant of molecules is a function of molecular size, one can obtain (roughly) size-based sorting of biomolecules in these systems.

Whether this technique could be used for sorting other biomolecules including proteins remains to be seen, since there are several issues to be resolved in the design of the system.^76,77 One of them is the fact that molecular/particle diffusion could also be affected by fluid flow that goes around the asymmetric obstacles, disrupting the energy landscape for asymmetric diffusion significantly.

Hydrodynamic sorting

The steric hindrance mechanism for sieving, previously mentioned in relation with Ogston sieving, would also work for larger length scales (∼1 µm or greater). One can capitalize on this to design efficient size-sorting microdevices for larger particles, such as large DNA, cells, and other bioparticles. Seki and coworkers⁷⁸ demonstrated ‘pinched flow fractionation’ by pushing the particles to the microchannel wall and allowed differently-sized particles to stream into different directions via laminar flow. Huang et al.⁷⁹ developed so-called ‘bump array’, where similar sieving processes can be repeated many times in a large array of pillars, for better separation accuracy. In this system, molecules and particles are pushed against this regular array of pillars, and differently-sized species are routed in different directions. Huang and coworkers demonstrated highly efficient DNA and particle separation using this device, in a continuous-flow format. These hydrodynamic sorting systems are ideally suited for cell sorting and separation,⁸⁰ which is an important problem not only in sample preparation but also in diagnostics.

The unique feature of this idea is that the particle motion and interaction with the sieving structure (pillars and microchannel walls) would be deterministic, which could lead to highly specific and accurate size sorting. (This is largely due to the fact that, at this size scale, random Brownian motion would be much less of a factor.) Therefore, one could possibly get a separation that inherently does not suffer from random motion and dispersion, especially for rigid particles such as micron-sized beads and nanoparticles. However, in practice, most biomolecules (large DNA) and cells are rather flexible (not rigid) and deformable, which would create some dispersion in the sorting process.

In fact, these are conceptually related to the old technique of field-flow fractionation (FFF),^81,82 where the hyperbolic flow profile is coupled with differential analyte distribution profiles at the capillary wall, in order to provide various types of separation. In this class of techniques, analytes are driven (by electric field, sedimentation, and other driving forces) toward the wall differentially (based on the difference in mobility or diffusion constant, or based on steric interaction). For example, steric FFF of micron-size particles⁸³ have already been demonstrated, although using a relatively large (>250 µm) fluidic chamber with a high flow rate (∼mL min^–1).

Continuous-flow molecular sieving systems

For efficient biomolecule separation using nanofilters and nanopores, system-level design is perhaps as important as the nanopore/nanofilter fabrication. For conventional, elution-type separation, many sieving nanofilters or nanopores are arranged in a linear array, and biomolecules assume a different velocity in the system as they pass through the sieving filter array (for example, see Fig. 6). Different analytes will elute out of the system at different times, but all the analytes will pass the same sieving filters. Essentially, separation is achieved by multiple filtration (dialysis) steps as molecules pass through the system. Such a design of nanofilter systems (linear array of nanofilters), while conceptually simple, has many practical drawbacks. First, this design critically suffers from the clogging of filters or molecular sieves in use. Most biosample preparation involves fractionation/separation of very complex samples, containing cells, organelles, large and small biomolecules. Since both large and small analytes in the sample have to go through the same nanofilters, it is likely that large particles (or debris) will clog the system quickly and affect the separation performance. Second, sieving steps at each nanofilter tend to be a stochastic, field-driven energy barrier crossing process, each of which could generate dispersion. This produces unnecessarily large dispersions for the analyte peaks, especially for late-eluting analytes, and therefore degrades the separation resolution. Third, elution-type separations are operated in a batch-processing mode, which limits the overall sample throughput of the separation. Low sample throughput is especially undesirable in proteomic sample preparation, where a certain amount of target molecules should be processed to be detected in the downstream detectors.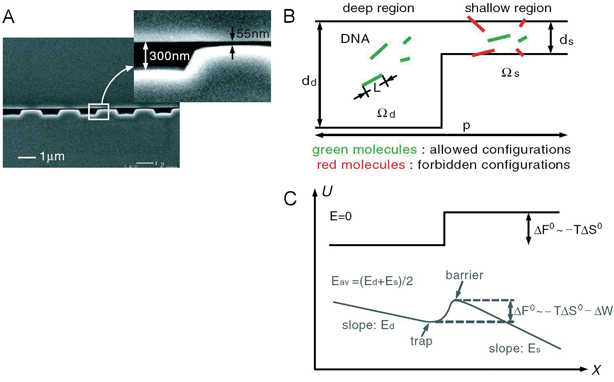

Fig. 6 Nanofilter array for Ogston sieving of proteins and rod-like short DNA molecules (from ref. 5, copyright (2006) by the American Physical Society). A: Cross sectional SEM image of the nanofilter array, with ∼55 nm deep nanofilters. B: Schematic diagram for Ogston sieving in the system. Longer DNA would have more configurations that are prohibited by steric hindrance, therefore would have lower probability to enter the nanofilter. C: Free energy diagram of the system. The energy barrier is determined by the confinement effect (TΔS°) and another electric field dependent term (ΔW). This field-dependent portion of the energy barrier is part of the reason for the field-dependent mobility shift at high electric field conditions.

Many of these issues can be overcome by adapting separation systems into a continuous-flow format. This idea is certainly not new,⁸³ and there has been several (even commercial) development of continuous-flow type protein separation systems,^84–86 mostly in a macroscopic scale. In microfluidics format, isoelectric focusing,^87–89isotachophoresis,⁹⁰ and free-solution capillary electrophoresis^91–93 have been implemented in a continuous-flow format. These systems are very effective in achieving high sample volume processing rates, but the use of liquid sieving media (carrier ampholytes and liquid sieving gel) somewhat limits the choice and function of downstream detectors. In addition, the ideal separation parameter for complex biosamples would be the size and the pI value, rather than the free solution electrophoretic mobility.

Various gel-free, continuous-flow separation systems have been recently developed. Macounova et al. developed a continuous-flow isoelectric focusing device which utilizes natural pH gradient from the electrolysis of buffer at the electrodes.⁹⁴ Song et al. developed a continuous-flow binary sorting system based on the pI value of the protein.⁹⁵ Austin and coworkers^{54,73,74,78,79} have been developing various types of continuous-flow DNA sorting systems, utilizing different sorting mechanisms described previously. These systems allow highly efficient and accurate size-based sorting of large DNA molecules, microparticles, and even blood cells. More recently, an anisotropic nanofilter array (ANA) for separation of small DNA molecules and proteins have been demonstrated⁶⁴ (Fig. 7). Using the same device, the authors were able to separate small DNA and proteins (Ogston sieving), and large DNA molecules (entropic trapping), and proteins based on the pI values (electrostatic sieving). As a result of these contributions, systematic separation and sorting of all the key entities in typical biosamples (blood) now would be possible. These are red and white blood cells, cell nucleus and organelles, viruses, and small and large biomolecules, ranging 5 nm–15 µm in terms of size ranges. Development of such a continuous-flow (high-throughput) biosample fractionation/sorting tool would have a high impact on biological research and biosensing.

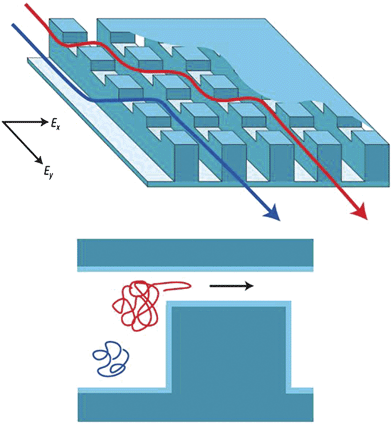Fig. 7 Concept of the anisotropic nanofilter array (ANA), from ref. 65 and 99. (Reprinted by permission from Macmillan Publishers Ltd: Nature Nanotechnology, copyright (2007).) Instead of being driven into the same nanofilters, molecules are given a choice at the junction, and molecules follow different paths based on their sieving properties (size, charge and other properties).

One important advantage of these engineered molecular sieving systems is the ability to position and integrate various sieving structures and fluidic channels in an optimized fashion. For example, a gradient pillar array (with varying pore size),^96,97 or micro/nanochannels with varying width⁹⁸ can be designed, for stretching of long DNA molecules before near-field optical genotype scanning. Another example can be found in the ANA system⁶⁴ (Fig. 7), where different analytes in the mixture are given a choice (by applying a field simultaneously in two orthogonal directions) between molecular sieve (nanofilter) and open road (microchannel), thanks to the structural anisotropy of the system. Then, molecules that are hindered more severely from the nanofilters (e.g. bigger molecules) will get preferentially routed along the microchannel, without the need for them to cross as many nanofilters as the molecules that are favoured to enter the nanofilters (e.g. smaller molecules). As a result, the ANA system has one distinct advantage over other conventional filtration/dialysis membranes: It is much less prone to clogging, since larger analytes will simply be driven away from the nanofilters, or go through only a small number of nanofilters. This could lead to a continuous-flow filtration/sieving of complex biosamples without suffering from system failure due to clogging, especially if the idea of gradually decreasing (increasing) nanofilter sizes (‘gradient’ nanofilter systems) is implemented.⁹⁹ In addition, a similar idea could be applied to any sieving mechanism (either size-, charge-, or even reverse-phase(hydrophobicity) separations), as long as one can create a separation system that is ‘anisotropic’ in nature. We expect more examples like this will emerge in the coming years.

4. Concluding remarks

While molecular filtration and sieving has been studied for a long time, recent development of regular nanopores and nanofluidic molecular filters provide exciting opportunities for further enrichment in our understanding of molecular sieving phenomena. Biomolecules can interact with sieving nanostructures (nanofilters) in diverse modes, each of which could lead to unique molecular separation and filtration methods. Perhaps the biggest benefit one can get from these artificial membrane systems would be the flexibility in sieving system design, which could lead to novel membrane/filter functions. Careful design of nanofilter separation systems could bring about new opportunities in molecular separation.

For wider applications of artificial sieving systems, sample throughput of these systems should be further enhanced. While nanofilter fabrication using substrate etching and bonding¹⁰⁰ provide an accurately sized nanochannels, alternative fabrication techniques should be developed for high-throughput applications. Bottom-up fabrication techniques, such as bead templating,¹⁰¹ are available, but integration with other microfluidic systems has been a challenge. Top-down fabrication of massively parallel, regular nanopore/nanofilter systems with good pore size/chemistry control has been sought by many researchers,^{30,32,102,103} and in our view, it still remains as one of the major challenges in the field. With numerous novel fabrication techniques and ideas, we are reasonably optimistic about achieving this goal in the near future.

Acknowledgements

The authors acknowledge support from the SMA-II CE programme, NIH grant EB005743, and NSF grant CTS-0347348 (CAREER).

References

1. W. M. Deen, AIChE J., 1987, 33, 1409.
2. W. D. Volkmuth and R. H. Austin, Nature, 1992, 358, 600.
3. I. Rubinstein and B. Zaltzman, Phys. Rev. E, 2000, 62, 2238.
4. S. J. Kim, Y.-C. Wang, J. H. Lee, H. Jang and J. Han, Phys. Rev. Lett., 2007, 99, 044501.
5. J. Fu, J. Yoo and J. Han, Phys. Rev. Lett., 2006, 97, 018103.
6. N. Laachi, C. Declet, C. Matson and K. D. Dorfman, Phys. Rev. Lett., 2007, 98, 098106.
7. J. D. Ferry, J. Gen. Physiol., 1936, 20, 95.
8. J. R. Pappenheimer, E. M. Renkin and L. M. Borrero, Am. J. Physiol., 1951, 167, 13.
9. E. M. Renkin, J. Gen. Physiol., 1954, 38, 225.
10. D. M. Malone and J. L. Anderson, Chem. Eng. Sci., 1978, 33, 1429.
11. F. G. Smith and W. M. Deen, J. Colloid Interface Sci., 1983, 91, 571.
12. C. P. Bean, M. V. Doyle and G. Entine, J. Appl. Phys., 1970, 41, 1454.
13. J. A. Quin, J. L. Anderson, W. S. Ho and W. J. Petzny, Biophys. J., 1972, 12, 990.
14. R. I. Fleischer, H. W. Alter, S. C. Furman, P. B. Price and R. M. Walker, Science, 1972, 178, 255.
15. R. E. Beck and J. S. Schultz, Science, 1970, 170, 1302.
16. R. E. Beck and J. S. Schultz, Biochim. Biophys. Acta, 1972, 255, 273.
17. C. P. Bean, in Membranes, ed. G. Eisenman, Dekker, New York, 1972, vol. 1, p. 1.
18. J. L. Anderson and J. A. Quinn, J. Chem. Soc., Faraday Trans. 1, 1972, 68, 744.
19. J. L. Anderson and J. A. Quin, Biophys. J., 1974, 14, 130.
20. C. R. Martin, Adv. Mater., 1991, 3, 457.
21. C. R. Martin, Science, 1994, 266, 1961.
22. M. Nishizawa, V. P. Menon and C. R. Martin, Science, 1995, 268, 700.
23. K. B. Jirage, J. C. Hulteen and C. R. Martin, Science, 1997, 278, 655.
24. G. Che, B. B. Lakshmi, E. R. Fisher and C. R. Martin, Nature, 1998, 393, 346.
25. S. B. Lee, D. T. Mitchell, L. Trofin, T. K. Nevanen, H. Soderlund and C. R. Martin, Science, 2002, 296, 2198.
26. T.-C. Kuo, J. Donald M. Cannon, Y. Chen, J. J. Tulock, M. A. Shannon, J. V. Sweedler and P. W. Bohn, Anal. Chem., 2003, 75, 1861.
27. B. R. Flachsbart, K. Wong, J. M. Iannacone, E. N. Abante, R. L. Vlach, P. A. Rauchfuss, P. W. Bohn, J. V. Sweedler and M. A. Shannon, Lab Chip, 2006, 6, 667.
28. G. Kittilsland, G. Stemme and B. Norden, Sens. Actuators, A, 1990, 21–23, 904.
29. W. Chu and M. Ferrari, in SPIE Proceedings, 1995, vol. 2593, pp. 9–20.
30. W.-H. Chu, R. Chin, T. Huen and M. Ferrari, J. Microelectromech. Syst., 1999, 8, 34.
31. T. A. Desai, D. Hansford and M. Ferrari, J. Membr. Sci., 1999, 159, 221.
32. H. D. Tong, H. V. Jansen, V. J. Gadgil, C. G. Bostan, E. Berenschot, C. J. M. v. Rijn and M. Elwenspoek, Nano Lett., 2004, 4, 283.
33. C. C. Striemer, T. R. Gaborski, J. L. McGrath and P. M. Fauchet, Nature, 2007, 445, 749.
34. A. G. Ogston, Trans. Faraday Soc., 1958, 54, 1754.
35. C. J. O. R. Morris, Prot. Biol. Fluids, 1966, 14, 543.
36. D. Rodbard and A. Chrambach, Proc. Natl. Acad. Sci. U. S. A., 1970, 65, 970.
37. K. A. Ferguson, Metab., Clin. Exp., 1964, 13, 985.
38. J. C. Giddings, E. Kucera, C. P. Russell and M. N. Myers, J. Phys. Chem., 1968, 72, 4397.
39. D. Tietz, in Advanceds in Electrophoresis, 1988, vol. 2, p. 109.
40. J. L. Viovy, Rev. Mod. Phys., 2000, 72, 813.
41. J. Fu, P. Mao and J. Han, Appl. Phys. Lett., 2005, 87, 263902.
42. J. Han, S. W. Turner and H. G. Craighead, Phys. Rev. Lett., 1999, 83, 1688.
43. Y. Zeng and D. J. Harrison, Anal. Chem., 2007, 79, 2289.
44. M. Muthukumar, J. Non-Cryst. Solids, 1991, 131–133, 654.
45. G. W. Slater and S. Y. Wu, Phys. Rev. Lett., 1995, 75, 164.
46. G. I. Nixon and G. W. Slater, Phys. Rev. E, 1996, 53, 4969.
47. D. L. Smisek and D. A. Hoagland, Science, 1990, 248, 1221.
48. J. Rousseau, G. Drouin and G. W. Slater, Phys. Rev. Lett., 1997, 79, 1945.
49. D. Nykypanchuk, H. H. Strey and D. A. Hoagland, Science, 2002, 297, 987.
50. J. Han and H. G. Craighead, Science, 2000, 288, 1026.
51. S. W. P. Turner, M. Cabodi and H. G. Craighead, Phys. Rev. Lett., 2002, 88, 128013.
52. P. G. DeGennes, J. Chem. Phys., 1971, 55, 572.
53. W. D. Volkmuth, T. A. J. Duke, M. C. Wu, R. H. Austin and A. Szabo, Phys. Rev. Lett., 1994, 72, 2117.
54. O. Bakajin, T. A. J. Duke, J. Tegenfeldt, C.-F. Chou, S. S. Chan, R. H. Austin and E. C. Cox, Anal. Chem., 2001, 73, 6053.
55. L. R. Huang, J. O. Tegenfeldt, J. J. Kraeft, J. C. Sturm, R. H. Austin and E. C. Cox, Nat. Biotechnol., 2002, 20, 1048.
56. T. Sano, N. Iguchi, K. Iida, T. Sakamoto, M. Baba and H. Kawaura, Appl. Phys. Lett., 2003, 83, 4438.
57. M. Tabuchi, M. Ueda, N. Kaji, Y. Yamasaki, Y. Nagasaki, K. Yoshikawa, K. Kataoka and Y. Baba, Nat. Biotechnol., 2004, 22, 337.
58. N. Kaji, Y. Tezuka, Y. Takamura, M. Ueda, T. Nishimoto, H. Nakanishi, Y. Horiike and Y. Baba, Anal. Chem., 2004, 78, 15.
59. P. S. Doyle, J. Bibette, A. Bancaud and J.-L. Viovy, Science, 2002, 295, 2237.
60. R. B. Schoch and P. Renaud, Appl. Phys. Lett., 2005, 86 , 253111.
61. D. Stein, M. Kruithof and C. Dekker, Phys. Rev. Lett., 2004, 93, 035901.
62. F. G. Smith, III and W. M. Deen, J. Colloid Interface Sci., 1980, 78, 444.
63. A. Plecis, R. B. Schoch and P. Renaud, Nano Lett., 2005, 5, 1147.
64. R. B. Schoch, A. Bertsch and P. Renaud, Nano Lett., 2006, 6, 543.
65. J. Fu, R. R. Schoch, A. L. Stevens, S. R. Tannenbaum and J. Han, Nat. Nanotechnol., 2006, 2, 121.
66. M. von Smoluchowski, Phys. Z., 1912, 13, 1069.
67. J. Howard, A. J. Hudspeth and R. D. Vale, Nature, 1989, 342, 154.
68. S. M. Simon, C. S. Peskin and G. F. Oster, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 3770.
69. J. Rousselet, L. Salome, A. Ajdari. and J. Prost, Nature, 1994, 370, 446.
70. L. P. Faucheux, L. S. Bourdieu, P. D. Kaplan and A. J. Libchaber, Phys. Rev. Lett., 1995, 74, 1504.
71. D. Ertas, Phys. Rev. Lett., 1998, 80, 1548.
72. T. A. J. Duke and R. H. Austin, Phys. Rev. Lett., 1998, 80, 1552.
73. A. van Oudenaarden and S. G. Boxer, Science, 1999, 285, 1046.
74. C.-F. Chou, O. Bakajin, S. W. P. Turner, T. A. J. Duke, S. S. Chan, E. C. Cox, H. G. Craighead and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13762.
75. L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Anal. Chem., 2003, 75, 6963.
76. R. H. Austin, N. Darnton, R. Huang, J. Sturm, O. Bakajin and T. Duke, Appl. Phys. A: Mater. Sci. Process., 2002, 75, 279.
77. L. R. Huang, P. Silberzan, J. O. Tegenfeldt, E. C. Cox, J. C. Sturm, R. H. Austin and H. Craighead, Phys. Rev. Lett., 2002, 89, 178301.
78. M. Yamada, M. Nakashima and M. Seki, Anal. Chem., 2004, 76, 5465.
79. L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987.
80. J. A. Davis, D. W. Inglis, K. J. Morton, D. A. Lawrence, L. R. Huang, S. Y. Chou, J. C. Sturm and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14779.
81. J. C. Giddings, Sep. Sci., 1966, 1, 123.
82. J. C. Giddings, Unified Separation Science, John Wiley & Sons, Inc, New York, NY, 1991.
83. T. Koch and J. C. Giddings, Anal. Chem., 1986, 58, 994.
84. V. L. Locke, T. S. Gibson, T. M. Thomas, G. L. Corthals and D. B. Rylatt, Proteomics, 2002, 2, 1254.
85. M. Bier, Electrophoresis, 1998, 19, 1057.
86. P. G. Righetti, A. Castagna, B. Herbert, F. Reymond and J. S. Rossier, Proteomics, 2003, 3, 1397.
87. K. Macounova, C. R. Cabrera and P. Yager, Anal. Chem., 2001, 73, 1627.
88. Y. Xu, C.-X. Zhang, D. Janasek and A. Manz, Lab Chip, 2003, 3, 224.
89. H. Lu, S. Gaudet, M. A. Schmidt and K. F. Jensen, Anal. Chem., 2004, 76, 5705.
90. D. S. Janasek, M. Schilling, J. Franzke and A. Manz, Anal. Chem., 2006, 3815.
91. B. B. M. Fonslow, Anal. Chem., 2005, 77, 5706.
92. C.-X. Zhang and A. Manz, Anal. Chem., 2003, 75, 5759.
93. D. Kohlheyer, G. A. J. Besselink, S. Schlautmann and R. B. M. Schasfoort, Lab chip, 2006, 6, 374.
94. K. Macounova, C. R. Cabrera, M. R. Holl and P. Yager, Anal. Chem., 2000, 72, 3745.
95. Y.-A. Song, S. Hsu, A. Stevens and J. Han, Anal. Chem., 2006, 78, 3528.
96. H. Cao, J. O. Tegenfeldt, R. H. Austin and S. Y. Chou, Appl. Phys. Lett., 2002, 81, 3058.
97. J. O. Tegenfeldt, O. Bakajin, C.-F. Chou, S. S. Chan, R. H. Austin, W. Fann, L. Liou, E. Chan, T. Duke and E. C. Cox, Phys. Rev. Lett., 2001, 86, 1378.
98. G. C. Randall, K. M. Schultz and P. S. Doyle, Lab Chip, 2006, 6, 516.
99. R. H. Austin, Nat. Nanotechnol., 2007, 2, 79.
100. P. Mao and J. Han, Lab Chip, 2005, 5, 837.
101. D. J. Norris, E. G. Arlinghaus, L. Meng, R. Heiny and L. E. Scriven, Adv. Mater., 2004, 16, 1393.
102. S. Matthias and F. Müller, Nature, 2003, 424, 53.
103. P. Mao and J. Han, in Proceedings of the MicroTAS 2005 conference, Boston, MA, 2005, vol. 1, p. 678.
104. R. B. Schoch, PhD thesis, EPFL, Lausanne, Switzerland, 2006.

---