The impact of carbon capture and storage on climate
Emma J.
Stone
a,
Jason A.
Lowe
b and
Keith P.
Shine
*c
aSchool of Geographical Sciences, University of Bristol, Bristol, UK BS8 1SS
bMet Office Hadley Centre Reading Unit, Meteorology Building, University of Reading, Reading, UK RG6 6BB
cDepartment of Meteorology, University of Reading, Reading, UK RG6 6BB
First published on 28th November 2008
Abstract
Carbon capture and storage (CCS) is being widely discussed as a possible mitigation option for limiting the emissions of carbon dioxide (CO2) from fossil fuel burning power plants. The implementation of CCS requires the resolution of a number of difficult policy, engineering and economic issues. Here we address the efficacy of CCS from the perspective of climate science. Implementation of CCS makes power stations less efficient, in the sense that they produce more CO2 for a given output of electricity, a feature which is characterised by the so-called energy penalty. The captured CO2 is then stored in, for example, geological storage reservoirs, from which some small fraction is expected to leak back into the atmosphere each year.
We use a set of relatively simple models of carbon capture, the atmospheric carbon cycle and climate, to quantify, for a range of CCS engineering and implementation parameters, the amount of leakage from these reservoirs that can be tolerated to ensure that CCS leads to less, rather than more, climate change. We demonstrate that up to the year 2100, for almost all the parameters that we consider, application of CCS is beneficial. However, in some cases the benefit might be small. We also consider a much longer time horizon (out to the year 2500). We find that while many parameter combinations still lead to a benefit, there are some cases for which application of CCS leads to greater warming than had it not been applied at all. The largest single controlling factor is seen to be the storage reservoir retention time. Many previous studies focused on the use of those storage reservoirs with very long retention times, but we demonstrate that the use of less resilient reservoirs might also provide a climate benefit during the 100 to 500 year time horizon. The largest absolute benefits of CCS to global temperature are found for high future emission scenarios. These absolute benefits also increase as the climate sensitivity of the model is increased.
 Emma Stone | Emma Stone is currently in the final year of her PhD at the University of Bristol. Her research specialises in modelling climate-vegetation ice sheet interactions over Greenland. Her previous research interests have been interpreting palaeoclimate proxies during the mid-Jurassic period and modelling carbon capture and storage and its effects on future global warming. |
Jason Lowe is a Met Office Fellow and is currently leading the production of a new set of climate change scenarios for the UK Climate Change Committee, mapping multi-gas emissions scenarios onto probabilistic estimates of future climate change. In addition he manages a team focused on understanding coupled climate change, including sea level rise and ocean impacts, uncertainty in multi-model projections, and cryosphere changes. Jason has been extensively involved in the communication of science for the Met Office Hadley Centre, and has regularly presented his work to both scientists and policy makers. |
Keith Shine is Professor of Physical Meteorology at the University of Reading. He specialises in climate and climate change, with particular foci on the mechanisms which force climate change, and on the role of water vapour in radiative transfer in the Earth’s atmosphere. He has been a lead author on physical science assessments of the Intergovernmental Panel on Climate Change and World Meteorological Organization assessments of the state of the ozone layer. |
Broader contextCarbon capture and storage (CCS) is a possible mitigation option for limiting emissions of carbon dioxide (CO2) from fossil-fuel burning power stations. Implementation of CCS makes power stations less efficient, in the sense that they produce more CO2 for a given output of electricity. A small fraction of the captured CO2 is expected to leak from the storage reservoirs into the atmosphere each year. We use a set of relatively simple models to quantify, for a range of CCS engineering and implementation parameters, the amount of leakage that can be tolerated to ensure that CCS leads to less, rather than more, climate change. Up to the year 2100, for almost all parameters that we consider, CCS is beneficial, but over periods out to the year 2500, some CCS parameter combinations lead to a greater warming than had CCS not been applied at all. Many previous studies focused on the use of storage reservoirs with very long retention times. We demonstrate that less resilient reservoirs (leakage times less than 100 years) might provide a climate benefit during the 100 to 500 year time horizon. The largest absolute benefits of CCS to global temperature are found for high future emission scenarios. |
1. Introduction
The Fourth Assessment of the Intergovernmental Panel on Climate Change (IPCC) discusses the high likelihood of significant future global climate warming if emissions of greenhouse gases are not sizeably reduced.1 Numerous schemes have been suggested as possible ways of reducing greenhouse gas emissions into the atmosphere over coming decades (for instance ref. 2) of which Carbon Capture and Storage (CCS) has been attracting particular attention.In CCS, CO2 is captured from industrial and/or energy-related sources and transported to a storage location, where it is isolated from the atmosphere – for example in geological or ocean reservoirs. While, in principle, CCS may sound of clear benefit in reducing climate warming, in practice it is not obviously so. At the core of the problem are two facts. First, capture of CO2 requires energy, and the generation of this extra energy is referred to as the “energy penalty”; hence more CO2 is produced per unit energy generated than would be the case without the implementation of CCS. Second, the storage reservoirs will have potential pathways for CO2 leakage into the atmosphere. Clearly, if the CCS leakage rate and energy penalty were to be too high, the amount of CO2 in the atmosphere following CCS implementation could be higher than if CCS had not implemented.
A recent report on CCS by the IPCC3 focused on the potential global capacity of carbon storage reservoirs and highlighted many of the technical difficulties. However, it devoted surprisingly little space (part of Section 1.6.4) to the possibility that CCS might not lead to a reduction of climate change. Here we address the efficacy of CCS from the perspective of climate science; the engineering and economic perspective is covered in detail in IPCC.3 Ultimately, decisions on the implementation of CCS will depend on political, economic and engineering considerations (e.g.ref. 4–6) but it is also important to assess the climate change issues in isolation, as we do here, to understand which constraints are coming purely from this direction, unhindered by the different assumptions that have to be made in, for example, an analysis of the economics of CCS.
There are relatively few recent studies of this problem from a purely climate change perspective in the literature. Haugan and Joos7 considered a simple case whereby, for a given scenario of future CO2 emissions, 30% of those emissions were subject to CCS, and this 30% was subject to a 20% energy penalty. This is equivalent to 6% more CO2 being produced when CCS is implemented, but of course less CO2 is, at least in the first instance, emitted into the atmosphere. They considered annual leakage rates of 0.1% and 1%. They found that if the leakage rate was 1%, then after 300 years, the global warming exceeded that found without CCS, although it would be beneficial for times before this. This led them to consider a metric “global warming avoided”, which is the time-integral of the difference between the temperature change with and without the implementation of CCS. This metric showed that after 700 years, with the leakage rate of 1%, the global warming avoided became zero. By contrast, for a leakage rate of 0.1%, CCS remained strongly beneficial beyond the year 3000, the end point of their analysis.
More recently, Teng and Tondeur8 characterised the effectiveness of CCS in terms of the Global Warming Potential (GWP), which is the metric used within the Kyoto Protocol to the United Nations Framework Convention on Climate Change, to allow emissions of gases other than CO2 to be given a CO2 “equivalence”. The GWP is the time-integrated radiative forcing (i.e. the perturbation of the planetary energy balance) due to a pulse emission of a gas; for the Kyoto Protocol, and in Teng and Tondeur,8 this integration is performed over a 100 year period. Teng and Tondeur8 modified the GWP to consider the time-integrated radiative forcing as the result of storage and gradual leakage of CO2 following implementation of CCS. Using this framework, they defined a “maximum allowable leakage coefficient” and showed it to depend on the ratio of energy penalty and the fraction of CO2 captured by a given CCS technology. Annual leakage rates of 0.1% or less were found to be nearly as effective as perfect storage when considered on a 100 year timescale. For various types of proposed CCS technology, the maximum allowable leakage coefficients were equivalent to leakage rates of between 1% and 6% per year. These values appear significantly more optimistic than those from Haugan and Joos7 but this reflects the shorter timescale adopted in their analysis and perhaps is also influenced by their choice of metric.
CCS is also now included in some integrated assessment models, which try to credibly simulate economics, mitigation measures, the climate system and climate impacts.9 However, in these model studies, the precise role of CCS is not usually singled out for investigation and uncertainties are not often considered.
Several factors have to be taken into account when assessing the potential climate benefit of CCS, some of which are illustrated by these earlier studies. First, various different metrics are available to assess the climate impact of CCS—and the perception of the climate benefit depends on the metric chosen. Second, the perceived benefit of CCS depends on the time period over which the benefits are assessed; there is no obvious choice for this time-period and it is a value-laden decision that policymakers assessing CCS will need to make. Third, assumptions about the choice of the scenario of future emissions of CO2 are also a factor in determining the apparent effectiveness of CCS.
Here we use a set of relatively simple earth-system models (but of similar complexity to those used in the studies referred to above) and a carbon capture and storage model, to examine the impact on the climate system of CCS. Our approach is to examine the effect of applying CCS to the fossil-fuel emissions detailed in two policy-relevant emissions scenarios, based on the IPCC Special Report on Emissions Scenarios (SRES) B1 and A1FI.10 We investigate the effects on atmospheric CO2 abundance, radiative forcing and global warming in order to identify the point at which CCS becomes beneficial (and to investigate how this point depends on the choice of metric) and in order to quantify the magnitude of this benefit over two different timescales (up to 2100 and up to 2500). We choose the timescale up to 2100 because it is a more conventional planning timescale in climate change assessment work; nevertheless, many components of the climate system (such as sea level and ice sheets) respond on a much longer time scale and so it is useful to assess how our conclusions depend on the timescale up to 2500.
Our work considers a wider range of CCS parameters than Haugan and Joos7 and hence leads to a broader analysis of the allowable leakage rates. It also extends their analysis by considering the dependence of the results on the choice of the value of climate sensitivity. Teng and Tondeur's8 analysis was restricted to a 100 year time period and the use of a single metric (GWP)—our work examines, in addition, longer timescales, and extends it to a consideration of surface temperature change.
2. Engineering constraints of carbon capture and storage technology
The type of CCS we consider involves capturing CO2 by separating it from industrial and energy-related sources and transporting it to a storage location where it is isolated from the atmosphere, for example, in either geological or ocean reservoirs and mineral carbonates. Capture from large numbers of small mobile sources (e.g. road transport) is not treated. Several types of geological reservoirs exist, including enhanced oil recovery fields, depleted and disused oil and gas fields and deep unminable coal seams. Global storage capacity has been estimated to be between about 184 and 300 gigatonnes of carbon (Gt-C) for these reservoirs, which can be compared with current annual fossil-fuel emissions of about 6.8 Gt-C.3 If storage in deep saline aquifers were also used then the capacity might be as high as 2700 Gt-C3 but this estimate is very uncertain.Four fundamental parameters determine how effective CCS will be at limiting increases in future atmospheric CO2 abundance. These are illustrated in Fig. 1 and described below:
• The energy penalty
• The fraction of CO2 released to the atmosphere from a CCS plant
• The fraction of global fossil fuel emissions to which CCS is applied
• The retention time of CO2 in storage reservoirs.
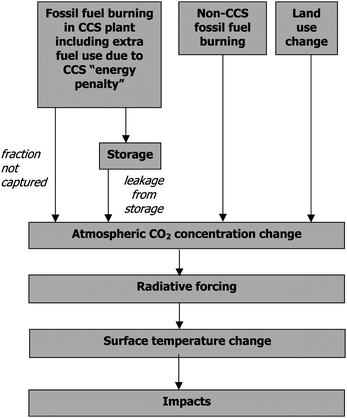 | ||
| Fig. 1 Cause-effect chain illustrating the four fundamental parameters that determine the efficacy of CCS in limiting increases of future CO2 abundances and how the implementation of CCS impacts the climate system. | ||
2.1 The energy penalty
The energy penalty describes the increased CO2 production resulting from the loss in overall efficiency of power plants or industrial processes due to the extra energy needed for the capture process. IPCC3 states that power plants equipped with a CCS system (and access to a geological/ocean storage sites) would need approximately 10–40% more energy than a plant of equivalent output without CCS, the range reflecting the type of power station to which CCS is applied. The majority of this is used for capture and compression. The energy penalty may also have a contribution from the transportation of captured CO2 from source to storage reservoir.2.2 The fraction of CO2 released to the atmosphere from a CCS plant
According to the IPCC,3 available technology is able to capture approximately 85–95% of the CO2 processed in a plant. Thus, only a small amount is not captured within any single CCS application.2.3 The fraction of global fossil fuel emissions to which CCS is applied
Although the capture process is proven to be very efficient for an individual source, not all point sources are suitable for carbon capture. Fossil-fuel based industrial sources are currently the best potential candidates for early implementation of CCS. From the SRES emission scenarios it has been projected that the number of large point sources will increase in the future; by 2050 about 21–45% of global fossil-fuel CO2 emissions could be technically suitable for capture.3 The range represents uncertainties of scenario and modelling analyses and the engineering limitations of applying CCS.2.4 The retention time of CO2 in the reservoir
Some fraction of the stored CO2 will return to the atmosphere each year, either through abrupt leakage, through injection well failure, and/or the gradual leakage through faults, fractures, or wells and molecular diffusion through cap rock. In the case of injection of carbon into the ocean, the retention time is a strong function of the depth of injection3,11—shallower injection is likely to be cheaper but subject to faster leakage rates. Leakage of CO2 during the transport process from point source to storage site is also possible.The development of CCS projects and monitoring is so recent that there has been insufficient time to obtain reliable observationally-based leakage values. Instead, computer modelling of leakage rates from geological and ocean reservoirs are being performed. IPCC3 state that for a well-selected, designed and operated CO2storage project, “the balance of evidence suggests … it is very likely that the fraction of stored CO2 retained is more than 99% over the first 100 years”. We will use a range of leakage rates, which are generally more pessimistic than this, allowing an assessment of whether there is utility in exploring the potential of using CCS with leakier reservoirs.
Our approach in this paper is to produce results for ranges of the parameters on which CCS is likely to depend. In this way our results can be seen as a sensitivity study providing the minimum targets for these engineering parameters, if particular climate benefits are to be required from this technology.
3. Methodology
The impacts of the CCS process on the climate system are illustrated in the cause-effect chain in Fig. 1. Here we describe the simple model framework used to quantify the effects of applying CCS. These components are a carbon cycle model, a carbon capture model and a climate model. The simple model framework is appropriate for exploring the sensitivity of the system to various parameters, and indeed necessary, given the large number of simulations that are required to explore the parameter space.3.1 The carbon cycle model
Complex carbon cycle models are often used to simulate the dynamics of the atmosphere-ocean-biosphere system in order to understand the fate of anthropogenic CO2 (e.g.ref. 12) However, while these provide spatial information and are able to deal, in a simplified manner, with non-linear effects, they are computationally expensive. If the focus is on global climate response, and we do not attempt to include the still quantitatively uncertain feedback of climate change onto the carbon cycle, as is the case here, then much simpler pulse-response function models can be used.13 The concentration of carbon dioxide (R(t)) following a unit mass pulse emission (at time, t (in years)) can then be approximated by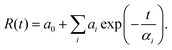 | (1) |
The atmospheric CO2 concentration (ppmv) at time t can then be represented as the sum of earlier emissions at time t′, multiplied by the fraction still remaining airborne after time t − t′ (e.g.ref. 13, 15) so that
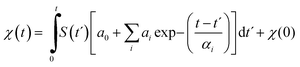 | (2) |
3.2 The CCS model
We have developed a simple global average CCS model that can be easily coupled to our other model components. The total CO2 production rate, ETOTAL, from a single CCS plant can be described by| ETOTAL = (1 + α)EFF | (3) |
The total fossil-fuel CO2 emissions rate into the atmosphere, EATM after CCS is applied comprises three terms: fossil-fuel emissions released from CCS point sources due to inefficiency in the capture process, the emissions released from non-CCS fossil-fuel sources, and the amount leaked from the CCS storage sites. This is expressed as
| EATM = (1 + α)βγEFF + (1 − γ)EFF + L | (4) |
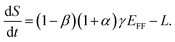 | (5) |
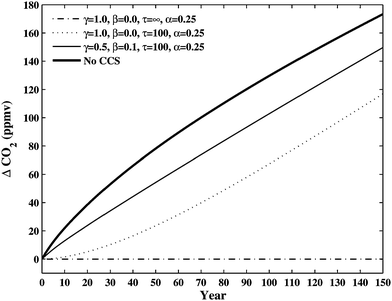
The quantity of CO2 lost from storage within a year is assumed here to be dependent on the cumulative amount of CO2 stored and the residence time of CO2 in the reservoir (τ), thus
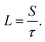 | (6) |
For simplicity, and in common with other recent studies,7,8 we have assumed that one generic value of retention time is appropriate for all storage sites. In reality, different storage sites will have different CO2retention times (which would have to be estimated before use) and we have assumed gradual leakage rather than catastrophic failure of a reservoir. This simple CCS model also neglects the time dependence of the energy penalty and the leakage rate. It is likely that in the future, with technological advancement, the energy penalty will be significantly reduced. Improvements in the monitoring of abandoned wells and understanding of the leakage processes in the geological reservoirs are likely to lead to a reduction in leakage rates with time. However, as the most resilient stores become full, this could be offset by a need to use reservoirs with inherently larger leakage rates.
The combined CCS-carbon cycle model was evaluated for a hypothetical scenario with a constant fossil-fuel emission rate of 6 Gt-C year−1 and an energy penalty of 0.25 for 150 years. Fig. 2 shows the cases for where all fossil-fuel emissions are captured (i.e.β = 0 and γ = 1) with no leakage, 100% capture with a 1% per year leakage rate (100 year storage retention time), 50% of sources subject to capture but where 10% of the CO2 from these sources is not captured with a 1% per year leakage rate and, for comparison, the case when CCS is not applied. The model manages to simulate each of these scenarios adequately. The 100% capture and no leakage case maintains a change in CO2 atmospheric mixing ratio of zero ppmv while the 100% capture case with leakage shows a linear increase with time as expected.
 | ||
| Fig. 2 Change in CO2 volume mixing ratio (ppmv) for three hypothetical CCS scenarios and the case where CCS is not applied using the combined CCS-carbon cycle model. The CO2 emission rate was taken to be 6 Gt-C year−1 and the model run for 150 years. | ||
3.3 Climate model
The simple climate model used here has two main components. First the estimate of radiative forcing (RF) is calculated from changes in the atmospheric abundance of CO2, and second the temperature change caused by the radiative forcing is determined. The first step uses the following expression, as given in the IPCC,16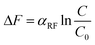 | (7) |
An upwelling-diffusion energy balance model (UD/EBM) (from ref. 15) was used to calculate the temperature response to forcing perturbations. UD/EBMs have been extensively used by the IPCC to evaluate projections of global-mean surface temperature change for a range of emissions scenarios (e.g.ref. 1, 16).
The model used here incorporates a number of climate system processes, including heat transport from the mixed layer of the ocean to the deep ocean via diffusion, advective heat transport by the ocean thermohaline circulation, and the inclusion of the land surface with heat exchange between the land and the ocean. It also simulates the difference in ocean and land warming and differences between the Northern and Southern Hemispheres. Appendix B in Shine et al.15 outlines the model parameters used here.
Although there is uncertainty in many of these parameters (see e.g.ref. 16) only the effect of uncertainty in climate sensitivity is investigated here, as it is probably the largest and most important of these uncertainties in the context of this work. Climate sensitivity provides a measure of the effect, on the global scale, of climate feedback processes, such as the response in cloud properties to climate change. Numerically it gives the equilibrium change in surface temperature for a unit radiative forcing and is often quoted, as we do here, as the change in equilibrium surface temperature that would result from a doubling of atmospheric CO2 concentrations. The value of the climate sensitivity impacts on the time-scale, as well as the magnitude, of the climate response. One advantage of using simple climate models, such as the UD/EBM, is that they allow the effect of uncertainties in climate sensitivity to be explored in a way that is impossible with more sophisticated climate models. The uncertainty in the climate sensitivity is one of the key, and chronic, uncertainties in climate modelling. We will show that the absolute benefit of CCS depends significantly on the value of climate sensitivity; it is a factor that has not been explored in earlier CCS studies.
3.4 Experimental design
The climate experiments we consider all begin in year 1850. Emissions of CO2 follow historic values up to year 2000 (from Marland et al., ref. 18) then follow one of two policy-relevant scenarios into the future. The SRES A1FI and B1 scenarios10 were used to contrast a world of rapid economic growth where the technological emphasis is fossil-fuel intensive (A1FI) with a world in which the introduction of clean and resource-efficient technologies takes place (B1).The SRES emissions are only specified up to 2100 so we extended them out to 2500 as follows. The fossil-fuel emissions for SRES B1 in 2100 were linearly decreased to 2 Gt-C year−1 over 50 years and kept constant thereafter. The same linear rate of emissions decrease was also applied to the A1FI scenario until the annual emissions rates reached 2 Gt-C year−1. Land use emissions were held constant at the 2100 value in both cases. Clearly, we are assuming that the original scenarios and their extensions can be achieved without applying CCS technology. If this were not the case, we would be double counting the effects of CCS.
Parallel to the B1 and A1FI baseline scenarios, a set of experiments were run with CCS being switched on in 2010. These experiments sampled a range of CCS parameters (α, β, γ and τ) as listed in Table 1. We quote the retention time τ as the e-folding time (eqn (6)); this can be approximately converted to leakage rates in % per year by taking the reciprocal of τ and multiplying by 100; so the values of τ of 10, 40, 100, 500 and 1000 years correspond to annual leakage rates of 10%, 2.5%, 1%, 0.2% and 0.1% respectively. The value of 99% retained after 100 years, cited in Section 2.4 above, is equivalent to 0.01% annual leakage. An important output of our work is a consideration of whether reservoirs with significantly higher leakage rates might, nonetheless, be of practical value in mitigation. The extreme values of these parameters come from a combination of literature synthesis and plausibility arguments, and we make no claim as to the relative probability of any particular set of CCS parameter values.
| Retention time, τ/years | Energy penalty, α | Fraction of fossil fuel emissions released from a single CCS plant, β | Fraction of global fossil fuels emissions subject to CCS, γ |
|---|---|---|---|
| 10 | 0.10 | 0.05 | 0.25 |
| 40 | 0.25 | 0.1 | 0.50 |
| 100 | 0.40 | 0.15 | |
| 500 | |||
| 1000 |
Several values of equilibrium climate sensitivity are used: 1.5 °C, 3 °C, 4.4 °C and 7.4 °C. These were chosen based on the IPCC,1 which reports that the equilibrium climate sensitivity is likely to be in the range 2 °C to 4.5 °C, and very unlikely to be less than 1.5 °C. Our higher value is included because IPCC1 indicates that values substantially in excess of 4.5 °C cannot be excluded.
4. Results and discussion
First we consider the effect of applying CCS on the atmospheric abundance of CO2. For this part of the study, the CCS-carbon cycle model combination was run for the baseline (no CCS) and 90 permutations of the parameters in the CCS model for each of the emissions scenarios up to the year 2500. This represents 177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 simulated years in total although, obviously, before CCS is applied in 2010, the simulations with CCS will be identical to the baseline cases.
450 simulated years in total although, obviously, before CCS is applied in 2010, the simulations with CCS will be identical to the baseline cases.
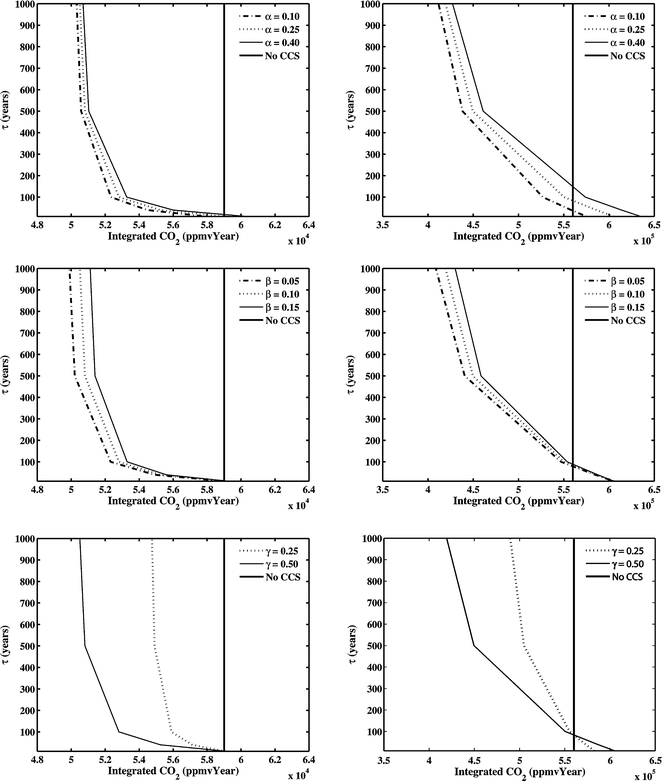
From time series plots of CO2 abundance for all permutations, the retention time of CO2 in storage sites was found to have the greatest effect on the results. To summarize and compare experiments we have calculated the time-integrated CO2 abundances (ppmv year−1) for the periods spanning 2000 to 2100, and 2000 to 2500. In each frame of Fig. 3 and 4 (the B1 and A1FI scenarios respectively), the dependence of the time-integrated CO2 is plotted against retention time, using the values of the other parameters as given in Table 1. In each plot, the vertical line is the non-CCS case, so that any parameter set leading to a value of the integrated CO2 to the right of this line means that CCS is increasing the amount of CO2 in the atmosphere.
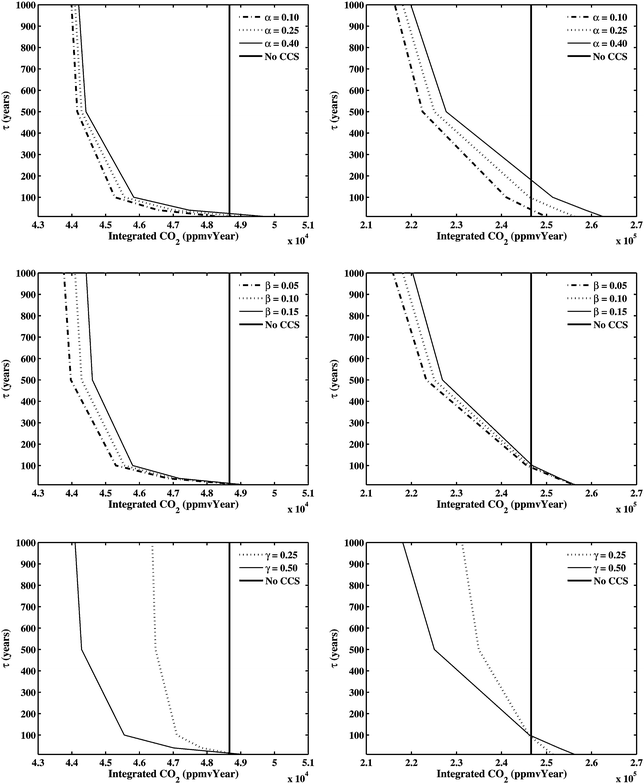 | ||
| Fig. 3 Integrated CO2 concentration (ppmv year−1) versusretention time, τ, for the B1 scenario. Top row: α variation with β = 0.1 and γ = 0.5, middle row: β variation with α = 0.25 and γ = 0.5 and bottom row: γ variation with α = 0.25 and β = 0.1. Left column: time horizon 2000 to 2100. Right column: time horizon 2000 to 2500. α is the energy penalty, β is the fraction of fossil fuel emissions released from a single CCS plant and γ is the fraction of global fossil fuel emissions subject to CCS. The vertical line in each frame shows the integrated CO2 concentration in the absence of CCS. | ||
 | ||
| Fig. 4 Integrated CO2 concentration (ppmv year−1) versusretention time, τ, for the A1FI scenario. Top row: α variation with β = 0.1 and γ = 0.5, middle row: β variation with α = 0.25 and γ = 0.5 and bottom row: γ variation with α = 0.25 and β = 0.1. Left column: time horizon 2000 to 2100. Right column: time horizon 2000 to 2500. α is the energy penalty, β is the fraction of fossil fuel emissions released from a single CCS plant and γ is the fraction of global fossil fuel emissions subject to CCS. The vertical line in each frame shows the integrated CO2 concentration in the absence of CCS. | ||
Focusing on the B1 scenario (Fig. 3) we first note that there is a set of parameter values for which CCS leads to a greater integrated CO2 abundance than in the no CCS case. The maximum benefit from CCS comes, as expected, from applying the technology to as much of the global fossil fuel emissions as possible while having a low energy penalty and capturing the maximum percentage of CO2 produced in each plant. Once in the storage reservoir, the longest retention time leads to the greatest benefits. However, we note that a doubling of the retention time from 50 years will have a much greater effect on the integrated CO2 abundance (and the benefit of CCS) than a doubling of the retention time from 500 years, which has very little effect.
By comparing the left (2000–2100) and right (2000–2500) columns, it is apparent that it is much easier to achieve the break-even point for the shorter period than for the longer period. A retention time of greater than around 25 years is sufficient to result in a benefit up to 2100, whereas a retention time of between 30 and 180 years (depending on other parameter choices) is needed to achieve break-even for a 2500 time horizon. These values of retention time are consistent with Teng and Tondeur's8 analysis, which indicated that over a 100 year time period, annual leakage rates in excess of 1% (i.e.retention times of less than 100 years) could be tolerated. It also supports the view of Haugan and Joos7 that when longer time scales are considered, longer retention times are required—however annual leakage rates of much greater than 0.1% (i.e.retention times less than 1000 years) can still be effective over the 500 year time period.
Beyond the break-even point, for any given retention time, the greatest effect on the magnitude of the benefit comes from our chosen spread in γ, the fraction of global fossil fuel emissions to which CCS technology is applied. The effect on the benefit of CCS due to the spread in α, the energy penalty, and β, the fraction of fossil fuel emissions released from a single CCS plant, is much less. This is particularly interesting because it implies that provided suitably long retention times can be achieved, even quite large energy penalties can be tolerated. However, large energy penalties do have the added drawbacks that they would increase the fuel costs in CCS, so making it less attractive from an economic point of view and would also consume natural fuel resources at a faster rate.
Similar conclusions follow for the A1FI scenario (Fig. 4), although the exact values for the break-even point and magnitude of the benefit of CCS clearly change. Table 2 lists the break-even points for the two scenarios. Clearly a shorter retention time is necessary for break-even in the high emission scenario (A1FI), a difference that is found for all values of energy penalty explored here. This can be explained by considering the CO2 concentrations, in the non-CCS case. For the B1 scenario, concentrations peak by about 2075 and are approximately constant at about 500 ppmv thereafter. For A1FI, they continue to rise to about 1350 ppmv in about 2400, before declining very slowly. The time-integrated CO2 concentrations in the atmosphere for the A1FI case are found to be only 20% higher than B1 for the period 2000–2100. For the 2000–2500 period, by contrast, they are more than a factor of two higher. Hence, on introducing CCS, the amount of CO2 that will be taken into the storage reservoir by 2100 will be broadly similar in both the high and low scenarios, and hence the leakage rate into the atmosphere will also be broadly similar. However, in the B1 case, the leakage will have become a much larger proportion of the total emissions into the atmosphere than in the A1FI case, and hence the atmospheric concentrations will be more sensitive to that leakage.
| Scenario | Energy penalty | ||
|---|---|---|---|
| 0.1 | 0.25 | 0.40 | |
| A1FI | 36 | 83 | 125 |
| B1 | 42 | 96 | 144 |
Next we address the issue of whether similar conclusions can be made about the break-even point and benefit of CCS when climate indicators other than CO2 abundance are used. Here we use the time-integrated radiative forcing and the time-integrated global average temperature increase. Fig. 5 shows that, for a time horizon of 2000 to 2500 and default values of α, β and γ, the choice of indicator has little effect on the break-even point. However, the fractional benefit for a given retention time is greater if either radiative forcing or temperature are used. Clearly, the non-linearity in the forcing relationship (eqn (7)) is important to this result. The small additional benefit seen by choosing a temperature indicator over a forcing indicator implies the lag in temperature response to a radiative forcing change (e.g.ref. 19) actually has little effect on the overall fractional benefit.
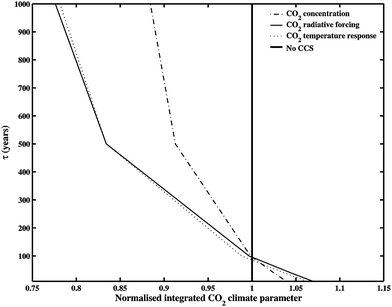 | ||
| Fig. 5 Impact of the choice of impact parameter (integrated CO2 concentration, integrated radiative forcing and integrated temperature change). The calculations are for the B1 scenario and time horizon 2000–2500. To plot these parameters on the same scale, they have all been normalised by dividing by the value of the parameters when CCS is not implemented. Hence the vertical line, at a value of 1, is the no-CCS case. | ||
Finally, we look in more detail at the temperature response with and without CCS for a range of different climate sensitivities (Fig. 6). The shaded regions encompass the temperature response for all permutations of the CCS model parameters; the red dashed lines correspond to the temperature response from the baseline case where CCS is not implemented.
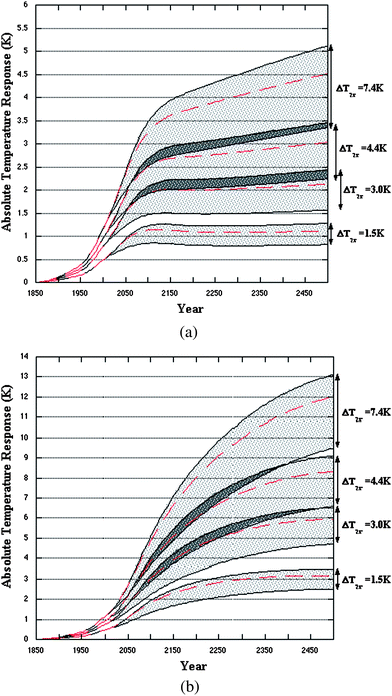 | ||
| Fig. 6 Temperature response (K) time series from 1850 to 2500 for different climate sensitivities (ΔT2x) for (a) the B1 and (b) the A1FI CO2 emission scenarios. The shaded area denotes the total CCS parameter space. The red dashed lines correspond to the temperature response for no CCS. | ||
First we note that up to 2100, for both scenarios, almost all the permutations of the CCS model parameters result in a temperature response equal to or lower than that for no CCS, although for some the benefit will be small. This is consistent with our earlier findings, using the CO2 abundance indicator, that relatively short retention times lead to break-even up to year 2100. After 2100, more cases with CCS give higher absolute temperature responses relative to the no-CCS situation. For the B1 scenario, where CO2 concentrations stabilise at around 490 ppmv, and considering a mid-range climate sensitivity of 3 °C, the maximum benefit of CCS for the parameter values we have considered is around 0.5 °C. Next we notice, as expected, that the maximum temperature reduction due to CCS, relative to the no-CCS cases, increases with increasing climate sensitivity. In the most extreme case of the A1FI scenario and for the highest climate sensitivity considered here (7.4 °C), this reduction is about 2.5 °C. The greater absolute benefit of CCS for higher emissions scenarios is consistent with Haugan and Joos7—see especially their supplementary electronic information—but they did not examine the dependence on the choice of climate sensitivity.
An increasingly important aspect of the climate debate is whether society will be exposed to a dangerous amount of climate change. Indeed, the objective of the United Nations Framework Convention on Climate Change (http://unfccc.int) is “stabilization of greenhouse gas concentrations in the atmosphere at a level that would prevent dangerous anthropogenic interference with the climate system”. While the meaning of “dangerous” remains a matter for debate, the European Union has adopted a target of limiting global average temperature increases since the industrial revolution to no more than 2 °C (http://www.europa.eu/bulletin/en/200503/i1010.htm). The red lines in Fig. 6a shows that for our extended B1 simulation without CCS it is likely that this target will be exceeded if the climate sensitivity is found to be greater than around 3 °C. However, it also shows that, given our full range of CCS parameter values, applying CCS to these B1 emissions might be sufficient to limit warming to less than 2 °C for climate sensitivities of less than around 4 °C. (This analysis, of course, neglects the contribution of other non–CO2 anthropogenic emissions to climate change.)
An aspect of the climate system that we have not included here is the feedback between the climate and the natural carbon cycle response. For most carbon cycle models, and for all but the largest temperature increases discussed in this paper, the natural carbon reservoirs are likely to still provide a net sink. However, coupled climate carbon cycle models typically show that the effect of temperature rise is to weaken the strength of this sink, so that the same anthropogenic emissions lead to a greater change in concentration. The details and magnitude of the temperature dependence of the natural sinks are currently very uncertain (e.g.ref. 12) This is likely to accentuate the benefits of applying CCS beyond the break-even point, especially at high climate sensitivity and for scenarios with high carbon dioxide emissions. Conversely, those cases that result in CCS leading to greater eventual warming than the baseline are likely to be made even worse.
5. Conclusions
The aim of this study was to assess how much difference CCS could make to global climate by investigating the impacts of the uncertainty ranges of the energy penalty, retention time of CO2 in storage sites, the fraction of emissions that is released by a point source after the capture process, the fraction of global fossil fuel emissions that are captured and the sensitivity of the climate system. We have focused our analysis on the effect of CCS to a range of existing emissions scenarios, assuming that the baseline scenario does not itself require CCS to be achieved and explored the impact of uncertainties in climate sensitivity. Our results confirm previous expectations (e.g. Haugan and Joos, Teng and Tondeur7,8) that in the short-term, CCS is likely to reduce the temperature response below that of cases where CCS is not implemented.Our study has found that:
• Break-even conditions are relatively insensitive to the energy penalty and the fraction of CO2 stored by CCS but they are sensitive to the reservoir retention times.
• Achieving break-even depends on the time horizon we consider, with longer time horizons (we considered 2100 and 2500) requiring longer reservoir retention times as also found by Haugan and Joos.7 This is seen most graphically in the temperature time series where almost all permutations of the CCS model give lower temperature compared to the no CCS case up to the year 2100, but by 2500 a significant minority of CCS parameter cases actually lead to greater warming.
• Consistent with Teng and Tondeur,8 we find that CCS implemented with quite modest retention times (less than 100 years, equivalent to annual leakage rates in excess of 1% per year) would still lead to a reduction in the resulting climate change over the next 100 year period.
• The benefit of applying CCS is, as expected, a strong function of reservoir retention times, although the benefit of increases in retention time are reduced as the retention time increases.
• The fractional benefit of CCS depends on the indicator chosen, with a greater benefit seen in terms of radiative forcing and temperature than in terms of atmospheric CO2 abundance alone.
• The absolute benefit from CCS differs between scenarios, with the greatest benefit seen for the highest emissions case, consistent with Haugan and Joos.7 We also show that the absolute benefit is greater for higher values of climate sensitivity.
The simulations for the lowest emission case of the SRES scenarios (B1) suggest that without applying CCS there is a significant probability that the global average temperature will rise by more than 2 °C above pre-industrial levels. With CCS (and for this extended B1 scenario) it might be possible to keep temperature increases below this level for climate sensitivities of less than 4 °C. We have not included emissions of other greenhouse gases, which would tend to produce further warming, or aerosol particles, which might offset some of this extra warming.
Although it has used relatively simple models, this study provides results that might be used to guide the CCS engineering and economics community as it works to operationalise the process on a large scale. Clearly it would not be sensible to proceed with sites that do not at least satisfy the “break-even” conditions, such as sites with the shortest retention time. Our work also gives preliminary guidance on the relative importance of focusing on improvements in reservoir retention time, energy penalty and fraction captured in a CCS plant, in terms of optimizing the climate benefits of implementing CCS.
An interesting aspect of our study is that it also highlights the potential climate benefits from using storage reservoirs that have in many previous studies been considered to have too high a leakage rate. To those currently thinking of the reservoirs being considered for CCS as providing permanent storage (i.e. longer than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years) it might seem strange to investigate the use of less resilient reservoirs. However, our results must be viewed in terms of the current climate mitigation debate. Some authors, such as den Elzen and van Vuuren,20 have discussed stabilisation scenarios in which the atmospheric abundance of greenhouse gases initially exceeds a target stabilisation level, returning to the stabilisation level from above sufficiently quickly that the climate system's thermal inertia prevents a corresponding stabilisation temperature target being exceeded. This is effectively storing extra carbon temporarily in the atmosphere and relying on the currently uncertain climate system inertia to avoid dangerous warming while this temporary store is used. Using CCS, even with the relatively high leakage rates we consider here, provides at least similar benefits (once the energy penalty is accounted for) to storing extra carbon temporarily in the atmosphere, while being a much lower risk option.
000 years) it might seem strange to investigate the use of less resilient reservoirs. However, our results must be viewed in terms of the current climate mitigation debate. Some authors, such as den Elzen and van Vuuren,20 have discussed stabilisation scenarios in which the atmospheric abundance of greenhouse gases initially exceeds a target stabilisation level, returning to the stabilisation level from above sufficiently quickly that the climate system's thermal inertia prevents a corresponding stabilisation temperature target being exceeded. This is effectively storing extra carbon temporarily in the atmosphere and relying on the currently uncertain climate system inertia to avoid dangerous warming while this temporary store is used. Using CCS, even with the relatively high leakage rates we consider here, provides at least similar benefits (once the energy penalty is accounted for) to storing extra carbon temporarily in the atmosphere, while being a much lower risk option.
Future climate modelling work in this area should focus on a probabilistic approach for both climate and CCS parameters and ought to include the feedback of climate onto the natural carbon cycle and other greenhouse gases.
Acknowledgements
This work was supported by the Joint Defra and MoD Programme, (Defra) GA01101 (MoD) CBC/2B/0417_Annex C5, and by the Natural Environment Research Council. We benefited from discussions with Tim Cockerill and Naser Odeh and thank the referees for their comments.References
- IPCC, Climate Change 2007, The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, ed. S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K. B. Avery, M. Tignor and H. L. Miller, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2007 Search PubMed.
- S. Pacala and R. Socolow, Stabilization wedges: solving the climate problem for the next 50 years with current technologies, Science, 2004, 305, 968–972 CrossRef CAS.
- IPCC, Special Report on CO2 Capture and Storage, ed. B. Metz, O. R. Davidson, H. de Coninck, L. M. Meyer, Cambridge University Press, Cambridge, 2005, p. 443 Search PubMed.
- M. Ha-Duong and D. W. Keith, Carbon storage: the economic efficiency of storing CO2 in leaky reservoirs, Clean Technol. Environ. Policy, 2003, 5, 181–189 Search PubMed.
- H. Herzog, K. Caldeira and J. Reilly, An issue of permanence: assessing the effectiveness of temporary carbon storage, Clim. Change, 2003, 59, 293–310 CrossRef CAS.
- B. van der Zwaan and K. Smekens, CO2 capture and storage with leakage in an energy-climate model, Environ. Modell. Assess., 2007 DOI:10.1007/s10666-007-9125-3 (online first).
- P. M. Haugan and F. Joos, Metrics to assess the mitigation of global warming by carbon capture and storage in the ocean and in geological reservoirs, Geophys. Res. Lett., 2004, 31, L18202 CrossRef.
- F. Teng and D. Tondeur, Efficiency of carbon storage with leakage: physical and economical approaches, Energy, 2007, 32, 540–548 CrossRef CAS.
- J. R. McFarland and H. J. Herzog, Incorporating carbon capture and storage technologies in integrated assessment models, Energy Econ., 2006, 28, 632–652 CrossRef.
- N. Nakicenovic, Greenhouse gas emissions scenarios, Technol. Forecasting Social Change, 2000, 65(2), 149–166 Search PubMed.
- K. Caldeira, M. E. Wickett and P. B. Duffy, Depth, radiocarbon, and the effectiveness of direct CO2 injection as an ocean carbon sequestration strategy, Geophys. Res. Lett., 2002, 29, 1766 CrossRef.
- P. Friedlingstein, P. Cox, R. Betts, L. Bopp, W. Von Bloh, V. Brovkin, P. Cadule, S. Doney, M. Eby, I. Fung, G. Bala, J. John, C. Jones, F. Joos, T. Kato, M. Kawamiya, W. Knorr, K. Lindsay, H. D. Matthews, T. Raddatz, P. Rayner, C. Reick, E. Roeckner, K. -G. Schnitzler, R. Schnur, K. Strassmann, A. J. Weaver, C. Yoshikawa and N. Zeng, Climate-carbon cycle feedback analysis: Results from the (CMIP)-M-4 model intercomparison, J. Clim., 2006, 19(14), 3337–3353 CrossRef.
- F. Joos, M. Bruno, R. Fink, U. Siegenthaler, T. F. Stocker, C. Le Quéré and J. L. Sarmiento, An efficient and accurate representation of complex oceanic and biospheric models of anthropogenic carbon uptake, Tellus, 1996, 48B, 397–417 Search PubMed.
- U. Siegenthaler and F. Joos, Use of a simple model for studying oceanic tracer distributions and the global carbon cycle, Tellus, 1992, 44B, 186–207 Search PubMed.
- K. P. Shine, J. S. Fuglestvedt, K. Hailemariam and N. Stuber, Alternatives to the global warming potential for comparing climate impacts of emissions of greenhouse gases, Clim. Change, 2005, 68, 281–302 CrossRef CAS.
- IPCC, Climate Change: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change, ed. J. T. Houghton, Y. Ding, D. J. Griggs, M. Noguer, P. J. van Der Linden, X. Dai, K. Maskell and C. A Johnson, Cambridge University Press, Cambridge, 2001, p. 892 Search PubMed.
- V. Ramaswamy, O. Boucher, J. Haigh, D. Hauglustaine, J. Haywood, G. Myhre, T. Nakajima, G. Y. Shi, S. Solomon, Radiative Forcing of Climate Change, in Climate Change 2001: The Scientific Basis, ed. J. T. Houghton, Y. Ding, D. J. Griggs, M. Noguer, P. J. van Der Linden, X. Dai, K. Maskell and C. A. Johnson, Cambridge University Press, Cambridge, 2001, pp. 349–416 Search PubMed.
- G. Marland, T. A. Boden and R. J. Andres, Global, Regional, and National Fossil Fuel CO2 Emissions, in Trends: A Compendium of Data on Global Change. Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge, TN, USA, 2006, http://cdiac.ornl.gov/trends/emis/tre_glob.html Search PubMed.
- D. L. Hartmann, Global Physical Climatology, Academic Press, San Diego, 1994, p. 411 Search PubMed.
- M. G. J. den Elzen and D. P. van Vuuren, Peaking profiles for achieving long-term temperature targets with more likelihood at lower costs, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17931–17936 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2009 |
