On the efficiency limit of triplet–triplet annihilation for photochemical upconversion
Yuen Yap
Cheng
a,
Tony
Khoury
a,
Raphaël G. C. R.
Clady
a,
Murad J. Y.
Tayebjee
a,
N. J.
Ekins-Daukes
b,
Maxwell J.
Crossley
a and
Timothy W.
Schmidt
*a
aSchool of Chemistry, The University of Sydney, NSW 2006, Australia. E-mail: t.schmidt@chem.usyd.edu.au; Fax: +61 2 9351 3329; Tel: +61 2 9351 2781
bDepartment of Physics and the Grantham Institute for Climate Change, Imperial College, London, UK SW7 2AZ
First published on 3rd November 2009
Abstract
Photochemical upconversion is performed, whereby emitter triplet states are produced through triplet energy transfer from sensitizer molecules excited with low energy photons. The triplet emitter molecules undergo triplet–triplet annihilation to yield excited singlet states which emit upconverted fluorescence. Experiments comparing the 560 nm prompt fluorescence when rubrene emitter molecules are excited directly, using 525 nm laser pulses, to the delayed, upconverted fluorescence when the porphyrin sensitizer molecules are excited with 670 nm laser pulses reveal annihilation efficiencies to produce excited singlet emitters in excess of 20%. Conservative measurements reveal a 25% annihilation efficiency, while a direct comparison between the prompt and delayed fluorescence yield suggests a value as high as 33%. Due to fluorescence quenching, the photon upconversion efficiencies are lower, at 16%.
Introduction
Upconversion is the process whereby a stream of light of a given photon energy is converted into one of a higher energy. While this can be achieved under high light intensities using non-linear optical techniques and pulsed lasers, there has been recent interest in low-power, incoherent upconversion due to triplet–triplet annihilation (TTA).1–4 In this scheme, the upconverted light is produced through the reaction of triplet molecules in solution and can thus be effected under incoherent light sources such as the sun.5 If this process can be made significantly efficient, it could be applied to single-threshold solar cells to harvest that unused part of the solar spectrum of energy lower than the band-gap, boosting energy conversion efficiencies by about one-third.6,7 Despite the importance of low-power upconversion, there is still no consensus as to the theoretical upper limit for the TTA process, with various figures quoted from 11.1% to 40%.4,8 In this article, we describe an experiment in which we demonstrate annihilation efficiencies in excess of 20%, and argue that the upper limit depends on the energy level structure of the annihilating species.Triplet–triplet annihilation upconversion (TTA-UC) is performed in a mixture of two species in solution: a sensitizer and an emitter. The sensitizer absorbs low energy light through its S0–S1 transition, and is chosen so that it undergoes rapid intersystem crossing to the T1 state, sacrificing only a few kBT of energy in the process. This triplet energy is transferred to the second species, the emitter, which possesses a long-lived T1 state lower in energy than that of the sensitizer, but higher than half of the energy of its own S1 state. When two emitter molecules in their T1 states come together in solution, they form encounter complexes of singlet, triplet and quintet spin multiplicities. The singlet encounter complex, which forms with one-ninth probability, undergoes internal conversion to a state whereby one moiety is in its S1 state, and the other is in its ground state, S0. The excited moiety promptly fluoresces to yield an upconverted photon. If all triplet state emitters reacted in such a way, then N/2 upconverted photons would be produced for every N photons absorbed. In this communication, we define this as 100% upconversion efficiency. If N/2 excited emitter molecules are generated, but do not necessarily emit light, then we define this as 100% annihilation efficiency.
Singlet dioxygen production by triplet molecules, as used in photodynamic cancer therapies, is a (hetero) TTA process.9 The difference is that dioxygen is a triplet molecule in its ground state (Fig. 1a). It has been shown that molecules such as C60 can yield 1Δg O2 in 100% yield.10
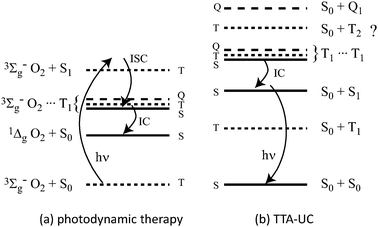 | ||
| Fig. 1 The energy level structures involved in (a) photodynamic therapy and (b) TTA-UC. In the former, when only the singlet encounter complex can undergo internal conversion, singlet oxygen is produced in high yield. In TTA-UC, only the singlet encounter complex can decay unless the T2 state is lower than the sum of two T1 states. | ||
This is easily rationalised in terms of the fates of the triplet and quintet encounter complexes. The quintet must simply dissociate back into the reactants since there is no lower quintet state into which the system can internally convert. In principle, the triplet encounter complex may decay into the ground state reactants. However, this is essentially reverse intersystem crossing of the sensitizer, which will not be assisted by the dioxygen moiety to any significant degree. As such, despite only a 1/9 chance of forming the singlet encounter complex, the triplet and quintet complexes need not quench any excited triplet energy from the system and the dioxygen yield can approach unity, as experimentally verified. This principle also operates in TTA-UC.
In TTA-UC, it is true that on purely statistical grounds only 1/9 of the encounter complexes will form the singlet state required to liberate a photon. However, claims of an 11.1% limit to upconversion efficiency based on this point are predicated upon the quintet and triplet encounter complexes quenching directly to the singlet ground states. This is highly unlikely and, as will be shown below experimentally, must be untrue. As before, the quintet encounter complex cannot undergo a spin-allowed radiationless transition to a lower state. It is thus likely that it dissociates back into triplets, preserving the stored photon energies. The triplet encounter complex may convert into a near isoenergetic state in which one moiety is in its T2 state, providing that the T2 energy is lower than twice the T1 energy. The T2 state will quite likely decay into T1. Upon dissociation of the encounter complex, one of the T1 emitters will have been quenched. In this scenario, of every four encounter complexes formed, being the three triplets and one singlet (ignoring quintets), five T1 emitters are quenched for the formation of one upconverted photon. This is 40% of the maximum yield. If the quintet encounter complexes find their way into the triplet channel, and then follow the fate of this channel as outlined above, then a 20% yield would be predicted.
The 40% limit can be broken in various ways. Firstly, it is known that some T2 states can undergo an amount of reverse intersystem crossing into S1, which would yield some fluorescence from the T2 channel.11 Secondly, if the T2 energy is higher than twice the T1 energy, and exceeds this by many times kBT, then the triplet channel may behave as does the quintet and, as long as the triplet and quintet channels remain benign, 100% TTA-UC yields can be imagined, as for singlet oxygen production by C60.10
Polycyclic aromatic hydrocarbons (PAHs) are known to often undergo an amount of intersystem crossing from S1 to yield T1 states, thereby depressing the fluorescence quantum yield. It has been shown that it is the position of the T2 state which controls this, and that a T2 state, energetically inaccessible from the S1 state, does not quench the fluorescence. Several PAH molecules are known with very high fluorescence quantum yields, including diphenylanthracene and rubrene (tetraphenyltetracene).12 Indeed, an Arrhenius study of rubrene revealed a high-lying T2 state.13 In this work, we report a test of the limits to TTA-UC efficiencies in the rubrene emitter system, sensitized with a unique porphyrin sensitizer, a tetrakisquinoxalinoporphyrin palladium(II) (PQ4Pd). In the following experiment, we measure the yield of delayed fluorescence, Fd, following excitation of the porphyrin sensitizer, and make a comparison between this and the prompt fluorescence observed by exciting the rubrene emitter directly, Fp. Since, in both cases, the molecular fluorescence is from an identical environment, any fluorescence quenching that occurs will cancel and the triplet–triplet annihilation yield is then calculated by
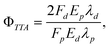 | (1) |
The upconversion yield is determined by multiplication by the quantum yield of the prompt fluorescence and the yield of triplet energy transfer from sensitizer to emitter, which is assumed to be unity,
| ΦUC = ΦTTΦTTAΦFp. | (2) |
Experimental details
PQ4Pd and/or rubrene were dissolved in toluene in a custom-built vacuum cuvette and deaerated through several freeze-pump-thaw cycles under high vacuum (10−5 mbar) to remove oxygen.Two series of experiments were performed. In the first, the delayed and prompt fluorescence was recorded by pumping the molecular mixture with 670 nm and 525 nm, respectively the absorption maxima of the sensitizer and emitter. In order to provide a means of making a conservative estimate of the annihilation yield, we also performed a series of prompt fluorescence measurements on pure rubrene solutions at various concentrations.
In all measurements, the cuvette was illuminated by the tunable output of a TOPAS OPA laser pumped by a Clark MXR CPA 2101 femtosecond laser operating at 1 kHz. The ∼1 mm2 fluorescent spot on the front face of the cuvette was entirely imaged, with a 10 cm focal length lens, through the slits of a spectrograph fitted with an iCCD detector (Acton/Princeton). The delayed fluorescence was integrated for 500 μs from 220 ns after the laser pulse, capturing the TTA-UC in its entirety while ignoring any prompt fluorescence of rubrene (which was undetectable). Under identical imaging conditions, the prompt fluorescence, due to direct excitation of the rubrene at 525 nm, was integrated for 500 ns from 30 ns before the laser pulse.
PQ4Pd (the synthesis and detailed characterization of which will be reported elsewhere) has a molar extinction coefficient in the Q-band exceeding 105 M−1 cm−1. As such, at concentrations above 10−4 M, 90% of the 670 nm photons, at the Q-band maximum, do not propagate more than about 1 mm into the cuvette. Likewise, this condition holds for rubrene excitation at concentrations above 10−3 M, with the large majority of fluorescence occurring very close to the cuvette face. As the fluorescence in both cases is due to rubrene, there was no need to take account of the detection efficiencies, and the yields could be compared directly. The use of the OPA lasers allowed for the rapid changeover from 670 nm pumping to 525 nm pumping, ensuring otherwise identical experimental conditions. The effect of laser power on both delayed and prompt fluorescence yields was determined by varying the pump laser energies from 500 nJ to 10 μJ, allowing the determination of ΦTTA.
Prompt fluorescence lifetimes were determined for rubrene, in deaerated toluene, at various concentrations using time-correlated single photon counting (TCSPC) in the front-face geometry (Halcyone/Ultrafast Systems). The samples were illuminated at 1 kHz using the femtosecond laser system as above. Signal levels were kept below 200 photons s−1.
Results and discussion
Delayed fluorescence measurements
In Fig. 2, the time-resolved emission of rubrene following laser excitation of the sensitizer at 670 nm is plotted. Importantly, the emission peaks some microseconds after the laser pulse and persists for tens of microseconds as the triplet rubrene molecules annihilate to yield upconverted photons, demonstrating the true incoherent nature of this type of upconversion.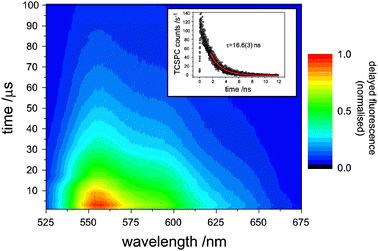 | ||
| Fig. 2 The time-dependence of upconverted rubrene fluorescence after excitation at 670 nm. The delayed fluorescence peaks within a few μs after the laser pulse and lasts for 10s of μs, demonstrating its incoherence. Inset: a time-correlated single-photon counting trace of prompt rubrene fluorescence (8 × 10−4 M) induced by a 525 nm pulse. | ||
The integrated TTA-UC yield was explored as a function of the porphyrin concentration and the 670 nm laser power, with rubrene in excess ([Rub] = 8 × 10−3 M). These results are plotted in Fig. 3 on a dual logarithmic scale. As can be seen, the laser powers employed span the region between a quadratic power dependence, where the plot exhibits a slope of 2, and a linear region where the slope is unity. In the quadratic region, the dominant triplet decay pathway is (quasi) first order (phosphorescence, quenching and intersystem crossing to S0), while in the linear region, the TTA-UC yield is maximized. Thus, increases in laser power bring about a linear response in the integrated delayed fluorescence. This may occur for two reasons. Firstly, as the energy is dumped into the system instantaneously, the triplet concentration is so high that they essentially all find an annihilation partner. If all triplets react through TTA rather than decaying by quasi-first order processes, then the delayed fluorescence yield must have a linear relationship to the number of triplets, which itself is linear in the number of photons. Secondly, even in the presence of quasi-first order triplet decay, if the sensitizer excitation is saturated, then transient bleaching occurs and TTA-UC occurs to a greater depth in the sample without increasing the local triplet concentration. A combination of these two is likely to be occurring in our experiment. Once the delayed fluorescence yield is linear in the excitation intensity, the efficiency has reached its limit, since the numerator and denominator in eqn (1) both scale linearly.
![The dependence of delayed fluorescence intensity on 670 nm excitation pulse energy at various sensitizer concentrations: [PdPQ4] = 8.0 × 10−4 M (▲), 4.0 × 10−4 M (▼), 2.0 × 10−4 M (●) and 1.2 × 10−4 M (■). In all plots [Rub] = 8.0 × 10−3 M. The response spans the range where quadratic dependence is observed (slope = 2) and where the efficiency is maximized and a linear dependence is observed (slope = 1).](/image/article/2010/CP/b913243k/b913243k-f3.gif) | ||
| Fig. 3 The dependence of delayed fluorescence intensity on 670 nm excitation pulse energy at various sensitizer concentrations: [PdPQ4] = 8.0 × 10−4 M (▲), 4.0 × 10−4 M (▼), 2.0 × 10−4 M (●) and 1.2 × 10−4 M (■). In all plots [Rub] = 8.0 × 10−3 M. The response spans the range where quadratic dependence is observed (slope = 2) and where the efficiency is maximized and a linear dependence is observed (slope = 1). | ||
The highest absolute TTA-UC yields are for a porphyrin concentration of [PdPQ4] = 4 × 10−4 M. Increases beyond this seem to decrease the absolute upconverted photon yield, probably due to quenching of the S1 emitter fluorescence by ground state porphyrin molecules.
Prompt fluorescence measurements
In order to determine the yield of S1 rubrene molecules from 670 nm photons, and thus the TTA yield, ΦTTA, the prompt fluorescence yield was measured as a function of 525 nm laser power on the same samples. These results are plotted in Fig. 4 (solid markers), on a scale allowing comparison with the delayed fluorescence results in Fig. 3. Generally, the yields are about tenfold higher per μJ, and are largely linear. However, the dependence is actually slightly sub-linear, indicating absorption (and hence waste) of photons due to excited species, a point which is addressed below.![The dependence of prompt fluorescence intensity on 525 nm excitation pulse energy at various sensitizer concentrations: [PdPQ4] = 8.0 × 10−4 M (▲), 4.0 × 10−4 M (▼), 2.0 × 10−4 M (●) and 1.2 × 10−4 M (■), with [Rub] fixed at 8.0 × 10−3 M. Also, the fluorescence observed from pure rubrene samples is plotted for 9.0 × 10−3 M (△), 4.8 × 10−3 M (▽), 2.1 × 10−3 M (○), 7.7 × 10−4 M (□), 7.3 × 10−4 M (◇) and 3.6 × 10−4 M ().](/image/article/2010/CP/b913243k/b913243k-f4.gif) | ||
Fig. 4 The dependence of prompt fluorescence intensity on 525 nm excitation pulse energy at various sensitizer concentrations: [PdPQ4] = 8.0 × 10−4 M (▲), 4.0 × 10−4 M (▼), 2.0 × 10−4 M (●) and 1.2 × 10−4 M (■), with [Rub] fixed at 8.0 × 10−3 M. Also, the fluorescence observed from pure rubrene samples is plotted for 9.0 × 10−3 M (△), 4.8 × 10−3 M (▽), 2.1 × 10−3 M (○), 7.7 × 10−4 M (□), 7.3 × 10−4 M (◇) and 3.6 × 10−4 M (![[hexagon open, flat-side down]](https://www.rsc.org/images/entities/char_e1c0.gif) ). ). | ||
Accounting for a very small percentage which is absorbed by the porphyrin (which is easily calculated from absorption spectra), it is assumed that the remaining 525 nm photons promote rubrene to its S1 state. Since any quenching of delayed fluorescence will be identical to the prompt fluorescence, this comparison provides a measurement of ΦTTA, the annihilation yield. However, while quenching is not a problem for an estimate of ΦTTA, the assumption that each 525 nm photon produces an excited rubrene (but not necessarily a photon of fluorescence) must be satisfied. To this end, we fitted the plots in Fig. 4 (on a linear scale) to a 2nd-order polynomial, and extrapolated the slope to small photon flux. As such, any laser power effects which may reduce the size of the denominator in the ΦTTA expression (eqn (1)) are eliminated.
To investigate the effect of the porphyrin on prompt fluorescence measurements, a series of measurements were performed on pure rubrene samples of various concentrations up to that employed in the TTA-UC measurements. These are also plotted in Fig. 4 and the extrapolations of dFp/dEp to Ep = 0 were performed as above. The pure rubrene prompt fluorescence yields are significantly higher than those with porphyrin, indicating quenching due to the sensitizer.
Triplet–triplet annihilation yields
To take account of the effects of laser intensity on the prompt fluorescence measurements, the fluorescence per unit of laser pulse energy was extrapolated to zero energy. The appropriately modified expression for the annihilation yield is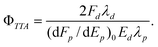 | (3) |
![The dependence of annihilation efficiency on 670 nm excitation pulse energy at various sensitizer concentrations: [PdPQ4] = 8.0 × 10−4 M (▲), 4.0 × 10−4 M (▼), 2.0 × 10−4 M (●) and 1.2 × 10−4 M (■). (a) The prompt fluorescence reference is performed in situ, taking account of all quenching processes occurring in the upconversion experiments. (b) The prompt fluorescence reference is for pure rubrene, [Rub] = 8.0 × 10−3 M, thus providing a pessimistic estimate of the annihilation yield.](/image/article/2010/CP/b913243k/b913243k-f5.gif) | ||
| Fig. 5 The dependence of annihilation efficiency on 670 nm excitation pulse energy at various sensitizer concentrations: [PdPQ4] = 8.0 × 10−4 M (▲), 4.0 × 10−4 M (▼), 2.0 × 10−4 M (●) and 1.2 × 10−4 M (■). (a) The prompt fluorescence reference is performed in situ, taking account of all quenching processes occurring in the upconversion experiments. (b) The prompt fluorescence reference is for pure rubrene, [Rub] = 8.0 × 10−3 M, thus providing a pessimistic estimate of the annihilation yield. | ||
Photon upconversion yield
An estimate of the actual upconversion yield, which is of practical interest, as opposed to the annihilation yield, which is of fundamental interest, requires knowledge of the quantum yield for prompt fluorescence (eqn (2)). It is known that dilute rubrene, under deaerated conditions in toluene has a fluorescence quantum yield near unity (0.98 ± 0.02).13 However, under our conditions, it is almost certainly less than this. In the presence of dynamic quenching, a reduced fluorescence quantum yield manifests as a shortened fluorescence lifetime. However, TCSPC measurements of the fluorescence lifetime revealed an increase of lifetime with increasing rubrene concentration (Fig. 6). This is due to reabsorption-reemission effects and has been observed before for the similar diphenyl anthracene molecule.14 Our lowest concentration lifetime measurement (10−6 M, not plotted), at 13 ns, is shorter than the natural lifetime of 16.4 ns, probably due to quenching by oxygen (although we attempted to remove this by several freeze-pump-thaw cycles, identical to the TTA measurements). The quantum yield is thus 0.8 at these low concentrations, and may be reduced at high concentrations if self quenching is important. The plot of (dFp/dEp)0 against rubrene concentration (Fig. 6) reveals a peak near 8 × 10−4 M, where the laser beam is effectively stopped within 1 mm of the cuvette face. Further increases in concentration reveal a small drop in prompt fluorescence. This may be due to very inefficient self-quenching, which would be within the range of error at 8 × 10−4 M. For the purposes of a pessimistic upconversion yield estimate, we take (dFp/dEp)0 at [Rub] = 8 × 10−4 M and utilize the quantum yield of 0.8, as determined from fluorescence lifetime measurements under dilute conditions. These numbers combine to give an upconversion yield, ΦUC, of (16 ± 1)%. However, the main purpose of the present article is to disprove the 11.1% limit to the annihilation yield, which shall be the focus of the remainder of the discussion.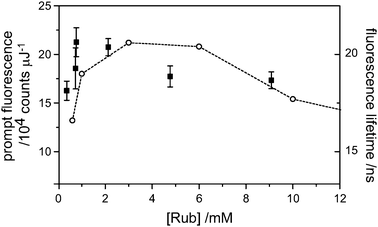 | ||
| Fig. 6 The integrated prompt fluorescence yields (dFp/dEp) of rubrene (only) solutions in deaerated toluene (■). The yield peaks at 1 mM as the fluorescence imaging is optimized and is hardly diminished over a further 10-fold increase in concentration, indicating minimal self-quenching. The observed fluorescence lifetimes (○) increased above the natural lifetime (16.4 ns) due to re-absorption effects. | ||
Implications
If the encounter complexes of pairs of triplet emitters in solution form statistically, then we expect 5/9 quintets, 3/9 triplets, and 1/9 singlets. As such, for every 18 triplets that react, 10 will react through the quintet channel, six through the triplet channel, and two through the singlet channel. The maximum number of upconverted photons possible from 18 triplets (which themselves originate from 18 low energy photons) is nine. Taking this as 100%, then, if only the singlet channel produces photons, and the other channels completely quench the triplet energy, we will generate one upconverted photon from 18 input photons, which is 11.1% of the maximum yield.We report a conservative estimate of the annihilation yield of 25 ± 2%, which is comfortably in excess of the 11.1% scenario. This implies incomplete quenching of the triplet by the quintet and triplet channels. Hund’s rule alone suggests that the quintet channel should be the lowest energy of the three. However, while Hund’s rule applies generally for well overlapped orbitals, the ordering of spin states for separated but coupled spins is a matter of ferromagnetic versus antiferromagnetic coupling. In the case of the O2·O2 dimer, the two ground state triplets interact to bring about potential energy surfaces of singlet, triplet and quintet multiplicities. A recent extensive ab initio study of the ordering of these spin states reveals the singlet state to be the most strongly bound, and the quintet to have the highest energy, as expected for antiferromagnetic coupling.15 We expect the rubrene triplet states to behave similarly, with the quintet encounter complex having an energy higher than the triplet, which is in turn higher than the singlet.
Just as the singlet channel promotes a near isoenergetic decay onto the S1 + S0 potential, analogously, the triplet channel should promote a crossing to the T2 + S0 potential, providing this is energetically accessible. This is the scheme favoured by Bachilo and Weisman, who devised a method to determine triplet yields by comparing prompt and delayed fluorescence.16 The T2 state will most likely decay almost exclusively non-radiatively to the T1 state. The dimer can then dissociate, returning a triplet emitter to the reaction bath.
The quintet channel cannot undergo any spin-allowed decay. If one were to suppose that it could decay into the triplet channel then one may ask why the triplet channel in turn does no decay into the singlet channel. If, for the sake of argument, the quintet channel could lead the complex onto the triplet surface, and if it reacted as above, quenching one triplet state, then from the 18 triplets reacting statistically, five would be quenched in the quintet channel, three in the triplet channel, and two in the singlet channel, yielding a single S1 emitter molecule. In this case, there is one S1 emitter produced from 10 triplets which is 20% of the maximum. Our conservative annihilation yield of 25% comfortably exceeds this, which implies that the quintet encounters must dissociate back into two triplets, as previously assumed.8,16 We favour this mechanism, where the quintet channel does not participate. As such, quenching three triplets in the triplet channel and two in the singlet channel for one excited emitter molecule is 40% of the maximum. Our conservative 25% and more realistic 33% annihilation measurements are consistent with this upper limit.
At low triplet concentrations in continuous-wave illumination experiments,4 a quadratic dependence of TTA-UC yield is observed, which should smoothly evolve into a linear dependence as the efficiency approaches a maximum.17 As explained above, it is a necessary requirement of approaching maximum efficiency that the TTA-UC yield exhibits a near-linear dependence with light intensity. It can thus be concluded that any experiment which exhibits a quadratic dependence must still be limited by the quasi-first order processes, such as reaction with ambient O2.
While the laser intensity during the laser pulse in our experiments is as high as 13 GW cm−2, this only brings about a certain population of triplets during the 150 fs of the laser pulse, and should not itself be considered comparable to continuous excitation at 13 GW cm−2. The average power is actually 2 W cm−2, but since the triplets decay within about 30 ms, and the laser repetition rate is 1 kHz, one may estimate that one needs 30 times higher continuous wave (cw) intensities to reach the same steady-state triplet concentration, i.e. 60 W cm−2. The lowest intensities employed are therefore equivalent to cw excitation with about 1.5 W cm−2, only one order of magnitude higher than sunlight. At the lowest intensity, our best annihilation yield was a few percent, and thus under sunlight, one would expect less than 1%. However, under a modest solar concentration, this would be increased considerably.
Conclusions
We have demonstrated annihilation efficiencies conservatively estimated at 25%, far in excess of the widely accepted 11.1% limit. Our direct comparison between prompt and delayed fluorescence suggests a higher annihilation yield of 33%. The corresponding photon upconversion efficiency is estimated to be 16%.The 25% result on its own indicates that the quintet and triplet complexes most likely do not dissociate into ground state monomers, but that triplet emitters are returned to the milieu to be granted a second chance at performing TTA-UC. It remains to be shown if efficiencies in excess of 40% can be obtained, which would indicate that the quintet and triplet channels are both attenuated. If this can be achieved, it will be with an emitter with an exceptionally high energy T2 state.
Notes and references
- S. Baluschev, V. Yakutkin, T. Miteva, Y. Avlasevich, S. Chernov, S. Aleshchenkov, G. Nelles, A. Cheprakov, A. Yasuda, K. Müllen and Gerhard Wegner, Angew. Chem., Int. Ed., 2007, 46, 7693 CrossRef CAS.
- S. Baluschev, V. Yakutkin, G. Wegner, T. Miteva, G. Nelles, A. Yasuda, S. Chernov, S. Aleshchenkov and A. Cheprakov, Appl. Phys. Lett., 2007, 90, 181103 CrossRef.
- T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. A, 2009, 113, 5912 CrossRef CAS.
- T. N. Singh-Rachford, A. Haefele, R. Ziessel and F. N. Castellano, J. Am. Chem. Soc., 2008, 130, 16164 CrossRef CAS.
- S. Baluschev, T. Miteva, V. Yakutkin, G. Nelles, A. Yasuda and G. Wegner, Phys. Rev. Lett., 2006, 97, 143903 CrossRef CAS.
- T. Trupke, A. Shalav, B. Richards, P. Würfel and M. Green M, Sol. Energy Mater. Sol. Cells, 2006, 90, 3327 CrossRef CAS.
- N. J. Ekins-Daukes and T. W. Schmidt, Appl. Phys. Lett., 2008, 93, 063507 CrossRef.
- P. P. Levin, Dokl. Phys. Chem., 2003, 388, 10–12 CrossRef CAS.
- A. J. McLean and T. G. Truscott, J. Chem. Soc., Faraday Trans., 1990, 86, 2671 RSC.
- J. W. Arbogast, A. P. Darmanyan, C. S. Foote, Y. Rubin, F. N. Diederich, M. M. Alvarez, S. J. Anz and R. L. Whetten, J. Phys. Chem., 1991, 95, 11 CrossRef CAS.
- S. Kobayashi, K. Kikuchi and H. Kokubun, Chem. Phys. Lett., 1976, 42, 494 CrossRef CAS.
- C. Burgdorff, T. Kircher and H.-G. Löhmannsröben, Spectrochim. Acta, Part A, 1988, 44, 1137 CrossRef.
- F. Lewitzka and H.-G. Löhmannsröben, Z. Phys. Chem. Neue Folge, 1986, 150, 69 CAS.
- J. M. G. Martinho, A. L. Maçanita and M. N. Berberan-Santos, J. Chem. Phys., 1989, 90, 53 CrossRef CAS.
- M. Bartolomei, M. I. Hernandez, J. Campos-Martinez, E. Carmona-Novilloa and R. Hernandez-Lamoneda, Phys. Chem. Chem. Phys., 2008, 10, 5374–5380 RSC.
- S. M. Bachilo and R. B. Weisman, J. Phys. Chem. A, 2000, 104, 7711 CrossRef CAS.
- J. E. Auckett, Y. Y. Cheng, T. Khoury, R. G. C. R. Clady, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Conf. Ser., 2009, 185, 012002 CrossRef.
| This journal is © the Owner Societies 2010 |
