Pseudorotation in pyrrolidine: rotational coherence spectroscopy and ab initio calculations of a large amplitude intramolecular motion†
Maksim
Kunitski
a,
Christoph
Riehn
b,
Victor V.
Matylitsky
a,
Pilarisetty
Tarakeshwar
*c and
Bernhard
Brutschy
*a
aInstitut für Physikalische und Theoretische Chemie, Goethe-Universität Frankfurt am Main, Max-von-Laue-Straße 760438 Frankfurt am Main, Germany. E-mail: brutschy@chemie.uni-frankfurt.de; Fax: +49 (0)69 798 29560; Tel: +49 (0)69 798 29424
bDepartment of Chemistry, Technische Universität Kaiserslautern, Erwin-Schrödinger-Straße 52, 67663 Kaiserslautern, Germany
cDepartment of Chemistry, University of Nevada Las Vegas, 4505 Maryland Parkway, Las Vegas, NV 89154, USA. E-mail: tarakesh@unlv.nevada.edu
First published on 9th November 2009
Abstract
Pseudorotation in the pyrrolidine molecule was studied by means of femtosecond degenerate four-wave mixing spectroscopy both in the gas cell at room temperature and under supersonic expansion. The experimental observations were reproduced by a fitted simulation based on a one-dimensional model for pseudorotation. Of the two conformers, axial and equatorial, the latter was found to be stabilized by about 29 ± 10 cm−1 relative to the former one. The barrier for pseudorotation was determined to be 220 ± 20 cm−1. In addition, quantum chemical calculations of the pseudorotational path of pyrrolidine were performed using the synchronous transit-guided quasi-Newton method at the MP2 and B3LYP levels of theory. Subsequent CCSD(T) calculations yield the energy preference of the equatorial conformer and the barrier for pseudorotation to be 17 and 284 cm−1, respectively.
1. Introduction
Paths presenting low energy barriers to conformational change are of special interest because they govern the progress of many important processes in chemistry and biology.1–3 Amongst the several factors controlling the conformation of molecules, pseudorotation (PR) is one of the most widely invoked but least understood intramolecular motions.1,2,4,5 Though more than 60 years have elapsed since Kilpatrick et al.4 put forward the concept of PR to explain the anomalously high entropy of cyclopentane, little is known about its energetic relevance in complex molecular systems.PR is an inherent property of saturated five-membered rings. It is an out-of-plane ring-puckering vibration that causes the ring atoms to move in such a way that the phase of the puckering rotates around the ring. Since it is a periodic motion it is convenient to use an angle (ϕ) as the pseudorotational coordinate. An important aspect of PR is that it represents a lower energy path between molecular conformations as compared to ring inversion.6 This is illustrated in Fig. 1 at the example of the pyrrolidine molecule. PR plays an important role in a wide range of biomolecules such as the deoxyribose/ribose of DNA/RNA,7 the amino acid proline, nicotine and numerous drugs containing the 5-membered thiazolidine ring, such as penicillin. For instance a recent study has shown that the side-chain flexibility of the proline residue, which largely arises from PR, is coupled to the backbone conformation of a protein.8
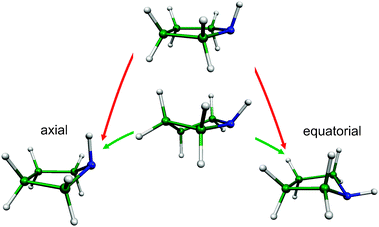 | ||
| Fig. 1 Two ways of interconversion of the axial (ϕ = 0°) and equatorial (ϕ = 180°) conformers of pyrrolidine: pseudorotation (green, <300 cm−1) and ring inversion (red, ∼1500 cm−1).6 | ||
Pyrrolidine (PYR) was chosen as an archetypical system for studying PR since it is an essential component of several biologically important molecules and the relatively sparse experimental information available about PR in this molecule.
Several experimental techniques have been utilized for studying ring-puckering vibration and PR.1,2 Vibrational spectroscopy1 is used to investigate energetical but not structural aspects of PR. Concerning PYR, however, only one vibrational mode corresponding to PR was reported so far, but it was not sufficient for gaining information about the energetics of PR in this molecule.9,10 Nuclear magnetic resonance11 and electron diffraction (ED)11,12 enable the determination of energetic preferences and structures of lower pseudorotational states, however, information about the complete pseudorotational potential usually remains beyond their scope. The gas-phase ED study of the conformational preferences in pyrrolidine in conjunction with ab initio calculations indicated that the axial conformer is energetically the most stable one,13 an assignment which was revised later by microwave spectroscopy.14 However it was conceded that the signal intensity was not very sensitive to the conformation.13 Microwave spectroscopy (MW) is a straightforward approach for precise determination of both potential energy and structural changes along a pseudorotational pathway15,16 but is not suitable for molecules lacking or possessing a small dipole moment. This was the reason why the equatorial conformer of PYR was not observed in early microwave investigations17 and as a consequence, the axial conformer was assumed to be the most stable structure. Only later under better cooling conditions in a free jet experiment the equatorial conformer turned out to be the most stable structure.14,18 The energy difference between the axial and equatorial minima was estimated to be lower than 220 cm−1.14
High resolution rotationally resolved infrared spectroscopy was shown to be applicable for studing ring puckering in four-membered ring compounds.19–21 The assignment of the spectra however is not an easy task, mainly due to their congestion. To the best of our knowledge, no high resolution infrared spectra of molecules undergoing PR have been reported so far. Recently single molecule vibrational spectroscopy22 was exploited for studying a pyrrolidine molecule attached to the Ag(001) surface at a temperature of 9 K. The frequency of 298 cm−1 was reported and assigned to the barrier for PR. This mode however may be also attributed to ring inversion, as shown in several other vibrational studies.6,9,10
In a recent theoretical study on PYR Carballeira et al.6 revised the previous findings23 and showed that the calculated energy difference between the axial and equatorial conformers strongly depends both on the quantum chemistry method and the basis set. The pseudorotational path of pyrrolidine was also modeled by constrained optimization of several points along the pseudorotational path. Subsequent single point calculations yielded the energy barrier for pseudorotation of 248 cm−1 at MP2 and 236 cm−1 at B3LYP levels of theory with the 6-311++G(3df,3pd) basis set. It was also stated that explicit inclusion of electron correlation and zero-point energies corrections would lower the estimated barrier for PR down to 150 cm−1. The barrier to ring inversion was estimated to be around 1500 cm−1.
Femtosecond degenerate four-wave mixing (fs DFWM), an ultrafast pump–probe laser technique, enables in its many different implementations to study different kinds of molecular dynamics.24–27 In the scheme utilized in rotational coherence spectroscopy, which is used in the present study, fs DFWM allows for the time-domain observation of the coherent rotation of a molecular ensemble. Being a Raman type spectroscopy, fs DFWM has proven to be a powerful tool for investigating the structure of large molecular systems at thermal equilibrium, even if they do not possess a permanent dipole moment.28,29 Recently fs DFWM was applied to obtain accurate rotational constants for several lower vibrational states of cyclobutane30 and cyclooctatetraene.31
In this work fs DFWM spectroscopy was applied for the first time to study such a large amplitude intramolecular motion as PR at example of the pyrrolidine molecule. The interpretation of the experimental fs DFWM spectra was done by means of the simulation based on a one-dimensional quantum mechanical model for PR. This allowed for determination of the energy potential and the rotational constants along the pseudorotational path. The experimental findings were additionally supplemented by unrestrained high level quantum chemistry calculations.
The paper is organized as follows. We initially discuss the theoretical background of PR in five-membered ring compounds. Than follows the description of experimental details, the simulation procedure and the quantum chemical methods utilized in the current work. Subsequently we discuss the results.
2. Theoretical framework
2.1 Pseudorotation
The theory of ring puckering in five-membered saturated rings was developed by Harris et al.32 For such a system there are 5–3 = 2 out-of-plane skeletal modes consisting of a bend and a twist. Assuming that rotation and other vibrations may be separated from these two modes, the Hamiltonian may be written as follows: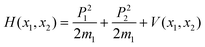 | (1) |
The Hamiltonian (1) may also be written in polar coordinates in the way that the radial coordinate expresses the amplitude of the ring puckering and the angular coordinate relates to the puckering phase. While the motion in the radial coordinate is nothing else than ring inversion, the puckering phase motion was termed pseudorotation.4,32 In PYR the barrier for inversion through the planar ring is much higher than the barrier for PR.6 Therefore, the puckering amplitude mode can be separated from the puckering phase mode. Then, PR alone can be described with the following one-dimensional Hamiltonian:32
| H(ϕ) = BpP2ϕ + V(ϕ) | (2) |
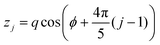 | (3) |
 | ||
| Fig. 2 The envelope structures of pyrrolidine and the corresponding pseudorotational angles ϕ. In all these structures four atoms of the ring are in one plane, while the fifth one (indicated by a red arrow) is not. This pucker rotates around the ring during pseudorotation. | ||
The solution of the Schrödinger equation that corresponds to Hamiltonian (2) can be numerically obtained in the free rotor basis set.34 For this purpose the potential V(ϕ) can be parameterized in the following way:
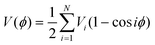 | (4) |
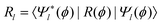 | (5) |
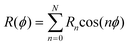 | (6) |
2.2 Pseudorotational potential
Previous studies on PYR6,14 favor a shape of the pseudorotational potential where two energetically non-identical minima (the axial and equatorial forms) are separated by a barrier (Fig. 3). The energy difference of the two minima was experimentally estimated to be lower than 220 cm−1.14 The analysis of the solutions of the one-dimensional model for PR indicated that depending on the barrier height two limiting cases may be observed in experiment. The first one occurs when the barrier for PR is rather high (related to the thermal energy), so that only a few of the lowest pseudorotational states are populated. The average geometries of these states are very close to those of the axial and equatorial conformers, since the molecule is localized in the regions of the two minima, namely close to the pseudorotational angles of 0° and 180°. Therefore the spectrum will appear mainly as a superposition of the spectra of two structures. The second case is when the barrier for pseudorotation is low. In this case, a number of pseudorotational levels will be populated and contribute to the experimental spectrum.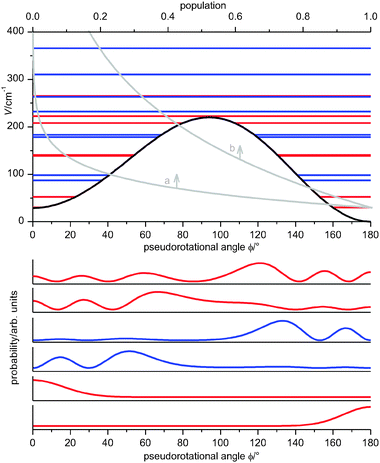 | ||
| Fig. 3 Top: Pseudorotational potential and corresponding levels with their relative Boltzmann populations at temperatures of 68 K (a) and 298 K (b). Bottom: The probability density functions of the first six pseudorotational levels. The parity of levels is shown by red (even) and blue (odd) colors. The levels above 300 cm−1 are doubly degenerated. | ||
These two limiting cases can be illustrated by considering a potential with a barrier height of 220 cm−1 and the energy difference between the axial and equatorial conformers of 29 cm−1 (these values will be obtained below from the fitted simulation of the room-temperature fs DFWM spectrum of PYR, see Table 2). The calculated pseudorotational energy levels and their populations at two temperatures 68 K and 298 K are shown on the top of Fig. 3. On the bottom the probability density functions of the first six pseudorotational states are depicted. As one can see the higher the state the more delocalized is the molecule on the pseudorotational path. Thus at low temperatures (about 68 K and below) only the structures close to 0° and 180° will be observed in experiment. With increase of the temperature more and more conformations along the pseudorotational path will contribute to the spectrum.
2.3 Simulation of the fs DFWM spectrum
Simulation of the fs DFWM spectrum of a single species in the semirigid rotor approximation has been previously discussed in detail.28,29,35 Briefly, the typical time-resolved fs DFWM spectrum of a single species consists of equidistant signal peaks called transients or recurrences. The period of such a transient sequence relates to the rotational constants (structural parameters) of the molecule under investigation. Quantitative simulation of the fs DFWM spectrum requires the following molecular properties to be known: rotational constants, centrifugal distortion constants, rotational temperature and anisotropy of the polarizability tensor. In order to reduce the number of parameters in the simulation, the following approximations were made. Only two terms of quartic centrifugal constants ΔJ, ΔJK were included, since the other terms have a negligible influence on the spectrum in case of a nearly symmetric top and, in particular, when no K-type transients are observed.28 Only diagonal elements of the polarizability tensor were considered, which is justified by the fact that the off-diagonal elements are usually much smaller. The diagonal components of the tensor might be further parameterized by only one parameter φ.35 Therefore, in total, seven parameters are required for the simulation of a fs DFWM spectrum of a single species.A fs DFWM spectrum of a mixture of several species or of one species with several low-frequency vibrations may be constructed as a coherent superposition of the individual contributions with certain weights, which in the latter case correspond to the Boltzmann populations of the vibrational states.26,30,31
As was already mentioned, pseudorotation causes significant changes in the molecular structure and therefore the rotation of the molecule cannot be described within the scope of a semirigid rotor approximation. In order to consider pseudorotation in the simulation each pseudorotational level is considered as a single species with its own set of averaged molecular properties such as rotational constants, polarizability, centrifugal distortion constants. Thus the complete simulation procedure consists of the following steps. First the pseudorotational levels are calculated relying on the pseudorotational potential and the kinetic term constant Bp. Next the expectation values of the rotational constants, centrifugal distortion constants and polarizability parameter φ are evaluated using eqn (5). With these data the fs DFWM spectra are generated for each pseudorotational state in the way as for a single species using a semirigid rotor approximation. A coherent superposition of all individual fs DFWM spectra weighted by the Boltzmann population of the corresponding pseudorotational levels yields the complete fs DFWM spectrum.
The above discussion is not limited to the case of PR, but may be applicable to other kinds of intramolecular motions such as ring-puckering in four-membered ring compounds or rotation around a central bond in n-butane-like molecules. For further details see Supp. Inf.
3. Methods and material
3.1 Experimental
The femtosecond degenerate four-wave mixing spectra of PYR were recorded using an experimental setup that has been previously described in detail.28,29 The vapour pressure of PYR in the gas cell was about 65 mbar at a temperature of 298 K. The supersonic expansion was produced by a slit nozzle of dimensions: 0.1 × 3 mm. Under the low-concentration conditions of a supersonic expansion, a slit nozzle provides a much better signal-to-noise ratio than a round orifice of the same cross section. This is due to the fact that a four-wave mixing signal depends on the square of the interaction length of the laser beams. Helium at 0.4 bar stagnation pressure was bubbled through liquid PYR and expanded adiabatically into a vacuum chamber at a background pressure of 10−4 bar. The interaction region of the three laser beams was located at a distance of approximately 2mm from the nozzle. PYR (= 98.0%, purum grade) was obtained from Fluka and used without further purification.3.2 Quantum chemistry calculations
The synchronous transit-guided quasi-Newton (STQN) method36,37 was applied for generating various points along the pseudorotational pathway of PYR. Compared to previous simulations of the pseudorotational barrier,6 the STQN approach enables a more detailed following the pseudorotational pathway without resorting to artificial geometric constraints. The STQN calculations were carried out at both the second order Møller–Plesset perturbation (MP2) and density functional (B3LYP) levels of theory using the aug-cc-pVXZ (X = D,T) basis sets. Additionally, CCSD(T) calculations38,39 with aug-cc-pVD(T)Z basis sets were performed. The energy difference between the axial and equatorial conformers of PYR was also calculated at the MP2 level of theory with (aug)-cc-pCVXZ (X = D,T,Q) basis sets.4. Results and discussion
4.1 Experimental fs DFWM spectra of pyrrolidine
The fs DFWM spectra of PYR were recorded both in the gas cell (298 K) and in the supersonic expansion. Sixteen recurrences of the room temperature spectrum and ten of the supersonic expansion spectrum are shown in Fig. 4 and 5.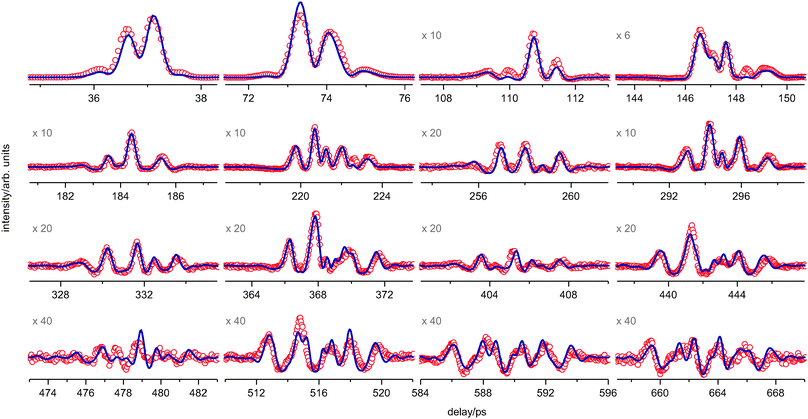 | ||
| Fig. 4 The experimental fs DFWM spectrum (red) of PYR at room temperature (298 K) and the fitted simulation (blue) using the one-dimensional model for PR. The magnification factor of some weak recurrences is given. | ||
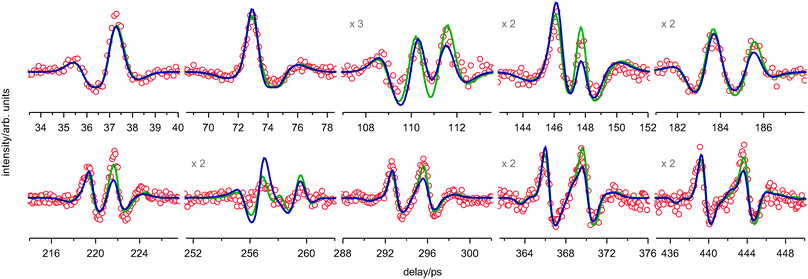 | ||
| Fig. 5 The experimental fs DFWM spectrum (red) of PYR measured under supersonic expansion and the fitted simulations: green—using only 2 conformers, blue—using the pseudorotational model with parameters taken from the fit of the room-temperature spectrum. The magnification factor of some weak recurrences is given. | ||
One can clearly see that the supersonic jet spectrum (Fig. 5) contains a permanent signal component, which results in the negative signal modulations (relative to the background level). This occurs at higher laser intensity, which had to be employed to increase the signal under the conditions of the supersonic expansion. A very small permanent signal component is present in the cell spectrum as well. This can be recognized on the late recurrences, which are of rather small intensity (Fig. 4, ×20 and ×40). It can be explained by non-linear field effects, formation of an ion grating or a plasma and additional scattering thereof.40,41 In the first approximation these high field effect can be satisfactorily described by means of a local field oscillator,28,42 which was also included in the simulation procedure.28
The shapes of the rotational recurrences of the experimental spectra appear to be much more complex than those of a single rigid molecule. Therefore the first attempt to explain the experimental observations was based on the assumption that the spectra result from a mixture of two conformers, axial and equatorial, as identified in previous studies.6,13,14,17 As shown in Fig. 5 (green) the spectrum measured under supersonic expansion conditions can be satisfactorily fitted with two structures. The obtained rotational constants A and B (Table 1) are in good agreement (within their error bars) with the ones assigned to the axial and equatorial conformers in previous MW studies.14,17,18 Since PYR is a nearly oblate top, the fs DFWM signal is only slightly sensitive to the rotational constant C. Therefore, this constant was fixed in all fits.
| Supersonic expansiona | Cellb | MW spectroscopy18 | ||||
|---|---|---|---|---|---|---|
| eq | ax | eq | ax | eq | ax | |
| a Fitted using two conformers. b Fitted using the pseudorotational model; the equatorial and axial conformers correspond to the first and second pseudorotational levels (see Fig. 3). c Fixed in the fit. d Calculation based on the obtained pseudorotational potential. | ||||||
| A/GHz | 6.864(5) | 6.837(5) | 6.866(4) | 6.835(4) | 6.864704(6) | 6.834536(8) |
| B/GHz | 6.788(5) | 6.680(5) | 6.787(4) | 6.682(4) | 6.791908(5) | 6.677856(8) |
| C/GHz | 3.9004c | 3.888062c | 3.895c | 3.895c | 3.9004(42) | 3.888062(8) |
| Rotational T/K | 66(9) | 298c | 10 | |||
| Relative population (ax/eq) | 1.6(3) | 0.9d | <1.0 | |||
However, the two conformers fit yields one inconsistency, namely, that the axial conformer has a greater contribution to the simulated spectrum than the equatorial one (Table 1). This indicates an energetic preference of the axial conformer over the equatorial one, which is in qualitative disagreement to the assignment reported in the literature.14
The room temperature spectrum of pyrrolidine can in no way be reproduced by a simulation using only the axial and equatorial conformers (Fig. 6). As was discussed above this is evidence that the barrier for pseudorotation is not very high-presumably below 1000 cm−1—since the signals of more than two structures are superimposed in the room temperature spectrum.
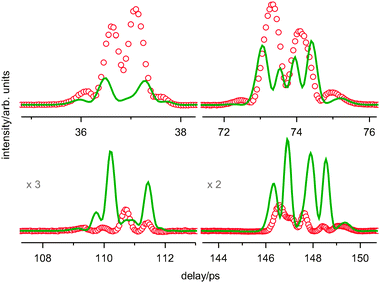 | ||
| Fig. 6 The first four recurrences of fs DFWM spectrum of pyrrolidine at room temperature: red—experimental, green-fitted simulation by only two conformers: axial and equatorial, the rotational constants are taken from microwave spectroscopy.18 | ||
4.2. Vibrational analysis in the low frequency region
In order to gain insights into the experimental spectra we proceed with the identification of vibrations that are populated at room temperature and consequently contribute to the spectrum.30,31 The infrared and Raman spectra of PYR were reported by Billes et al.9 and El-Gogary et al.10 The normal mode assignment of the spectral lines was based on scaled quantum mechanical force fields.6,9,10 The lowest frequency reported by Billes et al.9 at 65 cm−1 in the infrared spectrum (gas phase) and 71 cm−1 in the Raman spectrum (liquid) was attributed to PR.6 El-Gogary et al.10 measured the infrared and Raman spectra of liquid PYR. The lowest frequency they reported was 162 cm−1, which was not detected by Billes and coworkers.9 This mode was assigned to an out-of-plane twist of the ring, which is commonly attributed to PR.1,32 The next higher frequency of 299 cm−1 reported in both works9,10 was assigned to the ring bending mode, in other words to ring inversion. All other frequencies were measured to be higher than 580 cm−1 and therefore they are omitted from our discussion. The main conclusion from this analysis is that only two vibrations assigned to PR and ring inversion may have an influence on the room temperature fs DFWM spectrum. However, in the following, we will consider only PR on the ground state of the ring inversion vibration. This can be justified by two arguments. The first one is that the population of the first excited ring inversion state (299 cm−1) at room temperature amounts to only about 24% of the ground state. The second argument is that the pseudorotational motion on the first excited ring inversion state should not differ too much from the one in the ground state, since the barrier to ring inversion is rather high so that this vibration at the bottom of its potential minima may be considered as harmonic, which means that the ring puckering amplitude q (see eqn (3)) remains almost the same in the ground and the first excited state of ring inversion. Therefore, the contribution of the state at 299 cm−1 is very similar to that of the ground state, but much weaker in intensity and thus should affect mainly amplitude of the spectrum, but not its structure.4.3 Quantum chemistry calculations
The STQN method36 was applied for optimization of 21 and 19 points along the pseudorotational path of PYR with the aug-cc-pVDZ basis set at the B3LYP and MP2 levels of theory, respectively. Additionally, the 3 points STQN optimization was carried out at the MP2 level of theory using the aug-cc-pVTZ basis set. The obtained geometries were further used for single point CCSD(T)/aug-cc-pVTZ calculations. The pseudorotational angle ϕ and the maximum puckering amplitude q (see eqn (3)) were constructed for each calculated structure using the procedure described by Cremer and Pople33 (for the dependence of q on ϕ see Fig. S1 of Supp. Inf.). The calculated potential energy along the pseudorotational path is depicted in Fig. 7. Despite the shift of the potentials both methods yield very similar barrier heights with the aug-cc-pVDZ basis set, namely 318 cm−1 (B3LYP) and 307 cm−1 (MP2). The MP2 optimization with aug-cc-pVTZ basis set and subsequent single point CCSD(T) calculations give a smaller value of about 285 cm−1. The structure with the highest energy on the pseudorotational path at B3LYP/aug-cc-pVDZ corresponds to the pseudorotational angle of 94° and is the twisted form (Fig. 7, top). The energetically highest structure at MP2/aug-cc-pVDZ relates to 104°, which is very close to the envelope form at 108°, shown in Fig. 2. The MP2 calculations with a larger basis set (aug-cc-pVTZ) yield the potential maximum being shifted even further towards the equatorial conformer, at a pseudorotational angle of about 112°. Both the MP2 and B3LYP methods give the equatorial conformer being stabilized by about 55–70 cm−1 with respect to the axial one. It has been noted earlier that most current theoretical methods are able to reproduce the relative experimental conformer energy differences within about 100 cm−1.43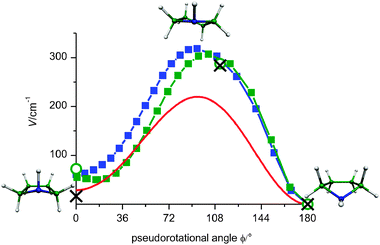 | ||
| Fig. 7 Potential energy of PR: calculated using aug-cc-pVDZ at B3LYP (blue) and MP2 (green squares). The MP2/aug-cc-pVTZ calculations are shown by green circles. Single point CCSD(T)/aug-cc-pVTZ calculations on the MP2/aug-cc-pVTZ geometries are shown by black crosses. The potential obtained from the fitted simulation of the fs DFWM cell spectrum at room temperature is plotted in red. The structures shown are those optimized at the B3LYP level. | ||
However, since the size of the basis set was found to be crucial for the energy calculation,6 we have determined the energy difference between axial and equatorial conformers at different basis sets and levels of theory (see Table 2, Fig. S2 of ESI†).
| ϕ max/° | V max/cm−1 | ΔVax–eq/cm−1 | |
|---|---|---|---|
| a Single point calculations on geometries optimized at MP2/aug-cc-pVTZ. | |||
| Fitted simulation | 94.5(2) | 220(20) | 29(10) |
| B3LYP/aug-cc-pVDZ | 94 | 318 | 61 |
| MP2/aug-cc-pVDZ | 104 | 307 | 55 |
| MP2/aug-cc-pVTZ | 112 | 288 | 72 |
| MP2/aug-cc-pVQZ | — | — | 84 |
| CCSD(T)/aug-cc-pVDZ | — | — | 7 |
| CCSD(T)/aug-cc-pVTZa | 112a | 284 | 17 |
The MP2 calculations with larger basis sets progressively favor the equatorial form, converging at a value of about 90 cm−1 (Fig. S2 of the ESI†). The CCSD(T) optimization with the aug-cc-pVDZ basis set indicates a significantly smaller stabilization (only by 7 cm−1) of the equatorial conformer over the axial one. This energetic preference becames 17 cm−1 at single point CCSD(T)/aug-cc-pVTZ calculations, carried out on the MP2/aug-cc-pVTZ geometries.
According to the MP2 calculations with the aug-cc-pVDZ basis set (Fig. 7), the energy minimum on the left side of the barrier does not corresponds to the axial form (0°, Cs symmetry, envelope), but rather to the pseudorotational angle of 18° (C1 symmetry, twist). This outcome of the MP2 calculations was also reported by Carballeira et al.6 This is not the case when larger basis sets are used (Fig. S2 of the ESI,† starting from aug-cc-pCVTZ), giving the left minimum to be exactly at the pseudorotational angle of 0°. However the lowest frequency of 16 cm−1 indicates that this minimum is rather flat.
The calculated rotational constants A and B are shown in Fig. 8. They are systematically lower than those obtained in MW studies. Thus, both theoretical methods, MP2 and B3LYP, overestimate the bond lengths at the aug-cc-pVDZ basis set. An enlargement of the basis set increases the magnitude of rotational constants, whereas consideration of higher order correlation and anharmonic effects in calculations tends to decrease it (see Table S2 of the ESI† and ref. 44). Thus, one can expect a better agreement between calculated and experimental values when larger basis sets are used and higher order correlation along with anharmonic effects are taken into account.
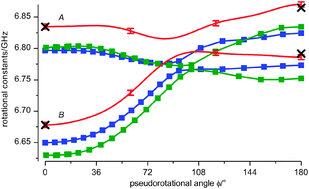 | ||
| Fig. 8 Rotational constants A and B of PYR as functions of the pseudorotational angle ϕ: calculated at B3LYP/aug-cc-pVDZ (blue) and MP2/aug-cc-pVDZ (green); obtained from the fitted simulation of the fs DFWM cell spectrum at room temperature (red). MW values for the axial and equatorial conformers18 are shown with black crosses (at ϕ = 0° and ϕ = 180°). | ||
Additionally we calculated the barrier for ring inversion (the structure with a planar ring) using the aug-cc-pVDZ basis set at the B3LYP and MP2 levels of theory. The calculations yield the values of 1422 cm−1 (B3LYP) and 1634 cm−1 (MP2). These results are in agreement with those reported by Carballeira et al.6 Thus the barrier for ring inversion in PYR is indeed about five times larger than that for PR.
4.4 Fitted simulation of the fs DFWM spectra with consideration of pseudorotation
The one-dimensional model for PR was incorporated into the simulation of the fs DFWM spectrum as described heretofore. In order to obtain an initial guess of the rotational constants we have scaled the calculated dependencies of rotational constants (Fig. 8) by normalizing their values at 0 and 180° close to those of the axial and equatorial conformers earlier determined by fitted simulation of the supersonic jet spectrum (Table 1). The fitted simulation of the fs DFWM spectrum of pyrrolidine at room temperature is depicted in Fig. 4. It shows very good agreement with the experimental spectrum. The energetic parameters of PR obtained from both the fitted simulation and quantum chemistry calculations are collected in Table 2 (see also Table S1 of the ESI).† The pseudorotational potential found from the fit is depicted in Fig. 7 (red). It indicates that the equatorial form of PYR is stabilized by 29 cm−1 with respect to the axial one. This value is smaller than those calculated at the MP2 and B3LYP levels of theory (55–92 cm−1). However, as was pointed out above, the calculated energetic stabilization of the equatorial conformer decreases when the calculations are carried out using higher levels of correlation. We believe that CCSD(T) calculations using larger basis sets might yield energetics which are in better agreement with experiment.The energetical preference of the equatorial form over the axial one, though being small, could be understood in terms of two electronic effects: steric repulsion and hyperconjugation stabilization. It is however difficult to determine which of these two effects has the greater contribution. Natural bond orbital analysis on the HF/6-31G** wavefunctions23 showed that the hyperconjugation interactions were greater than steric repulsion in the equatorial conformer of PYR, what consequently favored this conformer over the axial one. We also believe that the nitrogen lone pair plays an important role in the stabilization of the equatorial conformer because SCRF calculations of PYR carried out in the presence of polar solvent like water reverses the energetical order of the conformers (see Fig. S3 of the ESI).† Additionally, the enhanced dipole moment of the axial conformer as compared to the equatorial one can also explain its lower energy in polar solutions.
The fitted simulation yields the pseudorotational barrier height of 220 cm−1, which is lower by about 100 cm−1 than that derived from the calculations with the aug-cc-pVDZ basis set at the MP2 and B3LYP levels of theory. This discrepancy however becomes smaller (64 cm−1) when the MP2 method with a larger basis set, aug-cc-pVTZ, is used. The twisted conformation at the pseudorotational angle of about 94° was found to have the highest energy on the pseudorotational path. This value is very close to the one obtained in the calculation at the B3LYP level of theory.
It should be pointed out that the barrier for PR in PYR is higher than that in analogous five-membered saturated ring compounds such as cyclopentane (CYC, <25 cm−1)45 and tetrahydrofuran (THF, ∼30 cm−1).46 This difference is related to the subtle interplay of steric repulsion and hyperconjugation, whose contributions depend sensitively on the individual molecular structure and electronic configuration. Thus, we cannot give a simple explanation for this observation. The ongoing debate on the origin of the torsional barrier of ethane demonstrates that this analysis is a demanding task.47,48
The pseudorotational constant Bp was found to be 3.8 ± 0.1 cm−1, which is also higher than those reported for CYC (2.9 cm−1)45 and THF(3.2 cm−1).46
The fitted rotational constants A and B as functions of the pseudorotational coordinate are presented in Fig. 8. They show a similar dependence on the pseudorotational angle as the calculated ones, especially those of the MP2 level of theory, being however systematically shifted to higher values. The rotational constant C was fixed in the fit to the value of 3.895GHz (see the ESI)† since, as was stated above, its influence on the fs DFWM spectrum of PYR was found to be insignificant.
Using the fitted parameters we calculated the average values of rotational constants for the first two pseudorotational states, which correspond to the equatorial and axial conformers (see Fig. 3). These constants are collected in Table 1. They are in good agreement with the values obtained from the two-structure-fit of the spectrum measured under supersonic expansion and also close to those of previous MW studies.18
Next we checked whether the simulation based on the pseudorotational model can reproduce the experimental fs DFWM spectrum measured under supersonic expansion. All parameters required for the simulation, with the exception of the vibrational and rotational temperatures, were taken from the fit of the room-temperature spectrum. The resulting fitted simulation is shown in Fig. 5 (blue). Although the root mean-square deviation (chi-square) of this fit is higher than that using only two conformers (Fig. 5, green), the agreement with the experimental spectrum is still good. Moreover, the energetic preference of the equatorial conformer, as follows from the obtained pseudorotational potential (Fig. 7, red), is consistent with the finding of MW spectroscopy.14 This was not the case when only two structures have been considered (Table 1). From the fitted simulation the rotational and vibrational temperatures under supersonic expansion were found to be roughly the same and equal to about 68 K. This is very close to the value of 66 K obtained in the foregoing two-structure-fit (Table 1).
Thus, the invoked model for PR in PYR supported by ab initio calculations was successfully applied to the analysis and simulation of the experimental fs DFWM transients measured in a supersonic exspansion and in a gas cell.
5. Conclusions
The key findings of this study may be summarized as follows. Femtosecond degenerate four-wave mixing (fs DFWM, a pump–probe rotational coherence spectroscopic scheme) was applied successfully to the characterization of pseudorotation (PR) in gaseous pyrrolidine (PYR). The structural and energetic implications of this large amplitude motion were deduced from the detailed analysis of the fs DFWM spectra at different temperatures. It turned out that a mixture of two conformers (axial and equatorial) is definitely not sufficient to explain the fs DFWM spectrum of PYR at room temperature. Hence, it is pertinent to consider the energetics and dynamics of PR in terms of its potential and the evolution of the rotational constants (structure) along the pseudorotational path. These data were obtained by means of fitted simulations of the experimental fs DFWM spectra. Thus, the equatorial conformer of PYR was found to be by 29 ± 10 cm−1 more stable than the axial one. The barrier for PR was determined to be 220 ± 20 cm−1. As a consequence we have confirmed the results of former experimental studies on the relative stability of the axial and equatorial conformers with an independent spectroscopic method. However, clear differences and significant refinements in the quantitative analysis give evidence that the energy difference between both conformers is much smaller than estimated in previous experimental studies. Moreover, for the first time we provide for PYR the pseudorotational path, including its barrier, deduced from the fitted simulation of experimental data. Our experimental findings are in satisfactory agreement with results from high level quantum chemistry calculations, namely, the stabilization of the equatorial conformer and the pseudorotational barrier were calculated to be 17 cm−1 and 284 cm−1, respectively (single point CCSD(T)/aug-cc-pVTZ on the MP2/aug-cc-pVTZ geometries).Thus we have with fs DFWM a method at hand that allows for the analysis of conformational transformations of molecules possessing no dipole moment even under the spectroscopically often inaccessible condition of a high temperature equilibrium. The method outlined here may be applied in addition to PR for studying the wide range of large amplitude intramolecular motions, such as the puckering inversion in four-membered rings or the internal rotation along the central bond in bithiophene- and n-butane-like molecules.
Acknowledgements
M.K. and C.R. thank the Deutsche Forschungsgemeinschaft (DFG RI 749/5-1) and the Goethe University Frankfurt for financial support and M. Gelin for lots of discussions. The authors gratefully acknowledge support by the Frankfurt Centre for Scientific Computing as well as the donations of the “Messer-Foundation” and of the “Friends and Sponsors of the Goethe University”.References
- A. C. Legon, Chem. Rev., 1980, 80, 231–262 CrossRef CAS.
- H. L. Strauss, Annu. Rev. Phys. Chem., 1983, 34, 301–328 CrossRef CAS.
- D. M. Leitner, M. Havenith and M. Gruebele, Int. Rev. Phys. Chem., 2006, 25, 553–582 CrossRef CAS.
- J. E. Kilpatrick, K. S. Pitzer and R. Spitzer, J. Am. Chem. Soc., 1947, 69, 2483–2488 CrossRef CAS.
- A. F. Sax, Chem. Phys., 2008, 349, 9–31 CrossRef CAS.
- L. Carballeira, I. Perez-Juste and C. Van Alsenoy, J. Phys. Chem. A, 2002, 106, 3873–3884 CrossRef CAS.
- W. K. Olson and J. L. Sussman, J. Am. Chem. Soc., 1982, 104, 270–278 CrossRef CAS.
- B. K. Ho, E. A. Coutsias, C. Seok and K. A. Dill, Protein Sci., 2005, 14, 1011–1018 CrossRef CAS.
- F. Billes and E. Geidel, Spectrochim. Acta, Part A, 1997, 53, 2537–2551 CrossRef.
- T. M. El-Gogary and M. S. Soliman, Spectrochim. Acta, Part A, 2001, 57, 2647–2657 CrossRef CAS.
- G. V. Girichev, N. I. Giricheva, A. Bodi, P. I. Gudnason, S. Jonsdottir, A. Kvaran, I. Arnason and H. Oberhammer, Chem.–Eur. J., 2007, 13, 1776–1783 CrossRef CAS.
- H. Oberhammer, G. V. Girichev, N. I. Giricheva, A. V. Krasnov and U. Klingebiel, Inorg. Chem., 2004, 43, 3537–3542 CrossRef CAS.
- G. Pfafferott, H. Oberhammer, J. E. Boggs and W. Caminati, J. Am. Chem. Soc., 1985, 107, 2305–2309 CrossRef CAS.
- W. Caminati, A. Dell’ Erba, G. Maccaferri and P. G. Favero, J. Mol. Spectrosc., 1998, 191, 45–48 CrossRef CAS.
- G. G. Engerholm, A. C. Luntz, W. D. Gwinn and D. O. Harris, J. Chem. Phys., 1969, 50, 2446–2457 CAS.
- A. K. Mamleev, L. N. Gunderova, R. V. Galeev and A. A. Shapkin, J. Struct. Chem., 2004, 45, 960–965 CrossRef CAS.
- W. Caminati, H. Oberhammer, G. Pfafferott, R. R. Filgueira and C. H. Gomez, J. Mol. Spectrosc., 1984, 106, 217–226 CAS.
- B. Velino, A. Millemaggi, A. Dell'Erba and W. Caminati, J. Mol. Struct., 2001, 599, 89–93 CrossRef CAS.
- H. Li, C. C. Miller and L. A. Philips, J. Chem. Phys., 1994, 100, 8590–8601 CrossRef CAS.
- G. Moruzzi, M. Kunzmann, B. P. Winnewisser and M. Winnewisser, J. Mol. Spectrosc., 2003, 219, 152–162 CrossRef CAS.
- T. A. Blake, E. A. Glendening, R. L. Sams, S. W. Sharpe and S. S. Xantheas, J. Phys. Chem. A, 2007, 111, 11328–11341 CrossRef CAS.
- J. Gaudioso and W. Ho, J. Am. Chem. Soc., 2001, 123, 10095–10098 CrossRef CAS.
- L. Carballeira and I. Perez-Juste, J. Chem. Soc., Perkin Trans. 2, 1998, 1339–1345 RSC.
- M. Motzkus, S. Pedersen and A. H. Zewail, J. Phys. Chem., 1996, 100, 5620–5633 CrossRef CAS.
- H. M. Frey, P. Beaud, T. Gerber, B. Mischler, P. P. Radi and A. P. Tzannis, Appl. Phys. B: Lasers Opt., 1999, 68, 735–739 CrossRef CAS.
- M. Dantus, Annu. Rev. Phys. Chem., 2001, 52, 639–679 CrossRef CAS.
- C. Riehn, Chem. Phys., 2002, 283, 297–329 CrossRef CAS.
- V. V. Matylitsky, W. Jarzeba, C. Riehn and B. Brutschy, J. Raman Spectrosc., 2002, 33, 877–883 CrossRef CAS.
- V. V. Matylitsky, C. Riehn, M. F. Gelin and B. Brutschy, J. Chem. Phys., 2003, 119, 10553–10562 CrossRef CAS.
- D. S. Kummli, H. M. Frey and S. Leutwyler, J. Phys. Chem. A, 2007, 111, 11936–11942 CrossRef CAS.
- D. S. Kummli, S. Lobsiger, H. M. Frey, S. Leutwyler and J. F. Stanton, J. Phys. Chem. A, 2008, 112, 9134–9143 CrossRef CAS.
- D. O. Harris, G. G. Engerholm, C. A. Tolman, A. C. Luntz, R. A. Keller, H. Kim and W. D. Gwinn, J. Chem. Phys., 1969, 50, 2438–2445 CrossRef CAS.
- D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358 CrossRef CAS.
- J. D. Lewis, T. B. Malloy, T. H. Chao and J. Laane, J. Mol. Struct., 1972, 12, 427–449 CrossRef CAS.
- C. Riehn, V. V. Matylitsky and M. F. Gelin, J. Raman Spectrosc., 2003, 34, 1045–1050 CrossRef CAS.
- P. Y. Ayala and H. B. Schlegel, J. Chem. Phys., 1997, 107, 375–384 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. Montgomery, J. A. T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- J. F. Stanton, J. Gauss, M. E. Harding and P. G. Szalay, CFOUR, Coupled-cluster techniques for computational chemistry, a quantum-chemical program package with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, E. Bernholdt, Y. J. Bomble, O. Christiansen, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A. Matthews, T. Metzroth, D. P. O’Neill, D. R. Price, E. Prochnow, K. Ruud, F. Schiffmann, S. Stopkowicz, J. Vázquez, F. Wang and J. D. Watts and the integral packages/MOLECULE/(J. Almlöf and P. R. Taylor),/PROPS/ (P. R. Taylor), /ABACUS/ (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen Search PubMed; M. E. Harding, T. Metzroth, J. Gauss and A. A. Auer, J. Chem. Theory Comput., 2008, 4, 64 Search PubMed.
- J. F. Stanton, J. Gauss, J. D. Watts, M. Nooijen, N. Oliphant, S. A. Perera, P. G. Szalay, W. J. Lauderdale, S. A. Kucharski, S. R. Gwaltney, S. Beck, A. Balkov, D. E. Bernholdt, K. K. Baeck, P. Rozyczko, H. Sekino, C. Hober and R. J. Bartlett, ACES II is a program product of the Quantum Theory Project, University of Florida, pp. Integral packages included are VMOL (J. Alml and P. R. Taylor); VPROPS (P. Taylor) ABACUS; (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, J. Olsen, and P. R. Taylor). J. F. Stanton, J. Gauss, M. E. Harding and P. G. Szalay, ACES II Search PubMed.
- V. G. Stavros, E. Harel and S. R. Leone, J. Chem. Phys., 2005, 122, 064301 CrossRef.
- A. Rouzee, V. Renard, S. Guerin, O. Faucher and B. Lavorel, J. Raman Spectrosc., 2007, 38, 969–972 CrossRef CAS.
- V. G. Stavros and S. R. Leone, Chem. Phys. Lett., 2008, 452, 33–37 CrossRef CAS.
- K. B. Wiberg and Y. G. Wang, J. Comput. Chem., 2004, 25, 1127–1132 CrossRef CAS.
- C. Riehn, V. V. Matylitsky, W. Jarzeba, B. Brutschy, P. Tarakeshwar and K. S. Kim, J. Am. Chem. Soc., 2003, 125, 16455–16462 CrossRef CAS.
- L. E. Bauman and J. Laane, J. Phys. Chem., 1988, 92, 1040–1051 CrossRef CAS.
- D. G. Melnik, S. Gopalakrishnan, T. A. Miller and F. C. De Lucia, J. Chem. Phys., 2003, 118, 3589–3599 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, Angew. Chem., Int. Ed., 2003, 42, 4183–4188 CrossRef CAS.
- Y. R. Mo and J. L. Gao, Acc. Chem. Res., 2007, 40, 113–119 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A flash movie with pseudorotation in pyrrolidine; further details on the fitted simulation of the fs DFWM spectrum; calculated dependences of the maximum pseudorotational amplitude q on the pseudorotational angle ϕ; the energy difference between the axial and equatorial conformers of pyrrolidine calculated with different methods and basis sets; the experimental and calculated rotational constants of the axial and equatorial conformers of pyrrolidine; SCRF calculations of the pseudorotational pathway of pyrrolidine. See DOI: 10.1039/b917362e |
| This journal is © the Owner Societies 2010 |
