Monte Carlo study for the growth of α-Fe₂O₃ nanowires synthesized by thermal oxidation of iron

Abstract

The growing mechanism of α-Fe₂O₃ nanowires synthesized by thermal oxidation of iron is studied by the Monte Carlo method. Using a model of diffusion, the effects of synthesizing temperature, oxygen density and annealing on the morphology of the nanowires have been simulated. The results show that nanowires with a large head can only be obtained under the correct temperature and a sufficiently high density of oxygen. Under a low temperature or a low density of oxygen, particles can be obtained. And under a high temperature or after annealing, the nanowires will become thicker. The results are consistent with our experiments. This fact indicates that the growth of α-Fe₂O₃ nanowires should be a diffusion process and provides an approach for improving the quality of the nanowires.

---

Introduction

Due to their special compositions, shapes, physical and chemical properties, and their diverse applications, metal oxide nanowires have been the focus of research efforts in the recent years.^1–5 Recently, the thermal oxidation method has been widely used to prepare metal oxide nanowires of single crystals and high quality, such as α-Fe₂O₃,^6–10 CuO,¹¹ Co₃O₄¹² and V₂O₅.⁴ By reactions of SO₂, CO₂, N₂, and vapor with iron substrates, Fu et al. first used this method to obtain successfully α-Fe₂O₃ nanowires.^6,10 The method was then improved and extended. For example, by carefully controlling the temperature, α-Fe₂O₃ nanowires were also synthesized by oxidization in flowing O₂,⁸ oxygen plasma⁹ or only in air.¹³ These improvements make the method simpler, more convenient, and widely used. Some efforts have also been made for the mechanisms of the thermal oxidation method.^7–9 Because the reactive temperature (about 400–800 °C) is very low and without catalyst, two widely used mechanisms for nanowires growing in the gas phase, i.e. vapor–liquid–solid (VLS) and vapor–solid (VS), should be excluded. We⁷ once suggested a diffusion mechanism for growing α-Fe₂O₃ nanowires based on the fact that the ratio of Fe/O became smaller from the bottom to top of the nanowires. Wang⁸ and Fu¹⁰ also considered that the nanowires should grow through iron diffusion to the top. However, the mechanism lacked simulations and theoretical analyses. In this paper, we study the growing mechanism based on diffusion using the Monte Carlo (MC) method, and show that the nanowires' growth should be a process of diffusion. From the results of the simulation, a suggestion is also given to improve the quality and growing conditions of the nanowires.

Model

The experiments show that α-Fe₂O₃ nanowires grow from points on the iron surface, and along a specific direction, usually the [110] direction.^7,8 For simplicity, a square two-dimensional structure is considered. The units of energy, temperature and the lattice length are chosen as 1. One MO_x unit cell is supposed to be in a lattice. Here, M and O represent metal and oxygen, respectively, and x is chosen as 1 for simplicity. As the crystal lattice of α-Fe₂O₃ is larger than that of iron, the volume of N₁ metal unit cells is supposed to equal that of one MO in our model, i. e., there are N₁ “fixed” metal atoms in a metal lattice. On the effect of diffusion, no more than N₂ “dissociative” metal atoms can be in a lattice. Here we take N₁ = 3 and N₂ = 2. When one metal atom is oxidized successfully, it changes to MO, and other metal atoms in the lattice become dissociative. If the MO already exists in the lattice, the nanowire would grow. The sketches are shown in Fig. 1. The program is written in C code, and the detail algorithm is given below.

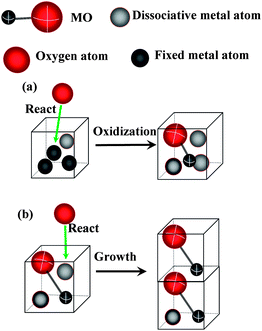Fig. 1 Sketches of the simulation. (a) Oxidation of a metal lattice with a dissociative atom. (b) A growth process.

Initialization

A line with a given length (L) on the bottom is thought to be a growing point. L is set to be 6 in the computation. Every lattice in the point contains one MO and N₂ metal atoms. As the metal atoms with high energy around the point would diffuse to it, it is convenient to consider that they do not take part in the reaction on other parts of the bottom.

Reaction

The density of oxygen molecules can be described as the trial times of all the surface lattices in a unit time (N_O), because only the atoms there can react. Metal atoms can be oxidized only if the activation energy of them and oxygen molecules is larger than the binding energy (E_C). Considering that the metal atoms in the solid phase always have low dynamic energy, we only take oxygen molecules into account. Here, we suppose that the molecules obey the Maxwell velocity distribution law and can only move along one direction. The probability of successful oxidization of one metal atom in a trial is

p = erfc(E_C/T) (1)

The atom can only react with the oxygen molecules, the kinetic energy of which is larger than E_C at the temperature of T. The metal atoms should be more stable with higher E_C. Here, we set E_C = 0.25.

Diffusion

We simulate the process of diffusion of metal ions using MC/Metropolis algorithm.¹⁴ Considering the two dimensions of the model, the trial times for the diffusion of each dissociative metal atom is

N_d = DT (2)

Here, D is set to be 200. The details of the algorithm about diffusion in a MC step are as following:

Suppose that a metal atom diffuses to a B site from an A site. we set

ξ = min{1,exp[−(ρ_B + ε − ρ_A)/T]} (3)

Here, ρ_A and ρ_B are the density of the metal atoms in A and B sites, respectively, and ε is the energy barrier, which the metal atoms should overcome in the diffusion. Given a random number η(0 < η < 1), and we accept the trial state of diffusion (B) only if η < ξ.

The diffusion should be related to the numbers of metal atoms and the kind of the lattice. The density of the metal atoms is calculated differently in different conditions. As there are N₂ metal atoms in a MO lattice at most, here we set the density ρ = m/N₂, and m is the number of metal atoms in the lattice. For the metal lattice, the density ρ = m/(N₁ + N₂). For different conditions, ε is also set to be different values. Diffusion mainly exists in the MO lattices. According to the experiments,^8,10 α-Fe₂O₃ nanowires grow along the <110> crystal direction. Wang⁸ showed that iron atoms prefer to transfer in that direction in the growing process, because of the deficiency of them in the (110) plane. The vertical direction is chosen as preferred, with ε is set to be 0.1, while 1.5 is used for the traverse direction. For diffusion from the metal lattices to MO, or in the metal, we set ε = 0 for simplicity. The iron atoms should be absorbed on the surface of α-Fe₂O₃ lattices. To simulate the absorption, ε is set to be 0.1 if the distance to the MO lattice in the space is shorter than S, and 10 for the others. S is chosen to be 3 in the calculation.

Results and discussion

First, the growing process of the nanowires with cooling is simulated. Here T_a is the reaction temperature, and t is the reaction time. The sample is cooled naturally after reaction. Using the Fourier law, we get

ΔT/Δt = −χ(T − T_r) (4)

Here, T_r is room temperature, and set to be 0.01 in the simulation. The coefficient χ = 0.01 here.

When T_a = 0.2, N_O = 100, t = 600, the morphology of the nanowire obtained from the simulation is shown in Fig. 2a. Han et al. showed that the Fe/O ratio decreased from the bottom to top, but in some places, for example, the large head on the top, it is larger than in the surroundings. The places with high Fe/O ratio usually correspond to the dark areas of the scanning electron microscopy (SEM) images.⁷ In our results, the number of the metal atoms in a unit lattice also decreases from the bottom to top in general, and in some places it is larger than the surroundings. It is the result of the nonequilibrium process of diffusion. There is also a large head with larger metal content in the nanowire, which is also in accord with the experiment in ref. 7 (see Fig. 2b). A nanowire without cooling is also shown in Fig. 2a for comparison. There is no large head on it. The head should be formed in the cooling process. The probability of oxidation is p = erfc(E_C/T). When temperature decreasing, it decreases more quickly than the diffusion coefficient does. As a result, metal atoms assemble on the top. Comparing with the computational and experimental results, it is reasonable to say that the growth of α-Fe₂O₃ nanowires should be a diffusion process.

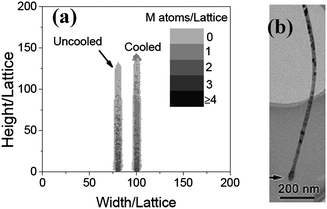Fig. 2 (a) The morphologies of the nanowires simulated (naturally cooled and uncooled, respectively) when T_a = 0.2, t = 600 and N_O = 200. (b) An image of a typical α-Fe₂O₃ nanowire with a large head.⁷

Secondly, the effect of the oxygen density and temperature on the growing process is investigated. In the former experiment, the α-Fe₂O₃ nanowires is obtained by heating iron foils at about 550–650 °C for 10 h in a weak oxidizing mixed gas (containing 18% CO₂, 70% N₂ and 0.16% SO₂) and vapor.⁶ In order to investigate the effect of the oxygen content on the morphology, the iron foils were heated in a mixed gas (argon + 0.001% oxygen) at 600 °C for 10 h. Particle-like structures with dimensions of about 2–4 μm were formed on the surface of the foil (see Fig. 3a). Fig. 3b shows the computational results of the morphologies of MO, when N_O = 1. The reacting temperature and time is kept the same as those of Fig. 2a. The sample grown with the lower oxygen density is particle-like, which is similar to that obtained in the experiment shown in Fig. 3a. From these results, it can be seen that the oxygen density affects the morphologies of the sample. In the low oxygen density, the metal atoms diffusing to the MO surface could not be oxidized immediately, and would diffuse along the surface. Some of them on the surface would be oxidized, which results in the particle forms.

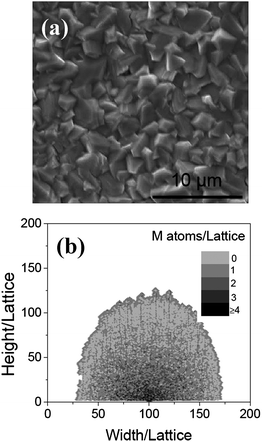Fig. 3 (a) The SEM image of the surface of iron, after annealing at 600 °C in Ar for 10 h. Particle-like structures are formed on the surface. (b) The morphologies of the nanowire obtained at N_O = 1 when T_a = 0.2, L = 6, and t = 600.

With N_O = 100, and T_r = 0.01, the effect of temperature on the morphology is also investigated. Fig. 4 shows the nanowires grown at the temperatures of 0.1 and 0.4, respectively. It can be seen that when T_a = 0.1, a particle is formed, which is similar to that shown in Fig. 2. The reason should be also same as the particle grown in a low oxygen density. At high temperature (T_a = 0.4), a wide (the width is about 30 lattices on average) wire is obtained. The growth of the wide wires can be explained as following: as the temperature increases, the probability of the diffusion of the metal atoms in the traverse direction will become bigger. As a result, the nanowire becomes wider. To test the reliability of the simulated results, the experiment was carried out at different temperatures. The iron foils were heated at 450 °C and 750 °C for 10 h in a mixed gas and water vapor. The detailed condition was the same as that in ref. 6. Fig. 5 shows the SEM images of the samples. Comparing the simulated (Fig. 4) with the experimental results (Fig. 5) demonstrates that both the theoretical and experimental results match well.

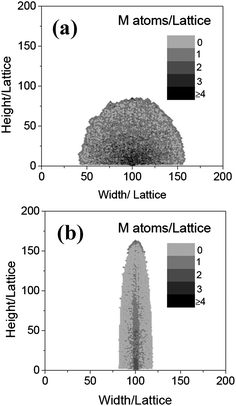Fig. 4 The morphologies of the nanowires obtained at T_a = 0.1 (a) and 0.4 (b), respectively, when N_O = 0.2, L = 6, and t = 600.

Fig. 5 The SEM images of the surface of iron annealed at 450 °C (a) and 750 °C (b) in the mixed gas shown in ref. 6.

Fourthly, using this model, the effects of annealing on morphology are also investigated. We have shown that the annealing can make the nanowires thicker in ref. 15. However, no explanation was given. In this simulation, a wire is first obtained by natural cooling, when T_a = 0.2, t = 300, and N_O = 100, and then annealed with the same temperature, reacting time and oxygen density. In this case, the wire becomes wider, as shown in Fig. 6. From the process of the simulation, it can be seen that when annealing, iron atoms with a large head would diffuse along the surface. As the diameter of the head is larger than the wire, the wire becomes wider. Comparing with the nanowire growth with t = 600 (see Fig. 6), it demonstrates that after annealing, the diffusion of the iron atoms in the large head, formed in the cooling process, makes the nanowire thicker.

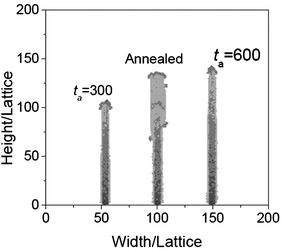Fig. 6 The morphologies of the nanowires obtained when t = 300, T_a = 0.2, N_O = 100, and annealed with the same temperature, reacting time and oxygen density. The nanowire obtained at t = 600 is shown here for comparison.

The variation of E_C and ε can also affect the morphology of the nanowires. According to eqn(1), larger E_C can bring on less-reactive oxygen molecules. The situation is like that at low oxygen density: as a result particles will be obtained. In order to investigate the effect of ε, the condition is kept the same as that in Fig. 2a, and the value of ε in the traverse direction is changed to 1.0. The result is shown in Fig. 7: a particle is obtained. Different values of ε in different crystalline directions are related to the anisotropy of the metal crystal. If the anisotropy is weak, not nanowires but particles should be obtained by thermal oxidation. The parameters E_C and ε are relative with the intrinsic properties of the metal. It means that the nanowires of some oxides might not be synthesized by oxidizing corresponding metals directly.

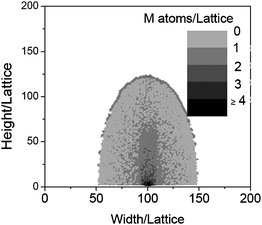Fig. 7 The morphologies of the nanowire simulated when ε = 1.5 in the traverse directionand other parameters are kept same as those in Fig. 2.

Experimental details

The iron (99.96 wt% Fe) foils were used as substrates. The details are shown in ref. 6. The surface morphology of the samples is characterized by field emission environmental scanning electron microscopy (FEI Quanta 200 FEG).

Conclusion

Using Monte Carlo method, a model of diffusion is first applied to simulate the growth process of an α-Fe₂O₃ nanowire synthesized by the thermal oxidization method. The simulated results, such as the big head on the nanowire and particles obtained under low oxygen density or low temperature, are consistent with experiment, indicating that the growth mechanism is a process of diffusion. The simulation also gives a direction for improving the quality of the nanowires. It is known that the nanowires can only be obtained under the right temperature and a sufficiently high density of oxygen When annealing, the nanowires will become thicker: this would be a restriction on applications. Fortunately, from our simulations, peeling off the nanowires from the iron substrate would be a useful method to solve this problem. Considering different parameters, the effect of the stability and the anisotropy of diffusion in the metal are also studied. It is found that the some oxide nanowires might not be synthesized by oxidizing corresponding metals directly.

Acknowledgements

The authors are grateful for the support of State Key Laboratory for Mesoscope Physics at Peking University and National Natural Science Foundation of China under grant No. 10434010. We thank Mr Xin Liang for his help in programming skills.

References

1. G. Shen, P.-C. Chen, K. Ryu and C. Zhou, J. Mater. Chem., 2009, 19, 828.
2. Z. L. Wang, J. Nanosci. Nanotechnol., 2008, 8, 27.
3. E. Comini, G. Faglia, M. Ferroni, A. Ponzoni, A. Vomiero and G. Sberveglieri, J. Mol. Catal. A: Chem., 2009, 305, 170.
4. S. Rackauskas, A. G. Nasibulin, H. Jiang, Y. Tian, V. I. Kleshch, J. Sainio, E. D. Obraztsova, S. N. Bokova, A. N. Obrazstsov and E. I. Kauppinen, Nanotechnology, 2009, 20, 165603.
5. H. E. Unalan, Y. Zhang, P. Hiralal, S. Dalal, D. Chu, G. Eda, K. B. K. Teo, M. Chhowalla, W. I. Milne and G. A. J. Amaratunga, Appl. Phys. Lett., 2009, 94, 163501.
6. Y. Y. Fu, J. Chen and H. Zhang, Chem. Phys. Lett., 2001, 350, 491.
7. Q. Han, Y. Y. Xu, Y. Y. Fu, H. Zhang, R. M. Wang, T. M. Wang and Z. Y. Chen, Chem. Phys. Lett., 2006, 431, 100.
8. X. Wen, S. Wang, Y. Ding, Z. L. Wang and S. Yang, J. Phys. Chem. B, 2005, 109, 215.
9. U. Cvelbar, Z. Chen, M. K. Sunkara and M. Mozetič, Small, 2008, 4, 1610.
10. Y. Y. Fu, R. M. Wang, J. Xu, J. Chen, Y. Yan, A. V. Narlikar and H. Zhang, Chem. Phys. Lett., 2003, 379, 373.
11. Y. W. Zhu, T. Yu, F. C. Cheong, X. J. Xu, C. T. Lim, V. B. C. Tan, J. T. L. Thong and C. H. Sow, Nanotechnology, 2005, 16, 88.
12. Z. Dong, Y. Fu, Q. Han, Y. Xu and H. Zhang, J. Phys. Chem. C, 2007, 111, 18475.
13. L.-C. Hsu, Y.-Y. Li and C.-Y. Hsiao, Nanoscale Res. Lett., 2008, 3, 330.
14. D. P. Landau, K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, World Publishing Corporation, Beijing, 2008. p. 127.
15. X. Zhang, Q. Han, Z. Dong, Y. Xu and H. Zhang, J. Mater. Sci. Technol., 2008, 24, 594.

---