Integration of sol–gel derived inorganic nanonetworks into polymers
Sebastian
Wohlrab
*ab,
Andreas
Schönhals
b,
Harald
Goering
b and
Jörg F.
Friedrich
b
aLeibniz-Institut für Katalyse e.V. an der Universität Rostock, Albert-Einstein-Str. 29a, D-18059, Germany. E-mail: Sebastian.wohlrab@catalysis.de; Fax: +49 382 128151328; Tel: +49 381 1281328
bBundesanstalt für Materialforschung und –prüfung, Unter den Eichen 87, D-12205, Berlin, Germany
First published on 18th June 2010
Abstract
Nanoparticulate networks as fillers for polymer based nanocomposites offer an optimized, surfactant free distribution of the inorganic component. Additionally, their non-aggregated but interconnected nanoparticulate subunits can lead to new properties owing to special inherent solid state properties and/or spacial restrictions to the polymeric parts. In particular, polymer nanocomposites based on poly(methyl methacrylate) (PMMA) or poly(hydroxyethyl methacrylate) (PHEMA), filled with different nanoparticulate networks of AlOOH were synthesized using two advanced synthesis techniques. An ex situ method, in which a preformed AlOOH-gel was solvent exchanged by methyl methacrylate (MMA) and an in situ method, in which the AlOOH scaffold was prepared within hydroxyethyl methacrylate (HEMA), have been used to produce the materials described here through polymerization. On the MMA based composites the particles were removed by etching, yielding porous polymers. Promising for a broad variety of crystallisable networks within polymers, the phase transition of amorphous AlOOH within PMMA towards crystalline boehmite was performed using a hydrothermal method. The materials were characterized using transmission electron microscopy, X-ray diffraction, gel permeation chromatography, differential scanning calorimetry, IR-spectroscopy, UV/Vis spectroscopy and hardness measurements. Special material properties were investigated using thermogravimetry, thermomechanical analysis and dynamic mechanical analysis. Furthermore, interactions between PMMA segments and the AlOOH network were detailed studied using dielectric spectroscopy.
Introduction
Polymer-inorganic hybrid materials possess fascinating structures and show versatile possibilities in synthesis, composition and manipulation of properties.1 Some of these nanocomposites are characterized by a network architecture of the inorganic part. This inorganic framework can consist of preformed nano-, meso- or microporous scaffolds. For instance, investigations regarding the incorporation of polymers into zeolites are well studied with respect to electrical conductive polymers2 or the infiltration of mesoporous materials with monomers and their subsequent polymerization resulting in novel hybrid materials or even in new synthesis procedures for polymers.3 However, in order to combine the properties of inorganic materials with polymeric materials the inorganic content of the later composite has to be reduced compared to the above mentioned examples. This state can be achieved while using porous nanostructures with larger pore sizes. However, in this case, it is difficult to start from a preformed, more fragile scaffold in which polymerization of monomers or impregnation with polymers has to be performed. Not least, due to the problems during the preparation of aerogels from lyogels, the integration of polymers within such dry porous structures is often restricted and synthesis routes have to be modified.Important precursors for the preparation of such inorganic nanoscale networks are metal alkoxides.4 Beside this application, the usage of alkoxides for the preparation of inorganic nanocomposite components is demonstrated in the synthesis of organic-inorganic hybrids with inorganic nanobuilding blocks.5 Consequentially, polymer nanocomposites, where interconnected particles are incorporated in situ within a polymeric matrix, were developed following different sol–gel approaches. However, only the simple hydrolysis conditions of silicon based alkoxides lead to an almost exclusive applicability of silica nanoscaffolds as inorganic fillers.6 For instance, Novak and Davies describe such a composite via hydrolysis and condensation of tetraalkenyl orthosilicates forming a SiO2 matrix and a subsequent polymerization of the eliminated unsaturated alcohol.7 Furthermore, poly(vinyl alcohol)/SiO2 hybrids were prepared by hydrolysis of poly(vinyl acetate) in a sol–gel reaction mixture with tetramethoxy silane,8 hybrids consisting of polystyrene gels and silica gels were generated using an in situ polymerization/condensation route.9 An in situ condensation of tetramethoxy silane within a polyimide precursor which was subsequently cyclised was reported by Wang et al.10 Moreover, silicic acid oligomers and poly(silicic acid esters) are suitable reactants for the in situ generation of composites with higher inorganic contents as referred before.11
The incorporation of functional networks into polymers promises complete new material aspects for nanocomposites. However, during their generation the usage of preformed porous materials is restricted and in situ methods are limited. Examples, like the use of natural clay derived aerogels,12 or the impregnation of dried amorphous silica gels with polymers are rare. The latter principle was shown on amorphous silica gel/PMMA composites by Pope and co-workers who use dried, porous silica gels as inorganic network precursors which were filled with organic monomers to generate nanocomposites after polymerization.13 Also the readily synthesized PMMA was shown to be usable for the impregnation of such silica gels.14 However, these methods have been surpassed by other more convenient procedures, but with a lack of restrictions mainly in the choice of polymers and fillers.15
In order to overcome the existing problems of handling and processing and to exploit new fields of nanocomposite preparation, two advanced methods for the integration of such crystallisable structures within polymers are presented with this work. A material different from the known silica containing composites was chosen for the inorganic network part in order to show the advantage of the methods presented. In particular, networks of needlelike AlOOH from conventional sol–gel approaches were filled with acrylic polymers. The advantage of the methods described is characterized by the simplicity of the formation of a lyogel which doesn't have to be converted into an aerogel. It is assumed, that these methods should be applicable to other lyogel structures obtained from different synthetic routes. According to the synthetic routes described in this work, with special inherent solid state functionalities like ferroelectric PZT or related gels,16 conductive polypyrrole/vanadium pentoxide structures17 and carbon gels18 or semi conductive titania gels19 a new pool of nanocomposites would be possible to generate.
The AlOOH/polyacrylate composites presented here are characterized by three dimensional reticulate structures formed by needlelike nanoparticles surrounded by polymer as main component of the nanocomposite. The considered networks are comparable to known structures of aero-4 or lyogels20 and show a maximum dispersability within the composite at a high filler degree. The influence of the network onto composite properties was investigated in detail using different analytical techniques. The obtained materials were further treated in order to demonstrate the potential of the structures presented. For instance, dissolution of the filler yields porous polymers or hydrothermal crystallization of the incorporated inorganic network leads to advanced hybrids. In this study mostly fundamental aspects of polymers with integrated nanoparticulate networks are discussed.
Results and discussion
Two methods were applied for the preparation of the nanocomposites as drafted in Scheme 1 and documented in Table 1.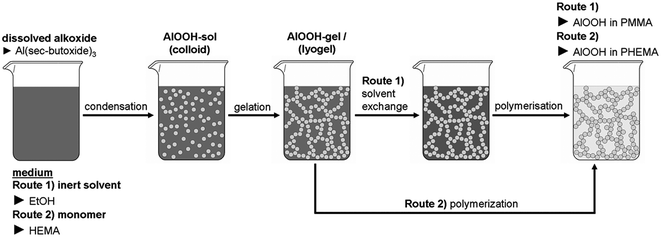 | ||
| Scheme 1 An illustration of two possible procedures for the preparation of polymer integrated nanoparticulate networks (PINNs). | ||
| Sample | Molar ratioa | AlOOH content within the PINNb | Shrinkage after solvent-exchangec | Surface area after HCl treatment and drying (BET) | M w and PDId of the polymers |
|---|---|---|---|---|---|
| a EtOH(PINN1–2)/HEMA(PINN3) to Al(OC4H9)3 ratio; formation of the lyogel. b from TG measurements for PINN1–2 and calculated for PINN3. c calculated from weight loss after extraction. d polydispersity index (PDI), denoted as Mw/Mn. | |||||
| PMMA | no additive | 0.0 wt. % | — | — | 991 000 g mol−1; PDI = 2.55 |
| PINN1a | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.047 0.047 |
4.9 wt. % | 35% | 5.5 m2 g−1 | 541 000 g mol−1; PDI = 2.95 |
| PINN1b | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.094 0.094 |
9.9 wt. % | 31% | 21.2 m2 g−1 | 353 000 g mol−1; PDI = 4.25 |
| PINN1c | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.188 0.188 |
14.4 wt. % | 24% | 1.6 m2 g−1 | 156 000 g mol−1; PDI = 2.45 |
| PMMA:EGDMA(10%) | no additive | 0.0 wt. % | — | — | cross linked |
| PINN2a | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.047 0.047 |
4.2 wt. % | 30% | 5.9 m2 g−1 | cross linked |
| PINN2b | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.094 0.094 |
8.8 wt. % | 32% | 13.7 m2 g−1 | cross linked |
| PINN2c | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.188 0.188 |
14.0 wt. % | 26% | 1.4 m2 g−1 | cross linked |
| PHEMA | No additive | 0.0 wt. % | — | — | — |
| PINN3a | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.056 0.056 |
2.5 wt. % | none | pore collapse | — |
| PINN3b | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.114 0.114 |
5.0 wt. % | none | pore collapse | — |
| PINN3c | 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.170 0.170 |
7.5 wt. % | none | pore collapse | — |
In route 1, a lyogel consisting of an AlOOH nanoparticulate network in ethanol was obtained from a sol according to the method of Yoldas with aluminium tri-sec-butoxide as source.21 The inorganic components of this lyogel build a three dimensional nanoscale network22 of low crystalline γ-AlOOH (boehmite) particles.23 Using this lyogel as starting point a variety of nanocomposites with interconnected nanoparticles can be synthesized after substitution of the ethanol phase by variably monomer/initiator mixtures. This time consuming procedure can be bypassed using route 2 where the lyogel is directly generated within a reactive monomer. Polymerization of the monomers within the inorganic network results in the polyacrylate impregnated AlOOH gels described here. Using thermogravimetric measurements on freshly ground samples the completeness of this preparation step was controlled.
Even though route 1 is more time consuming than route 2, route 1 is of fundamental interest due to the potential application to a broad library of monomers, which can substitute the alcohol from the preformed lyogel chosen. Therefore, materials obtained from route 1 are discussed in detail in the following.
First, ethanol in the preformed lyogel was extracted with a solution of 1.0 mol% BPO in MMA. The extraction steps were carried out three times, taking 24 h for each step until the remaining ethanol concentration was ≤ 0.1%. For such a low ethanol content and only traces of water and sec-butanol the reactive polymer precursor can be polymerized inside the inorganic network yielding the materials PINN1a-c (AlOOH content: a = 4.9 wt. %, b = 9.9 wt. %, c = 14.4 wt. %). The products are transparent to slight milky, and stable against water and organic solvents. Good solvents for PMMA, like tetrahydrofuran, only etch the composites. Additionally, in comparison to the unfilled polymer the composites are shape resistant against temperature until degradation. It is noteworthy that the swelling degree of the inorganic networks after extraction depends mainly on the quality of the solvent. For the considered system, after three extraction steps a remarkable shrinkage of the preformed lyogel of 35% takes place during the preparation of PINN1a, which is characterized with a relatively low filler content. Depending on the inorganic content of the lyogel the shrinkage is reduced to 24% in the case of PINN1c with the highest AlOOH content, while PINN1b with a medium amount of inorganic filler also shows medium shrinkage behaviour of 31%. The more or less flexible inorganic network adapts to its environment even when shrinkage occurs during polymerization. This flexibility of the network is a key property to produce phase compatible and mechanical stable composites from these structures. When the volume of the organic phase is lowered by shrinking due to polymerization, the network has to be flexible enough to fit to its changed environment. The phase interaction and the compatibility between the inorganic network material and the polymer were investigated using different analytical methods as described below.
The microscopic structure and therefore the structural integrity of the AlOOH network within the polymer was investigated with ultra-thin sections using transmission electron microscopy. Fig. 1 shows electron micrographs of such ultra-thin sections of PINN1b with an AlOOH content of 9.9 wt. %. The integrity of the nanoparticulate networks is confirmed and a structure comparable to AlOOH cryogels24 or aerogels can be observed.25
 | ||
| Fig. 1 Transmission electron micrographs; ultra-thin sections of PINN1b: 9.9 wt. % AlOOH as the network (darker regions) within a PMMA matrix (brighter regions), obtained from an AlOOH/MMA/BPO lyogel after polymerization. The right part of the micrograph with low magnification corresponds to the embedding material. | ||
The shrinking process described does not lead to a disintegration of the inorganic network. Elongated particles 80–120 nm in length and 10–20 nm in width build a compact network which is filled out with polymer. The dark appearing AlOOH needles are surrounded by brighter areas which in the present are case ascribable to PMMA. Samples with different amounts of filler are comparable to this structure and the observed particles sizes and shapes—the composites differ only in their inorganic contents. However, densities of PINN1a–c do not increase as much as would be assumed from calculated values. Considering an ideal mixture of AlOOH in PMMA a density increase from 1.20 g cm−3 for pure PMMA to 1.37 g cm−3 for PINN1c would occur (derived from measured values for PMMA and AlOOH with ρ(AlOOH) = 2.44 g cm−3). Effectively, the composites PINN1a–c show increasing densities from 1.26 g cm−3 for PINN1a, 1.29 g cm−3 for PINN1b and up to 1.32 g cm−3 for PINN1c. Assuming strong polymer/particle interactions, as it will be shown by reference to dielectric measurements later, the polymer has to have a lower effective density in the confined space than pure PMMA possesses. Due to polymerization within the matrix the formed macromolecules are limited to arrange in an energetically preferred manner. Furthermore, by means of these results the formation of hollow spaces during composite synthesis cannot be excluded finally.
The polymeric parts of the as received PINNs were determined regarding their polymerisation state. Therefore the inorganic network was dissolved out of the PINNs using a 5 N HCl solution and the weight average molecular weights (Mw) were measured using gel permeation chromatography (GPC) with THF as solvent for the macromolecules. The values are dependent on the cavities where the polymerisation takes place. While the pure PMMA is polymerised unhindered and appears in the GPC with a Mw value of 991,000 g mol−1, the limitation of the network content to the polymerisation becomes obvious. For the PINN1a, which has a more open network, Mw is found to be 541,000 g mol−1. The average molecular weight decreases with increasing network content to 156,000 g mol−1 for PINN1c. The Mw for the PINN1b, which has a medium inorganic content, is found to be 353,000 g mol−1. When looking to the polydispersity index no clear trend is found. The values vary between 2.45 and 4.25 (Table 1).
When the inorganic network is dissolved out of the nanocomposite the remaining polymer was expected to be porous, for example applicable as exotemplate as shown previously.26 Therefore, the resulting surface areas of the materials produced in this way were measured on washed and dried samples using scanning electron microscopy and the BET method using nitrogen as adsorptive (Table 1). In Fig. 2 the pores are imaged on the former sample PINN1b.
 | ||
| Fig. 2 Scanning electron microscopy images of the PINN1b (9.9 wt. % AlOOH) sample after etching the AlOOH network; (a) the surface of the etched sample after washing and drying under vacuum, (b) the inner structure of the porous material can be observed on artificial fractures. | ||
In Fig. 2a the surface of the previous nanocomposite is shown. On the former AlOOH places now holes can be observed in the size range of the single particles. The inner structure also shows a continuous porosity. For visualization the etched and dried samples were fractured to get these deeper insights (Fig. 2b). PINN1a and PINN1b showed surface areas according to calculated values of 5.5 m2 g−1 and 21.2 m2 g−1, respectively, while PINN1c was not significantly porous. In the latter case, when the inorganic material is dissolved through addition of concentrated HCl the polymer shows a pore collapse at a theoretical high pore fraction. In comparison, even the relatively stiff material polybenzimidazole showed a loss of surface area during hard templating experiments due to pore collapses when decreasing the crosslinker density.27
In order to stabilize the polymer of the PINNs against vapour pressure and therewith to achieve higher surface areas from PINNs with high inorganic contents, the polymer was crosslinked with 10% ethylene glycol dimethacrylate yielding PINN2a–c (AlOOH content: a = 4.2 wt. %, b = 8.8 wt. %, c = 14.0 wt. %). Polymers derived from this approach showed that the pore collapse seems to occur even at medium filler degrees. In order to produce porous polymers via lyogels the method described here should be applied to more rigid polymers.
In order to investigate molecular interactions between inorganic network and polymer spectroscopic investigations were carried out. These measurements revealed that information given by PINN1 samples result only due to an overlap of the IR-spectra of AlOOH and PMMA. A clear signal from interactions at the phase boundary could not be seen. In order to get this information, the materials were studied using dielectric spectroscopy. Here only two filler concentrations and some key aspects are discussed. Fig. 3 gives the dielectric loss ε′′ versus frequency and temperature in a 3D representation for pure PMMA.
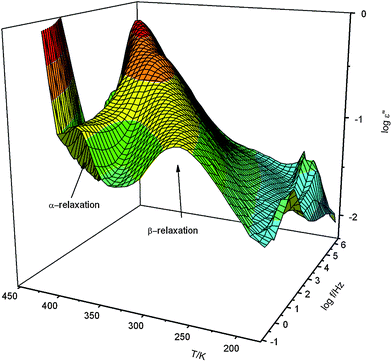 | ||
| Fig. 3 Dielectric loss ε′′ of pure PMMA versus frequency and temperature in a 3D representation. | ||
As it is well known in literature28 two relaxation processes are observed for PMMA indicated by peaks in the dielectric loss. The process at higher frequencies (lower temperatures) corresponds to β-relaxation which is assigned to fluctuations of the ester group with a partial involvement of the main chain.29 The relaxation mode at lower frequencies (higher temperatures) corresponds to the segmental motion related to the dynamic glass transition (α-relaxation). As it is well known for conventional synthesized PMMA the dielectric strength of the β-relaxation is much stronger than that of the α-process.
The model function of Havriliak/Negami (HN-function)30 is used to analyze the dielectric measurements quantitatively. It reads
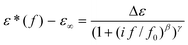 | (1) |
Fig. 4 compares the dielectric loss ε′′ versus frequency at constant temperature for pure PMMA and PINN1a. Like for pure PMMA the β- and α- relaxation are also visible as peaks in the dielectric loss for the nanocomposite. Compared to pure PMMA for the composite with the lowest concentration of AlOOH the intensity of the β-process is strongly reduced. This indicates a strong influence of the inorganic network on the molecular mobility of the organic PMMA phase.
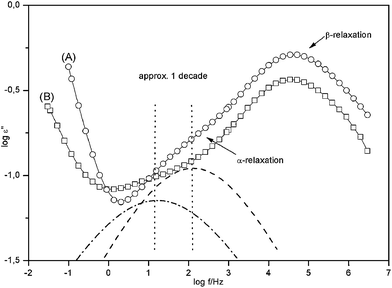 | ||
| Fig. 4 Dielectric loss ε′′ versus frequency for T = 404 K for pure PMMA (A) and the nanocomposite with 4.9 wt. % AlOOH (PINN1a) (B). The solid lines are guides for the eyes. The dashed line gives the contribution of the α-relaxation to the dielectric loss of pure PMMA where the dashed-dotted line gives the same for the nanocomposite. | ||
In the inset of Fig. 5 the relaxation rate of the β-relaxation is plotted versus inverse temperature. As expected the data can be described by the Arrhenius law with an activation energy of ca. 79 kJ mol−1. As it is already obvious from raw data (see Fig. 3) temperature dependency of the relaxation rate on the β-process is not influenced by the nanofiller. This effect is expected because the β-relaxation is more or less a localized relaxation process.32 The dielectric relaxation strength Δε of this relaxation process behaves differently (Fig. 3). The raw data show that the dielectric strength of the composite is decreased in comparison to pure PMMA.
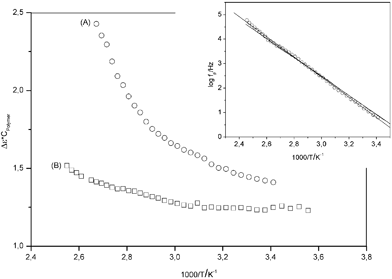 | ||
| Fig. 5 Dielectric relaxation strength normalized by the volume concentration of the polymer cPolymerversus inverse temperature: (A) pure PMMA; (B) 4.9 wt. % AlOOH (PINN1a). The inset gives the relaxation fpversus inverse temperature for the β-relaxation. The lines are linear regressions to the data. | ||
The Debye theory of dielectric relaxation generalized by Kirkwood and Fröhlich32 predicts the temperature dependence of the dielectric relaxation strength
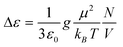 | (2) |
In Fig. 5 Δε, the dielectric relaxation strength normalized by the volume concentration of the polymer cPolymer, versus the inverse temperature is compared for pure PMMA and PINN1b. For pure PMMA Δε increases strongly with increasing temperatures as it is well known for the β-relaxation.32 This is explained by an increase of the number density of dipoles with increasing temperature. For the composite as it can be seen already from the raw data the relaxation strength is decreased compared to pure PMMA. This result means that a part of the molecular dipoles in the composite does not contribute to the β-relaxation. The dipoles either are immobilized by the interaction of PMMA segments with AlOOH or they are simply spacial restricted due to confinements of the network. More importantly, the temperature dependence of Δε for the nanocomposite is much weaker than for pure PMMA. As mentioned before the increase of Δε with temperature is due to an increase of the number density of dipoles. In the case of the composite much less dipoles become mobile with increasing temperature compared to pure PMMA. This result underlines the strong influence of the polymer segments with the AlOOH framework.
Compared to the more localized β-process the α-relaxation corresponds to cooperative segmental fluctuations. During this dynamic glass transition the relaxation strength is strongly reduced (see Fig. 3). Unfortunately, as it is known for PMMA, the α-process is strongly overlaid by the β-relaxation. Therefore the temperature dependence of the relaxation strength of the dynamic glass transition could not be analyzed in detail.
In addition to the decreased intensity of the dynamic glass transition the maximum position of the dynamic glass transition is shifted to lower frequencies. This corresponds to an increase of the glass transition temperature. In Fig. 6 the temperature dependence of the relaxation rate of the dynamic glass transition is compared for both systems.
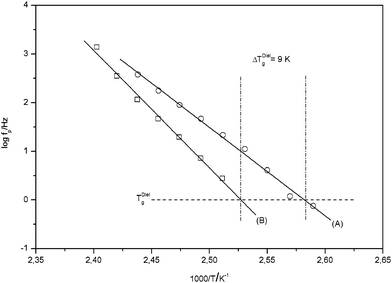 | ||
| Fig. 6 Relaxation fpversus inverse temperature for the α-relaxation: (A) pure PMMA; (B) 4.9 wt. % AlOOH (PINN1a). The solid lines are linear regressions to the data. The dashed-dotted lines indicate the dielectric Tg. | ||
A dielectric glass transition temperature TgDiel is defined by TgDiel = T(fp = 1 Hz). For the composite TgDiel is shifted at approximately 9 K to higher temperatures. This strong shift in Tg is a further proof of how the polymer interacts with AlOOH network. Even though an increase of the local free volume of the polymer within the composite is assumed, Tg increases due to these interactions. The Tg itself increases due to the confinement of the PMMA within PINN1a–c in a range from 9 to 12 K in comparison to pure PMMA (Table 2). This result was confirmed by DSC measurements. With this second method Tg was found to be 5 to 8 K higher in PINN samples then for pure PMMA with a Tg of 378 K (Table 2). At this point it has to be remarked that Tg can be influenced strongly by confinements either to higher or lower values. For instance, Tran et al. described an increase of Tg of syndiotactic PMMA confined between layers of organophilic montmorillonite indicating strong interactions between substrate and polymer.33 The polymer nanocomposite described here has therefore to be seen as a polymer which is stabilized by the inorganic network, which itself was further densified by shrinking during the solvent exchange.
Macroscopic differences in the stabilizing effect of the filler are clearly recognizable. It became obvious that the nanoparticulate network has also a strong influence on the hardness of the materials. In Table 2 Shore-D values measured on PMMA and PINN1a–c are presented. With increasing filler content the hardness also increases, in the present case from 81 (without AlOOH) to 95 (14.4 wt. % AlOOH). Upcoming brittleness can be overcome by hydrothermal treatment, where even hardness is further increased through crystallization as it is discussed later.
Thermomechanical analysis (TMA) on PINN1a–c samples gave information concerning the linear coefficient of expansion α below Tg which is documented in Table 2. A general expansion behaviour of the samples is shown in Fig. 7.
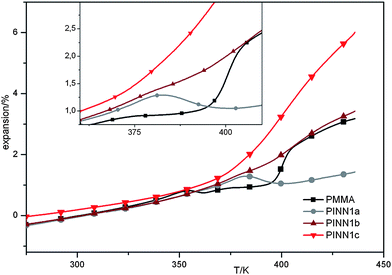 | ||
| Fig. 7 Plots from thermo mechanical analysis on the samples PINN1a–c and the PMMA reference. | ||
The force chosen to be applied to the samples was very small, with 10 mN applied by a punch with 1 mm in diameter in order to get direct information about α. A different expansion characteristic for each PINN1 sample becomes obvious. The glass transition can be seen in the volatile rise of the expansion curve which results from the measurement of the expansion during linear temperature changes of the samples and was found to be comparable to the results of the DSC measurements. Below this temperature a similar behaviour of the PINN1 samples in comparison to PMMA is observed. In the glass transition range a different behaviour of the PINNs is determined. The temperature dependant expansion is intensified at high degrees of filler and reduced at low inorganic contents.
The network also influences the thermal degradation of the polymer due to shielding. In Fig. 8 DTG (differential thermogravimetry) plots vs. temperature are shown for the samples PINN1a–c recorded under air and nitrogen atmosphere. In presence of the network degradation is suppressed and a relative higher thermal stability is found (Fig. 8a). The thermal degradation of PINNs occur at broader temperature ranges ending at higher temperatures at ca. 630 K. In comparison, pure PMMA is completely degraded at approximately 580 K. PINN1b shows a significant peak at approximately 535 K which is in the region of pure PMMA decomposition. The other composite samples give only a small signal here. At the first glance a strong peak for PINN1a in the region of pure PMMA degradation would have been expected when looking at the PINN1b behaviour. The obvious absence can be clarified by DTG investigations under nitrogen atmosphere. Hatada et al. divide the degradation mechanism of pure PMMA into two parts. At 543 K chain-end degradation and at 633 K scissions of the head-to-head linkages are reported.34 According to Fig. 8b the influence on the inorganic network density has a strong influence on the nature of the thermal degradation. PINN1a shows stronger chain-end degradation than pure PMMA. The caged polymer of the nanocomposite with the highest network content (PINN1c) shows no significant decomposition before 620 K. This result indicates that depending on the confined space which is defined by the inorganic network, different degradation mechanisms are active.
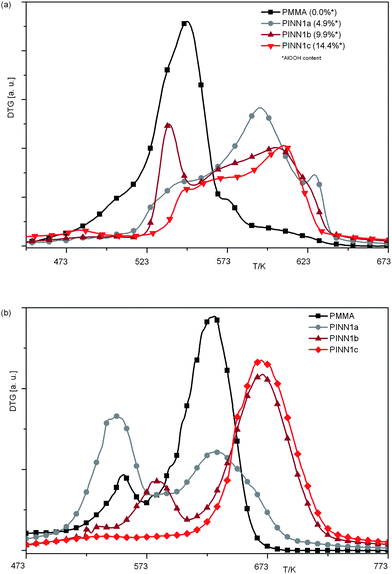 | ||
| Fig. 8 DTG vs.T plots of PINNs consisting of different amounts of confined PMMA within nanoparticulate AlOOH networks; (a) measurements under air; (b) under nitrogen atmosphere; heating rate 10 K min−1. | ||
With the highest filler content the degradation mechanism becomes a nearly head-to-head type while a medium filler degree of 9.9 wt. % causes a temperature shift of the chain-end degradation towards higher values. This strong influence of the inorganic network onto the mechanism of degradation should also be responsible for the unexpected behaviour of PINN1b degradation under air at around 535 K. The influence of inorganic networks on the thermal degradation of polymers is up to now only described for carbon nanotube/polymer composites.35 However, the influence of a dimensional restriction of PMMA on its thermal degradation was found by Blumstein in 196536 and can also be applied to PINN1 samples. Here adsorption on the inorganic matter and steric restrictions can be counted as factors which influence degradation.
The limitation of the polymer flexibility within the inorganic network results also in a different behaviour in elasticity. Due to the inorganic network the material shows no thermoplastic behaviour macroscopically as a simple experiment showed. When the PINN1 material is heated above Tg to 423 K no deformation can be achieved as in the reference case using pure PMMA by pressing with 5 N mm−2. This effect can be explained as the inorganic network does not allow the polymer chains to deform. Above the softening point for PMMA which is defined above its Tg of about 380 K the material stays durable in its geometry when it is under stress. A detailed investigation is not possible due to limitations in the measuring parameters of the TMA and the necessary sample geometry, which could not be prepared using route 1. However, on materials resulting from route 2 this behaviour could be investigated in detail using DMA as it is discussed later.
The characterization of the inorganic parts of the hybrid was performed using XRD. Derived xerogels consist of particles with a very low crystalline boehmite structure detected by XRD. Assuming a similar crystallization state of the inorganic networks in PINNs it was not surprising to detect no reflex pattern in these samples due to their high polymer content. However, it is a challenge to crystallize particles within these composites in order to improve the materials properties. Temperature treatments under atmospheric conditions from 393 K to 523 K (the starting temperature of thermal decomposition of PMMA under air) in steps of 10 K and holding this temperature for 2 h did not lead to crystallization of the filler as in situ XRD measurements proved. Under vacuum the heating temperature can be increased to 573 K with less decomposition of the PMMA. In order to investigate the crystallization behaviour in a vacuum a larger temperature range from 393 K to 573 K was applied also using in situ XRD investigations at 50 K steps. Up to the temperature of 573 K no crystallization could be confirmed by means of the XRD data. However, using a third, hydrothermal way the inorganic filler could finally be crystallized. When the freshly prepared nanocomposite is hydrothermally treated for 4 d at a temperature of 433 K crystalline reflexes appear in the XRD pattern of the obtained product, which are definitively assignable to diffractions of a boehmite lattice (Fig. 9).
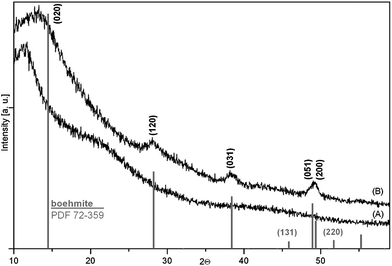 | ||
| Fig. 9 XRD patterns recorded on PINN1c after synthesis (A) and after hydrothermal treatment at 435 K for 4 d (B). For comparison, a calculated pattern of pure boehmite according to the Powder Diffraction File (PDF) 72-259 from the Inorganic Crystal Structure Database (ICSD). | ||
Hydrothermal treatments at 375 K, 393 K and 413 K for 4 d, each, gave no crystalline signals in the XRD signal. It has to be concluded that the crystallization temperature under the applied terms lies between 413 K and 433 K. For comparison, Bokhimi et al. reported on the crystallization possibility of similar prepared AlOOH gels and water as a mineralizing agent under hydrothermal conditions at 473 K for 3 d, without a mineralizing agent no mineralization occurs.23
In the case under consideration at a temperature of 433 K the polymer is above its glass transition temperature and it acts on the one hand as a distance holder between the particles and on the other hand as a crystallization medium for the inorganic filler. The surrounding water should also play an important role during the crystallization process, because the crystallization experiments under air and in vacuum failed. It can be assumed that the small amount of dissolved water within the PMMA acts as mineralising agent. A temperature treatment at 433 K for 4 d at atmospheric pressure did not lead to a comparable result. Here no crystallization was detected using the applied XRD method.
An increase of the E-modulus at 298 K was found when the inorganic network in the PINN1c was crystallized via the described hydrothermal method. The untreated PINN1c shows an E-modulus of 420 MPa. After hydrothermal treatment this value increases up to ca. 5 times to 2010 MPa. This behaviour has to be partially related to the crystallization event within the nanocomposite. Another influencing variable is the thermal curing of the PMMA under the applied hydrothermal conditions. A pure PMMA reference sample shows an E-modulus in the range of the untreated PINN1c composite. After curing also the E-modulus increases, but only to a value of 1190 MPa. It can be concluded that the higher value of the E-modulus of the hydrothermally treated PINN1c can be regarded as being due to the crystalline network.
The samples resulting from route 1 have no defined shape, meaning that some investigations are impossible to carry out. For instance when the samples were cut into 200 μm thin sections for transparency measurements (Fig. 10a), the cutting procedure is not suitable for producing materials of normal PMMA standard transparency due to scratching effects. Although samples with low filler degrees show pleasing transparencies, with increasing inorganic content the samples lose a lot of their original clarity due to cutting. More disadvantages of materials from route 1 are, besides the lengthy procedure, the already mentioned restrictions in geometry. To get information on the elasticity of materials samples which are larger in size and well shaped are often required. Moreover, samples, which can easily be produced in molds, are more attractive for applications. To improve synthesis regarding time consumption and to overcome geometric restrictions route 2 was developed. Here the lyogel consists of the polymer precursor from the beginning on, no extraction steps are necessary anymore and the shaping of the materials becomes much easier for special applications. However, this method is limited to the monomer nature. Hydrophobic monomers like MMA, styrene or related ones are not suitable for lyogel formation, while hydroxyl group bearing monomers, like HEMA can be used during the lyogel formation yielding PINN3 samples after subsequent photopolymerization. The microscopic structure of the obtained materials is comparable to the situation in Fig. 1 where a sample of 9.9 wt. % AlOOH in PMMA is shown.
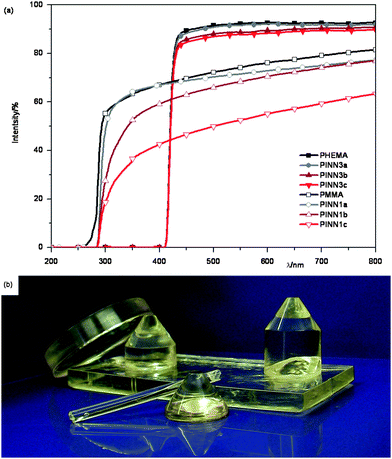 | ||
| Fig. 10 The transparency of the obtained composites. (a) UV/Vis spectra of PINN1 and PINN3 with different amounts of nanoparticulate network consisting of AlOOH, sample thicknesses PINN1 = 200 μm, PINN3 = 1 cm; (b) photograph of PINN3b containing 5 wt. % AlOOH. | ||
Fortunately, with the more specialized synthesis route 2 the previously mentioned problems can be overcome. Using this route it is possible to fabricate samples of various geometries and sizes easily. Samples with transparencies in the range of the unfilled reference polymer, different in size and geometry, were produced (Fig. 10a and Fig. 10b).
Now it is possible to get information on the temperature dependence of elasticity in comparison to the pure polymers. Therefore, dynamic mechanical analysis (DMA) was performed in order to understand the influence of molecular structure as indicated by molecular mobility to flexibility. The temperature of the complex shear modulus G* was measured at a fixed frequency f. The real part G′ is the storage modulus, which is related to the stiffness of the material. The imaginary part of G* is the loss modulus G′′ as a value for the dissipated vibration energy by molecular dynamics due to the given morphology. G′′/G′ = tanδ is called mechanical loss factor. The glass transition range is characterized in the G′(T) curve as a drop of G′ in the relevant temperature range, while tanδ passes a maximum. In Fig. 11 G′ and tan δ with dependence on temperature are shown for PHEMA and for PINN3b.
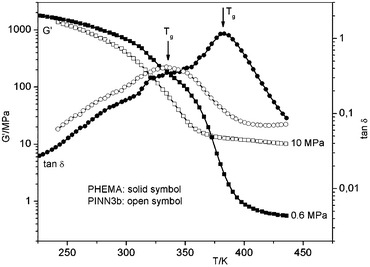 | ||
| Fig. 11 Dynamic mechanical analysis of PMMA and PINN3b (5.0 wt. % AlOOH). | ||
The DMA diagrams show a dramatic decrease of the Tg of PINN3b in relation to PMMA. For the pure polymer, PHEMA, a Tg of 382 K can be derived, while for the PINN3b a much lower temperature of Tg = 335 K is required (from temperature position at maximum tanδ at f = 1 Hz). The first assumption of this behaviour may be based on large residual monomer content within the polymer or present side products from the condensation process during the network formation. These possible reasons can be excluded as thermoanalytic and spectroscopic investigations on the corresponding PINN3 materials reveal. The dramatic decrease of Tg of PHEMA in the pores of the network has to be relativised after subsequent repeating DMA measurements. With each repetition of the experiment Tg increases. After six DMA runs Tg was found to be at a value of 375 K, which is near to pure PHEMA. It has to be stated that in comparison to the PMMA-composites the Tg of PHEMA-composites is lowered and it has to be assumed that the increase of this characteristic material parameter via multiple measuring cycles has to be ascribed to a thermomechanical optimization of the network-polymer assembly. For instance, morphology related dependence of Tg was observed for clay/poly(vinyl alcohol) composites12 while an increase of Tg is ascribed to restricted motions of polymer chains between the filler37 and a decrease of Tg is a consequence of an increase of the local free volume.38 In the case of PINN3-samples, during the fast polymerization at room temperature only less shrinkage of the inorganic network occurs. A simple thermal curing does also not lead to a structural optimisation. That means the inorganic network remains in nearly constant dimensions. After polymerization within the AlOOH scaffold the polymer has a higher local free volume than pure PHEMA. Under a coupled thermal and vibrational influence these frozen conditions change towards a more dense structure.
Another essential message from these measurements can be found in the G′(T) regime above Tg. Due to strong polymer/particle interactions the motion of the polymer chains between these particles becomes more restrictive. It was found that G′ is essentially 17 times higher for the composite PINN3b with 10.1 MPa than the value for pure PHEMA with 0.6 MPa. Additionally, it has to be noted that after six measurement cycles on the sample PINN3b G′ is only slightly increased to 11.2 MPa.
The in situ method according to route 2 is limited to an inorganic filler degree up to 7.5 wt. % AlOOH in the case of a PHEMA-filling. Above this value irregularities in the AlOOH network are obtained, due to uncontrollable gelation of the nanoparticulate network.
Conclusions
Two advanced possibilities of integrating inorganic networks of crystallisable particles within polymers were presented. An ex situ method was described where a preformed inorganic network was solvent exchanged by a polymerizable solution and an in situ method was shown where the inorganic scaffold was produced within the polymer precursor. As polymer component macromolecules from the acrylates MMA and HEMA were used. As inorganic scaffold AlOOH derived from an alkoxide source was applied which gives after hydrothermal treatment crystalline boehmite when present in the composite. The appearing inorganic needlelike particles and the scaffolds derived therefrom provide a macroscopic isotropic character to the material even at high filler degrees above 10%. Isolation of the needles from the nanocomposites results in porous polymers. The molecular interactions of the materials were mainly investigated using dielectric spectroscopy showing a strong influence of the AlOOH scaffold to the relaxation characteristics of the polymer indicating strong interactions of the components. The effect of the inorganic filler on the polymer was studied on further material properties. It can be stated that an enhanced thermal stability and different thermomechanical behaviour can be achieved. Considerations regarding an optimized particle distribution within the polymer and a stabilizing effect by the inorganic network would let assume significantly improved materials properties. However, compared to traditional prepared composites no crucial advancements can be registered. Nevertheless, the methodologies described should be transferable to other crystallisable networks in order to integrate their inherent solid state properties into polymers.Experimental section
Chemicals
Aluminium tri-sec-butoxide (≥97.0%) was purchased from Aldrich and it was used without further purification. Ethanol (≥99.8%, without additive) was purchased from Fluka and stored over molecular sieve 4 Å. Acetic acid (≥99.0%), methanol (≥99.5%), MMA (methyl methacrylate) (≥99.0%) and benzoyl peroxide (BPO) were purchased from Merck. Diphenyl(2,4,6-trimethylbenzoyl)phosphine oxide was purchased from Aldrich. MMA, ethylene glycol dimethacrylate (EGDMA, Fluka, ≥97.0%) and HEMA (hydroxyethyl methacrylate) (Fluka, ≥ 97.0%) were distilled under vacuum before use. Any liquids except Aluminium tri-sec-butoxide were purged with nitrogen for ½ h.Synthesis
For a better understanding the prepared samples are shortened to PINNs, which is derived from polymer integrated nanoparticulate networks.PINN1
In a typical synthesis ethanol was mixed with aluminium tri-sec-butoxide in certain ratios (Table 1) in a nitrogen purged three-necked flask at 298 K. Afterwards, 10% of double distilled water related to the alkoxide content was added at 333 K. The resulting white suspension was stirred for 30 min until a nearly clear solution was formed. The produced sol was gelled in nitrogen purged casting molds made from polypropylene after the addition and mixing of a mixture of methanol, acetic acid and water (ratio: 1.0 mol : 0.089 mol : 0.025 mol). The weight ratio of the AlOOH-sol to this mixture was 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17. The weight of a typical lyogel ranges from 5 to 7 g. Samples of this gel were dried for 24 h at 295 K under vacuum to give a reference powder of AlOOH. The formed lyogels were transferred to a solution of 1.0 mol % BPO in MMA at 298 K. The amount of the added monomer/initiator-mixture was adjusted to a tenfold excess. This extraction was carried out under nitrogen for 24 h and repeated for two times. Afterwards the excess on MMA/BPO was exhausted and the monomer in the resulting lyogel was polymerized at 333 K for 8 h under nitrogen in the closed molds. As a reference MMA was polymerized with BPO under the same conditions as those which were applied for the composites. The resulting materials were cured for 2 h at 393 K and 10−3 bar. For the preparation of porous polymers the inorganic components were dissolved out of crushed PINNs by treatment of 5 N HCl over 14 d at 298 K. The samples were washed three times with deionised water for 24 h each time and dried under vacuum at 298 K at 10−8 bar. Furthermore, the obtained PINN samples were partially cured hydrothermal using a pressure digestion vessel (DAB II, Berghof Instruments, Germany) equipped with a 50 ml Teflon insert. For the crystallization of the inorganic network 0.2 g of freshly prepared PINN1c (without thermal curing) and 25 ml deionised water were filled in the Teflon insert. Afterwards, hydrothermal treatment at temperatures of 373 K, 393 K, 413 K and 433 K for 4 d each was performed. Temperature treatment under air and in vacuum were performed in an in situ measuring chamber in the temperature range of 393 K to 523 K (10 K steps holding for 2 h) or 323 K to 573 K (50 K steps holding for 2 h), respectively.
17. The weight of a typical lyogel ranges from 5 to 7 g. Samples of this gel were dried for 24 h at 295 K under vacuum to give a reference powder of AlOOH. The formed lyogels were transferred to a solution of 1.0 mol % BPO in MMA at 298 K. The amount of the added monomer/initiator-mixture was adjusted to a tenfold excess. This extraction was carried out under nitrogen for 24 h and repeated for two times. Afterwards the excess on MMA/BPO was exhausted and the monomer in the resulting lyogel was polymerized at 333 K for 8 h under nitrogen in the closed molds. As a reference MMA was polymerized with BPO under the same conditions as those which were applied for the composites. The resulting materials were cured for 2 h at 393 K and 10−3 bar. For the preparation of porous polymers the inorganic components were dissolved out of crushed PINNs by treatment of 5 N HCl over 14 d at 298 K. The samples were washed three times with deionised water for 24 h each time and dried under vacuum at 298 K at 10−8 bar. Furthermore, the obtained PINN samples were partially cured hydrothermal using a pressure digestion vessel (DAB II, Berghof Instruments, Germany) equipped with a 50 ml Teflon insert. For the crystallization of the inorganic network 0.2 g of freshly prepared PINN1c (without thermal curing) and 25 ml deionised water were filled in the Teflon insert. Afterwards, hydrothermal treatment at temperatures of 373 K, 393 K, 413 K and 433 K for 4 d each was performed. Temperature treatment under air and in vacuum were performed in an in situ measuring chamber in the temperature range of 393 K to 523 K (10 K steps holding for 2 h) or 323 K to 573 K (50 K steps holding for 2 h), respectively.
PINN2
According to the synthesis of PINN1, here a mixture of 1.0 mol % BPO and 10.0 mol % EGDMA in MMA was used to extract the ethanol from the lyogels. The further treatments are analogue to the PINN1 procedures.PINN3
HEMA was divided in two equal parts. In the first part aluminium tri-sec-butoxide with variable ratios (Table 1) and 2% of diphenyl(2,4,6-trimethylbenzoyl)phosphine oxide were dissolved to produce a clear solution. To form lyogels, to this mixture the second part of HEMA with 2.0 wt. % water was added at 298 K. The whole procedure was carried out under nitrogen. Gelation was performed in casting molds made from polypropylene different in size and shape. Polymerization was carried out after careful evaporation (12 h) of the mean content of the fluid side products of the gelation step. Irradiation with UV light using a HPW125 mercury discharge source (Philips, Turnhout, Belgium) for 1 h (25 cm distance to the sample) was applied to polymerize the polymer precursor at 298 K. Residual monomer and solvents were evaporated for 24 h at 393 K in a vacuum drier.Techniques
TEM images of ultra-thin cross sections were recorded using an Omega 912 TEM instrument (Carl Zeiss, Oberkochen, Germany). Microtoming was performed after the materials were integrated into an epoxy resin (LRWhite Resin). After embedding, the samples were cured for several days and afterwards cut using a diamond knife (Leica EM Trim, Wetzlar, Germany).Densities were determined using a calibrated pycnometer of 1 ml in volume. For measurements 500–600 mg samples were placed into the vial. After bubble free complete filling with cyclohexane at 20 °C densities were calculated based on the mass of solvent required.
Gel permeation chromatography (GPC) was performed on a HP 1050 system by Agilent equipped with three different columns (PL-Gel, 10 μm mixed B, 300 × 8 mm ID; PL-Gel, 10 μm mixed E, 300 × 8 mm ID; PL-Gel, 3 μm 100 Å, 300 × 8 mm ID), an evaporative light scattering detector (ELSD) and 100% THF as eluent (T = 308 K, flow = 1 ml min−1, injection = 100 μl at a concentration of ca. 4–5 mg polymer per ml THF).
Hydrothermal treated samples and the thermal treatments on PINN1 samples were investigated on a STADI P transmission diffractometer from STOE (Darmstadt) with a curved germanium monochromator in the incident beam path selecting Cu-Kα1 radiation (λ = 0.15406 nm) and a 6° linear position sensitive detector (PSD). The alignment was checked by the use of a silicon standard. The phase composition of the samples was determined using the program suite WINXPow by STOE&CIE GmbH with inclusion of the Powder Diffraction File PDF2 of the ICDD (International Centre of Diffraction Data).
The Young modulus of the synthesised material is calculated from the loading and unloading function after the imprint of a Bercovich tip using a Hysitron nanomechanical test system. The indentation depth and the applied force are recorded at constant temperature of high stability. The force-displacement function is measured by the nanoindentation of surfaces of the samples as obtained by the synthesis. The stiffness of the material can be read from the slope of the indentation function. Shore D values were detected with the help of a Bareiss tester (Barreis, Germany).
UV/Vis spectra were recorded on 200 μm thin sections of PINN1 obtained from an Accutom-5 (Struers, Willich, Germany). Samples of PINN3 with a given dimension of 10 mm by the polypropylene casting mould were measured as received. To record the spectra, a UV/Vis spectrometer of the type Cary 300 UV (Varian, Palo Alto, USA) was used. On these samples also IR spectra were measured using a FTIR-Spektrometer Nexus 8700 (Nicolet, USA).
BET measurements were performed on an ASAP 2010 system (Micromeritics, Mönchengladbach, Germany) using nitrogen as adsorptive. The samples were activated in vacuum at room temperature overnight.
Thermogravimetric (TG) measurements were carried out on a TGA/SDTA 851 (Mettler/Toledo, Gießen, Germany) applying nitrogen 5.0 or synthetic air of 30 ml min−1. Samples of about 5 mg were heated in alumina pans from 293 K to 1073 K at a heating rate of 10 K min−1. The measurements were repeated two times.
Dielectric relaxation spectroscopy in the frequency range from 10−1 Hz to 107 Hz was applied to investigate the nanocomposites with respect to their molecular mobility including the dynamic glass transition Tg. The complex dielectric function ε*(f) = ε′(f) − iε′′(f) (f—frequency, ε′ and ε′′—real and imaginary part of the complex dielectric function) was measured by a high resolution ALPHA analyzer equipped with a Quatro cryosystem with a stability better than 0.1 K from Novocontrol (Hundsangen, Germany).
Differential scanning calorimetry (DSC) was performed using a DSC 204 F1 Phoenix (Netzsch Gerätebau GmbH, Germany) under a nitrogen 5.0 flow of 20 ml min−1 at a heating rate of 10 K min−1. The samples were placed in Al crucibles (diameter, 6 mm) with pierced lids. The mass of the samples was in the range of 5 to 10 mg. The measurements were repeated for three times. The glass temperature Tg is defined as the temperature position of the midpoint of the measured heat flow.
Thermomechanical analysis (TMA) was performed at a Seiko system TAM/SS 120C. Cylindrical samples of 5 mm in diameter and 4 mm in thickness were tempered to the starting temperature. After tempering a punch of 1 mm in diameter and 10 mN in bearing-strength was placed on the sample. The position of the punch was registered during a time linear heating rate of 2 K min−1. During the measurement the samples were purged with nitrogen at a flow of 100 ml min−1. Tg is defined as the temperature of the intersection of the two tangents of the linear parts of the curve.
Dynamic mechanical analysis (DMA) was achieved with a torsional pendulum ATM3 (Myrenne GmbH, Germany). The measurements were carried out in a temperature range from 93 K to 453 K with a cascaded temperature increase of 3.5 K after 4 min in each case. The measuring frequency was 1 Hz ± 0.1 Hz. For the measurement samples with dimensions of 45 × 4 × 1 mm were used. Tg (DMA) was determined as the temperature position of the relative mechanical loss factor maximum.
Acknowledgements
We thank Dr Jana Falkenhagen, Dr Franziska Emmerling, Dr Werner Österle, Dr Jürgen Hartmann, Rona Pitschke, Frank Neuber, Dr Asmus Meyer-Plath and Prof. Dr A. Thünemann for helpful discussions and analytical support. The authors are grateful for the advisory support of Norbert Hofbauer.Notes and references
- (a) J. E. Mark, Acc. Chem. Res., 2006, 39, 881 CrossRef CAS; (b) P. Judeinstein and C. Sanchez, J. Mater. Chem., 1996, 6, 511 RSC; (c) S. C. Tjong, Mater. Sci. Eng., R, 2006, 53, 73 CrossRef.
- (a) G. A. Ozin, Angew. Chem., Int. Ed. Engl., 1989, 28, 359 CrossRef; (b) T. Bein, ACS Symp. Ser., 1992, 499, 274 CAS; (c) F. Márquez, R. Roque-Malherbe, J. Ducongé and W. del Valle, Surf. Interface Anal., 2004, 36, 1060 CrossRef CAS.
- (a) C. G. Wu and T. Bein, Science, 1994, 264, 1757 CrossRef CAS; (b) D. J. Cardin, S. P. Constantine, A. Gilbert, A. K. Lay, M. Alvaro, M. S. Galletero, H. Garcia and F. Marquez, J. Am. Chem. Soc., 2001, 123, 3141 CrossRef CAS; (c) M. S. Galletero, M. Alvaro, H. Garcia, C. J. Gomez-Garcia and A. K. Lay, Phys. Chem. Chem. Phys., 2002, 4, 115 RSC; (d) X. Ji, J. E. Hampsey, Q. Hu, J. He, Z. Yang and Y. Lu, Chem. Mater., 2003, 15, 3656 CrossRef CAS.
- A. C. Pierre and G. M. Pajonk, Chem. Rev., 2002, 102, 4243 CrossRef CAS.
- C. Sanchez, G. J. de A. A. Soler-Illia, F. Ribot, T. Lalot, C. R. Mayer and V. Cabuil, Chem. Mater., 2001, 13, 3061 CrossRef CAS.
- B. M. Novak, Adv. Mater., 1993, 5, 422 CrossRef CAS.
- B. M. Novak and C. Davies, Macromolecules, 1991, 24, 5481 CrossRef CAS.
- R. Tamaki and Y. Chujo, Appl. Organomet. Chem., 1998, 12, 755 CrossRef CAS.
- R. Tamaki and Y. Chujo, J. Mater. Chem., 1998, 8, 1113 RSC.
- S. Wang, Z. Ahmad and J. E. Mark, Chem. Mater., 1994, 6, 943 CrossRef CAS.
- (a) B. M. Novak and M. W. Ellsworth, Mater. Sci. Eng., A, 1993, 162, 257 CrossRef; (b) M. W. Ellsworth and B. M. Novak, Chem. Mater., 1993, 5, 839 CrossRef CAS.
- S. Bandi and D. A. Schiraldi, Macromolecules, 2006, 39, 6537 CrossRef CAS.
- E. J. A. Pope, M. Asami and J. D. Mackenzie, J. Mater. Res., 1989, 4, 1018 CrossRef CAS.
- M. C. Nobrega, L. C. F. Gomes, G. P. LaTorre and J. K. West, Mater. Charact., 1998, 40, 1 CrossRef CAS.
- A. B. Wojcik and L. C. Klein, Appl. Organomet. Chem., 1997, 11, 129 CrossRef CAS.
- S. Geis, J. Fricke and P. Lobmann, J. Eur. Ceram. Soc., 2002, 22, 1155 CrossRef CAS.
- H. P. Wong, B. C. Dave, L. Leroux, J. Harreld, B. Dunn and L. F. Nazar, J. Mater. Chem., 1998, 8, 1019 RSC.
- R. W. Pekala, J. C. Farmer, C. T. Alviso, T. D. Tran, S. T. Mayer, J. M. Miller and B. Dunn, J. Non-Cryst. Solids, 1998, 225, 74 CrossRef CAS.
- (a) G. Dagan and M. Tomkiewicz, J. Phys. Chem., 1993, 97, 12651 CrossRef CAS; (b) L. K. Campbell, B. K. Na and E. I. Ko, Chem. Mater., 1992, 4, 1329 CrossRef CAS.
- C. J. Brinker, G. W. Scherer, Sol–Gel Science, Academic Press, New York, 1990, ch. 1, p. 9 Search PubMed.
- B. E. Yoldas, J. Mater. Sci., 1975, 10, 1856 CrossRef CAS.
- J. F. Poco, J. H. Satcher Jr. and L. W. Hrubesh, J. Non-Cryst. Solids, 2001, 285, 57 CrossRef CAS.
- X. Bokhimi, J. Sánchez-Valente and F. Pedraza, J. Solid State Chem., 2002, 166, 182 CrossRef CAS.
- T. Osaki, K. Nagashima, K. Watari and K. Tapiri, J. Non-Cryst. Solids, 2007, 353, 2436 CrossRef CAS.
- A. Corrias, M. F. Casula, A. Falqui and G. Paschina, Chem. Mater., 2004, 16, 3130 CrossRef CAS.
- S. Wohlrab, M. Weiss, H. Du and S. Kaskel, Chem. Mater., 2006, 18, 4227 CrossRef CAS.
- J. Weber, M. Antonietti and A. Thomas, Macromolecules, 2007, 40, 1299 CrossRef CAS.
- A. Schönhals, Molecular Dynamics in Polymer Model Systems In: Broadband Dielectric Spectroscopy, F. Kremer, A. Schönhals, ed.; Springer: Berlin, 2002; p 225 Search PubMed.
- A. S. Kulik, H. W. Beckham, K. Schmidt-Rohr, D. Radloff, U. Pawelzik, C. Boeffel and H. W. Spiess, Macromolecules, 1994, 27, 4746 CrossRef CAS.
- (a) S. Havriliak and S. Negami, Polymer, 1967, 8, 161 CAS; (b) S. Havriliak and S. Negami, J. Polym. Sci., Part C: Polym. Symp., 1966, 16, 99 Search PubMed.
- A. Schönhals and F. Kremer, Analysis of dielectric spectra, in Broadband Dielectric Spectroscopy, ed. F. Kremer, A. Schönhals, Springer, Berlin, 2002, p 59 Search PubMed.
- A. Schönhals, F. Kremer, in Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer Verlag, Berlin, 2002, pp. 1–ff Search PubMed.
- T. A. Tran, S. Said and Y. Grohens, Macromolecules, 2005, 38, 3867 CrossRef CAS.
- K. Hatada, T. Kitayama, N. Fujimoto and T. Nishiura, J. Macromol. Sci., Part A: Pure Appl. Chem., 1993, 30, 645 Search PubMed.
- T. Kashiwagi, F. Du, J. F. Douglas, K. I. Winey, R. H. Harris Jr. and R. J. Sields, Nat. Mater., 2005, 4, 928 CrossRef CAS.
- (a) A. Blumstein, J. Polym. Sci., Part A: Gen. Pap., 1965, 3, 2653 CrossRef CAS; (b) A. Blumstein, J. Polym. Sci., Part A: Gen. Pap., 1965, 3, 2665 CrossRef CAS.
- (a) H. R. Brown and T. P. Russell, Macromolecules, 1996, 29, 798 CrossRef CAS; (b) J. H. Gibbs and E. A. DiMarzio, J. Chem. Phys., 1958, 28, 373 CAS.
- (a) E. A. DiMarzio and J. H. Gibbs, J. Chem. Phys., 1958, 28, 807 CrossRef CAS; (b) C. L. Jackson and G. B. McKenna, J. Non-Cryst. Solids, 1991, 221, 131.
| This journal is © The Royal Society of Chemistry 2010 |
