Symmetry and polar-π effects on the dynamics of enshrouded aryl-alkyne molecular rotors†
Arif R.
Karim
,
Anthony
Linden
,
Kim K.
Baldridge
* and
Jay S.
Siegel
*
Organisch-chemisches Institüt, Universität Zürich, Winterthurerstrasse 190, Zürich, CH-8057, Switzerland. E-mail: kimb@oci.uzh.ch; jss@oci.uzh.ch
First published on 24th May 2010
Abstract
The central ring of a 1,4-bis(arylethynyl)arene (ditolan) can be viewed as a molecular rotor with an extremely low barrier to rotation in the gas phase or solution. The torsional energy profile of that ring is shown to be dependent on the relative conformation of the end capping arenes. When the capping arenes are sterically bulky m-terphenyl units, it is possible to rationalize the conformational dynamics of the central ring by a factorization analysis, involving perturbation of the basic torsional energy profile by polar-π, and dispersion interactions between the flanking rings of the cap and the central ring of the ditolan. The symmetry of the construct can modulate the effect of these interactions. These principles apply to the design of materials in which a steric shroud excludes packing distortions.
Introduction
Control of the conformation and dynamics1,2 of molecular rotors3,4 is a key aspect of designing mechanical devices be they molecules5,6 or materials.7–9 Molecular rotors based on tolans (1,4-(arylethynyl)arenes) and ditolans (1,4-bis(arylethynyl)arenes) display extremely low barriers to rotation and weak conformational preferences in solution.10–16 In contrast, their solid phase structures tend to be conformationally fixed according to the dictates of the crystal packing.17–23 Two issues of control thus arise: (1) how can one modulate the inherent barrier to rotation in ditolans; (2) how can one decouple the conformational profile of a ditolan from its crystal packing interactions? One answer to question 1 comes in the form of a molecular design in which symmetry and stereoelectronic factors work hand in hand to modulate the inherent barrier to rotation of the central ring in a ditolan. Question 2 can be addressed by creating a steric shroud, which shields the rotator from the external environment,24 while providing the specific symmetry and internal interactions25 that control the conformational profile.10–13 Specific to this study, the utility of molecular fragments based on 2,6-diaryltolan,26–32 and molecular interactions of the polar-π type,33,34 are investigated.A well-known principle of conformational analysis is that, for otherwise equal systems, an increase in the symmetry of the conformational profile results in a decrease in the barrier to rotation.35 This idea may be viewed as a stereochemical corollary to the Hammond postulate in so far as conformations that are close in structure tend to be close in energy, and arriving back at the same conformation in fewer radians implies a closer structural, hence closer energetic, relation of the intermediate conformations.36
In tolan, there are two principal arenes (A and B), one at each end of the alkyne, with a slight preference to align coplanar with one another across the alkyne.12 The structure of 2,6-diaryltolans displays an umbrella-like conformation in which the alkyne is nestled between the two flanking arenes situated in the ortho positions of ring A (Fig. 1). In the idealized CPK model geometry of conformation α, the ortho-hydrogen atoms of ring B sit just outside vdW contact with the face of the flanking rings. Thus, no direct steric repulsion ensues; however, the possibility of CH-π/polar-π as well as attractive dispersive interactions still exists. A 90° rotation of ring B (conformation β) eliminates the CH-π interaction and places ring B orthogonal to ring A.
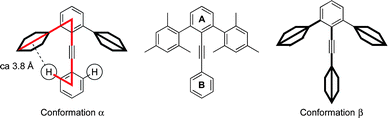 | ||
| Fig. 1 Principal conformations (α and β) of a 2,6-diaryltolan. | ||
Extending the structure to a ditolan (1,4-bis(arylethynyl)arene) makes for three principal rings (A, B, and A′) and creates four fundamental high symmetry conformations: two in which rings A and A′ are coplanar (||α/||β) and two in which they are orthogonal to one another (⊥α/⊥γ). Conformations ||α and ||β interconvert by 90° rotation of ring B; and conformations ⊥α and ⊥γ interconvert by 45° rotation of ring B (Fig. 2).
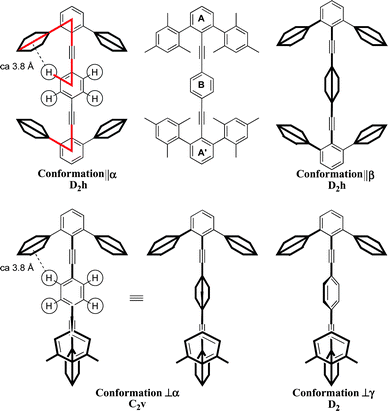 | ||
| Fig. 2 Principal conformations of a generic tetraarylditolan: (top) rings A and A′ are coplanar (||) and ring B is either coplanar (α) or orthogonal (β); (bottom) rings A and A′ are orthogonal (⊥) and ring B is either coplanar to one ring A or A′ (α), or skewed to both (γ). | ||
In type ||, the 90° rotation of ring B interconverts diastereomeric conformations, each of D2h symmetry, which represent the maximum and minimum of a 2-fold conformational profile. In ⊥, the 90° rotation of ring B interconverts homomeric conformations of D2d symmetry, which represent equipotential conformations on a 4-fold conformational profile; a skewed structure with equal torsion angles of 45° between ring B and either ring A or A′ is the transition structure. Thus, control of the relative conformation of the end terphenyls (acting as stators) changes the symmetry of the conformational profile of the central ring (acting as rotator).
The hypothesis is that conformations of type || will display higher than “normal” barriers to rotation in 2,2′,6,6′-tetraarylditolans, and those of type ⊥ will lead to barriers lower than “normal.” Furthermore, conformations of type ⊥ could set up a steric shield around ring B, which could allow similar rotational dynamics in the crystal as in solution. The caveat here is always the uncertainty as to what extent crystal packing forces will cause structural perturbation.37
The magnitude of the difference between rotational barriers of types || and ⊥ will depend to a large extent on the nature and strength of the CH-π interaction in these systems.38,39 Thus, umbrella-like 2,6-diaryltolans provide a useful model system for experimental and computational assessment of these interactions. Data on the umbrella-like systems provide a basis for creating an empirical factorization of effects on the barrier to rotation, the additivity of which can be tested in the 2,2′,6,6′-tetraarylditolans of family 2.
CH-π and polar-π interactions
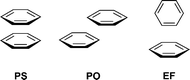
The relative orientations of interacting arenes have been categorized in three general classes (Fig. 3): parallel-stack (PS), parallel-offset (PO), and edge-to-face (EF).40Several model systems have been studied to parse out aspects of the aryl-aryl interaction.41–43 Specific studies into the so-called polar-π effect have led to a model for aryl-aryl interactions that includes dispersion, static polarity, and induced dipolar effects.44–47 Such a model is further supported by extensive theoretical work predicting the repulsive nature of the PS disposition and the attractive nature of both the PO and EF dispositions.48 This model provides a simple empirical way to rationalize the nature of a variety of arene-arene interactions.49–53
Until recently, quantum-mechanical methods that account for dispersive interactions well were too resource intensive to implement for systems of 30–60 non-hydrogen atoms. Commonly used DFT methods like B3LYP neglect dispersive interactions.54,55 More modern DFT functionals attempt to include effects due to dispersive terms.56,57 The combination of results from both DFT method types provides an impression of the relative importance of dispersive interactions in a specific system.
In the present study, the EF and PO arrangements most closely model the α and β conformations of ring B, respectively. Given the energy difference between α and β conformations in the parent tolan, one can assume that the change in ΔE(β − α) is a measure of the ΔE(PO − EF) in this system. This assumption is not an absolute but a useful working model for deducing semi-quantitatively the factors that contribute to such arene-arene interactions. The EF interaction has also been considered as a CH-π interaction.58
Chemical synthesis
Three families of molecules serve as targets for this study (Fig. 4): (1) umbrella-like 2,6-diaryltolans; (2) 2,2′,6,6′-tetraarylditolans; and (3) macrocyclic ditolans (cyclophanes/catenanes). The basic strategies for each follow some standard retrosynthetic principles, such that the base fragments are 2,6-diarylphenyl-X compounds, which we shall refer to as m-terphenyl-X fragments.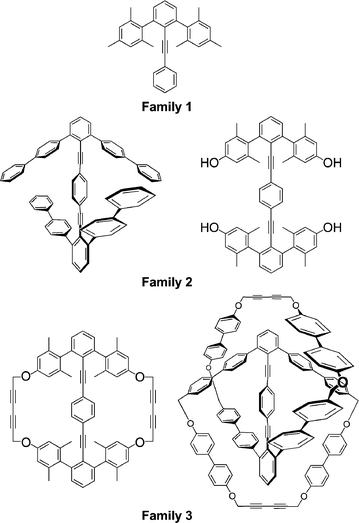 | ||
| Fig. 4 Families 1 (umbrella tolans), 2 (ditolans), and 3 (ditolylcyclophanes/catenanes). | ||
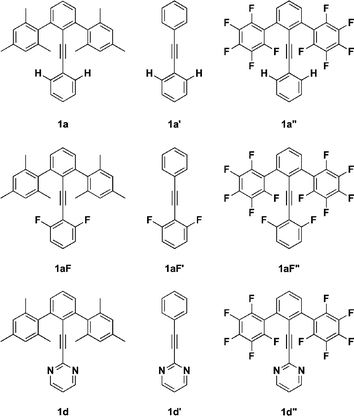
The synthesis of family 1 derivatives starts with an alkynyl coupling to 2,6-dibromoiodobenzene and passes through intermediates 6a–d (Scheme 1).59 Subsequent Negishi coupling with mesitylzinc chloride yields 1a–d:60,61 Ar = phenyl (1a), 2-pyridyl (1b), 3-pyridyl (1c), and 2-pyrimidyl (1d).
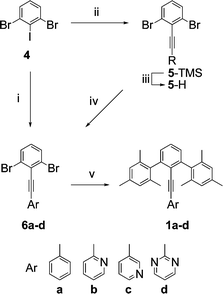 | ||
| Scheme 1 i. ArCCH, Pd(PPh3)2Cl2, CuI, TEA; ii. TMSCCH, Pd(PPh3)4, CuI, TEA; iii. K2CO3, MeOH; iv. 2-iodopyrimidine, Pd(PPh3)4, TEA; v. MesitylZnCl, Pd(PPh3)4, THF. | ||
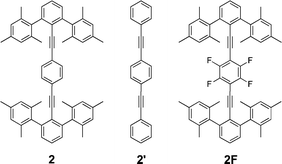
Members of family 2 were prepared from 5-TMS by Pd mediated coupling with m-anisyl zincate to make intermediate 7-TMS/Me (Scheme 2). Desilylation of 7-TMS/Me with carbonate and subsequent coupling with diiodobenzene, 2-bromo-5-iodopyridine or diiodobiphenyl resulted in 2a-Me, 2b-Me or 2c-Me, respectively. The synthesis of the desmethyl version of 2a-Me (2a-H) began with protection of 4-bromo-3,5-dimethylphenol with tert-butyldimethylsilylchloride, from which the arylzinc halide was prepared and used to couple with 5-TMS under Pd mediated Negishi conditions.60,61 The resulting m-terphenylacetylene (7-TMS/TBDMS) was deprotected and then set to couple with 1,4-diiodobenzene under Pd mediated Sonogashira conditions to produce 2a-H.59
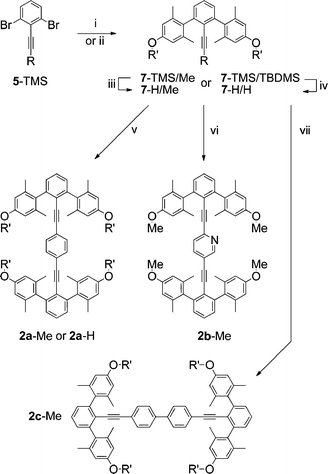 | ||
| Scheme 2 i. 2,6-diMe-4MeOPhZnCl, Pd(PPh3)4, THF; iii. K2CO3, MeOH; (ii. 2,6-diMe-4TBDMSOPhZnCl, Pd(PPh3)4, THF; iv. K2CO3, MeOH); v. 1,4-diiodobenzene, Pd(PPh3)2Cl2, CuI, TEA; vi. 2-bromo-5-iodopyridine, Pd(PPh3)4, TEA; vii. 4,4′-diiodobiphenyl, Pd(PPh3)4, CuI, TEA. | ||
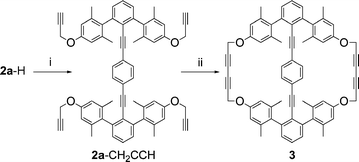
A cyclophane of family 3 was prepared by alkylation of 2a-H with propargyl bromide to provide 2a-CH2CCH, the precursor to cyclophane 3 (Scheme 3), which was obtained by intramolecular oxidative alkyne–alkyne coupling mediated by copper(II).62 As a set, 2a, 2b, and 3 are all targets to mimic type || systems.
A catenane of family 3 has not yet been completed, but an analog of the desired twisted type III conformation was prepared by extending the flanking 2,2′,6,6′ arenes as rigid biphenyls (2d) (Scheme 4). The zinc halide reagent of 4-(4-bromo-3,5-dimethylphenyl)anisole was used to couple with 5-TMS under Pd mediated Negishi conditions. The resulting m-terphenylacetylene (8) was deprotected and then set to couple with 1,4-diiodobenzene under Pd mediated Sonogashira conditions to produce 2d, a potential precursor to a concatenated ditolan.
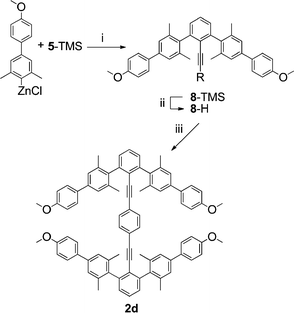 | ||
| Scheme 4 i. Pd(PPh3)4, THF; ii. K2CO3, MeOH; iii. 1,4-diiodobenzene, Pd(PPh3)4, CuI, TEA. | ||
A side reaction of the Sonogashira reaction of 7-H/Me led to the diyne dimer (9), presumably through a Pd mediated version of an alkyne-coupling reaction (Scheme 5). Though not directly cogent to our discussion of tolan based rotors, its structure depicts well how steric effects alone might achieve the same goals as the catenane.
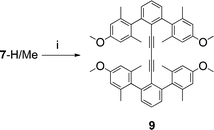 | ||
| Scheme 5 i. Cu(OAc)2·H2O, EtOH. | ||
Structural studies – X-ray crystallography/quantum chemical computations
Family 1 – umbrella tolans
The structure and conformational analysis of family 1 derivatives (1a–d) serves as the reference for comparative behavior in families 2 and 3. Key features to consider are the computational energetic preferences of conformations α vs. β, as well as the degree of angle bending of the alkyne axis in conformer α (parameters θexo and θendo), and the position of the CH bond vector relative to the flanking arene in conformation α (parameters dplane and datom).Initial computational studies focused on three symmetrical derivatives of family 1 with flanking mesityl rings on ring A, and phenyl (1a), 2,6-difluorophenyl (1aF), or 2-pyrimidyl (1d) as ring B, all compared against either a reference (parent) compound without flanking rings (1a′, 1a′F and 1d′), or a cognate with pentafluorophenyls instead of mesityl (1a′′, 1a′′F and 1d′′). From this series, the parent conformational preference, ΔE(ref), in the absence of flanking arenes can be established from the difference in energy of the β and α conformations of the reference compound (1a′, 1a′F or 1d′). The difference in energy of the β and α conformations of the aryl substituted compounds, ΔE(β − α), for (1a′, 1a′F and 1d′) or (1a′′, 1a′′F and 1d′′) are assumed to comprise a component arising from the parent ΔE(ref) and a component attributable to the interaction between the edge of ring B and the face of ring A, ΔE(edge/face).
On the basis of previous studies,34–37 mesityl (M) and pentafluorophenyl (P) should have opposite electrostatic effects, with mesityl showing larger interaction energies, (E(estat)). In contrast, polarizability and dispersion (E(disp)) effects of the arene π face should operate in both cases to a similar end. From the perspective of the edge side of the interaction, CH should be δ+, whereas CF and N: should be δ−. The magnitude of the dispersive interactions of these three groups should follow the order, N: < CH < CF.
This admittedly simple analysis provokes an empirical formula of the following form:
| ΔE(β − α) = ΔE(ref) + E(edge/face) |
| E(edge/face) = E(estat)X/Y + E(disp)X/Y |
| X = N:, CH, or CF and Y = M or P |
| N:/M < CF/M < CH/P < 0.0 kcal mol−1 < N:/P < CF/P < CH/M |
| N:/M = N:/P < CH/M = CH/P < CF/M = CF/P |
Using the data in Table 1, along with the acknowledgement that B3LYP does not account for dispersion effects,63 whereas B97-D does,64 one comes to a presumptive set of basic quantitative values for the interaction terms: (1) the E(estat)X/Y series follows as N:/M (−1.2) < CF/M (−0.7) < CH/P (−0.3) < 0.0 kcal mol−1 < N:/P (0.4) < CF/P (0.9) = CH/M (0.9); and (2) the E(disp)X/Y series follows as N:/M = N:/P (0.3) < CH/M = CH/P (0.6) < CF/M = CF/P (1.0) kcal mol−1. Adding the two terms together, one arrives at E(edge/face) terms of N:/M (−0.9) < CF/M (0.3) < CH/P (0.3) < N:/P (0.7) < CH/M (1.5) < CF/P (1.9) kcal mol−1. ΔE(ref) is between 1.1 and 1.3 kcal mol−1.
| Modela | 1a | 1a′ | 1a′′ | 1d | 1d′ | 1d′′ | 1aF | 1a′F | 1a′′F |
|---|---|---|---|---|---|---|---|---|---|
| a A: B3LYP/DZV(2d,p); B: B97-D/DZV(2d,p); C: MP2/DZV(2d,p); D: M06/DZV(2d,p); E: Empirically fit. | |||||||||
| A | 1.86 | 0.98 | 0.65 | 0.20 | 1.43 | 1.65 | 0.58 | 1.26 | 2.15 |
| B | 2.47 | 1.11 | 1.39 | 0.50 | 1.53 | 1.96 | 1.62 | 1.40 | 3.29 |
| C | 3.09 | 0.65 | — | 0.21 | 0.94 | — | 1.26 | 0.98 | — |
| D | 2.59 | 0.87 | 1.37 | 0.41 | 1.31 | 1.87 | 1.66 | 1.18 | 3.03 |
| E | 2.6 | 1.1 | 1.4 | 0.4 | 1.3 | 2.0 | 1.6 | 1.3 | 3.2 |
These values not only account for the set of 9 basis compounds, but they also predict the conformational energies in family 2 quite well. Although, no general transferability of these values is warranted, this analysis supports the hypothesis that these effects are energetically small and additive within the scope of this model. It shows that standard intuition concerning the reduction of these interactions into qualitative physical organic components results in a simplifying abstract model. It further highlights the importance of dispersive effects, especially in the context of F for H replacement.47
X-Ray diffraction quality crystals of 1a–1d were grown, diffraction data sets collected, and structures solved/refined.† No derivative of family 1 adopts an idealized α or β conformation in the crystal. The dihedral angles between the planes of the A and B arenes are intermediate between conformations α and β, and the alkyne axis is bent substantially away from linearity (Table 2, Fig. 5, Fig. 6). Computations starting from the crystal structure geometry of 1a predict a very small distortion energy, optimizing back to the idealized 1a in the α conformation as the minimum energy structure. Therefore, one can assume that the potential energy surface is very soft about the ideal α conformation and the distortions in the crystal structure are due to packing forces.
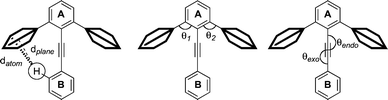 | ||
| Fig. 5 Geometrical parameters considered in Table 2. | ||
| Compound | A//Ba | θ 1 | θ 2 | θ exo | θ endo | d plane | d atom |
|---|---|---|---|---|---|---|---|
| a A//B = dihedral angle between rings A and B. b 1a_α is the computational geometry for 1a in the α conformation. | |||||||
| 1a | 34.32(11) | 118.39(16) | 119.48(16) | 173.2(2) | 173.1(2) | 2.89 | 2.95 |
| 1a_αb | 0.0 | 121.17 | — | 180.0 | 180.0 | 3.89 | 4.10 |
| 1b | 33.97(7) | 118.28(10) | 119.26(10) | 171.03(13) | 174.12(12) | 2.90 | 2.95 |
| 1c | 23.30(11) | 120.54(17) | 120.19(17) | 177.7(2) | 176.9(2) | 3.71 | 3.89 |
| 41.75(11) | 119.59(18) | 121.38(18) | 177.0(2) | 177.6(2) | 3.60 | 3.79 | |
| 1d | 47.5(6) | 119.05(15) | 119.05(15) | 177.2(15) | 180.0 |
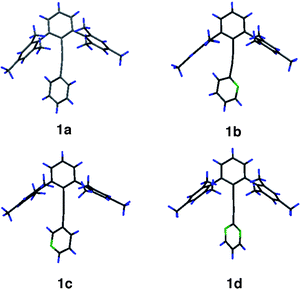 | ||
| Fig. 6 X-Ray diffraction structures of 1a–1d. | ||
In the series 1a–1d, the ortho positions of ring B are two CH bonds, one CH bond, and one N: lone pair, or two N: lone pairs. In all cases where a CH bond is present, the B ring twists to place the CH vector roughly over the position ortho to the methyl groups of the mesitylene, and the alkyne axis bends in favor of a closer CH to arene interaction. Where no CH bond is presented, the arene A-to-B dihedral angle is large and approximates a conformation of the β type. This mode of alkyne bending in the X-ray crystal structure presents itself also in compounds of family 2, albeit placing the CH vector over the methyl bearing carbon (see below). Although no such distortion is predicted by the computations, the energy needed to distort into this conformation is predicted to be very low. It is likely that these crystal structures represent a low energy mode of distortion caused by packing forces.
Family 2 – tetraarylditolans
In family 2, computations were restricted to 2, 2′ (ditolan), and 2F, in conformations ||α, ||β, ⊥α and ⊥γ. Type || structures showed a marked increase in preference for the α conformation, which is attributed to the two-fold barrier and the increase in the number of CH-to-arene interactions. In contrast, type ⊥ structures, where the symmetry of the barrier is four-fold and no conformation displays all four CH-to-arene interactions, show little if any conformational preference, with a rotational barrier on the order of 0.25 kcal mol−1. Applying to the series 2, 2′ and 2F, the empirical factors derived above from family 1, one finds a reasonable agreement for the difference in conformational energies (Table 3). This analysis supports the factorization model of effects within this limited series of compounds.|
|
|||||
|---|---|---|---|---|---|
| Method | 2-|| | 2-⊥ | 2′-|| | 2′-⊥ | 2F-|| |
| B3LYP | 3.96 | −0.05 | 2.19 | −0.23 | 1.51 |
| B97-D | 5.31 | −0.16 | 2.53 | −0.30 | 3.76 |
| MP2 | — | — | 1.48 | −0.09 | — |
| M06 | 5.38 | −0.42 | 1.98 | −0.22 | 3.67 |
| Empirical | 5.2 | 2.2 | 3.2 | ||
Synthetic derivatives (2a, 2b and 2c) of family 2 provided solvated crystals suitable for X-ray crystallographic analysis (Fig. 7). In 2c, there are two geometrically similar molecules in the asymmetric unit. They all adopt a type ||α structure and show a serpentine distortion of the ditolan axis, again favoring proximity between an ortho CH bond and the face of a flanking arene. The molecules of 2a and 2b sit across crystallographic centres of inversion. As a consequence, the N: atom and related para CH group in 2b are disordered over two sites, both of which lie to the wayward side of the ditolan-to-arene interaction. The consistent structural distortion across families 1 and 2 and the consistent placement of CH proximal and N: distal to the flanking arene further speaks of a stabilizing CH-to-arene interaction. In all cases, the closest CH bond to arene-ring-atom contact is at the carbon ortho to the methoxy substituent (3.00 Å [2a], 3.05 Å [2b] and 3.29 Å as the avg. of 3.10, 3.26, 3.34 and 3.45 Å [2c]). The central biaryls of 2c adopt a torsion angle close to 15°, suggesting no torsional inhibition of conjugation from end to end of the conjugated π system.
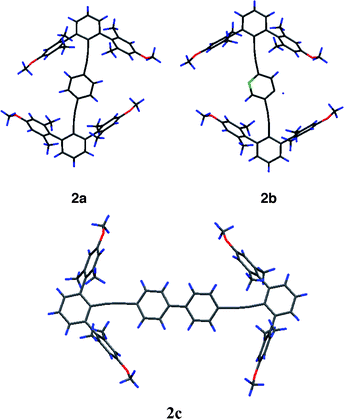 | ||
| Fig. 7 X-Ray diffraction structures of 2a, 2b and 2c (molecule A). | ||
The fourth synthetic derivative (2d) of family 2 bears extended diaryl arms in the 2,2′,6,6′ positions (Fig. 8). These were designed to create steric repulsion between substituents on ring A and ring A′, and thereby distort the conformation away from type || toward type ⊥. Crystals of 2d suitable for X-ray crystallographic analysis were grown and the structure solved. The conformation of 2d twists away from type || as predicted; however the dihedral angle between rings A and A′ (42.37(9)°) is intermediate between type || and ⊥. The relationship between rings A and B presents a relatively small dihedral angle of ca. 10°, whereas the dihedral angle between rings B and A′ is close to 33°. The angle distortion of the alkynes is now very small, with an average close to 178°. The distances between the hydrogen atoms on ring B and the carbon atoms of the flanking arenes are also much larger, the closest being 3.39 Å from a carbon meta to the aryl substituent. Most of the contacts exceed 3.6 Å, thus well outside the vdW radii of H and a carbon π system. These structural parameters support the idea that conformations of type ⊥ will display no preferential interactions and therefore manifest effectively high symmetry conformational profiles and lower barriers to rotation.
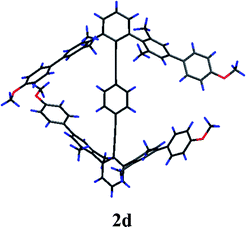 | ||
| Fig. 8 X-Ray diffraction structure of 2d. | ||
The full potential of this steric exclusion design has not been achieved but there is still promise in this approach. The side product 9, although not in the tolan series, gives some insight into what would happen if the steric interactions among the flanking rings could be increased.65 The crystal structure of 9 (Fig. 9) shows a dihedral angle between the terminal aryl rings of over 50°. Extremely bulky and rigid units such as tetraarylmethanes or centaryltricornans could induce such structures to adopt conformations even closer to the type ⊥ ideal.
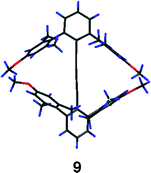 | ||
| Fig. 9 X-Ray diffraction structure of 9. | ||
Family 3 – macrocyclic ditolans
Two target topologies were the design of family 3: a macrocycle and a catenane. The macrocyclic structure was achieved synthetically as 3, a crystal of which yielded a structure with a conformation very close to type ||α (Fig. 10). In this structure the macrocyclic linkers were kept relatively short to discourage twisting of ring A relative to A′. The design results in a structure with dihedral angles between rings A and B and between B and A′ of only 6.4(2)° and 3.3(2)°, respectively. Rings A and A′ are almost coplanar. The alkynes distort in the now characteristic serpentine fashion (Table 4) and two trans-disposed hydrogen atoms of ring B are near to the carbon atom bearing the oxygen atom of the flanking rings.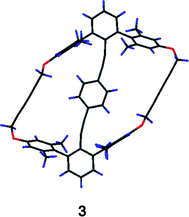 | ||
| Fig. 10 X-Ray diffraction structure of macrocycle 3. | ||
| Compound | A//Ba | θ exo | θ endo | d atom |
|---|---|---|---|---|
| a A//B = dihedral angle between rings A and B. b Two molecules in the asymmetric unit. c Dihedral angles are not representative, torsion angles are about 3, 8, 12, and 22°, see X-ray data. | ||||
| 2a | 7.57(11) | 174.6(2) | 174.1(2) | 3.00 |
| 2b | 6.70(14) | 174.5(2) | 174.0(2) | 3.05 |
| 2c | —c | 174.6(4) | 173.1(4) | 3.10 |
| 175.3(4) | 171.8(4) | 3.26 | ||
| 176.8(4) | 174.1(4) | 3.34 | ||
| 175.4(4) | 177.0(4) | 3.45 | ||
| 2d | 10.06(9) | 178.1(2) | 176.5(2) | 3.39 m |
| [A//B] | [A] | [A] | 3.63 o | |
| 33.57(9) | 177.6(2) | 178.3(2) | ||
| [B//A′] | [A′] | [B] | ||
| 42.37(9) | ||||
| [A//A′] | ||||
| 3 | 6.4(2) | 174.7(5) | 169.9(5) | 2.86 |
| 3.3(2) | 173.6(5) | 169.4(5) | 2.90 |
Conclusions
Conformational analysis of a series of umbrella-like diaryltolans has led to the design of tetraarylditolan structures for which rotation of the internal benzene ring should be essentially barrierless. The design involves a strategy that places m-terphenyl capping groups in an orthogonal conformation on opposite ends of the ditolan, thus sterically shielding the central arene from its external environment, while increasing the symmetry of the central ring's torsional energy profile. The ideal reduction to practice is seen as a bridged catenane, where the non-bonding repulsion of the interlocked rings enforces the orthogonal conformation of the capping arenes. Despite all the positives of these design principles, one remains at the mercy of unpredictable crystal packing forces, which can strongly perturb the structure of even relatively stiff systems. Further rigidification of these systems should minimize these distortions and the effect of encroachment by neighboring molecules in the solid state – a challenge for further research. The elucidation of this conformational control opens the possibility to study the physical properties, such as luminescence, as a systematic correlation with respect to internal structure.Computational methods
The conformational analyses of the molecular systems described in this study, including structural and orbital arrangements as well as property calculations, were carried out using the GAMESS66 software package. Structural computations of all compounds were performed using the B97-D,64 M06,67 and B3LYP68–70 density functional methods, with a subset additionally computed using conventional perturbation theory methods, MP2.71 The Dunning double-ζ polarized basis set, DZV(2d,p), was employed.72 Full geometry optimizations were performed and uniquely characterized via second derivative (Hessian) analysis to determine the number of imaginary frequencies (0 = minima; 1 = transition state). For details see the ESI.† Molecular orbital contour plots, used as an aid in the analysis of results, were generated and depicted using the programs QMView73 and WebMO.74Crystallographic data
Crystallographic data are provided in Table 5 and in the ESI.†| a Weighting scheme: w−1 = σ2(Fo2) + (aP)2 + bP where P = (Fo2 + 2Fc2)/3. b Non-merohedrally twinned by a 2-fold rotation about b*, with a major twin fraction of 0.68. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Compound | 1a | 1b | 1c | 1d | 2a | 2b | 2c | 2d | 9 | 3 |
| Crystallised from | CH2Cl2 | CH2Cl2–EtOH | CH2Cl2–MeOH | CH2Cl2–EtOH | CH2Cl2–hexane | CH2Cl2–EtOH | CH2Cl2–EtOH | CH2Cl2–EtOH | CH2Cl2–EtOH | CH2Cl2 |
| Empirical formula | C32H30 | C31H29N | C31H29N | C30H28N2 | C66H72Cl4O4 | C61H61Cl8NO4 | C64H58O4 | C82H70O4 | C52H50O4 | C66H50O4 |
| Formula weight/g mol−1 | 414.59 | 415.58 | 415.58 | 416.56 | 1071.10 | 1155.78 | 891.16 | 1119.45 | 738.96 | 907.12 |
| Crystal colour, habit | Yellow, prism | Colourless, prism | Colourless, prism | Pale-yellow, plate | Colourless, tablet | Colourless, prism | Colourless, tablet | Colourless, prism | Colourless, plate | Colourless, prism |
| Crystal dimensions/mm | 0.12 × 0.27 × 0.30 | 0.20 × 0.20 × 0.25 | 0.12 × 0.25 × 0.27 | 0.05 × 0.20 × 0.25 | 0.10 × 0.17 × 0.40 | 0.15 × 0.20 × 0.25 | 0.10 × 0.25 × 0.30 | 0.20 × 0.20 × 0.30 | 0.03 × 0.17 × 0.28 | 0.13 × 0.18 × 0.23 |
| T/K | 160 (1) | 160(1) | 160 (1) | 160(1) | 160(1) | 160(1) | 160(1) | 1601) | 160(1) | 160(1) |
| Crystal system | Triclinic | Triclinic | Triclinic | Orthorhombic | Triclinic | Triclinic | Monoclinic | Monoclinic | Monoclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Pnna |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/c | P21/c | Pc | Cc |
| Z | 2 | 2 | 4 | 4 | 1 | 1 | 8 | 4 | 4 | 4 |
| Reflections for cell determination | 4275 | 6886 | 8433 | 2427 | 5006 | 52011 | 18356 | 13211 | 7705 | 4677 |
| 2θ range for cell determination/° | 4–50 | 4–60 | 4–50 | 4–50 | 4–50 | 4–50 | 4–50 | 4–52 | 4–50 | 4–50 |
| Unit cell parameters | ||||||||||
| a/Å | 8.4200(4) | 8.3091(2) | 10.1034(4) | 18.9732(7) | 9.5378(3) | 9.5501(2) | 21.7475(7) | 29.4698(4) | 12.9195(3) | 35.618(1) |
| b/Å | 10.4450(4) | 10.5240(2) | 14.8715(6) | 14.5707(5) | 11.7657(4) | 11.9607(3) | 36.719(1) | 13.9924(2) | 26.1804(7) | 9.3960(3) |
| c/Å | 15.4972(7) | 15.4592(3) | 17.8686(7) | 8.6223(4) | 13.6855(6) | 13.4618(3) | 12.9048(4) | 16.0684(2) | 13.8321(3) | 14.9250(4) |
| α/° | 81.045(3) | 80.8186(9) | 74.014(3) | 90 | 85.769(2) | 85.759(2) | 90 | 90 | 90 | 90 |
| β/° | 74.819(3) | 74.994(1) | 75.146(2) | 90 | 88.725(2) | 88.837(1) | 95.539(1) | 102.4965(8) | 114.575(1) | 92.473(2) |
| γ/° | 68.224(3) | 67.878(1) | 78.920(2) | 90 | 71.627(2) | 71.180(1) | 90 | 90 | 90 | 90 |
| V/Å3 | 1218.90(10) | 1206.70(4) | 2473.3(2) | 2383.7(3) | 1453.51(9) | 1451.48(6) | 10257.0(6) | 6468.9(2) | 4254.7(2) | 4990.2(3) |
| F(000) | 444 | 444 | 888 | 888 | 568 | 602 | 3792 | 2376 | 1576 | 1912 |
| D x /g cm−3 | 1.130 | 1.144 | 1.116 | 1.161 | 1.224 | 1.322 | 1.154 | 1.149 | 1.154 | 1.207 |
| μ(Mo-Kα)/mm−1 | 0.0634 | 0.0653 | 0.0637 | 0.0674 | 0.251 | 0.434 | 0.0703 | 0.0690 | 0.0713 | 0.0737 |
| Scan type | ω | ϕ and ω | ω | ω | ω | ω | ω | ϕ and ω | ϕ and ω | ω |
| 2θ(max)/° | 50 | 60 | 50 | 50 | 50 | 50 | 50 | 52 | 50 | 50 |
| Transmission factors (min; max) | — | — | — | — | — | 0.889; 0.967 | — | — | — | — |
| Total reflections measured | 17941 | 30830 | 32418 | 28593 | 19536 | 19022 | 101722 | 99005 | 65817 | 36176 |
| Symmetry independent reflections | 4301 | 7037 | 8627 | 2112 | 5099 | 5070 | 18117 | 95938 | 7536 | 4402 |
| R int | 0.059 | 0.046 | 0.055 | 0.089 | 0.069 | 0.067 | 0.100 | 0.088 | 0.084 | 0.090 |
| Reflections with I > 2σ(I) | 3093 | 4918 | 6228 | 1506 | 2948 | 3558 | 9010 | 67864 | 5363 | 3928 |
| Reflections used in refinement | 4298 | 7032 | 8625 | 2109 | 5094 | 5069 | 18108 | 95938 | 7532 | 4402 |
| Parameters refined | 296 | 296 | 590 | 178; 36 | 287 | 287 | 1250 | 789 | 1034; 2 | 639; 2 |
| Final R(F) [I > 2σ(I) reflections] | 0.0530 | 0.0558 | 0.0546 | 0.0485 | 0.0661 | 0.0786 | 0.0876 | 0.0868 | 0.0526 | 0.0724 |
| wR(F2) (all data) | 0.1430 | 0.1591 | 0.1458 | 0.1312 | 0.1903 | 0.2454 | 0.2100 | 0.2708 | 0.1166 | 0.1890 |
| Weighting parameters a; ba | 0.0552; 0.3424 | 0.0734; 0.1784 | 0.0574; 0.7937 | 0.0612; 0.3266 | 0.1087; 0 | 0.1749; 0 | 0.0359; 7.7552 | 0.1085; 11.9 | 0.0555; 0.0332 | 0.1465; 0.7217 |
| Goodness of fit | 1.067 | 1.054 | 1.055 | 1.060 | 0.965 | 1.018 | 1.104 | 1.153 | 1.091 | 1.073 |
| Secondary extinction coefficient | 0.033(5) | 0.027(7) | 0.017(2) | 0.008(2) | 0.030(5) | 0.06(1) | 0.0008(2) | 0.0110(3) | 0.0215(9) | — |
| Final Δmax/σ | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.05 | 0.001 |
| Δρ (max; min)/e Å−3 | 0.23; −0.18 | 0.27; −0.27 | 0.19; −0.16 | 0.22; −0.19 | 0.26; −0.21 | 0.27; −0.29 | 0.41; −0.20 | 0.67; −0.64 | 0.19; −0.19 | 0.40; −0.28 |
Acknowledgements
This work was supported by the Swiss National Science Foundation. David Wolstenholme, Dalhousie University, is thanked for assistance with the crystal structure determination for 2b.References
- T. Akutagawa and T. Nakamura, Dalton Trans., 2008, 6335–6345 RSC.
- S. D. Karlen and M. A. Garcia-Garibay, Top. Curr. Chem., 2005, 262, 179–227 CAS.
- For a general review of artificial molecular rotors, see: G. S. Kottas, L. I. Clarke, D. Horinek and J. Michl, Chem. Rev., 2005, 105, 1281 Search PubMed.
- In the nomenclature of ref. 1, the term molecular rotor refers to the entire molecule, and comprises a stator and rotator that are linked by an axle.
- For a perspective on molecular rotors as gyroscopes see: M. A. Garcia-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10771 Search PubMed.
- For an overview of molecular structures that emulate certain aspects of macroscopic gyroscopes, see: K. Skopek, M. C. Hershberger and J. A. Gladysz, Coord. Chem. Rev., 2007, 251, 1723 Search PubMed.
- T. Akutagawa, H. Koshinaka, D. Sato, S. Takeda, S.-I. Noro, H. Takahashi, R. Kumai, Y. Tokura and T. Nakamura, Nat. Mater., 2009, 8, 342–347 CrossRef CAS.
- S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695–704 Search PubMed.
- J. Seo, R. Matsuda, H. Sakamoto, C. Bonneau and S. Kitagawa, J. Am. Chem. Soc., 2009, 131, 12792–12800 CrossRef CAS.
- Solution studies of tolans (ref. 10–13): M. Barzoukas, A. Fort, G. Klein, A. Boeglin, C. Serbutoviez, L. Oswald and J. F. Nicoud, Chem. Phys., 1991, 153, 457 Search PubMed.
- K. Inoue, H. Takeuchi and S. Konaka, J. Phys. Chem. A, 2001, 105, 6711 CrossRef CAS.
- A. Liberles and B. Matlosz, J. Org. Chem., 1971, 36, 2710 CrossRef CAS.
- K. Okuyama, T. Hasegawa, M. Ito and N. Mikami, J. Phys. Chem., 1984, 88, 1711 CrossRef CAS.
- Solution studies of ditolans (ref. 14–16): A. Beeby, K. Findlay, P. J. Low and T. B. Marder, J. Am. Chem. Soc., 2002, 124, 8280 Search PubMed.
- S. J. Greaves, E. L. Flynn, E. L. Futcher, E. Wrede, D. P. Lydon, P. J. Low, S. R. Rutter and A. Beeby, J. Phys. Chem. A, 2006, 110, 2114 CrossRef CAS.
- M. Levitus, K. Schmieder, H. Ricks, K. D. Shimizu, U. H. F. Bunz and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2001, 123, 4259 CrossRef CAS.
- Crystal structure of tolan (ref. 17–21): A. V. Abramenkov, A. Almenningen, B. N. Cyvin, S. J. Cyvin, T. Jonvik, L. S. Khaikin, C. Roemming and L. V. Vilkov, Acta Chem. Scand., Ser. A, 1988, 42a, 674 Search PubMed.
- A. A. Espiritu and J. G. White, Z. Kristallogr., Kristallgeom., Kristallphys., Kristallchem., 1978, 147, 177 Search PubMed.
- A. Mavridis and I. Moustakali-Mavridis, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 3612 CrossRef.
- J. M. Robertson and I. Woodward, Proc. R. Soc. London, Ser. A, 1938, 164, 436 CrossRef CAS.
- R. Thomas, S. Lakshmi, S. K. Pati and G. U. Kulkarni, J. Phys. Chem. B, 2006, 110, 24674 CrossRef CAS.
- Crystal structure of ditolan (ref. 22,23): S. W. Watt, C. Dai, A. J. Scott, J. M. Burke, R. L. Thomas, J. C. Collings, C. Viney, W. Clegg and T. B. Marder, Angew. Chem., Int. Ed., 2004, 43, 3061 Search PubMed.
- L. Zhao, I. F. Perepichka, F. Türksoy, A. S. Batsanov, A. Beeby, K. S. Findlay and M. R. Bryce, New J. Chem., 2004, 28, 912 RSC.
- M. A. Garcia-Garibay and C. E. Godinez, Cryst. Growth Des., 2009, 9, 3124–3128 CrossRef CAS.
- P. D. Jarowski, K. N. Houk and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2007, 129, 3110–3117 CrossRef CAS.
- This motif can be seen in tris(ethynylphenyl)triphenylbenzene, see ref. 26–28: A. J. Chalk and R. A. Jerussi, Tetrahedron Lett., 1972, 13, 61–62 Search PubMed.
- H.-F. Hsu, M.-C. Lin, W.-C. Lin, Y.-H. Lai and S.-Y. Lin, Chem. Mater., 2003, 15, 2115 CrossRef CAS.
- W. Hübel and R. Merényi, Chem. Ber., 1963, 96, 930–943.
- M. Kozaki, H. Tujimura, S. Suzuki and K. Okada, Tetrahedron Lett., 2008, 49, 2931–2934 CrossRef CAS.
- M. Kozaki, A. Uetomo, S. Suzuki and K. Okada, Org. Lett., 2008, 10, 4477–4480 CrossRef CAS.
- More general is the use of m-terphenyl as a shroud to shield an atom or functional group, see ref. 22,23: C.-T. Chen and J. S. Siegel, J. Am. Chem. Soc., 1994, 116, 5959–5960 Search PubMed.
- J. A. C. Clyburne and N. McMullen, Coord. Chem. Rev., 2000, 210, 73 CrossRef CAS.
- S. L. Cockroft, J. Perkins, C. Zonta, H. Adams, S. E. Spey, C. M. R. Low, J. G. Vinter, K. R. Lawson, C. J. Urch and C. A. Hunter, Org. Biomol. Chem., 2007, 5, 1062 RSC.
- Review: E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250 Search PubMed.
- S. D. Karlen, C. E. Godinez and M. A. Garcia-Garibay, Org. Lett., 2006, 8, 3417–3420 CrossRef CAS.
- J. P. Lowe, Prog. Phys. Org. Chem., 1968, 6, 1 CAS.
- S. D. Karlen, S. I. Khan and M. A. Garcia-Garibay, Mol. Cryst. Liq. Cryst., 2006, 456, 221–230 CrossRef CAS.
- M. Nishio, M. Hirota and Y. Umezawa, The CH/π Interaction: Evidence, Nature, and Consequences, Wiley-VCH, Zürich, 2001 Search PubMed.
- S. Tsuzuki and A. Fujii, Phys. Chem. Chem. Phys., 2008, 10, 2584 RSC.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- For EF-oriented arenes see: F. J. Carver, C. A. Hunter, D. J. Livingstone, J. F. McCabe and E. M. Seward, Chem.–Eur. J., 2002, 8, 2847 Search PubMed.
- For PO-oriented arenes see: F. Cozzi, R. Annunziata, M. Benaglia, M. Cinquini, L. Raimondi, K. K. Baldridge and J. S. Siegel, Org. Biomol. Chem., 2003, 1, 157–162 Search PubMed.
- For studies on model systems featuring PS-oriented arenes see: F. Cozzi and J. S. Siegel, Pure Appl. Chem., 1995, 67, 683–689 Search PubMed.
- F. Cozzi, M. Cinquini, R. Annunziata, T. Dwyer and J. S. Siegel, J. Am. Chem. Soc., 1992, 114, 5729–5733 CrossRef CAS.
- F. Cozzi, M. Cinquini, R. Annuziata and J. S. Siegel, J. Am. Chem. Soc., 1993, 115, 5330–5331 CrossRef CAS.
- F. Cozzi, F. Ponzini, R. Annunziata, M. Cinquini and J. S. Siegel, Angew. Chem., Int. Ed. Engl., 1995, 34, 1019 CrossRef CAS.
- For a study that reached a similar conclusion about H– vs. F–arene interactions, see: F. Cozzi, R. Annunziata, M. Benaglia, K. K. Baldridge, G. Aguirre, Y. Sritana-Anant and J. S. Siegel, Phys. Chem. Chem. Phys., 2008, 10, 2686–2694 Search PubMed.
- Review: C. A. Hunter, Angew. Chem., Int. Ed. Engl., 1993, 32, 1584 Search PubMed.
- Additional analysis and critique of this model recently appeared in which the experimental and theoretical results that form the basis for our model have been confirmed. The discussion remains open concerning the relative importance of specific factors. See ref. 50–53.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430 CrossRef.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10656–10668 CrossRef CAS.
- S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10854 CrossRef CAS.
- S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2009, 5, 2301 CrossRef CAS.
- P. Hobza, J. Sponer and T. Reschel, J. Comput. Chem., 1995, 16, 1315–1325 CrossRef CAS.
- S. Kristyán and P. Pulay, Chem. Phys. Lett., 1994, 229, 175 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108–034115 CrossRef.
- R. Peverati and K. K. Baldridge, J. Chem. Theory Comput., 2008, 4, 2030–2048 CrossRef CAS.
- M. Nishio, CrystEngComm, 2004, 6, 130–158 RSC.
- K. Sonogashira, Y. Tohda and N. Hagihara, Tetrahedron Lett., 1975, 16, 4467 CrossRef.
- E.-I. Negishi, Acc. Chem. Res., 1982, 15, 340 CrossRef CAS.
- E.-I. Negishi, A. O. King and N. Okudado, J. Org. Chem., 1977, 42, 1821–1823 CrossRef CAS.
- G. Eglinton and A. R. Galbraith, Chem. Ind. (London, U. K.), 1956, 737 Search PubMed.
- S. Grimme, C. Mück-Lichtenfeld and J. Antony, Phys. Chem. Chem. Phys., 2008, 10, 3327 RSC.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef.
- S. Toyota, T. Iida, C. Kunizane, N. Tahnifuji and Y. Yoshida, Org. Biomol. Chem., 2003, 1, 2298 RSC.
- M. Schmidt, K. K. Baldridge, J. A. Boatz, S. Elbert, M. Gordon, J. H. Jenson, S. Koeski, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- K. K. Baldridge and J. P. Greenberg, J. Mol. Graphics, 1995, 13, 63 CrossRef CAS.
- http://www.webmo.net/index.html .
Footnote |
| † Electronic supplementary information (ESI) available: Computational methods and coordinate files, experimental procedures and analytical data for compounds prepared in this work. CCDC reference numbers 763789–763798. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c0sc00117a |
| This journal is © The Royal Society of Chemistry 2010 |