Correlated single quantum dot blinking and interfacial electron transfer dynamics†
Shengye Jina, Jung-Cheng Hsiangb, Haiming Zhua, Nianhui Songa, Robert M. Dicksonb and Tianquan Lian*a
aDepartment of Chemistry, Emory University, Atlanta, GA 30322, USA. E-mail: tlian@emory.edu
bSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, GA 30332-0400, USA
First published on 31st August 2010
Abstract
The electron transfer (ET) dynamics from core/multi-shell (CdSe/CdS3MLZnCdS2MLZnS2ML) quantum dots (QDs) to adsorbed Fluorescein (F27) molecules have been studied by single particle spectroscopy to probe the relationship between single QD interfacial electron transfer and blinking dynamics. Electron transfer from the QD to F27 and the subsequent recombination were directly observed by ensemble-averaged transient absorption spectroscopy. Single QD-F27 complexes show correlated fluctuation of fluorescence intensity and lifetime, similar to those observed in free QDs. With an increasing ET rate (controlled by F27-to-QD ratio), the lifetime of on states decreases and relative contribution of off states increases. It was shown that ET is active for QDs in on states, the excited state lifetime of which reflects the ET rate, whereas in the off state QD excitons decay by Auger relaxation and ET is not a competitive quenching pathway. Thus, the blinking dynamics of single QDs modulate their interfacial ET activity. Furthermore, interfacial ET provides an additional pathway for generating off states, leading to correlated single QD interfacial ET and blinking dynamics in QD-acceptor complexes. Because blinking is a general phenomenon of single QDs, it appears that the correlated interfacial ET and blinking and the resulting intermittent ET activity are general phenomena for single QDs.
Introduction
Understanding exciton quenching dynamics in quantum dots (QDs) is essential to their many applications, ranging from solar cells1,2 and light emitting diodes3 to biological imaging.4 Interest in exciton dissociation by interfacial charge transfer has been intensified by recent reports of multiple exciton generation in some QDs.5–7 This novel phenomenon may provide a new approach to improve the efficiency of QD-based solar cells,8,9 although its mechanism and efficiency are still subjects of intense debate.10–16 Furthermore, it is unclear how to dissociate multiple excitons prior to their annihilation on the 10s-100s picosecond time scale.7,17 One potential approach may be to dissociate excitons in QDs by ultrafast electron transfer (ET) to acceptors on the surface.18–27 To gain further insight into the dynamics of charge transfer from QDs, ET on the single QD level has been investigated.28–31Single QDs exhibit correlated fluctuation of fluorescence intensity (i.e.“blinking”) and lifetime.32–53 It was shown that states with higher fluorescence intensity (on state) have longer exciton lifetimes, and states of low intensity (off state) have shorter lifetimes, suggesting a fluctuation of the nonradiative decay rate. For most QDs, the probabilities of the QD remaining in the on and off states obey a power-law dependence with an exponent of ∼ 1.5.33,40,49,53 The formation of off states has been attributed to photoinduced charging of QDs by Auger ionization and/or charge transfer to trap states in QDs and the surrounding matrix.32–35,39,43,52,53 The trapped charge can recombine with the charged QD, returning it to the on state. The power-law dependence in the on- and off-time distributions suggests a broad distribution and fluctuation of the transition rates between the on and off states. Although the nature of the trap states and the microscopic origin of these fluctuating transition rates remains unclear, models assuming diffusion-controlled ET33,46–49 and fluctuating tunneling barriers for ET to and from trap states39,52 can account for the power-law on- and off-time distribution functions. These insights have led to the development of novel materials and schemes for suppressing the blinking of QDs.31,53–60
Recently, we and others have shown that in single QD-molecular electron acceptor complexes the blinking dynamics and lifetime fluctuations persist, suggesting intermittent ET activities.28,29 The origin of the intermittent ET activity remains unclear. Two possibilities exist. In the first case, the fluctuating lifetime may be caused by a corresponding fluctuation of ET rates. As a result, states with short and long lifetimes have fast and slow ET rates, respectively.28,29 In the second scenario, the lifetime of the off states is dominated by the Auger relaxation process in charged QDs, similar to single QDs on ET inactive substrates. In these off states, exciton quenching by ET is not competitive with Auger relaxation and QDs become ET inactive.30 If the latter model is correct, the intermittent ET activity is a general characteristic of single QDs because most of them have been shown to undergo blinking under continuous illumination.32–43,45–60 In a more recent study of single QDs on TiO2, we compared ensemble-averaged and single QD fluorescence decays and suggested that the second scenario described above is the origin of the intermittent ET activities of single QDs.30 Unfortunately, in that system, the ET process was not directly identified and cannot be readily controlled to assess the validity of the model.
In this paper, we compare ensemble-averaged and single QD ET dynamics of QD-Fluorescein 27 (F27) complexes. The ET rates in these complexes can be varied by adjusting the number of adsorbates on QDs. The rates of charge separation and charge recombination are directly studied by ensemble-averaged transient absorption and fluorescence decay. On the single QD level, blinking dynamics persist in these complexes, showing correlated fluorescence fluctuations of lifetime and intensity, consistent with our previous report.28 With increased ET rate, the on state probability density of single QDs decreases and the off state probability density increases. We show that both the ensemble-averaged and single QD fluorescence decay can be described by a model that assumes a Poisson distribution of the number of adsorbates on QDs. The lifetime of the on states of single QDs correlates with the charge separation rates whereas the lifetime of the off states is dominated by Auger relaxation. ET activity is modulated due to the blinking dynamics of the QDs. Furthermore, interfacial ET produces positively charged (optically dark) QDs and reduced adsorbates, providing another pathway for generating off states and leading to correlated single QD blinking and interfacial ET dynamics.
Results and discussion
Ensemble-averaged ET dynamics
The core/multi-shell (CdSe/CdS3MLZnCdS2MLZnS2ML) QDs chosen for this study have their lowest energy exciton absorption band at 605 nm. For the ensemble-averaged transient absorption (TA) and fluorescence (FL) decay measurements, three samples were prepared in heptane solution: free QDs and QD-F27 complexes with low (sample A) and high (sample B) F27-to-QD ratios. The exact ratios are initially not known because the extinction coefficient of these QDs has not been determined. However, the ratio in sample B is about twice that of sample A according to the UV-vis. absorption spectra shown in Figure S1.† Most F27 molecules are believed to be bound on the QDs because of their negligible solubility in heptane, but their mode of attachment is not known. In general, excitons in QDs can be quenched by energy, electron and hole transfer to adsorbates. In this system, exciton quenching by energy transfer from the QD to F27 is not possible because of the lack of spectral overlap of the QD emission with F27 absorption. The estimated core radius is 1.7 nm and the estimated 1S exciton oxidation and reduction potentials are −0.85 and +1.05 V (vs SCE), respectively, for the QDs used in this study (see supporting information for details†).31 Compared to the reduction and oxidation potentials of F27 (at −0.81 and +1.57 V SCE, respectively61), hole transfer from QD to F27 is not energetically allowed. This suggests that ET from the QD to F27 is the only pathway for the quenching of QD excitons. The ET process leads to the formation of oxidized QDs and the reduced F27 molecules, which eventually recombine to regenerate the QD and F27 ground state. The charge separation and recombination process can be described in the following equation: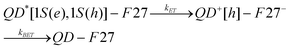 | (1) |
Here, QD*[1S(e), 1S(h)] denotes an excited QD with an electron in the 1S(e) level and a hole in the 1S(h) level, and QD+[h] denotes an oxidized QD with a hole in the valence band or a trap state.
To directly probe the ET process, we have compared transient absorption spectra of free QDs and QD-F27 complexes. Shown in Fig. 1a are the TA spectra of QD-F27 complexes (sample B) at different delay times. These samples were excited at 400 nm, which selectively excited QDs (see Figure S1†). Similar TA spectra for free QDs and sample A are shown in Figure S3.† These spectra show an initial bleach and subsequent recovery of the exciton bands. The exciton bleach results from the filling of the 1S electron level in excited QDs.7,18 The bleach formation is instrument response time (0.5 ns) limited in this measurement. Subpicosecond transient absorption studies of similar samples (shown in Figure S4†) shows QD exciton bleach formation on the subpicosecond time scale and negligible bleach recovery in the first 500 ps. As shown in Fig. 1b, the exciton bleach recovery of these samples (probed around 605 nm) occurs on the few nanosecond time scale and the bleach recovery rate increases in samples with higher F27-to-QD ratios. This trend can be attributed to ET from the QD to F27, which reduces the lifetime of the 1S electron and leads to a faster QD 1S exciton bleach recovery.
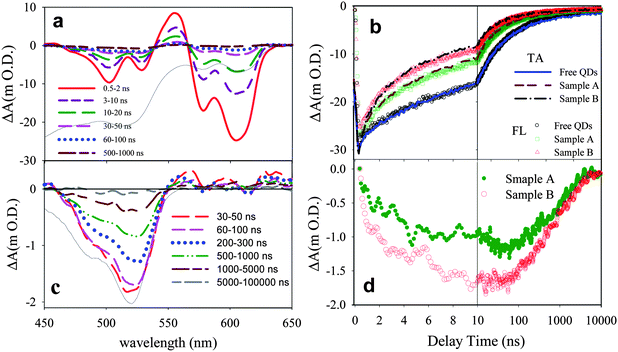 | ||
| Fig. 1 (a) Transient absorption spectra at indicated delay times following 400 nm excitation of QDs-F27 complexes (sample B). The black solid line is the ground state absorption spectrum of QD-F27 complex (inverted for better comparison). (b) Transient absorption (TA, solid lines) kinetics at ∼ 605 nm (averaged from 601 to 610 nm) and ensemble averaged fluorescence (FL, open symbols) decays of free QDs and QD-F27 complexes. The FL kinetics have been inverted and normalized for better comparison with the TA kinetics. (c) Transient spectra of F27 in sample B obtained by subtracting the QDs signals (see text for details). Also shown is the ground state absorption spectrum of F27 (black solid line, inverted for better comparison). (d) The kinetics of F27 bleach at ∼525 nm (averaged from 521∼530 nm) for sample A (green solid circles) and sample B (red open circles). | ||
Furthermore, the ET process should also lead to the depletion of F27 ground state and the formation of reduced F27. The latter has a spectral feature at ∼390 nm and is not observed in this study due to the limited spectral range of the white light probe.62 The bleach of F27 ground state absorption can be observed in the 450∼540 nm region for the QD-F27 complex. Because the amplitudes of the F27 signals are much smaller than those of the QD, we have subtracted out the QD signal to produce transient spectra that contain the contribution of the F27 signal only, as shown in Fig. 1c. In the subtraction procedure, the free QD signal has been scaled such that its bleach amplitude matches that of QD-F27 at 605 nm (where the signal is caused by QD exciton bleach only) and the scaled QD signal has been subtracted from the total signal shown Fig. 1a. The kinetics of F27 bleach formation and recovery are shown in Fig. 1d. The kinetics of F27 bleach formation follows the QD exciton bleach recovery, reflecting the forward ET process. These kinetics deviate from each other after 10 ns due to the presence of back ET from F27 to QDs. The recombination of electrons in F27 with the holes in the QD leads to the regeneration of the F27 (and QD) ground state and can be monitored by the F27 bleach recovery kinetics at 525 nm. As shown in Fig. 1d, the recovery of the F27 bleach is non-single-exponential, with half lifetimes of 0.8 and 0.7 μs for sample A and B, respectively. It should be noted that the bleach recovery contains a small but non-negligible component that is slower than the 10 μs observation window of this transient absorption study.
As shown in Fig. 1b, the exciton bleach recovery kinetics are in good agreement with the ensemble-averaged fluorescence decay of these samples, suggesting that fluorescence quenching also results from ET and that the fluorescence lifetime provides a reliable measurement of ET dynamics in these samples. This agreement enables the study of ET dynamics in single QD-F27 complexes using single QD fluorescence decays, which will be discussed later. Furthermore, these transient absorption and fluorescence decay measurements show that the ET rate from QD to F27 increases in QDs with more adsorbed F27. Comparison of the bleach recovery of free QD vs. QD-F27 complexes allows an estimate of the ensemble-averaged ET time. As will be further discussed below, ET in this system occurs on the few to 10s of nanosecond timescale. This ET rate is considerably slower than those from core only CdSe QDs to other molecular adsorbates, such as rhodamine B and methylene blue, in which ET occurs on the few to 10s of picosecond time scales.27,63 The slower rate in this system can be attributed to a smaller driving force for ET and a smaller electronic coupling strength between the QD and adsorbate (due to the presence of ZnS shells).
Single QD ET dynamics
Three samples were prepared for single QD studies: sample 1 is free QDs without F27, and samples 2 and 3 are QD-F27 complexes with low and high F27-to-QD ratios, respectively. The exact ratios will be determined as fitting parameters from the measured single QD ET rate distributions (see below). Raster-scanned single particle fluorescence images show well-separated single QDs (see Figure S2†). The samples were excited at 400 nm with an average power of 150 nW. The emission between 540 and 675 nm from single QDs was detected, and collected photons were labeled by their arrival time (relative to the start of the experiments) and decay time (relative to the excitation pulse). The number of photons binned over a 50-ms window of arrival times was calculated to construct trajectories of fluorescence intensity (in units of counts per second or Hz) as a function of (arrival) time. Delay time histograms of detected photons within 1-s windows were constructed and fit by single exponential decays to determine their fluorescence lifetimes, from which the lifetime trajectories were constructed. Typical fluorescence intensity and lifetime trajectories for these samples are shown in Fig. 2 a1–a3.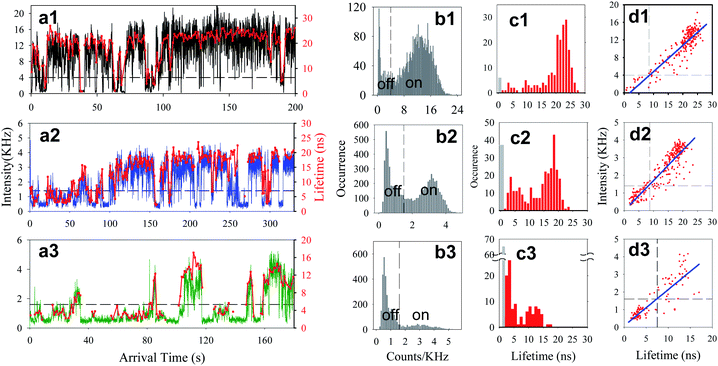 | ||
| Fig. 2 ai) Typical fluorescence intensity (black, blue or green) and lifetime (red) trajectories, bi) histograms of fluorescence intensity, ci) histograms of fluorescence lifetime, and di) fluorescence intensity vs. lifetime for a typical single QD from each sample i (i = 1 for free QDs, and i = 2, and 3 for low and high ratio QD-F27 complexes, respectively). The dashed lines in panels b1–b3 indicate the thresholds separating the on and off states. The black bars in lifetime histograms (panels c1–c3) indicate the occurrence of low-fluorescence intensity points along the trajectories, for which the lifetimes have been assumed to be < 0.5 ns. In panels d1–d3, the blue solid lines are linear fits and the dashed lines indicate the intensity and lifetime thresholds separating the on and off states. | ||
As shown in Fig. 2 b1, the intensity distribution of this free QD (without F27) shows two peaks at ∼12 kHz and 0.54 kHz (background level). The high-intensity peak has been assigned to the QD on state and the low-intensity peak to the off state.33–41,43,45–57,64 The fluorescence intensity trajectories of QD-F27 complexes shows considerably more off states in the intensity histogram, as shown in Fig. 2 b2 and b3. To determine the threshold intensity that separates the on and off states, the distribution was fit by a sum of two Gaussian functions. The points where these two Gaussians cross were taken as the threshold intensity, which for QDs shown in panels a1, a2, a3 of Fig. 2 are at 4.0, 1.4 and 1.6 kHz, respectively. Any point in the trajectory with intensity above (below) the threshold level was assigned to on (off) state. The same analysis was applied to all studied QDs in sample 1 (45 QDs), 2 (47 QD-F27 complexes) and 3 (42 QD-F27 complexes) to determine their individual threshold values and occurrence of on and off states.
To quantify the occurrence of on and off states for each sample, we calculate probability densities P(t) of QDs at on or off states for a duration time of t:40
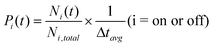 | (2) |
| Pi(t) = Bit−αiexp(−Γit) (i = on or off) | (3) |
| Sample # | αon | 1/Γon/s | αoff | 1/Γoff/s |
|---|---|---|---|---|
| 1 | 1.20 ± 0.05 | 20 ± 3 | 1.80 ± 0.1 | 10 ± 3 |
| 2 | 1.35 ± 0.02 | 17 ± 2 | 1.51 ± 0.06 | 13 ± 2 |
| 3 | 1.50 ± 0.07 | 13 ± 2 | 1.38 ± 0.06 | 20 ± 4 |
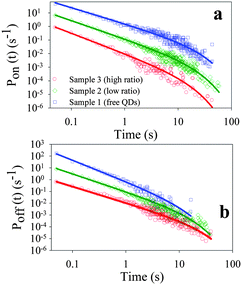 | ||
| Fig. 3 Probability density of (a) on states (Pon(t)) and (b) off states (Poff(t)) of the ensembles of single QDs from sample 1 (blue squares), sample 2 (green diamonds) and sample 3 (red circles). The solid lines are the best fits to eqn (3) (see text). These curves have been displaced vertically for clarity. | ||
As shown in panels a1–a3 and d1–d3 in Fig. 2, the fluctuations in fluorescence intensity are accompanied by positively correlated fluctuations in lifetime for both single QDs and QD-F27 complexes, consistent with previously reported blinking dynamics in QDs and QD-ET acceptor complexes.28,37,43,51 Due to a limited number of photons, when the fluorescence intensity is near the background level, the lifetimes could not be accurately determined and were assumed to be < 0.5 ns on the basis of the positive correlation. The total decay rate (1/lifetime) histogram (H′(k)) for the ensembles of single QDs in samples 1, 2 and 3 are shown in panels a, b and c in Fig. 4, respectively. These histograms are the summation of the decay rate histograms for all single QDs in these samples. The peaks at 2 ns−1 (1/500 ps) indicates the occurrence of low fluorescence intensity (background) points whose lifetimes are assumed to be <500 ps. For comparison we also plotted the on state decay rate histograms (H(k)) which differ from the total decay rate histograms at > ∼0.2 ns−1. It is clear that as the F27-to-QD ratio increases, the on state rate distributions shift to higher rates and broaden, while the relative contribution of off states increases. The increase (decrease) of relative contributions of off (on) states with F27-to-QD ratio is consistent with the trends of the on and off state probability densities shown in Fig. 3. These results suggest a correlation between the single QD blinking dynamics and interfacial ET dynamics in QD-F27 complexes.
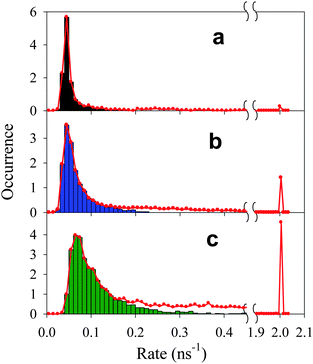 | ||
| Fig. 4 Total (H′(k), red solid lines) and on state (H(k), black, blue and green bars) decay rate (1/lifetime) histograms of single QDs in (a) sample 1, (b) sample 2, and (c) sample 3. The peaks at 2 ns−1 indicate the occurrences of low fluorescence intensity points whose lifetimes are assumed to be <0.5 ns. | ||
The total fluorescence decay rate (k0) of free QDs is a sum of radiative (kr) and nonradiative (knr) decay rates. The fluorescence decay rate distribution I(k0) of free QDs in Fig. 4a indicates the variation of k0 among different QDs and at different times. For QD-F27 complexes, the fluorescence decay rate is given by k = k0+kET, where kET is the interfacial ET rate. The measured distributions of decay rates of QD-F27 complexes (H(k) and H′(k)) are dependent on both the distributions of the interfacial ET rates (F(k) and F′(k)) and the intrinsic decay rates of QDs (I(k0)):
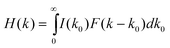 | (4) |
From the measured total (H′(k)) and on state (H(k)) decay rate distributions, and using the on state decay rate distribution of free QDs (I(k0)), ET rate distributions F′(kET) and F(kET) for samples 2 and 3 can be obtained according to eqn (4), as shown in Fig. 5b and c.
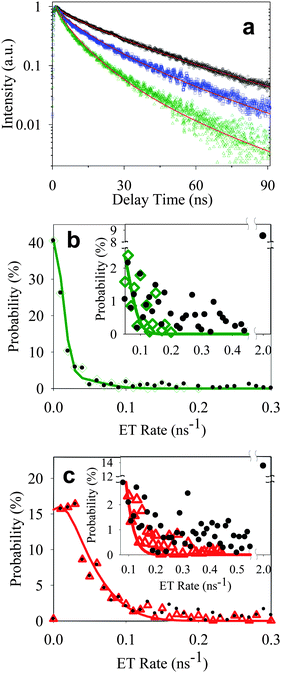 | ||
| Fig. 5 (a) Ensemble-averaged fluorescence decays of free QDs (black circle) and QD-F27 complexes from samples A′ (blue square) and B′ (green triangle) obtained under the same experimental conditions (on glass cover slip and dried in air) as single QD measurements. Solid lines are fits according to eqn (8). Distributions of ET rates in single QD-F27 complexes from sample 2 (b) and 3 (c). On state (green open diamonds in panel b and red open triangles in panel c) and total ET rate (black solid circles) distributions are obtained from on state (H(k)) and total (H′(k)) rate distributions. Solid lines are fits according to eqn (7). The insets show the expanded view of the distributions at higher rates. The best fits to a, b, and c yield k1 = 0.03 ns−1 and w = 0.06 ns−1. | ||
Comparison of ensemble and single QD ET dynamics
Both the total decay and ET rate distributions of single QD-F27 complexes contain fast decay components of > (0.5 ns)−1 that are not observed in the ensemble-averaged fluorescence decay or transient absorption data shown in Fig. 1 and S4.† These data were obtained with samples in heptane solution whereas the single QDs were measured on glass cover slips in the absence of solvent. To ensure that the solvent environment was not the cause of the observed difference, we also measured the ensemble-averaged fluorescence decays of QD-F27 complexes under the same conditions as the single QD measurements. Shown in Fig. 5a are the ensemble-averaged fluorescence decays of free QDs and QD-F27 complexes (samples A′ and B′) cast on glass cover slips and exposed to air. They were prepared from the samples A and B after ∼10-fold dilution, and have estimated QD-F27 complex concentrations of ∼106 higher than those used for single QD measurements. During the measurements, the samples were scanned at a speed of 0.1 μm s−1 to avoid photoinduced charging of the QDs. The decay curves are qualitatively similar to those shown in Fig. 1b, indicating a lack of any decay components that are > (0.5 ns)−1. In a previous study of single QDs on TiO2 nanoparticles, we showed that ensemble-averaged fluorescence decay agrees with the sum of on state decay of single QDs and lacks the fast off state decay rates of single QDs.30 It suggests that the lifetime of the off states does not reflect the ET time and is dominated by Auger relaxation rate in charged QDs. Unfortunately, similar comparisons cannot be carried out here because the F27-to-QD ratio (and therefore ET rates) varies with the concentration of the sample under single molecule conditions.To provide further evidence for the assignment of the on and off state lifetimes in QD-F27 complexes and to gain insight into the heterogeneous distribution of ET rates, we propose the following model to describe both the single QD and ensemble-averaged fluorescence decay rates. In our previous studies of ensemble-averaged electron or hole transfer dynamics between QDs and adsorbed molecules, we have shown that there is a distribution of the number of adsorbates on QDs.63,67 If the adsorption process is random, then the number of adsorbed molecules per QD should obey the Poisson distribution:63,67,68
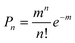 | (5) |
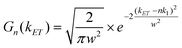 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 QD-F27 complex. We have assumed that the ET rate constant is linearly proportional to the number of adsorbates n and the width is same for QD-F27 complexes of different ratios. The distribution of ET rates F(kET) of QD-F27 complexes with an average adsorbate number of m is given by:
1 QD-F27 complex. We have assumed that the ET rate constant is linearly proportional to the number of adsorbates n and the width is same for QD-F27 complexes of different ratios. The distribution of ET rates F(kET) of QD-F27 complexes with an average adsorbate number of m is given by: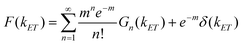 | (7) |
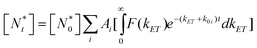 | (8) |
The ensemble fluorescence decay of QD-F27 complexes on glass cover slips, and single QD-F27 ET on state ET rate distributions, F(kET), for samples 2 and 3 are fit by eqn (8) and (7), respectively. The same k1 and w values, and different m values (to account for different adsorbate/QD ratios) are used in these fits. As shown in Fig. 5a, b and c, these data can be well fit by this model, yielding average F27-to-QD ratios of 0.7, 2.6, 0.3 and 0.9 for samples A, B, 2, and 3, respectively, and an averaged ET rate k1 of 0.03 ns−1 and a width w of 0.06 ns−1. This result suggests that the on state decay rate distribution in QD-F27 complexes can be well described by considering interfacial ET in addition to the intrinsic decay of free QDs.
However, the total ET rate distributions, F′(kET), which includes the contribution of both on and off states, cannot be fit by eqn (7). The discrepancy is caused by the much larger off state contribution in QD-F27 complexes than in free QDs, as shown in the insets in Fig. 5 b and c. If the off state decay rate is dominated by interfacial ET, it would require a ET rate of > 2 ns−1, which is not observed in the ensemble averaged transient absorption and fluorescence decay measurements, as shown in Fig. 1 and S4.† Thus the off state decay rate is dominated by other nonradiative decay pathways.
As shown in Fig. 6, the off state of free QDs has been attributed to positively charged QDs, which are formed by photoinduced Auger ionization of neutral QDs, producing a hole in the QD and an electron trapped on the QD surface or the surrounding materials.32,34 Optical excitation of the positively charged QDs generates a positive trion (an exciton plus a hole), which can undergo fast nonradiative Auger relaxation. The biexciton Auger relaxation time for CdSe QDs with radius of 2.3 nm has been reported to be ∼ 45 ps.69 The Auger relaxation of trions in these core/multi-shell quasi type II structures has not been extensively studied. They are expected to be slower than those in core-only QDs of similar size due to the reduced electron/hole overlap.70
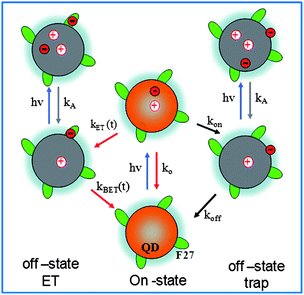 | ||
| Fig. 6 A model for on and off states in single QD-F27 complexes. In free QDs, on states correspond to those in neutral QDs, and off states are positively charged QDs formed by Auger ionization. In QD-acceptor complexes, ET from QDs to acceptors provides an additional pathway for forming off states, leading to correlated single QD interfacial ET and blinking dynamics. | ||
Photoinduced electron transfer from the QD to F27 generates a reduced F27 and a QD with a valence band hole, as shown in Fig. 6. Optical excitation of the QDs in the charge-separated state also generates positive trions in the QDs, which are similar to those formed by Auger ionization of free QDs. These trion states should also be short-lived and optically dark under single QD conditions. Thus interfacial ET provides an effective additional pathway for producing off states. The lifetime of these off states is determined by the charge recombination rate between the reduced adsorbate and the QD. As shown in Fig. 1d, although the majority of the recombination occurs on the ∼1-μs time scale, this process is not completed by 10 μs. It is possible that the charge-separated state can have finite probability at the 50-ms to 10-s timescale that was probed in the single QD studies. Thus, the interfacial ET process reduces (increases) the on (off) time probability density, affecting the single QD blinking dynamics. With the increase of ET rates, the probability of creating an off state increases, leading to higher contribution of off states in samples with higher F27-to-QD ratios, as shown in Fig. 4 and 6.
Conclusions
The electron transfer dynamics from CdSe core multi-layer shell QDs to adsorbed F27 molecules have been studied by both ensemble-averaged and single particle spectroscopy to probe the relationship between single QD interfacial ET and blinking dynamics. Interfacial ET from the QD to F27 is directly probed by TA studies of QD-F27 complexes, which show a faster QD exciton bleach recovery in the presence of F27, the formation of the F27 bleach, and a charge-separation rate that increases with the F27-to-QD ratio. The charge recombination process was found to occur on the 1-μs time scale, but the process is non-single exponential and is not completed by 10 μs. Single QD-F27 complexes show correlated fluctuations of fluorescence intensity and lifetime, similar to those observed in free QDs. With increasing ET rate (controlled by F27-to-QD ratio), the lifetime of on states decreases and the relative contribution of off states increases. Comparison of single QD and ensemble-averaged fluorescence decays shows that the distribution of on state decay rates can be well-described by a model that assumes a Poisson distribution of the number of adsorbed F27 on QDs, revealing an ET rate of 0.03 ns−1 in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 QD-F27 complex. The fluorescence decay rate of the off state is much faster than the ET rate, and is believed to be controlled by Auger relaxation in the charged QDs. In the off state, ET is not a competitive pathway for exciton quenching. As a result, the blinking dynamics of single QDs modulate their interfacial ET activity. Interfacial ET generates QDs in the charge-separated state with an electron trapped on the adsorbate and hole in the QD. Excited QDs in the charge-separated state should also decay mostly by fast non-radiative Auger relaxation process and be optically dark. As a result, interfacial ET provides an additional pathway for generating off states in the QD-F27 complexes, affecting the single QD blinking dynamics. With increasing ET rates, the probability for generating off states increases, which leads to correlated single QD interfacial ET and blinking dynamics in QD-acceptor complexes. Because blinking is a general phenomenon of single QDs, we believe that the correlated interfacial ET and blinking and the resulting intermittent ET activity is a general phenomenon for QDs.
1 QD-F27 complex. The fluorescence decay rate of the off state is much faster than the ET rate, and is believed to be controlled by Auger relaxation in the charged QDs. In the off state, ET is not a competitive pathway for exciton quenching. As a result, the blinking dynamics of single QDs modulate their interfacial ET activity. Interfacial ET generates QDs in the charge-separated state with an electron trapped on the adsorbate and hole in the QD. Excited QDs in the charge-separated state should also decay mostly by fast non-radiative Auger relaxation process and be optically dark. As a result, interfacial ET provides an additional pathway for generating off states in the QD-F27 complexes, affecting the single QD blinking dynamics. With increasing ET rates, the probability for generating off states increases, which leads to correlated single QD interfacial ET and blinking dynamics in QD-acceptor complexes. Because blinking is a general phenomenon of single QDs, we believe that the correlated interfacial ET and blinking and the resulting intermittent ET activity is a general phenomenon for QDs.
Acknowledgements
The work was supported by the National Science Foundation under grant number CHE-0848556 and the Petroleum Research Fund (PRF #49286-ND6). R. M. D. acknowledges support from NIH R01-GM086195.Notes and references
- W. U. Huynh, J. J. Dittmer and A. P. Alivisatos, Science, 2002, 295, 2425–2427 CrossRef CAS.
- I. Robel, V. Subramanian, M. Kuno and P. V. Kamat, J. Am. Chem. Soc., 2006, 128, 2385–2393 CrossRef CAS.
- P. O. Anikeeva, J. E. Halpert, M. G. Bawendi and V. Bulovic, Nano Lett., 2007, 7, 2196–2200 CrossRef CAS.
- S. Nie, Y. Xing, G. J. Kim and J. W. Simons, Annu. Rev. Biomed. Eng., 2007, 9, 257–288 CrossRef CAS.
- R. D. Schaller and V. I. Klimov, Phys. Rev. Lett., 2004, 92, 186601–186604 CrossRef CAS.
- R. J. Ellingson, M. C. Beard, J. C. Johnson, P. Yu, O. I. Micic, A. J. Nozik, A. Shabaev and A. L. Efros, Nano Lett., 2005, 5, 865–871 CrossRef CAS.
- V. I. Klimov, Annu. Rev. Phys. Chem., 2007, 58, 635–673 CrossRef CAS.
- A. J. Nozik, Phys. E., 2002, 14, 115–120 CrossRef CAS.
- V. I. Klimov, Appl. Phys. Lett., 2006, 89, 123118 CrossRef.
- G. Nair and M. G. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 081304 CrossRef.
- A. Shabaev, A. L. Efros and A. J. Nozik, Nano Lett., 2006, 6, 2856–2863 CrossRef CAS.
- V. I. Rupasov and V. I. Klimov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125321 CrossRef.
- O. V. Prezhdo, Chem. Phys. Lett., 2008, 460, 1 CrossRef CAS.
- A. Franceschetti, J. M. An and A. Zunger, Nano Lett., 2006, 6, 2191 CrossRef CAS.
- G. Allan and C. Delerue, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125340 CrossRef.
- J. A. McGuire, J. Joo, J. M. Pietryga, R. D. Schaller and V. I. Klimov, Acc. Chem. Res., 2008, 41, 1810 CrossRef CAS.
- A. J. Nozik, Annu. Rev. Phys. Chem., 2001, 52, 193–231 CrossRef CAS.
- J. Huang, D. Stockwell, Z. Huang, D. L. Mohler and T. Lian, J. Am. Chem. Soc., 2008, 130, 5632–5633 CrossRef CAS.
- A. Boulesbaa, A. Issac, D. Stockwell, Z. Huang, J. Huang, J. Guo and T. Lian, J. Am. Chem. Soc., 2007, 129, 15132–15133 CrossRef CAS.
- R. Rossetti, S. M. Beck and L. E. Brus, J. Am. Chem. Soc., 1984, 106, 980–984 CrossRef CAS.
- R. Rossetti and L. E. Brus, J. Phys. Chem., 1986, 90, 558 CrossRef CAS.
- J. J. Ramsden and M. Gratzel, Chem. Phys. Lett., 1986, 132, 269 CrossRef CAS.
- A. Henglein, Pure Appl. Chem., 1984, 56, 1215–1224 CAS.
- S. Logunov, T. Green, S. Marguet and M. A. El-Sayed, J. Phys. Chem. A, 1998, 102, 5652–5658 CrossRef CAS.
- C. Burda, T. C. Green, S. Link and M. A. El-Sayed, J. Phys. Chem. B, 1999, 103, 1783–1788 CrossRef CAS.
- V. V. Matylitsky, L. Dworak, V. V. Breus, T. Basche and J. Wachtveitl, J. Am. Chem. Soc., 2009, 131, 2424 CrossRef CAS.
- J. Huang, Z. Huang, Y. Yang, H. Zhu and T. Lian, J. Am. Chem. Soc., 2010, 132, 4858–4864 CrossRef CAS.
- A. Issac, S. Jin and T. Lian, J. Am. Chem. Soc., 2008, 130, 11280–11281 CrossRef CAS.
- S.-C. Cui, T. Tachikawa, M. Fujitsuka and T. Majima, J. Phys. Chem. C, 2008, 112, 19625–19634 CrossRef CAS.
- S. Jin and T. Lian, Nano Lett., 2009, 9, 2448–2454 CrossRef CAS.
- S. Jin, N. Song and T. Lian, ACS Nano, 2010, 4, 1545–1552 CrossRef CAS.
- A. L. Efros and M. Rosen, Phys. Rev. Lett., 1997, 78, 1110–1113 CrossRef CAS.
- K. T. Shimizu, R. G. Neuhauser, C. A. Leatherdale, S. A. Empedocles, W. K. Woo and M. G. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 205316 CrossRef.
- T. D. Krauss, S. O'Brien and L. E. Brus, J. Phys. Chem. B, 2001, 105, 1725–1733 CrossRef CAS.
- M. Nirmal, B. O. Dabbousi, M. G. Bawendi, J. J. Macklin, J. K. Trautman, T. D. Harris and L. E. Brus, Nature, 1996, 383, 802–804 CrossRef CAS.
- S. Empedocles and M. Bawendi, Acc. Chem. Res., 1999, 32, 389–396 CrossRef CAS.
- B. R. Fisher, H.-J. Eisler, N. E. Stott and M. G. Bawendi, J. Phys. Chem. B, 2004, 108, 143–148 CrossRef CAS.
- I. Chung and M. G. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 165304 CrossRef.
- M. Kuno, D. P. Fromm, S. T. Johnson, A. Gallagher and D. J. Nesbitt, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125304 CrossRef.
- M. Kuno, D. P. Fromm, H. F. Hamann, A. Gallagher and D. J. Nesbitt, J. Chem. Phys., 2001, 115, 1028–1040 CrossRef CAS.
- M. Kuno, D. P. Fromm, A. Gallagher, D. J. Nesbitt, O. I. Micic and A. J. Nozik, Nano Lett., 2001, 1, 557–564 CrossRef CAS.
- J. J. Peterson and D. J. Nesbitt, Nano Lett., 2009, 9, 338–345 CrossRef CAS.
- K. Zhang, H. Chang, A. Fu, A. P. Alivisatos and H. Yang, Nano Lett., 2006, 6, 843–847 CrossRef CAS.
- D. Montiel and H. Yang, J. Phys. Chem. A, 2008, 112, 9352–9355 CrossRef CAS.
- M. Pelton, G. Smith, N. F. Scherer and R. A. Marcus, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14249–14254 CrossRef.
- J. Tang and R. A. Marcus, J. Chem. Phys., 2006, 125, 044703 CrossRef.
- J. Tang and R. A. Marcus, J. Chem. Phys., 2005, 123, 054704 CrossRef.
- J. Tang and R. A. Marcus, Phys. Rev. Lett., 2005, 95, 107401 CrossRef.
- J. Tang and R. A. Marcus, J. Chem. Phys., 2005, 123, 204511 CrossRef.
- A. Issac, C. von Borczyskowski and F. Cichos, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 161302 CrossRef.
- G. Schlegel, J. Bohnenberger, I. Potapova and A. Mews, Phys. Rev. Lett., 2002, 88, 137401–137401 CrossRef.
- R. Verberk, A. M. van Oijen and M. Orrit, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 233202 CrossRef.
- K. T. Shimizu, W. K. Woo, B. R. Fisher, H. J. Eisler and M. G. Bawendi, Phys. Rev. Lett., 2002, 89, 117401 CrossRef CAS.
- Y. Chen, J. Vela, H. Htoon, J. L. Casson, D. J. Werder, D. A. Bussian, V. I. Klimov and J. A. Hollingsworth, J. Am. Chem. Soc., 2008, 130, 5026–5027 CrossRef CAS.
- V. Fomenko and D. J. Nesbitt, Nano Lett., 2008, 8, 287–293 CrossRef CAS.
- B. Mahler, P. Spinicelli, S. Buil, X. Quelin, J.-P. Hermier and B. Dubertret, Nat. Mater., 2008, 7, 659 CrossRef CAS.
- S. Hohng and T. Ha, J. Am. Chem. Soc., 2004, 126, 1324–1325 CrossRef CAS.
- X. Wang, X. Ren, K. Kahen, M. A. Hahn, M. Rajeswaran, S. Maccagnano-Zacher, J. Silcox, G. E. Cragg, A. L. Efros and T. D. Krauss, Nature, 2009, 459, 686 CrossRef CAS.
- M. Y. Odoi, N. I. Hammer, K. T. Early, K. D. McCarthy, R. Tangirala, T. Emrick and M. D. Barnes, Nano Lett., 2007, 7, 2769–2773 CrossRef CAS.
- N. I. Hammer, K. T. Early, K. Sill, M. Y. Odoi, T. Emrick and M. D. Barnes, J. Phys. Chem. B, 2006, 110, 14167–14171 CrossRef CAS.
- P. S. Rao and E. Hayon, J. Am. Chem. Soc., 1974, 96, 1287 CrossRef CAS.
- A. I. Ponyaev, V. P. Martynova and A. V. El′tsov, Russ. J. Gen. Chem., 2001, 71, 1744–1750 CrossRef CAS.
- A. Boulesbaa, Z. Huang, D. Wu and T. Lian, J. Phys. Chem. C, 2010, 114, 962–969 CrossRef CAS.
- M. Kuno, D. P. Fromm, H. F. Hamann, A. Gallagher and D. J. Nesbitt, J. Chem. Phys., 2000, 112, 3117–3120 CrossRef CAS.
- S. Wang, C. Querner, T. Emmons, M. Drndic and C. H. Crouch, J. Phys. Chem. B, 2006, 110, 23221–23227 CrossRef CAS.
- A. Mandal, J. Nakayama, N. Tamai, V. Biju and M. Isikawa, J. Phys. Chem. B, 2007, 111, 12765–12771 CrossRef CAS.
- J. Huang, Z. Huang, S. Jin and T. Lian, J. Phys. Chem. C, 2008, 112, 19734–19738 CrossRef CAS.
- T. Pons, I. L. Medintz, X. Wang, D. S. English and H. Mattoussi, J. Am. Chem. Soc., 2006, 128, 15324 CrossRef CAS.
- V. I. Klimov, A. A. Mikhailovsky, D. W. McBranch, C. A. Leatherdale and M. G. Bawendi, Science, 2000, 287, 1011–1013 CrossRef CAS.
- F. Garcia-Santamaria, Y. Chen, J. Vela, R. D. Schaller, J. A. Hollingsworth and V. I. Klimov, Nano Lett., 2009, 9, 3482–3488 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Absorption spectra, single molecule image, and transient spectra. See DOI: 10.1039/c0sc00334d |
| This journal is © The Royal Society of Chemistry 2010 |
