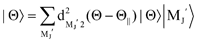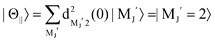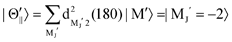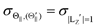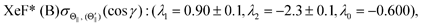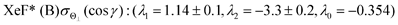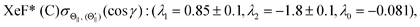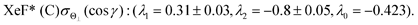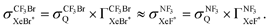Multidimensional steric effect for the XeF* (B, C) formation in the oriented Xe* (3P2, MJ = 2) + oriented NF3 reaction
Received
21st May 2010
, Accepted 25th August 2010
First published on 21st October 2010
Abstract
Steric effect for the XeF* (B, C) formations in the oriented Xe* (3P2, MJ = 2) + oriented NF3 reaction has been observed as a function of the mutual configuration between the molecular orientation and the atomic orientation in the collision frame. Molecular steric opacity function has been determined as a function of the atomic orbital alignment (LZ′) in the collision frame. The larger reactivity at the side with the smaller reactivity at the molecular axis direction is observed for the XeF* (B, C) channels at each atomic orbital alignment. A good correlation between the shape of the molecular steric opacity function and the molecular geometry of NF3 is recognized. The LZ′ selectivity in the molecular steric opacity function is different between the XeF* (B, C) channels; in the sideways direction, the XeF* (B) channel is favorable at LZ′ = 0, while the XeF* (C) channel is favorable at |LZ′| = 1. In contrast, at the molecular axis direction, the XeF* (B) channel is favorable at |LZ′| = 1, while the XeF* (C) channel is favorable at LZ′ = 0. We propose the collision-induced harpoon mechanism for the XeF* (B, C) formation in the Xe* (3P2) + NF3 reaction.
Introduction
Steric effect is one of the important factors to control the reaction dynamics. A variety of molecular beam experiments has provided direct observation of steric requirements in chemical reactions. So far, the steric effect on the reactive collision has been studied by using the electrostatic hexapole method,1–17 the brute force method,18–20 and the optical pumping method.21–23 In general, the steric effect in the reaction dynamics should essentially be seen from a multidimensional perspective because the reaction dynamics between two reactants having anisotropic structure should depend on the mutual orientation between two reactants. Although the multidimensional perspective of the steric effect on reactive collision is one of the important subjects in stereodynamics, the experimental studies on steric effect are still limited to the stereo-anisotropy related to only one of the reactants even in the small number of atom-molecular reaction systems. The direct experimental studies on the multidimensional steric effects on reactive collision are extremely limited.13–17
The formation of electronically excited rare-gas halide RgX* from the reactions of metastable rare-gas Rg* (3P2) with polyatomic halogen containing molecules RX is important as a benchmark system to study the multidimensional steric effects on reactive collisions because Rg* (3P2) has an anisotropic electronic structure, (n − 1)p5ns1. The non-closed shell of Rg+ gives rise to two different excited rare gas halide product states, RgX* (B, Ω = 1/2) and RgX* (C, Ω = 3/2), that correlate with Rg+ (2P3/2) and X−(1S0). The RgX* formation is known to proceed via the “harpoon” mechanism24–29 like the metal halide MX formations in the reactions of alkali-metal atoms M, for which steric effects have been widely studied using the oriented molecules.1–12,18–21 For the KI formation in the K + CF3I reaction system, it has been reported that the molecular orientation exerts an influence on only the angular distribution of KI with comparable reaction probability at the two ends.3 In contrast, for the KBr formation in the K + CF3Br reaction, it has been reported that the Br-end is about three fold more reactive than the CF3-end, and that the KBr is scattered backward in the Br-end orientation and forward in the CF3-end orientation.8 The difference in the orbital configuration between the Rg* ((n − 1)p5ns1) and the M ((n − 1)p6ns1) should provide an interesting contrast in stereoselectivity.
Most recently, we have studied the multidimensional steric effects for the excimer (XeX*) formations in the reactions of the oriented Xe* (3P2, MJ = 2) with the oriented molecules having a molecular geometry like CY3X (e.g., CF3I, CH3I, CF3Br)14–16 and CX3Y (e.g., CCl3F)17 which commonly have relatively large quenching cross sections (σQ ∼ a few hundred Å2).24–29 Although the X(or X3)-end is commonly most reactive as expected from the chemical intuition like “steric hindrance” due to the non-reactive bulky group CY3 (or Y), every system exhibits a wide range of molecular orientation (and alignment) dependence affected by the atomic orbital alignment which does not correlate well with the chemical intuition. Especially, every system commonly shows poor reactivity at the side with the molecular steric opacity function despite the large difference in the crossing distance (rc = 3.9–6.4 Å)14–17 between the covalent entrance potential surface [Xe*(3P2) + CY3X (or CX3Y)] and the ionic surface [Xe+ (2P3/2) + CY3X− (or CX3Y−)], and in the branching fraction to the excimer (XeX*) formation (ΓXeX* = 0.01–0.25).24–29 We have proposed an indirect mechanism for the dark channels (Xe + X + CY3 (or CX2Y)) via the back electron transfer from the CY3 segment (or dissociating CY3⋯X−) (or CX2Y segment; CX2Y⋯X−) to Xe+ as the origin of the poor reactivity at the side with the molecular steric opacity function. This indirect process to the dark channel (Xe + X + CY3 (or CX2Y)) should cause the small branching fraction to the XeX* formation in the Xe* (3P2) + CY3X (or CX3Y) reaction systems. Therefore, it is expected that the proposed indirect mechanism for the dark channel is the general process in the Xe* (3P2) + RX reaction systems that have a relatively large quenching cross section with the small branching fraction to the XeX* formation. In order to give an additional evidence of the generality of the proposed mechanism, further studies on the other reaction systems that have the small quenching cross sections are important and interesting.
Here we report on the multidimensional steric effects for the XeF* (B, C) formations in the oriented Xe* (3P2, MJ = 2) + oriented NF3 reaction that has a small quenching cross section 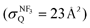 .28 The larger reactivity at the side with the smaller reactivity in the molecular axis direction is observed in contrast with the other molecular systems that commonly show poor reactivity at the side. A good correlation between the direction of the reactive lobe and the F atoms direction from the center-of-mass of NF3 is recognized. We propose the collision-induced harpoon mechanism for the XeF* (B, C) formations.
.28 The larger reactivity at the side with the smaller reactivity in the molecular axis direction is observed in contrast with the other molecular systems that commonly show poor reactivity at the side. A good correlation between the direction of the reactive lobe and the F atoms direction from the center-of-mass of NF3 is recognized. We propose the collision-induced harpoon mechanism for the XeF* (B, C) formations.
II. Experimental
The experimental setup and the procedures are similar to our previous study.13–17 The apparatus is composed of two state-selectors. One is a 40-cm long electrostatic hexapole for the oriented molecular beam. The other is a 35-cm long magnetic hexapole for the oriented atomic beam. In the present study, the oriented NF3 molecular beam is oriented to the homogeneous electric orientation field E, and the oriented Xe* (3P2, MJ = 2) atomic beam is oriented to the homogeneous magnetic orientation field B. For the collision processes, however, the relative velocity vector (vR) serves as the other relevant quantization axis (i.e., collision frame). The cross section is then a function of the angle between those quantization axes. We have accomplished the doubly orientation-control by using both the oriented NF3 molecular beam and the oriented Xe* (3P2, MJ = 2) atomic beam whose configurations in the collision frame are independently controlled.13–17 A NF3 molecular beam was generated from a pulsed valve with a stagnation pressure of 50 Torr, and then state-selected by the electrostatic hexapole. The velocity distribution of the NF3 molecular beam was determined as the stream velocity of vs = 400 ms−1, and the translational temperature of Ttrans = 200 K by using a conventional time-of-flight measurement.30 The molecular orientation in the collision frame was controlled by changing the direction of a uniform electric orientation field E at the beam crossing point. The electric orientation field (E = 600 V cm−1) was prepared by a pair of electrode plates tilted at an angle of 45° (i.e., the direction of the relative velocity, vR) with respect to the direction of Xe* (3P2) beam axis. An oriented metastable Xe* (3P2, MJ = 2) beam was generated by a pulsed glow discharge with a pulse width of 100 μs, and then state-selected by the magnetic hexapole. The MJ state distribution of the state-selected Xe* (3P2) beam at the beam crossing point (1000 mm downstream from the Xe* (3P2) beam source) was directly determined by separating each MJ state using a Stern-Gerlach type inhomogeneous magnetic state-selector (SGIM) as a function of the arrival time, t0.13,31 The state-selected metastable Xe* (3P2) beam within the arrival time region (2.45 ≤ t0 ≤ 2.75 ms) (corresponds to vs = 395 ± 30 ms−1) is composed of almost pure Xe* (3P2, MJ = 2) (more than 95%). The emission signal produced from the collision with Xe* (3P2, MJ = 2) within this time region (I) was used for the present study. The atomic orientation in the collision frame was controlled by rotating the direction of the magnetic orientation field B that was prepared by four pieces of ferrite magnets mounted on a motor driven rotatable stage.
Fig. 1(A) shows a schematic drawing of the configurations for the oriented NF3 molecule (i.e., the direction of the uniform electric orientation field E) and for the oriented Xe* (3P2, MJ = 2) atom (i.e., the direction of the magnetic orientation field B) with respect to vR. For the atomic orientation of Xe* (3P2, MJ = 2), three configurations were representatively selected, i.e. parallel (Θ∥), perpendicular (Θ⊥), and antiparallel 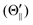 . Similarly, three representative configurations were selected for the molecular orientation, i.e. parallel (Φ∥: N-end), antiparallel (
. Similarly, three representative configurations were selected for the molecular orientation, i.e. parallel (Φ∥: N-end), antiparallel (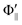 : F3-end), and orientation field off (Φoff: random orientation). Under the doubly-orientation controlled conditions, the oriented Xe* (3P2, MJ = 2) atomic beam collides with the oriented NF3 molecular beam at the beam crossing point. The emission from the products XeF* (B, C) was separated through the band-pass filters (B: Asahi Spectra (SUX300), λ = 210–300 nm; C: Optical Coatings Japan (SPF570), λ = 380–570 nm) and detected by a cooled and magnetic shielded photomultiplier. Only the signal enhanced by applying the electric hexapole field (V0 = 12 kV) was used as the chemiluminescence signal from the oriented NF3 + oriented Xe* (3P2, MJ = 2) reaction. For the subtraction of the background signal, the signal at V0 = 0 kV was used as the background signal. The emission intensities (I(Θ,Φ)) from the products XeF* (B, C) were measured at the nine mutual configurations between the atomic orientation Θ and molecular orientation Φ.
: F3-end), and orientation field off (Φoff: random orientation). Under the doubly-orientation controlled conditions, the oriented Xe* (3P2, MJ = 2) atomic beam collides with the oriented NF3 molecular beam at the beam crossing point. The emission from the products XeF* (B, C) was separated through the band-pass filters (B: Asahi Spectra (SUX300), λ = 210–300 nm; C: Optical Coatings Japan (SPF570), λ = 380–570 nm) and detected by a cooled and magnetic shielded photomultiplier. Only the signal enhanced by applying the electric hexapole field (V0 = 12 kV) was used as the chemiluminescence signal from the oriented NF3 + oriented Xe* (3P2, MJ = 2) reaction. For the subtraction of the background signal, the signal at V0 = 0 kV was used as the background signal. The emission intensities (I(Θ,Φ)) from the products XeF* (B, C) were measured at the nine mutual configurations between the atomic orientation Θ and molecular orientation Φ.
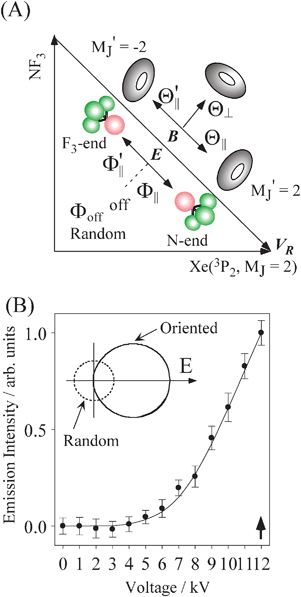 |
| | Fig. 1 (A) Geometric relationship between the molecular orientation (parallel (Θ∥: N-end), antiparallel (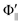 : F3-end), and orientation field off (Φoff: random orientation)) and the atomic configuration (parallel (Θ∥), perpendicular (Θ⊥), and antiparallel : F3-end), and orientation field off (Φoff: random orientation)) and the atomic configuration (parallel (Θ∥), perpendicular (Θ⊥), and antiparallel 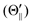 ) with respect to the direction of relative velocity vR with a Newton diagram for the title reaction. (B) Focusing curve for the XeF* formation; experimental (●), calculated one via the trajectory simulation with the rotational temperature of Trot = 200 K (solid line). (inner panel) Polar coordination representation of the orientational distribution of the molecular axis with respect to the electric orientation field E for the state-selected NF3 beam at V0 = 12 kV (solid line) and random orientation (broken line). ) with respect to the direction of relative velocity vR with a Newton diagram for the title reaction. (B) Focusing curve for the XeF* formation; experimental (●), calculated one via the trajectory simulation with the rotational temperature of Trot = 200 K (solid line). (inner panel) Polar coordination representation of the orientational distribution of the molecular axis with respect to the electric orientation field E for the state-selected NF3 beam at V0 = 12 kV (solid line) and random orientation (broken line). | |
We calibrated the relative intensity XeF* (B)/XeF* (C) by using the branching ratio (Γ (B/C) ∼ 2.8) reported in ref. 29. Needless to say, the uncertainty of Γ (B/C) gives no influence on the shape of the molecular steric opacity function for each XeF* channel, and changes only the relative intensity of the molecular steric opacity function between the XeF* (B, C) channels.
The molecular orientation configuration Φ was changed every 500 beam pulses in turn at each atomic orientation configuration Θ. The atomic orientation configuration was changed every 1500 beam pulses in turn. To obtain an acceptable signal to noise ratio, the data were accumulated up to 6.0 × 104 beam pulses at each mutual configuration condition.
A Orientational distribution of the oriented NF3 beam
In order to estimate the orientational distribution W(cos γE) of the molecular axis with respect to the electric orientation field direction (E), the trajectory simulation for the state-selection in the hexapole field was carried out for the oriented NF3 molecular beam.32 Here, γE is the orientation angle of the NF3 molecular axis with respect to E. Fig. 1(B) shows the focusing curve that is defined as the emission intensity from the product XeF* at the random orientation condition as a function of the hexapole voltage (V0). The calculated focusing curve with a rotational temperature of Trot = 200 K is in good agreement with the experimental one, which is shown in Fig. 1(B) as a solid line. According to the trajectory simulation, the orientational distribution of the molecular axis W(cos γE) with respect to E was calculated for the experimental conditions at V0 = 12 kV.33,34 The calculated W(cos γE) is shown in the inner panel in Fig. 1(B). The nth Legendre moments, 〈Pn〉, for the orientational distribution are summarized to be 〈P1〉 = 0.60, 〈P2〉 = 0.22, 〈P3〉 = 0.022, 〈P4〉 = −0.021, 〈P5〉 = −0.007, 〈P6〉 = 0.003, 〈P7〉 = 0.002. The error of the Legendre moments is estimated to be less than 10%.
B Atomic orbital alignment in the oriented Xe* (3P2, MJ = 2) beam
For the configuration of the oriented Xe* (3P2, MJ = 2) beam in the collision frame, three configurations were representatively selected, i.e. parallel (Θ∥), perpendicular (Θ⊥), and antiparallel 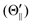 . Although the Xe* (3P2, MJ = 2) beam is oriented in the homogeneous magnetic orientation field B in the present study, we can observe only the atomic alignment effect due to the experimental condition with a cylindrical symmetry (i.e., we observed only the total cross section).31 By using Wigner's d function,34
. Although the Xe* (3P2, MJ = 2) beam is oriented in the homogeneous magnetic orientation field B in the present study, we can observe only the atomic alignment effect due to the experimental condition with a cylindrical symmetry (i.e., we observed only the total cross section).31 By using Wigner's d function,34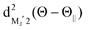 , the Xe* (3P2, MJ = 2) states |Θ〉 at the three atomic orientation configurations can be simply expressed as
, the Xe* (3P2, MJ = 2) states |Θ〉 at the three atomic orientation configurations can be simply expressed as
in terms of the magnetic MJ′ sub-states |MJ′〉 in the collision frame;
| | 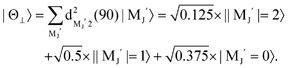 | (1) |
Recently, we have reported that the atomic alignment effect on the XeF* (B, C) formations has no notable rank 4 moment term.35 No contribution of rank 4 moment directly signifies that J (=2) is not the proper quantum number to describe the essential dynamics of the present system. Rather, the physics of the process is dominantly determined by the orbital angular momentum L (=1) and its components LZ′ in the collision frame.31 That is, the atomic alignment effects on the XeF* (B, C) formations are dominantly controlled by the alignment of the unpaired 5p electron of Xe* (3P2, MJ = 2) in the collision frame.31 In this case, the cross-section (σM J′) for each MJ′ state can be alternatively expressed by the cross sections (σLZ′) based on the |L,S,LZ′,SZ′〉 basis using the standard recoupling procedure through the Clebsch–Gordan coefficients.34 Since the SZ′ and the sign of LZ′ gives no effect on the reactivity in the excimer formation, the cross-section σ|MJ′| can be directly related with σ|LZ′| as below,
| σ|MJ′| = 1 = ½ × σ|LZ′| = 1 + ½ × σLZ′ = 0 |
| | | σMJ′ = 0 = ⅓ × σ|LZ′ = 1 + ⅔ × σLZ′ = 0. | (2) |
From eqn (1), the cross sections (σΘ) at three atomic orientation configurations (Θ∥, Θ⊥, and 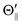 ) can be expressed as follows by using the cross section (σ|LZ′|) at each atomic orbital alignment (|LZ′|) in the collision frame,
) can be expressed as follows by using the cross section (σ|LZ′|) at each atomic orbital alignment (|LZ′|) in the collision frame,
| | | σ|Θ⊥| = 0.5 × σLZ′ = 0 + 0.5 × σ|LZ′| = 1. | (3) |
II. Results and discussion
A Multidimensional steric effect
Fig. 2 shows the emission intensities I(Θ,Φ) of XeF* (B, C) under the nine mutual configurations between the molecular orientation configuration (Φ∥, 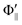 , and Φoff) and the atomic orientation configuration (Θ∥, Θ⊥, and
, and Φoff) and the atomic orientation configuration (Θ∥, Θ⊥, and  ). The N-end configuration is extremely less reactive than the F3-end and the random configurations. In addition, the reactivity at the random configuration is most reactive at each atomic alignment configuration. The Θ-dependence is extremely different between the XeF* (B, C) channels at each molecular orientation configuration. The XeF* (B) channel shows poor Θ-dependence at every molecular orientation configuration, while the XeF* (C) channel shows significant Θ-dependence that depends on the molecular orientation configuration. The XeF* (C) intensity is lower for Θ⊥ than for Θ∥ (and
). The N-end configuration is extremely less reactive than the F3-end and the random configurations. In addition, the reactivity at the random configuration is most reactive at each atomic alignment configuration. The Θ-dependence is extremely different between the XeF* (B, C) channels at each molecular orientation configuration. The XeF* (B) channel shows poor Θ-dependence at every molecular orientation configuration, while the XeF* (C) channel shows significant Θ-dependence that depends on the molecular orientation configuration. The XeF* (C) intensity is lower for Θ⊥ than for Θ∥ (and  ) at both the F3-end and the random configurations, while the N-end configuration shows the opposite Θ-dependence.
) at both the F3-end and the random configurations, while the N-end configuration shows the opposite Θ-dependence.
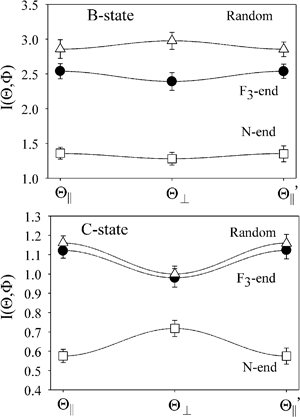 |
| | Fig. 2 Θ-dependence of the chemiluminescence intensity of XeF* (B, C) under the three molecular orientation configurations; N-end collision (□), F3-end collision (●), and random (△). The error bar shows the confidence interval for 95% confidence coefficient. The relative intensity XeF* (B)/XeF* (C) was calibrated by the branching ratio (Γ(B/C) = 2.8) reported in ref. 29. | |
In order to accentuate the steric effects, we define the orientation term (O(Θ)) and the alignment term (A(Θ)) by
| | 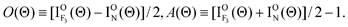 | (4) |
Here, I
ON(Θ) and
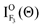
is the relative emission intensity at the N-end configuration (Φ
∥) and at the F
3-end configuration
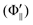
to that at the random orientation (Φ
off), respectively.
| | 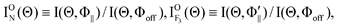 | (5) |
The orientation (
O(Θ)) and alignment (
A(Θ)) terms are shown in
Fig. 3 as a function of the atomic orientation configuration (Θ).
Fig. 3 shows that the orientation terms
O(Θ) for the XeF* (B, C) channels are positive at each Θ configuration. The Θ-dependence of the orientation term
O(Θ) is different between the XeF* (B, C) channels; the XeF* (B) channel shows little Θ dependence, while
O(Θ
⊥) is smaller than
O(Θ
∥) (and
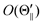
) for the XeF* (C) channel.
Fig. 3 further shows that the alignment terms
A(Θ) for the XeF* (B, C) channels are negative at each Θ configuration. The Θ-dependence of
A(Θ) is different between the XeF* (B, C) channels;
A(Θ
⊥) is smaller than
A(Θ
∥) (and
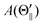
) for the XeF* (B) channel, while
A(Θ
⊥) is larger than
A(Θ
∥) (and
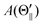
) for the XeF* (C) channel.
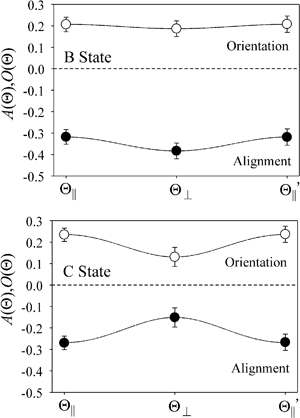 |
| | Fig. 3 Molecular orientation O(Θ) and alignment A(Θ) terms for the XeF* (B, C) formation under the three configurations for the atomic orientation (parallel (Θ∥), perpendicular (Θ⊥), and antiparallel 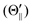 );O(Θ) (○), A(Θ) (●). The error bar shows the confidence interval for 95% confidence coefficient. );O(Θ) (○), A(Θ) (●). The error bar shows the confidence interval for 95% confidence coefficient. | |
B Molecular steric opacity function as a function of atomic orbital alignment
In general, the observed emission intensity I(Θ,Φ) can be expressed in terms of the molecular steric opacity function as below,| | 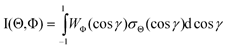 | (6) |
where γ is the orientation angle of the NF3 molecular axis in the collision frame (i.e., with respect to vR), σΘ(cos γ) is the molecular steric opacity function at each atomic orientation configuration (Θ), WΦ(cos γ) is the orientational distribution of the molecular axis for the NF3 molecular beam in the collision frame at each molecular orientation configuration (Φ). Since the observed stereo-anisotropies depend on the orientational distribution WΦ(cos γ), it is suitable to represent them in the form of the molecular steric opacity function σΘ(cos γ) in order to quantitatively evaluate the observed steric effects.
Here, we obtain the molecular steric opacity functions σΘ(cos γ) at three atomic orientation configurations (Θ∥, Θ⊥,  ) by applying the Engel-Levine function model described below,36
) by applying the Engel-Levine function model described below,36
| | 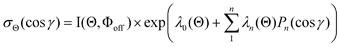 | (7) |
where P
n(cos
γ) is the
nth Legendre function,
λn(Θ) are the fitting parameters, and
λ0(Θ) is the normalization factor. In this model calculation, only two parameters
λ1(Θ) and
λ2(Θ) are sufficient for reproducing the present experimental results. By reproducing the experimental emission intensities I(Θ,Φ), the fitting parameters (
λ1,
λ2) and
λ0 can be determined as below,
The cross section σ(cos γ, α) as a function of the molecular orientation angle (γ) and the atomic orbital alignment angle (α) in the collision frame can be expressed as below by using eqn (3),34
| | | σ(cos γ,α) = |d100(α)|2 × σLZ′=0(cos γ) + |d1|1|0(α)|2 × σ|LZ′|=0(cos γ) = 2cos2α × σΘ⊥(cos γ) + (1 − 2 cos2α) × σΘ∥(cos γ). | (8) |
In particular, the molecular steric opacity functions at the specific atomic orbital alignment (|L
Z′| = 0, 1) can be expressed as below,
σ|LZ′|=1(cos γ) ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) σ(cos γ, α = 90) = σΘ∥(cos γ) σ(cos γ, α = 90) = σΘ∥(cos γ) |
| | σLZ′=0(cos γ) ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) σ(cos γ, α = 0) = 2 × σΘ⊥(cos γ) − σΘ∥(cos γ). σ(cos γ, α = 0) = 2 × σΘ⊥(cos γ) − σΘ∥(cos γ). | (9) |
The representative values of
σ(cos
γ,
α) are shown in
Fig. 4. The alignment (
α) of the unpaired 5p electron in the collision frame has a significant effect on both the shape of molecular steric opacity function
σ|LZ′|(cos
γ) and the branching to the XeF* (B, C) channels. We can observe a good correlation between the shape of the molecular steric opacity function and the geometry of NF
3 (
i.e., the direction of F atom (designated by the asterisk) from the center-of-mass of NF
3).
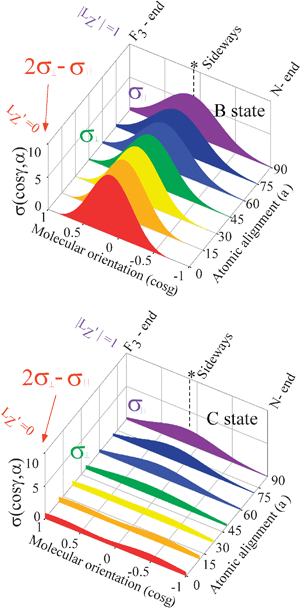 |
| | Fig. 4 Molecular steric opacity function for the XeF * (B, C) channels obtained by the Engel-Levine function model (expansion up to n = 2) as a function of the atomic orbital alignment angle (α) (painted projection drawings). The molecular steric opacity function at each atomic orbital alignment angle (α) was calculated by the relationship of eqn (9). The asterisk shows the direction of the F atom from the center-of-mass of NF3. | |
C Correlation between the molecular orientation and the atomic orbital alignment
The shapes of the molecular steric opacity functions for the XeF* (B, C) channels are similar to each other except for the XeF* (C) channel at LZ′ = 0. The side (or the direction of F atom (designated by the asterisk) from the center-of-mass of NF3) is most reactive with the poor reactivity at the molecular axis direction at each atomic orbital alignment. The LZ′ dependence in the molecular steric opacity function is different between the XeF* (B, C) channels; for the XeF* (B) channel, LZ′ = 0 is favorable sideways, and |LZ′| = 1 is favorable at the molecular axis direction. On the contrary, for the XeF* (C) channel, |LZ′| = 1 is favorable sideways, and LZ′ = 0 is favorable in the molecular axis direction.
D Comparison with the harpoon mechanism
If the XeF* formation is initiated by the “harpoon” mechanism, the cross section can be approximated as πrc2 by using rc of eqn (10),37| | | e2/rc ≈ IE(Xe(3P2)) − EA(NF3) | (10) |
where IE (Xe (3P2)) is the ionization energy of Xe*(3P2), EA (NF3) is the electron affinity of NF3, and rc is the crossing distance between the covalent entrance potential surface [Xe*(3P2) + NF3] and the ionic surface [Xe+ (2P3/2) + NF3−]. The reactivity is essentially determined by the crossing distance (rc) at which the 6s electron jump takes place because Coulomb forces between the ions [Xe+ (2P3/2) − F−(1S0)] essentially ensure XeF* formation.
The (adiabatic) electron affinity of NF3, EAad(NF3), has been reported to be EAad(NF3) = 1.71 eV.39 According to IE (Xe (3P2)) = 3.82 eV38 and EAad(NF3) = 1.71 eV,39 the crossing distance radc is calculated to be 6.8 Å. Although rc is not well-defined for a polyatomic system, we can expect little steric effect according to the sufficiently large crossing distance radc = 6.8 Å. Indeed, for the KI formation in the K + CF3I reaction system which has an large crossing distance of rc = 5.2 Å (IE (K) = 4.35 eV40 and EA (CF3I) = 1.57 eV38), it has been reported that the molecular orientation exerts an influence on only the angular distribution of KI with comparable reaction probability at the two ends.4 Moreover, for the KCl formation in the K + CHCl3 reaction system which has a shorter crossing distance of rc = 3.9 Å2 (IE (K) = 4.35 eV40 and EA (CHCl3) = 0.62 eV41), it has been reported that the molecular orientation has no influence on the reaction probability and on the angular distribution of KCl.3 Therefore, the observed large steric effects for the XeF* formations are distinctly different from the expectation from the large crossing distance radc estimated from the adiabatic electron affinity of NF3.
E Collision-induced harpooning mechanism
The quenching cross section 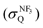 of Xe* (3P2) by NF3 has been reported to be
of Xe* (3P2) by NF3 has been reported to be 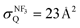 .28 This cross section is extremely smaller than the estimated cross section, π(radc)2 ≈ 150 Å2. Density function theory (DFT) calculations have predicted that the geometry of NF3− is far from the geometry of the neutral NF3.42 In addition, it has been reported that the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) has an activation energy of Ea = 0.1 ± 0.05 eV42 (and/or the larger activation energy of Ea = 300 ± 60 meV has been reported in the flowing afterglow experiment43). In other words, the curve crossing between NF3 and NF3− takes place out of the Frank-Condon region. This situation is schematically described in Fig. 5 in terms of a simplified one-dimensional potential energy diagram with Q as the relevant coordinates for the dissociative attachment reaction. The data were cited from ref. 42 as the values calculated by DFT. The Franck–Condon transition (0.5–3.5 eV) creates the transient negative ion NF3− in its electronic ground state. If the harpooning takes place within the Frank-Condon region of NF3, we have to adapt the vertical electron affinity (EAver (NF3)) of NF3 instead of the adiabatic electron affinity of EAad (NF3) to estimate the crossing distance rc. According to IE (Xe* (3P2)) = 3.82 eV38 and EAver (NF3) = (−0.5–−3.5) eV,39 the crossing distance rverc is calculated to be 2.0 Å < rverc < 3.3 Å. The geometry of NF3 molecule with the molecular steric opacity function for the XeF* (B) channel at |LZ′| = 1 is shown in Fig. 6. As can be seen in Fig. 6, a good correlation between the direction of the reactive lobe and the F atom direction (designated by the asterisk) from the center-of-mass of NF3 is recognized. Dashed lines indicate the van der Waals surface for NF3 and Xe* (3P2) as the approximate position of the repulsive wall. Since the rverc is located medial to the repulsive wall, it is unlikely that the 6s electron jump (harpooning) takes place via the vertical transition at the shorter intermolecular distance (2 Å < rverc < 3.3 Å). Therefore, in order for the harpooning for the NF3− formation to take place, the collisional deformation of NF3 (and/or collisional activation of the internal mode of NF3) is necessary to reach the curve crossing point between NF3 and NF3− located out of the Frank-Condon region. Here, we apply the word “collision-induced harpoon mechanism” to such a specific harpooning process induced by the collisional deformation of NF3. According to this mechanism, the good correlation between the molecular geometry and the shape of the molecular steric opacity function seems to be plausible because the Xe*(3P2) must have a close encounter with NF3 at the short intermolecular distance to induce the deformation of NF3.
.28 This cross section is extremely smaller than the estimated cross section, π(radc)2 ≈ 150 Å2. Density function theory (DFT) calculations have predicted that the geometry of NF3− is far from the geometry of the neutral NF3.42 In addition, it has been reported that the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) has an activation energy of Ea = 0.1 ± 0.05 eV42 (and/or the larger activation energy of Ea = 300 ± 60 meV has been reported in the flowing afterglow experiment43). In other words, the curve crossing between NF3 and NF3− takes place out of the Frank-Condon region. This situation is schematically described in Fig. 5 in terms of a simplified one-dimensional potential energy diagram with Q as the relevant coordinates for the dissociative attachment reaction. The data were cited from ref. 42 as the values calculated by DFT. The Franck–Condon transition (0.5–3.5 eV) creates the transient negative ion NF3− in its electronic ground state. If the harpooning takes place within the Frank-Condon region of NF3, we have to adapt the vertical electron affinity (EAver (NF3)) of NF3 instead of the adiabatic electron affinity of EAad (NF3) to estimate the crossing distance rc. According to IE (Xe* (3P2)) = 3.82 eV38 and EAver (NF3) = (−0.5–−3.5) eV,39 the crossing distance rverc is calculated to be 2.0 Å < rverc < 3.3 Å. The geometry of NF3 molecule with the molecular steric opacity function for the XeF* (B) channel at |LZ′| = 1 is shown in Fig. 6. As can be seen in Fig. 6, a good correlation between the direction of the reactive lobe and the F atom direction (designated by the asterisk) from the center-of-mass of NF3 is recognized. Dashed lines indicate the van der Waals surface for NF3 and Xe* (3P2) as the approximate position of the repulsive wall. Since the rverc is located medial to the repulsive wall, it is unlikely that the 6s electron jump (harpooning) takes place via the vertical transition at the shorter intermolecular distance (2 Å < rverc < 3.3 Å). Therefore, in order for the harpooning for the NF3− formation to take place, the collisional deformation of NF3 (and/or collisional activation of the internal mode of NF3) is necessary to reach the curve crossing point between NF3 and NF3− located out of the Frank-Condon region. Here, we apply the word “collision-induced harpoon mechanism” to such a specific harpooning process induced by the collisional deformation of NF3. According to this mechanism, the good correlation between the molecular geometry and the shape of the molecular steric opacity function seems to be plausible because the Xe*(3P2) must have a close encounter with NF3 at the short intermolecular distance to induce the deformation of NF3.
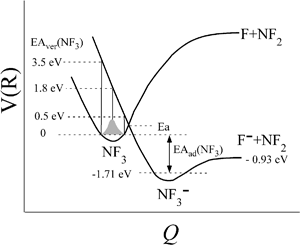 |
| | Fig. 5 Schematic drawings of the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) in terms of a simplified one-dimensional potential energy diagram with Q as the relevant coordinates for the dissociative attachment reaction that has activation energy Ea = 0.1 ± 0.05 eV. The data are cited from the ref. 42. The curve crossing between NF3 and NF3− takes place out of the Frank-Condon region (grey painted region). Franck–Condon transitions (0.5–3.5 eV) create the transient negative ion NF3− in its electronic ground state. | |
![Schematic drawings of the collision-induced harpooning mechanism with the geometry of NF3 molecule and the molecular steric opacity function for the XeF* (B) channel at |LZ′| = 1 (red line). A good correlation is recognized between the direction of the reactive lobe and the F atom direction (*) from the center-of-mass of NF3. The crossing distances (rverc) between the covalent potential surface [Xe*(3P2) + NF3] and the ionic surface [Xe+ (2P3/2) + NF3−] within the Franck–Condon region (−0.5 > EAver (NF3) > −3.5 eV) are shown by the dashed-dotted line circles for each vertical electron affinity (EAver (NF3)) of NF3; rverc = 2.0 Å for EAver (NF3) = −3.5 eV, rverc = 3.3 Å for EAver (NF3) = −0.5 eV. Dashed line indicates the van der Waals surface of NF3 and Xe*(3P2) as the approximate position of the repulsive wall. The painted arrow indicates the sideways relative velocity (vR). γ is the molecular orientation angle and α is the atomic orbital alignment angle with respect to the relative velocity vector (vR). The outline arrow indicates the relative velocity (vR) for the axial direction. The LZ′ selectivity expected from the LZ′ conservation model at each collision geometry is shown for the XeF* (B, C) channels.](/image/article/2011/CP/c0cp00648c/c0cp00648c-f6.gif) |
| | Fig. 6 Schematic drawings of the collision-induced harpooning mechanism with the geometry of NF3 molecule and the molecular steric opacity function for the XeF* (B) channel at |LZ′| = 1 (red line). A good correlation is recognized between the direction of the reactive lobe and the F atom direction (*) from the center-of-mass of NF3. The crossing distances (rverc) between the covalent potential surface [Xe*(3P2) + NF3] and the ionic surface [Xe+ (2P3/2) + NF3−] within the Franck–Condon region (−0.5 > EAver (NF3) > −3.5 eV) are shown by the dashed-dotted line circles for each vertical electron affinity (EAver (NF3)) of NF3; rverc = 2.0 Å for EAver (NF3) = −3.5 eV, rverc = 3.3 Å for EAver (NF3) = −0.5 eV. Dashed line indicates the van der Waals surface of NF3 and Xe*(3P2) as the approximate position of the repulsive wall. The painted arrow indicates the sideways relative velocity (vR). γ is the molecular orientation angle and α is the atomic orbital alignment angle with respect to the relative velocity vector (vR). The outline arrow indicates the relative velocity (vR) for the axial direction. The LZ′ selectivity expected from the LZ′ conservation model at each collision geometry is shown for the XeF* (B, C) channels. | |
F Comparison with the LZ′ conservation model
Recently, we have suggested the Ω′-conservation model for the excimer formation in which the angular momentum (Ω′) of the unpaired 5p electron of Xe* (3P2, MJ = 2) in the collision frame is assumed to be conserved in the course of ion pair [Xe+ (2P3/2)–NF3−] formation.35 According to this assumption, we can estimate the atomic orbital alignment (LZ′) selectivity owing to the correlation between the LZ′ and the projection (Λ) of the electronic angular momentum of XeF* on the diatomic axis in the ion pair [Xe+ (2P3/2)–NF3−].44 If we assume the “collision-induced harpoon mechanism”, the Xe*(3P2) must have a close encounter with NF3 to induce the harpooning via the deformation of the NF3. Therefore, the hard collision with F atom from the side with a small impact parameter must be favorable for the XeF* formation. In this case, we can expect a normal correlation between LZ′ and Λ (i.e., the LZ′ = 0 alignment is favorable for the XeF* (B, Σ) channel, and the |LZ′| = 1 alignment is favorable for the XeF* (C, Π) channel) for sideways XeF* formation because the diatomic axis of the product XeF* is parallel to the relative velocity, vR. While the inverse correlation (i.e., the LZ′ = 0 alignment is favorable for XeF* (C, Π) formation, and the |LZ′| = 1 alignment is favorable for XeF* (B, Σ) formation) should be expected for the collision with a large impact parameter from the molecular axis direction due to the rotational coupling because the diatomic axis of the product XeF* formed is perpendicular to the relative velocity. The LZ′ selectivities expected from the LZ′ conservation model are summarized in Fig. 6 for the XeF* (B, C) channels at each collision geometry. Overall, the collision-induced harpoon processes with the LZ′-conservation fairly explain the characteristics in the LZ′ dependent molecular steric opacity functions for the XeF*(B, C) channels.
G Effect of dark channel
In the Xe* (3P2) + NF3 reaction, it has long been thought that the branching fraction 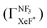 to the XeF* formation is unity,
to the XeF* formation is unity, 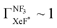 .24,25 However, the
.24,25 However, the 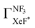 value has been revised downward in the most recent report;45
value has been revised downward in the most recent report;45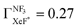 . An analogous discrepancy has been observed for the activation energy (Ea) in the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) studied under different experimental conditions; the crossed beam42 (Ea = 0.1 ± 0.05 eV), and the flowing afterglow43 (Ea = 300 ± 60 meV). These discrepancies might reflect the significant influence of the experimental conditions on reactivity because the harpoon process induced by the collisional deformation of NF3 (and/or activation of the internal mode) should be sensitive to the experimental conditions.
. An analogous discrepancy has been observed for the activation energy (Ea) in the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) studied under different experimental conditions; the crossed beam42 (Ea = 0.1 ± 0.05 eV), and the flowing afterglow43 (Ea = 300 ± 60 meV). These discrepancies might reflect the significant influence of the experimental conditions on reactivity because the harpoon process induced by the collisional deformation of NF3 (and/or activation of the internal mode) should be sensitive to the experimental conditions.
Unfortunately, we cannot determine the branching fraction 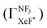 in the present study, independently. However we can expect the large branching fraction
in the present study, independently. However we can expect the large branching fraction 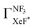 at least in our experimental conditions because we have observed about the same XeF* emission intensity as compared with the XeBr* emission intensity in the Xe* (3P2) + CF3Br reaction;
at least in our experimental conditions because we have observed about the same XeF* emission intensity as compared with the XeBr* emission intensity in the Xe* (3P2) + CF3Br reaction;
The branching fraction 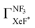 can be roughly estimated to be
can be roughly estimated to be 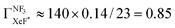 based on the quenching cross section of CF3Br
based on the quenching cross section of CF3Br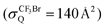 ,28 the branching fraction of
,28 the branching fraction of 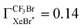 ,23 and the quenching cross section of NF3
,23 and the quenching cross section of NF3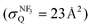 .28 It is likely that the XeF* formation is the dominant channel in the quenching process with minor contribution from the dark channel in our experimental conditions. The good correlation between the molecular shape and the shape of the steric opacity function seems to be consistent with the large branching fraction to the XeF* formation. Exceptionally, we can observe the notable depletion in the molecular steric opacity function for the sideways XeF* (C, Π) channel at |LZ′| = 1. It seems likely that this depletion is caused by the dark channelvia a similar indirect process that have been commonly proposed in the other reaction systems; i.e., the NF3* formation via the back-electron transfer from the dissociating (NF2⋯F−) to Xe+ which may be favorable for the sideways collision. The electron transfer from the NF2 segment to Xe+ might be energetically possible because the ionization energy of Xe (IE (Xe) = 12.13 eV41) is slightly larger than that of NF2 (IE (NF2) = 11.8 ± 0.4 eV46). In addition, since the direct coupling between the entrance surface [Xe*(3P2) + NF3] and the exit surface [Xe + NF3*] via a mechanism like electron exchange is expected at the short intermolecular distance, the NF3* formation via direct coupling might have some effect on the stereo-anisotropy of the XeF* formation, too.
.28 It is likely that the XeF* formation is the dominant channel in the quenching process with minor contribution from the dark channel in our experimental conditions. The good correlation between the molecular shape and the shape of the steric opacity function seems to be consistent with the large branching fraction to the XeF* formation. Exceptionally, we can observe the notable depletion in the molecular steric opacity function for the sideways XeF* (C, Π) channel at |LZ′| = 1. It seems likely that this depletion is caused by the dark channelvia a similar indirect process that have been commonly proposed in the other reaction systems; i.e., the NF3* formation via the back-electron transfer from the dissociating (NF2⋯F−) to Xe+ which may be favorable for the sideways collision. The electron transfer from the NF2 segment to Xe+ might be energetically possible because the ionization energy of Xe (IE (Xe) = 12.13 eV41) is slightly larger than that of NF2 (IE (NF2) = 11.8 ± 0.4 eV46). In addition, since the direct coupling between the entrance surface [Xe*(3P2) + NF3] and the exit surface [Xe + NF3*] via a mechanism like electron exchange is expected at the short intermolecular distance, the NF3* formation via direct coupling might have some effect on the stereo-anisotropy of the XeF* formation, too.
In conclusion, we have studied the steric effect of the XeF* (B, C) formation in the oriented Xe* (3P2, MJ = 2) + oriented NF3 reaction under doubly orientation-controlled conditions. Clear multidimensional stereo-selectivity depending on the mutual orientation between two reactants is recognized. The larger reactivity at the side with the smaller reactivity in the molecular axis direction is observed for the XeF* (B, C) channels at each atomic orbital alignment (LZ′) in contrast with the other molecular systems that commonly show poor reactivity at the side. A good correlation between the direction of the reactive lobe in the molecular steric opacity function and the F atom direction from the center-of-mass of NF3 is recognized. We propose the collision-induced harpoon mechanism for the XeF* (B, C) formations in the Xe* (3P2) + NF3 reaction.
References
- P. R. Brooks, Science, 1976, 193, 11 CAS.
- R. J. Beuhler Jr and R. B. Bernstein, Chem. Phys. Lett., 1968, 2, 166 CrossRef.
- P. R. Brooks, Faraday Discuss. Chem. Soc., 1973, 55, 299 RSC.
- G. Marcelin and P. R. Brooks, J. Am. Chem. Soc., 1975, 97, 1710 CrossRef CAS.
- D. H. Parker, K. K. Chakravorty and P. R. Bernstein, J. Phys. Chem., 1981, 85, 466 CrossRef CAS.
- D. H. Parker and R. B. Bernstein, Annu. Rev. Phys. Chem., 1989, 40, 561 CrossRef CAS.
- J. Bulthuis, J. J. van Leuken and S. Stolte, J. Chem. Soc., Faraday Trans., 1995, 91, 205 RSC.
- H. S. Carman, P. W. Harland and P. R. Brooks, J. Phys. Chem., 1986, 90, 944 CrossRef CAS.
- M. H. M. Janssen, D. H. Paker and S. Stolte, J. Phys. Chem., 1996, 100, 16066 CrossRef CAS.
- P. R. Brooks and S. A. Harris, J. Chem. Phys., 2002, 117, 4220 CrossRef CAS.
- A. Gijsbertsen, H. Linnartz, G. Rus, A. E. Wiskerke, S. Stolte, D. W. Chandler and J. Klos, J. Chem. Phys., 2005, 123, 224305 CrossRef CAS.
- P. R. Brooks, J. Chem. Phys., 2009, 130, 151102 CrossRef.
- D. Watanabe, H. Ohoyama, T. Matsumura and T. Kasai, Phys. Rev. Lett., 2007, 99, 043201 CrossRef CAS.
- H. Ohoyama, F. Kubo and T. Kasai, J. Chem. Phys., 2009, 131, 134306 CrossRef CAS.
- H. Ohoyama and T. Kasai, Phys. Chem. Chem. Phys., 2010, 12, 6949 RSC.
- H. Ohoyama and T. Kasai, J. Chem. Phys., 2010, 132, 234316 CrossRef CAS.
- H. Ohoyama, J. Phys. Chem. A, 2010 DOI:10.1021/jp104314s.
- H. J. Loesch and A. Remscheid, J. Chem. Phys., 1990, 93, 4779 CrossRef CAS.
- B. Friedrich and D. R. Herschbach, Z. Phys. D: At., Mol. Clusters, 1991, 18, 153 CAS.
- H. J. Loesch and J. Möller, J. Chem. Phys., 1992, 97, 9016 CrossRef CAS.
- M. S. de Vries, V. I. Srdanov, C. P. Hanrahan and R. M. Martin, J. Chem. Phys., 1983, 78, 5582 CrossRef CAS.
- Z. Karny, R. C. Estler and R. N. Zare, J. Chem. Phys., 1978, 69, 5199 CrossRef CAS.
-
W. R. Simpson, T. P. Rakitzis, S. A. Kandel, A. J. Orr-Ewing and R. N. Zare, Proc. Stereodynamics and Active Control in Chemical Reactions, CNRS, Gif sur Yvette, 1994, p. 2 Search PubMed.
- K. Tamagake, D. W. Setser and J. H. Kolts, J. Chem. Phys., 1981, 74, 4286 CrossRef CAS.
- J. H. Kolts, J. E. Velazco and D. W. Setser, J. Chem. Phys., 1979, 71, 1247 CrossRef CAS.
- N. Sadeghi, M. Cheaib and D. W. Setser, J. Chem. Phys., 1989, 90, 219 CrossRef CAS.
- D. Zhong, D. W. Setser, R. Sobczynski and W. Gadomski, J. Chem. Phys., 1996, 105, 5020 CrossRef CAS.
- J. E. Velazco, J. H. Kolts and D. W. Setser, J. Chem. Phys., 1976, 65, 3468 CrossRef CAS.
- D. W. Setser, T. D. Dreiling, H. C. Brashears Jr and J. H. Kolts, Faraday Discuss. Chem. Soc., 1979, 67, 255 RSC.
-
R. B. Bernstein, Chemical Dynamics via Molecular Beam and Laser Techniques, Oxford University Press, New York, 1982, ch. 3 Search PubMed.
- D. Watanabe, H. Ohoyama, T. Matsumura and T. Kasai, J. Chem. Phys., 2006, 125, 084316 CrossRef CAS.
- H. Ohoyama, T. Ogawa and T. Kasai, J. Phys. Chem., 1995, 99, 13606 CrossRef CAS.
- S. Stolte, K. K. Chakravorty, R. B. Bernstein and D. H. Parker, Chem. Phys., 1982, 71, 353 CrossRef CAS.
-
R. N. Zare, Angular Momentum, Understanding Spatial Aspects in Chemistry and Physics, Wiley, New York, 1998 Search PubMed.
- H. Ohoyama, K. Yasuda and T. Kasai, J. Phys. Chem. A, 2009, 113, 14785 CrossRef CAS.
- Y. M. Engel and R. D. Levine, Chem. Phys., 1984, 91, 167 CrossRef CAS.
-
R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics and Chemical Reactivity, Oxford University Press, New York, 1987 Search PubMed.
-
C. E. Moore, Atomic Energy Levels, Government Printing Office, Washinton, DC, 1952 Search PubMed.
- R. N. Compton, P. W. Reinhardt and C. D. Cooper, J. Chem. Phys., 1978, 68, 4360 CrossRef CAS.
- R. L. Kelly, J. Phys. Chem. Ref. Data, 1987, 16(S1), 1 CAS.
- H. Schafer, H. Rabeneck and Z. Anor, Z. Anorg. Allg. Chem., 1987, 545, 224 CrossRef.
- N. Ruchhaberle, L. Lehmann, S. Matejcik, E. Illenberger, Y. Bouteiller, V. Periduet, L. Museur, C. Desfrancois and J. P. Schermann, J. Phys. Chem. A, 1997, 101, 9942 CrossRef CAS.
- T. M. Miller, J. F. Friedman, A. E. S. Miller and J. F. Pauson, Int. J. Mass Spectrom. Ion Processes, 1995, 149–150, 111 CrossRef.
-
J. C. Whitehead, Selectivity in Chemical Reactions, Kluwer, London, 1988, p. 473 Search PubMed.
- D. Lin, Y. C. Yu and D. W. Setser, J. Chem. Phys., 1984, 81, 5830 CrossRef CAS.
- V. Tarnovsky, A. Levin and K. Becker, J. Chem. Phys., 1994, 100, 5626 CrossRef CAS.
|
| This journal is © the Owner Societies 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 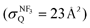 .28 The larger reactivity at the side with the smaller reactivity in the molecular axis direction is observed in contrast with the other molecular systems that commonly show poor reactivity at the side. A good correlation between the direction of the reactive lobe and the F atoms direction from the center-of-mass of NF3 is recognized. We propose the collision-induced harpoon mechanism for the XeF* (B, C) formations.
.28 The larger reactivity at the side with the smaller reactivity in the molecular axis direction is observed in contrast with the other molecular systems that commonly show poor reactivity at the side. A good correlation between the direction of the reactive lobe and the F atoms direction from the center-of-mass of NF3 is recognized. We propose the collision-induced harpoon mechanism for the XeF* (B, C) formations.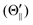 . Similarly, three representative configurations were selected for the molecular orientation, i.e. parallel (Φ∥: N-end), antiparallel (
. Similarly, three representative configurations were selected for the molecular orientation, i.e. parallel (Φ∥: N-end), antiparallel (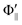 : F3-end), and orientation field off (Φoff: random orientation). Under the doubly-orientation controlled conditions, the oriented Xe* (3P2, MJ = 2) atomic beam collides with the oriented NF3 molecular beam at the beam crossing point. The emission from the products XeF* (B, C) was separated through the band-pass filters (B: Asahi Spectra (SUX300), λ = 210–300 nm; C: Optical Coatings Japan (SPF570), λ = 380–570 nm) and detected by a cooled and magnetic shielded photomultiplier. Only the signal enhanced by applying the electric hexapole field (V0 = 12 kV) was used as the chemiluminescence signal from the oriented NF3 + oriented Xe* (3P2, MJ = 2) reaction. For the subtraction of the background signal, the signal at V0 = 0 kV was used as the background signal. The emission intensities (I(Θ,Φ)) from the products XeF* (B, C) were measured at the nine mutual configurations between the atomic orientation Θ and molecular orientation Φ.
: F3-end), and orientation field off (Φoff: random orientation). Under the doubly-orientation controlled conditions, the oriented Xe* (3P2, MJ = 2) atomic beam collides with the oriented NF3 molecular beam at the beam crossing point. The emission from the products XeF* (B, C) was separated through the band-pass filters (B: Asahi Spectra (SUX300), λ = 210–300 nm; C: Optical Coatings Japan (SPF570), λ = 380–570 nm) and detected by a cooled and magnetic shielded photomultiplier. Only the signal enhanced by applying the electric hexapole field (V0 = 12 kV) was used as the chemiluminescence signal from the oriented NF3 + oriented Xe* (3P2, MJ = 2) reaction. For the subtraction of the background signal, the signal at V0 = 0 kV was used as the background signal. The emission intensities (I(Θ,Φ)) from the products XeF* (B, C) were measured at the nine mutual configurations between the atomic orientation Θ and molecular orientation Φ.
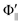 : F3-end), and orientation field off (Φoff: random orientation)) and the atomic configuration (parallel (Θ∥), perpendicular (Θ⊥), and antiparallel
: F3-end), and orientation field off (Φoff: random orientation)) and the atomic configuration (parallel (Θ∥), perpendicular (Θ⊥), and antiparallel 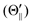 ) with respect to the direction of relative velocity vR with a Newton diagram for the title reaction. (B) Focusing curve for the XeF* formation; experimental (●), calculated one via the trajectory simulation with the rotational temperature of Trot = 200 K (solid line). (inner panel) Polar coordination representation of the orientational distribution of the molecular axis with respect to the electric orientation field E for the state-selected NF3 beam at V0 = 12 kV (solid line) and random orientation (broken line).
) with respect to the direction of relative velocity vR with a Newton diagram for the title reaction. (B) Focusing curve for the XeF* formation; experimental (●), calculated one via the trajectory simulation with the rotational temperature of Trot = 200 K (solid line). (inner panel) Polar coordination representation of the orientational distribution of the molecular axis with respect to the electric orientation field E for the state-selected NF3 beam at V0 = 12 kV (solid line) and random orientation (broken line).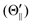 . Although the Xe* (3P2, MJ = 2) beam is oriented in the homogeneous magnetic orientation field B in the present study, we can observe only the atomic alignment effect due to the experimental condition with a cylindrical symmetry (i.e., we observed only the total cross section).31 By using Wigner's d function,34
. Although the Xe* (3P2, MJ = 2) beam is oriented in the homogeneous magnetic orientation field B in the present study, we can observe only the atomic alignment effect due to the experimental condition with a cylindrical symmetry (i.e., we observed only the total cross section).31 By using Wigner's d function,34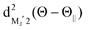 , the Xe* (3P2, MJ = 2) states |Θ〉 at the three atomic orientation configurations can be simply expressed as
, the Xe* (3P2, MJ = 2) states |Θ〉 at the three atomic orientation configurations can be simply expressed as 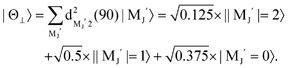
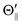 ) can be expressed as follows by using the cross section (σ|LZ′|) at each atomic orbital alignment (|LZ′|) in the collision frame,
) can be expressed as follows by using the cross section (σ|LZ′|) at each atomic orbital alignment (|LZ′|) in the collision frame,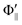 , and Φoff) and the atomic orientation configuration (Θ∥, Θ⊥, and
, and Φoff) and the atomic orientation configuration (Θ∥, Θ⊥, and 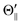 ). The N-end configuration is extremely less reactive than the F3-end and the random configurations. In addition, the reactivity at the random configuration is most reactive at each atomic alignment configuration. The Θ-dependence is extremely different between the XeF* (B, C) channels at each molecular orientation configuration. The XeF* (B) channel shows poor Θ-dependence at every molecular orientation configuration, while the XeF* (C) channel shows significant Θ-dependence that depends on the molecular orientation configuration. The XeF* (C) intensity is lower for Θ⊥ than for Θ∥ (and
). The N-end configuration is extremely less reactive than the F3-end and the random configurations. In addition, the reactivity at the random configuration is most reactive at each atomic alignment configuration. The Θ-dependence is extremely different between the XeF* (B, C) channels at each molecular orientation configuration. The XeF* (B) channel shows poor Θ-dependence at every molecular orientation configuration, while the XeF* (C) channel shows significant Θ-dependence that depends on the molecular orientation configuration. The XeF* (C) intensity is lower for Θ⊥ than for Θ∥ (and 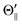 ) at both the F3-end and the random configurations, while the N-end configuration shows the opposite Θ-dependence.
) at both the F3-end and the random configurations, while the N-end configuration shows the opposite Θ-dependence.

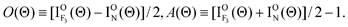
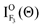 is the relative emission intensity at the N-end configuration (Φ∥) and at the F3-end configuration
is the relative emission intensity at the N-end configuration (Φ∥) and at the F3-end configuration 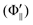 to that at the random orientation (Φoff), respectively.
to that at the random orientation (Φoff), respectively.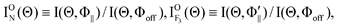
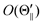 ) for the XeF* (C) channel. Fig. 3 further shows that the alignment terms A(Θ) for the XeF* (B, C) channels are negative at each Θ configuration. The Θ-dependence of A(Θ) is different between the XeF* (B, C) channels; A(Θ⊥) is smaller than A(Θ∥) (and
) for the XeF* (C) channel. Fig. 3 further shows that the alignment terms A(Θ) for the XeF* (B, C) channels are negative at each Θ configuration. The Θ-dependence of A(Θ) is different between the XeF* (B, C) channels; A(Θ⊥) is smaller than A(Θ∥) (and 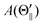 ) for the XeF* (B) channel, while A(Θ⊥) is larger than A(Θ∥) (and
) for the XeF* (B) channel, while A(Θ⊥) is larger than A(Θ∥) (and 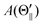 ) for the XeF* (C) channel.
) for the XeF* (C) channel.

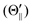 );O(Θ) (○), A(Θ) (●). The error bar shows the confidence interval for 95% confidence coefficient.
);O(Θ) (○), A(Θ) (●). The error bar shows the confidence interval for 95% confidence coefficient.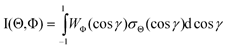
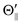 ) by applying the Engel-Levine function model described below,36
) by applying the Engel-Levine function model described below,36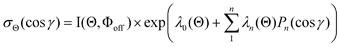
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) σ(cos γ, α = 90) = σΘ∥(cos γ)
σ(cos γ, α = 90) = σΘ∥(cos γ)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) σ(cos γ, α = 0) = 2 × σΘ⊥(cos γ) − σΘ∥(cos γ).
σ(cos γ, α = 0) = 2 × σΘ⊥(cos γ) − σΘ∥(cos γ).
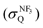 of Xe* (3P2) by NF3 has been reported to be
of Xe* (3P2) by NF3 has been reported to be 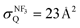 .28 This cross section is extremely smaller than the estimated cross section, π(radc)2 ≈ 150 Å2. Density function theory (DFT) calculations have predicted that the geometry of NF3− is far from the geometry of the neutral NF3.42 In addition, it has been reported that the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) has an activation energy of Ea = 0.1 ± 0.05 eV42 (and/or the larger activation energy of Ea = 300 ± 60 meV has been reported in the flowing afterglow experiment43). In other words, the curve crossing between NF3 and NF3− takes place out of the Frank-Condon region. This situation is schematically described in Fig. 5 in terms of a simplified one-dimensional potential energy diagram with Q as the relevant coordinates for the dissociative attachment reaction. The data were cited from ref. 42 as the values calculated by DFT. The Franck–Condon transition (0.5–3.5 eV) creates the transient negative ion NF3− in its electronic ground state. If the harpooning takes place within the Frank-Condon region of NF3, we have to adapt the vertical electron affinity (EAver (NF3)) of NF3 instead of the adiabatic electron affinity of EAad (NF3) to estimate the crossing distance rc. According to IE (Xe* (3P2)) = 3.82 eV38 and EAver (NF3) = (−0.5–−3.5) eV,39 the crossing distance rverc is calculated to be 2.0 Å < rverc < 3.3 Å. The geometry of NF3 molecule with the molecular steric opacity function for the XeF* (B) channel at |LZ′| = 1 is shown in Fig. 6. As can be seen in Fig. 6, a good correlation between the direction of the reactive lobe and the F atom direction (designated by the asterisk) from the center-of-mass of NF3 is recognized. Dashed lines indicate the van der Waals surface for NF3 and Xe* (3P2) as the approximate position of the repulsive wall. Since the rverc is located medial to the repulsive wall, it is unlikely that the 6s electron jump (harpooning) takes place via the vertical transition at the shorter intermolecular distance (2 Å < rverc < 3.3 Å). Therefore, in order for the harpooning for the NF3− formation to take place, the collisional deformation of NF3 (and/or collisional activation of the internal mode of NF3) is necessary to reach the curve crossing point between NF3 and NF3− located out of the Frank-Condon region. Here, we apply the word “collision-induced harpoon mechanism” to such a specific harpooning process induced by the collisional deformation of NF3. According to this mechanism, the good correlation between the molecular geometry and the shape of the molecular steric opacity function seems to be plausible because the Xe*(3P2) must have a close encounter with NF3 at the short intermolecular distance to induce the deformation of NF3.
.28 This cross section is extremely smaller than the estimated cross section, π(radc)2 ≈ 150 Å2. Density function theory (DFT) calculations have predicted that the geometry of NF3− is far from the geometry of the neutral NF3.42 In addition, it has been reported that the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) has an activation energy of Ea = 0.1 ± 0.05 eV42 (and/or the larger activation energy of Ea = 300 ± 60 meV has been reported in the flowing afterglow experiment43). In other words, the curve crossing between NF3 and NF3− takes place out of the Frank-Condon region. This situation is schematically described in Fig. 5 in terms of a simplified one-dimensional potential energy diagram with Q as the relevant coordinates for the dissociative attachment reaction. The data were cited from ref. 42 as the values calculated by DFT. The Franck–Condon transition (0.5–3.5 eV) creates the transient negative ion NF3− in its electronic ground state. If the harpooning takes place within the Frank-Condon region of NF3, we have to adapt the vertical electron affinity (EAver (NF3)) of NF3 instead of the adiabatic electron affinity of EAad (NF3) to estimate the crossing distance rc. According to IE (Xe* (3P2)) = 3.82 eV38 and EAver (NF3) = (−0.5–−3.5) eV,39 the crossing distance rverc is calculated to be 2.0 Å < rverc < 3.3 Å. The geometry of NF3 molecule with the molecular steric opacity function for the XeF* (B) channel at |LZ′| = 1 is shown in Fig. 6. As can be seen in Fig. 6, a good correlation between the direction of the reactive lobe and the F atom direction (designated by the asterisk) from the center-of-mass of NF3 is recognized. Dashed lines indicate the van der Waals surface for NF3 and Xe* (3P2) as the approximate position of the repulsive wall. Since the rverc is located medial to the repulsive wall, it is unlikely that the 6s electron jump (harpooning) takes place via the vertical transition at the shorter intermolecular distance (2 Å < rverc < 3.3 Å). Therefore, in order for the harpooning for the NF3− formation to take place, the collisional deformation of NF3 (and/or collisional activation of the internal mode of NF3) is necessary to reach the curve crossing point between NF3 and NF3− located out of the Frank-Condon region. Here, we apply the word “collision-induced harpoon mechanism” to such a specific harpooning process induced by the collisional deformation of NF3. According to this mechanism, the good correlation between the molecular geometry and the shape of the molecular steric opacity function seems to be plausible because the Xe*(3P2) must have a close encounter with NF3 at the short intermolecular distance to induce the deformation of NF3.

![Schematic drawings of the collision-induced harpooning mechanism with the geometry of NF3 molecule and the molecular steric opacity function for the XeF* (B) channel at |LZ′| = 1 (red line). A good correlation is recognized between the direction of the reactive lobe and the F atom direction (*) from the center-of-mass of NF3. The crossing distances (rverc) between the covalent potential surface [Xe*(3P2) + NF3] and the ionic surface [Xe+ (2P3/2) + NF3−] within the Franck–Condon region (−0.5 > EAver (NF3) > −3.5 eV) are shown by the dashed-dotted line circles for each vertical electron affinity (EAver (NF3)) of NF3; rverc = 2.0 Å for EAver (NF3) = −3.5 eV, rverc = 3.3 Å for EAver (NF3) = −0.5 eV. Dashed line indicates the van der Waals surface of NF3 and Xe*(3P2) as the approximate position of the repulsive wall. The painted arrow indicates the sideways relative velocity (vR). γ is the molecular orientation angle and α is the atomic orbital alignment angle with respect to the relative velocity vector (vR). The outline arrow indicates the relative velocity (vR) for the axial direction. The LZ′ selectivity expected from the LZ′ conservation model at each collision geometry is shown for the XeF* (B, C) channels.](/image/article/2011/CP/c0cp00648c/c0cp00648c-f6.gif)
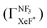 to the XeF* formation is unity,
to the XeF* formation is unity, 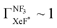 .24,25 However, the
.24,25 However, the 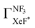 value has been revised downward in the most recent report;45
value has been revised downward in the most recent report;45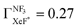 . An analogous discrepancy has been observed for the activation energy (Ea) in the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) studied under different experimental conditions; the crossed beam42 (Ea = 0.1 ± 0.05 eV), and the flowing afterglow43 (Ea = 300 ± 60 meV). These discrepancies might reflect the significant influence of the experimental conditions on reactivity because the harpoon process induced by the collisional deformation of NF3 (and/or activation of the internal mode) should be sensitive to the experimental conditions.
. An analogous discrepancy has been observed for the activation energy (Ea) in the dissociative attachment (DA) reaction (e− + NF3 → NF2 + F−) studied under different experimental conditions; the crossed beam42 (Ea = 0.1 ± 0.05 eV), and the flowing afterglow43 (Ea = 300 ± 60 meV). These discrepancies might reflect the significant influence of the experimental conditions on reactivity because the harpoon process induced by the collisional deformation of NF3 (and/or activation of the internal mode) should be sensitive to the experimental conditions.
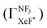 in the present study, independently. However we can expect the large branching fraction
in the present study, independently. However we can expect the large branching fraction 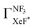 at least in our experimental conditions because we have observed about the same XeF* emission intensity as compared with the XeBr* emission intensity in the Xe* (3P2) + CF3Br reaction;
at least in our experimental conditions because we have observed about the same XeF* emission intensity as compared with the XeBr* emission intensity in the Xe* (3P2) + CF3Br reaction;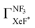 can be roughly estimated to be
can be roughly estimated to be 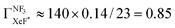 based on the quenching cross section of CF3Br
based on the quenching cross section of CF3Br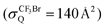 ,28 the branching fraction of
,28 the branching fraction of 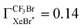 ,23 and the quenching cross section of NF3
,23 and the quenching cross section of NF3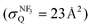 .28 It is likely that the XeF* formation is the dominant channel in the quenching process with minor contribution from the dark channel in our experimental conditions. The good correlation between the molecular shape and the shape of the steric opacity function seems to be consistent with the large branching fraction to the XeF* formation. Exceptionally, we can observe the notable depletion in the molecular steric opacity function for the sideways XeF* (C, Π) channel at |LZ′| = 1. It seems likely that this depletion is caused by the dark channelvia a similar indirect process that have been commonly proposed in the other reaction systems; i.e., the NF3* formation via the back-electron transfer from the dissociating (NF2⋯F−) to Xe+ which may be favorable for the sideways collision. The electron transfer from the NF2 segment to Xe+ might be energetically possible because the ionization energy of Xe (IE (Xe) = 12.13 eV41) is slightly larger than that of NF2 (IE (NF2) = 11.8 ± 0.4 eV46). In addition, since the direct coupling between the entrance surface [Xe*(3P2) + NF3] and the exit surface [Xe + NF3*] via a mechanism like electron exchange is expected at the short intermolecular distance, the NF3* formation via direct coupling might have some effect on the stereo-anisotropy of the XeF* formation, too.
.28 It is likely that the XeF* formation is the dominant channel in the quenching process with minor contribution from the dark channel in our experimental conditions. The good correlation between the molecular shape and the shape of the steric opacity function seems to be consistent with the large branching fraction to the XeF* formation. Exceptionally, we can observe the notable depletion in the molecular steric opacity function for the sideways XeF* (C, Π) channel at |LZ′| = 1. It seems likely that this depletion is caused by the dark channelvia a similar indirect process that have been commonly proposed in the other reaction systems; i.e., the NF3* formation via the back-electron transfer from the dissociating (NF2⋯F−) to Xe+ which may be favorable for the sideways collision. The electron transfer from the NF2 segment to Xe+ might be energetically possible because the ionization energy of Xe (IE (Xe) = 12.13 eV41) is slightly larger than that of NF2 (IE (NF2) = 11.8 ± 0.4 eV46). In addition, since the direct coupling between the entrance surface [Xe*(3P2) + NF3] and the exit surface [Xe + NF3*] via a mechanism like electron exchange is expected at the short intermolecular distance, the NF3* formation via direct coupling might have some effect on the stereo-anisotropy of the XeF* formation, too.