Thermodynamics of liquids: standard molar entropies and heat capacities of common solvents from 2PT molecular dynamics†
Tod A.
Pascal
ab,
Shiang-Tai
Lin
c and
William A.
Goddard III
*ab
aMaterials and Process Simulation Center, California Institute of Technology, Pasadena, CA 91125, USA. E-mail: wag@wag.caltech.edu
bGraduate School of EEWS, Korea Advanced Institute of Science and Technology, Daejeon, Korea 305-701
cDepartment of Chemical Engineering, National Taiwan University, Taipei 10617, Taiwan
First published on 23rd November 2010
Abstract
We validate here the Two-Phase Thermodynamics (2PT) method for calculating the standard molar entropies and heat capacities of common liquids. In 2PT, the thermodynamics of the system is related to the total density of states (DoS), obtained from the Fourier Transform of the velocity autocorrelation function. For liquids this DoS is partitioned into a diffusional component modeled as diffusion of a hard sphere gas plus a solid component for which the DoS(υ) → 0 as υ → 0 as for a Debye solid. Thermodynamic observables are obtained by integrating the DoS with the appropriate weighting functions. In the 2PT method, two parameters are extracted from the DoS self-consistently to describe diffusional contributions: the fraction of diffusional modes, f, and DoS(0). This allows 2PT to be applied consistently and without re-parameterization to simulations of arbitrary liquids. We find that the absolute entropy of the liquid can be determined accurately from a single short MD trajectory (20 ps) after the system is equilibrated, making it orders of magnitude more efficient than commonly used perturbation and umbrella sampling methods. Here, we present the predicted standard molar entropies for fifteen common solvents evaluated from molecular dynamics simulations using the AMBER, GAFF, OPLS AA/L and Dreiding II forcefields. Overall, we find that all forcefields lead to good agreement with experimental and previous theoretical values for the entropy and very good agreement in the heat capacities. These results validate 2PT as a robust and efficient method for evaluating the thermodynamics of liquid phase systems. Indeed 2PT might provide a practical scheme to improve the intermolecular terms in forcefields by comparing directly to thermodynamic properties.
I. Introduction
Modern quantum mechanics (QM) methods provide powerful means for predicting the energetics and enthalpies of molecules at low temperatures, including accurate estimates for solvation energies.1–3 However, neither QM nor molecular dynamics (MD) using forcefields (FF) have proved feasible for predicting accurate free energies from practical first principles calculations, primarily due to uncertainty in calculating entropy. Numerous methods have thus been proposed to calculate accurate entropies, although there is usually a tradeoff between accuracy and efficiency. Most perturbation MD methods,4 based on Kirkwood–Zwanzig thermodynamic integration,5,6 have shown to be very accurate for a range of systems and can in principle lead to accurate free energy change from a reference system A to the target system B. However, complexities related to the choice of appropriate approximation formalism limit their straightforward application.Alternatively, the free energy can be obtained from potential of mean-force simulations,7 which are markedly simpler, but not as accurate. Widom particle insertion8 schemes yield the chemical potential but require extensive sampling for all but the simplest of systems. Alternatively, Jorgensen and others have shown9–13 that Monte Carlo (MC) methods14 coupled with intermolecular forcefields can lead to accurate free energies of solution, but again this usually involves very long simulations to reduce the statistical uncertainty. Indeed, except in the context of thermodynamic integration using umbrella sampling, MD has not generally been useful for predicting the free energy or entropy of complex molecular systems.
It would be quite useful to have efficient ways to estimate the entropy directly from MD (thereby preserving the dynamical information lost from MC techniques). Indeed, entropy is expected to be the driving force behind most biochemical processes, ranging from protein folding and ligand/protein binding,15–17 to DNA transformations and recognition18 and hydrophobic effects.19,20 In particular, solubility and therefore miscibility of molecules in organic liquids may be dominated by changes in entropy,21–23 making accurate measures of the standard molar entropy critical to understanding solvation phenomena.
We propose here a practical approach to obtain accurate thermodynamics from short MD trajectories, which we validate by predicting entropies and specific heats of 15 standard solvents. Our approach is based on the 2PT method24 for extracting absolute standard molar entropies and free energies from classical MD trajectories. In the 2PT paradigm, the entropy of the system is derived from the atomic velocity autocorrelation function C(t) extracted from a 20 ps trajectory. The process is first to calculate the total density of states (DoS), from a Fast Fourier Transform of C(t) to obtain DoS(υ). Obtaining the thermodynamic properties from the DoS(υ) of a liquid is complicated by diffusional effects (a finite DoS at υ = 0), which would lead to infinite values for the entropy for the standard harmonic oscillator partition function.
In the 2PT model, we assume that the DoS can be partitioned into a solid like component, DoS(υ)solid, and a diffusional component, DoS(υ)diff. This DoS(υ)diff component is modeled in terms of a gas of hard spheres, completely described by DoS(υ=0), the zero frequency intensity of the total DoS and f, the fraction of the 3N degrees of freedom (dof) that are diffusional. These parameters DoS(υ) and f are extracted from the total DoS, leading to the vibrational DoS(υ)solid that can be analyzed using the standard harmonic oscillator partition function to account for the vibrational and librational components.
The original validation of the 2PT method was for a Lennard-Jones fluid, where very extensive MC calculations were available for the free energies for all regimes of the phase diagram, including solid, liquid, gas, supercritical, metastable, and unstable. Lin et al.24 showed that 2PT from short 10 ps simulations gave excellent agreement with the MC for the entropies and free energies for all phases, including metastable and unstable regions.
The 2PT method has since been applied to several complex, condensed phase systems. For example, Lin et al.25 showed that the water molecules in a full solvent simulation (∼40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules) of a generation 4 PAMAM Dendrimer (one molecule with 2244 atoms) leads to dramatically different entropies for the inner hydrophobic region, compared to the surface and bulk waters. Similarly, Jana et al.26 used 2PT to show that the entropies of water molecules in the grooves of DNA are significantly lower than in bulk water. More recently, Pascal et al.27 used 2PT to examine the entropic effects in binding a disaccharide (chitobiose) to the outer membrane protein A on Escherichia coli (a system involving 2589 atoms in the protein, 114 in the ligand and 42
000 water molecules) of a generation 4 PAMAM Dendrimer (one molecule with 2244 atoms) leads to dramatically different entropies for the inner hydrophobic region, compared to the surface and bulk waters. Similarly, Jana et al.26 used 2PT to show that the entropies of water molecules in the grooves of DNA are significantly lower than in bulk water. More recently, Pascal et al.27 used 2PT to examine the entropic effects in binding a disaccharide (chitobiose) to the outer membrane protein A on Escherichia coli (a system involving 2589 atoms in the protein, 114 in the ligand and 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 solvent/lipid atoms). Here it was shown that various mutations led to a significant change in the contribution of entropy to the binding, so that enthalpies alone did not correlate well with experimental invasion rates, but that the 2PT derived free energies led to an excellent correlation. This work demonstrated the feasibility of calculating accurate ligand binding free energies and entropies on proteins embedded in a phospholipid membrane with explicit water molecules and salt.
600 solvent/lipid atoms). Here it was shown that various mutations led to a significant change in the contribution of entropy to the binding, so that enthalpies alone did not correlate well with experimental invasion rates, but that the 2PT derived free energies led to an excellent correlation. This work demonstrated the feasibility of calculating accurate ligand binding free energies and entropies on proteins embedded in a phospholipid membrane with explicit water molecules and salt.
While 2PT has been applied successfully to these and other complex systems,28,29 its performance in computing the absolute entropy and free energy of liquids other than water has not been demonstrated. In this paper, we use the 2PT method to calculate standard molar entropies and molar heat capacities of 15 common organic liquids. Of course the 2PT analysis cannot be better than the forcefield used, so we test the accuracy of several forcefields: AMBER-2003,30,31 General Amber Force Field (GAFF),32 OPLS AA/L11,33 and Dreiding II.34 Overall, we find good agreement with experiment from all these forcefields, but OPLS AA/L, derived to fit MC simulations of liquids, was the best. Perhaps more importantly, we find that after equilibration 20 ps of MD leads to deviations in the standard molar entropy of 0.25 cal mol−1 K−1 (or 0.6%).
In the 2PT framework, the heat capacity is calculated (as any other thermodynamic quantity) directly from the DoS by applying the appropriate weighting function. In this paper we show that the calculated molar heat capacities are in very good agreement with experiment and in excellent agreement with other theoretical methods, further validating the 2PT method.
Finally, we present the partition of the total entropy of these solvents into the rotational, translational and internal vibrational components. We find that 46% of the entropy of the liquids arises from translation, 37% from rotation and 17% from intra-molecular vibrations, with large variations depending on the nature of the liquid. This is the first time that such a theoretical component analysis has been reported for these organic liquids. We expect that such analyses may be useful in formulating macroscale methods of estimating entropies of solvation.
Taken together, we demonstrate that the 2PT method can be applied without reparameterization to study liquids, producing precise results from standard molecular dynamics forcefields and simulation codes. The remainder of the paper is organized as follows: Section II presents the major results with discussions. Section III presents the theoretical background of the 2PT method and details for the application to the systems considered here.
II. Results and discussion
II.a Applicability of forcefields for liquid simulations
Table 1 compares the computed static dielectric constants (see Appendix A.II.3 of ESI†) of the 15 liquids in this study. We find that all forcefields (FF) underestimate the dielectric constants, with the magnitude of the error depending on the nature of the solvent. This is expected since these FF all use fixed charges and hence cannot account for the molecular polarizability contribution to the dielectric constant. We plan later to use the QEq method35 to include such polarization effects.| Expa | AMBER 2003b,c,d | Dreidingc,e | GAFF b,c,d | OPLS AA/Lf | |||||
|---|---|---|---|---|---|---|---|---|---|
| a Ref. 64. b Undefined valence and vdW parameters obtained from Antechamber78 atom typing program. c Structures optimized HF/6-31G* level using Jaguar 7.079 electronic structure package. d Charges from RESP37 charge fitting scheme. e Charges from Mulliken population analysis.80 f Parameters and charges from MacroModel 9.7program.81 | |||||||||
| Non-polar | |||||||||
| Benzene | 2.283 | 1.031 | 0.000 | 1.018 | 0.000 | 1.014 | 0.000 | 1.027 | 0.000 |
| Chloroform | 4.807 | 2.136 | 0.000 | 1.738 | 0.000 | 3.236 | 0.001 | 3.636 | 0.001 |
| 1,4-Dioxane | 2.219 | 1.082 | 0.000 | 1.079 | 0.000 | 1.055 | 0.000 | 1.057 | 0.000 |
| furan | 2.940 | 1.232 | 0.001 | 1.160 | 0.000 | 1.668 | 0.000 | 1.534 | 0.000 |
| Toluene | 2.379 | 1.049 | 0.000 | 1.182 | 0.000 | 1.039 | 0.000 | 1.204 | 0.000 |
| M.A.D. | — | 0.456 | — | 0.587 | — | 0.106 | — | 0.078 | 0.456 |
| RMS error | — | 0.626 | — | 0.812 | — | 0.152 | — | 0.103 | 0.626 |
| Polar-aprotic | |||||||||
| Acetonitrile | 36.640 | 18.843 | 0.126 | 17.908 | 0.113 | 22.429 | 0.186 | 14.468 | 0.069 |
| Acetone | 21.100 | 12.319 | 0.047 | 19.535 | 0.138 | 12.343 | 0.048 | 14.417 | 0.069 |
| DMSO | 47.240 | 53.590 | 1.205 | 45.723 | 0.865 | 59.147 | 1.500 | 49.221 | 0.975 |
| THF | 7.520 | 10.263 | 0.030 | 16.701 | 0.095 | 9.487 | 0.023 | 5.340 | 0.005 |
| M.A.D. | — | 8.918 | — | 7.787 | — | 9.211 | — | 7.454 | 8.918 |
| RMS error | — | 11.034 | — | 11.547 | — | 11.599 | — | 10.550 | 11.034 |
| Polar protic | |||||||||
| Acetic acid | 6.200 | — | — | 4.623 | 0.001 | — | — | 4.311 | 0.002 |
| Ethanol | 25.300 | 16.020 | 0.083 | 7.796 | 0.015 | 16.184 | 0.072 | 19.075 | 0.120 |
| Ethylene glycol | 41.400 | 37.212 | 0.514 | 13.284 | 0.042 | 11.708 | 0.013 | 30.389 | 0.350 |
| Methanol | 33.000 | 24.678 | 0.228 | 14.965 | 0.074 | 33.399 | 0.423 | 25.540 | 0.249 |
| NMA | 179.000 | 85.662 | 0.836 | 69.445 | 1.794 | 99.101 | 1.748 | 62.611 | 1.599 |
| TFE | 27.680 | 13.437 | 0.054 | 33.408 | 0.422 | 14.294 | 0.064 | 23.931 | 0.201 |
| M.A.D. | — | 26.986 | — | 27.126 | — | 22.765 | — | 30.645 | 26.986 |
| RMS error | — | 37.883 | — | 41.704 | — | 31.856 | — | 45.148 | 37.883 |
For non-polar solvents, the OPLS AA/L FF has the best performance, with a mean absolute deviation—MAD—error of 0.078 (2.5%) and a root mean squared—RMS—error (a measurement of the variance) of 0.103. The next best is GAFF (3.6% error), the AMBER 2003 FF (15.5%) and finally the Dreiding FF (20%). The excellent performance of OPLS AA/L might be expected since the charges of benzene,10chloroform,10furan36 and toluene10 were explicitly parameterized to reproduce the experimental dielectric properties.
The gas-phase RESP37 charges in GAFF generally are more polar than the solution phase fitted charges in OPLS (Table S1, ESI†). Perhaps unsurprisingly, the calculated gas phase dipole moments (Table 2) are closer to the experimental gas phase values. This relatively good performance of GAFF indicates that these gas phase static charges are transferable for simulations of non-polar liquids, greatly simplifying FF development. The relatively poor performance of the AMBER 2003 FF compared to the GAFF is also not surprising, since the AMBER forcefield was not optimized for simulations of liquids. We find that the Mulliken charges used with the generic Dreiding FF are more polar than the RESP charges of GAFF, leading Dreiding to overestimate the gas phase dipole moments, relative to GAFF and charges that are not transferable to the condensed phase.
| Expa | AMBER 03 | Dreiding | GAFF | OPLS AA/L | |
|---|---|---|---|---|---|
| a Ref. 82. | |||||
| Acetic acid | 1.70 | 1.678 | 2.307 | 1.506 | 1.542 |
| Acetone | 2.88 | 3.226 | 3.608 | 3.194 | 3.111 |
| Acetonitrile | 3.92 | 4.035 | 4.681 | 4.030 | 4.129 |
| Benzene | 0.00 | 0.000 | 0.000 | 0.000 | 0.000 |
| Chloroform | 1.04 | 1.085 | 0.934 | 1.083 | 1.462 |
| 1,4-Dioxane | 0.45 | 0.000 | 0.000 | 0.000 | 0.000 |
| DMSO | 3.96 | 4.933 | 5.450 | 4.711 | 4.700 |
| Ethanol | 1.69 | 1.876 | 1.921 | 1.900 | 2.323 |
| Ethylene glycol | — | 0.000 | 0.000 | 0.000 | 0.000 |
| Furan | — | 0.868 | 0.429 | 0.843 | 0.732 |
| Methanol | 1.70 | 2.150 | 2.060 | 2.177 | 2.274 |
| NMA | 4.04 | 4.414 | 4.881 | 4.378 | 4.030 |
| THF | 1.75 | 2.621 | 3.617 | 2.690 | 1.972 |
| Toluene | 0.36 | 0.211 | 0.606 | 0.221 | 0.566 |
| TFE | — | 3.563 | 4.640 | 3.624 | 4.087 |
The agreement with experimental dielectric constants deteriorates considerably for polar solvents. We find MAD errors of 8.92, 7.79, 9.21 and 7.5 (33%, 28%, 32% and 27%) for the aprotic solvents for the AMBER, Dreiding, GAFF and OPLS, respectively, and significantly worse agreement for the protic solvents, with errors greater than 50% for all but the GAFF forcefield (44%). The largest errors are observed for NMA (the most polar solvent), where the dielectric constant is underestimated by 93.4, 109.6, 80.0 and 116.4 respectively (cf. the experimental value of 179.0). We again attribute these large errors to the lack of charge polarization in these forcefields. Indeed Anisimov et al.38 showed that the dielectric constants of common alcohols are underestimated by 36% using non-polorizable forcefields compared to polarizable forcefields, and that polarizable forcefields show significantly better agreement to experiments.
The AMBER, GAFF and OPLS forcefields slightly underestimate the liquid densities and molar volumes, with average errors of −1.4%, −2.2% and −1.6%, respectively, across all liquids (Table 3). Since the density of the liquid is a parameter used in fitting these forcefields, the better performance compared to the dielectric constant (usually not a fitting parameter except the cases of OPLS outlined above) is to be expected. This indicates that the vdW parameters, and specifically the equilibrium distance R0, are tuned to compensate for inaccuracies in the electrostatics. The Dreiding underestimates the densities by 10%, which might be expected due to the generic nature of this FF. The results obtained here could be used to optimize the Dreiding vdW parameters.
| Density 〈ρ〉/g cm−3 | Molar volumeb〈V〉/cm3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Expc | AMBER 2003 | Dreiding | GAFF | OPLS AA/L | Expc | AMBER 2003 | Dreiding | GAFF | OPLS AA/L | |||||
| a Estimations of the statistical uncertainties are obtained by fluctuation auto-correlation analysis via the estimation of correlation times τ.83 b Calculated from molecular weight. c NIST Reference Database Number 69.64 | ||||||||||||||
| Acetic acid | 1.045 | 1.020 | (99) | 1.047 | (16) | 95.45 | 97.75 | 95.19 | ||||||
| Acetone | 0.785 | 0.757 | (19) | 0.697 | (32) | 0.764 | (31) | 0.777 | (26) | 122.9 | 127.33 | 138.41 | 126.25 | 124.11 |
| Acetonitrile | 0.786 | 0.729 | (18) | 0.730 | (18) | 0.705 | (27) | 0.711 | (71) | 86.75 | 93.53 | 93.37 | 96.62 | 95.92 |
| Benzene | 0.877 | 0.827 | (31) | 0.802 | (54) | 0.796 | (62) | 0.913 | (26) | 147.96 | 156.82 | 161.77 | 162.90 | 141.98 |
| Chloroform | 1.479 | 1.380 | (34) | 1.331 | (55) | 1.412 | (34) | 1.447 | (82) | 134.03 | 143.59 | 148.96 | 140.40 | 136.96 |
| 1,4-Dioxane | 1.034 | 1.088 | (26) | 0.871 | (27) | 1.068 | (37) | 0.987 | (24) | 141.51 | 134.49 | 167.89 | 137.03 | 148.15 |
| DMSO | 1.101 | 1.096 | (28) | 1.089 | (15) | 1.103 | (35) | 1.095 | (23) | 117.82 | 118.38 | 119.09 | 117.59 | 118.42 |
| Ethanol | 0.789 | 0.790 | (27) | 0.642 | (34) | 0.785 | (33) | 0.783 | (18) | 96.90 | 96.83 | 119.11 | 97.38 | 97.66 |
| Ethylene glycol | 1.114 | 1.166 | (12) | 0.997 | (44) | 1.115 | (50) | 1.064 | (24) | 92.55 | 88.38 | 103.31 | 92.38 | 96.83 |
| Furan | 0.951 | 0.959 | (29) | 0.852 | (32) | 0.950 | (32) | 0.972 | (37) | 118.80 | 117.86 | 132.64 | 118.96 | 116.25 |
| Methanol | 0.791 | 0.801 | (27) | 0.644 | (29) | 0.799 | (27) | 0.766 | (24) | 67.22 | 66.42 | 82.62 | 66.57 | 69.49 |
| NMA | 0.937 | 0.954 | (18) | 0.847 | (24) | 0.952 | (21) | 0.952 | (20) | 129.50 | 127.14 | 143.32 | 127.47 | 127.54 |
| THF | 0.883 | 0.909 | (32) | 0.826 | (19) | 0.901 | (43) | 0.786 | (24) | 135.53 | 131.68 | 144.98 | 132.84 | 152.25 |
| Toluene | 0.862 | 0.816 | (23) | 0.782 | (10) | 0.822 | (21) | 0.900 | (33) | 177.41 | 187.47 | 195.57 | 186.09 | 170.06 |
| TFE | 1.384 | 1.300 | (20) | 1.354 | (52) | 119.99 | 127.79 | 122.68 | ||||||
II.b Convergence, efficiency and precision of the 2PT method
Lin et al.24 showed that the entropies predicted with 2PT for a LJ gas converge for just 10 ps of dynamics. To validate the time needed for convergence, we calculated the properties of benzene using OPLS AA/L for 5 independent 1 ns trajectories, calculating the properties for various length trajectories: 1 ps, 4 ps, 10 ps, 20 ps, 40 ps, 100 ps and 200 ps (Fig. 3). We find that by 20 ps the entropy and heat capacity are converged, while the self-diffusivity took 50 to 100 ps to converge (Fig. S1, ESI†). This convergence in the thermodynamic quantities is consistent with a recent study of Lin et al.39 that found that the entropy of liquid water converges after 10 to 50 ps.Due to the short 20 ps trajectories required and the efficiency of FFTs, the 2PT calculations presented here require only a trivial increase in additional computation time. This allows one to calculate the system thermodynamics on-the-fly during dynamics. Such calculations provide a rigorous check of numerical stability and precision of the method.
Fig. 4 reports the standard molar entropies and heat capacities for acetic acid, benzene and DMSO with OPLS AA/L. Here, we used the last 20 ps of dynamics to evaluate the thermodynamic properties every 100 ps during the 2.5 ns dynamics, for a total of 25 data points. Convergence is observed after only 300 ps of equilibration, with fluctuations of 0.36 cal mol−1 K−1 in specific heat (0.6%). This indicates that 2PT gives robust and precise thermodynamic quantities from short MD trajectories. The additional simulation and computational time is also minimal, with the trajectories generated automatically during regular dynamics and the post trajectory analysis taking less than 2% of the total simulation time. For example, the total time to simulate 512 molecules of benzene for 2.5 ns with LAMMPS took approximately 110 CPU hours on a 3.2 GHz Intel Xenon processor, while the additional analysis of the 25 NVT trajectories to obtain the 2PT prediction took an additional 16 minutes (0.2%). Further, the average values of the entropy and heat capacity calculated every 500 ps (5 trajectories) are within 0.1% of the average calculated every 100 ps, showing that accurate thermodynamics can be obtained from uncorrelated or correlated trajectories.
In all our simulations, we chose not to constrain the motion of the hydrogen atoms by the SHAKE40 algorithm, as is commonly the practice in the AMBER/GAFF and OPLS forcefields. While these constraints would presumably not affect the dynamics,41 the calculated thermodynamics depends on integrating over the entire DoS, thus SHAKE might affect the thermodynamics. Conversely, the high frequency of the vibrations may render any effect due to SHAKE minimal, as high frequency modes contribute exponentially less to the thermodynamics than low frequency modes. We note however that the 2PT formalism allows for accurate calculation of thermodynamic quantities regardless of external constraints, by accounting for the removed degrees of freedom (Dof): the Dof is used to calculate the system's temperature from the atomic velocities.
II.c Comparison of standard molar entropies vs. experiment
Fig. 5 and Table 4 present the standard molar entropies S0. Contributions due to configurational entropy are included by statistical averaging over 5 discrete and uncorrelated microstates, obtained from 20 ps trajectories every 500 ps of the 2.5 ns dynamics, as described previously. Effects due to configurational changes are captured in the diffusive component and explicitly included in our model.| Solvent | Expa | Best estimatec | AMBER 03 | Dreiding | GAFF | OPLS AA/L | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg | ± | Avg | ± | Avg | ± | Avg | ± | |||
| a NIST Reference Database Number 69. 64 b Mean absolute deviation. c No experimental values are available for chloroform, NMA and TFE. We estimate their values here but subtracting the average error from the calculated OPLS AA/L values. | ||||||||||
| Acetic acid | 37.76 | 32.23 | 0.25 | 37.79 | 2.35 | 30.67 | 0.17 | 35.13 | 0.22 | |
| Acetone | 47.90 | 44.72 | 0.15 | 44.26 | 0.26 | 44.79 | 0.21 | 47.27 | 0.08 | |
| Acetonitrile | 35.76 | 38.06 | 0.15 | 34.08 | 0.21 | 34.75 | 0.28 | 33.99 | 0.22 | |
| Benzene | 41.41 | 40.58 | 0.22 | 39.01 | 0.25 | 38.37 | 0.52 | 41.19 | 0.16 | |
| 1,4-Dioxane | 46.99 | 39.47 | 0.22 | 41.71 | 0.27 | 38.00 | 0.20 | 42.82 | 0.26 | |
| DMSO | 45.12 | 39.57 | 0.25 | 38.71 | 0.13 | 37.99 | 0.24 | 39.10 | 0.12 | |
| Ethanol | 38.21 | 33.92 | 0.33 | 41.97 | 0.13 | 30.36 | 0.13 | 33.63 | 0.16 | |
| Ethylene glycol | 39.89 | 30.43 | 0.05 | 40.13 | 0.31 | 28.95 | 0.18 | 33.62 | 0.16 | |
| Furan | 42.22 | 39.09 | 0.00 | 38.88 | 0.38 | 37.60 | 0.25 | 40.03 | 0.23 | |
| Methanol | 30.40 | 28.61 | 0.10 | 25.87 | 0.26 | 26.13 | 0.12 | 29.12 | 0.08 | |
| THF | 48.71 | 41.89 | 0.22 | 48.45 | 0.12 | 38.01 | 0.18 | 46.96 | 0.28 | |
| Toluene | 52.81 | 48.98 | 0.23 | 45.91 | 0.24 | 45.30 | 0.19 | 48.67 | 0.23 | |
| M.A.D.b | 2.39 | 2.48 | 2.62 | 1.72 | ||||||
| Avg. error | −4.13 | −2.53 | −6.36 | −2.97 | ||||||
| RMS error | 3.17 | 3.12 | 3.15 | 2.03 | ||||||
| R 2 | 0.75 | 0.74 | 0.76 | 0.90 | ||||||
| Chloroform | 43.01 | 47.47 | 0.10 | 47.44 | 0.30 | 53.88 | 0.22 | 45.98 | 0.31 | |
| NMA | 40.23 | 41.86 | 0.29 | 33.51 | 0.24 | 40.18 | 0.14 | 43.20 | 0.07 | |
| TFE | 43.54 | 48.54 | 0.30 | 46.07 | 0.08 | 44.30 | 0.23 | 46.51 | 0.22 | |
All FF underestimate S0, with average errors of −4.13, −2.12, −6.36, −2.97 cal mol−1 K−1 for AMBER 2003, Dreiding, Gaff and OPLS AA/L, respectively, or approximately 5 to 15%. As was the case with the dielectric constant, the largest discrepancy occurs in the polar solvents, in particular ethylene glycol (average of 16% error) and DMSO (average of 15% error). This may again point to the deficiency of using a fixed charge model, since the diffusion constant of other liquids42 is known to be also affected by the lack of polarization. Self-diffusion and other low frequency librational modes contribute most to the entropy calculated from approaches that rely on the DoS such as 2PT.
While none of the forcefields reproduce the experimental S0, the OPLS forcefield shows the best overall correlation with experiment, with a 1.72 cal mol−1 K−1MAD and a 90% correlation. Particularly exciting here is the performance of the Dreiding forcefield (2.5 cal mol−1 K−1MAD and 74% correlation), since no parameters related to the thermodynamics of liquids were used in determining the forcefield parameters. The AMBER and GAFF forcefields have performance similar to Dreiding: 2.39 and 2.67 cal mol−1 K−1MAD and 75% and 76% correlation respectively. We find that 2PT predicts standard molar entropies of these pure liquids to within 0.25 cal mol−1 K−1 (0.6%) standard deviation over all forcefields.
Since there are no experimental standard molar entropy values for chloroform, NMA and TFE, we provide here a priori predictions based on the OPLS AA/L forcefield average error of −2.97 cal mol−1 K−1: 43.01 for chloroform, 40.23 for NMA and 43.54 cal mol−1 K−1 for TFE.
II.d Comparison of molar heat capacities vs. experiment
In 2PT we prefer to keep the volume constant (NVT MD) leading to Cv and Helmholtz free energies, because we consider this to be the least ambiguous framework for describing the DoS. However experiments are generally carried out under conditions of NPT, leading to Cp and Gibbs free energies. To compare the Cv from 2PT to the Cp from experiment, we apply a correction: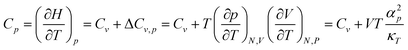 | (1) |
Overall, all forcefields reproduce the experimental heat capacities to within 5%. More importantly, the values calculated using the 2PT approach show a 96% correlation to the approach used by Jorgensen and coworkers9,10,12,13,36,43 with the OPLS forcefield, which was based on extensive Monte Carlo sampling. This validates that 2PT can capture the essential physics in these systems from short 20 ps MD trajectories. Further, the statistical deviations in our calculated heat capacities are 0.2 cal mol−1 K−1, or 0.5% (Table 5).
| Expb | Best Estimate | AMBER 2003 | Dreiding | GAFF | OPLS AA/L | Other calculated values | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg | ± | Avg | ± | Avg | ± | Avg | ± | ||||
| a C p is obtained from the calculated Cv by eqn (1). The corrections to the heat capacity ΔCv are all <0.25 cal mol−1 K−1 (Table S4, ESI1). b NIST Reference Database Number 69. 64 | |||||||||||
| Acetic acid | 29.42 | 26.44 | 0.76 | 26.76 | 0.12 |
26.069
29.484 30.643 |
|||||
| Acetone | 29.98 | 29.37 | 0.10 | 28.29 | 0.12 | 29.31 | 0.14 | 30.88 | 0.13 | 30.284 | |
| Acetonitrile | 21.91 | 23.38 | 0.07 | 22.90 | 0.10 | 20.75 | 0.23 | 19.45 | 0.09 | 19.4312 | |
| Benzene | 32.43 | 29.35 | 0.21 | 26.73 | 0.13 | 23.52 | 0.25 | 30.73 | 0.17 |
31.210
31.884 |
|
| Chloroform | 27.31 | 26.10 | 0.18 | 25.16 | 0.17 | 30.23 | 0.09 | 25.18 | 0.17 | — | |
| 1,4-Dioxane | 35.77 | 34.32 | 0.13 | 33.00 | 0.07 | 33.15 | 0.27 | 36.74 | 0.18 | 36.085 | |
| DMSO | 35.71 | 31.39 | 0.17 | 30.80 | 0.14 | 30.64 | 0.13 | 32.15 | 0.14 |
36.086
34.7587 |
|
| Ethanol | 26.86 | 24.82 | 0.26 | 24.41 | 0.13 | 23.46 | 0.11 | 26.03 | 0.12 |
26.113
23.988 |
|
| Ethylene | |||||||||||
| glycol | 35.80 | 28.39 | 0.09 | 27.88 | 0.15 | 27.38 | 0.20 | 29.98 | 0.15 | — | |
| Furan | 27.38 | 24.91 | 0.10 | 23.24 | 0.14 | 22.07 | 0.16 | 26.22 | 0.08 | 26.6836 | |
| Methanol | 19.00 | 18.69 | 0.19 | 18.46 | 0.16 | 18.07 | 0.17 | 19.37 | 0.09 |
20.013
26.043 22.588 |
|
| THF | 29.66 | 30.81 | 0.14 | 28.91 | 0.12 | 29.31 | 0.09 | 33.33 | 0.20 | 31.943 | |
| Toluene | 37.55 | 37.40 | 0.15 | 33.87 | 0.10 | 31.19 | 0.11 | 39.08 | 0.14 | — | |
| M.A.D. | 1.93 | 2.02 | 2.62 | 2.00 | |||||||
| Avg. error | −1.75 | −3.05 | −3.93 | −0.90 | |||||||
| RMS error | 3.01 | 3.84 | 4.92 | 2.62 | |||||||
| R 2 | 0.79 | 0.78 | 0.70 | 0.83 | |||||||
| NMA | 36.60 | 34.49 | 0.12 | 32.76 | 0.13 | 33.10 | 0.09 | 35.70 | 0.07 | 39.743,63 | |
| TFE | 36.46 | 35.39 | 0.16 | 35.23 | 0.09 | 34.54 | 0.10 | 35.56 | 0.14 | — | |
II.e Components of liquid entropy
An attractive feature of 2PT is the facility to separate the individual components of the entropy as detailed in Section III.c.ii. We performed this decomposition for all the liquids, with the OPLS AA/L forcefield (Table 6). Here we find the ratio of the contributions to the entropy of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 for valence vibrations
5 for valence vibrations![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rotation
rotation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) translation across all molecules, leading to a non-negligible contribution of 17% to the entropy from the internal vibrations. As expected, the vibrational entropy is greatest for the large flexible solvents (31%, 24% and 21% for NMA, TFE and ethylene glycol respectively) and least for the small rigid solvents (3% and 6% for acetonitrile and methanol respectively). Since the vibrational component of the total DoS is analogous to the experimental IR and Raman spectra, forcefields that more closely reproduce the experimental vibrational frequencies should lead to improved entropies. For illustrative purposes, we show the vibrational DoS for chloroform using the OPLS AA/L forcefield in Fig. 2b. The vibrational frequencies are on average 15 cm−1 too low, which we estimate would account for a 1–2 cal mol−1 K−1 (2%) increase in the total entropy.
translation across all molecules, leading to a non-negligible contribution of 17% to the entropy from the internal vibrations. As expected, the vibrational entropy is greatest for the large flexible solvents (31%, 24% and 21% for NMA, TFE and ethylene glycol respectively) and least for the small rigid solvents (3% and 6% for acetonitrile and methanol respectively). Since the vibrational component of the total DoS is analogous to the experimental IR and Raman spectra, forcefields that more closely reproduce the experimental vibrational frequencies should lead to improved entropies. For illustrative purposes, we show the vibrational DoS for chloroform using the OPLS AA/L forcefield in Fig. 2b. The vibrational frequencies are on average 15 cm−1 too low, which we estimate would account for a 1–2 cal mol−1 K−1 (2%) increase in the total entropy.
| Standard molar entropy S0/cal mol−1 K−1 | Fluidicity factor | D × 10−5/cm2 s−1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S vib | S rot | S trans | f trans | f rot | MSD a | GK b | Expc | ||||
| Avg | ± | Avg | ± | Avg | ± | ||||||
| a Calculated from mean squared deviation—equation A.II.2a, ESI†. b Calculated from Green–Kubo formalism—equation A.II.2b, ESI†. c Ref. 92–94. d Values for F3C, SPC/E and TIP4P-Ew below taken from ref. 39. | |||||||||||
| Acetic acid | 6.28 | 0.06 | 13.38 | 0.08 | 15.48 | 0.10 | 0.16 | 0.12 | 1.03 | 1.18 | |
| Acetone | 11.08 | 0.04 | 16.84 | 0.04 | 19.35 | 0.05 | 0.34 | 0.29 | 4.39 | 5.09 | |
| Acetonitrile | 0.93 | 0.02 | 13.86 | 0.08 | 19.20 | 0.14 | 0.40 | 0.30 | 7.25 | 7.93 | |
| Benzene | 4.74 | 0.06 | 16.63 | 0.06 | 19.83 | 0.09 | 0.30 | 0.29 | 3.45 | 3.77 | |
| Chloroform | 5.65 | 0.02 | 19.20 | 0.15 | 21.12 | 0.16 | 0.33 | 0.30 | 3.22 | 3.76 | |
| 1,4-Dioxane | 8.43 | 0.05 | 16.43 | 0.09 | 17.97 | 0.15 | 0.20 | 0.20 | 1.69 | 1.82 | |
| DMSO | 8.87 | 0.06 | 13.93 | 0.08 | 16.31 | 0.10 | 0.16 | 0.13 | 0.63 | 1.09 | |
| Ethanol | 4.51 | 0.01 | 13.16 | 0.06 | 15.95 | 0.09 | 0.20 | 0.15 | 1.54 | 1.82 | |
| Ethylene glycol | 6.94 | 0.02 | 12.03 | 0.08 | 14.66 | 0.08 | 0.16 | 0.10 | 0.33 | 0.39 | |
| Furan | 3.40 | 0.04 | 16.76 | 0.12 | 19.87 | 0.12 | 0.35 | 0.30 | 3.55 | 4.85 | |
| Methanol | 1.71 | 0.01 | 11.38 | 0.04 | 16.03 | 0.06 | 0.32 | 0.20 | 3.39 | 3.68 | 2.2 |
| NMA | 13.29 | 0.01 | 13.59 | 0.04 | 16.32 | 0.03 | 0.21 | 0.10 | 1.52 | 1.73 | 1.2 |
| THF | 9.01 | 0.06 | 17.90 | 0.07 | 20.05 | 0.15 | 0.33 | 0.31 | 3.92 | 4.63 | |
| Toluene | 11.45 | 0.09 | 17.45 | 0.07 | 19.77 | 0.11 | 0.26 | 0.23 | 2.75 | 3.00 | |
| TFE | 11.21 | 0.04 | 16.54 | 0.11 | 18.75 | 0.12 | 0.20 | 0.16 | 1.32 | 1.56 | 0.6 |
| Water d | |||||||||||
| F3C 89 | 0.04 | 0.00 | 11.54 | 0.06 | 50.50 | 0.25 | 0.25 | 0.06 | |||
| SPC/E90 | — | — | 12.03 | 0.03 | 53.05 | 0.14 | 0.29 | 0.07 | |||
| TIP4P-Ew 91 | — | — | 9.53 | 0.07 | 49.79 | 0.07 | 0.24 | 0.05 | |||
The almost 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 partition between the translational and rotational entropies is in contrast with the case of water, where a ratio of 2
1 partition between the translational and rotational entropies is in contrast with the case of water, where a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was obtained by Henchman44 and 4
1 was obtained by Henchman44 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 from Lin et al.39 The liquids considered here are significantly larger than water, with far weaker hydrogen bonds, in the case of the polar protic solvents. Consequently, the rotations in these systems are not as hindered as in water, which has been shown to reorganize by a jump rather than continuous mechanism.45–47 Lower frequency rotations contribute more to the total entropy than higher frequency rotations and the “solid-like” rotations (hindered-rotors) contribute at least 70% to the rotational entropy, as determined by the rotational fluidicity factor frot (Table 6).
1 from Lin et al.39 The liquids considered here are significantly larger than water, with far weaker hydrogen bonds, in the case of the polar protic solvents. Consequently, the rotations in these systems are not as hindered as in water, which has been shown to reorganize by a jump rather than continuous mechanism.45–47 Lower frequency rotations contribute more to the total entropy than higher frequency rotations and the “solid-like” rotations (hindered-rotors) contribute at least 70% to the rotational entropy, as determined by the rotational fluidicity factor frot (Table 6).
We find a large correlation (85%) between the translation entropy and the self-diffusion constants, which is not surprising as the low frequency librational modes contribute most to the translational (as well as the overall) entropy. We note that the translational entropy includes components due to pure diffusion (a hard-sphere gas) as well as solid-like translations, as determined by the fluidicity parameter ftrans (Table 6). The fraction of the translational degrees of freedom that are diffusional range from 0.16 for DMSO to 0.35 for furan, thus over 65% of the translational entropy arises from solid-like translation.
We find that 2PT is somewhat insensitive to the self-diffusion constant. The self-diffusion constants for all 15 liquids are calculated over the 20 ps trajectory using the Green–Kubo (GK) approach (equation A.II.2b, ESI†). This can be compared to the more common mean-squared displacement (MSD) approach, which is evaluated over the entire 2.5 ns MD. We find that the GK diffusion constants are not converged (as noted previously, convergence is only obtained after ∼100 ps) and are 19% higher than the converged MSD diffusion constants. Additionally, both methods overestimate the experimental diffusion constants by 90%, for the 3 of the 15 liquids for which such experimental self-diffusion constants are available. In spite of these errors, the standard molar entropies show good agreement with experiment.
To examine one specific example, consider methanol. The diffusion constant is overestimated by 112% using GK and 82% using MSD, compared to experiments. Since translations contribute 55% to the total entropy, errors due to overestimating the diffusion constant could be significant. However, the calculated entropy of methanol with OPLS AA/L of 29.12 cal mol−1 K−1 is in excellent agreement with the experimental value of 30.40 cal mol−1 K−1. This indicates that the rotational and internal vibrational entropies are correspondingly underestimated, but only by 10%, as diffusion only contributes 19% to the translational entropy.
It would thus be practical to use such 2PT calculations for entropy (the enthalpy/internal energy can also be evaluated in the same framework) to refine the forcefield against accurate experimental data at room temperature. Usually, forcefields are fitted to data at 0 K, say from QM, leading usually to poor equilibrium densities at 300 K. A possible improvement would be to use 2PT to match the experimental thermodynamics and the bulk properties simultaneously. Of course, since 2PT needs only ∼20 ps of MD, it could also be used with ab initioQM MD to avoid forcefields all together. However most QM methods have difficulty in describing the London dispersion (van der Waals attraction)48–50 so important in molecular solvents.
II.f Comparisons to previous methods
There has been no comprehensive study of the entropy of the 15 pure liquids presented here using alternative methods. There has however been considerable computational effort dedicated towards calculating accurate entropies of water: the simplest liquid and most important solvent. White and Meirovitch51,52 used a hypothetical scanning method to determine the absolute entropy and free energy and obtained excellent agreement to experiments. Lazaridis and Karplus53 later obtained standard molar entropies of water using truncated expansion of molecular pair correlation functions,54 and Sharma et al.55 using the atom–atom pair correlation function. Tyka et al.56 demonstrated the determination of absolute entropy of water using thermodynamic integration with a harmonic reference state. More recently, Henchman57 proposed a cell theory which provides reliable entropies of liquid water based on harmonic approximations.In spite of the good agreements to experiment, it is not clear how these newer methods would be applied to systems other than water.39 Further, asymmetry in hydrogen bonding may dictate that the simple harmonic approximations of these methods break down for conditions other than the ambient ones considered. Finally, except for the Cell Method of Henchman,57 the computational cost of the aforementioned approaches would still be prohibitive for studying large biomolecular systems.
A recent study by Lin et al.39 showed that 2PT is accurate in predicting the absolute thermodynamics of liquid water and vapor phases along the vapor–liquid equilibrium curve, from the triple point to the critical point. 2PT achieves the same accuracy as other more common methods, while being orders of magnitude more efficient.
III. Computational methods
The standard molar entropy S0, molar heat capacity Cp and heat of vaporization ΔHvap are the three important observables used to characterize the thermodynamics of condensed phase systems. We have devoted most of our efforts in presenting the results of S0 which we calculate self-consistently from the dynamics, since it is an exact quantity that does not rely on a predefined reference state.58–60 We note that S0 is not directly accessible to methods such as umbrella sampling14 and thermodynamic integration,4 which provide the more familiar change in entropy ΔS.61Since the Cp tests the response of the entropy to small changes in temperature, we presented our predictions of Cp, directly from the DoS. This was compared to experiments and to other theoretical studies that are based on either numeric differentiation of simulated enthalpies over a range of temperatures or on Kirkwood type fluctuation analysis,62 both of which require much longer trajectories. We also calculated ΔHvap, though since this has been characterized for these systems in other studies,9,10,12,13,36,43,63 we do not discuss these results in the text. For completeness, the calculated ΔHvap for all 15 liquids is presented in Table S2 (ESI†).
Finally, we evaluated the various nonbonded parameters of each forcefield by calculating physical properties that are sensitive to variations therein: density, self-diffusion constant, static dielectric constant, isothermal compressibility and coefficient of thermal expansion. The methods used to obtain these measures are detailed in Appendix II.2 of ESI.†
III.a Choice of liquids and forcefields
We classify organic liquids into three broad categories, according to their dielectric constants (Table 1), miscibility in water, and their ability to participate in hydrogen bonding:1. Non-polar—low dielectric constant/not miscible in watere.g.benzene.
2. Polar aprotic—low dielectric constant/miscible in water/cannot hydrogen-bond (HB) e.g.acetone.
3. Polar protic—high dielectric constant/miscible in water/can HB e.g.acetic acid.
We selected 15 of the most common solvents used in organic reactions (Fig. 1) to test the accuracy of the various forcefields. Eleven of these liquids have high quality S0 measurements from experiment.64 The remaining three (chloroform, NMA and 2,2,2-triflouroethanol—TFE) were presented here as a priori predictions.
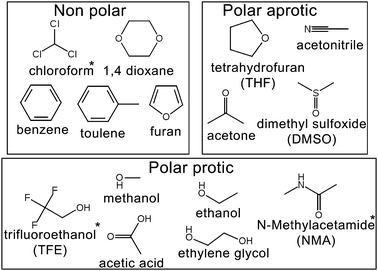 | ||
| Fig. 1 The 15 organic liquids used in this study. Molecules with * symbol (TFE, chloroform and NMA) have no experimentally determined standard molar entropies and are presented here as a proiri predictions. | ||
![(a) Velocity autocorrelation function (VACF) of chloroform from 20 ps NVT MD, using the OPLS AA/L forcefield. (b) The corresponding density of states (DoS), obtained from the Fourier Transform of the VACF. The 6 valence infrared and Raman active modes (a1: 3001 cm−1 C–H stretch, 634 cm−1CCl3 symmetric stretch and 301 cm−1CCl3 symmetric deform. e: 1355 cm−1 CH bend, 875 cm−1CCl3 asymmetric stretch and 239 cm−1CCl3 asymmetric deform) are labeled. These can be compared to 3034, 680, 363, 1220, 774 and 261 from experiment.95 (c) The 2PT partitioning of the translational component of the DoS into the solid (DoSsolid) and gas (DoSdiffuse) components. Note that DoSvib = 0 at v = 0, while the gas component has value DoS(0) = 32.4 at v = 0 and smoothly decays to 0 over 150 cm−1. The fraction of the modes in the gas phase (the f—fludicity—factor), and hence the rate of decay of DoSdiffuse, is determined self-consistently from the diffusivity of the systems (f = 0.32 in this system). The f factor and DoS(0) parameters of the 2PT method are extracted directly from the MD trajectory. (d) The low frequency librational modes (0–250 cm−1) including the translational DoStrans and rotational DoSrot components (log scale). Here, the value of the DoS at v = 0 [DoS(0)] = 32.4, which would lead to an infinite contribution to the entropy if the harmonic approximation was employed. The thermodynamic properties of the system are obtained by applying the 2PT correction and integrating over the DoS with the appropriate weighting functions.](/image/article/2011/CP/c0cp01549k/c0cp01549k-f2.gif) | ||
| Fig. 2 (a) Velocity autocorrelation function (VACF) of chloroform from 20 ps NVT MD, using the OPLS AA/L forcefield. (b) The corresponding density of states (DoS), obtained from the Fourier Transform of the VACF. The 6 valence infrared and Raman active modes (a1: 3001 cm−1 C–H stretch, 634 cm−1CCl3 symmetric stretch and 301 cm−1CCl3 symmetric deform. e: 1355 cm−1 CH bend, 875 cm−1CCl3 asymmetric stretch and 239 cm−1CCl3 asymmetric deform) are labeled. These can be compared to 3034, 680, 363, 1220, 774 and 261 from experiment.95 (c) The 2PT partitioning of the translational component of the DoS into the solid (DoSsolid) and gas (DoSdiffuse) components. Note that DoSvib = 0 at v = 0, while the gas component has value DoS(0) = 32.4 at v = 0 and smoothly decays to 0 over 150 cm−1. The fraction of the modes in the gas phase (the f—fludicity—factor), and hence the rate of decay of DoSdiffuse, is determined self-consistently from the diffusivity of the systems (f = 0.32 in this system). The f factor and DoS(0) parameters of the 2PT method are extracted directly from the MD trajectory. (d) The low frequency librational modes (0–250 cm−1) including the translational DoStrans and rotational DoSrot components (log scale). Here, the value of the DoS at v = 0 [DoS(0)] = 32.4, which would lead to an infinite contribution to the entropy if the harmonic approximation was employed. The thermodynamic properties of the system are obtained by applying the 2PT correction and integrating over the DoS with the appropriate weighting functions. | ||
![The molar heat capacity Cv (squares) and standard molar entropy S0 (circles) of benzene using the OPLS AA/L forcefield. The left y-axis is the Cv, the right y-axis is the S0 and the x-axis is the log scale of the trajectory length. Convergence in both thermodynamic quantities is observed from 20 ps trajectories. The uncertainty in the measurements [0.14 cal mol−1 (0.6%) for Cv and 0.25 cal mol−1 K−1 (0.7%) for S0] is obtained from 5 independent trajectories and scale by a factor of 5 for presentation purposes.](/image/article/2011/CP/c0cp01549k/c0cp01549k-f3.gif) | ||
| Fig. 3 The molar heat capacity Cv (squares) and standard molar entropy S0 (circles) of benzene using the OPLS AA/L forcefield. The left y-axis is the Cv, the right y-axis is the S0 and the x-axis is the log scale of the trajectory length. Convergence in both thermodynamic quantities is observed from 20 ps trajectories. The uncertainty in the measurements [0.14 cal mol−1 (0.6%) for Cv and 0.25 cal mol−1 K−1 (0.7%) for S0] is obtained from 5 independent trajectories and scale by a factor of 5 for presentation purposes. | ||
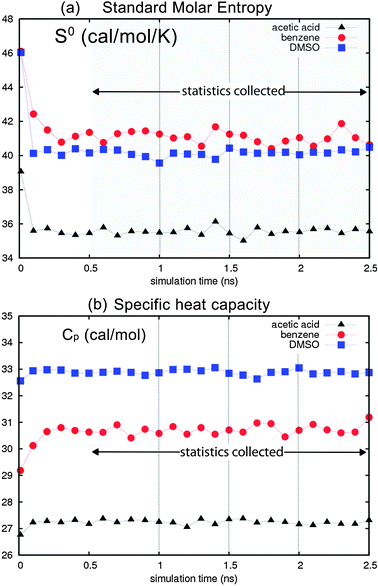 | ||
| Fig. 4 (a) Standard molar entropy S0 for acetic acid (triangles), benzene (circles) and DMSO (squares) using the OPLS AA-L forcefield, evaluated every 100 ps during 2.5 ns dynamics. (b) Molar heat capacity Cp convergence is observed after 500 ps, validating the simulation protocol. Statistics are obtained every 500 ps after equilibration; the average calculated from the 5 discrete points is within 0.1% of the running average calculated every 100 ps. We find average fluctuations in S0 of 0.36 cal mol−1 K−1 (0.9%) and in Cp of 0.12 cal mol−1 K−1 (0.6%). | ||
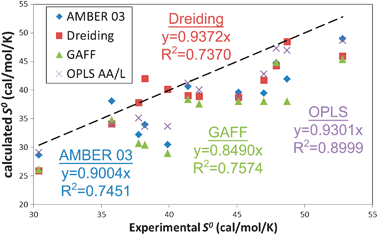 | ||
| Fig. 5 Comparison of experimental and calculated standard molar entropies S0 (cal mol−1 K−1) for 12 of the 15 liquids in this study. No experimental data are available for chloroform, NMA and TFE; the calculated values of 43.01, 40.23 and 43.54 cal mol−1 K−1, respectively, are presented as a prori predictions. The precision in the calculated values is ∼0.25 cal mol−1 K−1. The dashed line indicates exact matching between simulation and experiment. All four of the forcefields underestimate S0. The OPLS AA/L forcefield provides the best performance with a 90% correlation. The generic Dreiding forcefield (74%) is as accurate as the AMBER class of forcefields. | ||
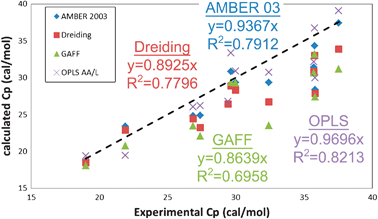 | ||
| Fig. 6 Comparison of constant pressure heat capacity Cp (cal mol−1) for the 12 liquids with experimental data. The dashed black line indicates exact matching between simulation and experiment. The Cp is obtained from the calculated Cv according to eqn (1) (see Table S4, ESI†). The OPLS AA/L forcefield provides the best agreement with experiment, with a correlation coefficient of 82%, while the GAFF forcefield has the worse agreement (70%). | ||
The non-polar liquids provide a rigorous test of the van der Waals (vdW) parameters, the polar protic molecules test primarily the atom centered charges and any effect due to the missing charge polarization, while the polar aprotic molecules is a good test of both and the accuracy of the HB description in the FF. We include four flexible liquids (NMA, TFE, ethylene glycol and ethanol) in our test set. Accurate determination of the thermodynamics of flexible molecules is more computationally challenging than rigid molecules, due to the need for extensive torsional sampling. The selected molecules thus provide simultaneously a rigorous test of the precision of the 2PT method and the accuracy of the forcefields.
The four forcefields in this study are commonly used for biomolecular simulations and solvation calculations, thus their ability to reproduce the experimental S0 and Cp is of interest:
(a) AMBER 200330,31—the AMBER99 forcefield, with the PARMBSC031 modifications, is a standard for molecular simulations of proteins and nucleic acids.
(b) GAFF32—the General Amber Forcefield was created for rational drug design and simulations of small organic molecules.
(c) OPLS AA/L11,33—a variant of the all atom OPLS all atom forcefield, parameterized to reproduce the solvation free energies of various organic liquids from Monte Carlo simulations.
(d) Dreiding34—a generic forcefield useful for predicting structures and dynamics of organic, biological, and main-group inorganic molecules.
Dreiding is the simplest of the forcefields considered here, with just seven parameters to describe all valence interactions. Dreiding is also the only forcefield with an explicit three-body hydrogen bonding term (see Appendix I (ESI†) for the description of the forcefields).
III.b Liquid simulations
All simulations were performed using the LAMMPS65,66 simulation engine, which affords the flexibility of using various forcefields in a common framework (we modified LAMMPS to include the full Dreiding FF, including 3-body HB). Long-range coulombic interactions were calculated using the particle–particle particle–mesh Ewald method67 (with a precision of 10−5 kcal mol−1), while the van der Waals interaction was computed with a cubic spline (an inner cutoff of 11 Å and an outer cutoff of 12 Å). We used the spline to guarantee that the energies and forces go smoothly to zero at the outer cutoff, preventing energy drifts that might arise from inconsistent forces. We also tested the effect of the cutoff by computing the energy of benzene with cutoffs ranging from 8 to 20 Å and found converged results at 12 Å.For each system, we used the Continuous Configurational Boltzmann Biased (CCBB) Monte Carlo (MC) method68,69 to generate a random starting structure of 512 solvent molecules packed to minimize the system interaction energy. To rapidly equilibrate the systems, we used our standard procedure:70–72 after an initial conjugant gradient minimization to an RMS force of 10−4 kcal mol−1 Å−1, the system was slowly heated from 0 K to 298 K over a period of 100 ps using a Langevin thermostat in the constant temperature, constant volume canonical (NVT) ensemble. The temperature coupling constant was 0.1 ps and the simulation timestep was 1.0 fs.
This equilibration was followed by 1 ns of constant-pressure(iso-baric), constant-temperature (NPT) dynamics at 298 K and 1 atm. The temperature coupling constant was 0.1 ps while the pressure piston constant was 2.0 ps. The equations of motion used are those of Shinoda et al.,73 which combine the hydrostatic equations of Martyna et al.74 with the strain energy proposed by Parrinello and Rahman.75 The time integration schemes closely follow the time-reversible measure-preserving Verlet integrators derived by Tuckerman et al.76 Production dynamics was then run for a further 2.5 ns in the NPT ensemble, with coordinates and velocities saved every 4 ps for post-trajectory analysis.
III.c Obtaining thermodynamic properties: the 2PT method
The 2PT-MD method uses the following protocol to obtain free energies from the 2.5 ns of NPT MD: we analyzed the trajectory in 500 ps blocks and selected the snapshot with volume closest to the average value. Then using the coordinates and dynamics from this snapshot we ran a short 20 ps NVT MD, saving the coordinates and velocities every 4 fs (needs to be shorter than the fastest vibrational levels which have periods of ∼10 fs for a 3000 cm−1 vibration), for a total of 5000 structures. The quoted thermodynamic values are taken as the statistical average over these 5 trajectories.For each 20 ps trajectory, we calculated the velocity autocorrelation function (VAC) for each atom,
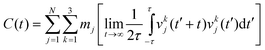 | (2) |
The total density of states (DoS) DoS(v) (also referred to as the power spectrum or spectral density) is obtained from a fast Fourier Transform (FFT) of eqn (2) (Fig. 2):
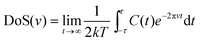 | (3) |
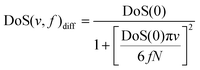 | (4) |
(1) the total DoS(0) at υ = 0, this is,
| DoS(0) = DoS(0)diff | (5) |
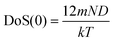 , where N is the number of molecules in the system and m is the mass of a molecule], and
, where N is the number of molecules in the system and m is the mass of a molecule], and
(2) the “fluidicity” parameter f, which is the fraction of the 3Ntranslation or rotation modes corresponding to the fluid or diffusional parts of the dynamic system, i.e.
| ∫∞0 DoS(v,f)diff dv = 3 fN | (6) |
| 2Δ−9/2f15/2 − 6Δ−3f5 − Δ−3/2f7/2 + 6Δ−3/2f5/2 + 2f − 2 = 0 | (7) |
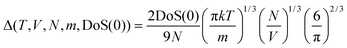 | (8) |
| ln Q = ∫∞0DoS(v)solidqHO(v)dv | (9) |
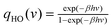 is the quantum harmonic oscillator partition function, β = 1/kT and h the Planck's constant. S0 and Cv are then obtained directly from the standard statistical mechanical expressions:
is the quantum harmonic oscillator partition function, β = 1/kT and h the Planck's constant. S0 and Cv are then obtained directly from the standard statistical mechanical expressions: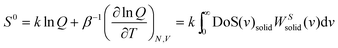 | (10a) |
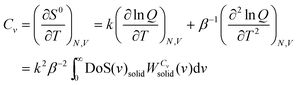 | (10b) |
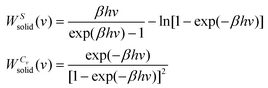 | (11) |
The total standard molar entropy and heat capacity are then obtained as:
| S0 = k∫∞0 [DoS(v)diffWSdiff(v) + DoS(v)solidWSsolid(v)]dv | (12a) |
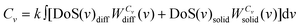 | (12b) |
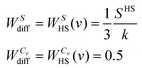 | (13) |
• Strans: the center of mass translational contribution to the total velocity (Vtrans) (for molecule i and total mass Mi) is obtained as the center of mass velocity of that molecule:
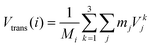 | (14) |
• Srot: the rotational contribution (Vrot) is obtained by calculating the angular velocity (Vang), treating the system as a quantum rigid rotor:
| Vrot(i) = ω(i) × Vtot(i) | (15a) |
| ω(i) = I−1i × L(i) | (15b) |
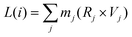 | (15c) |
The rotational entropy is obtained by substituting Vang into eqn (2), with weighting functions:
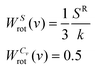 | (16) |
• Svib: the internal vibrational component (Vvib) to the velocity is taken as the remaining velocity after subtracting the first two contributions: Vvib(i) = Vtot(i) − [Vtrans(i) + Vrot(i)]. The vibrational entropy is obtained by substituting Vvib into eqn (2). There is no decomposition of the DoS here, as DoSvib(v) has no diffusional component (i.e. the fluidicity is zero).
IV. Conclusions
We have characterized the thermodynamics of 15 pure organic liquids using the 2PT method. Good agreement with experiment is obtained in the calculated standard molar entropies and excellent agreement is obtained for the molar heat capacities with all four common empirical forcefields. Overall, the highly optimized OPLS AA/L forcefield is the most accurate for obtaining thermodynamics of these liquids.We partitioned the molar entropies into the contributions arising from translation, rotation and internal vibration, and find that a non-negligible 17% of the entropy arises from intra-molecular vibrations, possibly indicating the need for future forcefields to be better tuned to reproduce experimental vibrational frequencies.
Thus 2PT offers a consistent, parameter free method for accurately determining the standard molar entropy and heat capacity of arbitrary liquids, with a high thermodynamic precision. Due to its efficiency (adding ∼0.2% to the total simulation time), we foresee future uses in obtaining entropies of more complex, condensed phased systems.
Acknowledgements
The authors acknowledge Mario Blanco, and Prabal Maiti for useful discussions. This project was partially supported by grants to Caltech from National Science Foundation (CMMI-072870, CTS-0608889). This work is supported by the WCU program (31-2008-000-10055-0) through the National Research Foundation of Korea and the generous allocation of computing time from the KISTI supercomputing center. TAP thanks the US Department of Energy CSGF and the National Science Foundation for graduate fellowships. Prof. Goddard acknowledges the WCU program at KAIST for financial support.References
- B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788 CrossRef CAS.
- D. J. Tannor, B. Marten, R. Murphy, R. A. Friesner, D. Sitkoff, A. Nicholls, M. Ringnalda, W. A. Goddard and B. Honig, J. Am. Chem. Soc., 1994, 116, 11875–11882 CrossRef CAS.
- F. J. Webster, J. Schnitker, M. S. Friedrichs, R. A. Friesner and P. J. Rossky, Phys. Rev. Lett., 1991, 66, 3172–3175 CrossRef CAS.
- X. Kong and C. L. Brooks Iii, J. Chem. Phys., 1996, 105, 2414–2423 CrossRef.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CAS.
- R. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CAS.
- E. Darve and A. Pohorille, J. Chem. Phys., 2001, 115, 9169–9183 CrossRef CAS.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- J. M. Briggs, T. B. Nguyen and W. L. Jorgensen, J. Phys. Chem., 1991, 95, 3315–3322 CrossRef CAS.
- W. L. Jorgensen and D. L. Severance, J. Am. Chem. Soc., 1990, 112, 4768–4774 CrossRef CAS.
- W. L. Jorgensen and J. Tiradorives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS.
- W. L. Jorgensen and J. M. Briggs, Mol. Phys., 1988, 63, 547–558 CAS.
- W. L. Jorgensen, J. Phys. Chem., 1986, 90, 1276–1284 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- G. D. Rose and R. Wolfenden, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 381–415 CrossRef CAS.
- P. L. Privalov and G. I. Makhatadze, J. Mol. Biol., 1993, 232, 660–679 CrossRef CAS.
- E. M. Boczko and C. L. Brooks, Science, 1995, 269, 393–396 CAS.
- R. S. Spolar and M. T. Record, Science, 1994, 263, 777–784 CAS.
- D. M. Huang and D. Chandler, J. Phys. Chem. B, 2002, 106, 2047–2053 CrossRef CAS.
- G. Hummer, S. Garde, A. E. Garcia, M. E. Paulaitis and L. R. Pratt, J. Phys. Chem. B, 1998, 102, 10469–10482 CrossRef CAS.
- B. Guillot, Y. Guissani and S. Bratos, J. Chem. Phys., 1991, 95, 3643–3648 CrossRef CAS.
- T. Lazaridis and M. E. Paulaitis, J. Phys. Chem., 1992, 96, 3847–3855 CrossRef CAS.
- B. Lee, Biopolymers, 1991, 31, 993–1008 CAS.
- S. T. Lin, M. Blanco and W. A. Goddard, J. Chem. Phys., 2003, 119, 11792–11805 CrossRef CAS.
- S. T. Lin, P. K. Maiti and W. A. Goddard, J. Phys. Chem. B, 2005, 109, 8663–8672 CrossRef CAS.
- B. Jana, S. Pal, P. K. Maiti, S. T. Lin, J. T. Hynes and B. Bagchi, J. Phys. Chem. B, 2006, 110, 19611–19618 CrossRef CAS.
- T. A. Pascal, R. Abrol, R. Mittal, Y. Wang, N. V. Prasadarao and W. A. Goddard, J. Biol. Chem., 2010 DOI:10.1074/jbc.M110.122804.
- Y. Y. Li, S. T. Lin and W. A. Goddard, J. Am. Chem. Soc., 2004, 126, 1872–1885 CAS.
- S. S. Jang, S. T. Lin, P. K. Maiti, M. Blanco, W. A. Goddard, P. Shuler and Y. C. Tang, J. Phys. Chem. B, 2004, 108, 12130–12140 CrossRef CAS.
- D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS.
- A. Perez, I. Marchan, D. Svozil, J. Sponer, T. E. Cheatham, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829 CrossRef CAS.
- J. M. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- A. K. Rappe and W. A. Goddard, J. Phys. Chem., 1991, 95, 3358–3363 CrossRef CAS.
- N. A. McDonald and W. L. Jorgensen, J. Phys. Chem. B, 1998, 102, 8049–8059 CrossRef CAS.
- T. Fox and P. A. Kollman, J. Phys. Chem. B, 1998, 102, 8070–8079 CrossRef CAS.
- V. M. Anisimov, I. V. Vorobyov, B. Roux and A. D. MacKerell, J. Chem. Theory Comput., 2007, 3, 1927–1946 CrossRef CAS.
- S. T. Lin, P. K. Maiti and W. A. Goddard, J. Phys. Chem. B, 2010, 114, 8191–8198 CrossRef CAS.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef.
- M. R. Shirts and V. S. Pande, J. Chem. Phys., 2005, 122, 134508–134513 CrossRef.
- T. Yan, C. J. Burnham, M. G. Del Popolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 11877–11881 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- R. H. Henchman, J. Chem. Phys., 2007, 126, 064504 CrossRef.
- D. Laage and J. T. Hynes, Science, 2006, 311, 832–835 CrossRef CAS.
- B. Mukherjee, P. K. Maiti, C. Dasgupta and A. K. Sood, J. Phys. Chem. B, 2009, 113, 10322–10330 CrossRef CAS.
- V. Molinero, T. Cagin and W. A. Goddard, J. Phys. Chem. A, 2004, 108, 3699–3712 CrossRef CAS.
- Y. Zhang, X. Xu and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 4963–4968 CrossRef CAS.
- C. D. Sherrill, B. G. Sumpter, M. O. Sinnokrot, M. S. Marshall, E. G. Hohenstein, R. C. Walker and I. R. Gould, J. Comput. Chem., 2009, 30, 2187–2193 CAS.
- C. D. Sherrill, T. Takatani and E. G. Hohenstein, J. Phys. Chem. A, 2009, 113, 10146–10159 CrossRef CAS.
- R. P. White and H. Meirovitch, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9235–9240 CrossRef CAS.
- R. P. White and H. Meirovitch, J. Chem. Phys., 2004, 121, 10889–10904 CrossRef CAS.
- T. Lazaridis and M. Karplus, J. Chem. Phys., 1996, 105, 4294–4316 CrossRef CAS.
- L. Wang, R. Abel, R. A. Friesner and B. J. Berne, J. Chem. Theory Comput., 2009, 5, 1462–1473 CrossRef CAS.
- R. Sharma, M. Agarwal and C. Chakravarty, Mol. Phys., 2008, 106, 1925–1938 CrossRef CAS.
- M. D. Tyka, R. B. Sessions and A. R. Clarke, J. Phys. Chem. B, 2007, 111, 9571–9580 CrossRef CAS.
- R. H. Henchman, J. Chem. Phys., 2007, 126, 064504 CrossRef.
- G. S. Parks, W. D. Kennedy, R. R. Gates, J. R. Mosley, G. E. Moore and M. L. Renquist, J. Am. Chem. Soc., 1956, 78, 56–59 CrossRef CAS.
- G. S. Parks, H. M. Huffman and M. Barmore, J. Am. Chem. Soc., 1933, 55, 2733–2740 CrossRef CAS.
- G. S. Parks, H. M. Huffman and S. B. Thomas, J. Am. Chem. Soc., 1930, 52, 1032–1041 CrossRef CAS.
- Y. Marcus, Pure Appl. Chem., 1987, 59, 1093–1101 CAS.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS.
- G. Kaminski and W. L. Jorgensen, J. Phys. Chem., 1996, 100, 18010–18013 CrossRef CAS.
- NIST, Chemistry WebBook, National Institute of Standards and Technology, Reference Database Number 69 edn, 2000.
- S. J. Plimpton, R. Pollock and M. Stevens, Proceedings of the Eighth SIAM Conference on Parallel Processing for Scientific Computing, Minneapolis, MN, 1997 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, Taylor & Francis, New York, 1989 Search PubMed.
- P. K. Maiti, T. Cagin, G. Wang and W. A. Goddard, Macromolecules, 2004, 37, 6236–6254 CrossRef CAS.
- T. Cagin, G. F. Wang, R. Martin, N. Breen and W. A. Goddard, Nanotechnology, 2000, 11, 77–84 CrossRef CAS.
- P. K. P. Maiti, A. T. Pascal, N. Vaidehi and W. A. Goddard, J. Nanosci. Nanotechnol., 2007, 7, 1712–1720 CrossRef CAS.
- P. K. Maiti, T. A. Pascal, N. Vaidehi, J. Heo and W. A. Goddard, Biophys. J., 2006, 90, 1463–1479 CrossRef CAS.
- P. K. Maiti, T. A. Pascal, N. Vaidehi and W. A. Goddard, Nucleic Acids Res., 2004, 32, 6047–6056 CrossRef CAS.
- W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103 CrossRef.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- M. E. Tuckerman, J. Alejandre, R. Lopez-Rendon, A. L. Jochim and G. J. Martyna, J. Phys. A: Math. Gen., 2006, 39, 5629–5651 CrossRef CAS.
- N. F. Carnahan and K. E. Starling, J. Chem. Phys., 1970, 53, 600–603 CrossRef CAS.
- J. M. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS.
- Jaguar, version 7.0, Schrödinger, New York, NY, 2007 Search PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CAS.
- MacroModel, version 9.7, Schrödinger, New York, NY, 2009 Search PubMed.
- A. L. Macclellan, Tables of experimental dipole moments, Rahara Enterprises, El Cerrito, California, 1974 Search PubMed.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- R. Shaw, J. Chem. Eng. Data, 1969, 14, 461–465 CrossRef CAS.
- P. Brocos, E. Calvo, R. Bravo, M. Pintos, A. Amigo, A. H. Roux and G. Roux-Desgranges, J. Chem. Eng. Data, 1999, 44, 67–72 CrossRef CAS.
- E. Calvo, P. Brocos, R. Bravo, M. Pintos, A. Amigo, A. H. Roux and G. Roux-Desgranges, J. Chem. Eng. Data, 1998, 43, 105–111 CrossRef CAS.
- F. Comelli, R. Francesconi, A. Bigi and K. Rubini, J. Chem. Eng. Data, 2006, 51, 665–670 CrossRef CAS.
- J. Gao, D. Habibollazadeh and L. Shao, J. Phys. Chem., 1995, 99, 16460–16467 CrossRef CAS.
- M. Levitt, M. Hirshberg, R. Sharon, K. E. Laidig and V. Daggett, J. Phys. Chem. B, 1997, 101, 5051–5061 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS.
- K. R. Harris, P. J. Newitt and Z. J. Derlacki, J. Chem. Soc., Faraday Trans., 1998, 94, 1963–1970 RSC.
- K. Krynicki, C. D. Green and D. W. Sawyer, Faraday Discuss. Chem. Soc., 1978, 66, 199–208 RSC.
- K. J. Tauer and W. N. Lipscomb, Acta Crystallogr., 1952, 5, 606–612 CrossRef.
- T. Shimanouchi, Tables of Molecular Vibrational Frequencies Consolidated Volume I, National Bureau of Standards, 1972, pp. 1–160 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Description of forcefield parameters, heats of vaporization, coefficient of thermal expansions and isothermal compressibilities. See DOI: 10.1039/c0cp01549k |
| This journal is © the Owner Societies 2011 |
