An ab initio insight into the Cu(111)-mediated Ullmann reaction†
Manh-Thuong
Nguyen
*,
Carlo A.
Pignedoli
and
Daniele
Passerone
*
EMPA - Swiss Federal Laboratories for Materials Science and Technology, nanotech@surfaces Laboratory, Überlandstrasse 129, CH-8600 Dübendorf, Switzerland. E-mail: manh-thuong.nguyen@empa.ch; daniele.passerone@empa.ch; Tel: + 41 44 823 48 77
First published on 26th October 2010
Abstract
The coupling process of phenyl radicals—the important intermediates in the prototypal Ullmann reaction—on Cu(111) is addressed using density functional theory. Consistent with experiments, we prove that the fragments interact attractively already at relatively large distances. An intermediate state involving a “popping-out” surface atom is reached through a non-trivial surface diffusion path. The overall process of coupling to the final biphenyl state (with a barrier of 0.38 eV) is governed by a subtle electronic mechanism that reminds the concepts postulated by Hoffmann about the alignment of molecular frontier orbitals with the metallic Fermi level. Our results can be applied to more complex surface processes in the field of molecular self-assembly.
1. Introduction
The coupling reaction of halobenzenes to form biaryls catalyzed by copper was first discovered by Ullmann and Bielecki more than one century ago.1 Since these days, this class of chemical reactions has been a highly interesting topic of catalysis, in terms of both basic understanding and applications.The Ullmann coupling reaction on several metal surfaces, for various molecular coverages, has been studied intensively by means of different techniques.2–12 In this reaction, one of the fundamental steps is the cleavage of C–X bonds (X = Cl, Br, I), which is usually activated by using thermal,5,6photon-stimulated8 and electron-induced10 treatments. Resulting phenyl groups (PGs), the important intermediates in the prototypal Ullmann coupling reaction, are stable on the metal surfaces over a certain range of temperatures, before forming biphenyl molecules. The other products of the cleavage, the halogen atoms, diffuse around on the metal surfaces and are desorbed after the recombination of PGs. The range of temperatures for these processes strongly depends on the nature of substrates. For instance, at sub-monolayer coverages, the C6H5–I dissociation occurs at 175 K on Cu(111),5,6 at 200–250 K on Au(111)9 and below 200 K on Ag(111).8 By contrast, the biphenyl formation temperatures are higher on Cu(111) (over 300 K5,6), and lower on Au(111) (165 − 180 K9) and on Ag(111) (110 K4).
In the recent years, among many fascinating applications that involve the Ullmann reaction, the surface-mediated synthesis of conjugated polymers has attracted particular interest. For instance, a method of synthesizing porous graphene with atomic precision13 or the synthesis of polyphenylene molecular wires14 has been reported. This field of synthesis potentially opens new opportunities in nano-electronics.
Although there are numerous experimental studies related to the Ullmann reaction, an understanding of the surface-mediated reaction mechanisms from an atomistic point of view is missing. Thanks to new advanced numerical methods and computing facilities, quantum mechanical simulations have enabled to describe catalytic reactions in detail, even at a level that is presently not accessible by experiments. It is therefore desirable to have a theoretical investigation collating with previous measurements.
As a first step towards understanding the surface-mediated Ullmann reaction, here we investigate, using density functional theory (DFT),15,16 the fundamental steps of the basic coupling between PGs on Cu(111). The cleavage of the C–X bond (X is a generic halogen atom), a precursor event is not discussed in the present study. Our findings, concerning the surface diffusion process, the approaching of two PGs and their recombination path to form biphenyl, are compatible with all available experimental data. Furthermore, we explain in detail the mechanism of the reaction and the electronic structure counterpart.
2. Computational method
DFT simulations are carried out with the CP2K code17 using the PBE exchange–correlation functional.18 Van der Waals (vdW) corrections to the PBE density functional in the Grimme implementation19 are also included. We exploit the Gaussian and Plane-wave (GPW) hybrid basis set scheme:20 the localized Gaussian-based basis sets used are DZVP for Cu, and TZV2P for H and C. The cutoff for the plane wave expansion of the charge density is 280 Ry. The nuclei and core electrons are described through norm conserving pseudo-potentials of the Goedecker-Teter-Hutter (GTH) type.21 For calculations of the reactants in vacuum we used a spin-polarized scheme due to the presence of unpaired electrons; at the surface the radicals are saturated by Cu electrons, and spin-polarized and non-spin-polarized calculations are equivalent as revealed by test calculations. Therefore, all calculations at the surface were performed within the non-spin-polarized scheme.The convergence threshold for the maximum force component in geometry optimizations is 10−4 hartree/bohr. The surface diffusion events and coupling reactions are investigated using the climbing image nudged elastic band (CI-NEB) method.22 The maximum force component for a band optimization is fixed to 3 × 10−3 hartree/bohr. For the NEB simulations we guarantee an adequate separation between consecutive images (<1.0 Å) considering up to 16 images.
To describe the substrate, we use a slab made up of three 8 × 6 Cu(111) layers with 48 atoms each (test calculations performed including an additional Cu layer revealed that adsorption energies, geometries and activation barriers do not change significantly). In order to avoid interactions between the slab and its periodic images along the direction of the surface normal, a 25 Å vacuum region is added. The lateral size of our slab is 17.8 × 15.42 Å2. This surface supercell containing 1–2 PGs mimics a low molecular coverage condition, reflected by available experiments; the lateral interaction energy between PGs and their periodic replicas was verified to be negligible. In all geometry optimizations, only PGs and top layer atoms of the substrate are relaxed, the others are kept fixed at the bulk positions; the bulk lattice constant is fixed to the model equilibrium value (3.64 Å), consistent with the pseudo-potential in use.
3. Results and discussion
We investigate here the following chain of reactions:| 2C6H5X + Cu(111) → (2C6H5 @Cu(111)) [+ 2X@Cu(111)] → (C6H5–Cu–C6H5) @ Cu(111) → C12H10 @ Cu(111) |
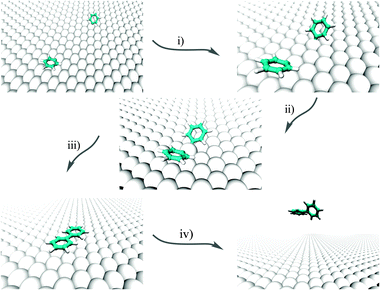 | ||
| Fig. 1 Pictorial representation of the overall formation of phenyl from two PGs on Cu(111). | ||
As a starting point, we determine the energetically favorable geometries of the reactants.
3.1 PG adsorbed on Cu(111)
Possessing a singly occupied molecular orbital (SOMO) (Fig. 2A and Fig. S1, ESI), the radical PG, as expected, can strongly bind to metal surfaces. Experimentally, the adsorption of PG on the (111) surface of the sd metals Au, Ag and Cu has been well documented.4,5,10 A notably observed feature is that PG, rather than oriented in a flat-lying fashion, is adsorbed in such a way that the π-ring is substantially inclined, making it possible to form a metal–carbon σ-bond.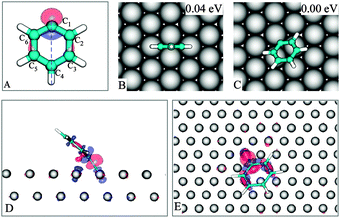 | ||
| Fig. 2 PG and its SOMO (A). The most stable geometries of PG on Cu(111) (B–C). The 0.004 a.u. iso-surface of induced charge density in the PG/Cu(111) system with accumulation (red) and depletion (blue) regions: side view (D), top view (E). | ||
In Fig. 2B–C we show the lowest energy adsorpiton geometries for PG; other configurations are presented in the ESI. In the 2C structure, C1 is nearly located at a hollow site with the SOMO pointing towards a copper atom. The tilt angle (see Fig. S1B, ESI for definition†) of the phenyl plane with respect to the surface is 36°, in agreement with the experimental values of 43 ± 5°,24 or 30°.5 A similar finding was also reported in a recent theoretical study.25
The induced charge density (Fig. 2D–E, defined as the difference between the charge density of the equilibrium system and the charge density of the isolated components (adsorbate and surface) each constrained to the geometry of the whole system, characterizes a covalent bond between PG and Cu(111), which is further supported by a 2.04 Å C1–Cu bond length and a large binding energy of −1.80 eV.
3.2 Surface diffusion of PG
To describe the diffusion of “single” PGs on Cu(111) we assume that PG is located in its favorable position (Fig. 2C) with C1 bound to Cu0 (see Fig. 3A). From this initial state (IS), PG can migrate to one of the six nearest neighbors of Cu0—the final state (FS) of a diffusion event. It is found that PG is highly mobile at the surface.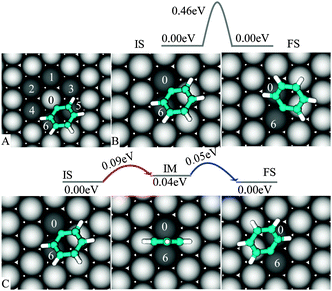 | ||
| Fig. 3 Diffusion of PG on Cu(111): PG migrates from Cu0 to one of the neighboring metal atoms (A), direct Cu0–C6 transition (B) and indirect Cu0–Cu6 transition (C). | ||
As an initial guess for the NEB simulation of a reaction pathway, we adopt a linear interpolation of the nuclear coordinates between IS and FS.
We first consider the Cu0–Cu6 transition (similar to Cu5). For this particular event, we propose two mechanisms (Fig. 3B–C): either (a) PG directly hops from one site (Cu0) to the other one (Cu6) or (b) it goes through an intermediate (IM), before jumping to the destination, thus this consists of two “small” consecutive pathways. The direct transition requires overcoming an energy barrier of 0.46 eV, and is unlikely to be accessible as compared to the indirect path, which is characterized by a 0.09 eV barrier. This low activation energy agrees well with the fact that PG still diffuses on Cu(111) at 77 K.26
The direct Cu0–Cu2 and Cu0–Cu4 pathways are also unfavorable (see ESI). Therefore, the indirect pathway (Fig. 3C) can be viewed as the basic mechanism underlying the migration of PG between any two sites on Cu(111).
3.3 The interactions between two PGs on Cu(111)
In an experimental work on the Ullmann reaction, Weiss and co-workers,26 by using STM measurements at low temperature (77 K), evinced that PGs on Cu(111) interact attractively. We will show that both reactant–surface and direct reactant–reactant interactions are driving forces for this attraction.Without considering the long-range interactions mediated by a surface-state band,27 we inspect two distant PGs approaching each other and obtain that down to a separation of 4.8 Å, the interaction between two PGs is negligible. Our starting configuration (Fig. 4A) corresponds to both PGs in the minimum energy structure for the single ones (Fig. 2C). When the spacing between two PGs is reduced and they bind to two neighboring surface atoms (Fig. 4B), the total energy is lowered by 0.02 eV. We consider this structure as the onset for the interactions between the PGs.
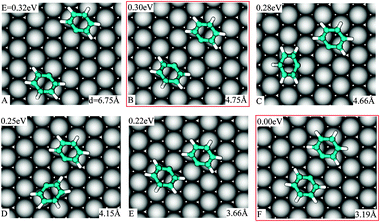 | ||
| Fig. 4 Adsorption position, energy relative to the lowest one and C1–C1 separation in various geometries of the two PGs staying in the favorable position of single ones on Cu(111) when they approach each other. | ||
Various locally stable configurations are possible for two PGs binding to adjacent surface atoms (Fig. 4B–E, and see the ESI†). Eventually, both reactants stick to the same surface atom (see ESI) and the global minimum of the two separate PGs is reached (Fig. 4F). It is evident that the energy on average depends on the C1–C1 spacing. We rationalize the total energies as a function of the C1–C1 separation in Fig. 5. From the graph, the attraction effect between the fragments is obvious.
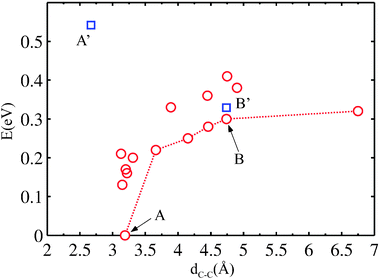 | ||
| Fig. 5 Energy of two PGs at the surface vs. C1–C1 separation (red circles). The dotted line identifies configurations in Fig. 4 (others provided in the ESI†). Points A and B correspond to the geometries 4F and 4B, respectively. Points A′ and B′ (blue squares) correspond to a modification of A and B constraining the substrate to the ideal Cu(111) geometry. | ||
The most stable configuration (Fig. 4F) could be seen as counter-intuitive since two fragments share the same metal atom: first, when a substrate atom is bound to one PG, it can become more inert with respect to the other PG,28 and the total adsorbate–surface interaction might consequently be weakened; second, the two PGs are equally polarized by the surface, and the electrostatic repulsions come therefore into action. In addition, the shared Cu is 0.6 Å lifted up from its initial equilibrium position, accordingly, decreasing the surface coordination.
Nevertheless, the following considerations are consistent with our finding.
We first analyze results of PG dimers in vacuum with their coordinates taken from configurations in Fig. 4B and F. The understanding of these gas-phase systems enriches the information about the interactions between two adsorbed PGs. In vacuum, the two close PGs are 0.29 eV more stable than when they are well separated. The plots in Fig. 6A reveal the onset of chemical bonding between the two fragments when their spacing is reduced. Obviously, there is a wave-function overlap portion between the two fragments despite a pretty large C1–C1 separation (Fig. 6A, bottom panel), leading to attractive interactions.
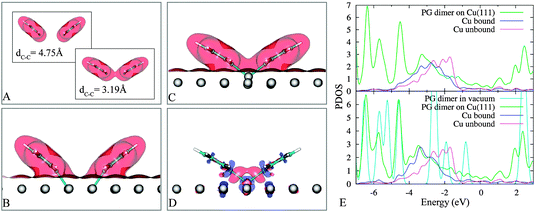 | ||
| Fig. 6 Electron densities of PG dimers in vacuum (panel A: top and bottom) and on Cu(111) (panel B and C) of 4B and 4F (see Fig. 4), respectively, at the iso-surface value of 0.01 a.u. Induced charge density of 4B (panel D) at the iso-surface value of 0.004 a.u red (blue): charge accumulation (depletion). The projected density of states (PDOS) of 4B and 4F (panel E: upper and lower, respectively) show a favourable hybridization between the popping-out metal atom and the PG dimer, “Cu unbound” indicates a surface atom that is far away from two PGs. | ||
We then check that in presence of a flat surface with fixed clean surface positions, a configuration that is favorable when the surface is relaxed ceases to be stable (point A′ in Fig. 5).
This configures an intermediate situation between the bonding of single fragments to the surface and the final surface-supported biphenyl: in this intermediate set of distances an additional source of electrons is necessary, represented by the popping out Cu atom.
To be more specific, we analyse the two structures in Fig. 4B and F and we compare the situation in vacuum (Fig. 6A) with the one on the surface (Fig. 6C–B). In the former case (Fig. 4B and 6B) the two individual PG radicals are saturated each by a surface atom. In the latter case (Fig. 4F and 6C), the popping out Cu atom actively participates in the bonding with a “bridge” between the two unsaturated carbon atoms (Fig. 6D) and the hybridization between this Cu and PGs is more pronounced with respect to the state in 4B (Fig. 4B), as is evident by the projected density of states (PDOS) (Fig. 6E).
A possible reason is that the popping out atom becomes less coordinated (or more adatom-like) when it is lifted up from its initial equilibrium position. Given the fact that low coordinated metal atoms generally provide stronger chemical bonding, the adsorption stability due to the lifting up of the shared atom can overcome the loss of coordination within the metallic surface. In other words, the local restructuring enhances the covalently bonded interactions between adsorbates and surfaces. The net gain in energy upon closing up of the two fragments is an expression of the favorable balance between loss of coordination and enhanced reactivity of the out-of-plane copper atom. We note that a minor role could also be played by the attractive vdW interactions between two PGs.
A final issue is still missing in the description of the diffusion of the PGs at the surface: if we consider two PGs in 4B we have to understand how they could reach 4F. Obviously, PGs can not reach the final geometry by repeating the favorable diffusion pathway of single PGs on Cu(111). For this case (the diffusion from 4B to 4F) we investigate only one pathway (detailed in the ESI†), and obtain a barrier of 0.09 eV.
3.4 The coupling of two PGs on Cu(111)
We now discuss the final coupling step leading to the formation of an adsorbed byphenyl (Fig. 1iii). We set up a NEB calculation where the starting point is 4F (IS0). Using a linear interpolation as a guess for the NEB trajectory could result in a starting point too far from the optimal path, thus, to obtain a reasonable guess, we perform a series of geometry optimizations constraining the C1–C1 separation from its initial value of 3.19 Å down to 1.5 Å. The FS configuration is then obtained by fully relaxing the last component of the constraint optimization series.Geometries obtained by the series of constrained calculations constitute the input for the NEB calculation. The snapshots in Fig. 7A display pathway–0, which reveals that the two reactants equally move toward each other along the reaction pathway. This can be viewed as a result of the nearly symmetric arrangement of the reactants about the surface normal crossing the shared copper atom. The tilt angle of the phenyl rings varies from 30° (IS0) to 22° (TS0) and ends up with 0° (FS0) with a corresponding C1–C1 distance of 3.19, 2.34 and 1.49 Å, respectively. Once the TS0 is reached, the tilt angle and the total energy quickly decrease. The activation energy for this process is 0.38 eV, which is in line with the experimental finding that the onset temperature for the coupling is over 300 K.5 The simulation results show that the coupling of two phenyl fragments is strongly exothermic, i.e., the enthalpy of the system is decreased by 1.9 eV. The energy barrier for the reverse pathway is 2.28 eV, which is much higher than the 1.3 eV adsorption energy of biphenyl on Cu(111), indicating that the biphenyl decomposition leading back to PGs is unlikely at the temperatures typical of biphenyl desorption. By comparison, we found that in the gas phase the enthalpy gain with respect to the two separate radicals is 4.9 eV and the event is barrierless.
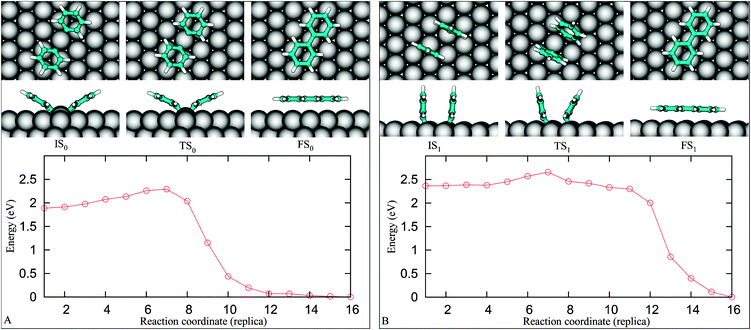 | ||
| Fig. 7 The coupling pathway-0 (A) and pathway-1 (B) of two PGs on Cu(111). | ||
We further inspect a possibility that the reactants couple without passing through the IS0 (Fig. 4F). With IS being one of some geometries given in Fig. 4 and Fig. S4 (see ESI),† only one pathway, named pathway–1 (Fig. 7B), is activated with an apparently low barrier of 0.29 eV. Nevertheless, the pathway–1 is not probable as it is evident exploring the pathway connecting IS1 and IS0. We find the energy barrier for the system to go from IS1 to IS0 is 0.04 eV. The energy landscape depicted in Fig. 8 implies that IS1 is a metastable state, if two distant PGs can reach IS1, they are easily trapped to IS0. Up to a first approximation, the activation energy needed for the reactants to reach the FS1 from IS0 is E(IS1)–E(IS0) + ΔE3 = 0.62 eV (see the red dashed line in Fig. 8). Needless to say, the ratio between the transition rates from IS0 to FS0 and from IS0 to FS1, r(IS0 → FS0/IS0 → FS1), which can be approximated by the ratio of the Boltzmann factors, e(0.62 eV−0.38 eV)/(kT), is very large (approximately 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times at T = 300 K). Consequently, the pathway–1 is unlikely to happen.
000 times at T = 300 K). Consequently, the pathway–1 is unlikely to happen.
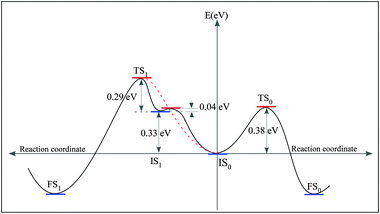 | ||
| Fig. 8 Energy diagram representing the energy landscape of the coupling pathway −0 and −1, and the pathway connecting IS1 and IS0. | ||
Armed with the fact that the two reactants are highly attractive on the surface and they can easily reach for their global minimum IS0, we believe that the reactants do not directly couple when they bind to two neighboring surface atoms, alternatively, they should bind to the same copper atom, in the IS0 position, before completing the recombination. Obviously, the attractive interactions between the PGs on the surface—the driving forces bringing two PGs close together—are extremely important factors in determining the mechanism of biphenyl formation.
Analyzing the electronic evolution of the system along the reaction pathway can provide further insight into reactant–substrate and reactant–reactant interactions.
To this end, we inspect the frontier molecular orbitals (FMOs) for gas phase dimers in the same configurations of the adsorbed molecules in IS0, TS0 and FS0. Then we compute the projection of each state of the corresponding adsorbed systems IS0, TS0 and FS0 on the gas phase FMOs; we can thus extract the state with the closest character to the FMOs of the gas phase.
Concerning IS0, the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the molecules in the gas phase (Fig. 9) show the sigma bonding (σ) and antibonding (σ*) characteristics, respectively. On the surface, states with this character are both positioned below the Fermi energy, EF. This is also verified by the amount of charge that the reactants receive from the metal (Fig. 10). In the TS0, the σ* shape of the gas-phase LUMO seems to remain the same, however, states of the full system with this character rise in energy, approaching EF, in correspondence to a back donation from the molecules to the substrate. Unlike the LUMO, the gas phase HOMO becomes a π state with antibonding character (π*), signaling the onset of the conjugation and of the biphenyl formation. States with the character of the σ-like gas phase HOMO of IS0 are thus pushed down to a much lower energy level. When biphenyl is formed, the π antibonding characteristic of the gas phase HOMO is unchanged.
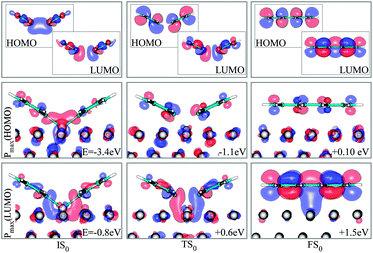 | ||
| Fig. 9 FMOs (HOMO and LUMO) of the reactants in vacuum (top panel) and the states of the full system that show maximum projection on them, labeled as Pmax(HOMO) and Pmax (LUMO), in the three states IS0 , TS0 and FS0. Energies are relative to EF. | ||
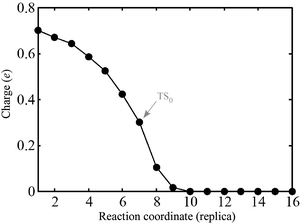 | ||
| Fig. 10 Amount of charge gained by PGs in the pathway-0 from the Bader analysis.30 | ||
However, the LUMO appears to be a π state with bonding character (π), above EF. The state with σ*-LUMO of TS0 is then raised up to a higher energy region.
In many respects, this description is similar to the model for alkyl coupling on a metal surface proposed by Hoffmann:23,29 along the reaction pathway, the C–C antibonding state (IS0–LUMO) is pushed above EF, signaling a back-donation to the surface. However, from our calculations, in the TS0, this antibonding state delocalized around EF and the reactants are still charged by 0.3 electrons (Fig. 10). Further inspection of the geometry and electronic states of the system reveals that TS0 is more IS0-like, explaining why the coupling barrier is relatively low in our study.
4. Conclusions
In this work we have first described in detail the mechanism of diffusion of PG, and explained the experimentally observed low-temperature mobility. Then, we analyzed the reaction process toward an intermediate state involving a bridging, “popping out” copper atom; finally, we computed and discussed the final path leading to the formation of the planar biphenyl. With respect to the literature hypotheses about the overall activation energies, we find a lower barrier of 0.38 eV, which could in turn lead to a lower reaction temperature with respect to the experimentally observed 300–400 K.5Our results could be effected by the limitations of transition state theory or of the particular density functional approximation adopted here, and, similarly, the estimates about activation barriers derived from experimental desorption data are always problematic.
More importantly, we found a viable mechanism through which in the reaction the presence of the Cu(111) surface promotes this fundamental reaction.
Through the projection of the electronic ground state on selected molecular orbitals calculated in the gas phase, we verified the applicability of Hoffmann's concepts about bonding and antibonding orbitals and their alignment with the metallic Fermi surface, and discovered that in this case the situation is more complex: when the radicals are far apart, the HOMO and the LUMO involve, as expected, the bonding and antibonding orbitals built from the radical carbon atoms. As the reaction proceeds, the conjugation typical of biphenyl acquires importance; the bonding in the gas phase would be favored by a twist of one group with respect to the other; here instead, the surface allows the complex to adopt planar configuration; at the same time, the former LUMO gets emptied as suggested by Hoffmann.
Summarizing, we delivered a complete description of a simple yet still not understood reaction and we believe that the same conclusions can be applied to more complex systems of technological and fundamental interest.
Acknowledgements
We gratefully acknowledge financial support from the Swiss National Science Foundation (project no. 200021–116073) as well as computer support by the Swiss National Supercomputing Center (CSCS). We thank Teodoro Laino and Riccarda Caputo for critical reading of the manuscript and for constructive discussions.References
- F. Ullmann and J. Bielecki, J. Ber. Dtsch. Chem. Ges., 1901, 34, 174 Search PubMed.
- X.-L. Zhou and J. M. White, J. Chem. Phys., 1990, 92, 5612 CrossRef CAS.
- X.-L. Zhou, M. E. Castro and J. M. White, Surf. Sci., 1990, 238, 215 CrossRef CAS.
- Y. Song, P. Gardner, H. Conrad and A. M. Bradshaw, Surf. Sci., 1991, 248, L279 CrossRef CAS.
- M. Xi and B. E. Bent, Surf. Sci., 1992, 278, 19 CrossRef CAS.
- M. Xi and B. E. Bent, J. Am. Chem. Soc., 1993, 115, 7426 CrossRef CAS.
- M. Xi and B. E. Bent, Langmuir, 1994, 10, 505 CrossRef CAS.
- G. J. Szulczewski and J. M. White, Surf. Sci., 1998, 399, 305 CrossRef CAS.
- D. Syomin and B. E. Koel, Surf. Sci., 2001, 490, 265 CrossRef CAS.
- D. Syomin, J. Kim, B. E. Koel and G. B. Ellison, J. Phys. Chem. B, 2001, 105, 8387 CrossRef CAS.
- S.-W. Hla, G. Meyer and K.-H. Rieder, Chem. Phys. Lett., 2003, 370, 431 CrossRef CAS.
- M. M. Blake, S. U. Nanayakkara, S. A. Claridge, L. C. Fernandez-Torres, E. C. H. Sykes and P. S. Weiss, J. Phys. Chem. A, 2009, 113, 13167 CrossRef CAS.
- M. Bieri, M. Treier, J. Cai, K. Aït-Mansour, P. Ruffieux, O. Groening, P. Groening, M. Kastler, R. Rieger, X. Feng, K. Müllen and R. Fasel, Chem. Commun., 2009, 6919–6921 RSC.
- J. A. Lipton-Duffin, O. Ivasenko, D. F. Perepichka and F. Rosei, Small, 2009, 5, 592 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103 CrossRef CAS ; http://cp2k.berlios.de/.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92(3), 477–487 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter, 1996, 54, 1703 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- C. Zheng, Y. Apeloig and R. Hoffmann, J. Am. Chem. Soc., 1988, 110, 749 CrossRef CAS.
- M. X. Yang, M. Xi, H. Yuan, B. E. Bent, P. Stevens and J. M. White, Surf. Sci., 1995, 314 Search PubMed.
- D. Jiang, B. G. Sumpter and S. Dai, J. Am. Chem. Soc., 2006, 128, 6030 CrossRef CAS.
- P. S. Weiss, M. M. Kamna, T. M. Graham and S. J. Stranick, Langmuir, 1998, 14, 1284 CrossRef CAS.
- P. Hyldgaard and M. Persson, J. Phys.: Condens. Matter, 2000, 12, L13 CrossRef CAS.
- P. J. Feibelman, Phys. Rev. B: Condens. Matter, 1988, 38, 12133 CrossRef CAS.
- R. Hoffmann, Rev. Mod. Phys., 1988, 60, 601 CrossRef CAS.
- R. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, New York, 1990 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: More adsorption geometries of PG, 2 PGs and biphenyl on Cu(111) and other details. See DOI: 10.1039/c0cp00759e |
| This journal is © the Owner Societies 2011 |
