A suggested periodic table up to Z ≤ 172, based on Dirac–Fock calculations on atoms and ions
Pekka
Pyykkö
*
Department of Chemistry, University of Helsinki, POB 55 (A. I. Virtasen aukio 1), FI-00014 Helsinki, Finland. E-mail: Pekka.Pyykko@helsinki.fi; Fax: +358 9 19150169
First published on 22nd October 2010
Abstract
Extended Average Level (EAL) Dirac–Fock calculations on atoms and ions agree with earlier work in that a rough shell-filling order for the elements 119–172 is 8s < 5g ≤ 8p1/2 < 6f < 7d < 9s < 9p1/2 < 8p3/2. The present Periodic Table develops further that of Fricke, Greiner and Waber [Theor. Chim. Acta 1971, 21, 235] by formally assigning the elements 121–164 to (nlj) slots on the basis of the electron configurations of their ions. Simple estimates are made for likely maximum oxidation states, i, of these elements M in their MXi compounds, such as i = 6 for UF6. Particularly high i are predicted for the 6f elements.
1. Introduction
The Periodic Table (PT) is a compact, approximate way to summarise both the electronic shell structure of individual atoms, or their ions, and chosen aspects of the chemical behaviour of the elements. The history of the PT was recently discussed by Kaji,1 Gordin2 and Scerri.3 We also quote the study on certain (n, l) (‘Madelung’) rules by Ostrovsky4 and the attempts at a group-theoretical classification of the elements by Kibler.5 The underlying electronic principles were discussed by Schwarz et al.6–8A modern, 18-column, shape of the PT is shown in Fig. 1. The latest two essential additions were the addition of the 5f or actinide elements by Seaborg (see ref. 10) and the now completed transactinide series up to Z = 118. The last of them was the case Z = 117, reported in 2010 by Oganessian et al.11 One often speaks of ‘Superheavy Elements (SHE)’. Chemically speaking, decades of both experimental12–14 and theoretical15,16 work give good reason to regard at least the elements 104–109 as a fourth, 6d transition-metal series. A drastic change of the covalent radii may occur from E110 (Darmstadtium, Ds) onwards, see Fig. 2. The experimental chemical studies on the elements Z ≤ 118, and maybe beyond, are of the type ‘one atom at a time’. In cases where the nuclear lifetimes now are too short for chemical studies, new, more neutron-rich isotopes may help. Studies on the bulk chemistry are expected to remain computational, only.
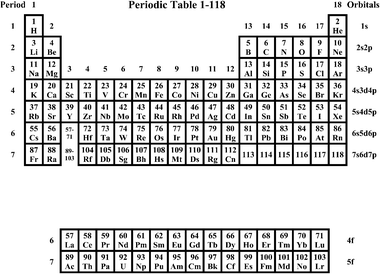 | ||
| Fig. 1 The Periodic Table of the 118 experimentally known elements. The numbers g = 1–18 are the Groups. The IUPAC PT9 coincides with this table, but so far only includes the elements, up to Rg. | ||
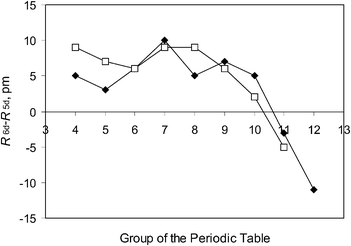 | ||
| Fig. 2 The collapse after Group 10 of the 7th Period (‘6d’) covalent radii, compared to 6th-Period (‘5d’) ones. Black diamonds: Single-bond radii.17 Open squares: Triple-bond radii.18 | ||
The values l = 0,1,2,3,4 are denoted by the symbols s, p, d, f, g respectively. When necessary, the lower spin–orbit (SO) split component j = l − ½ is denoted by a star, e.g. p* = p1/2. The principal quantum number n of the s and p shells coincides with the number of the period in Fig. 1. It should be stressed that, while nuclear charges are well defined, the concept of an electron configuration, both for atoms and molecules, is only approximate. For both systems, the true many-electron wave function can be a superposition of a large number of effective electron configurations. This aspect especially affects the transition metals.
The filling of such shells up to Z = 172 was studied using Dirac-Slater (DS) theory by Fricke et al.19,20 for single, jj-coupled electron configurations in this approximate form of density functional theory (DFT). It was found that, approximately for Z = 121–143, 8p1/2 and 5g shells become occupied in neutral atoms. The full 6f and 7d series are completed around Z = 144–154 and 155–164, respectively. The following row contained the 9s, 9p1/2 and 8p3/2 elements 165–166, 167–168 and 169–172, respectively, see Fig. 10 of ref. 19. The heaviest atom treated seems to be E184.21 The primary, numerical DS data are listed in ref. 22.
Already slightly earlier, Waber23,24 found 5g electrons in the atomic ground state from E125 on. Lu et al.25 also provided DS data up to Z = 126. At Dirac–Fock (DF) level, Mann26 noticed the particular stability of the 8p* shell and Mann and Waber27 reported results for E118–E131. The general conclusion is that, around E121–131, both 8p, 7d, 6f and 5g orbitals may enter the atomic ground states.
At this point one should point out that a realistic finite nuclear size keeps the lowest (1s) eigenvalue within the normally allowed range ε > −2mc2 (a free electron being taken as ε = 0). For the 1s state of a one-electron atom, and the available nuclear models, the critical limit, Zcr has been put at Z = 175,28 > 17029 or 171.5.30 The screening from the other electrons should raise that limit.
Zel'dovich and Popov31,32 actually point out that the electron wave functions remain localized beyond Zcr but this behaviour has not been implemented in any atomic codes yet.
It is not obvious how to treat the quantum electrodynamical (QED) effects in the supercritical domain Z > 137. Here they are hence simply dropped out. In the range Z = 50–100, they are typically −1% of the one-electron, Dirac-level relativistic effects,33–35 on the valence ns orbital binding energies of neutral or nearly neutral atoms. For a recent summary on the QED aspects, see Indelicato et al.36 Because their sign on s levels is repulsive, they should also increase Zcr.
Average-of-configurations Dirac–Fock (DF) calculations for the elements 1–120 were reported by Desclaux.37 Umemoto and Saito38 also found 5g electrons to appear at E126 at DS level. Very precise relativistic coupled-cluster calculations were reported by the group of Kaldor on individual atoms and their ions, such as E122.39 Multiconfiguration, MCDF-level calculations on the atomic ground configurations for elements 119–164 were reported by Nefedov et al.40 who, however, do not specify the exact computational method used, nor the value of the total atomic angular momentum, J.
Little molecular work has been done on superheavy elements beyond the rare gas E118 (which has an electron affinity41,42). The exceptions comprise an MS Xα study of 5g1 complexes of E12543(entirely supporting the present PT), a single-configuration DF study on diatomic (E126)F44 and a study on (E119)H and (E120)H+.45
The purpose of present work is to extend the previous work on neutral atoms to chemically plausible ions, fully realising the difference between free ions and ions in chemical compounds, at a—still approximate—but realistic DF level, in order to see how a 21st-Century Periodic Table could possibly be shaped in its most compact, approximate form.†
2. Methods
The calculations were performed using the latest version of the MCDF program of Desclaux and Indelicato,46 at the Extended Average Level (EAL) level. Because many atomic levels can be mixed in chemical-bond formation, as emphasized by Schwarz and coworkers,6 this may actually be a desirable approximation. The EAL is useful, as long as the spin–orbit (SO) effects are not excessive, or can be separately checked.The nuclear charge distribution was taken as a Fermi one with the parameters
| ρ(r) = ρ0/[1 + exp((r − c)(4 ln 3)/t)], | (1) |
| A = 0.00733Z2 + 1.3Z + 63.6. | (2) |
Some calibration results are compared to earlier ones in the Table 1.
3. Results
3.1 A broad mapping
A compact, very schematic grouping of the elements up to Z = 172 is shown in Fig. 3. The underlying atomic results are shown in Tables 2–4.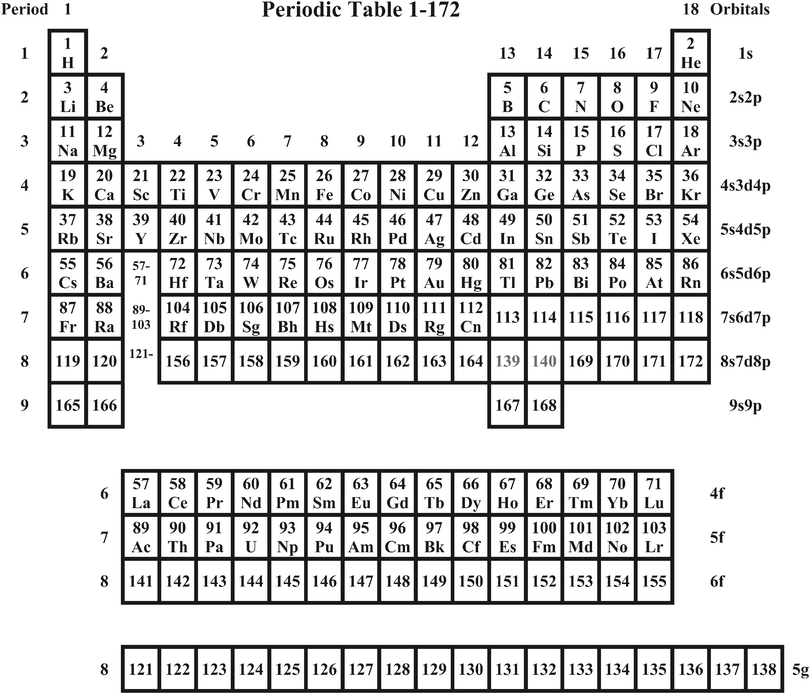 | ||
| Fig. 3 The new, compact Periodic Table for elements 1–172. The numbers 1–18 are the Groups. For Periods 8 and 9, the Groups 13–14 are interpreted as p* (p1/2) states and the Groups 15–18 as p (p3/2) states. Please note that, in this most compact version and respecting the ‘Orbitals’ assignment in the right-hand marginal, the Z values do not increase systematically. An alternative were to break present Period 8 into the pieces 8a (119–120), 8b (139–140) and 8c (156–164, 169–172). | ||
| Z | q | El. conf. | I/a.u. | Exc. en. | |
|---|---|---|---|---|---|
| 119 | 0 | 8s1 | r | ||
| 120 | 0 | 8s2 | r | ||
| 121 | 0 | 8s28p1 | 0.113 | r | |
| 8s27d1 | +0.0042 | r | |||
| +1 | 8s2 | ||||
| 123 | +4 | 6f1 | 1.374 | r | |
| 124 | +5 | 6f1 | 1.918 | r | |
| 5g1 | +0.0948 | r | |||
| 125 | +6 | 5g1 | 2.721 | r | |
| +7 | 5g0 | ||||
| 126 | +6 | 5g2 | 2.714 | r | |
| 6f15g1 | +0.2091 | r | |||
| +7 | 5g1 | 3.677 | |||
| 133 | +6 | 5g9 | r | ||
| 136 | +2 | 8s26f35g11 | |||
| +6 | 5g12 | ||||
| 138 | +5 | 8s25g13 | 2.089 | ||
| 8s15g14 | +0.0977 | ||||
| 6f25g13 | +0.2146 | ||||
| 6f15g14 | +0.2923 | ||||
| 6f35g12 | +0.3779 | ||||
| 8p15g14 | +0.7159 | ||||
| +6 | 8s15g13 | r | |||
| 6f15g13 | +0.0225 | ||||
| 5g14 | +0.0360 | ||||
| 6f25g12 | +0.2509 | ||||
| 8p15g13 | +0.7033 | ||||
| 140 | +2 | 8s25g168p2 | |||
| 8s25g178p1 | +0.2921 | ||||
| +4 | 8s26f25g14 | ||||
| +6 | 6f15g15 | 2.428 | r | ||
| 8s25g13 | +0.6637 | ||||
| +7 | 5g14 |
| Z | q | El. conf. | I/a.u. | Exc. en. | |
|---|---|---|---|---|---|
| 143 | +6 | 8s15g18 | 2.652 | ||
| 6f15g18 | +0.2473 | ||||
| +7 | 5g18 | ||||
| 144 | +5 | 8s26f15g18 | 2.139 | ||
| +6 | 8s25g18 | 2.760 | r | ||
| +7 | 8s15g18 | 3.185 | |||
| 6f15g18 | +0.1269 | ||||
| +8 | 5g18 | ||||
| 6f15g17 | +0.4306 | ||||
| 8s15g17 | +0.4908 | ||||
| 7d15g17 | +1.0658 | ||||
| 6f15g17 | +1.5227 | ||||
| 145 | +6 | 5g188s26f1 | 2.783 | r | |
| 5g188s16f2 | +0.1737 | ||||
| +7 | 5g188s2 | 3.303 | |||
| 5g188s16f1 | +0.0443 | ||||
| 5g186f2 | +0.1755 | ||||
| +8 | 5g186f1 | 3.755 | |||
| 5g188s1 | +0.0025 | ||||
| +9 | 5g18 | ||||
| 146 | +8 | 5g188s16f1 | 3.836 | ||
| 5g186f2 | +0.0031 | ||||
| 5g188s2 | +0.0887 | ||||
| +9 | 5g186f1 | 4.494 | |||
| 5g188s1 | +0.1388 | ||||
| +10 | 5g18 | ||||
| 147 | +10 | 5g186f1 | 5.272 | ||
| 5g188s1 | +0.2800 | ||||
| 148 | +11 | 5g186f1 | 6.088 | ||
| 149 | +12 | 5g186f1 | 6.940 |
| Z | q | El. conf. | I/a.u. | Exc. en. | |
|---|---|---|---|---|---|
| a Single-configuration jj-coupled DF, ref. 50. | |||||
| 153 | +1 | 8s26f14 | 0.380 | ||
| +2 | 8s26f13 | 0.872 | |||
| +3 | 8s26f12 | 1.415 | |||
| 8s16f13 | +0.5810 | ||||
| 6f14 | +1.2253 | ||||
| +4 | 8s26f11 | 1.999 | |||
| +5 | 8s26f10 | 2.619 | |||
| +6 | 8s26f9 | 3.270 | r | ||
| +7 | 8s26f8 | ||||
| 155 | +3 | 8s26f14 | 1.484 | ||
| +4 | 8s26f13 | 2.084 | |||
| +5 | 8s26f12 | 2.720 | r | ||
| 8s16f13 | +0.4201 | ||||
| 6f14 | +0.9189 | ||||
| +6 | 8s26f11 | ||||
| 156 | +3 | 8p1 | 1.177 | ||
| 7d1 | +0.0538 | ||||
| +4 | 8s2 | 2.126 | |||
| +5 | 8s26f13 | 2.770 | r | ||
| 8s16f14 | +0.4434 | ||||
| +6 | 8s26f12 | ||||
| 158 | +3 | 7d18p2 | |||
| 164 | +1 | 7d98s28p2 | 0.888 | ||
| 0.600a | |||||
| +2 | 7d88s28p2 | 1.300 | r | ||
| +3 | 7d78s28p2 | 1.741 | |||
| +4 | 7d68s28p2 | ||||
| 166 | +2 | 7d108p2 | |||
| 9s17d98p2 | +0.5826 | ||||
| 9s27d88p2 | +1.2594 | ||||
| 168 | +2 | 8p4 | |||
| 9s18p3 | +1.0742 | ||||
| 9s28p2 | +2.2027 |
3.2 Elements 119–126 and the beginning of a 5g series
As discussed before, elements 119 and 120 are 8s1 and 8s2, and thus belong to Groups 1 and 2, respectively.19,37,48,49 For neutral E121, the present EAL calculations prefer 8p, with 7d only slightly above. The one-electron ions E1234+ and E1245+ switch the 8s ground state for a 6f. From E1256+ onwards, a 5g1 state is preferred, as seen in Table 2. The one-electron ions E1256+ and E1267+ being clearly 5g1, this motivates placing these elements in Groups 7 and 8, of a beginning 5g row, respectively. A chemical example on the former would be the (E125)F6 of Makhyoun.43 For the next element, the (E126)F6 are then expected to be 5g2 systems. An analog for the one-electron ions is Ce3+, 4f1, placed in Group 4. Further analogs are U5+ and Np6+, both 5f1, placed in Groups 6 and 7, respectively. There is room for 18 elements E121–E138 on this 5g row. We repeat that we do not mind if other orbitals, such as 8p*, 7d, or 6f ones could be occupied in some early members of a row, or in low oxidation states of these elements. They are nevertheless counted as members of the 5g series.Note that, depending on the oxidation state, the 8s occupation may vary from 0 to 2. In this sense the 8s and 5g levels cross. Concerning the filling of the 5g shell, in the neutral-atom calculations, this does not occur until E144.19
The size of the 5g orbitals being very small (see Section 4), their direct involvement in chemical bonding is unlikely, just as in the case of the 4f orbitals of the lanthanides.
3.3 The 8p* shell
Mann and Waber26,27 found in their single-configuration jj-coupled DF calculations that, in the neutral atoms, one 8p* electron appeared at E121–E125, and two at E126-. In the DS calculations of Fricke et al.19 the limits were E121–E126 and E127-, respectively.For our electron book-keeping, we put the 8p* shell at E139 and E140. As seen in Table 2 for the previous element, E1385+, 6+, the available electrons will be placed in a full, 8s2 shell, the rest going to the 5g shell, and none yet to the 8p shell. This supports the present placement.
3.4 The 6f series
We here have a choice of keeping the 8s2 shell, or ionizing it away. If we keep it, we can place the 15 following elements E141–E155 below the actinides Ac-Lr. (Note that in the upper part of the PT, there is a slot at Group 3, and Ac, 7s26d1, is usually included on the actinide row, giving fifteen items. In contrast to the actinides, which lose their 7s electrons in compounds, the present series, in their lower oxidation states, keep their 8s2 but formally lose the (8p*)2 electrons.Taking as example the system E144+5 (see Table 3), it has an 8s26f15g18 configuration, and belongs in this sense to a 6f series. As its analog U5+ (5f1), E144 in its lower oxidation state hence does belong to Group 6 on the 6f row of Period 8. More generally, for the lower oxidation state of the 6f series, we expect an E118 core + a 5g188s2 semicore+the remaining electrons, going to the 6fk shell with
| k = Z − 138 − i, | (3) |
For the 6f series we also have the higher oxidation state, such as E1448+, where the 8s shell is ionized away. In fact, as the last electron above a 5g18 core, the 6f replaces the 8s starting from E1458+. The E1468+ has one of each, an 8s16f1 configuration in the EAL model. This underlines the similar binding energies of the 8s and 6f electrons in this neighbourhood.
This situation may create for the 6f elements a large range of high oxidation states, as discussed in Chapter 5. This is also a bit analogous with the Groups 13–15 of Period 6, with the choice between Tl(I,III), Pb(II,IV) or Bi(III,V).
As seen from Table 4, at E1533+ the 8s shell is already clearly under the 6f. Similarly, in the pentavalent state, E1555+, the 8s electrons are kept but the 6f shell is ionized to 6f.12
For the higher oxidation state, the number of 6f electrons is
| k = Z − 136 − i, | (4) |
3.5 The 7d series
After the 6f series, we assign the nine elements E156–E164 formally to a 7d series in Groups 4–12.Table 3 suggest 8p to lie slightly below 7d for E1563+. The 8p* eigenvalue of −1.91 au is clearly below the SO-averaged 7d one of −1.14 au. Note that trivalent Ti, Zr and Hf are d1 while E1563+ is p1 but has a low-lying d1 state.
As seen from Table 4, E1564+ is 8s26f14. If ionized further to 5+ or 6+, the electrons are taken from the 6f, not from the 8s.
At the end of the series, the chemical properties of eka-copernicium, E164, were discussed by Penneman et al.50 It was mainly predicted to be divalent, but oxidation states +IV and +VI were also expected. The calculated Ii for i = 2–4 in Table 3 lie above the limiting line in Fig. 6, suggesting at most borderline chemical stability. Notice that, unlike Zn–Hg, but like Cn,51 the ions of E164 keep both 8s electrons but remove 7d ones, which lie clearly higher. The 8s27d10 ground-state configuration of E164 is analogous to all of Zn–Cn, which motivates keeping E164 in Group 12 of Period 8. This also fixes the positions of the preceding 7d elements.
3.6 The last main-group elements
The 9s1 and 9s2 elements E165 and E166 are now in Groups 1 and 2, respectively. Unlike the ns elements of Periods 3–8, which have an underlying np6 core, the E165 and E166, however, have an underlying 7d10 core. In that sense, they would have a chance of rather being analogs to Au and Hg, or to Rg and Cn, and being members of Groups 11–12 of the Period 9, next to E167.As seen from Table 3, the dication E1662+ strongly prefers a 7d109s0 configuration to the alternatives 7d99s1 or 7d89s2. We recall here that Rg (E111) prefers a 6d98s2 ground state.52 Due to this orbital order 7d < 9s, we therefore let E165 and E166 stay in Groups 1 and 2, as done by Fricke et al.19
For the elements E167–E172 we likewise follow them in taking the energetic order as 9s < 9p1/2 < 8p3/2. Note that the SO splittings are so large that they are making two SO-split suborbitals with different n nearly degenerate.
4. Orbital radii
4.1 The nodeless 5g orbital
It is well-known that the first orbital with every l (1s, 2p, 3d, 4f, 5g,…) is much more compact than the following orbitals with the same l. This was noticed for 3d and 4f orbitals by Jørgensen,53 who related it to the number of radial nodes (actually ‘maxima’, see his p. 46). Similar later arguments exist for the shells 2p54,55 and 1s.56 Also Slater57 comments that the rmax of the 3d shells of Sc–Ni, given earlier by himself,58 are ‘much smaller than those for the 4s, even though the energies are about the same’. He mentions their ‘different shapes’. Qualitatively one could say that the higher levels with the same l feel a primogenic repulsion59 from the first, nodeless orbital. For a recent review on this problem, see Kaupp.60How compact is the 5g shell, compared with its counterparts? We show in Table 5 typical radii, 〈r〉, for the four series. The 5g shell is compact, but rather comparable with the other three series.
| Series | Beginning | End | ||
|---|---|---|---|---|
| Atom | 〈r〉 | Atom | 〈r〉 | |
| 1s | H | 1.5 | He | 0.927 |
| 2p | B | 2.205 | Ne | 0.964 |
| 3d | Sc | 1.692 | Cu | 0.998 |
| 4f | Ce | 1.041 | Lu | 0.702 |
| 5g | E1245+ | 0.756 | E1406+ | 0.593 |
Estimates for the ionic radii of E104–E120 and E156–E172 were provided by Fricke and Waber61 as the rmax of the outermost occupied orbital. The neutral atom rmax of Waber et al.24 for the 6f and 5g shells from E124 to E132 are comparable with the present values for their ions in Fig. 4.
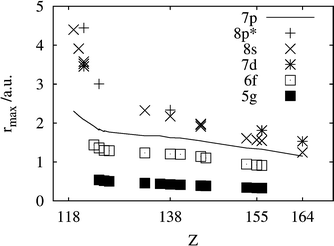 | ||
| Fig. 4 The distances for maximum electron density for the orbitals 7p, 8s, 8p*, 7d, 6f and 5g for the systems indicated by an ‘r’ in Tables 2–4. Note that 7p (given by the line) remains the outermost core orbital until about E153. | ||
Because of the small size of the 5g shell, the 5g elements may rather chemically form a group of superlanthanides, in the sense of systematic magnetic behaviour, and non-participation of the ‘label orbital’ 5g in the formation of bonds. The difference is that the lanthanides use 6s and 5d in their covalent bonds, but the 5g series has the panoply of 8s, 8p*, 7d and 6f for the purpose. For factors determining the ionic radii, see the subsection on 7p3/2 orbitals.
4.2 Magic numbers
The Lewis octets, corresponding to a formally filled ns2np6 electron configuration, are well-known. Likewise, the 18-electron rule with a formal ns2np6(n − 1)d10-like configuration at the central atom is well-known; for its history and actual interpretation, see ref. 62. The next step is a 32-electron closed-shell structure around a central atom. Recently, both the predicted Pu@Pb1263 or Pu@Sn1264 and the experimentally observed U@C2865 isoelectronic series were found to form good examples on such 32-electron systems.To obtain the next, 50-electron magic number, the first chance would be the 6g shell which, however, remains outside the elemental range, studied here.
4.3 The 7p3/2 semicore orbital
In the PT, the 5p orbital is filled at Xe and becomes the core orbital of the lanthanides. Similarly, the 6p orbital is filled at Rn and becomes the semicore orbital of the actinides. Although so far not formally oxidized, it can strongly hybridize with the valence orbitals in systems like uranyl or UF6 (for some references, see ref. 66). We now notice that the 7p3/2 orbital, filled at E118, remains the largest core orbital up to about E164. It is only slightly more compact than the 8s one, when this becomes permanently occupied around E153. The rmax values are shown in Fig. 4.5. Ionization potentials and oxidation states
Concerning the possible SHE oxidation states, Jørgensen67 guessed for E126 an oxidation state of +IV (5g4), while Fricke et al.19 thought its normal oxidation state could be as high as +8. Along the series, they expected a reduction to +6 at E132, and to +3 or +4 around E144.As well-known in the chemical literature (e.g.ref. 68 and 69), for electrons removed from the same atomic shell, the ionization potentials In systematically increase. Pyper and Grant70,71 rationalized this observation considering the atomic integrals involved.
How far along the atomic In sequence can we go in chemical compounds, assuming that the sum of the ionization energies is paid back by combined interionic Coulomb attractions and covalent bonding? Moreover it should be noticed that e.g. the Mulliken charges of the central atom can be roughly half of the formal oxidation state. An early example on this rule of thumb were the XeFn; n = 2–6, (see ref. 66, Fig. 4).
Experimentally, oxidation states up to +VIII are now known in oxides and fluorides.72 Himmel et al.,73 suggest gas-phase IrO4+ as a possible chemical system with oxidation state +IX. Parenthetically, the octahedral UO6 has been predicted to exist as a local high-energy minimum.74,75 It is not really a U(XII) compound, in the sense of oxidizing the 6p semicore levels, and has, moreover, lower-lying peroxido and superoxido isomers.
Can we relate the ionization energies, Ii of the free ions to the maximum oxidation states in compounds? Certain Ii values are shown in Table 6 and a correlation between the two numbers is shown in Fig. 5. This, rather Gordian, empirical attempt may give some idea of the possible oxidation states, if the Ii is known.
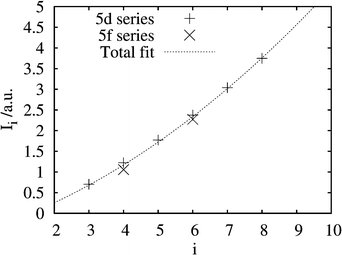 | ||
| Fig. 5 The correlation between the free-ion last ionization energies, Ii, and the maximum known oxidation state, i for certain 5d and 5f elements. The data are taken from Table 6. | ||
We then compare some calculated ionization energies for the present SHE in Fig. 6. For the nominal 5g series, the last valence electron is 8s, 6f and 5g for E121–122, E123–124 and E125–126, respectively. The values reach the line of Fig. 5 at I8. A further ionization, leading to a 7p5 configuration, would have a much higher ionization energy, e.g. an I7 of 3.184 au for E124.
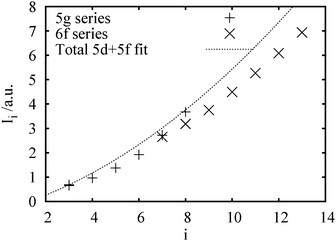 | ||
| Fig. 6 A comparison of some present calculated ionization energies with the fit to experimentally known maximum ones in Fig. 5. The ‘6f’ series corresponds to the higher oxidation state. | ||
The curve for the higher oxidation state of the 6f series lies below the experimentally known cases, making them also plausible, possibly to some very high i values, such as i = 12 for the hypothetical (E148)O6. A further study would require molecular calculations.
6. Multi-shell transition metals?
Taking an example, it is known that the Gd atom ground state is 6s25d14f7, with open 5d and 4f shells. For neutral or nearly neutral SHE this also is a common occurrence. Could this occur in compounds, or the present highly-charged ions?Table 2 has E138+6 with a low-lying 6f15g13 configuration. E140+6 has a 6f15g15 ground state. Thus some 6f–5g overlap may occur in this neighbourhood.
7. Possible new molecules
Some characteristic molecules for the presently studied 5g, 6f and 7d elements are given in Table 7. Their theoretical verification must be left to future quantum chemical studies. The 5g0 cases in the beginning are analogs of lanthanides in the sense of having a compact, inner shell, being filled.| Class | Molecules | Analogs |
|---|---|---|
| a Done in ref. 43. | ||
| 8s05g0 | (E121)X3 | LaX382 |
| (E122)X4 | ||
| (E123)X5 | ||
| (E124)X6,… | ||
| (E126)O4 | ||
| 8s05g1 | (E125)X6a | |
| 8s2(8p*)06f05g18 | (E142)X4 | ThF4 |
| (E144)X6 | UF6 | |
| (E144)O22+ | UO22+ | |
| 8s0(8p*)06f05g18 | (E144)F8 | PuF883 |
| (E144)O4 | PuO483 | |
| (E148)O6 | UO674,75 | |
| (E142)X6 | ||
| 8s2(8p*)07d06f145g18 | (E158)X6 | WF6, SgF6 |
| (E160)O4 | OsO4, HsO4 | |
| 8s0(8p*)07d06f145g18 | (E158)X8 | |
| (E158)O4 | ||
| 8s2(8p*)07d106f145g18 | (E164)X2 | HgX2 |
| 8s2(8p*)07d86f145g18 | (E164)X4 | HgF484 |
8. Conclusions
Based on the present ionic calculations, we have found a way to split the very long row E121–E164 of Fricke et al.19 to the suggested 5g, 6f and 7d segments, used in the present Fig. 3. Especially the 6f series may possess some very high oxidation states.While most experimental verifications may take a while, relativistic quantum chemistry could be used to show that e.g. (E125)F6 is indeed 5g1, as calculated by Makhyoun.43 It is similarly expected that (E143)F6 and/or (E145)F6 would be 6f1 systems, and so on.
Acknowledgements
The author belongs to the Finnish Centre of Excellence of Computational Molecular Science (CMS). Dr Jean-Paul Desclaux provided the version of the Dirac–Fock program used.46 Dr Michiko Atsumi showed, how to use Excel for making the Fig. 1 and 3. Dr Valeria Pershina suggested and provided Fig. 2.References
- M. Kaji, Found. Chem., 2003, 5, 189–214 Search PubMed
.
-
M. D. Gordin, A Well-Ordered Thing: Dmitrii Mendeleev and the Shadow of the Periodic Table, Basic Books, New York, 2004 Search PubMed
.
-
E. R. Scerri, The Periodic Table. Its Story and Its Significance, Oxford Univ. Press, Oxford, 2007 Search PubMed
.
- V. N. Ostrovsky, Ann. N. Y. Acad. Sci., 2003, 988, 182–192 CrossRef CAS
.
- M. Kibler, Found. Chem., 2007, 9, 221–234 Search PubMed
.
- S.-G. Wang and W. H. E. Schwarz, Angew. Chem., Int. Ed., 2009, 48, 3404–3415 CrossRef CAS
.
- W. H. E. Schwarz and S.-G. Wang, Int. J. Quantum Chem., 2010, 110, 1455–1465 CAS
.
- W. H. E. Schwarz and R. L. Rich, J. Chem. Educ., 2010, 87, 435–443 CrossRef CAS
.
- Anon., old.iupac.org/reports/periodic_table, Downloaded 20 August 2010.
- G. T. Seaborg, J. Chem. Soc., Dalton Trans., 1996, 3899–3907 RSC
.
- Yu. Ts. Oganessian, F. Sh. Abdullin, P. D. Bailey, D. E. Benker, M. E. Bennett, S. N. Dmitriev, J. G. Ezold, J. H. Hamilton, R. A. Henderson, M. G. Itkis, Yu. V. Lobanov, A. N. Mezentsev, K. J. Moody, S. L. Nelson, A. N. Polyakov, C. E. Porter, A. V. Ramayya, F. D. Riley, J. B. Roberto, M. A. Ryabinin, K. P. Rykaczewski, R. N. Sagaidak, D. A. Shaughnessy, I. V. Shirokovsky, M. A. Stoyer, V. G. Subbotin, R. Sudowe, A. M. Sukhov, Yu. S. Tsyganov, V. K. Utyonkov, A. A. Voinov, G. K. Vostokin and P. A. Wilk, Phys. Rev. Lett., 2010, 104, 142502 CrossRef
.
- M. Schädel, J. Nucl. Radiochem. Sci., 2002, 3, 113–120 Search PubMed
.
- M. Schädel, Angew. Chem., Int. Ed., 2006, 45, 368–401 CrossRef
.
-
D. C. Hoffman, in The Robert A. Welch Foundation Conference on Chemical Research. XXXIV. Fifty Years With Transuranium Elements, Houston, Texas, 1990, pp. 255–276 Search PubMed
.
-
V. Pershina, in Relativistic Electronic Structure Theory. Part 2. Applications, ed. P. Schwerdtfeger, Amsterdam, 2004, pp. 1–80 Search PubMed
.
- V. Pershina, Radiochim. Acta, 2005, 93, 125–131 CrossRef CAS
.
- P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197 CrossRef
.
- P. Pyykkö, S. Riedel and M. Patzschke, Chem.–Eur. J., 2005, 11, 3511–3520 CrossRef
.
- B. Fricke, W. Greiner and J. T. Waber, Theor. Chim. Acta, 1971, 21, 235–260 CrossRef CAS
.
- B. Fricke, Struct. Bonding, 1975, 21, 89–144 CAS
.
- B. Fricke and J. T. Waber, Actinides Rev., 1971, 1, 433–485 Search PubMed
.
- B. Fricke and G. Soff, At. Data Nucl. Data Tables, 1977, 19, 83–95 CrossRef CAS
.
-
J. T. Waber, in Proc. 13th R A Welch Foundation Conf. on Chem. Res., The Transuranium Elements, Houston, TX, 1969, pp. 353–443 Search PubMed
.
- J. T. Waber, D. T. Cromer and D. Liberman, J. Chem. Phys., 1969, 51, 664–668 CrossRef CAS
.
- C. C. Lu, T. A. Carlson, F. B. Malik, T. C. Tucker and C. W. Nestor Jr., At. Data, 1971, 3, 1–131 CrossRef CAS
.
- J. B. Mann, J. Chem. Phys., 1969, 51, 841–842 CrossRef CAS
.
- J. B. Mann and J. T. Waber, J. Chem. Phys., 1970, 53, 2397–2406 CrossRef CAS
.
- I. Pomeranchuk and J. Smorodinsky, J. Phys. (USSR), 1945, 9, 97–99 Search PubMed
.
- F. G. Werner and J. A. Wheeler, Phys. Rev., 1958, 109, 126–144 CrossRef CAS
.
- B. Müller, J. Rafelski and W. Greiner, Nuovo Cimento A, 1973, 18, 551–573 Search PubMed
.
- Ya. B. Zel'dovich and V. S. Popov, Usp. Fiz. Nauk, 1971, 105, 403–440 (
Sov. Phys. Usp.
, 1972
, 14
, 673
) Search PubMed
.
- V. S. Popov, Phys. At. Nucl., 2001, 64, 367–392 (
Yad. Fiz.
, 2001
, 64
, 421
) CrossRef CAS
.
- P. Pyykkö, M. Tokman and L. N. Labzowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, R689–R692 CrossRef CAS
.
- L. Labzowsky, I. Goidenko, M. Tokman and P. Pyykkö, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 2707–2711 CrossRef CAS
.
- P. Pyykkö and L.-B. Zhao, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, 1469–1478 CrossRef CAS
.
- P. Indelicato, J. P. Santos, S. Boucard and J.-P. Desclaux, Eur. Phys. J. D, 2007, 45, 155–170 CrossRef CAS
.
- J. P. Desclaux, At. Data Nucl. Data Tables, 1973, 12, 311–406 CrossRef CAS
.
- K. Umemoto and S. Saito, J. Phys. Soc. Jpn., 1996, 65, 3175–3179 CrossRef
.
- E. Eliav, A. Landau, Y. Ishikawa and U. Kaldor, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 1693–1700 CrossRef CAS
.
- V. I. Nefedov, M. B. Trzhaskovskaya and V. G. Yarzhemskii, Dokl. Phys. Chem., 2006, 408, 149–151 CrossRef CAS
.
- E. Eliav, U. Kaldor, Y. Ishikawa and P. Pyykkö, Phys. Rev. Lett., 1996, 77, 5350–5352 CrossRef
.
- I. Goidenko, L. Labzowsky, E. Eliav, U. Kaldor and P. Pyykkö, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 020102 CrossRef
.
- M. A. Makhyoun, J. Chim. Phys., 1988, 85, 917–924 CAS
.
- G. L. Malli, J. Chem. Phys., 2006, 124, 071102 CrossRef
.
- C. Thierfelder, P. Schwerdtfeger, A. Koers, A. Borschevsky and B. Fricke, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 022501 CrossRef
.
- J. P. Desclaux and P. Indelicato, The relativistic atomic program MCDFGME V 2005.10, Published at http://dirac.spectro.jussieu.fr/mcdf/ on August 17, 2005, 2005.
- E. Eliav, S. Shmulyian, U. Kaldor and Y. Ishikawa, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 3954–3958
.
- T. H. Dinh, V. A. Dzuba, V. V. Flambaum and J. S. M. Ginges, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 022507 CrossRef
.
- T. H. Dinh, V. A. Dzuba, V. V. Flambaum and J. S. M. Ginges, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 054501 CrossRef
.
- R. A. Penneman, J. B. Mann and C. K. Jørgensen, Chem. Phys. Lett., 1971, 8, 321–326 CrossRef CAS
.
- E. Eliav, U. Kaldor and Y. Ishikawa, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 2765–2769 CrossRef CAS
.
- E. Eliav, U. Kaldor, P. Schwerdtfeger, B. A. Hess and Y. Ishikawa, Phys. Rev. Lett., 1994, 73, 3203–3206 CrossRef
.
-
C. K. Jørgensen, Energy Levels of Complexes and Gaseous Ions, Thesis, Gjellerups Forlag, Copenhagen, 1957 Search PubMed
.
- P. Pyykkö, J. Chem. Res. (S), 1979, 1979, 380–381 Search PubMed
.
- W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 23, 272–295 CrossRef
.
- P. Pyykkö, Int. J. Quantum Chem., 2001, 85, 18–21 CrossRef CAS
.
-
J. C. Slater, Quantum Theory of Atomic Structure, McGraw-Hill, New York, 1st edn, 1960, vol. 1 Search PubMed
.
-
J. C. Slater, Introduction to Chemical Physics, McGraw-Hill, New York, 1st edn, 1939 Search PubMed
.
- P. Pyykkö, Phys. Scr., 1979, 20, 647–651 CrossRef CAS
.
- M. Kaupp, J. Comput. Chem., 2007, 28, 320–325 CrossRef CAS
.
- B. Fricke and J. T. Waber, J. Chem. Phys., 1972, 56, 3246 CrossRef CAS
.
- P. Pyykkö, J. Organomet. Chem., 2006, 691, 4336–4340 CrossRef
.
- J.-P. Dognon, C. Clavaguéra and P. Pyykkö, Angew. Chem., Int. Ed., 2007, 46, 1427–1430 CrossRef CAS
.
- J.-P. Dognon, C. Clavaguéra and P. Pyykkö, C. R. Chim., 2010, 13, 884–888 CrossRef CAS
.
- J.-P. Dognon, C. Clavaguéra and P. Pyykkö, J. Am. Chem. Soc., 2009, 131, 238–243 CrossRef CAS
.
- S. Larsson and P. Pyykkö, Chem. Phys., 1986, 101, 355–369 CrossRef CAS
.
- C. K. Jørgensen, Chem. Phys. Lett., 1968, 2, 549–550 CrossRef
.
- C. K. Jørgensen, Angew. Chem., Int. Ed. Engl., 1973, 12, 12–19 CrossRef
.
-
C. S. G. Phillips and R. J. P. Williams, Inorganic Chemistry. I, Clarendon Press, Oxford, 1965, See pp. 47–52 Search PubMed
.
- N. C. Pyper and I. P. Grant, Proc. R. Soc. London, 1978, 360, 525–543
.
- N. C. Pyper and I. P. Grant, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1885–1900 RSC
.
- S. Riedel and M. Kaupp, Coord. Chem. Rev., 2009, 253, 606–624 CrossRef CAS
.
- D. Himmel, C. Knapp, M. Patzschke and S. Riedel, ChemPhysChem, 2010, 11, 865–869 CrossRef CAS
.
- H. Xiao, H.-S. Hu, W. H. E. Schwarz and J. Li, J. Phys. Chem. A, 2010, 114, 8837–8844 CrossRef CAS
.
- P. Pyykkö, N. Runeberg, M. Straka and K. G. Dyall, Chem. Phys. Lett., 2000, 328, 415–419 CrossRef CAS
.
- W. C. Martin, L. Hagan, J. Reader and J. Sugar, J. Phys. Chem. Ref. Data, 1974, 3, 771–779 CrossRef CAS
.
-
CRC Handbook of Chemistry and Physics, 90th edn, 2009–2010, ed. D. R. Lide, CRC, Boca Raton, FL, 2010 Search PubMed
.
- B. Fricke, E. Johnson and G. M. Rivera, Radiochim. Acta, 1993, 62, 17–25 CAS
.
- E. Johnson, V. Pershina and B. Fricke, J. Phys. Chem. A, 1999, 103, 8458–8462 CrossRef CAS
.
- J. Sugar and V. Kaufman, J. Opt. Soc. Am., 1979, 69, 141–143 CrossRef CAS
.
- C. R. A. Catlow, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1901–1908 RSC
.
- C. Clavaguéra, J.-P. Dognon and P. Pyykkö, Chem. Phys. Lett., 2006, 429, 8–12 CrossRef CAS
.
- M. Straka, K. G. Dyall and P. Pyykkö, Theor. Chem. Acc., 2001, 106, 393–403 CrossRef CAS
.
- X.-F. Wang, L. Andrews, S. Riedel and M. Kaupp, Angew. Chem., Int. Ed., 2007, 46, 8371–8375 CrossRef CAS
.
Footnote |
| † The present work was done in preparation for a lecture at the 150th Anniversary Congress of “Weltkongress Chemie” in 1860 at Karlsruhe on 3–4 September, 2010. |
| This journal is © the Owner Societies 2011 |
