Holstein–Peirls–Hubbard trimer as a model for quadrupolar two-photon absorbing dyes†
Robertino
Pilot
and
Renato
Bozio
*
Consorzio INSTM, UdR Padova, Department of Chemical Sciences, Via Marzolo 1, 35131 Padua, Italy. E-mail: roberto.pilot@unipd.it; renato.bozio@unipd.it; Fax: +39 049 827 5135
First published on 16th November 2010
Abstract
The linear and nonlinear optical properties of a Donor–Acceptor–Donor system have been investigated by using a two-electron three-point-site model system. Some basic features of electron correlations are included in the model by means of a bi-electronic density matrix. The polarizabilities and second hyperpolarizabilities have been computed with a modified version of the Collective Electronic Oscillators (CEO) method which allowed us to include the electron–phonon coupling. Both singly- and doubly-excited states are taken into account in the computation of (hyper-)polarizabilities. The effects of electron–phonon coupling on the two-photon absorption and on the third harmonic generation in the infrared region are discussed.
I. Introduction
The microscopic requirement for obtaining large and fast nonlinear optical (NLO) responses is that molecules possess easily polarizable electronic charge as delocalized π electrons.1 Among other properties, large two-photon absorption (TPA) cross sections are promising for a wealth of applications, including two-photon excited fluorescence microscopy,2 optical limiting3–5 three dimensional optical data storage and up-conversion lasing.Design strategies for improving the cross section of organic molecules have pointed out that symmetric charge transfer from the ends of a conjugated system to the middle, or vice versa, upon excitation is normally associated with large TPA cross sections.6 For instance, symmetric π-conjugated molecules such as E-stilbene show small values of the cross section,7 whereas the presence of two electron Donors (D) at the ends of the E-stilbene, enhances the cross section by 20 times.6 Also quadrupolar structures A–π–D–π–A, where A is an electron Acceptor and π a conjugated bridge, are known to possess very good cross sections.6
The theoretical studies about the nonlinear properties of Donor–Acceptor systems have been following different routes to shed light on the relation between the molecular structure and its optical properties. They differ from each other in mainly two points: (a) the way in which the non-interacting system is treated and (b) the method employed to work out an expression for the dynamic (hyper-)polarizabilities as a function of molecular quantities, within a perturbative approach for the light–matter interaction. By means of the techniques mentioned above, the effect of electron–phonon coupling8–11 has been investigated as well as the role of electron correlation.12,13
Concerning point (a), the approaches commonly exploited to investigate the structure–property relationships rely on two conceptually different ideas. The first one is to treat molecules with oversimplified models where only the processes that are expected to play the main role in the optical response (like intramolecular charge transfer or energy transfer) are included. In spite of the simplicity of the model, this provides a deep insight into the origin of the nonlinearity, making it possible to find out simple relations between electronic parameters (such as the electron donating or withdrawing strengths) and the hyperpolarizabilities.14–17 The second approach involves detailed quantum mechanical calculations performed on series of molecules in which only one characteristic at a time is varied (for instance, the type or length of the π bridge connecting D and A). In this case it is possible to make a direct comparison of the calculated quantities with experiments but, on the other hand, it is more difficult to spot a clear correlation among electronic and structural parameters and the calculated optical properties.
As for point (b), the most widely employed technique is the Sum Over States (SOS) one. It involves the computation of all the eigenenergies and transition dipoles; the polarisabilities are finally expressed as formally infinite sums over excited states.18,19
An alternative approach proposed by Mukamel and his co-workers,20–23 consists in abandoning the eigenstate representation altogether and considering the material system as a collection of “Collective Electronic Oscillators” (CEO). Within this framework, the system is mapped onto the dynamics of coupled electronic oscillators representing the electron-hole pair components of the single-electron reduced density matrix. The principal advantage of the CEO method is that it avoids the calculation of the complete information of a quantum system, that is its set of many electron eigenstates and eigenenergies, thus providing a computational advantage especially useful in the investigation of large systems like linear polyenes, and photosynthetic light harvesting systems.24,25
Another issue in the computation of optical nonlinearities concerns the role that electron–phonon coupling can play in determining NLO dynamical properties. Theoretical studies on vibronic profiles of TPA (especially of large molecules) are not so many: we mention, for instance, the work by Painelli et al. who found quite a strong contribution to TPA due to electron-vibration coupling in Donor–Acceptor molecules (D–A), by employing analytical models.8 Moreover the same subject has been investigated by Agren et al. with a quantum chemical approach, yielding a weak or strong contribution depending on the features of the system.9–11 As for the electron correlation, its importance to the ordering of the levels and to the estimation of the matrix elements of the dipole moments (especially in low dimensional systems such as conjugated polymers or push–pull molecules) has been demonstrated by large scale numerical full configuration interaction calculations.12,13 Moreover, Nakano and co-workers pointed out the role played by the electron correlation in determining the diradical character of open-shell systems and thereby on the (static) second hyper-polarizability of such systems.26
Some features of electron correlation can be included in the calculations, to a very simple level, by defining a two-electron density matrix:33 in this approach both one-electron and two-electron excitations are included
This kind of excited states could be expected to play an important role in the computation of nonlinear polarizabilities, since it implies the displacement of a double amount of charge both from ground to excited state and from excited to excited states. Moreover, the contribution of high energy states, especially to the nonlinear response, is well documented in the literature and represents one of the main drawbacks of the SOS method: truncating the summations limits the accuracy for large systems in particular because the response results from dramatic cancellation between very large positive and negative contributions.27–29
Within the framework outlined above, in this paper we calculate linear and nonlinear properties of a A–π–D–π–A structure treated as a two-electron–three-site system. The polarizabilities are computed with a modification of the CEO approach that implements the electron–phonon coupling.33 Its contribution is estimated both in the IR region and at optical frequencies for the linear and the third order responses. A complete basis set, including single and double excitation, is used.
As a final remark, it must be pointed out that the simulations presented here focus on a single (isolated) molecule, however practical devices are based on solid-state systems. Microscopic properties can be related to macroscopic quantities only under the hypothesis of non-interacting molecules. In particular, spatial coherence of electronic states may yield remarkable enhancements of the nonlinear responses as shown, e.g. for excitonic interactions in J-aggregates.30 On the other hand, many applications of TPA, such as optical limiting, multiphoton up-converted emission and two-photon induced polymerization, utilize composite solid materials in which the active species are present at low concentration levels. Under these circumstances, macroscopic properties are derived by simply summing single molecule contributions and taking into account Lorentz-type local field corrections.
II. Theoretical model
In our approach, a trimer like that shown in Fig. 1 is approximated by a linear three-site, two-electron system (Fig. 2). This scheme is somewhat analogous to the molecules-in-molecule approach sometimes used for quantum chemical calculations. However, in our model the sites are simple point charges that can be occupied by two electrons. The one-electron energies correspond to those of a LUMO localized on the Acceptor group or to a HOMO localized on the Donor group. Making use of bielectronic operators, we also account for the correlation energy of two electrons occupying the same site. The basis states are two-electron configurations corresponding to different ways of distributing electrons with a definite spin among the three sites: six singlet and nine triplet states make up the complete basis set. However, the basis set can be limited to the six singlet configurations, since we rule out any interaction allowing states with different spin functions to mix together.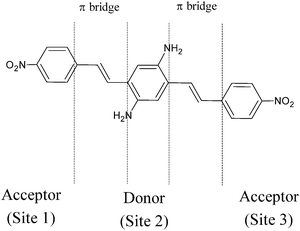 | ||
| Fig. 1 Example of an Acceptor–Donor–Acceptor structure. | ||
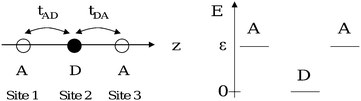 | ||
| Fig. 2 Energy scheme for the Donor and Acceptor orbital energies; all of the sites lie along the same axis (z) and are numbered from the left. tAD allows the electron transfer between 1 and 2 and tDA between 2 and 3. | ||
The trimer can be modelled by means of a Holstein–Peierls–Hubbard Hamiltonian:31
| ĤHPH = ĤH + ĤEMV + ĤEIP + ĤV | (1) |
II. 1 Electronic Hamiltonian
The electronic part of the Hamiltonian (ĤH) is expressed as follows:ĤH = ε(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 1 + 1 + ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 3) + Ud 3) + Ud![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 2↑ 2↑![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 2↓ + Ua( 2↓ + Ua(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 1↑ 1↑![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 1↓ + 1↓ + ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 3↑ 3↑![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 3↓) − tAD 3↓) − tAD![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) AD − tDA AD − tDA![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) DA DA | (2) |
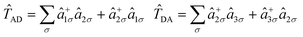 | (3) |
| tAD = 〈ψsite1LUMO|H|ψsite2HOMO〉; tDA = 〈ψsite2LUMO|H|ψsite3HOMO〉 | (4) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) iσ = â+iσâiσ is the number operator for the electrons with spin σ on site i. Ud and Ua are the correlation energy for two-electrons occupying the Donor and Acceptor, respectively. ε is the energy of the LUMO (Acceptor) with respect to the HOMO (Donor): the HOMO energy is set to 0. tAD is the charge transfer integral between the first Acceptor (site 1) and the Donor (site 2); tDA has analogous meaning (Fig. 2). If no electron–phonon coupling takes place, the presence of an inversion center in the trimer implies that tAD = tDA
iσ = â+iσâiσ is the number operator for the electrons with spin σ on site i. Ud and Ua are the correlation energy for two-electrons occupying the Donor and Acceptor, respectively. ε is the energy of the LUMO (Acceptor) with respect to the HOMO (Donor): the HOMO energy is set to 0. tAD is the charge transfer integral between the first Acceptor (site 1) and the Donor (site 2); tDA has analogous meaning (Fig. 2). If no electron–phonon coupling takes place, the presence of an inversion center in the trimer implies that tAD = tDA ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) t. Details about the six singlets used as basis states are given in the ESI (Table S-1).†
t. Details about the six singlets used as basis states are given in the ESI (Table S-1).†
In the literature, the commonly adopted point-site models make use of a reduced description, where only the three lowest states are taken into account:14,48 this approach only accounts for single excitations and it is appropriate to describe the system provided these states are well separated in energy from the upper lying ones (i.e. ε − Ud small compared to ε). Under this assumption, the Hamiltonian eqn (2) simplifies to:
ĤH = ε(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 1 + 1 + ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 3) + Ud 3) + Ud![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 2↑ 2↑![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 2↓ − tAD 2↓ − tAD![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) AD − tDA AD − tDA![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) DA DA | (5) |
The parameter Δ = ε − Ud represents the energy required to go from the neutral configuration with two electrons in D to the ionic configuration with one electron in D and one in A: in other words, it enters in determining, together with the transfer integral t, the weight of the configurations (or resonance structures) [A − D − A],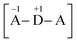 and
and 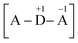 in the ground state. Moreover, in the three-level system, the relation Δ = E21 − E32 holds, where Eij is the energy difference between the eigenstates i and j. It is straightforward to show that
in the ground state. Moreover, in the three-level system, the relation Δ = E21 − E32 holds, where Eij is the energy difference between the eigenstates i and j. It is straightforward to show that 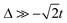 is associated to a mostly neutral ground state,
is associated to a mostly neutral ground state, 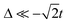 to a mostly ionic one; if
to a mostly ionic one; if 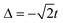 all the ionic and neutral resonance structures have the same weight and this condition is often referred to as the cyanine-limit.32 In this case one electron is still bound in the Donor site and the other one is equally distributed among the three sites, so that the charge distribution is like
all the ionic and neutral resonance structures have the same weight and this condition is often referred to as the cyanine-limit.32 In this case one electron is still bound in the Donor site and the other one is equally distributed among the three sites, so that the charge distribution is like 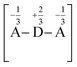 . Notice, however, that the two-photon resonance is simultaneously resonant with the one-photon one (E31 = 2E21) for Δ = 0. From now on, in this paper we shall assume Δ > 0: this is consistent with structures like that shown in Fig. 1, which are usually closed-shell with a neutral ground state.
. Notice, however, that the two-photon resonance is simultaneously resonant with the one-photon one (E31 = 2E21) for Δ = 0. From now on, in this paper we shall assume Δ > 0: this is consistent with structures like that shown in Fig. 1, which are usually closed-shell with a neutral ground state.
II. 2 Vibronic Hamiltonian
We can physically single out two kinds of vibronic coupling, the bond-order (BOV) and the site energy (SEV) ones.33 Keeping in mind that every point-site in our model represents a moiety (i.e. Donor or Acceptor groups), BOV modes account for the modulation of the distance between adjacent sites induced by the vibrational modes of the π-bridges in Fig. 1; on the other hand, SEV modes modulate the HOMO and LUMO energies of the moieties (and therefore the site-energies εAcceptorLUMO and εDonorHOMO). By introducing a linear dependence of the Acceptor and Donor energies on the SEV and a linear dependence of the charge transfer integrals (tAD and tDA) on the BOV, the following terms are obtained (see the ESI,† Appendix 1 for details):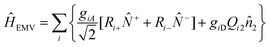 | (6) |
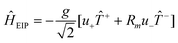 | (7) |
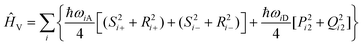 | (8) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ± = ± = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) AD ± AD ± ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) DA DA![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) ± = ± = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 3 ± 3 ± ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 1 1 | (9) |
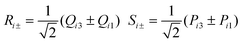 | (10) |
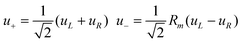 | (11) |
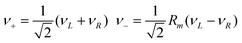 | (12) |
 | (13) |
Q ij , Pij and ωij are the dimensionless coordinates, momenta and the angular frequencies of the i-th SEV normal mode localized on the j-th moiety (for example, with reference to Fig. 1, Qi1 would represent the i-th vibrational mode of nitro-benzene); uL (uR) are the dimensionless coordinates for BOV modes, that is the “stretching” mode between Acceptor 1 and Donor (uL) and between Donor and Acceptor 3 (uR). νL, νR and ω+, ω− are the corresponding dimensionless momenta and angular frequencies. giA and giD are, respectively, the coupling constants for the Acceptor and the Donor SEV modes. Notice that j = 1,3 are the Acceptors on the left and on the right in Fig. 2 respectively, j = 2 is the Donor. The Hellman–Feynman theorem guarantees that only symmetric modes have got non zero SEV coupling constants.31 Symmetric modes belonging to different moieties (Qi1 and,Qi3) can be recast as symmetric (Ri+) and antisymmetric (Ri−) combinations with respect to the inversion centre of the whole molecule. Similarly, u+ and u− are defined as normalized in-phase and out-phase combination of uL and uR.
Fig. 3 gives a pictorial view of the BOV modes u+ and u−. Notice that two states of the same parity (g-states or u-states) can be coupled both by BOV (u+) and by the symmetric SEV modes (Ri+,Qi2). In the same way, an u- and a g-state can be coupled by the antisymmetric combination of the SEV modes of the Acceptors (Ri−) and by a BOV antisymmetric vibration (u−).
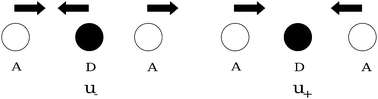 | ||
| Fig. 3 BOV modes. | ||
II. 3 Interaction hamiltonian with the external field
The interaction of the system with an external electromagnetic field is defined by the term:HEXT = −![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) E(t) E(t) | (14) |
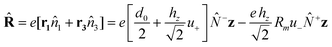 | (15) |
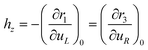 | (16) |
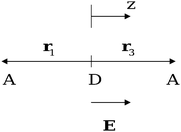 | ||
| Fig. 4 E is polarized along the axis of the trimer (z). | ||
II. 4 The calculation of polarizabilities and hyperpolarizabilities
The procedure we use to work out polarizabilities and hyperpolarizabilities has been already described in a previous publication:33 here, we point out only the main features of this calculation, applied to the trimer structure.To retain the most advantageous feature of the Hubbard model, that is considering explicitly the electron correlation, a variant of the CEO method is employed, by making use of a bielectronic density matrix defined, in second quantization, as:
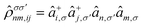 | (17) |
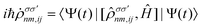 | (18) |
We remind that, once the density matrix is known, the expectation value of any operator (Ô) is known through the relation 〈Ô〉 = Tr[〈Ô〉![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ]: in particular polarizabilities are related to the expectation value of the dipole operator (
]: in particular polarizabilities are related to the expectation value of the dipole operator (![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) ).
).
In order to solve eqn (18) and therefore work out the density matrix elements, the following procedure is adopted.
1. It can be verified that, if the expressions for the vibrational operators are considered explicitly in eqn (18), the equation of motion is not closed because the right term contains three-electron terms. To close the equation of motion, then we employ the Random Phase Approximation (RPA),35 which consists in replacing all the vibrational operators with their expectation values. Appendix 2 in the ESI† provides the expressions for the vibrational operators and their expectation values.
If Ĥ in eqn (18) is replaced with its RPA analogous (ĥT) we get:
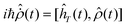 | (19) |
Eqn (19) can now be solved to work out ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) . Eqn (19), recast in the Liouville space, is expanded in power series of the electrical field and an equation is generated at each order (eqn (A4-13)–(A4-15)). A Fourier transform is finally used to solve the differential equations (see Appendix 4† for more details). Once the density operator is known at the first three orders, expressions for polarizabilities and hyperpolarizabilities are easily calculated from the expectation values of the dipole operator (see relations in Appendix 5, ESI†).
. Eqn (19), recast in the Liouville space, is expanded in power series of the electrical field and an equation is generated at each order (eqn (A4-13)–(A4-15)). A Fourier transform is finally used to solve the differential equations (see Appendix 4† for more details). Once the density operator is known at the first three orders, expressions for polarizabilities and hyperpolarizabilities are easily calculated from the expectation values of the dipole operator (see relations in Appendix 5, ESI†).
The basis vectors for the Liouville space are obtained starting from the eigenstates of ĤH (either eqn (2) or (5)). As shown in Appendix 3 in the ESI,† they are not exactly eigenfunctions of the complete Hamiltonian. The convention followed to write the expressions for the polarizabilities and the electrical field is the same as that adopted by Butcher and Cotter.36
At the first order, the equations for the three-level system can be solved analytically and the explicit expression for α is (see Appendix 2 for details and complete explanation of symbols)
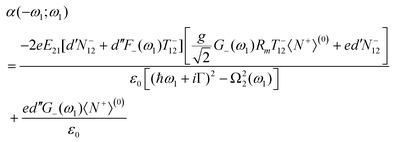 | (20) |
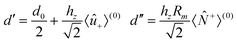 | (21) |
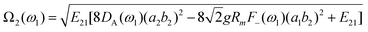 | (22) |
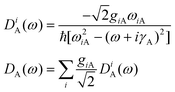 | (23) |
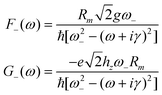 | (24) |
In eqn (20), d′ is the equilibrium distance corrected by the displacement of the potential energy minimum due to the symmetric mode u+ and d′′ stems from the dependence of the distance on u−. d′ and d′′ are responsible for the vibrational contribution to the static hyperpolarizabilities.37,38 The dynamic one is brought about by the propagators F−(ω1), G−(ω1) and DA(ω1). As underlined in the ESI† (Appendix 2), F−(ω1) and G−(ω1) derive from the modulation of the charge transfer integral and of the distance on u− respectively; DA(ω1) is due to the modulation of the site energy on Ri−. As predictable by symmetry considerations, only antisymmetric modes can affect the linear dynamic properties and then appear in the absorption spectrum.
III. Results and discussion
In this section numerical simulations of linear and nonlinear optical properties of the trimer are presented. The simulations are carried out using the following set of parameters, unless differently specified: γi = 20 cm−1; t = 0.30 eV; Ud = Ua = 1 eV; ε = 2 eV; d0 = 6 Å; Γ11 = 100 cm−1; Γ1j = Γj1 = 750 cm−1 (j = 2,3,..,6); Γij = Γji = 1500 cm−1 (i and j = 2,3,..,6); ωA = 2000 cm−1; gA = 0.05 eV; ωD = 1800 cm−1; gD = 0.05 eV; ω+ = 1400; ω− = 1600; g h−1z = 0.5 eV Å−1.31,39,40 They represent typical values adopted for D–A systems. All of the spectra are calculated making use of the complete six-state basis set (unless differently specified) and including both kind of electron phonon coupling. Moreover, the analysis is performed between 0 and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 where the phenomena dependent on the three lowest states are expected to appear.
000 cm−1 where the phenomena dependent on the three lowest states are expected to appear.
III. 1 Effects of electron–phonon coupling
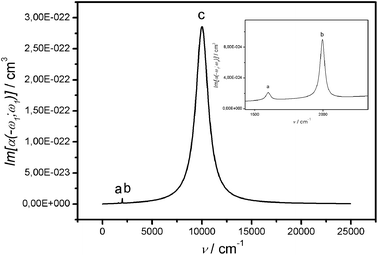 | ||
| Fig. 5 Linear absorption spectrum: imaginary part of α(−ω;+ω). | ||
| Peak | Vib. mode | ω i/cm−1 | Ω i/cm−1 |
|---|---|---|---|
| a | ω − | 1599 | 1600 |
| b | ω A | 1996 | 2000 |
| Peak | Electr. Resonance | Freq./cm−1 | |
|---|---|---|---|
| c | |1〉 → |2〉 | 10 010 | |
With respect to a symmetric dimer case33 the antisymmetric modes include both SEV (Ri−) and BOV ones (u−); the peak intensity of the vibrational resonances, relative to the CT transition, is of the same order of magnitude as in the symmetric dimer studied in ref. 33. Notice that this is just a vibronic contribution that adds up to the usual “ionic” component of the infrared intensity.
The linear coupling introduced by eqn (6) and (7) produces an energy shift of the minima of the electronic surfaces which is non-zero for the symmetric modes (Ri+, Qi2, u+) and zero for the antisymmetric ones (Ri−, u−): the demonstration is straightforward if we recall the equation of motion for the vibrational modes in the time domain (Ri+ for example) from Appendix 2† (eqn (A2-4)):
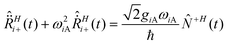 | (A2-4) |
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) −(t)〉 = 〈
−(t)〉 = 〈![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −(t)〉 = 0). As already mentioned in ref. 33, although a well-known spectroscopic consequence of the minimum shift is the appearance of vibronic progressions, the RPA adopted here does not allow us to see them since it reduces the vibrational operators to semiclassical variables.
−(t)〉 = 0). As already mentioned in ref. 33, although a well-known spectroscopic consequence of the minimum shift is the appearance of vibronic progressions, the RPA adopted here does not allow us to see them since it reduces the vibrational operators to semiclassical variables.
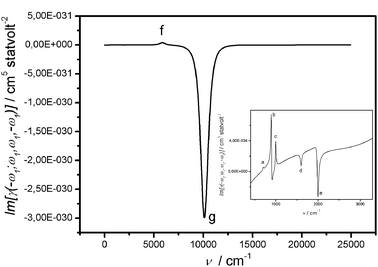 | ||
| Fig. 6 Imγ(−ω1;+ω1,+ω1,−ω1) calculated including electron phonon coupling. | ||
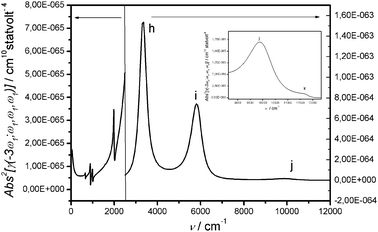 | ||
| Fig. 7 |γ(±3ω1;∓ω1,∓ω1,∓ω1)|2 calculated including electron phonon coupling. | ||
| Peak | Vibr. modea | Frequency/cm−1 |
|---|---|---|
| a | ω + (2 ph) | 700 |
| b | ω D (2 ph) | 894 |
| c | ω A (2 ph) | 1000 |
| d | ω − (1 ph) | 1598 |
| e | ω A (1 ph) | 1998 |
| Peak | Electr. resonancea | Frequency/cm−1 |
|---|---|---|
| a In brackets it is indicated whether the peak is a one, two or three photon resonance. b The frequency of the vibrational modes (peaks from “a” to “g”) is read from the Imγ(−3ω;+ω,+ω,+ω) (Fig. S-11). | ||
| h | |1〉 → |2〉(3ph) | 3352 |
| i | |1〉 → |3〉(2ph) | 5802 |
| j | |1〉 → |2〉(1ph) | 9752 |
| k | |1〉 → |5〉(3ph) | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 560 560 |
The trimer is a centrosymmetric structure: g → u electronic transitions are allowed as one-photon resonances (Kerr component) or as one- and three-photon ones (THG component) and g → g electronic transitions are allowed as two-photon resonances (Kerr and THG component). Similarly, antisymmetric modes appear as one-photon resonances (Kerr) or one- and three-photon ones (THG) and symmetric modes appear as two-photon resonances (Kerr and THG component). As in the linear spectrum, the calculated vibrational frequencies (ωi) are downshifted with respect to the input frequencies (Ωi) (Kerr and THG).31,33 In comparison with the symmetric dimer,33 vibrations show resonances which are much weaker, particularly so for the THG components.
Out of resonance, the electron–phonon coupling affects the spectra only by 1–3%, both in the Kerr and in the THG spectra. We remind however that, as already mentioned in ref. 33 and section II.4, within our approach vibronic progressions are not reproduced: only the redistribution of intensity among charge transfer resonances and vibrational resonances in the infrared are accounted for. In ref. 9–11 vibronic coupling is introduced in the calculation of TPA spectra through a Herzberg–Teller approach. Vibronic progressions and intensity redistributions are properly accounted for as a result of the coupling of the two-photon state with a number of other excited states not limited to charge transfer ones. This makes the comparison with our approach of limited value.
Summarizing, the vibronic coupling, treated as explained in section II.2, accounts for the following spectral effects:
1. Downshift of the input vibrational frequency in the linear, Kerr and THG spectra.
2. In the infrared region, appearance of: antisymmetric modes (one-photon resonant in the linear and Kerr spectrum, one- and three-photon resonant in the THG spectrum) and symmetric modes (two-photon resonant in the Kerr and the THG spectrum).
III. 2 TPA properties of the trimer
An interesting characteristic of the quadrupolar structures is that they can be good candidates for applications that exploit the TPA phenomenon.14 The latter can be enhanced if the incident fundamental frequency is near (but not quite inside) that of an allowed transition, thus in our case when the three levels are almost equally spaced. This condition is fulfilled for Δ = 0: it should be noticed that the same situation does not exist in a radical dimer structure because U cannot be zero. The enhancement condition for TPA is known in the literature for example from the work of Brédas et al.,13,32,42,43 Rebane et al.44 and Blanchard-Desce and Barzoukas.14Fig. 8 shows that decreasing ε results in a decrease of Δ, and thus drives the system towards the condition Δ = 0 (solid and dashed lines correspond to the complete and reduced basis set respectively). It is worth noting that for small ε the upper-lying levels get closer to the three lowest levels. Although in terms of eigenenergies this does not cause large corrections (both in the reduced and in the complete description the lowest 3 levels have roughly the same energy), the inclusion in the model of the higher-lying states increases the number of terms in the expression for γ; moreover, as already mentioned, they correspond to double excitations and are consequently associated to large charge displacements in the molecule.
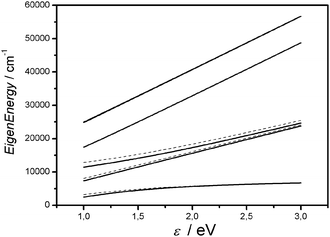 | ||
| Fig. 8 Electronic energies for the six level model (solid line) and for the three level one (dashed line) as a function of ε. The highest two levels are almost degenerate. | ||
Fig. 9 shows how the TPA cross section changes as a function of Δ (the cross section is defined in the ESI,† Appendix 6): solid and dashed lines correspond to the complete and reduced basis set respectively. Delta (Δ), defined as Δ = E21 − E32,45 was varied by changing the value of ε (from 1.75 to 3 eV in 0.25 eV steps). The electron–phonon coupling has not been included because of its very low contribution to the NLO response at optical frequencies. The trend agrees with the resonance enhancement expected. Fig. 10 reports the TPA peak cross section as a function of Δ: the circles and the squares correspond respectively to full and reduced basis set calculation. It can be noticed that the inclusion of double excitations lowers the computed cross sections: this effect is more remarkable in pre resonant conditions, in fact it amounts to about 20% for ε = 1.75 eV and to about 5% for ε = 3 eV. Fig. 11 shows the detuning between the one-photon absorption band (Γ12 = 750 cm−1) and the photon frequencies (2hν = E31) at different values of ε (vertical lines: label 6 → ε = 3 eV, label 5 → ε = 2.75 eV and so on). Along with Fig. 10, Fig. 11 provides a correlation between the detuning and the trend of σ2. As we can see, shifting the detuning from 8100 cm−1 (label 6) to 3200 cm−1 (label 1) provides a five-fold enhancement of σ2. Notice that in tuning the value of ε not only are the relative energies of the levels modified, but also the transition dipole moments.
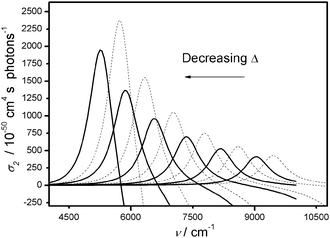 | ||
| Fig. 9 Decreasing Δ shifts the TPA peaks to lower frequencies and increases their intensities. Dashed lines refer to the calculation performed with the reduce basis set (3 states) and solid lines to the full basis set (6 states). Negative values of σ2 indicate saturation of the one-photon transition. ν is the photon frequency. | ||
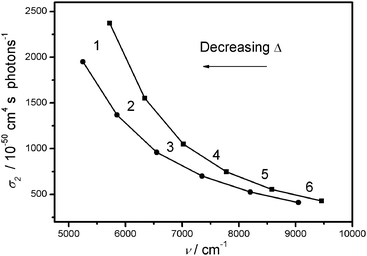 | ||
| Fig. 10 Maxima of TPA cross section as a function of the transition frequency. Squares refer to the calculation performed with the reduce basis set (3 states) and circles to the full basis set (6 states) (label 6 → ε = 3 eV, label 5 → ε = 2.75 eV and so on). | ||
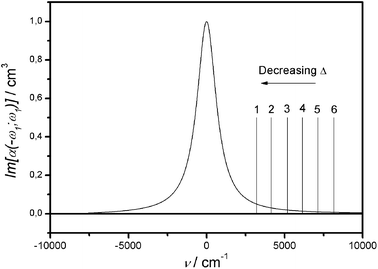 | ||
| Fig. 11 Detuning between the one-photon absorption band (Γ12 = 750 cm−1) and the photon frequencies (2hν = E31) at different values of ε (vertical lines: label 6 → ε = 3 eV, label 5 → ε = 2.75 eV and so on). | ||
The parameter ε represents the difference between the energy of the Acceptor LUMO and of the Donor HOMO, that is approximately the difference between the electronic affinity of A and the ionisation energy of D: ε is then related to the relative strength of D and A. It can be experimentally modified in molecule in Fig. 1, for example, either substituting the kind of D and A or just modifying the polarity of the solvent.14,46 For instance, more polar solvents and stronger D and A play a similar effect on the system in the sense that they both tend to increase the ground state ionicity and to reduce the transition energy. In the end, by inspection of a simplified formula, valid for the reduced three level system,47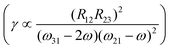 it can be verified that, in analogy to what is already known from the literature, decreasing Δ increases both the transition dipoles and it creates simultaneously resonant factors in the denominator.14 Moreover, the relation between the transition dipole moment and Δ agrees with the work of Cho who found an analogous trend for linear quadrupolar molecules both employing a valence-bond charge-transfer model16 and by using ab initio calculation methods.48
it can be verified that, in analogy to what is already known from the literature, decreasing Δ increases both the transition dipoles and it creates simultaneously resonant factors in the denominator.14 Moreover, the relation between the transition dipole moment and Δ agrees with the work of Cho who found an analogous trend for linear quadrupolar molecules both employing a valence-bond charge-transfer model16 and by using ab initio calculation methods.48
In conclusion, concerning the validity of the reduced model within the set of parameters we have adopted, from Fig. 10 and 11 we can see that when the photon energy is about 3000 cm−1 (Γ12 = 750 cm−1) the corrections to the values of TPA are already around 20%. Therefore, this suggests some care in the use of an essential state model when close to pre-resonant conditions. The pre resonant enhancement has been experimentally demonstrated in porphyrins by Rebane et al.44,49and in symmetric substituted diacetylene by Kondo et al.50 In some other classes of compounds like perylene derivatives,51porphyrin dimers52 and substituted donor–acceptor squaraines,53 a pre-resonant effect has been claimed as a mechanism for explaining the unusually large TPA cross sections (even normalized per number of electrons) measured at small detuning energies. A quantitave estimation of the pre-resonant effect has been undertaken by Brèdas et al.43 in fluorene derivatives (both dipolar (D–π–A) and centrosymmetric (D–π–D)) by degenerate and nondegenerate two-photon absorption spectroscopy. The latter technique allowed them to tune independently the frequency of two laser beams so that one could be set at the desired detuning from the one-photon allowed transition while keeping the sum of the two frequencies two-photon resonant. The Intermediate Resonance Enhancement (ISRE) has been evaluated comparing the TPA cross sections in conditions of “large” and “small” detuning. They found for the symmetric compound a ISRE of 4.8 going from 0.2 eV (1600 cm−1) to 1.2 eV (9000 cm−1). Although a comparison with the simulations presented in this paper is difficult (calculated TPA cross sections are degenerate; varying Δ means tailoring the Donor–Acceptor strengths and therefore the relative energy of the levels) we may consider our data at least comparable to the experimental results in ref. 43.
III. 3 Comparison of the optical response between the symmetric dimer and the trimer
It is worth comparing the analytical expression available for the polarizabilities and hyperpolarizabilities of the trimer and of the symmetric dimer (see ref. 33). Since electron–phonon coupling did not show a large contribution at optical frequencies in any of the two cases, it has not been included. Table S-3 in the ESI† summarises the expressions for the above mentioned systems.Looking at the expressions for the transition energies shown in Table S-3,† it can be realised that choosing the parameter Δ for the trimer equal to the parameter U for the dimer the three levels exhibit the same energy difference in both systems: it is worth noticing that Δ and U have, for each structure, the same physical meaning, in fact they correspond to the energy necessary to transfer an electron from the ground configuration to the first excited one. If we assume that d and d/2 are the equilibrium distances for the trimer and the dimer respectively it can be easily shown that
| (R231)D = (R221)T (R223)D = (R232)T | (25) |
Then
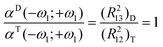 | (26) |
It is obvious that with the parameter set chosen to compare the dimer and the trimer, not only will the linear response be the same, but also the non-linear one: we are working in fact with two systems that have the same transition energies and the same transition dipoles. In conclusion we can expect that, in these conditions, the equalities
| (γ(−ω;ω,ω,−ω))D = (γ(−ω;ω,ω,−ω))T | (27) |
| (γ(−3ω;ω,ω,ω))D = (γ(−3ω;ω,ω,ω))T | (28) |
Summarizing, based on very simple quantum mechanical models, we can say that the optical properties of the dimer and of the trimer should be comparable, provided the difference between electronic affinity and ionization energy of the acceptor and the donor is the same in both systems. It should be noticed that, while in the dimer it is the same moiety that works as a donor and as an acceptor, in the trimer donor and acceptor are different units. As already mentioned, however, only in the trimer the electron affinity and the ionization potential of A and D can be separately varied to tailor the TPA properties of the molecule.
IV. Conclusions
Making use of a simple quantum chemical model, the goal of our investigation has been to study the NLO responses of a symmetric A–π–D–π–A structure. Since we focused on the role of the CT interactions from the standpoint of describing its electronic properties, the trimer has been treated as a two-electron three-point-site system. In order to derive the final expressions for the polarizability and the second hyperpolarizability, we made use of a modified version of the CEO method implementing the linear electron phonon coupling and a bi-electronic density matrix.The use of a bielectronic density matrix in a two electron system allowed us to account for electron correlation (on-site correlation only); double excited states were included in the calculation along with single excited ones. It has been recognized that higher CT states come into play especially in pre-resonant conditions, thus when the system is simultaneously two-photon resonant and “nearly” one-photon resonant. TPA cross sections calculated with the full basis set turned out to be from 20% (small Δ) to 5% (large Δ) lower that the ones calculated with the reduced basis set. Notice that this effect could not be recognized in models14,17 that took into account one-electron energies only. These data suggest that care must be taken when calculating TPA cross-sections in pre-resonant conditions with a reduced model: within our set of parameters, for a detuning of about 3000 cm−1, 20% corrections arise. The use of a calculation technique based on a bi-electronic density matrix is expected to be of relevance for tackling the study of strongly correlated systems with more than two electrons (i.e. more complex systems than the one studied in this paper).
As for the vibronic coupling in the first order spectrum the order of magnitude of the vibrational transition intensity (compared to the charge transfer transition) is roughly the same as in the dimer structure in ref. 33; in third order spectra the vibrational resonance intensities are remarkably weaker in the trimer than in the dimer, particularly so for the THG spectra. Moreover, two and three photon vibrational resonances show up in the third order spectra.
The effect of vibronic coupling at optical frequency was recognized to be quite small (about 1–3%): however, since within our approach vibronic progressions are not reproduced, only the redistribution of intensity among charge transfer resonances and vibrational resonances in the infrared was included in our estimation. The lack of vibronic progressions in our spectra is not surprising due to the use of the Random Phase Approximation.
Finally, we recognized that varying Δ to reduce the detuning from ∼8000 cm−1 to ∼3200 cm−1 in degenerate TPA provides a five-fold enhancement of σ2, within our choice of parameters.
Numerical methods
All numerical simulations were performed by a FORTRAN program written by the author (RP) and running on a LINUX platform.Acknowledgements
Financial support by the Italian Ministry of Education, University and Research through the FIRB Contract No. RBNE033KMA and by the National Research Council through the CNR-INSTM programme PROMO is gratefully acknowledged.Notes and references
- P. N. Prasad and D. G. Williams, Introduction to Nonlinear Optical Effects in Molecules and Polymers, John Wiley & sons, New York, 1991 Search PubMed.
- R. H. Kohler, J. Cao, W. R. Zipfel, W. W. Webb and M. R. Hansen, Science, 1997, 276, 2039 CrossRef CAS.
- J. E. Ehrlich, X. L. Wu, I. Y. S. Lee, Z. Y. Hu, H. Rockel, S. R. Marder and J. W. Perry, Opt. Lett., 1997, 22(24), 1843 Search PubMed.
- A. A. Said, C. Wamsley, D. J. Hagan, E. W. Van Stryland, B. A. Reinhard, P. Roderer and A. G. Dillard, Chem. Phys. Lett., 1994, 228, 646 CrossRef CAS.
- G. S. He, R. Gvishi, P. N. Prasad and B. A. Reinhardt, Opt. Commun., 1995, 117, 133 CrossRef CAS.
- M. Albota, D. Beljonne, J. L. Brédas, J. E. Ehrlich, J. Y. Fu, A. A. Heikal, S. E. Hess, T. Kojey, M. D. Levin, S. R. Marder, D. McCord-Maughon, J. W. Perry, H. Rockel, M. Rumi, C. Subramaniam, W. W. Webb, X. L. Wu and C. Xu, Science, 1998, 281, 1653 CrossRef CAS.
- R. J. M. Anderson, G. R. Holtom and W. M. McClain, J. Chem. Phys., 1979, 70(9), 4310 CrossRef CAS.
- A. Painelli, L. Del Freo and F. Tereziani, Chem. Phys. Lett., 2001, 346, 470 CrossRef CAS.
- Y. Luo, P. Norman and H. Agren, Chem. Phys. Lett., 1999, 303, 616 CrossRef CAS.
- P. Macak, Y. Luo and H. Agren, Chem. Phys. Lett., 2000, 330, 447 CrossRef CAS.
- N. Lin, X. Zhao, A. Rizzo and Y. Luo, J. Chem. Phys., 2007, 126, 244509 CrossRef.
- S. Etemand and Z. G. Zoos, Spectroscopy of Advanced Materials, Wiley, Chichester, 1991 Search PubMed.
- E. Zojer, D. Beljonne, T. Kogej, H. Vogel, S. R. Marder, J. W. Perry and J. L. Brédas, J. Chem. Phys., 2002, 116, 3646 CrossRef CAS.
- M. Barzoukas and M. Blanchard-Desce, J. Chem. Phys., 2000, 113, 3951 CrossRef CAS.
- A. Painelli, Chem. Phys. Lett., 1998, 285, 352 CrossRef CAS.
- S. Hahn, D. Kim and M. Cho, J. Phys. Chem. B, 1999, 103, 8221 CrossRef CAS.
- W. H. Lee, H. Lee, J. A. Kim, J. H. Choi, M. Cho, S. J. Jeon and B. R. Cho, J. Am. Chem. Soc., 2001, 123, 10658 CrossRef CAS.
- D. S. Chemla and J. Zyss, Nonlinear Optical Properties of Organic Molecules and Crystals, Academic Press, New York, 1978 Search PubMed.
- J. L. Brédas, C. Adant, P. Tackyx, A. Persoon and B. M. Pierce, Chem. Rev., 1994, 94, 243 CrossRef CAS.
- A. Takahashi and S. Mukamel, J. Chem. Phys., 1994, 100, 2366 CrossRef CAS.
- G. Chen and S. Mukamel, J. Am. Chem. Soc., 1995, 117, 4945 CrossRef CAS.
- S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171 CrossRef CAS and references therein.
- S. Mukamel, Principles of Nonlinear Spectroscopy, Oxford University Press, New York, 1995 Search PubMed.
- G. Chen and S. Mukamel, Chem. Phys. Lett., 1995, 240, 296 CrossRef CAS.
- S. Mukamel, S. Tretiak, T. Wagersreiter and V. Chernyak, Science, 1997, 277, 781 CrossRef CAS.
- M. Nakano, R. Kishi, S. Ohta, H. Takahashi, T. Kubo, K. Kamada, K. Ohta, E. Botek and B. Champagne, Phys. Rev. Lett., 2007, 99, 033001 CrossRef.
- A. Garito, J. R. Heflin, K. Y. Wong and O. Zamani-Khamiri, Organic Materials for Nonlinear Optics, Royal Society of Chemistry, London, 1989 Search PubMed.
- Z. Shuai, D. Beljonne and J. L. Brédas, J. Chem. Phys., 1992, 97, 1132 CrossRef CAS.
- D. Beljonne, Z. Shuai and J. L. Brédas, J. Chem. Phys., 1993, 98, 8819 CrossRef CAS.
- E. Collini, C. Ferrante and R. Bozio, J. Phys. Chem. B, 2005, 109, 2 CrossRef CAS.
- R. Bozio and C. Pecile, Spectroscopy of Advanced Materials, Wiley, Chichester, 1991 Search PubMed.
- T. Kogej, D. Beljonne, F. Meyers, J. W. Perry, S. R. Marder and J. L. Brédas, Chem. Phys. Lett., 1998, 298, 1 CrossRef CAS.
- R. Pilot and R. Bozio, J. Phys. Chem. B, 2005, 109, 19082 CrossRef CAS.
- An analytical expression for hz can be easily obtained choosing m1 = m2: then
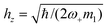 .
. - J. M. Ziman, Elements of Advanced Quantum Theory, Cambridge University Press, Cambridge, 1969 Search PubMed.
- P. N. Butcher and D. Cotter, The Elements of Nonlinear Optics, Cambridge University Press, Cambrige, 1990 Search PubMed.
- A. Painelli, Chem. Phys. Lett., 1998, 285, 352 CrossRef CAS.
- L. Del Freo, F. Terenziani and A. Painelli, J. Chem. Phys., 2002, 116, 755 CrossRef.
- R. Bozio, R. Feis, I. Zanon and C. Pecile, J. Chem. Phys., 1989, 91, 13 CrossRef CAS.
- D. Pedron, A. Speghini, V. Mulloni and R. Bozio, J. Chem. Phys., 1995, 103, 2795 CrossRef CAS.
- G. Fisher, Vibronic Coupling, Academic Press, New York, 1984 Search PubMed.
- S. Ohira, I. Rudra, K. Schmidt, S. Barlow, S.-J. Chung, Q. Zhang, J. Matichack, S. R. Marder and J.-L. Brédas, Chem.–Eur. J., 2008, 14, 11082 CrossRef CAS.
- J. M. Hales, D. J. Hagan, E. W. Van Stryland, K. J. Schafer, A. R. Morales, K. D. Belfield, P. Pacher, O. Kwon, E. Zojer and J. L. Brédas, J. Chem. Phys., 2004, 121(7), 3152 CrossRef CAS.
- M. Drobizhev, A. Karotiki, M. Kruk and A. Rebane, Chem. Phys. Lett., 2002, 355, 175 CrossRef CAS.
- We remind that in the three-level system Δ can be defined either as Δ = ε-Ud or as Δ = E21-E32. However, in the six-level system the equality ε-Ud = E21-E32 is no longer valid and we have chosen to define Δ = E21-E32.
- M. Barzoukas, C. Runser, A. Fort and M. Blanchard-Desce, Chem. Phys. Lett., 1996, 257, 531 CrossRef CAS.
- R. Bozio, E. Cecchetto, G. Fabbrini, C. Ferrante, M. Maggini, E. Menna, D. Pedron, R. Ricco’, R. Signorini and M. Zerbetto, J. Phys. Chem. A, 2006, 110, 6459 CrossRef CAS.
- W. H. Lee, M. Cho, S. J. Jeon and B. R. Cho, J. Phys. Chem. A, 2000, 104, 11033 CrossRef CAS.
- M. Drobizhev, Y. Stephanenco, Y. Dzenis, A. Karokti, A. Rebane, P. N. Taylor and H. L. Anderson, J. Am. Chem. Soc., 2004, 126, 15352 CrossRef CAS.
- K. Kamada, K. Ohta, Y. Iwase and K. Kondo, Chem. Phys. Lett., 2003, 372, 386 CrossRef CAS.
- D. S. Correa, S. L. Oliveira, L. Misoguti, S. C. Zilio, R. F. Aroca, C. J. L. Costantino and C. R. Mendoça, J. Phys. Chem. A, 2006, 110, 6433 CrossRef CAS.
- K. Ogawa, A. Ohashi, Y. Kobuke, K. Kamada and K. Ohta, J. Phys. Chem. B, 2005, 109, 22003 CrossRef CAS.
- S. J. Chung, S. Zheng, T. Odani, L. Beverina, J. Fu, L. A. Padilha, A. Biesso, J. M. Hales, X. Zhan, K. Schmidt, A. Ye, E. Zojer, S. Barlow, D. J. Hagan, E. Van Stryland, Y. Yi, Z. Shuai, G. A. Pagani, J. L. Brédas, J. W. Perry and S. R. Marder, J. Am. Chem. Soc., 2006, 128, 14444 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Further details and appendices. See DOI: 10.1039/c0cp00998a |
| This journal is © the Owner Societies 2011 |
