Structure and dynamics of the Zr4+ ion in water
Received
27th July 2010
, Accepted 13th October 2010
First published on 22nd November 2010
Abstract
The four-times positively charged zirconium ion in aqueous solution was simulated, using an ab initio quantum mechanical charge field molecular dynamics approach. As no hydrolysis reaction occurred during the simulation time of 10 ps, the target of this study was the evaluation of the structure and dynamics of the monomeric hydrated zirconium(IV) ion. The ion forms three hydration shells. In the first hydration shell the ion is 8-fold coordinated with a maximum probability of the Zr–O distance at 2.25 Å. While no exchanges occurred between the first and second shell, the mean residence time of the water molecules in the second shell is 5.5 ps. A geometry of the first hydration shell in-between a bi-capped trigonal prism and a square antiprism was found and a Zr–O force constant of 188 N m−1 was evaluated.
1. Introduction
In nature, zirconium occurs as the mineral Zircon (ZrSiO4) or as Baddeleyite (ZrO2).1 Zirconium's excellent resistance to corrosion and its low cross-section for thermal neutrons make this metal important in the nuclear industry.1 Pumps, valves and surgical implants are further applications that make use of its resistance to corrosion.1,2 The chemistry of the Zr4+ ion in water is very complex due to hydrolysis reactions and polymer formations. While Ti4+, an element of the same group, is not stable in aqueous solutions, hydrated Zr4+ and Hf4+ are reported to be stable in solutions with a pH below 0 and a concentration smaller than 10−4 mol dm−3.3,4 In more concentrated and less acidic solutions the hydrolysis product [Zr4(OH)8(OH2)16]8+ is the dominant species.4,5 Experimental4,6,7 and theoretical studies8,9 have investigated the structure of the hydrolysis products but only the experimental studies4 have investigated the structure of monomeric hydrated zirconium(IV).
2. Methods
2.1 Simulation method
The quantum mechanical charge field (QMCF) molecular dynamcs (MD) approach10 is, like conventional quantum mechanics/molecular mechanics (QM/MM) methods,11,12 based on the partition of the simulation box. The chemically most relevant part is described by a quantum mechanical technique and the remaining part is treated by means of classical mechanics. The main difference between these two simulation techniques is the QM region which in the case of the QMCF approach is larger and consists of 2 subregions: the core zone and the solvation layer. The core region contains the solute and the first hydration shell and the solvation layer includes another shell of solvent molecules. Due to the large radius of the QM region, non-coulombic interactions between the molecules located in the core region and in the MM zone are negligible and thus this method does not require the construction of any other potential functions except those for solvent–solvent interactions. In conventional QM/MM simulations, the construction of suitable solute–solvent potentials is a time consuming and sometimes infeasible step, especially for strongly polarizing ions like Zr(IV).| | 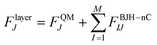 | (2) |
| | 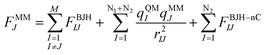 | (3) |
The forces acting on a particle J in the core zone FJcore are treated by QM (eqn (1)). In the solvation layer the quantum mechanical forces are supplemented by the interactions of the particles with the MM atoms obtained from the BJH-CF2 water model13,14 (eqn (2)). In the MM region the forces are composed of the forces of the BJH-CF2 water model augmented by the coulombic forces exerted by all the atoms in the core region (N1) and the solvation layer (N2), and the non-coulombic forces exerted by all atoms in the solvation layer (N2) (eqn (3)). For the calculation of the QM/MM coulomb contributions, the partial charges of the particles in the QM region are obtained via Mulliken population analysis15 which has proven most compatible with the BJH-CF2 water model.21 The influence of the particles in the MM region onto the QM region is taken into account via a perturbation term of the core Hamilton operator:| | 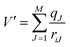 | (5) |
where M is the number of particles in the MM zone and qJ the partial charges of these atoms. To guarantee a smooth transition of the molecules between the solvation layer and the MM region a smoothing function is employed for the atoms of the molecules located in the so-called smoothing region (usually 0.2 Å thick):| | | FjSmooth = S(r)(Fjlayer − FjMM) + FjMM | (6) |
where,| | 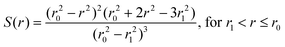 | (8) |
r is the distance of a given solvent molecule (centre of mass) from the center of the box, r0 the radius of the QM region and r1 the inner border of the smoothing region.
The choice of the basis set is a crucial step for QMCF MD simulations. While the DZP basis set (Dunning)16 was used for oxygen and hydrogen, different basis sets (LANL2DZ ECP,17SBKJC ECP18 and Def2-SV(P))19 were tested for zirconium(IV) by performing geometry optimisations for [Zr(H2O)n]4+ (n = 1, 2, 3, 4, 6 and 8) species in the gas phase with the software package GAUSSIAN 03.
All basis sets delivered good results concerning binding energies and Zr–O distances. LANL2DZ ECP17 was chosen for this simulation based on its favourable computation time. To estimate the effect of electron correlation during the simulation, cluster calculations at HF, MP2, B3LYP and CCSD levels with the LANL2DZ ECP basis set were performed (Tables 1 and 2). The average hydration energies calculated by HF show a negligible difference compared to the correlated CCSD method. In the case of the semiempirical B3LYP approach the effect of electron correlation was overestimated and the difference became more significant. Due to the fact that only HF and B3LYP are computationally affordable at present, HF was to be preferred and, therefore, used for this simulation. Generally in a strongly polarized system like Zr(IV) in water the energy contribution resulting from electron correlation is small compared to the electrostatic energy contributions.
Table 1 Binding energies in kcal mol−1 obtained from cluster calculations at HF, MP2, CCSD and B3LYP levels
|
N
|
HF
|
MP2 |
CCSD
|
B3LYP |
| 1 |
−213 |
−235 |
−226 |
−265 |
| 2 |
−183 |
−196 |
−191 |
−218 |
| 3 |
−172 |
−183 |
−178 |
−201 |
| 4 |
−159 |
−168 |
−164 |
−182 |
| 6 |
−136 |
−142 |
— |
−151 |
| 8 |
−115 |
−121 |
— |
−127 |
Table 2 Bond distances in Å obtained from cluster calculations at HF, MP2, CCSD and B3LYP levels
|
N
|
HF
|
MP2 |
CCSD
|
B3LYP |
| 1 |
1.97 |
1.99 |
1.99 |
1.98 |
| 2 |
2.05 |
2.06 |
2.06 |
2.07 |
| 3 |
2.06 |
2.06 |
2.06 |
2.06 |
| 4 |
2.10 |
2.09 |
2.10 |
2.10 |
| 6 |
2.18 |
2.17 |
— |
2.18 |
| 8 |
2.27 |
2.25 |
— |
2.26 |
QMCF MD simulations have been performed with various metal cations at the HF level with double ζ basis sets and have delivered excellent results at a manageable computational effort.20–22
2.2 Evaluation of structure and dynamics
In order to evaluate the structure, besides the radial distribution functions (RDF) and the angular distribution functions (ADF), the local density corrected three-body distribution functions23 were also used, which are denoted as f(3)O–X–O(s,r,s) and formulated as follows:| | 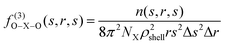 | (10) |
where NX is the number of species X and n(s,r,s) is the average number of O–X–O triples with X–O distances ranging from s − (Δs/2) (inner border of the shell) to s + (Δs/2) (outer border of the shell). ρshell is the average density of the shell:| | 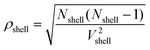 | (11) |
The local density corrected three body distribution functions were evaluated in order to get qualitative and quantitative information about the solvent structure in a given solvation shell by comparing it to the bulk structure.
To obtain information about the dynamics, the vibrational spectrum was calculated using velocity autocorrelation functions (VACF):
| | 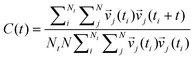 | (12) |
N is the number of particles,
Nt is the number of time origins
ti, and
vj denotes a certain velocity component of the particle. Choosing 2000 time origins the vibrational spectrum was obtained
via Fourier transformation. The force constant was calculated using
eqn (13), where
μ is the reduced mass and
ν the frequency.
In Hartree–Fock calculations the frequencies are frequently scaled by a factor of 0.89
24,25 in order to correct the missing treatment of electron correlation and the vacuum environment. The values of this study were not scaled by this factor, as this simulation provided a
solvent environment and the contribution of electron correlation was, as proven by cluster calculations, small.
The mean residence time (MRT) of a ligand in a certain shell was calculated by the direct method:26
| | 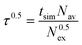 | (14) |
where
tsim is the duration of the simulation,
Nav is the average number of particles in the respective shell and
N0.5ex is the number of exchanges with a
ligand displacement time of more than 0.5 ps which is the mean lifetime of a hydrogen bond, determined by femtosecond laser-pulse
spectroscopy.
27
R
ex, which indicates the number of attempts needed for a successful exchange, is given by the ratio of the total number of exchange attempts and the number of exchanges with a displacement of more than 0.5 ps (eqn (15)).
| | 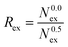 | (15) |
2.3 Simulation protocol
For the QMCF MD simulation a cubic box with side length of 31.1 Å was used, containing one Zr4+ ion and 1000 water molecules. The periodic boundary conditions were employed and a canonical NVT ensemble was chosen, whose temperature was kept constant at 298.15 K using the Berendsen algorithm28 (relaxation time 0.1 ps). The density of the system was fixed at 0.997 g cm−3, which is the density of pure water at 298.15 K. For the description of the MM water molecules the flexible BJH-CF2 water model13,14 was used, which has proven in previous simulations that a continuous transition between QM and MM regions is granted. To solve the equations of motion a predictor–corrector algorithm with 0.2 fs timesteps was employed. The radius of the core zone was set to 3.0 Å and the solvation layer ranged from 3.0 Å to 5.7 Å. The smoothing function extended from 5.5 Å to 5.7 Å. To correct the cutoff of long-range electrostatic interactions the reaction field method was employed.29 Sampling was performed every fifth step and the whole simulation time was 10 ps. As a starting geometry the final geometry of a previous MM simulation of As(III) in aqueous solution was taken. Before sampling the system was equilibrated for 3ps with an intermediate heating to 600 K.
3. Results and discussion
During the simulation time of 10 ps the four-times positively charged zirconium ion was stable. Simulations at higher temperatures (>600 K) showed, however, a reproducible hydrolysis reaction, resulting in a hydroxy group in the first shell and a hydronium ion in the second shell. Despite this tendency toward hydrolysis, suggesting hydrolysis reactions to be also observed at 298 K at longer simulation times, the target of this study was the structure and dynamics of the monomeric hydrated zirconium(IV), and further discussion will therefore be focused on this species.
3.1 Structure
As shown in the radial distribution functions of Zr–O and Zr–H (Fig. 1) the Zr4+ ion forms two well defined hydration shells and even beyond the second shell there seems to be a slight ordering of water molecules. In Table 3 the peak maxima and minima of the Zr–O and Zr–H RDF are listed.
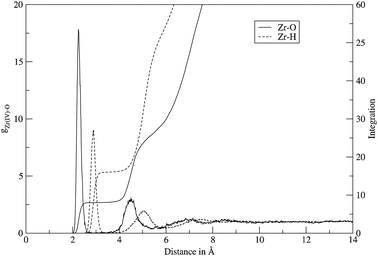 |
| | Fig. 1 The Zr–O (solid line) and Zr–H (dashed line) radial distribution functions and integration for Zr4+ in aqueous solution obtained from the QMCF MD simulation. | |
Table 3 Values for maxima rM and minima rm of the radial distribution functions in Å and the average coordination numbers for the first (CNav,1) and second shell (CNav,2)
| |
r
M1
|
r
m1
|
r
M2
|
r
m2
|
CN
av,1
|
CN
av,2
|
| Zr–O |
2.25 |
3.89 |
4.48 |
5.68 |
8 |
17.8 |
| Zr–H |
2.89 |
3.95 |
5.03 |
5.98 |
16 |
35.6 |
For the first hydration shell the Zr–O maximum was found at 2.25 Å which is in reasonable agreement with the extended X-ray absorption fine structure spectroscopic study of Hagfeldt et al. that reported a Zr–O distance of 2.19 Å,4 considering the strongly different conditions of the experiment (0.3 M anhydrous zirconium(IV) chloride in 10.5 M perchloric acid). The coordination number of the first shell is eight (which was also found by the experiments of Hagfeldt et al.)4 and the zero value between the first and second peak indicates that no exchanges took place between the shells.
For the second shell a peak maximum was found at a Zr–O distance of 4.48 Å. The average number of water molecules in this layer is 17.8 but as there are exchanges with the bulk the coordination number of the second shell ranges from 15 to 21 (Fig. 2).
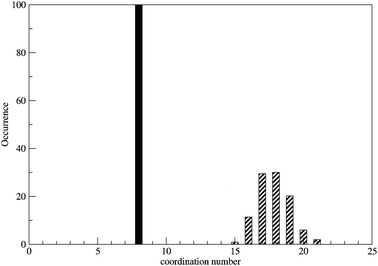 |
| | Fig. 2 Coordination number distribution for the first and second shell of Zr4+ ion in water. | |
For a more detailed analysis of the structure, the local density corrected three-body distribution functions (f(3)O–X–O (s,r,s)) were calculated for different hydration shells obtained from the ion–oxygen RDF. For the first hydration shell the function shows two sharp peaks at positions 2.7 Å and 4.3 Å (Fig. 3(a)). The arrangement of water molecules in this shell differs totally from the arrangement in the bulk and in the discussion of the ADF it will be elaborated to which geometry this structure corresponds. The influence of the ion on the second shell's water molecules is also enormous (Fig. 3(b)), as almost no oxygen–oxygen distances of ∼2.8 Å (peak maximum of the reference function for the bulk) were found. This indicates that no hydrogen bonds exist between the water molecules inside this shell. For the third shell's function (Fig. 3(c)) a peak at ∼2.8 Å was found (as in the case of the reference function), but as this peak is not as high as in the reference function, there is still some ordering effect of the zirconium ion. The water dipoles orientate with the negative partial charge towards the ion, resulting in shorter lifetimes of the hydrogen bonds. As the “fourth shell's” (Fig. 3(d)) function is similar to that of the reference bulk function, it can be concluded that the zirconium ion has no influence on the water structure beyond the third shell.
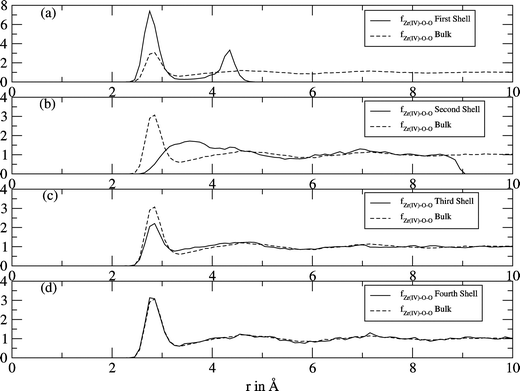 |
| | Fig. 3 Local density corrected three-body distributions for the first (a), second (b), third (c) and “fourth” (d) shells of Zr4+ (solid line), compared with that of bulk (dashed line). | |
A further tool to analyse the hydration structure is the angular distribution function of the first hydration layer which is shown in Fig. 4 in comparison with the structures of the standard 8-fold coordinated geometries. The square antiprism and the bi-capped trigonal prism seem to match best to the [Zr(H2O)8]4+ structure. As this complex is not a solid-state and liquids are characterized by vigorous dynamics it can be concluded that the water molecules around the ion assume structures in-between the bi-capped trigonal prism and the square antiprism. Fig. 5 shows snapshots of geometries similar to the square antiprism (Fig. 5(a)) and the bi-capped trigonal prism (Fig. 5(b)). This seems to be in agreement with the experimental work of Hagfeldt et al. that reported a more or less well-defined square antiprismatic configuration.4
![Comparison of the angular distribution functions of [Zr(H2O)8]4+ with that of standard 8-fold coordinated geometries.](/image/article/2011/CP/c0cp01330g/c0cp01330g-f4.gif) |
| | Fig. 4 Comparison of the angular distribution functions of [Zr(H2O)8]4+ with that of standard 8-fold coordinated geometries. | |
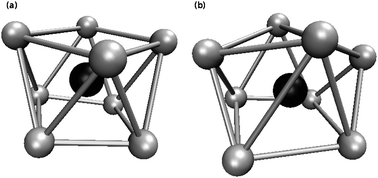 |
| | Fig. 5 Snapshots of two different coordination geometries. The grey spheres are oxygen atoms and the black sphere is the zirconium(IV) ion. | |
3.2 Dynamics
As already discussed in connection with the RDF, no exchanges took place between the first and second shells during the simulation time of 10 ps. To characterise the zirconium(IV)–oxygen bond, the Zr–O stretching frequency and the corresponding force constant were evaluated. In Table 4 these values are compared to values of other strongly polarising ions (Be(II),30U(IV),20Al(III))21 obtained from QMCF MD simulations. As mentioned earlier the Zr–O frequency was not scaled in order to get the force constant but one should consider that in the case of beryllium(II)30 a scaling factor of 0.89 was applied, which lead to difficulties in comparison. Nevertheless it can be concluded that the Zr–O bond (k = 188 N m−1) has a similar strength to the Al–O bond and seems to be even stronger than the Be–O bond.
Table 4 Mean residence times (MRT) of second shell, ion–oxygen stretching frequencies (Qion–O) and the corresponding force constants (kion–O) of Zr(IV), Al(III),21Be(II)30 and U(IV)20 obtained from QMCF MD simulations
| Ion |
MRT/ps |
Q
ion–O/cm−1 |
k
ion–O/N m−1 |
R
ex
|
|
Zr4+ |
5.5 |
484 |
188 |
6.8 |
|
Al3+ |
17.7 |
560 |
194 |
15 |
|
Be2+ |
4.8 |
653 |
144 |
— |
|
U4+ |
8.1 |
— |
— |
6 |
In contrast to the first shell, multiple exchanges occurred between the second and third shell and the third shell and the bulk. The MRT for the water molecules in the second shell was 5.5 ps which is, compared to other strongly structure-forming ions (Table 4), in-between the MRT of Be(II) (4.8)30 and U(IV) (8.1).20 With an MRT value of 17.7 ps, Al(III)21 has by far the most rigid second shell within these ions.
The Rex value, indicating the number of attempts needed for a successful exchange, of zirconium's second shell is 6.8, which is similar to the corresponding value of U(IV).20 The high value of Al(III)21 confirms again the higher stability of aluminium's second hydration shell (Table 4).
The analysis of hydrogen bonds between the water molecules of the first and second shell showed, that the average lifetime of a H(first shell)–O(second shell) bond is 0.6 ps, which is slightly longer than the lifetime of a hydrogen bond in pure water (0.5 ps).27
4. Conclusion
This theoretical study of the monomeric hydrated zirconium(IV) ion based on QMCF MD simulation methology has proven successful in obtaining structural and dynamical data. As the hydrated Zr4+ ion was stable (at least at room temperature) during the simulation time of 10 ps, it is one of the very few four-times positively charged ions observable in aqueous solution. Another example for a stable fourfold charged ion in aqueous solution is U4+,20 while simulations of ions of the elements of the fourth main group namely Ge4+, Sn4+ or Pb4+ have shown immediate hydrolysis.31 Available experimental data like the Zr–O distance, coordination number and geometry of the first hydration shell were excellently reproduced by this simulation. The QMCF MD framework proved besides its accuracy again the applicability to highly charged ions with its advantage that no solute–solvent potentials have to be constructed. Cluster calculations showed that the effect of electron correlation is small and that Hartree–Fock gives a sufficiently accurate description of the system, while B3LYP overestimates the effect of electron correlation. Any improvement could only be achieved, therefore, with ab initio correlated methods, which are not affordable at present with today’s computational facilities.
Acknowledgements
Financial support for this work from the Austrian Science Foundation (FWF) is gratefully acknowledged.
References
-
E. Wiberg, A. F. Holleman and N. Wiberg, Lehrbuch der Anorganischen Chemie, Walter De Gruyter, 2007 Search PubMed.
-
L. L. Hench and J. Wilson, An Introduction to Bioceramics, World Scientific Pub Co, 1993 Search PubMed.
- A. J. Zielen and R. E. Connick, J. Am. Chem. Soc., 1956, 78, 5785–5792 CrossRef CAS.
- C. Hagfeldt, V. Kessler and I. Persson, Dalton Trans., 2004, 2142–2151 RSC.
-
C. F. Baes and R. E. Mesmer, The Hydrolysis of Cations, Wiley New York, 1976 Search PubMed.
- D. H. Devia and A. G. Sykes, Inorg. Chem., 1981, 20, 910–913 CrossRef CAS.
- A. Singhal, L. M. Toth, J. S. Lin and K. Affholter, J. Am. Chem. Soc., 1996, 118, 11529–11534 CrossRef CAS.
- N. Rao, M. N. Holerca, M. L. Klein and V. Pophristic, J. Phys. Chem. A, 2007, 111, 11395–11399 CrossRef CAS.
- N. Rao, M. Holerca and V. Pophristic, J. Chem. Theory Comput., 2008, 4, 145–155 CrossRef CAS.
- B. M. Rode, T. S. Hofer, B. R. Randolf, C. F. Schwenk, D. Xenides and V. Vchirawongkwin, Theor. Chem. Acc., 2006, 115, 77 CrossRef CAS.
- M. J. Field, P. A. Bash and M. Karplus, J. Comput. Chem., 1990, 11, 700–733 CrossRef CAS.
- D. Bakowies and W. Thiel, J. Phys. Chem., 1996, 100, 10580–10594 CrossRef CAS.
- F. H. Stillinger and A. Rahman, J. Chem. Phys., 1978, 68, 666–670 CrossRef CAS.
- P. Bopp, G. Janscó and K. Heinzinger, Chem. Phys. Lett., 1983, 98, 129–133 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1962, 36, 3428 CrossRef CAS.
- T. H. Dunning, Jr., J. Chem. Phys., 1970, 53, 2823 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284 CrossRef CAS.
- W. Stevens, M. Krauss, H. Basch and P. Jasien, Can. J. Chem., 1992, 70, 612–630 CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. J. Frick, A. B. Pribil, T. S. Hofer, B. R. Randolf, A. Bhattacharjee and B. M. Rode, Inorg. Chem., 2009, 48, 3993–4002 CrossRef CAS.
- T. S. Hofer, B. R. Randolf and B. M. Rode, J. Phys. Chem. B, 2008, 112, 11726–11733 CrossRef CAS.
- L. H. Lim, A. B. Pribil, A. E. Ellmerer, B. R. Randolf and B. M. Rode, J. Comput. Chem., 2009, 31, 1195–1200.
- A. Bhattacharjee, T. S. Hofer and B. M. Rode, Phys. Chem. Chem. Phys., 2008, 10, 6653–6657 RSC.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
- D. J. DeFrees and A. D. McLean, J. Chem. Phys., 1985, 82, 333 CrossRef CAS.
- T. S. Hofer, H. T. Tran, C. F. Schwenk and B. M. Rode, J. Comput. Chem., 2004, 25, 211–217 CrossRef.
-
A. J. Lock, S. Woutersen and H. Bakker, Femtochemistry and Femtobiology, World Scientific, Singapore, 2001 Search PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- D. J. Adams, E. M. Adams and G. J. Hills, Mol. Phys., 1979, 38, 387–400 CAS.
- S. S. Azam, T. S. Hofer, A. Bhattacharjee, L. H. V. Lim, A. B. Pribil, B. R. Randolf and B. M. Rode, J. Phys. Chem. B, 2009, 113, 9289–9295 CrossRef CAS.
-
L. H. V. Lim, PhD Thesis, University of Innsbruck, 2010 Search PubMed.
|
| This journal is © the Owner Societies 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 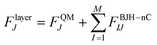
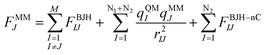
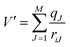
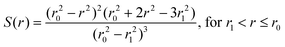
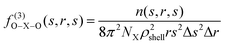

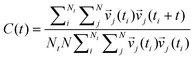
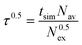
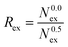



![Comparison of the angular distribution functions of [Zr(H2O)8]4+ with that of standard 8-fold coordinated geometries.](/image/article/2011/CP/c0cp01330g/c0cp01330g-f4.gif)

