Theory of gold on ceria

Abstract

The great promise of ceria-supported gold clusters as catalysts of the future for important industrial processes, such as the water gas shift reaction, has prompted a flurry of activity aimed at understanding the molecular-level details of their operation. Much of this activity has focused on experimental and theoretical studies of the structure of perfect and defective ceria surfaces, with and without gold clusters of various sizes. The complicated electronic structure of ceria, particularly in its reduced form, means that at present it is highly challenging to carry out accurate electronic structure simulations of such systems. To overcome the challenges, the majority of recent theoretical studies have adopted a pragmatic and often controversial approach, applying the so-called DFT + U technique. Here we will briefly discuss some recent studies of Au on CeO₂{111} that mainly use this methodology. We will show that considerable insight has been obtained into these systems, particularly with regard to Au adsorbates and Au cluster reactivity. We will also briefly discuss the need for improved electronic structure methods, which would enable more rigorous and robust studies in the future.

---

Angelos Michaelides

Angelos Michaelides obtained a PhD in Theoretical Chemistry in 2000 from Queen's University Belfast (supervised by Peijun Hu). He then moved to David King's group in Cambridge and in 2002 was awarded a junior research fellowship from Gonville and Caius College. In 2004 he moved to the Fritz Haber Institute, Berlin, first as an Alexander von Humboldt fellow and then later as a staff scientist, in Matthias Scheffler's Theory Department. In 2006 he moved to UCL and became Professor in 2009. Angelos' current research (www.chem.ucl.ac.uk/ice) involves the application and development of electronic structure methods to study catalytic and environmental interfaces.

Stephen J. Jenkins

Stephen Jenkins studied Theoretical Physics at the University of Exeter, completing his PhD in 1995 (supervised by G.P. Srivastava and John Inkson). After a spell as a post-doc in Exeter, he joined David King's group in Cambridge in 1997. Awarded a Royal Society University Research Fellowship in 2001, Stephen was appointed to a University Lectureship in Physical Chemistry in 2009, and succeeds David King as head of the Cambridge Surface Chemistry group. His current research (www-jenkins.ch.cam.ac.uk) includes the fundamentals of adsorption and catalysis, surface structure and chirality, and the surface and interface properties of spintronic materials.

---

1. Introductory remarks

Amongst the least reactive of all bulk metals, gold would, until relatively recently, have seemed an odd choice of material to investigate for its potential as a catalyst. Since the seminal work of Haruta,¹ however, it has become clear that gold nanoparticles can show dramatic chemical activity in certain contexts when suitably prepared, and this unexpected observation has prompted concerted efforts both to explain this phenomenon and to expand its range of application.^2–19 Today, research into catalysis by gold is a thriving field, driven not only by the economic attractions of the material (historically one of the more abundant and cheaper of the precious metals) but also by its highly desirable propensity to catalyse reactions at relatively low temperatures. Various theories have been put forward to explain the activity of nanoparticulate gold, including those based on structural effects (the presence of step and kink sites), on electronic effects (the presence of non-metallic and/or ionic sites), and on support effects (either through the stabilisation of unusual structural/electronic features, or through reactions occuring across the particle/support interface itself). The reality may well be that all such phenomena are important at some time or another in varying proportions in different scenarios and for different reactions.

One of the more exotic materials considered as a possible support for nanoparticulate gold is cerium dioxide (ceria, CeO₂). A highly reducible oxide, ceria has found applications as an oxygen buffer, as a catalyst, as a catalyst support, and as a solid electrolyte.²⁰ These uses typically rely upon the easy creation and diffusion of oxygen vacancies within the material. When the oxide is stoichiometric, the constituent cerium atoms exist in the Ce⁴⁺ oxidation state, but in the partially reduced form each missing lattice oxygen atom implies the existence of two Ce³⁺ ions in sites close to (though not necessarily immediately adjacent to²¹) the vacancy. The stoichiometric oxide is therefore characterised by a completely empty f-band (located in an energy gap between the occupied O 2p states and the unoccupied Ce 5d states) whilst the partially reduced oxide features highly-localised partially-occupied f orbitals split-off below the unoccupied f states (see Fig. 1).

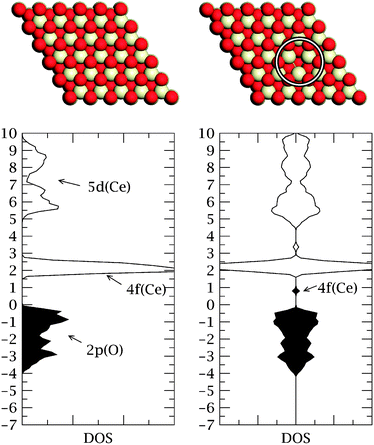Fig. 1 Top: Schematic representations of the stoichiometric (left) and reduced (right) CeO₂{111} surface. White atoms are cerium, red atoms oxygen, and the oxygen vacancy is circled. Bottom: Electronic structure of the stoichiometric CeO₂{111} surface (left) and the reduced surface (right) with occupied states shaded and unoccupied states unshaded. The density of states for the reduced surface is shown spin-resolved. The Fermi levels are set at zero and the units of the energy (y) axis are in eV.

A variety of experimental studies has provided evidence to suggest that gold nanoparticles supported on ceria may be of great interest from the catalytic viewpoint.^22–34 These studies in turn have prompted significant theoretical efforts to understand the physical nature of the particle/support interaction in this system, and its effect on catalytic activity.^35–41 In this short perspective article, we aim to provide a selective but representative overview of progress in this direction over recent years, highlighting not only the key areas in which consensus appears to be emerging, but also what we believe to be some of the most pertinent open questions that remain.

2. Theoretical approaches

Electronic structure simulations of nanoparticles on oxide surfaces are challenging for a number of reasons. First, there is the inevitable difficulty of describing finite clusters attached to extended surfaces. This implies that the structures are complex and system sizes rather large, and that neither localised nor periodic basis functions are without significant drawbacks. Second, and more challenging fundamentally, is the question of identifying a suitable electronic structure method with the requisite accuracy to describe the properties of interest. Of the many electronic structure techniques that have been developed, density functional theory (DFT) is the most popular and robust theoretical approach currently available for solving the electronic structures of solid surfaces. However, DFT with standard exchange–correlation functionals (e.g. generalised gradient functionals, such as PW91⁴² or PBE⁴³) is far from a panacea and suffers from a number of well-known deficiencies. The one most relevant to the present topic of gold on ceria is an inability to correctly treat the strongly correlated nature of the cerium f electrons.

The problem of strongly correlated electrons is easily explained, though much less easily remedied. Essentially, one should recall that the electron–electron interactions included within standard DFT exchange–correlation functionals are only mean-field approximations to what are, in reality, a set of complex dynamical phenomena. In most situations, this approach works remarkably well, allowing orbitals to be calculated within an independent particle picture. In contrast, however, when an orbital is very highly localised (as occurs, of course, for f orbitals in the cerium atom) the Coulomb repulsion is sufficient to provide a strong disincentive towards instantaneous double occupancy of that orbital. That is, the probability of a specific electron being found in such an orbital at any given moment is strongly modified by whether another electron is or is not already there at the time: the motion of electrons then becomes “strongly correlated”. Effects of this nature cannot be captured by a pure mean-field approach, since this assumes that electrons can be treated as independent particles, so standard DFT exchange–correlation functionals are doomed to failure; a classic example of such a situation is to be found in NiO, where DFT incorrectly predicts a metallic bandstructure and must be augmented in some more or less sophisticated manner in order to achieve a physically reasonable result.⁴⁴

Although alternative explictly correlated electronic structure methods for solids have recently begun to emerge, e.g. the Random Phase Approximation⁴⁵ and Quantum Monte Carlo,⁴⁶ a pragmatic ad hoc correction known as the “Hubbard U” has much more commonly been applied in practical calculations.⁴⁷ Its application is, however, not free from controversy, as it includes within DFT an additional potential, given the symbol U, which effectively penalises double occupancy of highly localised orbitals. In doing so, one steps outside the bounds of “pure” DFT, but experience shows that the results of DFT + U calculations can be considered reliable, so long as the value of U is appropriately chosen.⁹⁷ To further complicate matters, reports in the literature often cite an effective parameter, U_eff, defined as the difference between the spherically averaged value of U and the screened exchange interaction parameter, J. In addition, the Hubbard correction is typically applied only to a subset of orbitals (i.e. the most strongly localised ones) which in this case corresponds to the Ce 4f electrons.

The issue of choosing the value of U_eff thus assumes considerable importance in assessing calculations reported in the literature for ceria. Values employed for cerium oxides typically range between 3–6 eV. One should note that the DFT + U approach is generally implemented in the context of either the local density approximation (LDA + U) or the generalised gradient approximation (GGA + U);^48,49 the latter may itself be sub-divided according to the particular flavour of GGA functional used, which in the present context has tended to be of either the PW91 or the PBE variety. On the basis of studies for bulk CeO₂ and bulk Ce₂O_3,^50–53 various authors have favoured U_eff values ranging between 5–6 eV for LDA + U and between 3–5 eV for GGA + U.^21,53–58 How well any of these conclusions may safely be carried over to surface calculations, however, has proved to be a point of significant contention, as will be seen below. Moreover, it has been pointed out (e.g.ref. 52) that there probably exists no single value of U_eff that is optimal for calculation of all material properties, which is to say that a value of U_eff that yields excellent results for one property (e.g. lattice constant) may yield poor results for another (e.g. band gap) and vice versa.

3. The nature of the clean ceria surface with and without defects

The most stable surface of ceria is the CeO₂{111} facet,^57–60 and it is this that has been the subject of most study to date. This surface exhibits three-fold rotational symmetry and may be thought of in terms of stacked O–Ce–O trilayers (Fig. 1). Removal of a single oxygen atom at the surface leaves three undercoordinated cerium atoms to accommodate the two resulting excess electrons (3Ce⁴⁺ → 2Ce³⁺ + Ce⁴⁺). An early confirmation of the necessity to account for strong correlation effects in any theoretical assault on this system may, however, be gleaned from the fact that standard DFT calculations incorrectly predict delocalisation of these excess electrons across all three undercoordinated cerium atoms (3Ce⁴⁺ → 3Ce^3.33+). Correct localisation is obtained when U_eff values of around 5 eV are employed.^{21,56–58,61,62} The energy cost for removal of an oxygen atom (i.e. creation of a surface oxygen vacancy) has been calculated by Zhang et al.⁶³ using GGA + U with U_eff = 5 eV to be 2.23 eV; in contrast, the creation of a cerium vacancy has been calculated in the same work to require an energy of 4.67 eV.

Removal of a single subsurface oxygen atom leads to an electronic structure almost indistinguishable from that of a single surface oxygen vacancy.^58,62,63 Their energy difference is on the order of 0.1 eV, which is very small compared to the vacancy formation energy of well over 2.0 eV. These theoretical conclusions are in good agreement with the elegant high-resolution scanning tunneling microscopy work of Esch et al.,⁶⁴ which showed that the two types of defect (i.e. surface oxygen vacancy and subsurface oxygen vacancy) are present with almost equivalent concentrations. In addition to the single vacancies, Esch et al.⁶⁴ further discovered that upon prolonged annealing vacancy clusters appear, with linear vacancy clusters being dominant and triangular vacancy clusters being the next most abundant. Interestingly, those vacancy clusters expose exclusively Ce³⁺ ions. Because electrons left behind by the released oxygen atoms are localised at adjacent Ce ions, these observations suggest that electron localisation plays an important role in shaping the vacancy clusters.^64,65

In order to address this issue, Zhang et al.⁶² carried out a systematic DFT + U study on a series of vacancy clusters. A correlation between the coordination number of each Ce³⁺ ion and the energy of its f states was identified: specifically, the higher the coordination number, the less stable the Ce³⁺ ion would be. Because the Ce ions neighboring the vacancies have lower coordination numbers than those that are further away from the vacancies, this correlation explains well the electronic features of the vacancy clusters. However, Zhang et al.⁶² predicted that a triangular surface vacancy cluster is actually more stable than the linear vacancy clusters, which disagrees with the experimental observations. Conesa⁶⁶ also used DFT + U to study the defects containing two and three vacancies. Whilst the author identified a similar correlation between the coordination number of Ce³⁺ ions and their energies, he also found the electronic configuration with the lowest energy is not that which contains the Ce³⁺ ions located as immediate neighbors to the vacancies, although the energy differences between them are small (less than 0.1 eV per vacancy). Because the reduction of Ce ions leads to displacements of neighboring O atoms, such electronic configurations as predicted in Conesa's work would produce different O structural features than are observed in the STM images. These apparent disagreements suggest a need for further experiments and calculations on vacancy clusters. Another important issue deserving of further study is the mobility of oxygen vacancies. Experimentally, whilst Namai et al. reported the defect mobility at room temperature,^67,68 Esch et al.⁶⁴ suggested that the diffusion of oxygen vacancies requires temperature higher than 400 °C. In theory, energy barriers for vacancy diffusion have been computed with interatomic potential approaches⁶⁹ and DFT methods,^70,71 and the obtained values vary in the range of ∼0.5–1.1 eV. Nolan et al.⁷² employed the DFT + U method to calculate the diffusion for a single vacancy in a (2×2×2) unit cell (CeO_1.96) and obtained an energy barrier of 0.53 eV. Substituting the calculated barrier in the classical transition-state theory expression yields a rate of less than 10⁻⁸ps⁻¹ at 300 K (assuming a standard pre-exponential factor of 10¹³), which suggests very low mobility for the vacancy at room temperature.

4. Gold adatoms on stoichiometric ceria surfaces

The first theoretical calculation to address the adsorption of gold on ceria was that of Liu et al.,³⁵ in which single adatoms were considered on both the stoichiometric and the partially reduced CeO₂{111} surface. Significantly, the adsorption energy was found to be rather larger when the adatom occupied an oxygen vacancy site (1.86 eV) than when it sat atop an oxygen atom on the ideal surface (1.26 eV) pointing towards a possible role for such vacancies as nucleation sites for larger clusters. Furthermore, these calculations also indicated that the charge state of gold adatoms could be profoundly altered by their local environment. On the stoichiometric surface, the calculations indicated that the 6s orbital of the gold atom became depopulated in favour of an adjacent cerium atom upon adsorption (Ce⁴⁺ → Ce³⁺); the adatom itself acquired a net positive charge of +0.35|e|⁹⁸ (see Fig. 2) and was found to retain no net spin, in sharp contrast to an isolated gold atom for which the 6s orbital hosts a single unpaired spin.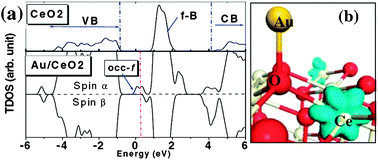

Fig. 2 Electronic structure of a single Au adatom on the stoichiometric CeO₂{111} surface (atop site). In (a) the top panel shows the density of states (DOS) for the clean surface, similar to the bottom left panel of Fig. 1. The lower panel in (a) shows the spin-polarised DOS that arises from adsorption of Au in an atop site, highlighting the existence of a single occupied f-orbital (occ-f). In (b) the blue isosurface shows net spin associated with this occupied f-orbital, localised on one of the Ce ions neighbouring the Au adatom. Reprinted with permission from Liu et al.³⁵ Copyright (2005), American Physical Society.

It is worth mentioning that these early calculations for gold on ceria were not carried out using the DFT + U technique that underlies more recent work. Neither, however, were they carried out without due regard to the issue of strong correlation. In fact, an alternative method of achieving localisation of f electrons was employed, via a technical adjustment to the self-consistency procedure adopted during iterative solution of the Kohn–Sham equations of DFT, perhaps best described as “pruned density mixing”.⁹⁹ Nevertheless, it is certainly fair to say that the “pruned density mixing” technique is not trivial to apply, and that careful adjustment of parameters was required to achieve convergence in its one application to date.³⁵ The DFT + U method suffers from the ambiguity noted above, regarding the correct choice for U_eff, but does benefit from being by now rather standard, implying both that DFT + U is readily available as an option in many modern DFT codes, but also that calculations performed using this method are more straightforwardly comparable with others in the literature obtained by similar means; convergence is also routinely achieved without the extensive optimisation efforts necessary in application of the “pruned density mixing” approach. For those reasons alone, the present authors have adopted the GGA + U methodology in all of their joint publications on this system.

Our recent GGA + U (U_eff = 5 eV) results⁵⁵ for individual gold adatoms on the CeO₂{111} surface are, indeed, in qualitative agreement with the earlier work, albeit the adatom charge (+0.17|e|) and adsorption energy (0.96 eV) for the atop site are both rather smaller than before. Upon investigating alternative adsorption sites, however, we discovered that a position bridging between two oxygen atoms was, in fact, preferred (adsorption energy 1.17 eV, adatom charge +0.32|e|); interestingly, the unpaired spin resulting from depopulation of the gold 6s orbital was found to be located not on the nearest cerium atom, but instead upon the third nearest⁵⁵ (see Fig. 3). A very similar configuration (both in terms of energy and electronic structure) was reported subsequently by Hernández et al.,⁷³ using a near-identical computational set-up, although they additionally point out the existence of multiple, slightly less stable, electronic local minima associated with some of the adsorption sites they considered. Camellone and Fabris⁷⁴ also concur with the same basic picture, using U_eff = 4.5 eV.

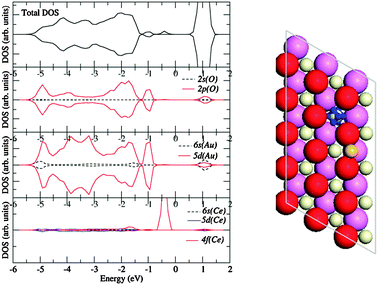Fig. 3 Electronic structure of a single Au adatom on the stoichiometric CeO₂{111} surface (bridge site). In the left panel, the total density of states (DOS) and atom-resolved projected density of states (PDOS) of the Au adsorbed on the bridge site, the latter of which are rescaled so that characteristic features can be seen more clearly. The Ce and O atoms in the PDOS refer to the reduced Ce (i.e.Ce³⁺) and the O between Ce³⁺ and the Au atom, respectively. In the right panel is depicted the three-dimensional isosurface plot of the spin density (blue areas) of the system. Reprinted with permission from Zhang et al.⁵⁵ Copyright (2008), American Chemical Society.

Castellani et al.,⁷⁵ however, adopt a mixed methodology whereby LDA + U (U_eff = 5 eV) is used to obtain optimised geometries, and then a single-point GGA + U (U_eff = 3 eV) calculation is performed to obtain energies, charges and spin moments. These choices are motivated by evidence from bulk ceria compiled by Loschen et al.,⁵¹ but in light of other work on the clean reduced surface^57,62 it is questionable whether the relatively low value of U_eff used in the GGA + U calculations will correctly reproduce the localisation of charge on cerium f orbitals. Certainly, the results for gold adsorption presented by Castellani et al.⁷⁵ are in marked disagreement with those of Zhang et al.,⁵⁵ Hernández et al.⁷³ and Camellone and Fabris,⁷⁴ both regarding the location and the charge state of the adatom; they conclude that it sits atop an oxygen atom and remains essentially neutral. Use of the same mixed methodology by Branda et al.⁷⁶ yields a different preferred adsorption site for Au, bridging between an O and a Ce atom, but again indicates a neutral charge state; results in line with previous work^55,73,74 are obtained when a purely GGA + U (U_eff = 5 eV) approach is adopted.⁷⁶ Our view is that the low U_eff values suggested by Loschen et al.⁵¹ are intended to provide a balanced description of both CeO₂andCe₂O₃, whereas a better representation of CeO₂alone may be achieved with higher U_eff values. Furthermore, the lower lattice constant achieved through use of LDA + U in the structural calculation would, we believe, tend to favour unphysical delocalisation of charge between neighbouring cerium atoms, owing to their closer proximity. Alternatively, one might say that whilst charge localisation is most strongly controlled by the choice of U_eff, an important secondary effect arises due to the influence of strain (relative to the prevailing calculated lattice constant) on the stability of the large Ce³⁺ cation versus the smaller Ce⁴⁺ cation (i.e. compressive strain disfavours the reduction of individual ions, Ce⁴⁺ → Ce³⁺, implied by localisation).⁷⁷ It should nevertheless be granted, of course, that the lower lattice constant obtained with LDA + U lies closer to the experimental value than does that calculated with GGA + U.

A valuable analysis has now been provided by Branda et al.,⁷⁸ addressing precisely the subtle interplay between lattice constant and the chosen U_eff value in determining the charge transfer between adatom and surface. They demonstrate that, for gold adsorbed atop an oxygen atom, GGA + U (U_eff = 3 eV) consistently predicts zero or minimal charge transfer at lattice constants in the range 5.35–5.55 eV, whereas GGA + U (U_eff = 5 eV) consistently predicts full charge transfer at lattice constants above about 5.40 eV (and very little charge transfer at lattice constants below). If one accepts the larger U_eff value and any reasonable lattice constant, the unequivocal conclusion is that significant charge transfer occurs. If, on the other hand, one prefers the smaller U_eff value, the result is a less clearcut preference for a lack of charge transfer, since metastable solutions with some degree of charge transfer lie within a few tens of meV from the ground state. Branda et al.⁷⁸ avoid drawing a firm conclusion over which picture is correct, but we feel it is important to note that their results obtained at smaller (essentially experimental) lattice constants reveal an unphysical (albeit small) delocalisation of charge amongst cerium f orbitals, whereas those obtained at larger lattice constants do not.

Out of interest, we have now performed GGA + U (U_eff = 3 eV) and GGA + U (U_eff = 5 eV) calculations for the clean reduced CeO₂{111} surface, holding the lattice constant fixed at the LDA + U (U_eff = 5 eV) value reported by Castellani et al.⁷⁵ (i.e. 5.39 Å). In the former case, we find unphysical delocalisation of charge amongst three cerium atoms, rather than the physically correct solution showing localisation on just two. Only with the larger U_eff value do we obtain properly localised solutions, and even then only when the initial guess for the electron distribution is carefully chosen. It seems clear, therefore, that use of the lower lattice constant (5.39 Å) produces unphysical results unless the higher U_eff value is used for the GGA + U calculations, and risks error even then. Since we and others have also previously reported^57,62 that GGA + U (U_eff = 3 eV) produces similarly spurious results for oxygen vacancies even at larger lattice constants, it seems to us on balance that the most consistent choice is to use GGA + U (U_eff ≈ 5 eV) at its own theoretically obtained (albeit somewhat too large) lattice constant. Such a choice for CeO₂{111}/Au leads to adsorption at the bridge site, with full charge transfer from the gold adatom to a single cerium atom, as described by Zhang et al.,⁵⁵ Hernández et al.,⁷³ Camellone and Fabris,⁷⁴ and Branda et al.⁷⁶

As a final comment on the subject of adatom adsorption on the stoichiometric surface, we note that Branda et al.⁷⁸ report the results of hybrid functional (HSE⁷⁹) calculations (as opposed to DFT + U) which favour a solution with no charge transfer over a second solution with strong charge transfer, but only by a very small margin. Given the uncertainties inherent in hybrid functional DFT, its application on ceria systems is not free of problems. Indeed, as Da Silva et al.⁸⁰ and Kullgren et al.⁸¹ have found, whilst hybrid functionals such as PBE0,⁸² HSE⁷⁹ or B3LYP⁸³ give a reasonably good prediction on bulk CeO₂ and Ce₂O₃ systems, the overall description of the electronic properties (particularly band gaps) can actually be substantially worse than obtained when using LDA + U or GGA + U with adjustable U parameters.

5. Gold adatoms on defective ceria surfaces

Notwithstanding the complexities of gold adsorption on stoichiometric surfaces, it is highly likely that adsorption at defect sites will play a major (possibly even dominant) role under catalytically relevant conditions. Certainly the adsorption energy associated with depositing single gold adatoms into either cerium or oxygen vacancy sites is agreed to be rather greater than for the stoichiometric surface. Various calculations have, for instance, indicated a preference for adsorption into an oxygen vacancy site relative to the stoichiometric surface (see Table 1) the most reliable results being, we believe, those presented recently by Zhang et al.⁵⁵ (1.58 eV preference), Hernández et al.⁷³ (1.26 eV preference) and Camellone and Fabris⁷⁴ (1.11 eV preference). The work of Chen et al.⁸⁴ appears accurately to represent the structure and energetics of the gold adatom in the oxygen vacancy site, but overstates the relative preference for that site because the most stable site for adsorption on the stoichiometric surface is not considered in that work. The adsorption energy of 1.86 eV reported by Liu et al.³⁵ for the oxygen vacancy site now looks conspicuously low in relation to these four GGA + U calculations. All works that address explicitly the calculated electronic structure,^55,73,74 however, agree with the original finding of Liu et al.³⁵ that the direction of charge transfer is reversed relative to adsorption on the stoichiometric surface; one of the two reduced cerium atoms associated with the oxygen vacancy donates an electron (2Ce³⁺+Ce⁴⁺ → Ce³⁺ + 2Ce⁴⁺) to the adatom, which gains a substantial net negative charge in the vicinity of −0.60|e| due to filling of the 6s orbital (see Table 2 and Fig. 4).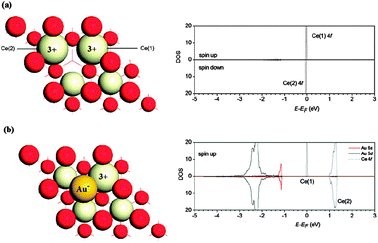

Fig. 4 Electronic structure of a single Au adatom adsorbed into an O vacancy on the CeO₂{111} surface. In (a) the left panel shows schematically the structure and the formal charges of atoms surrounding the bare vacancy, while the right panel shows the density of states (DOS) projected onto the f-orbitals of the two Ce³⁺ ions. In (b) the left panel shows the structure and formal charges after adsorption of Au into the vacancy site, while the right panel shows the DOS projected onto the f-orbitals of the single remaining Ce³⁺ ion and the s- and d-orbitals of the Au adatom. Reprinted with permission from Hernández et al.⁷³ Copyright (2009), Royal Society of Chemistry.

Table 1 Calculated adsorption energies for a single gold atom on the stoichiometric (Stoich.) and defective (O-Vac. and Ce-Vac.) CeO₂{111} surfaces. The “PW91+” calculations employed the “pruned density mixing” technique. For the various DFT + U calculations, we adopt the notation of Branda et al.,⁷⁸ whereby “Ln” indicates LDA + U with U_eff = n eV, and “Gm” indicates GGA + U with U_eff = m eV. All the GGA-based calculations used the PW91 functional, except for those reported by Camellone & Fabris⁷⁴ which employed the PBE functional. The notation “L5 → G3” implies that geometry optimisation was done wholly within the L5 approach (and at the L5 lattice constant) followed by a single-point calculation for adsorption energy and electronic structure carried out within the G3 approach. For the stoichiometric surface, results marked with a superscript dagger correspond to adsorption atop an O atom, those marked with a double-dagger are for adsorption in a Ce–O bridge site, and the remaining plain entries are for adsorption in the O–O bridge site. In all cases at the O-Vac. and Ce-Vac. surfaces, the adatom bonds directly into the vacancy site.

	Functional	Stoich.	O-Vac.	Ce-Vac.
Liu et al.^35	PW91+	1.26^†	1.86	—
Chen et al.^84	G5	0.88^†	2.58	5.65
Branda et al.^78	G5	0.96^†	—	—
Zhang et al.^55	G5	1.17	2.75	5.94
Hernandez et al.^73	G5	1.15	2.41	—
Camellone & Fabris^74	G4.5	1.18	2.29	5.68
Branda et al.^76	G5	1.15	—	—
Branda et al.^76	L5 → G3	0.71^††	—	—
Castellani et al.^75	L5 → G3	0.66^†	—	—
Branda et al.^78	L5 → G3	0.61^†	—	—
Branda et al.^78	G5	0.96^†	—	—

---

Table 2 Calculated charge states for a single gold atom adsorbed on the stoichiometric (Stoich.) and defective (O-Vac. and Ce-Vac.) CeO₂{111} surfaces. The key to the “Functional” column is explained in the caption to Table 1. For the stoichiometric surface, results marked with a superscript dagger correspond to adsorption atop an O atom, those marked with a double-dagger are for adsorption in a Ce–O bridge site, and the remaining plain entries are for adsorption in the O–O bridge site. In all cases at the O-Vac. and Ce-Vac. surfaces, the adatom bonds directly into the vacancy site

	Functional	Stoich.	O-Vac.	Ce-Vac.
Liu et al.^35	PW91+	+0.35^†	−0.58	—
Branda et al.^78	G5	+0.32^†	—	—
Zhang et al.^55	G5	+0.32	−0.62	+1.23
Hernandez et al.^73	G5	+0.34	−0.6	—
Branda et al.^76	G5	+0.33	—	—
Branda et al.^76	L5 →G3	−0.06^††	—	—
Castellani et al.^75	L5 → G3	−0.02^†	—	—
Branda et al.^78	L5 →G3	+0.05^†	—	—
Branda et al.^78	G5	+0.32^†	—	—

---

An alternative scenario involves the adsorption of gold into cerium vacancies, the energetics of which were first considered by Hu and co-workers^84,85 who report an extremely high adsorption energy of 5.65 eV in this site. Subsequent work by Zhang et al.⁵⁵ confirms a similarly high adsorption energy (5.94 eV) and adds the observation that the substitutional gold atom gains a very large positive charge of +1.23|e|. Camellone and Fabris⁷⁴ report an adsorption energy of 5.68 eV for such a site. These high adsorption energies do not, however, necessarily imply that cerium vacancies will dominate the adsorption properties of gold, since the creation of a cerium vacancy itself requires significant energy.

In order to address this issue, Zhang et al.⁶³ extended their work to include a first-principles thermodynamic analysis of gold adsorption, allowing both oxygen and cerium vacancies to compete with the stoichiometric surface for gold adatoms. As mentioned in the section dealing with clean surfaces above, the formation energy for a single cerium vacancy (4.67 eV) far exceeds that of a single oxygen vacancy (2.23 eV) when calculated within the GGA + U (U_eff = 5 eV) methodology.⁶³ Application of thermodynamic arguments then leads to the conclusion that the free energy of an oxygen vacancy is much less than that of a cerium vacancy, under conditions similar to those found in, for example, the water gas shift (WGS) reaction (400–800 K, with partial pressure ranging from 1 kPa to 100 kPa). Indeed, the free energy of the oxygen vacancy is comparable with that of the stoichiometric surface in the relevant range, whereas the cerium vacancy is unstable by a margin of around 8 eV. Even composite defects including both ceriumandoxygen vacancies together are found to be unstable by more than 2 eV. Accordingly, one expects that oxygen vacancies will be abundant under these conditions, whereas cerium vacancies ought to be extremely rare. The inclusion of gold within the model makes only a quantitative difference to the outcome under WGS conditions.⁶³ Coupling the creation of a cerium vacancy with gold adsorption into the vacant site is strongly disfavoured, from a free energy perspective, by around 7 eV relative to adsorption of gold on the stoichiometric surface. And once again, composite defects involving both ceriumandoxygen vacancies together are also disfavoured. Adsorption of gold into oxygen vacancies is, however, still strongly favoured over adsorption onto the stoichiometric surface, even when the cost of creating the oxygen vacancy is included within the free energy.

In a rare investigation of the less stable {110} and {100} surfaces of CeO₂, Nolan et al.⁸⁶ considered the effect of substitutional gold on the formation of oxygen vacancies. They found that occupancy of a Ce site with Au rendered nearby lattice O thermodynamically unstable, implying that substitutional gold would almost inevitably be accompanied by an oxygen vacancy under near-equilibrium conditions. In effect, therefore, these results indicate that substitution of an isolated Au atom into a Ce vacancy is unstable relative to adsorption of Au into a composite defect comprising both Ce and O vacancy sites. Furthermore, the cost of creating the Ce vacancy in the first place was not included in the analysis, so the likely concentration of substitutional Au defects cannot be directly addressed. We anticipate that, similar to the {111} surface, such defects will be rare under conditions relevant to WGS catalysis. Heavily oxygen-rich conditions would, of course, tend to favour cerium vacancies over oxygen vacancies, so under such circumstances it may be that substitutional gold becomes important.

In the case of Au substituting Ce, there is another dimension of complexity worthy of our attention. Substitution of Au, with a lower valency (Au⁺ or Au³⁺), on a Ce⁴⁺ site could result in an electronic hole localized on the neighbouring oxygen ion(s). This phenomenon, also referred to as polaronic localization, is quite common in many metal oxides⁸⁷: despite the existence of several equivalent oxygen sites surrounding a metal ion defect in oxides, the hole-lattice coupling often favours hole localization at a single oxygen, and thus breaks the space group symmetry. This poses a challenge in theoretical treatments, as standard DFT often fails to predict the correct hole localization and the associated lattice distortion.^88–90 The origin of this problem has been tracked back to the inability of standard DFT to cancel the electron self-interaction. There have been some recent theoretical efforts in tackling this problem, among which the DFT + U approach with the Hubbard correction applied to the oxygen p orbitals has shown some promising improvement.^91–94 As the current DFT + U studies of ceria-based systems often treat only the Ce f orbitals with the Hubbard correction, it would be interesting to see the effects on electronic structure, ionic structure and energetics when the correction also applies on the oxygen p orbitals.

Another category of surface defect worthy of serious consideration is to be found in the form of step sites, but these have been the subject of comparatively little study to date. To our knowledge, only Castellani et al.⁷⁵ have investigated the binding of Au adatoms at step sites, working with a model structure incorporating both convex and concave step morphology. In most of the adsorption sites considered, these authors find adsorption energies in the range 0.52–0.69 eV, with a trivial degree of charge transfer between surface and adsorbate. Although such results would seem distinctive relative to the findings on planar surfaces reported by the majority of recent works^35,55,73,74 it should, however, be noted that the particular methodology employed by Castellani et al.⁷⁵ does in fact yield similarly weakly bound and neutral adsorption for the planar case. Indeed, the clearest message that may be understood from this work is that Au adsorption in most of the step-related adsorption sites is remarkably unperturbed relative to the planar surface.⁷⁵ We might therefore expect that calculations performed using methodologies that provide stronger binding and greater charge transfer on the planar surface are likely also to do so on the stepped surface; unfortunately such calculations have not, to our knowledge, been performed to date. In just one adsorption site, involving the concave step, is a significantly enhanced adsorption energy of 2.36 eV reported by Castellani et al.,⁷⁵ accompanied by a charge transfer that leaves the Au adatom with a significant positive charge of +0.32|e|.

6. Gold clusters on ceria

Although a great deal of attention has been lavished on the adsorption of single gold adatoms on ceria surfaces (see above) it is of course essential to ask whether these isolated entities are likely to be plentiful under reaction conditions. In general, we should think in terms of gold clusters, whose size distribution will depend critically upon both thermodynamic and kinetic aspects of the surface preparation. Since the adsorption energies reported for gold on the stoichiometric and reduced surfaces of ceria fall well below the calculated cohesive energy of bulk gold, it is expected that high temperatures will allow sintering, ultimately resulting in relatively large gold particles. Low temperature preparation, in contrast, may kinetically stabilise small particles, and this may be further accentuated by low gold loading.

The earliest calculations to address gold clusters on ceria were those of Liu et al.³⁵ on CeO₂{111}, where up to four adatoms were considered (i.e.Au₁, Au₂, Au₃ and Au₄ clusters). The first of these adatoms was assumed to occupy an oxygen vacancy site, and the others to progressively occupy adjacent sites lying nearly atop oxygen atoms. The adsorption energy for each additional gold atom was in the range 1.84–2.45 eV, which was noted to be much higher than the 1.26 eV calculated in the same work for adsorption on the stoichiometric surface. It was therefore concluded that, once the number of adsorbed gold atoms exceeded the number of oxygen vacancies, clusters would grow preferentially around these gold-filled vacancies, rather than nucleating elsewhere on patches of stoichiometric surface. Moreover, although the first gold atom in each cluster was found to be negatively charged, consistent with its occupation of an oxygen vacancy site, the additional gold atoms all achieved a net positive charge, in the range +0.10–0.19|e|, somewhat less than that associated with an isolated gold adatom on the stoichiometric surface (+0.35|e|).

Sporadic attention has been paid to cluster morphology on CeO₂{111} in subsequent GGA + U calculations, for example a Au₂ cluster anchored to an oxygen vacancy site was considered by Camellone et al.⁷⁴ (U_eff = 4.5 eV) and a Au₃ cluster anchored to a cerium vacancy site studied by Chen et al.⁹⁵ (U_eff = 5 eV). These latter authors also reported calculations on a Au₁₀ cluster, constructed by depositing a cluster of assumed shape onto the stoichiometric surface, performing molecular dynamics as a form of simulated annealing, and then re-optimising; the stability of this cluster against others of differing size and general shape was, however, not discussed.⁹⁵

Gold clusters of up to 11 atoms were studied more systematically in very recent work by Zhang et al.⁹⁶ based on the GGA + U (U_eff = 5 eV) methodology. Assuming the particles to be anchored at a single oxygen vacancy, they built up a sequence of clusters, one gold atom at a time, optimising each structure before adding another atom and calculating the next (see Fig. 5). Molecular dynamics calculations were also performed for some clusters, to test stability against unexpected rearrangements. Both two- and three-dimensional clusters were considered, and the latter was found to be energetically favoured in general, with the exception of the Au₇ case. For the larger clusters, Au₁₀ and Au₁₁, it is possible to discern the beginnings of face-centred cubic (fcc) and hexagonal close-packed (hcp) stacking patterns, and it is notable that these have very similar energies; the preference for fcc stacking in bulk gold must emerge at rather larger cluster sizes. This observation raises the fascinating prospect that the smallest gold clusters (we speculate that this means those having fewer than about 35 atoms) may exhibit fcc/hcp polymorphism. This in turn may have catalytic consequences, in terms of the number and type of active step and kink sites exposed by the clusters. We believe that state-of-the-art scanning transmission electron microscopy may now be approaching sufficient resolution to confirm or refute these intriguing structural predictions.

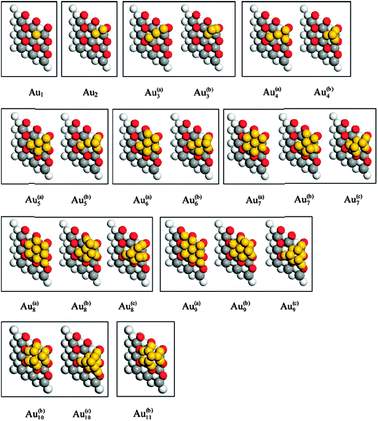Fig. 5 Au clusters anchored to an O vacancy on CeO₂{111}. Planar two-dimensional clusters are denoted with a superscript (a). Clusters forming a series leading eventually to hcp stacking are given a superscipt (b), and those forming a series leading eventually to fcc stacking are highlighted with a superscript (c). Reprinted with permission from Zhang et al.⁹⁶ Copyright (2009), American Chemical Society.

In addition to the structural issues raised by these cluster studies, the work of Zhang et al.⁹⁶ also confirmed that unusual electronic properties were retained even for the largest clusters considered. Specifically, although the net negative charge residing on the gold atom sitting directly in the vacancy site was found typically to be lessened by the addition of more gold neighbours, the net positive charge found on other gold atoms in direct contact with the oxide remained high. In the hcp-stacked Au₁₁ cluster, for example, the gold atom located directly on top of the central oxygen vacancy retained a net negative charge of −0.03|e| (cf. −0.62|e| for a single gold atom), while six other gold atoms in the first layer of the cluster displayed net positive charges averaging +0.17|e| per atom; three further gold atoms in the second layer of the cluster showed a net negative charge averaging −0.03|e|, and the single gold atom in the third layer of the cluster had a net negative charge of −0.12|e|. These results strongly suggest that the gold layer in immediate contact with the ceria surface will display a significant positive charge, even for much larger clusters.

7. Reaction mechanisms

The first theoretical discussion of a reaction occurring on a gold particle at a ceria surface addressed the WGS process (i.e.CO + H₂O → CO₂ + H₂) on a planar Au₄ cluster anchored at an oxygen vacancy on CeO₂{111}.³⁵ The first step in the proposed mechanism involved adsorption of CO onto one of the positively charged Au atoms clustered around the negative one that sits in the vacancy site itself, with an adsorption energy of 1.22 eV.³⁵ This immediately highlights one of the most important consequences of the Au charge state, namely that it strongly affects adsorption energies. Indeed, Liu et al.³⁵ reported that CO adsorption energies on single adatoms ranged from 0.09 eV in the case of negatively charged Au located in an oxygen vacancy site, through to 2.37 eV in the case of positively charged Au located atop an oxygen atom on the stoichiometric surface. The lesser positive charges found for Au atoms in the basal layer of clusters are thus likely to provide moderate adsorption energies, of which the value quoted above for the Au₄ cluster is probably fairly typical.

After adsorption of CO, the next stage in the mechanism proposed by Liu et al.³⁵ is partially dissociative adsorption of H₂O, calculated to be almost thermoneutral, and with an activation barrier of 0.59 eV (see Fig. 6). The resulting OH moiety can then react with CO to form COOH, via a transition state activated by just 0.10 eV, releasing 0.37 eV at this step. A barrier of 1.08 eV must then be overcome in order to remove H from COOH onto the cluster, in an almost thermoneutral step that releases CO₂ into the gas phase. And finally, recombination of H adatoms to give gas-phase H₂ requires input of 0.90 eV. Since the adsorption of an H₂O molecule onto the cluster involves only a very small binding energy, it is far from inevitable that there will a reasonable probability of each one encountering a CO molecule on the same cluster during its short adsorbed lifetime; clearly this will depend sensitively upon the lifetime of adsorbed CO at the ambient temperature. The observation that the adsorption energy of CO (1.22 eV) exceeds the highest reaction barrier (1.08 eV) is therefore highly relevant, implying that a favourable state of affairs can be achieved through selection of an appropriate temperature for the reaction, without recourse to prohibitive pressures. The efficacy of gold clusters on ceria for the WGS reaction is therefore explicitly linked to the unusual charge state of its constituent atoms.³⁵

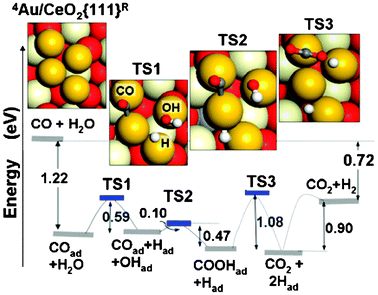Fig. 6 Reaction mechanism for the WGS reaction at a model Au₄ cluster anchored to an O vacancy on CeO₂{111}. After initial adsorption of CO, subsequent steps involve dissociative adsorption of H₂O, reaction of the resulting OH moiety with CO to form COOH, loss of H from COOH to form gas-phase CO₂, and finally recombinative desorption of H₂. Reprinted with permission from Liu et al.³⁵ Copyright (2005), American Physical Society.

More recent work, by Camellone and Fabris,⁷⁴ confirms through the use of GGA + U (U_eff = 4.5 eV) the qualitative conclusions asserted by Liu et al.³⁵via “pruned density mixing” for the dependence of CO adsorption energy on the Au charge state. Specifically, they report that adsorption of CO onto a single Au adatom initially located in its favoured bridge site on the stoichiometric CeO₂{111} surface results in a spontaneous relocation of the adatom into a neighbouring site atop an oxygen atom, with an adsorption energy of 2.48 eV. On a Au₂ cluster, anchored at an oxygen vacancy site, the preferred adsorption geometry features CO bound to the Au atom furthest from the vacancy, and with a somewhat lower adsorption energy of 1.60 eV, consistent with the assumption that the Au atom in question has a lower positive charge than that of a single adatom on the stoichiometric surface. The negatively charged single Au adatoms found anchored into oxygen vacancies are again reported as essentially inert towards CO adsorption.⁷⁴

Alternative pathways for the WGS reaction on CeO₂{111} have been investigated by Chen et al.,⁹⁵ working with both a Au₃ cluster anchored at a cerium vacancy and with a Au₁₀ cluster located on the stoichiometric surface (GGA + U, U_eff = 5 eV). They consider first a “redox” mechanism, in which H₂O dissociates stepwise at an oxygen vacancy site resulting finally in filling of the vacancy with the O atom, and creation of an H₂ molecule on the cluster. The H₂ molecule can then desorb from the cluster, whilst CO is proposed to be oxidised by an O atom from the lattice, thus regenerating an oxygen vacancy adjacent to the cluster. Details of the CO oxidation step itself are not reported, as the authors focus instead upon the OH dissociation step, which they believe to be kinetically limiting. To avoid the necessity for OH dissociation involving only the oxide substrate or the gold cluster, Chen et al.⁹⁵ secondly consider a “formate” mechanism, in which CO adsorbed on the cluster first abstracts H from OH adsorbed at an oxide oxygen vacancy, then reacts with the remaining O atom. The result is once again to fill the vacancy, but this time by creating a formate moiety adsorbed adjacent to the cluster; this in turn can decompose via various routes to produce gas-phase CO₂ and H₂. The calculated activation energy of formate production is, however, even higher than those calculated for OH dissociation in the “redox” pathway. The authors conclude that both pathways are limited by the need to refill oxygen vacancies, since their view is that the substrate is the proximal source of oxygen in the CO oxidation step.⁹⁵ This is a fundamental difference from the pathway proposed by Liu et al.³⁵ in which OH adsorbed on the cluster supplied the necessary oxygen atom (without itself dissociating prior to CO oxidation) and the substrate was not directly involved other than to induce a positive charge state on the gold cluster.

Camellone and Fabris,⁷⁴ meanwhile, have proposed a detailed mechanism for CO oxidation at a single Au adatom on the stoichiometric surface (see Fig. 7). Such a mechanism could constitute the CO oxidation step within the “redox” WGS pathway proposed by Chen et al.,⁹⁵ or could indeed stand alone in a process of CO oxidation by molecular O₂. After initial adsorption of CO (exothermic by 2.48 eV) the molecule rotates towards the surface in a “spillover” step, surmounting an activation barrier of 0.86 eV and achieving eventually a metastable state in which the molecule bonds not only to the Au adatom but also to one of the lattice oxygen atoms. The conversion to this metastable state is endothermic by 0.24 eV, and subsequent extraction of the lattice oxygen atom to form desorbing CO₂ requires an activation energy of only another 0.24 eV. The Au adatom left behind by the departing CO₂ molecule migrates into the nascent oxygen vacancy during this last step. As a means of CO oxidation, therefore, this process is inherently self-limiting, since further CO cannot adsorb on Au located in such a site. The authors suggest, however, that clusters of Au atoms might allow spillover to occur whilst being relatively more resistant to deactivation.⁷⁴ Such a situation might, for instance, allow sufficient time for the vacancy to be refilled, either directly by dissociation of molecular O₂ in some manner, or via the adsorption and dissociation of H₂O as part of the “redox” or “formate” pathways of the WGS reaction.⁹⁵

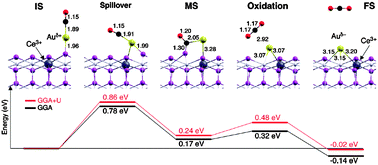Fig. 7 Reaction mechanism for CO oxidation at Au adsorbed on stoichiometric CeO₂{111}. After initial adsorption of CO on Au, the spillover step leads to a metastable configuration in which the molecule binds not only to Au but also to a lattice O atom. In the subsequent oxidation step, this lattice O atom forms part of the departing CO₂ molecule, leaving an O vacancy into which the Au atom migrates. Reprinted with permission from Camellone and Fabris.⁷⁴ Copyright (2009), American Chemical Society.

In addition, Camellone and Fabris⁷⁴ report on a highly exothermic (by 3.24 eV) and barrierless oxidation of CO to CO₂ by lattice oxygen when interacting with substitutional Au located in a cerium vacancy (see Fig. 8). It is suggested that molecular O₂ can then adsorb in the oxygen vacancy created by this first oxidation step, with an adsorption energy of 1.18 eV, and that a further CO molecule can then abstract an oxygen atom from this molecule in a second oxidation step leading to CO₂ (exothermic by 2.76 eV and again barrierless). The final state of the surface is identical to the initial state, so the catalytic cycle is closed, with an overall release of around 3.59 eV per CO₂ molecule formed (including the contribution from the O₂ adsorption energy). These results show substitutional gold in cerium vacancies to be highly active towards CO oxidation, although it remains uncertain whether such sites typically exist in substantial concentration under realistic reaction conditions.

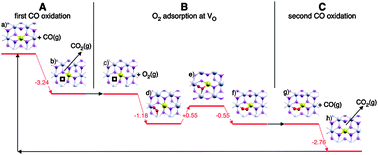Fig. 8 Reaction mechanism for CO oxidation at Au substituted for Ce on CeO₂{111}. Step A involves abstraction of lattice O by CO, forming gas-phase CO₂. Step B covers the adsorption of molecular O₂ into the O vacancy created in the previous step, including thermoneutral in siturearrangement. Step C involves abstraction of O from the adsorbed O₂ molecule by CO, forming gas-phase CO₂. The surface at the end of Step C has returned to its condition at the start of Step A. Energy is in eV. Reprinted with permission from Camellone and Fabris.⁷⁴ Copyright (2009), American Chemical Society.

8. Conclusions

In this brief perspective article we have discussed some of the recent theoretical studies of relevance to gold at the surface of ceria. In view of our aim to highlight only the key issues, we have of course barely scratched the surface of the details to be found within the wide literature on this topic. Inevitably, the views we have put forward reflect primarily our own accumulated experience of calculations on the gold/ceria system, rather than a settled consensus accepted by all workers in the field. We hope, however, that the current review will serve to point readers in the direction of the original works, and references therein, which will reveal both the great progress that has recently been made (for example in predicting realistic adsorption geometries for small gold clusters, plausible mechanisms for important catalytic reaction pathways, and the role of different vacancies in modulating the properties of gold) and the significant work that still remains to be done. Indeed, the work carried out to date in this area has not been free from controversies. Mainly these have focussed upon discussions over what might be the best value of U to use, and the physical implications of this choice in terms of adsorption structure and energetics. Such discussions arise because, as is widely recognised, DFT + U is merely an ad hoc pragmatic approach to a profound many-body problem. It is nevertheless the most useful approach we currently have available in the light of contemporary computational resources. We hope, however, that more rigorous approaches will soon be applied to these systems, resolving many of the intriguing controversies that have stimulated so much active debate.

Acknowledgements

We warmly thank Ricardo Grau-Crespo and Franscesc Illas for constructive criticism on a draft version of this work. S.J.J. is grateful to The Royal Society for a University Research Fellowship; C.Z. thanks the Isaac Newton Trust for post-doctoral funding; and A.M.'s work is supported by the EURYI scheme (www.esf.org/euryi), EPSRC and the European Research Council.

References

1. M. Haruta, N. Yamada, T. Kobayashi and S. Iijima, Gold catalysts prepared by coprecipitation for low-temperature oxidation of hydrogen and of carbon monoxide, J. Catal., 1989, 115, 301.
2. H. Sakurai, A. Ueda, T. Kobayashi and M. Haruta, Low-temperature water–gas shift reaction over gold deposited on TiO₂, Chem. Commun., 1997, 271.
3. D. Andreeva, V. Idakiew, T. Tabakova, A. Andreev and R. Giovanoli, Low-temperature water–gas shift reaction on Au/α-Fe₂O₃ catalyst, Appl. Catal., A, 1996, 134, 275.
4. D. Andreeva, T. Tabakova, V. Idakiew, P. Christov and R. Giovanoli, Au/α-Fe₂O₃ catalyst for water–gas shift reaction prepared by deposition-precipitation, Appl. Catal. A., 1996, 169, 9.
5. D. Andreeva, V. Idakiew, T. Tabakova, I. Ilieva, P. Falaras, A. Bourlinos and A. Travlos, Low-temperature water–gas shift reaction over Au/CeO₂ catalysts, Catal. Today, 2002, 72, 51.
6. A. Venugopal, J. Aluha, D. Mogano and M. S. Scurrell, The gold–ruthenium–iron oxide catalytic system for the low temperature water–gas-shift reaction: The examination of gold–ruthenium interactions, Appl. Catal., A, 2003, 245, 149.
7. J. Hua, K. Wei, Q. Zheng and X. Lin, Influence of calcination temperature on the structure and catalytic performance of Au/iron oxide catalysts for water–gas shift reaction, Appl. Catal., A, 2004, 259, 121.
8. D. L. Trimm, Minimisation of carbon monoxide in a hydrogen stream for fuel cell application, Appl. Catal., A, 2005, 296, 1.
9. D. Boyd, S. Golunski, G. R. Hearne, T. Magadzu, K. Mallick, M. C. Raphulu, A. Venugopal and M. S. Scurrell, Reductive routes to stabilized nanogold and relation to catalysis by supported gold, Appl. Catal., A, 2005, 292, 76.
10. C. H. Kim and L. T. Thompson, Deactivation of Au/CeO_x water gas shift catalysts, J. Catal., 2005, 230, 66.
11. M. Haruta, Catalysis: Gold rush, Nature, 2005, 437, 1098.
12. C. W. Corti, R. J. Holliday and D. T. Thompson, Progress towards the commercial application of gold catalysts, Top. Catal., 2007, 44, 331.
13. M. S. Chen and D. W. Goodman, Catalytically active gold: From nanoparticles to ultrathin films, Acc. Chem. Res., 2006, 39, 739.
14. A. S. K. Hashmi and G. J. Hutchings, Gold catalysis, Angew. Chem., Int. Ed., 2006, 45, 7896.
15. J. A. Rodriguez, S. Ma, P. Liu, J. Hrbek, J. Evans and M. Perez, Activity of CeO_x and TiO_x nanoparticles grown on Au(111) in the water–gas shift reaction, Science, 2007, 318, 1757.
16. M. C. Kung, R. J. Davis and H. H. Kung, Understanding Au-catalyzed low-temperature CO oxidation, J. Phys. Chem. C, 2007, 111, 11767.
17. J. A. van Bokhoven, Catalysis by Gold: Why Size Matters, Chimia, 2009, 63, 257.
18. N. R. Shiju, N. Raveendran and V. V. Guliants, Recent developments in catalysis using nanostructured materials, Appl. Catal., A, 2009, 356, 1.
19. G. Bond and D. Thompson, Formulation of mechanisms for gold-catalysed reactions, Gold Bull., 2009, 42, 247.
20. A. Trovarelli, Catalysis by Ceria and Related Materials, Imperial College Press, London, 2002.
21. (a) M. Veronica Ganduglia-Pirovano, J. L. F. Da Silva and J. Sauer, Density-functional calculations of the structure of near-surface oxygen vacancies and electron localization on CeO₂(111), Phys. Rev. Lett., 2009, 102, 026101; (b) H.-Y. Li, H.-F. Wang, X.-Q. Gong, Y.-L. Guo, Y. Guo, G. Lu and P. Hu, Multiple configurations of the two excess 4f electrons on defective CeO₂(111): Origin and implications, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 193401.
22. J. A. Rodriguez, X. Wang, P. Liu, W. Wen, J. C. Henson, J. Hrbek, M. Perez and J. Evans, Gold nanoparticles on ceria: importance of O vacancies in the activation of gold, Top. Catal., 2007, 44, 73.
23. M. Han, X. J. Y. Shen, C. H. Tang, G. S. Li and R. L. Smith, Preparation of Highly Active, Low Au-Loaded, Au/CeO₂ Nanoparticle Catalysts That Promote CO Oxidation at Ambient Temperatures, J. Phys. Chem. C, 2010, 114, 793.
24. Q. Fu, H. Saltsburg and M. Flytzani-Stephanopoulos, Active Nonmetallic Au and Pt Species on Ceria-Based Water–Gas Shift Catalysts, Science, 2003, 301, 935.
25. Q. Fu, W. Deng, H. Saltsburg and M. Flytzani-Stephanopoulos, Activity and stability of low-content gold-cerium oxide catalysts for the watergas shift reaction, Appl. Catal., B, 2005, 56, 57.
26. G. Jacobs, P. M. Patterson, L. Williams, E. Chenu, D. Sparks, G. Thomas and B. H. Davis, Water–gas shift: In situ spectroscopic studies of noble metal promoted ceria catalysts for CO removal in fuel cell reformers and mechanistic implications, Appl. Catal., A, 2004, 262, 177.
27. H. Sakurai, T. Akita, S. Tsubota, M. Kiuchi and M. Haruta, Low-temperature activity of Au/CeO₂ for water gas shift reaction, and characterization by ADF-STEM, temperature-programmed reaction, and pulse reaction, Appl. Catal., A, 2005, 291, 179.
28. W. Deng, J. De Jesus, H. Saltsburg and M. Flytzani-Stephanopoulos, Low-content gold-ceria catalysts for the water–gas shift and preferential CO oxidation reactions, Appl. Catal., A, 2005, 291, 126.
29. A. M. Venezia, G. Pantaleo, A. Longo, G. D. Carlo, M. P. Casaletto, F. L. Liotta and G. Deganello, Relationship between structure and CO oxidation activity of ceria-supported gold catalysts, J. Phys. Chem. B, 2005, 109, 2821.
30. J. T. Miller, A. J. Kropf, Y. Zha, J. R. Regalbuto, L. Delannoy, C. Louis, E. Bus and J. A. van Bokhoven, The effect of gold particle size on Au–Au bond length and reactivity towards oxygen in supported catalysts, J. Catal., 2006, 240, 222.
31. T. Tabakova, F. Boccuzzi, M. Manzoli, J. W. Sobczak, V. Idakiev and D. Andreeva, A comparative study of nanosized IB/ceria catalysts for low-temperature water–gas shift reaction, Appl. Catal., A, 2006, 298, 127.
32. R. Burch, Gold catalysts for pure hydrogen production in the water–gas shift reaction: Activity, structure and reaction mechanism, Phys. Chem. Chem. Phys., 2006, 8, 5483.
33. U. R. Pillai and S. Deevi, Highly active gold-ceria catalyst for the room temperature oxidation of carbon monoxide, Appl. Catal., A, 2006, 299, 266.
34. J. B. Park, J. Graciani, J. Evans, D. Stacchiola, S. D. Senanayake, L. Barrio, P. Liu, J. F. Sanz, J. Hrbek and J. A. Rodriguez, Gold, Copper, and Platinum Nanoparticles Dispersed on CeO_x/TiO₂(110) Surfaces: High Water–Gas Shift Activity and the Nature of the Mixed-Metal Oxide at the Nanometer Level, J. Am. Chem. Soc., 2010, 132, 356.
35. Z.-P. Liu, S. J. Jenkins and D. A. King, Origin and activity of oxidised gold in water–gas-shift catalysis, Phys. Rev. Lett., 2005, 94, 196102.
36. V. Shapovalov and H. Metiu, Catalysis by doped oxides: CO oxidation by Au_xCe_1−xO₂, J. Catal., 2007, 245, 205.
37. C. S. Chretien, S. K. Buratto and H. Metiu, Catalysis by very small Au clusters, Curr. Opin. Solid State Mater. Sci., 2007, 11, 62.
38. P. Liu and J. A. Rodriguez, Water–gas-shift reaction on metal nanoparticles and surfaces, J. Chem. Phys., 2007, 126, 164705.
39. J. Graciani, J. J. Plata, J. F. Sanz, P. Liu and J. A. Rodriguez, A theoretical insight into the catalytic effect of a mixed-metal oxide at the nanometer level: the case of the highly active metal/CeO_x/TiO₂(110) catalysts, J. Chem. Phys., 2010, 132, 104703.
40. M. V. Ganduglia-Pirovano, A. Hofmann and J. Sauer, Oxygen vacancies in transition metal and rare earth oxides: Current state of understanding and remaining challenges, Surf. Sci. Rep., 2007, 62, 219.
41. R. T. Kinch, C. R. Cabrera and Y. Ishikawa, A Density-Functional Theory Study of the Water–Gas Shift Mechanism on Pt/Ceria(111), J. Phys. Chem. C, 2009, 113, 9239.
42. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids and surfaces-applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter, 1992, 46, 6671.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
44. I. P. R. Moreira, F. Illas and R. L. Martin, Effect of Fock exchange on the electronic structure and magnetic coupling in NiO, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155102.
45. J. Harl and G. Kresse, Accurate bulk properties from approximate many-body techniques, Phys. Rev. Lett., 2009, 103, 056401.
46. R. J. Needs, M. D. Towler, N. D. Drummond and P. L. Rios, Continuum variational and diffusion quantum Monte Carlo calculations, J. Phys.: Condens. Matter, 2010, 22, 023201.
47. V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter, 1991, 44, 943.
48. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, First-principles calculations of the electronic structure and spectra of strongly correlated systems: The LDA + U method, J. Phys.: Condens. Matter, 1997, 9, 767.
49. A. Rohrbach, J. Hafner and G. J. Kresse, Electronic correlation effects in transition-metal sulfides, J. Phys.: Condens. Matter, 2003, 15, 979.
50. D. A. Andersson, S. I. Simak, B. Jahansson, I. A. Abrikosov and N. V. Skorodumova, Modeling of CeO₂, Ce₂O₃, and CeO_2−x in the LDA + U formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035109.
51. C. Loschen, J. Carrasco, K. M. Neyman and F. Illas, First-principles LDA + U and GGA + U study of cerium oxides: Dependence on the effective U parameter, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035115.
52. C. W. M. Castleton, J. Kullgren and K. Hermansson, Tuning LDA + U for electron localization and structure at oxygen vacancies in ceria, J. Chem. Phys., 2007, 127, 244704.
53. S. Fabris, S. de Gironcoli, S. Baroni, G. Vicario and G. Balducci, Taming multiple valency with density functionals: A case study of defective ceria, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 041102.
54. M. Nolan, S. C. Parker and G. W. Watson, Density functional theory studies of the structure and electronic structure of pure and defective low index surfaces of ceria, Surf. Sci., 2005, 595, 223.
55. C. Zhang, A. Michaelides, D. A. King and S. J. Jenkins, Structure of gold atoms on stoichiometric and defective ceria surfaces, J. Chem. Phys., 2008, 129, 194708.
56. B. Herschend, M. Baudin and K. Hermansson, Oxygen vacancy formation for transient structures on the CeO₂(110) surface at 300 and 750 K, J. Chem. Phys., 2007, 126, 234706.
57. M. Nolan, S. Grigoleit, D. C. Sayle, S. C. Parker and G. W. Watson, The electronic structure of oxygen vacancy defects at the low index surfaces of ceria, Surf. Sci., 2005, 576, 217.
58. S. Fabris, G. Vicario, G. Balducci, S. de Gironcoli and S. Baroni, Electronic and atomistic structures of clean and reduced ceria surfaces, J. Phys. Chem. B, 2005, 109, 22860.
59. J. C. Conesa, Computer modeling of surfaces and defects on cerium dioxide, Surf. Sci., 1995, 339, 337.
60. N. V. Skorodumova, M. Baudin and K. Hermansson, Surface properties of CeO₂ from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 075401.
61. P. R. L. Keating, D. O. Scanlon and G. W. Watson, Intrinsic ferromagnetism in CeO₂: Dispelling the myth of vacancy site localization mediated superexchange, J. Phys.: Condens. Matter, 2009, 21, 405502.
62. C. Zhang, A. Michaelides, D. A. King and S. J. Jenkins, Oxygen vacancy clusters on ceria: Decisive role of cerium f electrons, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 075433.
63. C. Zhang, A. Michaelides, D. A. King and S. J. Jenkins, Anchoring sites for gold nanoparticles on ceria: O vacancy versus Ce vacancy, J. Phys. Chem. C, 2009, 113, 6411.
64. F. Esch, S. Fabris, L. Zhou, T. Montini, C. Africh, P. Fornasiero, G. Comelli and R. Rosei, Electron localization determines defect formation on ceria substrates, Science, 2005, 309, 752.
65. C. T. Campbell and C. H. F. Peden, Oxygen vacancies and catalysis on ceria surfaces, Science, 2005, 309, 713.
66. J. C. Conesa, Surface anion vacancies on ceria: Quantum modelling of mutual interactions and oxygen adsorption, Catal. Today, 2009, 143, 315.
67. Y. Namai, K. Fukui and Y. Iwasawa, Atom-resolved noncontact atomic force microscopic and scanning tunneling microscopic observations of the structure and dynamic behavior of CeO₂(111) surfaces, Catal. Today, 2003, 85, 79.
68. Y. Namai, K. Fukui and Y. Iwasawa, Atom-resolved noncontact atomic force microscopic observations of CeO₂(111) surfaces with different oxidation states: Surface structure and behavior of surface oxygen atoms, J. Phys. Chem. B, 2003, 107, 11666.
69. G. Balducci, J. Kašpar, P. Fornasiero, M. Graziani, M. S. Islam and J. D. Gale, Computer simulation studies of bulk reduction and oxygen migration in CeO₂–ZrO₂ solid solutions, J. Phys. Chem. B, 1997, 101, 1750.
70. C. Frayret, A. Villesuzanne, M. Pouchard and S. Matar, Density functional theory calculations on microscopic aspects of oxygen diffusion in ceria-based materials, Int. J. Quantum Chem., 2005, 101, 826.
71. D. A. Andersson, S. I. Simak, N. V. Skorodumova, I. A. Abrikosov and B. Johansson, Optimization of ionic conductivity in doped ceria, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3518.
72. M. Nolan, J. E. Fearon and G. W. Watson, Oxygen vacancy formation and migration in ceria, Solid State Ionics, 2006, 177, 3069.
73. N. C. Hernández, R. Grau-Crespo, N. H. de Leeuw and J. F. Sanz, Electronic charge transfer between ceria surfaces and gold adatoms: A GGA + U investigation, Phys. Chem. Chem. Phys., 2009, 11, 5246.
74. M. F. Camellone and S. Fabris, Reaction mechanisms for the CO oxidation on Au/CeO₂ catalysts: Activity of substitutional Au³⁺/Au⁺ cations and deactivation of supported Au⁺ adatoms, J. Am. Chem. Soc., 2009, 131, 10473.
75. N. J. Castellani, M. M. Branda, K. M. Neyman and F. Illas, Density functional theory study of the adsorption of Au atom on cerium oxide: Effect of low-coordinated surface sites, J. Phys. Chem. C, 2009, 113, 4948.
76. M. M. Branda, N. C. Hernández, J. F. Sanz and F. Illas, Density functional theory study of the interaction of Cu, Ag, and Au atoms with the regular CeO₂(111) surface, J. Phys. Chem. C, 2010, 114, 1934.
77. R. Grau-Crespo, private communication.
78. M. M. Branda, N. J. Castellani, R. Grau-Crespo, N. H. de Leeuw, N. C. Hernández, J. F. Sanz, K. M. Neyman and F. Illas, On the difficulties of present theoretical models to predict the oxidation state of atomic Au adsorbed on regular sites of CeO₂(111), J. Chem. Phys., 2009, 131, 094702.
79. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106.
80. J. L. F. Da Silva, M. Veronica Ganduglia-Pirovano, J. Sauer, V. Bayer and G. Kresse, Hybrid functionals applied to rare-earth oxides: The example of ceria, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045121.
81. J. Kullgren, C. W. M. Castleton, C. Muller, D. M. Ramo and K. Hermansson, B3LYP calculations of cerium oxides, J. Chem. Phys., 2010, 132, 054110.
82. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158.
83. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter, 1988, 37, 785.
84. Y. Chen, P. Hu, M. H. Lee and H. Wang, Au on (111) and (110) surfaces of CeO₂: A density-functional theory study, Surf. Sci., 2008, 602, 1736.
85. D. Tibiletti, A. Amieiro-Fonseca, R. Burch, Y. Chen, J. M. Fisher, A. Goguet, C. Hardacre, P. Hu and A. Thompsett, DFT and in situ EXAFS investigation of gold/ceria-zirconia low-temperature water gas shift catalysts: Identification of the nature of the active form of gold, J. Phys. Chem. B, 2005, 109, 22553.
86. M. Nolan, V. S. Verdugo and H. Metiu, Vacancy formation and CO adsorption on gold-doped ceria surfaces, Surf. Sci., 2008, 602, 2734.
87. O. F. Schirmer, O-bound small polarons in oxide materials, J. Phys.: Condens. Matter, 2006, 18, R667.
88. A. Chainani, M. Mathew and D. D. Sarma, Electronic structure of La_1−xSr_xFeO₃, Phys. Rev. B: Condens. Matter, 1993, 48, 14818.
89. R. H. Potze, G. A. Sawatzky and M. Abbate, Possibility for an intermediate-spin ground state in the charge-transfer material SrCoO₃, Phys. Rev. B: Condens. Matter, 1995, 51, 11501.
90. M. D'Avezac, M. Calandra and F. Mauri, Density functional theory description of hole-trapping in SiO₂: A self-interaction-corrected approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205210.
91. D. O. Scanlon, A. Walsh, B. J. Morgan, M. Nolan, J. Fearon and G. W. Watson, Surface sensitivity in lithium-doping of MgO: a density function theory study with correction for on-site Coulomb interactions, J. Phys. Chem. C, 2007, 111, 7971.
92. S. Lany and A. Zunger, Polaronic hole localization and multiple hole binding of acceptors in oxide wide-gap semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085202.
93. J. A. Chan, S. Lany and A. Zunger, Electronic correlation in anion p orbitals impedes ferromagnetism due to cation vacancies in Zn chalcogenides, Phys. Rev. Lett., 2009, 103, 016404.
94. B. J. Morgan and G. W. Watson, Polaronic trapping of electrons and holes by native defects in anatase TiO₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 233102.
95. Y. Chen, J. Cheng, P. Hu and H. Wang, Examining the redox and formate mechanisms for water–gas shift reaction on Au/CeO₂ using density functional theory, Surf. Sci., 2008, 602, 2828.
96. C. Zhang, A. Michaelides, D. A. King and S. J. Jenkins, Positive charge states and possible polymorphism of gold nanoclusters on reduced ceria, J. Am. Chem. Soc., 2010, 132, 2175.
97. To reiterate, although the expression DFT + U is widely used, the DFT approach itself is formally exact and its failure to reproduce the behaviour of strongly correlated electronic systems is a failure of standard mean-field exchange–correlation functionals.
98. The charge on the atoms is typically estimated in such calculations with a scheme such as Mulliken or Bader charge analysis.
99. In order to avoid problematic oscillations in the approach to self-consistency, it is standard practice in DFT to mix the electron density calculated at each new iteration with some contribution from previous iterations, prior to using this in formulating the potential to be employed in calculating the next iteration. In essence, the work of Liu et al.³⁵ “switched off” this mixing procedure for the components of the density matrix most likely to correspond to the f orbitals (i.e. those corresponding to large reciprocal lattice vectors and/or those whose magnitudes varied dramatically from one iteration to the next, the latter criterion being continually reassessed dynamically during the course of the calculation). The result is to “lock-in” localised behaviour for the f electrons, whilst still benefitting from improved convergence properties for the s, p and d electrons.

---