Solvent structural relaxation dynamics in dipolar solvation studied by resonant pump polarizability response spectroscopy
Received
21st July 2010
, Accepted 11th October 2010
First published on 23rd November 2010
Abstract
Resonant pump polarizability response spectroscopy (RP-PORS) was used to study the isotropic and anisotropic solvent structural relaxation in solvation. RP-PORS is the optical heterodyne detected transient grating (OHD-TG) spectroscopy with an additional resonant pump pulse. A resonant pump excites the solute–solvent system and the subsequent relaxation of the solute–solvent system is monitored by the OHD-TG spectroscopy. This experimental method allows measuring the dispersive and absorptive parts of the signal as well as fully controlling the beam polarizations of incident pulses and signal. The experimental details of RP-PORS were described. By performing RP-PORS with Coumarin 153(C153) in CH3CN and CHCl3, we have successfully measured the isotropic and anisotropic solvation polarizability spectra following electronic excitation of C153. The isotropic solvation polarizability responses result from the isotropic solvent structural relaxation of the solvent around the solute whereas the anisotropic solvation polarizability responses come from the anisotropic translational relaxation and orientational relaxation. The solvation polarizability responses were found to be solvent-specific. The intramolecular vibrations of CHCl3 were also found to be coupled to the electronic excitation of C153.
1. Introduction
Understanding chemical and physical processes occurring in solutions requires detailed knowledge about the solvent dynamics in such processes. Solvent interacts with chemical species during the processes in many different ways by activating reactants, stabilizing activated complexes or any intermediates, and releasing excess energy from products, and thus determine the outcome of the processes.1 However, an accurate measurement of solvent dynamics in such processes is not straightforward. Instead, the simpler process of solvation has been widely studied for fundamental understanding of the solvent dynamics.2
As schematically shown in Fig. 1, solvation is a relaxation of solute–solvent system after a sudden change in electronic structure of the solute following the electronic excitation of the solute as the surrounding solvent undergoes the time-dependent structural reorganization to minimize the free energy of the system.3–6 The solvent reorganization occurs on subpicosecond and picosecond timescales. Solvation dynamics have been extensively studied by time-resolved fluorescence Stokes shift (TRFSS)7–9 and photon echo peak shift (PEPS)5,10–13 measurements. In TRFSS, the relaxation of the solute–solvent system is monitored by measuring the solute's emission spectra of which the time-dependent shift gives information on solvent relaxation. On the other hand, in PEPS, the solvent fluctuations have a direct influence on the solute's electronic energy gap correlation function. In both methods, the solute's spectroscopic properties are used to probe the solvent relaxation or fluctuation. Under the fluctuation-dissipation theorem, both methods give the same information, which is the timescale of the solvation. The major finding from TRFSS and PEPS is that the solvation is bimodal, exhibiting inertial and diffusive motions of the solvent.5,14 Inertial motion plays an important role at very early times and is represented by a Gaussian function while the diffusive motion is responsible for solvation at longer times and is well described by exponential functions. The relative contribution of the inertial and diffusive motions is solvent-dependent. In highly polar solvents, the inertial motion is dominant while the diffusive motion is more important in weakly polar and nondipolar solvents.14 Computer simulations have also been performed with simple solute–solvent systems for detailed molecular-level understanding of solvation in terms of the nature of interactions between the solute and solvent as well as the changes in solute charge, size, and polarizability.15,16
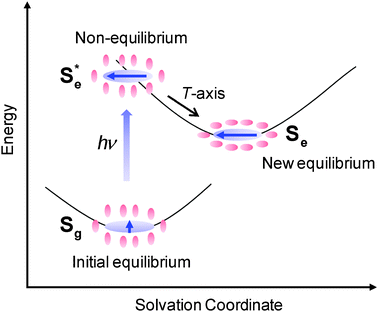 |
| | Fig. 1 Schematic representation of the solvation dynamics. Sg represents an initial equilibrium state between the ground state solute and solvents while Se represents a new equilibrium state between the excited state solute and solvents. 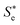 is a nonequilibrium state created by an electronic excitation of the solute. is a nonequilibrium state created by an electronic excitation of the solute. | |
The current level of understanding of the solvation is achieved by the experimental results from TRFSS and PEPS as well as the results of computer simulations. However, despite these advances, our insight into the solvent responses in solvation is still incomplete. One major reason for this is that the solute is used as a probe molecule such that what is measured is a change in the solute's property associated with the solvent relaxation or fluctuation. Therefore, the quantities measured in TRFSS and PEPS give indirect information on what the solvent is actually doing. It also stems partially from the difficulty of direct measurements of the solvent responses in solvation. Recently, optical-pump terahertz-probe spectroscopy was employed to measure the low-frequency solvent modes in solvation.17–19 A terahertz pulse has spectral bandwidth of 10–100 cm−1 which covers much of the spectral range of the solvent intermolecular motions. However, the terahertz pulses are not short enough to resolve the solvent dynamics at early times. More recently, Blank and coworkers showed an experimental method in which the third-order Raman spectroscopy was combined with a resonant pump, which was termed “RAPTORS”.20,21 In their method, a time-dependent solvent scattering signal was used as a local oscillator. Unfortunately, this complicated the interpretation of the experimental results because many degenerate signals were able to be measured in the same phase matching direction as well as the dispersive and absorptive parts of the signal were not able to be measured separately.
As a first effort of direct measurements of the solvent response in solvation, we had developed a two-color optical Kerr effect (OKE) spectroscopy where only the anisotropic solvent response around the solute was able to be measured.22 As an extension of the two-color OKE spectroscopy, we have developed an experimental method, termed “resonant pump polarizability response spectroscopy (RP-PORS)” with a time-independent local oscillator as opposed to RAPTORS.23–25 This method utilizes the optical heterodyne detected transient grating (OHD-TG) spectroscopy in which the phase of the local oscillator is fully controlled with respect to the signal and therefore it is possible to selectively measure the dispersive and absorptive parts of the third-order signal.26–29 In addition, the full control of the beam polarizations of incident pulses and signal in the OHD-TG geometry is feasible so that both isotropic and anisotropic solvent responses can be measured as opposed to the two-color OKE spectroscopy. Recently, the detailed theoretical description and simulation for the RP-PORS were presented.24 The RP-PORS was theoretically considered as a fifth-order spectroscopy where the resonant pulse created the ground (hole) and excited state (particle) wavepackets that evolved until the polarizability spectrum was probed by three incident nonresonant pulses and a fourth local oscillator pulse. The model simulation showed that the PORS signal generation could result from (1) the structural relaxation induced resonance and (2) the dephasing induced resonance.24 The lineshapes obtained from both the model simulation based on two mechanisms and the RP-PORS experiments had suggested that the structural relaxation induced resonance was more important than the dephasing induced resonance.24 Mathies and coworkers developed femtosecond stimulated Raman spectroscopy (FSRS) that could, in principle, measure the same dynamics as the RAPTORS and RP-PORS when the actinic pump pulse and the Raman probe pulses were resonant and nonresonant with the electronic transition of the solute, respectively.30–34 However, the FSRS has been applied to study the high frequency vibrational resonances (>300 cm−1).
In the present work, RP-PORS was performed with Coumarin 153 (C153) in CH3CN and CHCl3 to measure the solvation polarizability spectra. In the RP-PORS setup, a resonant pump is added to the optical heterodyne detected transient grating (OHD-TG) spectrometer. As shown in Fig. 1, a resonant pump, which is resonant with C153 and is nonresonant with the solvents, electronically excites the C153–solvent system which is in an initial equilibrium state (Sg). This creates a nonequilibrium state 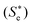 of the C153–solvent system which will relax to a new equilibrium state (Se) as a result of the solvent reorganization around C153. The relaxation of the nonequilibrium C153–solvent system is monitored by selectively measuring the dispersive part (i.e. index of refraction of the system; polarizability response) of the OHD-TG signal which is termed “polarizability response spectroscopy (PORS)”.
of the C153–solvent system which will relax to a new equilibrium state (Se) as a result of the solvent reorganization around C153. The relaxation of the nonequilibrium C153–solvent system is monitored by selectively measuring the dispersive part (i.e. index of refraction of the system; polarizability response) of the OHD-TG signal which is termed “polarizability response spectroscopy (PORS)”.
2. Experimental
A home-built cavity-dumped Ti:Sapphire oscillator is used to generate 20 nJ and ∼20 fs pulses centered at 800 nm.35 The 800 nm pulses are amplified in a home built cavity-dumped Ti:Sapphire amplifier with chirped mirrors producing pulses of 1.5 μJ at repetition rates ranging from 10 to 250 kHz.36,37 The 400 nm second harmonic pulse, which is used as a resonant pump in RP-PORS, is generated with a 200 μm thick BBO crystal. Both 800 and 400 nm pulses are properly precompensated for material dispersion with two different pairs of BK7 prisms giving 35 fs pulse duration of 800 nm and 70 fs pulse duration of 400 nm at the sample position, respectively.
The overall RP-PORS setup is shown in Fig. 2. Basically, it is the OHD-TG setup with a resonant pump added. The OHD-TG setup is built with diffractive optical element (DOE) and its basic design and performance have been previously shown.26,38–40 The design of our OHD-TG setup is based on the Newtonian telescope. By using parabolic mirrors for collimating and focusing in our OHD-TG setup, any beam distortion (spherical aberration, astigmatism, and chromatic aberration) can be minimized. The 800 nm beam is split into two beams with a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity ratio. Their relative time delay is controlled before the DOE. The weak beam passes through a variable time delay line while the intense beam has a fixed path. As shown in Fig. 2, two beams, which are vertically-polarized (P1 and P2), are focused onto the DOE with an achromat lens (L1, f.l. = 15 cm). The DOE is specially designed and manufactured such that the total diffraction efficiency for the first-order (±1) beams is more than 80% at 800 nm (HoloEye Photonics AG, Germany). The first-order (±1) diffraction beams, whose angle is 10°, are collimated and focused with parabolic mirrors (CM1, f.l. = 20 cm and CM2, f.l. = 15 cm, respectively) in a box-car geometry and recollimated with an achromat lens (L2, f.l. = 10 cm). A phase-matched beam geometry after the sample is shown in the upper right corner of Fig. 2. A mask (M1) is used to block higher-order diffraction beams from the DOE and another mask (M2) after the sample is used to block all incident beams except the signal and local oscillator.
1 intensity ratio. Their relative time delay is controlled before the DOE. The weak beam passes through a variable time delay line while the intense beam has a fixed path. As shown in Fig. 2, two beams, which are vertically-polarized (P1 and P2), are focused onto the DOE with an achromat lens (L1, f.l. = 15 cm). The DOE is specially designed and manufactured such that the total diffraction efficiency for the first-order (±1) beams is more than 80% at 800 nm (HoloEye Photonics AG, Germany). The first-order (±1) diffraction beams, whose angle is 10°, are collimated and focused with parabolic mirrors (CM1, f.l. = 20 cm and CM2, f.l. = 15 cm, respectively) in a box-car geometry and recollimated with an achromat lens (L2, f.l. = 10 cm). A phase-matched beam geometry after the sample is shown in the upper right corner of Fig. 2. A mask (M1) is used to block higher-order diffraction beams from the DOE and another mask (M2) after the sample is used to block all incident beams except the signal and local oscillator.
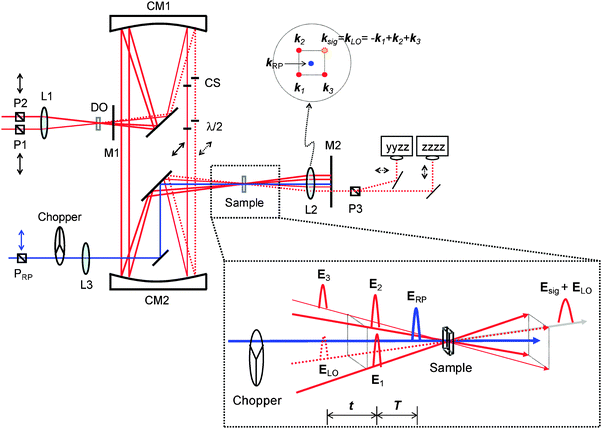 |
| | Fig. 2 Layout of RP-PORS experimental setup. P1, P2, and PRP, Glan Taylor polarizers; P3, Rochon polarizer; DO, diffractive optical element; CM, parabolic mirrors; CS, cover slips; M, mask; L, lens; λ/2, half waveplates. | |
In the TG geometry, two pump pulses, E1(k1) and E2(k2), are temporally and spatially overlapped in the sample creating an interference pattern. Interactions of the two pump pulses with the sample lead to a spatially modulated complex refractive index of the sample (transient grating) in the crossing region.27,41–46 The time-delayed probe pulse, E3(k3) (+1 diffraction order), is diffracted off the grating at the Bragg angle and is detected as a signal, Esig(ksig = −k1 + k2 + k3), to a new phase-matched direction. In the DOE-based OHD-TG setup, the signal is automatically collinear and coherent with the local oscillator, ELO(kLO) (−1 diffraction order, LO), providing a convenient way to implement the optical heterodyne detection. Identical achromat half waveplates (λ/2) are inserted in the probe and LO beams after the collimating parabolic mirror (CM1). A 150 μm thick microscope cover slip (CS) is inserted between CM1 and the half waveplate in the probe and LO beams. One face of the CS placed in the LO beam path is coated with gold particles such that it gives 5% transmission at 800 nm. The CS in the LO is mounted on a rotational stage whose fine adjustment controls the relative phase of the LO with respect to the signal. The rotation of the CS results in the change in the relative optical pathlength of the LO leading to the phase shift. A π-phase change is made by rotating the CS by ∼3°.
Neat solvent is used to calibrate the relative phase of the OHD-TG signal with respect to the LO. The phase scan is made in neat solvent at t = 0 ps by rotating the CS in the LO beam. The absorptive part of the OHD-TG signal from the neat solvent is negligible because the neat solvent is nonresonant with 800 nm. The OHD-TG signal is dependent on the relative phase of the LO with respect to the signal. The peaks and valleys in the phase scan determine the ±π/2 conditions within the pulse envelope. The relative phase of the signal is calibrated with respect to the LO such that the maximum peak in the phase scan within the pulse envelope is set to be π/2 phase. Fig. 3(A) shows the calibrated relative phase of the OHD-TG signal with respect to the LO. The relative phase is checked before and after each experiment to ensure no significant phase drift during data acquisition. The phase drift is measured to be less than 5° over a few days. Fig. 3(B) shows the OHD-TG signals that are measured with neat CH3CN at four different LO phases. The dispersive parts (ϕ = 90 and 270°) of the signal are opposite in sign and similar in amplitude while the absorptive parts (ϕ = 0 and 180°) are negligible. For the remainder of the present paper, the polarizability response spectroscopy (PORS) represents selective measurements of the dispersive part of the signal in the OHD-TG method.
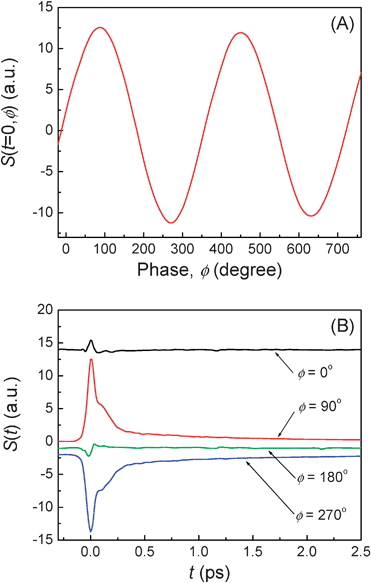 |
| | Fig. 3
Phase control in the OHD-TG measurement. (A) The relative phase of the LO with respect to the signal in neat CH3CN. (B) The OHD-TG signals at four different phases of the LO. | |
For the electronic excitation, a resonant pump is added to the OHD-TG setup. The resonant pump is focused with an achromat lens (L3, f.l. = 30 cm). The resonant beam is vertically polarized (PRP). The polarizations of incoming fields are defined as ERP/E1/E2/E3/ELO = 0°/0°/0°/45°/45°. The vertical and horizontal components of the OHD-TG signal are decomposed before the detection by a Rochon polarizer (P3) and are measured simultaneously. In RP-PORS, a resonant pump pulse, ERP(kRP), excites a chromophore (i.e. solute) at T = 0 ps. At a time delay, T, the two nonresonant pump pulses, E1(k1) and E2(k2), are temporally and spatially overlapped leading to a modulation of the complex index of refraction of the sample. At a time delay, T + t, the probe, E3(k3), stimulates the emission of the signal, Esig(ksig = −k1 + k2 + k3), to a new phase matched direction. The emitted signal field is interferometrically mixed with the LO allowing the optical heterodyne detection. In our experimental geometry, the LO, ELO(kLO), is also overlapped with other incoming pulses (En(kn) = ERP(kRP), E1(k1), E2(k2), and E3(k3)) in the sample and the degenerate pump–probe signals 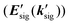 in the same phase-matched direction
in the same phase-matched direction 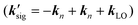 are also measured together with the OHD-TG signal
are also measured together with the OHD-TG signal 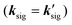 . However, the degenerate pump–probe signals are always in-phase with the LO while the OHD-TG signal is dependent upon the phase of the LO. Therefore, the dispersive and absorptive parts of the OHD-TG signal at a given T can be obtained by a dual phase scan method
. However, the degenerate pump–probe signals are always in-phase with the LO while the OHD-TG signal is dependent upon the phase of the LO. Therefore, the dispersive and absorptive parts of the OHD-TG signal at a given T can be obtained by a dual phase scan method
| | | Sdisp(t;T) = S(t,ϕ = π/2;T) − S(t,ϕ = 3π/2;T) ∝ Re[P(3)(t;T)] | (1) |
| | | Sabs(t;T) = S(t,ϕ = 0;T) − S(t,ϕ = π;T) ∝ Im[P(3)(t;T)] | (2) |
In practice, the RP-PORS signals are obtained by measuring the OHD-TG signals with two π/2 out-of-phase local oscillators and taking their difference.
Fig. 4 describes the dual phase scan method. The RP-PORS signals are collected with the LO phase of 90° and 270°. The RP-PORS signals are superimposed on top of the degenerate pump–probe signals. These degenerate pump–probe signals (
ERP and
ELO) are a time-dependent background. However, they are independent of the phase of the LO and thus, can be removed by the dual phase scan method.
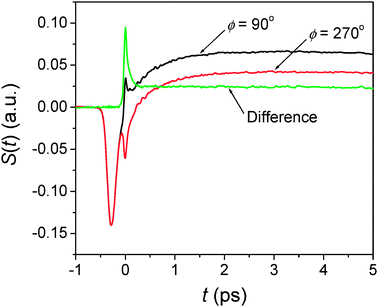 |
| | Fig. 4 Dual phase scan method in RP-PORS. At T = 0.3 ps, two scans are made with two different LO phases (ϕ = 90° and 270°) and the RP-PORS signal is obtained by taking their difference. | |
Sample C153 purchased from Acros was used as received. CH3CN (acetonitrile) and CHCl3 (chloroform) used in the experiments were HPLC-grade. 0.30 mM C153 solutions were prepared by directly dissolving C153 in each solvent. The C153 solution sample was circulated in a flow-through cell during the measurement to avoid photobleaching and thermal heating. The repetition rate of pulses from the laser system was 123 kHz so that the time interval between pulses in a train of pulses was 8 μs ensuring that C153, whose lifetime in the excited state was ∼5 ns, relaxed back to the ground state before the next pulse arrives. Two sets of identical detector and lock-in amplifier are used to measure both Szzzz(t) and Syyzz(t) at the same time by chopping the resonant pump at 2.51 kHz. For accurate measurements of the isotropic and anisotropic tensor elements (i.e. Siso(t) and Saniso(t)), the polarizations of the probe and LO were carefully adjusted to 45° with respect to those of the nonresonant pumps. Siso(t) and Saniso(t) of CCl4 reconstructed from the measured Szzzz(t) and Syyzz(t) were in excellent agreement with the previously reported results.47 A low-pass color filter (cutoff at 715 nm) was placed right before the detectors to block the scattering of the resonant pump (400 nm) from the sample cell.
In RP-PORS, the signals are collected by chopping the resonant pump (RP). In other words, the solute–solvent system is probed by the PORS with the resonant pump on and off, which allows a selectivity of the molecular responses that are induced only by the resonant pump,
| | | S(t;T) = SRP-On(t;T) − SRP-Off(t;T) | (3) |
where
SRP-On(
t;
T) and
SRP-Off(
t;
T) represent the molecular responses with the resonant pump on and off, respectively. The resonant pump is resonant with the solute (
i.e. C153) and nonresonant with the
solvent. Therefore, the RP-PORS measures only the molecular responses that are influenced by the electronic excitation of the solute. That is to say, the
solvent molecular response in bulk is not measured in RP-PORS. It will be discussed in terms of molecular contributions in RP-PORS in more detail in the following section.
3. Results and data analysis
3.1 RP-PORS signal
The RP-PORS signal, S(t;T), can be collected by scanning t at a series of T. T is a waiting time before the PORS measurement is performed as shown in Fig. 2. In this particular case, T-axis is denoted “the solvation axis”. As mentioned earlier, the RP-PORS signal results from the structural relaxation of the solvent molecules around the solute (the solute–solvent system) following the electronic excitation of the solute.24 When T is shorter than Teq (i.e. the complete solvation time, the time for completion of solvent relaxation), the structural relaxation of the solvent molecules around the excited solute is taking place while the t scan is being made. Accordingly, the RP-PORS signal includes nonequilibrium solvent relaxation dynamics. On the other hand, when T is larger than Teq, the solvent reorganization is finished and thus the solute–solvent system reaches a new equilibrium state as shown in Fig. 2. The RP-PORS signal measured at any time larger than Teq (denoted S(t;Teq) for simplicity) includes the equilibrium structural change of the solvent molecule around the solute in the excited state (S1) and ground state (S0). This is referred to as “the solvation response” throughout this paper. The structural change arises mainly from the translational and orientational relaxations of the solvent molecules around the solute. The solvent structural relaxations can be separated into the isotropic and anisotropic responses based on their symmetry. The isotropic and anisotropic PORS signals are obtained by| | 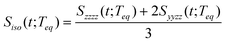 | (4) |
| | 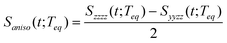 | (5) |
where Szzzz(t;Teq) and Syyzz(t;Teq) are experimentally measured at Teq.
3.2 The solvation axis (T-axis) scan
The T-axis scan in Fig. 5(A) is made with C153 in CH3CN at t = 0 ps with all nonresonant pulses overlapped. In this case, the T-axis scan measures how the electronic polarizability response of the excited solute–solvent system changes as the time-dependent solvent reorganization takes place around the solute. It should be sensitive to the solvent structural relaxation around the solute. Therefore, the T-axis scan gives information on the timescale of the solvent reorganization. In practice, T scan with any fixed t time can also give the same timescale of the solvent reorganization even though the nature of the signals is different. In other words, the T scan at t = 0 ps (T-axis scan) is the relaxation of the electronic response function while the T scan at t > 0 ps (more accurately, t should be greater than the pulse duration) is the relaxation of the nuclear response function. For example, T scan at t = 1.0 ps measures how the nuclear polarizability response at t = 1.0 ps changes as the solvation proceeds. Fig. 5(A) shows the anisotropic PORS signal, S(T,t = 0), as a function of T at t = 0 ps. In Fig. 5(A), the instrumental response function appears at T = 0 ps. Subsequently, a fast rise is followed by the long time decay component. The initial fast rise results from the solvent reorganization and its timescale is the same with that measured from TRFSS while the long time decay components are related to dynamics of C153. From the result of the T-axis scan, the complete solvation time (Teq) can be determined. As shown in Fig. 5(A), the solvent reorganization is very fast in CH3CN and it can be reasonably assumed that solvation is completely finished at T = 4 ps. Fig. 5(B) displays the anisotropic PORS signal from C153 in CH3CN as a function of t at T = Teq = 4 ps.
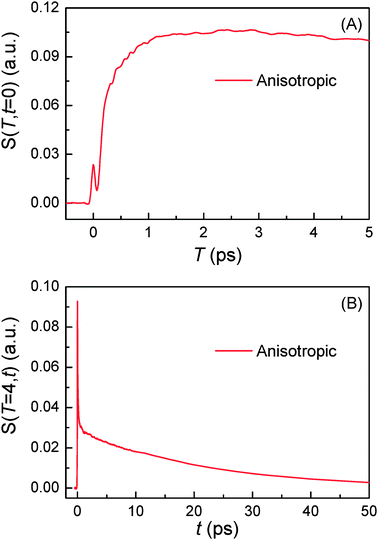 |
| | Fig. 5 Anisotropic PORS signals of C153 in CH3CN. (A) T-axis scan is made at t = 0 ps to determine the complete solvation time (Teq). (B) The anisotropic PORS signals are measured at Teq = 4 ps. | |
3.3 Solvation polarizability responses at Teq
As mentioned earlier, the isotropic and anisotropic PORS signals give information on the isotropic and anisotropic structural relaxation of the solvent molecules around the solute, respectively. Fig. 6 displays the isotropic and anisotropic PORS signals measured with C153 in CH3CN and CHCl3. The isotropic PORS signals have a constant offset at long times while the anisotropic PORS signals decay to zero. The molecular dynamics observed in both PORS signals are separable in time ranging from subpicosecond to nanosecond. The constant offset in the isotropic PORS signal is related to the isotropic change in the solvent local density around C153. On the other hand, the longest time decay component in the anisotropic PORS signal results from the orientational relaxation of the excited state C153. The time constants of the longest time decay components in the anisotropic PORS signals in different solvents are in excellent agreement with the reorientation times of C153 in such solvents obtained previously from time-resolved fluorescence Stokes shift (TRFSS) measurements.48 The constant offset in the isotropic PORS signal and the solute reorientation in the anisotropic PORS signal are associated with the dynamics occurring on much longer timescales than the time-dependent solvent reorganization around C153. Therefore, the solvent reorganization at short times and the dynamics at long times can be temporally separable in both isotropic and anisotropic PORS signals.
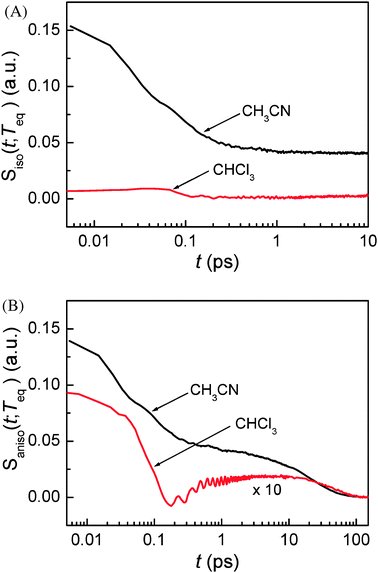 |
| | Fig. 6 (A) Isotropic and (B) anisotropic PORS signals of C153 in CH3CN and CHCl3. Teq = 4 ps is determined for CH3CN and Teq = 25 ps for CHCl3. | |
3.4 Data analysis
The PORS signal at Teq can be written in terms of the convolution of the polarizability response function, Rijkl(t;Teq), and the instrumental response function, G(t),
| Sijkl(t;Teq) = ∫dτG(τ)Rijkl(τ − t;Teq) |
| | | Rijkl(t;Teq) = Relijkl(t;Teq) + Rnucijkl(t;Teq) | (6) |
where Rijkl(t;Teq) can be written as the sum of the electronic response function, Relijkl(t;Teq), and nuclear response function, Rnucijkl(t;Teq), within the Born–Oppenheimer approximation. The nuclear response function, Rnucijkl(t;Teq), includes all nuclear dynamics that are observed in the PORS. The nuclear response function can be further separated into two contributions at a given Teq| | | Rnucijkl(t;Teq) = Rsolventijkl(t;Teq)+Rsoluteijkl(t;Teq) | (7) |
where Rsoluteijkl(t;Teq) represents the long time decay component observed in the PORS signal and Rsolventijkl(t;Teq) describes all nuclear dynamics occurring on shorter timescales than Rsoluteijkl(t;Teq). The long time decay component of the anisotropic PORS signal is well fit with a single exponential function while the long time decay component of the isotropic PORS signal is a constant in our experimental time window as shown in Table 1. They can be removed from the PORS signal,| | 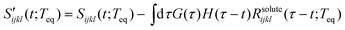 | (8) |
where H(t) is the Heaviside step function. Here, 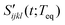 is referred to as the solvation polarizability response. Fig. 7 shows the procedure to remove the long time decay component from the anisotropic PORS signal measured with C153 in acetonitrile. As shown in Table 1, the orientational relaxation time (22 ps) of the excited C153 in CH3CN is larger than the solvent reorganization time (less than 1 ps) of CH3CN. In this analysis, it was assumed that the dynamics at long times would be Markovian and the solvent dynamics at short times would be separated from the long time decay component.22 The RP-PORS signal at early times is attributed to the solvent organization dynamics. As will be mentioned later, the RP-PORS signal at early times is solvent-dependent. Rzzzz(t;Teq) and Ryyzz(t;Teq) are defined in the laboratory frame. Rsolventzzzz(t;Teq) and Rsolventyyzz(t;Teq) are the quantities defined in the molecular frame and denote the polarizability tensor elements that are parallel and perpendicular to the transition dipole of C153, respectively, as will be discussed later.
is referred to as the solvation polarizability response. Fig. 7 shows the procedure to remove the long time decay component from the anisotropic PORS signal measured with C153 in acetonitrile. As shown in Table 1, the orientational relaxation time (22 ps) of the excited C153 in CH3CN is larger than the solvent reorganization time (less than 1 ps) of CH3CN. In this analysis, it was assumed that the dynamics at long times would be Markovian and the solvent dynamics at short times would be separated from the long time decay component.22 The RP-PORS signal at early times is attributed to the solvent organization dynamics. As will be mentioned later, the RP-PORS signal at early times is solvent-dependent. Rzzzz(t;Teq) and Ryyzz(t;Teq) are defined in the laboratory frame. Rsolventzzzz(t;Teq) and Rsolventyyzz(t;Teq) are the quantities defined in the molecular frame and denote the polarizability tensor elements that are parallel and perpendicular to the transition dipole of C153, respectively, as will be discussed later.
Table 1 Single exponential fit to the long time decay components in the isotropic and anisotropic PORS signals
| |
|
A/10−3 |
τ/ps |
|
Reorientational time of C153 in each solvent.
Constant offset in the isotropic PORS signal.
|
|
CH3CN
|
Anisotropic |
42.3 |
22.0a |
| |
Isotropic |
40.8b |
|
|
CHCl3 |
Anisotropic |
2.92 |
33.9a |
| |
Isotropic |
3.42b |
|
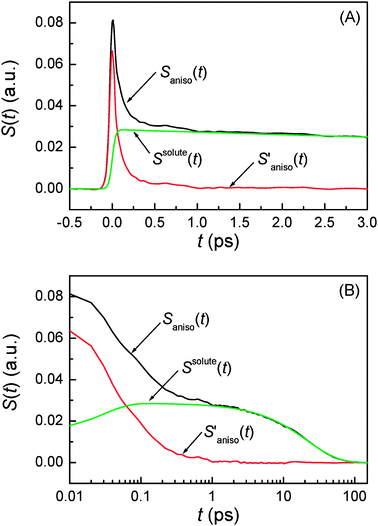 |
| | Fig. 7 Removal of the long time decay component, Ssolute(t), from the anisotropic PORS signal, Saniso(t), of C153 in CH3CN obtained at Teq = 4 ps. (A) A linear scale in the t-axis at short times. (B) A log scale in the t-axis is used to show a long time behavior. | |
Solvation polarizability spectrum at Teq is obtained by Fourier transformation of S′(t;Teq) followed by deconvolution of the pulse spectrum (i.e. Fourier deconvolution method),22,49,50
| | 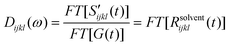 | (9) |
where
FT[⋯] denotes the Fourier transformation and
Dijkl(
ω) = Re[
Dijkl(
ω)] +
iIm[
Dijkl(
ω)].
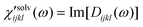
is denoted polarizability
spectrum of solvation and captures all nuclear motions that are present in
Rsolventijkl(
t;
Teq). The isotropic and anisotropic
solvation polarizability
spectra,
χ′
solv(
ω), measured with CH
3CN and CHCl
3 are shown in
Fig. 8.
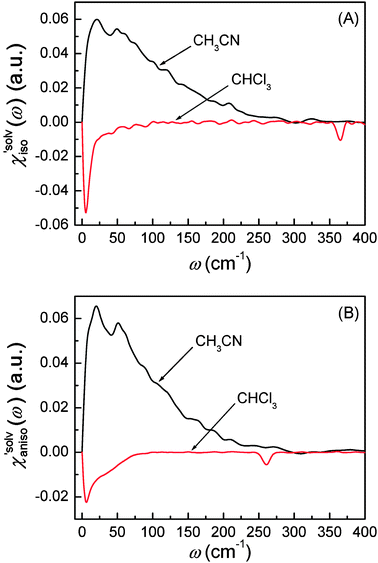 |
| | Fig. 8 (A) Isotropic solvation polarizability spectra and (B) anisotropic polarizability spectra obtained from C153 in CH3CN and CHCl3. | |
4. Discussion
During the solvation, the solute–solvent system relaxes by translational and orientational motions of the solvent molecules. The motions of the solvent intermolecular relaxation can be separated into the isotropic and anisotropic motions based on their symmetry. In liquids composed of the symmetric top molecules, three types of the solvent (collective) intermolecular motions can be involved in solvation; isotropic translational, anisotropic translational, and orientational motions. The isotropic translational motion is observed in the isotropic PORS signal while the anisotropic translational and orientational motions are measured in the anisotropic PORS signal.
4.1 Isotropic solvation response
In RP-PORS, the isotropic solvation PORS signal, 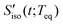 , provides information on the isotropic change in the solvent local density around the solute that is induced by the isotropic solvent translational motions (i.e. isotropic contraction or isotropic expansion of the solvent cage). The isotropic solvation PORS signal is defined with respect to the beam polarization of the resonant pump (ERP) which is parallel to the solute transition dipole,
, provides information on the isotropic change in the solvent local density around the solute that is induced by the isotropic solvent translational motions (i.e. isotropic contraction or isotropic expansion of the solvent cage). The isotropic solvation PORS signal is defined with respect to the beam polarization of the resonant pump (ERP) which is parallel to the solute transition dipole,| | 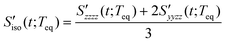 | (10) |
where 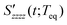 and
and 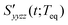 denote the polarizability tensor elements that are parallel and perpendicular to the solute transition dipole, respectively, in the molecular frame. The isotropic solvation polarizability spectra,
denote the polarizability tensor elements that are parallel and perpendicular to the solute transition dipole, respectively, in the molecular frame. The isotropic solvation polarizability spectra, 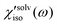 , of CH3CN and CHCl3 are shown in Fig. 8(A). The sign of
, of CH3CN and CHCl3 are shown in Fig. 8(A). The sign of 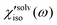 is positive in CH3CN but negative in CHCl3 in the low frequency region. The sign of the isotropic solvation polarizability spectrum,
is positive in CH3CN but negative in CHCl3 in the low frequency region. The sign of the isotropic solvation polarizability spectrum, 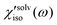 , is directly related to the direction of changes in the solvent local density around C153. In general, when the density of a liquid increases, the index of refraction increases. Upon electronic excitation of C153, C153 has a large increase in its dipole moment (Δμ = 7–8 Debye) and polarizability (Δα = ∼50%). The increase in the polarizability of C153 reflects the increase in its size (volume) leading to pushing the solvent molecules outward. On the other hand, the increase in its dipole moment gives rise to an enhanced intermolecular interaction between C153 and the surrounding solvent molecules. This results in pulling the solvent molecules inward. As a result, these two effects are competing in different solvents upon electronic excitation of C153. In CH3CN (a highly polar solvent), the solvent local density increases (i.e. the solvent cage contracts isotropically) because the increased intermolecular interaction between C153 and CH3CN molecules plays a dominant role while in CHCl3 (a weakly polar solvent) the solvent local density decreases (i.e. the solvent cage expands isotropically) because the increased polarizability of C153 has a larger effect.
, is directly related to the direction of changes in the solvent local density around C153. In general, when the density of a liquid increases, the index of refraction increases. Upon electronic excitation of C153, C153 has a large increase in its dipole moment (Δμ = 7–8 Debye) and polarizability (Δα = ∼50%). The increase in the polarizability of C153 reflects the increase in its size (volume) leading to pushing the solvent molecules outward. On the other hand, the increase in its dipole moment gives rise to an enhanced intermolecular interaction between C153 and the surrounding solvent molecules. This results in pulling the solvent molecules inward. As a result, these two effects are competing in different solvents upon electronic excitation of C153. In CH3CN (a highly polar solvent), the solvent local density increases (i.e. the solvent cage contracts isotropically) because the increased intermolecular interaction between C153 and CH3CN molecules plays a dominant role while in CHCl3 (a weakly polar solvent) the solvent local density decreases (i.e. the solvent cage expands isotropically) because the increased polarizability of C153 has a larger effect.
Before we close this section, it should be mentioned that the molecular properties of CH3CN and CHCl3 are quite different. Interestingly, the permanent dipole moment of CH3CN is parallel to its most polarizable axis while the permanent dipole moment of CHCl3 is orthogonal to its most polarizable axis. Upon the excitation of C153, the dipole–dipole interaction between the excited C153 and solvent molecules was turned on. In CH3CN, librational and translational motions were induced resulting in an increase in the solvent local density without a significant change in relative orientation. However, in CHCl3, the solvent reorganization occurred through the orientational motion of CHCl3 molecules. Therefore, the relative orientations of two solvent molecules are expected to be different around the ground state C153 and excited C153.22
4.2 Anisotropic solvation response
The anisotropic solvation PORS signal, 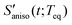 , measures the difference of two polarizability tensor elements that are parallel and perpendicular to the solute transition dipole, respectively. The anisotropic solvation PORS signal is defined with respect to the beam polarization of the resonant pump (ERP) which is parallel to the solute transition dipole,
, measures the difference of two polarizability tensor elements that are parallel and perpendicular to the solute transition dipole, respectively. The anisotropic solvation PORS signal is defined with respect to the beam polarization of the resonant pump (ERP) which is parallel to the solute transition dipole,| | 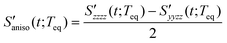 | (11) |
The anisotropic solvation PORS signal contains information on the anisotropic solvent relaxation resulting from the anisotropic (asymmetric) translational motion (i.e. anisotropic contraction and expansion of the solvent cage) and/or the orientational motion of the solvent molecules around the solute. In case that the anisotropic translational relaxation in solvation is less important, the relative orientation of the solvent molecules with respect to the solute transition dipole is not changed for 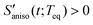 while the relative orientation of the solvent molecules around the solute is significantly changed for
while the relative orientation of the solvent molecules around the solute is significantly changed for 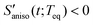 . When the orientational relaxations of the solvent molecules are negligible, the anisotropic contraction of the solvent cage along the solute transition dipole gives
. When the orientational relaxations of the solvent molecules are negligible, the anisotropic contraction of the solvent cage along the solute transition dipole gives 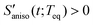 and the anisotropic expansion of the solvent cage along the solute transition dipole gives
and the anisotropic expansion of the solvent cage along the solute transition dipole gives 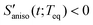 . Anisotropic solvation polarizability spectra,
. Anisotropic solvation polarizability spectra, 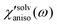 , are shown in Fig. 8(B). The sign of the anisotropic polarizability spectra,
, are shown in Fig. 8(B). The sign of the anisotropic polarizability spectra, 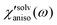 , is positive in CH3CN and is negative in CHCl3. As explained in the previous section, it can be interpreted that the solvent cage contracts anisotropically along the solute transition dipole in CH3CN and the relative orientation of CH3CN is not changed. In CHCl3, the solvent cage expands anisotropically and the solvent molecules are also reoriented with respect to the solute transition dipole.
, is positive in CH3CN and is negative in CHCl3. As explained in the previous section, it can be interpreted that the solvent cage contracts anisotropically along the solute transition dipole in CH3CN and the relative orientation of CH3CN is not changed. In CHCl3, the solvent cage expands anisotropically and the solvent molecules are also reoriented with respect to the solute transition dipole.
4.3 Solvent-dependent PORS signals
In RP-PORS experiments performed with two different solvents in terms of their dipole moments and polarizabilities, the PORS signals are highly solvent-dependent as shown in Fig. 8. The dynamics at short times are separated by removing the longer time decay component. As mentioned above, the dynamics at short times may contain the intramolecular vibrational relaxation (IVR) of C153. If the IVR of C153 were significantly large, the RP-PORS spectra obtained from different solvents shouldn't depend upon the solvent. However, the results shown in Fig. 8 are completely solvent-dependent suggesting that there is no clear indication of contribution of the IVR of C153 to the RP-PORS signal. Therefore, it can be reasonably assumed that the contribution of the IVR of C153 to the RP-PORS signal is negligible in the present experiments. It may suggest that the IVR is much faster than the solvent relaxation around C153 as was previously observed in fluorescence Stokes shift measurements.8 The solvation polarizability spectra are solvent-specific.
The intramolecular vibrational modes of CHCl3 (CCl3 deformation modes; 260 cm−1 and 363 cm−1) are observed in Fig. 8. It indicates that these intramolecular motions are driven in the electronic excitation of C153. This means that they are different around the ground state (S0) and excited state (S1) of C153. The present results show that there is no significant change in their frequencies. The isotropic intramolecular mode (363 cm−1) of CHCl3 oscillates with larger amplitude around the excited state of C153. On the other hand, the anisotropic intramolecular modes of CHCl3 (260 cm−1) oscillate in a different oriented configuration around the excited state of C153.
4.4 Isotropic and anisotropic responses of solvation and neat CH3CN
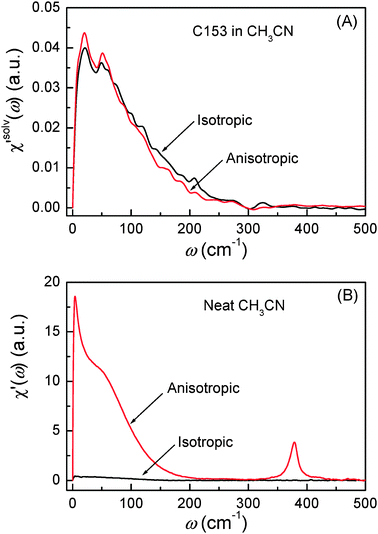
The solvation polarizability spectra (χ′solv(ω)) are shown in Fig. 9(A) representing the difference in the structural fluctuation of CH3CN molecules around C153 in S1 and S0. Fig. 9(B) displays the polarizability spectra (χ′(ω)) of neat CH3CN. χ′solv(ω) represents the solvent intermolecular modes of CH3CN that are driven in solvation while χ′(ω) represents the equilibrium intermolecular modes of CH3CN that are present in neat CH3CN.
 |
| | Fig. 9 (A) Isotropic and anisotropic solvation polarizability spectra (χ′solv(ω)) obtained from C153 in CH3CN. (B) Isotropic and anisotropic polarizability spectra (χ′(ω)) from neat CH3CN. The amplitudes of the spectra in (A) and (B) can be directly compared. | |
In Fig. 9, χ′solv(ω) has a few noticeable features when compared with χ′(ω). First, the isotropic and anisotropic solvation polarizability spectra (χ′solv(ω)) of CH3CN are very similar in amplitude and shape while the anisotropic polarizability spectrum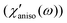 is much larger than the isotropic polarizability spectrum
is much larger than the isotropic polarizability spectrum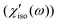 in neat CH3CN. The anisotropic molecular motions are predominant in neat solvent because the orientational and anisotropic translational motions are more likely than isotropic translational motion. However, the isotropic and anisotropic motions of CH3CN are comparably driven in the solvation process of C153 and their frequency distributions are very similar. Second, χ′solv(ω) is broader and contains higher-frequency intermolecular modes that are not present in χ′(ω). It indicates that the higher frequency modes of CH3CN molecules are driven in the solvation process of C153 when compared with the molecular modes in bulk (i.e. neat CH3CN). Third, the low frequency peak near 4 cm−1, which is due to diffusive reorientation of CH3CN, is not observed in χ′solv(ω). It reflects that the solvation responses of CH3CN are inertial and fast. Fourth, the intramolecular vibrational mode (methyl-cyano bending, 380 cm−1) of CH3CN is not observed in χ′solv(ω) suggesting that the methyl-cyano bending mode is not significantly influenced by the electronic excitation of C153 in terms of its amplitude or the relative orientation of CH3CN.
in neat CH3CN. The anisotropic molecular motions are predominant in neat solvent because the orientational and anisotropic translational motions are more likely than isotropic translational motion. However, the isotropic and anisotropic motions of CH3CN are comparably driven in the solvation process of C153 and their frequency distributions are very similar. Second, χ′solv(ω) is broader and contains higher-frequency intermolecular modes that are not present in χ′(ω). It indicates that the higher frequency modes of CH3CN molecules are driven in the solvation process of C153 when compared with the molecular modes in bulk (i.e. neat CH3CN). Third, the low frequency peak near 4 cm−1, which is due to diffusive reorientation of CH3CN, is not observed in χ′solv(ω). It reflects that the solvation responses of CH3CN are inertial and fast. Fourth, the intramolecular vibrational mode (methyl-cyano bending, 380 cm−1) of CH3CN is not observed in χ′solv(ω) suggesting that the methyl-cyano bending mode is not significantly influenced by the electronic excitation of C153 in terms of its amplitude or the relative orientation of CH3CN.
In summary, the solvation polarizability spectra (χ′solv(ω)) of CH3CN are quite different in many aspects and cannot be simply approximated from χ′(ω) which is the polarizability spectrum representing the equilibrium solvent modes of CH3CN molecules in bulk. The features discussed in this section are quite interesting as an example of the solvation response of a small and highly polar molecule like CH3CN. However, some of the features may be generally applicable to and true for other solvents.
5. Concluding remarks
Resonant-pump polarizability response spectroscopy (RP-PORS) was developed and used to measure directly the solvent structural relaxation in solvation. RP-PORS allows direct measurements of isotropic and anisotropic solvation polarizability spectra of CH3CN and CHCl3 in the solvation process of C153. The solvent molecular motions driven in solvation are solvent-specific and are different from the equilibrium solvent modes that are present in neat solvent.
Direct measurements of the solvent relaxation dynamics in solvation are shown to have advantages over the previously performed experiments (TRFSS and PEPS) where the solvation dynamics have been investigated by probing the solute. First, the timescale of the solvation is obtained, which is really the only information extracted from TRFSS and PEPS measurements. Second, polarization-controlled measurements enable us to separate the solvent relaxation around the solute into the isotropic and anisotropic solvent reorganization. The isotropic solvation polarizability spectra give information on the isotropic changes in the solvent local density around the solute arising from the isotropic translational relaxation of the solvent molecules. The anisotropic polarizability spectra allow estimating the solvent structural changes caused by anisotropic translational and orientational motions of the solvent molecules. Third, one can even observe the solvent intramolecular vibrational modes driven in solvation. Both isotropic and anisotropic polarizability spectra allow estimation of the solvent structural changes around the solute. RP-PORS gives molecular level understandings of the solvent relaxation dynamics in solvation.
In RP-PORS, the dispersive and absorptive parts of the third-order signal can be separately measured. The dispersive part is sensitive to molecular dynamics associated with a change in the index of refraction while the absorptive part is sensitive to changes in absorption, which are associated with the solute. Therefore, the dynamics of the excited state solute can also be studied by selectively measuring the absorptive part of the signal. In addition, RP-PORS can be applied to study the non-fluorescent solute–solvent systems where TRFSS cannot be used.
Here, we measured the overall solvation polarizability spectra during the solvation by performing the PORS at Teq after the solvation is complete. However, it should be more interesting to measure the instantaneous solvation polarizability spectra in the solvation process. This can be achieved by measuring the PORS signal as a function of waiting time (T) which will be reported elsewhere in the future.
Acknowledgements
This research is supported by National Science Foundation (CHE0317009). We thank Margaret Hershberger for assistance with the measurements. S. Park thanks Korea University for a new faculty grant.
References
-
C. Reichardt, Solvents and Solvent Effects in Organic Chemistry, VCH, New York, 1990 Search PubMed.
- P. F. Barbara and W. Jarzeba, Adv. Photochem., 1990, 15, 1–68 CAS.
- B. Bagchi, D. W. Oxtoby and G. R. Fleming, Chem. Phys., 1984, 86, 257–267 CrossRef CAS.
- R. M. Stratt and M. Maroncelli, J. Phys. Chem., 1996, 100, 12981–12996 CrossRef CAS.
- G. R. Fleming and M. Cho, Annu. Rev. Phys. Chem., 1996, 47, 109–134 CrossRef.
- B. Bagchi and B. Jana, Chem. Soc. Rev., 2010, 39, 1936–1954 RSC.
- M. A. Kahlow, W. Jarzeba, T. J. Kang and P. F. Barbara, J. Chem. Phys., 1989, 90, 151–158 CrossRef CAS.
- M. L. Horng, J. A. Gardecki and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311–17337 CrossRef CAS.
- L. Reynolds, J. A. Gardecki, S. J. V. Frankland, M. L. Horng and M. Maroncelli, J. Phys. Chem., 1996, 100, 10337–10354 CrossRef CAS.
- T. Joo, Y. Jia, J.-Y. Yu, M. J. Lang and G. R. Fleming, J. Chem. Phys., 1996, 104, 6098–6108.
- W. P. de Boeij, M. S. Pshenichnikov and D. A. Wiersma, Annu. Rev. Phys. Chem., 1998, 49, 99–123 CrossRef CAS.
- C. J. Bardeen, S. J. Rosenthal and C. V. Shank, J. Phys. Chem. A, 1999, 103, 10506–10516 CrossRef CAS.
- D. S. Larsen, K. Ohta and G. R. Fleming, J. Chem. Phys., 1999, 111, 8970–8979 CrossRef CAS.
- E. W. J. Castner and M. Maroncelli, J. Mol. Liq., 1998, 77, 1–36 CrossRef.
- M. Maroncelli, P. V. Kumar and A. Papazyan, J. Phys. Chem., 1993, 97, 13–17 CrossRef CAS.
- V. Tran and B. J. Schwartz, J. Phys. Chem. B, 1999, 103, 5570–5580 CrossRef CAS.
- G. Haran, W.-D. Sun, K. Wynne and R. M. Hochstrasser, Chem. Phys. Lett., 1997, 274, 365–371 CrossRef CAS.
- B. N. Flanders, D. C. Arnett and N. F. Scherer, IEEE J. Sel. Top. Quantum Electron., 1998, 4, 353–359 CrossRef CAS.
- M. C. Beard, G. M. Turner and C. A. Schmuttenmaer, J. Phys. Chem. B, 2002, 106, 7146–7159 CrossRef CAS.
- D. F. Underwood and D. A. Blank, J. Phys. Chem. A, 2003, 107, 956–961 CrossRef CAS.
- D. F. Underwood and D. A. Blank, J. Phys. Chem. A, 2005, 109, 3295–3306 CrossRef CAS.
- S. Park, B. N. Flanders, X. Shang, R. A. Westervelt, J. Kim and N. F. Scherer, J. Chem. Phys., 2003, 118, 3917–3920 CrossRef CAS.
-
S. Park, J. Kim and N. F. Scherer, in Ultrafast Phenomena XIV, ed. T. Kobayashi, T. Okada, T. Kobayashi, K. A. Nelson and S. D. Silvestri, Springer, New York, 2005, pp. 557–559 Search PubMed.
- A. M. Moran, S. Park and N. F. Scherer, Chem. Phys., 2007, 341, 344–356 CrossRef CAS.
- A. M. Moran, R. A. Nome and N. F. Scherer, J. Chem. Phys., 2007, 127, 184505 CrossRef.
- M. Khalil, N. Demirdoven, O. Golonzka, C. J. Fecko and A. Tokmakoff, J. Phys. Chem. A, 2000, 104, 5711–5715 CrossRef CAS.
- Q.-h. Xu, Y.-Z. Ma, I. V. Stiopkin and G. R. Fleming, J. Chem. Phys., 2002, 116, 9333–9340 CrossRef CAS.
- G. D. Goodno and R. J. Dwayne Miller, J. Phys. Chem. A, 1999, 103, 10619–10629 CrossRef CAS.
- I. A. Heisler and S. R. Meech, Science, 2010, 327, 857–860 CrossRef CAS.
- D. W. McCamant, P. Kukura and R. A. Mathies, J. Phys. Chem. A, 2003, 107, 8208 CrossRef CAS.
- P. Kukura, D. W. McCamant and R. A. Mathies, J. Phys. Chem. A, 2004, 108, 5921 CrossRef CAS.
- D. W. McCamant, P. Kukura, S. Yoon and R. A. Mathies, Rev. Sci. Instrum., 2004, 75, 4971 CrossRef CAS.
- P. Kukura, D. W. McCamant, S. Yoon, D. B. Wandschneider and R. A. Mathies, Science, 2005, 310, 1006 CrossRef CAS.
- P. Kukura, D. W. McCamant and R. A. Mathies, Annu. Rev. Phys. Chem., 2007, 58, 461–488 CrossRef CAS.
- Y.-H. Liau, A. N. Unterreiner, D. C. Arnett and N. F. Scherer, Appl. Opt., 1999, 38, 7386–7391 CrossRef CAS.
- A. J. Ruggiero, N. F. Scherer, G. M. Mitchell, G. R. Fleming and J. N. Hogan, J. Opt. Soc. Am. B, 1991, 8, 2061–2067 CAS.
- T. B. Norris, Opt. Lett., 1992, 17, 1009–1011 Search PubMed.
- A. A. Maznev and K. A. Nelson, Opt. Lett., 1998, 23, 1319–1321 Search PubMed.
- G. D. Goodno, V. Astinov and R. J. Dwayne Miller, J. Phys. Chem. B, 1999, 103, 603–607 CrossRef CAS.
- Q.-h. Xu, Y.-Z. Ma and G. R. Fleming, Chem. Phys. Lett., 2001, 338, 254–262 CrossRef CAS.
- K. A. Nelson, R. Casalegno, R. J. Dwayne Miller and M. D. Fayer, J. Chem. Phys., 1982, 77, 1144–1152 CrossRef CAS.
- D. A. Wiersma and K. Duppen, Science, 1987, 237, 1147–1154 CrossRef CAS.
- P. Vohringer and N. F. Scherer, J. Phys. Chem., 1995, 99, 2684–2695 CrossRef CAS.
- T. Tahara and S. Matsuo, Chem. Phys. Lett., 1997, 264, 636–642 CrossRef.
- G. D. Goodno, G. Dadusc and R. J. D. Miller, J. Opt. Soc. Am. B, 1998, 15, 1791–1794 Search PubMed.
- J.-C. Gumy, O. Nicolet and E. Vauthey, J. Phys. Chem. A, 1999, 103, 10737–10743 CrossRef CAS.
- M. Khalil, O. Golonzka, N. Demirdoven, C. J. Fecko and A. Tokmakoff, Chem. Phys. Lett., 2000, 321, 231–237 CrossRef CAS.
- M. L. Horng, J. A. Gardecki and M. Maroncelli, J. Phys. Chem. A, 1997, 101, 1030–1047 CrossRef CAS.
- D. McMorrow and W. T. Lotshaw, J. Phys. Chem., 1991, 95, 10395–10406 CrossRef CAS.
- Y. J. Chang and E. W. J. Castner, J. Phys. Chem., 1996, 100, 3330–3343 CrossRef CAS.
|
| This journal is © the Owner Societies 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 
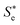 is a nonequilibrium state created by an electronic excitation of the solute.
is a nonequilibrium state created by an electronic excitation of the solute.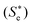 of the C153–solvent system which will relax to a new equilibrium state (Se) as a result of the solvent reorganization around C153. The relaxation of the nonequilibrium C153–solvent system is monitored by selectively measuring the dispersive part (i.e. index of refraction of the system; polarizability response) of the OHD-TG signal which is termed “polarizability response spectroscopy (PORS)”.
of the C153–solvent system which will relax to a new equilibrium state (Se) as a result of the solvent reorganization around C153. The relaxation of the nonequilibrium C153–solvent system is monitored by selectively measuring the dispersive part (i.e. index of refraction of the system; polarizability response) of the OHD-TG signal which is termed “polarizability response spectroscopy (PORS)”.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∶
∶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity ratio. Their relative time delay is controlled before the DOE. The weak beam passes through a variable time delay line while the intense beam has a fixed path. As shown in Fig. 2, two beams, which are vertically-polarized (P1 and P2), are focused onto the DOE with an achromat lens (L1, f.l. = 15 cm). The DOE is specially designed and manufactured such that the total diffraction efficiency for the first-order (±1) beams is more than 80% at 800 nm (HoloEye Photonics AG, Germany). The first-order (±1) diffraction beams, whose angle is 10°, are collimated and focused with parabolic mirrors (CM1, f.l. = 20 cm and CM2, f.l. = 15 cm, respectively) in a box-car geometry and recollimated with an achromat lens (L2, f.l. = 10 cm). A phase-matched beam geometry after the sample is shown in the upper right corner of Fig. 2. A mask (M1) is used to block higher-order diffraction beams from the DOE and another mask (M2) after the sample is used to block all incident beams except the signal and local oscillator.
1 intensity ratio. Their relative time delay is controlled before the DOE. The weak beam passes through a variable time delay line while the intense beam has a fixed path. As shown in Fig. 2, two beams, which are vertically-polarized (P1 and P2), are focused onto the DOE with an achromat lens (L1, f.l. = 15 cm). The DOE is specially designed and manufactured such that the total diffraction efficiency for the first-order (±1) beams is more than 80% at 800 nm (HoloEye Photonics AG, Germany). The first-order (±1) diffraction beams, whose angle is 10°, are collimated and focused with parabolic mirrors (CM1, f.l. = 20 cm and CM2, f.l. = 15 cm, respectively) in a box-car geometry and recollimated with an achromat lens (L2, f.l. = 10 cm). A phase-matched beam geometry after the sample is shown in the upper right corner of Fig. 2. A mask (M1) is used to block higher-order diffraction beams from the DOE and another mask (M2) after the sample is used to block all incident beams except the signal and local oscillator.

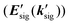 in the same phase-matched direction
in the same phase-matched direction 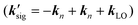 are also measured together with the OHD-TG signal
are also measured together with the OHD-TG signal 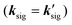 . However, the degenerate pump–probe signals are always in-phase with the LO while the OHD-TG signal is dependent upon the phase of the LO. Therefore, the dispersive and absorptive parts of the OHD-TG signal at a given T can be obtained by a dual phase scan method
. However, the degenerate pump–probe signals are always in-phase with the LO while the OHD-TG signal is dependent upon the phase of the LO. Therefore, the dispersive and absorptive parts of the OHD-TG signal at a given T can be obtained by a dual phase scan method
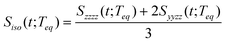
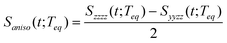


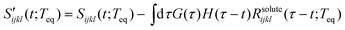
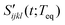 is referred to as the solvation polarizability response. Fig. 7 shows the procedure to remove the long time decay component from the anisotropic PORS signal measured with C153 in acetonitrile. As shown in Table 1, the orientational relaxation time (22 ps) of the excited C153 in CH3CN is larger than the solvent reorganization time (less than 1 ps) of CH3CN. In this analysis, it was assumed that the dynamics at long times would be Markovian and the solvent dynamics at short times would be separated from the long time decay component.22 The RP-PORS signal at early times is attributed to the solvent organization dynamics. As will be mentioned later, the RP-PORS signal at early times is solvent-dependent. Rzzzz(t;Teq) and Ryyzz(t;Teq) are defined in the laboratory frame. Rsolventzzzz(t;Teq) and Rsolventyyzz(t;Teq) are the quantities defined in the molecular frame and denote the polarizability tensor elements that are parallel and perpendicular to the transition dipole of C153, respectively, as will be discussed later.
is referred to as the solvation polarizability response. Fig. 7 shows the procedure to remove the long time decay component from the anisotropic PORS signal measured with C153 in acetonitrile. As shown in Table 1, the orientational relaxation time (22 ps) of the excited C153 in CH3CN is larger than the solvent reorganization time (less than 1 ps) of CH3CN. In this analysis, it was assumed that the dynamics at long times would be Markovian and the solvent dynamics at short times would be separated from the long time decay component.22 The RP-PORS signal at early times is attributed to the solvent organization dynamics. As will be mentioned later, the RP-PORS signal at early times is solvent-dependent. Rzzzz(t;Teq) and Ryyzz(t;Teq) are defined in the laboratory frame. Rsolventzzzz(t;Teq) and Rsolventyyzz(t;Teq) are the quantities defined in the molecular frame and denote the polarizability tensor elements that are parallel and perpendicular to the transition dipole of C153, respectively, as will be discussed later.

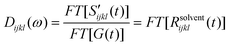
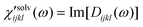 is denoted polarizability spectrum of solvation and captures all nuclear motions that are present in Rsolventijkl(t;Teq). The isotropic and anisotropic solvation polarizability spectra, χ′solv(ω), measured with CH3CN and CHCl3 are shown in Fig. 8.
is denoted polarizability spectrum of solvation and captures all nuclear motions that are present in Rsolventijkl(t;Teq). The isotropic and anisotropic solvation polarizability spectra, χ′solv(ω), measured with CH3CN and CHCl3 are shown in Fig. 8.

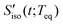 , provides information on the isotropic change in the solvent local density around the solute that is induced by the isotropic solvent translational motions (i.e. isotropic contraction or isotropic expansion of the solvent cage). The isotropic solvation PORS signal is defined with respect to the beam polarization of the resonant pump (ERP) which is parallel to the solute transition dipole,
, provides information on the isotropic change in the solvent local density around the solute that is induced by the isotropic solvent translational motions (i.e. isotropic contraction or isotropic expansion of the solvent cage). The isotropic solvation PORS signal is defined with respect to the beam polarization of the resonant pump (ERP) which is parallel to the solute transition dipole,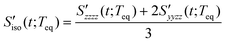
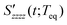 and
and 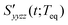 denote the polarizability tensor elements that are parallel and perpendicular to the solute transition dipole, respectively, in the molecular frame. The isotropic solvation polarizability spectra,
denote the polarizability tensor elements that are parallel and perpendicular to the solute transition dipole, respectively, in the molecular frame. The isotropic solvation polarizability spectra, 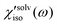 , of CH3CN and CHCl3 are shown in Fig. 8(A). The sign of
, of CH3CN and CHCl3 are shown in Fig. 8(A). The sign of 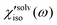 is positive in CH3CN but negative in CHCl3 in the low frequency region. The sign of the isotropic solvation polarizability spectrum,
is positive in CH3CN but negative in CHCl3 in the low frequency region. The sign of the isotropic solvation polarizability spectrum, 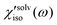 , is directly related to the direction of changes in the solvent local density around C153. In general, when the density of a liquid increases, the index of refraction increases. Upon electronic excitation of C153, C153 has a large increase in its dipole moment (Δμ = 7–8 Debye) and polarizability (Δα = ∼50%). The increase in the polarizability of C153 reflects the increase in its size (volume) leading to pushing the solvent molecules outward. On the other hand, the increase in its dipole moment gives rise to an enhanced intermolecular interaction between C153 and the surrounding solvent molecules. This results in pulling the solvent molecules inward. As a result, these two effects are competing in different solvents upon electronic excitation of C153. In CH3CN (a highly polar solvent), the solvent local density increases (i.e. the solvent cage contracts isotropically) because the increased intermolecular interaction between C153 and CH3CN molecules plays a dominant role while in CHCl3 (a weakly polar solvent) the solvent local density decreases (i.e. the solvent cage expands isotropically) because the increased polarizability of C153 has a larger effect.
, is directly related to the direction of changes in the solvent local density around C153. In general, when the density of a liquid increases, the index of refraction increases. Upon electronic excitation of C153, C153 has a large increase in its dipole moment (Δμ = 7–8 Debye) and polarizability (Δα = ∼50%). The increase in the polarizability of C153 reflects the increase in its size (volume) leading to pushing the solvent molecules outward. On the other hand, the increase in its dipole moment gives rise to an enhanced intermolecular interaction between C153 and the surrounding solvent molecules. This results in pulling the solvent molecules inward. As a result, these two effects are competing in different solvents upon electronic excitation of C153. In CH3CN (a highly polar solvent), the solvent local density increases (i.e. the solvent cage contracts isotropically) because the increased intermolecular interaction between C153 and CH3CN molecules plays a dominant role while in CHCl3 (a weakly polar solvent) the solvent local density decreases (i.e. the solvent cage expands isotropically) because the increased polarizability of C153 has a larger effect.
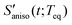 , measures the difference of two polarizability tensor elements that are parallel and perpendicular to the solute transition dipole, respectively. The anisotropic solvation PORS signal is defined with respect to the beam polarization of the resonant pump (ERP) which is parallel to the solute transition dipole,
, measures the difference of two polarizability tensor elements that are parallel and perpendicular to the solute transition dipole, respectively. The anisotropic solvation PORS signal is defined with respect to the beam polarization of the resonant pump (ERP) which is parallel to the solute transition dipole,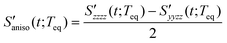
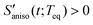 while the relative orientation of the solvent molecules around the solute is significantly changed for
while the relative orientation of the solvent molecules around the solute is significantly changed for 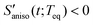 . When the orientational relaxations of the solvent molecules are negligible, the anisotropic contraction of the solvent cage along the solute transition dipole gives
. When the orientational relaxations of the solvent molecules are negligible, the anisotropic contraction of the solvent cage along the solute transition dipole gives 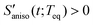 and the anisotropic expansion of the solvent cage along the solute transition dipole gives
and the anisotropic expansion of the solvent cage along the solute transition dipole gives 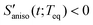 . Anisotropic solvation polarizability spectra,
. Anisotropic solvation polarizability spectra, 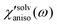 , are shown in Fig. 8(B). The sign of the anisotropic polarizability spectra,
, are shown in Fig. 8(B). The sign of the anisotropic polarizability spectra, 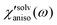 , is positive in CH3CN and is negative in CHCl3. As explained in the previous section, it can be interpreted that the solvent cage contracts anisotropically along the solute transition dipole in CH3CN and the relative orientation of CH3CN is not changed. In CHCl3, the solvent cage expands anisotropically and the solvent molecules are also reoriented with respect to the solute transition dipole.
, is positive in CH3CN and is negative in CHCl3. As explained in the previous section, it can be interpreted that the solvent cage contracts anisotropically along the solute transition dipole in CH3CN and the relative orientation of CH3CN is not changed. In CHCl3, the solvent cage expands anisotropically and the solvent molecules are also reoriented with respect to the solute transition dipole.

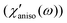 is much larger than the isotropic polarizability spectrum
is much larger than the isotropic polarizability spectrum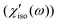 in neat CH3CN. The anisotropic molecular motions are predominant in neat solvent because the orientational and anisotropic translational motions are more likely than isotropic translational motion. However, the isotropic and anisotropic motions of CH3CN are comparably driven in the solvation process of C153 and their frequency distributions are very similar. Second, χ′solv(ω) is broader and contains higher-frequency intermolecular modes that are not present in χ′(ω). It indicates that the higher frequency modes of CH3CN molecules are driven in the solvation process of C153 when compared with the molecular modes in bulk (i.e. neat CH3CN). Third, the low frequency peak near 4 cm−1, which is due to diffusive reorientation of CH3CN, is not observed in χ′solv(ω). It reflects that the solvation responses of CH3CN are inertial and fast. Fourth, the intramolecular vibrational mode (methyl-cyano bending, 380 cm−1) of CH3CN is not observed in χ′solv(ω) suggesting that the methyl-cyano bending mode is not significantly influenced by the electronic excitation of C153 in terms of its amplitude or the relative orientation of CH3CN.
in neat CH3CN. The anisotropic molecular motions are predominant in neat solvent because the orientational and anisotropic translational motions are more likely than isotropic translational motion. However, the isotropic and anisotropic motions of CH3CN are comparably driven in the solvation process of C153 and their frequency distributions are very similar. Second, χ′solv(ω) is broader and contains higher-frequency intermolecular modes that are not present in χ′(ω). It indicates that the higher frequency modes of CH3CN molecules are driven in the solvation process of C153 when compared with the molecular modes in bulk (i.e. neat CH3CN). Third, the low frequency peak near 4 cm−1, which is due to diffusive reorientation of CH3CN, is not observed in χ′solv(ω). It reflects that the solvation responses of CH3CN are inertial and fast. Fourth, the intramolecular vibrational mode (methyl-cyano bending, 380 cm−1) of CH3CN is not observed in χ′solv(ω) suggesting that the methyl-cyano bending mode is not significantly influenced by the electronic excitation of C153 in terms of its amplitude or the relative orientation of CH3CN.