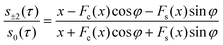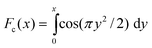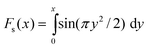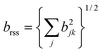Selective internuclear coupling estimation in the solid-state NMR of multiple-spin systems

Abstract

A new solid-state NMR method is presented for estimating homonuclear dipole–dipole couplings for selected groups of nuclear spins in a multiple-spin coupled network. The methodology combines off-magic-angle spinning, frequency selective spin echoes, and multiple quantum filtering. The new method is insensitive to incoherent relaxation effects and may be used to estimate weak couplings. Internuclear ¹³C–¹³C couplings are estimated in uniformly ¹³C-labelled L-Histidine·HCl·H₂O. Weak intermolecular couplings between ¹³C nuclei separated by distances exceeding 6 Å are estimated.

---

Solid-state nuclear magnetic resonance (NMR) provides important molecular structural information on samples that are unsuitable for X-ray crystallography. The measurement of internuclear dipole–dipole (DD) couplings allows the estimation of internuclear distances.^1–7 However, the measurement of individual couplings is difficult if the sample contains clusters of many magnetic nuclei, for example ¹³C nuclei in organic solids with a high density of ¹³C labeling, or proton nuclei in almost any organic material. The difficulty of obtaining quantitative structural data from multiply-labelled samples is a major drawback, especially in biomolecular solid-state NMR. In this communication we demonstrate significant progress towards a general solution of this problem.

Sample rotation about an axis at the angle arctan √2 ≅ 54.74° with respect to the magnetic field (magic-angle spinning, MAS) is essential for obtaining chemical shift resolution in solids, but strongly attenuates the effect of the DD couplings. Rotor-synchronized “recoupling” pulse sequences restore the DD coupling effects, but usually generate strongly-coupled spin Hamiltonians, for which the effect of individual spin–spin couplings cannot be disentangled. An exception is found in heteronuclear systems, where frequency-selective pulses may be used to pick out individual spin–spin couplings.¹

In the homonuclear case, several techniques have been proposed for selecting individual couplings in multiple-spin clusters, but except for short-distance couplings they rarely provide quantitative agreement between theory and experiment.^2–8

A relatively simple method for introducing DD couplings is to offset the angle between the spinning axis and the magnetic field slightly away from the magic angle. The residual dipolar couplings (RDCs) may be estimated by a spin echo procedure, and analyzed to obtain internuclear distance information.⁹ Frequency selective pulses may be used to pick out individual couplings from clusters of closely-spaced spins.¹⁰ This works because off-magic-angle spinning (offMAS) is a mild technique that, in most cases, preserves the weakly-coupled nature of the spin system.

However, frequency-selective offMAS is not capable, by itself, of estimating weak internuclear couplings. Long-range RDCs induce a monotonic decay of nuclear magnetization that resembles the incoherent decay caused by fluctuating magnetic fields.¹⁰ We now show that a multiple-quantum filtering scheme may be used to distinguish the effects of small RDCs from incoherent decay. The pulse sequence may either be implemented at a fixed rotation angle or in conjunction with mechanical switching of the spinning angle¹¹ in order to restore full spectral resolution during signal detection.¹²

The pulse sequence for the fixed-angle version of the experiment is shown in Fig. 1. Standard cross-polarization of ¹³C transverse magnetization is followed by two spin echo sequences conducted in the presence of a proton decoupling field and bracketing two strong 90° pulses. Each spin-echo block has a duration τ/2 and consists of a shaped 180° pulse and two variable evolution intervals. In the experiments discussed here, the rf field amplitude profile during the 180° pulses is either a Gaussian function of time (for single-band selection) or a Gaussian function of time multiplied by a cosine wave (for dual-band selection). In the latter case, the modulation parameters are chosen to rotate the quantum states of nuclei precessing within two sharply-defined ranges of Larmor frequencies.^10,13

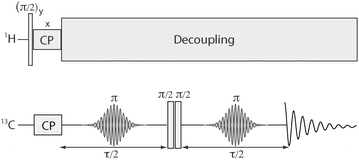Fig. 1 Pulse sequence for measuring selected internuclear ¹³C–¹³C dipolar couplings in ¹³C-labelled organic solids. The sample is rotated around an axis which has a known constant deviation from the magic angle with respect to the magnetic field. The shaped π pulses are tuned to invert the magnetizations of nuclei resonating within 1 or 2 narrow frequency regions. In practice, these selective pulses have a very small amplitude. The phases of the adjacent π/2 pulses are cycled to filter out signals that pass through either zero-quantum coherence (ZQC) or double-quantum coherence (DQC) at the junction of the pulses. Comparison of the ZQ and DQ-filtered signal amplitudes as a function of τ permits estimation of the internuclear couplings.

The effects of the selective pulses and the spinning angle offset are shown in Fig. 2 for the case of [U-¹³C,¹⁵N]-L-His·HCl·H₂O powder. Fig. 2(b) shows the magic-angle-spinning¹³C spectrum, while in (c) and (d) the sample was rotated at an angle of 53.94° ± 0.05° with respect to the magnetic field, as determined by a Hall effect angle sensor.¹⁴ The −0.8° spinning axis deviation from the magic angle causes tolerable line broadening. To obtain Fig. 2(d), a cosine-modulated Gaussian pulse was used to invert the z-magnetizations of two selected ¹³C peaks, before exciting transverse magnetization with a 90° pulse. This spectrum shows a clean magnetization inversion of the two selected chemical sites. The coupling between the members of the selected spin pair is estimated by repeating the pulse sequence in Fig. 1 for several values of the total interval τ. Phase cycling¹⁵ is used to filter the experimental NMR signals through either zero-quantum coherences (ZQC) or double-quantum coherences (DQC) at the junction of the two π/2 pulses. The amplitudes of the zero-quantum-filtered signals s₀(τ) and double-quantum-filtered signals s_±2(τ) are obtained for several values of total duration τ. The ratio s_±2(τ)/s₀(τ) is compared with theoretical results to obtain an estimate of the internuclear coupling strength. This estimate is highly insensitive to incoherent effects causing signal decay during the evolution interval.

Fig. 2 (a) Molecular structure and labelling scheme of the L-histidinium ion. (b) Cross-Polarization (CP) magic-angle spinning¹³C spectrum of [U-¹³C,¹⁵N]-L-His·HCl·H₂O. (c) CP ¹³C spectrum obtained while spinning around an axis with an offset of −0.8° from the magic angle. (d) as in (c) but using a cosine-modulated Gaussian 180° pulse to invert the ¹³C magnetizations of sites C2 and C5. All spectra were obtained at 9.4 T and a spinning frequency of 14.00 kHz.

In favourable cases, the set of coupled spins selected by the 180° pulses contain a single dominant internuclear coupling. In this case, the system may be approximated as an ensemble of isolated spin-1/2 pairs. The following analytical formula for the ratio s_±2(τ)/s₀(τ) is derived in the ESI†:

where:

φ = ½(b_RDC − 2πJ)τ_eff

x = (3b_RDCτ_eff/π)^½

b_RDC = b½(3cos²β − 1)

τ_eff = τ − 2τ_sh

and the Fresnel integrals are defined as follows:

The dipole–dipole coupling strength for the selected spin pair is given, in the case of static molecular geometry, by b = −(μ₀/4π)γ²ℏr⁻³ where r is the internuclear distance between the coupled spins. The residual dipolar coupling in the presence of off-magic-angle spinning is denoted b_RDC. The angle subtended by the spinning axis and the static magnetic field is denoted β. The symbol τ_sh indicates the time shift associated with the finite duration of a frequency-selective pulse, which may be estimated from the pulse shape.¹⁰

Fig. 3(a) shows the experimental ratios of the DQF and ZQF signal amplitudes for [U-¹³C,¹⁵N]-L-Histidine·HCl·H₂O, selecting ¹³C nuclei in sites C2 and C5 by cosine-modulated Gaussian pulses, as shown in Fig. 2. Fitting the experimental amplitude ratio s_±2(τ)/s₀(τ) to the theoretical expression (assuming a zero value for the J-coupling, but taking into account the confidence limits in the spinning angle) provides an internuclear coupling estimate of −744 Hz ± 29 Hz. This corresponds to an internuclear distance estimate of 217 ± 3 pm, which agrees with the intramolecular C2–C5 distance of 220 pm from X-ray crystallography.¹⁶

Fig. 3 Experimental ratios of the DQ and ZQ-filtered ¹³C NMR signal amplitudes in [U-¹³C, ¹⁵N]-L-Histidine·HCl·H₂O powder, plotted against the pulse-sequence duration τ. (a) Selection of ¹³C nuclei in the C2 and C5 sites, using a spinning-angle offset of −0.8° from the magic angle. The data were obtained from the amplitude of the C2 peak (open symbols) and the C5 peak (black symbols). The error bars derive from an analysis of the noise in the individual multiple-quantum-filtered spectra. (b) Selection of ¹³C in CO sites, using a spinning-angle offset of −3.0° from the magic angle (filled circles). The solid curves are the theoretical DQ/ZQ ratio functions for dipolar coupling strengths of (a) −744 Hz and (b) −82 Hz.

In general, the group of spins which resonate within the bandwidth(s) of the frequency-selective pulses are connected by many internuclear couplings of different magnitudes. This case may be treated approximately by replacing the single dominant coupling by the root-sum-square coupling¹⁷ for the selected spins, defined as follows:

where the sum is taken over all nuclei resonating within the inversion bandwidth (or bandwidths) of the selective 180° pulses.

Fig. 3(b) shows an experimental example. In this case, the magic-angle offset was set to −3.00° ± 0.05°, and single-bandwidth Gaussian pulses were used to invert the quantum states of ¹³C nuclei in CO sites (left-hand peak in Fig. 2). The experimental signal ratio s_±2(τ)/s₀(τ) is consistent with a root-sum-square coupling with a magnitude of 82 ± 4 Hz.

The crystal structure of L-Histidine·HCl·H₂O shows that each CO site has two nearest CO neighbours, each at a distance of 601 pm, and two more distant neighbours, each at a distance of 688 pm. The root-sum-square coupling corresponding to the 4 nearest CO neighbours of a given CO site is 60 Hz. If 10 nearest CO neighbours are taken into account, the estimated root-sum-square coupling is equal to 80 Hz, while if more than 100 nearest CO neighbours are taken into account, the root-sum-square coupling converges to a value of 89 Hz. The experimental signal ratio s_±2(τ)/s₀(τ) for ¹³C in CO sites is therefore reasonably consistent with the known crystal structure of L-Histidine·HCl·H₂O, providing that at least 10 nearest-neighbour contacts are taken into account. Each of these interactions is at a distance exceeding 600 pm.

These results show that the method is capable of quantifying interactions between relatively remote ¹³C nuclei. An internuclear coupling of −82 Hz corresponds to a single ¹³C–¹³C distance of 453 pm. Distances of this order are of great interest in the field of biomolecular structure determination.

In its current form, the method has the disadvantage of degraded spectral resolution during the detection interval, due to the participation of chemical shift anisotropy when the spinning axis is offset from the magic angle. This disadvantage may be avoided by storing the magnetization along the static field and switching the spinning angle to the magic angle before signal detection.¹² Experiments of this type will be reported elsewhere.

We have also implemented a variant of the method which uses spherical tensor analysis of the NMR signals,¹⁸ instead of multiple-quantum filtration. In principle this procedure can lead to increased signal strength.

The method works well when the monitored peak belongs to a site that has no coupling partners that are close in both space and in resonance frequency, but may give unreliable results when this condition is not fulfilled. We anticipate that refinement of the selective pulse shapes will reduce these interference effects.

Conclusions

In summary, the combination of a small spinning angle offset, frequency-selective spin echoes and multiple-quantum filtration provides quantitative long-range homonuclear coupling estimations in samples containing a high density of magnetic nuclei. This is of great potential interest for the estimation of molecular structures and supramolecular organization in biomolecules, organic solids and inorganic materials. Extensions to multiple dimensions, and to other coupled nuclei, including protons in some cases, should be feasible.

Acknowledgements

This research was funded by EPSRC (UK). We thank O. G. Johannessen, G. Pileio, S. Mamone, M. C. D. Tayler, P. K. Madhu, S. P. Brown and M. Carravetta for help and discussions.

Notes and references

1. C. P. Jaroniec, B. A. Tounge, J. Herzfeld and R. G. Griffin, J. Am. Chem. Soc., 2001, 123, 3507.
2. R. Ramachandran, V. Ladizhansky, V. S. Bajaj and R. G. Griffin, J. Am. Chem. Soc., 2003, 125, 15623.
3. V. Ladizhansky and R. G. Griffin, J. Am. Chem. Soc., 2004, 126, 948.
4. A. K. Paravastu and R. Tycko, J. Chem. Phys., 2006, 124, 194303.
5. R. Tycko, Phys. Rev. Lett., 2007, 99, 187601.
6. I. Marín Montesinos, G. Mollica, M. Carravetta, A. Gansmüller, G. Pileio, M. Bechmann, A. Sebald and M. H. Levitt, Chem. Phys. Lett., 2006, 432, 572.
7. L. A Straasø, M. Bjerring, N. Khaneja and N. C. Nielsen, J. Chem. Phys., 2009, 130, 225103.
8. V. Ladizhansky, Solid State Nucl. Magn. Reson., 2009, 36, 119.
9. G. Pileio, Y. Guo, T. N. Pham, J. M. Griffin, M. H. Levitt and S. P. Brown, J. Am. Chem. Soc., 2007, 129, 10972.
10. G. Pileio, S. Mamone, G. Mollica, I. Marín Montesinos, A. Gansmüller, M. Carravetta, S. P. Brown and M. H. Levitt, Chem. Phys. Lett., 2008, 456, 116.
11. T. Terao, T. Fujii, T. Onodera and A. Saika, Chem. Phys. Lett., 1984, 107, 145–148.
12. R. Tycko, J. Am. Chem. Soc., 1994, 116, 2217.
13. L. Emsley, I. Burghardt and G. Bodenhausen, J. Magn. Reson., 1990, 90, 214.
14. S. Mamone, A. Dorsch, O. G. Johannessen, M. V. Naik, P. K. Madhu and M. H. Levitt, J. Magn. Reson., 2008, 190, 135.
15. G. Bodenhausen, H. Kogler and R. R. Ernst, J. Magn. Reson., 1984, 58, 370–388.
16. H. Fuess, D. Hohlwein and S. A. Mason, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 654.
17. V. E. Zorin, S. P. Brown and P. Hodgkinson, Mol. Phys., 2006, 104, 293.
18. J. D. van Beek, M. Carravetta, G. C. Antonioli and M. H. Levitt, J. Chem. Phys., 2005, 122, 244510.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental parameters, details of the phase cycling, error analysis and derivation of analytical formulae. See DOI: 10.1039/c0cp01262a

---