Vibrationally promoted electron emission at a metal surface: electron kinetic energy distributions

Abstract

We report the first direct measurement of the kinetic energy of exoelectrons produced by collisions of vibrationally excited molecules with a low work function metal surface exhibiting electron excitations of 64% (most probable) and 95% (maximum) of the initial vibrational energy. This remarkable efficiency for vibrational-to-electronic energy transfer is in good agreement with previous results suggesting the coupling of multiple vibrational quanta to a single electron.

---

Understanding the interactions of molecules with solid surfaces is important to the development of predictive theories of surface chemistry,^1,2 which up to now routinely assume electronic adiabaticity. According to this assumption, one may calculate an effective potential energy surface upon which the atoms move based on the Born–Oppenheimer approximation, where the system remains in its electronic ground state. While this approach enables highly detailed calculations to be carried out, it neglects possible energy transfer channels between nuclear motion and electronic degrees of freedom in the metal.

Reports of laboratory observations of electronically nonadiabatic influences on molecule–surface interactions are now becoming increasingly available,^3–5 yet it remains an open question whether such effects are important enough to require major adjustments to the electronically adiabatic picture.⁶ For example, including nonadiabatic influences such as electronic friction, employing a weak coupling approximation, has been remarkably successful in addressing the inadequacies of the adiabatic assumption in describing vibrational lifetimes of small molecules on metal surfaces.⁷ Specifically, adiabatic theories predict millisecond lifetimes whereas electronic friction calculations result in picosecond lifetimes, in good agreement with experiment.⁸ The successes of friction theory suggest that major adjustments to the adiabatic picture might not be necessary.

Recently, multi-quantum vibrational relaxation,⁹ vibrationally promoted electron emission^10,11 and electron mediated vibrational overtone excitation¹² in molecule–surface scattering have been reported by our group. It is unclear if these phenomena can be described by electronic friction theories. For example, multi-quantum vibrational relaxation of NO(v = 14,15) on Au(111) is at least semi-quantitatively reproduced by friction-like theories.¹³ However, good agreement with experiment is also found using a multi-state (independent electron surface hopping) model,^14–16 where a single electron transfer mechanism is operative.

Putting it another way, a fundamental unknown is the fraction of molecular vibration that can be converted to single electron excitation and vice versa. For example, one might envision that a single highly excited electron in a solid could transfer nearly all of its excitation energy to a molecule at the surface. If that were possible, time reversal suggests that a highly excited molecule would be able to transfer all (or nearly all) of its excitation energy to a single electron in the surface.

In this work, we report the first direct measurements of electron kinetic energy distributions produced by vibrationally promoted electron emission at a metal surface. Here, the available vibrational energy of the molecule (E_vib = 3.3 eV) exceeds the work function of the surface (Φ = 1.6 eV ± 0.1 eV)¹⁷ and therefore a vibrational relaxation event results in electron ejection.^10,11 The derived electron translational energy distribution peaks at 0.5 eV with respect to the vacuum level, that is, the most probable electron excitation energy is 2.1 eV with respect to the Fermi level. Furthermore, the electron energy distribution extends nearly to the energetic limit imposed by the initial vibrational energy, assuming the latter is the only source of electronic excitation.

These observations demonstrate the efficiency with which molecular vibration may be converted to single electron excitation in molecule surface collisions and suggest that conditions might be found where electronic excitation in solids can be efficiently converted to molecular vibration.

These experiments were carried out in a molecule–surface scattering apparatus that will be described in detail in another publication.¹⁸ Briefly, a supersonic pulsed molecular beam with ∼430 m s⁻¹ RMS velocity was formed by expanding 1% NO seeded in Kr through a 10 Hz repetition rate piezo-electrically actuated nozzle at 23 psi stagnation pressure.

After passing through a 2 mm electroformed skimmer (Ni Model 2, Beam Dynamics, Inc.), NO molecules were optically excited to v = 16 by stimulated emission pumping (SEP).¹⁹ Excitation of ground state NO molecules to the intermediate A²Σ⁺ (v = 2) state was achieved using 204.6 nm (1 mJ per pulse) light produced by a home-built OPO-SFG light source²⁰via the R₁₁(0.5)/Q₂₁(0.5) line. Stimulated emission down to X²Π_1/2 (v = 16) was accomplished by 450.4 nm (10 mJ per pulse) fundamental of a Nd:YAG (LabPRO-200, Spectra-Physics) pumped dye laser (PRSC-DA-24, Sirah) via the same rotational line with an efficiency of ∼20% monitored by fluorescence depletion using a photo-multiplier tube (R7154, Hamamatsu).

The prepared NO(v = 16) molecules were then scattered from a low work function Cs/Au(111) surface^10,11,17 in a UHV chamber (base pressure 1 × 10⁻¹⁰ Torr) outfitted with a home-built retarding field hemispherical electron energy analyzer (EEA), which will be described in detail in another publication.¹⁸ Exoelectrons were collected over a solid angle of Ω = 1.2π sr and focused onto a micro-channel plate (30392, Burle) detector connected to an oscilloscope (LT344, LeCroy) for data acquisition.

Fig. 1 shows typical EEA transmission curves recorded by raising the retarding potential and thus gradually rejecting exoelectrons with ever-increasing energies until the signal disappears completely. Although most of the exoelectron signal (open squares, Fig. 1) is caused by SEP-prepared NO(v = 16) molecules, it always contains a portion originating from the vibrationally excited molecules produced by spontaneous emission (Franck–Condon pumping, FCP) from the intermediate A²Σ⁺ (v = 2) state. In order to derive the electron signal coming from NO(v = 16) (open circles, Fig. 1), transmission curves of one-laser (FCP induced electron signal) were recorded (open triangles, Fig. 1) and used to correct the two-laser signal using a procedure described in ref. 21. The intensities of all curves in Fig. 1 are adjusted accordingly, normalizing NO(v = 16) contribution to unity, which is then fitted with a sum of two error functions shown as a solid line in Fig. 1.

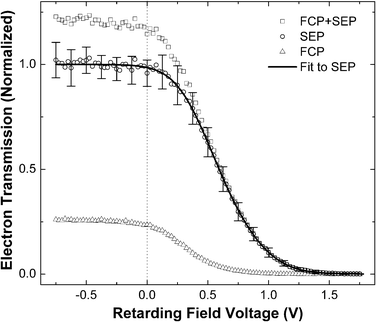Fig. 1 Transmission of vibrationally promoted exoelectrons as a function of retarding potential. See text.

The desired exoelectron kinetic energy distributions can be obtained by differentiation of the experimentally measured transmission curves. In Fig. 2, the direct numerical derivative of the experimental data (scattered symbols) is shown together with the derivative of the fit (dashed line).

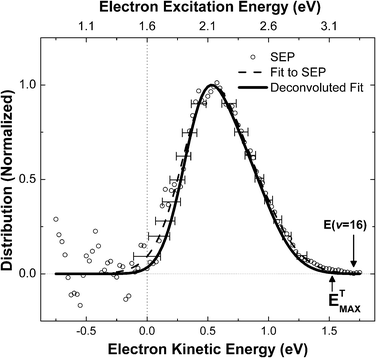Fig. 2 Kinetic energy distribution of vibrationally promoted exoelectrons derived from the data in Fig. 1. See text.

It should be noted that the energy axes on both figures were adjusted to account for the contact potential difference between the low work function Cs/Au(111) surface and the instrument by using measured kinetic energy distributions of photoelectrons produced by a HeNe laser (hν = 1.96 eV) as calibration. This procedure allows us to define the zero of the kinetic energy with respect to the vacuum level, and to subsequently derive electronic excitation energy as the sum of electron kinetic energy and the work function of the surface, assuming that the electrons originate from the Fermi level. See upper axis in Fig. 2.

We derived the instrument broadening function of the EEA by comparing electron energy distributions produced by HeNe laser induced photoemission to those reported in ref. 17, where a high resolution electron energy analyzer was used. The broadening function was used to deconvolute the apparent energy distribution (dashed line Fig. 2) to obtain the solid line of Fig. 2.²²

Inspection of Fig. 2 reveals that the most probable exoelectron kinetic energy is 0.5 eV (2.1 eV excitation energy). The available vibrational energy of NO(v = 16) is 3.3 eV. Thus the most probable fraction of vibrational energy converted to electronic excitation is 0.64. This value could be higher if the excited electrons originate below the Fermi level. A 2.1 eV electronic excitation implies a vibrational transition from NO(v = 16) to at least as low as NO(v = 5), i.e. Δv = 11. This is qualitatively similar to previous state-to-state survival probabilities measurements of NO(v = 15) on Au(111), where Δv = 7,8 transitions were found to be the most probable.⁹

The maximum observed electron kinetic energy E^T_MAX can be read from Fig. 2 as 1.52 ± 0.05 eV. This corresponds to an electronic excitation energy of 3.12 ± 0.09 eV, again assuming the electrons originate from the Fermi level. This leads to a value of 0.95 ± 0.03 for the maximum fraction of vibrational energy appearing as electronic excitation. This is qualitatively in agreement with the reported threshold for vibrationally promoted electron emission since the vibrational threshold (v = 8) is nearly isoenergetic with the surface work function.¹⁰

In a previous work, we outlined a possible mechanism for the energy transfer, which we referred to as vibrationally promoted autodetachment.¹¹ In this picture, as the vibrationally excited NO approaches the surface, an electron hops from the surface to the NO, forming a transient NO⁻ anion stabilized mostly by its image charge. The NO⁻ subsequently ejects an electron reforming NO. It is thought that in the course of the electron hopping process, the molecule can relax to a lower vibrational state, transferring the excess energy to the electron. The electron energy distribution reported here is consistent with this mechanism, showing in particular that: (1) a large fraction of the vibrational energy can be transferred to a single electron and (2) the limit for the exoelectron kinetic energy is given by the available vibrational energy.

It is interesting to note that the electron energy distribution is not monotonically decreasing with increasing energy, as might be expected based on recent theoretical work, albeit describing somewhat different systems.^23,24 As these new theories do not attempt to characterize the electron escape dynamics, this discrepancy may relate to the energy dependence of the electron escape probability. If low energy electrons are more easily recaptured by the surface after excitation than high energy electrons, one might hope to reconcile the experiments to the theories of Mizielinski et al.^23,24

Finally, we comment that the exoelectron kinetic energy distribution is broad with no apparent substructure, despite the fact that the NO vibrational spacing is about 0.2 eV. Of course, this may reflect the nature of the vibrational autodetachment mechanism. Broadening of the electron energy distribution could result from excitation of NO rotation, surface phonons or from electrons originating below the Fermi level. Nevertheless, it is important to note that the energy resolution and the signal to noise of the present experiment can be improved. For instance, the energy convolution function of the retarding field analyzer obtained in this work has a width of ∼0.15 eV and the need to take the derivative of the transmission curve to obtain the energy distribution introduces a great deal of noise. Moreover, significant experimental improvements can be made, such as increasing the energy resolution to better than 0.005 eV by using a high resolution hemispherical energy analyzer. In addition to studies of this sort, we plan to carry out additional measurements, such as the dependence on collision energy and vibrational quantum number.

Summary

We have observed direct quantitative conversion of vibrational energy to electronic excitation in collisions of NO(v = 16) with a low work function Cs/Au(111) surface. These results clearly cannot be described within the adiabatic picture even when weak coupling corrections like electronic friction are employed. Additional developments of nonadiabatic theories will be needed to correctly account for these observations. We hope that the results presented here will provide a good benchmark against which future developments might be evaluated.

References

1. N. H. Nahler and A. M. Wodtke, Mol. Phys., 2008, 106, 2227.
2. A. M. Wodtke, D. Matsiev and D. J. Auerbach, Prog. Surf. Sci., 2008, 83, 167.
3. B. Gergen, H. Nienhaus, W. H. Weinberg and E. W. McFarland, Science, 2001, 294, 2521.
4. R. Grobecker, H. Shi, H. Bludau, T. Hertel, T. Greber, A. Böttcher, K. Jacobi and G. Ertl, Phys. Rev. Lett., 1994, 72, 578.
5. C. T. Rettner, F. Fabre, J. Kimman and D. J. Auerbach, Phys. Rev. Lett., 1985, 55, 1904.
6. P. Nieto, E. Pijper, D. Barredo, G. Laurent, R. A. Olsen, E. J. Baerends, G. J. Kroes and D. Farias, Science, 2006, 312, 86.
7. V. Krishna and J. C. Tully, J. Chem. Phys., 2006, 125, 054706.
8. M. Morin, N. J. Levinos and A. L. Harris, J. Chem. Phys., 1992, 96, 3950.
9. Y. H. Huang, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 2000, 290, 111.
10. J. D. White, J. Chen, D. Matsiev, D. J. Auerbach and A. M. Wodtke, Nature, 2005, 433, 503.
11. J. D. White, J. Chen, D. Matsiev, D. J. Auerbach and A. M. Wodtke, J. Chem. Phys., 2006, 124, 064702.
12. R. Cooper, I. Rahinov, Z. Li, D. Matsiev, D. J. Auerbach and A. M. Wodtke, Chem. Sci., 2010, 1, 55.
13. S. Monturet and P. Saalfrank, Phys. Rev. B: Condens. Matter, 2010, 82.
14. S. Roy, N. A. Shenvi and J. C. Tully, J. Chem. Phys., 2009, 130, 174716.
15. N. Shenvi, S. Roy and J. C. Tully, Science, 2009, 326, 829.
16. N. Shenvi, S. Roy and J. C. Tully, J. Chem. Phys., 2009, 130, 174107.
17. J. L. LaRue, J. D. White, N. H. Nahler, Z. Liu, Y. Sun, P. A. Pianetta, D. J. Auerbach and A. M. Wodtke, J. Chem. Phys., 2008, 129, 024709.
18. J. L. LaRue, T. Schäfer, D. Matsiev, L. Velarde, N. H. Nahler, D. J. Auerbach and A. M. Wodtke, 2010, in preparation.
19. M. Silva, R. Jongma, R. W. Field and A. M. Wodtke, Annu. Rev. Phys. Chem., 2001, 52, 811.
20. L. Velarde, D. P. Engelhart, D. Matsiev, J. LaRue, D. J. Auerbach and A. M. Wodtke, Rev. Sci. Instrum., 2010, 81, 063106.
21. N. H. Nahler, J. D. White, J. LaRue, D. J. Auerbach and A. M. Wodtke, Science, 2008, 321, 1191.
22. The instrument broadening function was independently estimated using photoemission from 730 nm laser light (hν = 1.70 eV), and found to be in agreement with these results.
23. M. S. Mizielinski, D. M. Bird, M. Persson and S. Holloway, J. Chem. Phys., 2007, 126, 034705.
24. M. S. Mizielinski and D. M. Bird, J. Chem. Phys., 2010, 132, 184704.

---