Polyelectrolyte uptake by PEMs: Impact of salt concentration†
Xingjie
Zan
a,
Bo
Peng
a,
David A.
Hoagland
b and
Zhaohui
Su
*a
aState Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun, 130022, P. R. China. E-mail: zhsu@ciac.jl.cn; Fax: (+86)431-85262126; Tel: (+86)431-85262854
bPolymer Science and Engineering Department, University of Massachusetts, Amherst, MA 01003, USA
First published on 27th September 2011
Abstract
In a two-step process, polyelectrolytes are added to existing layer-by-layer (LbL)-constructed polyelectrolyte multilayer films (PEMs), generating versatile new films as well as fundamental insights into LbL assembly mechanisms. First, PEM swelling is affected by exposure to aqueous salt solutions of high concentration, and second, polyelectrolyte is added to the swollen PEM at the same high salt concentration. Our strategy is illustrated by adding poly(styrene sulfonate) (PSS) to poly(diallyldimethylammonium chloride)/PSS PEMs swollen by NaCl, the rebuilding steps tracked by the quartz crystal microbalance with dissipation, or QCM-D, approach. From the swelling after the first step, the association free energy of polycation and polyanion units is derived, ∼−7.0 kJ mol−1. Swelling by salt strongly affects the rate of attachment, depth of permeation, and rate of diffusion of PSS. At low salt ([NaCl] less than ∼1 M for PEMs constructed at [NaCl] = 0.5 M), PSS is added only at/near the PEM surface, while at high salt ([NaCl] greater than ∼1 M for the same PEMs), PSS fully permeates the PEM, contributing a PSS mass that can approach or exceed that already present; higher salt leads to greater PSS uptake. Even with sizable PSS addition, uptake kinetics is closely diffusive, characterized by surprisingly large and sharply [NaCl]-dependent diffusion coefficients (∼10−14–10−12 cm2s−1). The kinetics at high salt concentreation offer no evidence of slow PEM reorganization, although at low salt concentration, such reorganization remains possible.
Introduction
Electrostatically driven layer-by-layer deposition, LbL, has attracted much interest due to its simplicity, flexibility, and robustness.1 For the resulting polyelectrolyte multilayer films (PEMs), a broad spectrum of applications, such as sensors, optical devices, separation membranes, and drug delivery vehicles, have been proposed.2,3 The LbL assembly mechanism is complicated, and depending on conditions, experiments reveal a role for many factors.4 Two growth modes are known: linear and exponential. Studies have examined LbL growth under conditions of differing solvent quality,4 temperature,5,6 salt concentration,7 pH,8 and polyelectrolyte charge density.9 Of these, salt concentration affords the easiest manipulation of growth mode and PEM morphology.10–13 Under low or salt-free growth conditions, PEM thickness and mass rise linearly with the number of deposited layers N; at high salt growth conditions, thickness and mass increase exponentially with N. Various explanations for the two growth modes have emerged, and among the factors cited are: (i) continuous increase in the area active for adsorption;10,14 (ii) charge overcompensation and polyelectrolyte conformation in the outermost layer;15 (iii) increase of the charge penetration length;16 and (iv) in-and-out diffusion of polyelectrolytes.17–23Polyelectrolyte complexes (PECs), a related class of electrostatically assembled polyelectrolyte structures, spontaneously form during the solution mixing of oppositely charged polyelectrolytes, and their formation kinetics combine a fast first step, involving irreversible polyanion–polycation association, with a slow second step, involving structural rearrangement mediated by polyelectrolyte exchange with the surrounding solution. When a guest polyelectrolyte (GPE) is mixed into a solution of PECs, the GPE can either displace polyelectrolytes from the PEC, a substitution reaction, or bolster PEC mass, an addition reaction.24–26 Both scenarios entail complex intramolecular and intermolecular rearrangements. PEMs support a similar substitution reaction. For example, dissolved poly(styrene sulfonate) (PSS) has been reported to replace existing poly(methacrylic acid) (PMA) in PMA/poly(diallyldimethylammonium chloride) (PDDA) PEMs due to the stronger electrostatic interactions of the more highly ionized sulfonic acid units.27 The substitution reaction of PECs has also been examined by thermodynamic measurements.28 Mean-field theories suggest that polyelectrolytes will add to existing PEMs swollen by salt and water,16 and the addition reaction will clearly alter the PEM composition and internal structure. To our knowledge, although argued from theory, the addition reaction has not been verified by experiment. From the fundamental perspective, observing the addition will aid in the understanding of PEM growth, and from the practical perspective, offer a flexible route to new PEM functionalities. Going further, understanding replacement/addition reactions should yield insights into the stability of PEMs exposed to salt-containing polyelectrolyte solutions.
The quartz crystal microbalance with dissipation method (QCM-D), based on an acoustomechanic transducer principle, noninvasively monitors the properties of surface films in real time. By measuring the shifts in resonant frequency (Δf) and the energy dissipation factor (ΔD) of an oscillating sensor crystal to which a film is adhered, adsorbed mass and mechanical properties information are obtained in situ. QCM-D has most frequently been chosen to investigate protein adsorption,29 but LbL assembly has been explored by the method as well.30–32
The present study demonstrates that dissolved PSS in an overlying salt solution can adhere and then permeate PDDA/PSS PEMs capped by PSS. The PSS uptake and transport processes have been examined by QCM-D as a function of salt concentration for salt concentrations above the one used for PEM construction. From the monitored Δf and ΔD trends, the swelling of PEMs by salt and the subsequent PSS entry and permeation of PEMs by diffusion are quantified. Furthermore, the polycation–polyanion association energy is calculated, and the PSS diffusion kinetics fit to simple model equations.
Experimental
Materials
Poly(styrene sulfonate) (PSS, MW ∼ 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1), poly(diallyldimethylammonium chloride) (PDDA, 20 wt% in water, MW ∼ 200
000 g mol−1), poly(diallyldimethylammonium chloride) (PDDA, 20 wt% in water, MW ∼ 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–350 000 g mol−1), and sodium chloride (NaCl) were purchased from Aldrich and used as received. Polished silicon wafers and quartz were purchased from Shanghai Wafer Works Corporation. Water for rinsing and preparing all solutions was purified with a Millipore Simplicity 185 purification unit (18.2 MΩ cm).
000–350 000 g mol−1), and sodium chloride (NaCl) were purchased from Aldrich and used as received. Polished silicon wafers and quartz were purchased from Shanghai Wafer Works Corporation. Water for rinsing and preparing all solutions was purified with a Millipore Simplicity 185 purification unit (18.2 MΩ cm).
QCM-D measurements
The QCM-D system (Q-sense E1) consists of a fluid cell housing a rigidly mounted, disc-shaped, AT-cut piezoelectric quartz crystal with gold electrodes on its opposing faces. The cell provides rapid, non-perturbing exchange of the probe liquid, which contacts only one crystal face. Applying a RF voltage of ∼5 MHz across the electrodes excites the composite of the crystal and any adhered film into the thickness shear mode resonance at their coupled fundamental frequency f. Less than 3 nm (rms), crystal roughness had no impact on f.33 Measurements of f and D were obtained by switching the voltage to the piezoelectric crystal on and off periodically.34 When off, the voltage over the crystal decayed as an exponentially damped sinusoid. Numerically fitting the decay to this mathematical form, the series resonant frequency and the dissipation factor were obtained simultaneously. Serial measurements could be made at the rate of voltage switching.Soft matter adsorbed to the crystal surface creates a resonant frequency shift Δf, related to the attached mass Δm (including coupled water), and a shift in the dissipation factor ΔD, related to the frictional (viscous) losses in this mass. The described experimental system provided both film parameters at a time resolution of less than 1 s. When the adsorbed mass is uniformly distributed across the surface, unable to slip on the electrode, and sufficiently rigid and/or thin to have negligible internal friction, Δf is proportional to Δm for small values of this parameter:
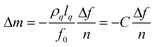 | (1) |
Due to the invalidity of the Sauerbrey equation for PEMs, thicknesses were obtained by fitting data to the model predictions of a Voigt mechanical representation (parallel spring/dashpot arrangement) for the films. The fitting procedure is described in the literature.12 In brief, the densities of both adsorbed polymer and solution (water) were set to 1 g cm−3, and the solution viscosity was set to 1 × 10−3 Pa s.
The quartz resonators were first cleaned in an ammonium peroxide mixture (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, water
1, water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH3 (25%)
NH3 (25%)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2 (30%)) at 75 °C, then rinsed with water, and finally dried in a stream of N2. LbL deposition in the liquid cell was initiated by switching the probe liquid from polyelectrolyte-free salt solution, at 0.5 M NaCl, to a PDDA-salt solution (1 mg mL−1, 0.5 M NaCl). The PDDA was allowed to adsorb to the gold resonator surface for 25 min after which rinsing with water ensured uniform coating of a positive charge. After this first adsorption of PDDA, PSS and PDDA solutions (1.0 mg mL−1, 0.5 M NaCl) were alternately injected into the cell as continuous streams for 25 min, with each solution crossover interrupted by a rinse with salt solution (0.5 M NaCl). After eight paired deposition cycles, the PEM was designated (PDDA/PSS)8; the last deposition was of PSS.
H2O2 (30%)) at 75 °C, then rinsed with water, and finally dried in a stream of N2. LbL deposition in the liquid cell was initiated by switching the probe liquid from polyelectrolyte-free salt solution, at 0.5 M NaCl, to a PDDA-salt solution (1 mg mL−1, 0.5 M NaCl). The PDDA was allowed to adsorb to the gold resonator surface for 25 min after which rinsing with water ensured uniform coating of a positive charge. After this first adsorption of PDDA, PSS and PDDA solutions (1.0 mg mL−1, 0.5 M NaCl) were alternately injected into the cell as continuous streams for 25 min, with each solution crossover interrupted by a rinse with salt solution (0.5 M NaCl). After eight paired deposition cycles, the PEM was designated (PDDA/PSS)8; the last deposition was of PSS.
Salt swelling and PSS diffusion into (PDDA/PSS)8
After an assembly of (PDDA/PSS)8, a solution of the desired higher salt concentration was injected into the liquid cell, and when both Δf and ΔD had stabilized (defined by Δf and ΔD fluctuations over 10 min of less than 3 Hz and 1 × 10−6, respectively), a PSS solution of identical salt concentration was injected into the cell. For the sequence of salt swelling and PSS diffusion, Δf and ΔD are reported as the average of three or more measurements.UV-vis characterization
Flat quartz substrates were immersed in boiling piranha solution (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 98% H2SO4 and 30% H2O2) for 20 min and then rinsed with copious amounts of water. (PDDA/PSS)8PEMs were assembled as just described.36 The PEM-coated substrates were then exposed to NaCl-containing PSS solutions (1.0 mg mL−1) for a time (12 h) sufficient to reach steady state. After rinsing with copious water and drying with N2, UV-vis spectra of the modified PEMs were collected with a Shimadzu UV-2450 spectrophotometer.
1 mixture of 98% H2SO4 and 30% H2O2) for 20 min and then rinsed with copious amounts of water. (PDDA/PSS)8PEMs were assembled as just described.36 The PEM-coated substrates were then exposed to NaCl-containing PSS solutions (1.0 mg mL−1) for a time (12 h) sufficient to reach steady state. After rinsing with copious water and drying with N2, UV-vis spectra of the modified PEMs were collected with a Shimadzu UV-2450 spectrophotometer.
Results and discussion
Fig. 1 shows typical changes of Δf and ΔD during (PDDA/PSS)8LbL assembly (section A), subsequent swelling of the formulated PEM by exposure to a high NaCl concentration (section B), and PSS uptake into the swollen PEM (section C). For each section, characteristic Δf and ΔD shifts were recorded at high signal-to-noise as near-continuous functions of time t. As described in the preceding discussion, negative Δf is expected as mass adds to an adsorbed layer, and here, the magnitude of Δf for each section was in the range of a few hundred Hz. Shifts of ΔD are more pronounced, especially in section A, where dissipation oscillated as the two polyelectrolytes were alternately deposited. Signal transients occurred at the changeovers of liquid input streams, but the transients were limited to a few seconds, allowing extraction of the long-term kinetics associated with alterations of the layer structure and composition.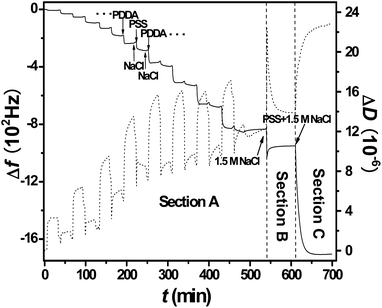 | ||
| Fig. 1 Shifts of Δf (solid line) and ΔD (dotted line) during LbL deposition of (PDDA/PSS)8 at 0.5 M NaCl (section A), swelling of the (PDDA/PSS)8PEM in 1.5 M NaCl (section B), and PSS penetration at 1.5 M NaCl into the swollen PEM (section C). | ||
Fig. 2 plots film properties as functions of N during section A. The monotonic decrease of Δf and the oscillated increase of ΔD displayed in Fig. 2a are the expected trends that have been described elsewhere.12 It has been shown that at this salt concentration (0.5 M NaCl) the multilayer growth is exponential in the first several layers, and then becomes linear afterwards with a rather constant Δf associated with each PSS deposition.12 This common feature has been attributed to the decaying excess charge profile from the surface.16 Also in the linear regime, the Δf for each PDDA deposition is greater than that for PSS because the former is more hydrated and exhibits stronger interactions between the ion pair than the latter.37PEM thickness H, plotted in Fig. 2b, was derived by the Voigt model fitting at n equal to 3, 5, and 7. The linear H rise for N > 3 is consistent with the linear Δf drop for the same N range, and similar linear PEM growth has been much reported in the LbL literature.2,10 For (PDDA/PSS)8 (N = 16), H reached 180 nm, sufficient for large QCM-D signals in the subsequent salt swelling and PSS penetration experiments. During the latter experiment, H is greater than the coil size, or even the contour length, of penetrating PSS, which are estimated to be ∼5 and ∼85 nm, respectively.
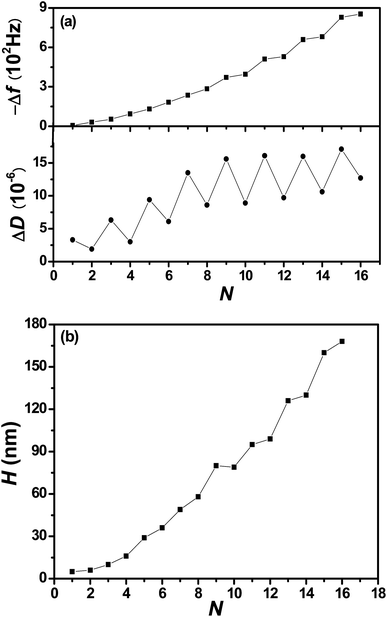 | ||
| Fig. 2 Δf and ΔD (a) and H (b) plotted as functions of N. Odd N is after PDDA deposition and even N is after PSS deposition. Lines are to guide the eye. | ||
Upon exposure to 1.5 M NaCl, after a short transient, Δf for (PDDA/PSS)8 dropped rapidly over a period of several tens of seconds even while ΔD rose over a slightly longer period (section B of Fig. 1); both trends reflected PEM thickening by fast uptake of small ions and water. Ion and its hydration water are considered together in this work because contribution of each separately to the Δf cannot be determined. At this high salt concentration, PEM swelling saturated to a steady state in ∼1 min. After achieving this state, a PSS solution of equal salt concentration was injected into the liquid cell, and then, as shown for section C of Fig. 1, Δf and ΔD evolved over a period of several tens of seconds, the magnitude of their changes comparable to or greater than those seen when the PEM was previously swollen in salt solution. These Δf and ΔD trends establish further PEM thickening, but due to pre-equilibration with solutions of the same salt concentration, the new thickening can only be ascribed to PSS diffusion into the PEM. Another important feature of the QCM-D data in section C is the large increase in dissipation associated with the PSS adsorption step, indicative of a more viscous film. This is opposite to that occurring at each PSS deposition in section A and in QCM-D studies on PSS/PDDA assembly by others,12 where a decrease in dissipation indicates a less viscous layer. This difference can be attributed to hydration water and small counterions: in section A, the PSS deposited forms complex with PDDA and a lot of small counterions and hydration water molecules are released, resulting in a less viscous layer and decrease in dissipation. In section C, however, when PSS diffuses into the PEM capped with PSS, no extra PDDA is added to form a complex with the PSS, and small counterions (sodium ions) and hydration water are introduced into the PEM along with the PSS, resulting in a more viscous layer and increase of dissipation.
To probe the swelling by salt and the uptake of PSS more deeply, (PDDA/PSS)8PEMs were swollen at different salt concentrations before the uptake of PSS. The sesults are shown in Fig. 3. Both swelling and PSS uptake increased as the salt concentration rose above its value during PEM formulation.
![Δf during salt swelling and subsequent PSS addition to (PDDA/PSS)8 at different constant [NaCl].](/image/article/2011/PY/c1py00280e/c1py00280e-f3.gif) | ||
| Fig. 3 Δf during salt swelling and subsequent PSS addition to (PDDA/PSS)8 at different constant [NaCl]. | ||
At elevated [NaCl], Cl− and Na+ ions of the contacting aqueous solution partition into the PEM, where they establish an internal equilibrium between solvated ions, intrinsically compensated polyelectrolytes, designated as Poly+Poly−, and extrinsically compensated polyelectrolytes, designated as Poly+Cl− and Poly−Na+:38
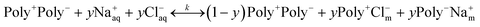 | (2) |
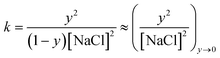 | (3) |
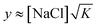 | (4) |
Fig. 3 reveals a shift of Δf with increasing [NaCl] for section B, and the measured trend, made more explicit in Fig. 4, tracks almost linearly with [NaCl] as predicted by eqn (4). A reasonable starting assumption is that the fractional change in Δf is proportional to NaCl uptake, i.e., y ∼ Δfsalt/ΔfPEMs, where Δfsalt and ΔfPEMs are the respective frequency shifts observed during salt swelling and after original deposition of (PDDA/PSS)8. A plot of y vs. [NaCl] derived under this assumption is given as the inset to Fig. 4, and the inset data are well fit by the linear equation y = 0.237([NaCl] − 0.5) − 0.026. The fit's small offset at [NaCl] = 0.5 M can be explained in three ways: (1) some extrinsic sites were trapped during PEM growth due to sluggish polyelectrolyte diffusion; (2) some intrinsic sites were trapped during swelling, again due to sluggish polyelectrolyte diffusion; or (3) the experimental estimate of the extrinsic fraction is not quantitatively correct. (The ratio of water uptake to salt uptake may change over the course of swelling.) Going further in this analysis, if during swelling Δf is strictly proportional to the overall mass uptake of the PEM, the inset's slope can be combined with eqn (4) to find K. Inserting the obtained value, 0.056, into the expression ΔG = −RTlnK−1, reveals that the association free energy for the pairing of PDDA and PSS repeat units is ∼−7.0 kJ mol−1, in line with a previous report.39 This simple analysis' success implies that the association energy is not measurably impacted by [NaCl]. Note that values along the inset's y-axis are appreciable in comparison to unity; a substantial fraction of polyanion–polycation contacts are displaced by salt even when the salt concentration is only moderately above the one employed for PEM construction.
![Impact for section B of [NaCl] on Δf for a (PDDA/PSS)8PEM formulated at 0.5 M NaCl. The inset plots y (approximated from Δf as described in the text) vs. [NaCl] for the latter above 0.5 M.](/image/article/2011/PY/c1py00280e/c1py00280e-f4.gif) | ||
| Fig. 4 Impact for section B of [NaCl] on Δf for a (PDDA/PSS)8PEM formulated at 0.5 M NaCl. The inset plots y (approximated from Δf as described in the text) vs. [NaCl] for the latter above 0.5 M. | ||
Steady state Δf values for section C are plotted as a function of the salt concentration in Fig. 5, and their increased magnitude at higher salt concentration illustrates the importance of PEM swelling to PSS uptake. For the (PDDA/PSS)8PEMs assembled in section A from 0.5 M NaCl, no PSS uptake in section C occurred for [NaCl] at or below 0.5 M, this absence presumably attributable to the large electrostatic repulsion between excess PSS chains at the PEM surface and PSS chains in solution. This barrier falls with rising the salt concentration, and consequently, PSS chains attach at higher salt concentration until a new barrier of approximately the original height re-develops, again blocking the PSS attachment. Since chain adsorption to PEMs is irreversible,40 the attachment process cannot be understood by thermodynamics alone. Further, within the PEM bulk, rising salt levels enhance the extrinsic compensation of polyelectrolyte charges, leading to greater polyelectrolyte mobility as well as more opportunities for PSS to displace Cl− in Poly+Cl− pairs. As neutralizing small ions in the PEM are released by growing intrinsic compensation, entropy is gained; each absorbed chain frees to the overlying solution twice as many counterions as the chain's total number of fixed charges, since release is from both polycation and polyanion. Better quantifying the entropy gained by counterion release is difficult, as unambiguously distinguishing a neutralizing ion from a free ion is not trivial, and ions in the PEM may be hydrated differently than ions in the overlying solution.
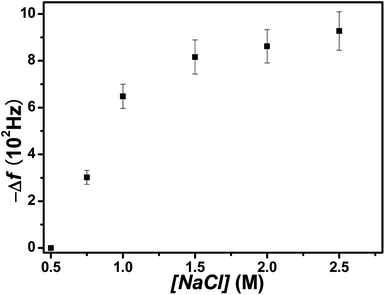 | ||
| Fig. 5 Steady state Δf value for section C as a function of salt concentration. | ||
Evidence of enhanced PSS uptake at high salt concentration was also gathered by UV-vis, as illustrated in Fig. 6, which shows spectra taken at steady state for section C. The spectra show the characteristic PSS absorbance maximum at 225 nm consistently increasing with salt concentration, confirming the uptake trend deduced from QCM-D. Closer examination of either UV-vis or QCM-D data, but especially the latter, reveals weakening of the uptake's salt dependence for [NaCl] > 1 M, suggesting a possible change in the uptake mechanism. A similar crossover in the salt dependence has been reported in PEM formation, with PEM growth becoming less dependent on salt concentration when this concentration exceeds a high threshold.11,12
![UV-vis spectra of (PDDA/PSS)8 after 12 h immersion in PSS solutions of different [NaCl]. Absorbance of the 225 nm peak is plotted against [NaCl] in the inset.](/image/article/2011/PY/c1py00280e/c1py00280e-f6.gif) | ||
| Fig. 6 UV-vis spectra of (PDDA/PSS)8 after 12 h immersion in PSS solutions of different [NaCl]. Absorbance of the 225 nm peak is plotted against [NaCl] in the inset. | ||
To elucidate better how salt controls PSS uptake in section C, thicker (PDDA/PSS)12PEMs were prepared by LbL depositions at 0.5 M NaCl, and after swelling at salt concentrations of 0.75 and 2.5 M, PSS uptakes for the new PEMs were compared to those for (PDDA/PSS)8. Section B and section C QCM-D parameters for both PEMs at the two salt concentrations are listed in Table 1. HA is the initial film thickness, and ΔfB represents the mass uptake for Section B. If the taken up mass is distributed uniformly across the films, ΔfB is proportional to HA; on the other hand, if ΔfB is the same irrespective of film thickness, uptake probably occurs only at/near the film surface, presumably as a modified layer of thickness independent of the film thickness. So the ratio ΔfB/HA is a good indicator of whether the behavior is surface- or bulk-related. In 0.75 M NaCl, for example, the ratios of ΔfB to HA for (PDDA/PSS)8 and (PDDA/PSS)12 are much the same, 0.14 and 0.15, respectively. This similarity convincingly argues that small ions (and their associated water molecules) uniformly penetrated both PEMs. However the trends for section C at steady state are less straightforward. In 2.5 M NaCl, the ratios of ΔfC to HA for (PDDA/PSS)8 and (PDDA/PSS)12 are comparable, 5.2 and 5.0, respectively, again showing full PSS penetration. However in 0.75 M NaCl, ΔfC is essentially the same for the two PEMs, indicating incomplete penetration, with uptake likely constrained to surface zones of equal thickness. Furthermore, the times to reach steady state uptake were similar for the PEMs at 0.75 M NaCl, but at 2.5 M NaCl, the uptake time was larger for the thicker film.
| [NaCl] (M) | PEM thickness (nm) | steady state Δf (Hz) | diffusion coefficient D (10−14 cm2s−1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H A | H B | H C | −ΔfB | −ΔfC | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a Subscript A, B, and C indicates the value at the end of Section A, B, and C, respectively. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (PDDA/PSS)8 | 0.75 | 180 | 185 | 249 | 25 | 298 | 5.0 ± 0.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.00 | 196 | 329 | 65 | 648 | 5.5 ± 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.50 | 214 | 384 | 170 | 816 | 170 ± 40 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.00 | 235 | 412 | 254 | 862 | 400 ± 100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.50 | 267 | 459 | 405 | 903 | 420 ± 100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (PDDA/PSS)12 | 0.75 | 296 | 305 | 364 | 44 | 271 | 46 ± 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.50 | 434 | 761 | 652 | 1548 | 700 ± 200 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The substantial mass of PSS added at high salt argues for permeation of the polyelectrolyte across the PEM. The magnitude of the addition can be seen in Fig. 6, where at 2.5 M NaCl, the 225-nm PSS absorbance peak approximately doubles during section C uptake, suggesting a doubling of PSS mass. The QCM-D data of Fig. 1 build the following picture: the sum of Δf shifts during the PSS additions of section A nearly matches the total Δf shift of section C, again indicating a doubling of mass. How so much mass might be accommodated in only a portion of the PEM is unclear. On the other hand, at low salt, the PSS addition for section C is much less, and confinement of PSS mass to just a portion of the PEM seems more reasonable. For example, at 0.75 M, the section C addition corresponds to just ∼20% of the PSS mass in the as-formed PEM.
The preceding results help to clarify the LbL assembly mechanism (section A), and more specifically, they readily explain the two growth modes described in the Introduction. At low salt concentration, LbL thickness and mass increase linearly with N, as polyelectrolytes are added mainly at/near the PEM surface. At high salt concentration, the thickness and mass increase more than linearly with N, almost exponentially, due to a surface and bulk uptake of polyelectrolytes. The crossover salt concentration, ∼1 M NaCl in the current case, is likely sensitive to polyelectrolyte identities, and through the strength of polyelectrolyte–ion associations, counterion identities as well. Although in a different context, i.e., PEM addition rather than LbL growth, these conclusions differ little from those of Schlenoff et al.16
The Δf vs. t curves of Fig. 3 admit a more quantitative analysis of PSS uptake kinetics. Letting Δf0 and Δf∞ be the initial and steady state section C values of Δf, the ratio (Δf0 − Δf)/(Δf0 − Δf∞) defines a normalized addition parameter q that rises from zero to unity with t. If uptake is diffusive, the small t slope of a plot of q vs. t1/2 manifests the diffusion coefficient D,41
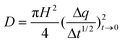 | (5) |
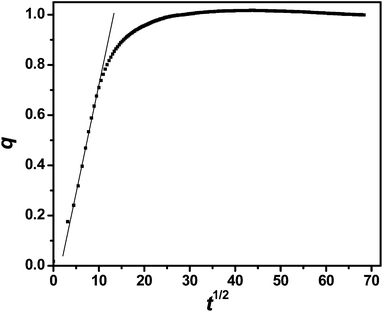 | ||
| Fig. 7 PSS uptake for (PDDA/PSS)8 at 2.0 M NaCl plotted as q vs. t1/2. The initial slope reflects D. | ||
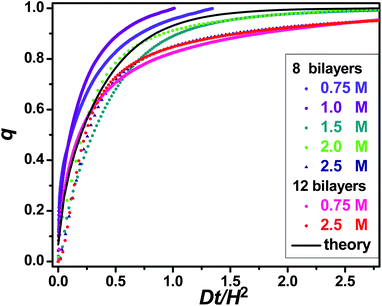
If diffusion at constant D and H is maintained throughout section C, the uptake will follow the theoretical Fickian form,
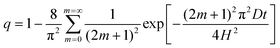 | (6) |
 | ||
| Fig. 8 Section C uptake curves for different salt concentrations and PEM thicknesses. | ||
Closer examination of Fig. 8 uncovers small discrepancies that admit, for some experimental conditions, the possibility of secondary uptake effects. As already mentioned, at low salt concentration the initial PSS uptake is not linear, a feature not immediately evident in the expanded format of Fig. 8. The deviations are consistent with elevated D at early times. An obvious explanation is faster diffusion in a more highly salt-swollen surface region than in the PEM bulk; once PSS has penetrated this surface region, diffusion slows down. Modeling of the diffusion in this case would require a two-layer PEM model, not considered here. Further, some of the experiments were not of sufficient duration to reach PSS saturation; in such cases, much better experiment-theory agreement can be obtained by adjusting Δf∞ upward to account for the lack of saturation. Despite such details, the diffusion in PEM dominating the uptake is clear. No evidence is found, at least for high salt, of any slow PEM reorganization that would limit the rate of PSS uptake; at low salt concentration this possibility remains, although for the conditions examined any effect would be small. Different PEM organizations/interactions at high and low salt concentration (above and below 1 M) offer a clear explanation for the gross D trend.
The identity of the diffusive process that dictates D is not established. Naively, since PSS uptake kinetics were examined, D might be assigned to PSS migration within a fixed PEM matrix. However, nothing in the current study conclusively makes this assignment, and other possibilities exist. For example, the rate of PSS migration might be limited by PDDA diffusion. In such coupled diffusion scenarios, PDDA and PSS molecular weights did not vary in this study, and would both significantly impact the value of D; ongoing experimental studies are addressing this possibility.
Several alternatives to diffusion-controlled uptake kinetics were assessed, and in particular, the biexponential addition kinetics considered for PECs24,25 was pursued for PEMs. In this scenario, q vs. t data are fitted to the sum of two exponentials, introducing three adjustable model parameters (two decay rates and a factor weighting the relative amplitudes of two exponentials). The biexponential model affords an excellent fit to all section C data sets, better than those found by the diffusion-controlled depiction. However, the latter introduces only one fitting parameter (D), and the value of this parameter is in line with expectation; the physical interpretations of the biexponential model's parameters are less clear. The biexponential model might be superior at very low salt concentration (less than ∼0.75 M NaCl), where there is limited evidence for uptake by a combination of diffusion and PEM reorganization, but the data for this condition are too limited to reach definite conclusions.
The principles underlying salt-mediated polyelectrolyte uptake into existing PEM can now be discussed with some confidence. Salt at a concentration above that used for PEM construction quickly swells an existing PEM, the salt partitioning into and across the PEM almost uniformly; perturbations are restricted to interfacial zones near the solid substrate and the solution surface. The overall swelling is well described by a mass action law that shifts the existing charge pairing balance toward greater extrinsic compensation with rising the external salt level. Along with ion hydration, the weakening and reduced number of contacts between the oppositely charged hydrophilic polyelectrolytes favors water adsorption. Swelling of the PEM bulk by counterions and water is accompanied by redistribution of the existing PSS surface excess into the PEM bulk. The reasons for this redistribution go beyond enhanced PSS mobility: the swollen matrix affords greater configurational freedom (thus raising the chain entropy) and heightened counterion concentration (lowering the PSS chemical potential). Eventually, the PSS re-equilibrates to approximately uniform concentration across the PEM (including the surface zone).
When the salt-equilibrated PEM is next challenged with PSS solution, as the previous PSS surface excess was lost by salt-swelling, there is no longer a significant electrostatic barrier to PSS adsorption, enabling PSS uptake that eventually generates a new barrier, one of approximately the same height as the one maintained before salt swelling. With adsorption at the surface rapid, redistribution of PSS by diffusion across the PEM becomes rate-limiting. As this process proceeds, a raised concentration of PSS remains at the surface, just as happens during LbL assembly. In all likelihood, this surface excess develops for thermodynamic reasons, perhaps as previously proposed for LbL assembly, because of the greater configurational freedom for segments in a surface zone.16 Ultimately, the new electrostatic barrier precludes additional adsorption and PSS uptake stops.
A key part of this argument is diffusion-controlled equilibration of PSS across the PEM. PSS chains inside the PEM appear to have sufficient mobility after salt-swelling to diffuse and mix uniformly across the PEM bulk in a timescale of seconds to minutes. Although the level of PSS mass uptake is not thermodynamically controlled, the PSS captured within the PEM readily equilibrates, which leads to approximately constant PSS concentration (again, surface excess is expected).
Although the mechanism appears clear, the factors that dictate the level of uptake and the rate of uptake are hard to quantify. While higher salt concentration favors greater PSS uptakes, predicting the level of uptake will require a better understanding of the interactions within the PEM, especially those involved in the delicate interplay of ion-pairing near the PEM surface, where enhanced chain configurational freedom must be ultimately responsible for the electrostatic barrier to PSS adsorption. Quantifying the factors controlling diffusion within the PEM bulk is an equally daunting task, one that must consider the complex coupling of polycation and polyanion mobilities as mediated by the dynamics of counterion exchange. The high diffusion coefficients found here at high salt concentration suggest surprisingly facile transport, at polymer mobility more typical of a moderately concentrated polymer solution than a polymer solid.
As the concentration of salt drops toward the value employed in PEM construction, equilibration of PSS within PEM at steady state appears incomplete. Incomplete equilibration is illustrated, for example, by PEM thickness-independent mass uptake, a result suggestive of a finite zone of PSS surface enrichment. Presumably, at low salt concentrations, swelling of the PEM bulk by salt is insufficient to accommodate the entire existing PSS surface excess, and consequently, any subsequent PSS addition is lessened. But more importantly, equilibration of the added PSS across the PEM bulk is not achieved. This low salt regime was not extensively explored in the current study, and its limits are not yet defined. While thickness-independent mass uptake was observed at 0.75 M NaCl, uptake kinetics at this salt constant were consistent with diffusive redistribution of mass across the entire PEM. The apparent discrepancy argues for a gradual crossover, not a sharp change, in uptake dynamics at ∼0.75–1.0 M NaCl.
The most striking indication of a change in uptake dynamics is seen in D, plotted in Fig. 9 as a function of [NaCl] for (PDDA/PSS)8. A two orders-of-magnitude rise in D begins somewhere between 1.0 and 1.5 M [NaCl]. Although large changes of PEM thickness occur during uptake at high [NaCl], an effect responsible for the large plotted uncertainties in D, these uncertainties are minor compared to the almost two-orders-of-magnitude upward shift in D. The steepness and magnitude of the rise argue for origins in the increased transience, with rising salt, of intrinsic contacts between PDDA and PSS. Analogies might be found in the dynamics associated with lateral diffusion of surface-bound polymers of high molecular weight, where similar transient chain contacts determine D; in each case, a small molecule displacer at concentration insufficient to desorb the chains can increase lateral mobility.
![D as a function of [NaCl] for (PDDA/PSS)8.](/image/article/2011/PY/c1py00280e/c1py00280e-f9.gif) | ||
| Fig. 9 D as a function of [NaCl] for (PDDA/PSS)8. | ||
The dynamics of PSS uptake considered here differ only in detail from those offered by Schlenoff et al.16 in the context of LbL growth; at high salt, both depictions envisage that polyelectrolyte motions allow equilibration across PEM thickness. In essence, the two polyelectrolytes, sometimes viewed as approximately layered in the original PEM, mix by diffusion throughout the PEM bulk, excepting a layer of surface excess for one, here PSS. At low salt concentration, mixing is confined to a finite surface zone. A major distinction is, of course, the definition of high and low salt, referenced here against the salt concentration of PEM construction. Fig. 10 offers a pictorial view of polyelectrolyte mixing.
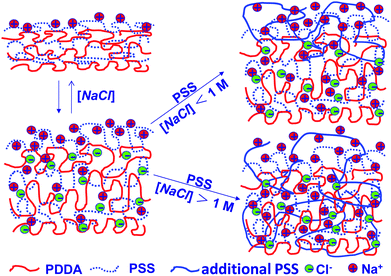 | ||
| Fig. 10 Mechanism of swelling and PSS addition at low and high salt concentrations. | ||
Conclusions
Exposure to elevated salt concentration facilitates a dramatic addition of one polyelectrolyte to a previously constructed PEM, in some cases causing a doubling of the polyelectrolyte's mass in the PEM. The addition at high salt, defined relative to the salt concentration of PEM construction, is rapid, with diffusive uptake across the PEM characterized by D as large as ∼4 × 10−12 cm2s−1. At lower salt concentration, the uptake is less dramatic, and the penetration of polyelectrolyte across the PEM is slower and probably incomplete. Nevertheless, in either salt situation is the uptake sufficiently rapid to make this new two-step approach practical as a means to tailor PEM composition and reactivity, necessary in many proposed PEM applications. Indeed, although the modification is gross rather than incremental, the effort to rebuild a PEM is not much greater than that required to deposit an additional layer via the LbL technique. A key to this approach is careful control of the salt concentration, which dictates the extent of pre-swelling and, in turn, the added mass and the time for steady state addition. The findings provide fundamental insights into the LbL assembly mechanism. Future reports will discuss the impacts of molecular weight, salt identity and polyelectrolyte concentration.Acknowledgements
Z.S. thanks the National Natural Science Foundation of China (50921062) for support, and D.A.H. acknowledges support of the U.S. National Science Foundation-funded UMass MRSEC.References
- G. Decher, Science, 1997, 277, 1232 CrossRef CAS.
- X. Zhang, H. Chen and H. Y. Zhang, Chem. Commun., 2007, 1395 RSC.
- W. Schrof, S. Rozouvan, E. Van Keuren, D. Horn, J. Schmitt and G. Decher, Adv. Mater., 1998, 10, 338 CrossRef CAS.
- S. T. Dubas and J. B. Schlenoff, Macromolecules, 1999, 32, 8153 CrossRef CAS.
- K. Buscher, K. Graf, H. Ahrens and C. A. Helm, Langmuir, 2002, 18, 3585 CrossRef.
- H. L. Tan, M. J. McMurdo, G. Q. Pan and P. G. Van Patten, Langmuir, 2003, 19, 9311 CrossRef CAS.
- S. L. Clark, M. F. Montague and P. T. Hammond, Macromolecules, 1997, 30, 7237 CrossRef CAS.
- D. Yoo, S. S. Shiratori and M. F. Rubner, Macromolecules, 1998, 31, 4309 CrossRef CAS.
- K. Glinel, A. Moussa, A. M. Jonas and A. Laschewsky, Langmuir, 2002, 18, 1408 CrossRef CAS.
- R. A. McAloney, M. Sinyor, V. Dudnik and M. C. Goh, Langmuir, 2001, 17, 6655 CrossRef CAS.
- N. Laugel, C. Betscha, M. Winterhalter, J. C. Voegel, P. Schaaf and V. Ball, J. Phys. Chem. B, 2006, 110, 19443 CrossRef CAS.
- G. M. Liu, S. R. Zou, L. Fu and G. Z. Zhang, J. Phys. Chem. B, 2008, 112, 4167 CrossRef CAS.
- L. Richert, P. Lavalle, E. Payan, X. Z. Shu, G. D. Prestwich, J. F. Stoltz, P. Schaaf, J. C. Voegel and C. Picart, Langmuir, 2004, 20, 448 CrossRef CAS.
- D. M. DeLongchamp, M. Kastantin and P. T. Hammond, Chem. Mater., 2003, 15, 1575 CrossRef CAS.
- G. Ladam, P. Schaad, J. C. Voegel, P. Schaaf, G. Decher and F. Cuisinier, Langmuir, 2000, 16, 1249 CrossRef CAS.
- J. B. Schlenoff and S. T. Dubas, Macromolecules, 2001, 34, 592 CrossRef CAS.
- P. M. Biesheuvel and M. A. C. Stuart, Langmuir, 2004, 20, 4764 CrossRef CAS.
- J. M. Garza, P. Schaaf, S. Muller, V. Ball, J. F. Stoltz, J. C. Voegel and P. Lavalle, Langmuir, 2004, 20, 7298 CrossRef CAS.
- C. Porcel, P. Lavalle, V. Ball, G. Decher, B. Senger, J. C. Voegel and P. Schaaf, Langmuir, 2006, 22, 4376 CrossRef CAS.
- C. Porcel, P. Lavalle, G. Decher, B. Senger, J. C. Voegel and P. Schaaf, Langmuir, 2007, 23, 1898 CrossRef CAS.
- L. Jourdainne, Y. Arntz, B. Senger, C. Debry, J. C. Voegel, P. Schaaf and P. Lavalle, Macromolecules, 2007, 40, 316 CrossRef CAS.
- P. Lavalle, V. Vivet, N. Jessel, G. Decher, J. C. Voegel, P. J. Mesini and P. Schaaf, Macromolecules, 2004, 37, 1159 CrossRef CAS.
- E. Hübsch, V. Ball, B. Senger, G. Decher, J. C. Voegel and P. Schaaf, Langmuir, 2004, 20, 1980 CrossRef.
- K. N. Bakeev, V. A. Izumrudov, S. I. Kuchanov, A. B. Zezin and V. A. Kabanov, Macromolecules, 1992, 25, 4249 CrossRef CAS.
- H. L. Chen and H. Morawetz, Macromolecules, 1982, 15, 1445 CrossRef CAS.
- V. A. Kabanov, A. B. Zezin, V. A. Izumrudov and T. K. Bronich, Makromol. Chem., 1985, 13, 137 CrossRef CAS.
- H. W. Jomaa and J. B. Schlenoff, Langmuir, 2005, 21, 8081 CrossRef CAS.
- V. Ball, F. Bernsmann, C. Betscha, C. Maechling, S. Kauffmann, B. Senger, J. C. Voegel, P. Schaaf and N. Benkirane-Jessel, Langmuir, 2009, 25, 3593 CrossRef CAS.
- Y. Lin, Q. R. Huang and Z. H. Su, Chin. J. Appl. Chem., 2010, 27, 505 Search PubMed.
- N. F. Steinmetz, E. Bock, R. P. Richter, J. P. Spatz, G. P. Lomonossoff and D. J. Evans, Biomacromolecules, 2008, 9, 456 CrossRef CAS.
- G. M. Liu, J. P. Zhao, Q. Y. Sun and G. Z. Zhang, J. Phys. Chem. B, 2008, 112, 3333 CrossRef CAS.
- J. J. I. Ramos, S. Stahl, R. P. Richter and S. E. Moya, Macromolecules, 2010, 43, 9063 CrossRef.
- S. J. Martin, G. C. Frye, A. J. Ricco and S. D. Senturia, Anal. Chem., 1993, 65, 2910 CrossRef CAS.
- M. Rodahl, F. Höök, A. Krozer, P. Brzezinski and B. Kasemo, Rev. Sci. Instrum., 1995, 66, 3924 CrossRef CAS.
- T. Serizawa, K. Yamamoto and M. Akashi, Langmuir, 1999, 15, 4682 CrossRef CAS.
- G. J. Wu and Z. H. Su, Chem. Mater., 2006, 18, 3726 CrossRef CAS.
- J. B. Schlenoff, A. H. Rmaile and C. B. Bucur, J. Am. Chem. Soc., 2008, 130, 13589 CrossRef CAS.
- H. W. Jomaa and J. B. Schlenoff, Macromolecules, 2005, 38, 8473 CrossRef.
- S. T. Dubas and J. B. Schlenoff, Langmuir, 2001, 17, 7725 CrossRef CAS.
- J. B. Schlenoff, in Multilayer Thin Films, ed. G. Decher and J. B. Schlenoff, Wiley-VCH, Weinheim, 2003p. 118 Search PubMed.
- J. Crank, The Mathematics of Diffusion, 2nd edn, Oxford University Press, Oxford, 1975 Search PubMed.
- P. Nazaran, V. Bosio, W. Jaeger, D. F. Anghel and R. von Klitzing, J. Phys. Chem. B, 2007, 111, 8572 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: q vs. t1/2 plots for all salt concentrations at small t. See DOI: 10.1039/c1py00280e |
| This journal is © The Royal Society of Chemistry 2011 |
