The formation of NH+ following the reaction of N22+ with H2
Jessica F.
Lockyear
,
Claire L.
Ricketts†
,
Michael A.
Parkes
and
Stephen D.
Price
*
University College London, Department of Chemistry, 20 Gordon Street, London, WC1H 0AJ, United Kingdom. E-mail: s.d.price@ucl.ac.uk
First published on 24th September 2010
Abstract
The nitrogen molecular dication (N22+) has been proposed as a minor but significant component of the ionosphere of Saturn's moon Titan with an abundance comparable to that of several key monocations. It has also been suggested that the reactions of N22+ with H2 can provide a source of N2H2+ in Titan's atmosphere. This paper reports the results from experiments, using a position-sensitive coincidence technique, which reveal the chemical reactions forming pairs of monocations following collisions of the N22+ dication with H2(D2) at a centre-of-mass collision energy of 0.9(1.8) eV. These experiments show, in addition to single electron-transfer processes, a bond-forming pathway forming NH+ + H+ + N and allow an estimate to be made of the reaction cross section and the rate coefficient for this reaction. The correlations between the product velocities revealed by the coincidence experiments show that NH+ is formed via N atom loss from a primary encounter complex [N2H2]2+ to form NH22+, with this triatomic daughter dication then fragmenting to yield NH+ + H+. A computational investigation of stationary points on the lowest energy singlet and triplet [N2H2]2+ potential energy surfaces confirms the mechanistic deductions from the experiments and indicates that the formation of NH+ occurs solely, and efficiently, from the reaction of the c3Σ+u excited electronic state of N22+.
1. Introduction
Due to their large intramolecular Coulomb repulsion, the majority of the electronic states of small molecular di-positive ions (dications), such as N22+, are dissociative. Population of these electronic states results in very short lived species which fragment rapidly to give a pair of monocations:| N22+ → N+ + N+ | (1) |
Given the above behaviour, one would not immediately expect that these highly energetic ions could exhibit an extensive bond-forming chemistry. However, the possibility of dicationic bimolecular chemical reactions has been apparent since 1930, when the observation of CO2+ using a mass spectrometric experiment was reported.1 Since a variety of small molecular dications are detectable via standard mass spectrometric techniques, these ions must possess electronic states with a lifetime of at least a few microseconds. These longer-lived states of small molecular dications are commonly termed “metastable” and arise as a result of energy barriers which confer kinetic stability on species2,3 which are usually4,5 thermodynamically unstable with respect to dissociation to a pair of monocations (reaction (1)). Extensive experimental and theoretical work over many years has revealed that many small molecular dications possess at least one metastable electronic state, and molecular dication lifetimes of the order of seconds have been reported.6 Thus, in a variety of environments, such as planetary ionospheres, metastable dications are sufficiently long-lived to experience collisions with neutral molecules and undergo chemical transformations. However, it is only comparatively recently that the extensive chemistry which occurs in such low-energy collisions between molecular dications and neutral molecules has begun to be revealed and the implications of this chemistry for the composition of energized media explored.2,4,7,8
The potential role of the chemistry of gas-phase monocations in extreme environments, such as the interstellar medium and planetary ionospheres, has long been appreciated.9,10 In addition to their postulated role in some regions of the interstellar medium,10,11 recent modelling has strongly suggested a contribution from molecular dications to the chemistry of planetary ionospheres.12–14 For example, CO22+ has been predicted to be a measurable constituent of the Martian ionosphere and N22+ has been implicated in the chemistry of the upper atmospheres of Earth and Saturn's moon Titan.13,14 In fact modelling indicates that optical emission from N22+ should be observable in Titan's ionosphere.14 Dicationic chemistry has also been proposed as a mechanism for the synthesis of larger hydrocarbons in Titan's atmosphere as well as elsewhere.15
The chemistry of Titan's atmosphere has been described as “the richest … in the Solar System”.16 Measurements taken by the Cassini spacecraft, and their subsequent modelling, have revealed a highly complex ionospheric composition, both on the day-side and the night-side of this moon.16–19 These observations indicate that molecular growth starts in the upper atmosphere of Titan and results in large positively and negatively charged ions, which are probably the precursors for even larger molecules and eventually aerosols.16–19 Successful attempts to replicate the general themes of this molecular synthesis in the laboratory have recently been reported.20 Modelling has indicated that the abundance of N22+ in Titan's ionosphere, at altitudes of approximately 1000 km, is comparable with that of several key minor ions such as CN+ and C2H+.14 Indeed, the presence of dications in Titan's ionosphere is supported by the tentative assignment of N2+ in the ion abundances recorded by Cassini.17 Recent investigations have concluded that to improve the agreement between models and observations of Titan's ionospheric ion abundances, beyond the current factors of 2-3, requires a more detailed knowledge of the ion/neutral chemistry.19 Thus, since N2 is the most abundant molecule in Titan's ionosphere, it is highly pertinent to examine the reactions of N22+ with other key ionospheric species.
This paper reports a study of the reactivity of N22+ with H2, as models indicate that H2 is the third most abundant molecular species in Titan's atmosphere.19 The principal loss mechanisms for ionospheric molecular dications are electron recombination and reaction with neutral species.14 Thus, our experimental investigation of the consequences of N22+ collisions with H2 is of particular relevance to the fate of N22+ in Titan's ionosphere. More specifically, recent computational studies21 have investigated the structure of N2H2+. These calculations showed that the ground state of N2H2+ is metastable and, in addition, that many of the excited N2H2+ electronic states also possess local minima. The authors of this computational study suggested that interactions between N22+ and H2 may provide a source of long-lived N2H2+ ions in Titan's ionosphere. Such bond-forming reactions are, in general, more likely to occur at low collision energies (below 10 eV), where there is significant interaction time between the reactants.22,23
Stimulated by the relevance to Titan's ionosphere, and the intriguing possibility of the formation of N2H2+, we report in this paper an experimental study of the reactivity of N22+ with H2(D2) using a position-sensitive coincidence (PSCO) experiment. This experiment clearly identifies the reactions which generate pairs of singly-charged ions following dication-neutral collisions, revealing NH+ + H+ are formed following collisions of N22+ with H2. Examination of the correlations between the velocities of the product ions shows that the NH+ + H+ ion pair is formed via an NH22+ reaction intermediate, a conclusion supported by an accompanying computational investigation. Analysis of the experimental results also allows the estimation of the reaction cross section and the thermal rate coefficient for this reaction. Coupled with the results of the computational investigation, these estimates indicate that the bond forming reactivity is solely due to reaction of the first excited triplet state of N22+, and this state reacts with H2 to form NH+ at close to the collisional rate.
2. Experimental section
The PSCO technique involves the mass-spectrometric detection of the pairs of monocations, formed from dication-neutral reactions, on an event by event basis at a position-sensitive detector. This methodology allows us to determine the masses and the velocities of each of the product ions and, by conservation of momentum, the velocity of any accompanying neutral product.8,22 These data both identify the different dicationic reactions which form pairs of positive ions from a given collision system and also reveal the dynamics of these reactions.8The details of the operation of the PSCO experiment have been described elsewhere and will only be summarized very briefly here.8,24 The reactant dications are generated via electron ionization of N2 and are energy monochromatized, pulsed and mass selected before they are decelerated to encounter an effusive jet of the neutral reactant. It is important to note that the ion beam is mass selected at m/z = 14 for N22+. Of course, this mass selection means that the beam of N22+ also contains a considerable number of N+ ions. However, since the PSCO spectrometer only records events that result in the formation of a pair of product ions, the N+ ions do not contribute any true coincidences to the experimental spectra.
Interactions with H2(D2) occur, under single collision conditions, in the field-free source region of a specially designed time-of-flight mass spectrometer (TOF-MS). Immediately after these interactions, the product ions, and any un-reacted dications are extracted and accelerated to strike a position sensitive detector (PSD).25
For events where two ions arrive at the detector following a single repeller plate pulse, we record the flight time of both of the ions and the position at which each ion hits the detector. The experimental conditions ensure such events are dominated by the reactions of individual dications. The experiment accumulates these coincidences for least 105 pair events, which usually takes several days.
We process the experimental dataset off-line. Firstly, a two-dimensional histogram of the pairs of flight times for the detected reactive events is constructed to give a pairsspectrum (Fig. 1). The different dicationic reaction channels, which generate different pairs of monocations, appear as distinct peaks in the pairs spectrum. To prevent a significant number of false coincidences due to the N+ ions in the N22+ beam, we inhibit the acquisition of pairs involving a narrow range of flight times close to m/z = 14. We can easily allow for real coincidences lost in this excluded region when assessing the intensity of the different product channels.26 The time and positional data corresponding to each reaction channel identified in the pairs spectrum can then be selected from the experimental dataset for kinematic analysis. From the positions of the ionic impacts on the detector and the ionic flight times, together with the known collision energy (ECM), we can determine the velocities of the product ions in the centre of mass (CM) frame of the N22+-H2 collision system: w(X+).8,24 Then the CM velocity vector of any accompanying neutral species can be derived from the velocity vectors of the two charged species via conservation of momentum. Subsequently we examine, for each reactive channel, the correlations between the velocities of the products and the relationship of these velocities to the original velocity vector of the reactant dication. These correlations have been shown to be a powerful probe of the mechanisms of the chemical reactions of molecular dications.8,22,26–28
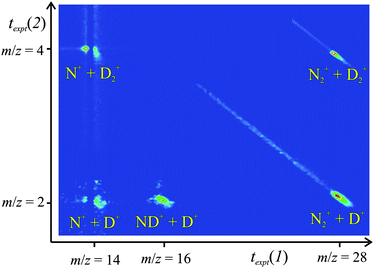 | ||
| Fig. 1 The pairs spectrum recorded following the collisions of N22+ with D2 at ECM = 1.8 eV. The peaks involving coincidences with N+ have a “split” shape due to the exclusion of a strip of false coincidences resulting from the N+ ions present in the reactant ion beam. See text for details. | ||
3. Results and discussion
Our experimental technique gives us the masses and the CM velocities of the product ions formed following the collisions of N22+ with H2(D2). We can also determine the velocity of any accompanying neutral products. These data immediately (Fig. 1) identify the different dicationic reactions which form pairs of positive ions and examining the correlations between the product and reactant velocities reveals the dynamics of the reactions.8Five bimolecular reactions are clearly observed in the PSCO pairs spectrum recorded following collisions of N22+ with H2 (Table 1). Experiments with D2 show analogous reactivity to that observed for H2 (Table 1).
| Reaction | R (N22+ + H2) | R (N22+ + D2) | |
|---|---|---|---|
| (2) | N22+ + H2 → N2+ + H2+ | 53.1 | 61.2 |
| (3) | N22+ + H2 → N+ + H2+ + N | 31.5 | 23.6 |
| (4) | N22+ + H2 → N2+ + H+ + H | 10.3 | 12.1 |
| (5) | N22+ + H2 → N+ + H+ + (N + H) | 3.4 | 1.6 |
| (6) | N22+ + H2 → NH+ + H+ + N | 1.7 | 1.5 |
The reactivity we observe comprises four reactions (2)–(5) (Table 1) which involve transfer of a single electron from H2(D2) to N22+. Three of these reactions, (3)–(5), involve subsequent decay of the monocation products (N2+ + H2+) of this initial electron transfer. Our PSCO data (Table 1, Fig. 1) also clearly shows the formation of NH+ + H+ following N22+ collisions. However, in contrast to the theoretical predictions discussed above, we see no signals due to N2D2+ or N2H2+ in the mass spectra we collect in parallel with the PSCO data.29
The branching ratios (Table 1) of the different reactions in the pairs spectrum (Fig. 1), do not place the rates of these reactions on an absolute scale and such absolute measurements are those of real value to ionospheric modelling. To obtain estimates of the rate coefficient for the formation of NH+ + H+ from the signals in our pairs spectra we have adopted two different approaches. Firstly we have extrapolated the absolute measurements of the cross section for forming N2+ from reactions between N22+ and H2 of Agee et al.30 to our collision energy and then used the measured relative intensity of the channels forming N2+ and NH+ (Table 1) to deduce that the absolute cross section for forming NH+ under our experimental conditions is 1.0 × 10−17 cm2.31 To estimate the corresponding thermal rate constant for this reaction from this cross section we assume the limiting ECM−½ dependence of an ion-molecule reaction cross section and perform the standard integration over a Boltzmann distribution.32 This procedure yields an estimated rate coefficient k6 for the formation of NH+ at 300 K of 1.0 × 10−11 molecule−1 cm3s−1.
The other approach to estimate k6 is to assume product formation occurs at every close approach of the reactants, at the so-called Langevin rate,33 and partition this rate between the various channels in proportion to our measured branching ratios (Table 1). This calculation results in an estimate of k6 = 5.4 × 10−11 molecule−1 cm3s−1, a value independent of temperature and in good accord with our first estimate.34
We now consider the mechanisms of the reactions we observe following collisions of N22+ with H2(D2) (Table 1). The detailed dynamics of dicationic electron transfer reactions at low collision energies (below ECM = 10 eV) have been extensively investigated in recent years.22,28,35,36 Experimental work shows that in this low energy regime the electron is transferred from the neutral to the dication at a significant (3–6 Å) interspecies separation, where the interaction potential between the reactants is not strong.8 Thus, most electron transfer events simply involve the dication and neutral flying past each other and exchanging an electron. Such electron transfer forms monocationic products which move in the same direction as the reactant from which they were formed. Thus, in reaction (2) the N2+ is formed with a velocity vector which is closely aligned with that of the reactant N22+. This strong alignment between the product and reactant velocities is termed forward scattering. The electron transferreactions (2)–(5) we observe in the N22+ + H2 collision system all exhibit the expected forward scattering and will not be discussed further.
The mechanism of the bond-forming reaction which generates NH+ + H+ is far more unusual and complex than that of the electron transfer processes. To reveal the kinematics of this chemical process we examine the correlations between the product and reactant velocities by generating a variety of scattering diagrams from our PSCO data. We present here the data for the N22+ + D2 collision system, which displays identical correlations to those we observe for N22+ + H2. Fig. 2 shows the CM frame scattering diagram for the ND+ and D+ ions generated by reaction (6). This scattering diagram is a radial histogram where, for all the reactive events detected in the ND+ + D+ channel, we plot the angle θ between a product ion's CM velocity and the initial CM velocity of the N22+ reactant (0° ≤ θ ≤ 180°) as the angular co-ordinate. The radial co-ordinate in these diagrams is the magnitude of the product ion's CM velocity, |w(X+)|. The data for ND+ is plotted in the upper semicircle of Fig. 2 and the data for D+ in the lower semicircle. Fig. 2 shows that there is little correlation between the velocities of the products of reaction (6) with the velocity of the reactant N22+. Although not shown in Fig. 2, a similar lack of correlation is observed for the CM scattering of the product N atom. This lack of correlation is a clear indication that a collision complex [N2–H2]2+ is involved in the reaction pathway, before the formation of any of the observed products.33 If the collision complex lives for at least a few rotational periods then the products have no “memory” of the original direction of the reactant N22+ ion, as we observe in Fig. 2.
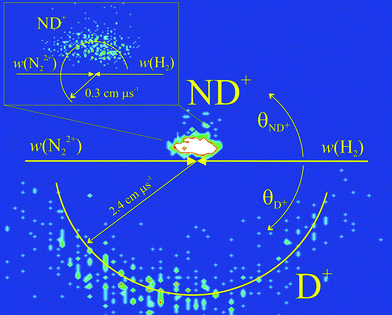 | ||
| Fig. 2 The CM frame scattering diagram for the reaction N22+ + D2 → ND+ + D+ + N, showing the scattering of ND+ and D+, relative to the direction of the reactant dication velocity w(N22+), derived from PSCO data recorded at ECM = 1.8 eV. The inset shows the scattering of the ND+ fragment on a larger scale. See text for details. | ||
To probe the mechanism of reaction (6) in more detail we examine the correlations between the product velocities in the “internal frame”, the frame defined by the velocities of the product ions themselves.8 In an internal frame scattering diagram, another radial histogram, the radial co-ordinate is again |w(X+)|or |w(X)|. However, the angular co-ordinate ϕ is now the scattering angle between the velocity of the product of interest and the velocity of another reference product. For example, Fig. 3a shows the scattering of w(ND+) and w(N) with respect to the direction of w(D+). Fig. 3b and Fig. 3c show internal frame scattering diagrams with reference to the velocities of N and ND+ respectively.
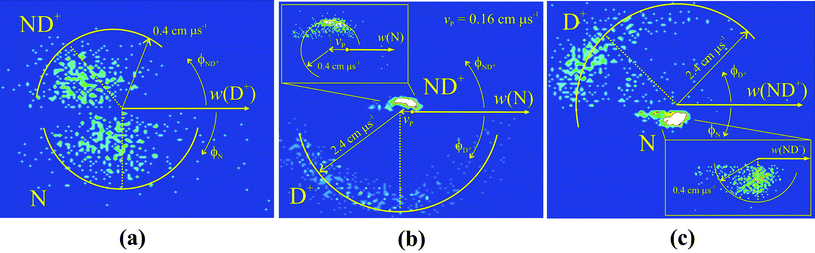 | ||
| Fig. 3 The internal frame scattering diagrams from reaction (6) in the N22+ + D2 collision system at ECM = 1.8 eV. Fig. 3a shows the scattering of ND+ and N relative to w(D+), Fig. 3b shows the scattering of the ND+ and D+ relative to w(N) and Fig. 3c shows the scattering of D+ and N relative to w(ND+). The insets in (b) and (c) show the scattering of the ND+ and N fragments respectively on a larger scale. See text for details. | ||
There are four possible mechanisms (7)–(10) for the formation of ND+ + D+ + N, given that, as discussed above, the CM scattering data (Fig. 2) shows that the first step in this mechanism is the formation of a collision complex:
| N22+ + D2 → [N2D2]2+ → ND+ + N + D+ | (7) |
| N22+ + D2 → [N2D2]2+ → ND+ + ND+ then ND+ → N + D+ | (8) |
| N22+ + D2 → [N2D2]2+ → N2D+ + D+ then N2D+ → ND+ + N | (9) |
| N22+ + D2 → [N2D2] 2+ → ND22+ + N then ND22+ → ND+ + D+ | (10) |
The form of Fig. 3 immediately allows us to discount the concerted fragmentation of the collision complex in mechanism (7). Such concerted reactions give internal frame scattering diagrams where there are fixed angular relationships between the velocity vectors of the products.37 The scattering diagrams in Fig. 3 clearly do not show such fixed angular relationships between the product velocity vectors.
From inspection of Fig. 3, the sequential mechanism (8) can also readily be discounted. Charge separation of the [N2H2]2+ collision complex to form two ND+ ions would form these primary products with significant velocities. A typical dicationic charge separation involves an energy release of approximately 6 eV, which would give the ND+ ions velocities of the order 0.6 cm μs−1. Extraction of the CM velocity distributions of the product ions from our data (Fig. 4) shows that the average value of w(ND+) is markedly lower than this expected value of 0.6 cm μs−1. Furthermore, following the secondary fragmentation of one of the ND+ ions in mechanism (8), the velocity of the N atom will remain close to that of the precursor ND+ due to conservation of momentum and energy. Thus, mechanism (8) would predict ND+ to have a significant velocity which will be strongly anticorrelated with w(N). None of these predicted features are apparent in Fig. 3.
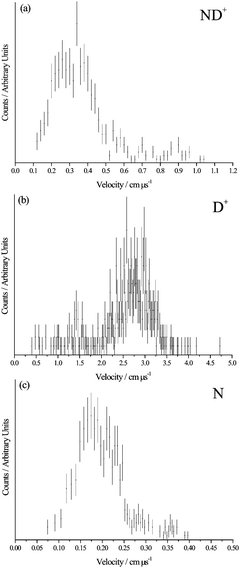 | ||
| Fig. 4 Product velocity distributions for reaction (6). | ||
Mechanism (9) involves the charge separation of the initial collision complex and then subsequent secondary fragmentation of the N2D+ product of this initial decay. If this mechanism is operating we can determine the average velocity of this N2D+ precursor to be 0.18 cm μs−1via conservation of momentum from the measured modal value of w(D+) = 2.75 cm μs−1 (Fig. 4). We would then expect the velocities of ND+ and N to be isotropically distributed about w(N2D+), the velocity of the precursor ion, as we have observed before for such secondary fragmentations.35Fig. 3a clearly does not show such a characteristic distribution for the N atom. In addition, the secondary fragmentation of N2D+ should not involve a significant kinetic energy release, in comparison to the large kinetic energy released upon the charge separation of the doubly-charged collision complex. Thus, we would expect the average value of w(ND+) to be similar to that of the precursor ion w(N2D+) = 0.18 cm μs−1. As shown in Fig. 4, the average value of w(ND+) is almost twice this value. Hence, the scattering is clearly not in accord with mechanism (9).
In mechanism (10) the collision complex first loses an N atom to form NH22+ and this daughter dication then undergoes a two-body charge separation to form the observed products. For this mechanism we would expect w(N) to be broadly anticorrelated with w(D+) and w(ND+), as we observe in Fig. 3b. From the measured average value of w(N) of 0.2 cm μs−1 we can estimate, using conservation of momentum, the average value of w(ND22+) to be 0.16 cm μs−1. The scattering of ND+ and D+ should then be centred about this value of w(ND22+), as is also clearly visible in Fig. 3b where w(ND22+) is marked as vp. Thus, the only reaction mechanism in full accord with the PSCO data is mechanism (10).
To lend further support to the above mechanistic conclusions we have investigated the stationary points on the N22+ + H2 potential energy surface (PES) computationally.38 We initially restricted our calculations to the singlet potential energy surface, as experiments have indicated that the majority of dications in N22+ beams are in the ground X1Σ+g state.39 Stationary points were located by B3LYP/aug-ccVTZ optimization and their energies characterized by CCSD(T)/aug-ccVTZ single point calculations. B3LYP frequency analysis was used to identify minima and transition states, and the connectivity of the transition states was confirmed by the IRC methodology and inspection of imaginary frequencies.23 The geometries of several of the reactant and product species have been determined before either theoretically or experimentally.40–42 In these cases our calculated geometries agree well with the literature values. The energy of any excited states of the atomic products were determined by adding spectroscopic excitation energies43 to our calculated energies of the relevant ground states. This procedure generates a calculated reaction exothermicity of −2.8 eV (Fig. 5) for reaction (6), which on the singlet PES forms NH+ and N in doublet states, in excellent agreement with literature thermodynamics (−2.8 eV).40,44
![Stationary points on the singlet [N2H2]2+ potential energy surface. All energies include zero point energies and are expressed relative to the infinitely separated singlet reactants. The levels labelled TS are transition states with a critical vibration shown by the double headed arrow. Bond lengths are in Ångströms and angles in degrees.](/image/article/2011/SC/c0sc00344a/c0sc00344a-f5.gif) | ||
| Fig. 5 Stationary points on the singlet [N2H2]2+ potential energy surface. All energies include zero point energies and are expressed relative to the infinitely separated singlet reactants. The levels labelled TS are transition states with a critical vibration shown by the double headed arrow. Bond lengths are in Ångströms and angles in degrees. | ||
Fig. 5 reveals two pathways from N22+(X1Σ+g) + H2 on the singlet [N2H2]2+ surface to reach pairs of monocations with new chemical connectivity; one of these pathways leads to the formation of the experimentally observed products NH+ + H+ + N (Rxn. 6). Both pathways proceed via the formation of a collision complex (1).45 The lowest energy reaction pathway involves charge-separating decay of 1, via a transition state 2, to form NH2+ (3) + N+. We observe no evidence of this pathway in our PSCO spectra. Clearly there are dynamic or energetic constraints in the formation of N+ + NH2+via this pathway that are not revealed by our calculated stationary points.
The second reactive pathway revealed by our calculations (Fig. 5) corresponds exactly to the experimentally determined mechanism (10) for forming the observed NH+ + H+ + N products. Specifically, the theoretical pathway involves the loss of a nitrogen atom from 1 to yield an NH22+ dication 4 in a doublet state. This loss of an N atom appears not to involve a transition state. The NH22+ ion (4) then decays via a transition state (5) to yield the experimentally observed products. However, the energetics revealed in Fig. 5 indicate that this pathway proceeds via structures (4 and 5) which are energetically inaccessible to reactants in their ground vibrational levels, even allowing for the contribution of the CM collision energy. The N22+(X1Σ+g) ions in our reactant beam are not necessarily in their ground vibrational states. However, investigations of the population of the ground electronic state of N22+ following photoionization clearly show the population of the three lowest vibrational levels is favoured, giving a maximum vibrational energy of 0.5 eV.44 Thus, if the vibrational distribution of the N22+ reactant ions in our beam is similar to that formed by photoionization, then the N22+(1Σ+g) + H2 collision system should not be able to energetically access the observed products via intermediates 4 and 5.
To resolve the above inconsistency between the calculated energetics on the singlet surface of [N2H2]2+ and the experimental observation of reaction (6) we note that it is well established that beams of N22+ contain a small proportion of ions in the metastable triplet c3Σ+u state.39 This state lies 1.5 eV above the ground electronic state of N22+.42,46 Thus, given the difficulties in explaining the observation of the formation of NH+ + H+via a singlet PES we have also calculated (Fig. 6) stationary points on the triplet [N2H2]2+ surface.
![Stationary points on the triplet [N2H2]2+ potential energy surface. All energies include estimated zero point energies and are expressed relative to the infinitely separated singlet reactants (see Fig. 5); the energy zero is the same in both Fig. 5 and 6. The levels labelled TS are transition states with a critical vibration shown by the double headed arrow. All bond lengths are in Ångströms and angles in degrees. Note the vertical scale breaks at −2 eV and −8 eV.](/image/article/2011/SC/c0sc00344a/c0sc00344a-f6.gif) | ||
| Fig. 6 Stationary points on the triplet [N2H2]2+ potential energy surface. All energies include estimated zero point energies and are expressed relative to the infinitely separated singlet reactants (see Fig. 5); the energy zero is the same in both Fig. 5 and 6. The levels labelled TS are transition states with a critical vibration shown by the double headed arrow. All bond lengths are in Ångströms and angles in degrees. Note the vertical scale breaks at −2 eV and −8 eV. | ||
The triplet surface we calculate (Fig. 6) is qualitatively similar to that of the singlet surface (Fig. 5) with the same two series of stationary points leading to NH+ + H+ + N and NH2+ + N+.47 However, inspection of the triplet surface (Fig. 6) reveals that the stationary points on the pathway to form NH+ + H+ + N(4S) now all lie at energies below the N22+(c3Σ+u) asymptote. Thus, our computational results strongly indicate that NH+ formation proceeds via the reaction of the metastable triplet N22+ ions in our dication beam. No quantitative evaluation of the relative abundances of the X and c states of N22+ in dication beams is available. Previous investigations of the electron transfer reactivity of N22+ with the rare gases, show that reactions of the ground (singlet) electronic state of the dication dominate the ion yield when such channels are accessible. Hence, it is likely that the N22+(c3Σ+u) species are a distinct minority species in our dication beam, and the small yield of NH+ + H+ in our experiments is indicative of a large reaction cross section for NH+ formation from the N22+(c3Σ+u) state. If, as might be expected, less than 10% of the N22+ ions in our ion beam are in the c3Σ+u state then our data would indicate that the c3Σ+u state reacts with H2 to form NH+ on almost every encounter.
Given the above results, it seems clear that a long-term goal should be a fully state-resolved investigation of the reactivity of N22+ ions with H2. With regard to the ionospheric chemistry of Titan, clearly improved models of dicationic chemistry need to differentiate the long-lived X and c electronic states of N22+. If a significant fraction of the N22+ ions present in Titan's ionosphere are in the c3Σ+u state, the reactions of such ions with H2 to form NH+ + H+ + H may contribute significantly to the observed ionic abundances.
4. Conclusions
We have investigated the chemical reactions forming pairs of monocations following collisions of the N22+ dication with H2(D2) at a centre-of-mass collision energy of 0.9(1.8) eV. These experiments reveal, in addition to single electron transfer reactions, a bond-forming pathway forming NH+ + H+ + N. Correlations between the velocities of the products of this bond-forming channel show that NH+ is formed via N atom loss from a primary encounter complex [N2H2]2+ to form NH22+. This triatomic dication then fragments to yield NH+ + H+. No evidence for the involvement of an N2H2+ ion is observed. A computational investigation of the [N2H2]2+ potential energy surfaces confirms the mechanistic deductions from the experiments and indicates that the formation of NH+ occurs solely, and efficiently, from the reaction of the c3Σ+u excited electronic state of N22+ with H2.Acknowledgements
This work was supported by funding from the EPSRC (EP/E038522/1) and UCL.Notes and References
- R. Conrad, Physik. Z., 1930, 31, 888 Search PubMed.
- S. D. Price, J. Chem. Soc., Faraday Trans., 1997, 93, 2451–2460 RSC.
- D. Mathur, Phys. Rep., 2004, 391, 1–118 CrossRef CAS.
- D. Schroder and H. Schwarz, J. Phys. Chem. A, 1999, 103, 7385–7394 CrossRef.
- C. Heinemann, D. Schroder and H. Schwarz, J. Phys. Chem., 1995, 99, 16195–16198 CrossRef CAS.
- L. H. Andersen, J. H. Posthumus, O. Vahtras, H. Agren, N. Elander, A. Nunez, A. Scrinzi, M. Natiello and M. Larsson, Phys. Rev. Lett., 1993, 71, 1812–1815 CrossRef CAS.
- D. Mathur, Phys. Rep., 1993, 225, 193–272 CrossRef CAS; Z. Herman, Int. Rev. Phys. Chem., 1996, 15, 299–324 CrossRef CAS; S. D. Price, Phys. Chem. Chem. Phys., 2003, 5, 1717–1729 RSC.
- S. D. Price, Int. J. Mass Spectrom., 2007, 260, 1–19 Search PubMed.
- D. Smith and P. Spanel, Mass Spectrom. Rev., 1995, 14, 255–278 CAS.
- S. Petrie and D. K. Bohme, Mass Spectrom. Rev., 2007, 26, 258–280 CrossRef CAS.
- J. Roithova and D. Schroder, J. Am. Chem. Soc., 2006, 128, 4208–4209 CrossRef CAS; S. Leach, J. Electron Spectrosc. Relat. Phenom., 1986, 41, 427–438 CrossRef CAS.
- O. Witasse, O. Dutuit, J. Lilensten, R. Thissen, J. Zabka, C. Alcaraz, P. L. Blelly, S. W. Bougher, S. Engel, L. H. Andersen and K. Seiersen, Geophys. Res. Lett., 2002, 29, 1263 CrossRef; G. Gronoff, J. Lilensten, C. Simon, O. Witasse, R. Thissen, O. Dutuit and C. Alcaraz, Astron. Astrophys., 2007, 465, 641–645 CrossRef CAS.
- C. Simon, J. Lilensten, O. Dutuit, R. Thissen, O. Witasse, C. Alcaraz and H. Soldi-Lose, Ann. Geophys., 2005, 23, 781–797 Search PubMed.
- J. Lilensten, O. Witasse, C. Simon, H. Solidi-Lose, O. Dutuit, R. Thissen and C. Alcaraz, Geophys. Res. Lett., 2005, 32, L03203 CrossRef.
- J. Roithova, C. L. Ricketts and D. Schroder, Int. J. Mass Spectrom., 2009, 280, 32–37 Search PubMed; C. L. Ricketts, D. Schroder, C. Alcaraz and J. Roithova, Chem.–Eur. J., 2008, 14, 4779–4783 CrossRef CAS; D. Ascenzi, J. Roithova, D. Schroder, E. L. Zins and C. Alcaraz, J. Phys. Chem. A, 2009, 113, 11204–11210 CrossRef CAS.
- V. Vuitton, R. V. Yelle and P. Lavvas, Philos. Trans. R. Soc. London, Ser. A, 2009, 367, 729–741 CrossRef CAS.
- T. E. Cravens, I. P. Robertson, J. Clark, J. E. Wahlund, J. H. Waite, S. A. Ledvina, H. B. Niemann, R. V. Yelle, W. T. Kasprzak, J. G. Luhmann, R. L. McNutt, W. H. Ip, V. De La Haye, I. Muller-Wodarg, D. T. Young and A. J. Coates, Geophys. Res. Lett., 2005, 32, L12108 CrossRef.
- I. P. Robertson, T. E. Cravens, J. H. Waite, R. V. Yelle, V. Vuitton, A. J. Coates, J. E. Wahlund, K. Agren, K. Mandt, B. Magee, M. S. Richard and E. Fattig, Planet. Space Sci., 2009, 57, 1834–1846 CrossRef CAS.
- T. E. Cravens, I. P. Robertson, J. H. Waite, R. V. Yelle, V. Vuitton, A. J. Coates, J. E. Wahlund, K. Agren, M. S. Richard, V. La Haye, A. Wellbrock and F. M. Neubauer, Icarus, 2009, 199, 174–188 CrossRef.
- R. Thissen, V. Vuitton, P. Lavvas, J. Lemaire, C. Dehon, O. Dutuit, M. A. Smith, S. Turchini, D. Catone, R. V. Yelle, P. Pernot, A. Somogyi and M. Coreno, J. Phys. Chem. A, 2009, 113, 11211–11220 CrossRef CAS.
- V. Brites and M. Hochlaf, J. Phys. Chem. A, 2009, 113, 11107–11111 CrossRef CAS; V. Brites and M. Hochlaf, Chem. Phys. Lett., 2009, 477, 48–51 CrossRef CAS.
- C. L. Ricketts, D. Schroder, J. Roithova, H. Schwarz, R. Thissen, O. Dutuit, J. Zabka, Z. Herman and S. D. Price, Phys. Chem. Chem. Phys., 2008, 10, 5135–5143 RSC.
- D. Ascenzi, P. Tosi, R. J., C. L. Ricketts, D. Schröder, J. F. Lockyear, M. A. Parkes and S. D. Price, Phys. Chem. Chem. Phys., 2008, 10, 7121–7128 RSC.
- W. P. Hu, S. M. Harper and S. D. Price, Meas. Sci. Technol., 2002, 13, 1512–1522 CrossRef CAS.
- I. Ali, R. Dorner, O. Jagutzki, S. Nuttgens, V. Mergel, L. Spielberger, K. Khayyat, T. Vogt, H. Brauning, K. Ullmann, R. Moshammer, J. Ullrich, S. Hagmann, K. O. Groeneveld, C. L. Cocke and H. Schmidt-Bocking, Nucl. Instrum. Methods Phys. Res., Sect. B, 1999, 149, 490–500 CrossRef CAS; A. Oelsner, O. Schmidt, M. Schicketanz, M. Klais, G. Schonhense, V. Mergel, O. Jagutzki and H. Schmidt-Bocking, Rev. Sci. Instrum., 2001, 72, 3968–3974 CrossRef CAS.
- C. L. Ricketts, S. M. Harper, S. W. P. Hu and S. D. Price, J. Chem. Phys., 2005, 123, 134322 CrossRef.
- M. A. Parkes, J. F. Lockyear and S. D. Price, Int. J. Mass Spectrom., 2009, 280, 85–92 Search PubMed.
- J. F. Lockyear, M. A. Parkes and S. D. Price, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 145201 CrossRef.
- The bond-forming reaction we detect, which forms NH+ + H+ + N cannot proceed via a N2H2+ intermediate, as the reaction viaN2H2+ must involve the formation of an H atom. A contribution to reactions (4) and (5) from decay of an N2H2+ intermediate is excluded by the strong forward scattering exhibited by these channels clearly showing that these reactions proceed by simple dissociative electron transfer.
- J. H. Agee, J. B. Wilcox, L. E. Abbey and T. F. Moran, Chem. Phys., 1981, 61, 171–179 CrossRef CAS.
- This reaction cross section is likely to be a lower limit because the assumed linear decrease in the cross section for forming N2+ with collision energy probably results in an underestimate of the cross section for N2+ formation at our collision energies.
- S. H. Lin and H. Eyring, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 402 CrossRef CAS.
- R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics and Chemical Reactivity, Oxford Univeristy Press, Oxford, 1987 Search PubMed.
- The incident dications, which are produced by electron ionization cannot be considered to be equilibrated to a thermal temperature. Thus, as is usually the case with ion beam work, the rate coefficients derived should be considered as simply indicative for thermalised reactant ions.
- W. P. Hu, S. M. Harper and S. D. Price, Mol. Phys., 2005, 103, 1809–1819 CAS.
- S. M. Harper, W.-P. Hu and S. D. Price, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 4409–4423 CrossRef CAS; L. Mrazek, J. Zabka, Z. Dolejsek, J. Hrusak and Z. Herman, J. Phys. Chem. A, 2000, 104, 7294–7303 CrossRef CAS; Z. Herman, J. Zabka, Z. Dolejsek and M. Farnik, Int. J. Mass Spectrom., 1999, 192, 191–203 Search PubMed.
- S. M. Harper, S. W. P. Hu and S. D. Price, J. Chem. Phys., 2004, 120, 7245–7248 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98 (Revision A.9), Gaussian, Inc., Pittsburgh, PA, 1998 Search PubMed.
- H. R. Koslowski, H. Lebius, V. Staemmler, R. Fink, K. Wiesemann and B. A. Huber, J. Phys. B: At., Mol. Opt. Phys., 1991, 24, 5023–5034 CrossRef CAS; E. Y. Kamber, K. Akgungor, C. P. Safvan and D. Mathur, Chem. Phys. Lett., 1996, 258, 336–341 CrossRef CAS.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg MD, 20899 (http://webbook.nist.gov), 2003 Search PubMed.
- P. R. Taylor and H. Partridge, J. Phys. Chem., 1987, 91, 6148–6151 CrossRef CAS; B. J. Olsson, G. Kindvall and M. Larsson, J. Chem. Phys., 1988, 88, 7501–7507 CrossRef CAS; D. Cossart, F. Launay, J. M. Robbe and G. Gandara, J. Mol. Spectrosc., 1985, 113, 142–158 CrossRef CAS.
- R. W. Wetmore and R. K. Boyd, J. Phys. Chem., 1986, 90, 5540–5551 CrossRef CAS.
- W. C. Martin, J. R. Fuhr, D. E. Kelleher, A. Musgrove, L. Podobedova, J. Reader, E. B. Saloman, C. J. Sansonetti, W. L. Wiese, P. J. Mohr and K. Olsen, NIST Atomic Spectra Database 2.0 (http://physics.nist.gov/asd), National Institute of Standards and Technology, Gaithersburg, MD., 2002 Search PubMed.
- J. H. D. Eland, Chem. Phys., 2003, 294, 171–186 CrossRef CAS.
- We have also located a low lying H-NN–H2+ minimum (E = −13.6 eV, r(HN) = 1.104 Å, r(NN) = 1.073 Å) on the singlet PES, of D∞h symmetry. This minimum does not appear to readily connect to the observed products.
- M. Lundqvist, D. Edvardsson, P. Baltzer and B. Wannberg, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, 1489–1499 CrossRef CAS.
- We also find a 3[H–NN–H]2+ minimum, of C2h geometry [r(H–N) = 1.108 Å, r(N–N) = 1.280 Å, ∠(HNN) = 125.7°, E = −7.1 eV]. This minimum does not appear to lie on a pathway to the observed products.
Footnote |
| † Current Address: Space Science Division, NASA Ames Research Center, Moffett Field, CA 94035, USA |
| This journal is © The Royal Society of Chemistry 2011 |
