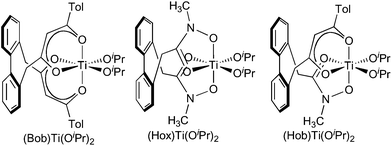
Gauging electronic dissymmetry in bis-chelates of titanium(IV) using sterically and electronically variable 2,2′-biphenoxides†
Natcharee
Kongprakaiwoot
,
Mauricio
Quiroz-Guzman
,
Allen G.
Oliver
and
Seth N.
Brown
*
Department of Chemistry and Biochemistry, 251 Nieuwland Science Hall, University of Notre Dame, Notre Dame, IN 46556-5670, USA. E-mail: Seth.N.Brown.114@nd.edu; Fax: +01 574 631 6652; Tel: +01 574 631 4659
First published on 27th October 2010
Abstract
3,3′,5,5′-Tetrasubstituted-2,2′-biphenolate complexes of titanium(IV) with bis(diketonate) (Bob), bis(hydroxamate) (Hox) and mixed diketonate–hydroxamate (Hob) ligands have been prepared from the corresponding diisopropoxide complexes. Four of the twelve compounds have been characterized crystallographically, and in the solid state all show the (Δ,R)/(Λ,S) relative stereochemistry at titanium and the biaryloxide, respectively, as previously observed in (acac)2Ti(1,1′-bi-2-naphtholate) complexes. In solution the compounds epimerize by atropisomerization of the biphenolate moiety with ΔG‡ ≈ 14 kcal mol−1. The bis(diketonate) complexes show high diastereoselectivity except for the most electron-poor tetranitrobiphenolate. In contrast, the bis(hydroxamate) shows low to moderate selectivity which correlates with the steric but not electronic properties of the biphenolates (Br < CH3 < NO2 < tBu). The mixed diketonate–hydroxamate complexes show intermediate behaviour. These observations are rationalized on the basis of MO arguments regarding ligand-metal π bonding. Symmetrical chelates such as diketonates foster mixing of two dπ orbitals and create a dissymmetric electronic environment. This mixing does not take place with unsymmetrical ligands such as hydroxamates, which therefore do not create an environment where electronic effects contribute significantly to binding stereoselectivity.
Introduction
A molecule’s chirality derives from its dissymmetric three-dimensional structure. In trying to understand how chirality is transferred from one molecule to another, as in asymmetric catalysis, chemists have generally relied on models involving the direct interaction of the shapes of catalyst and substrate—steric repulsions or attractive van der Waals or hydrogen bonding interactions. This general model has been refined extensively over the years, but fundamentally dates back to the ‘lock and key’ model of enzyme action proposed by Fischer.1The three-dimensional shape of molecules also affects their electronic structure. However, while electronic effects obviously affect the geometry of binding between reagent and substrate,2 and while they can modulate the degree of stereoselectivity based on their modulation of reactivity and hence transition state geometry,3 electronic effects have seldom been invoked as determinants in and of themselves of the sense of enantioselectivity. At least part of this scarcity is due to the omnipresence of steric effects masking possible electronic influences. A handful of cases have been developed where isosteric but electronically disparate groups—nitrosylvs.carbonyl,4 or nitrogenvs. phosphorus5—have been used as the sources of chirality in metal-based reagents or catalysts (Fig. 1). In these examples, the observed stereoselectivities must attest to the electronic desymmetrization of the allyl group by the unsymmetrical metal center.
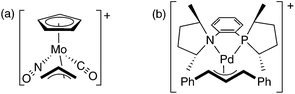 | ||
| Fig. 1 Complexes that are sterically mirror-symmetric but are rendered chiral by virtue of electronically unsymmetrical groups. (a) ref. 4. (b) ref. 5. | ||
The enantiomers of 1,1′-bi-2-naphtholate (BINOL2−) bind differentially to the chiral cis-(dike)2TiIV fragment (dike = β-diketonate), with very high diastereoselectivities (> 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in some cases).6 Here the basis for enantiodiscrimination was also attributed (principally) to electronic effects due to dπ-pπ bonding on the basis of the striking differences in selectivity between the quasi-isostructural titanium and tin complexes.
1 in some cases).6 Here the basis for enantiodiscrimination was also attributed (principally) to electronic effects due to dπ-pπ bonding on the basis of the striking differences in selectivity between the quasi-isostructural titanium and tin complexes.
Unlike the previously cited cases, the (dike)2TiIV fragment is C2-symmetric and the two available binding sites are therefore homotopic. The C1-symmetric molecules in Fig. 1 can direct an incoming nucleophile preferentially to one side of the allyl ligand because the electronic properties of the two sides are inequivalent, a distinction that could be termed electronic asymmetry. Any stereodiscrimination exerted by the symmetrical (dike)2TiIV fragment cannot arise by this mechanism. Instead, it must arise from the chirality of the electronic environment of each individual binding site, an effect that can be termed electronic dissymmetry.
This work raises the more general question of what kinds of environments would give rise to effective levels of electronic dissymmetry in metal complexes. For example, are all cis-bis(chelate)titanium(IV) complexes equally useful in this regard, or are there specific features of the ligands that are important? Here, we address this issue by comparing the stereoselectivities of biphenolate binding of bis(diketonate)titanium(IV) complexes with those displayed by analogous bis(hydroxamate) and mixed hydroxamate–diketonate complexes. The behaviour of a series of 3,3′,5,5′-tetrasubstituted biphenolates with substituents of varying electronic and steric character also sheds light on the origins of stereoselectivity in these complexes.
Results and discussion
Origin of electronic dissymmetry in bis(chelate)titanium(IV) complexes
The origin of electronic dissymmetry is most easily analyzed in a C2-symmetric complex such as (acac)2TiCl2 (acac = acetylacetonate). In an octahedral complex such as this one, the σ bonding is nearly C2v-symmetric and so does not contribute appreciably to any dissymmetry. In contrast, the π bonding (between the acac ligands and Ti) is intrinsically chiral by virtue of the propeller-type chirality at the titanium centre. Since this is a d0 complex, the relevant π bonding interactions would appear to be ligand-to-metal π donation. For the diketonate ligand, the only good π donor orbital is the πnb orbital, which has two nodes and thus has in-phase components on the two oxygen atoms (Fig. 2). There are thus two acac-based donor orbitals, an A combination (symmetric with respect to the twofold axis) and a B combination (antisymmetric with respect to the twofold axis). In an octahedral complex, there are three dπ orbitals (the t2g set in true Oh symmetry), which transform as 2A + B in the C2 point group. The key phenomenon occurs in the A manifold, since there are two acceptor orbitals but only one donor orbital. This ligand-based donor orbital can overlap with both dπ orbitals of A symmetry and thus mixes them together. One combination of metal orbitals overlaps strongly with the ligand orbital and forms a bonding and antibonding combination with it; the second combination has essentially no overlap and forms a nonbonding (metal-centred) orbital. This orbital has two critical features: (1) It is the LUMO of the complex (since the other two dπ orbitals have been raised in energy through π interactions with the filled acac π orbitals), so any filled π donor orbitals on a substrate that would displace the chloride ligands should preferentially maximize overlap with this orbital. (2) While either one of the ‘usual’ A-symmetry dπ orbitals is spatially mirror-symmetric with respect to the two mirror planes of the TiCl2 fragment, their linear combination is not. Instead, it has a noticeable inclination with respect to this plane (Fig. 3a). To maximize overlap with the LUMO, then, the substrate would be expected to bind so as to have its π-donor orbitals align as closely as possible with this inclined LUMO. This gives a mechanism for the communication of chirality from titanium to substrate, one based on a purely electronic phenomenon, namely a virtual orbital.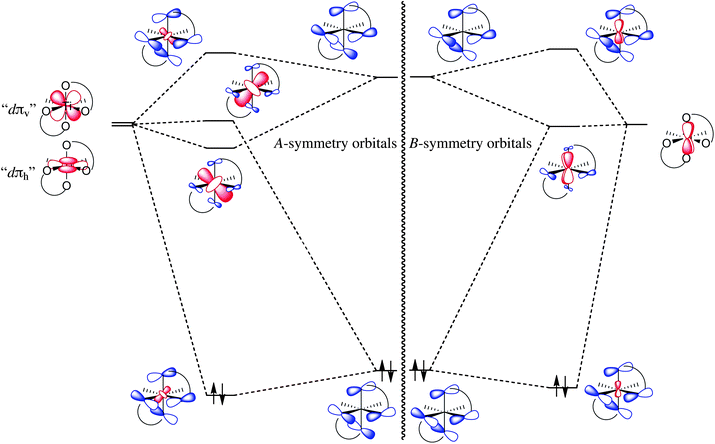 | ||
| Fig. 2 Qualitative molecular orbital diagram of the (acac)2Ti fragment, illustrating the mixing of the titanium dπ orbitals (red) with acac πnb and π* orbitals (blue). | ||
![Kohn–Sham LUMOs of (a) (acac)2TiCl2 (b) (CH3CON[CH3]O)2TiCl2 and (c) (acac)(CH3CON[CH3]O)TiCl2 (B3LYP, 6-31G*).](/image/article/2011/SC/c0sc00468e/c0sc00468e-f3.gif) | ||
| Fig. 3 Kohn–Sham LUMOs of (a) (acac)2TiCl2 (b) (CH3CON[CH3]O)2TiCl2 and (c) (acac)(CH3CON[CH3]O)TiCl2 (B3LYP, 6-31G*). | ||
Density functional theory calculations (B3LYP, 6-31G* basis set, see ESI for details†) bear out this qualitative picture quite well. In particular, they confirm both the shape of the LUMO (Fig. 3a) and its significant energetic separation from the next highest A-symmetry orbital (ΔE = 0.39 eV). An intriguing addendum to the qualitative discussion above that is suggested by the calculation is that because titanium is highly electropositive, the empty acac π* orbitals are actually closer in energy to the titanium dπ orbitals than are the filled acac πnb orbitals. Because the acac π* orbitals have the opposite relative phase on the oxygen atoms compared to the πnb orbitals, their A-symmetry combination interacts strongly with the dπ LUMO, pushing it down in energy, and has almost no overlap with the higher-lying A-symmetry dπ orbital. Thus this interaction acts synergistically with the π-donor interaction to increase the splitting between the two dπ orbitals of A symmetry.
Generation of a LUMO that is of appropriate shape to allow potential enantiodiscrimination requires mixing of the vertical ‘dπv’ orbital with the horizontal ‘dπh’ orbital, since either of these orbitals by itself is spatially mirror-symmetric with respect to the TiX2 plane. This in turn requires that there be similar strength of π donation from the apical sites of the chelate ligand (which can donate only into dπv) and from the equatorial sites (which can only donate into dπh). Clearly this condition is satisfied by the essentially symmetric7diketonate ligand, but might well not be met by an unsymmetrical ligand. Indeed, calculations confirm that the C2-symmetric isomer of the N-methylacetohydroxamate complex (CH3CON[CH3]O)2TiCl2 with equatorial carbonyl groups has a LUMO which looks like an almost unperturbed dπh orbital (Fig. 3b). Since the negative charge is principally on the NOoxygen, it is a much stronger π donor than the carbonyl oxygen, so dπv is raised in energy and does not mix appreciably with the lower-lying dπh orbital. Thus bis(hydroxamate) complexes would be expected to possess little electronic dissymmetry. A mixed diketonate–hydroxamate complex is more difficult to analyze qualitatively because of its lower symmetry, but the calculated LUMO of (acac)(CH3CON[CH3]O)TiCl2 does appear to be interpolated between the two symmetric complexes (Fig. 3c). A π donor orbital on a substrate donor atom cis to the acac would enjoy maximal overlap at a substantial inclination to the equatorial plane (high electronic dissymmetry), while a π donor orbital cis to the hydroxamate would overlap best if it lay in the equatorial plane (low electronic dissymmetry).
 | ||
| Fig. 4 Inclination of A-symmetric π donor orbital of a 2,2′-biaryloxide. | ||
Inversion of configuration at titanium, which occurs rapidly in bis(diketonate)titanium(IV) complexes by a trigonal twist mechanism,8 interconverts the diastereomers and allows measurement of the equilibrium dr by NMR (at low temperature). This strategy is not well-suited to analysis of bis(hydroxamate) complexes, however, because of the possibility of forming geometric isomers with this unsymmetrical ligand. Analysis of a mixed hydroxamate–diketonate complex would be further complicated by its possible disproportionation into bis(diketonate) and bis(hydroxamate) species.
These complications of geometry and stoichiometry can be bypassed through the use of 2,2′-bis(methylene)biphenyl bridged bis(diketonate) (‘Bob’),9bis(hydroxamate) (‘Hox’) and hydroxamate–diketonate (‘Hob’)10 ligands. These have been shown to bind tightly to titanium(IV) to form monomeric complexes with complete control of geometry (the carbonyl groups α to the methylene groups are equatorial and only the (S,Δ)/(R,Λ) diastereomer is observed). In contrast to unlinked bis(chelate) complexes, (Bob)Ti complexes have very high barriers to racemization,11 so equilibration of the diastereomeric complexes with optically stable BINOL would require ligand exchange reactions, which are relatively slow and can give rise to side products such as monodentate BINOLH complexes.12
We therefore prepared complexes of 2,2′-biphenolate ligands, which are known to undergo facile inversion of configuration,13 in order to assess the diastereoselectivity of binding (eqn (1)). A variety of 3,3′,5,5′-tetrasubstituted biphenolate complexes may be synthesized by protonolysis of the titanium diisopropoxides by the 2,2′-biphenols R4C12H4(OH)2 (R = CH3, Br,14NO215 and tBu16). (The unsubstituted 2,2′-biphenolate complexes of (Bob)Ti and (Hox)Ti were also prepared, but proved too insoluble for NMR characterization and were not examined in detail.) The reactions take place readily at room temperature, except for those of the tetra-tert-butylbiphenol, which require heating overnight at 108 °C (see ESI for synthetic details and spectroscopic characterization†).
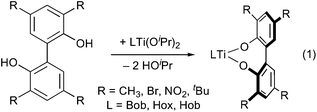 | (1) |
All three titanium complexes of tetramethylbiphenolate, as well as (Hox)Ti(O2C12H4[NO2]4), were characterized in the solid state by X-ray crystallography (Fig. 5). The three tetramethylbiphenolate complexes are strikingly similar to each other and to previously characterized bis(diketonate)titanium(IV) binaphtholate6,11 and biphenolate complexes,17 both in their metrical data (Table 1) and in the exclusive presence of the (Λ,S)/(Δ,R) diastereomer in the crystal. (This is the diastereomer expected to exhibit maximum alignment of the biaryloxide π donor orbitals with the LUMO of the (acac)2Ti fragment, see Fig. 3 and 4.6) As expected due to the lower basicity of the tetranitrobiphenoxide, its complex has on average 0.069 Å longer Ti-aryloxide distances, and 0.051 Å shorter equatorial chelate distances, than in (Hob)Ti(O2C12H4[CH3]4). The tetranitrobiphenoxide complex also shows a substantial twisting and tilting of the biaryloxide away from pseudo-C2 symmetry, as witnessed by differences in the Ti–O–C angles (131.19(17)° and 120.19(16)° at O5 and O6, respectively) and O–Ti–O–C dihedral angles (25.8° and 65.4°, respectively). (In contrast, the corresponding angles differ by less than 1°, and the dihedrals by less than 4°, in (Hob)Ti(O2C12H4[CH3]4).)
| (Bob)Ti (O2C12H4Me4) | (Hox)Ti (O2C12H4Me4) | (Hob)Ti (O2C12H4Me4) | (Hob)Ti (O2C12H4[NO2]4) | |
|---|---|---|---|---|
| Ti-O1 | 2.040(3) | 2.0701(11) | 2.0398(13) | 1.9960(19) |
| Ti-O2 | 1.966(3) | 1.9580(11) | 1.9500(13) | 1.9264(19) |
| Ti-O3 | 2.022(3) | 2.0565(11) | 2.0730(13) | 1.9929(19) |
| Ti-O4 | 1.970(3) | 1.9551(11) | 1.9382(13) | 1.9524(19) |
| Ti-O5 | 1.840(3) | 1.8575(11) | 1.8469(13) | 1.9224(19) |
| Ti-O6 | 1.854(3) | 1.8582(11) | 1.8470(13) | 1.9264(19) |
| O1-Ti-O2 | 83.01(12) | 75.94(4) | 81.96(5) | 83.66(8) |
| O3-Ti-O4 | 82.99(12) | 75.97(5) | 75.88(5) | 76.18(8) |
| O5-Ti-O6 | 92.28(12) | 91.00(5) | 90.23(6) | 88.14(8) |
| Ti-O5-C52 | 129.6(3) | 124.40(9) | 128.42(11) | 131.19(17) |
| Ti-O6-C62 | 124.1(3) | 127.56(9) | 128.10(11) | 120.19(16) |
![Thermal ellipsoid plots of (a) (Bob)Ti(O2C12H4[CH3]4), (b) (Hox)Ti(O2C12H4[CH3]4), (c) (Hob)Ti(O2C12H4[CH3]4) and (d) (Hob)Ti(O2C12H4[NO2]4). Hydrogen atoms and solvents of crystallization are omitted for clarity.](/image/article/2011/SC/c0sc00468e/c0sc00468e-f5.gif) | ||
| Fig. 5 Thermal ellipsoid plots of (a) (Bob)Ti(O2C12H4[CH3]4), (b) (Hox)Ti(O2C12H4[CH3]4), (c) (Hob)Ti(O2C12H4[CH3]4) and (d) (Hob)Ti(O2C12H4[NO2]4). Hydrogen atoms and solvents of crystallization are omitted for clarity. | ||
Diastereoselectivity of binding in bis(chelate)titanium(2,2′-biphenoxide) complexes
At room temperature, the 1H and 13C NMR spectra of the (Bob)Ti(biphenoxide) and (Hox)Ti(biphenoxide) complexes show the number of resonances expected for a single C2-symmetric species, and those of (Hob)Ti(biphenoxide) show the number of resonances expected for a single C1-symmetric species. However, as the temperature is lowered, seven of the twelve complexes show reversible temperature-dependent changes in their 1H NMR spectra, with the room-temperature resonances decoalescing into signals for two distinct complexes (e.g., Fig. 6). While the dynamics of exchange have not been analyzed in detail, all of the compounds show the onset of linebroadening between −30 and −20 °C, corresponding to ΔG‡ ≈ 14 kcal mol−1.18 The invariance of the barrier is consistent with its being due to inversion of configuration of the biaryloxide, and hence the two species observed at low temperature are the diastereomers of LTi(biphenoxide). The similarity of the barrier to that observed for atropisomerization in Me2Ge(O2C12H4tOct4) (ΔG‡ = 13.8 kcal mol−1)19 also supports this analysis. Note that ring formation lowers the barrier to atropisomerization (e.g., by 3.4 kcal mol−1 in the germacycle relative to the free biphenol19), presumably because the ring decreases the steric clash between the 6,6′-hydrogens in the planar transition state. The effect of the germanium and titanium centers should be quite similar, since the slightly shorter Ge–O distances (1.770(2) Å in Me2Ge(O2C12H4tBu4)20) will be balanced by a slightly larger O–Ge–O angle (106.85(13)°).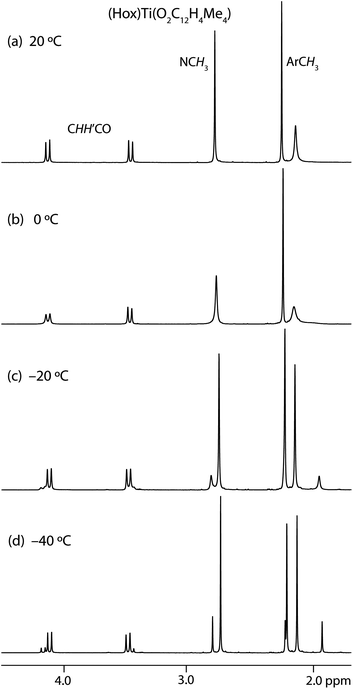 | ||
| Fig. 6 1H NMR spectra of (Hox)Ti(O2C12H4Me4) (500 MHz, CD2Cl2, aliphatic region) at (a) 20 °C, (b) 0 °C, (c) −20 °C and (d) −40 °C. | ||
At −30 °C in CD2Cl2, exchange between diastereomers is slow enough for them to show well-separated resonances, so the equilibrium constant for their interconversion can be measured (Table 2). The five compounds that show no definitive signals for minor diastereomers are presumed to have much higher diastereoselectivities. The two possible alternative explanations for the lack of decoalescence seem improbable: the consistency of interconversion rates as a function of biphenoxide substituents and ancillary ligands strongly suggests that these diastereomers do not interconvert unusually quickly (and spectra are unchanged down to −70 °C), and the good dispersion of chemical shifts observed between diastereomers in the seven other compounds makes it unlikely that the diastereomers have all resonances accidentally degenerate in these cases.
| Complex | R = Br | R = CH3 | R = NO2 | R = tBu |
|---|---|---|---|---|
| a Several signals of 4% of the intensity of the major species appeared at or below −30 °C and may be due to a minor diastereomer, but the signals were too weak to permit a definitive assignment. b Reported values represent minimum dr′s based on the signal-to-noise limits of the 1H NMR spectra. | ||||
| (Hox)Ti(O2C12H4R4) | 1.0 | 3.9 | 6.3 | 7.9 |
| (Bob)Ti(O2C12H4R4) | ≥ 24a | >90b | 11.3 | >90b |
| (Hob)Ti(O2C12H4R4) | 8.3 | >50b | 11.6 | >50b |
The four biphenolate substituents vary in both electronic and steric profile. The electronic trends are unambiguous, with electron donation increasing in the order NO2 ≪ Br ≪ CH3 ≈ tBu (for example, the Hammett σp constants are +0.78, +0.23, −0.17 and −0.20, respectively21). Apart from the obvious conclusion that tert-butyl is the largest of the four substituents, steric effects are more sensitive to context and thus harder to rank; different schemes for ranking steric effects can be found to place any of the other three as the smallest group.22 However, the most relevant gauge is probably the Taft ES scale, since it is based on sterics of the ortho substituent in hydrolysis of benzoate esters; by this measure, size increases in the order Br ≈ CH3 < NO2 (ES = +0.01, 0.00 and −0.71, respectively).23
It is clear that the selectivities exhibited by the bis(hydroxamate) complexes (Hox)Ti(biphenoxide), while modest in all cases, correlate well with the steric demand of the biphenoxide substituents R and not at all with their electronic character. In particular, the tert-butyl derivative is the most selective, and the methyl derivative is intermediate in selectivity between the bromo and nitro compounds. The lack of correlation with electronics supports the orbital analysis of these compounds discussed earlier, since with a nearly horizontal LUMO the biaryloxide–titanium π bonding would be expected to be nearly equivalent in both diastereomers. The modest size of the steric effect is consistent with the very small steric profile of the hydroxamate ligands.
In contrast, the bis(diketonate) complexes (Bob)Ti(biphenoxide) show very high selectivity except for the most electron-poor derivative with R = NO2. In particular, both small and large electron-donating substituents show high diastereoselectivity. This agrees with a model where electronic effects are sufficient to impart high stereoselectivity, but where in the absence of strong π donation from the aryloxide, the intrinsic (presumably largely sterically-induced) selectivity is modest. These results are completely consistent with the high stereoselectivities previously observed with sterically undemanding (ortho-unsubstituted) binaphthoxides of unlinked6 or linked11bis(β-diketonate)titanium complexes. The recently published NMR spectra of the bis(diketonate) complexes of unsubstituted 2,2′-biphenoxide (PhCOCHCOCX3)2Ti(O2C12H8) (X = H, F) at −60 °C, where both the titanium centre and the biaryloxide should be nonfluxional, show only the expected resonances from geometrical isomers due to the unsymmetrical diketonates, with no sign of diastereomers, consistent with high diastereoselectivity in this case as well.17b
The mixed-ligand complexes (Hob)Ti(biphenoxide) show behaviour intermediate between those of the bis-hydroxamate and bis-diketonate complexes. When π donation is strong, selectivity is high regardless of the size of the substituent, but for R = Br, the weaker π donation is not enough to give high selectivity, though the selectivity is noticeably greater than would be expected based on steric effects alone for such a small substituent (compare the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 selectivity observed in the bis(hydroxamate) complex). This is consistent with an electronic effect being present, but not as strong as in the bis(diketonate), as predicted by the orbital analysis. Note that the similarity of the diastereoselectivity in the tetranitrobiphenoxides across the entire series, where π donation is minimal, indicates that the steric profile of the diketonate is not much different from the hydroxamate. The modest selectivities with this ligand suggest that these tied-back bidentate chelates are, as expected, rather small and impinge only weakly on the biphenoxides.
1 selectivity observed in the bis(hydroxamate) complex). This is consistent with an electronic effect being present, but not as strong as in the bis(diketonate), as predicted by the orbital analysis. Note that the similarity of the diastereoselectivity in the tetranitrobiphenoxides across the entire series, where π donation is minimal, indicates that the steric profile of the diketonate is not much different from the hydroxamate. The modest selectivities with this ligand suggest that these tied-back bidentate chelates are, as expected, rather small and impinge only weakly on the biphenoxides.
Conclusions
The diastereoselectivities of binding of 3,3′,5,5′-tetrasubstituted biphenoxide complexes of linked bis(chelate) complexes of titanium have been measured. The bis(hydroxamate) shows low diastereoselectivity which is based on sterics, not electronics, while the bis(β-diketonate) shows high selectivity as long as the donating ability of the aryloxides is appreciable. The mixed hydroxamate–diketonate complex shows intermediate selectivity. These observations confirm the electronic origin of selectivity previously observed in similar bis(diketonato)titanium(IV) complexes, indicating that this fragment presents an electronically dissymmetric environment to bound substrates. Molecular orbital analyses indicate that a critical feature in establishing the electronic dissymmetry is that the β-diketonate chelates are symmetric in terms of their donor properties, which causes the two dπ orbitals of A symmetry to mix and form a LUMO that is tilted with respect to the plane formed by the titanium atom and the two ligating atoms from the biphenolate. Thus, in contrast to diketonates, the electronically unsymmetrical hydroxamates are not able to create a disymmetric electronic environment at titanium.Acknowledgements
This work was supported by the U.S. National Science Foundation (CHE-0518243). The sample of (Bob)Ti(O2C12H4[CH3]4)·0.5 C6H14 was submitted for synchrotron crystallographic analysis through the SCrALS (Service Crystallography at Advanced Light Source) program. Crystallographic data were collected at Beamline 11.3.1 at the Advanced Light Source (ALS), Lawrence Berkeley National Laboratory. The ALS is supported by the U.S. Dept. of Energy, Office of Energy Sciences, under contract DE-AC02-05CH11231.Notes and references
- (a) E. Fischer, Ber. Dtsch. Chem. Ges., 1894, 27, 2985–2993 CrossRef CAS; (b) F. W. Lichtenthaler, Angew. Chem., Int. Ed. Engl., 1994, 33, 2364–2374 CrossRef.
- J. A. Gladysz and B. J. Boone, Angew. Chem. Int. Ed., 1997, 36, 551–583 CrossRef.
- J. W. Faller, B. J. Grimmond and D. G. D'Alliessi, J. Am. Chem. Soc., 2001, 123, 2525–2529 CrossRef CAS and references therein.
- (a) R. D. Adams, D. F. Chodosh, J. W. Faller and A. M. Rosan, J. Am. Chem. Soc., 1979, 101, 2570–2578 CrossRef CAS; (b) J. W. Faller and D. L. Linebarrier, J. Am. Chem. Soc., 1989, 111, 1937–1939 CrossRef CAS.
- (a) R. Stranne, J.-L. Vasse and C. Moberg, Org. Lett., 2001, 3, 2525–2528 CrossRef CAS; (b) J.-L. Vasse, R. Stranne, R. Zalubovskis, C. Gayet and C. Moberg, J. Org. Chem., 2003, 68, 3258–3270 CrossRef CAS.
- S. N. Brown, E. T. Chu, M. W. Hull and B. C. Noll, J. Am. Chem. Soc., 2005, 127, 16010–16011 CrossRef CAS.
- While free acac is symmetrical, bound acac is not perfectly so, since the differential trans influences of acac and the equatorial ligand cause the Ti–Oax distances to be slightly different from the Ti–Oeq distances.
- (a) D. C. Bradley and C. E. Holloway, J. Chem. Soc. A, 1969, 282–285 RSC; (b) N. Baggett, D. S. P. Poolton and W. B. Jennings, J. Chem. Soc., Dalton Trans., 1979, 1128–1134 RSC; (c) R. C. Fay and A. Lindmark, J. Am. Chem. Soc., 1983, 105, 2118–2127 CrossRef CAS.
- V. Ugrinova, B. C. Noll and S. N. Brown, Inorg. Chem., 2006, 45, 10309–10320 CrossRef CAS.
- N. Kongprakaiwoot, B. C. Noll and S. N. Brown, Inorg. Chem., 2008, 47, 11902–11909 CrossRef CAS.
- N. Kongprakaiwoot, J. B. Armstrong, B. C. Noll and S. N. Brown, Dalton Trans., 2010, 39, 10105–10115 RSC.
- L. T. Dulatas, S. N. Brown, E. Ojomo, B. C. Noll, M. J. Cavo, P. B. Holt and M. Wopperer, Inorg. Chem., 2009, 48, 10789–10799 CrossRef CAS.
- A. van der Linden, C. J. Schaverien, N. Meijboom, C. Ganter and A. G. Orpen, J. Am. Chem. Soc., 1995, 117, 3008–3021 CrossRef CAS.
- O. Diels and A. Bibergeil, Ber. Dtsch. Chem. Ges., 1902, 35, 302–313 CrossRef CAS.
- J. van Alphen, Recueil des Travaux Chimiques des Pays-Bas, 1932, 51, 179–184 Search PubMed.
- T. Yamato, K. Hasegawa, Y. Saruwatari and L. K. Doamekpor, Chem. Ber., 1993, 126, 1435–1439 CrossRef CAS.
- (a) T. A. Tsotetsi, A. Kuhn, A. Muller and J. Conradie, Polyhedron, 2009, 28, 209–214 CrossRef CAS; (b) A. Kuhn, T. A. Tsotetsi, A. Muller and J. Conradie, Inorg. Chim. Acta, 2009, 362, 3088–3096 CrossRef CAS.
- J. W. Faller, in Encyclopedia of Inorganic Chemistry, ed. R. B. King, John Wiley and Sons, New York, 1994, pp. 3914–3933 Search PubMed.
- S. D. Pastor, A. Carinci, N. Khoury and D. N. Rahni, Inorg. Chem., 2001, 40, 3830–3832 CrossRef CAS.
- S. D. Pastor, D. N. Rahni, N. Khoury and S. A. Koch, Phosphorus, Sulfur Silicon Relat. Elem., 2006, 181, 1951–1956 Search PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- H. Förster and F. Vögtle, Angew. Chem., Int. Ed. Engl., 1977, 16, 429–441 CrossRef.
- R. W. Taft, J. Am. Chem. Soc., 1952, 74, 3120–3128 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Preparative and spectroscopic details for all compounds, details of X-ray crystallography and DFT calculations. CCDC reference numbers 791673–791676. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c0sc00468e |
| This journal is © The Royal Society of Chemistry 2011 |