DOI:
10.1039/C0SC00392A
(Edge Article)
Chem. Sci., 2011,
2, 326-330
O2insertion into a palladium(II)-hydride bond: Observation of mechanistic crossover between HX-reductive-elimination and hydrogen-atom-abstraction pathways†
Received
24th July 2010
, Accepted 17th September 2010
First published on 13th October 2010
Abstract
The reaction of molecular oxygen with palladium(II)–hydrides is a key step in Pd-catalyzed aerobic oxidation reactions, and the mechanism of such reactions has been the focus of considerable investigation and debate. Here we describe the reaction of O2 with a series of electronically varied PdII–H complexes of the type trans-(IMes)2Pd(H)(O2CAr), with different para-substituted benzoates as the ArCO2− ligand. Analysis of the oxygenation rates of these complexes revealed a non-linear Hammett plot, and further kinetic studies demonstrated that reaction of O2 with the most electron-rich para-methoxybenzoate derivative proceeds via two parallel mechanisms, one initiated by rate-limiting reductive elimination of the carboxylic acid (HXRE) and the other involving hydrogen-atom abstraction by O2 (HAA). DFT computational studies support these conclusions and reveal that the preferred mechanism for the O2insertion reaction changes from HAA to HXRE as the para substituent on the benzoate ligand shifts from electron-donating to electron-withdrawing.
Introduction
The scope of Pd-catalyzed aerobic oxidation reactions has expanded significantly over the past decade1 and these developments have been complemented by a number of mechanistic studies of the reaction of O2 with reduced Pd complexes.2,3 Efficient reoxidation of the Pd catalysts by O2 is essential to avoid irreversible Pd0 decomposition into metallic Pd (Scheme 1).
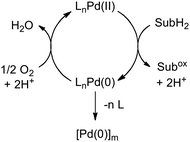 |
| | Scheme 1 Simplified catalytic cycle for Pd-catalyzed aerobic oxidation reactions (SubH2 = reduced organic substrate). | |
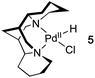
Many Pd-catalyzed aerobic oxidation reactions proceed viaPdII–hydride intermediates, and several research groups have proposed that such species react directly with O2 in catalytic reactions to form a PdII–hydroperoxide (eqn (1)).4,5 The first well-defined examples of O2insertion reactions with PdII–hydrides were reported only recently for two different complexes: a bis-N-heterocyclic-carbene-ligated Pd complex (1a, eqn (2))2d,e,g and a PCP-pincer-ligated Pd complex (3, eqn (3)).3b,c Experimental and computational studies demonstrated that these reactions proceed via two different mechanisms. Oxygenation of 1a proceeds via an HX-reductive-elimination (HXRE) pathway (Scheme 2A),2d,g in which reductive elimination of the carboxylic acid is the rate-determining step. In contrast, oxygenation of 3 proceeds via a hydrogen-atom-abstraction (HAA) mechanism, in which abstraction of the hydrogen atom by O2 is rate-determining (Scheme 2B).3b,c These mechanisms lead to very different experimental observations: oxygenation of 1a exhibits a zero-order dependence on [O2] and a very small isotope effect [kPd–H/kPd-D = 1.3(1)], whereas the reaction of 3 with O2 exhibits a first-order dependence on [O2] and a large primary kinetic isotope effect [kPd–H/kPd-D = 5.8(5)]. Another PdII–hydride complex, [(–)-sparteine]Pd(H)Cl (5), has been proposed to undergo oxygenation via the HAA pathway on the basis of DFT computational studies.3a,d To date, this complex has not been synthesized or investigated experimentally.
| | | L2(X)PdII–H + O2 → L2(X)PdII–OOH | (1) |
| | 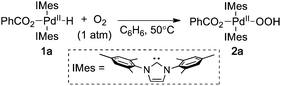 | (2) |
| | 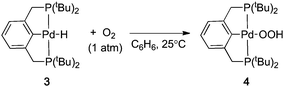 | (3) |
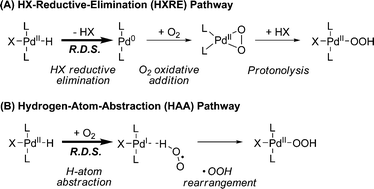 |
| | Scheme 2 Two mechanistic pathways that have been established experimentally for O2insertion into a PdII–hydride bond. | |
These previous results demonstrate that O2insertion into a PdII–H bond can occur by different mechanisms, and the preferred pathway will depend upon the identity of the Pd complex. In the present study, we show that bothHXRE and HAA pathways proceed in parallel for a single PdII–hydride complex. Close agreement is observed between experimental and computational results, both of which demonstrate that crossover between the two mechanisms occurs for a narrow series of related PdII–hydride complexes.
Results and discussion
Hammett analysis of the reaction of O2 with trans-(IMes)2Pd(H)(O2CAr) complexes
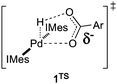
The reaction of PdII–hydride complexes trans-(IMes)2Pd(H)(O2CAr) with O2 was shown previously to proceed nearly eight-fold more rapidly with the para-nitrobenzoate derivative 1b than with 1a.2g Computational studies suggested that this rate difference could be explained by the build-up of anionic charge on the carboxylate ligand in the rate-limiting O–H reductive elimination step via transition state 1TSTS.2e A subsequent, more-thorough analysis of the electronic effects on the formal O2insertion reaction in eqn (2) led to some unexpected results, and these are the focus of the present study.
A systematic series of trans-(IMes)2Pd(H)(O2CAr) complexes were prepared with different substituents in the para position of the benzoate ligand: the previously reported –H (1a) and -NO2 (1b) derivatives, and the new -Cl (1c), -Me (1d) and -OMe (1e) derivatives. Spectroscopic characterization of these complexes suggests that these complexes exhibit systematic differences that vary as a function of the para substituent. For example, 1H NMR spectra of these complexes reveal a monotonic correlation between the Pd–H chemical shift (δ) and the Hammett σp parameter for the substituents (Fig. 1).
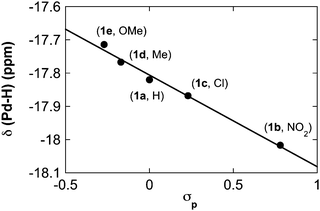 |
| | Fig. 1 Dependence of δ(Pd–H) (C6D6, 25 °C) on σp for different (IMes)2Pd (H)(O2CC6H4-pX) complexes. | |
Each of these complexes reacts with O2 (1 atm) in C6D6 solution at 51 °C to afford the corresponding PdII–hydroperoxide complexes 2a–e (eqn (4)). The rates of the oxygenation reactions were determined for each of the derivatives 1a–e,6 and the data were used to construct a Hammett plot. As shown in Fig. 2, the log(kX/kH) values for four of the complexes, 1a–d, exhibit a positive, approximately linear correlation with the σp Hammett parameter (ρ = 0.91), indicating that the rate increases with more-electron-deficient benzoate ligands. In contrast, the para-methoxy-substituted derivative 1e reacts with O2 much faster than expected and does not fit the Hammett correlation. This anomalous kinetic result contrasts the systematic behavior exhibited by the ground-state PdII–hydride complexes (e.g., Fig. 1), and it could arise from a change in the rate-determining step of the HXRE mechanism or the onset of a different O2-insertion mechanism. The former possibility can be excluded by noting that RCO2H reductive elimination (the RDS of the HXRE mechanism) is expected to be slowest with the p-MeO derivative (cf.1TSTS),2g and the second step of the HXRE mechanism, O2 oxidative addition of (IMes)2Pd0 should be unaffected by the identity of the carboxylate or carboxylic acid. Moreover, independent studies of the reaction between (IMes)2Pd0 and O2 have shown that oxidative addition of O2 to the Pd0 center proceeds very rapidly, even at −78 °C.2c These considerations suggested that the discontinuity in the Hammett plot reflects the onset of a different O2insertion mechanism.
| | 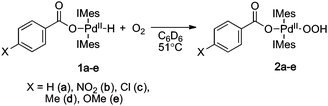 | (4) |
![Hammett correlation for the rate of oxygenation of (IMes)2Pd(H)(O2CC6H4X), 1a–e. Reaction conditions: [1a–e]0 = 0.5 mM, 1 atm O2, 51 °C, 0.4 mL C6D6.](/image/article/2011/SC/c0sc00392a/c0sc00392a-f2.gif) |
| | Fig. 2 Hammett correlation for the rate of oxygenation of (IMes)2Pd(H)(O2CC6H4X), 1a–e. Reaction conditions: [1a–e]0 = 0.5 mM, 1 atm O2, 51 °C, 0.4 mL C6D6. | |
Kinetic studies of the oxygenation of 1e
The HXRE mechanism established for the oxygenation of 1a (Scheme 2A) exhibits two diagnostic kinetic features: (1) a zero-order dependence on the O2 pressure and (2) a small deuterium kinetic isotope effect. In this context, the rate of oxygenation of the p-methoxybenzoate derivative 1e was measured in the presence of different O2 pressures, from 0.45–4.1 atm.7 The data exhibit a linear first-order dependence of the rate on O2 pressure, but they also exhibit a non-zero y-intercept (filled circles, Fig. 3). These results implicate a two-term rate law for the oxygenation of 1e, one term zero-order in [O2] and the other first-order in [O2] (eqn (5)).| | | Rate = k1[1e] + k2[1e][O2] | (5) |
![Effect of O2 pressure on the observed rate constant for the oxygenation of 1e (●) and 1e-dd (♦). Reaction conditions: [1e]0 = 1 mM, [1e-dd]0 = 0.5 mM, pO2 = 0.28–4.1 atm, [NBu4O2CC6H4OMe] = 10 mM, 0.4 mL C6D6, 75 °C.](/image/article/2011/SC/c0sc00392a/c0sc00392a-f3.gif) |
| | Fig. 3 Effect of O2 pressure on the observed rate constant for the oxygenation of 1e (●) and 1e-dd (♦). Reaction conditions: [1e]0 = 1 mM, [1e-dd]0 = 0.5 mM, pO2 = 0.28–4.1 atm, [NBu4O2CC6H4OMe] = 10 mM, 0.4 mL C6D6, 75 °C. | |
Subsequently, we prepared the PdII–deuteride complex, 1e-dd and examined its reaction under conditions similar to those used in the oxygenation of 1e. The data (filled diamonds, Fig. 3) resemble those obtained with 1e, with a less pronounced first-order dependence on the O2 pressure. A linear least-squares fit of the data enables rate constants k1 and k2 to be obtained for the oxygenation of 1e and 1e-dd, and these values were used to determine the deuterium kinetic isotope effects (KIEs). The KIE for k1 is 1.1(1), and the KIE for k2 is 3.1(2).
The two-term rate law, together with the different isotope effects for the k1 and k2 steps, suggest that the oxygenation of 1e proceeds via two parallel pathways. The zero-order [O2]-dependence and negligible isotope effect for the k1 term in the rate law are consistent with the HXRE oxygenation mechanism (Scheme 2A), and the first-order [O2]-dependence and sizable primary KIE for the k2 term are consistent with the HAA pathway (Scheme 2B).8 In order to probe this hypothesis further, electronic effects on the oxygenation of trans-(IMes)2Pd(H)(O2CAr) complexes were examined by DFT computational methods.
Computational analysis of electronic effects on the oxygenation of trans-(IMes)2Pd(H)(O2CAr)
Our computational studies to probe the electronic effects on O2insertion employed the model complexes (IMe)2Pd(H)(O2CC6H4X) (6), which differ from the experimental complexes by the presence of methyl, rather than mesityl, groups on the NHC ligand (IMe).9 This study builds upon our previous DFT analysis of O2insertion into the PdII–H bond of the closely related complex, (IMe)2Pd(H)(OAc) (7). This previous study revealed that the HXRE and HAA pathways are energetically favored, relative to other mechanisms for this reaction,10 and it suggested that the barrier for the HAA pathway is lower in energy than the HXRE pathway by 4.5 kcal mol−1. The latter conclusion was contradicted by our subsequent experimental study of 1a, which provided clear evidence for an HXRE mechanism (see discussion above). This experimental-computational discrepancy was attributed to the uncertainties in the computational methods, such as potential errors in the calculated entropic effects and possible problems with solvation models, particularly when used for two chemically different mechanisms. The results presented here resolve this apparent discrepancy and demonstrate remarkable agreement between the computational and experimental data.
Our previous studies established that the HXRE and HAA pathways proceed via the stepwise sequences illustrated in Scheme 2, with the first step calculated to be the rate-determining step (RDS) in each case.2e Building on these results, we calculated the ground-state and transition-state energies associated with the HXRE and HAA pathways for (IMe)2Pd(H)(O2CPh) (6a) (Fig. 4).9 The results reveal that free energies of activation are nearly identical for the two mechanisms: ΔG‡HXRE = 24.1 kcal mol−1 and ΔG‡HAA = 24.3 kcal mol−1. Similar calculations were then carried out for a series of closely related complexes in which benzoate was replaced with a variety of para-substituted benzoate ligands (p-XC6H4CO2−, X = NO2, Cl, CF3, F, H, Me, OMe, NH2, NMe2).
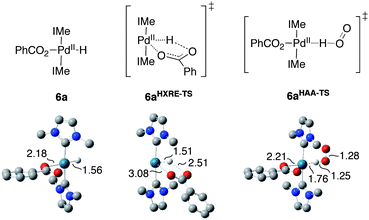 |
| | Fig. 4 Optimized ground-state structure for (IMe)2Pd(H)(O2CPh) and the rate-determining transition states for the HXRE and HAA mechanisms of O2insertion into the Pd–H bond. | |
Analysis of the ground-state structures for para-substituted benzoate analogs of 6a revealed two primary trends: the Pd–O bond distance shortened and the Pd–H bond distance lengthened with increasing electron-donating character of the para substituent. These trends correlated with electronic effects observed on the activation barriers calculated for the HXRE and HAA mechanistic pathways. In the transition state for the HXRE mechanism, the Pd–O bond is almost completely broken, dPd–O = 3.08 Å (Fig. 4), and the carboxylate fragment has substantial negative charge build-up (see discussion of 1TSTS above). Electron-withdrawing substituents favor both of these properties, and the activation barrier for the HXRE mechanism decreases with more-electron-withdrawing substituents. The electronic dependence for the HAA pathway is more subtle, but it exhibits the opposite trend: the barrier decreases with more-electron-donating substituents. This trend is best rationalized on the basis of the increased trans effect of benzoate ligands with electron-donating substituents.11
The computed free energies of activation (ΔG‡calc) for the HXRE and HAA were used to prepare a Hammett plot (Fig. 5A). A V-shaped plot is evident upon fitting linear trendlines to two groups of data: (1) those for the para –NMe2, –NH2, –OMe and –Me derivatives; and (2) those for the para –OMe, –Me, –F, –Cl, –CF3 and –NO2 derivatives. The scatter in the plot and the large deviation for the parent benzoate derivative 6a reflects the substantial scatter in calculated ΔS‡ values.11 The scatter is eliminated (by cancelation) in the Hammett plot based on the relative free energies of activation for the HXRE and HAA pathways, ΔΔG‡calc = ΔG‡HAA–ΔG‡HXRE. In this case, a linear Hammett correlation is observed (Fig. 5B). The positive slope reflects an increasing preference for the HXRE mechanism with more-electron-withdrawing substituents, and the calculations predict a mechanistic crossover (ΔΔG‡calc = 0) with the parent benzoate or para-fluorobenzoate ligands. This conclusion is qualitatively close to the conclusion from our experimental studies, which provide evidence for mechanistic crossover with the para-methoxybenzoate ligand (Fig. 2). Moreover, the calculated ΔΔG‡ values for the para–H, –F and –OMe derivatives differ by only 1 kcal mol−1.
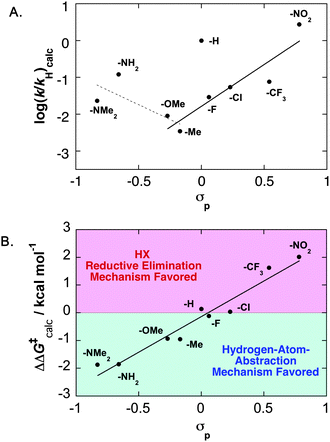 |
| | Fig. 5 (A) Hammett plot based on calculated rate constants (kHXRE + kHAA) for O2insertion into the PdII–H bond of (IMe)2Pd(H)(O2CC6H4X) complexes.11 The p-H derivative is not included in the two trendlines. (B) Hammett plot of the relative calculated free-energies of activation (ΔΔG‡calc = ΔG‡HAA–ΔG‡HXRE) for the hydrogen-atom-abstraction (HAA) and HX-reductive-elimination (HXRE) pathways. | |
Mechanistic implications for previous studies and catalytic reactions
The above results provide a rationale for the discrepancy between mechanistic conclusions reached from previous experimental and computational studies. The experimental study of (IMes)2Pd(H)(O2CPh) (1a) supported the HXRE pathway, whereas the computational study of (IMe)2Pd(H)(OAc) (7) supported the HAA pathway. The trend illustrated in Fig. 5 demonstrates that the acetate ligand in 7, which is substantially more basic than the benzoate ligand in 1a, would favor the HAA mechanism. Thus, the discrepancy is resolved by the fact that the preferred mechanism changes, depending on the electronic properties of the carboxylate ligand.
Another important outcome of the present study is the experimental validation of DFT methods as a quantitatively useful tool in assessing the mechanism of reactions between O2 and PdII–hydride complexes. This conclusion has important implications for understanding the mechanism of aerobic oxidation of Pd in catalytic reactions. Thus far, PdII–hydride intermediates in aerobic oxidation have not been directly observed or studied under catalytically relevant conditions, and the well-defined PdII–hydride complexes 1a–e and 3 (eqn (1) and (2)) are not effective catalysts for aerobic oxidation reactions. Insights into the aerobic oxidation of catalytically relevant PdII–hydride species, such as [(–)-sparteine]Pd(H)X (X = Cl, OAc)3a,d,i and (pyridine)2Pd(H)OAc,2h,3j have been limited to computational studies. The latter studies suggest that labile neutral-donor ligands (e.g., pyridine, triethylamine, dimethyl sulfoxide) and carboxylate ligands strongly favor the HXRE pathway for PdII–H oxidation. Only [(–)-sparteine]Pd(H)Cl, which lacks both labile neutral-donor and carboxylate ligands, has been proposed to favor an HAA mechanism on the basis of DFT calculations.
Conclusions
The present study demonstrates that two different mechanisms are energetically accessible in the reaction of O2 with PdII–hydride complexes trans-(IMes)2Pd(H)(O2CC6H4X). Experimental and computational data reveal that mechanistic crossover occurs between HX-reductive-elimination (HXRE) and hydrogen-atom-abstraction (HAA) pathways as the electronic properties of the benzoate ligand are varied. Electron-deficient benzoates favor the HXRE pathway and electron-donating benzoates favor the HAA pathway. The close correlation between experiment and theory evident from these results provides an important foundation for future computational studies of Pd catalyst systems, especially for the study of catalytic intermediates that are difficult to access viaexperimental methods.
Acknowledgements
We thank C. R. Landis for valuable discussions during the course of this work and I. A. Guzei for X-ray crystallographic characterization of compound 1d. We are grateful to the National Science Foundation for financial support of the research (CHE-0543585) and computational resources (CHE-0840494 and TG-CHE-070040).
Notes and references
- For reviews, see:
(a) R. A. Sheldon, I. W. C. E. Arends, G. J. Ten Brink and A. Dijksman, Acc. Chem. Res., 2002, 35, 774–781 CrossRef CAS;
(b) S. S. Stahl, Angew. Chem., Int. Ed., 2004, 43, 3400–3420 CrossRef CAS;
(c) T. Nishimura and S. Uemura, Synlett, 2004, 201–216 CAS;
(d) S. S. Stahl, Science, 2005, 309, 1824–1826 CrossRef CAS;
(e) M. S. Sigman and D. R. Jensen, Acc. Chem. Res., 2006, 39, 221–229 CrossRef CAS;
(f) K. M. Gligorich and M. S. Sigman, Chem. Commun., 2009, 3854–3867 RSC;
(g) X. Chen, K. M. Engle, D.-H. Wang and J.-Q. Yu, Angew. Chem., Int. Ed., 2009, 48, 5094–5115 CrossRef CAS.
-
(a) S. S. Stahl, J. L. Thorman, R. C. Nelson and M. A. Kozee, J. Am. Chem. Soc., 2001, 123, 7188–7189 CrossRef CAS;
(b) C. R. Landis, C. M. Morales and S. S. Stahl, J. Am. Chem. Soc., 2004, 126, 16302–16303 CrossRef CAS;
(c) M. M. Konnick, I. A. Guzei and S. S. Stahl, J. Am. Chem. Soc., 2004, 126, 10212–10213 CrossRef CAS;
(d) M. M. Konnick, B. A. Gandhi, I. A. Guzei and S. S. Stahl, Angew. Chem., Int. Ed., 2006, 45, 2904–2907 CrossRef CAS;
(e) B. V. Popp and S. S. Stahl, J. Am. Chem. Soc., 2007, 129, 4410–4422 CrossRef CAS;
(f) B. V. Popp, J. E. Wendlandt, C. R. Landis and S. S. Stahl, Angew. Chem., Int. Ed., 2007, 46, 601–604 CrossRef CAS;
(g) M. M. Konnick and S. S. Stahl, J. Am. Chem. Soc., 2008, 130, 5753–5762 CrossRef CAS;
(h) B. V. Popp and S. S. Stahl, Chem.–Eur. J., 2009, 15, 2915–2922 CrossRef CAS;
(i) B. V. Popp, C. M. Morales, C. R. Landis and S. S. Stahl, Inorg. Chem., 2010, 49, 8200–8207 CrossRef CAS.
-
(a) J. M. Keith, R. J. Nielsen, J. Oxgaard and W. A. Goddard, III, J. Am. Chem. Soc., 2005, 127, 13172–13179 CrossRef CAS;
(b) M. C. Denney, N. A. Smythe, K. L. Cetto, R. A. Kemp and K. I. Goldberg, J. Am. Chem. Soc., 2006, 128, 2508–2509 CrossRef CAS;
(c) J. M. Keith, R. P. Muller, R. A. Kemp, K. I. Goldberg, W. A. Goddard, III and J. Oxgaard, Inorg. Chem., 2006, 45, 9631–9633 CrossRef CAS;
(d) J. M. Keith, W. A. Goddard, III and J. Oxgaard, J. Am. Chem. Soc., 2007, 129, 10361–10369 CrossRef CAS;
(e) S. Chowdhury, I. Rivalta, N. Russo and E. Sicilia, Chem. Phys. Lett., 2007, 443, 183–189 CrossRef CAS;
(f) S. Chowdhury, I. Rivalta, N. Russo and E. Sicilia, J. Chem. Theory Comput., 2008, 4, 1283–1292 CrossRef CAS;
(g) S. Chowdhury, I. Rivalta, N. Russo and E. Sicilia, Chem. Phys. Lett., 2008, 456, 41–46 CrossRef CAS;
(h) E. A. Katayev, H. V. Lavrova and V. N. Khrustaleva, J. Porphyrins Phthalocyanines, 2008, 12, 1137–1145 CrossRef CAS;
(i)
J. M. Keith, California Institute of Technology, Pasadena, California, 2008, p. 117;
(j) J. M. Keith and W. A. Goddard, J. Am. Chem. Soc., 2009, 131, 1416–1425 CrossRef CAS.
- See, for example:
(a) J. Muzart and J. P. Pete, J. Mol. Catal., 1982, 15, 373–376 CrossRef CAS;
(b) K. Takehira, T. Hayakawa, H. Orita and M. Shimizu, J. Mol. Catal., 1989, 53, 15–21 CrossRef CAS;
(c) T. Hosokawa and S. Murahashi, Acc. Chem. Res., 1990, 23, 49–54 CrossRef CAS;
(d) T. Hosokawa, T. Nakahira, M. Takano and S. Murahashi, J. Mol. Catal., 1992, 74, 489–498 CrossRef CAS;
(e) T. Nishimura, T. Onoue, K. Ohe and S. Uemura, J. Org. Chem., 1999, 64, 6750–6755 CrossRef CAS;
(f) T. Nishimura, N. Kakiuchi, T. Onoue, K. Ohe and S. Uemura, J. Chem. Soc., Perkin Trans. 1, 2000, 1915–1918 RSC.
- For leading references on the reactions of other metal hydride complexes with O2 to form metal hydroperoxo complexes see:
(a) J. H. Bayston and M. E. Winfield, J. Catal., 1964, 3, 123–128 CrossRef CAS;
(b) T. T. Wenzel, Stud. Surf. Sci. Catal., 1991, 66, 545–554 CAS;
(c) A. Bakac, J. Am. Chem. Soc., 1997, 119, 10726–10731 CrossRef CAS;
(d) D. D. Wick and K. I. Goldberg, J. Am. Chem. Soc., 1999, 121, 11900–11901 CrossRef CAS;
(e) A. Bakac, J. Photochem. Photobiol., A, 2000, 132, 87–89 CrossRef;
(f) S. Thyagarajan, C. D. Incarvito, A. L. Rheingold and K. H. Theopold, Chem. Commun., 2001, 2198–2199 RSC;
(g) W. Cui and B. B. Wayland, J. Am. Chem. Soc., 2006, 128, 10350–10351 CrossRef CAS;
(h) M. Schlangen and H. Schwarz, Helv. Chim. Acta, 2008, 91, 379–386 CrossRef CAS;
(i) J. L. Look, D. D. Wick, J. M. Mayer and K. I. Goldberg, Inorg. Chem., 2009, 48, 1356–1369 CrossRef CAS;
(j) E. Szajna-Fuller and A. Bakac, Inorg. Chem., 2010, 49, 781–785 CrossRef CAS.
- The oxygenation rates were determined by the method of initial rates. We have shown previously that hydrogen bond donors, including the Pd–OOH product, accelerate the rate of oxygenation and lead to non-exponential decay of the Pd–H species in reactions of this type. For further discussion and characterization of this effect, see: ref. 2g.
- Addition of NBu4(O2CC6H4OMe) had no effect on the reaction rate, and, as described in ref. 2g, allowed us to obtain full exponential reaction timecourses for 1e. Tetrabutylammoniumpara-methoxybenzoate NBu4(O2CC6H4OMe), was synthesized through an established literature procedure from tetrabutylammonium hydroxide and para-methoxybenzoic acid: Y. Sato, H. Fujisawa and T. Mukaiyama, Chem. Lett., 2005, 34, 1188–1189 Search PubMed.
- It should be noted that the rates in Fig. 2 and Fig. 3 cannot be compared directly because the data were acquired at different temperatures (51 and 75 °C, respectively). In the [O2]-dependence experiments (Fig. 3), higher temperatures were found to minimize complications associated with decomposition of the Pd-hydroperoxide, which is accelerated at higher O2 pressures. Qualitatively, the proportion of the reaction that proceeds via the [O2]-dependence HAA pathway becomes much more pronounced at lower temperatures, as implied by the Hammett plot in Fig. 2.
- Computational method: All computations were performed with the Gaussian 03 program. Geometry optimizations were performed using the B3LYP functional with the Stuttgart RSC 1997 ECP basis set for Pd and 6-31+G* for all other atoms. Spin-unrestricted methodology was used for the calculations. At the calculated stationary points, solvation-corrected single-point-energy calculations were carried out with the Pd basis detailed above and the 6-311++G** basis for all other atoms. These calculations were used to predict the solvation free energy close to experimental conditions (toluene solvent at 50 °C).
- Other mechanisms analyzed in the previous study included an O2-coordination/insertion pathway and an O2-oxidative-addition/O–H-reductive-elimination sequence. These mechanisms exhibited barriers much higher in energy than those for the HXRE and HAA pathways (≥10–30 kcal mol−1). See ref. 2e for further details.
- Calculated entropies of activation (ΔS‡) exhibit substantial scatter in a Hammett plot (ΔS‡calcvs. σp; Fig. S2), and this scatter is propagated in the calculated ΔG‡ values and rate constants (Figs. 5A and S1). More-systematic Hammett trends are evident for the calculated ΔE‡ and ΔH‡ values (Figs. S3 and S4). The scatter introduced by the calculated ΔS‡ values is also cancelled in the plot of ΔΔG‡vs. σp (Fig. 5B). See the supplementary information for details†.
Footnote |
| † Electronic supplementary information (ESI) available: Data for new compounds, experimental procedures, and computational data. CCDC reference number 785942. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c0sc00392a |
|
| This journal is © The Royal Society of Chemistry 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 





![Hammett correlation for the rate of oxygenation of (IMes)2Pd(H)(O2CC6H4X), 1a–e. Reaction conditions: [1a–e]0 = 0.5 mM, 1 atm O2, 51 °C, 0.4 mL C6D6.](/image/article/2011/SC/c0sc00392a/c0sc00392a-f2.gif)
![Effect of O2 pressure on the observed rate constant for the oxygenation of 1e (●) and 1e-dd (♦). Reaction conditions: [1e]0 = 1 mM, [1e-dd]0 = 0.5 mM, pO2 = 0.28–4.1 atm, [NBu4O2CC6H4OMe] = 10 mM, 0.4 mL C6D6, 75 °C.](/image/article/2011/SC/c0sc00392a/c0sc00392a-f3.gif)