Excited states and optical absorption of small semiconducting clusters: Dopants, defects and charging

Abstract

Spatially confined semiconductors form an exciting type of material with potential for numerous applications, many of which rely on the material's optical properties and excitation dynamics. For successful realization of the applications a detailed analysis of excitations in these materials is needed, extending beyond the ideal case and including various defects, such as photoionization, doping and surface dangling bonds. High-level ab initio electronic structure calculations on two representative classes of semiconducting clusters have lead to much progress on achieving a thorough understanding of the excitation properties of these materials when they are altered with charging, doping or dangling bonds. The calculations show that the defects introduce new intra-band transitions, blue-shift the optical absorption spectra and push the normal excitonic and multiexcitonic transitions to higher energies. Generally, doping and charging have similar effects on the excited state properties, while introduction of dangling bonds cause less severe changes, since the latter defect can be partially accommodated by reorganization in the local bonding pattern.

---

Electronic excitations in spatially confined, semiconducting materials, known as nanocrystals (NCs),^1–6 are of fundamental importance and interest. NCs form the basis for a variety of applications, including biological probes,⁷ quantum information devices,⁸ thermopower machines,⁹ spintronic systems,¹⁰ quantum antennas,¹¹ field-effect transistors,¹² light-emitting diodes,¹³ lasers,¹⁴ and photovoltaic cells.^15,16 Understanding of the nature of electronic excitations in NCs is crucial to realizing the full potential of all these applications.

Types of excitations in ideal and imperfect nanoclusters

In pure, ideal semiconductors the picture of excitations is relatively straightforward; a photon incident on the material excites an electron across the band gap from the valence band (VB) to the conduction band (CB), thereby producing an interacting electron-hole pair, the so-called exciton, that is stabilized by the Coulomb interaction of the two charges in the semiconducting material. Additionally, if the energy of the incident photon is at least twice the energy of the band gap, then a phenomenon known as multiple exciton generation (MEG) can occur, in which more than one exciton is created through the absorption of a single photon. Because MEG has the potential to increase the photoinduced current in a material and thus increase the maximum efficiency of solar cells by about a third,¹⁷ there is much interest in trying to understand and maximize this phenomenon. Currently, there is considerable debate over the mechanism^15,18–26 responsible for MEG in confined materials and the efficiency^16,27–39 at which MEG occurs in these materials.

In contrast to molecules, whose composition and structure are well-defined, semiconductors, whether bulk or confined, are likely to exhibit a variety of defects, such as missing or extra atoms, dopants, and excess charges. Deviations from the ideal structure can occur either by design, as in the case of doping Si with phosphorous or boron in order to create an n- or p-type material,⁴⁰ or by inherent surface defects⁴¹ such as dangling bonds, or through inadvertent photoionization of the material. Materials containing defects have more complicated excitation profiles, because they contain new types of transitions beyond single excitons (SEs) and multiexcitons (MEs).^42,43 Shown diagrammatically in the bottom of Fig. 1, these new excitations result from a disruption of the normal electronic structure of the material. If the material becomes charged, an extra charge carrier appears in the VB or CB, and additional electronic transitions within these bands become possible. A similar situation results from the introduction of a heterovalent dopant atom. Then, a defect state is created near a band edge, and an extra charge carrier enters the VB or CB when the dopant atom ionizes, either through thermal activation or confinement effects.⁴⁴ Dangling bonds can also introduce states into the band gap of the material; however, unlike the dopant case, the gap-states (GSs) created by dangling bonds are not necessarily near either band edge. These GSs can be occupied or unoccupied.

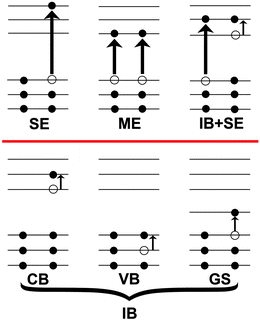Fig. 1 Possible electronic transitions in the semiconducting clusters. Single exciton (SE) and multi-exciton (ME) transitions can occur in all the systems, while conduction band (CB), valence band (VB), and gap-state (GS) transitions, collectively referred to as intra-band (IB) transitions, become possible when the material is modified from the ideal cluster. Combinations of IB and SE/ME transitions (e.g. IB + SE) can also occur.

For brevity we will refer to these VB, CB, and GS transitions by the collective term intra-band (IB) transitions. While IB transitions do create excitons, these excitons are contained within either the VB or CB and, therefore, are not of use to photovoltaic applications, which need to separate the charges across the band gap. Nor are they of use to any application that relies on radiative recombination, since the charges will relax and recombine non-radiatively. At sufficiently high energies, the excitations get more complicated, as these IB transitions can occur in conjunction with SEs (IB + SE), resulting in a multi-electron excitation that involves the creation of only one new electron-hole pair spanning the band gap. While formally these transitions are MEs, in photovoltaic applications they are equivalent to SEs. They cannot be viewed as ordinary MEs, since the latter create two electron-hole pairs spanning the gap, potentially doubling the photocurrent. Going to even higher energies, IB transitions can occur in conjunction with ME transitions. Since excitations involving more than two electrons contribute rather minimally (≤5%) to the NC excited states discussed below, the excitations that are combinations of IB and ME transitions are categorized as just MEs.

We note that the concept of a charged exciton⁴⁵ is often used in NC literature. A charged exciton consists of either two electrons and one hole or two holes and one electron. A charged biexciton involves three electrons and two holes or vice versa. Application of this nomenclature to non-ideal clusters—charged, doped or with dangling bonds—implies that a SE should be called a charged exciton, IB + SE becomes a biexciton, and ME becomes a charged biexciton. According to this nomenclature, a biexciton in a neutral cluster is a two band-gap excitation, while a biexciton in a charged cluster involves only one band-gap excitation. In order to avoid this inconsistency, we use the notation introduced above in Fig. 1.

Much work has already been accomplished towards the understanding and realization of doping in semiconducting NCs.^44,46–57 Progress has also been made in elucidating the effects of excess charges in NCs,^45,58,59 as well as surface defects.^60,61 In self-assembled quantum dots, the absorption and emission energies red-shift relative to the neutral dots as electrons are loaded into the quantum dots.^45,59 A pseudopotential study on CdSe quantum dots predicted that the shift in the absorption energies are dependent on the relative localization of the hole state as compared to the electron state.⁵⁸ These studies focused on the first few transitions, covering an excitation window of approximately 1 eV. A detailed, ab initio description of the excited states and the optical absorption of confined semiconductors across a substantial energy range has been lacking.

Simulation details

In order to gain insight into the nature of the electronically excited states in spatially confined semiconducting materials, as well as to study the effects caused by modifications to the ideal structure, high level ab initio electronic structure calculations were performed that could properly model SE, ME, and IB excited state configurations. The calculations used the symmetry adapted cluster theory with configuration interaction (SAC-CI) method,^62–64 as implemented within the Gaussian 03 computational package,⁶⁵ the LANL2DZ basis set and pseudopotentials, with all valence orbitals included in the active space. The calculation begins by using the Hartree–Fock ground state determinant as a reference wavefunction in a cluster expansion of the true wavefunction, thereby including correlation effects into the ground state. The excited state wavefunctions are determined by first defining a set of basis functions, which are created by applying symmetry adapted excitation operators^66,67 to the ground state wavefunction. The excited states are then constructed from linear combinations of these basis functions. For the calculations discussed here, excitation operators up to at least quadruples were utilized. Some computational savings can be achieved by reducing the SAC-CI expansion from quadruples to doubles.^22,42,43 The excited states are classified according to the types of transitions that comprise each excited state.

It is important to emphasize that the eigenstates of the SAC-CI Hamiltonian consist of mixtures of single and multiple excitations. At the single particle description, only SEs can be optically excited, and MEs always remain dark. The mixing of SEs and MEs described by SAC-CI makes MEs optically active, since they can couple to light due to the presence of a non-zero SE component in the SAC-CI eigenstates.

The excited states calculated with this method are the many-electron eigenstates of the electronic Hamiltonian that includes electron correlation, excitonic effects at a high level of ab initio description. These states describe initial photoexcitations that can evolve further by a number of mechanisms, including Auger processes^19,20 phonon-induced dephasing^23,24,68,69 and electron–phonon relaxation.^41,70 The subsequent evolution of the photoexcited states can produce transitions between states of difference character, e.g.SEs and MEs, loss of coherence in superpositions of various types of transitions and electronic energy losses to heat.

As a consequence of the complexity of the calculation and the supremely large number of states (>1000) needed to span a meaningful energy range, only very small clusters of atoms were used in the calculations. Nevertheless, quantum-mechanical calculations in combination with classical theories of optical absorption demonstrate universality of the optical response. For instance, the optical response of the Si–Si bond was found independent of bonding configuration, and the classical theory remained valid from bulk Si down to atomic-scale clusters, as small as Si₈ and even Si₅.⁷¹ While we would like to stress that the results and conclusion obtained here are for small clusters, there is reason to think that some of the effects observed in these small clusters may be present in larger systems. First, the single-particle band structure of small clusters was found to be qualitatively similar to that of much larger clusters.²²Second, the key features of the absorption spectra of Si clusters were observed to be independent of cluster size over almost an order of magnitude in the number of atoms in the cluster.⁷² This suggests that the conclusions drawn here for small Si clusters could be directly relevant for mid-sized Si clusters. Third, there is correspondence between the small cluster results and calculations on larger NCs. Specifically, Franceschetti and Zunger⁵⁸ calculate a general red-shift of exciton transition energies for negative charging and blue-shift for positive charging. The small cluster results show that SEs are slightly red-shifted for anionic clusters as compared to neutral clusters, while SEs are blue-shifted for cationic clusters as compared to neutral clusters. The ME thresholds found in our ab initio calculations with small neutral clusters^22,43 agree with the experimental data^18,23,73,74 and the more empirical calculations on the larger particles.^20,30Finally, most of the arguments made concerning the cause of the observed effects are general and not expected to depend on the size of the system. For example, dopants and dangling bonds create defect states no matter the size of the system, and an extra electron in the CB allows new, low energy transitions, which have been observed in remote doping experiments on full-sized NCs.^52–54

Systems studied by the SAC-CI method include neutral clusters of PbSe, CdSe²² and Si,⁴³ in addition to positively and negatively charged clusters of PbSe⁴² and Si.⁴³ Further work has been carried out on PbSe and Si clusters involving dopants and dangling bonds.⁷⁵ The calculations employed the same geometric structure for the neutral and charged clusters, see top of Fig. 2. Both positive and negative charges were considered. The dopant case is represented here by replacing a Si atom from the original cluster with a P atom, as shown in the bottom left of Fig. 2. In this case, the dopant causes a modification similar to negatively charging the cluster since P introduces an extra electron into the CB. Dangling bonds were introduced into the PbSe cluster by removal of one of the Pb atoms, see bottom right of Fig. 2. Here, the dangling bonds introduced an unoccupied level into the band gap. This GS leads to similarity with a positively charged cluster, since electrons excited from the VB do not necessarily transition into the CB, but can also occupy the GS.

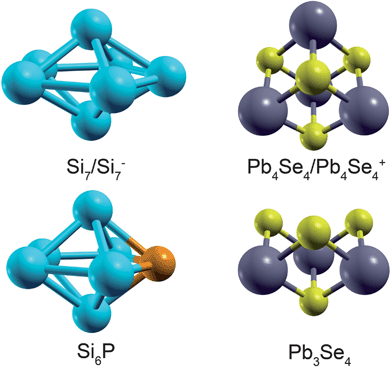Fig. 2 Geometries of the studied systems. The charged clusters have the same geometries as the respective neutral clusters.

Optical spectra

Fig. 3 shows the optical spectra generated from the SAC-CI calculations for each of the studied systems. The spectra were obtained non-perturbatively, by explicitly computing the transition dipole moment and oscillator strength for each transition. It has been shown for neutral Si clusters that the classical theory of optical absorption remains valid down to very small clusters, Si₈ and even Si₅, and that the optical response is generally independent of bonding configuration.⁷¹ Generally, the bands seen in the spectra are composed of multiple individual excitations. In the neutral clusters, at energies between 2.5 and 3 times the lowest excitation energy E_g, we observe a drop in the intensity of the individual excitations, see the top two panels in Fig. 3. This correlates with the change in the nature of excited states, which become predominantly MEs at these energies, Fig. 4. ME states are optically forbidden within the single-particle excitation picture. By including electron correlation effects caused by the Coulomb interaction, SAC-CI mixes SEs and MEs. At high energies, every SE is diluted in hundreds of MEs, and the intensity of a given excitation is determined by its SE component.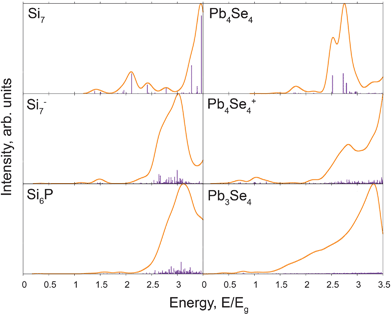

Fig. 3 Optical absorption spectra. Modifications to the systems result in a blue-shift of the absorption spectra. Adding a dopant or introducing a dangling bond causes a similar effect to charging the system. The energy scales for the Si and PbSe clusters are shown relative to the lowest excitation energies, i.e. band-gaps E_g, of the corresponding neutral cluster. Namely, E_g(Si₇) = 2.55 eV, E_g(Pb₄Si₄) = 2.72 eV.

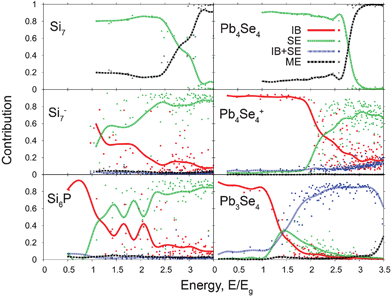Fig. 4 Contribution of the different electronic transitions to the excited state character for each of the studied systems. See Fig. 1 for the schematic of the transition types and Fig. 3 for the energy scales. Red (solid line, squares) gives the contribution of intra-band (IB) transitions, green (dashed line, triangles) depicts single exciton (SE) transitions, blue (dotted line, circles) corresponds to IB transitions combined with exciton transitions (IB + SE), and black (dash-dot line, asterisks) shows multi-exciton (ME) transitions. The data points are the squares of the SAC-CI expansion coefficients for the corresponding transition types. Only every fifth data point is plotted for clarity. The lines give the average behavior of the respective transition type.

At most excitation energies the density of excited states is high even in these very small clusters, justifying the general lack of the so-called “phonon bottleneck” for electron–phonon energy relaxation.^16,41,70,76 Our calculations confirm that the gaps between the states are larger at low energies, rationalizing observation of the phonon bottleneck for certain special cases.⁷⁷

The calculations show that a modification to the cluster from its ideal structure blue-shifts the main absorption peaks in the optical spectra, compare the top panels in Fig. 3 with the middle and bottom panels. This is seen with all types of defects, including doping, charging and dangling bonds. The effect has been observed experimentally and can be rationalized by Pauli blocking, whereby occupation of the lowest energy CB state in an n-type cluster prevents a transition into this state from a VB electron.^52–54 For the positively charged, p-type clusters, the effect is the same, but instead of the CB electron blocking the excitation of a VB electron, it is the lack of a VB electron that bleaches the lowest energy exciton transitions. While the modifications to the clusters open the possibility for much lower energy IB transitions, these transitions do not have a significant contribution to the absorption spectra. Typical oscillator strengths calculated for the IB transitions are on the order of 10⁻⁴ for the Si clusters and 10⁻² for the PbSe clusters, while they are on the order of 10⁻¹ for SE transitions in both materials. The role of defects should diminish in larger clusters, since the ratio of the density of state (DOS) of IB transitions to SE excitations will decrease substantially.

Nature of excited states

The contributions of each excited state configuration, as defined in Fig. 1, to the overall character of the excited states in the ideal and modified clusters are analyzed in Fig. 4. The data points shown in Fig. 4 are the squares of the expansion coefficients for a given excitation represented in the basis of the single- or multi-electron configurations defined in Fig. 1. For both ideal Si₇ and ideal Pb₄Se₄ clusters, the transformation from essentially all SEs to all MEs occurs between 2.5 and 3 times the first excitation energy, in agreement with the previous results on Si⁷⁴ and PbSe^18,20,23,73 NCs. The transformation is sharper in the PbSe cluster. In the ideal clusters, the ME contributions are significant even at lowest energies. This behavior is reminiscent of that for molecular chromophores⁷⁸ and occurs as a result of strong Coulomb interactions between electrons and holes. The coupling should decrease in larger clusters, and states with nearly 100% SE contributions can be seen even at high energies, according to the semiempirical calculations.^20,30

The transformation between different excitation types can be rationalized by statistical arguments. Fig. 5 shows DOS for various excitation types. At high energies there are many more possibilities to create multiple electron-hole pairs and excite MEs rather than SEs. In contrast, MEs are not allowed at lower energies by energy conservation. The DOS shown in Fig. 5 correlate with the data of Fig. 4. The correlation is not perfect, since the mixing of excitation types, reflected in their contributions to the excited states shown in Fig. 4, depends on the Coulomb coupling, which may vary with energy. The Coulomb coupling enters the SAC-CI Hamiltonian at the fundamental level of the electron-electron repulsion operator, 1/r. In comparison to other schemes,^20,30 it is not a parameter in our approach, and it cannot be plotted in a simple way.

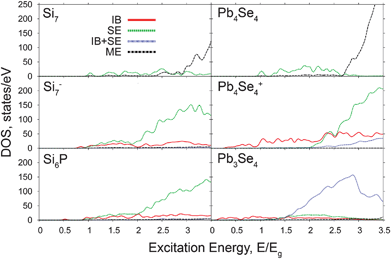Fig. 5 Densities of states for different transitions types. See Fig. 1 for the transition types and Fig. 3 for the energy scales.

The Si₇⁻ and Si₆P clusters show almost identical behavior, which is to be expected, since doping Si with P essentially amounts to adding an extra electron into the CB. The lowest excitation energy in these clusters are smaller than that of the ideal cluster, 2.11 and 1.34 eV vs. 2.55 eV, respectively. Nevertheless, MEs appear at much higher energies, see Fig. 4 and 5. This is because the lowest excitations in the modified clusters arise due to the IB transitions, Fig. 1. As the energy increases, the IB contributions gradually decrease in magnitude, and SEs become the dominant configuration. At the energies at which MEs overcome SEs in the ideal Si₇ cluster, SE configurations remain dominant in the Si₇⁻ and Si₆P clusters, reaching average contribution levels above 80%. While SEs begin to appear at about the same energy for the ideal and modified Si clusters, in the latter case the SE onset is not so sharp and SEs continue to contribute the most to the excited states until the end of the energy range shown in Fig. 4 and 5. The IB + SE and ME two-electron configurations begin contributing to the electronically excited states of the Si₇⁻ and Si₆P clusters at very high energies.⁴³ This shift of the multi-electron transitions to higher energies can be understood by a statistical argument. At the energies where SE and ME configurations begin to appear, the number of the IB and IB + SE configurations is significantly greater than the number of the SE and ME configurations in the charged and doped clusters. As a result, only a small percentage of the SE and ME configurations is seen initially, and the onsets of pure SE and ME transitions shift to higher energies.

The modified PbSe clusters show similar features to each other. IB configurations dominate at low energies in both modified PbSe clusters. At higher energies, the IB contributions fall and the SE contributions rise. The SE contribution never gets above 50% in the Pb₃Se₄ cluster, and it is rather quickly overcome by the IB + SE configurations. The cationic Pb₄Se₄⁺ cluster has significant contributions from SEs for a wider energy range. The magnitude of the average SE contribution reaches nearly 80%. The onset of SEs is shifted in the Pb₄Se₄⁺ cluster to energies that are twice higher than the SE onset energy in the neutral cluster. Correspondingly, the ME transitions are shifted to much higher energies as well.⁴² They are not seen at all within the current energy range shown in Fig. 4.

In contrast, MEs in the Pb₃Se₄ start at around the same absolute energy as in the ideal Pb₄Se₄ cluster. The fact that MEs appear at lower energies in the NC missing an atom, compared to the other modified NCs, is due to reorganization of the local bonding pattern that partially eliminates the dangling bonds.⁷⁹ The electrons of the dangling bonds can potentially pair up and move GSs closer to the VB. Unlike the charged and doped clusters, Pb₃Se₄ has an even number of electrons, which favors elimination of the defect. Analysis shows that two electrons are necessary to completely saturate all dangling bonds in this cluster, explaining why the GSs persist.

Conclusions

The high level ab initio electronic structure calculations on small semiconducting clusters demonstrate that single excitons become double excitons at energies of about 2.5 times the lowest excitation energy. Cluster modifications such as charging, doping, or incomplete passivation of dangling bonds lead to dramatic alterations in the types of excitations experienced by the material as well as changes in the optical absorption spectrum. New states are introduced by the defects, which mix with the original states to push multi-electron transitions to higher energies. Meanwhile, Pauli blocking causes a blue-shift in the absorption spectra, implying that SEs will not be observed experimentally in modified clusters until higher energies. Given the correspondence when going from small clusters to larger ones in density of states, absorption spectra, and shifting of excitonic transition energy upon charging,⁵⁸ the observed effects should be present in some form in larger systems. This conclusion is supported further by the general, size-independent nature of many arguments presented in this minireview. These effects caused by modifications to the cluster could significantly affect the performance of devices dependent upon band gap excitonic transitions in semiconductors. Adding a dopant has essentially the same effect as charging the cluster, while introducing dangling bonds has less severe consequences, provided that the electrons can pair up and new bonds can form. The ME and IB + SE configurations show a similar trend in the anionic and n-doped clusters, while the IB + SE configurations dominate the ME configurations in the cationic clusters. The detailed analysis of the excited state properties of the semiconducting nanoscale particles provided in this mini-review can help to understand and more fully exploit the unique properties of these materials.

Acknowledgements

The research was supported by grants from DOE DE-FG02-05ER15755, NSF CHE-1050405 and ACS PRF 41436-AC6.

References

1. A. L. Efros and A. L. Efros, Interband absorption of light in a semiconductor sphere, Sov. Phys. Semicond.+, 1982, 16, 772–775.
2. A. I. Ekimov and A. A. Onushchenko, Quantum size effect in the optical-spectra of semiconductor micro-crystals, Sov. Phys. Semicond.+, 1982, 16, 775–778.
3. L. E. Brus, Electron electron and electron-hole interactions in small semiconductor crystallites - the size dependence of the lowest excited electronic state, J. Chem. Phys., 1984, 80, 4403–4409.
4. A. I. Ekimov, A. L. Efros and A. A. Onushchenko, Quantum size effect in semiconductor microcrystals, Solid State Commun., 1985, 56, 921–924.
5. L. Brus, Electronic wave-functions in semiconductor clusters - experiment and theory, J. Phys. Chem., 1986, 90, 2555–2560.
6. A. P. Alivisatos, Semiconductor clusters, nanocrystals, and quantum dots, Science, 1996, 271, 933–937.
7. M. Dahan, S. Levi, C. Luccardini, P. Rostaing, B. Riveau and A. Triller, Diffusion dynamics of glycine receptors revealed by single-quantum dot tracking, Science, 2003, 302, 442–445.
8. D. S. Kilin, K. L. Tsemekhman, S. V. Kilina, A. V. Balatsky and O. V. Prezhdo, Photoinduced conductivity of a porphyrin-gold composite nanowire, J. Phys. Chem. A, 2009, 113, 4549–4556.
9. R. Scheibner, H. Buhmann, D. Reuter, M. N. Kiselev and L. W. Molenkamp, Thermopower of a kondo spin-correlated quantum dot, Phys. Rev. Lett., 2005, 95, 176602.
10. J. Berezovsky, M. H. Mikkelsen, N. G. Stoltz, L. A. Coldren and D. D. Awschalom, Picosecond coherent optical manipulation of a single electron spin in a quantum dot, Science, 2008, 320, 349–352.
11. J. N. Farahani, D. W. Pohl, H. J. Eisler and B. Hecht, Single quantum dot coupled to a scanning optical antenna: A tunable superemitter, Phys. Rev. Lett., 2005, 95, 017402.
12. D. V. Talapin and C. B. Murray, Pbse nanocrystal solids for n- and p-channel thin film field-effect transistors, Science, 2005, 310, 86–89.
13. S. Coe, W. K. Woo, M. Bawendi and V. Bulovic, Electroluminescence from single monolayers of nanocrystals in molecular organic devices, Nature, 2002, 420, 800–803.
14. V. I. Klimov, A. A. Mikhailovsky, S. Xu, A. Malko, J. A. Hollingsworth, C. A. Leatherdale, H. J. Eisler and M. G. Bawendi, Optical gain and stimulated emission in nanocrystal quantum dots, Science, 2000, 290, 314–317.
15. A. J. Nozik, Spectroscopy and hot electron relaxation dynamics in semiconductor quantum wells and quantum dots, Annu. Rev. Phys. Chem., 2001, 52, 193–231.
16. O. V. Prezhdo, Multiple excitons and the electron–phonon bottleneck in semiconductor quantum dots: An ab initio perspective, Chem. Phys. Lett., 2008, 460, 1–9.
17. A. J. Nozik, Nanoscience and nanostructures for photovoltaics and solar fuels, Nano Lett., 2010, 10, 2735–2741.
18. R. D. Schaller and V. I. Klimov, High efficiency carrier multiplication in PbSe nanocrystals: Implications for solar energy conversion, Phys. Rev. Lett., 2004, 92, 186601.
19. M. Califano, A. Zunger and A. Franceschetti, Efficient inverse auger recombination at threshold in CdSe nanocrystals, Nano Lett., 2004, 4, 525–531.
20. A. Franceschetti, J. M. An and A. Zunger, Impact ionization can explain carrier multiplication in PbSe quantum dots, Nano Lett., 2006, 6, 2191–2195.
21. R. D. Schaller, V. M. Agranovich and V. I. Klimov, High-efficiency carrier multiplication through direct photgeneration of multi-excitons via virtual single-exciton states, Nature Physics, 2005, 1, 189–194.
22. C. M. Isborn, S. V. Kilina, X. Li and O. V. Prezhdo, Generation of multiple excitons in PbSe and CdSe quantum dots by direct photoexcitation: First-principles calculations on small PbSe and CdSe clusters, J. Phys. Chem. C, 2008, 112, 18291–18294.
23. R. J. Ellingson, M. C. Beard, J. C. Johnson, P. R. Yu, O. I. Micic, A. J. Nozik and A. L. Efros, Highly efficient mutiple exciton generation in collodial PbSe and PbS quantum dots, Nano Lett., 2005, 5, 865–871.
24. A. Shabaev, A. L. Efros and A. J. Nozik, Multiexciton generation by a single photon in nanocrystals, Nano Lett., 2006, 6, 2856–2863.
25. A. Piryatinski and K. A. Velizhanin, An exciton scattering model for carrier multiplication in semiconductor nanocrystals: Theory, J. Chem. Phys., 2010, 133, 084508.
26. L. Silvestri and V. M. Agranovich, Direct photogeneration of biexcitons via virtual single-exciton and biexciton states in PbSe quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205302.
27. J. A. Mcguire, J. Joo, J. M. Pietryga, R. D. Schaller and V. I. Klimov, New aspects of carrier multiplication in semiconductor nanocrystals, Acc. Chem. Res., 2008, 41, 1810–1819.
28. A. J. Nozik, Multiple exciton generation in semiconductor quantum dots, Chem. Phys. Lett., 2008, 457, 3–11.
29. M. C. Beard, A. G. Midgett, M. Law, O. E. Semonin, R. J. Ellingson and A. J. Nozik, Variations in the quantum efficiency of multiple exciton generation for a series of chemically treated PbSe nanocrystal films, Nano Lett., 2009, 9, 836–845.
30. E. Rabani and R. Baer, Distribution of multiexciton generation rates in CdSe and InAs nanocrystals, Nano Lett., 2008, 8, 4488–4492.
31. M. T. Trinh, A. J. Houtepen, J. M. Schins, T. Hanrath, J. Piris, W. Knulst, A. P. L. M. Goossens and L. D. A. Siebbeles, In spite of recent doubts carrier multiplication does occur in PbSe nanocrystals, Nano Lett., 2008, 8, 1713–1718.
32. M. Ben-Lulu, D. Mocatta, M. Bonn, U. Banin and S. Ruhman, On the absence of detectable carrier multiplication in a transient absorption study of InAs/CdSe/ZnSe core/shell1/shell2 quantum dots, Nano Lett., 2008, 8, 1207–1211.
33. J.-W. Luo, A. Franceschetti and A. Zunger, Carrier multiplication in semiconductor nanocrystals: Theoretical screening of candidate materials based on band-structure effects, Nano Lett., 2008, 8, 3174–3181.
34. G. Nair, S. M. Geyer, L.-Y. Chang and M. G. Bawendi, Carrier multiplication yields in PbS and PbSe nanocrystals measured by transient photoluminescence, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125325.
35. C. Sevik and C. Bulutay, Auger recombination and carrier multiplication in embedded silicon and germanium nanocrystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125414.
36. M. Ji, S. Park, S. T. Connor, T. Mokari, Y. Cui and K. J. Gaffney, Efficient multiple exciton generation observed in colloidal PbSe quantum dots with temporally and spectrally resolved intraband excitation, Nano Lett., 2009, 9, 1217–1222.
37. J. J. H. Pijpers, R. Ulbricht, K. J. Tielrooij, A. Osherov, Y. Golan, C. Delerue, G. Allan and M. Bonn, Assessment of carrier-multiplication efficiency in bulk PbSe and PbS, Nat. Phys., 2009, 5, 811–814.
38. M. C. Beard, A. G. Midgett, M. C. Hanna, J. M. Luther, B. K. Hughes and A. J. Nozik, Comparing multiple exciton generation in quantum dots to impact ionization in bulk semiconductors: Implications for enhancement of solar energy conversion, Nano Lett., 2010, 10, 3019–3027.
39. J. B. Sambur, T. Novet and B. A. Parkinson, Multiple exciton collection in a sensitized photovoltaic system, Science, 2010, 330(6000), 63–66.
40. X. D. Pi, R. Gresback, R. W. Liptak, S. A. Campbell and U. Kortshagen, Doping efficiency, dopant location, and oxidation of Si nanocrystals, Appl. Phys. Lett., 2008, 92, 123102.
41. O. V. Prezhdo, Photoinduced dynamics in semiconductor quantum dots: Insights from time-domain ab initio studies, Acc. Chem. Res., 2009, 42, 2005–2016.
42. C. M. Isborn and O. V. Prezhdo, Charging quenches multiple exciton generation in semiconductor nanocrystals: First-principles calculations on small PbSe clusters, J. Phys. Chem. C, 2009, 113, 12617–12621.
43. S. A. Fischer, A. B. Madrid, C. M. Isborn and O. V. Prezhdo, Multiple exciton generation in small Si clusters: A high-level ab initio study, J. Phys. Chem. Lett., 2010, 1, 232–237.
44. D. J. Norris, A. L. Efros and S. C. Erwin, Doped nanocrystals, Science, 2008, 319, 1776–1779.
45. R. J. Warburton, C. S. Dürr, K. Karrai, J. P. Kotthaus, G. Medeiros-Ribeiro and P. M. Petroff, Charged excitons in self-assembled semiconductor quantum dots, Phys. Rev. Lett., 1997, 79, 5282–5285.
46. R. N. Bhargava, D. Gallagher, X. Hong and A. Nurmikko, Optical-properties of manganese-doped nanocrystals of ZnS, Phys. Rev. Lett., 1994, 72, 416–419.
47. Y. Wang, N. Herron, K. Moller and T. Bein, 3-Dimensionally confined diluted magnetic semiconductor clusters-Zn1-xmnxs, Solid State Commun., 1991, 77, 33–38.
48. D. A. Schwartz, N. S. Norberg, Q. P. Nguyen, J. M. Parker and D. R. Gamelin, Magnetic quantum dots: Synthesis, spectroscopy, and magnetism of Co²⁺- and Ni²⁺-doped ZnO nanocrystals, J. Am. Chem. Soc., 2003, 125, 13205–13218.
49. R. Beaulac, P. I. Archer, S. T. Ochsenbein and D. R. Gamelin, Mn²⁺-doped CdSe quantum dots: New inorganic materials for spin-electronics and spin-photonics, Adv. Funct. Mater., 2008, 18, 3873–3891.
50. S. T. Ochsenbein, Y. Feng, K. M. Whitaker, E. Badaeva, W. K. Liu, X. S. Li and D. R. Gamelin, Charge-controlled magnetism in colloidal doped semiconductor nanocrystals, Nat. Nanotechnol., 2009, 4, 681–687.
51. D. A. Bussian, S. A. Crooker, M. Yin, M. Brynda, A. L. Efros and V. I. Klimov, Tunable magnetic exchange interactions in manganese-doped inverted core-shell ZnSe-CdSe nanocrystals, Nat. Mater., 2009, 8, 35–40.
52. M. Shim, C. J. Wang, D. J. Norris and P. Guyot-Sionnest, Doping and charging in colloidal semiconductor nanocrystals, MRS Bull., 2001, 26, 1005–1008.
53. M. Shim and P. Guyot-Sionnest, n-type colloidal semiconductor nanocrystals, Nature, 2000, 407, 981–983.
54. D. Yu, C. J. Wang and P. Guyot-Sionnest, n-type conducting CdSe nanocrystal solids, Science, 2003, 300, 1277–1280.
55. M. Perego, C. Bonafos and M. Fanciulli, Phosphorus doping of ultra-small silicon nanocrystals, Nanotechnology, 2010, 21, 025602.
56. M. Fujii, K. Toshikiyo, Y. Takase, Y. Yamaguchi and S. Hayashi, Below bulk-band-gap photoluminescence at room temperature from heavily p- and b-doped Si nanocrystals, J. Appl. Phys., 2003, 94, 1990–1995.
57. S. C. Erwin, Z. Lijun, M. I. Haftel, A. L. Efros, T. A. Kennedy and D. J. Norris, Doping semiconducting nanocrystals, Nature, 2005, 436, 91–94.
58. A. Franceschetti and A. Zunger, Optical transitions in charged CdSe quantum dots, Phys. Rev. B: Condens. Matter, 2000, 62, R16287–R16290.
59. K. H. Schmidt, G. Medeiros-Ribeiro and P. M. Petroff, Photoluminescence of charged InAs self-assembled quantum dots, Phys. Rev. B: Condens. Matter, 1998, 58, 3597–3600.
60. M. Califano, A. Franceschetti and A. Zunger, Temperature dependence of excitonic radiative decay in CdSe quantum dots: The role of surface hole traps, Nano Lett., 2005, 5, 2360–2364.
61. A. Puzder, A. J. Williamson, J. C. Grossman and G. Galli, Surface chemistry of silicon nanclusters, Phys. Rev. Lett., 2002, 88, 097401.
62. H. Nakatsuji and K. Hirao, Cluster expansion of the wavefunction. symmetry-adapted-cluster expansion, its variational determination, and extension of open-shell orbital theory, J. Chem. Phys., 1978, 68, 2053–2065.
63. H. Nakatsuji, Cluster expansion of the wavefunction. excited states, Chem. Phys. Lett., 1978, 59, 362–364.
64. H. Nakatsuji, Description of two- and many-electron processes by the SAC-CI method, Chem. Phys. Lett., 1991, 177, 331–337.
65. M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; J. A. Montgomery, Jr.; T. Vreven; K. N. Kudin; J. C. Burant; J. M. Millam; S. S. Iyengar; J. Tomasi; V. Barone; B. Mennucci; M. Cossi; G. Scalmani; N. Rega; G. A. Petersson; H. Nakatsuji; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; M. Klene; X. Li; J. E. Knox; H. P. Hratchian; J. B. Cross; V. Bakken; C. Adamo; J. Jaramillo; R. Gomperts; R. E. Stratmann; O. Yazyev; A. J. Austin; R. Cammi; C. Pomelli; J. W. Ochterski; P. Y. Ayala; K. Morokuma; G. A. Voth; P. Salvador; J. J. Dannenberg; V. G. Zakrzewski; S. Dapprich; A. D. Daniels; M. C. Strain; O. Farkas; D. K. Malick; A. D. Rabuck; K. Raghavachari; J. B. Foresman; J. V. Ortiz; Q. Cui; A. G. Baboul; S. Clifford; J. Cioslowski; B. B. Stefanov; G. Liu; A. Liashenko; P. Piskorz; I. Komaromi; R. L. Martin; D. J. Fox; T. Keith; M. A. Al-Laham; C. Y. Peng; A. Nanayakkara; M. Challacombe; P. M. W. Gill; B. Johnson; W. Chen; M. W. Wong; C. Gonzalez; J. A. Pople, Gaussian 03, Revision E.01.
66. K. Hirao and H. Nakatsuji, Cluster expansion of wavefunction - structure of closed-shell orbital theory, J. Chem. Phys., 1978, 69, 4535–4547.
67. K. Hirao and H. Nakatsuji, Cluster expansion of wavefunction - open-shell orbital theory including electron correlation, J. Chem. Phys., 1978, 69, 4548–4563.
68. H. Kamisaka, S. V. Kilina, K. Yamashita and O. V. Prezhdo, Ultrafast vibrationally-induced dephasing of electronic excitations in PbSe quantum dot, Nano Lett., 2006, 6, 2295–2300.
69. A. B. Madrid, H.-D. Kim, B. F. Habenicht and O. V. Prezhdo, Phonon-induced dephasing of excitons in semiconductor quantum dots: Multiple exciton generation, fission, and luminescence, ACS Nano, 2009, 3, 2487–2494.
70. S. V. Kilina, D. S. Kilin and O. V. Prezhdo, Breaking the phonon bottleneck in PbSe and CdSe quantum dots: Time-domain density functional theory of charge carrier relaxation, ACS Nano, 2009, 3, 93–99.
71. J. C. Idrobo, A. Halabica, R. H. Magruder, III, R. F. Haglund, Jr., S. J. Pennycook and S. T. Pantelides, Universal optical response of Si–Si bonds and its evolution from nanoparticles to bulk crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125322.
72. K.-D. Rinnen and M. L. Mandich, Spectroscopy of neutral silicon clusters, Si₁₈–Si₄₁: Spectra are remarkably size independent, Phys. Rev. Lett., 1992, 69, 1823–1826.
73. R. D. Schaller, M. A. Petruska and V. I. Klimov, Effect of electronic structure on carrier multiplication efficiency: Comparative study of PbSe and CdSe nanocrystals, Appl. Phys. Lett., 2005, 87, 253102.
74. M. C. Beard, K. P. Knutsen, P. R. Yu, J. M. Luther, Q. Song, W. K. Metzger, R. J. Ellingson and A. J. Nozik, Multiple exciton generation in colloidal silicon nanocrystals, Nano Lett., 2007, 7, 2506–2512.
75. S. A. Fischer and O. V. Prezhdo, Dopant effects on single and multiple excitons in small Si clusters: High level ab initio calculations, J. Phys. Chem., 2010.
76. S. V. Kilina, C. F. Craig, D. S. Kilin and O. V. Prezhdo, Ab initio time-domain study of phonon-assisted relaxation of charge carriers in a PbSe quantum dot, J. Phys. Chem. C, 2007, 111, 4871–4878.
77. A. Pandey and P. Guyot-Sionnest, Slow electron cooling in collodial quantum dots, Science, 2008, 322, 929–932.
78. V. Blanchet, M. Z. Zgierski, T. Seideman and A. Stolow, Discerning vibronic molecular dynamics using time-resolved photoelectron spectroscopy, Nature, 1999, 401, 52–54.
79. A. Puzder, A. J. Williamson, F. Gygi and G. Galli, Self-healing of CdSe nanocrystals: first-principles calculations, Phys. Rev. Lett., 2004, 92, 217401.

---