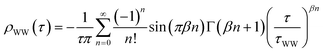Solvation dynamics of surface-trapped electrons at NH3 and D2O crystallites adsorbed on metals: from femtosecond to minute timescales
Julia
Stähler
*ab,
Michael
Meyer
ab,
Uwe
Bovensiepen
bc and
Martin
Wolf
ab
aFritz-Haber-Institut der Max-Planck-Gesellschaft, Abt. Physikalische Chemie, Faradayweg 4-6, 14195, Berlin, Germany. E-mail: staehler@fhi-berlin.mpg.de; Fax: +49-30-84135375; Tel: +49-30-84135125
bFreie Universität Berlin, Fachbereich Physik, Arnimallee 14, 14195, Berlin, Germany
cUniversität Duisburg-Essen, Fakultät für Physik, Lotharstr. 1, 47048, Duisburg, Germany
First published on 4th March 2011
Abstract
The creation and stabilization of localized, low-energy electrons is investigated in polar molecular environments. We create such excess electrons in excited states in ice and ammonia crystallites adsorbed on metal surfaces and observe their relaxation in real time using time-resolved photoelectron spectroscopy. The observed dynamics proceed up to minute timescales and are therefore slowed down considerably compared to ultrafast excited state relaxation in front of metal surfaces, which proceeds typically on femto- or picosecond time scales. It is the highly efficient wave function constriction of the electrons from the metal that ultimately enables the investigation of the relaxation dynamics over a large range of timescales (up to 17 orders of magnitude). Therefore, it gives novel insight into the solvated electron ground state formation at interfaces. As these long-lived electrons are observed for both, D2O and NH3 crystallites, they appear to be of general character for polar molecule–metal interfaces. Their time- and temperature-dependent relaxation is analyzed for both, crystalline ice and ammonia, and compared using an empirical model that yields insight into the fundamental solvation processes of the respective solvent.
1 Introduction
Since its first reported observation in 1808,1 solvated electrons have reached much attention; the impact of localized, low-energy electrons that are stabilized by surrounding polar molecules such as water or ammonia ranges from atmospheric chemistry2,3 to the field of radiation chemistry in nuclear reactors4 or of DNA.5 This wide-spread relevance led to an impressive number of studies on the solvated electron's ground and excited state properties in the solid and liquid phase. Yet, up to now, the precise characteristics of the hydrated electrons remain controversial; the traditional “cavity model”,6,7 which describes the excess electron density as being stabilized by a void in the water network, has just recently been challenged by molecular dynamics simulations that predict hydration of the electron even in denser regions of liquid water as opposed to a cavity.8The reactivity of solvated electrons, both in water and ammonia, has been thoroughly studied in the past decades, in particular with regard to hydrogen formation9 and also dissociative electron attachment (DEA) of chlorofluorocarbons (CFC), a process which can play a crucial role in ozone layer depletion.3 One attempt towards a better understanding of the underlying fundamental processes is the investigation of model systems prepared at surfaces under ultrahigh vacuum (UHV) conditions where chemical reactions can be mediated by the substrate and induced by hot electrons.10,11 This surface science approach offers well-defined preparation conditions in terms of structure and morphology of the solvent. In particular, the growth of amorphous and crystalline ice on various single crystal surfaces was investigated carefully in the past years,12,13,14,15 facilitating systematic study of such interfaces with respect to DEA. Representatively for the high number of investigations, we would like to mention the work of Ryu et al.16 and Lu and Sanche,17 who examined the electron-induced dissociation of CFCs at ice and ammonia vacuum interfaces. It is intuitively explicable that the cross section of such reactions is strongly connected to the excited electron lifetimes, because a longer availability of the localized charge enhances the probability of an encounter with the reactant. With regard to time-resolved studies of excess electrons in clusters7,18–21 and the liquid phase,8,22–25 it should be noted that these investigations have mainly focused on the dynamics occurring after photoexcitation from the ground (s-type) to the excited (p-type) state, i.e. the relaxation dynamics of the formerly equilibrated system that is perturbed by laser excitation. Complementarily, the study of excess electrons in ice or ammonia on surfaces created by fs-laser excitation aims to investigate the non-equilibrium dynamics of a previously neutral system that has not been exposed to trapped charges before. It has been shown that such molecule–metal or –semiconductor interfaces exhibit rich electron dynamics on ultrafast timescales, involving charge transfer, localization, and solvation phenomena.26–29
Recently, in our previous work, we have shown that it is possible to create trapped electrons at a crystalline ice–vacuum interface that exhibit residence times up to ten minutes.30 These electrons are generated by charge injection from a metal substrate, as opposed to irradiation with low-energy electrons17 or internal excitation as in refs 18,22. Our approach leads to the formation of E − Evac ≤ 0 eV electrons (i.e. bound with respect to the vacuum level), just a few Ångströms in front of a metal surface that are highly efficient in the dissociation of CFCl3.31 It is noteworthy that “typical” excited state lifetimes at molecule–metal interfaces on these distances are on the order of femto- or picoseconds.16,26,29,32 The remarkable increase in excess electron residence times was attributed30 to electron trapping in pre-existing defects at the crystalline ice–vacuum interface that very efficiently decrease the coupling of the excess charge to the continuum of (accepting) metal states. The decoupling results from a reduction of the wave function overlap of the excess electron with the metal. This is caused by the polar D2O network and can be regarded as screening of the electron by an interfacial potential barrier (see below). After this deep trapping of the electrons, the solvent response to the additional charge was monitored by the observation of energetic stabilization (increase in binding energy) of the excess charge ranging from femtoseconds up to minutes. In other words, the non-exponential relaxation dynamics spanned 17 orders of magnitude in time.30 Comparably rich dynamics are known in biomolecular systems where, for example, protein folding also occurs over a wide range of timescales.33,34 Phenomenologically, such processes are often described using stretched exponential functions; an approach that incorporates the macromolecules dynamics proceeding along conformational sub-states of the surrounding solvent.35
In the present work, we show that crystalline NH3—similar to D2O crystallites on Ru(001)—can be used to trap electrons outside the metal substrate for minutes. Their energetic relaxation spans, comparable to the dynamics observed for crystalline D2O,30 a wide range of timescales and continues up to minutes. As these long-lived electrons are observed for ice and ammonia crystallites, they appear to be a general phenomenon for adsorbed crystalline structures of polar molecules. Also, the time- and temperature-dependent energetic stabilization of excess electrons in crystalline water- and ammonia-ice is analyzed by means of relaxation along conformational sub-states of the solvent using the stretched exponential approach mentioned above. This empirical model yields, amongst other parameters, reorganization energies and characteristic relaxation times for crystalline D2O and NH3 that we discuss in the context of the microscopic properties of the two solvents. As, in addition to the crystallization of the solvents, also the morphology changes from wetting layers to crystallites, section 3.3 is devoted to the impact of morphology on the excess electron lifetimes. Finally, the implications of these results on the trapping site and general conclusions with respect to electron capture and solvation polar molecule–metal interfaces are drawn.
2 Experimental details
The experimental setup consists of a tunable femtosecond laser system and an ultrahigh vacuum (UHV) chamber. The former is used to excite (pump) and monitor (probe) the electron dynamics (see below), the latter for in situsample preparation and characterization. The Cu(111) and Ru(001) single crystal surfaces are prepared using standard surface science procedures.36,37 Adsorbate layers are grown onto the substrates by NH3 and D2O vapor deposition under ultrahigh vacuum conditions using a pinhole doser. Following established recipes,38 crystalline D2O is deposited onto Ru(001) at a sample temperature of 150 K. Subsequently, the temperature is increased to 162 K with the isothermal desorption yield being monitored until a constant desorption rate is reached, indicating complete crystallization of the D2O.Amorphous NH3 layers are grown on Cu(111) at a sample temperature of 30 K. Thermal desorption (TD) spectra of NH3/Cu(111) of various coverages (Fig. 1) are acquired using a quadrupole mass spectrometer (QMS). The two features at high temperatures, α1 and α2, are attributed to the desorption of the first monolayer (ML).39 The second monolayer β desorbs between 100 K and 120 K. For higher coverages, a multilayer peak γ with zero-order desorption kinetics evolves for T > 80 K. The integrated intensity of α1 and α2 is normalized to 1 ML and used as a mass equivalent for (crystalline and amorphous) coverages of ammonia. Analogous to the crystallization of amorphous ice on metal surfaces,38 the TD spectra exhibit a kink at ∼100 K (see arrow in Fig. 1), which is attributed to the vapor pressure reduction upon crystallization of the NH3. Accordingly, we prepare crystalline NH3/Cu(111) by annealing amorphous multilayers to 100 K until the desorption rate is constant.
 | ||
| Fig. 1 Thermal desorption spectra of amorphous NH3/Cu(111). The α1 and α2 feature correspond to the desorption of the first monolayer, which is used as a mass equivalent for coverage determination. β results from the second monolayer, and γ arises from the multilayer desorption. The transition from amorphous to crystalline ammonia is reflected by the kink in the multilayer desorption peak at 100 K (cf. arrow). | ||
Time-resolved two-photon photoelectron (2PPE) spectroscopy is performed using a commercial, regeneratively amplified femtosecond (Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
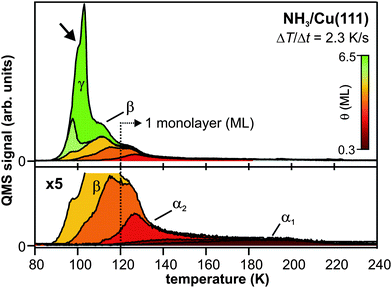
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa) laser system (Coherent RegA, 200–300 kHz repetition rate). Its output can either be frequency-doubled or used to drive an optical parametric amplifier (OPA) providing tunable laser light in the visible (VIS) range. Frequency-doubled ultraviolet (UV) pulses are used to pump (hνpump) the sample in the 2PPE experiment as depicted in the inset of Fig. 2a: the first pulse excites metal electrons from below the Fermi level EF to normally unoccupied states below the vacuum level Evac. The subsequent electron dynamics are monitored using a second, VIS laser pulse, which photoemits the excited electrons into the vacuum. Variation of the time delay between pump and probe pulse provides femtosecond (fs) time resolution. The kinetic energy of these photoelectrons is detected by an electron time-of-flight (TOF) spectrometer. Using the identity E − EF = Ekin + Φ − hνprobe (work function Φ), 2PPE spectra are plotted as a function of intermediate state energy with respect to the Fermi level. Surface charging effects are excluded by direct 2PPE measurement of the sample Fermi and vacuum level that are stable within the experimental resolution (20 meV).
Sa) laser system (Coherent RegA, 200–300 kHz repetition rate). Its output can either be frequency-doubled or used to drive an optical parametric amplifier (OPA) providing tunable laser light in the visible (VIS) range. Frequency-doubled ultraviolet (UV) pulses are used to pump (hνpump) the sample in the 2PPE experiment as depicted in the inset of Fig. 2a: the first pulse excites metal electrons from below the Fermi level EF to normally unoccupied states below the vacuum level Evac. The subsequent electron dynamics are monitored using a second, VIS laser pulse, which photoemits the excited electrons into the vacuum. Variation of the time delay between pump and probe pulse provides femtosecond (fs) time resolution. The kinetic energy of these photoelectrons is detected by an electron time-of-flight (TOF) spectrometer. Using the identity E − EF = Ekin + Φ − hνprobe (work function Φ), 2PPE spectra are plotted as a function of intermediate state energy with respect to the Fermi level. Surface charging effects are excluded by direct 2PPE measurement of the sample Fermi and vacuum level that are stable within the experimental resolution (20 meV).
 | ||
| Fig. 2 (a) Population decay traces of the solvated electron state (8.5 ML amorphous NH3/Cu(111), circles) and the image potential state (IPS) (mass equivalent of 3 ML crystalline NH3/Cu(111), diamonds). Fits to the data (solid lines) are exponential decays (based on rate equations) that are convoluted with the pump and probe laser pulse's cross correlation (XC). Inset: 2PPE scheme and illustration of the elementary processes of the electron dynamics for amorphous NH3 layers; electron injection (1), energetic stabilization (2), and transfer back to the substrate (3). (b) 2PPE spectra of the (crystalline) NH3/Cu(111) interface using hνUV = 3.0 eV (blue dashed) and hνVIS = 2.2 eV (red dotted). Spectral signature eT is excited by UV photons and probed by VIS light at delays > 3.3 μs after excitation. Note that the UV pulse duration was > 200 fs in order to suppress two-photon background signal. See text for details. | ||
3 Results and discussion
The interfacial electron dynamics at ice– and ammonia–metal interfaces are generally characterized by photoexcitation of electrons in the substrate with a UV pump pulse and charge injection into the adsorbed layers or crystallites. This is followed by electron localization and energetic stabilization of the injected excess electron due to reorganization of the solvent network of the polar adsorbate, accompanied by population decay from the excited state back to the unoccupied states of the metal.38 The respective development of these dynamics, however, depends crucially on the system investigated. The electron dynamics at interfaces of crystallineD2O and NH3 adsorbed at metal surfaces differ significantly from the ones of amorphous layers. For a better classification of the dynamics in the crystalline case, we start with a brief discussion of the electron dynamics in amorphous NH3 layers. A detailed analysis is found in ref. 40.The fundamental processes occurring at amorphous NH3/Cu(111) interfaces can be summarized as follows (see inset of Fig. 2a): after photoexcitation, electrons are transferred to the adsorbate layer by charge injection through the NH3 conduction band (CB, step 1 in the inset of Fig. 2a). They localize at the ammonia–vacuum interface, and the sudden increase of charge density initiates rearrangement of surrounding (polar) NH3 molecules that accommodate the excess charge. This process of electron solvation (step 2) is accompanied by a binding energy gain and the constriction of the excess electron's wave function that is thus becoming increasingly localized. The molecular rearrangement leads to the formation of an interfacial potential well,40 comparable to small polaron formation, that leads to a decreased wave function overlap of the excess charge with the metal. In other words, the electron is increasingly screened from the substrate.
Due to the continuum of unoccupied states in the metal, the excited, solvated electron population decays with increasing time delay. This electron transfer back to the metal (step 3) is, however, influenced by the concomitant, increasing screening of the excess electron by solvent molecules. The resulting competition between charge transfer and solvation is discussed in the following on the basis of the population decay trace for amorphous NH3 depicted in Fig. 2a (circles). The data show the 2PPE intensity as a function of pump–probe delay, integrated over the spectral signature of the solvated electrons eS (E − EF = 1.4–2.7 eV). At these energies, the electron transfer dynamics of the solvated electrons are superimposed by a contribution of hot electrons in the Cu(111) substrate at t ≤ 0 fs.41 Subtraction of this background leads to the dotted red curve in Fig. 2a which unveils a delayed intensity rise of the solvated electron state due to delayed charge localization from quasi-free, photoinjected electrons in the conduction band. The subsequent population decay, i.e.reduction of the population of the solvated electron state, is reflected by the slope of the population trace. With increasing time delay, the slope becomes flatter (non-exponential decay), unveiling that the population decay slows down. This retardation of electron transfer results from the above-mentioned competition of charge transfer and solvation: the further the solvation proceeds, the stronger the screening of the excess charge and the smaller the rate of electron transfer.
As discussed in detail in ref. 40, the characteristic times of electron transfer from the amorphous NH3 to the Cu(111) substrate depend, for pump–probe delays t > 300 fs, exponentially on the thickness d of the ammonia layer. This results from the fact that the electrons are localized at the NH3–vacuum interface and that their wave function is damped by screening in the ammonia layer. With increasing d, the electrons are driven further away from the metal, and their transfer probability is reduced reaching characteristic times of 600 ps for 18 ML (d = 26.5 Å).
3.1 Effect of NH3 crystallization
As will be shown in the following, the electron dynamics at the NH3/Cu(111) interface change radically when the ammonia adlayer is crystallized. We will first discuss the changes on ultrafast timescales and then address the excess electron dynamics occurring on minute timescales for NH3 crystallites.(i) Excitation. The spectrum shown by the blue, dashed curve in Fig. 2b is recorded using UV laser light (3.0 eV) only (bottom energy axis). It exhibits a wide peak, termed eT, at 1.7(1) eV above the Fermi level, which is excited and probed by UV photons. If this state at E − EF = 1.7 eV were directly excited (as opposed to an inelastic excitation channel), this should be possible using visible photons of 2.2 eV, too. In contrast, the red spectrum, which was taken using hν = 2.2 eV (red, dotted curve with corresponding energy scale on the top axis), does not exhibit a peak at 1.7 eV. Apparently, excitation of eT occurs non-resonantly, but along an inelastic pathway that requires photon energies higher than 2.2 eV.
(ii) Population and depopulation. The black spectrum shown in Fig. 2b is taken using both, UV and VIS pulses, in the sequence illustrated by the inset, i.e. the UV pulse hits the sample 3.3 μs before the VIS pulse. To elucidate which signatures result from correlation effects of UV and VIS photons, the non-correlated one-color spectra (blue and red curve, respectively) are subtracted from the black spectrum, resulting in the grey difference spectrum. The following two observations can be made:
(a) The UV-pumped and UV-probed signal of eT is quenched by the presence of VIS light (leading to the negative intensity of the difference plot).
(b) An additional peak occurs in the spectrum at 1.7 eV (energy scale on the top axis) or 0.9 eV (energy scale on the bottom axis), respectively, depending on whether it is probed by VIS or UV photons.
There is no straight forward interpretation of these results if excited state lifetimes in the fs to ns regime are considered. In this case, only time correlations between hνVIS and hνUV2 would affect the 2PPE signal and could cause signatures in the grey difference spectrum. It would, however, be unclear, how the preceding VIS laser pulse could affect the population of an excited state that is populated picoseconds after hνVIS hits the sample. We therefore take into account a very long lifetime of eT electrons, similar to the ones observed for crystalline D2O in ref. 30, and develop the following scenario.
After excitation of eT by hνUV1, the next laser pulse that hits the sample is hνVIS, probing the eT state. This course of events has two direct consequences:
(a) The intensity of the eT peak probed by UV photons (hνUV2) is reduced or even depleted by hνVIS (depending on the absorption cross section and fluence of the VIS light).
(b) The eT electron population probed by hνVIS appears at Δhν = hνUV − hνVIS lower energies in the spectrum.
Both consequences from the above scenario of the long-lived state eT fit to the observations (a) and (b) very well. In this picture, the eT population is excited by UV light and efficiently probed by VIS photons microseconds after excitation. This leads to two consequences for the correlated 2PPE intensity (grey curve in Fig. 2b): the signature eT (E − EF = 1.7 eV) is detected by VIS probe (top axis) and depleted for UV probe (E − EF = 1.7 eV, bottom axis). In the following, it will be shown that electrons in eT indeed have lifetimes exceeding the pulse separation of 3.3 μs, and that, moreover, these electrons reside in the excited state up to minutes.
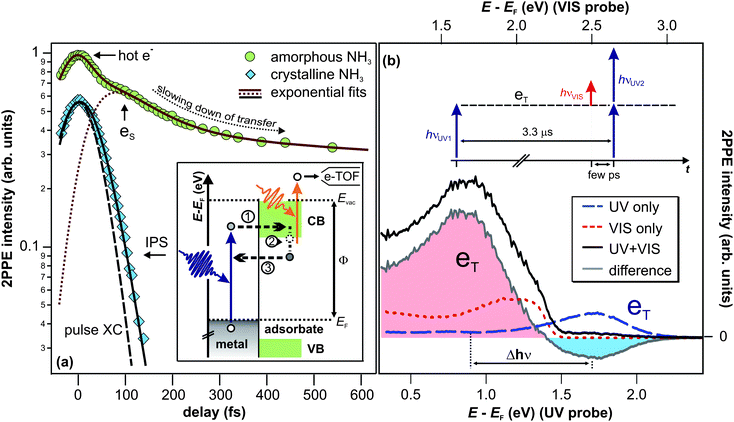
(iii) Lifetime. Fig. 3b (left) depicts UV-only spectra as a function of irradiation time (bottom axis) in false color representation. Again, the peak eT lies at 1.7 eV above the Cu(111) Fermi level (right axis). Integration of the eT 2PPE intensity (1.0–2.0 eV) yields the population of the excited state as a function of UV irradiation time, which is plotted in the bottom panel of Fig. 3b. It rises exponentially with a time constant of 0.25(10) s as indicated by the fit (black curve). This results from the formation of a photostationary state; as the eT lifetime exceeds τlaser, it is excited and probed (depopulated) by photons of several succeeding laser pulses. The equilibrium 2PPE intensity of eT is thus determined by the probabilities of population and depopulation by UV light, and, depending on the rates, this photostationary state would be reached with a characteristic time constant (0.25 s in Fig. 3b).
 | ||
| Fig. 3 (a) 2PPE scheme and illustration of the electron trapping process: electron localization at preexisting sites (1) and subsequent energetic stabilization proceeding on minute timescales (2), because electron transfer back to the substrate (3) is almost completely suppressed. See text for details. (b) Pump–probe experiment of crystalline NH3/Cu(111) on macroscopic timescales. (2PPE intensity is represented in false colors.) Left: the sample is irradiated by UV light for 5 s until the photostationary state is reached. The bottom panel depicts the intensity evolution (blue markers). The exponential fit (black curve) unveils a rise time of 0.25 s. Right: after 5 s of darkness, the trapped electron population is probed by VIS light and efficiently depopulated as apparent from the intensity trace at the bottom (orange markers). The dotted line indicates the constant background. | ||
The right panel of Fig. 3b, on the other hand, shows a similar measurement for VIS light only. For irradiation times t = 11–13 s, the plot shows similar 2PPE spectra (in false colors) as the red dotted spectrum in Fig. 2b. However, at t = 10 s, the 2PPE intensity peaks, clearly seen in the intensity trace at the bottom. The origin of this lies in the sequence of the experiment. First, the sample was irradiated with UV light, as shown in the left panel, which led to the formation of a photostationary population of the eT state. Then, the sample remained in darkness for 5 s. Finally, the 2PPE spectra in the right panel were measured using VIS light only. Note that the above mentioned intensity peak upon starting VIS light irradiation does not occur if the sample was not exposed to UV light before (not shown). It can therefore be concluded that the intensity of the VIS only spectrum at t = 10 s is correlated with the UV photons impinging the sample 5 s earlier; “UV pump” (cf.Fig. 3b) determines the non-equilibrium conditions probed by VIS light. In fact, the VIS spectrum at t = 10 s exhibits a maximum at 1.7 eV as indicated by the arrow in Fig. 3b, showing that the VIS photons probe electrons in eT. This means that the eT electrons exhibit residence times of more than 5 s.
Similar experiments with different dark times between UV and VIS light irradiation (i.e.pump–probe time delays) up to 120 s are performed, and the resulting 2PPE spectra are presented in Fig. 4a.42 The fact that the spectra differ for the different time delays demonstrates the correlation between UV pump and VIS probe. It can therefore be concluded that the electrons excited to eT can actually reside in the excited state up to two minutes. This increase in excited electron lifetimes compared to amorphous NH3/Cu(111) is a quite dramatic effect of ammonia crystallization. Analyzing the pump–probe data in Fig. 4a, it is observed that the peak maximum of eT shifts to lower intermediate state energies by 75 meV within 120 s, and its intensity decreases. After 120 s, the main part of its population has decayed. Comparing these population dynamics for crystalline NH3 with our results for solvated electrons in amorphousammonia layers on Cu(111),40 we find that the residence time of the excess electrons increases by 15 orders of magnitude, i.e. from ∼50 fs (for a 3 ML amorphous film) to one minute for crystallized ammonia (with a mass equivalent of 3 ML).
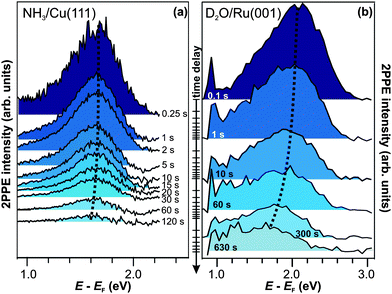 | ||
| Fig. 4 Time-resolved pump–probe photoelectron spectroscopy of (a) NH3/Cu(111) (hνprobe = 2.2 eV) and (b) D2O/Ru(001) (hνprobe = 1.95 eV). The trapped electron state is at lower energies in the case of crystalline ammonia-ice and exhibits a weaker energy shift than for D2O. Dotted curves are guides to the eye. | ||
The first-time observation of such a strong effect at a molecule–metal interface is reported in ref. 30 for the crystallization of D2O on Ru(001), as mentioned in the introduction. The corresponding pump–probe data are depicted in Fig. 4b for comparison with the electron relaxation on minute timescales at the NH3/Cu(111) interface. For D2O/Ru(001), the signature eT is detected at higher energies (2 eV above EF) and exhibits a stronger shift (∼0.2 eV within 120 s) towards the Fermi level than for the NH3/Cu(111) interface (dotted curve). However, the observation of the colossal change in excited electron lifetimes upon adsorbate crystallization to residence times on the order of minutes both for D2O- and NH3-ice strongly suggests that eT results from a qualitatively similar species of excess electrons. This assumption is supported by (i) the extraordinariness of an excited state > 1 eV above a metal's Fermi level exhibiting lifetimes that are orders of magnitude larger than picoseconds and the (ii) essentially comparable electron dynamics of amorphousD2O and NH3 on metal surfaces.43 To corroborate this picture, we now continue with a brief characterization of eT for crystalline D2O on Ru(001) based on the studies performed in ref. 30.
By variation of the excitation photon energy, it could be shown30 that the initial step for the creation of the long-lived electrons is population of n = 1 image potential state (IPS) at the D2O/Ru(001) interface, which is delocalized parallel to the surface. As the IPS at this interface exhibits a lifetime below 10 fs,44 a population transfer from this state to eT has to occur on ultrafast timescales, too. Furthermore, angle-resolved measurements of the (flat) dispersion of eT unveiled that electrons in eT are localized parallel to the surface, and Xe titration experiments45 showed that the trapped electrons reside at the ice–vacuum interface.30 These observations, combined with the long lifetime and the energetic relaxation on minute timescales, leads to the following understanding of the elementary processes of the electron dynamics at the D2O/Ru(001) interface as illustrated by Fig. 3a. Electrons are excited in the metal from below the Fermi level to the image potential state (IPS). Part of this IPS population localizes on fs-timescales at pre-existing potential minima at the ice–vacuum interface (1). The surrounding polar molecules accommodate the excess charge leading to a continuous energetic relaxation on minute timescales (2). This process is facilitated by the extraordinarily long lifetime of electrons in eT that indicates a very efficient suppression of the electron population decay back to the substrate (3). In accordance with ab initio calculations in ref. 30, these observations suggest that the excess electrons injected via the IPS are trapped at pre-existing defects at the ice–vacuum interface, being energetically stabilized by reorientations within the molecular lattice continuing even on minute timescales.
In the next section, we provide a quantitative analysis of the energetic relaxation of the trapped electrons at the NH3/Cu(111) and the D2O/Ru(001) interface as a function of time and temperature. The electronic coupling of eT with metal states is extremely small, as demonstrated by the exceptionally long residence times of the trapped electrons. Therefore, to simplify matters, we confine ourselves to the terms NH3 and D2O (crystallites) in the following without mentioning the corresponding substrates. However, all results presented in this article were either acquired at the NH3/Cu(111) or the D2O/Ru(001) interface.
3.2 Trapped electrons at NH3– and D2O–vacuum interfaces—a comparison
We have shown that the long-lived electrons are not a specific feature of D2O crystallites, but also occur for crystalline ammonia on Cu(111). The details of the electron dynamics are, however, different for the two solvents. As apparent by Fig. 4, the maximum of the trapped electron feature eT shifts towards lower energies with increasing time delay for crystalline NH3and D2O. However, as mentioned above, this energy shift is clearly larger in the case of D2O. For a quantitative analysis, both energy shifts of the peak maximum of eT are analyzed and depicted in Fig. 5a. In addition to this time-dependent stabilization, solvation of trapped electrons is also temperature-dependent as presented in Fig. 5b. Again, the energy shift is stronger for ice (circles) than for ammonia (diamonds). At first, this qualitative observation might appear counter-intuitive, as the weaker hydrogen bonding of NH3 compared to D2O (100 and 240 meV, respectively) could suggest a quicker reaction of the ammonia network. To address this question, we analyze the data using an empirical description with a stretched exponential law based on conformational sub-states (CSS).35 This approach is well-established for non-exponential relaxation dynamics ranging over many orders of magnitude33,34 and exhibiting strong temperature dependences.46,47 The basic idea is that relaxation proceeds through CSS that are characterized by local potential minima, which are separated by energy barriers Ea. In a realistic scenario, the sample exhibits a distribution of different trapping sites due to varying molecular surroundings. The stretched exponential approach accounts for such local variations by a distribution of relaxation times. Further below, a characteristic relaxation time τ0 will be determined that defines how quick energetic relaxation intrinsically evolves.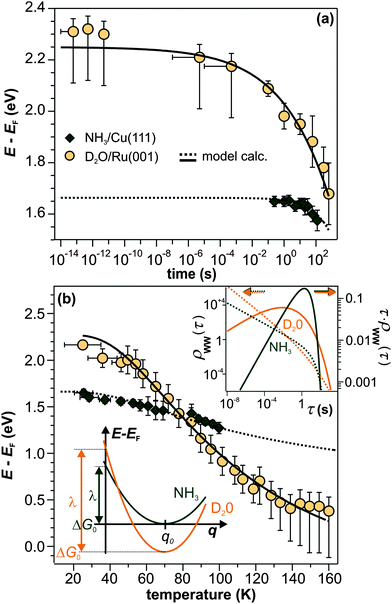 | ||
| Fig. 5 Comparison of the eT relaxation for NH3 and D2O. (a) Time-dependent shift of the peak maximum of the trapped electron distribution in ice (orange) and ammonia adlayers (green). (b) Temperature-dependent peak shift. Dashed and solid lines result from the model calculation based on conformational substates. Bottom inset: harmonic solvation potentials of NH3 and D2O. Top inset: distribution τ·ρWW(τ) (solid curves, right axis) and distribution density ρWW(τ) (dashed curves, left axis) of relaxation times of the NH3 (green) and D2O (orange) sample. | ||
As a starting point, we assume that the CSS minima follow a harmonic potential (bottom inset in Fig. 5b) as a function of the global solvation coordinate q:
| E(q) = λ·(q − q0)2 − ΔG0 | (1) |
Here, the reorganization energy λ is the potential energy that the system gains on its pathway that starts with the population of eT and that continues until equilibrium of the solvent–solute complex is reached. The Gibbs free energy ΔG0, on the other hand, is the energy difference of the eT minimum to the metal's Fermi level, i.e. the energy that the system gains/loses (ΔG0 < 0/ΔG0 > 0) when the fully equilibrated trapped electron is brought to the metal's Fermi level. Using the stretched exponential approach mentioned above, the following formula for time- and temperature-dependent energy shift can be derived:
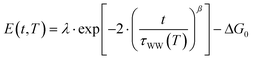 | (2) |
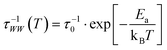 | (3) |
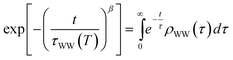 | (4) |
The black curves in Fig. 5 correspond to the best simultaneous fit to time- and temperature-dependent energy shift for NH3 (dotted curve) and D2O (solid curve), respectively. As seen in the figure, the data are reproduced well by the model. The resulting fit parameters for both solvents are depicted in Table 1. We start with the activation energy Ea, which determines the local barriers between different conformational sub-states, which is indeed larger for D2O (96 meV) than for NH3 (32 meV). This finding corresponds nicely to the stronger hydrogen bonding in the water-ice network compared to ammonia as mentioned earlier in the text (240 and 100 meV, respectively). However, at a first glance, larger activation energies for D2O imply that the relaxation should proceed slower in the case of water-ice than for ammonia, which would disagree with our observations. This apparent conflict results from the interplay of intrinsic relaxation times, reorganization energies, and stretching parameters, which favor quicker relaxation in the crystalline D2O network as will be discussed in the following.
| NH3/Cu(111) | D2O/Ru(001) | |
|---|---|---|
| λ/eV | 1.65(10) | 3.0(1) |
| E a/meV | 32(5) | 96(5) |
| τ 0/s | 0.9(1) | 0.004(1) |
| β | 0.4(1) | 0.16(3) |
| ΔG0/eV | 0.0(1) | 0.75(10) |
The intrinsic relaxation time τ0 (i.e. the threshold value of eqn (3) for infinite temperatures) is with 900 ms for NH3 substantially larger than for D2O (4 ms), indicating that stabilization occurs much quicker in ice than in ammonia. This means that comparable conformational changes of the solvent (molecular reorientation) lead to a larger binding energy gain of the excess electron in the case of D2O compared to NH3, an effect that could be caused by the difference in dipole moments of D2O (1.9 D) and NH3 (1.4 D). Also, the reorganization energy λ, i.e. the energy gained by the lattice deformation due to complete solvation of the excess charge, is larger for D2O. In other words, the driving force for energetic relaxation is stronger (or the potential is steeper) in crystalline water-ice compared to ammonia-ice as illustrated by the bottom inset in Fig. 5b.
We find that the stretching parameter β is smaller for D2O than for NH3, which means that water-ice exhibits a broader distribution of relaxation times τ·ρWW(τ) as shown in the upper inset of Fig. 5b. This does not necessarily imply that the crystalline D2O network has a higher number of possible molecular conformations, but could also indicate that a higher number of molecules is involved in the solvation process of the excess electron than for ammonia-ice. A wider distribution of relaxation times is generally in favor of faster energetic relaxation, as the distribution density ρWW(τ), which determines the population probability, is significantly higher for small τ (upper inset, Fig. 5b).
Summarizing the above, it can be concluded that the rigid hydrogen-bonded network of crystalline D2O resists—probably because of the stronger intramolecular bonds—conformational changes much more effectively than the ammonia-ice. Yet, energetic relaxation occurs quicker in crystalline water-ice, as fewer conformational changes of the molecules are required to achieve similar energetic relaxation, an effect that is reflected in the smaller relaxation time τ0 and the larger reorganization energy λ of D2O.
3.3 Influence of morphology
While the above section focused on the quantitative differences of the relaxation dynamics for D2O and NH3, the present one addresses the origin of the lifetime increase upon crystallization. The long residence times for crystalline solvents compared to amorphous NH3 and D2O must result from a more efficient decoupling of the excess electrons from the substrate. Such effect can either result from (i) a major change of the binding site of the excess electrons, which leads to a better screening, or (ii) simply from sufficiently large spatial separation of the trapped charge from the metal. Both aspects are influenced by the morphology changes going along with crystallization. Therefore, we first discuss the changes of morphology upon crystallization and then relate them to possible binding sites of the excess electrons.It is helpful to also consider the knowledge of the excess electron binding site for amorphoussolvents when discussing the influence of crystallization. As shown in ref. 40 and mentioned further above, the solvated electrons reside at the NH3–vacuum interface in the case of amorphous ammonia on Cu(111). This occurrence leads to the observation of residence times of the excited electrons that depend exponentially on the ammonia layer thickness (cf.Fig. 6a):
| τ(d) ∝ exp(β·d) | (5) |
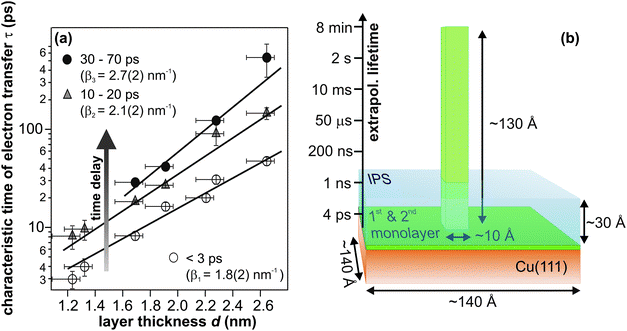 | ||
| Fig. 6 (a) Electron transfer time constants as a function of amorphous ammonia layer thickness in three different stages of solvation, i.e. at three different time delays. (b) Illustration of the required crystallite height formed by the material of the third NH3 layer) for electron residence times on minute timescales; extrapolating from panel (a) (taken from ref. 40). The blue-shaded area visualizes the dimension of the image potential state, which serves the excitation of eT. | ||
Both, the magnitude of the required distance (130 Å), which would entail rather implausible growth of adsorbate “towers”, and the prerequisite of proximity of eT and image potential state electrons for charge injection, direct to the conclusion that the residence time enhancement accompanying crystallization cannot solely result from an increased electron–metal distance due to the morphology change. Rather, the binding site of the excess electrons must be altered by crystallization leading to a more effective decoupling of the trapped electron state from the metal continuum. Moreover, the ultrafast injection of electrons (image potential state lifetime < 10 fs) suggests electron trapping at pre-existing sites, involving efficient screening of the excess charge. Plausible candidates for such trapping sites could be defects at the solvent–vacuum interface as suggested by density functional theory on D2O–vacuum interfaces in ref. 30. In particular, orientational defects involving reconstructions of the hydrogen-bonded network were found to very efficiently localize excess electrons and reduce the electron density already in the outer layer of ice by up to six orders of magnitude.
4 Summary and conclusions
In this paper, we have shown that crystallization of NH3 on Cu(111) leads to the observation of an excited state eT that remains populated even minutes after photoexcitation, similar to earlier observations at the D2O/Ru(001) interface. The long lifetime of these excess electrons has its origin in very efficient initial trapping of the electrons at preexisting defects at the vacuum interface of the respective crystallites. Before charge injection, the solvent structure is equilibrated, however, after population of eT, the system finds itself in a highly non-equilibrium situation and proceeds by molecular reorientation to its ground state. Due to the efficient screening of the excess electrons from the metal substrate, it is possible to follow the relaxation progression over many orders of magnitude in time. Comparison of this relaxation as a function of time and temperature for D2O and NH3 crystallites, yields microscopic insight into the solvation and trapping properties of the frozen solvents; trapped, long-lived electrons in front of a metal surface are not an ice-specific feature, but also occur for NH3–metal interfaces. This suggests that their occurrence is, in fact, not connected to particular properties of the D2O network, but requires the conjunction of the following prerequisites: (i) adequate trapping sites with quasi-instantaneous, efficient screening of the excess charge to allow for further relaxation, (ii) an excitation channel as the IPS, which, due to its delocalized character, enables electron trapping in the first place, and (iii) a solvent that continues stabilization of the excess electrons after initial trapping, which further extends their residence time. In principle, the latter two requirements can be fulfilled by a number of (polar) molecules (e.g.methane, alcohols) adsorbed on metal surfaces. However, also (i), a quite local corrugation of the potential that can lead to charge localization and efficient screening, is required. Whether such trapping sites, possibly resulting from defects, are available in the case of other solvents than NH3 or D2O, cannot be easily predicted and most probably depends crucially on the respective preparation conditions.Acknowledgements
The authors are grateful to C. Gahl, A. Nitzan, and A. Rubio for fruitful discussions and acknowledge funding by the Deutsche Forschungsgemeinschaft through Sfb 658, Sfb 450 and SPP 1093, and the German Israeli Foundation through the young investigator program and grant 961-92.5/2007.Notes and references
- H. Davy, Philos. Trans. R. Soc. London, 1808, 98, 333 CrossRef.
- Q.-B. Lu, Phys. Rep., 2010, 487, 141 CrossRef CAS.
- Q.-B. Lu and T. E. Madey, J. Chem. Phys., 1999, 111, 2861 CrossRef CAS.
- T. W. Marin, K. Takahashi, C. D. Jonah, S. D. Chemerisov and D. M. Bartels, J. Phys. Chem. A, 2007, 111, 11540 CrossRef CAS.
- T. G. Gantchev and D. J. Hunting, J. Mol. Model., 2008, 14, 451 CrossRef CAS.
- L. Kevan, Acc. Chem. Res., 1981, 14, 138 CrossRef CAS.
- O. Marsalek, F. Uhlig, T. Frigato, B. Schmidt and P. Jungwirth, Phys. Rev. Lett., 2010, 105, 043002 CrossRef.
- R. Larsen, W. J. Glover and B. J. Schwartz, Science, 2010, 329, 65 CrossRef CAS.
- N. G. Petrik and G. A. Kimmel, J. Chem. Phys., 2004, 121, 3736 CrossRef CAS.
- J. W. Gadzuk, Surf. Sci., 1995, 342, 345 CrossRef CAS.
- C. Frischkorn and M. Wolf, Chem. Rev., 2006, 106, 4207 CrossRef CAS.
- A. Hodgson and S. Haq, Surf. Sci. Rep., 2009, 64, 381 CrossRef CAS.
- M. Mehlhorn and K. Morgenstern, Phys. Rev. Lett., 2007, 99, 246101 CrossRef.
- G. A. Kimmel, N. G. Petrik, Z. Dohnalek and B. D. Kay, J. Chem. Phys., 2006, 125, 044713 CrossRef.
- G. A. Kimmel, N. G. Petrik, Z. Dohnalek and B. D. Kay, Phys. Rev. Lett., 2005, 95, 166102 CrossRef.
- S. Ryu, J. Chang, H. Kwon and S. K. Kim, J. Am. Chem. Soc., 2006, 128, 3500 CrossRef CAS.
- Q.-B. Lu and L. Sanche, J. Chem. Phys., 2004, 120, 2434 CrossRef CAS.
- G. B. Griffin, R. M. Young, O. T. Ehrler and D. M. Neumark, J. Chem. Phys., 2009, 131, 194302 CrossRef.
- T. Frigato, J. V. Vondele, B. Schmidt, C. Schütte and P. Jungwirth, J. Phys. Chem. A, 2008, 112, 6125 CrossRef CAS.
- D. H. Paik, I. R. Lee, D. S. Yang, J. S. Baskin and A. H. Zewail, Science, 2004, 306, 672 CrossRef CAS.
- L. Turi, W. S. Sheu and P. J. Rossky, Science, 2005, 309, 914 CrossRef CAS.
- K. R. Siefermann, Y. Liu, E. Lugovoy, O. Link, M. Faubel, U. Buck, B. Winter and B. Abel, Nat. Chem., 2010, 2, 274 CrossRef CAS.
- A. T. Shreve, T. A. Yen and D. M. Neumark, Chem. Phys. Lett., 2010, 493, 216 CrossRef CAS.
- M. Assel, R. Laenen and A. Laubereau, J. Chem. Phys., 1999, 111, 6869 CrossRef CAS.
- A. Migus, Y. Gauduel, J. L. Martin and A. Antonetti, Phys. Rev. Lett., 1987, 58, 1559 CrossRef CAS.
- J. E. Johns, E. A. Muller, J. M. J. Fréchet and C. B. Harris, J. Am. Chem. Soc., 2010, 132, 15720 CrossRef CAS.
- B. Li, J. Zhao, K. Onda, K. D. Jordan, J. Yang and H. Petek, Science, 2006, 311, 1436 CrossRef CAS.
- X.-Y. Zhu, Q. Yang and M. Muntwiler, Acc. Chem. Res., 2009, 42, 1779 CrossRef CAS.
- N.-H. Ge, C. M. Wong, R. L. Lingle Jr, J. D. McNeill, K. J. Gaffney and C. B. Harris, Science, 1998, 279, 202 CrossRef CAS.
- U. Bovensiepen, C. Gahl, J. Stähler, M. Bockstedte, M. Meyer, F. Baletto, S. Scandolo, X.-Y. Zhu, A. Rubio and M. Wolf, J. Phys. Chem. C, 2009, 113, 979 CrossRef CAS.
- M. Bertin, M. Meyer, J. Stähler, C. Gahl, M. Wolf and U. Bovensiepen, Faraday Discuss., 2009, 141, 293 RSC.
- J. Zhao, B. Li, K. Onda, M. Feng and H. Petek, Chem. Rev., 2006, 106, 4402 CrossRef CAS.
- H. Frauenfelder, P. W. Fenimore and B. H. McMahon, Biophys. Chem., 2002, 98, 35 CrossRef CAS.
- A. Ansari, C. M. Jones, E. R. Henry, J. Hofrichter and W. A. Eaton, Science, 1992, 256, 1796 CrossRef CAS.
- H. Frauenfelder, F. Parak and R. D. Young, Annu. Rev. Biophys. Biophys. Chem., 1988, 17, 451 CrossRef CAS.
- E. Knoesel, A. Hotzel and M. Wolf, Phys. Rev. B: Condens. Matter, 1998, 57, 12812 CrossRef CAS.
- S. Funk, M. Bonn, D. N. Denzler, C. Hess, M. Wolf and G. Ertl, J. Chem. Phys., 2000, 112, 9888 CrossRef CAS.
- R. S. Smith and B. D. Kay, Surf. Rev. Lett., 1997, 4, 781 CrossRef CAS.
- C. Benndorf and T. E. Madey, Surf. Sci., 1983, 135(1), 164 CrossRef CAS.
- J. Stähler, M. Meyer, D. O. Kusmierek, U. Bovensiepen and M. Wolf, J. Am. Chem. Soc., 2008, 130(27), 8797 CrossRef.
- These secondary, hot electrons are excited by VIS light and probed by UV photons.
- Spectra are corrected for the constant, non-correlated VIS-2PPE background (see Fig. 3b, t = 11–13 s). The spectrum at 0.25 s was extracted from the left panel in Fig. 3b.
- J. Stähler, U. Bovensiepen and M. Wolf. Electron dynamics at polar molecule–metal interfaces: Competition between localization, solvation, and transfer, in Dynamics at Solid State Surfaces and Interfaces, Volume I: Current Developements, U. Bovensiepen, H. Petek, M. Wolf (Ed.), 2010, Wiley-VCH, Berlin Search PubMed.
- U. Bovensiepen, C. Gahl, J. Stähler and M. Wolf, Surf. Sci., 2005, 584, 90 CrossRef CAS.
- Adsorption of a xenon overlayer on top of the D2O/Ru(001) leads to a vanishing of the eT feature, which demonstrates that the eT electrons are localized at the (Xe-covered) ice–vacuum interface and are influenced by the presence of the rare gas atoms. A detailed discussion of Xe titration experiments can be found in J. Stähler, M. Mehlhorn, U. Bovensiepen, M. Meyer, D. O. Kusmierek, K. Morgenstern and M. Wolf, Phys. Rev. Lett., 2007, 98, 206105 Search PubMed; M. Meyer, J. Stähler, D. O. Kusmierek, M. Wolf and U. Bovensiepen, Phys. Chem. Chem. Phys., 2008, 10, 4932 CrossRef CAS . For details on the titration of crystalline ice see refs. 30, 31.
- A. Ansari, S. V. Kuznetsov and Y. Shen, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 7771 CrossRef.
- M. Jäger, H. Nguyen, J. C. Crane, J. W. Kelly and M. J. Gruebele, J. Mol. Biol., 2001, 311, 373 CrossRef CAS.
- For a detailed discussion of the distribution density function
see C. P. Lindsey and G. D. Patterson, J. Chem. Phys., 1980, 73, 3348 Search PubMed. - A. Hodgson and S. Haq, Surf. Sci. Rep., 2009, 64, 381 CrossRef CAS.
- S. Haq and A. Hodgson, J. Phys. Chem., 2007, 111, 5946 Search PubMed.
- In ref. 30, we roughly estimated the average island height to be 4 BL (∼19 Å) on the basis of the IPS intensity.
| This journal is © The Royal Society of Chemistry 2011 |